1. Introduction
Regenerative heat exchangers are devices used for indirect heat exchange between hot and cold media. In these devices, heat is first transferred from a hot medium to a storage material and then is transferred to a cold medium. Thus, the hot and cold media are alternately in contact with the solid material forming the packed bed. In the hot cycle, heat is transferred from the medium to the packed bed, and, in the cold cycle, the cold medium absorbs the heat stored in the solid material. This cycle is the reason why regenerative heat exchangers must operate in pairs (they must have two beds) to work continuously. Regenerative heat exchangers are used mainly in the metallurgical industry, in air treatment, air preheating, or recovery of waste heat, and in turbine applications. However, the complexity of the calculations resulted in their limited expansion.
Although there are several approaches to calculating these devices, more accurate methods require the solution of differential equations. Their solution is quite time-demanding and they need the use of a computer. This paper describes the solution of the calculation of regenerative heat exchangers using the Willmott open method, which seems to be the best for computer use. This method shows great stability (convergence) and allows the inclusion of calculation of the equations describing heat transfer and pressure drop. The solution is performed by an iterative calculation, and the result is the distribution of gas temperatures and pressure over time and along the bed.
Another difficulty when calculating these devices is finding suitable computational equations to describe the heat transfer between the gas and the packed bed material. Although these equations can be found in the literature, they are usually given only for spherical shapes. In addition, different equations give different results. It is, therefore, necessary to choose a suitable calculation equation in order to get the best results. A better situation is in the calculation of pressure drops, for which many computational equations can be found in the literature. However, some of them give different results from those measured. This paper, therefore, provides an overview of suitable computational equations so that a complete computational algorithm of regenerative heat exchangers can be compiled.
2. Description of the Regenerator
2.1. Classification of Regenerative Heat Exchangers
Regenerators can be divided into two categories: fixed-bed and rotary regenerators. In the fixed-bed regenerator, a single fluid stream has cyclical or reversible flow. Valves are employed to switch the flow the hot and cold gas streams. In the rotary regenerator, the storage material rotates continuously through two counterflowing streams of fluids. Only one stream flows through a section of the storage material at a given time. However, both streams eventually flow through all sections of the storage material during one rotation.
Fixed-bed regenerators are commonly run in pairs. It means that two or more regenerators are used in parallel because of the requirement for a continuous stream of the gas. During one part of a cycle, the hot gas flows through one of the regenerators and heats up the storage material, while the cold gas flows through and cools down the storage material in the second regenerator. Both gases directly contact storage material in the regenerators, although not both at the same time, since each is in a different regenerator at any given time. After a sufficient amount of time, the cycle is switched such that the cooler storage material in the second regenerator is preheated with the hot gas, while the hot storage material in the first regenerator exchanges its heat into the cold gas. This cycle is permanently repeated.
The advantage of regenerators over recuperators is that they have a much higher surface area for a given volume. Hence, the regenerator usually has a smaller volume and weight than an equivalent recuperator. This means that regenerators are more economical in terms of materials and manufacturing. The storage material of regenerators also has a degree of self-cleaning characteristics, reducing fluid-side fouling and corrosion. Disadvantages include mixing the media as a result of alternating the passage of hot and cold media through the packed bed. Regenerators are, thus, ideal for gas–gas heat exchange.
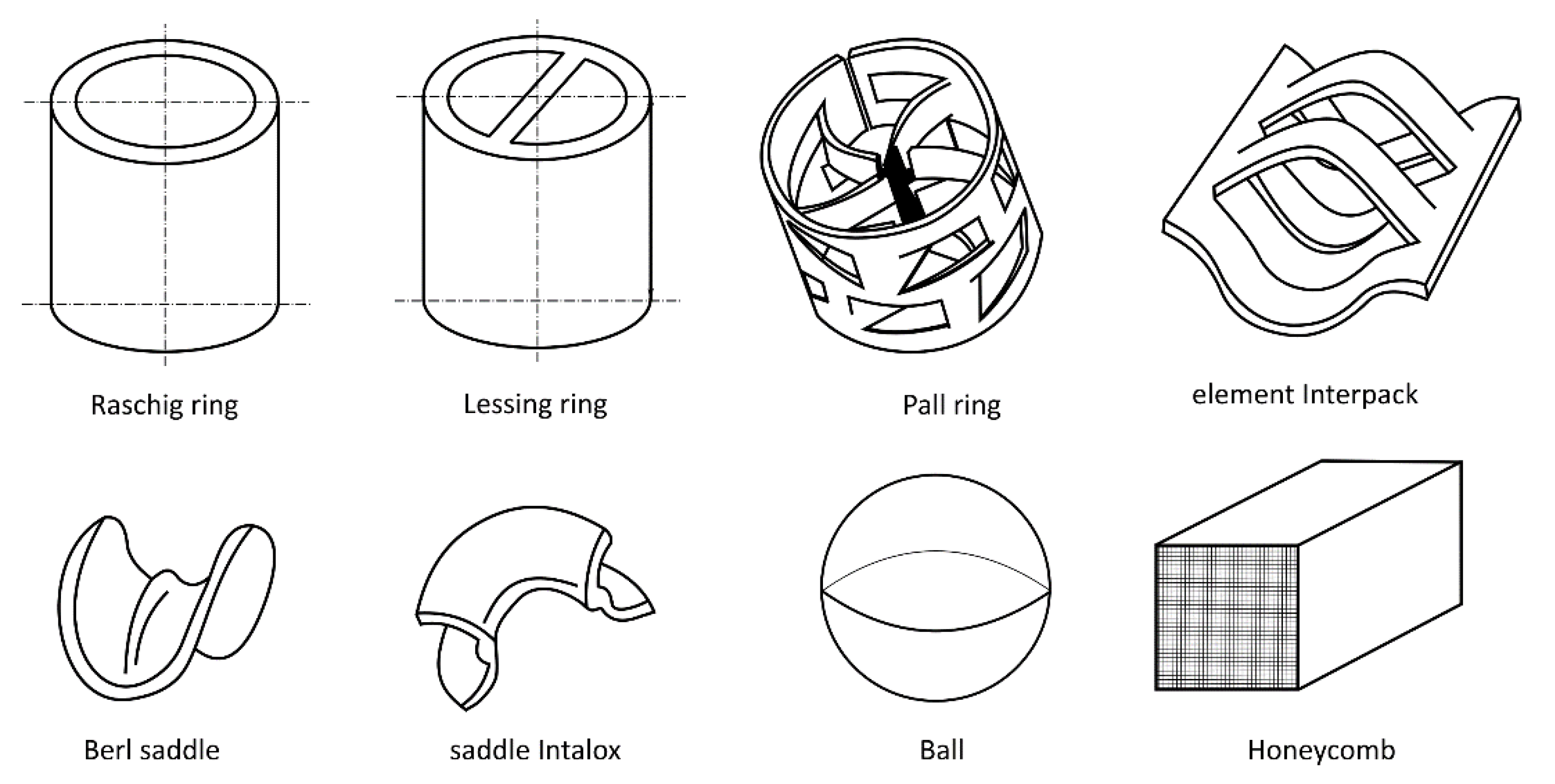
Various materials and shapes can be used as storage materials. Because solids have a very large heat capacity compared to gases, they are used as intermediary storage of the heat. Their selection depends on given conditions and requirements, especially temperature. For very high temperature, ceramic storage material should be used. For low or moderate temperatures, the heat storage material can be made of metal, e.g., steel or aluminum. There exist several types of storage shapes (see
Figure 1). For large regenerators, bricks can be used. For smaller regenerators, honeycombs, spherical particles, monoliths, saddles, rings, or Raschig rings can be used.
Regenerative heat exchangers can be used in various processes. The most common applications include the following:
The benefit of the exchanger is seen in the potential of its current multiple function. The exchanger could be used, for example, for simultaneous gas purification. This means that the storage material also serves as a catalyst on which the chemical reaction takes place.
2.2. Basic Geometric Characteristics of Packed Bed
Packed bed calculations use various geometric characteristics describing the packed bed. The main ones are specified in this section.
Voidage, -
An important parameter in the calculation of the flow in a packed bed is voidage. The voidage ε is defined as the ratio of the free volume of the packed bed to the total volume.
where
Vb is the total volume of the packed bed (m
3),
Vp is the volume of the packed bed material (m
3), and
Vm is the free volume of the packed bed (m
3).
Particle diameter, m
The particle diameter can be defined as the diameter of a sphere that has the same volume as the particle,
or as the equivalent particle diameter
dp (m), according to the specific surface given by Ergun [
2], which has the same ratio of the surface to the volume as the given particle and is given by
where
Ap is the particle surface area (m
2).
Sphericity, -
Sphericity is defined in Reference [
3] as the ratio of the surface area of the sphere to the surface area of the particle. The sphericity is 1 for a sphere and is less than 1 for any particle that is not a sphere.
where
As is the surface area of a sphere that has the same volume as the particle (m
2),
Ap is the particle surface area (m
2), and
Vp is the volume of the particle (m
3).
Hydraulic diameter of packed bed, m
where
rh is the hydraulic radius (m),
a is the absolute specific surface (m
2), and
ar is the relative specific surface (m
−1).
Absolute specific surface, (m−1)
Absolute specific surface is the ratio between the particle surface area and the volume of the packed bed.
Relative specific surface, (m−1)
Relative specific surface is the ratio between the particle surface area and the volume of the particle in the packed bed.
The relationship between relative and absolute specific surface is
3. Mathematical Model of the Regenerative Heat Exchanger
3.1. Energy Balance of the Regenerator
If the gas flows through the packed bed of the regenerator and the total heat transfer area between the bed and the gas is
Ap, then the mean temperature change of packed bed
Tb at time
t can be expressed in the form
where
Mb is the mass of packed bed (kg),
Tb is the mean temperature of packed bed (°C),
Tg is the temperature of the gas flowing through the bed (°C),
ht is the total heat transfer coefficient (W∙m
−2∙K
−1) between the flowing gas and the bed material,
Cp,b is the heat capacity of packed bed (J∙kg
−1∙K
−1), and
A is the total heat transfer area (m
2). In a cooling period, where the gas temperature,
Tg, is lower than the bed temperature,
Tb, the gas temperature increases over time while the bed temperature decreases
. During the heating period (
Tg >
Tb), the gas outlet temperature decreases with time, while the bed temperature increases
.
Heat is recovered or absorbed by the flowing gas through the packed bed of the regenerator. Since the gas flowing through the regenerator changes its temperature over time, we consider a change in the
y-axis (along the height of the regenerator).
where
mg is the mass flow rate of gas (kg∙s
−1),
Cp,g is the heat capacity of gas (J∙kg
−1∙K
−1),
Mg is mass of gas resident in the regenerator (kg), and
L is the height of regenerator (m).
The most important assumption in this model is that the thermal conductivity of the packing material is infinite in a direction perpendicular to gas flow (and zero in a direction parallel to the gas flow). This implies that, at any level in the regenerator, the solid material is isothermal in a direction perpendicular to gas flow, and this may be true or approximately true where the packing is thin or is made of materials of high conductivity. In this case, the coefficient ht is the surface heat transfer coefficient, usually a convective coefficient to which may be added a radiative component.
However, if the packing of the regenerator is constructed of material of low thermal conductivity and/or the thickness of packing around the channels through which the gases flow is comparatively large, then it is necessary to incorporate the resistances to heat transfer at the solid surface and within the solid into a lumped or total heat transfer coefficient. Hausen [
4] developed an equation to calculate this heat transfer coefficient in the following form:
where
n = 1 for slabs (plane walls) of thickness
d in (m),
n = 2 for solid cylinders of diameter
d in (m), and
n = 3 for spheres of diameter
d in (m),
λb is the thermal conductivity of packing material of regenerator (W∙m
−1∙K
−1),
hlum is the lumped heat transfer coefficient (W∙m
−2∙K
−1),
hc is the convective heat transfer coefficient (W∙m
−2∙K
−1), and
hr is the radiative heat transfer coefficient (W∙m
−2∙K
−1). The lumped heat transfer coefficient incorporates the surface convective heat transfer coefficient,
hc, and the resistance to heat transfer within the regenerator packing, as represented by the
therm. The total heat transfer coefficient can be used in the conventional model of the thermal performance of the regenerator, set out in the differential equations.
The function
, called Hausen factor, attempts to reproduce the effect of the very rapid temperature changes within the packing, immediately after a reversal, at the start of a hot or cold period. According to Reference [
5], this factor can be calculated in the case that
using equation
and, for other values,
where α is the thermal diffusivity (m
2∙s
−1),
P is the length of period for heating and cooling process (s),
ε = 2.7 for plates,
ε = 9.9 for cylinders, and
ε = 27.0 for spheres, Ω′ is the reduced time for hot period, and Ω″ is the reduced time for cold period.
This problem is described in more detail in Reference [
5].
3.2. Differential Equations
Equations (9) and (10) were rearranged by Hausen [
6] to the form
and
where
is the dimensionless length, and
is the dimensionless time.
and
When
t =
P and
y =
L, each period of regenerator operation is defined in terms of two dimensionless parameters given by Hausen [
6] “reduced period”, Π, and “reduced length”, Λ.
and
The effectiveness of regenerator behavior may be measured in terms of the thermal ratios, . The thermal ratio for the heating period is and that for the cooling period is . Ideally, the exit gas temperature in the hot or cold period should be equal to the inlet gas temperature in the opposite period. The thermal ratios, which are defined below, measure the degree to which this ideal is achieved.
For the heating period,
and, for the cooling period,
The term thermal ratio can be misleading in the sense that it is not always a measure of efficiency, and perhaps the term temperature ratio might be more appropriate.
In fixed-bed regenerators, the exit gas temperatures vary with time. The chronological average exit temperatures are, therefore, computed ( and ).
For the symmetric regenerator (Λ = Λ′ = Λ″, Π = Π′ = Π″, and
ηREG =
η’
REG =
η″
REG), an estimate of the thermal ratio is given by
It can be seen that a larger reduced length leads to a greater thermal ratio.
Let us suppose that we have a heat balance, once cyclic equilibrium is attained,
Dividing this equation by
, we get
If , the regenerator is said to be balanced and both thermal ratios are equal.
Equation (24) can be converted to the following form:
We can say that, in general, a regenerator is balanced if
If
k = 1, the regenerator is said to be symmetric. Equation (25) can be modified to the following form:
If γ = 1, the regenerator is balanced.
When
, this corresponds to the most general case where
,
, and the regenerator is said to be unbalanced. A summary of these classifications is presented in
Table 1.
The previous equations apply if the regenerative heat exchanger is symmetric. Hausen [
4] proposed that the performance of a balanced nonsymmetric regenerator can be accurately estimated using the symmetric regenerator model employing the harmonic reduced length
and the harmonic reduced period
in both hot and cold periods.
and
This proposal was verified as acceptable by Iliffe [
7], and its applicability was extended to unbalanced regenerators by Razelos [
8]. The thermal ratio than can be calculated using Equation (22).
A factor
K/K0 describing the effect of nonlinear variations of temperature using a factor is given in Reference [
4].
A smaller value of K/K0 results in a greater effect of both the nonlinear variations of temperature and the corresponding truncation error.
3.3. Calculation Methods
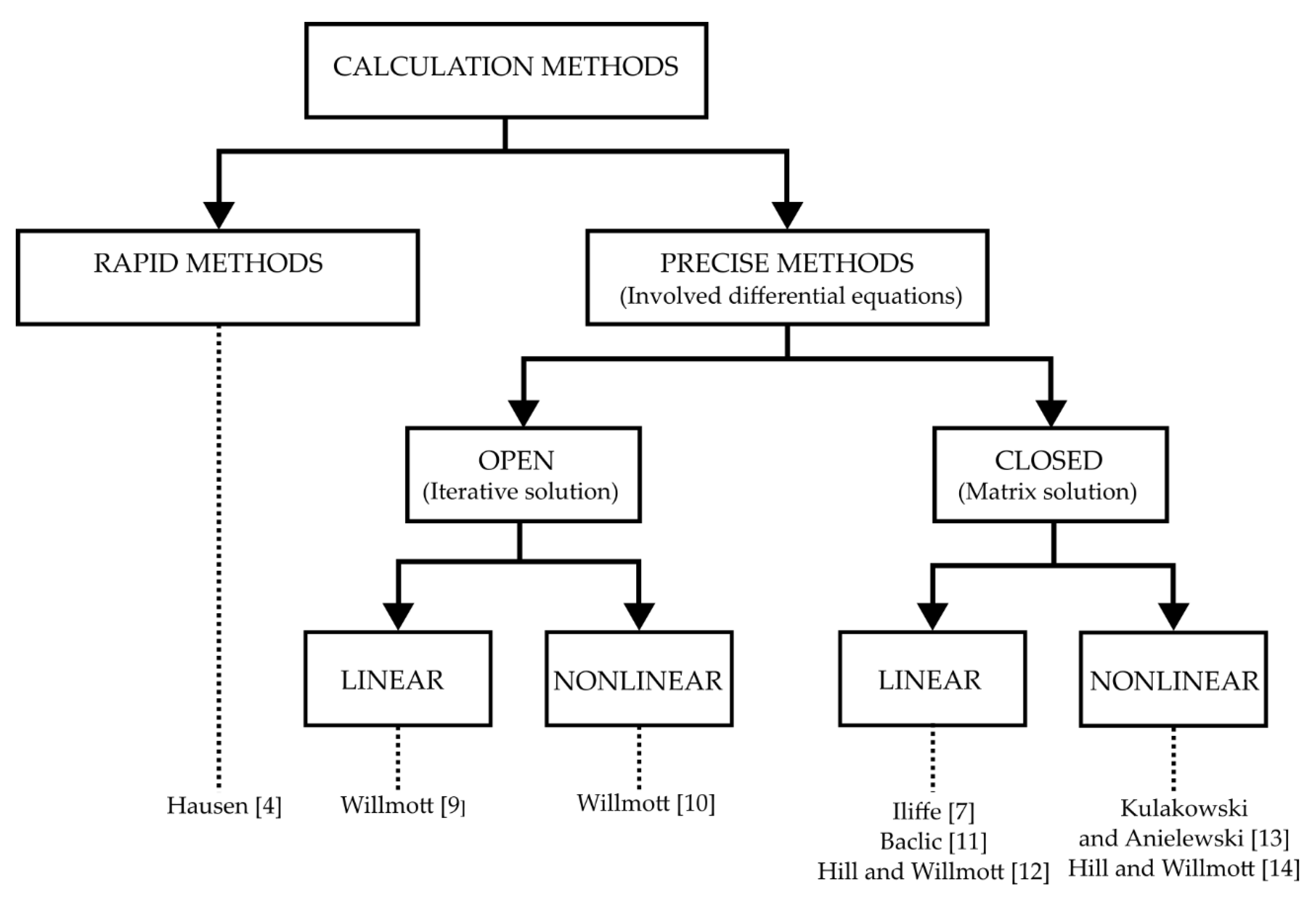
Several methods were developed to determine the solution of regenerative heat exchangers. Some of them are shown in
Figure 3. These methods can be divided into two groups: rapid and precise methods. Rapid methods are intended only for fast and preliminary calculation and do not provide sufficient accuracy. In addition, only the media outlet temperatures are the result. These methods are not suitable for the application of real calculations and designs. Rapid methods were created mainly before the expansion of computers. An example of a rapid method is given in Reference [
4].
The most suitable methods for the design of these heat exchangers are precise methods which involve the solution of differential equations, and the result is the variation of the media temperatures at the outlet over time. These methods can be classified into two groups: open and closed. Each of these two methods comprises two subgroups, namely, linear and nonlinear methods, according to the way in which thermophysical properties of the gas and the storage material are calculated.
In the open methods, the gas and solid temperatures are evaluated by solving differential equations over successive cycles of regenerator operation. The temperature profiles in each cycle and time are the result. We know the number of cycles to equilibrium at the end of the calculation. The closed methods are those in which the steady-state performance is calculated directly without the consideration of any previous cycles. In general, the closed methods are faster than open methods; however, when using modern computers, the difference is slight. The closed methods appear to be suitable for solving a linear problems, but are becoming extremely complicated (and sometimes unstable) in solving nonlinear problems, i.e., the thermophysical properties of both fluid and solids, including heat transfer coefficients, can vary spatially and temporally, depending on temperature and/or when mass flow rates of fluids in one or both periods of regeneration operation may vary with time. Open methods show great stability even when solving nonlinear problems. In these cases, open methods are preferable. Another advantage of open methods is their easy modification by including equations for calculating heat transfer coefficient and pressure drops.
For computer solutions, the open methods proposed by Willmott, given in References [
9,
10], seem to be the most suitable. These methods were chosen because they are relatively easy to program, and they involve the calculation of important parts (i.e., calculation of heat transfer coefficient, calculation of radiation influence, calculation of pressure losses, geometric characteristics). In addition, these methods enable including the effect of changes in the thermophysical properties of media flowing through the packed bed in time (nonlinear model) and are more stable.
3.4. Selected Mathematical Model
The selected Willmott open method can be further divided into a linear, quasi-linear, and nonlinear model. The difference between these models is in the calculation of the thermophysical properties of gas and bed.
The linear model calculates the thermophysical properties of the gas and bed based on the reference temperature, i.e., the properties are constant at each packed bed point and at every moment. The calculation is fast, but it may not be accurate enough in some cases, especially when the temperature changes significantly. The fluid properties are calculated at a reference temperature.
The quasi-linear model was described in Reference [
13]. This model uses a different reference temperature for hot and cold media.
The outlet temperatures are replaced by the newly calculated ones, and the reference temperatures are recalculated after each period or cycle. Based on these temperatures, all thermophysical properties of fluids, packed bed material, and related values are recalculated.
The nonlinear model considers the change in gas and bed properties at the place and time as a function of temperature. The heat transfer coefficient is then calculated from these properties at every moment and place. This is important for the most realistic simulation of high-temperature regenerators. The calculation is much more accurate but time-consuming. However, this is not a considerable problem with up-to-date computers.
Reference [
9] proposed a method for solving Equations (14) and (15) so that it could be used for the solution on computers. This method uses a trapezoidal method for the numerical solution of differential equations. This method of calculating the regenerator is known as the Willmott open method. The simplifications introduced to the derivation and calculation of these differential equations are as follows, according to Reference [
9]:
The effect of the reversals can be neglected, that is, the rapid gas temperature transients which are associated with the residual gas in the regenerator being replaced by the gas flowing in the opposite direction at the reversal can be ignored.
The entrance gas temperatures in both periods remain constant.
The mass flow rates of the heating and cooling gases do not vary throughout each period.
Heat transfer between gas and solid can be represented in terms of an overall heat transfer coefficient relating gas temperature to mean solid temperature. Furthermore, the rate of heat transfer in the packed bed at any height is represented by the time variation of the mean solid temperature.
The heat capacity of the gas in the channels of the packed bed at any instant is small relative to the heat capacity of the solid and, therefore, can be neglected.
The heat transfer coefficients and the thermal properties of the heat storing mass and the gas do not vary throughout a period and are identical at all parts of the regenerator in that period.
Longitudinal thermal conductivity is neglected.
Boundary conditions
There are determined two boundary conditions.
The inlet temperatures for both hot and cold cycles are constant.
The surface temperatures along the length of the regenerator at the end of the hot/cold period are the same as those at the beginning of the following cold/hot period. Since the gases flow in opposite directions in successive cycles, the boundary conditions are expressed by the equations
For the first cycle, the temperature along the bed is set arbitrarily, e.g., to ambient temperature. In the following cycles, the mentioned condition is already applied.
Using the trapezoidal numerical method, which provides excellent properties of numerical stability, the differential equations move to the following forms:
and
where
r refers to distance (
r = 0..
m) and
S refers to the time (
S = 0..
P). Thus, the distance step is
L/m and the time step is mostly 1 s.
3.4.1. Linear Model
In the case of the linear model, these equations can be further adjusted to form
and
where
In these equations, Λ is the reduced length, Π is the reduced time, m is the number of sections, and P is the cycle time.
These equations are the main equations needed to calculate the regenerative heat exchanger. For the proper solution of these equations, the bed needs to be divided into a suitable number of sections, in which the temperature calculations are gradually performed. The calculation is then a combination of the above and other supplementary equations. The calculation is solved by an iterative procedure for the given time over the entire length of the bed. This procedure is then repeated for all times and all periods (cooling and heating) until equilibrium is reached, i.e., for consecutive cooling cycles, abs (
Φ(
n) −
Φ(
n − 1)) must be less than the value given by the user. Then, the cycle (
n + 1) is the equilibrium cycle.
This is not an exhaustive description of the solution of differential Equations (33) and (34) using a trapezoidal rule for a linear model. See Reference [
9] for more information how to apply this method to the computer. This basic computational model was developed in GNU Octave software and then applied to several examples differing in reduced period value and reduced length. Subsequently, the influence of these reduced quantities on the calculation was evaluated.
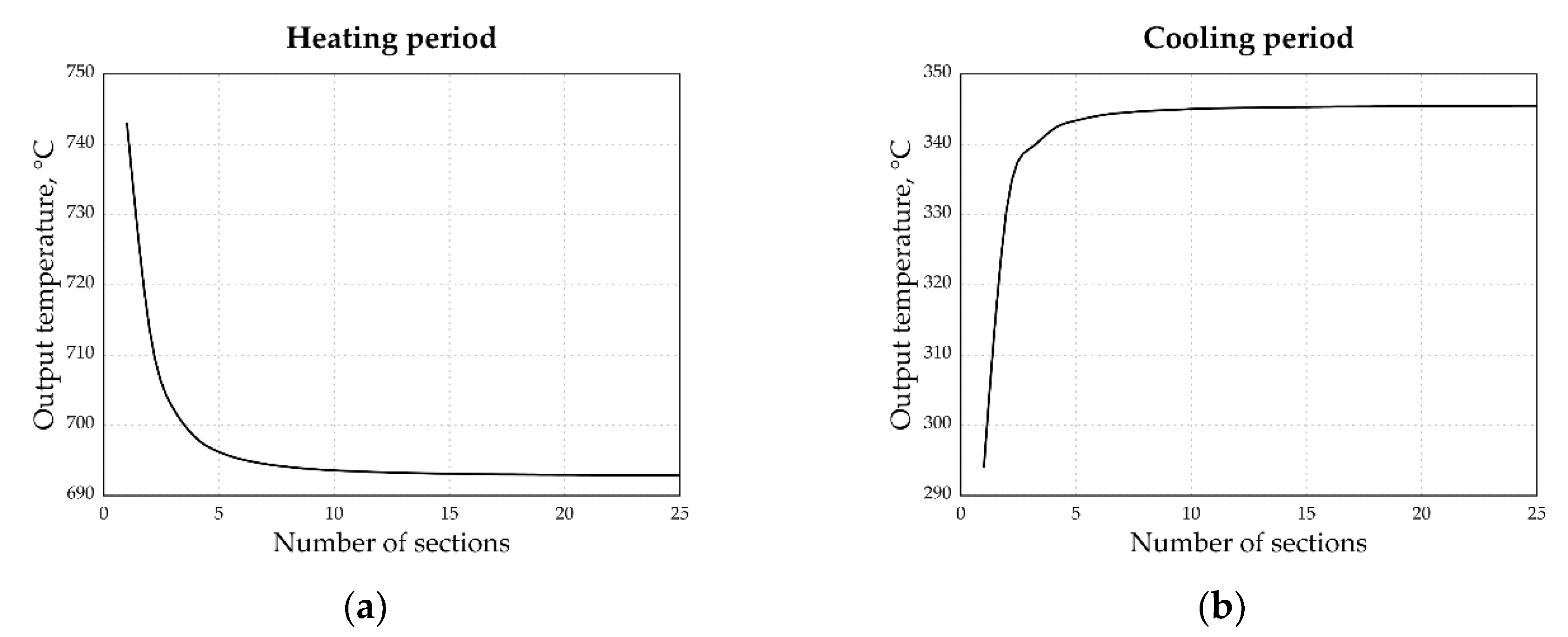
Case 1—taken from Reference [9] The input data of the calculation are given in
Table 2. The task was to calculate the outlet temperature of the hot and cold medium for the different number of sections
m. If we divide the regeneration bed into a small number of sections, the outlet temperature does not correspond to reality (see the results).
The results of the calculation are shown in graphical form in
Figure 4.
These calculations showed that the accuracy of the outlet temperature is dependent on the number of sections on which the regenerator (packed bed) is divided. In this case, the limit number of sections is 10. However, this is not true in all cases. From further calculations, it was possible to prove that, with a higher value of reduced length, the required number of sections on which the packed bed must be divided decreases; however, at the same time, the number of cycles needed to reach the equilibrium increases. On the other hand, as the reduced period increases, the number of sections (steps) increases, but the number of cycles necessary to establish equilibrium decreases. I suggest having a minimum of 50 sections. This is no problem for computers.
3.4.2. Nonlinear Model
The linear model considers only the constant properties of fluids. This means faster calculation; however, in some cases, the results may differ significantly from reality. Such a procedure is only suitable for preliminary calculations. More accurate results are obtained when changing the properties of fluid with a change in temperature. This model is called the nonlinear model.
In the case of the nonlinear model, Equations (33) and (34) can be further adjusted to form
and
where
These constants are calculated in every point and time with changing temperature. This is not an exhaustive description of the solution of differential Equations (33) and (34) using a trapezoidal rule for a nonlinear model. See Reference [
10] for more information how to apply this method to the computer.
4. Pressure Drops
A very important value in designing a regenerative heat exchanger or, generally, a device using a packed or structured material layer is the amount of pressure drop of the flowing gas. The general equation for its calculation is mostly defined as
where
is the velocity of gas based on the empty cross-section of the bed (m∙s
−1), and
λk is the friction factor, most often given in the form
where
k1 and
k2 are constants, and
b is the exponent.
Rem is the modified Reynolds number given by Ergun as follows:
Pressure drop in the packed bed is commonly calculated using the Ergun equation [
2].
According to Reference [
15], this equation very often over-predicts the respective value, and it is better to use special equation tailored to specific storage materials which are based on experimental data.
Ergun also defined the friction coefficient in the shape
Sometimes, friction coefficient proposed in Reference [
16] is used.
The Reynolds number is often also given in a modified form, which is defined by the equation
There are many correlations for calculating the friction coefficient. The best known is the Ergun equation mentioned above, but it overestimates pressure drop for a bed of randomly arranged smooth spheres for Rem > 700.
Based on an extensive comparison of the computational equations for determining the pressure drop through the packed bed performed in Reference [
17], the computational equations listed in
Table 3 were selected.
There are several other computational equations. These are mentioned, for example, in Reference [
15], which deals with the effect of particle shape, size distribution, packing arrangement, and roughness of particles on pressure drop.
The Eisfeld and Schnitlein equation (see
Table 3) using the constants
K1 = 190,
k1 = 2.00, and
k2 = 0.77 can be used for the cylindrical shapes of the particles. For other particles, the constants
K1 = 155,
k1 = 1.42, and
k2 = 0.83 can be used.
For non-spherical particles, Reference [
25] proposed altering the constants in the Ergun equation by means of the particle sphericity
ψ. For cylindrical particles, the friction factor is altered to
This equation is based on experimental data for Rem < 400.
Singh et al. [
26] presented a correlation for pressure drop through beds of differently shaped particles in the form
This is not an exhaustive list of all available computational equations to determine the friction coefficient as the medium flows through the packed bed. Other equations can be obtained in References [
15,
17].
For calculating the pressure drop across a layer consisting of a set of straight channels, e.g., honeycomb, the formulas for calculating pressure drop in a straight channel can be used.
where the friction factor can be calculated using the Swamee–Jain equation [
27].
where
e is the effective roughness height (m), and
dh is the hydraulic diameter (m).
An important value is the pressure drop of the sieve on which the bed is placed. This pressure drop must also be determined and included in the total pressure drop.
5. Voidage Calculation
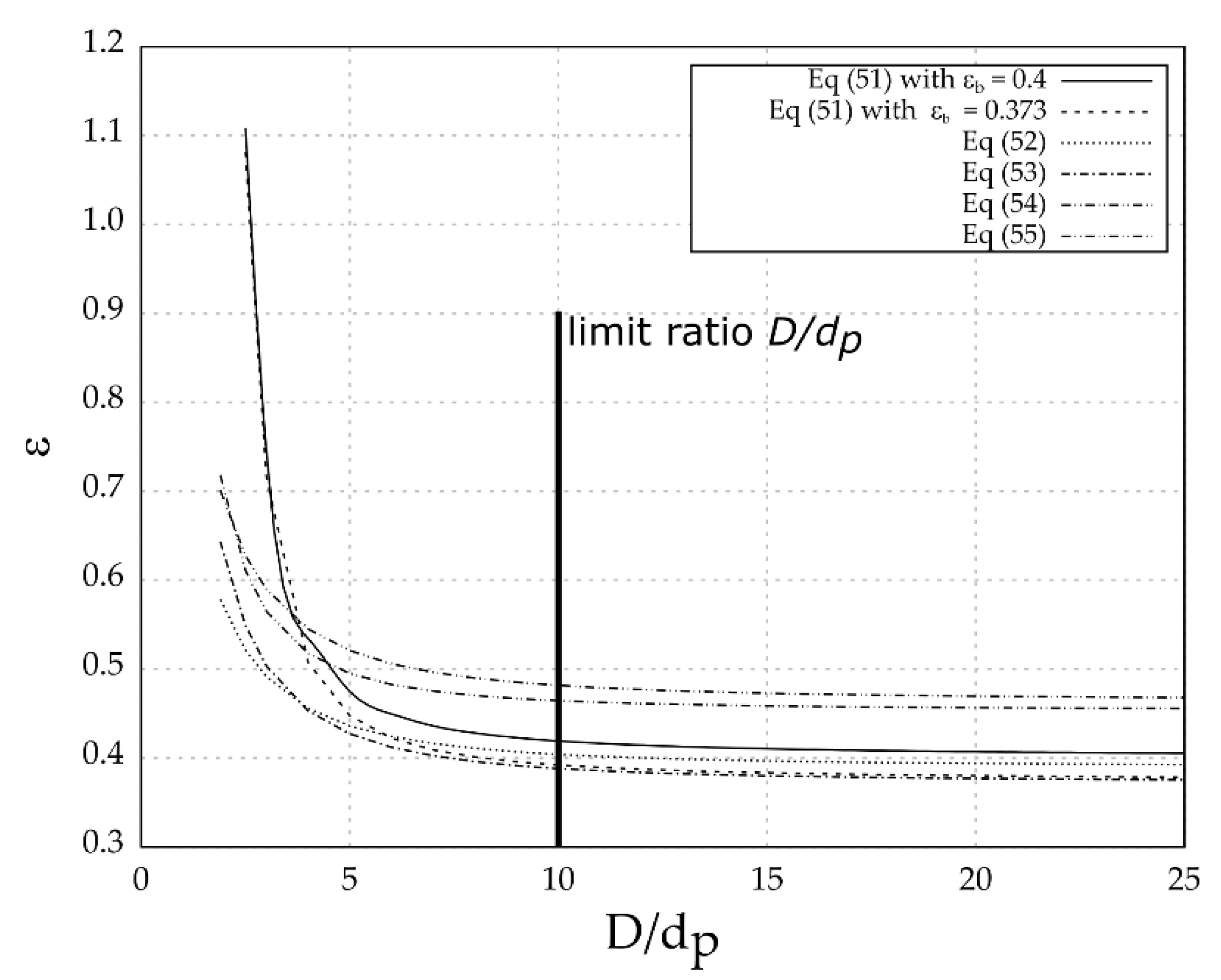
The pressure drop is strongly influenced by the mean voidage in the packed bed. In industrial practice, a large number of different non-spherical shaped particles are used, which form the bed and have different voidage. The most cited and experimentally verified effect on voidage is the ratio of regenerator diameter to equivalent particle diameter. This effect is most significant for a ratio of diameters less than 10 (see
Figure 5). If the bed consists of non-spherical particles, their diameter is expressed by the equivalent diameter
dp. In the randomly packed bed, other than spherical particles, the influence of particle orientation affects the local distribution of the voidage, which affects the mean voidage. This means that different medium voidage can be achieved with each filling of the packing.
Among the most used empirical formulas for calculating the voidage are those from References [
28,
29,
30,
31,
32]. These equations tend to be awkward and have too many parameters. Due to the complexity of using the mentioned equations, simpler but sufficiently accurate equations were developed to calculate the voidage. Some of them are listed below.
The equation designed by Zou and Yu [
33] and recommended by Di Felice and Gibilaro [
34] is in the form
for
.
By analyzing experimental data, Zou and Yu suggested a coefficient of
εb = 0.4, while Reference [
35] suggested that
εb = 0.373, a value derived from their own data (subscript
b means a bulk region).
Benyahia et al. [
36] developed the following equations based on the measured data:
For spherical particles (1.5 ≤
D/
dp ≤ 50),
For solid cylinders (1.7 ≤
D/
dp ≤ 26.3),
For hollow cylinders (1.9 ≤
D/
dp ≤ 14.5),
Pro general particles (1.5 ≤
D/
dp ≤ 50; 0.42 <
< 1.0),
The course of the voidage versus the
D/dp ratio is shown in
Figure 5. It can be seen that, up to value 10, the voidage strongly depends on this ratio. From this value, the voidage is approximately constant.
6. Heat Transfer Calculation
Determination of the heat transfer coefficient of the gas flowing through the packed bed is the most sensitive point of the calculation. Even if we set the correct number of sections and consider the variable properties of the fluids and the packed bed material, if we determine the wrong heat transfer coefficient, we get poor results.
The heat transfer coefficient mostly includes the effect of both convection and radiation for both streams. Heat transfer coefficient depends predominantly on the type of storage material. The respective equations for convective heat transfer were published, e.g., in Reference [
37], while those for radiative heat transfer were discussed, e.g., in Reference [
38].
The heat flux density
q between the gas and the packed bed material can be expressed as follows:
where
qc is the convective heat flux density (W∙m
−2),
qr is the radiative heat flux density (W∙m
−2), and the total heat transfer coefficient is defined as
The influence of the conductive transfer is negligible compared to the others. As mentioned previously, the convective component must be, in some cases, replaced by the effective heat transfer coefficient
hlum.
6.1. Convective Heat Transfer Coefficient
The choice of the heat transfer coefficient is a crucial factor. Many computational equations can be found to calculate the heat transfer coefficient in the literature. However, they can give different results. It is necessary to choose a computational equation that was verified for the particles that form the packed bed.
The equation for a randomly packed bed (Equation (59)), which was verified on experimental data, was recommended in Reference [
39].
for
Pr = 0.7–0.8,
Re > 100. Here,
λg is the thermal conductivity (W∙m
−1∙K
−1),
Re is the Reynolds number (-), and
Pr is the Prandtl number (-).
The heat transfer coefficient in the packed bed of spheres can be calculated according to Reference [
40] using the following equation:
for
Re = 500–50,000. This equation was also recommended in Reference [
41]. A significant wall effect was observed at ratios of bed diameter to particle diameter less than 20. Above that ratio, this equation is valid.
An equation for a packed bed formed with spheres was recommended in Reference [
42].
for
Re = 200–10,400.
Another suitable equation was mentioned in Reference [
40].
This equation takes into account the voidage, ε, and it is valid for a Reynolds number of 20–10,000.
The equation for flow in a packed bed can also be used [
43].
for 20 <
Re < 100,000.
As mentioned in Reference [
44], the heat transfer performances in a packed bed are usually formulated by traditional correlation as follows:
where
a1,
a2, and
n are model constants. The values of these constants given by Reference [
44] are
a1 = 2.0,
a2 = 1.1, and
n = 0.6. Values of these constant for different packed cells were mentioned in Reference [
45].
An experimental study was carried out to investigate the heat transfer of packed bed solar energy storage system having large-sized elements of storage material of different shapes [
26].
The heat transfer in the structured packed bed formed by straight channels can be determined using the following basic equation:
6.2. Radiative Heat Transfer Coefficient
In certain high-temperature applications, the heat exchanger is heated up by a flue gas containing significant proportions of CO2 and H2O vapor. In these circumstances, the radiation heat transfer must be considered.
The heat flux density due to gas–solid radiation is given by
where
εg and
αg are the emissivity and mean absorptivity of gases (-), respectively,
εb is the emissivity of bed material (-), and σ is Stefan Boltzmann’s constant, 5.67 × 10
−8 (W∙m
−2∙K
−1). The fraction of
is sometimes called the emissivity correction factor.
The values of emissivity and absorptivity are proportional to the percentage of carbon dioxide and water vapor in the gas and to the beam length. Both are functions of the gas temperature. These values can be obtained from Hottel’s charts [
46] or using the methods given in the literature.
According to Reference [
47], it is possible to calculate the radiative heat transfer
hr using the equation mentioned in Reference [
48].
More specifically, however, the emissivity and gas absorption can be determined based on the mean beam length (m), Lb, in a given space and on the partial pressures of the respective radiant gas components. Several methods can be found in the literature.
The mean beam length
Lb is determined from a known equation for the case when
Lb > 1 m,
and, for the case when
Lb < 1 m,
where
V is the mean channel volume (m
3), and
P is the mean inner surface of the channel in the packed bed (m
2).
The emissivity of gas can be calculated using the equation from Reference [
49].
where
εCO2 is the emissivity of carbon dioxide (-),
εH2O is the uncorrected emissivity of water vapor (-),
CH2O is Beer’s law correction factor for water vapor (-), and
CSO is the spectral overlap correction factor (-).
The emissivity of carbon dioxide (
εCO2) is a function of temperature and the product (
pCO2L), where
pCO2 is the partial pressure of carbon dioxide in the gases (Pa) and
Lb is the mean beam length (m). Thus,
The emissivity of water vapor (
εH2O) is a function of temperature and (
pH2OLb), where
pH2O is the partial pressure of water vapor (Pa) and
Lb is the mean beam length (m). Thus,
Mean absorptivity of gas (
αg) is estimated using the equation from Reference [
49].
where
n = 0.5 for
Tb < 500 °C,
n = 0.4 for
Tb > 900 °C, and
n = 0.45 for 500 °C <
Tb < 900 °C.
The emissivity of carbon dioxide (
εCO2) and water vapor (
εH2O), and the absorptivity of gases can be computed using methods available from the literature [
50,
51,
52,
53].
6.3. Heat Losses
If the wall of the regenerator is not sufficiently insulated, the heat losses through the wall of the equipment should also be included in the calculation.
These are defined as follows:
where
Aw is the wall area (m
2),
Tw is the wall temperature (°C),
Tinf is the ambient temperature (°C), and
ho is the outside convective heat transfer coefficient (W∙m
−2∙K
−1).
For vertical cylinders, the convective heat transfer coefficient
ho is calculated from a correlation of Churchill and Chu [
54] for plane surfaces as
where
H is the height of the regenerator (m), and
Ra is the Rayleigh number given as follows:
where
H is the height of the regenerator (m),
g is the gravity acceleration (m∙s
−2),
is the thermal expansion coefficient (K
−1),
α is the thermal diffusivity (m
2∙s
−1), and ν is the kinematic viscosity of gas (m
2∙s
−1) as defined in the temperature of
Tf. Validity of the correlation is in the range 10
−1 <
Ra < 10
12. This correlation can be used provided the curvature effect is not too significant. This represents the limit where boundary layer thickness is small relative to cylinder diameter
D. The correlations for vertical plane walls can be used when
D/L ≥
35/Gr0.25 where
Gr is the Grashof number.
7. Software Implementation of the Model
Since no software was found on the market to design regenerative heat exchangers, it had to be created. The abovementioned Willmott methods for the linear and nonlinear model, together with mentioned equations for determination of heat transfer and pressure drop, were used in creating the computational software. To make the software user-friendly, the JAVA environment was used to build the software. The created calculation software (see
Figure 6) enables effectively solving these types of heat exchangers, and it provides results in the form of text output and graphical dependencies of temperatures and pressure drops along the packed bed and over time. The software enables a user to print input data, text results, and various graphical dependencies. It is also possible to save these data and charts in various graphic file formats and copy dependencies in text form to Excel.
In order to perform the calculation, the user must specify the geometric characteristics of the packed bed, the media properties, the time of hot and cold period, the number of sections into which the packed bed is divided, and so on. Furthermore, the method of calculation and suitable equations for calculating heat transfer and pressure drop are selected.
The code of the created software has thousands of lines and it consists of many classes (for various methods, heat transfer, pressure drop, display results, saving, etc.); therefore, it is not possible to show all the code here. As mentioned in the article, the trapezoidal method is used to solve differential equations. A small part of the code for solving differential Equations (33) and (34) for the hot period is shown in the gray rectangle below.
![Energies 13 00759 i001]()
One possibility of how to improve the created software is to implement an open-source database of fluid properties. Currently, it is necessary to specify fluid properties using interpolation curves, which is not quite effective and delays the calculation. The user must firstly create interpolation curves and then insert their constants into the software. The next step would be to add the possibility of using the regenerative heat exchanger for flue gas cleaning. This means the software would be able to divide the packed bed into a part where heat accumulation or heat output occurs and a part where the chemical reactions (catalytic bed) take place.
The developed software was used to solve the regenerative heat exchanger. It should be noted the software is still being developed and improved.
Case Study
The task was to utilize the heat from the gas stream at an inlet temperature of 727 °C and to heat up the gas at an inlet temperature of 27 °C with the accumulated heat. Flow rates, hot and cold periods, and media properties are given in
Table 4. A regenerative heat exchanger with a packed bed diameter of 0.2 m and a height of 1 m should be used. The geometry of the regenerator and properties of the packed bed are given in
Table 5. The Willmott linear method was used for calculating the heat exchanger.
It should be noted that the cooling period means that the bed is cooling down and the heating period means that the bed is heating up.
Convergence is attained when the pseudo-thermal ratios given by Equation (37) in two subsequent cycles are numerically equal, with a difference of less than 1 × 10
−6. According to the calculation results, the equilibrium was reached after 18 cycles, and the calculation time was 48 milliseconds. It is obvious that the calculation is fast. The main results are shown in
Table 6, and graphical dependencies of temperatures and pressures are shown in the figures below. These are only basic graphical outputs provided by the software. Similarly, the output text protocol contains much more data than shown in
Table 6.
The basic graphical output is the course of the gas temperatures and the packed bed at the outlet as a function of time (see
Figure 7). It can be seen the temperature of the cold medium at the outlet is the highest at the beginning of the period. Gradually, the stored heat decreases and the outlet temperature of the cold gas falls. The opposite situation occurs with hot gas. The hot gas transfers most heat at the start of the period and, gradually, the ability of the bed to absorb energy decreases and the hot gas outlet temperature increases.
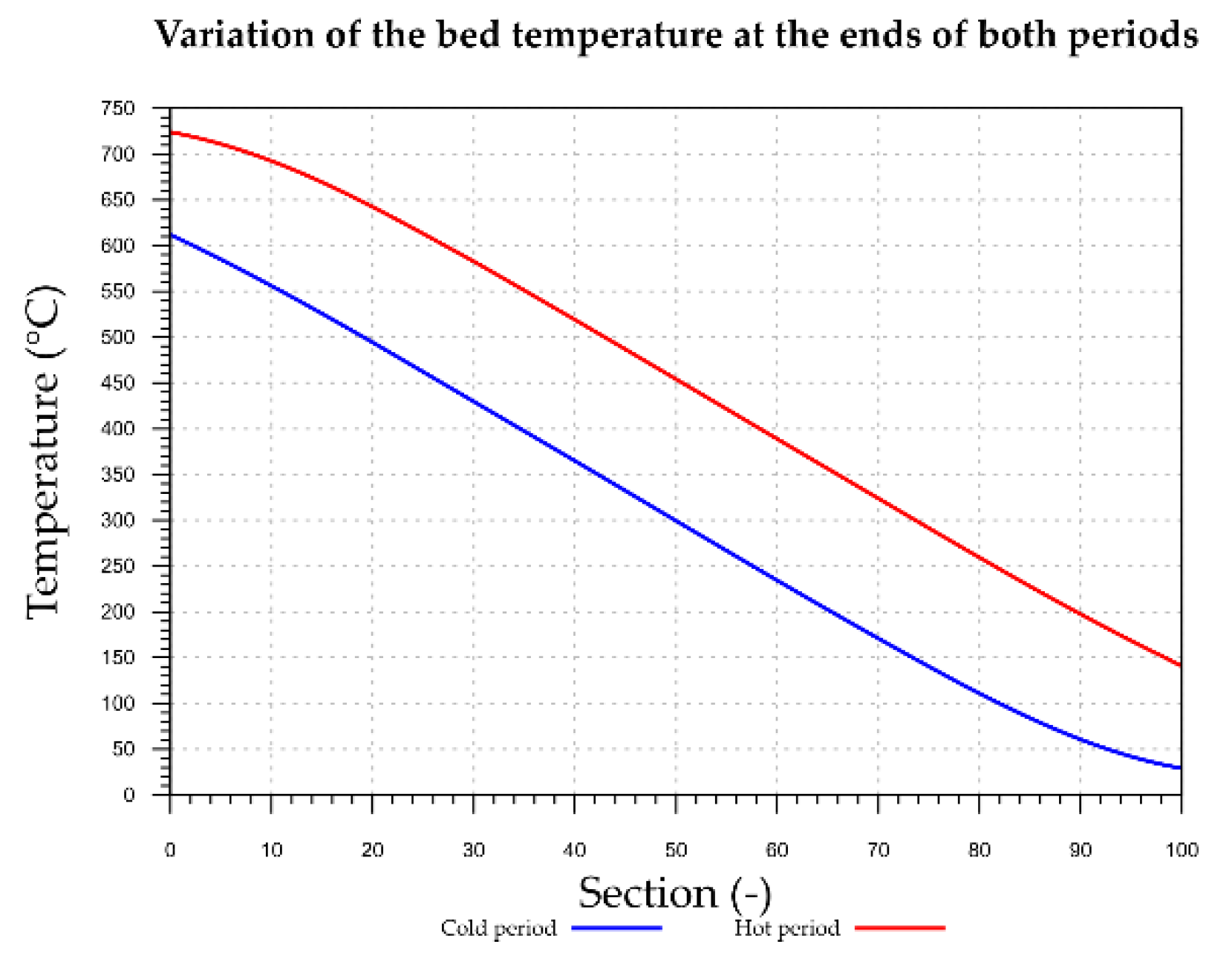
Figure 8 shows the temperature variations of the packed bed material along with its height for the hot and cold periods at steady state. It can be seen that the packed bed has the highest temperature in the first sections. With an increase in the height of the packed bed, the temperature decreases significantly. This is the reason why both media flow gradually in opposite directions.
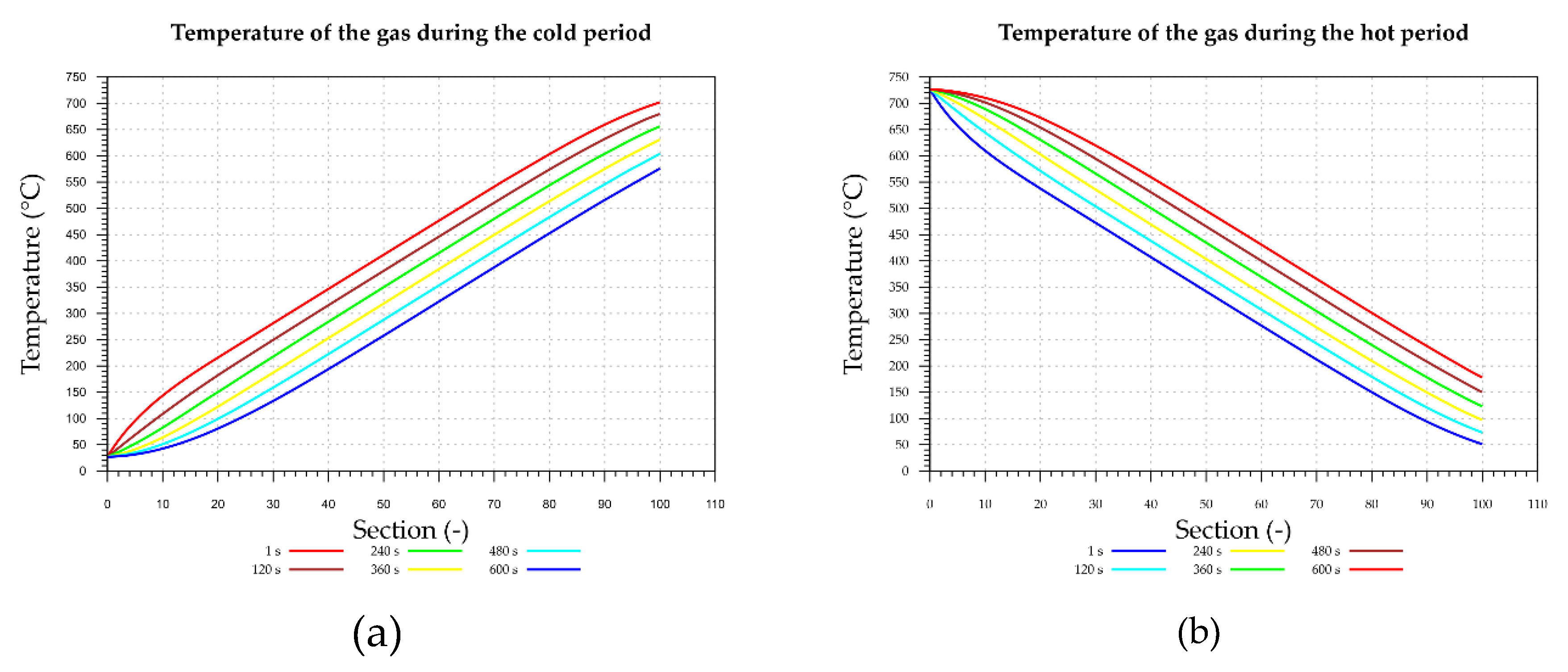
Figure 9a,b illustrates that the temperature profiles of the gaseous phase along the bed gradually change with time. In this calculation, they were obtained after a simulation of 18 cycles from the initial condition. Moreover, these figures predict the temperature variations at the same location of the bed but different time of the period.
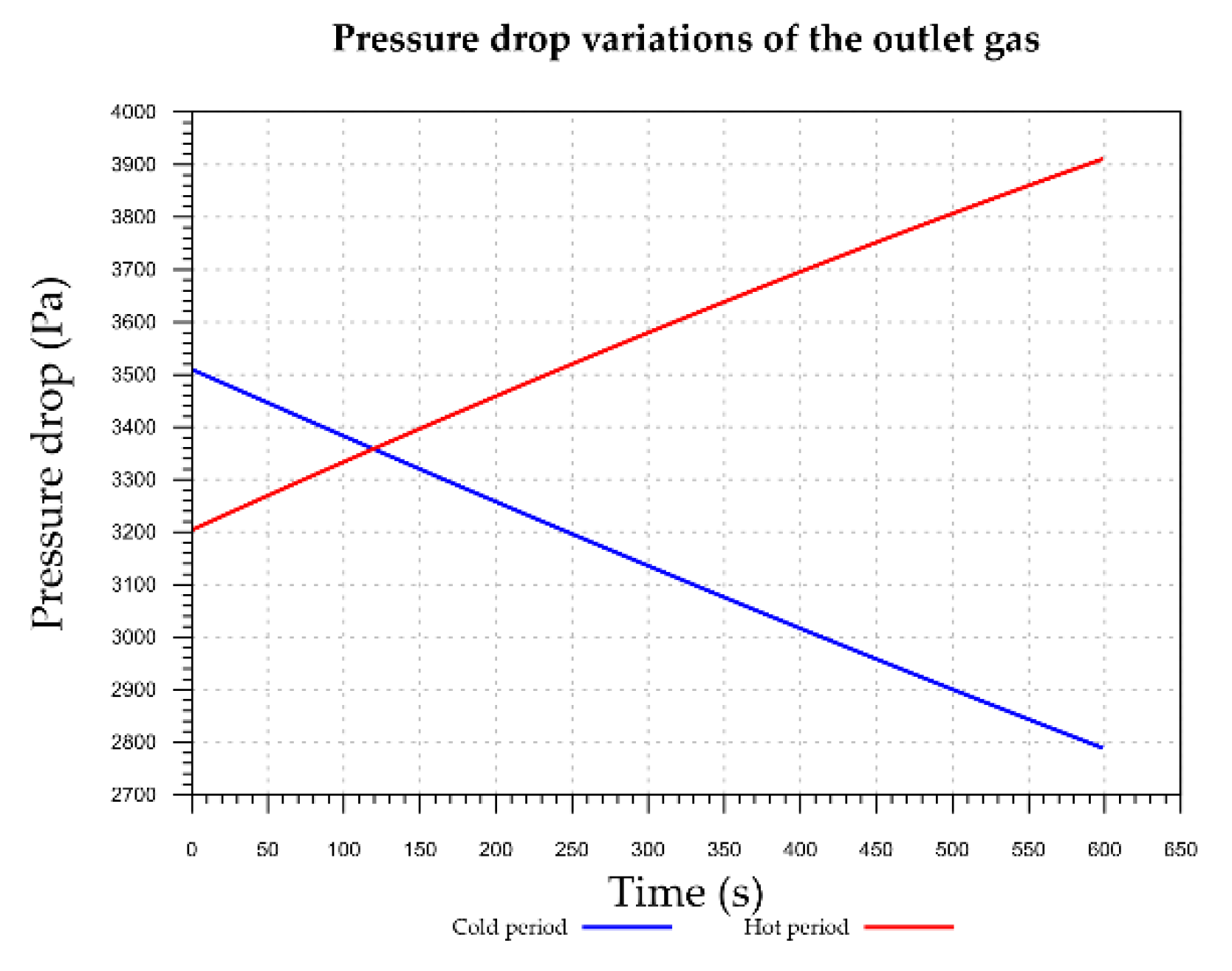
The pressure drop variations for the hot and cold periods over time is shown in
Figure 10. When calculating the pressure drop, the variable physical properties of the gases as a function of temperature were considered. The pressure drop increases with the temperature, while the gas volume increases with temperature and, hence, medium velocity increases. The pressure drop increases during the heating process and decreases during the cooling process with time. Thus, the pressure drop variations correspond to the temperatures shown in
Figure 7 and
Figure 9.
The text and graphical results shown in the paper are not complete results provided with the software. They represent only a selection of the main results.
8. Summary
Our task was to create software for calculating regenerative heat exchangers with a fixed bed at the request of an engineering office in the Czech Republic. Research revealed there are several computational methods that differ in accuracy and computational stability. It was shown that the open computational methods proposed by Willmott seem to be the most suitable for use on a computer. Although these methods are several years old, they were not suitable because of their complexity at the time of their creation. In subsequent years, the methods were simplified in order to facilitate and accelerate the calculation. This is because, for the exact solution of these types of exchangers, it is necessary to solve the system of differential equations. With the development of computers, however, the situation changed, and these methods are again up to date. The advantage of these methods is their stability and possibility to adjust them by adding suitable calculation formulas for the determination of heat transfer and pressure drop.
The impulse to create this paper was also to broaden the awareness of regenerative heat exchangers, to provide designers with an overview of suitable calculation methods and, thus, to extend the interest and use of these types of heat exchangers. This is the reason why not only calculation methods, but also equations for determining the heat transfer coefficient of convection and radiation and equations for predicting pressure drops are mentioned in the paper. Potential candidates for the calculations of these devices are given as an overview of suitable calculation methods and equations, and one does not need to extensively search for them in the available literature.