Abstract
Currently, natural gas provides more than a third of the energy used in European residential buildings. As part of the general decline of fossil fuels, this gas consumption is predicted to drop in several countries by 25–100% by 2050. We model a decline in gas consumption in 57 urban German distribution grids looking for the influence of grid-specific factors and different distribution network operator (DNO) strategies on grid charges. We find a functional relationship between grid length and customer amount described by a power law, with an exponent correlated with structural grid parameters. The disordered structure inherent to grids typically results in a decline in grid costs much slower than the corresponding demand. We introduce a simplified yearly cash flow calculation model based on the power law and validate it against mixed integer linear optimization. A comparison of the total costs of operation and resulting grid charges for several scenarios and strategies estimates the effects on DNO business models. Depending on a combination of DNO’s strategy and customers’ exit pattern, grid charges may increase, accelerating the substitution of gas-bound technologies that might develop into a self-reinforcing feedback loop, leading to grid defection.
1. Introduction
One fifth to one third of the global end-use of energy is consumed in the building sector. About 30% percent of it is used by electrical applications and 70% is needed for space heating (SH) as well as domestic hot water (DHW) generation [1,2,3]. Due to insulation measures and electrification of heating systems in new and existing buildings, most macroeconomic studies predict a decline in final energy demand and the use of fossil fuels in Europe [4,5]. The share of natural gas heating systems is predicted to drop by 25–100% until 2050 in Germany [6,7,8,9,10,11], as in other regions such as the USA [12,13,14,15] or China [16,17] studies predict a short- to medium-term increase. While an extensive gas infrastructure can be maintained under the assumption of a shift to renewable gas production even within a scenario of full decarbonization, most long-term scenarios find a decrease in gas demand more likely. Because of this, a transformation path of declining gas demand is a relevant scenario for the gas distribution network operators (DNO) in many areas worldwide that challenges existing business models.
With customer numbers and individual gas consumption dwindling, the profitability of the gas grid infrastructure is tending to decrease. Many European gas grid DNO operate under a regulatory model, where rising costs are passed on to grid users in the form of grid charges. Consequently, rising energy prices and grid charges might lead to customers substituting gas-based technologies especially in heating sector and therefore gas grid defection. This poses not only a risk for DNOs of losing their business model, but can also lead to macro-economic consequences: A large number of studies predict the importance of a gas network infrastructure as a flexibility option also for a fully electrified energy system [6,7,8,9,10,11]. Several studies address these questions at a macroscopic level [12,13,14,15], but there is a lack in the literature when it comes to the evaluation of such scenarios at grid level [18], especially for investigations based on real DNO, grid and customer data. Our study addresses three main questions relevant for DNOs, policy makers and creators of macro-economic models of the energy system:
- What is the trend of customer development?
- What are the grid-specific factors that influence the profitability of a natural gas grid?
- What are the options for grid operators, regulators and what are the impacts on grid users?
Therefore, we examine the development of grid charges and the DNO’s revenue cap for a gas exit scenario, analyzing in detail the effect of different local distributions of customer exits on the grid length and strategic options of the DNO for 57 grids in the German city of Bamberg. The paper is organized in two main sections: First, we perform a literature review to present the motivation as well as relevance of the topic and justify our assumptions. Second, we perform a structural and cost analysis for the real grid data. Within the review, we examine the current scenarios for the system-wide demand for natural gas, and how these exit scenarios are shaped by individual customers’ decisions (Section 2.1 and Section 2.2). Afterwards, we point out that there is a lack in the literature with respect to grid planning and the evaluation of distribution network operator strategies in face of decreasing gas demand (Section 2.3). Subsequently, in Section 2.4, we identify the economic factors that influence the total cost of operation of gas networks and how they scale with grid length, age and supplied energy. Finally, we analyze regulatory mechanisms and tag possible DNO strategies for scenarios with decreasing gas demand (Section 2.5). Based on the findings of the review, we perform a structural and economic analysis for 57 natural gas distribution grids described:
- Within a structural grid analysis, we estimate a functional relationship between required grid length and the amount of customers with a power law approach (Section 3.2.1) for different exit patterns in all grids (Section 4.2). Within a correlation analysis, we identify possible structural parameters for the prediction of the exponent k of the power law, a parameter which determines the disproportionality between grid length and number of customers when they leave the grid (Section 4.3).
- To calculate the total costs of grid operation within an economic analysis, we apply a mixed integer linear optimization model based on a yearly cash flow calculation and transform it into a simplified calculation model considering the functional relationship found in the previous section (Section 3.3.2 and Section 3.3.3). After a validation of the simplified model (Section 4.4.1 and Section 4.4.2), we compare the total costs of operation and resulting grid charges for several exit patterns and DNO investment strategies in Section 4.4.3.
Finally, we discuss the options, risks and conclusions for the different stakeholders, describe the transferability of the approach on other regulatory environments and analyze interdependencies between the decisions of different stakeholders to introduce the hypothesis of a self-reinforcing feedback loop that might lead to gas grid defection (Section 5). For a list of acronyms used, see Table A1 in Appendix A.
2. Literature Review
2.1. Scenarios for Gas Demand from an International and German Perspective
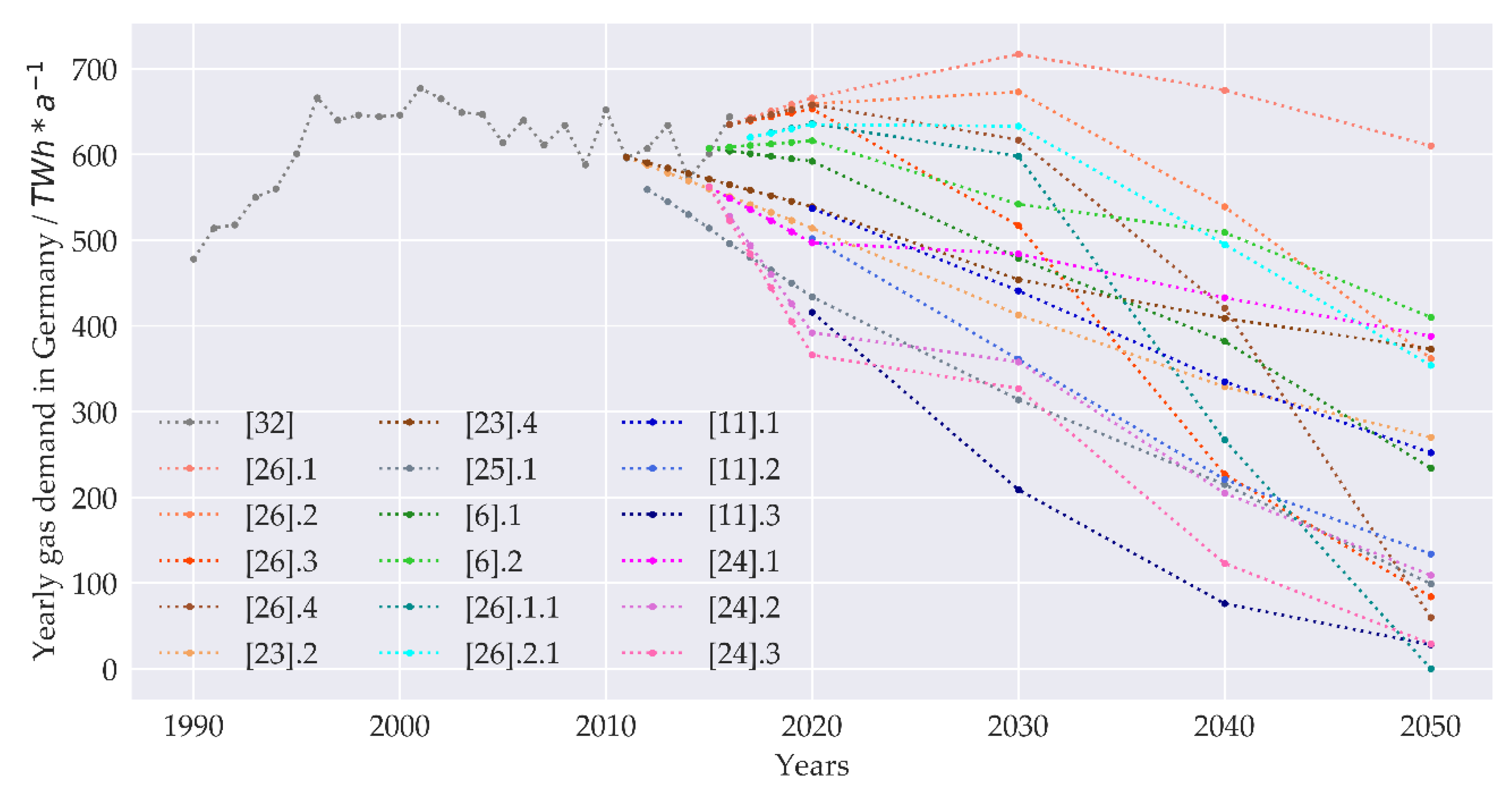
On a global scale, scenarios for future gas demand differ widely. While forecasts for China [16,17] or the USA [12,13,14,15] often predict an increase in gas demand over the next few years, many studies for European countries forecast a stagnation or decline. This also depends on the predicted technology development path: British and Irish publications in particular expect carbon capture technologies, hydrogen and bio-methane to be used to decarbonize the energy system while retaining gas grids [5,19,20,21,22]. Studies from Germany [6,11,23,24,25,26,27,28,29] or northern European countries [4,5], on the other hand, predict a decline in natural gas demand due to efficiency measures and electrification of the heating systems. In the long term, there could be two extreme transformation paths [14], either based on usage of synthetic gases, in which case the predicted demand fluctuates from a slight drop to an increase, or on an “all-electric” trend making the gas infrastructure obsolete.
In our paper, we will focus on the situation in Germany, where reduction targets for CO2 emissions are set to −55% in 2030 and −80% to −95% in 2050 compared to the values of 1990 [30,31]. The government emphasizes that the achievement of this goal should be “technology-neutral” and “open to innovation” [18,31]. Like other European studies, the German ones span the two extreme scenarios described above (Figure 1).
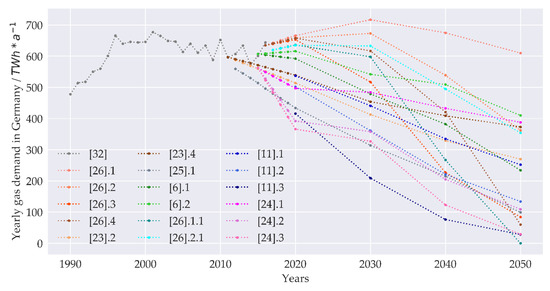
Figure 1.
Measured and predicted values of gas consumption for Germany in selected studies (Numbers: [cited source].scenario; linearly interpolated between projected years).
The trade, commerce and service (TCS) sector consumes 18% of natural gas in Germany, 41% go to the residential, 40% to the industry and 0.13% to the mobility sector [32]. While industry customers are mostly connected to high or medium pressure gas grids, TCS and residential clients are attached to medium or low-pressure distribution grids [18]. Gas mainly provides heating, especially storage heating and domestic hot water generation systems, which are currently used in more than 50% of buildings [9]. Typically, users decide for or against gas powered heating during a replacement of the heating system, often in combination with a renovation of the building envelope.
2.2. Investment Decisions in Building Sector and Their Influence on Grid Economics
The decreasing gas demand stems from a switch in investment decisions in building sector away from gas-bound technologies. When choosing modernization measures in buildings, individual owners decide based on renovation, operation and energy costs as well as building properties and available grid infrastructure [33,34]. The choice of optimal renovation measures in buildings has been the topic of several studies, which analyze building parts and perform optimization in terms of energy demand, costs or comfort issues [35,36,37]. Many approaches have multiple objectives, such as optimizing the building envelope and choosing the heating system in a holistic approach [35,38]. Studies usually calculate the annual energy demand based on individual building and usage characteristics and optimize the costs for a certain planning horizon. Since costs include the complete expenditures for energy related operation and maintenance, as well as for the building envelope and energy systems, owner decisions are based on available technologies, regulation and the energy market conditions.
R. Streblow et al. (2017) [38] compare CO2- and cost-optimized modernization measures for building envelope and heating between natural gas-based systems and electrical ones. They predict that gas-based solutions are more sensitive to fluctuations in energy procurement costs than electrical solutions based on heat pumps. From the perspective of the DNO, with a declining demand for natural gas, the profitability of the gas grid tends to decrease. Dependent on grid age, topology and load density as well as the DNO strategy, this might lead to rising grid charges [18], which can in turn influence building owner decisions against gas powered heating systems—a self-reinforcing effect.
2.3. Effects of Grid Structure and Asset Composition on Defection Scenarios
Grid costs do not only scale with the amount of transmitted energy, but even more with the length and age of the distribution grid [18,39]. This is the basis for strategic planning methods for natural gas grids, which focus on long term planning with the aim of finding cost optimal grid structures for given scenarios [40,41,42]. Very detailed work has been published on the planning of gas transmission [43,44,45,46,47] and distribution networks, with a focus on uncertainties [48] or the interconnection and energy conversion between the power and gas sectors [49,50,51]. These approaches mainly cover the construction, expansion and restructuring of existing network structures and often focus on building up a synthetic gas infrastructure based on bio-methane and hydrogen in combination with carbon capturing technologies. However, there is a lack in literature of how to deal with grid defection or a decreasing gas demand in natural gas grid planning.
While the relationship between grid length and supplied energy is currently often modeled as linear [18,39], studies about network connectivity postulate a non-linear dependency between network length and the number of connected users [52,53,54]. Depending on the connection structure of a network, a decreasing number of users can increase the network length per user needed to connect all participants. Several authors [52,53,54,55] have described the relationship between optimal network length and amount of nodes with a power law approach, where the exponent k differs with the disorder of the network. We will test this hypothesis on real distribution grid structures and calculate the effect this has on the resulting grid charges for the remaining customers. In addition to that, we will examine whether structural grid parameters allow a prediction on how problematic the effects of grid defection are.
2.4. Economic Factors of Operating a Natural Gas Infrastructure
Decreasing gas demand and the obligation to continue the operation of gas grids can lead to an increase of grid charges. Several works examine the future of natural gas grids on a macroscopic level, using top-down approaches without taking into account the costs of operating the network infrastructure [21,22,56]. Only [19] analyzes the costs for grid operation of distribution networks for several scenarios with a decreasing demand based on the quantitative structure of all grids in Ireland.
Grid charges as part of customer’s energy procurement costs are usually directly dependent on the DNO’s operating costs. In most countries, DNOs operate under public regulation with the goal of a secure, cost-efficient and stable grid operation [39,57]. In Germany, and in the most European countries, electricity and gas supply is vertically unbundled, which means that energy distribution networks will be operated separately from other parts of the value chain [57]. In this way, they are subject to a natural monopoly [58]. In the interest of maximizing welfare on a macroeconomic scale, optimum grid charges should correspond to marginal costs, where the sum of the revenues equals the grid costs. In reality, there is a risk for the network operator depending on the willingness of the grid users to pay. This risk requires the introduction of a return on equity that increases the network costs depending on the capital employed [59]. This is where regulation comes into play: Most regulatory approaches worldwide are based on one of the four basic models, the “cost-plus”, “rate-of-return”, “price-cap” or “revenue-cap” method, which are often supplemented by an incentive regulation to guarantee a cost-efficient and stable supply [59,60]. Table 1 gives an overview of the use of the different methods for several European countries.

Table 1.
Regulation mechanisms in different European countries [61].
The German regulatory regime basically follows the “revenue-cap” approach [62], whereby the DNO is granted a fixed interest rate on the capital required for operation. A government agency monitors the DNO and regulates it via a bonus-malus system. To reduce over-investment, the agency approves the revenue cap on the basis of supply efficiency and quality, which is finally passed on to the customer in the form of network charges depending on the grid usage of each customer [63]. Since the type and structure of the regulatory regimes of the individual countries differ in detail [61], we choose a simplified approach based on the “revenue-cap” method that is applicable to regulated as well as unregulated environments. Therefore, we add up the annual costs, considering network and demand-specific conditions. Depending on the DNO’s strategy, we limit the annual revenue cap via boundary conditions in three ways:
- “stable revenue cap”, an approach in which the DNO tries to keep the absolute revenue cap constant,
- “stable grid value”, an approach in which the revenue cap is constraint by a stable grid age, and
- “stable grid charges”, an approach in which the DNO tries to keep grid charges at a constant level.
Table 2 shows the cost components of the yearly revenue cap [18,19,64]. Costs that are part of the capital expenditure (CAPEX) have to be determined for every grid asset, so they scale with grid length as well as with asset age. Operational costs are also modeled as dependent on grid length, while the other operational expenditure (OPEX) components loss costs, upstream grid costs and concession fees are based on supplied energy.

Table 2.
Cost components of DNO’s revenue cap and their dependencies.
2.5. Different Strategies for Grid Operation
Under the regulatory regime, the DNO has limited options to maximize his return on equity since revenues are directly constrained by the costs. We concentrate on the aspect of grid planning: As measures, the grid operator can renew, operate or close each line in every year of the planning horizon. According to current German law, the DNO has to supply all customers non-discriminatorily until their exit from the grid [57], and can only close a line when no grid user is connected anymore.
By choosing when and where to invest, the DNO can follow various paths: Renewing and expanding the grid assets at a high rate would lead to a growing investment capital, resulting in a higher CAPEX value and grid charges, while a low rate would lead to a loss in capital but keep grid charges low. Among the strategies possible for dealing with a decrease in demand in a regulated system, we focus on three strategies [39,63,65]: Firstly the DNO can try to preserve his business model by stabilizing the yearly revenues; secondly, he can attempt to maintain a high grid value, by stabilizing grid age to ensure a reliable supply; thirdly, he can try to keep grid charges low to guarantee a cheap supply. In this paper, we examine the interdependence of these aspects based on an analysis of 57 urban and suburban natural gas grid areas in the German city Bamberg.
3. Data and Methods
3.1. Gas Grid Data and Software Tools
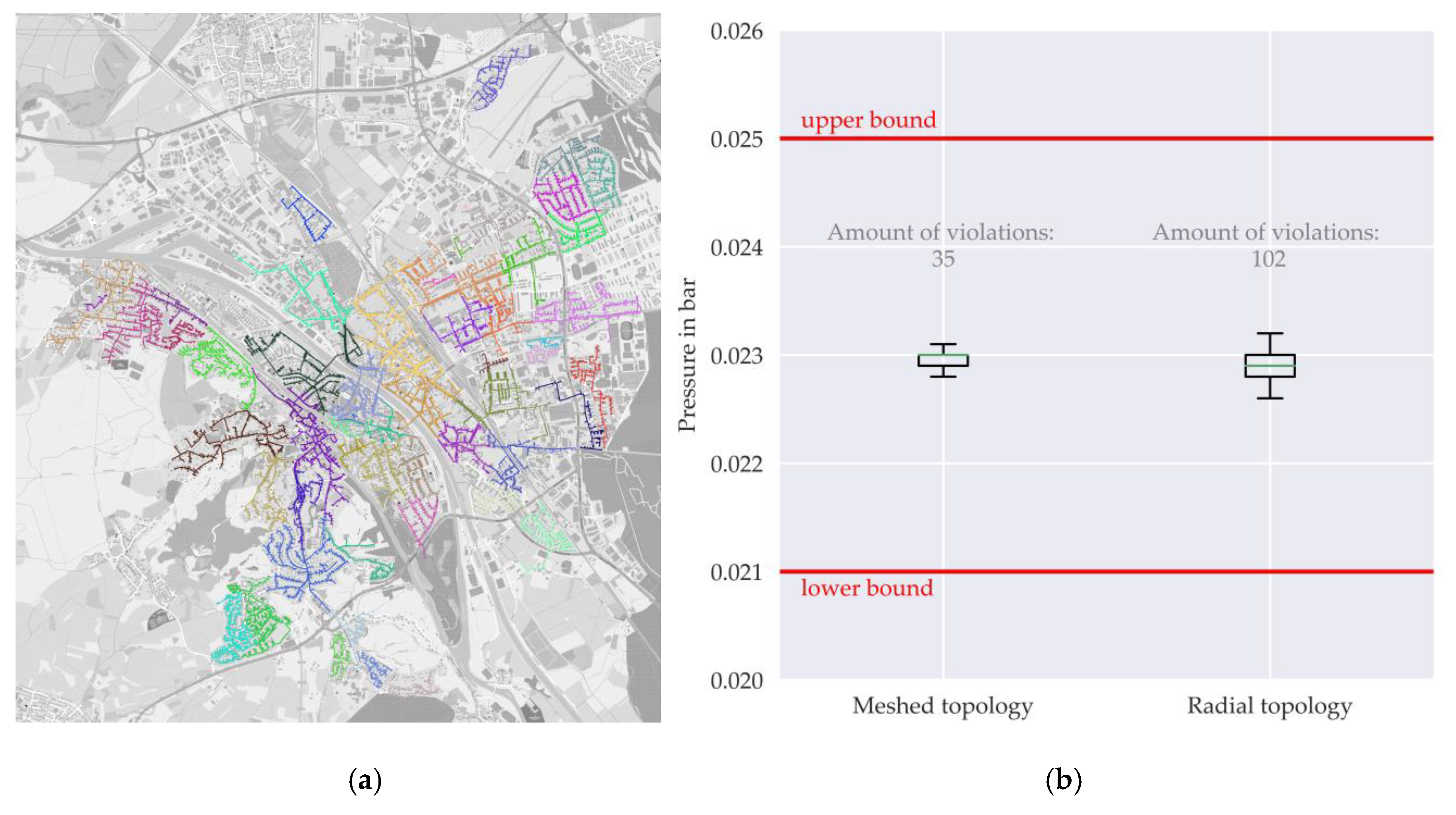
We base our evaluations on real gas grid data from the southern German city of Bamberg provided by the city’s DNO (Figure 2a). Bamberg has a high amount of customers using gas, with 85% of all buildings in the central city connected to the natural gas grid, of which approx. 90% use gas for space heating. The gas grid consists of a medium and a low-pressure stage operated in a meshed topology, with approx. 85% of all gas customers connected to the low-pressure stage. The total line length of the low-pressure grid is 258.6 km, which includes the house connection lines. The yearly gas demand of the 9118 grid users in the model is 351.9 GWh.
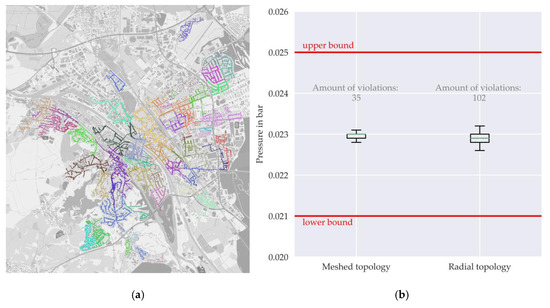
Figure 2.
(a) Separated radial grid areas [66]; (b) Pressure for all house connection points (n = 9118) in low-pressure stage for the original operated meshed topology and the radial topology (after demarcation of sub grid areas).
Data was provided by the city’s DNO as an excerpt from the geo-information system (grid line location, age and type information), internal asset database, and collected metering information of the individual grid users (energy consumption). The cost allocation sheet serves as the source for calculating the cost components of the revenue cap. The data was collected in 2018 for the financial year of 2017. All pressure loss calculations were performed with the commercial software STANET [67]. The other software-based models were created on a Python basis, using Pyomo [68,69] for optimization, NetWorkX [70] for graph analysis and the Scikit-learn [71] library for fitting. The commercial solver CPLEX [72] was used for optimization.
Before performing the structural network analysis, the low-pressure grid was divided into 57 subnetworks corresponding to the supply areas of pressure regulator stations by searching the shortest paths from every customer to each regulator station. The resulting 57 low-pressure grid areas are radial and represent the “initial grid length” (approx. 6% unnecessary lines). The process of demeshing the network was followed by a load flow calculation (load case corresponds to design case). Most of the connection points show a similar pressure level, where the number of violations is comparable for both network topologies (Figure 2b). For the subsequent structural analysis, the radial grid structure and line types of the sub-networks do not change: After a customer leaves the network, all lines that fall out of use are removed. With this approach, structural changes triggered by decreasing demand will only lead to decreases with regard to pressure losses and flow velocities in existing lines compared to the 100% case (Figure 2b). To verify this, pressure loss calculations were carried out for the 57 grids for a scenario of 0%, 25%, 50% and 75% customer decline (“random selection”, seed corresponds to the median of the 100 seeds from section Table 2).
3.2. Structural Network Analysis
3.2.1. Analysis of the Functional Relation between Grid Length and User Number
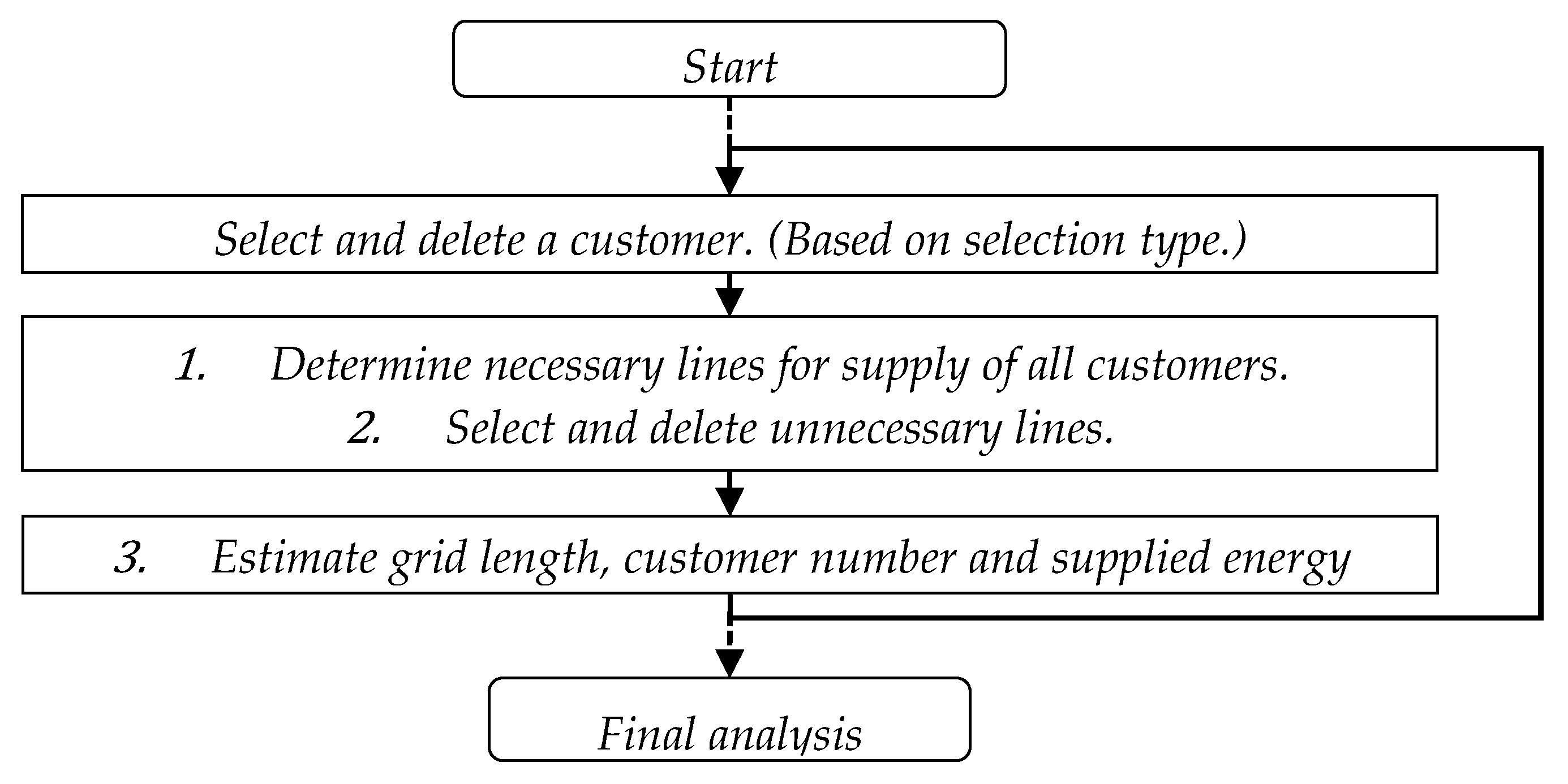
For all grids, the number of customers is scaled consecutively from 100% (current state) to zero. After the exit of each customer, a new grid structure results (Figure 3):
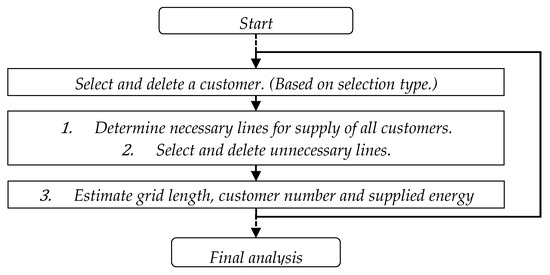
Figure 3.
Procedure for the determination of the grid length dependent on customer amount.
We explore several orders in which single customers leave the grid, which we call “selection types” (Table 3), based on principles of order theory [73]. Some selection types are deterministic (“Ranked selection”), while others are generated probabilistically (“Stochastic selection”) with 100 random distributions (seeds). Scenarios where users exit based on their distance to the station or their impact on grid length represent worst- or best-case scenarios. Others are stochastic or semi-stochastic selection types where users are chosen probabilistically from (in some cases weighted) distributions, based on building age or the starting point of procedure. These scenarios represent a range of realistic development paths and show the impact of local clustering of exits. While the “random selection” is used for cost analysis, all other types are only exploited within the structural analysis.

Table 3.
Selection types for user exits.
We fitted a power function (1) to the relationship of grid customers and resulting grid length , with the exponent k as a measure of the disorder of the network [52,53,54,55]. The best exponent of the power function was determined for every grid, selection type and seed by using a non-linear least squares approach [74]. Customer amount and grid length are stored for each run of the procedure of Figure 3. Before fitting, values are normalized to their initial values.
3.2.2. Correlation Analysis
As abstract measures for the classification of the grid structure, we use a broad selection of metrics and correlate these with the k values from the previous section. Correlation analyses are performed for each individual gas grid. The used parameters fall into four general classes:
- k values of Equation (1) (mean and standard deviation for “random selection”)
- Classical structural parameters [18,64]
- Path and length relations of the simplified graph [54]
- Graph theoretical metrics [75,76,77]
3.3. Cash Flow Analysis
3.3.1. Economic Parameters and Principles
Due to the transferability, we use a simplified approach that is based on the “revenue-cap” method from Section 2.4 used in most of the European countries [61] and Germany, respectively. The cost components are modeled directly depend on the length and age of the grid and the energy supplied (see Table 2). The starting point for the calculation represents the relative shares of cost components in 2017 (see Table 2). The revenue cap of the DNO in base year 2017 is about 10 M€. Since the model only includes the low-pressure stage of the grid, the medium pressure level will be considered in the cost parameter , which represents the upstream grid charges. Other cost parameters are set to the relative shares of the DNO’s actual revenue cap (Table 2). Whereas the CAPEX in the optimization model is calculated based on the rest book value, length and historical investment expenditures of every single line based on the chosen measures, within the cash flow calculation it is determined by the average grid age and costs as well as cumulated grid length.
The operational costs are modeled as a linear function of the grid length, whereas all other operational expenditures (OPEX) are depend on the supplied energy. Grid charges are modeled as energy related costs in directly derived from the revenue cap. Possible strategy patterns of the DNO regarding the allocation of grid charges on customer groups (e.g., trade, commercial, residential) are not considered. For detailed structural parameters of the sub grids see Appendix A and Table A4 in Appendix B.
3.3.2. Optimization Model
The renewal, operation and closure measures of lines will be selected to maximize the absolute return on equity over the planning horizon from 2018 to 2050. As the equity interest rate is a constant parameter over the planning horizon, the cumulative net book value is maximized. To avoid over-investment, a constraint is modeled for each DNO strategy to limit the investment budget. Since the optimization is just used to validate the cash flow calculation model, only one DNO strategy “stable grid value” is implemented, where the length dependent average mean age of the lines is limited to its initial value. Additional constraints for the measures are:
- Only one renewal per line allowed within the planning horizon.
- Lines have to stay in operation as long as customers are connected [57].
- Lines have to be closed if no customer is connected anymore.
Each line is modeled separately with its book value factor , length and historical investment expenditures . The relation between customers 𝒿 and lines ℓ are considered within a status matrix . The resulting optimization problem is to schedule the measures optimally within the planning horizon provided by the scenario. For a detailed description of the model, see Appendix A Table A2 and Appendix C.1. The optimization objective is to maximize the return on equity for every line under the fixed equity interest rate and equity amount for all lines under operation. Rest book value factor is a function of the binary decision variables for operation and renew as well as for closure of each line, see Appendix C.1.
Because of the regulatory regime, the DNO’s cumulated annual costs correspond to the revenues from grid charges, and form an upper bound:
The DNO strategy used in the optimization approach is to stabilize the length specific grid value. This forms an additional boundary: Since relative grid value depends on the grid age, this annual value, expressed by the length-dependent weighted average age for all operating lines, is not allowed to fall beneath its initial value.
3.3.3. Simplified Cash Flow Calculation
By only considering the cumulated rest book value and grid length of all lines or assets under operation when determining the capital expenditure, the optimization problem is transferred into a calculation model. The mean rest book value factor aggregates book values for the whole grid area based on (4):
By multiplying the mean rest book value factor with the average historical length specific costs and the current grid length based on a grid-specific power law function (1), it is possible to determine the capital expenditures (for the detailed formulation, see Appendix C.2):
The operational expenditures are a function of the grid length and the supplied energy:
Dependent on the DNO strategy, the mean book value factor or the grid charges are the variable. The mean book value factor is restricted to values between zero and one. In the simplified approach, we model three different DNO strategies:
- Stable grid charges: The grid charges are set to their initial value and is calculated, until its value reaches 0. After that, grid charges are a function of the yearly OPEX and supplied energy.
- Stable grid value: The mean rest book value factor is set to its initial value and the revenue cap is calculated.
- Stable revenue cap: The revenue cap is set to its initial value and the mean rest book value factor is calculated until its value reaches 1. After that, the revenue cap is a function of the yearly costs.
4. Results
4.1. Verification of Pressure Losses in the Distribution Grids
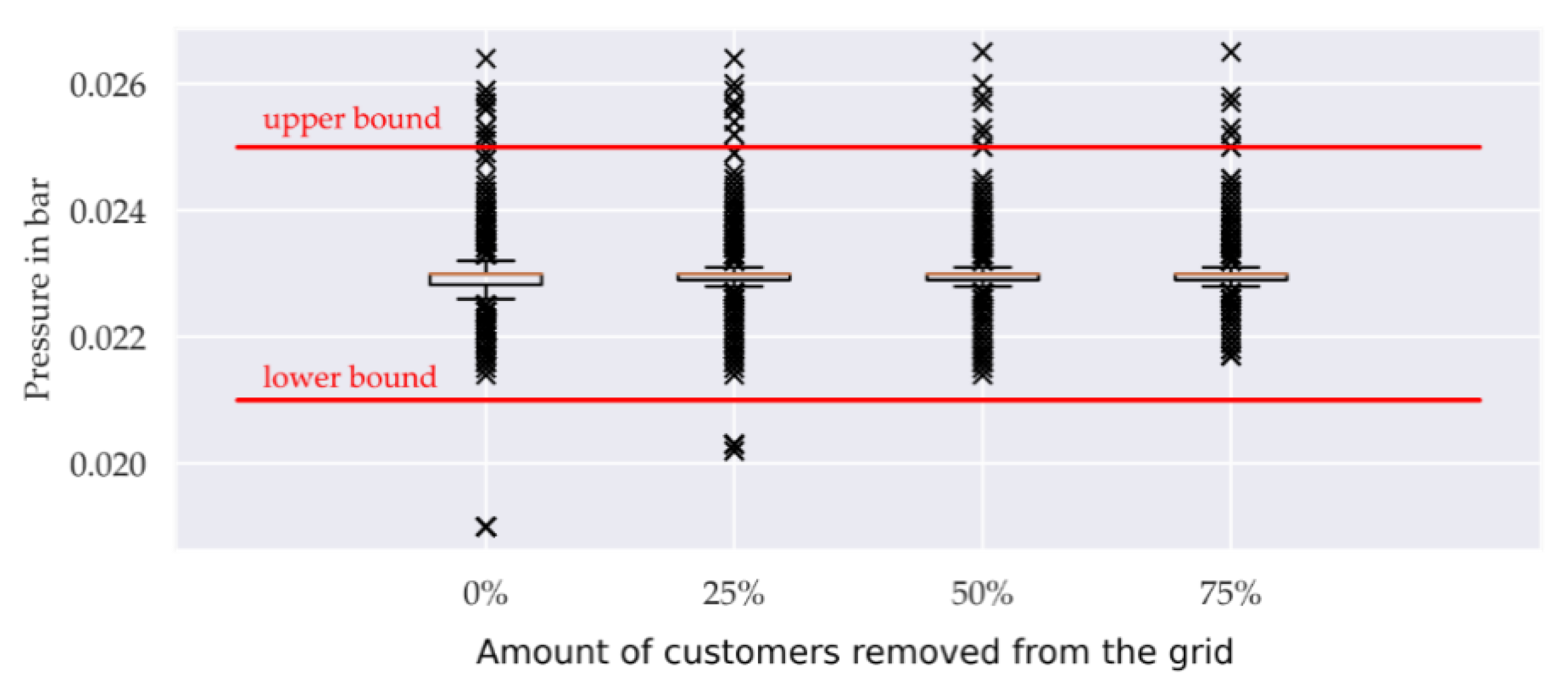
The amount of house connection points with a pressure level below 23 mbar decreases with the number of customers leaving the grid (Figure 4): 48.1% when no customer has left the grid, 43.5% for one quarter, 37.5% for one half and 30.1% for three quarter. The number of pressure violations decreases with the number of customers leaving the grid. When customers leave the grid, the gas demand decreases, thus reducing pressure losses in the radially operated network [78]. Since the grid is deconstructed from the customer to the substation in reality, successive subtrees are removed from the existing radial structure until the last user leaves the grid. The topology of each subtree remains the same during this process.
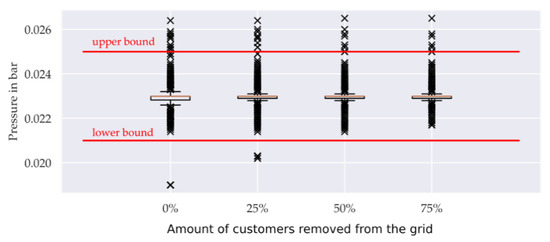
Figure 4.
Pressure of all house connection points for the median of the 100 scenarios of “random selection” for all 57 grids dependent on the number of customers leaving the grid from 0 up to 75%.
4.2. Structural Analysis
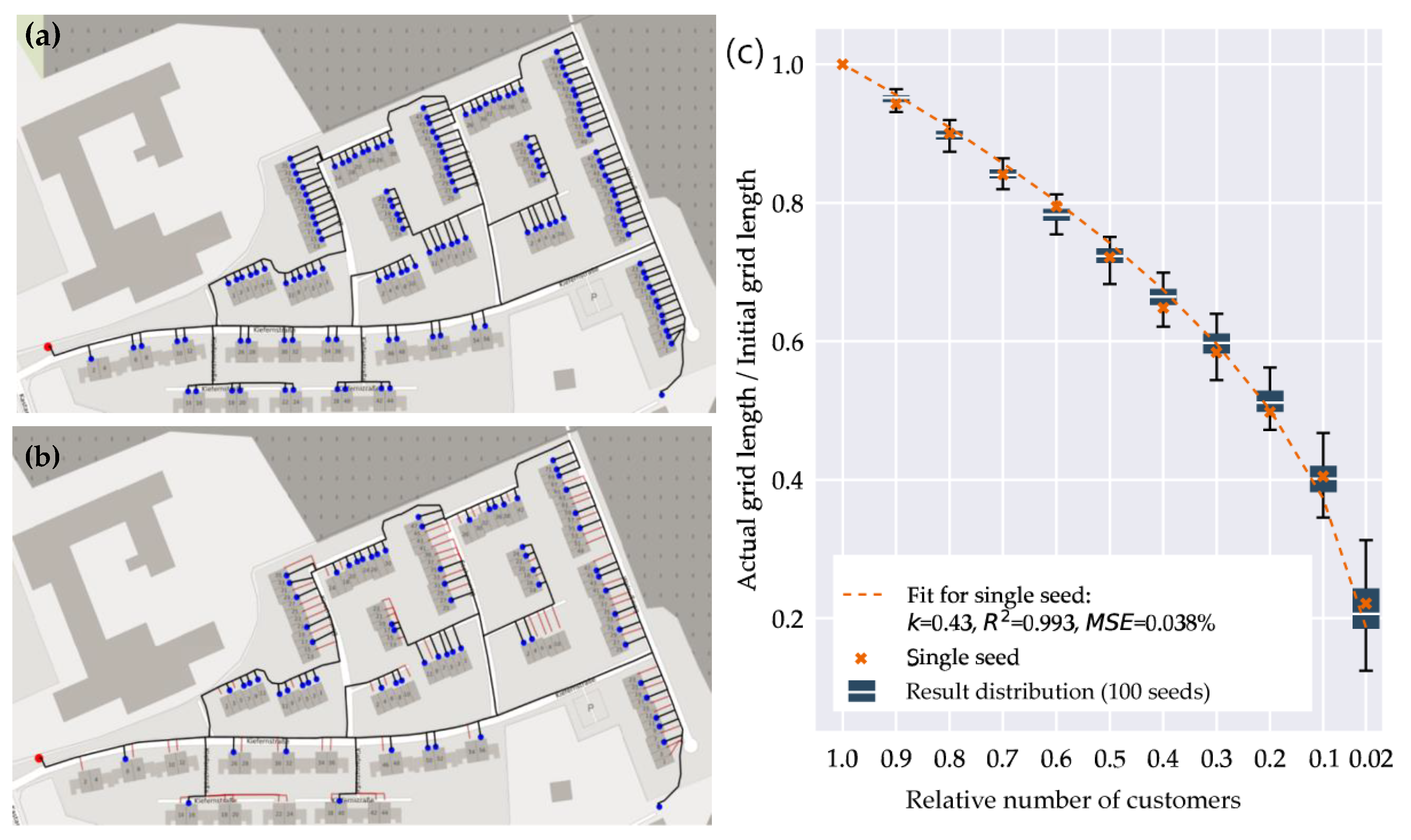
Figure 5a shows the exemplary grid area 18, (total line length: 3.21 km, 148 grid users, annual gas demand: 1.64 GWh, mean grid asset age: 17.0 years). For this grid, line length declines slower than the number of customers: After 50% of the grid users exit the network (“Random selection”), 71% of the grid is still in operation (Figure 5b). This trend is stable for different random seeds and can be well fitted with a power law function (Figure 5c).
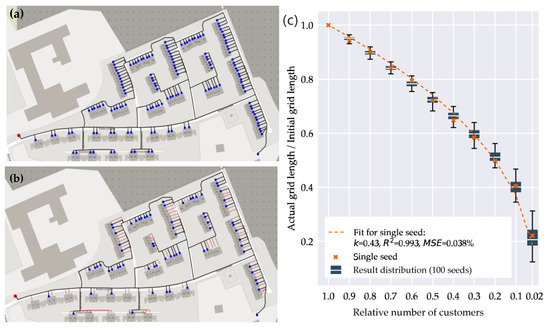
Figure 5.
Required grid length for declining customer numbers in a low-pressure gas grid. (a) Network structure of grid area 18 on the top with all customers, (b) with 50% of costumers (exemplary random selection, resulting grid length: 71%, background map in [66]). Blue dots: active customers, black lines: active lines, red: inactive lines, red dot: pressure regulator station. (c) Distribution of grid length for 100 random exit patterns (“Actual grid length” corresponds to black lines in (b), “Initial grid length” corresponds to all lines in B, Blue box: median and 25%/75% percentiles, whiskers: +/-1.5 IQD, red crosses: values for an example distribution, red dotted line: power law fit to example data).
The resulting k value (0.43 in the example) describes a deviation from a linear relationship of grid length and customer number: With a low k value, the DNO needs to maintain a proportionally large grid infrastructure in face of a decline in gas demand. The variance in k value between random seeds (Figure 5c) shows a sensitivity of grid length (and therefore grid costs) to different exit patterns (with “random selection” in Table 3).
To analyze the impact of different selection types of user exits on grid length, we calculated grid lengths for a wide range of possible distributions (Table 3) and determined the resulting exponent k (as either single or mean values). Basically, there are two different ranges of k:
- k < 1: The decrease of grid length is slower than the decrease of customer number .
- k > 1: The decrease of grid length is faster than the decrease of customer number .
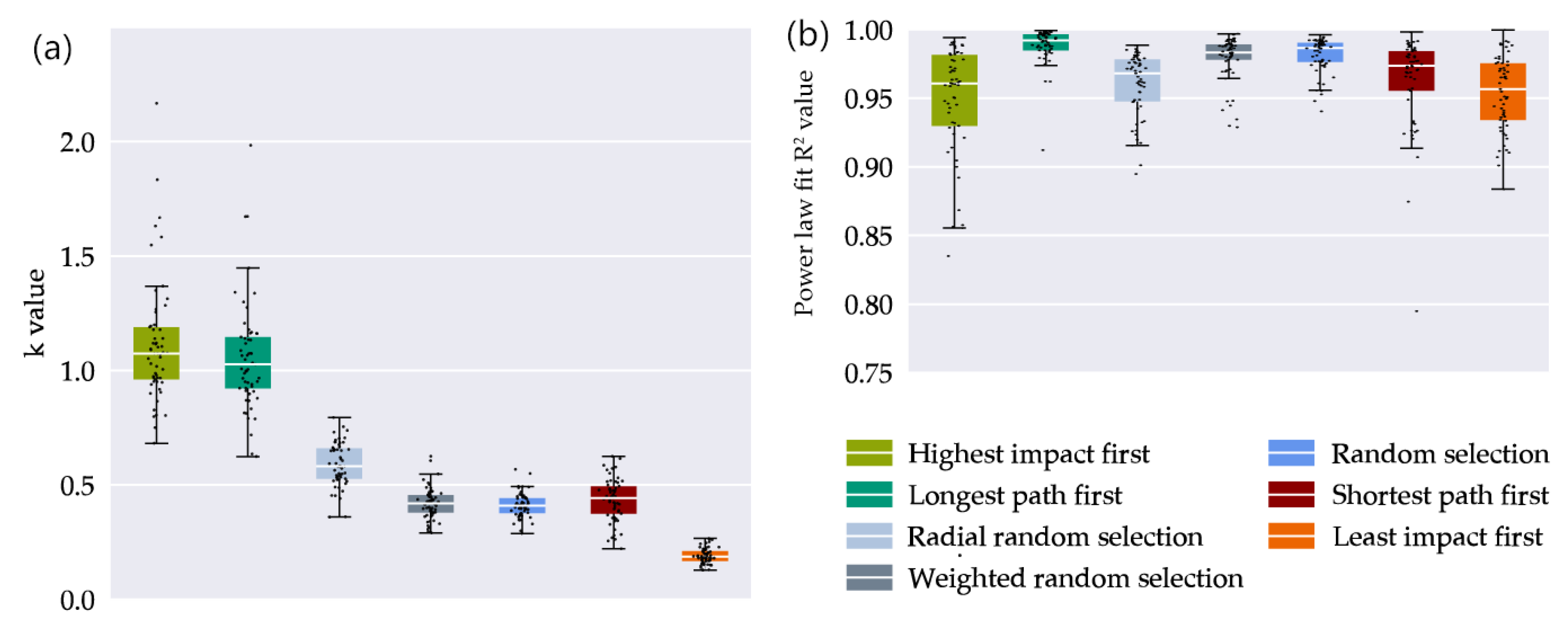
Figure 6a shows that while the “best-case” selections of highest impact and longest path first lead to k values close to and sometimes above 1, worst-case scenarios lead to a highly nonlinear relationship with k values around 0.2. In “weighted random selection” and the “radial random selection”, customers exit the grid in clusters. This increases the probability for the closure of entire grid sections, resulting in higher k values compared to “random selection” type. Fit quality is good (R2 values > 0.9, see Figure 6b) and generally rises with the amount of customers, with single outliers for small grid areas with less than 50 customers.
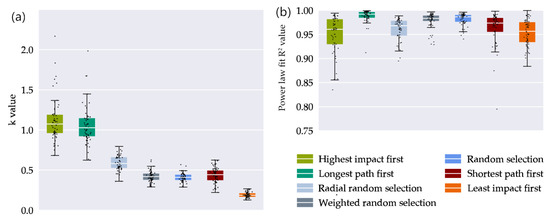
Figure 6.
(a) Dots: for ranked and for stochastic selection types of Table 2 for each of 57 grids with different selection types of user exits. (b) for ranked and for stochastic selection types of Table 2 for each of 57 grids with different selection types of user exits. Boxes: Median and 25%/75% percentiles of the distribution. Whiskers: +/-1.5 IQD).
Typical values for random selection types are in the range of 0.4 to 0.5. This fits with general predictions from network theory, which calculate k values of 1.0 for ordered and 0.33 for maximally disordered networks [54]. k values below 1 also indicates a grid structure that is expensive to maintain during a decline in demand from the DNO point of view, while a large spread of k values for different selection types could indicate a heterogeneous grid infrastructure with a mix of favorable and unfavorable customers.
4.3. Correlation Analysis
Both mean k values and k value variability are markedly different for individual grids. How does this characteristic depend on grid structure, and are there general predictors for the risk?
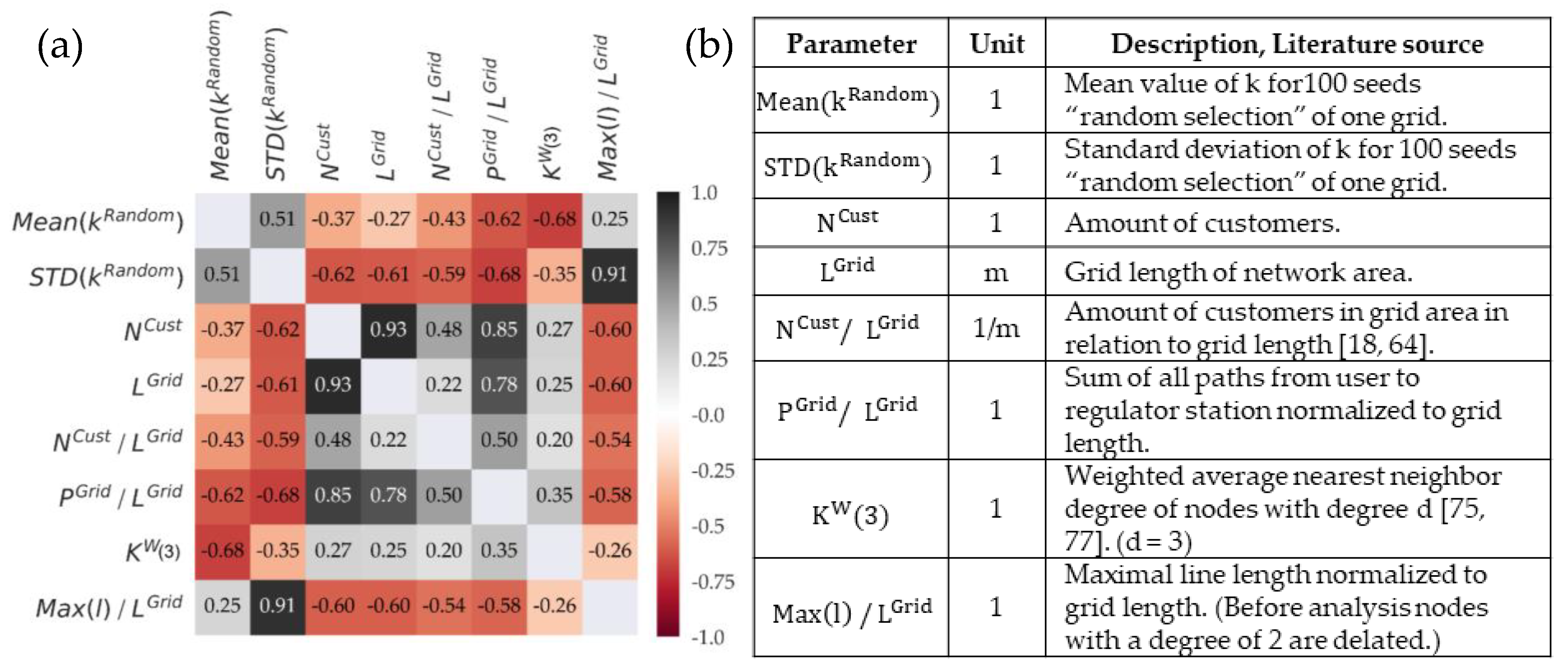
We examined a broad range of grid structure parameters (39) (see Table A3 in Appendix B) from our real grid data (57 grids) in a correlation analysis to examine their effect on k values (see Figure A1 in Appendix B). In following we discuss six selected parameters: three classical structural parameters (); and three with the strongest positive or negative correlation (, , ) with either or (Figure 7).
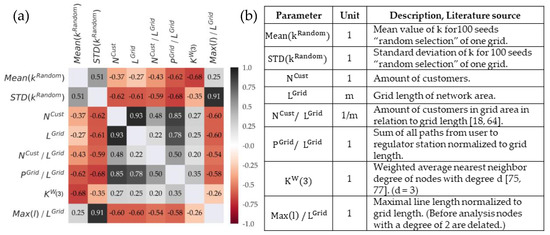
Figure 7.
(a) Correlation matrix; (b) Selected structural and graph theoretical parameters.
The “number of customers” and “grid length” are both descriptors for grid size and, as such, highly correlated in our dataset. We use as a normalization factor for the following density parameters, while is used as a baseline value in our economic analyses for declining grid demand. Both parameters show a moderate negative correlation with and , which suggests that larger grids tend to a slower but more reliable decrease in grid length, when customers exits grid (Figure 8b).
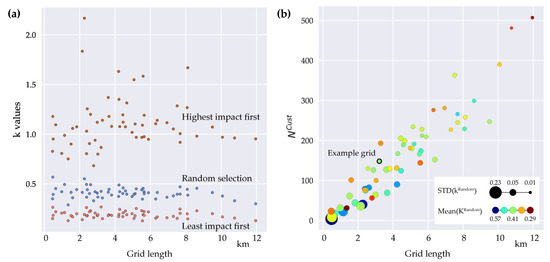
Figure 8.
k values for different grid sizes. (a) of each grid for different grid lengths; (b) Grid length and customer amount for individual grid areas.
The parameter “customers per grid length” describes grid density; therefore, it is higher for urban areas. As described for size, denser grids tend to k values which are lower and less variable for different seeds of “random selection”.
Grid structure is not only dependent on size and density, but also on the branching pattern of lines, a parameter that is difficult to quantify. We examine two path relation measures, which are also used as a general measure of network disorder [54]. Before calculating these parameters, we deleted all nodes with a degree of two (i.e., nodes located in the middle of an unbranched line) and merged the connected line properties.
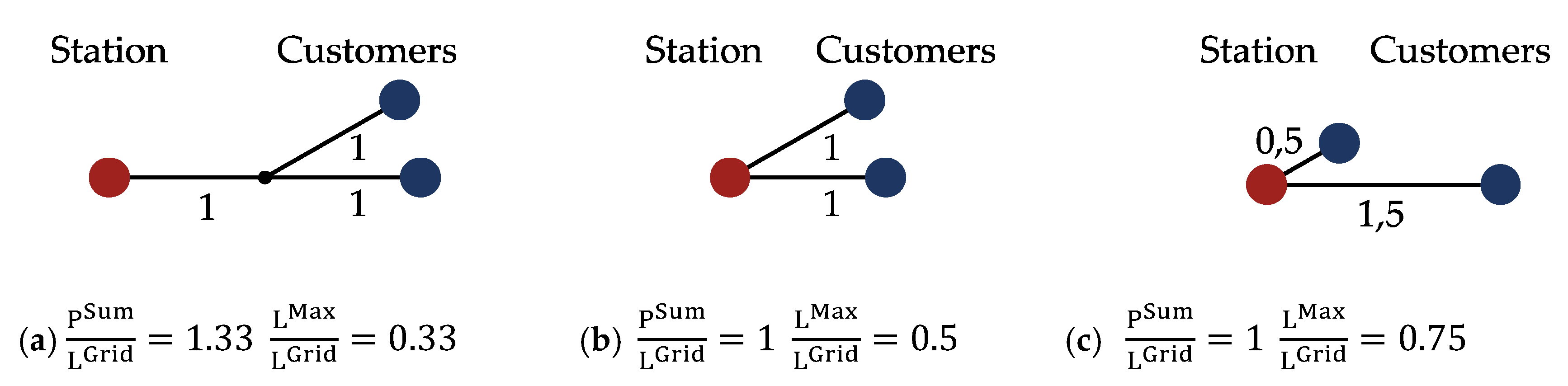
We use the “sum of all paths” , the cumulated line distance from each customer to the regulator station, normalized by grid length, as an indicator for the prevalence of shared assets. Since lines that route gas to more than one user contribute multiple times to cumulated path length, this descriptor is high for grids with a high number of customers connected to single lines (Figure 9). Even after normalization, a high number of shared assets strongly correlate with both, grid size and density in our dataset, which could indicate structural differences in grid planning. It is an even better predictor of lower k values than these parameters as expected, since shared lines have to stay in use until the last customer leaves.
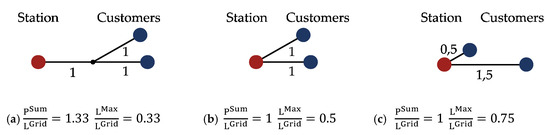
Figure 9.
Structural parameters for three simplified example grids. Numbers indicate line lengths.
After our removal of all degree 2 nodes, only nodes of degree 1 and 3 are left, the latter signifying branches in the grid structure (Figure 9a, black dot). The parameter , based on graph theory, describes the “weighted average degree” of nodes which are connected to these branching nodes. It is high in graphs with long and branching connection lines, and with multiple branches in sequence. The latter is also described as a measure of graph assortativity. High values are strongly correlated with low values of k, while showing only weak to moderate correlation with the other structural parameters.
The effect of single long grid lines on k can be seen in the “maximum relative line length” , which is most common in smaller, low-density grids. While the correlation with is only weak, long single lines lead to a high degree of randomness in how exit patterns shape grid lengths.
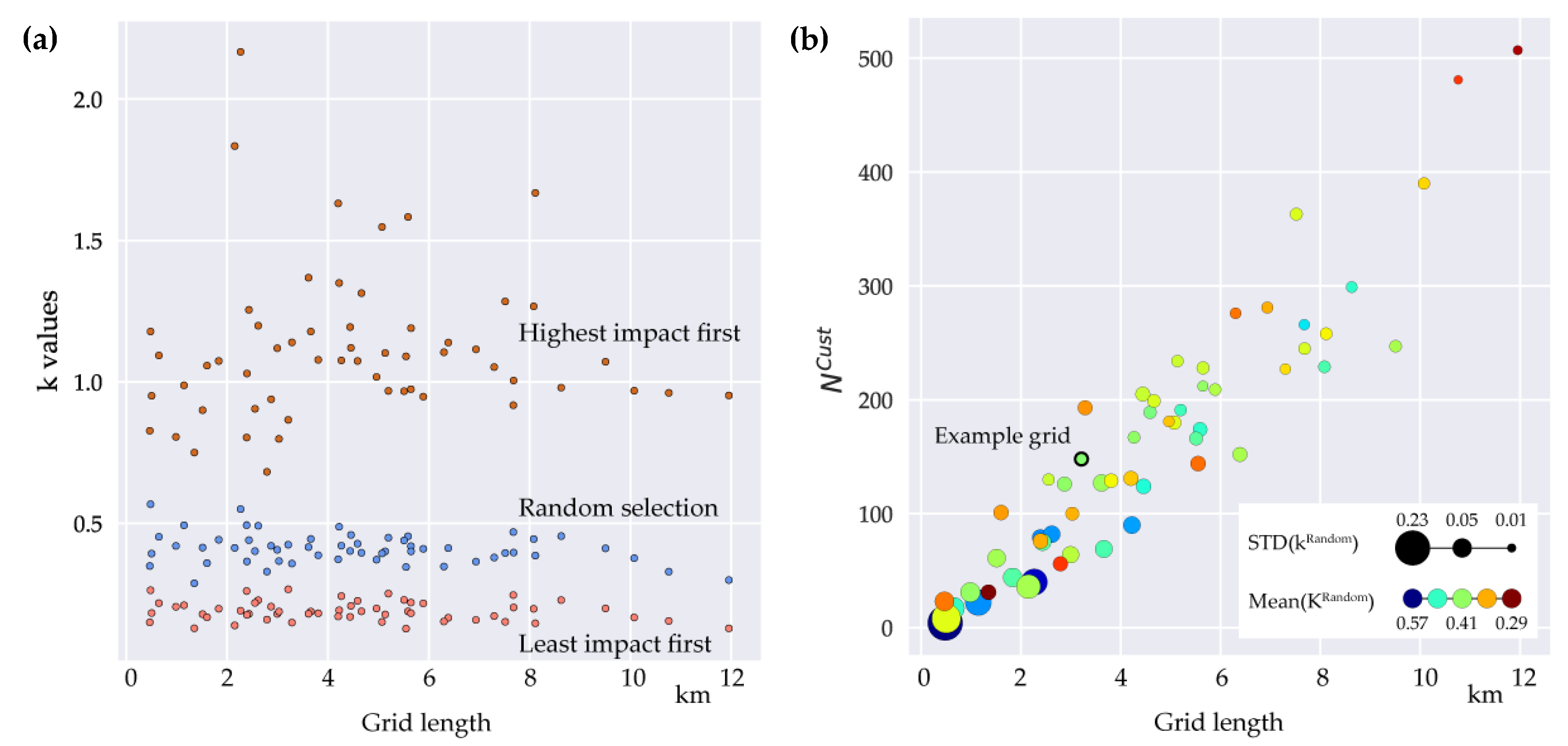
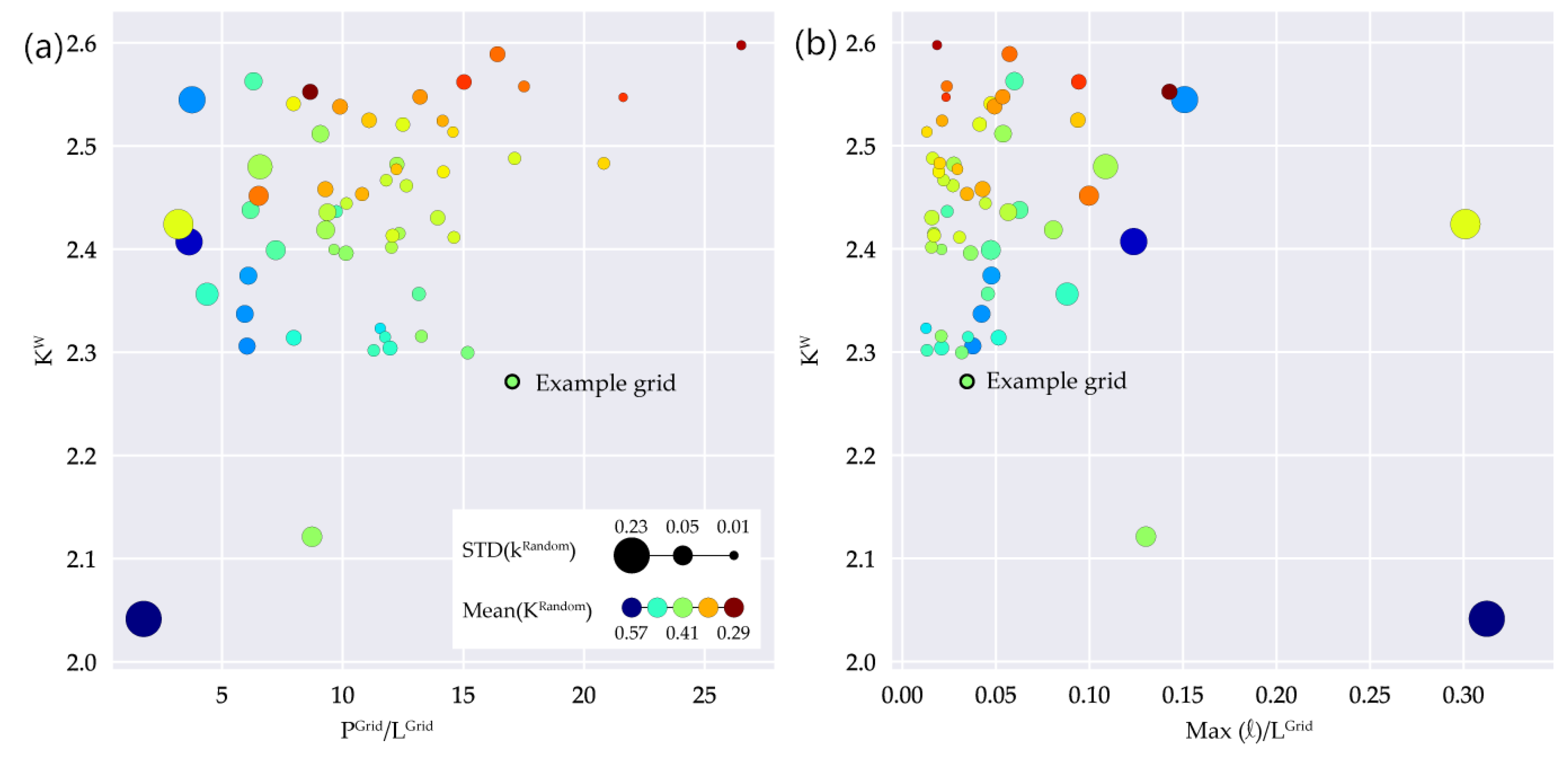
Figure 10 shows in detail how different structural parameters combine with mean and standard deviation of k in all single grids we examined. High values of are associated with high values of (Figure 10b), while low values of are correlated with high values of . The evaluation of these two parameters allows conclusions to be drawn on variance as well as the absolute value of k and thus on the risk of operating a disproportionately long network when customers leave the grid.
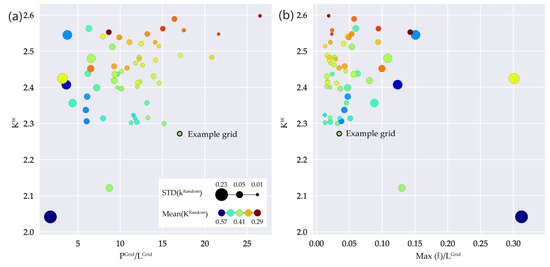
Figure 10.
k values for different structural parameters. (a) Weighted average nearest neighbor degree of nodes with degree 3 against sum of path lengths normalized to grid length; (b) Weighted average nearest neighbor degree of nodes with degree 3 against maximal line length normalized to grid length (Colors: , Sizes: ).
4.4. Cost Analysis
4.4.1. DNO Costs of Operating a Natural Gas Infrastructure
We see that grid structure has a strong influence on the network infrastructure needed to supply a declining number of customers. To quantify the economic consequences of this for a gas grid DNO, we use a complete linear decline in customers until 2050 as a scenario to the resulting costs for the example grid presented in Section 4.2. We model the DNO as an actor who can optimize his investment measures, i.e., when and where to renew individual gas lines, with the goal of achieving maximum revenues while still supplying all remaining customers. The DNO strategy we assume in this setting is to keep the average investment sum in grid assets constant. The normalization to line meters means that overall grid value still decreases in this scenario. The resulting investment plan influences only the CAPEX component of overall costs. For OPEX, operational costs depend on grid length, while the other OPEX components depend on the annually supplied energy (Table 2).
Figure 10 shows the resulting cost components for the optimized grid structure in each year as unhashed bars. Grid costs (and therefore the revenue cap) fall from 92.1k € to only about 60.5k € within 17 years, when 50% of all customers have already left the grid. Whereas the CAPEX drops from 38.0k € to 26.4k €, the decrease in OPEX is even higher, from 54.1k € to 34.1k €, where the operational cost drops about 29.5%, which raises the question of whether such a high reduction in operating expenses is possible in reality during this short period?
This full optimization for all lines and years provides detailed results, but is computationally demanding and not feasible for a high number of grids. In addition, it depends on access to a complete database of assets and their ages. We use the k values described in the previous section as base for a simplified model to estimate possible revenue cap and grid charge development paths for all our low-pressure grids.
4.4.2. Comparison of Optimization-Based and Simplified Cash Flow Calculations
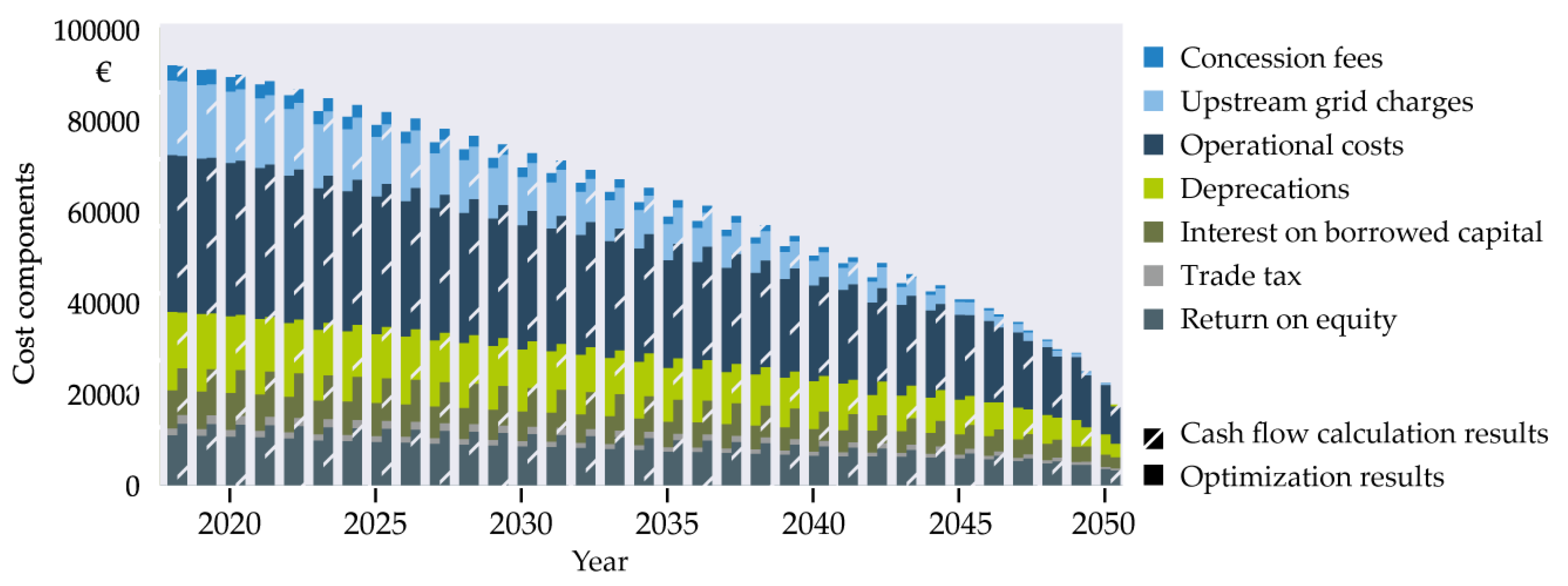
The hashed bars in Figure 11 show the results for the annual cost components calculated with the simplified approach.
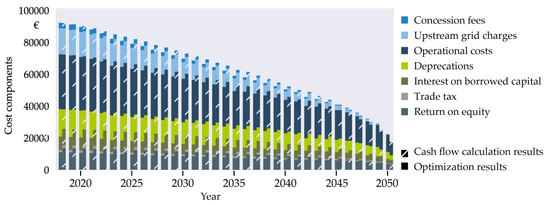
Figure 11.
Comparison of revenue caps for optimization (full) and simplified (hashed) cash flow calculation during declining gas demand in a single gas grid. Loss costs are modeled as 0. (Grid: #18, DNO strategy: constant grid value, selection type: random selection (mean k value), global scenario: linear decrease of gas demand 2018–2050).
Grid charges are calculated based on the revenue cap and energy demand. Like in the optimization model, the energy-based OPEX components are calculated directly, while the grid length for operational costs is determined with the power law relationship (1). CAPEX is also based on grid length and total grid value in this approach. Instead of cumulating all individual asset book values, we use a conversion factor derived from the mean asset age in the grid. This simplification resulted in speed increase by a factor of ~1000 in our calculations compared to the optimization approach. To emulate the “stable grid value” strategy, we use a fixed cumulated book value factor. The specific historical acquisition costs are used to calibrate the simplified cash flow model for the base year on the shares of the revenue cap of the real DNO.
The resulting total costs as well as the OPEX match the optimization results well. Since depreciations are modelled as a function of the cumulated residual book value in each year, we underestimate these costs, while modelling them based on the initial cumulated rest book value would overestimate them. Due to the fact that all other parts of the CAPEX are overestimated, we choose the first approach. For a comparison of the grid charges see Figure A2 in Appendix C.
4.4.3. Cash Flow Analysis for All 57 Grid Areas
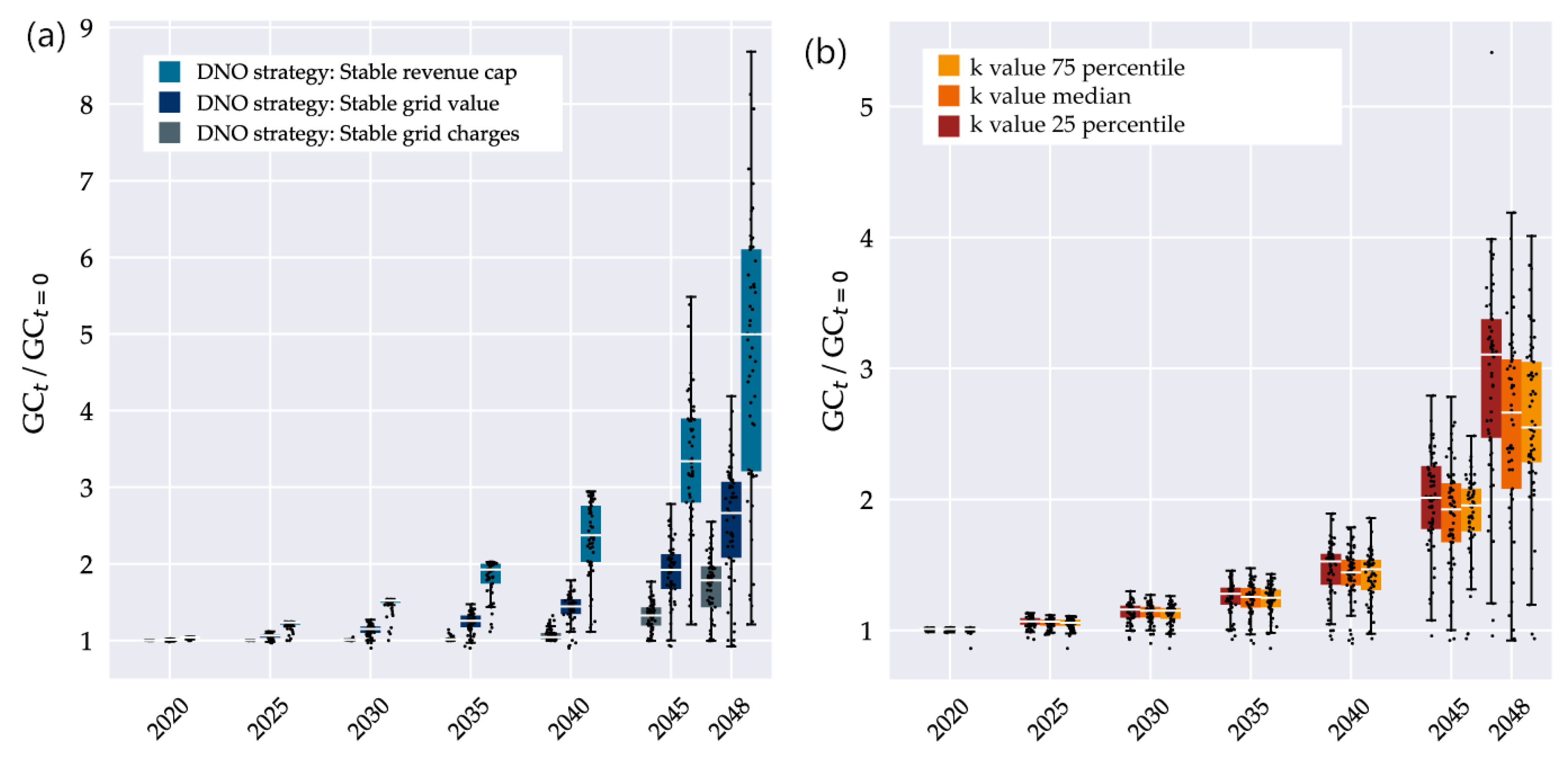
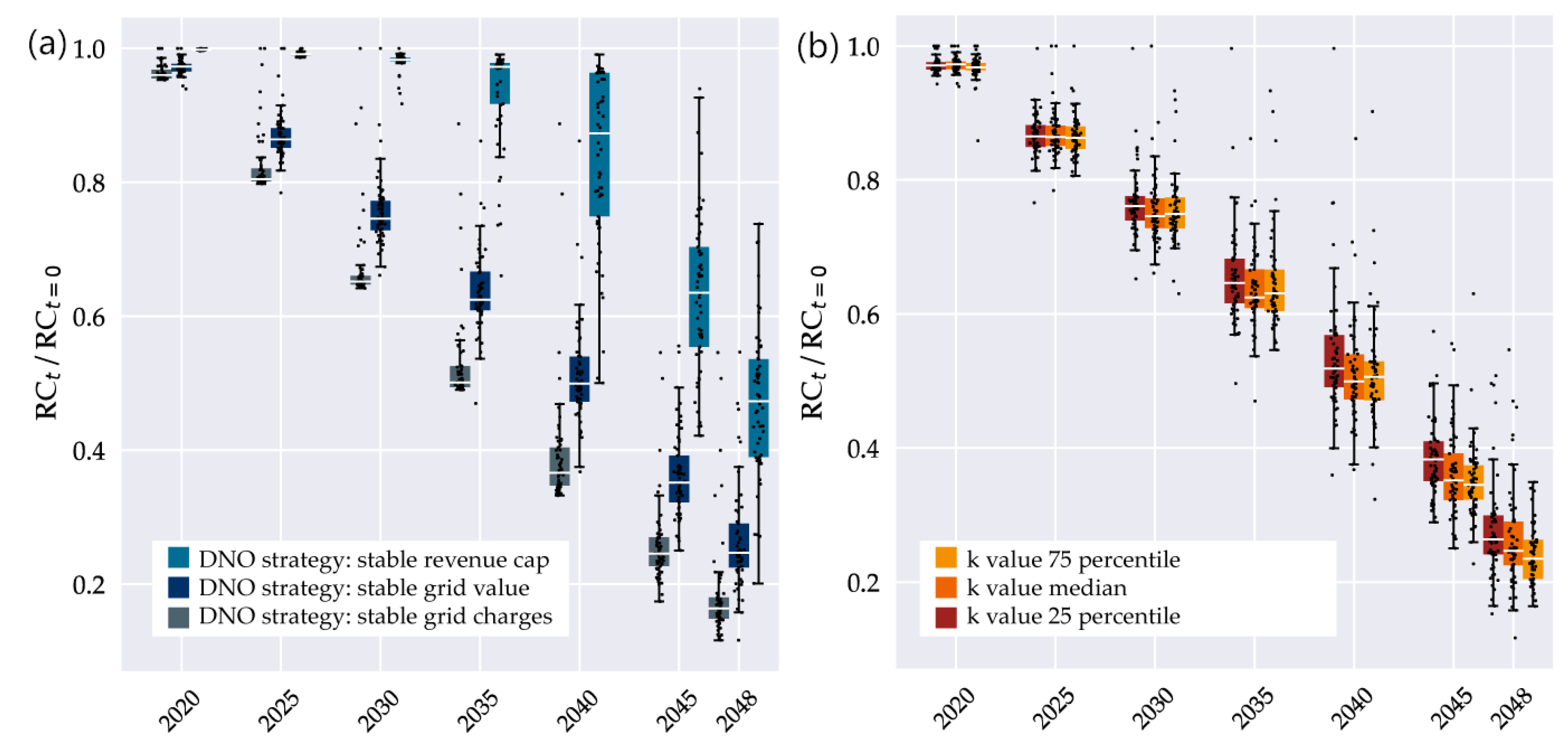
The simplified calculation allows a broad examination of how different DNO strategies and grid structures affect the economic results of declining gas demands. To investigate the impact of different DNO strategies, we used median k values as above and set either grid charges per customer (“stable grid charges”), book value conversion factor (“stable grid value”) or total costs to constant (“stable revenue cap”). To simulate different exit distributions, we applied the DNO strategy “stable grid value”, and used the 25, 50 and 75% percentile of grid specific k values of the 100 seeds of “random selection”. Figure 12 shows the resulting grid charges for all individual grids.
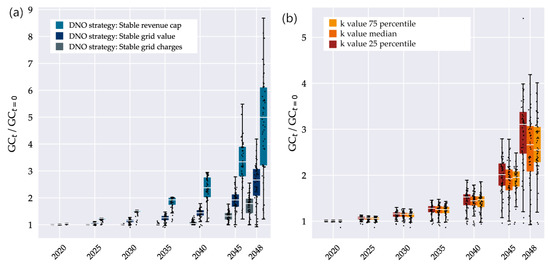
Figure 12.
(a) Grid charge development for individual grids at different DNO strategies with median k values. (b) Grid charge development for individual grids at different k values for the DNO strategy “stable grid value” (percentiles of random selection k values, 100 seeds). Dots: individual grids, boxes: median and 25%/75% percentiles of the resulting distribution, whiskers: +/-1.5 IQD.
Since grid length decreases slower than the number of grid users, grid charges rise for all different DNO strategies, but with a large spread among strategies and individual grids. When comparing different DNO strategies, grid charges remain below 200% over a long period until 2035, when gas demand decreases by 55% (Figure 12a). After 2040, GCs rise sharply, to between 140% in “stable grid charges” and 350% in “stable revenue cap” strategy in year 2045. “The stable grid charge” strategy, which represents a lower bound of the possible GC development, cannot keep GCs stable but at least successfully limits their rise.
A comparison of exit patterns, modeled by a variation in k values, leads to a much smaller spread in grid charges compared to differences between individual grids. As we have seen before, k values tend to be relatively stable for different random exit patterns in individual grids, so that the differences in grid charges are probably a result of structural parameters.
When looking at the total revenue cap (Figure 13), we see the same stronger dependency on DNO strategy than on exit distribution. The DNO strategy “stable revenue cap” is able to stabilize the RC until a drop in demand by 45% in 2035, while the other strategies lead to a drop between 35 to 50%. For different k-values, deviation between different exit distributions is small, and the spread between different grids is less pronounced than in the grid charges.
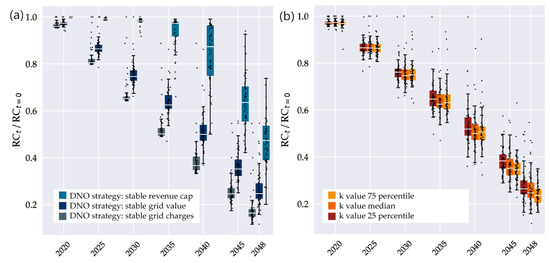
Figure 13.
(a) Revenue cap development for individual grids at different DNO strategies with median k values. (b) Revenue cap development for individual grids at different k values for the DNO strategy “stable grid value” (percentiles of random selection k values, 100 seeds). Dots: individual grids, boxes: median and 25%/75% percentiles of the resulting distribution, whiskers: +/-1.5 IQD.
The spread of grid charges among individual grids grows over time and is largest when there are few customers left. For the revenue cap, however, we see the highest amount on uncertainty for the earlier years that reaches a peak in 2040. This indicates that grid structure and strategy can lead to marked differences for the DNO’s business model already in earlier stages of grid defection.
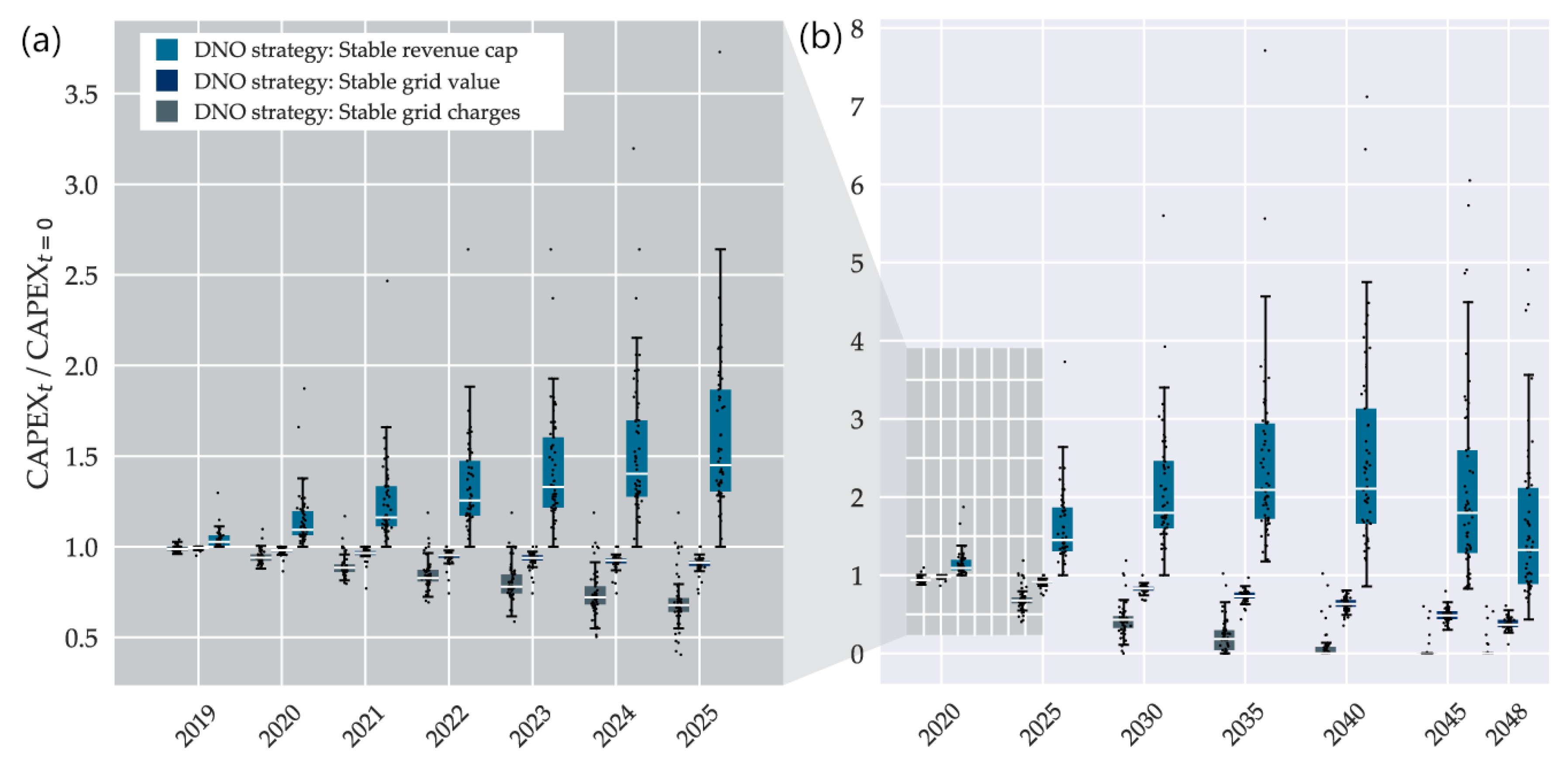
Development of capital expenditures dependent on DNO strategy (Figure 14):
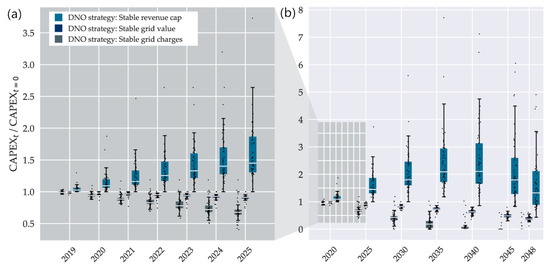
Figure 14.
CAPEX development for individual grids at different DNO strategies with median k values. (a) Selected years until 2025; (b) years until 2050. Dots: individual grids, boxes: median and 25%/75% percentiles of the resulting distribution, whiskers: +/-1.5 IQD.
Changes in CAPEX result from investments (renewals), annual deprecations and full deprecation in case of closure. While line replacement increases CAPEX, depreciation reduces them. The different DNO strategies lead to strongly diverging CAPEX values (Figure 14). While aiming for “stable grid charges” and “stable grid value” results in a fast or steady decrease in CAPEX, respectively, the “stable revenue cap” strategy first increase CAPEX by high investment into the grid, which then again falls when grid length shrinks strongly after 2040.
In this regard, our strategies “stable revenue cap” and “stable grid charges” represent extreme options of possible development paths. Grid operators in reality would probably generate an increase in RC with not only a higher CAPEX but also higher operational costs.
5. Discussion and Conclusions
5.1. Options, Risks and Conclusions for Distribution Network Operators
The complex system of interdependent actors and effects make detailed predictions difficult. For the cost analysis, different assumptions for the cost parameters were made. In the following, the three most influencing ones, the upstream grid charges, the operational cost and the costs of closure measures will be discussed.
The rise of grid charges in face of decreasing demand will probably affect all stages of the gas grid, not just the low-pressure stage described in this paper. This would lead to an increase in upstream grid charges, whereas we considered them to be constant. Assuming that the upstream grid charges increase at the same rate as the grid charges in our cost analysis, the revenue cap is raised by 10% in 2035 compared to the mean revenue cap of the cost analysis (mean value of the revenue cap of the 57 grids for the DNO Strategy “stable grid value”).
We also modeled operational costs just as a linear function of grid length, while it would be more realistic to treat them as step costs which also depend on grid age and supplied energy. If these remain at a stable level until 2035, the revenue ceiling is increased by 20% compared to the revenue cap of the cost analysis (same assumptions like above).
The costs of the closing, decommissioning and extraction of gas lines, which are often underground and not easy to access, are not modeled in this paper. For our DNO, the costs per closure measure are between 500–2500 €, depending on individual circumstances. Within such a scenario, we assume that the costs per measure are oriented towards the lower cost limit, as there is an overcapacity of personnel and measures can be partially coordinated. With 500 € closure measure costs, the revenue cap thus increases by 1.6% in the base year 2017 and by 2.6% in 2035 compared to the mean value of the cost analysis (same assumptions like above). In urban areas, gas pipes are usually laid under pavements or roads. After closing a line, it usually remains underground until the surface has to be opened up by other construction measures. Therefore, costs of deconstruction measures are not considered. In Germany, this is regulated in detail in the concession agreement conducted between the DNO and the concession grantor [79]. All these factors imply that the model in this paper rather lead to an under- than an overestimation of actual DNO costs.
From a DNO point of view, we identify several factors that could combine into a high economic risk when faced with decreasing demand: The nonlinear development of grid costs described by low k factors can result in a strong discrepancy of grid costs when most of the customers still remain in the grid. In these periods, we also see a strong variability of grid-dependent outcomes which could put an early strain on single grid areas. The risk-determining factors for individual areas are the age structure of the grid, the network topology, the cost structure of the DNO and the individual decisions of the grid users. Stranded investments are a relevant risk factor, when customer exits occur in areas which were not predicted by the DNO. While we model this customer behavior as random, in reality a prediction of customer exits is an effective way for the DNO to control parts of the resulting costs. From the perspective of a DNO, the decisions taken at this point are somewhat contradictory:
- Reducing the investment rate, and with that the CAPEX, leads to an increase of the grid age, thus its reliability drops, which in turn increases the operational costs.
- A changed capitalization strategy reduces the fixed capital and thus the risk for stranded investments, but increases operating costs, which in turn has a negative effect on the efficiency value of the DNO in the regulatory regime [18,63].
- Shortening the depreciation period of lines has the same effects like a changed capitalization strategy in the long term.
To reduce the risk for stranded investments, the DNO can develop its future investment roadmap under consideration of risk and return, where investment decisions regarding building heating systems determine the customers’ grid usage and thus the risk for the grid operator. The investment theory offers methods such as portfolio [80,81,82] or real options analysis [83,84], which enable the selection of risk- and return-optimal renewal measures under uncertainty.
5.2. Options, Risks and Conclusions for Grid Users
The regulated system [63] could incentivize DNOs to pursue a “stable revenue cap” in the first years of gas exit scenarios. We predict that this strategy could become non-sustainable after a 30%–40% decrease in demand, which would lead to a sharp rise in grid charges and thus gas costs for grid user. Facing this financial risk, customers can postpone investments in heating systems, invest in energy efficiency measures or combine gas-based systems with others such as electrical heat pumps or replace their heating systems with non-gas-based technologies. Ansorge et al. [85] provide an estimate for a tipping point that could trigger customer grid defection at a gas price increase by about 1.25 ct/kWh. In our study setup, this would correspond to an increase in grid charges by 50%–100%, which would be reached between 2035 and 2045 depending on DNO strategy. In result, this might lead to a sudden increase of grid charges and grid defection that might develop into a self-reinforcing feedback loop. Also, experience has shown that prosumers with a high degree of self-sufficiency tend to stay connected to power grids for the opportunity to sell surplus energy. While decentralized home production of synthetic gas, e.g., by small-scale electrolysis, is not common today, this factor might grow in importance in a global scenario of renewable gas production [38].
5.3. Macro-Economic Perspective and Regulatory Options
With our work we identify a future risk, that the operation of gas grid infrastructure as well as gas-bound heating systems will become uneconomical compared to other technologies, as the gas demand decreases in most predicted scenarios in Germany. This represents a macroeconomic risk, as numerous studies assume that gas-bound technologies are needed as a flexibility option for energy systems with a high penetration of renewable energy [6,11,23,24,25,26,29,32].
To counteract this development, the legislator can change individual aspects within the existing regulatory regime on the one hand, such as shortening the depreciation period, changing the return on equity or changing the benchmark system [62,63]. On the other hand, it is possible to change the regulatory regime itself, e.g., by introducing an energy carrier independent infrastructure charge, which takes into account the system-useful properties of the gas infrastructure.
5.4. Further Research
5.4.1. Limits and Transferability of the Approach
The general power-law relationship we use has been described for a widely different range of natural as well as human-made networks. It is, therefore, also most likely to apply to a wide variation of energy grids, although redundancy as in mesh structures might be an additional relevant factor which we did not examine. For the 57 grids, the values of the exponent k for a random exit pattern (median: 0.4) is in line with the literature [54], which describes a lowest value of 0.33 for highly disordered grids. Of the presented structural parameters, most can be generalized to a broad range of different grid infrastructures and are not specific to a single energy carrier, grid topology or scale. We assume that parameters for k values and variances can be estimated for other networks with a similar approach, which could also answer the question whether certain grid topologies are more or less sensitive to a decline in demand.
History shows that the regulatory regime of a country adapts to the respective technological and economic circumstances [62]. In this way it can be assumed that the regulatory system will adapt accordingly for transformation paths with strongly declining gas demand. As a result, DNOs will also adapt their strategy, leading to changed revenue cap and grid charge developments. Here, new work could start by examining the effects of changing regulatory regimes or DNO strategies within the transformation path. For this, the used regulatory mechanism can be transferred to other methods such as the “price-cap” or “rate-of-return” approach by adapting the formula relationships and adding additional cost elements if necessary, which also makes it possible to transfer the approach to other countries (see Table 1).
An evaluation of the gas demand scenario (Figure A3 in Appendix C.4) used for the cost analysis is difficult: On the one hand, the literature sources [6,11,23,24,25,26,29,32] show that the decline of the gas demand can also be of non-linear nature, which would further increase the economic risk for all stakeholders, since we have assumed a linear decline for the cost analysis. On the other hand, the majority of German studies predict a need for gas in the future energy system as a flexibility option, whereby renewable gases like bio-methane or synthetic gas produced by power-to-gas plants substitute the conventional natural gas. Studies agree that gas will become less important for space heating applications, but will be used for industrial process heat generation in the future [6,11,23,24,25,26,29,32]. In this way, the scenario used for the cost analysis represents a worst-case scenario.
5.4.2. Decisions of Single Actors
Many authors have developed building investment models with the aim of selecting cost and CO2 optimized renewal measures [35,36,38]. However, a validation of the German Energy Saving Ordinance shows that, especially in the residential sector, investment decisions are made on the basis of a wider spread of socio-economic factors [86,87]. To be able to quantify the risk of a customer’s exit from the gas network, models are needed that determine realistic refurbishment options for individual buildings respectively their owners. Based on these options, the risk in terms of future gas demand for individual network areas can be quantified and taken into account when planning renewal measures in the gas grid. For this purpose, existing investment valuation models, such as portfolio analysis as a one-period model or real options analysis as a multi-period model, which are already used in the energy economy, have to be adapted [88]. Moreover, the role of different regulatory regimes within such transformation paths should also be examined.
5.4.3. Interdependencies between the Decisions of Different Actors
The general problem of grid defection has been the topic of previous studies that focus on renewable power production, where the growing availability of residential PV systems and storage technology confronts utility businesses with the threat of grid defection. This effect is dubbed the “utility death spiral” and predicted as a possible positive feedback of rising grid charges and a decline in demand, which could lead to a thread to traditional utility business models [39,89,90]. Lessons learned from power grids could also serve as a model for gas grids: With the strong sensitivity to energy retail prices, both DNO pricing structures and national taxation models could help to control grid defection. For this reason, models should be developed to analyze the interdependencies between the decisions of the different stakeholders such as the regulator, the DNO and the grid user.
Author Contributions
Conceptualization, D.T., T.M.K. and M.B.; Data curation, J.B.; Funding acquisition, M.B.; Investigation, D.T. and J.B.; Methodology, D.T., C.S. and T.M.K.; Project administration, M.B.; Software, Daniel Then and Johannes Bauer; Supervision, T.M.K. and M.B.; Visualization, D.T. and C.S.; Writing—original draft, D.T. and C.S.; Writing—review & editing, C.S., T.M.K. and M.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
We would like to thank the Stadtwerke Bamberg energy and water supply company, Bamberg, Germany for providing us the data of loads, grids and costs components that form the basis for this work.
Conflicts of Interest
D.T. is an employee of the Stadtwerke Bamberg GmbH. The authors declare no conflict of interest.
Appendix A. Nomenclature and Parametrization

Table A1.
Acronyms.
Table A1.
Acronyms.
| Name | Acronym | Name | Acronym |
|---|---|---|---|
| Building owner | BO | Grid charges | GC |
| Capital expenditure | CAPEX | Operational expenditure | OPEX |
| Distribution network operator | DNO | Revenue cap | RC |
| Domestic hot water | DHW | Space heating | SH |

Table A2.
Nomenclature of formula symbols.
Table A2.
Nomenclature of formula symbols.
| Parameter | Description [unit] | Value |
|---|---|---|
| Variables | ||
| Renewal of line ℓ in year 𝓇 (Binary decision variable of optimization model) | ||
| Closure of line ℓ in year 𝒸 (Binary decision variable of optimization model) | ||
| Grid charges gas in year 𝓉 [€/kWh] | ||
| Rest book value factor of line ℓ in year 𝓉 as a function of the binary decision variables | ||
| Mean rest book value factor of the whole grid in year 𝓉 | ||
| Age of line ℓ in year 𝓉 as a function of the binary decision variables [a] | ||
| Binary variable representing if a line is within its technical lifetime (function of the binary decision variables) | ||
| Power law function | ||
| Customer number of the grid | ||
| Cumulated line length of the grid [m] | ||
| k | Exponent of the power law function | |
| MSE | Mean squared error of power law fit | |
| R2 | Correlation coefficient of power law fit | |
| Cost components of the revenue cap | ||
| Capital expenditures [€] | ||
| Operational expenditures [€] | ||
| Calculated return on equity [€] | ||
| Interest on borrowed capital [€] | ||
| Calculated trade tax [€] | ||
| Calculated interest on borrowed capital [€] | ||
| Operational costs [€] | ||
| Loss costs [€] | ||
| Upstream grid charges [€] | ||
| Concession fees [€] | ||
| Parameters used in Section 2 (methods and materials) | ||
| Supplied energy in year 𝓉 [kWh/a] | Scenario specific | |
| Historical acquisition expenditures for line ℓ [€/m] | 214 * | |
| Line length of line ℓ [m] | Line specific | |
| Interest rate equity capital of line ℓ | 0.0691 * | |
| Amount of equity capital of line ℓ | 0.4 * | |
| Interest rate borrowed capital of line ℓ | 0.035 * | |
| Amount of borrowed capital of line ℓ | 0.6 * | |
| Trade tax rate | 0.1365 * | |
| Technical lifetime of a line [a] | 40 | |
| Planning horizon [a] | 33 | |
| Specific costs of upstream grid charges [€/kWh] | 0.01 | |
| Specific costs for concession fees [€/kWh] | 0.002 | |
| Specific lost costs [€/kWh] | 0.008 | |
| Loss factor | 0 | |
| Specific operational costs [€/m] | 10.71 | |
| Line age at the begin of planning horizon [a] | Line specific | |
| Length-weighted average age of the grid [a] | Grid specific | |
| Additional Parameters used in optimization model | ||
| Status matrix for renewal measure 𝓇 in year 𝓉 | See Appendix C.1 | |
| Status matrix for operation of line ℓ in year 𝓉 | See Appendix C.1 | |
| Status matrix for closure measure 𝒸 in year 𝓉 | See Appendix C.1 | |
| Energy demand of building 𝒿 in year 𝓉 [kWh] | Building and scenario specific | |
| Status matrix of line ℓ in year 𝓉 | Line and scenario specific | |
| Indices and sets | ||
| A building 𝒿 of all buildings connected to the grid | ||
| A line ℓ of all lines in the grid | ||
| A year 𝓉 within the planning horizon | ||
| Year of renewal measure 𝓇 of all possible years within the planning horizon | ||
| Year of closure measure 𝒸 of all possible years within the planning horizon | ||
* Same values applied for all lines ℓ. Values are chosen on basis of local conditions in Bamberg, Germany (grid and DNO properties as well as regulatory aspects).
Appendix B. Correlation Analysis
Appendix B.1. Parameters of Correlation Analysis

Table A3.
Parameters of correlation analysis.
Table A3.
Parameters of correlation analysis.
| Parameter | Unit | Description, Literature source |
|---|---|---|
| 1 | k value for “highest impact first” selection type of one grid. | |
| 1 | k value for “longest path first” selection type of one grid. | |
| 1 | Mean value of k for 100 seeds “radial random selection” of one grid. | |
| 1 | Mean value of k for 100 seeds “weighted random selection” of one grid. | |
| 1 | Mean value of k for 100 seeds “random selection” of one grid. | |
| 1 | k value for “Shortest path first” selection type of one grid. | |
| 1 | k value for “Least impact first” selection type of one grid. | |
| 1 | Difference of k values “highest impact first” and “least impact first” of one grid. | |
| 1 | Standard deviation of k for 100 seeds “random selection” of one grid. | |
| m | Longest path of a grid. | |
| m | Shortest path of a grid. | |
| 1 | Average value of the detour factor of a grid (detour factor: path length normalized with linear distance). | |
| 1 | Standard deviation of the detour factor of a grid. | |
| m | Grid length of a grid. | |
| m | Average value of all paths lengths of a grid. | |
| m | Standard deviation of all paths lengths of a grid. | |
| kWh/a | Cumulated yearly energy demand of a grid. | |
| kWh/a | Average energy demand of customers of a grid. | |
| kWh/a | Standard deviation of the customer’s energy demands in a grid. | |
| kWh/a | Maximal energy demand of a customer in a grid. | |
| kWh/(a * m) | Cumulated energy of grid area normalized to grid length. | |
| 1/(a * m) | Number of customers in grid area in relation to grid length. | |
| 1 | Number of customers in a grid area. | |
| m2 | Area size. | |
| 1 | Sum of all paths from user to regulator station normalized to grid length in a grid. | |
| 1 | Standard deviation of path lengths normalized to sum of path lengths in a grid. | |
| 1 | Shortest path normalized to sum of path lengths in a grid. | |
| 1 | Longest path normalized to sum of path lengths in a grid. | |
| 1 | Variation coefficient of path lengths in a grid. | |
| 1 | Variation coefficient of line lengths in a grid (of simplified graph, see chapt. 2). | |
| m | Average line length (of simplified graph, see chapt. 2). | |
| 1 | Maximal line length normalized to grid length (of simplified graph, see chapt. 2). | |
| 1 | Mean value of page rank [76,77]. (weights = line lengths; dumping factor d = 0.85) | |
| 1 | Variation coefficient of page rank. | |
| m | Sum of shortest paths between every nodes of the graph normalized by squared customers number (weights = line lengths) [91]. | |
| 1 | Weighted average nearest neighbor degree of nodes with degree d [75,77]. (d = 1) | |
| 1 | Weighted average nearest neighbor degree of nodes with degree d. (d = 3) | |
| 1 | Diameter of the graph, which represents its maximum eccentricity. The eccentricity of a node v is the maximum distance from v to all other nodes in G [92]. | |
| 1 | Radius of the graph, which represents its minimum eccentricity [92]. |
Appendix B.2. Correlation Matrix of All Parameters
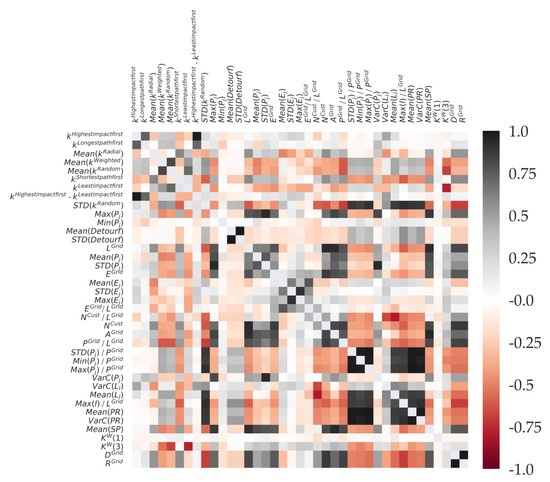
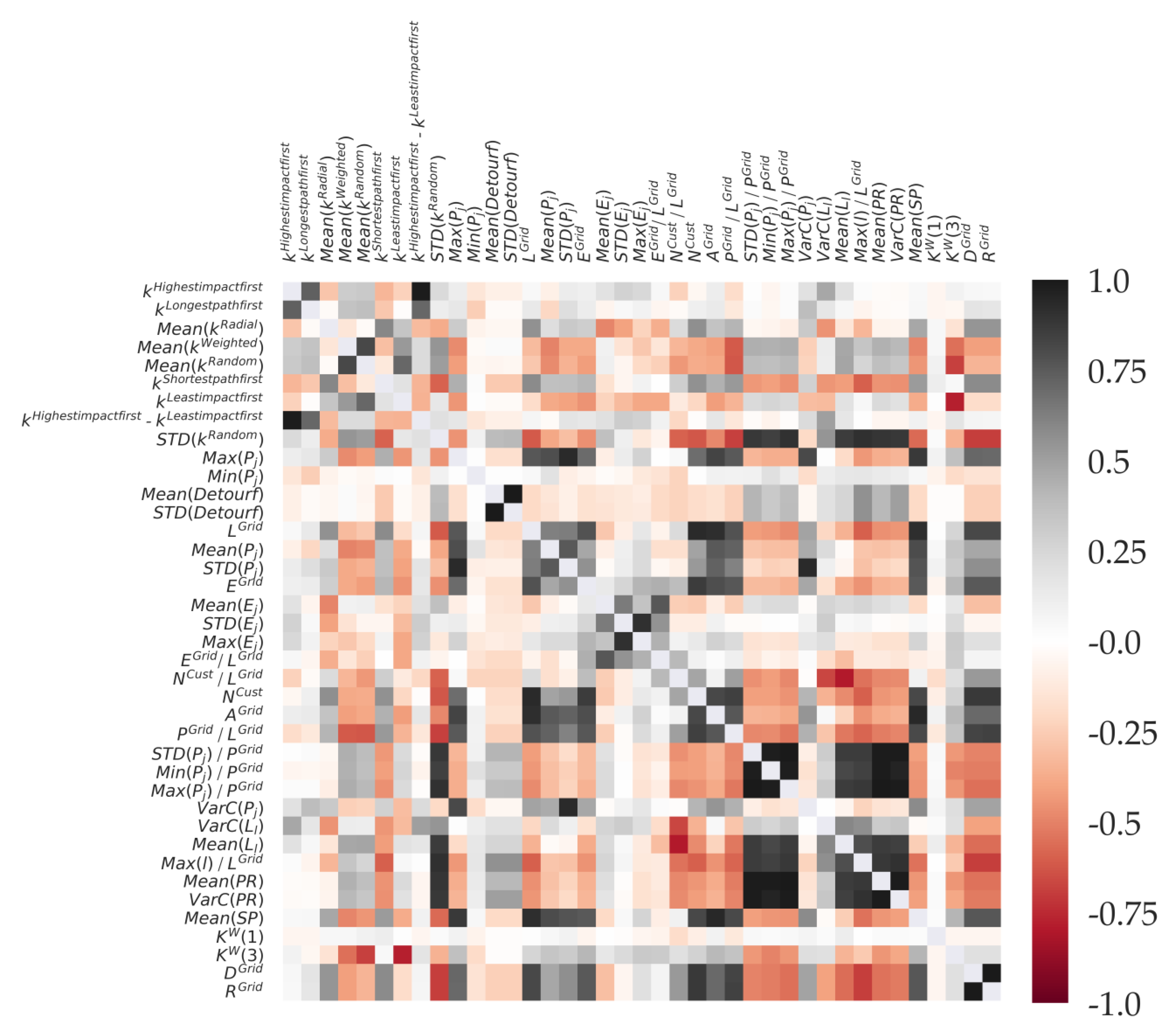
Figure A1.
Correlation matrix of all considered structural parameters and k values.
Figure A1.
Correlation matrix of all considered structural parameters and k values.
Appendix B.3. Structural Parameters of the 57 Grid Areas

Table A4.
Structural parameters of the grid areas.
Table A4.
Structural parameters of the grid areas.
| Grid | Length/m | Number of Customers | Yearly Energy Demand/MWh | Length Weighted Average Initial Age/a |
|---|---|---|---|---|
| 0 | 480 | 4 | 233 | 15.1 |
| 1 | 2270 | 40 | 2235 | 33.1 |
| 2 | 2390 | 79 | 2224 | 28.3 |
| 3 | 1140 | 22 | 2496 | 36.1 |
| 4 | 2620 | 82 | 4529 | 31.4 |
| 5 | 4220 | 90 | 1581 | 22.4 |
| 6 | 7680 | 266 | 6787 | 35.8 |
| 7 | 4460 | 124 | 8828 | 20.7 |
| 8 | 8630 | 299 | 8032 | 34.6 |
| 9 | 5590 | 174 | 4877 | 25.7 |
| 10 | 650 | 17 | 2335 | 29.0 |
| 11 | 5200 | 191 | 5445 | 27.1 |
| 12 | 3660 | 69 | 3625 | 22.9 |
| 13 | 8080 | 229 | 6524 | 24.5 |
| 14 | 1830 | 44 | 1575 | 29.9 |
| 15 | 2430 | 75 | 7457 | 29.1 |
| 16 | 5510 | 166 | 2284 | 20.4 |
| 17 | 4590 | 189 | 3889 | 28.6 |
| 18 | 3210 | 148 | 1638 | 17.0 |
| 19 | 4270 | 167 | 5633 | 22.7 |
| 20 | 2870 | 126 | 3009 | 29.1 |
| 21 | 980 | 31 | 1444 | 28.7 |
| 22 | 5650 | 212 | 4550 | 25.1 |
| 23 | 3620 | 127 | 4540 | 30.7 |
| 24 | 1510 | 61 | 2708 | 26.1 |
| 25 | 2150 | 36 | 2185 | 16.9 |
| 26 | 6390 | 152 | 5660 | 21.6 |
| 27 | 9510 | 247 | 7060 | 26.4 |
| 28 | 5890 | 209 | 4286 | 26.2 |
| 29 | 2990 | 64 | 4046 | 22.0 |
| 30 | 4440 | 205 | 5229 | 33.6 |
| 31 | 2550 | 130 | 2690 | 35.9 |
| 32 | 5650 | 228 | 7193 | 25.5 |
| 33 | 5140 | 234 | 8473 | 30.9 |
| 34 | 7680 | 245 | 9616 | 23.4 |
| 35 | 4660 | 199 | 9029 | 29.2 |
| 36 | 7520 | 363 | 19,092 | 29.9 |
| 37 | 5070 | 180 | 13,916 | 30.8 |
| 38 | 500 | 8 | 136 | 14.3 |
| 39 | 3810 | 129 | 3322 | 21.3 |
| 40 | 8110 | 258 | 13,229 | 31.3 |
| 41 | 7300 | 227 | 6336 | 35.1 |
| 42 | 10,080 | 390 | 16,786 | 27.2 |
| 43 | 4200 | 131 | 4694 | 27.0 |
| 44 | 4960 | 181 | 4626 | 21.4 |
| 45 | 3030 | 100 | 2583 | 28.6 |
| 46 | 2390 | 76 | 2133 | 26.3 |
| 47 | 6940 | 281 | 14,294 | 28.9 |
| 48 | 1600 | 101 | 3822 | 33.0 |
| 49 | 3290 | 193 | 8625 | 32.1 |
| 50 | 470 | 23 | 1538 | 35.8 |
| 51 | 6300 | 276 | 17,462 | 28.7 |
| 52 | 5550 | 144 | 8993 | 29.5 |
| 53 | 2790 | 56 | 4012 | 19.5 |
| 54 | 10,760 | 481 | 20,192 | 31.5 |
| 55 | 11,960 | 507 | 21,045 | 33.3 |
| 56 | 1350 | 31 | 1024 | 21.5 |
Appendix C. Cash Flow Analysis
Appendix C.1 Optimization Model
The objective is to maximize the earnings before interests and tax. The degree of freedom represents the scheduling of renewal measures within the planning horizon, which influences :
Subject to:
1. Costs equal revenues within every year 𝓉 of planning horizon:
2. Length-weighted mean age of grid for all lines under operation equal initial mean age for every year in planning horizon, where the age
is a function of chosen renewal measures:
The rest book value factor is a function of the binary decision variables for operation and renew as well as for closure of each line, where the sets and represents the years of the planning horizon in which a renewal or closure measure is possible. , are logical matrices that determine whether a line is operated, dependent on the chosen measure 𝓇 or 𝒸. is a logical matrix that determines whether a line ℓ is within its technical lifetime. Before optimization, the relation between each customer 𝒿 and line ℓ was figured out within a graph search and modeled by a logical matrix represents the substitute of the following relationship (15):
The rest book values before and after renewal can be described by:
and are a functions of chosen renewal measures and can be described as:
Additional constraints, regarding the choice of measures:
3. One renewal until closure allowed (lines must at least to be operated):
4. One closure measure allowed during planning horizon:
5. Closure measure only if no more customers are supplied:
6. Lines have to be closed when no customer is connected anymore:
The bilinear term was substituted to transform Equation (15) into a linear model [93]. Where an additional constraint 7 based on the substitute is necessary, in order to exclude renewals after shutdowns.
Appendix C.2. Simplified Cash Flow Model
In the following the calculation of each cost component of the revenue cap of the DNO used in this work is defined. Under consideration of the DNO strategies and the underlying scenario introduced in Section 2, as well as the functional relationships (1) and (3), grid charges and revenue cap can be determined.
Appendix C.3. Global Scenario of the Cost Analysis
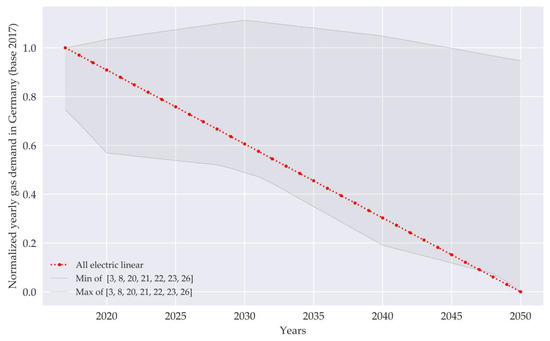
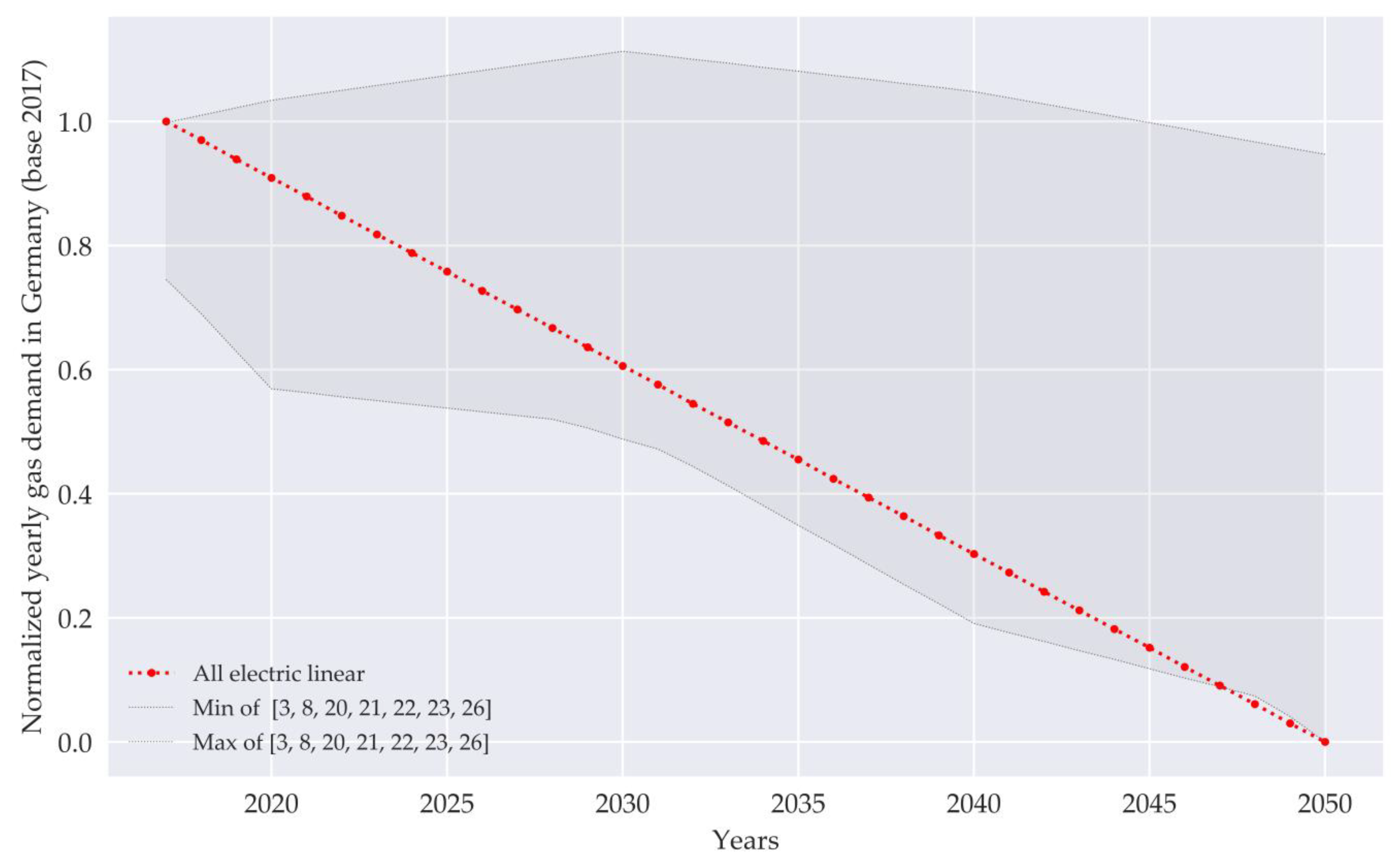
Figure A2.
Normalized scenario used as global scenario for the cash flow calculation compared to literature values for Germany (maximum and minimum of all sources).
Figure A2.
Normalized scenario used as global scenario for the cash flow calculation compared to literature values for Germany (maximum and minimum of all sources).
Appendix C.4. Results of the Cost Analysis
Grid 18 has a length-weighted mean initial age of 17.0 years. Therefore, the grid charges in 2018 are of above-average value.
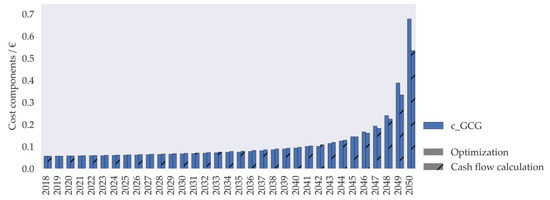
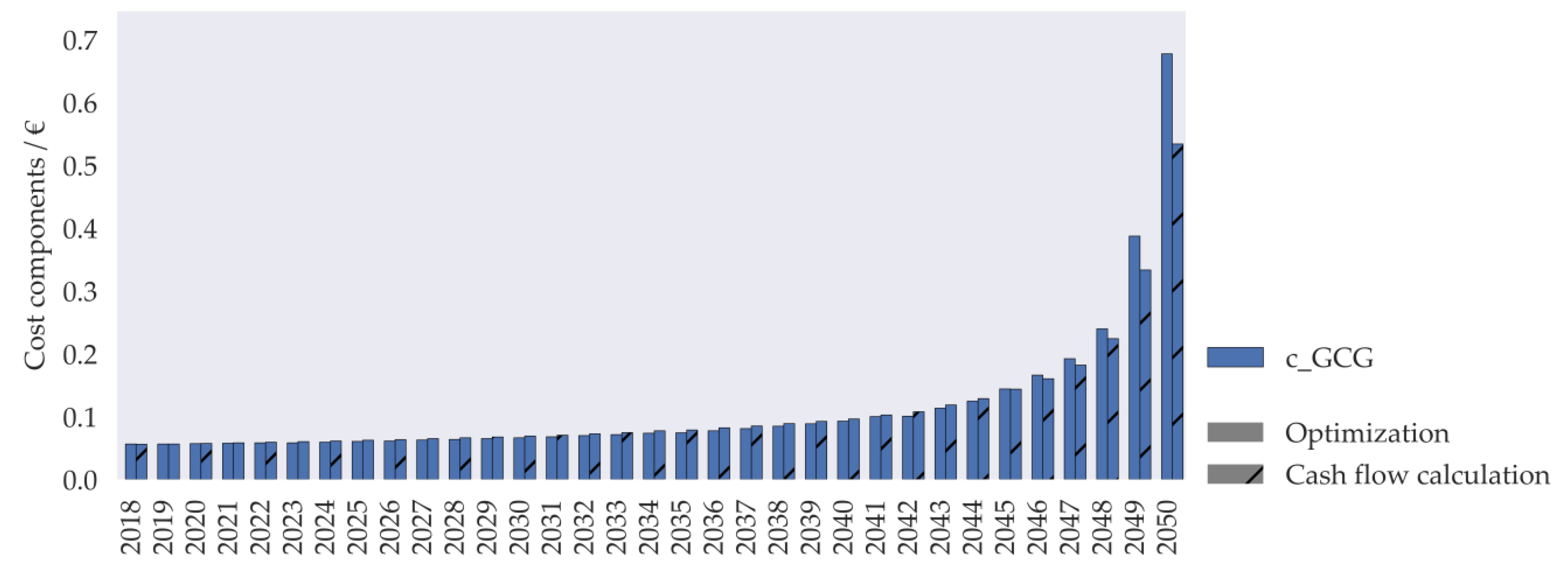
Figure A3.
Comparison of grid charges for optimization (full) and simplified (hashed) cash flow calculation during declining gas demand in a single gas grid. (Grid: #18, DNO strategy: constant grid value, selection type: random selection (mean k value), global scenario: linear decrease of gas demand 2018–2050).
Figure A3.
Comparison of grid charges for optimization (full) and simplified (hashed) cash flow calculation during declining gas demand in a single gas grid. (Grid: #18, DNO strategy: constant grid value, selection type: random selection (mean k value), global scenario: linear decrease of gas demand 2018–2050).
References
- Renewable Energy Policy Network for the 21st Century (REN21). Renewables 2018—Global Status Report; Renewable Energy Policy Network for the 21st Century (REN21): Paris, France, 2018. [Google Scholar]
- U.S. Energy Information Administration. International Energy Outlook 2019; U.S. Energy Information Administration: Washington, DC, USA, 2019.
- Global Energy Assessment Writing Team. Global Energy Assessment (GEA); Cambridge University Press: Cambridge, UK; New York, NY, USA; Melbourne, Australia, 2012; ISBN 9781107005198. [Google Scholar]
- Eurostat. Final Energy Consumption in Households. 2018. Available online: https://https://www.ec.europa.eu/eurostat/cache/metadata/EN/t2020_rk200_esmsip2.htm (accessed on 9 December 2019).
- Honoré, A. Decarbonisation of Heat in Europe: Implications for Natural Gas Demand; Oxford Institute for Energy Studies: Oxford, UK, 2018. [Google Scholar]
- Hecking, H.; Hintermayer, M.; Lencz, D.; Wagner, J. Energiemarkt 2030 und 2050—Der Beitrag von Gas-und Wärmeinfrastruktur zu Einer Effizienten CO2-Minderung; ewi Energy Research & Scenarios: Cologne, Germany, 2017. [Google Scholar]
- Bothe, D.; Janssen, M.; van der Poel, S.; Eich, T.; Bongers, T.; Kellermann, J.; Lück, L.; Chan, H.; Ahlert, M.; Borrás, C.A.B.; et al. Der Wert der Gasinfrastruktur für die Energiewende in Deutschland—Eine modellbasierte Analyse—Eine Studie im Auftrag der Vereinigung der Fernleitungsnetzbetreiber (FNB Gas e.V.); Frontier Eonomics: London, UK; Institut für Elektrische Anlagen und Energiewirtschaft (IAEW): Aachen, Germany; 4Management: Düsseldorf, Germany; EMCEL: Köln, Germany, 2017. [Google Scholar]
- Henning, H.M.; Palzer, A. Energiesystem Deutschland 2050; Fraunhofer-Institut für Solare Energiesysteme (ISE): Freiburg, Germany, 2013. [Google Scholar]
- Deutsch, M.; Gerhardt, N.; Sandau, F.; Becker, S.; Scholz, A.; Schumacher, P.; Schmidt, D. Wärmewende 2030—Schlüsseltechnologien zur Erreichung der mittel-und Langfristigen Klimaschutzziele im Gebäudesektor—Eine Studie im Auftrag der Agora Energiewende; Fraunhofer-Institut für Windenergie und Energiesystemtechnik (IWES): Bremerhaven, Germany; Fraunhofer-Institut für Bauphysik (IBP): Stuttgart, Germany, 2017. [Google Scholar]
- Fernleitungsnetzbetreiber Gas (FNB Gas). Prognos, Szenariorahmen für den Netzentwicklungsplan Gas 2018–2028 der Fernleitungsnetzbetreiber—Eine Studie im Auftrag der Deutschen; Fernleitungsnetzbetreiber (FNB): Berlin, Germany, 2017. [Google Scholar]
- Ziesing, H.J.; Repenning, J.; Emele, L.; Blanck, R.; Böttcher, H.; Dehoust, G.; Förster, H.; Greiner, B.; Harthan, R.; Henneberg, K.; et al. Klimaschutzszenario 2050—2. Endbericht—Eine Studie im Auftrag des Bundesministeriums für Umwelt, Naturschutz, Bau und Reaktorsicherheit; Fraunhofer-Institut für System-und Innovationsforschung: Karlsruhe, Germany, 2015. [Google Scholar]
- Mastorakos, S.; Madrigal, J.; Duffy, E.; Ebertin, M.; Bosso, E. The Future of Natural Gas in the United States; United States Ecologic Institute: Washington, DC, USA, 2017. [Google Scholar]
- Feijoo, F.; Iyer, G.C.; Avraam, C.; Siddiqui, S.A.; Clarke, L.E.; Sankaranarayanan, S.; Binsted, M.T.; Patel, P.L.; Prates, N.C.; Torres-Alfaro, E.; et al. The future of natural gas infrastructure development in the United states. Appl. Energy 2018, 228, 149–166. [Google Scholar] [CrossRef]
- Costello, K.W. Why natural gas has an uncertain future. Electr. J. 2017, 30, 18–22. [Google Scholar] [CrossRef]
- Mac Kinnon, M.A.; Brouwer, J.; Samuelsen, S. The role of natural gas and its infrastructure in mitigating greenhouse gas emissions, improving regional air quality, and renewable resource integration. Prog. Energy Combus. Sci. 2018, 64, 62–92. [Google Scholar] [CrossRef]
- Jianhong, Y. Analysis of sustainable development of natural gas market in China. Nat. Gas Ind. B 2018, 5, 644–651. [Google Scholar] [CrossRef]
- Ailin, J. Progress and prospects of natural gas development technologies in China. Nat. Gas Ind. B 2018, 5, 547–557. [Google Scholar] [CrossRef]
- Däuper, O.; Strasser, T.; Lange, H.; Tischmacher, D.; Fimpel, A.; Kaspers, J.; Koulaxidis, S.; Warg, F.; Baudisch, K.; Bergmann, P.; et al. Wärmewendestudie—Die Wärmewende und ihre Auswirkungen auf die Gasverteilnetze; Becker Büttner Held: München, Deutschland, 2018. [Google Scholar]
- Hickey, C.; Deane, P.; McInerney, C.; Gallachóir, B.Ó. Is there a future for the gas network in a low carbon energy system? Energy Policy 2019, 126, 480–493. [Google Scholar] [CrossRef]
- Speirs, J.; Balcombe, P.; Johnson, E.; Martin, J.; Brandon, N.; Hawkes, A. A greener gas grid: What are the options. Energy Policy 2018, 118, 291–297. [Google Scholar] [CrossRef]
- Qadrdan, M.; Fazeli, R.; Jenkins, N.; Strbac, G.; Sansorn, R. Gas and electricity supply implications of decarbonising heat sector in GB. Energy 2019, 169, 50–60. [Google Scholar] [CrossRef]
- McGlade, C.; Pye, S.; Ekins, P.; Bradshadw, M.; Watson, J. The future role of natural gas in the UK: A bridge to nowhere? Energy Policy 2018, 113, 454–465. [Google Scholar] [CrossRef]
- Schlesinger, M.; Hofer, P.; Kemmler, A.; Kirchner, A.; Koziel, S.; Ley, A.; Piégsa, A.; Seefeldt, F.; Straßburg, S.; Weinert, K.; et al. Entwicklung der Energiemärkte—Energiereferenzprognose—Projekt Nr. 57/12 Studie im Auftrag des Bundesministeriums für Wirtschaft und Technologie—Eine Studie im Auftrag des Bundesministeriums für Wirtschaft und Technologie; Energiewirtschaftliches Institut an der Universität zu Köln (EWI): Köln, Germany; Gesellschaft für Wirtschaftliche Strukturforschung mbH (GWS): Osnabrück, Germany; Prognos: Basel, Switzerland, 2014. [Google Scholar]
- Gerbert, P.; Herhold, P.; Burchardt, J.; Schönberger, S.; Rechenmaher, F.; Kirchner, A.; Kemmler, A.; Wünsch, M. Klimapfade für Deutschland—Eine Studie im Auftrag des Bundesverbandes der Deutschen Industrie e.V. (BDI); The Boston Consulting Group: Boston, MA, USA; Prognos: Basel, Switzerland, 2018. [Google Scholar]
- Gerhardt, N.; Sandau, F.; Scholz, A.; Hahn, H.; Schumacher, P.; Sager, C.; Bergk, F.; Kämper, C.; Knörr, W.; Kräck, J.; et al. Interaktion EE-Strom, Wärme und Verkehr—Analyse der Interaktion zwischen den Sektoren Strom, Wärme/Kälte und Verkehr in Deutschland in Hinblick auf steigende Anteile fluktuierender Erneuerbarer Energien im Strombereich unter Berücksichtigung der europäischen Entwicklung—Ableitung von optimalen strukturellen Entwiklungspfaden für den Verkehrs-und Wärmesektor; Fraunhofer-Institut für Windenergie und Energiesystemtechnik IWES: Bremerhaven, Germany; Fraunhofer-Institut für Bauphysik IBP: Stuttgart, Germany; Institut für Energie-und Umweltforschung IFEU: Heidelberg, Germany; Stiftung Umweltenergierecht: Würzburg, Germany, 2015. [Google Scholar]
- Enervis Energy Advisors GmbH. Klimaschutz durch Sektorenkopplung: Optionen, Szenarien, Kosten; Enervis Energy Advisors GmbH: Berlin, Germany, 2017. [Google Scholar]
- Nitsch, J. SZEN-15—Aktuelle Szenarien der Deutschen Energieversorgung unter Berücksichtigung der Eckdaten des Jahres 2014; Bundesverband Erneuerbare Energien e.V.: Berlin, Germany, 2015. [Google Scholar]
- Nitsch, J. SZEN-17—Erfolgreiche Energiewende nur mit Verbesserter Energieeffizienz—Aktuelle Szenarien 2017 der Deutschen Energieversorgungund einem Klimagerechten Energiemarkt; Bundesverband Erneuerbare Energien e.V.: Berlin, Germany, 2017. [Google Scholar]
- Klein, S.; Klein, S.W.; Steinert, T.; Fricke, A.; Peschel, D. Erneuerbare Gase—Ein Systemupdate der Energiewende; Eine Studie im Auftrag von der Initiative Erdgasspeicher; Bundesverband WindEnergie: Berlin, Germany; Enervis energy advisors GmbH: Berlin, Germany, 2017. [Google Scholar]
- Zukunft ERDGAS e.V. Wärmemarkt 2050—So Erreicht Deutschland Kosteneffizient das Klimaziel; Zukunft ERDGAS e.V.: Berlin, Germany, 2017. [Google Scholar]
- BMU, Arbeitsgruppe IK III 1. Klimaschutzplan 2050—Klimapolitische Grundsätze und Ziele der Bundesregierung; Bundesministerium für Umwelt, Naturschutz und Nukleare Sicherheit (BMU): Berlin, Germany, 2019. [Google Scholar]
- Wittke, F. Auswertungstabellen zur Energiebilanz Deutschland—1990 bis 2017; Arbeitsgemeinschaft Energiebilanzen e.V. AGEB: Berlin, Germany, 2018. [Google Scholar]
- FNB Gas; Prognos. Szenariorahmen für den Netzentwicklungsplan Gas 2018-2028 der Fernleitungsnetzbetreiber—Konsultationsdokument; Eine Studie im Auftrag; Fernleitungsnetzbetreiber: Berlin, Germany, 2017. [Google Scholar]
- Nymoen, H.; Siebert, K.; Niemann, E. Sanierungsfahrpläne für den Wärmemarkt: Wie Können sich Private Hauseigentümer die Energiewende Leisten? Eine Studie im Auftrag; Zukunft ERDGAS e.V.: Berlin, Germany; Nymoen Strategieberatung: Berlin, Germany, 2014. [Google Scholar]
- Evins, R. A review of computational optimisation methods applied to sustainable building design. Renew. Sustain. Energy Rev. 2013, 22, 230–245. [Google Scholar] [CrossRef]
- Machairas, V.; Tsangrassoulis, A.; Axarli, K. Algorithms for optimization of building design: A review. Renew. Sustain. Energy Rev. 2014, 31, 101–112. [Google Scholar] [CrossRef]
- Huang, Y.; Niu, J.-L. Optimal building envelope design based on simulated performance: History, current status and new potentials. Energy Build. 2016, 117, 387–398. [Google Scholar] [CrossRef]
- Ansorge, K.; Streblow, R. Genetischer Algorithmus zur Kombinatorischen Optimierung von Gebäudehülle und Anlagentechnik—Optimale Sanierungspakete für Ein-und Zweifamilienhäuser; Gebäude-Energiewende Arbeitspapier 7: Berlin, Germany, 2017. [Google Scholar]
- Appen, J.V.; Braun, M. Strategic decision making of distribution network operators and investors in residential photovoltaic battery storage systems. Appl. Energy 2018, 230, 540–550. [Google Scholar] [CrossRef]
- Huke, L. Energetische Optimierung der Öffentlichen Gasversorgung—Dissertation. Ph.D. Thesis, Technische Universität Bergakademie Freiberg, Freiberg, Germany, 2002. [Google Scholar]
- Sanft, S. Modell zur Wirtschaftlichkeitsbewertung von Instandhaltungsstrategien bei Gasverteilnetzen im regulierten deutschen Gasmarkt—Dissertation. Ph.D. Thesis, Ruhr-Universität Bochum, Bochum, Germany, 2015. [Google Scholar]
- Hübner, M.; Haubrich, H.-J. Long-Term Pressure-Stage Comprehensive Planning of Natural Gas Networks in Handbook of Networks in Power Systems II; Sorokin, A., Rebennack, S., Pardalos, P., Iliadis, N.A., Pereira, M.V.F., Eds.; Springer: Berlin, Germany, 2012; pp. 37–59. ISBN 978-3-642-44612-2. [Google Scholar]
- Zeng, Q.; Zhang, B.; Fang, J.; Chen, Z. A bi-level programming for multistage co-expansion planning of the integrated gas and electricity system. Appl. Energy 2017, 200, 192–203. [Google Scholar] [CrossRef]
- Unishuay-Vila, C.; Marangon-Lima, J.W.; Zambroni de Souza, A.C.; Perez-Arriaga, I.J.; Balestrassi, P.P. A model to long-term, multiarea, multistage, and integrated expansion planning of electricity and natural gas systems. IEEE Trans. Power Syst. 2010, 25. [Google Scholar] [CrossRef]
- Chaudry, M.; Jenkins, N.; Qadrdan, M.; Wu, J. Combined gas and electricity network expansion planning. Appl. Energy. 2014, 113, 1171–1187. [Google Scholar] [CrossRef]
- Odetayo, B.; MacCormack, J.; Rosehart, W.D.; Zareipour, H.; Seifi, A.R. Integrated planning of natural gas and electric power systems. Electr. Power Energy Syst. 2018, 103, 593–602. [Google Scholar] [CrossRef]
- Qiu, J.; Yang, Z.; Hua, J.; Meng, K.; Zheng, Y.; Hill, D.J. Low carbon oriented expansion planning of integrated gas and power systems. IEEE Trans. Power Syst. 2015, 30, 1035–1046. [Google Scholar] [CrossRef]
- Saldarriaga, C.A.; Hincapié, R.A.; Salazar, H. An integrated expansion planning model of electric and natural gas distribution systems considering demand uncertainty. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015. [Google Scholar] [CrossRef]
- Odetayo, B.; MacCormack, J.; Rosehart, W.D.; Zareipour, H. Integrated planning of natural gas and electricity distribution networks with the presence of distributed natural gas fired generators. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting, Boston, MA, USA, 17–21 July 2016. [Google Scholar] [CrossRef]
- Bakken, B.H.; Mindeberg, S.K. Linear models for optimization of interconnected gas and electricity networks. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009. [Google Scholar] [CrossRef]
- Zeng, Q.; Fang, J.; Li, J.; Chen, Z. Steady-State analysis of the integrated natural gas and electric power system with bi-directional energy conversion. Appl. Energy. 2016, 184, 1483–1492. [Google Scholar] [CrossRef]
- Wang, I.E.; Clandinin, T.R. The influence of wiring economy on nervous system evolution. Curr. Biol. 2016, 26, 1101–1108. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Braunstein, L.A.; Cohen, R.; Buldyrev, S.V.; Havlin, S. Optimal paths in disordered complex networks. Phys. Rev. Lett. 2003, 91. [Google Scholar] [CrossRef] [PubMed]
- Wen, Q.; Stepanyants, A.; Elston, G.N.; Grosberg, A.Y.; Chklovskii, D.B. Maximization of the connectivity repertoire as a statistical principle governing the shapes of dendritic arbors. Proc. Natl. Acad. Sci. USA 2009, 106, 12536–12541. [Google Scholar] [CrossRef] [PubMed]
- Peng, D.; Poudineh, R. A holistic framework for the study of interdependence between electricity and gas sectors. Energy Strategy Rev. 2016, 13–14, 32–52. [Google Scholar] [CrossRef]
- Bundesministerium der Justiz und Verbraucherschutz. Gesetz über die Elektrizitäts-und Gasversorgung (Energiewirtschaftsgesetz-EnWG); Energiewirtschaftsgesetz 7 July 2005; Bundesministerium der Justiz und Verbraucherschutz: Berlin, Germany, 2005.
- Christensen, L.R.; Greene, W.H. Economies of scale in U.S. electric power generation. J. Political Econ. 1976, 84, 655–676. [Google Scholar] [CrossRef]
- Erdmann, G.; Zweifel, P. Energieökonomik, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2010; ISBN 978-3-642-12777-9. [Google Scholar]
- Cambini, C.; Meletiou, A.; Bompard, E.; Masera, M. Market and regulatory factors influencing smart-grid investment in Europe: Evidence from pilot projects and implications for reform. Util. Policy 2016, 40, 36–47. [Google Scholar] [CrossRef]
- Andra, B. CEER Report: Report on Regulatory Frameworks for European Energy Networks; Council of European Energy Regulators: Brussels, Belgium, 2019. [Google Scholar]
- Diekmann, J.; Leprich, U.; Ziesing, H.-J. Regulierung der Stromnetze in Deutschland; Hans-Böckler-Stiftung: Düsseldorf, Germany, 2007; ISBN 978-3-86593-067-5. [Google Scholar]
- Bundesministerium der Justiz und Verbraucherschutz. Verordnung über die Anreizregulierung der Energieversorgungsnetze (Anreizregulierungsverordnung-ARegV); Anreizregulierungsverordnung vom 29 Oktober 2007; Bundesministerium der Justiz und Verbraucherschutz: Berlin, Germany, 2007.
- Agrell, P.; Bogetoft, P.; Koller, M.; Trinkner, U. Effizienzvergleich für Verteilernetzbetreiber Strom 2013—Ergebnisdokumentation und Schlussbericht; Swiss Economics: Zürich, Switzerland; SUMICSID: Stånga, Sweden, 2014. [Google Scholar]
- Bundesnetzagentur; Bundeskartellamt. Monitoringbericht 2018; Bundesnetzagentur: Bonn, Germany; Bundeskartellamt: Bonn, Germany, 2019.
- OpenStreetMap Contributors. 2019. Available online: https://wiki.openstreetmap.org/wiki/Researcher_Information (accessed on 10 December 2019).
- Fischer-Uhrig, I. STANET Netzberechnung—Für Gas, Wasser, Strom, Fernwärme und Abwasser. 2020. Available online: www.stafu.de/de/home.html (accessed on 9 January 2020).
- Hart, W.E.; Laird, C.D.; Watson, J.-P.; Woodruff, D.L.; Hackebeil, G.A.; Nicholson, B.L.; Siirola, J.D. Pyomo—Optimization Modeling in Python, 2nd ed.; Springer: Cham, Switzerland, 2017; ISBN 978-3-319-58821-2. [Google Scholar]
- Hart, W.E.; Watson, J.-P.; Woodruff, D.L. Pyomo: Modeling and solving mathematical programs in Python. Math. Program. Comput. 2011, 3, 219–260. [Google Scholar] [CrossRef]
- Hagberg, A.A.; Schult, D.A.; Swart, P.J. Exploring network structure, dynamics, and function using NetworkX. In Proceedings of the 7th Python in Science Conference (SciPy 2008), Pasadena, CA, USA, 19–24 August 2008; pp. 11–15. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine learning in Python. J. Mach. Learn. Res. 2012, 12, 2825–2830. [Google Scholar]
- IBM. IBM ILOG CPLEX Optimization Studio. 2020. Available online: https://www.ibm.com/products/ilog-cplex-optimization-studio (accessed on 9 January 2020).
- Rival, I. Algorithms and Order, 1st ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1989; ISBN 978-94-010-7691-3. [Google Scholar]
- The SciPy Community. SciPy Documentation—Scipy.optimize.curve_fit. 2019. Available online: https://www.docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.curve_fit.html (accessed on 9 December 2019).
- Barrat, A.; Barthélemy, M.; Pastor-Satorras, R.; Vespignani, A. The architecture of complex weighted networks. Proc. Natl. Acad. Sci. USA 2004, 101, 3747–3752. [Google Scholar] [CrossRef]
- Langville, A.N.; Meyer, C.D. A survey of eigenvector methods of web information retrieval. Soc. Ind. Appl. Math. Rev. 2005, 47, 135–161. [Google Scholar] [CrossRef]
- NetworkX Developers. NetworkX Documentation Reference. 2015. Available online: https://networkx.github.io/documentation/networkx-1.10/reference/index.html (accessed on 9 December 2019).
- Cerbe, G.; Lendt, B. Grundlagen der Gastechnik-Gasbeschaffung-Gasverteilung-Gasverwendung, 8th ed.; Brüggemann, K., Dehli, M., Gröschl, F., Heikrodt, K., Kleiber, T., Kuck, J., Mischner, J., Schmidt, T., Seemann, A., Thielen, W., Eds.; Carl Hanser Verlag: Munich, Germany, 2016; ISBN 978-3-446-44965-7. [Google Scholar]
- Bundesministerium der Justiz und Verbraucherschutz. Verordnung über die Vergabe von Konzessionen (Konzessionsvergabeverordnung—KonzVgV); Konzessionsvergabeverordnung vom 12 April 2016; Bundesministerium der Justiz und Verbraucherschutz: Berlin, Germany, 2016.
- Lee, C.W.; Ng, S.K.K.; Zhong, J. 2nd Broadband Convergence Networks BcN 2007. In Proceedings of the 2nd IEEE/IFIP International Workshop on Broadband Convergence Networks, 2007 (BcN ′07), Munich, Germany, 21 May 2007; IEEE: Piscataway, NJ, USA, 2007. [Google Scholar]
- Molina, J.D.; Contreras, J.; Rudnick, H. A risk-constrained project portfolio in centralized transmission expansion planning. IEEE Syst. J. 2017, 11, 1653–1661. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Zhang, W.; Wu, Z.; Zhang, Z.; Qiang, C. Co-Planning of generation and transmission capacity based on portfolio theory. In Proceedings of the 2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Xi’an, China, 25–28 October 2016. [Google Scholar]
- Schachter, J.A.; Mancarella, P. A critical review of Real Options thinking for valuing investment flexibility in Smart Grids and low carbon energy systems. Renew. Sustain. Energy Rev. 2016, 56, 261–271. [Google Scholar] [CrossRef]
- Odetayo, B.; MacCormack, J.; Rosehart, W.D.; Zareipour, H. A real option assessment of flexibilities in the integrated planning of natural gas distribution network and distributed natural gas-fired power generations. Energy 2018, 143, 257–272. [Google Scholar] [CrossRef]
- Ansorge, K.; Streblow, R. Gebäudesteckbriefe—Exemplarische Sanierungsstrategien für Wohngebäude am Beispiel von ausgewählten Prototypgebäuden; Gebäude-Energiewende Arbeitspapier 8: Berlin, Germany, 2017. [Google Scholar]
- Stieß, I.; van der Land, V.; Birzle-Harder, B.; Deffner, J. Handlungsmotive-hemmnisse und Zielgruppen für eine Energetische Gebäudesanierung—Ergebnisse einer Standardisierten Befragung von Eigenheimsanierern; Institut für Ökologische Wirtschaftsforschung IÖW: Berlin, Germany, 2010. [Google Scholar]
- Renz, I.; Hacke, U. Einflussfaktoren auf die Sanierung im Deutschen Wohngebäudebestand—Ergebnisse einer Qualitativen Studie zu Sanierungsanreizen und-Hemmnissen priater und intitutioneller Eigentümer—Eine Untersuchung im Auftrag der KfW Bankengruppe; Institut Wohnen und Umwelt IWU: Darmstadt, Germany, 2016. [Google Scholar]
- Hundt, M. Investitionsplanung Unter Unsicheren Einflussgrößen; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2015. [Google Scholar]
- Khalilpour, R.; Vassallo, A. Leaving the grid: An. ambition or a real choice? Energy Policy 2015, 82, 207–221. [Google Scholar] [CrossRef]
- Laws, N.D.; Epps, B.P.; Peterson, S.O.; Laser, M.S.; Wanjiru, G.K. On the utility death spiral and the impact of utility rate structures on the adoption of residential solar photovoltaics and energy storage. Appl. Energy 2017, 185, 627–641. [Google Scholar] [CrossRef]
- NetworkX Developers. NetworkX Documentation—Algorithms—Average_Shortest_Path_Length. 2015. Available online: https://networkx.github.io/documentation/networkx-1.10/reference/generated/networkx.algorithms.shortest_paths.generic.average_shortest_path_length.html (accessed on 11 December 2019).
- NetworkX Developers. NetworkX Documentation—Algorithms—Distance Measures. 2015. Available online: https://networkx.github.io/documentation/networkx-1.10/reference/algorithms.distance_measures.html (accessed on 11 December 2019).
- Bisschop, J. AIMMS Optimization Modeling; AIMMS B.V.: Haarlem, The Netherlands, 2019. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).