Increasing Energy Efficiency and Productivity of the Comminution Process in Tumbling Mills by Indirect Measurements of Internal Dynamics—An Overview
Abstract
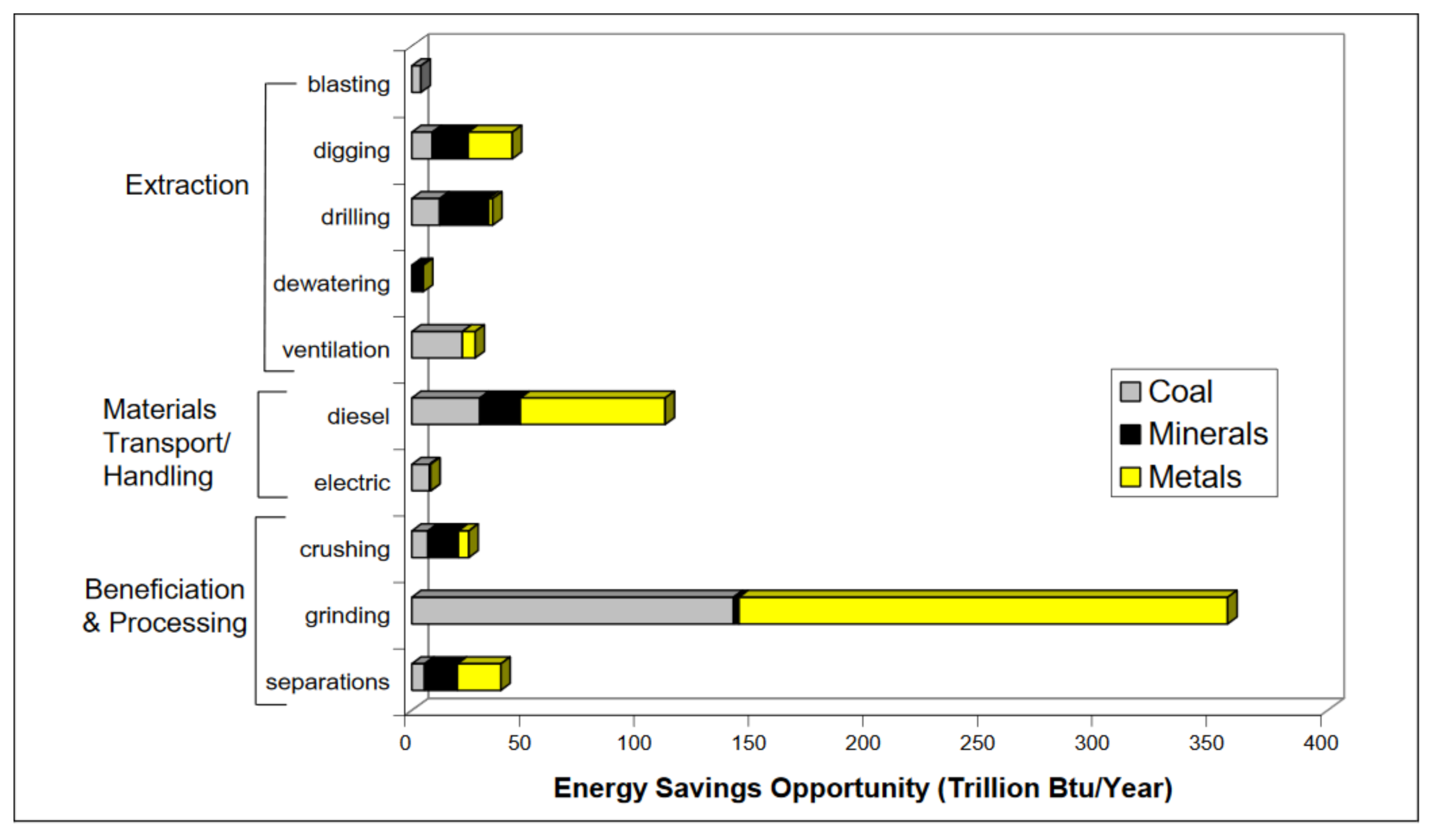
1. Introduction
2. State-of-the-Art in Mill Control
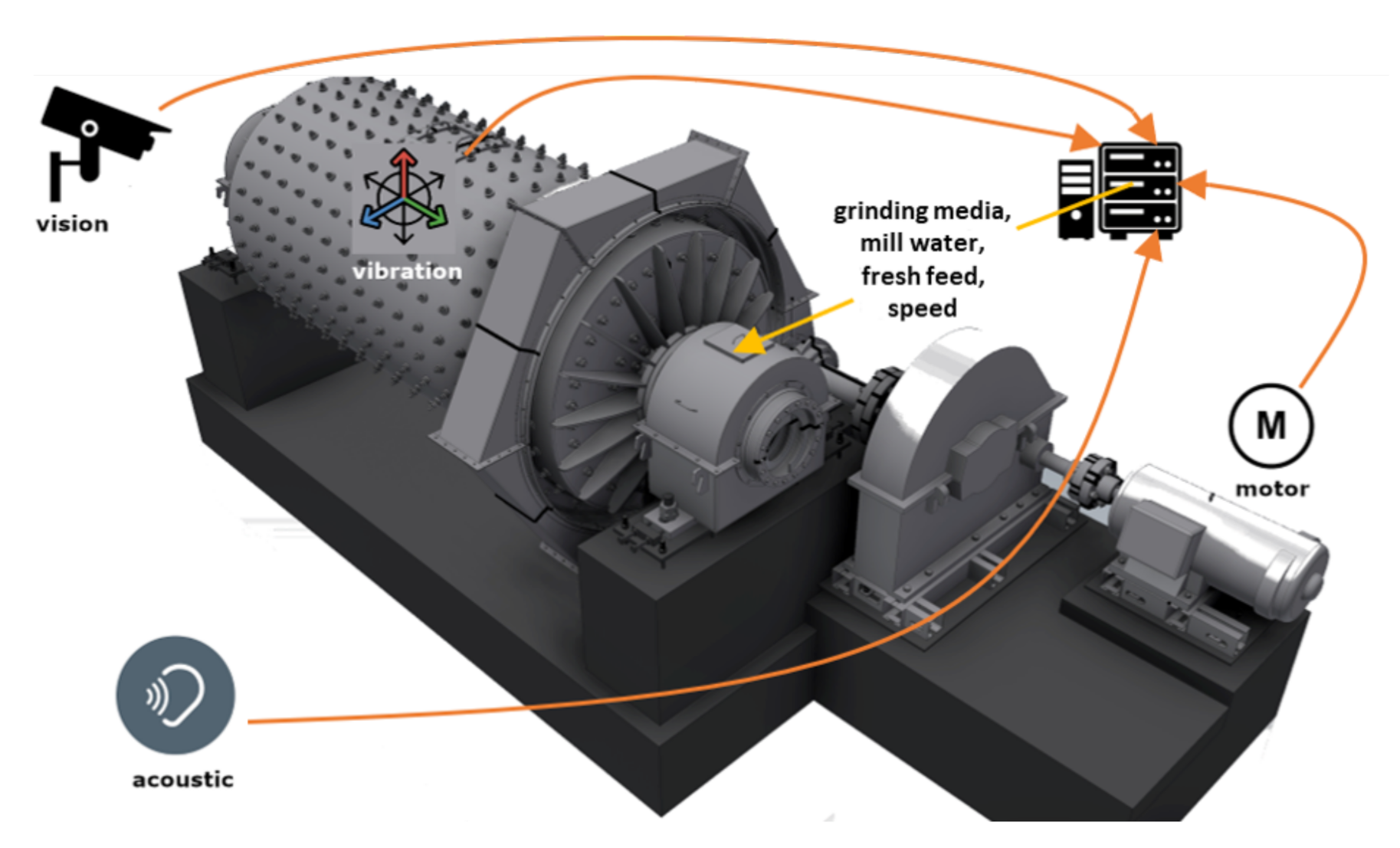
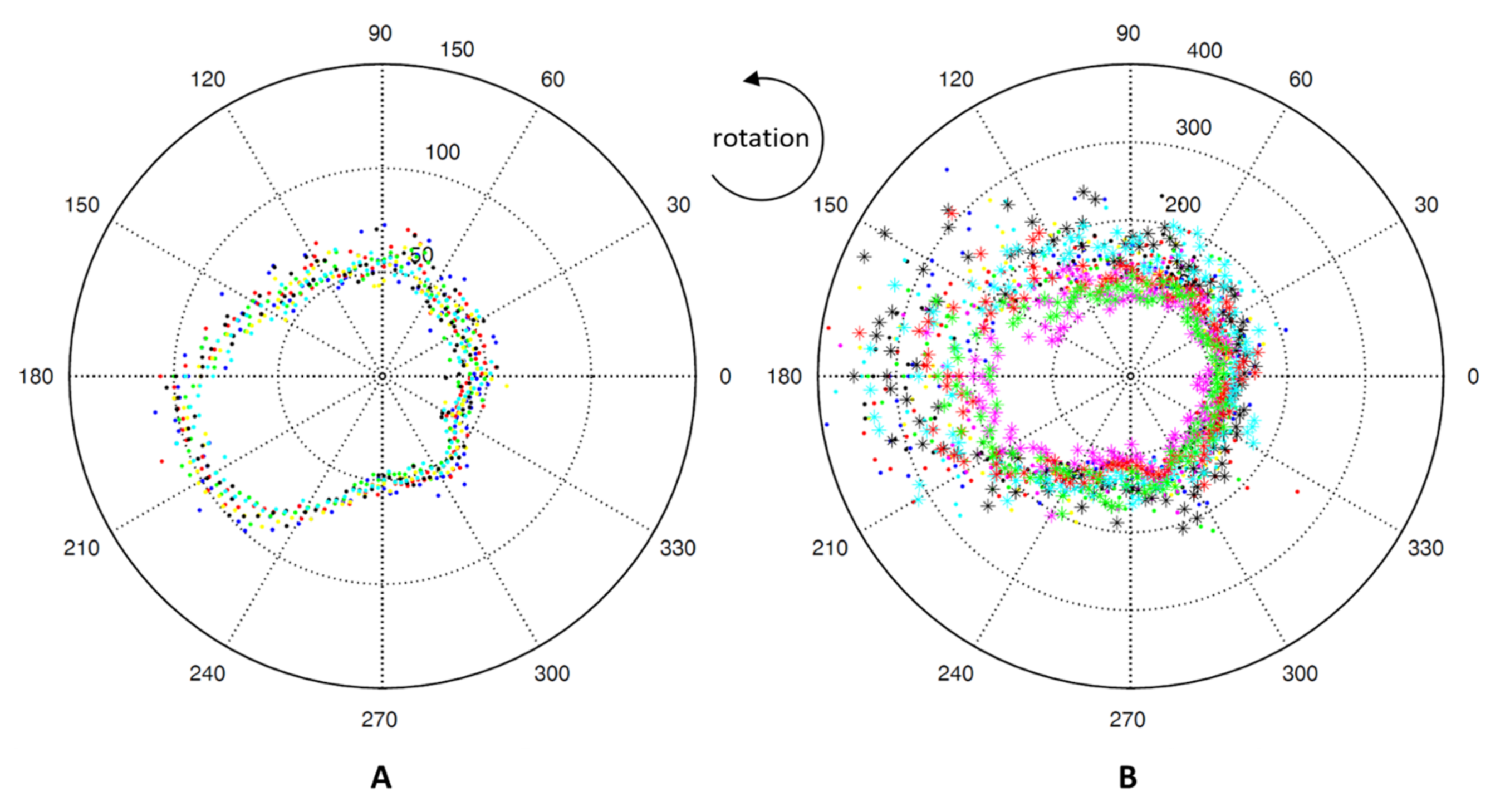
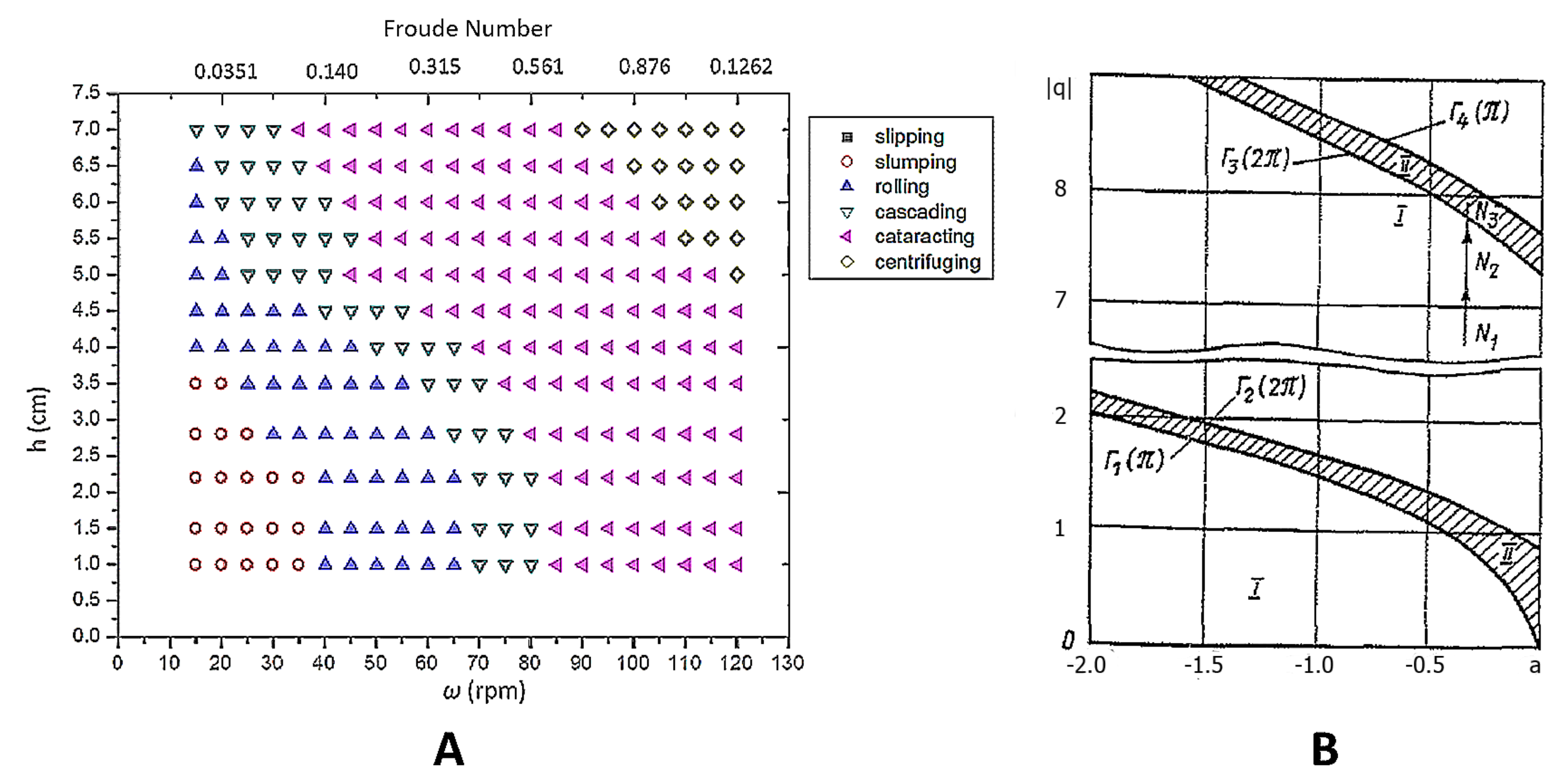
3. Methods of Measurements and Optimization of Tumbling Mills
- Data acquisition methods and instrumentation for such signals are well proven in the industry;
- The price of the equipment is relatively low;
- Probably most importantly—it does not require direct contact of the sensor with the processed, highly abrasive material.
4. Analytical Models of Grinding Process Dynamics
4.1. Mathematical Modelling
- Kick’s equation—for mm
- Bond’s equation—for 50 mm > d > 0.05 mm
- Von Rittinger’s equation—for mmwhere is the grinding work in kWh/t, are the work indexes, usually given in kWh/t, denotes pre-ground particle size, and —the size of the particle after comminution (the values of and are usually taken as from a granulometric curve, which describes the grain’s size, below which the cumulative sum of smaller ones gives 80 percent of material’s mass). However, it should be noted that energy consumption in the comminution processes still has not been theorized to a satisfactory degree [80].
- Quick relative displacements observed at low speeds of mutual sliding of surfaces disappear with increasing speed;
- The amplitude and frequency of the separate displacements depend on the sliding speed, the mass of the moving body and the rigidity of the system;
- The first displacement of contacted bodies is much larger than the subsequent ones.
4.2. Discrete Element Method
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Walkiewicz, J.; Clark, A.; McGill, S. Microwave-assisted grinding. IEEE Trans. Ind. Appl. 1991, 27, 239–243. [Google Scholar] [CrossRef]
- Musa, F.; Morrison, R. A more sustainable approach to assessing comminution efficiency. Miner. Eng. 2009, 22, 593–601. [Google Scholar] [CrossRef]
- BCS Incoprorated for the U.S. Department of Energy: U.S. Mining Industry Energy Bandwidth Study. Available online: https://www.energy.gov/sites/prod/files/2013/11/f4/mining_bandwidth.pdf (accessed on 5 December 2020).
- Jeswiet, J.; Szekeres, A. Energy consumption in mining comminution. Procedia CIRP 2016, 48, 140–145. [Google Scholar] [CrossRef]
- Fuerstenau, D.; Abouzeid, A.Z. The energy efficiency of ball milling in comminution. Int. J. Miner. Process. 2002, 67, 161–185. [Google Scholar] [CrossRef]
- Mular, A. Mineral Processing Plant Design, Practice, and Control Proceedings; Society for Mining, Metallurgy, and Exploration: New York, NY, USA, 2002. [Google Scholar]
- Chelgani, S.C.; Parian, M.; Parapari, P.S.; Ghorbani, Y.; Rosenkranz, J. A comparative study on the effects of dry and wet grinding on mineral flotation separation—A review. J. Mater. Res. Technol. 2019, 8, 5004–5011. [Google Scholar] [CrossRef]
- Wang, Y.; Forssberg, E. Enhancement of energy efficiency for mechanical production of fine and ultra-fine particles in comminution. China Particuol. 2007, 5, 193–201. [Google Scholar] [CrossRef]
- Wills, B.A.; Napier-Munn, T. Comminution. In Wills’ Mineral Processing Technology; Butterworth-Heinemann: Oxford, UK, 2005; Chapter 5; pp. 108–117. [Google Scholar] [CrossRef]
- Sosa-Blanco, C.; Hodouin, D.; Bazin, C.; Lara-Valenzuela, C.; Salazar, J. Economic optimization of a flotation plant through grinding circuit tuning. Miner. Eng. 2000, 13, 999–1018. [Google Scholar] [CrossRef]
- Gao, P.; Zhou, W.; Han, Y.; Li, Y.; Ren, W. Enhancing the capacity of large-scale ball mill through process and equipment optimization: An industrial test verification. Adv. Powder Technol. 2020, 31, 2079–2091. [Google Scholar] [CrossRef]
- Nagar, N.; Garg, H.; Sharma, H.; Angadi, S.; Gahan, C. Influence of Grinding Time on The Bioleaching of Copper from Copper Slag. Biosci. Biotechnol. Res. Commun. 2019, 12, 512–522. [Google Scholar] [CrossRef]
- Jonsen, P.; Palsson, B.; Haggblad, H.A.; Tano, K.; Berggren, A. Simulation of charge and structure behaviour in a tumbling mill. In Proceedings of the European LS-DYNA Users Conference, Strasbourg, France, 23–24 May 2011. [Google Scholar]
- Astrom, K.; Wittenmark, B. Computer-Controlled Systems: Theory and Design; Prentice Hall: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Craig, I. Grinding mill modeling and control: Past, present and future. In Proceedings of the 31st Chinese Control Conference, Anchui, China, 25–27 July 2012; pp. 16–21. [Google Scholar]
- Campbell, J.; Spencer, S.; Sutherland, D.; Rowlands, T.; Weller, K.; Cleary, P.; Hinde, A. SAG mill monitoring using surface vibrations. In Proceedings of the Third International Conference on Autogenous and Semiautogenous Grinding Technology (SAG2001), Vancouver, BC, Canada, 30 September–3 October 2001; Volume 2, pp. 373–385. [Google Scholar]
- Su, Z.; Wang, P.; Yu, X.; Lv, Z. Experimental investigation of vibration signal of an industrial tubular ball mill: Monitoring and diagnosing. Miner. Eng. 2008, 21, 699–710. [Google Scholar] [CrossRef]
- Bai, R.; Chai, T. Optimization control of ball mill load in blending process with data fusion and case-based reasoning. Huagong Xuebao/CIESC J. 2009, 60, 1746–1752. [Google Scholar]
- Tang, J.; Chai, T.; Zhao, L.; Yu, W.; Yue, H. Soft sensor for parameters of mill load based on multi-spectral segments PLS sub-models and on-line adaptive weighted fusion algorithm. Neurocomputing 2012, 78, 38–47. [Google Scholar] [CrossRef]
- Tang, J.; Zhao, L.; Yu, W.; Yue, H.; Chai, T. Soft Sensor Modeling of Ball Mill Load via Principal Component Analysis and Support Vector Machines. In Lecture Notes in Electrical Engineering; Springer: Berlin, Germany, 2010; pp. 803–810. [Google Scholar] [CrossRef]
- Tang, J.; Zhao, L.-j.; Zhou, J.-w.; Yue, H.; Chai, T.-y. Experimental analysis of wet mill load based on vibration signals of laboratory-scale ball mill shell. Miner. Eng. 2010, 23, 720–730. [Google Scholar] [CrossRef]
- Tang, J.; Zhao, L.; Yue, H.; Yu, W.; Chai, T. Vibration Analysis Based on Empirical Mode Decomposition and Partial Least Square. Procedia Eng. 2011, 16, 646–652. [Google Scholar] [CrossRef]
- Das, S.P.; Das, D.P.; Behera, S.K.; Mishra, B.K. Interpretation of mill vibration signal via wireless sensing. Miner. Eng. 2011, 24, 245–251. [Google Scholar] [CrossRef]
- Tang, J.; Chai, T.; Yu, W.; Zhao, L. Modeling Load Parameters of Ball Mill in Grinding Process Based on Selective Ensemble Multisensor Information. IEEE Trans. Autom. Sci. Eng. 2013, 10, 726–740. [Google Scholar] [CrossRef]
- Mohanty, S.; Gupta, K.K.; Raju, K.S. Vibration Feature Extraction and Analysis of Industrial Ball Mill Using MEMS Accelerometer Sensor and Synchronized Data Analysis Technique. Procedia Comput. Sci. 2015, 58, 217–224. [Google Scholar] [CrossRef][Green Version]
- Nayak, D.K.; Das, D.P.; Behera, S.K.; Das, S.P. Monitoring the fill level of a ball mill using vibration sensing and artificial neural network. Neural Comput. Appl. 2019, 32, 1501–1511. [Google Scholar] [CrossRef]
- Behera, B.; Mishra, B.; Murty, C. Experimental analysis of charge dynamics in tumbling mills by vibration signature technique. Miner. Eng. 2007, 20, 84–91. [Google Scholar] [CrossRef]
- Cho, K.S.; Kim, S.H.; Lee, Y.H. Correlation between Acoustic Intensity and Ground Particle Size in Alumina Ball Mill Process. J. Korean Ceram. Soc. 2018, 55, 275–284. [Google Scholar] [CrossRef]
- Aldrich, C.; Theron, D. Acoustic estimation of the particle size distributions of sulphide ores in a laboratory ball mill. J. S. Afr. Inst. Min. Metall. 2000, 100, 243–248. [Google Scholar]
- Pax, R.; Djordjevic, N.; Hocking, R. Non contact acoustics measurement and validation of SAG mill operation. In Proceedings of the XXII International Mineral Processing Congress, Cape Town, South Africa, 29 September–3 October 2003; SAIMM: Cape Town, South Africa, 2003; Volume 1, pp. 371–377. [Google Scholar]
- Wu, D.; Chen, W.; Yan, H.; Fischer, J.; Doolan, C. Identifying grinding mill dynamics using acoustic beamforming and numerical modelling. Powder Technol. 2020, 371, 231–243. [Google Scholar] [CrossRef]
- Zeng, Y.; Forssberg, E. Monitoring grinding parameters by signal measurements for an industrial ball mill. Int. J. Miner. Process. 1993, 40, 1–16. [Google Scholar] [CrossRef]
- Tang, J.; Liu, Z.; Wu, Y.J.; Zhao, L.J. Modeling Difficult-to-Measure Process Parameters Based on Intrinsic Mode Functions Frequency Spectral Features of Mechanical Vibration and Acoustical Signals. Adv. Mater. Res. 2014, 989–994, 3671–3674. [Google Scholar] [CrossRef]
- Tang, J.; Yu, W.; Chai, T.; Liu, Z.; Zhou, X. Selective ensemble modeling load parameters of ball mill based on multi-scale frequency spectral features and sphere criterion. Mech. Syst. Signal Process. 2016, 66–67, 485–504. [Google Scholar] [CrossRef]
- Tang, J.; Chai, T.; Yu, W.; Liu, Z.; Zhou, X. A Comparative Study That Measures Ball Mill Load Parameters Through Different Single-Scale and Multiscale Frequency Spectra-Based Approaches. IEEE Trans. Ind. Inform. 2016, 12, 2008–2019. [Google Scholar] [CrossRef]
- Tang, J.; Qiao, J.; Liu, Z.; Zhou, X.; Yu, G.; Zhao, J. Mechanism characteristic analysis and soft measuring method review for ball mill load based on mechanical vibration and acoustic signals in the grinding process. Miner. Eng. 2018, 128, 294–311. [Google Scholar] [CrossRef]
- Kolacz, J. Measurement system of the mill charge in grinding ball mill circuits. Miner. Eng. 1997, 10, 1329–1338. [Google Scholar] [CrossRef]
- Morrell, S. Power Draw of Grinding Mills—Its measurements and Prediction. In Proceedings of the 5th Mill Operators Conference, Roxby Downs, Australia, 16–20 October 1994. [Google Scholar]
- Melero, M.; Cano, J.; Norniella, J.; Pedrayes, F.; Cabanas, M.; Rojas, C.; Alonso, G.; Aguado, J.M.; Ardura, P. Electric motors monitoring: An alternative to increase the efficiency of ball mills. Renew. Energy Power Qual. J 2014, 849–854. [Google Scholar] [CrossRef]
- Pontt, J. MONSAG: A new monitoring system for measuring the load filling of a SAG mill. Miner. Eng. 2004, 17, 1143–1148. [Google Scholar] [CrossRef]
- Cleary, P. Predicting charge motion, power draw, segregation and wear in ball mills using discrete element methods. Miner. Eng. 1998, 11, 1061–1080. [Google Scholar] [CrossRef]
- Esteves, P.M.; Stopa, M.M.; Filho, B.J.C.; Galery, R. Charge behavior analysis in ball mill by using estimated torque. In Proceedings of the 2014 IEEE Industry Application Society Annual Meeting, Vancouver, BC, Canada, 5–9 October 2014. [Google Scholar] [CrossRef]
- Campbell, J.; Holmes, R.; Spencer, S.; Sharp, V.; Davey, K.; Barker, D.; Phillips, P. The collection and analysis of single sensor surface vibration data to estimate operating conditions in pilot-scale and production-scale AG/SAG mills. In Proceedings of the XXII International Mineral Processing Congress, Cape Town, South Africa, 29 September–3 October 2003; pp. 280–288. [Google Scholar]
- Martins, S.; Li, W.; Radziszewski, P.; Caron, S. Investigating the differences in charge dynamics due to a variation of the instrumented ball properties. IFAC Proc. Vol. 2007, 12, 463–468. [Google Scholar] [CrossRef]
- Martins, S.; Li, W.; Radziszewski, P.; Caron, S.; Aguanno, M.; Bakhos, M.; Petch, E.L. Validating the instrumented ball outputs with simple trajectories. Miner. Eng. 2008, 21, 782–788. [Google Scholar] [CrossRef]
- Martins, S.; Li, W.; Radziszewski, P.; Faucher, A.; Makni, S. Experimental and simulated instrumented ball in a tumbling mill—A comparison. Miner. Eng. 2013, 43–44, 79–84. [Google Scholar] [CrossRef]
- Coetzee, L. Stabilising and optimising a primary closed-loop milling circuit feeding a flotation circuit using StarCS RNMPC. In Proceedings of the 19th IFAC World Congress on International Federation of Automatic Controll Congress, Cape Town, South Africa, 24–29 August 2014; Volume 47, pp. 9786–9791. [Google Scholar] [CrossRef]
- Coetzee, L.; Ramonotsi, M. Applying StarCS RNMPC with Real-Time Optimiser to Pilanesberg Platinum Mines Primary UG2 Milling Circuit. IFAC-PapersOnLine 2016, 49, 78–83. [Google Scholar] [CrossRef]
- Outotec. Outotec Automation Solutions for Grinding Optimization. Available online: https://www.outotec.com/globalassets/products/analyzers-and-automation/ote_act_grinding_optimization_eng.pdf (accessed on 5 November 2020).
- FLSmidth. Maximize Grinding Efficiency with LoadIQ. Available online: https://www.kscape.com/loadiq (accessed on 5 November 2020).
- Thwaites, P. Developments in Process Control—Grinding Controls. 2015. Available online: https://xps.ca/files/31/Presentations/131/Developments-in-Process-Control—Grinding-Controls-by-P-Thwaites.pdf (accessed on 5 November 2020).
- AMEplus. MillVis: System for the Optimization of the Grinding Process Control. Available online: https://www.ameplus.pl/tag/millvis/ (accessed on 5 November 2020).
- Chai, T.; Ding, J. Integrated automation system for hematite ores processing and its applications. Meas. Control 2006, 39, 140–146. [Google Scholar]
- Kuzba, B.; Pawlos, W.; Konieczny, A.; Krzeminska, M. Optimisation Platform for copper ore processing at the Division of Concentrator of KGHM Polska Miedz SA. In Proceedings of the E3S Web of Conferences; EDP Sciences: Les Ulis, France, 2016; Volume 8, p. 01037. [Google Scholar]
- Zhou, P.; Chai, T.; Wang, H. Intelligent Optimal-Setting Control for Grinding Circuits of Mineral Processing Process. IEEE Trans. Autom. Sci. Eng. 2009, 6, 730–743. [Google Scholar] [CrossRef]
- Deineka, K.; Naumenko, Y. Revealing the effect of decreased energy intensity of grinding in a tumbling mill during selfexcitation of autooscillations of the intrachamber fill. Eastern-Eur. J. Enterp. Technol. 2019, 1, 6–15. [Google Scholar] [CrossRef]
- Maryuta, A. Frictional Oscillations in Mechanical Systems; Nedra: Moscow, Russia, 1993; p. 240. [Google Scholar]
- Naumenko, Y. Fundamentals of the Theory of Working Processes of Drum Mills; NUVGP: Rivne, Ukraine, 2014; p. 336. [Google Scholar]
- Deineka, K.; Naumenko, Y. Establishing the effect of a decrease in power intensity of self-oscillating grinding in a tumbling mill with a reduction in an intrachamber fill. Eastern-Eur. J. Enterp. Technol. 2019, 6, 43–52. [Google Scholar] [CrossRef]
- Alekseyev, M.; Alkhori, F. Automated control of ore-pebble mill charge by the signal of active power of magnetic separator electric motor. Sci. Bull. Natl. Min. Univ. Ukraine 2014, 3, 71–76. [Google Scholar]
- Atutxa, I.; Legarra, I. Stepping forward: Using variable speed drives for optimizing the grinding process in SAG and ball mills. In Proceedings of the Sixth International Conference on Semi-Autogenous High Pressure Grinding Technology, Vancouver, BC, Canada, 20–24 September 2015. [Google Scholar]
- Smotritskiy, A.; Smotritskiy, A.; Boriskov, F.; Chervyakov, S. Method for Grinding Materials in Rotating Drum Using Ferromagnetic Grinding Bodies. EU Patent EP3020483B1, 8 July 2013. [Google Scholar]
- Vertimill. Metso Mining. Available online: https://www.metso.com/products/grinding-mills/stirred-mills/vertimill/ (accessed on 5 November 2020).
- Isamill. Glencore Technology. Available online: https://www.isamill.com/en/downloads/Brochures/IsaMillBrochure.pdf (accessed on 5 November 2020).
- Krot, P. Telemetering systems for monitoring dynamic loads in drive lines of rolling mills. Vib. Mach. Meas. Reduct. Prot. 2008, 1, 46–53. [Google Scholar]
- Krot, P. Methods and instrumentation for measuring wear in drivelines of rolling mills. Metall. Process. Equip. 2003, 2, 45–53. [Google Scholar]
- Krot, P. Dynamics and diagnostics of the rolling mills drivelines with non-smooth stiffness characteristics. In Proceedings of the 3rd International Conference of Nonlinear Dynamic (ND-KhPI2010), Kharkov, Ukraine, 21–24 September 2012; pp. 115–120. [Google Scholar]
- Tang, J.; Chai, T.Y.; Cong, Q.M.; Liu, Z.; Yu, W. Modeling mill load parameters based on selective fusion of multi-scale shell vibration frequency spectra. Kongzhi Lilun Yu Yingyong/Control Theory Appl. 2015, 32, 1582–1591. [Google Scholar] [CrossRef]
- Meshcheryakov, L. Recognition of the operational state of the lining of drum mill. Sci. Bull. Natl. Min. Univ. Ukraine 2018, 53, 200–213. [Google Scholar]
- Vinogradov, B. Dynamics of Tumbling Mills; Economic Herald of State Higher Educational Institution, USUCT: Dnipro, Ukraine, 2004. [Google Scholar]
- Vinogradov, B.; Khristenko, A. The forced vibrations are in twin-engine synchronous drives of ball mills. Sci. Bull. Natl. Min. Univ. Ukraine 2012, 6, 72–76. [Google Scholar]
- Krot, P.V. Dynamical processes in a multi-motor gear drive of heavy slabbing mill. J. Vibroeng. 2019, 21, 2064–2081. [Google Scholar] [CrossRef]
- Borodai, V.; Borovyk, R.; Nesterova, O. Efficient transient modes of synchronous drive for mining and smelting mechanisms. Mech. Mater. Sci. Eng. J. 2017, 8. [Google Scholar] [CrossRef]
- Putnoki, A.; Klevtsov, O.; Ermolenko, A.; Verenev, V.; Krot, P. Evaluation of operation of equipment at the rolling mill. Stal 2003, 10, 56–58. [Google Scholar]
- Maryuta, A.; Kovalenko, A.; Meshcheryakov, L. Method for Determining Wear of Shaped Linings in Grinding Aggregate. Patent SU709173, 15 January 1980. [Google Scholar]
- Beke, B. The Process of Fine Grinding, 1st ed.; Springer: Dordrecht, The Netherlands, 1981; Volume 1. [Google Scholar] [CrossRef]
- Nussbaumer, H.J. Fast Fourier Transform and Convolution Algorithms; Springer: Berlin, Germany, 1982. [Google Scholar] [CrossRef]
- Konieczny, A.; Ogonowski, S.; Kurzydlo, M.; Foszcz, D. Vision systems in O/ZWR as a support tool for production management and optimization. In Proceedings of the Mineral Engineering Conference (MEC2014), Istebna, Poland, 15–18 September 2014. [Google Scholar]
- Thomas, A.; Filippov, L. Fractures, fractals and breakage energy of mineral particles. Int. J. Miner. Process. 1999, 57, 285–301. [Google Scholar] [CrossRef]
- Naziemiec, Z.; Saramak, D. Analiza energochłonności procesów rozdrabniania kruszyw mineralnych. Prace Naukowe Instytutu Górnictwa Politechniki Wrocławskiej. Studia i Materiały 2012, 134, 209–220. [Google Scholar]
- Weidenbaum, S.S. Mixing of solids. In Advances in Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 1958; Volume 2, pp. 209–324. [Google Scholar]
- Heim, A.; Gluba, T.; Obraniak, A. Bed dynamics during drum granulation. Fizykochemiczne Problemy Mineralurgii/Physicochem. Probl. Miner. Process. 2004, 38, 167–176. [Google Scholar]
- Maryuta, A.N. Analysis of motion of mechanical systems with frictional interaction. Sov. Appl. Mech. 1989, 25, 1031–1040. [Google Scholar] [CrossRef]
- Butikov, E.I. Analytical expressions for stability regions in the Ince–Strutt diagram of Mathieu equation. Am. J. Phys. 2018, 86, 257–267. [Google Scholar] [CrossRef]
- Mardiansyah, Y.; Khotimah, S.; Viridi, S. Characterization of motion modes of pseudo-two dimensional granular materials in a vertical rotating drum. J. Phys. Conf. Ser. 2016, 739, 012148. [Google Scholar] [CrossRef]
- Marjuta, A.; Krot, P. High frequency rolling mills chatter–mathematical identification and simulation. In Proceedings of the 1st International Symposium on “Multi-Body Dynamics Monitoring and Simulation Techniques”, Bradford, UK, 25–27 March 1997; pp. 407–419. [Google Scholar]
- Krot, P. Parametrical vibrations in the rolling mills. Collect. Sci. Pap. Natl. Min. Acad. Ukraine 2002, 3, 15–21. [Google Scholar]
- Krot, P. Investigation of ’ribbing’ defect and high-frequency oscillations of mills for strip cold rolling. Proizvod. Prokata 2002, 3, 21–23. [Google Scholar]
- Kragelsky, I.; Dobychin, M.; Kombalov, V. Friction and Wear: Calculation Methods; Pergamon Press: Oxford, UK, 1982; p. 474. [Google Scholar]
- Arbiter, N.; Harris, C. Scale-up and dynamics of large grinding mills-a case study. In Design and Installation of Comminution Circuits; AIME: New York, NY, USA, 1982; pp. 491–508. [Google Scholar]
- Moys, M. A model of mill power as affected by mill speed, load volume, and liner design. J. S. Afr. Inst. Min. Metall. 1993, 93, 135–141. [Google Scholar]
- Abou, S.C.; Tarasiewicz, S.; Remy, M. Mathematical modelling of ball mill charge slippage: Geometric approach. In Proceedings of the 4e Conférence International sur l’Automatisation Industrielle, Montréal, QC, Canada, 9–11 June 2003; CIAI: Montreal, QC, Canada, 2003. [Google Scholar] [CrossRef]
- Wang, Z.H.; Han, Y.X.; Chen, B.C. A Mathematical Model for Predicting the Internal Parameters of Ball Mill. Adv. Mater. Res. 2012, 454, 151–156. [Google Scholar] [CrossRef]
- Silva, M.; Casali, A. Modelling SAG milling power and specific energy consumption including the feed percentage of intermediate size particles. Miner. Eng. 2015, 70, 156–161. [Google Scholar] [CrossRef]
- Kozicki, J.; Donze, F. YADE-OPEN DEM: An opensource software using a discrete element method to simulate granular material. Eng. Comput. 2008, 26. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Mishra, B.; Rajamani, R.K. The discrete element method for the simulation of ball mills. Appl. Math. Model. 1992, 16, 598–604. [Google Scholar] [CrossRef]
- Mishra, B.K.; Rajamani, R.K. Motion Analysis in Tumbling Mills by the Discrete Element Method. KONA Powder Part. J. 1990, 8, 92–98. [Google Scholar] [CrossRef]
- Agrawala, S.; Rajamani, R.; Songfack, P.; Mishra, B. Mechanics of media motion in tumbling mills with 3d discrete element method. Miner. Eng. 1997, 10, 215–227. [Google Scholar] [CrossRef]
- Radiszewski, P. Comparing three DEM charge motion models. Miner. Eng. 1999, 12, 1501–1520. [Google Scholar] [CrossRef]
- Powell, M.; Nurick, G. A study of charge motion in rotary mills Part 1—Extension of the theory. Miner. Eng. 1996, 9, 259–268. [Google Scholar] [CrossRef]
- Mishra, B.; Rajamai, R.K. Simulation of charge motion in ball mills. Part 2: Numerical simulations. Int. J. Miner. Process. 1994, 40, 187–197. [Google Scholar] [CrossRef]
- Radziszewski, P.; Tarasiewicz, S. Ballmill simulation: Part II—Numerical solution to ballcharge model. Trans. Soc. Comput. Simul. 1989, 6, 75–88. [Google Scholar]
- Powell, M.; McBride, A. A three-dimensional analysis of media motion and grinding regions in mills. Miner. Eng. 2004, 17, 1099–1109. [Google Scholar] [CrossRef]
- Djordjevic, N. Influence of charge size distribution on net-power draw of tumbling mill based on DEM modelling. Miner. Eng. 2005, 18, 375–378. [Google Scholar] [CrossRef]
- Cleary, P.W.; Morrison, R.D. Prediction of 3D slurry flow within the grinding chamber and discharge from a pilot scale SAG mill. Miner. Eng. 2012, 39, 184–195. [Google Scholar] [CrossRef]
- Jahani Chegeni, M. Combined DEM and SPH simulation of ball milling. J. Min. Environ. 2019, 10, 151–161. [Google Scholar] [CrossRef]
- Walton, O. Particle-Dynamics Calculations of Shear Flow. In Mechanics of Granular Materials—New Models and Constitutive Relations; Elsevier: Amsterdam, The Netherlands, 1983; pp. 327–338. [Google Scholar] [CrossRef]
- Ting, J.M.; Khwaja, M.; Meachum, L.R.; Rowell, J.D. An ellipse-based discrete element model for granular materials. Int. J. Numer. Anal. Methods Geomech. 1993, 17, 603–623. [Google Scholar] [CrossRef]
- Cundall, P. Formulation of a three-dimensional distinct element model—Part I. A scheme to detect and represent contacts in a system composed of many polyhedral blocks. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1988, 25, 107–116. [Google Scholar] [CrossRef]
- Hocking, G. The discrete element method for analysis of fragmentation of discontinua. Eng. Comput. 1992, 9, 145–155. [Google Scholar] [CrossRef]
- Lin, X.; Ng, T.T. A three-dimensional discrete element model using arrays of ellipsoids. Geotechnique 1997, 47, 319–329. [Google Scholar] [CrossRef]
- Williams, J.R.; Pentland, A.P. Superquadrics and modal dynamics for discrete elements in interactive design. Eng. Comput. 1992, 9, 115–127. [Google Scholar] [CrossRef]
- Favier, J.; Fard, M.; Kremmer, M.; Raji, A. Shape representation of axi-symmetrical, non-spherical particles in discrete element simulation using multi-element model particles. Eng. Comput. Int. J. Comput.-Aided Eng. 1999, 16, 467–480. [Google Scholar] [CrossRef]
- Zhong, W.; Yu, A.; Liu, X.; Tong, Z.; Zhang, H. DEM/CFD-DEM modelling of non-spherical particulate systems: Theoretical developments and applications. Powder Technol. 2016, 302, 108–152. [Google Scholar] [CrossRef]

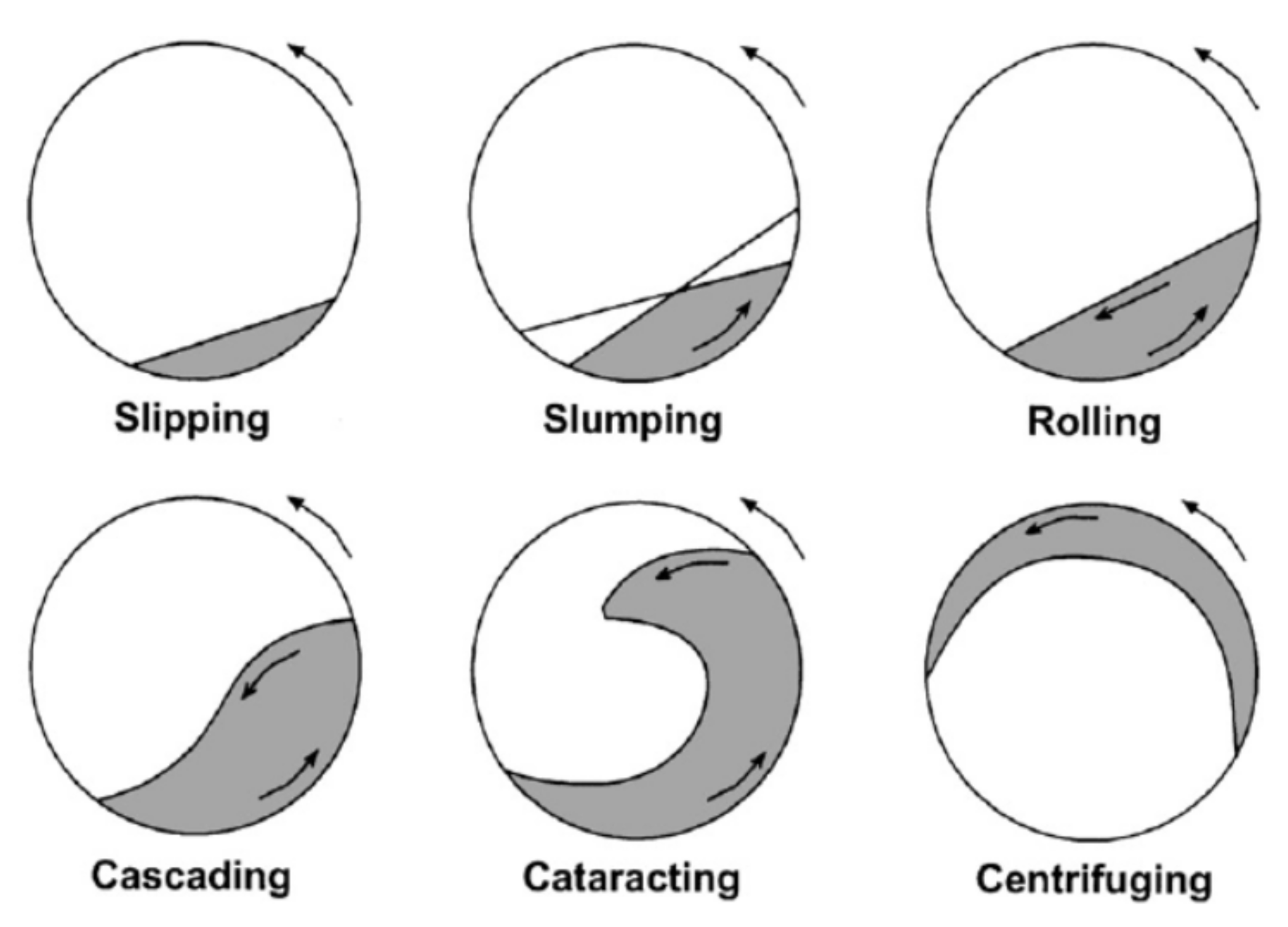
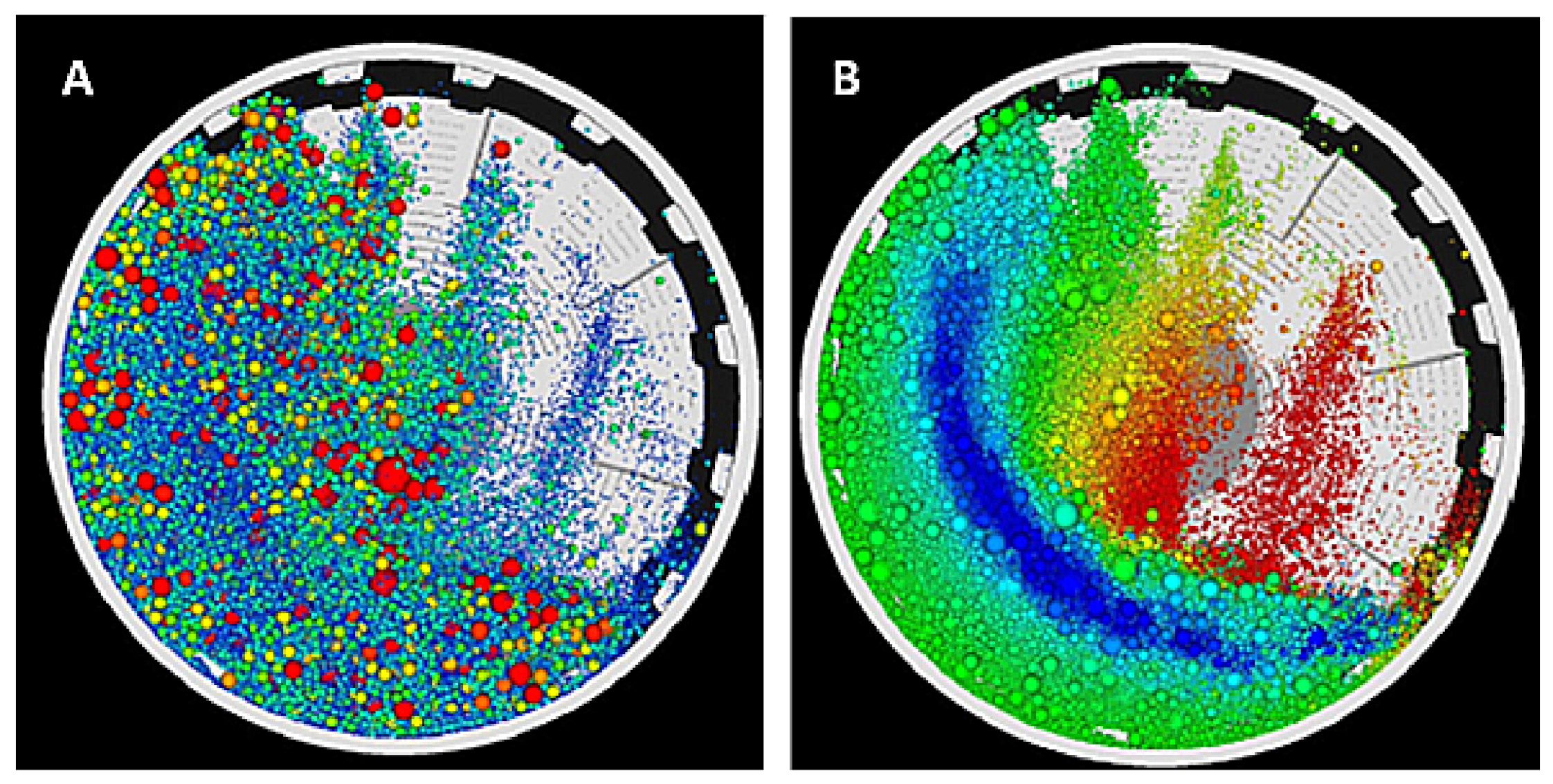
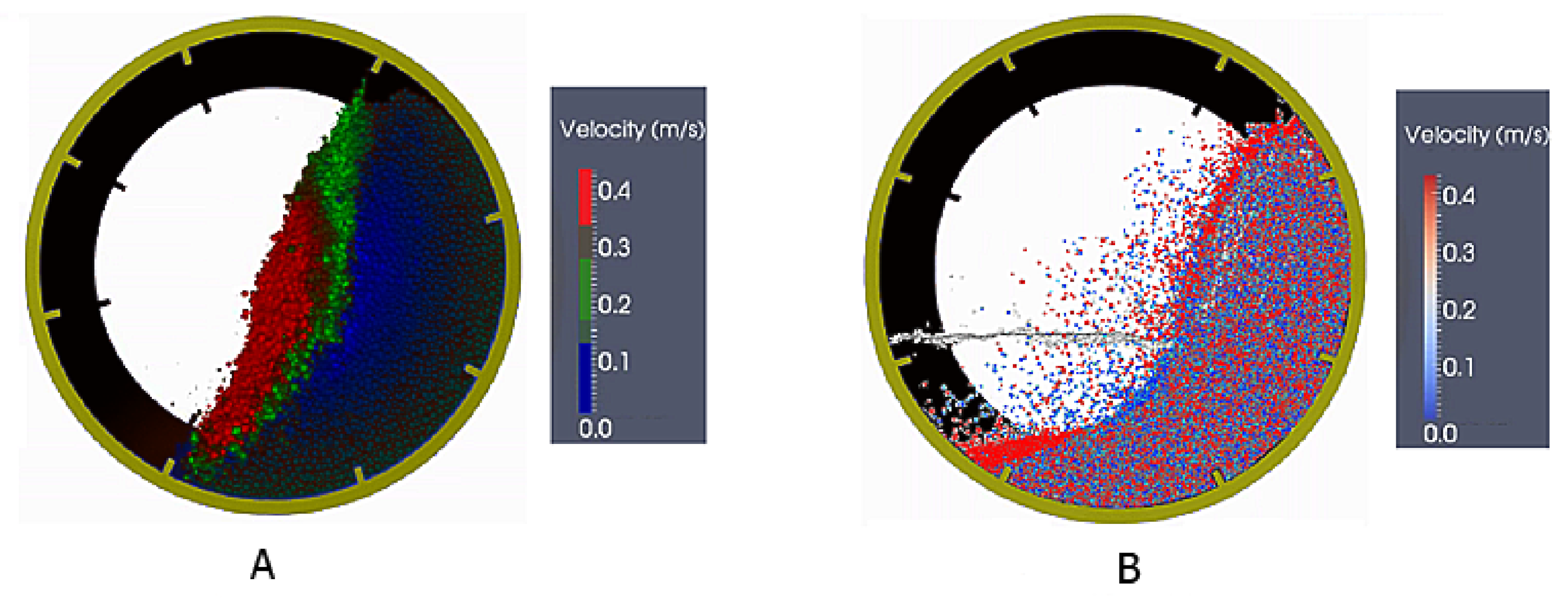
| Signal Monitored | Work |
|---|---|
| Vibration | [16,17,18,19,20,21,22,23,24,25,26,27,32,33,34,35,36,37,68] (with use of strain transducer), [43,51] (estimated based on torque), [54] |
| Acoustic Emission | [24,28,29,30,31,32,33,34,35,36,51,54] |
| Power Draw | [38,51,69] |
| Instrumented Ball | [44,45,46] |
| Vision | [46,51,54] |
| Other | [24]—motor current, [39]—torque, [40]—bearing pressure and motor vector control, [42]—torque signal estimated on the basis of angular position and motor electric signals, [55]—product particle size (PPS) soft sensor |
| Purpose of Measurement | Work |
|---|---|
| Power draw reduction | [32] |
| Wear reduction | [31,43,54] |
| Particle size distribution optimization | [25,28,29,32,51,54,55] |
| Detection of characteristic working conditions | [17,23,27,51] |
| Fill level/behaviour | [16,18,19,20,21,22,26,30,31,34,37,39,40,42,44,45,68] |
| Other | [32]—pulp temperature, [51,55]—throughput maximization, [46]—DEM tuning, [69]—wear diagnostics of liners |
| Signal Measured/Process Parameters | Fill Level | Balls Wear | Liners Wear | Particle Size Distribution |
|---|---|---|---|---|
| Acoustic | ✓ | ✓ | ✓ | |
| Vibration | ✓ | ✓ | ✓ | |
| Vision | ✓ | |||
| Power draw | ✓ | ✓ | ✓ | |
| Torque | ✓ | |||
| Other signals from electric motor | ✓ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Góralczyk, M.; Krot, P.; Zimroz, R.; Ogonowski, S. Increasing Energy Efficiency and Productivity of the Comminution Process in Tumbling Mills by Indirect Measurements of Internal Dynamics—An Overview. Energies 2020, 13, 6735. https://doi.org/10.3390/en13246735
Góralczyk M, Krot P, Zimroz R, Ogonowski S. Increasing Energy Efficiency and Productivity of the Comminution Process in Tumbling Mills by Indirect Measurements of Internal Dynamics—An Overview. Energies. 2020; 13(24):6735. https://doi.org/10.3390/en13246735
Chicago/Turabian StyleGóralczyk, Mateusz, Pavlo Krot, Radosław Zimroz, and Szymon Ogonowski. 2020. "Increasing Energy Efficiency and Productivity of the Comminution Process in Tumbling Mills by Indirect Measurements of Internal Dynamics—An Overview" Energies 13, no. 24: 6735. https://doi.org/10.3390/en13246735
APA StyleGóralczyk, M., Krot, P., Zimroz, R., & Ogonowski, S. (2020). Increasing Energy Efficiency and Productivity of the Comminution Process in Tumbling Mills by Indirect Measurements of Internal Dynamics—An Overview. Energies, 13(24), 6735. https://doi.org/10.3390/en13246735








