RAST-K v2—Three-Dimensional Nodal Diffusion Code for Pressurized Water Reactor Core Analysis
Abstract
1. Introduction
2. Calculation Models
2.1. Nodal Diffusion Analysis
2.2. Cross-Section Model
- Fuel temperature: 4 points, ranging from 293.6 K to 1500 K
- Moderator temperature: 12 points, ranging from 293.6 K to the input moderator temperature + 25 K
- Boron concentration: 4 points, ranging from 0.1 ppm to 2400 ppm
- Geometry: 4 points for geometry changes (generally for control rod)
- State points: burnup, fuel and moderator temperature, boron concentration, control rod
- Group-wise assembly/corner discontinuity factors
- 1-group power distribution (gamma smeared power distribution)
- 1-group form function for pin power reconstruction
- 1-group xenon and samarium chain data
- Group-wise macroscopic cross-section,
- Number density, and
- Delayed neutron and kinetics data
- Data for detector signal reconstruction
- Decay constants and fission yield data
2.3. Internal TH Solver
- The coolant flow is parallel to the channel; that is, the cross-flow is ignored.
- The core-exit coolant is sub-cooled.
- The power produced by the fuel rods within a node is deposited into the coolant in that node.
- The pressure drop across the core is assumed to be negligible.
- All water properties are evaluated at a single pressure.
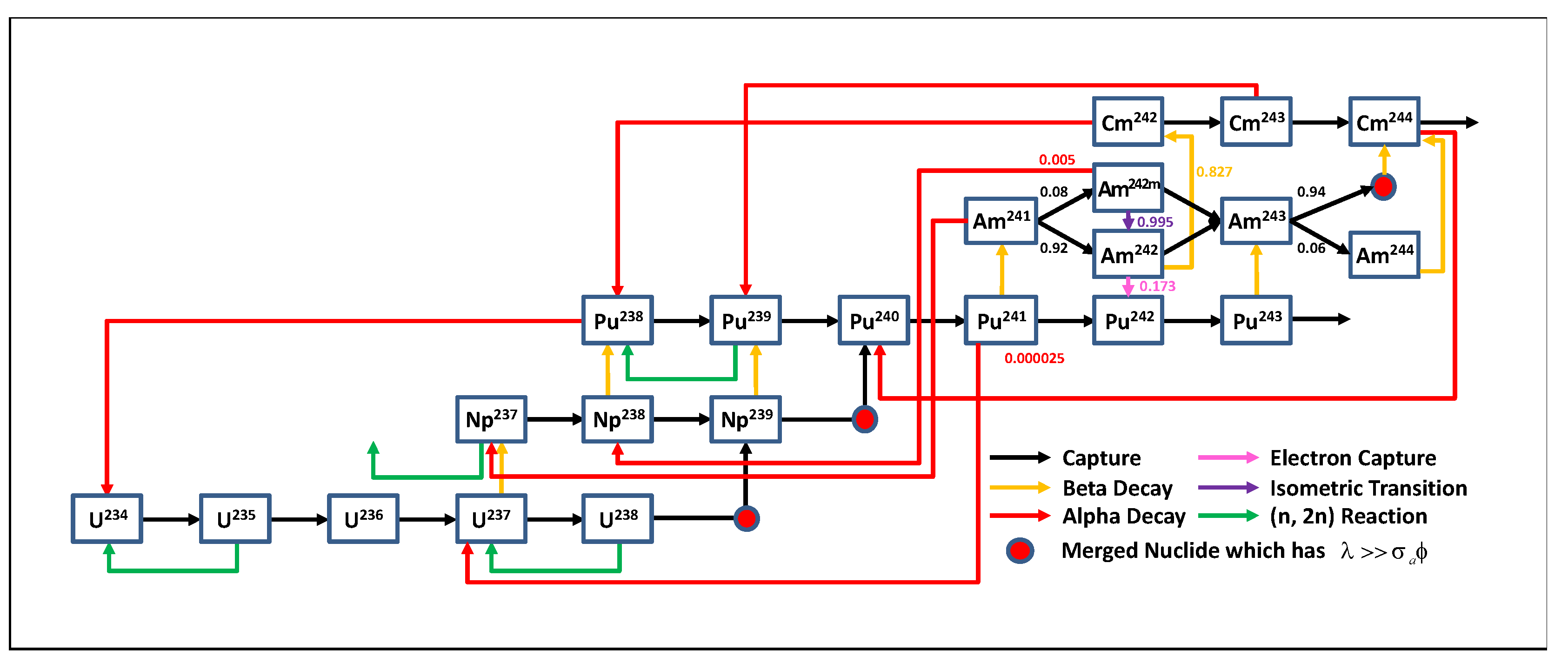
2.4. Fuel Cycle Analysis
3. Engineering Features
3.1. Multi-Cycle Simulation
3.2. Pin Power Reconstruction
3.3. Parameter Edits
3.4. Burnup Adaptation
3.5. CRUD Modeling
3.6. Spent Nuclear Fuel Analysis
4. Applications
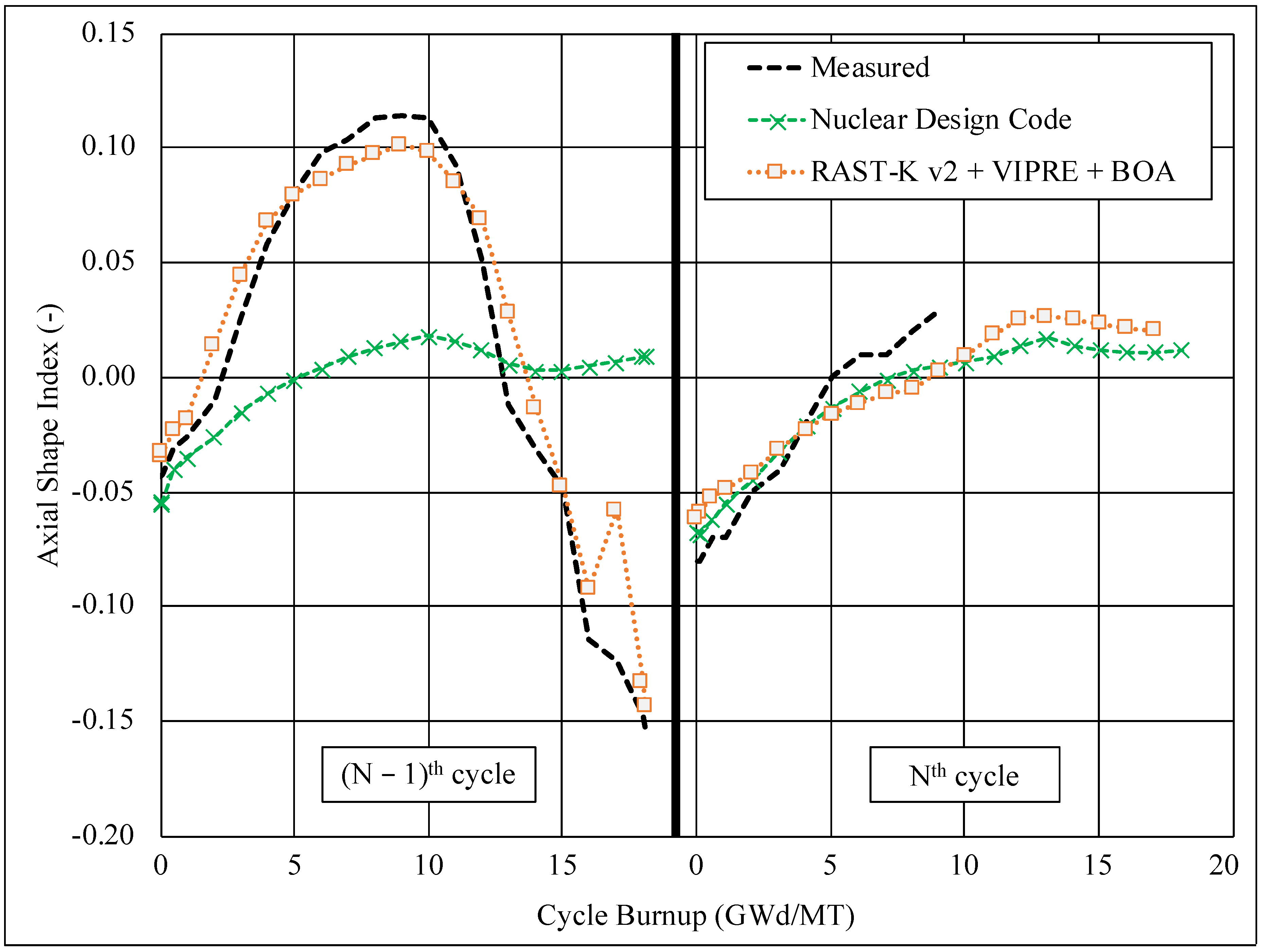
4.1. Verifications and Validation
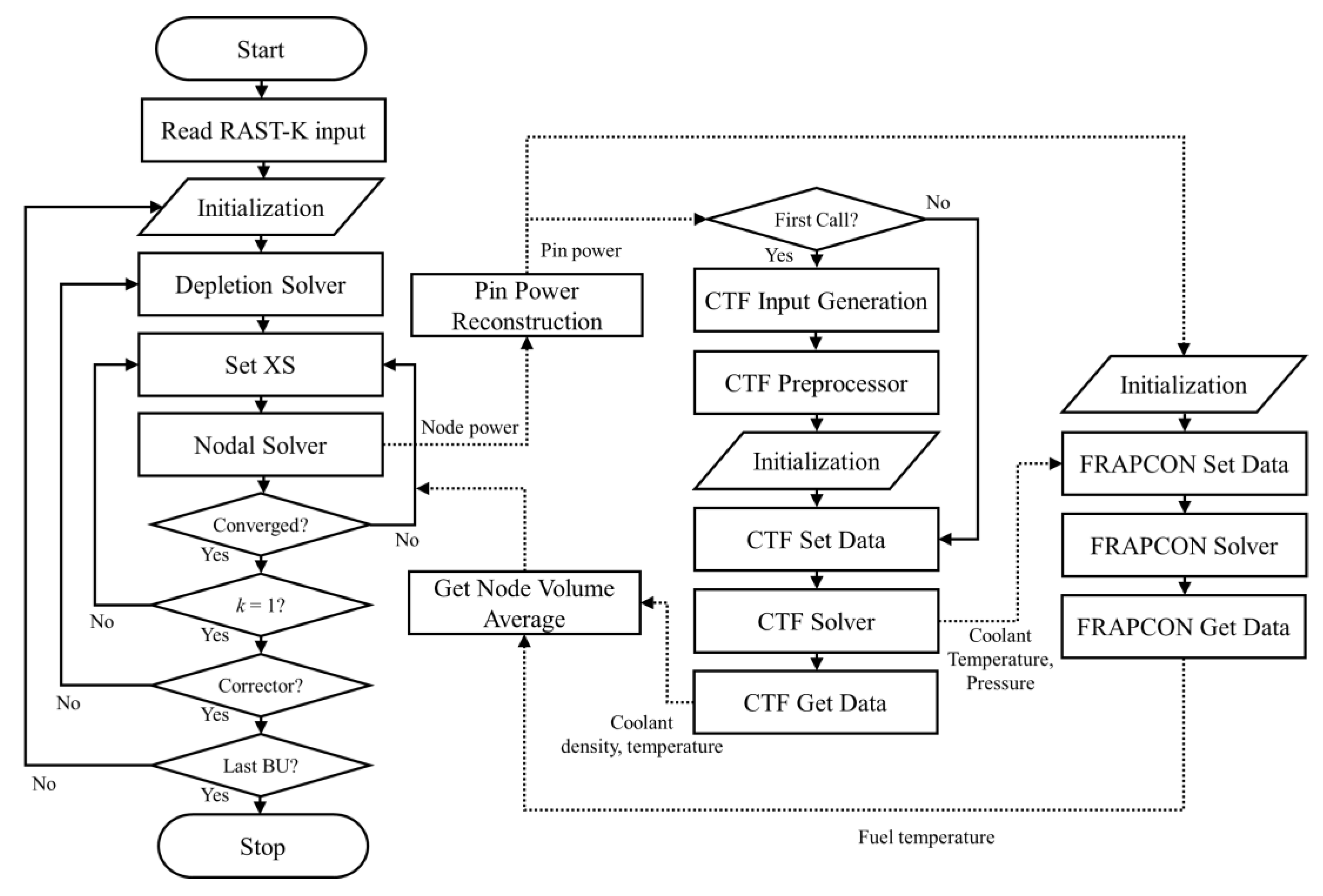
4.2. Internal Loose Coupling
4.3. External Loose Coupling
4.4. Machine Learning
- RAST-K v2 can provide an accurate solution for nuclear reactor cores with only a small difference compared to the measured data. Hence, RAST-K v2 can be used to develop ML models, which can be further used in a real nuclear power plant (NPP).
- Various reactor core models, even the ones whose operating conditions are unacceptable for safety reasons, can be modeled using RAST-K v2. Data on abnormal core conditions such as CRUD deposition can be employed to train ML models in a nuclear diagnostics system.
- RAST-K v2 can generate a substantial amount of nuclear data owing to the implemented acceleration methods, and such data can be used for efficiently training ML models within the stipulated time.
- RAST-K v2 can provide various nuclear reactor parameters for prioritizing LPs in SA algorithms or mimicking the core monitoring system of NPPs to develop a diagnostic system.
- Generation of normal and abnormal core models by randomly perturbing the input parameters such as the positions of the individual control rod and multiplication factor of the CRUD accumulation model,
- Running RAST-K v2 for all generated input files,
- Extraction of target output parameters from output files and writing them in a single train dataset file with “csv” format.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Studsvik Scandpower. SIMULATE-3: Advanced Three-Dimensional Two-Group Reactor Analysis Code User’s Manual; Technical Report No. SSP-09/447-U; Studsvik Scandpower: Nyköping, Sweden, 2009. [Google Scholar]
- Downar, T.; Xu, Y.; Seker, V. PARCS, v3.0 US NRC Core Neutronics Simulator User Manual; Technical report No. UM-NERS-09-0001; University of Michigan: Ann Arbor, MI, USA, 2013. [Google Scholar]
- Cho, J.; Song, J.; Lee, K. Three dimensional nuclear analysis system DeCART/CHORUS/MASTER. In Proceedings of the ANS Annual Meeting, Atlanta, GA, USA, 16–20 June 2013. [Google Scholar]
- Lee, C.; Cho, B.; Song, J.; Kim, J.; Kim, H.; Zee, S.; Joo, H. Verification of Extended Nuclide Chain of MASTER with CASMO-3 and HELIOS; Technical Report No. KAERI/TR-947/98; Korea Atomic Energy Research Institute: Yuseong-gu, Korea, 1998. [Google Scholar]
- Han, T.; Yoon, J.; Kim, J.; Lee, C.; Cho, B. Benchmark verification of the KARMA/ASTRA code with OECD/NEA and USNRC PWR MOX/UO2 transient problem. In Proceedings of the ICAPP 2011, Paris, France, 10 October 2011. [Google Scholar]
- Tatsumi, M.; Yamamoto, A. advanced PWR core calculation based on multi-group nodal-transport method in three-dimensional pin-by-pin geometry. J. Nucl. Sci. Technol. 2003, 40, 376–387. [Google Scholar] [CrossRef]
- Ober, T.G.; Stork, J.C.; Rickard, I.C.; Gasper, J.K. Theory, Capabilities, and Use of the Three-Dimensional Reactor Operation and Control Simulator (ROCS). Nucl. Sci. Eng. 1977, 64, 604–623. [Google Scholar] [CrossRef]
- African National Congress. A Westinghouse Advanced Nodal Computer Code; Technical Report No. WCAP-10965-P-A; African National Congress: Johannesburg, South Africa, 1986. [Google Scholar]
- Lee, E.K.; Shin, H.C.; Bae, S.M.; Lee, Y.K. New dynamic method to measure rod WORTHS in zero power physics test at PWR startup. Ann. Nucl. Energy 2005, 32, 1457–1475. [Google Scholar] [CrossRef]
- Kim, S.; Lee, E.; Kim, Y.; Lee, D. Development of a coupled code system based on SPACE safety analysis code and RAST-K three-dimensional neutronics code. In Proceedings of the NURETH-16, Chicago, IL, USA, 30 August–4 September 2015. [Google Scholar]
- Choe, J.; Choi, S.; Zhang, P.; Park, J.; Kim, W.; Shin, H.C.; Lee, H.S.; Jung, J.E.; Lee, D. Verification and Validation of STREAM/RAST-K for PWR Analysis. Nucl. Eng. Technol. 2019, 51, 356–368. [Google Scholar] [CrossRef]
- Tran, T.Q.; Cherezov, A.; Du, X.; Park, J.; Lee, D. Development of hexagonal-z geometry capability in RAST-K for fast reactor analysis. In Proceedings of the ICENES 2019, Bali, Indonesia, 6–9 October 2019. [Google Scholar]
- Jang, J.; Tran, T.Q.; Dzianisau, S.; Lee, W.; Lee, D. Verification of RAST-K hexagonal analysis module with SNR and VVER-440 benchmarks. In Proceedings of the KNS Winter Meeting, Korea (online), 16–18 December 2020. [Google Scholar]
- Jang, J.; Cherezov, A.; Jo, Y.; Tran, T.Q.; Dzianisau, S.; Lee, W.; Park, J.; Lee, D. Verification of RAST-K hexagonal transient solver with OECD/NEA benchmark problem of KALININ-3 NPP. In Proceedings of the KNS Winter Meeting, Korea (online), 16–18 December 2020. [Google Scholar]
- Smith, K.S. Nodal method storage reduction by nonlinear iteration. Trans. Am. Nucl. Soc. 1983, 44, 265–266. [Google Scholar]
- Smith, K.S. An Analytic Nodal Method for Solving the Two-Group, Multidimensional, Static and Transient Neutron Diffusion Equations. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1979. [Google Scholar]
- Joo, H.G.; Jiang, G.; Downar, T.J. A hybrid ANM/NEM interface current technique for the nonlinear Nodal calculation. In Proceedings of the ANS Conference Mathematics Computational, Saratoga, NY, USA, 5–9 October 1997. [Google Scholar]
- Lee, H. Unified Nodal Method for Static and Transient Analysis of Power Reactor. Ph.D. Thesis, Seoul National University, Seoul, Korea, 2001. [Google Scholar]
- Choi, S.; Lee, C.; Lee, D. Resonance treatment using pin-based pointwise energy slowing-down method. J. Comput. Phys. 2017, 330, 134–155. [Google Scholar] [CrossRef]
- Choi, S.; Lee, D. Three-dimensional method of characteristics/diamond-difference transport analysis method in STREAM for whole-core neutron transport calculation. Comput. Phys. Commun. 2020, 107332. [Google Scholar] [CrossRef]
- Choe, J.; Choi, S.; Zhang, P.; Kim, K.; Lee, D. Enhancement of cross-section feedback module for temperature coefficient in STREAM/RAST-K. In Proceedings of the KNS Spring Meeting, Jeju, Korea, 9–10 July 2020. [Google Scholar]
- Jung, Y.S.; Shim, C.B.; Lim, C.H.; Joo, H.G. Practical numerical reactor employing direct whole core neutron transport and subchannel thermal/hydraulic solvers. Ann. Nucl. Energy 2013, 62, 357–374. [Google Scholar] [CrossRef]
- Pacific Northwest National Laboratory. FRAPCON-4.0: A Computer Code for the Calculation of Steady-State, Thermal-Mechanical behavior of Oxide Fuel Rods for High Burnup; Technical Report No. PNNL-19418; Pacific Northwest National Laboratory: Richland, WA, USA, 2018; Volume 1, p. 2.
- Pennsylvania State University. COBRA-TF Subchannel Thermal-Hydraulics Code (CTF) Theory Manual Revision 0; Technical Report No. CASL-U-2015-0054-000; Pennsylvania State University: State College, PA, USA, 2015. [Google Scholar]
- Cetnar, J. General solution of Bateman equations for nuclear transmutations. Ann. Nucl. Energy 2006, 33, 640–645. [Google Scholar] [CrossRef]
- Pusa, M. Rational Approximations to the Matrix Exponential in Burnup Calculations. Nucl. Sci. Eng. 2011, 169, 155–167. [Google Scholar] [CrossRef]
- Pusa, M.; Leppänen, J. Computing the matrix exponential in burnup calculations. Nucl. Sci. Eng. 2010, 164, 140–150. [Google Scholar] [CrossRef]
- Isotalo, A.E.; Aarnio, P.A. Higher order methods for burnup calculations with Bateman solutions. Ann. Nucl. Energy 2011, 38, 1987–1995. [Google Scholar] [CrossRef]
- Kotlyar, D.; Shwageraus, E. Stochastic semi-implicit SUBSTEP method for coupled depletion Monte-Carlo codes. Ann. Nucl. Energy 2016, 92, 52–60. [Google Scholar] [CrossRef]
- Park, H.J.; Lee, D.H.; Jeon, B.K.; Shim, H.J. Monte Carlo burnup and its uncertainty propagation analyses for VERA depletion benchmarks by McCARD. Nucl. Eng. Technol. 2018, 50, 1043–1050. [Google Scholar] [CrossRef]
- Weiss, Z. A consistent definition of the number density of pseudo-isotopes. Ann. Nucl. Energy 1990, 17, 153–156. [Google Scholar] [CrossRef]
- Bahadir, T.; Lindahl, S.O.; Palmtag, S.P. SIMULATE-4 multigroup nodal code with microscopic depletion model. In Proceedings of the Mathematics and Computation, Super-Computing, Reactor Physics and Nuclear and Biological Applications, Palais des Papes, Avignon, France, 12–15 September 2005. [Google Scholar]
- Choe, J.; Choi, S.; Lee, D. Analysis of effective gadolinium depletion model. In Proceedings of the Transactions of the Korean Nuclear Society Spring Meeting, Jeju, Korea, 16–18 May 2018. [Google Scholar]
- Rempe, K.R.; Smith, K.S.; Henry, A.F. SIMULATE-3 pin power reconstruction: Methodology and benchmarking. Nucl. Sci. Eng. 1989, 103, 334–342. [Google Scholar] [CrossRef]
- Boer, R.; Finnemann, H. Fast analytical flux reconstruction method for nodal space-time nuclear reactor analysis. Ann. Nucl. Energy 1992, 19, 617–628. [Google Scholar] [CrossRef]
- Tong, L. Heat transfer in water-cooled nuclear reactors. Nucl. Eng. Des. 1967, 6, 301–324. [Google Scholar] [CrossRef]
- Zhang, P.; Choe, J.; Choi, S.; Lee, D. Burnup adaptation model in STREAM/RASTK code system. In Proceedings of the M & C 2019, Oregon, OR, USA, 25–29 August 2019. [Google Scholar]
- Jang, J.; Ebiwonjumi, B.; Kim, W.; Park, J.; Choe, J.; Lee, D. Validation of spent nuclear fuel decay heat calculation by a two-step method. Nucl. Eng. Technol. 2020. [Google Scholar] [CrossRef]
- Jang, J.; Ebiwonjumi, B.; Kim, W.; Park, J.; Lee, D. Verification and Validation of Back-end Cycle Source Term Calculation of the Nodal Code RAST-K. In Proceedings of the PHYSOR 2020, Cambridge, United Kingdom, 29 March–2 April 2020. [Google Scholar]
- Jonsson, A. The DIT nuclear fuel assembly physics design code. Nucl. Sci. Eng. 1988, 100, 363–374. [Google Scholar] [CrossRef]
- Ouisloumen, M.; Huria, H.; Mayhue, L.T.; Smith, R.M.; Park, S.W.; Kichty, M.J. Qualification of the Two-Dimensional Transport Code PARAGON; Technical Report No. WCAP-16045-NP Rev 0; Westinghouse Electric Company LLC: Pittsburgh, PA, USA, 2003. [Google Scholar]
- Nguyen, T.Q.; Hoskins, K.C.; Weber, M.M.; Srinilta, S.; Saji, E.; Disney, R.K.; Durston, C. Qualification of the PHOENIX-P/ANC Nuclear Design System for Pressurized Water Reactor Cores; Technical Report No. WCAP-11597-P-A; Westinghouse Electric Corp.: Pittsburgh, PA, USA, 1988. [Google Scholar]
- Choe, J.; Choi, S.; Park, J.; Lee, H.; Lemaire, M.; Shin, H.C.; Lee, H.S.; Lee, D. Verification of asymmetric fuel assembly treatment in STREAM/RAST-K 2.0. In Proceedings of the M&C 2019, Oregon, OR, USA, 25–29 August 2019. [Google Scholar]
- Cherezov, A.; Park, J.; Kim, H.; Lee, D. Fuel rod analysis program interface for tightly coupled multi-physics system. In Proceedings of the ANS Winter Meeting, Chicago, IL, USA, 16–19 November 2020. [Google Scholar]
- Cuta, J.M.; Koontz, A.S.; Stewart, C.W.; Montgomery, S.D.; Nomura, K.K. VIPRE-01: A Thermal-Hydraulic Code for Reactor Cores; Technical Report No. EPRI-NP--2511-CCM-A; Electric Power Research Institute: Palo Alto, CA, USA, 1989; Volume 1, p. 3.
- Deshon, J.; Hussey, D.; Westacott, J.; Young, M.; Secker, J.; Epperson, K.; McGurk, J.; Henshaw, J. Recent Development of BOA v3. In Proceedings of the NPC 2010 Conference, Quebec, QB, Canada, 3–8 October 2010. [Google Scholar]
- Gaston, D.R.; Permann, C.J.; Peterson, J.W.; Slaughter, A.E.; Andrš, D.; Wang, Y.; Short, M.P.; Perez, D.M.; Tonks, M.R.; Ortensi, J.; et al. Physics-based multiscale coupling for full core nuclear reactor simulation. Ann. Nucl. Energy 2015, 84, 45–54. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Q.; Ding, M. Review on neutronics/thermal-hydraulic coupling simulation methods for nuclear reactor analysis. Ann. Nucl. Energy 2020, 137, 1377–1386. [Google Scholar] [CrossRef]
- Cherezov, A.; Park, J.; Kim, H.; Choe, J.; Lee, D. MPCORE Multiphysics system for light-water reactor core safety analysis and accident simulation. Energies 2020. Accepted for publication. [Google Scholar]
- Cherezov, A.; Park, J.; Kim, H.; Lee, D. MPCORE code for OPR-1000 transient multi-physics simulation with adaptive time step size control. In Proceedings of the ANS Summer Meeting, USA (online), 8–11 June 2020. [Google Scholar]
- Yun, D.; Kim, D.; Kim, H.; Kong, C.; Lee, D. Fuel loading pattern optimization for OPR-1000 equilibrium cycle by simulated annealing algorithm. In Proceedings of the Transactions of the Korean Nuclear Society Virtual Spring Meeting, Korea (online), 9–10 July 2020. [Google Scholar]
- Jang, H.; Lee, H. Prediction of pressurized water reactor core design parameters using artificial neural network for loading pattern optimization. In Proceedings of the Transactions of the Korean Nuclear Society Virtual Spring Meeting, Korea (online), 9–10 July 2020. [Google Scholar]
- Dzianisau, S.; Kim, H.; Kong, C.; Yun, D.; Lee, D. Development of barcode model for prediction of PWR core design parameters using convolution neural network. In Proceedings of the Transactions of the Korean Nuclear Society Virtual Spring Meeting, Korea (online), 9–10 July 2020. [Google Scholar]
- Kim, H.; Yun, D.; Shin, H.; Moon, S.; Lee, D. Feasibility study on machine learning algorithm in nuclear reactor core diagnosis. In Proceedings of the Transactions of the Korean Nuclear Society Virtual Spring Meeting, Korea (online), 9–10 July 2020. [Google Scholar]






| Reactor Type | Parameter | Comparison | Mean | Abs. Std | RMS | Number of Data |
|---|---|---|---|---|---|---|
| OPR-1000 | CBC Diff. (ppm) | R a vs. M b | −23.7918 | 25.9309 | 35.0866 | 91 |
| R vs. N c | −3.6790 | 24.8926 | 25.1498 | 929 | ||
| ASI Diff. (-) | R vs. M | 0.0019 | 0.0119 | 0.0120 | 162 | |
| R vs. N | 0.0045 | 0.0158 | 0.0164 | 927 | ||
| FA Power Rel. Err. (%) | R vs. M | 0.3429 | 2.8076 | 2.8262 | 624 | |
| R vs. N | 0.3503 | 1.7976 | 1.8300 | 625 | ||
| APR-1400 | CBC Diff. (ppm) | R vs. M | −20.7710 | 12.4050 | 24.0414 | 21 |
| R vs. N | −24.5093 | 26.8268 | 36.1060 | 43 | ||
| ASI Diff. (-) | R vs. M | 0.0032 | 0.0088 | 0.0090 | 12 | |
| R vs. N | 0.0014 | 0.0089 | 0.0089 | 43 | ||
| FA Power Rel. Err. (%) | R vs. M | −0.0066 | 1.2684 | 1.2638 | 138 | |
| R vs. N | −0.0036 | 1.0694 | 1.0656 | 139 | ||
| WH-2L | CBC Diff. (ppm) | R vs. M | - | - | - | - |
| R vs. N | -12.8147 | 59.3517 | 60.6589 | 480 | ||
| ASI Diff. (-) | R vs. M | - | - | - | - | |
| R vs. N | 0.0011 | 0.0123 | 0.0123 | 228 | ||
| FA Power Rel. Err. (%) | R vs. M | - | - | - | - | |
| R vs. N | 0.352 | 2.200 | 2.230 | 3885 | ||
| WH-3L | CBC Diff. (ppm) | R vs. M | −34.8207 | 31.2628 | 46.7511 | 234 |
| R vs. N | −7.6617 | 15.9378 | 17.6601 | 303 | ||
| ASI Diff. (-) | R vs. M | −0.0074 | 0.0106 | 0.0130 | 248 | |
| R vs. N | −0.0134 | 0.0182 | 0.0225 | 182 | ||
| FA Power Rel. Err. (%) | R vs. M | 0.2694 | 1.5649 | 1.5874 | 1645 | |
| R vs. N | 0.3726 | 4.5802 | 4.5946 | 1646 |
| Design Parameters | Difference | ||
|---|---|---|---|
| BOC | MOC | EOC | |
| Cycle length (day) | −2 | ||
| CBC (ppm) | 3 | 10 | 7 |
| ASI (-) | −0.008 | −0.003 | 0.001 |
| FA power (%) | 1.333 | 0.749 | 0.359 |
| Peaking factor, Fxy (%) | −0.63 | 0.066 | −0.27 |
| FTC (%) | −3.71 | 0.05 | −3.32 |
| MTC (%) | 7.30 | 4.72 | 4.41 |
| Control rod worth (%) | 0.50 | 0.35 | 0.28 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.; Jang, J.; Kim, H.; Choe, J.; Yun, D.; Zhang, P.; Cherezov, A.; Lee, D. RAST-K v2—Three-Dimensional Nodal Diffusion Code for Pressurized Water Reactor Core Analysis. Energies 2020, 13, 6324. https://doi.org/10.3390/en13236324
Park J, Jang J, Kim H, Choe J, Yun D, Zhang P, Cherezov A, Lee D. RAST-K v2—Three-Dimensional Nodal Diffusion Code for Pressurized Water Reactor Core Analysis. Energies. 2020; 13(23):6324. https://doi.org/10.3390/en13236324
Chicago/Turabian StylePark, Jinsu, Jaerim Jang, Hanjoo Kim, Jiwon Choe, Dongmin Yun, Peng Zhang, Alexey Cherezov, and Deokjung Lee. 2020. "RAST-K v2—Three-Dimensional Nodal Diffusion Code for Pressurized Water Reactor Core Analysis" Energies 13, no. 23: 6324. https://doi.org/10.3390/en13236324
APA StylePark, J., Jang, J., Kim, H., Choe, J., Yun, D., Zhang, P., Cherezov, A., & Lee, D. (2020). RAST-K v2—Three-Dimensional Nodal Diffusion Code for Pressurized Water Reactor Core Analysis. Energies, 13(23), 6324. https://doi.org/10.3390/en13236324







