Abstract
This paper presents a methodology to calculate day-ahead wind speed predictions based on historical measurements done by weather stations. The methodology was tested for three locations: Colombia, Ecuador, and Spain. The data is input into the process in two ways: (1) As a single time series containing all measurements, and (2) as twenty-four separate parallel sequences, corresponding to the values of wind speed at each of the 24 h in the day over several months. The methodology relies on the use of three non-parametric techniques: Least-squares support vector machines, empirical mode decomposition, and the wavelet transform. Moreover, the traditional and simple auto-regressive model is applied. The combination of the aforementioned techniques results in nine methods for performing wind prediction. Experiments using a matlab implementation showed that the least-squares support vector machine using data as a single time series outperformed the other combinations, obtaining the least root mean square error (RMSE).
1. Introduction
At the end of the 20th century, a change in the trends of energy production began, promoted by concerns about pollution, climate change and the dependence of some countries on the importation of hydrocarbons. In this context, great interest is concentrated in the opportunities offered by renewable technologies as a source of supply in non-interconnected areas and as part of the integrated generation system that participates in the pool in the wholesale market [1,2].
Energy policies in many countries encourage the implementation, expansion and interconnection of alternative renewable energy sources such as photovoltaics, solar thermal, wind, geothermal, hydroelectric, wave, tidal and biofuel. An analysis of these technologies establishes wind energy as the most economical on a large scale [3]. It is remarkable that at the end of 2019 only a few countries had more than 20,000 MW of installed capacity of wind energy: China (236,402 MW), USA. (105,466 MW), Germany (61,357 MW), India (37,506 MW), Spain (25,808 MW) and the United Kingdom (23,515 MW). Currently, wind energy production is the fastest-growing energy generation technology, with a connected capacity in the world of 568,409 MW in 2019.
In Latin America [4], Brazil is the leader with 16,643 MW, followed by Chile with 2150 MW, Uruguay (1647 MW), Argentina (1604 MW), Costa Rica (459 MW), Nicaragua (635 MW), Honduras (274 MW) and Peru (375 MW). In Colombia, the advances associated with wind power generation are currently 0.10% of the national capacity, represented by the Jepirachi Wind Farm [5,6] which is regulated by UPME (Colombian Energy and Mining Planning Unit [7]). Since 2014, the Law 1715 [8] offers tax incentives that aims to boost the use of renewable energy sources in the Colombian electricity market (for capacities greater than 20 MW [9]) and in non-interconnected areas.
The entry of wind power into an electrical system brings with it the challenge of including non-dispatchable energy [10]. The difficulty lies in the stochastic characteristics of the wind and regardless of certainty that can be had when predicting its future values [11,12]. Prediction errors turn into technical and economic repercussions both for the market operator (due to the reprogramming involved) and for the owners of the generating parks. Modern wind turbines are in the capacity to turn to look for the direction of wind speed. This allows for the greatest possible power generation. Therefore, the prediction focuses on wind speed and not on its direction. [13,14]. However, the aforementioned does not reduce the complexity of the problem due to the wind’s characteristics and the influence exerted by factors such as latitude, altitude, relief, pressure, and temperature.
Several authors have faced the problem of wind prediction from different time horizons. Some researchers are focused on combining strategies to improve the estimation of power production in a wind farm as in [15]. In [16], authors propose a method for long-term estimation of the wind power, at 30, 25, 20, 15 and 10 days ahead, at any arbitrary site by using probability distribution functions. The proposed approach predicts the characteristic parameters of the wind speed probability distribution functions at different long-term future times and uses them to estimate the wind power at future times. The four ratings provided by [17] wind speed forecast models were reviewed, allowing a comparison based on three famous evaluation metrics. This allowed us to work in greater detail with our forecast model of the wind speed in each case.
Authors in [18] proposed a hybrid system for short-wind-speed prediction. The hybrid system combines simple implementation techniques such as autoregressive differential moving average (ARIMA) and machine learning techniques such as a three-layer neural network. The authors evaluate the performance of the technique using statistical indices: the mean square error (MSE), the root mean square error (RMSE), and the mean absolute percentage error (MAPE). The authors evaluate and conclude that the proposed hybrid technique has a good performance in predicting real-time series applied to wind speed. Hamed [19] proposes a hybrid forecasting model that sequentially uses wavelet-based neural networks, time series, and finally a Kalman filter to resulting data residuals. This shows that a combination of several techniques is crucial in achieving overall system stability and quality.
This paper presents a methodology for predicting wind speed in the short term (day-ahead market). The historical data is processing in series (time series) or parallel (prediction hours) using three non-parametric statistical regression techniques:
- Least-squares support vector machine (LSSVM)
- Empirical mode decomposition (EMD)
- Wavelet transform (WT)
The application of the methodology is illustrated using a software tool processed in MATLAB platform in the following cases: (1) Colombia: using historical wind data at the Puerto Bolívar weather station obtained from the Institute of Hydrology, Meteorology and Environmental Studies (IDEAM), (2) Ecuador: wind measurements recorded in the wind farm of San Cristóbal- Galápagos Island obtained by the park’s developer, EOLICSA and (3) Spain: wind data from Puerto de Santa María station in Cádiz. Figure 1 shows the locations studied.
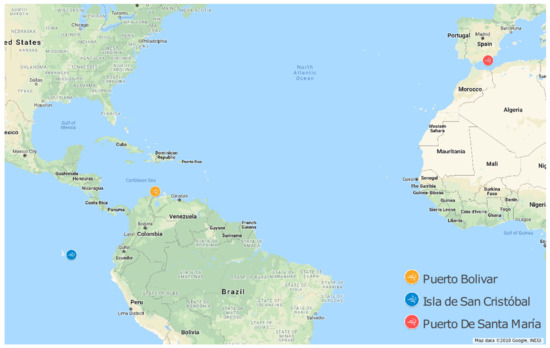
Figure 1.
Wind data measurements locations.
This article is organized as follows: Section 2 presents the materials and methods used for wind speed prediction. Section 2.1 offers a description of the WT technique and its application in signal decomposition. Section 2.2 introduces the EMD technique, and Section 2.3 presents the LSSVM technique. In addition, Section 3 exposes the results and tests conducted to measure the performance of every implemented hybrid techniques. Finally, Section 4 shows the conclusions reached from the evaluation of the nine wind speed prediction techniques in three different locations.
2. Materials and Methods: Wind Speed Prediction
This section presents a classification of the predictions based on the predicted time horizon. Besides, a description of the applied methodology is made. The prediction methods implemented in the platform are defined and description is made of the non-parametric techniques that are used: WT, EMD and LSSVM. According to [20] the predictions with time horizon are classified into 4 categories:
Predictions in the ultra short term: For ranges from a few minutes to an hour in advance, and its application focuses on adjustment markets, regulatory markets.
Short-term predictions: from one to several hours in advance. This type of prediction is appropriate to establish the availability proposals in the market of the previous day, which is carried out in the pool or the energy exchange.
Medium-term predictions: from several hours to a week in advance. It allows generation programming to be carried out; this programming must be adjusted with the information obtained with the short-term prediction minimizing the probabilities of deviations in the generation.
Long-term predictions: from one week to one year in advance. It is widely used in planning new wind projects, maintenance hours, and system expansion among others.
This methodology is developed to make a short-term prediction (day-ahead market) using statistical methods of non-parametric smoothing or regression. Different authors have worked and proved that decomposing the wind speed in time series partially removes their stochastic volatility. Historical wind speed data follow the composition of a stochastic plus a noisy signal [21,22,23].
Wind predictions are performed with each of the statistical techniques and make mixtures among them (hybrid techniques). The selected technique will be the one with the lowest RMSE (Equation (1)) where is the predicted data and is the actual data. Individual and hybrid statistical techniques take data in two ways: (1) Series: wind data in each hour of previous days, generating a single vector of data, and (2) Parallel: Wind data in every 24 h during previous days, generating 24 data vectors. Then decomposition, filtering, and reconstruction techniques are combined as follows:
- Method I (series prediction): SER-LSSVM.
- Method II (series prediction): EMD with WT, elimination of high variability component, signal reconstruction (REC) and then use of LSSVM (SER-WT-REC-LSSVM).
- Method III (series prediction): EMD, elimination of high variability component, signal reconstruction and then use of LSSVM (SER-EMD-REC-LSSVM).
- Method IV (series prediction): Decomposition with WT, elimination of high variability component, use of LSSVM to estimate each WT component and then signal reconstruction. (SER-WT-LSSVM-REC).
- Method V (series prediction): EMD, elimination of high variability component, use of LSSVM to estimate each EMD component and then signal reconstruction (SER-EMD-LSSVM-REC).
- Method VI (parallel prediction): Autoregressive model that estimates the wind in one hour using the simple average of the wind at that same time for previous days (PAR-AVE).
- Method VII (parallel prediction): LSSVM at hourly winds for several days (PAR-LSSVM).
- Method VIII (parallel prediction): Decomposition with WT at hourly winds for several days, eliminating the high variability component and then signal reconstruction. Subsequently, LSSVM is used to estimate winds in each of the 24 h (PAR-WT-REC-LSSVM).
- Method IX (parallel prediction): EMD at hourly winds for several days, elimination of the high variability component and then signal reconstruction. Subsequently, LSSVM is used to estimate winds in each of the 24 h (PAR-EMD-REC-LSSVM).
The methods will be analyzed considering the filtering and elimination of the components in the decomposition. As a result, the information of the wind speed trend is preserved and the component with the greatest variation is neglected. The reconstructed term refers to the elimination of the residues of the WT or the empirical decomposition, to then make the prediction using LSSVM. The purpose of eliminating residues is to have a smoothed signal so that the vector machine’s nonlinear regression fits in a better way to the input data of the model. Figure 2 shows a flowchart for the framework implemented in MATLAB.
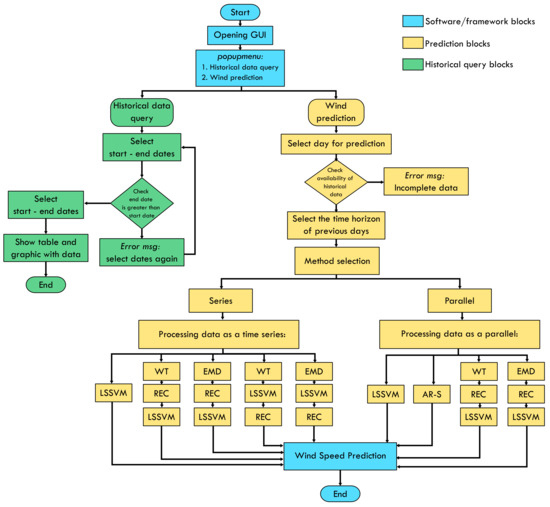
Figure 2.
Flowchart for software tool developed.
2.1. Wavelet Transform (WT)
The WT offers a solution to the problem of the temporal resolution balance compared to the frequency resolution, as presented in other more classical transforms such as Fourier [24]. WT is carried out using a function called mother wavelet, , with mother wavelet the signal of interest is split down in terms of different frequencies that make up a family of functions that are translations and expansions of the mother wavelet, represented as , where b performs the translation and a expansions or scales (Equation (2)).
Continuous wavelet transformation of a function of interest is obtained by Equation (3) where is the conjugate complex of . However, the continuous form contains a lot of redundant information. Thus, the use of the Discrete Wavelet Transform (DWT) is implemented [25]. DWT uses both the scaling and the translation parameter, values proportional to powers of 2. DWT allows a multi-resolution analysis (MRA). MRA can be seen as the process of passing the signal of interest through a low pass filter and a high pass filter. The output of the low pass filter is called approximation, while that of the high pass filter, detail. When the decomposition is done for multiple levels, the approach signal decomposes again into two subcomponents of low and high frequencies Figure 3.
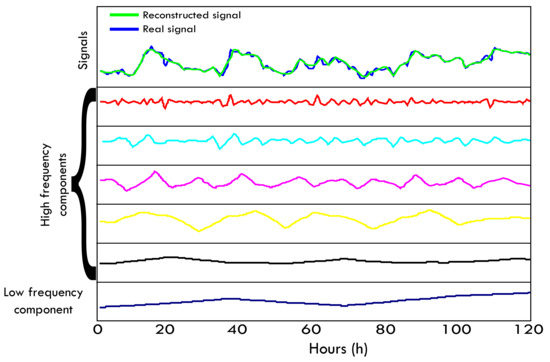
Figure 3.
Discrete wavelet transform decomposition level.
Gómez-Luna et al. [26] quantified the energy dispersion in the frequency of a large set of wavelets as a function of the number of coefficients of the filter that implements the decomposition. The result is that the Daubechies family has the smallest dispersion when the filter length is even, compared to other families such as symmlets, coiflets, biortogonal and inverse biortogonal.
For the prediction of the wind speed, a wavelet decomposition is performed using the mother wavelet Daubechies 3, which produces an equivalent filter of 6 coefficients. Besides, a decomposition is performed in 5 levels, that is, five detail signals and one approach signal. Multiple prediction experiments support the level of decomposition selected, as well as the choice of the mother wavelet. In the reconstruction of the filtered signal, one or more high-frequency components are neglected. High-frequency components contain information mostly of variability inherent in the wind speed and not of its tendency.
Figure 3 shows a wind speed signal for 120 h (5 days), and for its components after applying the DWT with the command waverec of the MATLAB tool, for 5 levels (five detail components in decreasing order of frequencies, and an approximation component). Mother wavelet db3 was implemented. The actual wind speed performance in that time and the reconstruction of this signal when the higher frequency component is neglected are shown in the first box. Note that even by neglecting the detail component of higher frequencies (), the reconstruction looks very similar to the original signal.
2.2. Empirical Mode Decomposition (EMD)
According to [27] EMD is applied to analyze signals rather than to predict them. Particularly, atmospheric signals have a high correlation linking them where EMD is useful. The objective of this technique is to decompose non-stationary and/or non-linear signals, in order to convert them into a series of stationary signals (Equation (4)). Where n is the number of empirical modes in which the original signal decomposes. In this specific case the wind speed signal is the component that is obtained from the decomposition of the signal in functions of intrinsic mode (IMF) and is the high-frequency residue [28].
2.3. Least Square Support Vector Machine (LSSVM)
LSSVM is properly related to classification and regression problems. Given a set of training examples (samples), we can label the classes and train an LSSVM to build a model that predicts a new sample class. LSSVM is a model that represents the sample points in space, separating the classes by a hyperplane as complete as possible. New samples are set in correspondence with the model, depending on their proximity [29].
For Method II and Method IV analysis of historical wind speed data reflects its non-linearity. For this reason, historical data were taken and divided as time series using the WT algorithm. The details or components that contributed greater randomness to the series were discarded, and finally the LSSVM model was used to predict the 24 h periods of one day [29,30]. The goal of the LSSVM model is to minimize the penalty error that arises from the regression. This penalty error is denoted as C and is shown in Equation (5) [31].
3. Test and Results
To evaluate the prediction techniques implemented, historical records of wind speeds were used. The records contain hourly wind speed information for each day of a year. For this data set, the prediction techniques that were processed in the computational tool were evaluated. The metric used to measure the performance of each prediction technique is the RMSE. RMSE is similar to the standard deviation when the average of the errors is small and the number of samples is large.
3.1. Test Case
We analyzed three locations: Puerto Bolivar (Colombia)—121336.7 N 715837.4 W, San Cristobal Island (Ecuador)—05207.2 S 892555.8 W, and Port of Santa Maria (Spain)—363456.3 N 61356.1 W. Concerning every location, we have data obtained from weather stations. The weather stations monitor temperature, humidity, rainfall, barometric pressure, solar radiation and wind speed/direction. From all the data loaded by the weather stations, we take exclusive the wind speed. The wind speed is measured and recorded hourly in a two-year database. The wind speed database is the only input random variable for predicting the next day’s wind speed using the proposed hybrid techniques.
3.2. Results
To predict with a filter with serial data, the n days before the one being predicted are taken, a vector is constructed with all the data as a continuous signal, and the next 24 points of that are predicted. For the preparation of serial data, five possible methods are designed (Figure 4a). To predict with a method with parallel data, the n days before the one being predicted are taken, 24 vectors are constructed with each hour of those n days. For example, by 7 o’clock a wind speed vector of those n days is built at 7 in the morning. With each of these vectors, the same time of the specific day selected is predicted. Four possible methods are designed for parallel data group (Figure 4b).
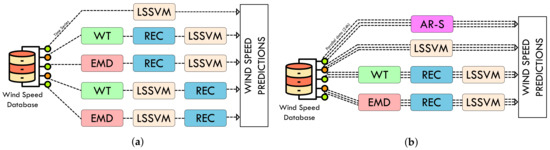
Figure 4.
Prediction methods implemented. (a) Series. (b) Parallel.
Initially, of the nine prediction methods implemented, the five best cases were selected. This previous selection of methods was made based on the histograms of the prediction errors. In Figure 5, the histograms obtained for each method are shown. Histograms discard those that have a platykurtic form; that is, they have the greatest standard deviations. From the above selection leads us to evaluate in detail the following methods:
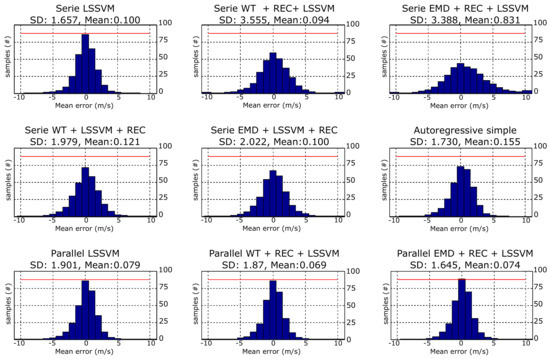
Figure 5.
Histograms of the predictions error for the nine prediction methods.
Series methods:
- Method I: LSSVM
- Method II: WT-LSSVM-REC
Parallel methods:
- Method VI: Autoregressive simple
- Method VII: LSSVM
- Method VIII: WT-REC-LSSVM
To calculate RMSE of the five selected methods, the next windy day (24 h) was predicted using a set day horizon. This experiment was performed 30 times with randomly selected days from the historical record. The error is calculated from the difference in the predicted value with the actual value of the wind speed. For each of the prediction techniques, RMSE is calculated by varying the horizon of days used in the prediction. In Figure 6a RMSEs obtained for the prediction techniques are presented varying the horizon of days used from 14 to 35. From Figure 6a it can be concluded that the support machine vector (LSSVM) and simple average (Autoregressive simple) are the prediction techniques that have a lower error.
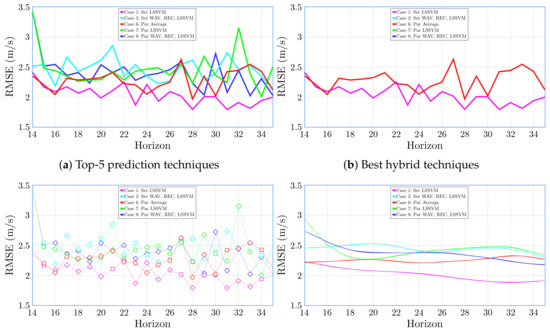
Figure 6.
Root mean square error (RMSE) for different horizons. Puerto Bolivar (Colombia).
To make the comparison between the two better curves easier for the reader, Figure 6b is presented with the results obtained for the LSSVM and the simple average. It is visible that initially both the simple average and the LSSVM have a comparable RMSE. However, as the horizon of days used increases, LSSVM has lower prediction errors than the simple average.
RMSEs are values that are calculated for each specific day horizon. Being a set of discrete values, a continuous plot may be a bit arbitrary. This is why in Figure 6c discrete points are shown joined by a dotted line that suggests a trend. To show the trend that RMSE follows in prediction techniques, a curve adjustment is made to each technique. The curve fit used is smoothing spline with a smoothing factor of 0.07. The curve adjustment described previously is shown in Figure 6d.
In addition to the site in La Guajira (Colombia), the same experiment was carried out for two sites located in the Galapagos Islands (Ecuador) and the Port of Santa María (Spain). The conclusions that were obtained in these different places follow the same statements that was obtained for the Colombian site. Figure 7 and Figure 8 show the results obtained for the locations in the Galapagos Islands and the Port of Santa María.
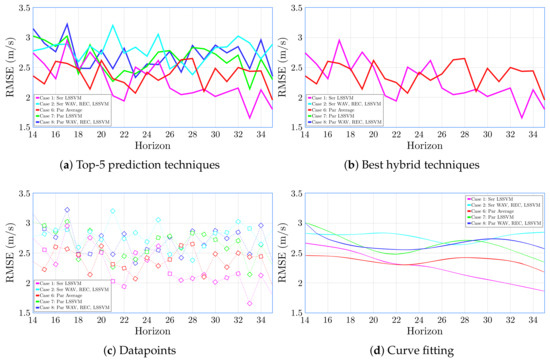
Figure 7.
RMSE for different horizons. The Galapagos Island (Ecuador).
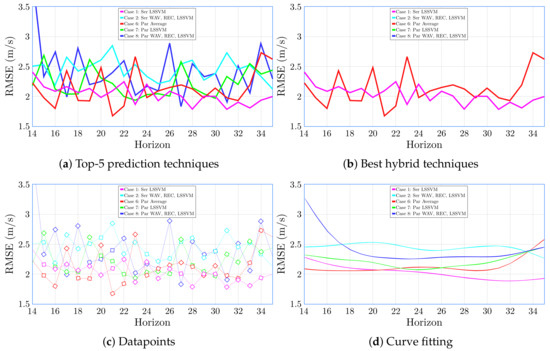
Figure 8.
RMSE for different horizons. Port of Santa Maria (Spain).
From the tests and results, it can be determined that the method of least average square error is LSSVM. To illustrate the prediction made by the LSSVM method on a given day, a prediction of the following 24 h is made. Figure 9 shows the values predicted by the LSSVM in green and the actual wind values for that particular day in the black.
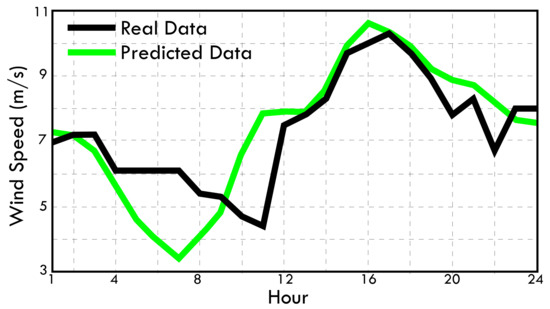
Figure 9.
Day-ahead prediction using least-squares support vector machine (LSSVM) for a typical day.
4. Conclusions
Historical wind speed data measured at three locations were used. The selected sites are monitored by weather stations that supply the wind speed database with the average hourly data. Besides, three non-parametric statistical techniques were implemented to perform wind prediction. The least-squares support vector machine, wavelet transform and empirical mode decomposition were implemented. WT and EMD were used as signal decomposition tools to eliminate the high-frequency variability of the wind speed signal and obtain the trend that is the variable of interest.
Combinations were made between the techniques implemented, seeking an improvement in the accuracy of the prediction values obtained. Nine prediction methods were implemented based on the program techniques. Five of these techniques make a time series treatment of wind data. Four of them make a parallel treatment of the prediction hours. From the implemented framework, it was concluded that parallel techniques generally have better wind prediction performance.
RMSE metric was used to compare the performance of the prediction methods. RMSE is measured after a sampling block of randomly selected day predictions. It was obtained that the two best prediction techniques for different time horizons (previous days took to make the prediction) were the LSSVM as a time series and the simple Autoregressive model as a parallel time prediction. For the LSSVM method, the lowest RMSEs were obtained in the time horizons between 25 and 30 days, achieving standard deviations of up to 1.2 m/s.
The recommendations and future work are suggested to incorporate new meteorological variables such as temperature, atmospheric pressure, and air density. The meteorological variables have a correlation between them that can improve the wind predictions that are obtained for the next day. On the other hand, it is recommended to explore larger time horizons to determine a substantial improvement in the wind forecast quality. Increasing the horizon of data taken as historical also increases the computational cost and the execution time of the implemented methods.
Author Contributions
Conceptualization, I.O.; Formal analysis, L.T.; Methodology, L.R.; Software, L.L.; Writing—original draft, L.T., G.S. and S.C.; Writing—review and editing, J.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Colombian Institute for the Development of Science and Technology Francisco José de Caldas—Colciencias Code 57598 Grant 037-2018
Acknowledgments
The authors thank Universidad del Norte for the support given through the Energy Strategic Area Program and for the availability of Renewable energy Laboratory, UniGrid. Also, We thank Universidad Politécnica de Madrid, specially to Sergio Martinez Gonzalez from Research Group "Generación Eléctrica con Energía Eólica".
Conflicts of Interest
The authors declare no conflict of interest.
References
- Perea-Moreno, M.A.; Hernandez-Escobedo, Q.; Perea-Moreno, A.J. Renewable energy in urban areas: Worldwide research trends. Energies 2018, 11, 577. [Google Scholar] [CrossRef]
- Hache, E.; Palle, A. Renewable energy source integration into power networks, research trends and policy implications: A bibliometric and research actors survey analysis. Energy Policy 2019, 124, 23–35. [Google Scholar] [CrossRef]
- Kumar, Y.; Ringenberg, J.; Depuru, S.S.; Devabhaktuni, V.K.; Lee, J.W.; Nikolaidis, E.; Andersen, B.; Afjeh, A. Wind energy: Trends and enabling technologies. Renew. Sustain. Energy Rev. 2016, 53, 209–224. [Google Scholar] [CrossRef]
- Wind, G.; Council, E. Global Wind Report 2019. Available online: https://gwec.net/global-wind-report-2019/ (accessed on 20 November 2020).
- The World Bank. Jepirachi Carbon Off Set Project in Colombia (2002–2024). Available online: https://projects.worldbank.org/en/projects-operations/project-detail/P074426 (accessed on 13 February 2020).
- Ochoa Suárez, M. Energía EóLica: Un Tema de Alto Voltaje para los Wayú. Press Article. Semana. 14 January 2020. Available online: https://sostenibilidad.semana.com/impacto/articulo/energia-eolica-un-tema-de-alto-voltaje-para-los-wayu/47189 (accessed on 13 February 2020).
- UPME. Unidad de Planeación Minero-Energética—Ministerio de Minas y Energía de Colombia. Available online: https://www1.upme.gov.co (accessed on 13 February 2020).
- UPME. Guía Práctica para la Aplicación de los Incentivos Tributarios de la Ley 1715 de 2014. Available online: https://www1.upme.gov.co/Documents/Cartilla_IGE_Incentivos_Tributarios_Ley1715.pdf (accessed on 20 April 2020).
- Comision de Regulacion de Energia y Gas. Código de Redes; CREG Online. Available online: http://apolo.creg.gov.co/Publicac.nsf/Indice01/Resoluci%C3%B3n-1995-CRG95025 (accessed on 20 November 2020).
- Perera, A.T.; Wickramasinghe, P.U.; Scartezzini, J.L.; Nik, V.M. Integrating renewable energy technologies into distributed energy systems maintaining system flexibility. In Proceedings of the 5th International Symposium on Environment-Friendly Energies and Applications, EFEA, Rome, Italy, 24–26 September 2018; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Huang, C.J.; Kuo, P.H. A short-term wind speed forecasting model by using artificial neural networks with stochastic optimization for renewable energy systems. Energies 2018, 11, 2777. [Google Scholar] [CrossRef]
- Dolatabadi, A.; Jadidbonab, M.; Mohammadi-Ivatloo, B. Short-Term Scheduling Strategy for Wind-Based Energy Hub: A Hybrid Stochastic/IGDT Approach. IEEE Trans. Sustain. Energy 2019, 10, 438–448. [Google Scholar] [CrossRef]
- Ackermann, T. Wind Power in Power Systems; Wiley Online Library: Hoboken, NJ, USA, 2005; Volume 140. [Google Scholar]
- Fallis, A. Developing wind power projects: Theory and Practice. J. Chem. Inf. Model. 2013, 53, 1689–1699. [Google Scholar]
- Famoso, F.; Brusca, S.; D’Urso, D.; Galvagno, A.; Chiacchio, F. A novel hybrid model for the estimation of energy conversion in a wind farm combining wake effects and stochastic dependability. Appl. Energy 2020, 280, 115967. [Google Scholar] [CrossRef]
- Borunda, M.; Rodríguez-Vázquez, K.; Garduno-Ramirez, R.; de la Cruz-Soto, J.; Antunez-Estrada, J.; Jaramillo, O.A. Long-term estimation of wind power by probabilistic forecast using genetic programming. Energies 2020, 13, 1885. [Google Scholar] [CrossRef]
- Hu, H.; Wang, L.; Tao, R. Wind speed forecasting based on variational mode decomposition and improved echo state network. Renew. Energy 2021, 164, 729–751. [Google Scholar] [CrossRef]
- Bai, Y.; Tang, L.; Fan, M.; Ma, X.; Yang, Y. Fuzzy First-Order Transition-Rules-Trained Hybrid Forecasting System for Short-Term Wind Speed Forecasts. Energies 2020, 13, 3332. [Google Scholar] [CrossRef]
- Aly, H.H. An intelligent hybrid model of neuro Wavelet, time series and Recurrent Kalman Filter for wind speed forecasting. Sustain. Energy Technol. Assessments 2020, 41, 100802. [Google Scholar] [CrossRef]
- Chang, W.Y. A Literature Review of Wind Forecasting Methods. J. Power Energy Eng. 2014, 2, 161–168. [Google Scholar] [CrossRef]
- Liu, D.; Niu, D.; Wang, H.; Fan, L. Short-term wind speed forecasting using wavelet transform and support vector machines optimized by genetic algorithm. Renew. Energy 2014, 62, 592–597. [Google Scholar] [CrossRef]
- Catalão, J.P.; Pousinho, H.M.; Mendes, V.M. Short-term wind power forecasting in Portugal by neural networks and wavelet transform. Renew. Energy 2011, 36, 1245–1251. [Google Scholar] [CrossRef]
- Wang, J.; Qin, S.; Zhou, Q.; Jiang, H. Medium-term wind speeds forecasting utilizing hybrid models for three different sites in Xinjiang, China. Renew. Energy 2015, 76, 91–101. [Google Scholar] [CrossRef]
- Liu, H.; wei Mi, X.; fei Li, Y. Wind speed forecasting method based on deep learning strategy using empirical wavelet transform, long short term memory neural network and Elman neural network. Energy Convers. Manag. 2018, 156, 498–514. [Google Scholar] [CrossRef]
- Liu, Y.; Guan, L.; Hou, C.; Han, H.; Liu, Z.; Sun, Y.; Zheng, M. Wind power short-term prediction based on LSTM and discrete wavelet transform. Appl. Sci. 2019, 9, 1108. [Google Scholar] [CrossRef]
- Gomez-Luna, E.; Aponte Mayor, G.; Pleite Guerra, J.; Silva Salcedo, D.F.; Hinestroza Gutierrez, D. Application of wavelet transform to obtain the frequency response of a transformer from transient signals—Part 1: Theoretical analysis. IEEE Trans. Power Deliv. 2013, 28, 1709–1714. [Google Scholar] [CrossRef]
- Bokde, N.; Feijóo, A.; Villanueva, D.; Kulat, K. A review on hybrid empirical mode decomposition models for wind speed and wind power prediction. Energies 2019, 12, 254. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Snin, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hubert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Cherkassky, V.; Ma, Y. Practical selection of SVM parameters and noise estimation for SVM regression. Neural Netw. 2004, 17, 113–126. [Google Scholar] [CrossRef]
- Kuh, A.; Manloloyo, C.; Corpuz, R.; Kowahl, N. Wind prediction using complex augmented adaptive filters. In Proceedings of the 1st International Conference on Green Circuits and Systems, ICGCS, Shanghai, China, 21–23 June 2010; pp. 46–50. [Google Scholar] [CrossRef]
- Wang, X.; LI, H. Multiscale prediction of wind speed and output power for the wind farm. J. Control Theory Appl. 2012, 10, 251–258. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).