Deep Reinforcement Learning Control of Cylinder Flow Using Rotary Oscillations at Low Reynolds Number
Abstract
1. Introduction
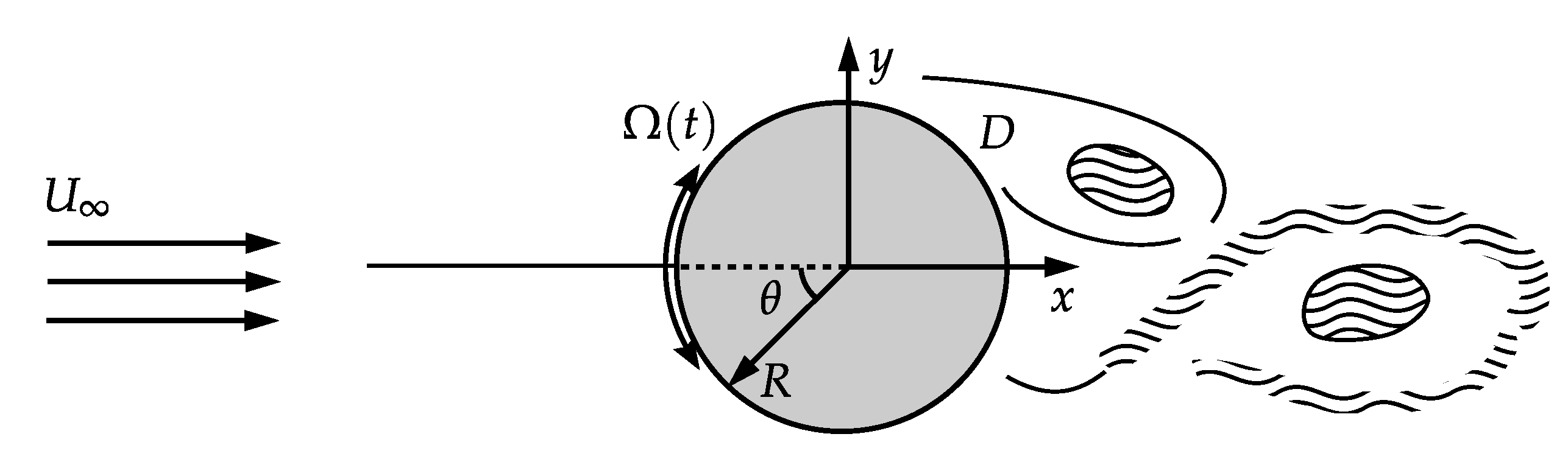
2. Problem Formulation and Computational Details
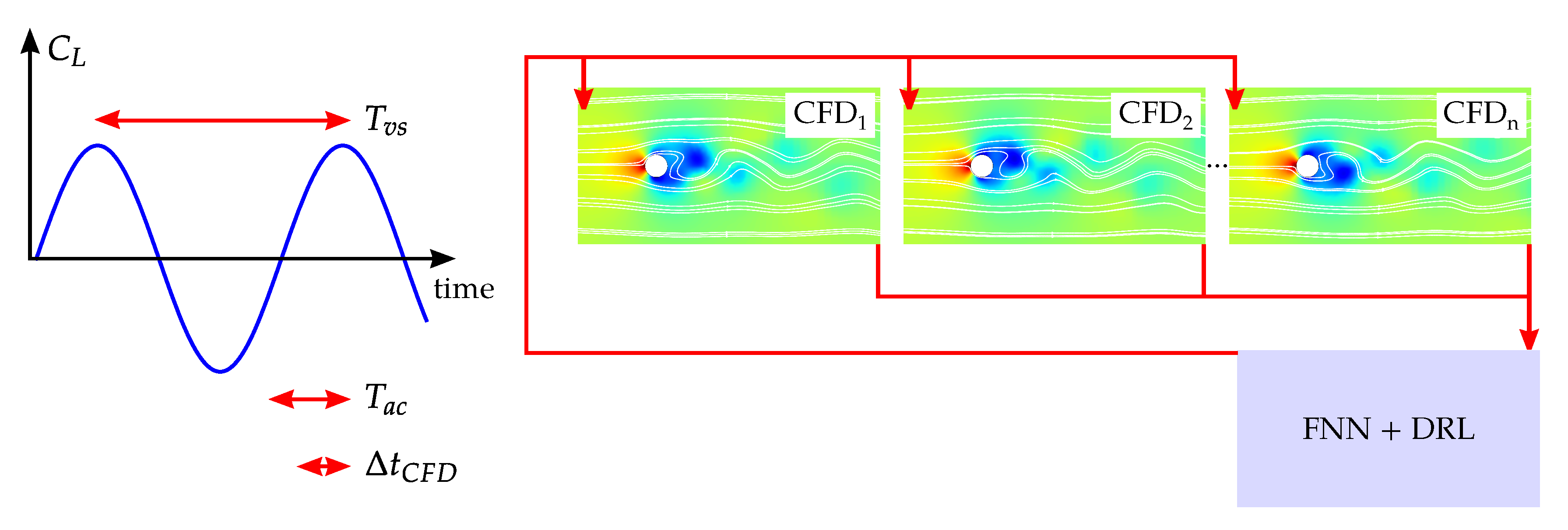
2.1. Flow Computations
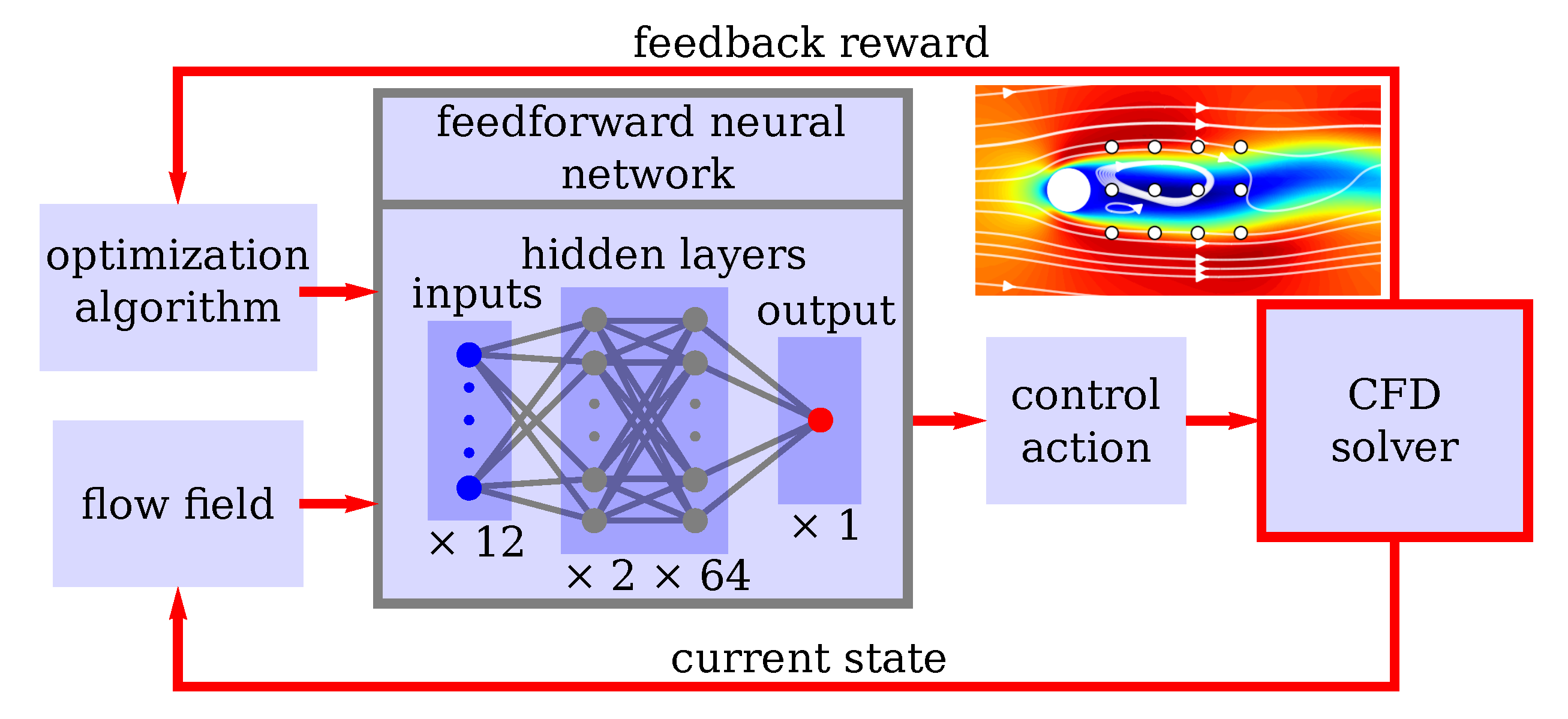
2.2. Machine-Learning Architecture, Feedback Loop and Parallelization
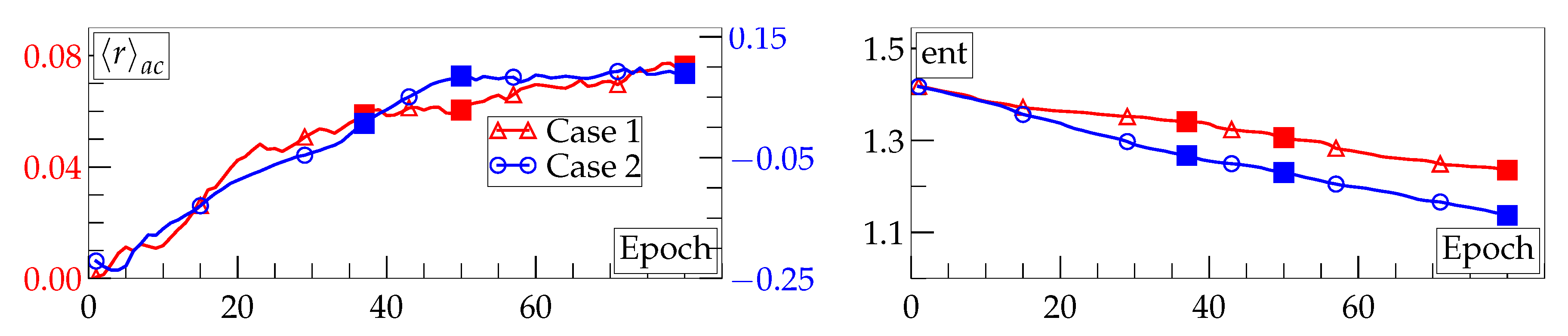
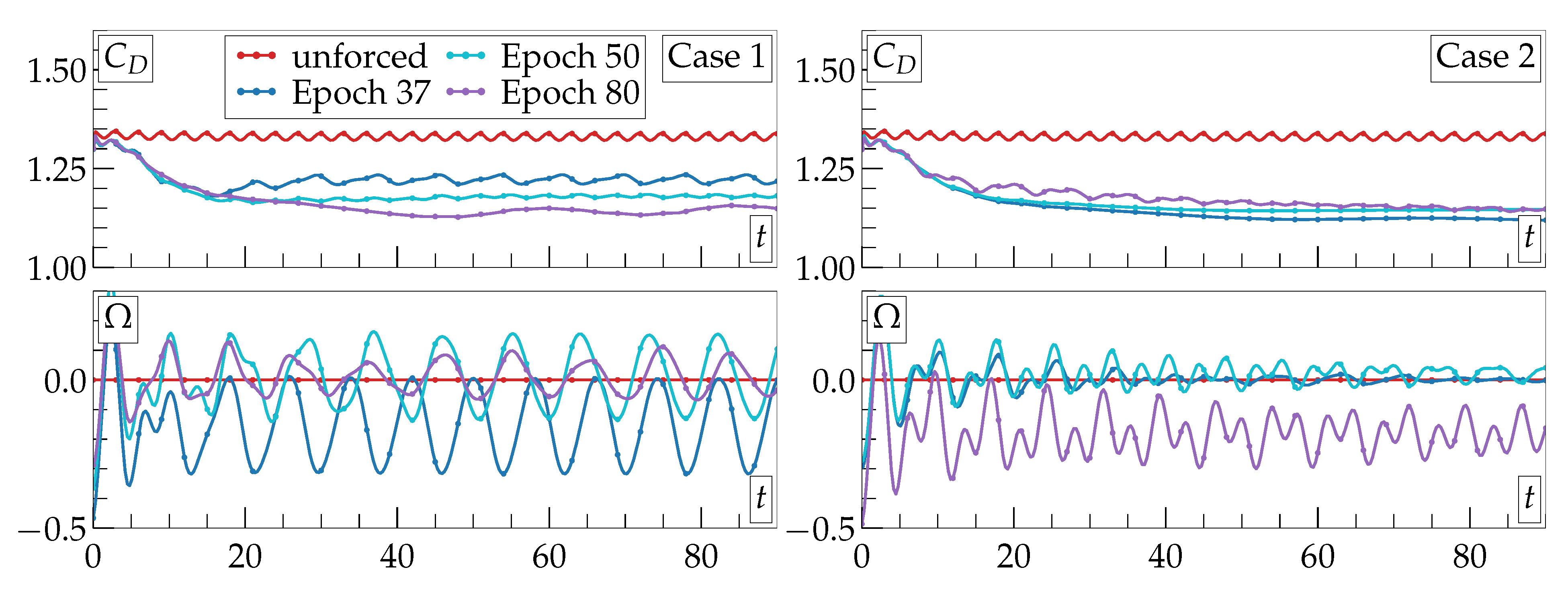
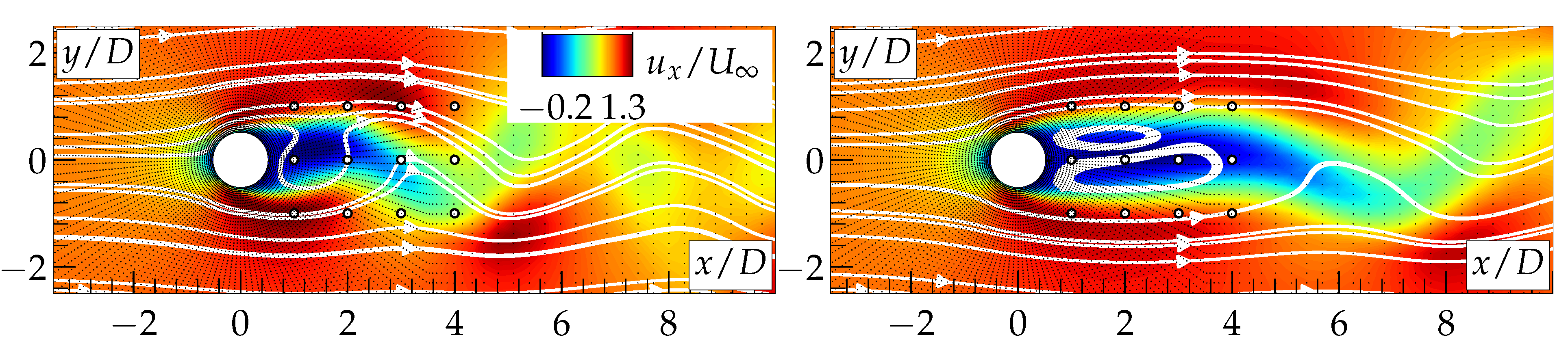
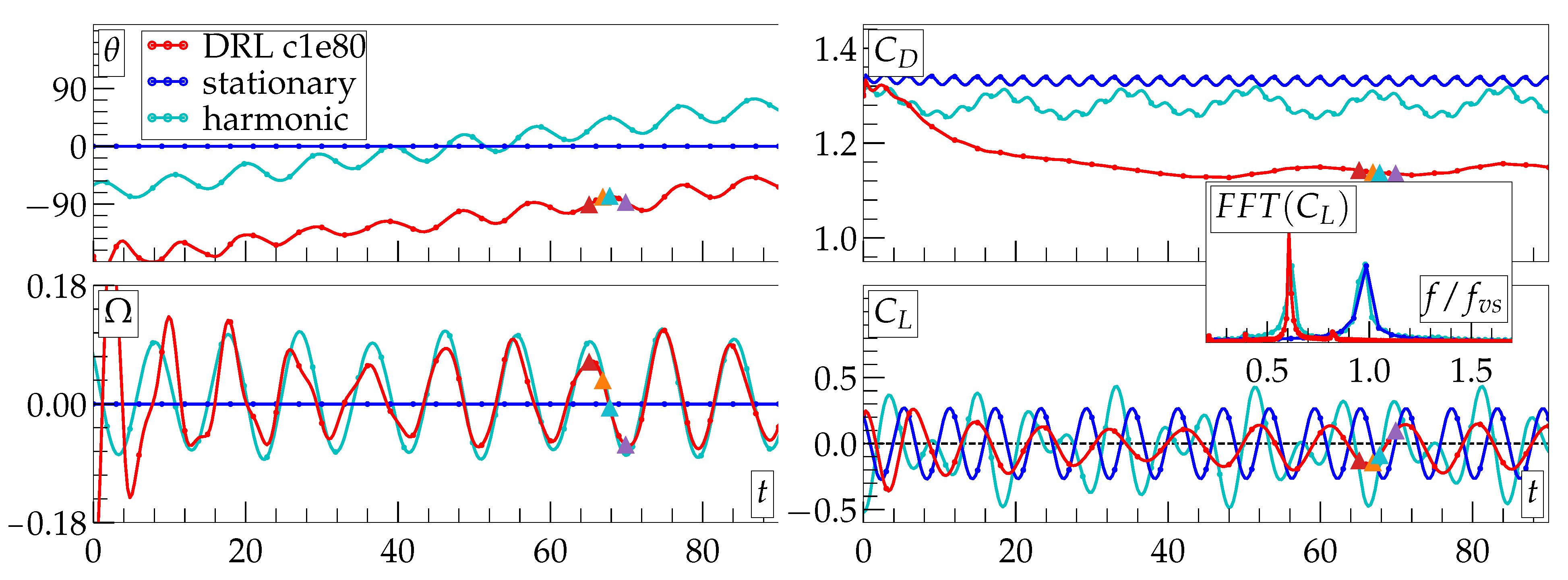
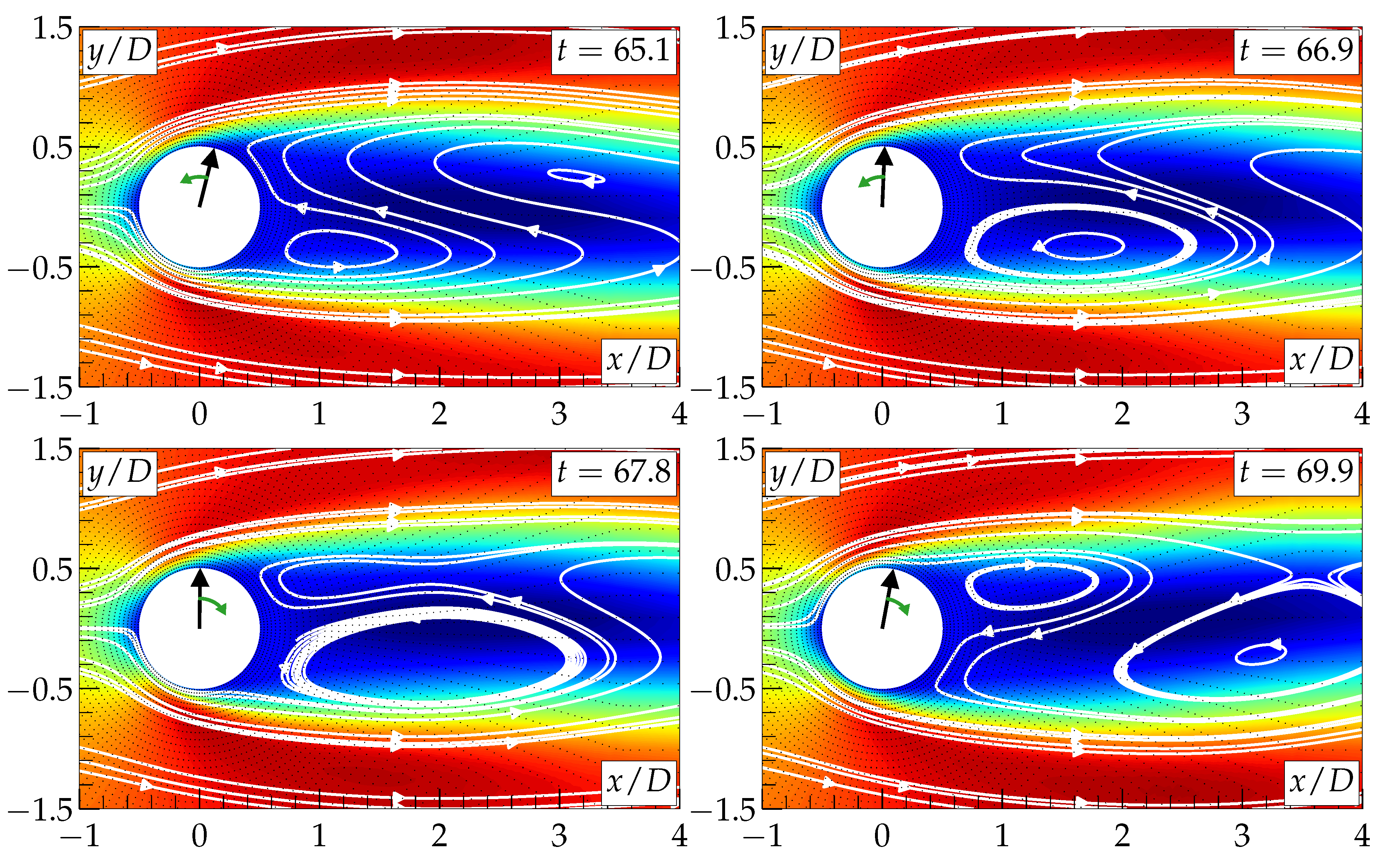
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Williamson, C. Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 1996, 28, 477–539. [Google Scholar] [CrossRef]
- Choi, H.; Jeon, W.P.; Kim, J. Control of flow over a bluff body. Annu. Rev. Fluid Mech. 2008, 40, 113–139. [Google Scholar] [CrossRef]
- Gad-el Hak, M. Flow Control: Passive, Active, and Reactive Flow Management; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Brunton, S.; Noack, B.; Koumoutsakos, P. Machine learning for fluid mechanics. Annu. Rev. Fluid Mech. 2020, 52, 477–539. [Google Scholar] [CrossRef]
- Weatheritt, J.; Sandberg, R. A novel evolutionary algorithm applied to algebraic modifications of the RANS stress-strain relationship. J. Comput. Phys. 2016, 325, 22–37. [Google Scholar] [CrossRef]
- Leoni, P.; Mazzino, A.; Biferale, L. Inferring flow parameters and turbulent configuration with physics-informed data assimilation and spectral nudging. Phys. Rev. Fluids 2018, 3, 104604. [Google Scholar] [CrossRef]
- Agostini, L. Exploration and prediction of fluid dynamical systems using auto-encoder technology. Phys. Fluids 2020, 32, 067103. [Google Scholar] [CrossRef]
- Bewley, T.; Moin, P.; Temam, R. DNS-based predictive control of turbulence: An optimal benchmark for feedback algorithms. J. Fluid Mech. 2001, 447, 179–225. [Google Scholar] [CrossRef]
- Müller, S.; Milano, M.; Koumoutsakos, P. Application of machine learning algorithms to flow modeling and optimization. Annu. Res. Briefs 1999, 169–178. [Google Scholar]
- Milano, M.; Koumoutsakos, P. A clustering genetic algorithm for cylinder drag optimization. J. Comput. Phys. 2002, 175, 79–107. [Google Scholar] [CrossRef]
- Parezanović, V.; Laurentie, J.; Fourment, C.; Delville, J.; Bonnet, J.; Spohn, A.; Duriez, T.; Cordier, L.; Noack, B.; Abel, M.; et al. Mixing layer manipulation experiment. Flow, turbulence and combustion. Flow Turbul. Combust. 2015, 94, 155–173. [Google Scholar] [CrossRef]
- Gautier, N.; Aider, J.; Duriez, T.; Noack, B.; Segond, M.; Abel, M. Closed-loop separation control using machine learning. J. Fluid Mech. 2015, 770, 442–457. [Google Scholar] [CrossRef]
- Antoine, D.; Von Krbek, K.; Mazellier, N.; Duriez, T.; Cordier, L.; Noack, B.; Abel, M.; Kourta, A. Closed-loop separation control over a sharp edge ramp using genetic programming. Exp. Fluids 2016, 57, 40. [Google Scholar]
- Li, R.; Noack, B.; Cordier, L.; Borée, J.; Harambat, F. Drag reduction of a car model by linear genetic programming control. Exp. Fluids 2017, 58, 103. [Google Scholar] [CrossRef]
- Li, R.; Noack, B.; Cordier, L.; Borée, J.; Kaiser, E.; Harambat, F. Linear genetic programming control for strongly nonlinear dynamics with frequency crosstalk. Arch. Mech. 2018, 70, 505–534. [Google Scholar]
- Bingham, C.; Raibaudo, C.; Morton, C.; Martinuzzi, R. Suppression of fluctuating lift on a cylinder via evolutionary algorithms: Control with interfering small cylinder. Phys. Fluids 2018, 30, 127104. [Google Scholar] [CrossRef]
- Ren, F.; Wang, C.; Tang, H. Active control of vortex-induced vibration of a circular cylinder using machine learning. Phys. Fluids 2019, 31, 093601. [Google Scholar] [CrossRef]
- Raibaudo, C.; Zhong, P.; Noack, B.; Martinuzzi, R. Machine learning strategies applied to the control of a fluidic pinball. Phys. Fluids 2020, 32, 015108. [Google Scholar] [CrossRef]
- Li, H.; Maceda, G.; Li, Y.; Tan, J.; Morzyński, M.; Noack, B. Towards human-interpretable, automated learning of feedback control for the mixing layer. arXiv 2020, arXiv:2008.12924. [Google Scholar]
- Sutton, R.; Barto, A. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.; Veness, J.; Bellemare, M.; Graves, A.; Riedmiller, M.; Fidjeland, A.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 7540, 529–533. [Google Scholar] [CrossRef]
- Rabault, J.; Ren, F.; Zhang, W.; Tang, H.; Xu, H. Deep reinforcement learning in fluid mechanics: A promising method for both active flow control and shape optimization. J. Hydrodyn. 2020, 32, 234–246. [Google Scholar] [CrossRef]
- Bingham, C.; Raibaudo, C.; Morton, C.; Martinuzzi, R. Feedback control of Karman vortex shedding from a cylinder using deep reinforcement learning. In Proceedings of the AIAA, Atlanta, GA, USA, 25–29 June 2018; p. 3691. [Google Scholar]
- Rabault, J.; Kuchta, M.; Jensen, A.; Reglade, U.; Cerardi, N. Artificial neural networks trained through deep reinforcement learning discover control strategies for active flow control. J. Fluid Mech. 2019, 865, 281–302. [Google Scholar] [CrossRef]
- Rabault, J.; Kuhnle, A. Accelerating deep reinforcement learning strategies of flow control through a multi-environment approach. Phys. Fluids 2019, 31, 094105. [Google Scholar] [CrossRef]
- Ren, F.; Rabault, J.; Tang, H. Applying deep reinforcement learning to active flow control in turbulent conditions. arXiv 2020, arXiv:2006.10683. [Google Scholar]
- Tang, H.; Rabault, J.; Kuhnle, A.; Wang, Y.; Wang, T. Robust active flow control over a range of Reynolds numbers using an artificial neural network trained through deep reinforcement learning. Phys. Fluids 2020, 32, 053605. [Google Scholar] [CrossRef]
- Paris, R.; Beneddine, S.; Dandois, J. Robust flow control and optimal sensor placement using deep reinforcement learning. arXiv 2020, arXiv:2006.11005. [Google Scholar]
- Belus, V.; Rabault, J.; Viquerat, J.; Che, Z.; Hachem, E.; Reglade, U. Exploiting locality and translational invariance to design effective deep reinforcement learning control of the 1-dimensional unstable falling liquid film. AIP Adv. 2019, 9, 125014. [Google Scholar] [CrossRef]
- Bucci, M.; Semeraro, O.; Allauzen, A.; Wisniewski, G.; Cordier, L.; Mathelin, L. Control of chaotic systems by deep reinforcement learning. Proc. R. Soc. A 2019, 475, 20190351. [Google Scholar] [CrossRef]
- Beintema, G.; Corbetta, A.; Biferale, L.; Toschi, F. Controlling Rayleigh-Bénard convection via Reinforcement learning. arXiv 2020, arXiv:2003.14358. [Google Scholar] [CrossRef]
- Han, Y.; Hao, W.; Vaidya, U. Deep learning of Koopman representation for control. arXiv 2020, arXiv:2010.07546. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Tokumaru, P.; Dimotakis, P. Rotary oscillation control of a cylinder wake. J. Fluid Mech. 1991, 224, 77–90. [Google Scholar] [CrossRef]
- Shiels, D.; Leonard, A. Investigation of a drag reduction on a circular cylinder in rotary oscillation. J. Fluid Mech. 2001, 431, 297–322. [Google Scholar] [CrossRef]
- Sengupta, T.; Deb, K.; Talla, S. Control of flow using genetic algorithm for a circular cylinder executing rotary oscillation. Comput. Fluids 2007, 36, 578–600. [Google Scholar] [CrossRef]
- Du, L.; Dalton, C. LES calculation for uniform flow past a rotationally oscillating cylinder. J. Fluids Struct. 2013, 42, 40–54. [Google Scholar] [CrossRef]
- Palkin, E.; Hadžiabdić, M.; Mullyadzhanov, R.; Hanjalić, K. Control of flow around a cylinder by rotary oscillations at a high subcritical Reynolds number. J. Fluid Mech. 2018, 855, 236–266. [Google Scholar] [CrossRef]
- Hadžiabdić, M.; Palkin, E.; Mullyadzhanov, R.; Hanjalić, K. Heat transfer in flow around a rotary oscillating cylinder at a high subcritical Reynolds number: A computational study. Int. J. Heat Fluid Flow 2019, 79, 108441. [Google Scholar] [CrossRef]
- Baek, S.; Sung, H. Numerical simulation of the flow behind a rotary oscillating circular cylinder. Phys. Fluids 1998, 10, 869–876. [Google Scholar] [CrossRef]
- He, J.; Glowinski, R.; Metcalfe, R.; Nordlander, A.; Periaux, J. Active control and drag optimization for flow past a circular cylinder: I. Oscillatory cylinder rotation. J. Comput. Phys. 2000, 163, 83–117. [Google Scholar] [CrossRef]
- Cheng, M.; Chew, Y.; Luo, S. Numerical investigation of a rotationally oscillating cylinder in mean flow. J. Fluids Struct. 2001, 15, 981–1007. [Google Scholar] [CrossRef]
- Protas, B.; Styczek, A. Optimal rotary control of the cylinder wake in the laminar regime. Phys. Fluids 2002, 14, 2073–2087. [Google Scholar] [CrossRef]
- Protas, B.; Wesfreid, J.E. Drag force in the open-loop control of the cylinder wake in the laminar regime. Phys. Fluids 2002, 14, 810–826. [Google Scholar] [CrossRef]
- Homescu, C.; Navon, I.; Li, Z. Suppression of vortex shedding for flow around a circular cylinder using optimal control. Int. J. Numer. Methods Fluids 2002, 38, 43–69. [Google Scholar] [CrossRef]
- Bergmann, M.; Cordier, L.; Brancher, J. Optimal rotary control of the cylinder wake using proper orthogonal decomposition reduced-order model. Phys. Fluids 2005, 17, 097101. [Google Scholar] [CrossRef]
- Ničeno, B.; Hanjalić, K. Unstructured large eddy and conjugate heat transfer simulations of wall-bounded flows. Model. Simul. Turbul. Heat Transf. 2005, 32–73. [Google Scholar]
- Ničeno, B.; Palkin, E.; Mullyadzhanov, R.; Hadžiabdić, M.; Hanjalić, K. T-Flows Web Page. 2018. Available online: https://github.com/DelNov/T-Flows (accessed on 27 October 2020).
- GitHub OpenAI Baselines Code Repository. Available online: https://github.com/openai/baselines (accessed on 27 October 2020).
- GitHub AICenterNSU Code Repository. Available online: https://github.com/AICenterNSU/cylindercontrol (accessed on 27 October 2020).
- Pastoor, M.; Henning, L.; Noack, B.; King, R.; Tadmor, G. Feedback shear layer control for bluff body drag reduction. J. Fluid Mech. 2008, 608, 161–196. [Google Scholar] [CrossRef]
- Flinois, T.; Colonius, T. Optimal control of circular cylinder wakes using long control horizons. Phys. Fluids 2015, 27, 087105. [Google Scholar] [CrossRef]
| c1e37 | c1e50 | c1e80 | c2e37 | c2e50 | c2e80 | |
|---|---|---|---|---|---|---|
| (%) | 8.1 | 11.3 | 13.9 | 16.1 | 13.7 | 14.7 |
| ) (%) | −50.5 | −21.8 | 29.6 | 92.8 | 86.1 | 76.8 |
| 0.158 | 0.139 | 0.082 | 0.008 | 0.031 | 0.126 | |
| () | −17.1 | 1.37 | 1.39 | 0.178 | 2.58 | −20.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tokarev, M.; Palkin, E.; Mullyadzhanov, R. Deep Reinforcement Learning Control of Cylinder Flow Using Rotary Oscillations at Low Reynolds Number. Energies 2020, 13, 5920. https://doi.org/10.3390/en13225920
Tokarev M, Palkin E, Mullyadzhanov R. Deep Reinforcement Learning Control of Cylinder Flow Using Rotary Oscillations at Low Reynolds Number. Energies. 2020; 13(22):5920. https://doi.org/10.3390/en13225920
Chicago/Turabian StyleTokarev, Mikhail, Egor Palkin, and Rustam Mullyadzhanov. 2020. "Deep Reinforcement Learning Control of Cylinder Flow Using Rotary Oscillations at Low Reynolds Number" Energies 13, no. 22: 5920. https://doi.org/10.3390/en13225920
APA StyleTokarev, M., Palkin, E., & Mullyadzhanov, R. (2020). Deep Reinforcement Learning Control of Cylinder Flow Using Rotary Oscillations at Low Reynolds Number. Energies, 13(22), 5920. https://doi.org/10.3390/en13225920





