Design Optimization of a Reluctance Lead Screw for Wave Energy Conversion
Abstract
1. Introduction
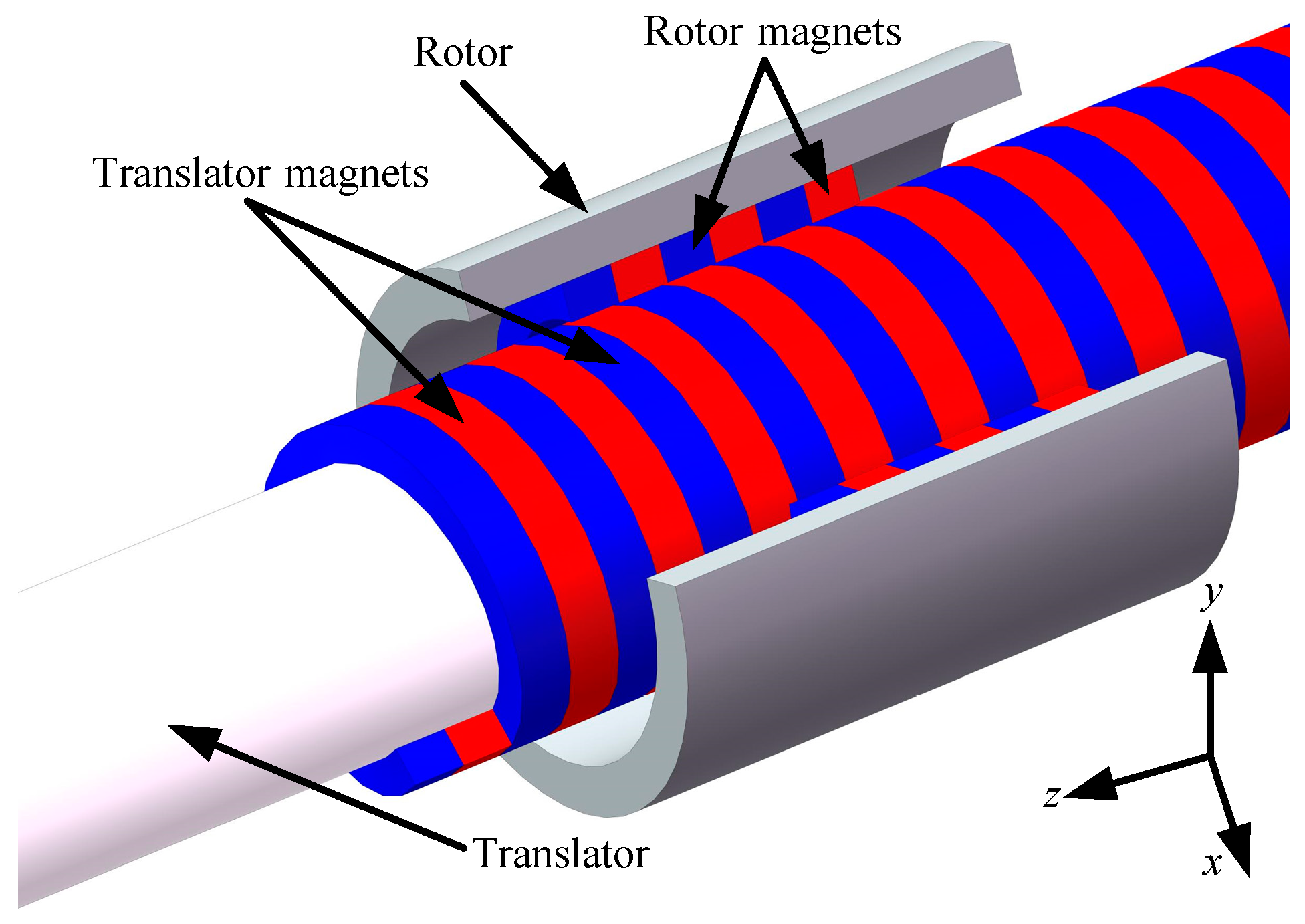
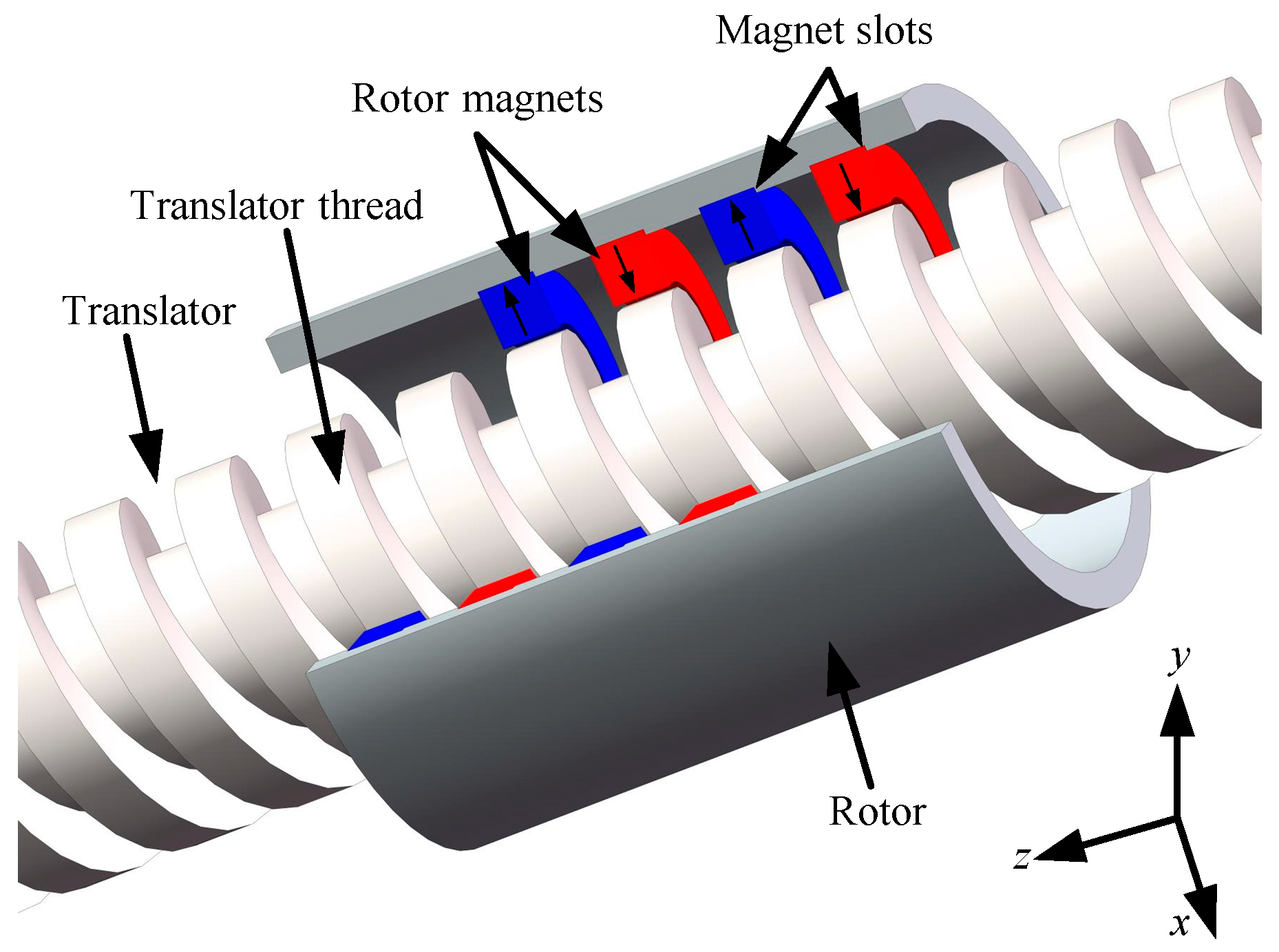
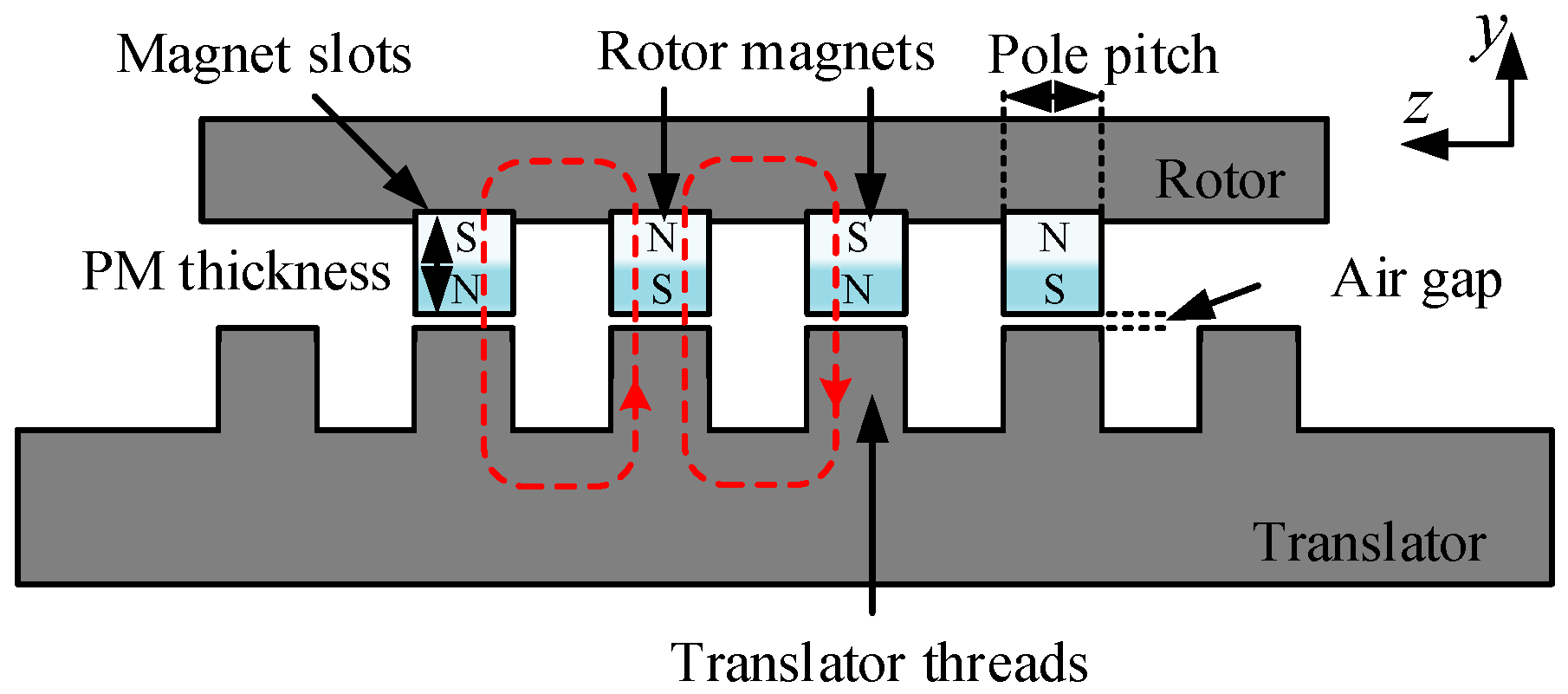
2. Fundamentals and Topology of the RLS
3. Design Optimization
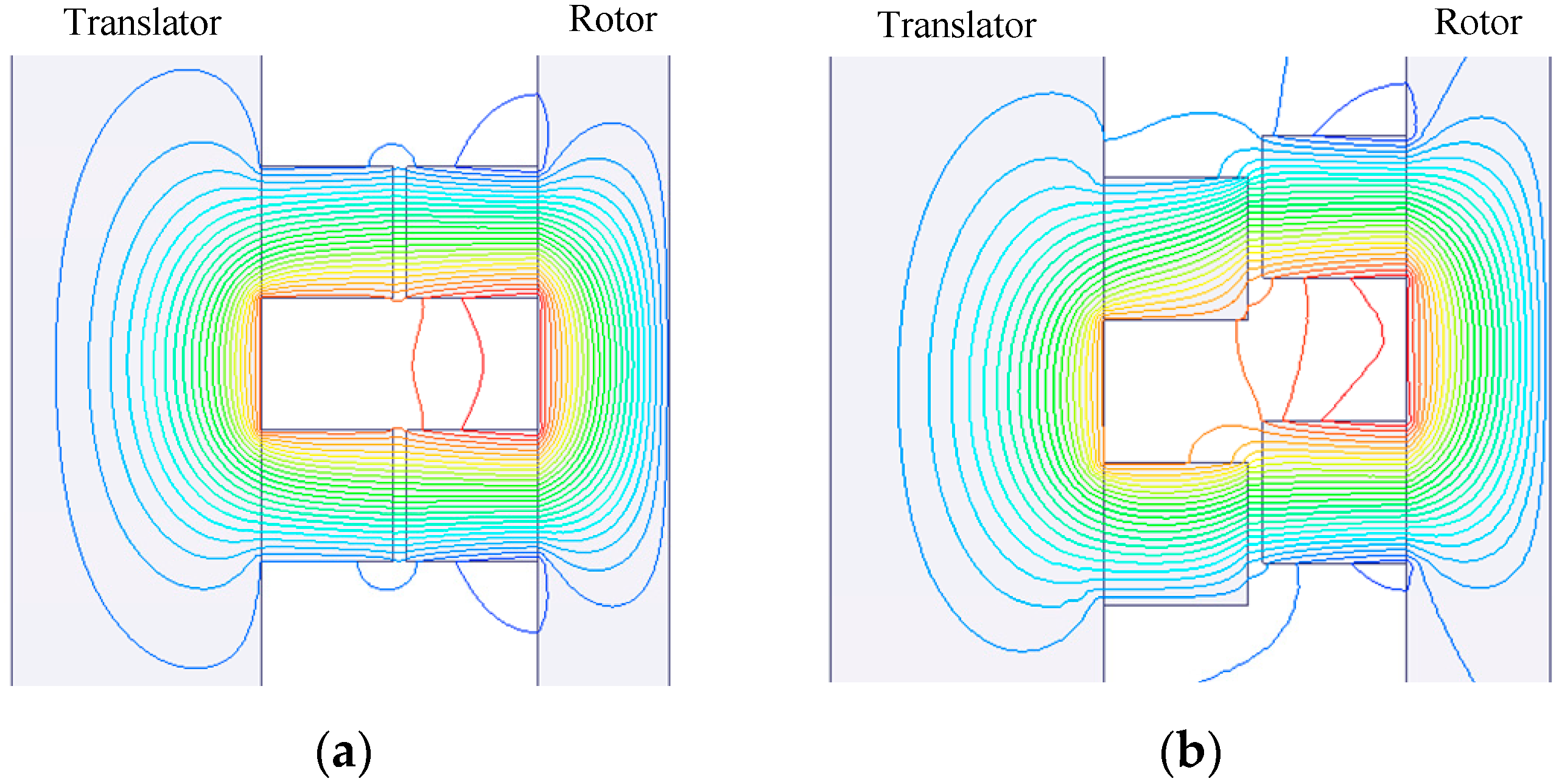
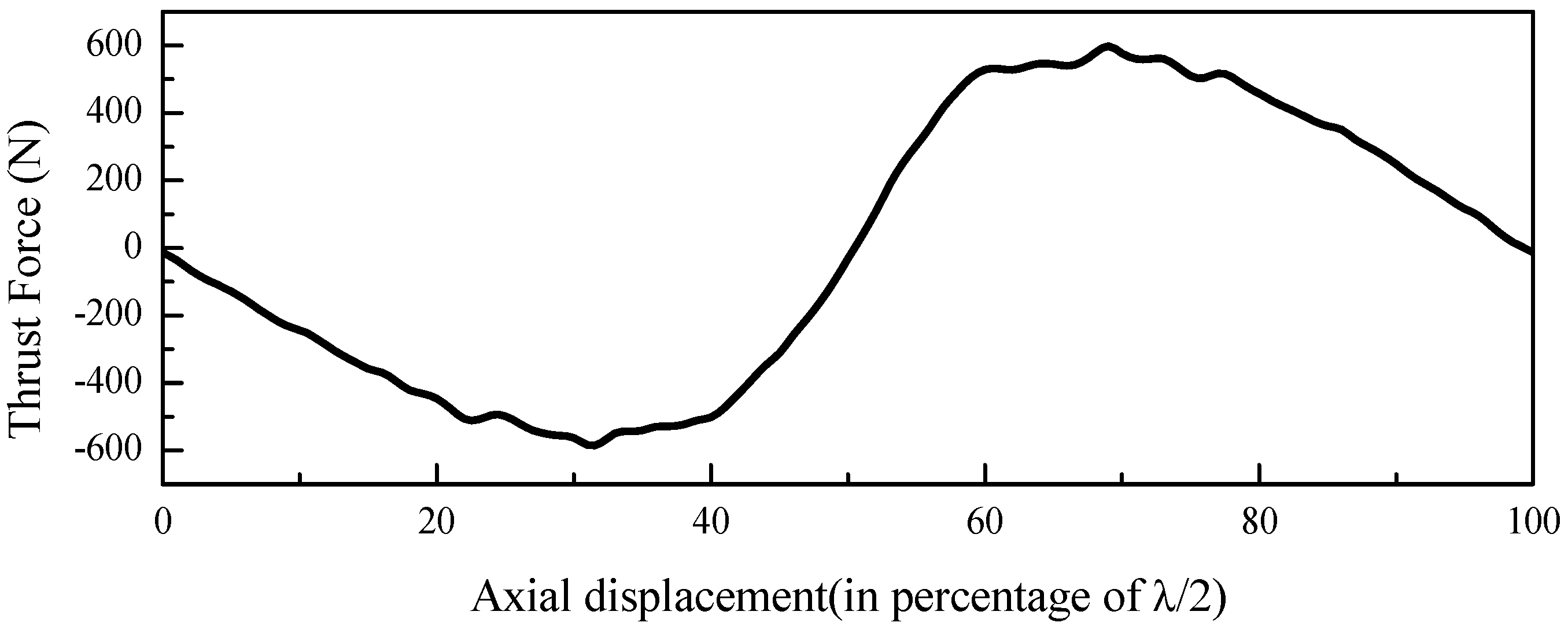
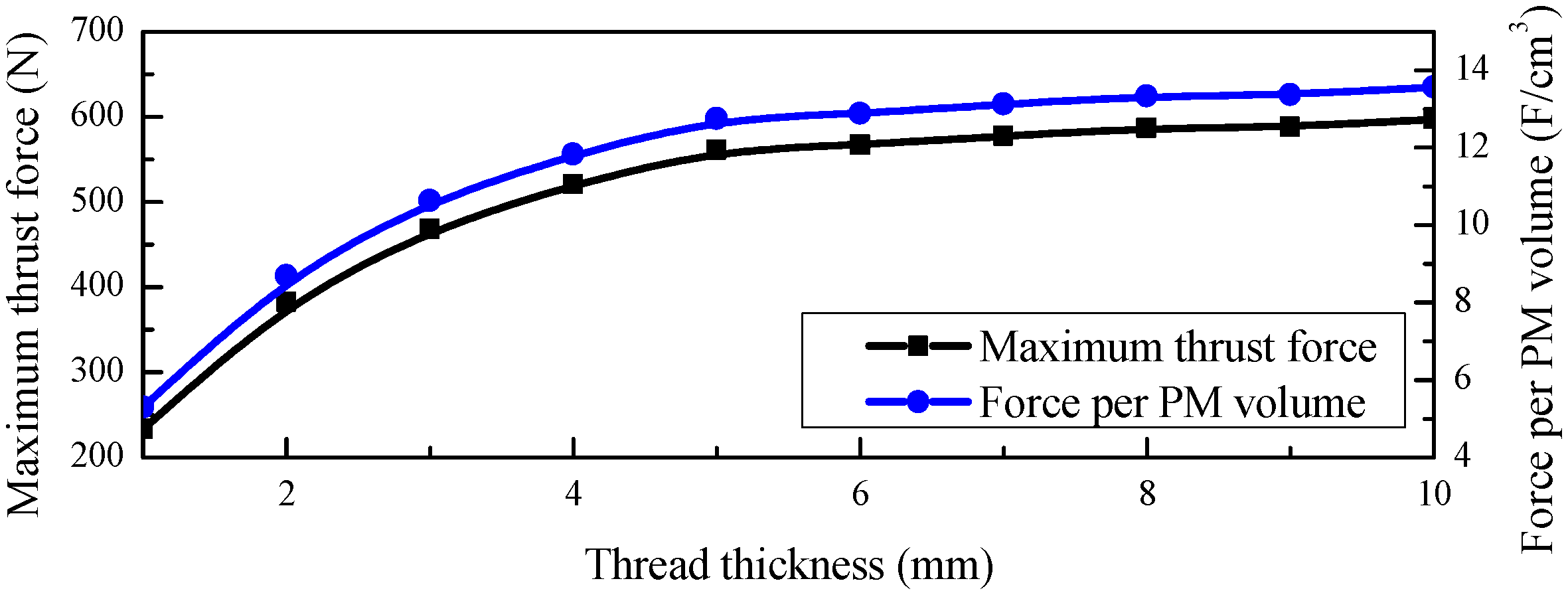
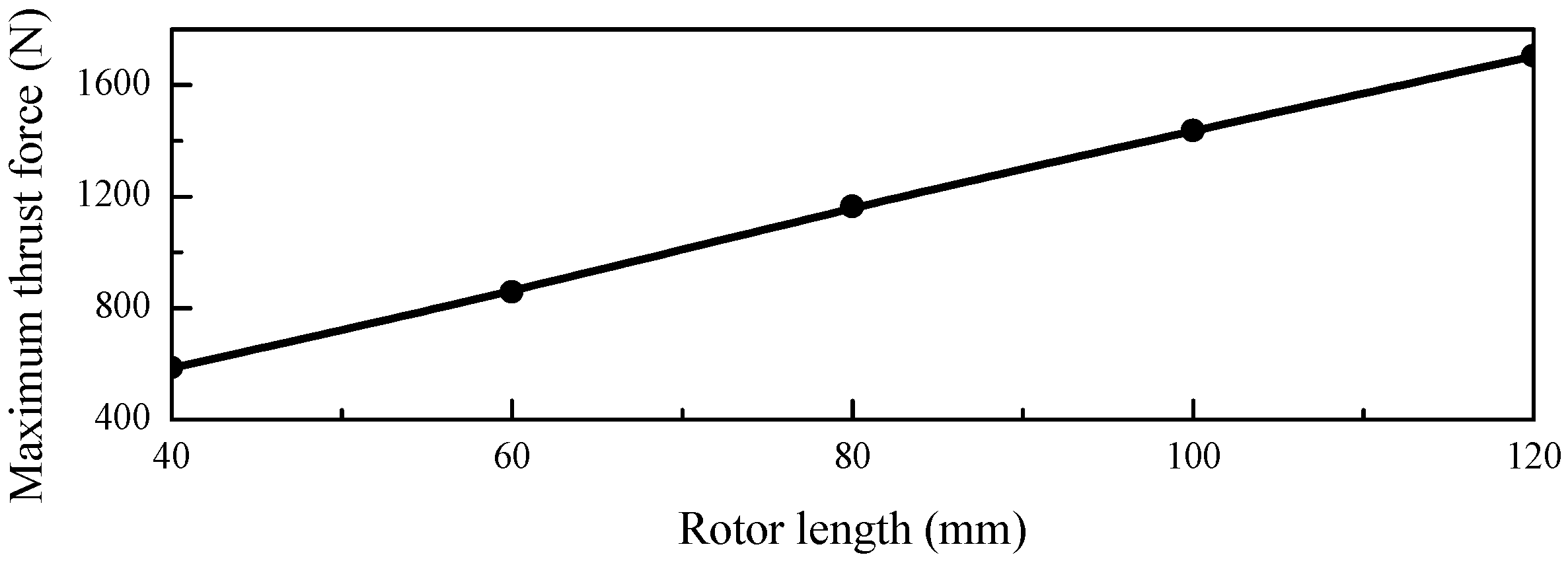
3.1. Ferromagnetic Structure Aspects
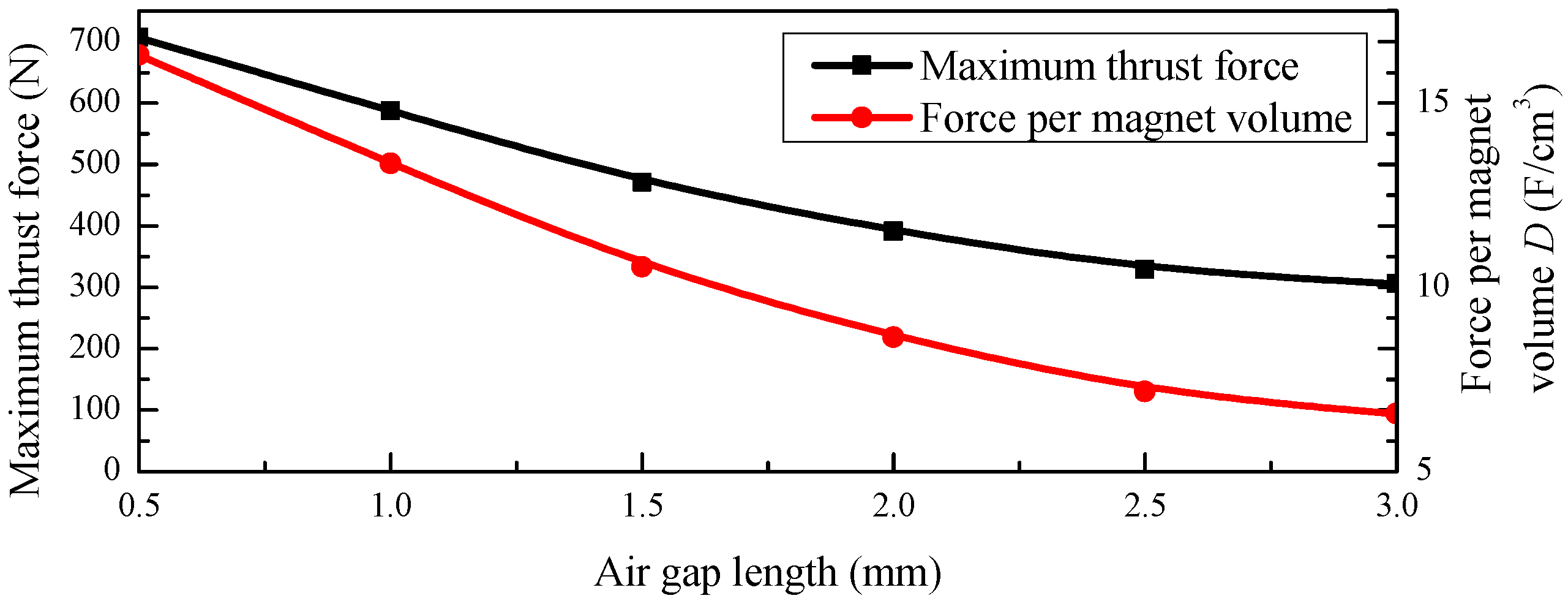
3.2. Magnet Aspects
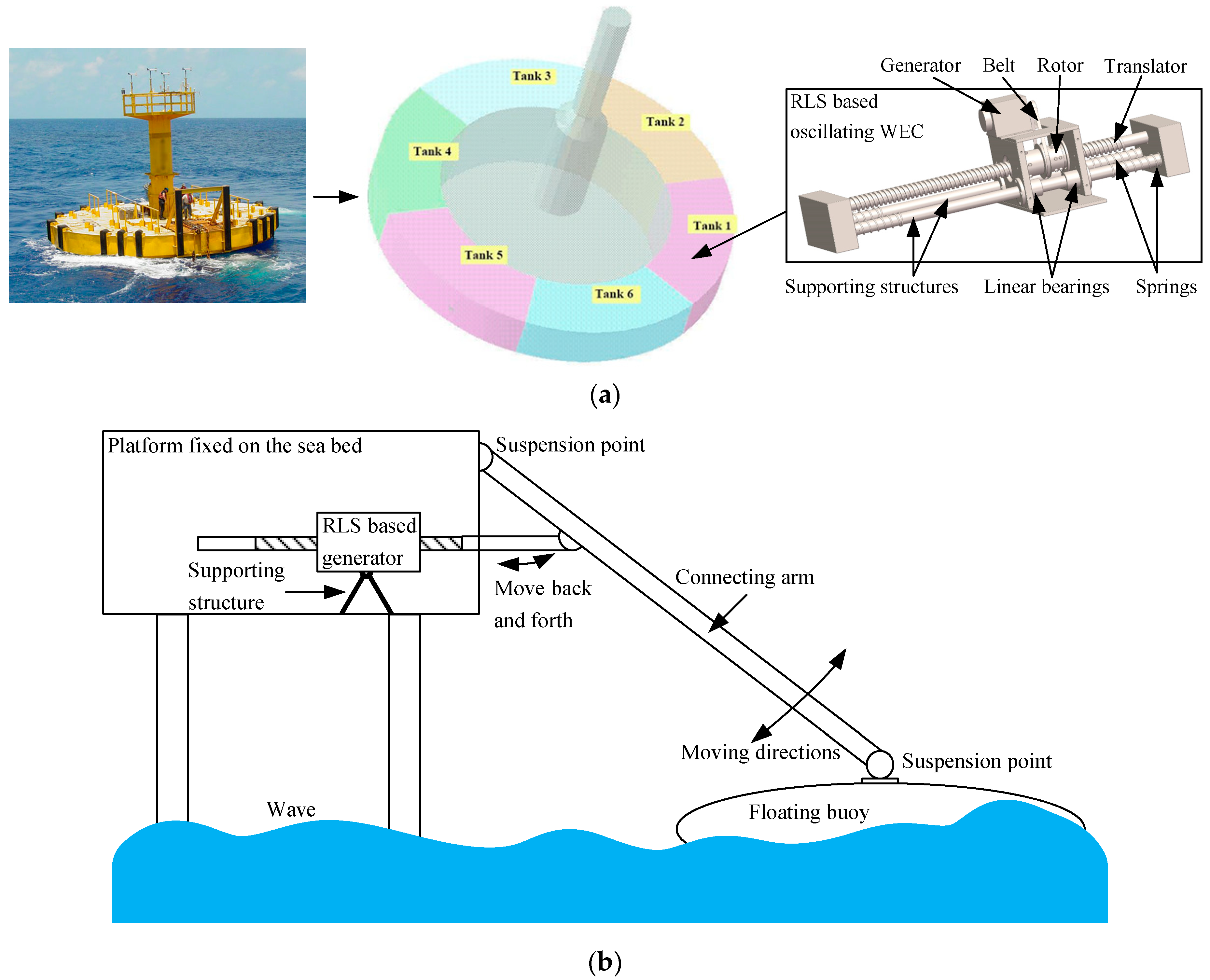
4. Prototype Design for WECs
4.1. RLS Prototype Design
4.2. Potential Applications in WECs
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mork, G.; Barstow, S.; Kabuth, A.; Pontes, M.T. Assessing the Global Wave Energy Potential. In Proceedings of the 29th International Conference on Ocean, Offshore and Arctic Engineering (OMAE), Shanghai, China, 6–11 June 2010; pp. 447–454. [Google Scholar]
- David, R. Power from the Waves; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Symonds, D.; Davis, E.; Ertekin, R. Low-power autonomous wave energy capture device for remote sensing and communications applications. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 2392–2396. [Google Scholar]
- Curto, D.; Frazitta, V.; Trapanense, M. Designing an innovative system for sea wave utilization. In Proceedings of the OCEANS 2018 MTS/IEEE Charleston, Charleston, SC, USA, 22–25 October 2018; pp. 1–6. [Google Scholar]
- Hansen, R.H.; Andersen, T.O.; Pedersen, H.C. Model based design of efficient power take-off systems for wave energy converters. In Proceedings of the 12th Scandinavian International Conference on Fluid Power, Tampere, Finland, 18–20 May 2011; pp. 18–20. [Google Scholar]
- Carpita, M.; Beltrami, T.; Besson, C.; Gavin, S. Multiphase active way linear motor: Proof-of-concept prototype. IEEE Trans. Ind. Electron. 2011, 59, 2178–2188. [Google Scholar] [CrossRef]
- Cao, R.; Cheng, M.; Zhang, B. Speed control of complementary and modular linear flux-switching permanent-magnet motor. IEEE Trans. Ind. Electron. 2015, 62, 4056–4064. [Google Scholar] [CrossRef]
- Choi, S.Y.; Lee, C.Y.; Jo, J.M.; Choe, J.H.; Oh, Y.J.; Lee, K.S.; Lim, J.Y. Sub-Sonic Linear Synchronous Motors Using Superconducting Magnets for the Hyperloop. Energies 2019, 12, 4611. [Google Scholar] [CrossRef]
- Polinder, H.; Damen, M.E.; Gardner, F. Linear PM generator system for wave energy conversion in the AWS. IEEE Trans. Energy Convers. 2004, 19, 583–589. [Google Scholar] [CrossRef]
- Spooner, E.; Grimwade, J. SnapperTM: An efficient and compact direct electric power take-off device for wave energy converters. In Proceedings of the World Maritime Technology Conference, London, UK, 6–10 March 2006; pp. 6–10. [Google Scholar]
- Hussain, H.A. A Novel Contactless Rotary-to-Linear Magnetic Actuator. In Proceedings of the 2019 IEEE International Electric Machines & Drives Conference (IEMDC), San Diego, CA, USA, 12–15 May 2019; pp. 1081–1086. [Google Scholar]
- Liu, X.; Liu, Y.; Li, X. Parametric Analysis and Design of Magnetic Lead Screw. In Proceedings of the 2019 IEEE International Electric Machines & Drives Conference (IEMDC), San Diego, CA, USA, 12–15 May 2019; pp. 1990–1995. [Google Scholar]
- Holm, R.K.; Berg, N.I.; Walkusch, M.; Rasmussen, P.O.; Hansen, R.H. Design of a magnetic lead screw for wave energy conversion. IEEE Trans. Ind. Appl. 2013, 49, 2699–2708. [Google Scholar] [CrossRef]
- Ling, Z.; Zhao, W.; Ji, J.; Liu, G. Design of a new magnetic screw with discretized PMs. IEEE Trans. Appl. Supercond. 2016, 26, 1–5. [Google Scholar] [CrossRef]
- Lu, K.; Wu, W. Electromagnetic lead screw for potential wave energy application. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Wang, J.; Atallah, K.; Wang, W. Analysis of a magnetic screw for high force density linear electromagnetic actuators. IEEE Trans. Magn. 2011, 47, 4477–4480. [Google Scholar] [CrossRef]
- Ling, Z.; Zhao, W.; Ji, J.; Zhu, J.; Mao, J. Design and Analysis of a New HTS Electromagnetic Screw. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Gao, F.; Wang, Q.; Jibin, Z. Analytical Modeling of 3-D Magnetic Field and Performance in Magnetic Lead Screws Accounting for Magnetization Pattern. IEEE Trans. Ind. Electron. 2019, 67, 4785–4796. [Google Scholar] [CrossRef]
- Heya, A.; Nakata, Y.; Sakai, M.; Ishiguro, H.; Hirata, K. Force Estimation Method for a Magnetic Lead-Screw-Driven Linear Actuator. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Gao, F.; Wang, Q.; Hu, Y.; Chen, B.; Zhao, B. Performance Evaluation of Magnetic Lead Screws Equipped With Skewed Arc Magnets Instead of Helical Ones. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Pakdelian, S.; Frank, N.W.; Toliyat, H.A. Magnetic design aspects of the trans-rotary magnetic gear. IEEE Trans. Energy Convers. 2014, 30, 41–50. [Google Scholar] [CrossRef]
- Cirolini, M.; Flores Filho, A.F.; Wu, Y.C.; Dorrell, D.G. Design Aspects of a Reluctance-Based Magnetic Lead Screw. IEEE Trans. Magn. 2019, 55, 1–6. [Google Scholar] [CrossRef]
- Ling, Z.; Ji, J.; Wang, J.; Zhao, W. Design optimization and test of a radially magnetized magnetic screw with discretized PMs. IEEE Trans. Ind. Electron. 2017, 65, 7536–7547. [Google Scholar] [CrossRef]
- Zhao, A.; Wu, W.; Jiang, J.; Zhu, L.; Lu, K.; Blaabjerg, F. Design and experiment of a magnetic lead screw for the point-absorbing wave energy conversion system. IET Electr. Power Appl. 2020, 49, 618–626. [Google Scholar] [CrossRef]







| Parameter | Quantity | Unit |
|---|---|---|
| Translator radius Rtl | 19 | mm |
| Translator length Ltl | 200 | mm |
| Rotor outer radius Rrto | 50 | mm |
| Rotor internal radius Rrti | 40 | mm |
| Rotor length Lrt | 80 | mm |
| magnet thickness hm | 10 | mm |
| Pole pitch τp | 10 | mm |
| Lead λ | 40 | mm |
| Air gap g | 1 | mm |
| Thread width wi | 10 | mm |
| Thread thickness hi | 10 | mm |
| PM remanence Br | 1.1 | T |
| PM coercivity Hc | 838.0 | kA/m |
| Parameters and Units | RLS | MLS |
|---|---|---|
| Translator radius/mm | 19 | 18 |
| Translator length/mm | 2000 | 2000 |
| Rotor outer radius/mm | 50 | 41 |
| Rotor length/mm | 120 | 36 |
| Maximum Force/kN | 1.8 | 1.5 |
| PM consumption/cm3 | 131.9 | 1543.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, T.; Wu, W.; Jiang, J.; Zhu, L.; Lu, K.; Blaabjerg, F. Design Optimization of a Reluctance Lead Screw for Wave Energy Conversion. Energies 2020, 13, 5388. https://doi.org/10.3390/en13205388
Tian T, Wu W, Jiang J, Zhu L, Lu K, Blaabjerg F. Design Optimization of a Reluctance Lead Screw for Wave Energy Conversion. Energies. 2020; 13(20):5388. https://doi.org/10.3390/en13205388
Chicago/Turabian StyleTian, Tian, Weimin Wu, Jiacheng Jiang, Lixun Zhu, Kaiyuan Lu, and Frede Blaabjerg. 2020. "Design Optimization of a Reluctance Lead Screw for Wave Energy Conversion" Energies 13, no. 20: 5388. https://doi.org/10.3390/en13205388
APA StyleTian, T., Wu, W., Jiang, J., Zhu, L., Lu, K., & Blaabjerg, F. (2020). Design Optimization of a Reluctance Lead Screw for Wave Energy Conversion. Energies, 13(20), 5388. https://doi.org/10.3390/en13205388








