Abstract
Parameter estimation based on the measurement data of the phasor measurement unit (PMU) is an important approach for identifying the Thévenin equivalent parameters (TEPs) of power systems. However, in the process of acquiring or transmitting data in PMU, measurement errors due to external interference or internal system faults will affect the accuracy of parameter estimation. In this paper, a TEP estimation algorithm based on local PMU measurement is proposed. The algorithm considers the errors of the PMU and introduces Huber function and projection statistics (PS) to eliminate the effects of outliers and leverage measurements, respectively. Additionally, a variable forgetting factor (VFF) is used to quickly eliminate the historical data with measurement deviation and track the changes of the system. The regularization technique is used to solve the divergence problem in the inverse process of the ill-conditioned matrix, thereby improving the stability and generalization performance of the algorithm. Finally, by minimizing the cost function of this algorithm, a recursive formula for the equivalent parameter estimation is derived. The effectiveness of the algorithm is verified on the IEEE 118-bus and IEEE 30-bus systems, and compared with recursive least squares (RLS) and Huber’s M-Estimation; the mean relative errors decreased by 94.75% and 84.77%, respectively.
1. Introduction
The Thévenin equivalent (TE) method is a method that can simplify the power system and increase the analysis rate. It is suitable for the current large-scale power grid, so it has been widely used in various circuit analysis situations, such as power system fault calculation [1], voltage stability analysis [2,3], power system adaptive protection scheme design [4], and rotor angle stability prediction [5], etc. Therefore, in order to make the analysis more effective, the accuracy of TEP estimation is very important. There are several methods for determining TEPs [6,7,8,9,10]. Based on the analysis of voltage-relaxation characteristics of pulse discharge and pulse charge experiments, the literature [6] applied the time domain method to extract the Resistor-Capacitance (RC) circuit parameters of the TE circuit battery model. In [7], the proposed algorithm can be simplified to a standard recursive least square algorithm, and after a limited time to track possible changes of parameters. In [8], the node–voltage equation was directly used to construct a complex high-dimensional linear system to obtain the equivalent voltage, and the LU factorization was used to achieve the rapid and accurate estimation of equivalent parameters.
In addition, the recognition of TEPs based on local measurement data of PMU has attracted the attention of scholars [11]. In these methods, no network topology but local measurement information is needed. These algorithms are based on the following premise: TEPs remain unchanged during the sampling period [12], and multiple cross-sectional data are used to identify the equivalent parameter. In [13], a method-based online measurement was proposed to determine multiport TE circuit parameters, where the equivalent was the reduction in the power flow model and was directly obtained by applying the least square method to the boundary bus measured value to determine. The fast tracking Thévenin parameter algorithm proposed in [14] can filter out oscillation without significantly delaying the recognition process. However, in practical applications, problems such as line tripping, shunt capacitor switches and generators reaching reactive power output limits will occur [15,16]. These problems lead to inaccurate assumptions of the above method. Therefore, the problem of parameter drift caused by time-varying operating conditions becomes very important [17]. In order to improve these methods, the literature [18] proposed a method to calculate impedance of the online Thévenin at the generator terminal, by using the frequency change rate available at the output of the PMU to correct the negative effects of phase drift. In [19], the expression of equivalent impedance was derived by using the Tellegen’s theorem and two measurements, and the Thévenin index based on sensitivity was further derived based on method [20].
In addition, due to external interference or internal failure of the system, the measured value of PMU data acquired or transmitted can be different from the actual value [21]. In order to deal with this issue, some scholars have tried to use state estimation methods to solve problems caused by erroneous data [21,22,23,24,25,26,27,28,29]. An optimal Thévenin model parameter estimation method was proposed in [22], which did not need to solve a system of nonlinear equations with measurement and quantization noise. In [23], based on the representation and manipulation of measured voltage phasors in the complex voltage plane, a graphical method for deriving TEPs was developed. An extended Kalman filtering method based on equivalence constraint was proposed in [25], which used a statistical projection algorithm to improve the robustness of leverage measurements. In [26], a robust recursive least square algorithm was applied to recognize measurement outliers and deal with missing data. Additionally, in [28], a regular term was introduced into the robust least-squares estimation to realize the prior conjecture of model parameters, and the anti-interference ability of measurement noise and gross error were improved. In addition, in [29], a generalized multivariate Huber loss function is proposed to realize parameter estimation in a linear model contaminated by non-Gaussian noise. The above methods have reduced the influence of erroneous measurement and noise in some PMU measurement data. However, their performances cannot solve the problem of algorithm divergence caused by the ill-conditioned matrix inverse and lack the robustness and adaptive tracking ability when the system changes. According to the analysis of the ill-conditioned Thevenin equivalent parameters equations, a method based on Schmidt’s orthogonalization transformation is presented in [30] to obtain precise solutions. A dynamic state estimation methodology was proposed in [31], which combined a new regularization-based method with a Markov model representation to improve estimation accuracy over classic methodologies based on static load pseudo measurements. The tracking capability of the robust recursive least square (RRLS) algorithm was improved by adaptive adjustment of the forgetting factor in [27], and this algorithm was used for estimating electromechanical modes of power systems. Based on [27], a dynamic regularization method was introduced in [28] to improve numerical performance for online estimation of power-system electromechanical modes.
Therefore, in order to reduce the influence of erroneous measurement of PMU and ill-conditioned matrix inverse on the estimation accuracy of TEPs, a Huber’s M-Estimation algorithm based on the variable forgetting factor (VFF) and projection statistics, abbreviated as HU-PS, is proposed in this paper. The M-estimation based on projection statistics is used to filter the measurement data and determine the TEPs through the recursion formula. In this way, the effect of erroneous measurement on the equivalent parameters is eliminated, and the problem of ill-conditioned matrix inversion is solved. Additionally, the real-time tracking capability of TEPs was also enhanced.
2. TEP Estimation Method
2.1. Variable Forgetting Factor
The forgetting factor is a fixed value in the classic RLS algorithm, which means that the influence of historical data is eliminated at a fixed rate. However, when the system structure suddenly changes or the measurements are wrong, the fixed forgetting factor cannot eliminate the influence of historical data in time, so errors will still occur in the subsequent period. An error-based VFF method is proposed, which can be adaptively adjusted according to the changes in the power system and erroneous measurements result.
When the system is running in a nonstationary state, the tracking ability of the algorithm can be enhanced by selecting a smaller forgetting factor and using data only in relatively recent times. In the stationary case, it is necessary to keep the forgetting factor around an appropriate value. The forgetting factor should be between 0.95 and 0.99 [32]. According to the analysis above, the VFF is represented by and defined as follows:
In Equation (1), and are the upper and lower limits of the VFF. is usually slightly smaller than 1, and the value of is related to a specific problem but should not be too small, so as not to affect the stability of the value. In Equation (2), is the estimated error at time ; and are error sensitivity coefficients, which are used to control the rate of forgetting factor. can maintain the stability of its value; can transfer the error size to the forgetting factor, so the forgetting factor can track changes of the system. For systems with large convergence errors, the value of is relatively small, while the value of is relatively large, and vice versa.
2.2. TEP Estimation Method Based on VFF, PS, and Huber’s M-Estimation
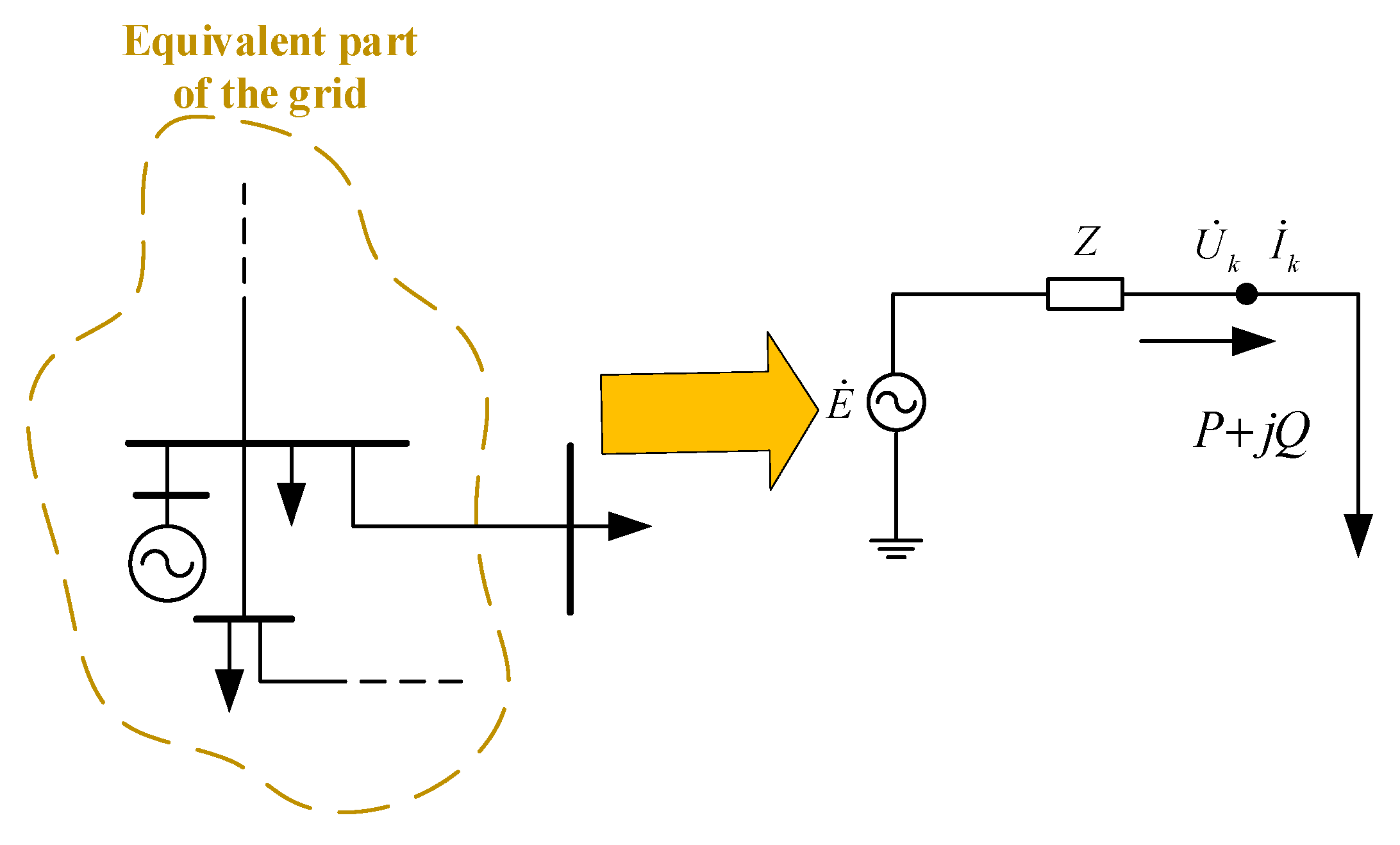
TE theorem states that in power systems analysis, a series model of equivalent impedance Z and equivalent power source E can be used to replace systems other than the load node under study. Figure 1 illustrates the TE circuit observed from the load side.
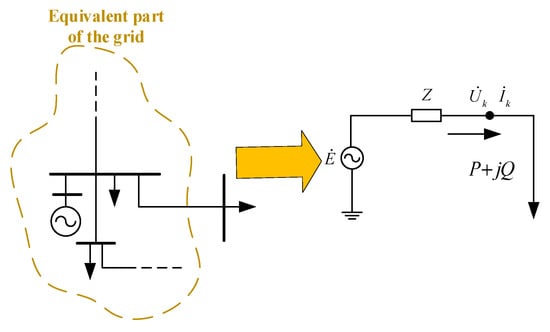
Figure 1.
TE circuit observed from load node.
In Figure 1, and are the voltage and current phase values of the load bus at time , respectively. They belong to the system boundary node information that can be obtained through PMU. and are equivalent potential and equivalent reactance of the TE model, respectively. The basic relationship of the TE circuit can be obtained from Kirchhoff’s Voltage Law, and then, dividing it into the real part and imaginary part, the following equation can be obtained:
where
where is the voltage measurement matrix at the kth time sample; is the measurement coefficient matrix at the kth time sample; is the TEP to be estimated; is the vector of random errors, which are caused by signal noises appearing on the input terminals of PMU [33].
When the voltage and current data measured by PMU are used for TE circuit parameter calculation, they are sometimes inaccurate due to measurement noise and the existence of PMU measurement error, which further leads to the large deviation between the solved TE circuit and the original circuit. In order to identify TEPs more accurately and reduce the systematic error of the TE circuit, a robust adaptive algorithm was adopted. The cost function of the algorithm can be expressed as:
The above formula can reduce the influence of erroneous measurement data on TEPs identification and improve the real-time tracking performance of TEPs. To further explain Equation (7), the first term is the positive definite term, which is used to solve the inverse problem of an ill-conditioned matrix, and at the same time, it can prevent overfitting, improve the generalization performance of the model, and enhance the anti-interference ability to system noise and erroneous data. The second term is used to reduce the influence of erroneous measurement data on TEP identification accuracy, where is the generalized regularization parameter; is the forgetting factor, which is used to weight the measurement data at different times, highlight the contribution of the new data by forgetting old data, and improve the real-time tracking capability of parameters; is the coefficient that characterizes the leverage measurement and is determined by applying PS on Equation (5).
where is the measure of the distance from the measured value to the center of the measured point and is usually set to 1.5 to produce good statistics under different distributions without increasing the deviation caused by the outliers. Additionally, in Equation (7), is the M-estimate function, which is used to constrain the influence of residuals and eliminate the influence of measured outliers on the equivalent process. In general, the Huber ρ-function is most widely used in the M-estimation [34,35], which is given as Equation (9).
where is a common choice in the Gaussian distribution [35] and
In Equation (10), is the standardized residual and is the robust scale estimate used to improve the robustness of M-estimation. In Equation (11), is to ensure the consistency of the method under Gaussian distribution [36] and is a correction factor under Gaussian distribution. Define:
then
In order to minimize the cost function (7), differentiate the cost function with respect to and set the result to zero, and then obtain:
where
Equations (16) and (17) can be written using the Sherman–Morrison–Woodbury formula [37] as:
It can be derived from (15) and (18):
Substituting (19) and (20) into (21) leads to:
where is the prior error, is the posterior error. It should be noted that in (22), the update calculation of TEPs requires the posteriori error as a known condition, but is not available when is unknown. Therefore, and are interdependent. When is unknown, the posterior error is approximately replaced by the prior error , and is used to replace the unknown for calculation in (19) and (22). Furthermore, (19) and (22) are rewritten as (24) and (25).
Therefore, the (20), (24), and (25) constitute the recursive calculation formula for the TEP estimation of HU-PS. Its pseudo code is given in Figure 2.

Figure 2.
Pseudo code of HU-PS.
3. Simulation Verification
To verify the effectiveness of the proposed method, the IEEE 118-bus system and IEEE 30-bus system were used for the simulation verification. At the same time, to simulate the noise of PMU measured data, a Gaussian distribution with the expected value of 0 and the standard deviation of 0.01 was added [25,31]. The node voltage and current were used as simulated PMU measurements.
Considering the influence of erroneous measurements on the accuracy of TEPs estimation, two different scenarios were set in case I which was simulated on the IEEE 118-bus system. However, when the system changes, it must also evaluate if the same level of accuracy can be obtained in the TEPs. To this end, different system lateral changes were simulated in case II on the IEEE 30-bus system, including the loss of generation capacity and branch cutting operations.
In TEP estimation, the classical RLS [11] and Huber’s M-Estimation [35] are popular because of their strong adaptability. Therefore, the calculation result of HU-PS was compared with the above two methods to verify its effectiveness. The parameters of the method were set as follows: , , . The maximum absolute error (MAER) and mean absolute error (MAE) are adopted as the evaluation indexes of the equivalent model, which are expressed as follows:
where and represent the results obtained from the equivalent model and the original model, respectively. is a variable, depending on the number of measurements.
3.1. Case I: Simulation Verification on IEEE 118-Bus System
As shown in Figure A1 (see Appendix A), this test was performed under the simulated measurements of the IEEE 118-bus system, which maintained everything except the load at bus 51. The load at this bus was changed at the 30th or 40th second of both the magnitude of voltage and current at this node, and was recorded and used as PMU measurements. The parameters were set as follows: , , , . Two scenarios were set as follows:
- (1)
- Scenario 1: The voltage and current values at the 30th second increased to 4 times and 6 times, respectively, and recorded as the leverage measurement. A fixed forgetting factor was applied in Huber’s M-Estimation algorithm.
- (2)
- Scenario 2: Increased the values at the 40th second to 6 times as outliers. A fixed forgetting factor was applied in Huber’s M-Estimation algorithm.
To compare the accuracy of the above three methods, random disturbance was added to the load at bus 51 (no more than 35%) in the original system, where everything else was kept constant. Then power flow calculation was carried on the original IEEE 118-bus system and the two-node TE systems. The voltage value of the original system was chosen as the real value, and the other voltage values will be compared with it. The experimental simulation results were as follows.
3.1.1. Scenario 1: Leverage in the Measurement Data
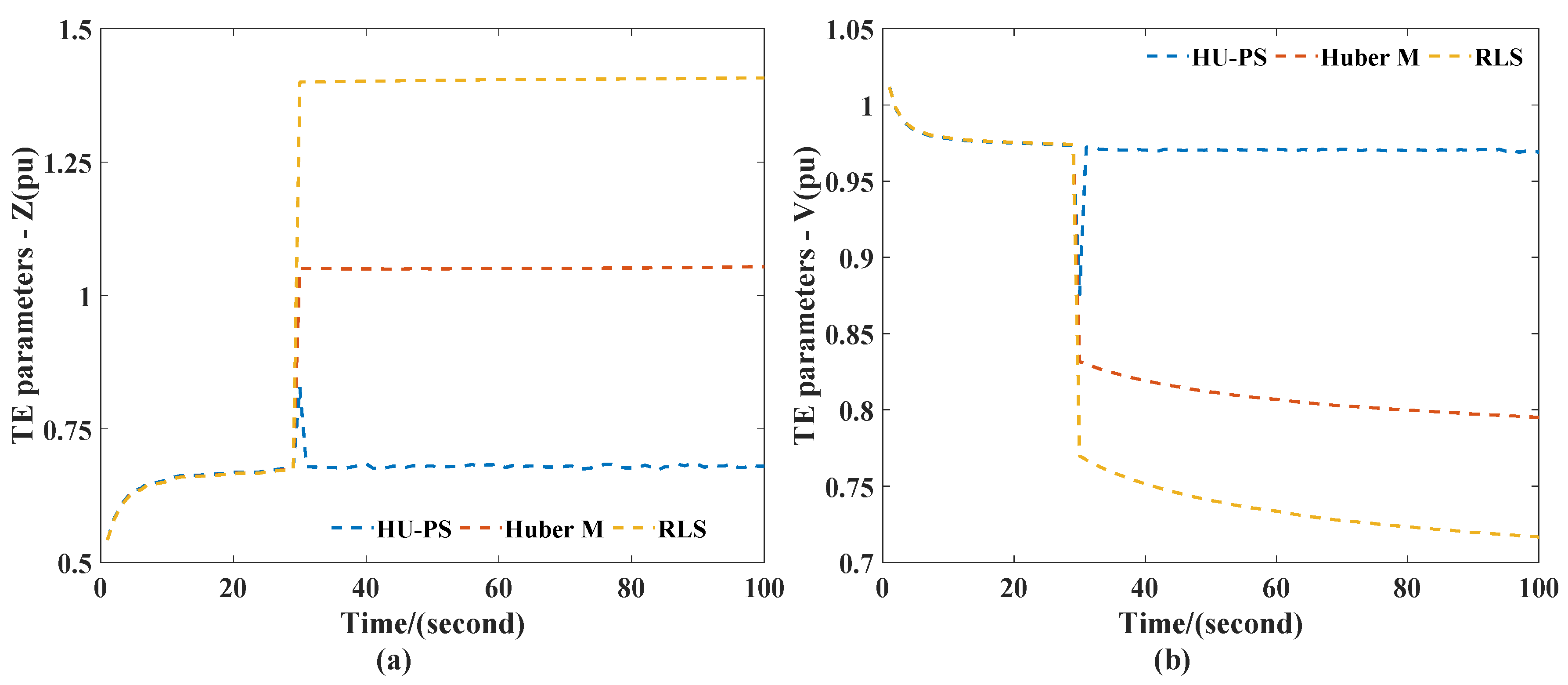
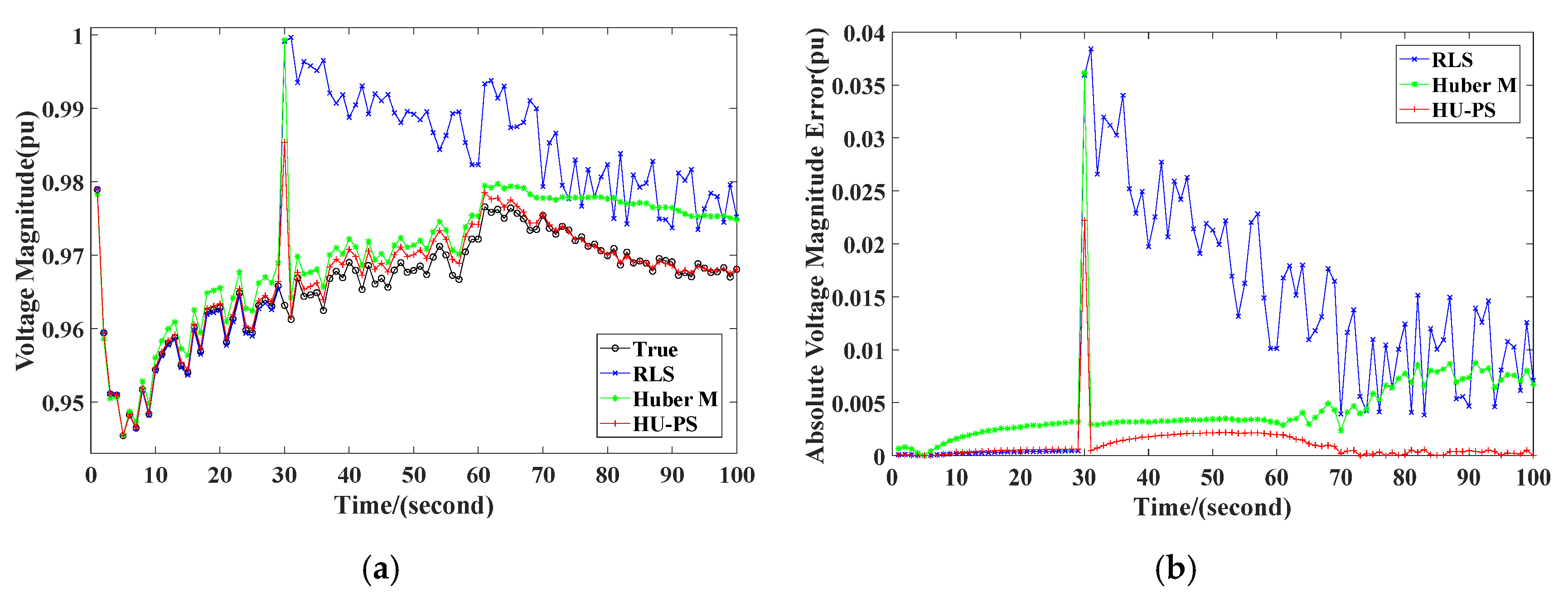
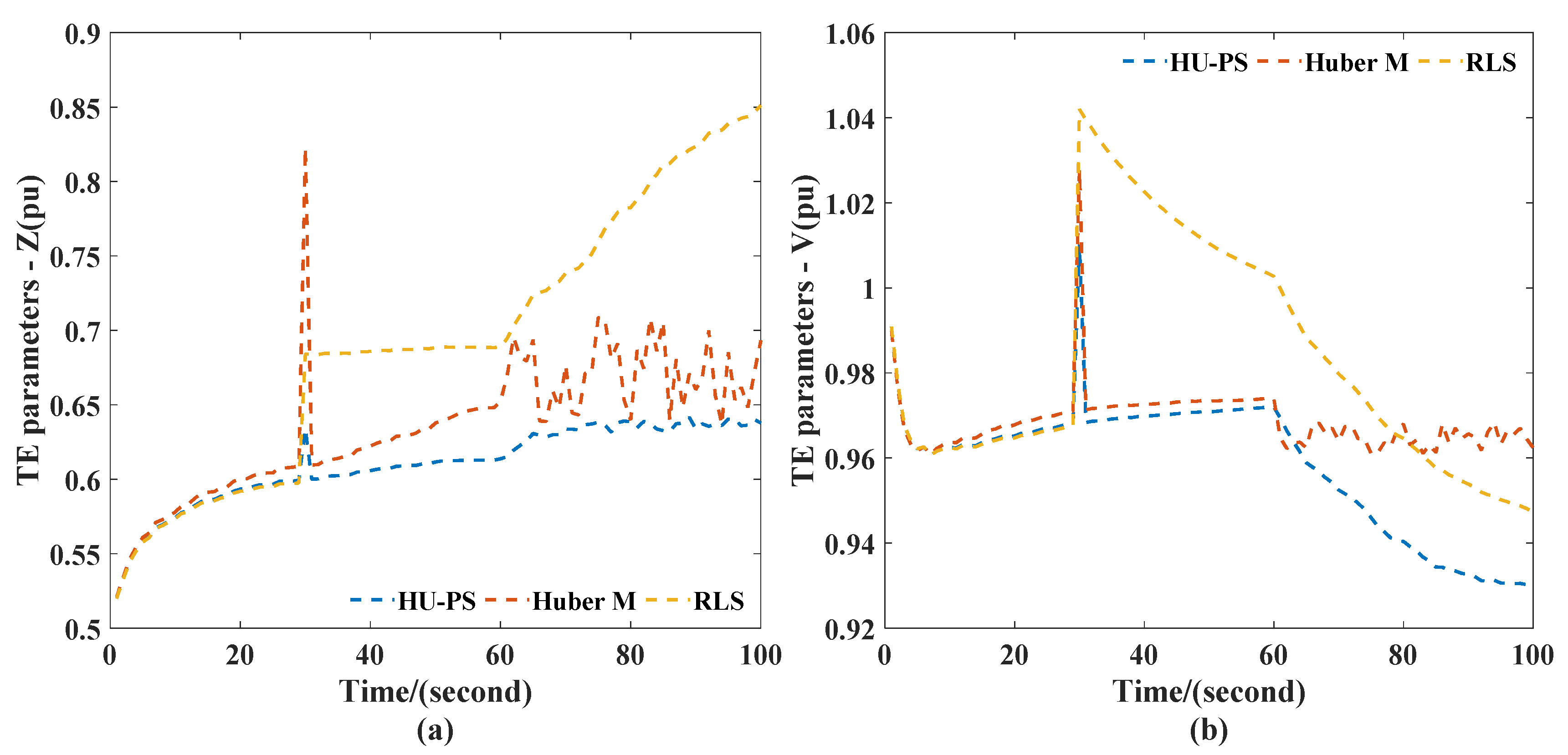
Based on the data measured by PMU, the TEPs were calculated using HU-PS, RLS, and Huber’s M-Estimation. The results are shown in Figure 3. It shows that the TEPs changed suddenly when leverage appeared. However, the TEPs obtained by HU-PS returned to their original values as soon as the change stopped, while the TEPs obtained by RLS and Huber’s M-estimation did not.
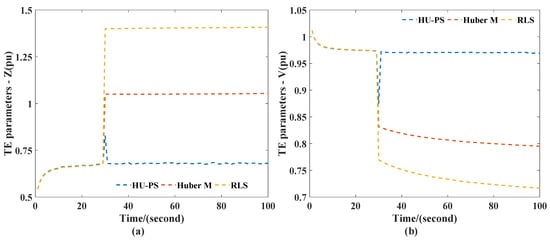
Figure 3.
TEPs obtained in case I scenario 1: (a) impedance, (b) voltage.
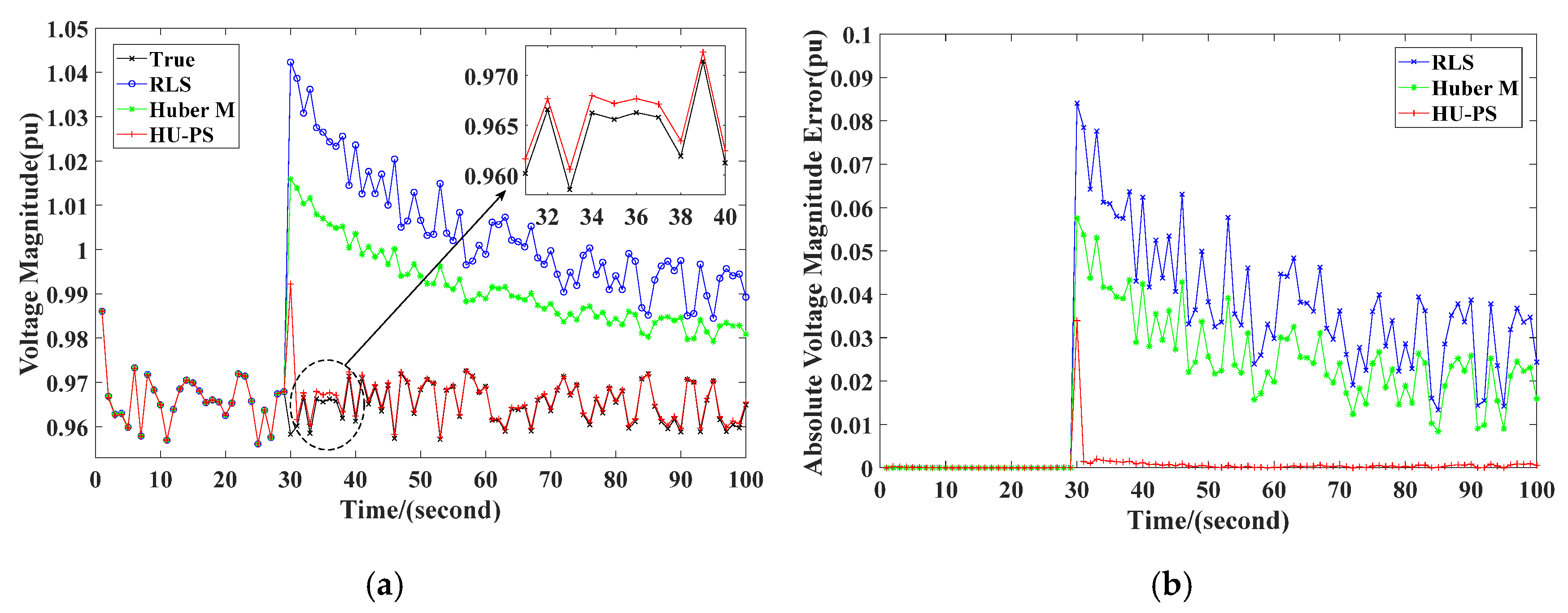
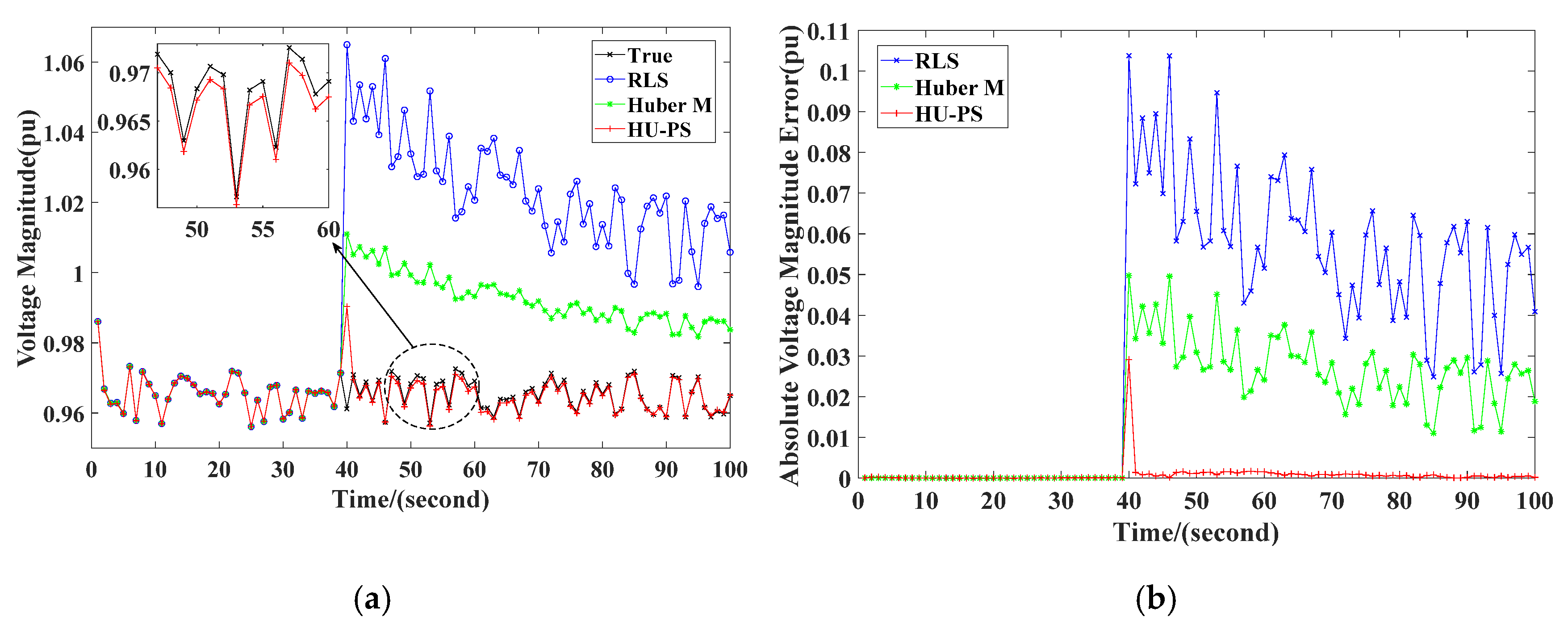
It can be seen from Figure 4 that RLS and Huber’s M-Estimation were very sensitive to the measurement of leverage measurement. When the leverage measurement appeared at the 30th second, the RLS error increased sharply and was affected by historical data, so it was not very easy to quickly recover to the tracking state of the system. Compared with RLS, Huber’s M-Estimation could effectively reduce the impact of leverage measurement, but there was still a significant deviation from the actual value. In contrast, HU-PS effectively suppressed the interference of leverage measurement by using PS, so it can be seen that the existence of leverage measurement did not significantly affect the estimation of TEPs. In addition, because of the use of VFF, HU-PS could eliminate the impact of historical data in time, and could accurately identify the TEPs of the system through new data, and track the system status again.
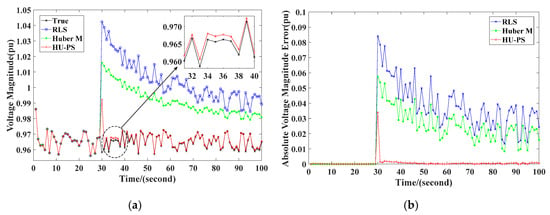
Figure 4.
Values in scenario 1: (a) voltage magnitude, (b) absolute voltage magnitude error.
3.1.2. Scenario 2: Outlier in the Measurement Data.
The same as scenario 1, the TEPs were calculated and the results are shown in Figure 5. It shows that the TEPs changed suddenly when the outlier appeared; however, the parameters obtained by HU-PS returned to their original values as soon as the change stopped, while the parameters obtained by other two methods did not.
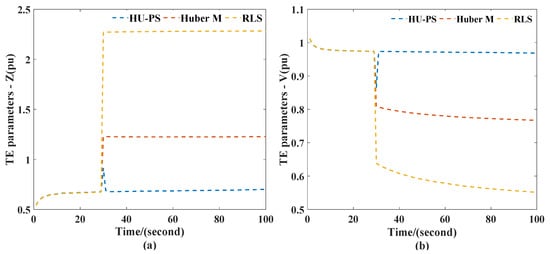
Figure 5.
TEPs obtained in case I scenario 2: (a) impedance, (b) voltage.
As shown in Figure 6, due to the outliers, at the 30th second, different degrees of errors appeared in the result of power flow calculation of the three equivalent methods. Because the Huber function was used in Huber’s M-Estimation and HU-PS, compared with RLS, the influence of outliers could be reduced to a certain extent. Additionally, compared with the other two methods, due to the use of VFF, HU-PS had higher steady-state recognition accuracy, which could eliminate the influence of old data in time, and the absolute error was smaller than the other two methods.
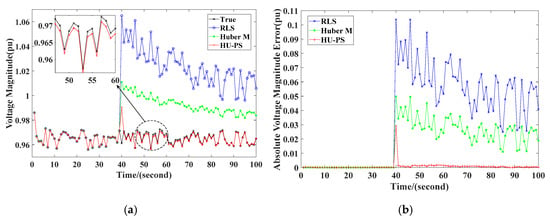
Figure 6.
Values in scenario 2: (a) voltage magnitude, (b) absolute voltage magnitude error.
As we can see from Table 1 and Figure 4 and Figure 6, MAER appeared when there was erroneous measurement. In both scenarios, the MAER of the HU-PS algorithm was the smallest, and it reduced by 65.80% and 58.64%, respectively, compared with RLS and Huber’s M-Estimation, which shows that the HU-PS algorithm in this paper had better robustness. In addition, compared with RLS and Huber’s M-Estimation, MAE of HU-PS reduced by 97.46% and 96.22%, respectively, which indicates that the accuracy of the HU-PS algorithm was higher.

Table 1.
Errors of TEPs estimation in case 1.
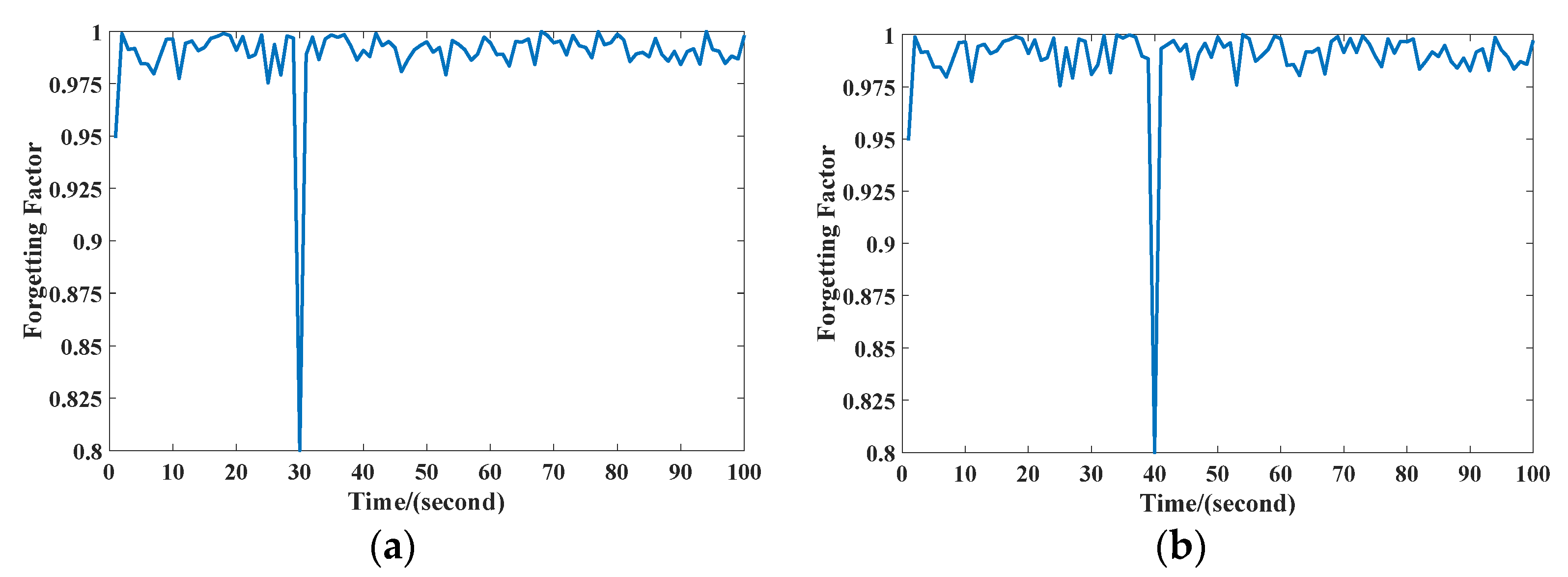
Figure 7a,b, respectively, reflect the changes of the forgetting factor in the parameter estimation process in the above two scenarios. It can be seen from Figure 7 that when the system was at the stationary state, the forgetting factor fluctuated around 0.9. When there was an erroneous measurement, the parameter estimation error increased sharply, and the forgetting factor rapidly decreased to an appropriate value to forget the historical data. As the system stabilized, the forgetting factor quickly returned to a very high value, thereby accurately tracking the system.
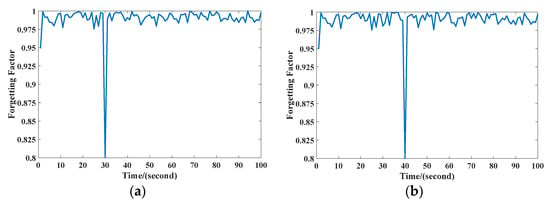
Figure 7.
Value of the forgetting factor: (a) scenario 1, (b) scenario 2.
3.2. Case II: Simulation Verification on IEEE 30-Bus System
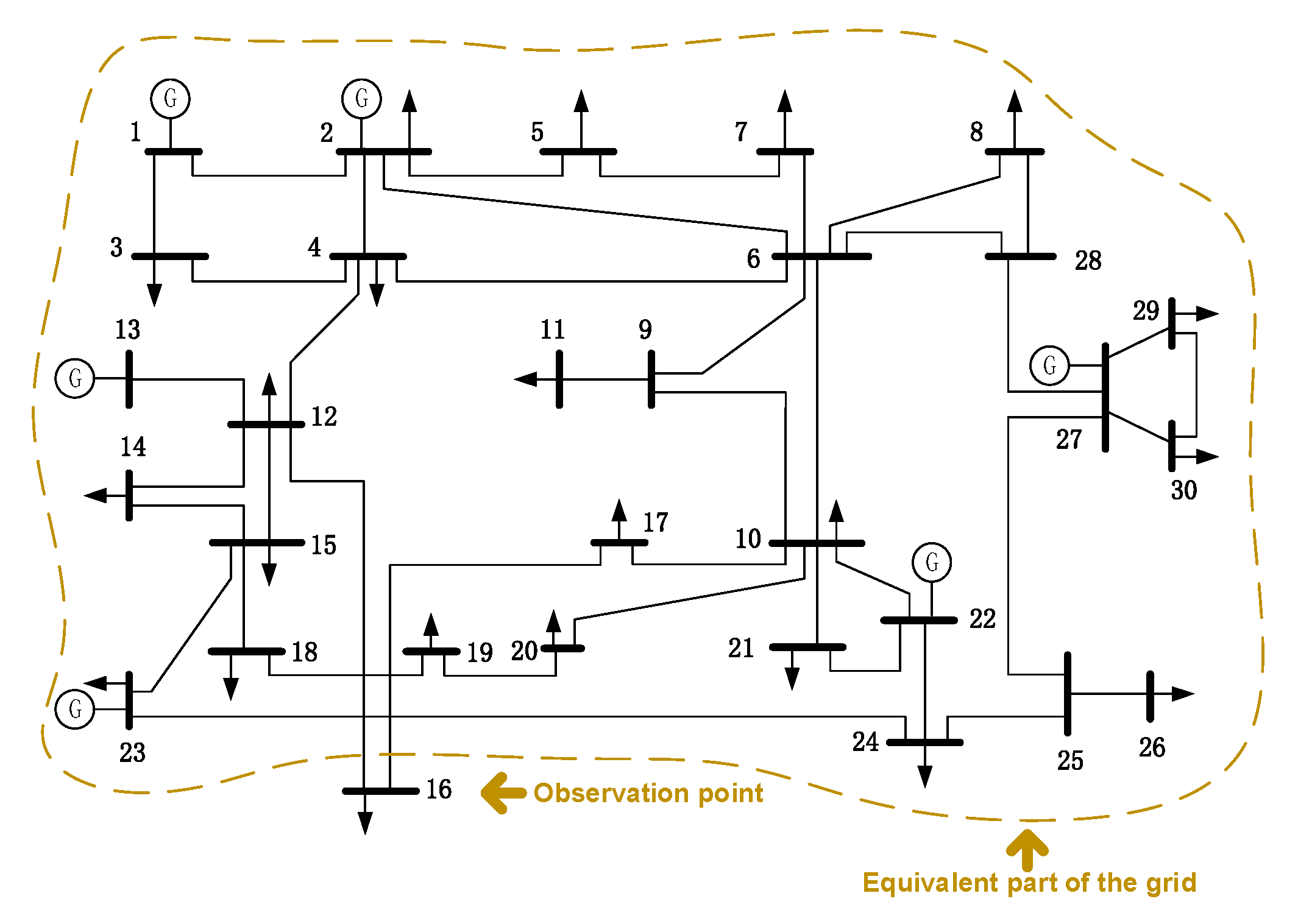
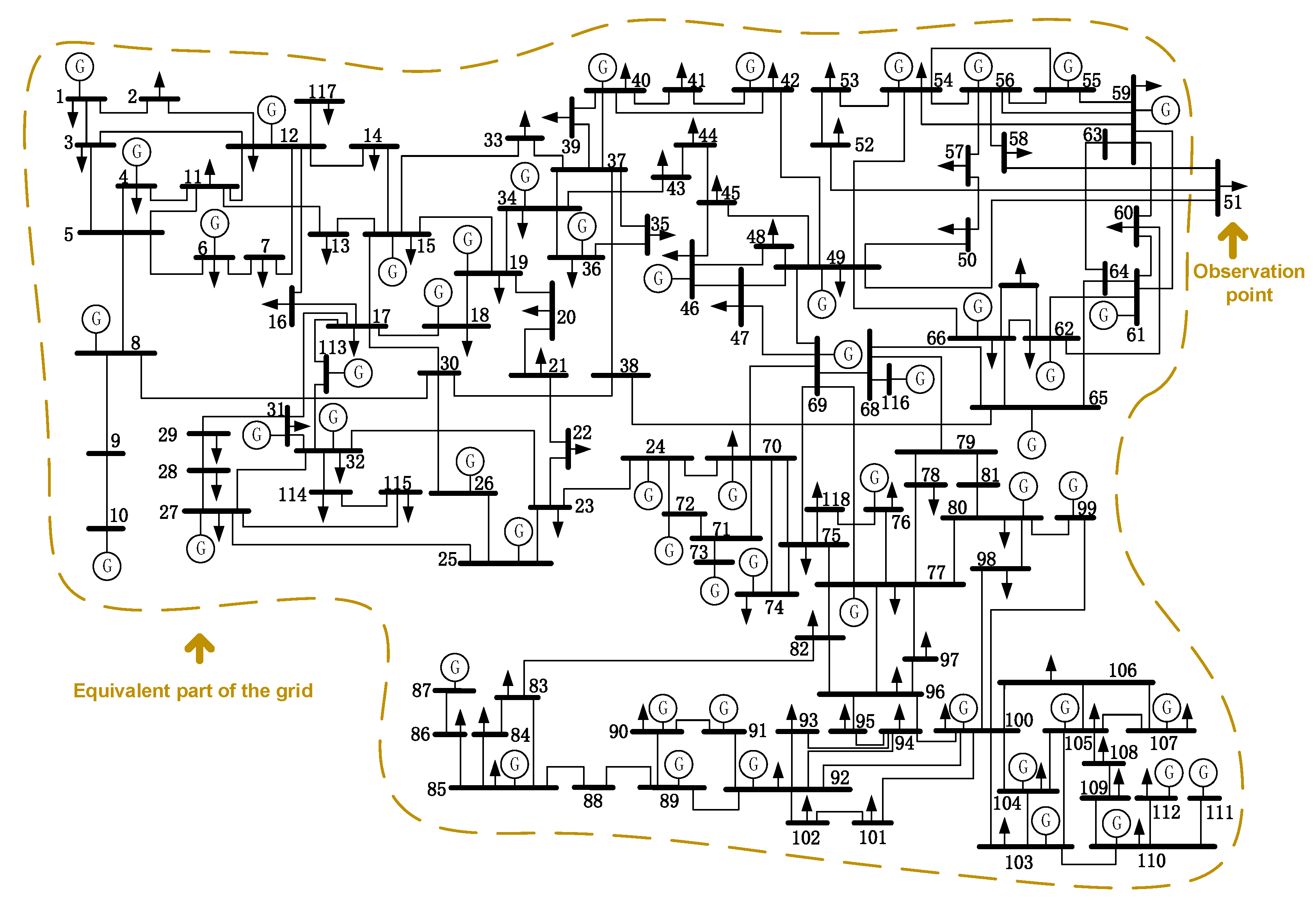
As shown in Figure 8, this test was conducted by simulated measurements of IEEE 30-bus system. In order to simulate the real-time fluctuation of user load, the load was set to increase at a rate of 4%, and the load on the bus 16 changed at the 30th second of the voltage and current. These data were recorded and used as PMU measurements. Considering the influence of erroneous measurements and changes in system structure on the accuracy of TEPs estimation, two different scenarios were set in case II. The parameters of the various methods were set as follows: , , , . Two scenarios were set as follows:
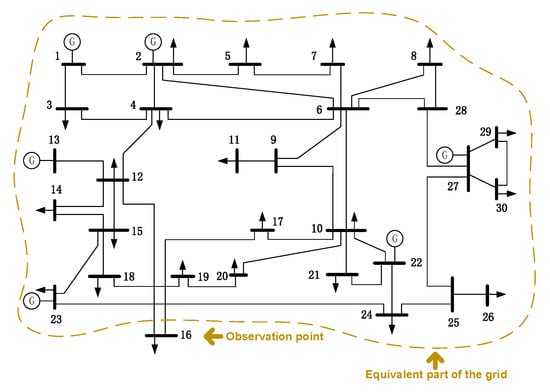
Figure 8.
The topology of the IEEE 30-bus system.
- (1)
- Scenario 1: selected the values at the 30th second as the original values, and increased the voltage and current values to 2.8 and 20 times, respectively, as the leverage measurement. VFF was used in the Huber’s M-Estimation algorithm. At the 60th second, the branch of node 26 was cut off.
- (2)
- Scenario 2: selected the values at the 30th second as the original values and increased them by 4 times as the outliers. VFF was used in the Huber’s M-Estimation algorithm. At the 60th second, the output of the generator of node 27 decreased.
To compare the accuracy of the above three methods, power flow calculations were performed on the original IEEE 30-bus system and the two-node TE systems. The voltage value of the original system was selected as the real value, and then the other voltage values were compared with the actual value. The experimental simulation results were as follows.
3.2.1. Scenario 1: System Branch Was Cut Off.
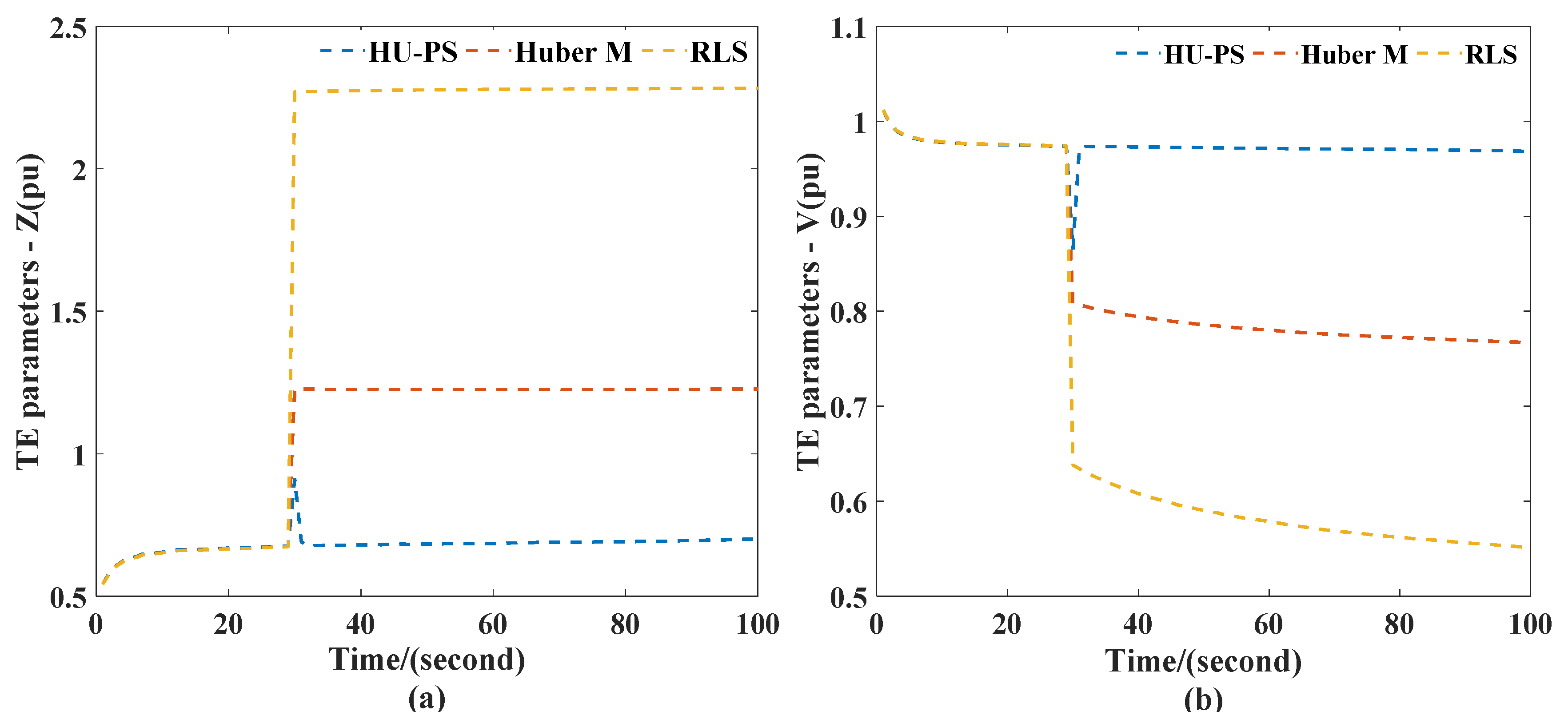
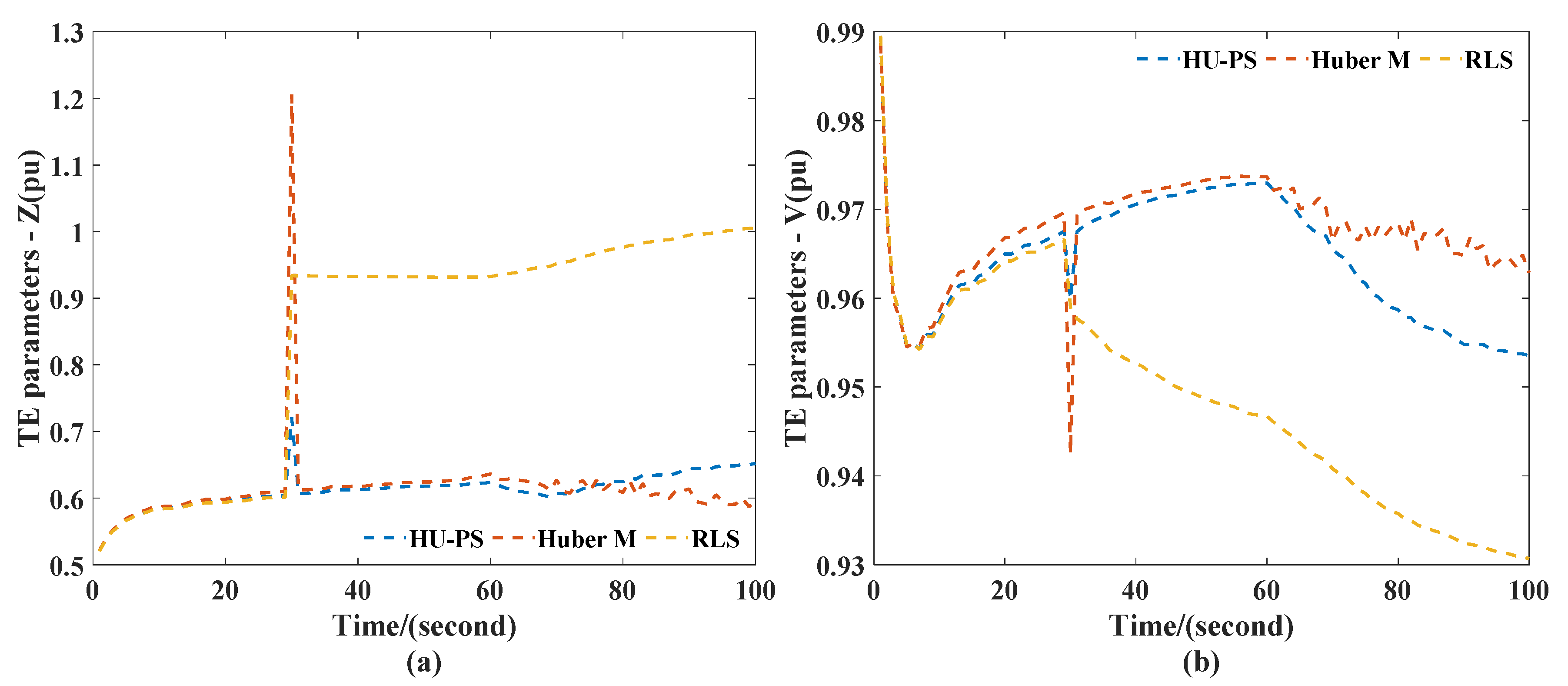
Base on the recorded data, the TEPs were calculated using HU-PS, RLS, and Huber’s M-Estimation. The results are shown in the Figure 9. When leverage appeared in PMU, the TEPs changed significantly, and the TEPs obtained by HU-PS were the least affected.
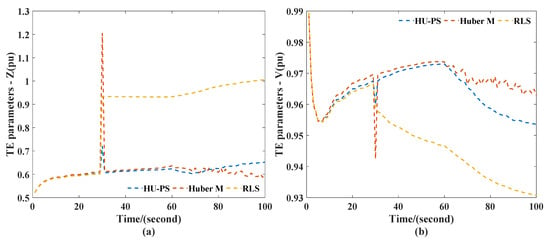
Figure 9.
TEPs obtained in case II scenario 1: (a) impedance (b) voltage.
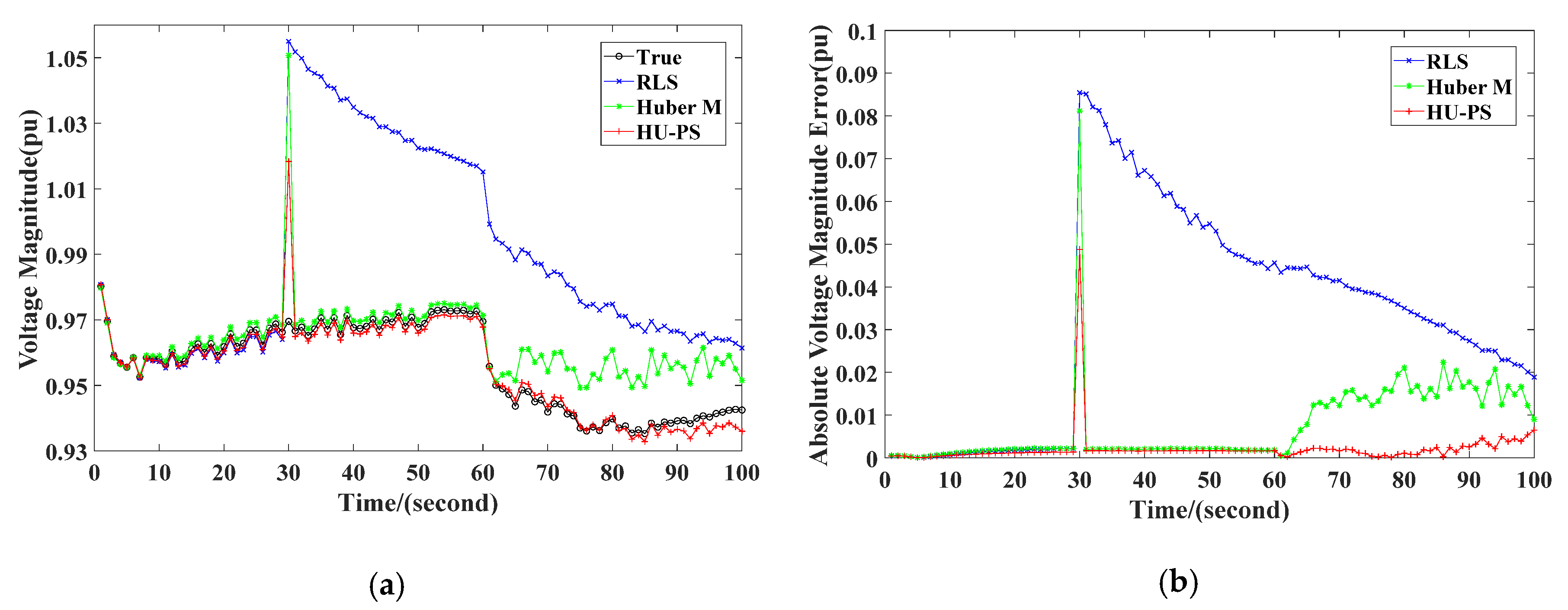
It can be seen from Figure 10 that at the 30th second, due to leverage measurement, there were certain errors in the power flow calculation results of the three equivalent methods. RLS was most affected by erroneous data. Although Huber’s M-Estimation could not eliminate the effects of inaccurate data completely, it could quickly return to the tracking state of the system after 30 s because of the use of VFF. The HU-PS could not only track the system changes quickly and accurately, but the absolute error was also smaller than the other two methods. In addition, since the bus 26 was cut off at the 60th second and the system topology changed, the voltage amplitude of the power flow calculation increased. The result of RLS for TE began to fluctuate. Huber’s M-Estimation showed a larger deviation, and the state tracking could not continue. However, due to the application of recursive theory, HU-PS could adjust in time according to the change of system topology and accurately track the equivalent parameters of the system; the absolute error was also controlled in a small range, and it had a dynamic performance.
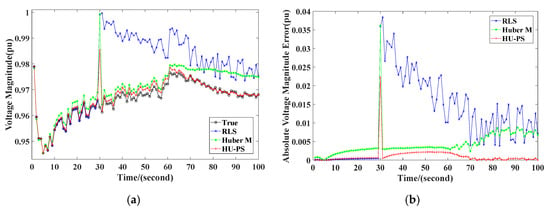
Figure 10.
Values in scenario 1: (a) voltage magnitude, (b) absolute voltage magnitude error.
3.2.2. Scenario 2: The Output of the System Generator Was Reduced.
The same as scenario 1, the TEPs were calculated and the results are shown in Figure 11. When outliers appeared in PMU, the TEPs changed significantly. However, the TEPs obtained by HU-PS were also the least affected.
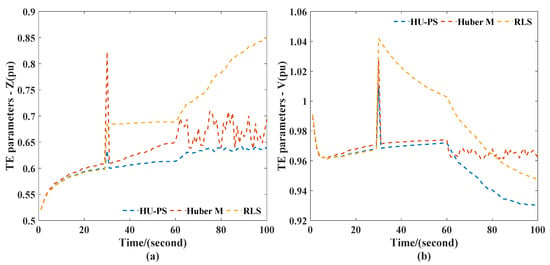
Figure 11.
TEPs obtained in case II scenario 2: (a) impedance, (b) voltage.
As can be seen from Figure 12, all three methods can track the system before outliers appear. However, at the 30th second, these three equivalent methods were affected by outliers. The power flow calculation of the TE models had a larger deviation than the actual value. Huber’s M-Estimation and HU-PS used the forgetting factor to eliminate the negative effects of the old data in time and use the new data to track the system. In addition, at the 60th second, the output of the generator at node 27 was reduced, and all three equivalent methods made corresponding responses. The calculation results of the system power flow using the Huber’s M-Estimation deviated from the actual values and caused substantial errors. However, HU-PS always tracked the state of the system with high accuracy.
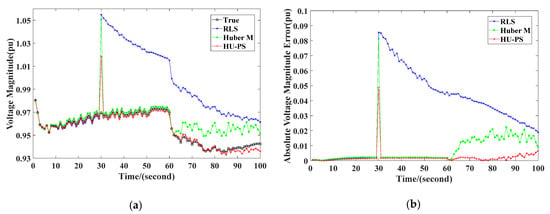
Figure 12.
Values in scenario 2: (a) voltage magnitude, (b) absolute voltage magnitude error.
Similarly, Table 2 shows that compared with RLS and Huber, the MAE of HU-PS decreased by 92.03% and 73.31%, and the MAER of HU-PS decreased by 42.52% and 39.17%, respectively. Additionally, it also shows that the HU-PS algorithm proposed in this paper had good tracking ability and adaptability when the system changed, of which MAE and MAER were the smallest in the three methods.

Table 2.
Errors of TEPs estimation in case 2.
In the above cases, there was a matrix inversion operation in the process of obtaining the node TEPs using RLS and Huber’s M-Estimation estimates. Once the algorithm caused a singular or pathological matrix, it would cause divergence problems, which would seriously affect the stability and practicability of the algorithm. However, due to the regularization technique introduced in HU-PS, the singularity of the matrix could be eliminated. It can be seen from the above simulation results that compared with the RLS algorithm and Huber’s M-Estimation algorithm, HU-PS had better adaptive tracking ability and robustness compared with RLS and Huber’s M-Estimation algorithms. For outliers, leverage values, and the system structure changes, HU-PS had higher precision for system Thévenin parameter estimation.
4. Conclusions
This paper proposes an equivalent parameter identification algorithm based on VFFs and PS. The functions of HU-PS algorithm are as follows:
- (1)
- Huber function and PS are introduced to eliminate the influence of erroneous measurements and model uncertainty in PMU measurement data.
- (2)
- With the proposed VFF, the shortcomings of the fixed forgetting factor that converges slowly when the system changes suddenly can be overcome, thereby further enhancing the real-time tracking ability and adaptability of online estimation.
- (3)
- The dynamic tracking ability and adaptability of the TEP solution algorithm are improved through recursion theory.
Finally, the HU-PS algorithm proposed in this paper was simulated on the IEEE 118-bus system and compared with the simulation results of RLS algorithm and Huber’s M-Estimation method, which demonstrates the robustness and advantages of HU-PS to eliminate the adverse effects of erroneous measurements. Simulation on the IEEE 30-bus system verifies that when the system structure changes, compared with RLS algorithm and Huber’s M-Estimation algorithm, the HU-PS algorithm can track the system changes in time and has better adaptability. In addition, using the HU-PS algorithm, the relative errors decreased by 94.75% and 84.77% compared with RLS and Huber’s M-estimation, respectively. In summary, when only PMU local measurement data are available, HU-PS algorithm has higher accuracy and better robustness in TEP estimation.
Author Contributions
Conceptualization, A.Z. and W.T.; methodology, A.Z.; software, W.T.; validation, M.C. and W.Y.; formal analysis, M.C.; writing—original draft preparation, A.Z.; writing—review and editing, W.T.; visualization, M.C. and W.Y.; supervision, A.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the scientific research starting project of National Key R&D Project under Grant 2017YFE0112600, Sichuan Province Science and Technology Support Program under Grant 2020YFQ0038, and the scientific research starting project of SWPU under Grant 2018QHZ028.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Figure A1.
The topology of the IEEE 118-bus system.
Figure A1.
The topology of the IEEE 118-bus system.
References
- Al-Mohammed, A.H.; Abido, M.A. A Fully Adaptive PMU-Based Fault Location Algorithm for Series-Compensated Lines. IEEE Trans. Power Syst. 2014, 29, 2129–2137. [Google Scholar] [CrossRef]
- Matavalam, A.R.R.; Singhal, A.; Ajjarapu, V. Monitoring Long Term Voltage Instability due to Distribution & Transmission Interaction using Unbalanced μPMU & PMU Measurements. IEEE Trans. Smart Grid 2019, 11, 873–883. [Google Scholar]
- Su, H.-Y.; Liu, C.-W. Estimating the Voltage Stability Margin Using PMU Measurements. IEEE Trans. Power Syst. 2015, 31, 3221–3229. [Google Scholar] [CrossRef]
- Shen, S.; Lin, D.; Wang, H.; Hu, P.; Jiang, K.; Lin, D.; He, B. An Adaptive Protection Scheme for Distribution Systems with DGs Based on Optimized Thevenin Equivalent Parameters Estimation. IEEE Trans. Power Deliv. 2015, 32, 411–419. [Google Scholar] [CrossRef]
- Mazhari, S.M.; Safari, N.; Chung, C.Y.; Kamwa, I. A Hybrid Fault Cluster and Thévenin Equivalent Based Framework for Rotor Angle Stability Prediction. IEEE Trans. Power Syst. 2018, 33, 5594–5603. [Google Scholar] [CrossRef]
- Hentunen, A.; Lehmuspelto, T.; Suomela, J. Time-Domain Parameter Extraction Method for Thévenin-Equivalent Circuit Battery Models. IEEE Trans. Energy Convers. 2014, 29, 558–566. [Google Scholar] [CrossRef]
- Arancibia, A.; Soriano–Rangel, C.A.; Mancilla-David, F.; Ortega, R.; Strunz, K. Finite–time identification of the Thévenin equivalent parameters in power grids. Int. J. Electr. Power Energy Syst. 2020, 116, 105534. [Google Scholar] [CrossRef]
- Yun, Z.; Cui, X.; Ma, K. Online Thevenin Equivalent Parameter Identification Method of Large Power Grids Using LU Factorization. IEEE Trans. Power Syst. 2019, 34, 4464–4475. [Google Scholar] [CrossRef]
- Vasquez, J.A.V.; Matavalam, A.R.R.; Ajjarapu, V. Fast calculation of Thévenin equivalents for real-time steady state voltage stability estimation. In Proceedings of the 48th North American Power Symposium (NAPS), Denver, CO, USA, 18–20 September 2016; pp. 1–7. [Google Scholar]
- Hashmi, U.; Choudhary, R.; Priolkar, J.G.; Umar, H. Online thevenin equivalent parameter estimation using nonlinear and linear recursive least square algorithm. In Proceedings of the 2015 IEEE International Conference on Electrical, Computer and Communication Technologies (ICECCT), Coimbatore, India, 5–7 March 2015; pp. 1–6. [Google Scholar]
- Vu, K.; Begovic, M.M.; Novosel, D.; Saha, M.M. Use of local measurements to estimate voltage-stability margin. IEEE Trans. Power Syst. 2002, 14, 1029–1035. [Google Scholar] [CrossRef]
- Wang, Y.; Li, W.; Lu, J. A new node voltage stability index based on local voltage phasors. Electr. Power Syst. Res. 2009, 79, 265–271. [Google Scholar] [CrossRef]
- Haji, M.M.; Xu, W. Online Determination of External Network Models Using Synchronized Phasor Data. IEEE Trans. Smart Grid 2016, 9, 635–643. [Google Scholar] [CrossRef]
- Corsi, S.; Taranto, G. A Real-Time Voltage Instability Identification Algorithm Based on Local Phasor Measurements. IEEE Trans. Power Syst. 2008, 23, 1271–1279. [Google Scholar] [CrossRef]
- Wang, Y.; Pordanjani, I.R.; Li, W.; Xu, W.; Chen, T.; Vaahedi, E.; Gurney, J. Voltage Stability Monitoring Based on the Concept of Coupled Single-Port Circuit. IEEE Trans. Power Syst. 2011, 26, 2154–2163. [Google Scholar] [CrossRef]
- Vanouni, M. Discussion of “Online tracking of Thévenin equivalent parameters using PMU measurements”. IEEE Trans. Power Syst. 2013, 28, 1899. [Google Scholar] [CrossRef]
- Abdelkader, S.; Morrow, D.J. Online Tracking of Thévenin Equivalent Parameters Using PMU Measurements. IEEE Trans. Power Syst. 2012, 27, 975–983. [Google Scholar] [CrossRef]
- Alinezhad, B.; Karegar, H.K.; Alinejad, B. On-Line Thévenin Impedance Estimation Based on PMU Data and Phase Drift Correction. IEEE Trans. Smart Grid 2016, 9, 1033–1042. [Google Scholar] [CrossRef]
- Smon, I.; Verbic, G.; Gubina, F. Local voltage-stability index using Tellegen’s theorem. IEEE Trans. Power Syst. 2006, 21, 1267–1275. [Google Scholar] [CrossRef]
- Matavalam, A.R.R.; Ajjarapu, V. Sensitivity based Thevenin index with systematic inclusion of reactive power limits. IEEE Trans. Power Syst. 2017, 33, 932–942. [Google Scholar] [CrossRef]
- Abdelkader, S.; Morrow, D.J. Online Thévenin Equivalent Determination Considering System Side Changes and Measurement Errors. IEEE Trans. Power Syst. 2014, 30, 2716–2725. [Google Scholar] [CrossRef]
- Burchett, S.M.; Douglas, D.; Ghiocel, S.G.; Liehr, M.W.A.; Chow, J.H.; Kosterev, D.; Faris, A.; Heredia, E.; Matthews, G.H.; Liehr, M. An Optimal Thévenin Equivalent Estimation Method and its Application to the Voltage Stability Analysis of a Wind Hub. IEEE Trans. Power Syst. 2018, 33, 3644–3652. [Google Scholar] [CrossRef]
- Abdelkader, S.; Eladl, A.; Saeed, M.A.; Morrow, D.J. Online Thévenin equivalent determination using graphical phasor manipulation. Int. J. Electr. Power Energy Syst. 2018, 97, 233–239. [Google Scholar] [CrossRef]
- Islam, M.N.; Ongsakul, W. Thevenin equivalent parameter tracking for on-line voltage stability assessment. In Proceedings of the 2015 IEEE Innovative Smart Grid Technologies—Asia (ISGT ASIA), Bangkok, Thailand, 3–6 November 2015; pp. 1–7. [Google Scholar] [CrossRef]
- Wang, C.; Qin, Z.; Hou, Y.; Yan, J. Multi-Area Dynamic State Estimation with PMU Measurements by an Equality Constrained Extended Kalman Filter. IEEE Trans. Smart Grid 2016, 9, 900–910. [Google Scholar] [CrossRef]
- Su, H.-Y.; Liu, T.-Y. Robust Thevenin Equivalent Parameter Estimation for Voltage Stability Assessment. IEEE Trans. Power Syst. 2018, 33, 4637–4639. [Google Scholar] [CrossRef]
- Zhou, N.; Pierre, J.W.; Trudnowski, D.J.; Guttromson, R.T. Robust RLS Methods for Online Estimation of Power System Electromechanical Modes. IEEE Trans. Power Syst. 2007, 22, 1240–1249. [Google Scholar] [CrossRef]
- Zhou, N.; Trudnowski, D.; Pierre, J.; Mittelstadt, W. Electromechanical Mode Online Estimation Using Regularized Robust RLS Methods. IEEE Trans. Power Syst. 2008, 23, 1670–1680. [Google Scholar] [CrossRef]
- Peker, E.; Wiesel, A. Fitting Generalized Multivariate Huber Loss Functions. IEEE Signal Process. Lett. 2016, 23, 1647–1651. [Google Scholar] [CrossRef]
- An, T.; Zhou, S.; Yu, J.; Lu, W.; Zhang, Y. Research on Illed-Conditioned Equations in Tracking Thevenin Equivalent Parameters with Local Measurements. In Proceedings of the 2006 International Conference on Power System Technology, Chongqing, China, 22–26 October 2006; pp. 1–4. [Google Scholar]
- Roca, I.L.; Carvalho, P.M. Solving Ill-Conditioned State-Estimation Problems in Distribution Grids with Hidden-Markov Models of Load Dynamics. IEEE Trans. Power Syst. 2020, 35, 284–292. [Google Scholar] [CrossRef]
- Kovacevic, B.; Milosavljevic, M.; Veinović, M. Robust recursive AR speech analysis. Signal Process. 1995, 44, 125–138. [Google Scholar] [CrossRef]
- IEEE Standard Association. C37.118.1-2011—IEEE Standard for Synchrophasor Measurements for Power Systems; IEEE Standard Association: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Chang, L.; Li, K.; Hu, B. Huber’s M-Estimation-Based Process Uncertainty Robust Filter for Integrated INS/GPS. IEEE Sens. J. 2015, 15, 3367–3374. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, W.; Yin, C.; Feng, Y. Huber-based Unscented Kalman Filters with the q-gradient. IET Sci. Meas. Technol. 2017, 11, 380–387. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, G.; Dong, Z.Y.; La Scala, M. Robust Forecasting Aided Power System State Estimation Considering State Correlations. IEEE Trans. Smart Grid 2016, 9, 2658–2666. [Google Scholar] [CrossRef]
- Golub, G.H.; van Loan, C.F. Matrix Computations; JHU Press: Baltimore, MD, USA, 2012; p. 65. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).