Abstract
This work couples high-fidelity moving-domain finite element compressible flow modeling with a Surrogate Management Framework (SMF) for optimization to effectively design a variable speed gas turbine stage. The superior accuracy of high-fidelity modeling, however, comes with relatively high computational costs, which are further amplified in the iterative design process that relies on parametric sweeps. An innovative approach is developed to reduce the number of iterations needed for optimal design, leading to a significant reduction in the computational cost without sacrificing the high fidelity of the analysis. The proposed design optimization approach is applied to a novel incidence-tolerant turbomachinery blade technology that articulates the stator- and rotor-blade positions of an annular single-stage high pressure turbine to achieve peak performance. This work also extends our understanding of rotor–stator interactions by simulating complex internal flows occurring during multi-speed turbine operation. Potential variable-speed gas turbine stage designs and the proposed optimization approach are presented to provide valuable insight into this new turbomachinery technology that can positively impact future propulsion systems.
1. Introduction
The demand for a variable-speed gas turbine engine (VSGTE) as a dynamic and reliable power source for aviation propulsion systems is consistently growing for commercial and military applications [1,2,3]. This comes from the ever-higher power, operational, and efficiency requirements of future aviation propulsion systems that traditional gas turbine engines are unable to effectively fulfill [1,2,3,4]. Previous works [2,3] reported that a VSGTE would be enabled by an adaptive blade technology, which articulates the stator and rotor blades to maintain optimal flow paradigms. While these works do not report any VSGTE designs, Welch [1] has noted that there exists significant industry interest for them.
Traditionally, gas turbine engine optimization has relied on the use of high-fidelity modeling coupled with parametric sweeps [3,5,6,7]. High-fidelity modeling delivers accuracy, however, when used in a highly iterative process involving parametric sweeps, its use often becomes complicated and expensive, both in terms of human and computational time [8]. This deficiency stems from the extensive user interaction required for geometric modeling and mesh generation, as well as the costly computational resources and long simulation times involved in executing the high-fidelity model. In addition, postprocessing of the computational results and interpreting the simulation data further contribute to the already intricate and time-consuming workflow. This complexity is amplified in designing a VSGTE because of its intricate geometry and parametric conditions, as well as the limited understanding of the internal flow dynamics. Consequently, the use of traditional methods for VSGTE development is not practical, creating a need for an innovative and effective design approach [1].
This work outlines a novel design approach that incorporates a Surrogate Management Framework (SMF) with high-fidelity moving-domain finite element compressible flow modeling and simulation of a gas turbine stage. First introduced by Booker et al. [9], the SMF is a cost-effective pattern search method that can facilitate design optimization using high-fidelity models without the need to compute complicated objective-function derivatives while keeping the theoretical guarantees of convergence. In order to create a rigorous and efficient SMF for the present application and beyond, the surrogate function, which acts as a predictive tool, is coupled to an extended version of the covariance matrix adaptation evolution strategy (CMA-ES) [10] with mesh adaptive direct search (MADS)-based polling [11]. In recent years, there has been an increase in the successful application of the SMF with high-fidelity modeling to design optimization of complex engineering systems, including subsonic wings [12], hydraulic arresting gears [13], and cardiovascular devices [14,15]. It is felt that propulsion system design could greatly benefit from these approaches, which largely motivates the developments in the present paper.
The paper is outlined as follows. In Section 2, we briefly describe our compressible-flow formulation and provide the details of a single-stage gas turbine model employed in this work. In Section 3, we describe the key technical elements of the SMF design optimization framework and its application to the optimization of the VSGTE stage. The results of the optimization and the analysis of the key flow phenomena governing the turbine stage performance are provided in Section 4. In Section 5, we draw conclusions.
2. High-Fidelity Modeling of Compressible Flow in a Gas Turbine Stage
2.1. Moving-Domain Finite Element Formulation of Compressible Flows
The flow in the turbine stage is governed by the Navier–Stokes equations of compressible flows and the ideal gas equation of state. The Navier–Stokes equations are posed on a moving domain to accommodate the motion of the rotor. The flow governing equations are discretized using the Streamline Upwind/Petrov–Galerkin (SUPG) [16,17,18,19,20,21,22,23,24,25,26,27,28,29] finite element formulation in the arbitrary Lagrangian–Eulerian (ALE) frame [30] to handle the domain motion. In addition to the SUPG stabilization, a residual-based discontinuity-capturing (DC) operator [31,32,33,34,35,36,37,38,39,40,41,42,43] is added to further stabilize the formulation in the presence of shocks. No-slip boundary conditions on the blade surfaces are enforced weakly [44,45,46,47,48], which allows the flow to slip on the solid surface and results in reasonably accurate solutions on coarse boundary-layer meshes. Finally, a sliding interface operator [49,50,51,52,53,54] is added at the interface between the moving-rotor and fixed-stator subdomains in order to enforce, in a weak sense, the continuity of the velocity, temperature, traction vector and heat flux at that location. To integrate the compressible-flow equations in time, we employ a generalized- time integrator [55,56,57], which is an implicit, unconditionally stable, second-order accurate method with control over high-frequency dissipation. At each time step, the solution of the nonlinear algebraic-equation system is performed using the Newton–Raphson technique. At each Newton–Raphson iteration the linear system is solved iteratively using a GMRES technique with block-diagonal preconditioning [58]. The mathematical details of the resulting discrete formulation may be found in Xu et al. [59,60].
2.2. Model of the Turbine Stage
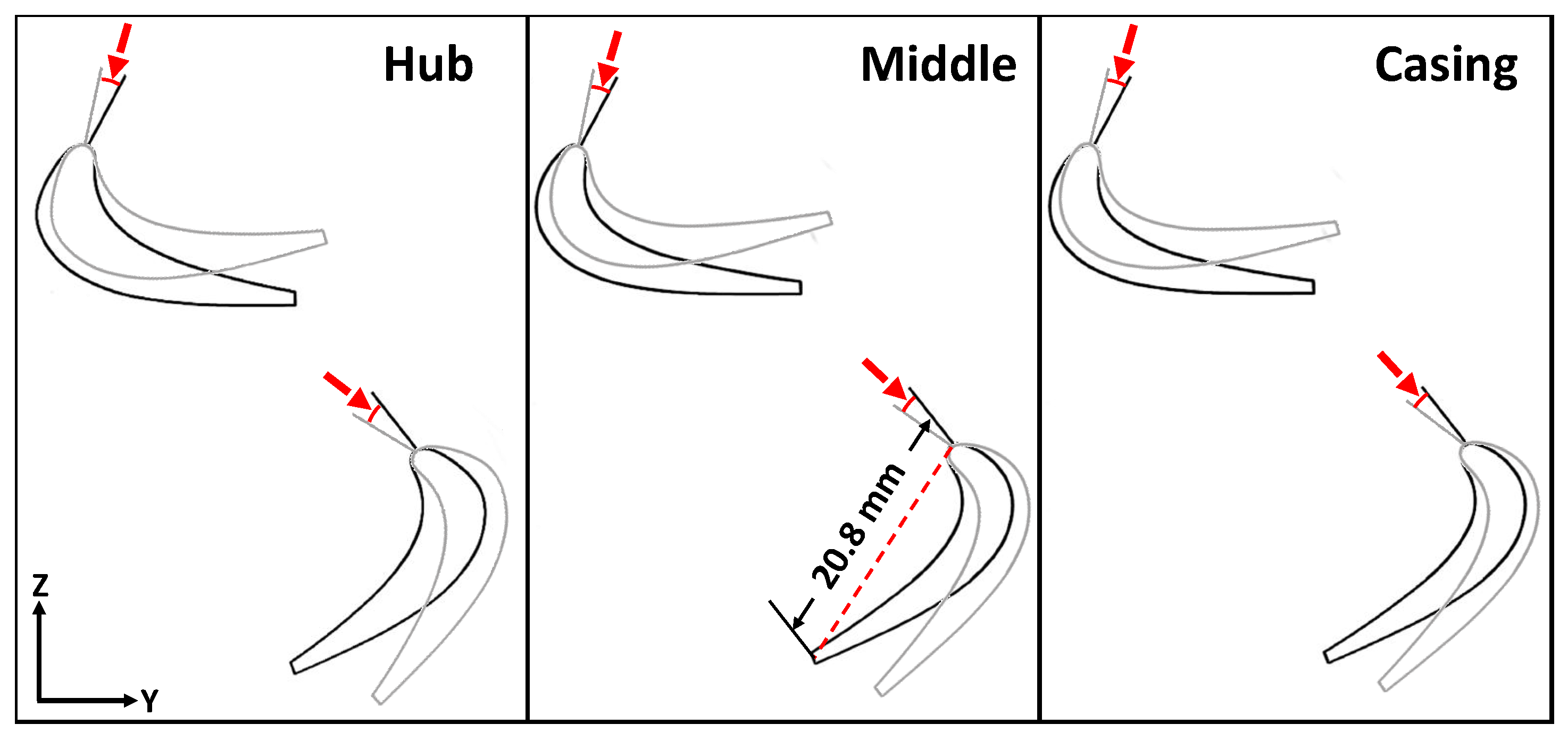
We study a single-stage high-pressure turbine composed of 24 stator and 34 rotor blades, resembling the engines found in rotorcraft like Apache and Black Hawk. We rely on the use of a parametric design tool proposed in Hsu et al. [61] to create the turbine geometry. This design tool enables us to automate and expedite the geometry modeling process by parametrically defining and pitching the stator and rotor blades in the computer-aided design (CAD) model through input parameters. These pitching angles are created by articulating the blades about their leading edge, where a positive angle represents a counterclockwise rotation. The airfoil profiles at three different blade heights are shown in Figure 1, where baseline positions (0) are colored in black and articulated positions are colored in gray. The turbine stage inner shaft radius is 77.7 mm, casing radius is 95.5 mm, and total length is 210 mm.
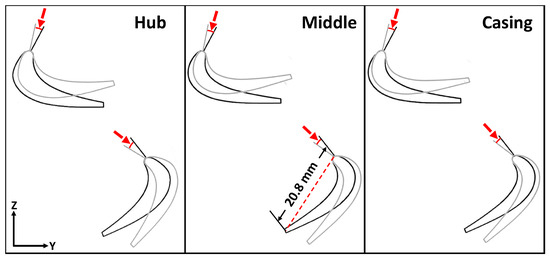
Figure 1.
Stator and rotor airfoil profiles at different blade heights and their baseline (0) and articulated positions. Baseline positions are colored in black and articulated positions are colored in gray. The articulation angle is shown by the red arc and highlighted using the red arrow. A positive angle corresponds to a counterclockwise articulation.
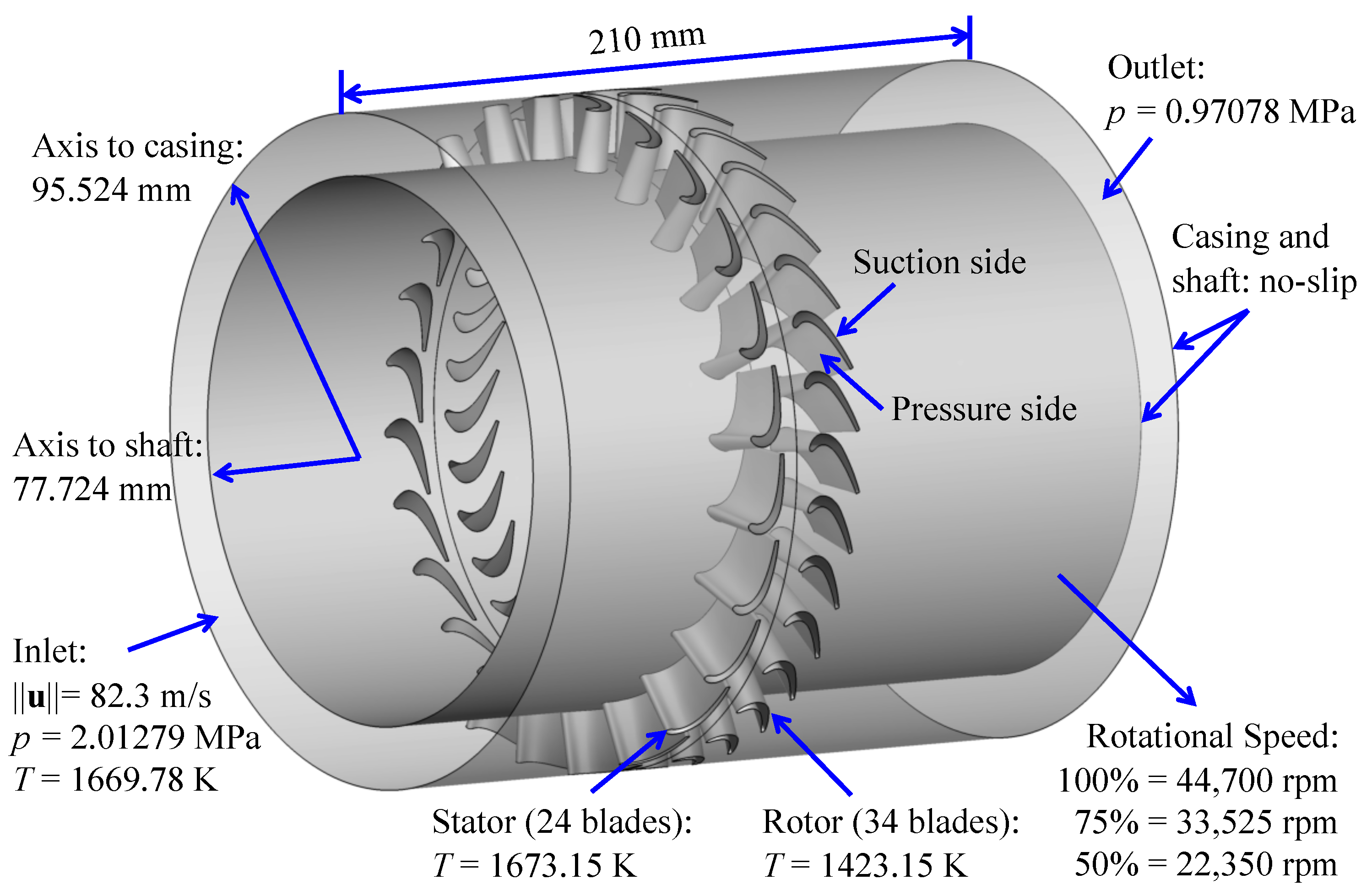
We consider the turbine stage at an off-design operating rotor speed of 22,350 rpm (50%), which is typical for rotorcraft cruising at constant speed. At the inlet boundary, we assume uniform axial inflow with velocity of 82.3 m/s, temperature of 1669.78 K, and pressure of 2.01279 MPa. The outlet boundary has a prescribed normal traction (i.e., pressure) of 0.97078 MPa. The temperature on the stator and rotor blades is specified as 1673.15 K and 1423.15 K, respectively. The inner shaft and outer casing surfaces have no-slip velocity and adiabatic conditions. The gas dynamic viscosity is kg/(m·s). The problem setup is summarized in Figure 2.
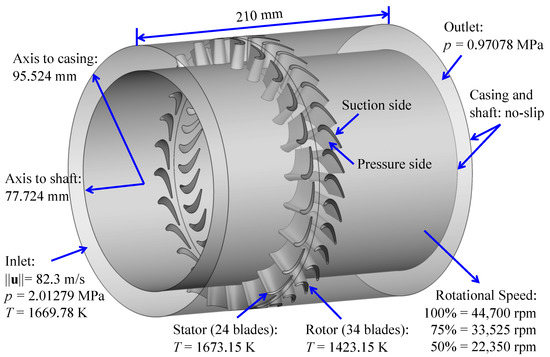
Figure 2.
Turbine stage problem setup.
The fluid domain of the gas turbine stage is discretized using linear tetrahedral elements with local refinement near the stator and rotor blades. The element size near the blades is 0.6 mm, while in the rest of the domain the maximum element size is 1.8 mm (for the reference, the rotor blade chord length is 20.8 mm). The mesh refinement study in Kozak et al. [6] showed that the current mesh resolution is sufficient to compute the quantities of interest needed for optimization.
3. Design Optimization Methodology
3.1. Surrogate Management Framework
The SMF optimization framework is driven by an objective function , which is minimized through an iterative process. The variables over which f is minimized take on real values, have upper and lower bounds, and are referred to as the design space. The SMF procedure begins with establishing an initial data set , , where N is a suitably chosen number of initial samples. This is done by applying a Latin Hypercube Sampling (LHS) technique [62,63], which gives a well distributed data set. The objective function is then evaluated at each of the initial data set to construct an initial surrogate function using Kriging method. This surrogate function interpolates the data, and estimates the values of the objective function at other locations in the design space. Note that each “evaluation” of the objective function amounts to generating the geometry and mesh for one turbine stage design, carrying out 3D, time-dependent, compressible-flow simulation, and postprocessing the results to obtain the key quantities of interest.
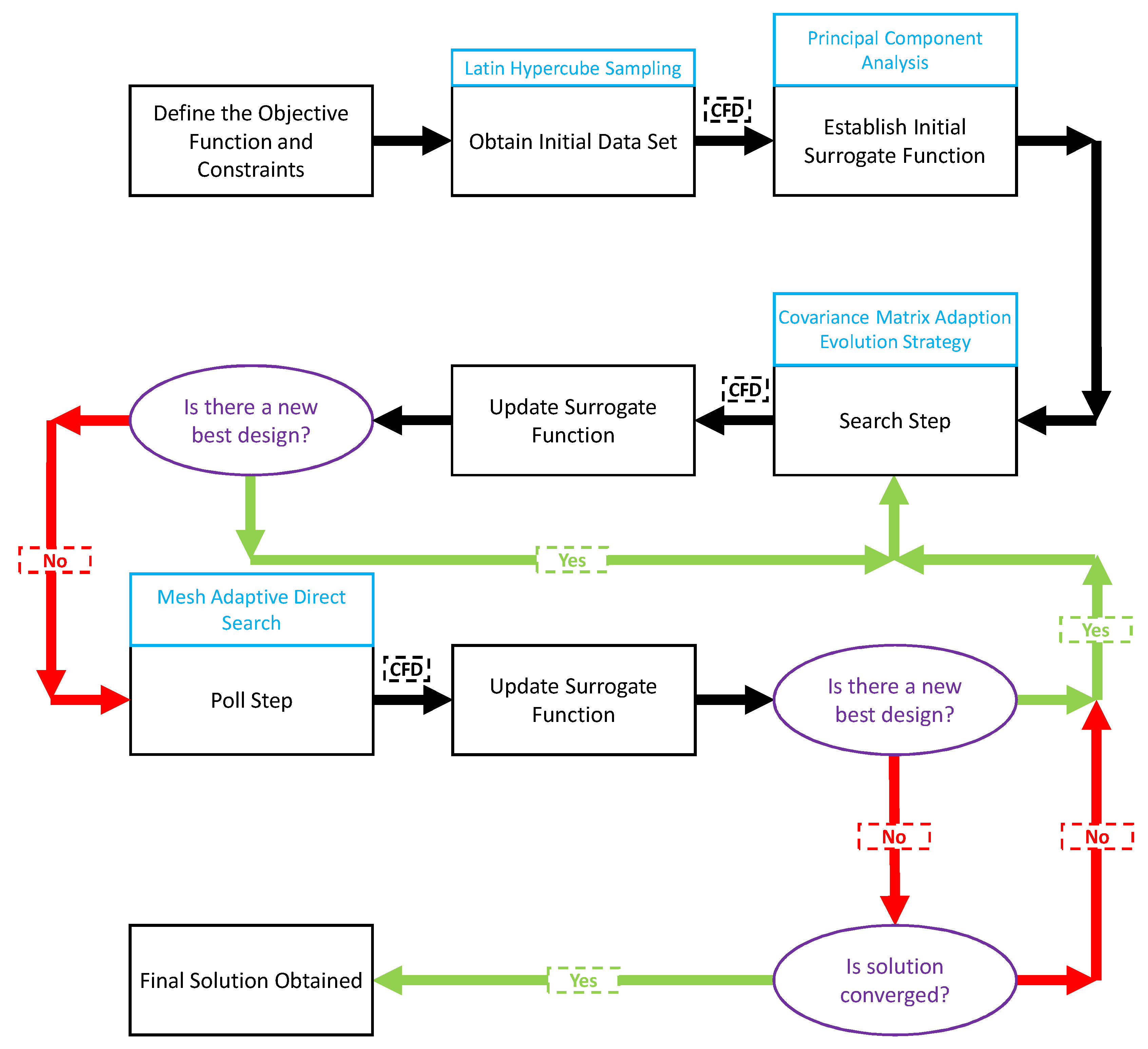
The SMF procedure continues with the search and poll steps. The search step uses the CMA-ES which is a gradient free approach to incrementally search for candidate cases with multivariate normal distributions and predict their objective function value with convex quadratic functions [64]. This step outputs a single candidate case that is expected to have a better result than the current best case. This candidate case is evaluated, and its corresponding objective function value is used to update the surrogate function. If the search step improves the surrogate function, then another search step will be executed. If the search step fails to improve the surrogate function, then the poll step is executed. The poll step uses MADS-based polling which is an iterative algorithm that randomly samples and predicts potential candidate cases near the current best case [11]. This step outputs a set of cases which are expected to improve the surrogate function. If the poll step determines the current best point remains the best, then the convergence of the function is evaluated. If the convergence criteria is met then, a solution has been found and the procedure terminates. If not, the minimal search distance between cases is reduced, and the algorithm returns to the search step. However, if the poll step determines a new local minimum, then the surrogate function is improved by this poll point and the algorithm returns to the search step. The search and poll steps are repeated until a converged solution, , is found. The SMF procedure is summarized in Figure 3.
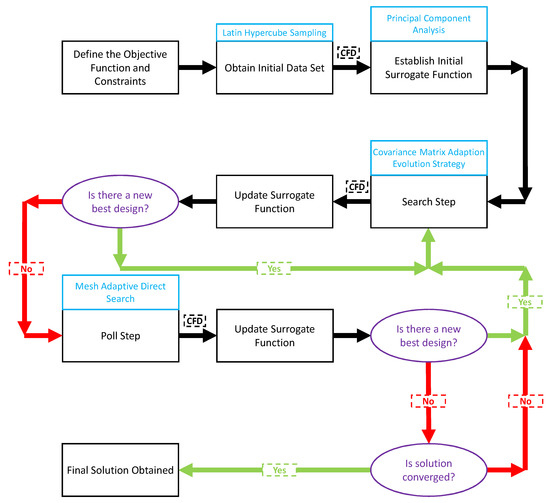
Figure 3.
Flowchart of the SMF procedure.
3.2. SMF Modifications for VSGTE Optimization
We introduce the following modifications to the SMF procedure as it applies to the VSGTE optimization. We restrict the articulation to integer-angle (measured in degrees) blade positions due to the limited articulation accuracy of the proposed VSTGE enabling mechanism [65]. Because the stator- and rotor-blade pitch angles constitute the 2D design space, is now restricted to a 2D integer grid. This, in turn, affects the LHS algorithm, the CMA-ES and the associated step-size adaptation of the search step as outlined in Hansen [10], and necessitates the introduction of a rounding function in the MADS-based polling technique as suggested in Audet et al. [66]. These modifications ensure that the LHS together with the search and poll steps only produce integer values as outputs, and thus constrain the optimizer to only examine integer stator- and rotor-blade positions.
3.3. Design and Analysis Spaces
Blade articulation is the primary VSGTE enabling technology as it maintains optimal flow paradigms and reduces excessive flow separation and recirculation attributed to off-design operation [2,3,6]. Therefore, we select the stator- and rotor-blade pitch angles and the operating rotor speed of the engine as our design space. We focus on two performance parameters, turbine stage adiabatic efficiency and output shaft torque, which we refer to as the analysis space.
Adiabatic efficiency is a key performance metric of a gas turbine engine as it provides insight into fuel consumption and environmental effects [5]. When associated with a rotorcraft, lower efficiency implies the need for larger fuel containers to maintain a reasonable operational range. This increase of fuel payload increases rotorcraft weight, and results in a reduction of the overall rotorcraft efficiency. Therefore, poor engine efficiency has multiple negative attributes associated with it as it simultaneously degrades both engine and rotorcraft performance. Inferior efficiency also negatively impacts the economic considerations of an engine [4]. Therefore, gas turbine engine efficiency is a key interest of analysis [1,2,3,8,67].
Another key parameter of a gas turbine engine performance is its power output. The power output determines how much thrust and lift the rotorcraft can produce, translating to how fast a rotorcraft can cruise and how much weight the rotorcraft can carry [8]. To match the demand of increased speeds and payloads [1,2,3], output power is a parameter of interest in our work. However, power output is dependent on operating rotor speed which is a design variable. We remove the relationship between this design and analysis parameter by specifying the rotor speed in the analysis, which makes the shaft rotor torque an equivalent performance metric.
3.4. Evaluation of Analysis-Space Parameters
The calculation of the analysis space parameters makes use of space- and time-averaging of the unsteady flow data coming from the compressible-flow simulations of the turbine stage. We develop the flow field by simulating 2.2 revolutions of the rotor, and time-average the flow data obtained by simulating an additional 3.3 revolutions for a total simulation time of 5.5 revolutions. Next, using the rotational symmetry of the problem geometry, a spatial averaging approach is used to extract the data. We obtain the mean pressure, temperature and Mach number entering and exiting the blade passage by averaging annular slices at 0.5 mm intervals between 3 mm and 7 mm upstream of the stator and downstream of the rotor. With these data, the adiabatic efficiency is computed as:
where and are the total temperature and pressure at the rotor outlet, respectively, and are the total temperature and pressure at the stator inlet, respectively, and is the heat capacity ratio corresponding to the temperature and pressure conditions inside the gas turbine. The rotor shaft torque is calculated by integrating the local torque contribution from the fluid traction over the entire rotor surface. The shaft power is obtained by multiplying the torque with the rotation speed.
3.5. Objective Function and Constraints
We aim to maximize the turbine stage torque output and efficiency at a given off-design operating speed by synchronously articulating the stator- and rotor-blade positions. To achieve this aim, we define our objective function as
where is the adiabatic efficiency for a given set of design variables, is the adiabatic efficiency of the baseline turbine stage design, is the torque acting on the drive shaft for a given set of design variables, is the torque acting on the drive shaft in the baseline turbine stage design, and ’s are the positive weights indicating the relative importance of the efficiency and torque. The efficiency of the baseline turbine stage design is % and torque is N·m, both quantities corresponding to the stator- and rotor-blade positions at 0.
We also introduce inequality constraints for our optimization problem. Firstly, we would like to discard the designs that have more than 2% drop in efficiency while operating at 50% rotor speed. In addition, we favor the designs which produce a 50% torque increase over the baseline. For this purpose we define two functions,
and
and employ an exterior penalty approach [68] to satisfy the desired constraints by minimizing an augmented objective function given by
The exterior penalty approach provides a direct and effective way to include constraints in the SMF framework, as well as in other optimization methods. In the above equation ’s are the penalty parameter weights given by
Finally, we impose restrictions on the design space to eliminate unfeasible designs. The restrictions are stated in terms of the allowable ranges of the blade pitch angles and rotor speeds:
In this work, we carry out optimization for the rotor speed of 50%, which typically corresponds to rotorcraft cruising conditions. Optimizing the blade pitch angles for a full range of rotor speeds will be considered in the future work.
4. Optimization Results
4.1. Convergence of the SMF Algorithm
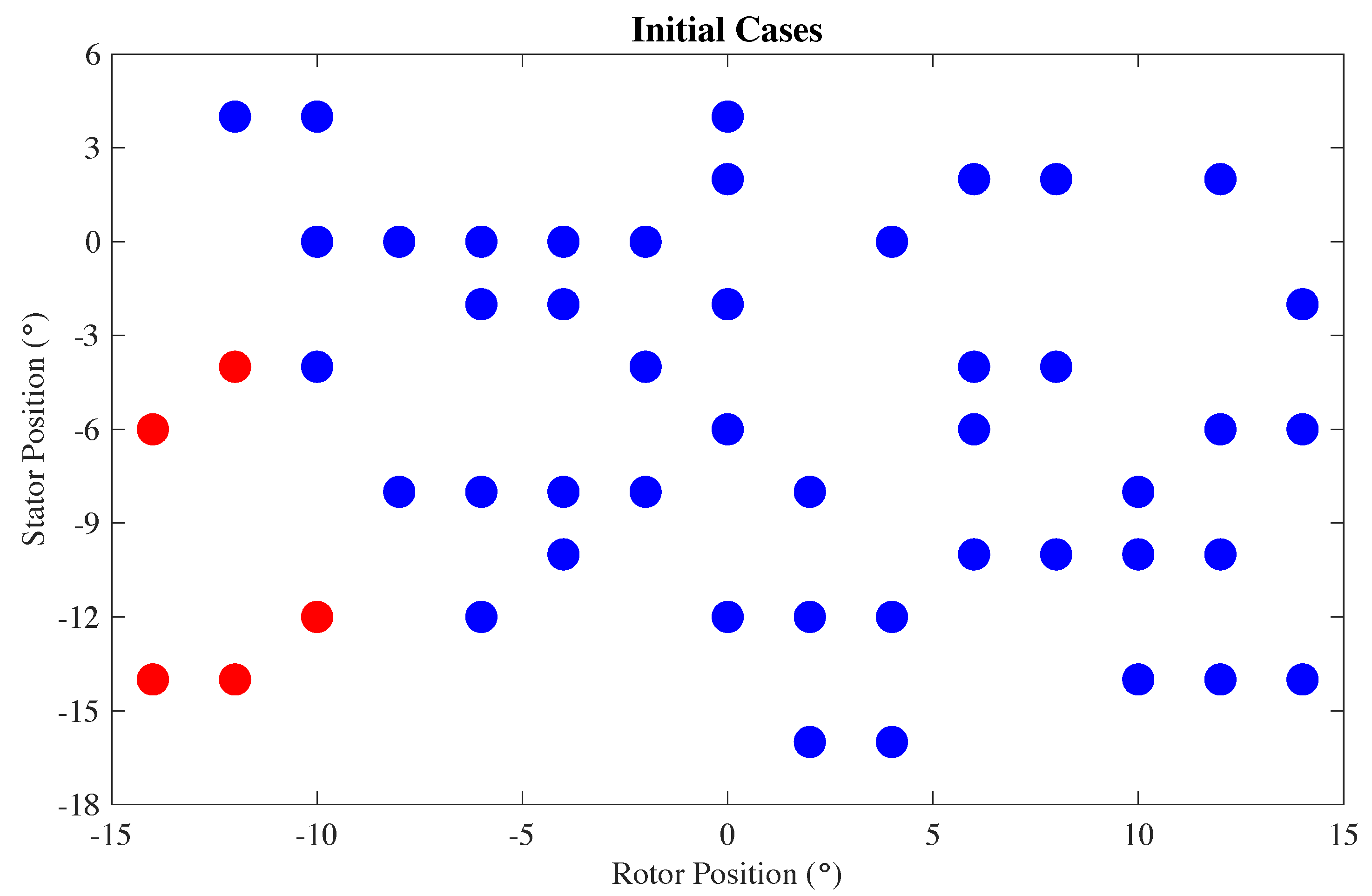
The LHS methodology produced an initial data set of 50 cases with varying stator- and rotor-blade orientations shown on a scatter plot in Figure 4. The corresponding geometric models were built and meshed using the parametric design framework [61] and subsequently analyzed using the compressible-flow solver described in Section 2.1. It is worth emphasizing that: 1. The geometry modeling and meshing pipeline handled all the cases without failure; 2. The same compressible-flow formulation and code were employed to simulate all the cases independent of the blade orientation. 3. The entire design-through-analysis pipeline exhibited the high level of robustness necessary for industrial practice.
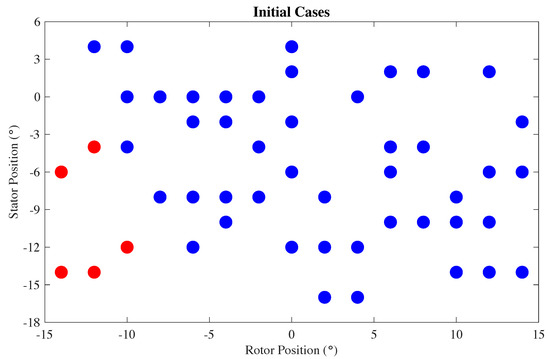
Figure 4.
Scatter plot of the 50 cases selected by the LHS approach that make up the initial data set. Unfeasible designs are colored in red.
The initial cases produced efficiency values ranging from 84.2% to 108% and torque values ranging from 62.2 to 272 N·m. Five out of the 50 cases achieved efficiencies above 100% and featured average torque values that were 37.8% below the baseline case. These cases, colored in red in Figure 4, were removed from the data set as unfeasible.
We do not attribute more importance to the efficiency or torque in the selection of the objective-function weights , and, as a result, we make them equal. In addition, a principal-component analysis (PCA) [69] of the initial data set suggests that the efficiency term needs to be additionally scaled by a factor seven to balance its contribution to the objective function.
The optimization was completed in five iterations featuring only seven additional cases. The five iterations include two poll steps and three search steps. The first poll step produced three candidate cases, while the second poll step only produced one candidate case. This small number of additional cases shows the effectiveness of the SMF in its ability to quickly arrive at an optimal design.
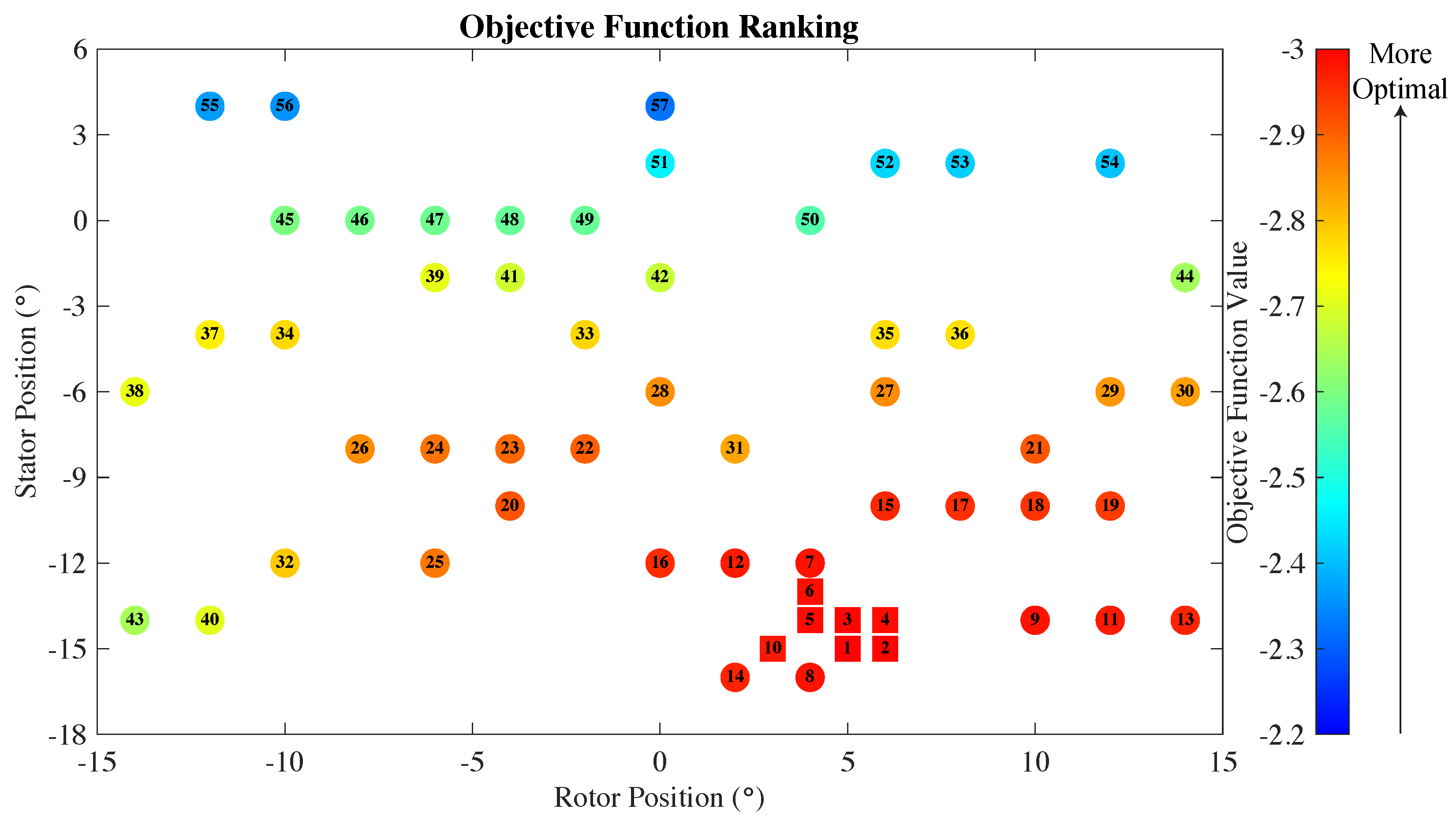
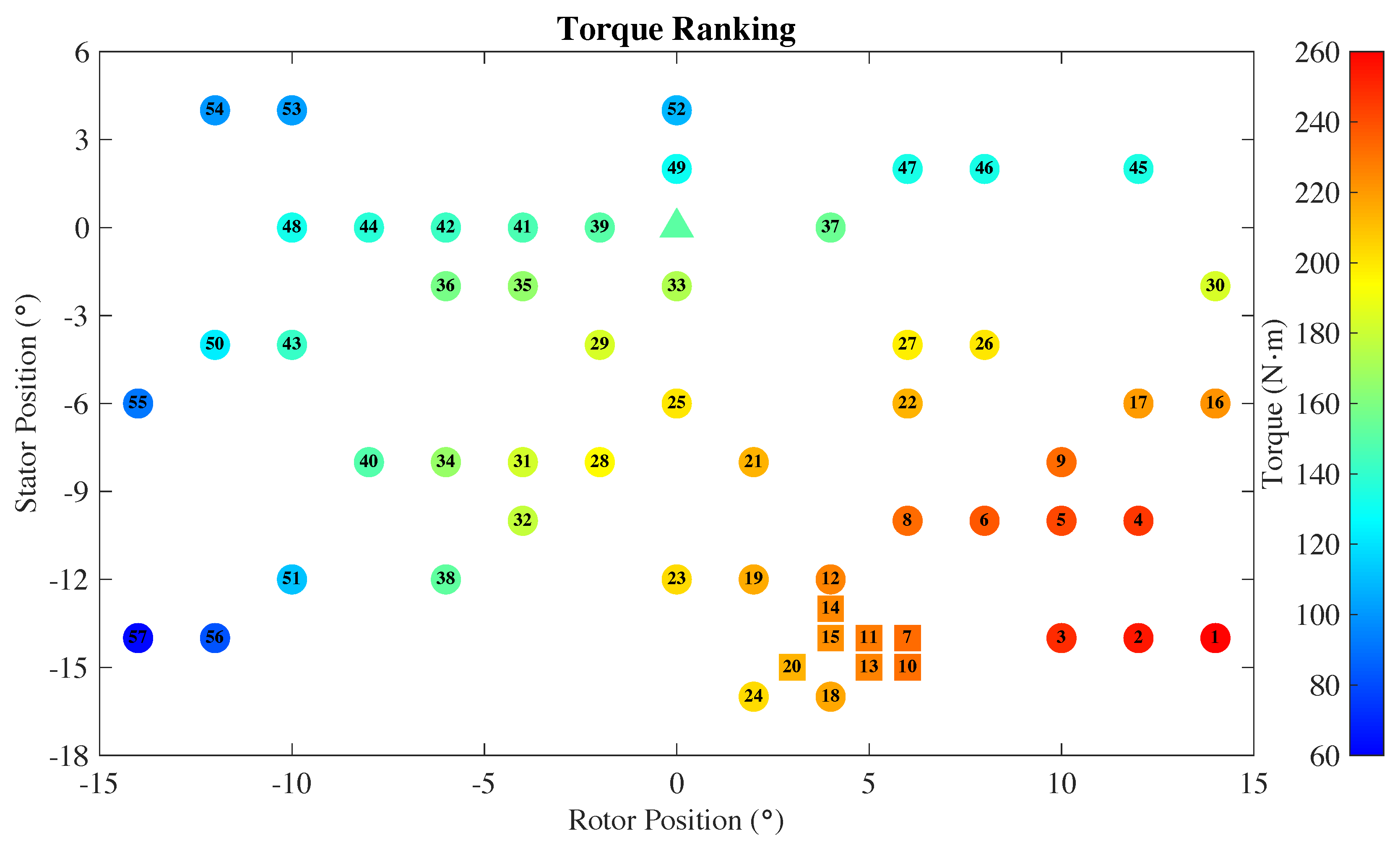
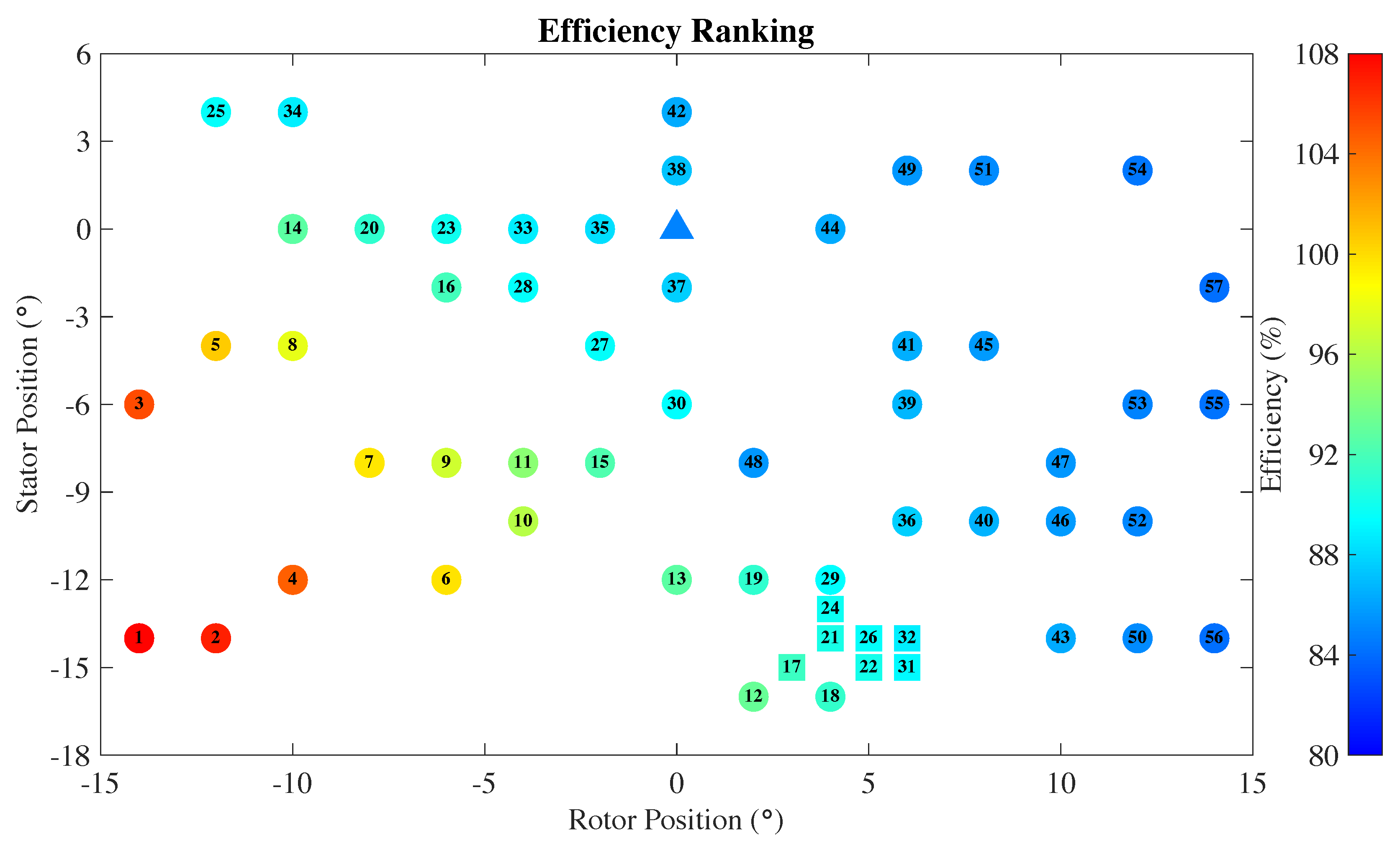
Figure 5 shows all the cases with their objective function ranks. Figure 6 and Figure 7 show the cases ranked individually by the torque and efficiency performance metrics. Cases from the initial data set are depicted using circles, while the additional seven cases are depicted using squares. The design with the best objective function has the stator pitched by and rotor pitched by from the baseline position. This design achieved an efficiency gain of 6.1% (22nd best) and a power gain of 49.3% (13th best).
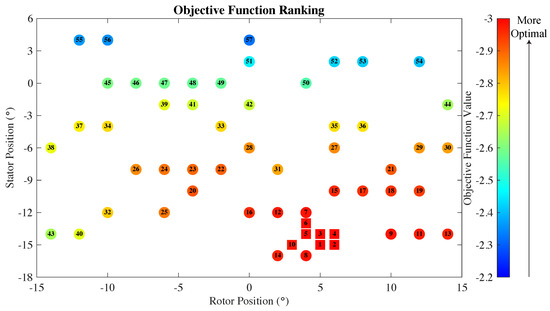
Figure 5.
Scatter plot of the cases ranked by the objective function value. Cases in the initial data set are denoted by circles while the remaining cases are denoted by squares. The color fill of the circles and squares corresponds to the value of the objective function.
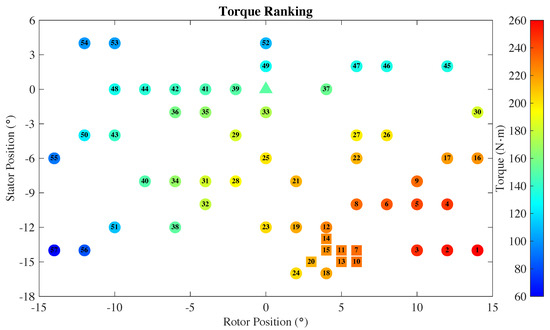
Figure 6.
Scatter plot of the cases ranked by the shaft torque value with rank 1 being the highest. Cases in the initial data set are denoted by circles while the remaining cases are denoted by squares. The color fill of the circles and squares corresponds to the value of the torque. The baseline design is denoted using a triangle with the torque value of N·m.
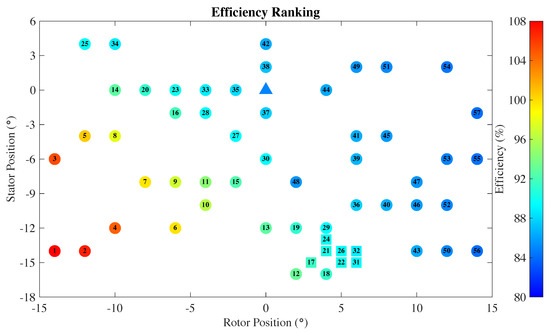
Figure 7.
Scatter plot of the cases ranked by the adiabatic efficiency value with rank 1 being the highest. Cases in the initial data set are denoted by circles while the remaining cases are denoted by squares. The color fill of the circles and squares corresponds to the value of the adiabatic efficiency. The baseline design is denoted using a triangle with the efficiency value of %.
Three important observations can be made from Figure 5, Figure 6 and Figure 7: 1. The prospective neighborhood of the optimal solution is quickly identified by the SMF, which may be inferred from all the squares, representing candidate cases computed after the initialization by the LHS approach, clustering together; 2. The SMF is able to arrive at an optimal solution without exhausting all options, which may be inferred from several cases near the optimal solution that were not chosen for the objective-function evaluation. 3: Adiabatic efficiency and shaft torque are clearly two competing performance metrics as the overall best design is not even in the top 20% as measured by the individual performance indicators.
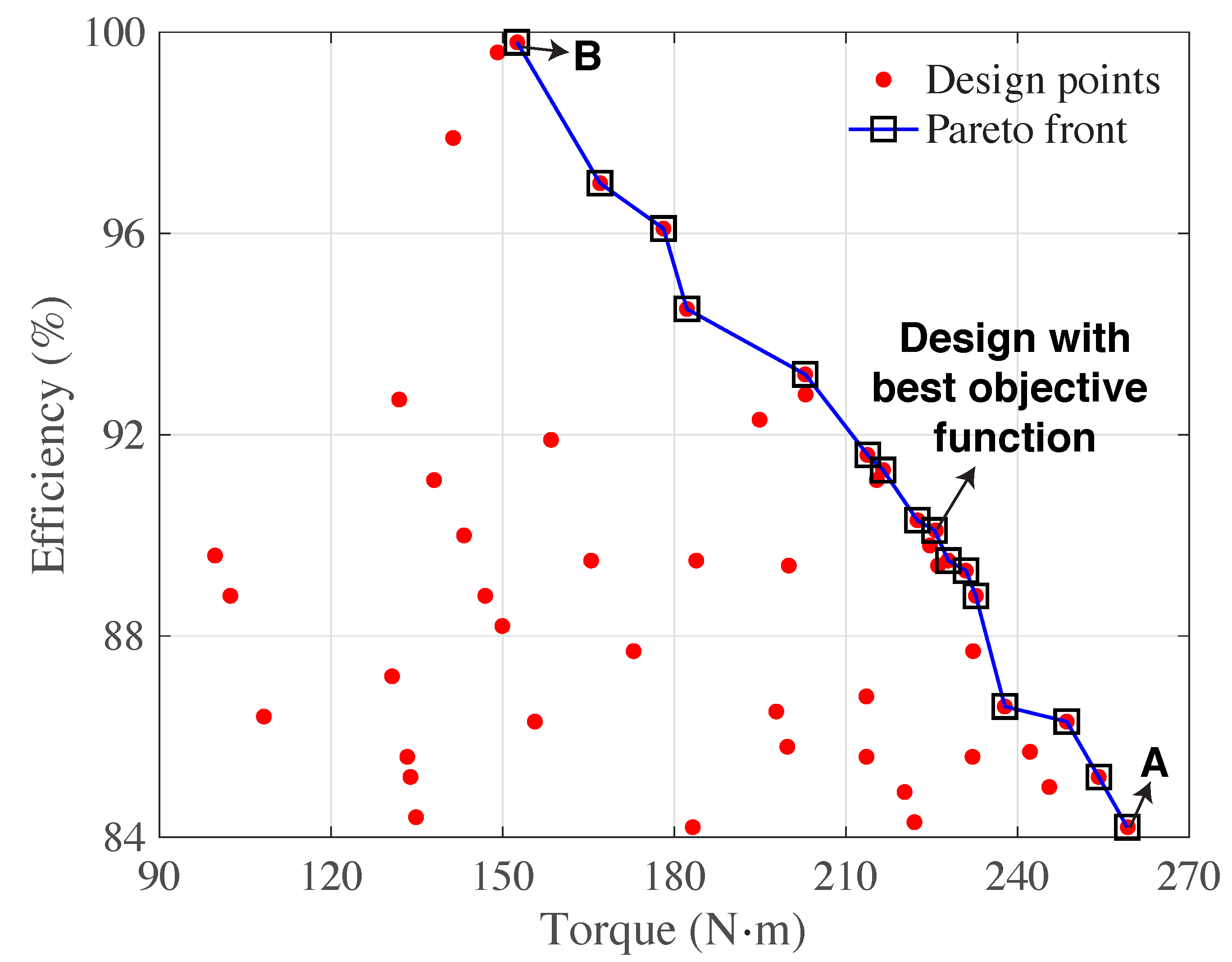
A scatter plot of efficiency vs. torque for all the cases along with the Pareto frontier is shown in Figure 8. From the standpoint of multi-objective optimization, all the designs on the Pareto frontier can be considered as optimal. In the figure, points A and B on the Pareto front represent the designs with the highest torque and efficiency values, respectively. The optimal design from the standpoint of the objective function chosen also lies on the Pareto frontier and is marked accordingly in the figure.
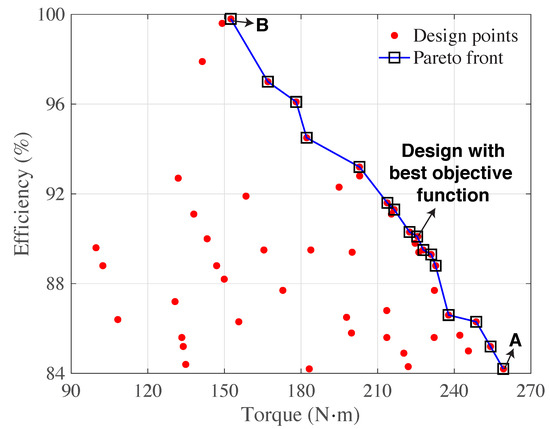
Figure 8.
Scatter plot of efficiency vs. torque for all the cases showing the Pareto optimal frontier.
4.2. Flow Analysis
Here we present a discussion of the flow phenomena observed in the simulations and how these translate into performance metrics considered. We first focus on the comparison between the optimal and baseline cases. We then discuss the flow phenomena observed in five other cases that are representative of the whole design space. We look at the instantaneous flow streamlines and vortical features depicted using the isosurfaces of Q-criterion, the second invariant of the velocity gradient that measures the relative importance of vorticity over strain rate, and that is part of the well-known Q-criterion used in the identification of vortical structures in the flow [70].
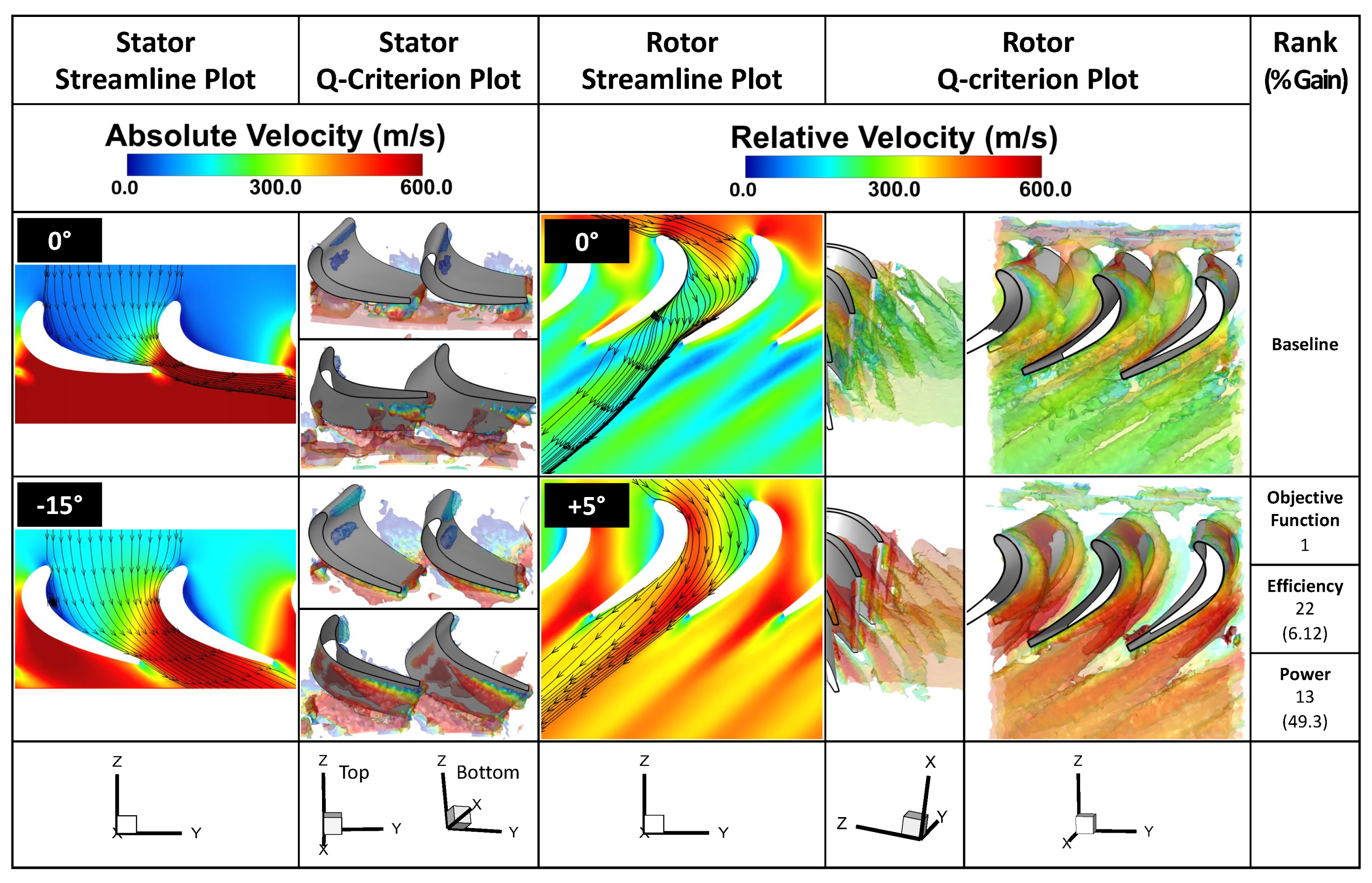
In Figure 9, we observe that pitching the stator blades results in the flow that is less blocked, with almost no separation, and reoriented in such a way that when it enters the rotor section it stays mainly attached to the suction side of the blade, thus creating a large suction pressure that drives the rotor. In contrast, the baseline case shows blocked flow at the stator and gives rise to premature flow separation on the suction side of the rotor blades with more flow recirculation than desired for high torque and efficiency output. Both the streamline and Q-criterion plots support these observations, which explain the performance gains of 6.1% for efficiency and 49.3% for torque for the optimal design.
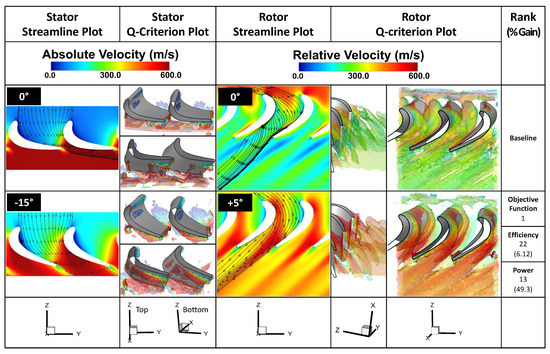
Figure 9.
Flow field comparison using streamline and Q-criterion plots between the optimal and baseline cases. The stator plots use absolute velocity while the rotor plots use relative velocity.
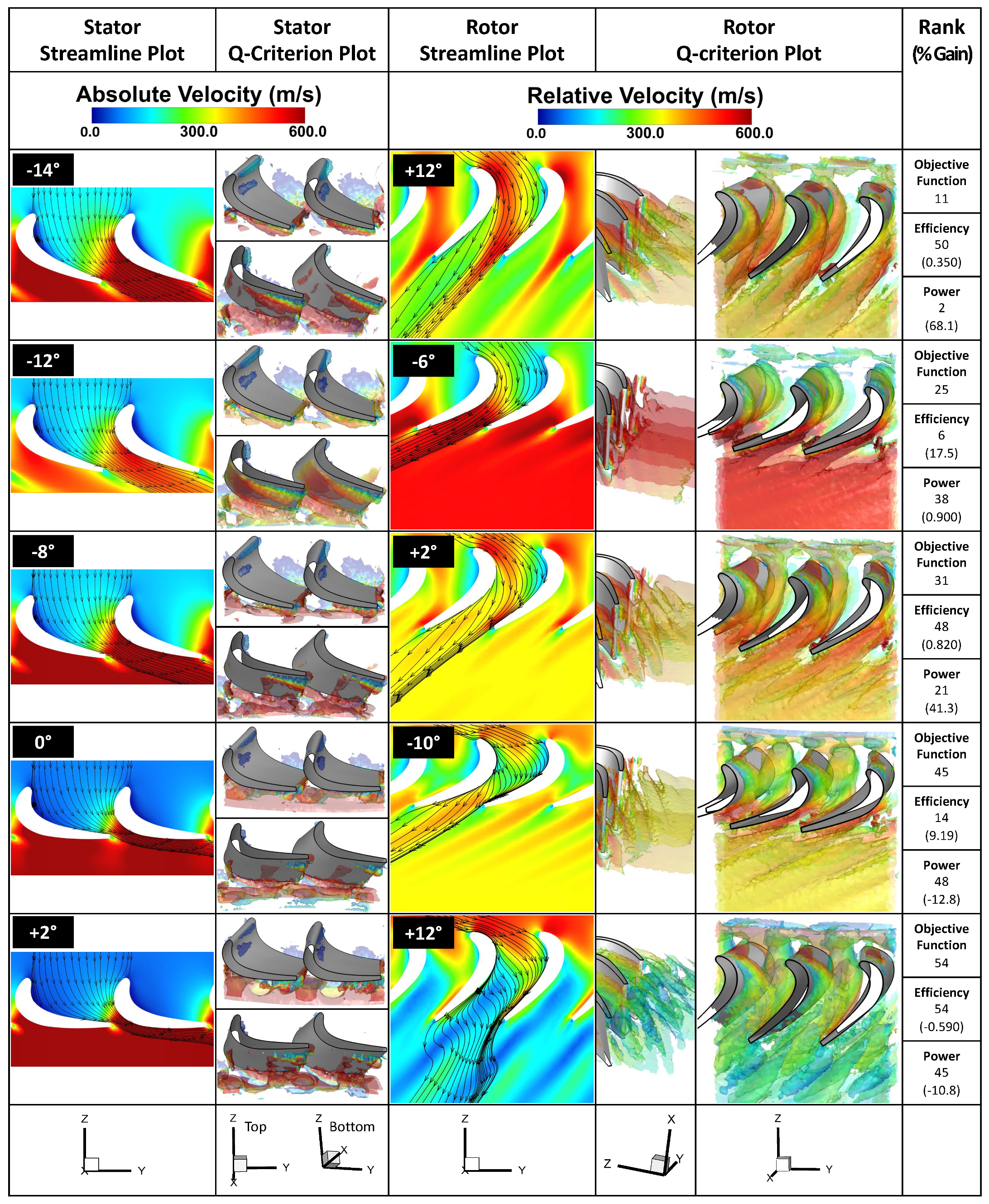
In Figure 10, the first case corresponds to the stator pitched at and rotor at 12 relative to the baseline. While the stator flow is not very different from the optimal case, and the rotor flow shows high speed on the suction side, the flow separation at the rotor blade appears to be slightly premature and the flow “strikes” the trailing edge of the pressure side of the neighboring blade. While this flow results in a high torque rating, the efficiency suffers tremendously due to flow striking the underside of the neighboring blade and creating unnecessarily high gradients leading to losses.
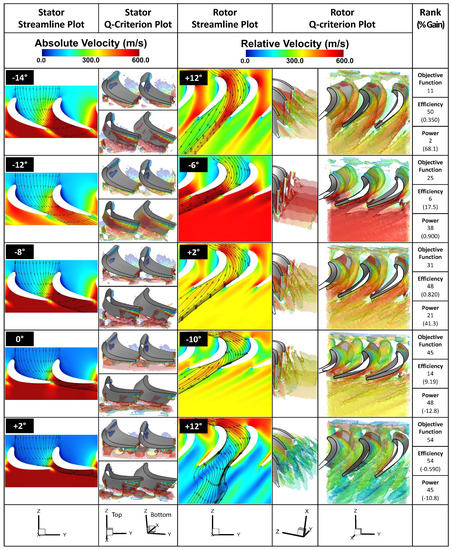
Figure 10.
Flow field comparison using streamline and Q-criterion plots between five different cases taken from the design space. The stator plots use absolute velocity while the rotor plots use relative velocity.
The second case in Figure 10, while showing very little flow separation and vorticity, and, as such, resulting in high efficiency, clearly shows excessive flow blockage in the rotor section. This blockage does not allow the flow to develop on the suction side and results in a low torque rating.
The third case in Figure 10 shows a little more blockage and flow reorientation in the stator, and a premature separation and striking of the neighbor-blade trailing edge in the rotor, resulting in a mediocre power ranking and bad efficiency.
The fourth case in Figure 10, where only the rotor is articulated to while the stator remained at the baseline position, shows premature flow separation at the rotor blade suction-side leading edge. However, because the rotor articulation is such that it tries to block the flow, the flow appears to reattach on the suction side without significant recirculation. This gives a good efficiency ranking, while the power ranking suffers due to insufficient flow speed near the suction side of the rotor blades.
The last case in Figure 10 shows a severe blockage of the stator flow and complete flow misalignment with the rotor section resulting in massive separation and 3D recirculation, and leading to bad efficiency and power rankings.
5. Conclusions
We presented a novel approach that couples a derivative-free Surrogate Management Framework for design optimization with high-fidelity finite element modeling of moving-domain compressible flows. The framework was demonstrated through the modeling, analysis, and optimization of a U.S. Army variable-speed gas turbine engine. We studied an annular single-stage high pressure turbine featuring a novel incidence-tolerant turbomachinery blade technology [65] that adapts to different operating conditions by synchronously articulating the stator and rotor blades. One of the objectives of this work was to determine the stator- and rotor-blade positions that achieved optimal turbine performance at an off-design condition of the engine operating at 50% of the nominal rotor speed, which is typical for rotorcraft cruising conditions. Using the proposed framework, we were able to achieve gains of 6.1% for the turbine stage adiabatic efficiency and 49.3% for the shaft output power.
The proposed framework exhibited remarkable robustness in that the geometry modeling, meshing, and compressible-flow analysis modules were able to handle nearly sixty gas turbine stage designs without failure and with minimal user intervention. Parallel to this very practical optimization focus, the work also examined the flow physics of rotor–stator interactions in a gas turbine stage and provided critical insights into an emerging turbomachinery blade technology that has the potential to positively impact the future propulsion systems.
Author Contributions
Conceptualization, N.K., M.M., L.B., A.G., M.-C.H. and Y.B.; Methodology, N.K., M.R.R., M.C.H.W., M.-C.H. and Y.B.; Software, N.K., M.R.R. and M.C.H.W.; Formal analysis, N.K. and Y.B.; Investigation, N.K., M.M. and L.B.; Data curation, N.K., M.M. and L.B.; Writing, N.K., M.-C.H. and Y.B.; Visualization, N.K.; Supervision, M.M., L.B., A.G., M.-C.H. and Y.B.; Project administration, A.G., M.-C.H. and Y.B.; Funding acquisition, A.G., M.-C.H. and Y.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the ARO Grant No. W911NF-14-1-0296.
Acknowledgments
N. Kozak was supported by the 2019 HPC Internship Program at the ARL Vehicle Technology Directorate. Computing resources used in this work were provided by the the Department of Defense High Performance Computing Modernization Program (HPCMP). This support is gratefully acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Welch, G.E. Assessment of aerodynamic challenges of a variable-speed power turbine for large civil tilt-rotor application. In Proceedings of the 66th American Helicopter Society International Annual Forum (AHS Forum 66), Phoenix, AZ, USA, 11–13 May 2010. [Google Scholar]
- Murugan, M.; Booth, D.; Ghoshal, A.; Thurman, D.; Kerner, K. Concept study for adaptive gas turbine rotor blade. Int. J. Eng. Sci. 2015, 4, 10–17. [Google Scholar]
- Murugan, M.; Ghoshal, A.; Xu, F.; Hsu, M.C.; Bazilevs, Y.; Bravo, L.; Kerner, K. Analytical Study of Articulating Turbine Rotor Blade Concept for Improved Off-Design Performance of Gas Turbine Engines. J. Eng. Gas Turbines Power 2017, 139, 102601. [Google Scholar] [CrossRef]
- Grossman, J.; Rubenson, D.; Sollfrey, W.; Steele, B. Vertical Envelopment and the Future Transport Rotorcraft; RAND Corporation: Santa Monica, CA, USA, 2003. [Google Scholar]
- Mcdonald, C.; Wilson, D. The utilization of recuperated and regenerated engine cycles for high-efficiency gas turbines in the 21st century. Appl. Therm. Eng. 1996, 16, 635–653. [Google Scholar] [CrossRef]
- Kozak, N.; Xu, F.; Rajanna, M.R.; Bravo, L.; Murugan, M.; Ghoshal, A.; Bazilevs, Y.; Hsu, M.C. High-fidelity finite element modeling and analysis of adaptive gas turbine stator–rotor flow interaction at off-design conditions. J. Mech. 2020. [Google Scholar] [CrossRef]
- Rajanna, M.R.; Xu, F.; Hsu, M.C.; Bazilevs, Y.; Murugan, M.; Ghoshal, A.; Bravo, L. Optimizing gas-turbine operation using finite-element cfd modeling. In Proceedings of the 2018 Joint Propulsion Conference, Cincinnati, OH, USA, 9–11 July 2018. [Google Scholar]
- Logan, E., Jr.; Roy, R. Handbook of Turbomachinery, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Booker, A.J.; Dennis, J.E., Jr.; Frank, P.D.; Serafini, D.B.; Torczon, V.; Trosset, M.W. A rigorous framework for optimization of expensive functions by surrogates. Struct. Optim. 1999, 17, 1–13. [Google Scholar] [CrossRef]
- Hansen, N. A CMA-ES for Mixed-Integer Nonlinear Optimization; Technical Report RR-7751; Institut National de Recherche en Informatique et en Automatique: Rocquencourt, France, 2011. [Google Scholar]
- Audet, C.; Dennis, J.E., Jr. Mesh adaptive direct search algorithms for constrained optimization. SIAM J. Optim. 2006, 17, 188–217. [Google Scholar] [CrossRef]
- Benaouali, A.; Kachel, S. A surrogate-based integrated framework for the aerodynamic design optimization of a subsonic wing planform shape. J. Aerosp. Eng. 2018, 232, 872–883. [Google Scholar] [CrossRef]
- Wu, M.C.H.; Kamensky, D.; Wang, C.; Herrema, A.J.; Xu, F.; Pigazzini, M.S.; Verma, A.; Marsden, A.L.; Bazilevs, Y.; Hsu, M.C. Optimizing fluid–structure interaction systems with immersogeometric analysis and surrogate modeling: Application to a hydraulic arresting gear. Comput. Methods Appl. Mech. Eng. 2017, 316, 668–693. [Google Scholar] [CrossRef]
- Long, C.C.; Marsden, A.L.; Bazilevs, Y. Fluid–structure interaction simulation of pulsatile ventricular assist devices. Comput. Mech. 2013, 52, 971–981. [Google Scholar] [CrossRef]
- Verma, A.; Wong, K.; Marsden, A.L. A concurrent implementation of the surrogate management framework with application to cardiovascular shape optimization. Optim. Eng. 2020. [Google Scholar] [CrossRef]
- Hughes, T.J.R.; Tezduyar, T.E. Finite element methods for first-order hyperbolic systems with particular emphasis on the compressible Euler equations. Comput. Methods Appl. Mech. Eng. 1984, 45, 217–284. [Google Scholar] [CrossRef]
- Hughes, T.J.R.; Franca, L.P.; Mallet, M. A new finite element formulation for computational fluid dynamics: I. Symmetric forms of the compressible Euler and Navier-Stokes equations and the second law of thermodynamics. Comput. Methods Appl. Mech. Eng. 1986, 54, 223–234. [Google Scholar] [CrossRef]
- Hughes, T.J.R.; Mallet, M. A new finite element formulation for computational fluid dynamics: III. The generalized streamline operator for multidimensional advective-diffusive systems. Comput. Methods Appl. Mech. Eng. 1986, 58, 305–328. [Google Scholar] [CrossRef]
- Hughes, T.J.R.; Franca, L.P.; Mallet, M. A new finite element formulation for computational fluid dynamics: VI. Convergence analysis of the generalized SUPG formulation for linear time-dependent multi-dimensional advective-diffusive Systems. Comput. Methods Appl. Mech. Eng. 1987, 63, 97–112. [Google Scholar] [CrossRef]
- Le Beau, G.J.; Ray, S.E.; Aliabadi, S.K.; Tezduyar, T.E. SUPG finite element computation of compressible flows with the entropy and conservation variables formulations. Comput. Methods Appl. Mech. Eng. 1993, 104, 397–422. [Google Scholar] [CrossRef]
- Aliabadi, S.K.; Tezduyar, T.E. Space–time finite element computation of compressible flows involving moving boundaries and interfaces. Comput. Methods Appl. Mech. Eng. 1993, 107, 209–223. [Google Scholar] [CrossRef]
- Hauke, G.; Hughes, T.J.R. A unified approach to compressible and incompressible flows. Comput. Methods Appl. Mech. Eng. 1994, 113, 389–396. [Google Scholar] [CrossRef]
- Hauke, G.; Hughes, T.J.R. A comparative study of different sets of variables for solving compressible and incompressible flows. Comput. Methods Appl. Mech. Eng. 1998, 153, 1–44. [Google Scholar] [CrossRef]
- Hauke, G. Simple sabilizing matrices for the computation of compressible flows in primitive variables. Comput. Methods Appl. Mech. Eng. 2001, 190, 6881–6893. [Google Scholar] [CrossRef]
- Hughes, T.J.R.; Scovazzi, G.; Tezduyar, T.E. Stabilized Methods for Compressible Flows. J. Sci. Comput. 2010, 43, 343–368. [Google Scholar] [CrossRef]
- Takizawa, K.; Tezduyar, T.E.; Kanai, T. Porosity models and computational methods for compressible-flow aerodynamics of parachutes with geometric porosity. Math. Model. Methods Appl. Sci. 2017, 27, 771–806. [Google Scholar] [CrossRef]
- Kanai, T.; Takizawa, K.; Tezduyar, T.E.; Tanaka, T.; Hartmann, A. Compressible-flow geometric-porosity modeling and spacecraft parachute computation with isogeometric discretization. Comput. Mech. 2019, 63, 301–321. [Google Scholar] [CrossRef]
- Castorrini, A.; Corsini, A.; Rispoli, F.; Venturini, P.; Takizawa, K.; Tezduyar, T.E. Computational analysis of performance deterioration of a wind turbine blade strip subjected to environmental erosion. Comput. Mech. 2019, 64, 1133–1153. [Google Scholar] [CrossRef]
- Castorrini, A.; Venturini, P.; Corsini, A.; Rispoli, F.; Takizawa, K.; Tezduyar, T.E. Computational Analysis of Particle-Laden-Airflow Erosion and Experimental Verification. Comput. Mech. 2020, 65, 1549–1565. [Google Scholar] [CrossRef]
- Hughes, T.J.R.; Liu, W.K.; Zimmermann, T.K. Lagrangian–Eulerian finite element formulation for incompressible viscous flows. Comput. Methods Appl. Mech. Eng. 1981, 29, 329–349. [Google Scholar] [CrossRef]
- Tezduyar, T.E.; Park, Y.J. Discontinuity capturing finite element formulations for nonlinear convection– diffusion–reaction equations. Comput. Methods Appl. Mech. Eng. 1986, 59, 307–325. [Google Scholar] [CrossRef]
- Hughes, T.J.R.; Mallet, M.; Mizukami, A. A new finite element formulation for computational fluid dynamics: II. Beyond SUPG. Comput. Methods Appl. Mech. Eng. 1986, 54, 341–355. [Google Scholar] [CrossRef]
- Hughes, T.J.R.; Mallet, M. A new finite element formulation for computational fluid dynamics: IV. A discontinuity-capturing operator for multidimensional advective-diffusive systems. Comput. Methods Appl. Mech. Eng. 1986, 58, 329–339. [Google Scholar] [CrossRef]
- Shakib, F.; Hughes, T.J.R.; Johan, Z. A new finite element formulation for computational fluid dynamics: X. The compressible Euler and Navier–Stokes equations. Comput. Methods Appl. Mech. Eng. 1991, 89, 141–219. [Google Scholar] [CrossRef]
- Almeida, R.C.; Galeão, A.C. An adaptive Petrov–Galerkin formulation for the compressible Euler and Navier–Stokes equations. Comput. Methods Appl. Mech. Eng. 1996, 129, 157–176. [Google Scholar] [CrossRef]
- Tezduyar, T.E. Finite element methods for fluid dynamics with moving boundaries and interfaces. In Encyclopedia of Computational Mechanics; Stein, E., Borst, R.D., Hughes, T.J.R., Eds.; Volume 3: Fluids; John Wiley & Sons: Hoboken, NJ, USA, 2004; Chapter 17. [Google Scholar]
- Tezduyar, T.E.; Senga, M. Stabilization and shock-capturing parameters in SUPG formulation of compressible flows. Comput. Methods Appl. Mech. Eng. 2006, 195, 1621–1632. [Google Scholar] [CrossRef]
- Tezduyar, T.E.; Senga, M.; Vicker, D. Computation of inviscid supersonic flows around cylinders and spheres with the SUPG formulation and YZβ shock-capturing. Comput. Mech. 2006, 38, 469–481. [Google Scholar] [CrossRef]
- Tezduyar, T.E.; Senga, M. SUPG finite element computation of inviscid supersonic flows with YZβ shock-capturing. Comput. Fluids 2007, 36, 147–159. [Google Scholar] [CrossRef]
- Rispoli, F.; Saavedra, R.; Corsini, A.; Tezduyar, T.E. Computation of inviscid compressible flows with the V-SGS stabilization and YZβ shock-capturing. Int. J. Numer. Methods Fluids 2007, 54, 695–706. [Google Scholar] [CrossRef]
- Rispoli, F.; Saavedra, R.; Menichini, F.; Tezduyar, T.E. Computation of inviscid supersonic flows around cylinders and spheres with the V-SGS stabilization and YZβ shock-capturing. J. Appl. Mech. 2009, 76, 021209. [Google Scholar] [CrossRef]
- Rispoli, F.; Delibra, G.; Venturini, P.; Corsini, A.; Saavedra, R.; Tezduyar, T.E. Particle tracking and particle–shock interaction in compressible-flow computations with the V-SGS stabilization and YZβ shock-capturing. Comput. Mech. 2015, 55, 1201–1209. [Google Scholar] [CrossRef]
- Takizawa, K.; Tezduyar, T.E.; Otoguro, Y. Stabilization and discontinuity-capturing parameters for space–time flow computations with finite element and isogeometric discretizations. Comput. Mech. 2018, 62, 1169–1186. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Hughes, T.J.R. Weak imposition of Dirichlet boundary conditions in fluid mechanics. Comput. Fluids 2007, 36, 12–26. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Michler, C.; Calo, V.M.; Hughes, T.J.R. Weak Dirichlet boundary conditions for wall-bounded turbulent flows. Comput. Methods Appl. Mech. Eng. 2007, 196, 4853–4862. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Michler, C.; Calo, V.M.; Hughes, T.J.R. Isogeometric variational multiscale modeling of wall-bounded turbulent flows with weakly enforced boundary conditions on unstretched meshes. Comput. Methods Appl. Mech. Eng. 2010, 199, 780–790. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Akkerman, I. Large eddy simulation of turbulent Taylor–Couette flow using isogeometric analysis and the residual-based variational multiscale method. J. Comput. Phys. 2010, 229, 3402–3414. [Google Scholar] [CrossRef]
- Hsu, M.C.; Akkerman, I.; Bazilevs, Y. Wind turbine aerodynamics using ALE–VMS: Validation and the role of weakly enforced boundary conditions. Comput. Mech. 2012, 50, 499–511. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Hughes, T.J.R. NURBS-based isogeometric analysis for the computation of flows about rotating components. Comput. Mech. 2008, 43, 143–150. [Google Scholar] [CrossRef]
- Hsu, M.C.; Akkerman, I.; Bazilevs, Y. Finite element simulation of wind turbine aerodynamics: Validation study using NREL Phase VI experiment. Wind Energy 2014, 17, 461–481. [Google Scholar] [CrossRef]
- Hsu, M.C.; Bazilevs, Y. Fluid–structure interaction modeling of wind turbines: Simulating the full machine. Comput. Mech. 2012, 50, 821–833. [Google Scholar] [CrossRef]
- Terahara, T.; Takizawa, K.; Tezduyar, T.E.; Bazilevs, Y.; Hsu, M.C. Heart Valve Isogeometric Sequentially-Coupled FSI Analysis with the Space–Time Topology Change Method. Comput. Mech. 2020, 65, 1167–1187. [Google Scholar] [CrossRef]
- Terahara, T.; Takizawa, K.; Tezduyar, T.E.; Tsushima, A.; Shiozaki, K. Ventricle-valve-aorta flow analysis with the Space–Time Isogeometric Discretization and Topology Change. Comput. Mech. 2020, 65, 1343–1363. [Google Scholar] [CrossRef]
- Otoguro, Y.; Takizawa, K.; Tezduyar, T.E.; Nagaoka, K.; Avsar, R.; Zhang, Y. Space–Time VMS Flow Analysis of a Turbocharger Turbine with Isogeometric Discretization: Computations with Time-Dependent and Steady-Inflow Representations of the Intake/Exhaust Cycle. Comput. Mech. 2019, 64, 1403–1419. [Google Scholar] [CrossRef]
- Chung, J.; Hulbert, G.M. A time integration algorithm for structural dynamics with improved numerical dissipation: The generalized-α method. J. Appl. Mech. 1993, 60, 371–375. [Google Scholar] [CrossRef]
- Jansen, K.E.; Whiting, C.H.; Hulbert, G.M. A generalized-α method for integrating the filtered Navier-Stokes equations with a stabilized finite element method. Comput. Methods Appl. Mech. Eng. 2000, 190, 305–319. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Calo, V.M.; Hughes, T.J.R.; Zhang, Y. Isogeometric fluid–structure interaction: Theory, algorithms, and computations. Comput. Mech. 2008, 43, 3–37. [Google Scholar] [CrossRef]
- Shakib, F.; Hughes, T.J.R.; Johan, Z. A multi-element group preconditioned GMRES algorithm for nonsymmetric systems arising in finite element analysis. Comput. Methods Appl. Mech. Eng. 1989, 75, 415–456. [Google Scholar] [CrossRef]
- Xu, F.; Moutsanidis, G.; Kamensky, D.; Hsu, M.C.; Murugan, M.; Ghoshal, A.; Bazilevs, Y. Compressible flows on moving domains: Stabilized methods, weakly enforced essential boundary conditions, sliding interfaces, and application to gas-turbine modeling. Comput. Fluids 2017, 158, 201–220. [Google Scholar] [CrossRef]
- Xu, F.; Bazilevs, Y.; Hsu, M.C. Immersogeometric analysis of compressible flows with application to aerodynamic simulation of rotorcraft. Math. Model. Methods Appl. Sci. 2019, 29, 905–938. [Google Scholar] [CrossRef]
- Hsu, M.C.; Wang, C.; Herrema, A.J.; Schillinger, D.; Ghoshal, A.; Bazilevs, Y. An interactive geometry modeling and parametric design platform for isogeometric analysis. Comput. Math. Appl. 2015, 70, 1481–1500. [Google Scholar]
- Huntington, D.E.; Lyrintzis, C.S. Improvements to and limitations of Latin hypercube sampling. Probabilistic Eng. Mech. 1998, 13, 245–253. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 2000, 42, 55–61. [Google Scholar] [CrossRef]
- Hansen, N.; Ostermeier, A. Completely derandomized self-adaptation in evolution strategies. Evol. Comput. 2001, 9, 159–195. [Google Scholar] [CrossRef]
- Murugan, M.; Ghoshal, A.; Bravo, L. Adaptable Articulating Axial-Flow Compressor/Turbine Rotor Blade. U.S. Patent Application 20180066671 A1, 8 March 2018. [Google Scholar]
- Audet, C.; Le Digabel, S.; Tribes, C. The mesh adaptive direct search algorithm for granular and discrete variables. SIAM J. Optim. 2019, 29, 1164–1189. [Google Scholar] [CrossRef]
- Schobeiri, M. Turbomachinery Flow Physics and Dynamic Performance; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Fletcher, R. Practical Methods of Optimization, 2nd ed.; John Wiley & Sons: Chichester, UK, 1987. [Google Scholar]
- Wold, S.; Esbensen, K.; Geladi, P. Principal Component Analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Jeong, J.; Hussain, F. On the identification of a vortex. J. Fluid Mech. 1995, 285, 69–94. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).