Abstract
A modified closed binary Brayton cycle model with variable isothermal pressure drop ratios is established by using finite time thermodynamics in this paper. A topping cycle, a bottoming cycle, two isothermal heating processes and variable-temperature reservoirs are included in the new model. The topping cycle is composed of a compressor, a regular combustion chamber, a converging combustion chamber, a turbine and a precooler. The bottoming cycle is composed of a compressor, an ordinary regenerator, an isothermal regenerator, a turbine and a precooler. The heat conductance distributions among the six heat exchangers are optimized with dimensionless power output as optimization objective. The results show that the double maximum dimensionless power output increases first and then tends to be unchanged while the inlet temperature ratios of the regular combustion chamber and the converging combustion chamber increase. There also exist optimal thermal capacitance rate matchings among the working fluid and heat reservoirs, leading to the optimal maximum dimensionless power output.
1. Introduction
Due to the characteristics of high power density (PD), small vibration, high automation, low operating pressure and easy lubrication, gas turbine plants (Brayton heat engine cycle) are extensively applied in the fields of aviation, energy, transportation, etc. According to the different working fluid (WF) circulation modes, the Brayton cycle is divided into open and closed cycles, and many works concerning the classical thermodynamic analyses and optimizations for various Brayton cycles have been performed [1,2,3]. The WF of closed Brayton cycle is not directly connected with the atmosphere, and does not participate in the combustion process. Hence, it is applied to convert nuclear energy, geothermal energy, solid fuel and other primary energy into electricity energy.
For the case of simple heating, the temperature of the gas elevates in the direction of a duct when the subsonic compressible gas flows through the smooth heating duct with a fixed cross-sectional area. For the case of simple cross-sectional area change, the temperature drops when the gas flows through the smooth adiabatic duct with a reduced cross-sectional area. Based on these two gas properties, the isothermal processes can be realized when the subsonic compressible gas flows through the smooth heating duct with a reduced cross-sectional area. Vecchiarelli et al. [4] presented a combustion chamber where the WF could be heated isothermally. The introduction of this type of combustion chamber could effectively improve the thermal efficiency (TEF) of the Brayton cycle, and reduce the emissions of nitrogen oxides and other harmful gases. Göktun and Yavuz [5] applied the isothermal heating combustion chamber to the regenerative Brayton cycle, and discovered the isothermal pressure drop ratio impacted the cycle performance significantly. Based on [5], Erbay et al. [6] compared the optimal performances of an isothermal heating regenerative Brayton cycle under maximum power output (PO) and maximum PD. Jubeh [7] found the exergy efficiency was enhanced by adding the isothermal heating combustion chamber in regenerative Brayton cycle. El-Maksoud [8] combined the isothermal concept and double Brayton cycle to establish a new cycle model. Based on [8], Qi et al. [9] derived the specific work and exergy efficiency, and analyzed the impacts of different parameters on the exergy efficiency. All those works were carried out by using classical thermodynamics.
Finite time thermodynamics (FTT) [10] have been extensively applied in the analyses and optimizations of many thermodynamic systems. The purpose of FTT is to reduce the irreversibilities of processes and cycles and to improve the energy utilization rates [11]. Plenty of FTT studies have been conducted for various heat engine cycles, including the Novikov engine [12], the Stirling engine [13], Rankine cycles [14,15,16,17,18,19,20,21], heated gas expansion process [22], thermoelectric generators [23,24,25,26], the fuel cell hybrid cycle [27], the gas–mercury combined cycle [28], the thermocapacitive heat engine [29], the Maisotsenko–Diesel cycle [30], the trigeneration cycle [31], Dual-Miller cycles [32,33,34], Feynman’s ratchet [35], the Kalina cycle [36] and so on.
For the Brayton cycles, FTT studies have been also conducted for simple cycles [37], regenerative cycles [38,39,40], multi-intercooling-and-regenerative cycles [41,42,43], the fuel cell–Brayton combined cycle [44], Maisotsenko–Brayton cycles [45,46], Brayton cycle-based cooling, heat and power combined cycles [47,48] and so on.
For the Brayton cycles with isothermal heating modification, Kaushik et al. [49] optimized the regenerative Brayton cycle with isothermal process whose optimization objective was the PO. Tyagi et al. [50,51,52,53,54,55,56] optimized the performances of the isothermal heating modified simple, regenerated and intercooling Brayton cycles with different optimization objectives. Based on [49,50,51,52,53,54,55,56], Wang et al. [57,58] and Tang et al. [59,60] analyzed and optimized the endoreversible simple, irreversible simple and irreversible regenerative Brayton cycles with isothermal processes. Arora et al. [61] optimized the regenerative Brayton cycle with isothermal process by employing the NSGA-II algorithm.
Based on El-Maksoud’s classical thermodynamic model [8], Qi et al. [62] established a closed endoreversible binary Brayton cycle model with two isothermal processes, without internal irreversibility, and coupled to constant-temperature reservoirs (CTRs). They derived the functional expressions of PO, TEF, PD and ecological function, respectively. The impacts of different thermodynamic parameters on the relationships among performance indexes and the pressure ratio of the topping cycle were analyzed, and the heat conductance distributions (HCDs) among heat exchangers were further optimized.
Based on the previously established cycle models in [8,62], a modified closed binary Brayton cycle (MCBBC) with variable isothermal pressure drop ratios and internal and external irreversibilities will be established by using FTT in this paper. The HCDs will be optimized with dimensionless PO. The influences of different thermodynamic parameters on the optimal performance will be analyzed, and the thermal capacitance rate matchings (TCRMs) among the WF and the heat reservoirs will be also discussed.
2. Cycle Model
Figure 1a shows the schematic diagram of the MCBBC with two isothermal heating processes [8]. A topping cycle and a bottoming cycle are included in the model. The topping cycle is composed of a compressor (Com1), a regular combustion chamber (RCC), a converging combustion chamber (CCC), a turbine (Tur1) and a precooler (PC1). The bottoming cycle is composed of a compressor (Com2), an ordinary regenerator (OR), an isothermal regenerator (IR), a turbine (Tur2) and a precooler (PC2).
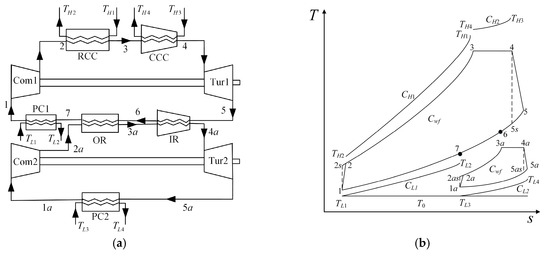
Figure 1.
(a) Schematic diagram of the cycle [8]; (b) T-s diagram of the cycle.
Figure 1b illustrates the T-s diagram of the MCBBC. In the figure, processes , , , , , and represent the irreversible adiabatic compression, isobaric heating, isothermal heating, irreversible adiabatic expansion and three isobaric exothermic processes of the WF in Com1, RCC, CCC, Tur1, IR, OR and PC1, respectively. Processes , , , and represent the irreversible adiabatic compression, isobaric heating, isothermal heating, irreversible adiabatic expansion and isobaric exothermic process of the WF in Com2, OR, IR, Tur2 and PC2, respectively. Processes , , and are the isentropic processes corresponding to the processes , , and respectively.
It is assumed that the WFs of the topping and bottoming cycles are the same, both of which are ideal gases. The specific heat at constant pressure, thermal capacity rate, specific heat ratio, mass flow rate and gas constant of the WF are , , , and , respectively, where and . The temperatures and pressures at different state points are signed as and (), and the ambient temperature is . The inlet temperatures of the outer fluids in the RCC, CCC, PC1 and PC2 are , , and , and the outlet temperatures of outer fluids in the RCC, CCC, PC and PC2 are , , and , respectively. The thermal capacity rates of outer fluids in the RCC, CCC, PC1 and PC2 are , , and , respectively. The pressure ratios in the Com1 and Com2 are and , and the isothermal pressure drop ratios at the CCC and IR are and , respectively. The heat conductances of the heat exchangers for the RCC, CCC, OR, IR, PC1 and PC2 are (), and the corresponding effectivenesses are ; namely:
where, , , , , and . The numbers of heat transfer units for the heat exchangers are calculated as:
When , and , Equations (1), (3) and (4) are simplified into:
The efficiencies in the Com1, Com2, Tur1 and Tur2 are , , and , respectively:
The heat absorbing rates of WF in the RCC, CCC, OR and IR are , , and , and the heat releasing rates in the PC1 and PC2 are and . They are calculated as:
The power output and thermal efficiency of the cycle are and , respectively:
Processes 3–4 and 3a–4a are the isothermal ones, and the heat absorbing rates of the two processes are:
Processes 1–2s, 1–2as, 4–5s and 4a–5as are the isentropic processes; namely:
where , , and are the parameters of temperature ratios which can be calculated by the pressure ratios.
The upper limits of and are 1, which means that the isothermal heating is not used. When or , the topping or bottoming cycle adopts the isothermal process. The isothermal pressure drop ratios must meet the following constraints:
where and ( and ) are the Mach numbers at the inlet and outlet of CCC (IR), respectively. If and , and get their maximum values of 1, and and get their minimum values of 0.4966. For the initial velocity of the WF, the Mach numbers satisfy and , and the corresponding minimum values of and are 0.5107. At the same time, must be greater than or equal to zero; otherwise, the cycle is meaningless.
The major difference between the model in this paper and that in [8] is that all the heat transfer losses in the six heat exchangers are considered in this paper. This is also the major difference between classical thermodynamic model and FTT model. The major differences between the model in this paper and that in [62] are two aspects: One is that the irreversible compression and expansion losses are considered in this paper; this is also the major difference between the endoreversible model and the irreversible one. Another is that the heat reservoirs are assumed to be variable-temperature ones in this paper; this is one of basic characteristics of practical closed engineering cycles.
According to the above model, the dimensionless PO and TEF can be given by:
where , , , and are listed in Appendix A.
If Equations (21) and (22) are not considered when solving Equations (28) and (29), the final analytical solutions for and of the cycle cannot be obtained. Considering Equations (21) and (22), the values of and in Equations (28) and (29) are obtained by numerical calculation, and the corresponding values of and can be obtained.
If , , , , , , , , , , , , and take different values, the model can be converted into different special models; Equations (28) and (29) can be reduced to the corresponding dimensionless PO and TEF respectively, which have a certain universality.
When , Equations (28) and (29) can be reduced to the dimensionless PO and TEF of a modified closed endoreversible binary Brayton cycle with two isothermal heating processes and coupled to variable-temperature heat reservoirs (VTHRs):
where , , , and are listed in Appendix A.
When , Equations (28) and (29) can be reduced to the dimensionless PO and TEF of a modified closed irreversible binary Brayton cycle with two isothermal heating processes and coupled to CTRs:
where , , , and are listed in Appendix A.
When and , Equations (28) and (29) can be reduced to the dimensionless PO and TEF of a modified closed endoreversible binary Brayton cycle with two isothermal heating processes and coupled to CTRs [62]:
where , , , and are listed in Appendix A.
When , Equations (28) and (29) can be reduced to the dimensionless PO and TEF of a modified closed irreversible Brayton cycle with an isothermal heating process and coupled to VTHRs:
where is listed in Appendix A.
When and , Equations (28) and (29) can be reduced to the dimensionless PO and TEF of a modified closed irreversible Brayton cycle with an isothermal heating process and coupled to CTRs:
When and , Equations (28) and (29) can be reduced to the dimensionless PO and TEF of a modified closed endoreversible Brayton cycle with an isothermal heating process and coupled to VTHRs [59,60]:
When 0, and , Equations (28) and (29) can be reduced to the dimensionless PO and TEF of a modified closed endoreversible Brayton cycle with an isothermal heating process and coupled to CTRs:
When , Equations (28) and (29) can be reduced to the dimensionless PO and TEF of a closed irreversible simple Brayton cycle coupled to VTHRs [37,63]:
When and , Equations (28) and (29) can be reduced to the dimensionless PO and TEF of a closed irreversible simple Brayton cycle coupled to CTRs [37,63]:
When and , Equations (28) and (29) can be reduced to the dimensionless PO and TEF of a closed endoreversible simple Brayton cycle coupled to VTHRs [64]:
When , and , Equations (28) and (29) can be reduced to the dimensionless PO and TEF of the closed endoreversible simple Brayton cycle coupled to CTRs [65,66]:
3. Optimal Heat Conductance Distributions
With as the optimization objective, the heat conductances of six heat exchangers will be optimized by fixing the total heat conductance (THC); namely, (). The HCDs in the RCC, CCC, OR, IR, PC1 and PC2 are defined as:
where must meet the following constraints:
The dimensionless PO of the MCBBC can be maximized by optimizing the HCDs. Finally, the maximum dimensionless PO () and the corresponding optimal HCDs (, , , , and ) can be obtained. Moreover, the optimal isothermal pressure drop ratios ( and ) can be calculated based on the optimal HCDs. The values or ranges of the variables are listed in Table 1. The flow chart of dimensionless PO optimization is displayed in Figure 2. Calculate the negative number of the dimensionless power output, and then the function “fmincon” in MATLAB is used to solve the minimum value. The parameters of “fmincon” are: “TolCon” is 10−6, “TolConSQP” is 300 and “TolFun” is 10−6.

Table 1.
Values or ranges of the variables.
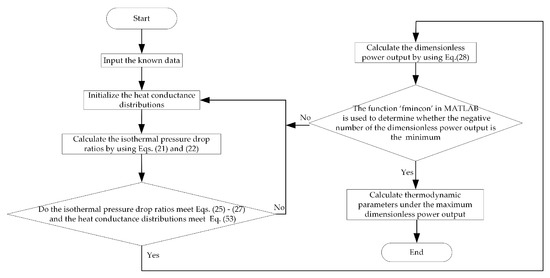
Figure 2.
Flow chart of dimensionless power output (PO) optimization.
Figure 3a,b, Figure 4a,b, Figure 5a,b and Figure 6 illustrate the relationships of the maximum dimensionless PO (), the corresponding dimensionless PO of the topping cycle, dimensionless PO of the bottoming cycle, TEF , isothermal pressure drop ratios ( and ) and HCDs (, , , , , and ) versus the pressure ratios ( and ) in the Com1 and Com2, respectively.
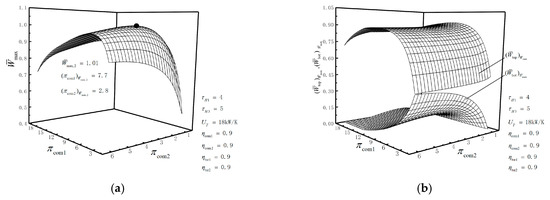
Figure 3.
(a) Relationships of versus and ; (b) relationships of and versus and .
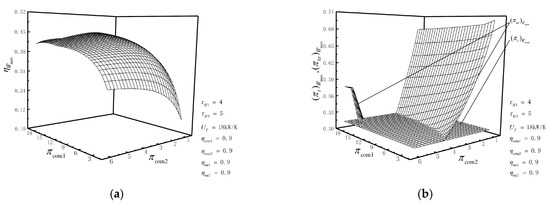
Figure 4.
(a) Relationships of versus and ; (b) relationships of and versus and .
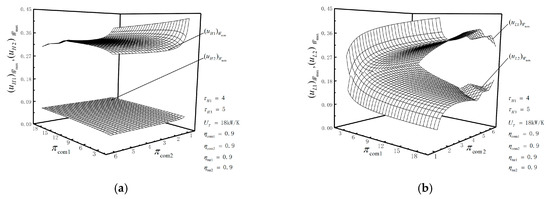
Figure 5.
(a) Relationships of and versus and ; (b) relationships of and versus and .
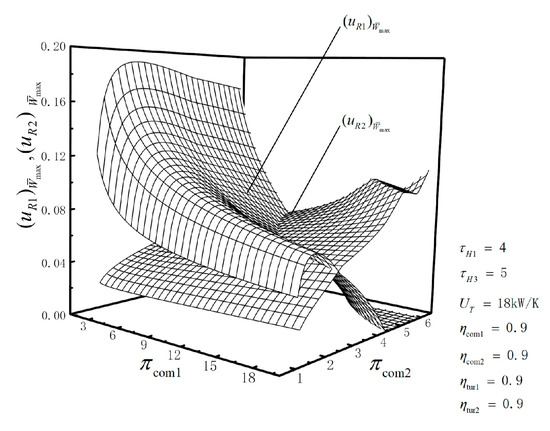
Figure 6.
Relationships of and versus and .
Figure 3a shows that increases first and then decreases as or increases. There is a set of optimal pressure ratios ( and ), so that achieves the double maximum dimensionless PO . This is because when gradually increases, , and gradually reduce, and slightly increases. With the increase in , decreases, decreases slightly, decreases first and then increases, and decreases. Under the given conditions, , and are approximately 1.01, 7.7 and 2.8, respectively.
Figure 3b shows that increases first; then decreases as increases; and remains substantially unchanged with the change of . decreases at first and then tends to remain unchanged with the increase in , the value of which is much smaller than that of . This is because decreases at first and then tends to be constant as increases. As increases, increases at first and then tends to be constant when is smaller; increases at first and then decreases to zero when is larger. That is, and can only be used to maintain the operation of the bottoming cycle. Figure 4a shows that increases at first and then becomes constant with the increase in or .
Figure 4b shows that remains unchanged as or increases, and is always located at the lower limit. This indicates that the degree of the isothermal heating in CCC always reaches the maximum. Therefore, only slightly changes with the change of or . When or is smaller, decreases slightly with the increase in and reaches the lower limit with the increase in . That indicates that under this condition, the degree of the isothermal heating in IR increases as or does; when and are larger, increases with the increase in or ; when is zero, remains substantially unchanged as or increases.
Figure 5a shows that when is not zero, increases slightly at first and then decreases slightly with the increase in ; decreases first and then tends to remain unchanged with the increase in . When is zero but both of and are not zero, decreases as or increases; when both of and are zero but is not zero, changing or does not change ; when , and are zero, decreases with the increase in or , and is far less than . With the decrease in , decreases, and then decreases. remains basically unchanged, is constant and the variation of is very small.
Figure 5b shows that when is not zero, increases as increases; it decreases first and then increases slightly as increases; decreases first and tends to remain unchanged with the increase in ; it increases first and then tends to be the same with the increase in . When is zero but both of and are not zero, decreases sharply with the increase in or , while increases sharply with the increase in or . When both of and are zero but is not zero, increases slightly with the increase in or , and remains basically unchanged with the increase in or . When , and are zero, decreases and increases as or increases.
Figure 6 shows that decreases to zero with the increase in , and increases at first and then decreases to zero as increases. When is not zero, increases with the increase in or . When is zero but is not zero, decreases with the increase in or . When both of and are zero, increases with the increase in or . Because increasing leads to the increases in and so as to avoid the negative value of , namely, inverse dimensionless PO of the bottoming cycle.
According to the numerical calculation, the influences of the temperature ratios, compressor efficiencies, turbine efficiencies and THC on optimization results are further analyzed. Figure 7a,b illustrates the relationships of the double maximum dimensionless PO () and the corresponding TEF () versus the temperature ratios ( and ). As can be seen from figure 7a,b, both and increase first and then tend to be unchanged with the increase in or . There is an optimal temperature ratio which makes reach the optimal. The corresponding fitting expression is , and the correlation coefficient is . As for , there also exists that satisfies the fitting expression: , and its correlation coefficient is also . In the actual design process, and should meet the relationship similar to or , in order to obtain as much and as possible and reduce the requirement for high temperature resistances of materials.
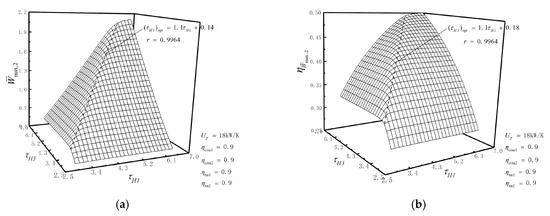
Figure 7.
(a) Relationships of versus and ; (b) relationships of versus and .
Figure 8a illustrates the relationships of , , and versus . It shows that , and increase and decreases slightly with the increase in . With the increase in , and basically increase. With the increase in , remains substantially unchanged, decreases and increases. The amount of change in is mainly affected by that in . It should be noted that when , , , and do not exist and are indicated by dashed lines.
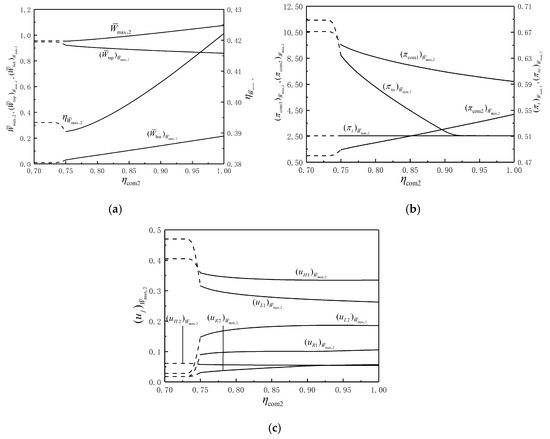
Figure 8.
(a) Relationships of , , and versus ; (b) relationships of , , and versus ; (c) relationships of versus .
Figure 8b illustrates the relationships of , , and versus . It shows that decreases and increases as
increases. The decrease in reduces , thereby increasing . Under the given condition, is less than when is less than or equal to 0.76. As increases, remains the lower limit, which indicates that the degree of the isothermal heating in CCC always reaches the maximum. As increases, decreases to the lower limit, which indicates that increasing improves the degree of the isothermal heating in IR.
Figure 8c illustrates the relationship of versus . It shows that as decreases, , and remains basically unchanged; decreases first and then tends to remain unchanged; increases first and then tends to be unchanged; increases.
Similarly, both of and increase as , and increase. The effects of and on and are greater than those of and . increases with the increases in and , while decreases with the increases in and . decreases with the increases in and , while increases with the increases in and . It should be noted that when , , , and also do not exist. When , the change of has little effects on and . Within the given range, the changes in and do not exceed 7% and 4%, respectively. In practical design of improving cycle performance, it is suggested to give priority to appropriately increasing and . Then one can choose to increase and , successively. Apart from this, and increase as increases.
4. Optimal Thermal Capacitance Rate Matchings
The of the cycle also affected by the TCRMs. By taking as the optimization objective, TCRMs are optimized. Figure 9a,b illustrates the relationships of and versus and when and . The figures show that both of and increase, and then tend to remain constant with the increase in or . These indicate that there is a set of the optimal and , so that gets the optimal value. Similarly, there is a set of the optimal and , so that gets the optimal value.
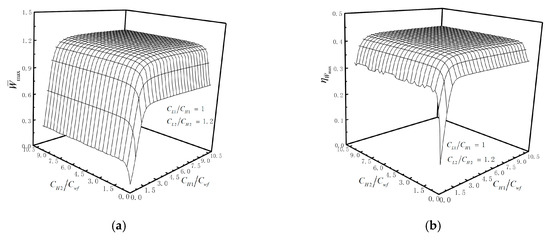
Figure 9.
(a) Relationships of versus and ; (b) relationships of versus and .
Figure 10 illustrates that the effects of on the characteristics of and when and . It shows that when and reach the optimal values, mainly reduces the corresponding , and has little effect on the optimal values of and . Similarly, mainly reduces the corresponding when and reach the optimal values, and has little effects on the optimal values of and .
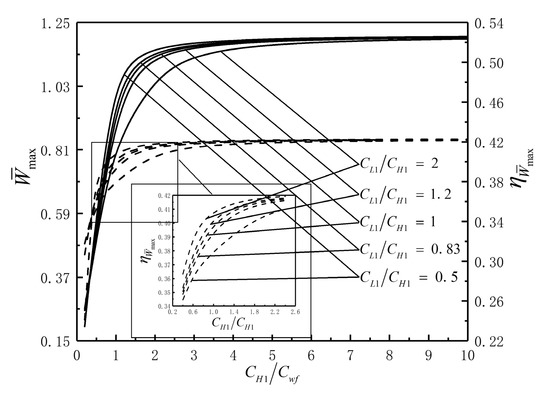
Figure 10.
Effects of on the characteristics of and .
5. Conclusions
Based on the previous established models in [8,62], a modified closed binary Brayton cycle model coupled to VTHRs with two isothermal heating processes and variable isothermal pressure drop ratios is established by using FTT in this paper. The HCDs of the six heat exchangers are optimized, and the effects of , , , , , , , and on the optimal performances are analyzed by taking as the optimization objective. The results show that there is a set of and which makes reach . and have certain linear relationship (, and the correlation coefficient is ), which makes optimal. increases with the increases in , , , and . It should be noted that when or , does not exist. increases first and then remain unchanged with the increases in and . This cycle can effectively improve energy efficiency and reduce emissions of nitrogen oxide and other harmful gases. Additionally, the optimal results can guide the practical designs for the gas turbine plants.
Author Contributions
C.T., L.C., H.F., W.W. and Y.G. collectively finished the manuscript. All authors have read and approved the final manuscript.
Funding
This research was funded the National Natural Science Foundation of China (project number 51779262).
Acknowledgments
The authors wish to thank the reviewers for their careful, unbiased and constructive suggestions, which led to this revised manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| a, b, c, d, e, m, x, y | Intermediate variables |
| C | Thermal capacity rate (kW/K) |
| Cp | Specific heat at constant pressure (kJ/(kg·K)) |
| E | Effectiveness of heat exchanger |
| k | Specific heat ratio |
| M | Mach number |
| N | Number of heat transfer units |
| Heat absorbing rate or heat releasing rate | |
| Rg | Gas constant (kJ/(kg·K)) |
| T | Temperature (K) |
| U | Heat conductance (kW/K) |
| u | Heat conductance distribution |
| W | Power output(kW) |
| Dimensionless power output | |
| Greek symbol | |
| Efficiency | |
| π | Pressure ratio |
| Temperature ratio | |
| Subscripts | |
| bot | Bottoming cycle |
| com | Compressor |
| H | Hot-side heat exchanger |
| L | Cold-side heat exchanger |
| R | Regenerator |
| s | Isentropic |
| t/ta | Converging combustion chamber/isothermal regenerator |
| tot | Total |
| tur | Turbine |
| top | Topping cycle |
| wf | Working fluid |
| 1,2,3,4,5,6,7,1a,2a,3a,4a,5a,2s,5s,2as,5as | State points |
Abbreviations
| CCC | Converging combustion chamber |
| CTR | Constant-temperature reservoir |
| FTT | Finite-time thermodynamics |
| HCD | Heat conductance distribution |
| IR | Isothermal regenerator |
| MCBBC | Modified closed binary Brayton cycle |
| PO | Power output |
| PD | Power density |
| OR | Ordinary regenerator |
| RCC | Regular combustion chamber |
| TCRM | Thermal capacitance rate matching |
| TEF | Thermal efficiency |
| THC | Total heat conductance |
| Tur | Turbine |
| VTHR | Variable-temperature heat reservoir |
| WF | Working fluid |
Appendix A
References
- Invernizzi, C.M. Prospects of mixtures as working fluids in real-gas Brayton cycles. Energies 2017, 10, 1649. [Google Scholar] [CrossRef]
- Wang, J.P.; Wang, J.; Lund, P.D.; Zhu, H.X. Thermal performance analysis of a direct-heated recompression supercritical carbon dioxide Brayton cycle using solar concentrators. Energies 2019, 12, 4358. [Google Scholar] [CrossRef]
- Jaszczur, M.; Dudek, M.; Kolenda, Z. Thermodynamic analysis of advanced gas turbine combined cycle integration with a high-temperature nuclear reactor and cogeneration unit. Energies 2020, 13, 400. [Google Scholar] [CrossRef]
- Vecchiarelli, J.; Kawall, J.G.; Wallace, J.S. Analysis of a concept for increasing the efficiency of a Brayton cycle via isothermal heat addition. Int. J. Energy Res. 1997, 21, 113–127. [Google Scholar] [CrossRef]
- Göktun, S.; Yavuz, H. Thermal efficiency of a regenerative Brayton cycle with isothermal heat addition. Energy Convers. Manag. 1999, 40, 1259–1266. [Google Scholar] [CrossRef]
- Erbay, L.B.; Göktun, S.; Yavuz, H. Optimal design of the regenerative gas turbine engine with isothermal heat addition. Appl. Energy 2001, 68, 249–264. [Google Scholar] [CrossRef]
- Jubeh, N.M. Exergy analysis and second law efficiency of a regenerative Brayton cycle with isothermal heat addition. Entropy 2005, 7, 172–187. [Google Scholar] [CrossRef]
- El-Maksound, R.M.A. Binary Brayton cycle with two isothermal processes. Energy Convers. Manag. 2013, 73, 303–308. [Google Scholar] [CrossRef]
- Qi, W.; Wang, W.H.; Chen, L.G. Exergy analysis and optimization for binary Brayton cycle with two isothermal heat additions. Therm. Turbine 2017, 46, 76–81. (In Chinese) [Google Scholar]
- Andresen, B.; Salamon, P.; Barry, R.S. Thermodynamics in finite time. Phys. Today 1987, 37, 62–70. [Google Scholar] [CrossRef]
- Chen, L.G.; Li, J. Thermodynamic optimization theory for Two-Heat-Reservoir cycles; Science Press: Beijing, China, 2020. [Google Scholar]
- Barranco-Jimenez, M.A.; Ramos-Gayosso, I.; Rosales, M.A.; Angulo-Brown, F. A proposal of ecologic taxes based on thermoeconomic performance of heat engine models. Energies 2009, 2, 1042–1056. [Google Scholar] [CrossRef]
- Chen, C.L.; Ho, C.E.; Yau, H.T. Performance analysis and optimization of a solar powered Stirling engine with heat transfer considerations. Energies 2012, 5, 3573–3585. [Google Scholar] [CrossRef]
- Gonca, G. Energy and exergy analyses of single and double reheat irreversible Rankine cycle. Int. J. Exergy 2015, 18, 402–422. [Google Scholar] [CrossRef]
- Han, Z.H.; Li, P.; Han, X.; Mei, Z.K.; Wang, Z. Thermo-economic performance analysis of a regenerative superheating organic Rankine cycle for waste heat recovery. Energies 2017, 10, 1593. [Google Scholar] [CrossRef]
- White, M.T.; Sayma, A.I. A generalised assessment of working fluids and radial turbines for non-recuperated subcritical organic Rankine cycles. Energies 2018, 11, 800. [Google Scholar] [CrossRef]
- Chen, W.J.; Feng, H.J.; Chen, L.G.; Xia, S.J. Optimal performance characteristics of subcritical simple irreversible organic Rankine cycle. J. Therm. Sci. 2018, 27, 555–562. [Google Scholar] [CrossRef]
- Vittorini, D.; Cipollone, R.; Carapellucci, R. Enhanced performances of ORC-based units for low grade waste heat recovery via evaporator layout optimization. Energy Convers. Manag. 2019, 197, 111874. [Google Scholar] [CrossRef]
- Koo, J.; Oh, S.R.; Choi, Y.U.; Jung, J.H.; Park, K. Optimization of an organic Rankine cycle system for an LNG-powered ship. Energies 2019, 12, 1933. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, W.; Feng, Y.Q.; Wang, X.; Wang, Q.; Liu, Y.Z.; Wang, Y.; Yao, L. Entropy, entransy and exergy analysis of a dual-loop organic Rankine cycle (DORC) using mixture working fluids for engine waste heat recovery. Energies 2020, 13, 1301. [Google Scholar] [CrossRef]
- Feng, H.J.; Chen, W.J.; Chen, L.G.; Tang, W. Power and efficiency optimizations of an irreversible regenerative organic Rankine cycle. Energy Convers. Manag. 2020, 220, 113079. [Google Scholar] [CrossRef]
- Chen, L.G.; Ma, K.; Feng, H.J.; Ge, Y.L. Optimal configuration of a gas expansion process in a piston-type cylinder with generalized convective heat transfer law. Energies 2020, 13, in press. [Google Scholar]
- Chen, L.G.; Meng, F.K.; Sun, F.R. Thermodynamic analyses and optimizations for thermoelectric devices: the state of the arts. Sci. China Technol. Sci. 2016, 59, 442–455. [Google Scholar] [CrossRef]
- Chen, J.L.; Li, K.W.; Liu, C.W.; Li, M.; Lv, Y.C.; Jia, L.; Jiang, S.S. Enhanced efficiency of thermoelectric generator by optimizing mechanical and electrical structures. Energies 2017, 10, 1329. [Google Scholar] [CrossRef]
- Feng, Y.L.; Chen, L.G.; Meng, F.K.; Sun, F.R. Influences of external heat transfer and Thomson effect on performance of TEG-TEC combined thermoelectric device. Sci. China Technol. Sci. 2018, 61, 1600–1610. [Google Scholar] [CrossRef]
- Li, G.; Wang, Z.C.; Wang, F.; Wang, X.Z.; Li, S.B.; Xue, M.S. Experimental and numerical study on the effect of interfacial heat transfer on performance of thermoelectric generators. Energies 2019, 12, 3797. [Google Scholar] [CrossRef]
- Açıkkalp, E.; Chen, L.G.; Ahmadi, M.H. Comparative performance analyses of molten carbonate fuel cell-alkali metal thermal to electric converter and molten carbonate fuel cell –thermoelectric generator hybrid systems. Energy Rep. 2020, 6, 10–16. [Google Scholar] [CrossRef]
- Gonca, G. Exergetic and thermo-ecological performance analysis of a Gas-Mercury combined turbine system (GMCTS). Energy Convers. Manag. 2017, 151, 32–42. [Google Scholar] [CrossRef]
- Lin, J.; Zhang, Z.H.; Zhu, X.Y.; Meng, C.; Li, N.; Chen, J.C.; Zhao, Y.R. Performance evaluation and parametric optimization strategy of a thermocapacitive heat engine to harvest low-grade heat. Energy Convers. Manag. 2019, 184, 40–47. [Google Scholar] [CrossRef]
- Zhu, F.L.; Chen, L.G.; Wang, W.H. Thermodynamic analysis and optimization of irreversible Maisotsenko-Diesel cycle. J. Therm. Sci. 2019, 28, 659–668. [Google Scholar] [CrossRef]
- Dumitrascu, G.; Feidt, M.; Popescu, A.; Grigorean, S. Endoreversible trigeneration cycle design based on finite physical dimensions thermodynamics. Energies 2019, 12, 3165. [Google Scholar]
- Wu, Z.X.; Chen, L.G.; Feng, H.J. Thermodynamic optimization for an endoreversible Dual-Miller cycle (DMC) with finite speed of piston. Entropy 2018, 20, 165. [Google Scholar] [CrossRef]
- You, J.; Chen, L.G.; Wu, Z.X.; Sun, F.R. Thermodynamic performance of Dual-Miller cycle (DMC) with polytropic processes based on power output, thermal efficiency and ecological function. Sci. China Technol. Sci. 2018, 61, 453–463. [Google Scholar] [CrossRef]
- Abedinnezhad, S.; Ahmadi, M.H.; Pourkiaei, S.M.; Pourfayaz, F.; Mosavi, A.; Feidt, M.; Shamshirband, S. Thermodynamic assessment and multi-objective optimization of performance of irreversible Dual-Miller cycle. Energies 2019, 12, 4000. [Google Scholar] [CrossRef]
- Ding, Z.M.; Ge, Y.L.; Chen, L.G.; Feng, H.J.; Xia, S.J. Optimal performance regions of Feynman’s ratchet engine with different optimization criteria. J. Non-Equilib. Thermodyn. 2020, 45, 191–207. [Google Scholar] [CrossRef]
- Feng, H.J.; Qin, W.X.; Chen, L.G.; Cai, C.G.; Ge, Y.L.; Xia, S.J. Power output, thermal efficiency and exergy-based ecological performance optimizations of an irreversible KCS-34 coupled to variable temperature heat reservoirs. Energy Convers. Manag. 2020, 205, 112424. [Google Scholar] [CrossRef]
- Chen, L.G.; Sun, F.R.; Wu, C. Performance analysis of an irreversible Brayton heat engine. J. Inst. Energy 1997, 70, 2–8. [Google Scholar]
- Sadatsakkak, S.A.; Ahmadi, M.H.; Ahmadi, M.A. Thermodynamic and thermo-economic analysis and optimization of an irreversible regenerative closed Brayton cycle. Energy Convers. Manag. 2015, 94, 124–129. [Google Scholar] [CrossRef]
- Naserian, M.M.; Farahat, S.; Sarhaddi, F. Finite time exergy analysis and multi-objective ecological optimization of a regenerative Brayton cycle considering the impact of flow rate variations. Energy Convers. Manag. 2015, 103, 790–800. [Google Scholar] [CrossRef]
- Jansen, E.; Bello-Ochende, T.; Meyer, J.P. Integrated solar thermal Brayton cycles with either one or two regenerative heat exchangers for maximum power output. Energy 2015, 86, 737–748. [Google Scholar] [CrossRef]
- Sánchez-Orgaz, S.; Medina, A.; Calvo Hernández, A. Thermodynamic model and optimization of a multi-step irreversible Brayton cycle. Energy Convers. Manag. 2010, 51, 2134–2143. [Google Scholar] [CrossRef]
- Sanchez-Orgaz, S.; Pedemonte, M.; Ezzatti, P.; Curto-Risso, P.L.; Medina, A.; Calvo Hernández, A. Multi-objective optimization of a multi-step solar-driven Brayton plant. Energy Convers. Manag. 2015, 99, 346–358. [Google Scholar] [CrossRef]
- Chen, L.G.; Feng, H.J.; Ge, Y.L. Power and efficiency optimization for open combined regenerative Brayton and inverse Brayton cycles with regeneration before the inverse cycle. Entropy 2020, 22, 677. [Google Scholar] [CrossRef]
- Açıkkalp, E. Performance analysis of irreversible solid oxide fuel cell–Brayton heat engine with ecological based thermo-environmental criterion. Energy Convers. Manag. 2017, 148, 279–286. [Google Scholar] [CrossRef]
- Zhu, F.L.; Chen, L.G.; Wang, W.H. Thermodynamic analysis of an irreversible Maisotsenko reciprocating Brayton cycle. Entropy 2018, 20, 167. [Google Scholar] [CrossRef]
- Chen, L.G.; Shen, J.F.; Ge, Y.L.; Wu, Z.X.; Wang, W.H.; Zhu, F.L.; Feng, H.J. Power and efficiency optimization of open Maisotsenko-Brayton cycle and performance comparison with traditional open regenerated Brayton cycle. Energy Convers. Manag. 2020, 217, 113001. [Google Scholar] [CrossRef]
- Feng, H.J.; Tao, G.S.; Tang, C.Q.; Ge, Y.L.; Chen, L.G.; Xia, S.J. Exergoeconomic performance optimization for a regenerative gas turbine closed-cycle heat and power cogeneration plant. Energy Rep. 2019, 5, 1525–1531. [Google Scholar] [CrossRef]
- Chen, L.G.; Yang, B.; Feng, H.J.; Ge, Y.L.; Xia, S.J. Performance optimization of an open simple-cycle gas turbine combined cooling, heating and power plant driven by basic oxygen furnace gas in China’s steelmaking plants. Energy 2020, 203, 117791. [Google Scholar] [CrossRef]
- Kaushik, S.C.; Tyagi, S.K.; Singhal, M.K. Parametric study of an irreversible regenerative Brayton cycle with isothermal heat addition. Energy Convers. Manag. 2003, 44, 2013–2025. [Google Scholar] [CrossRef]
- Tyagi, S.K.; Kaushik, S.C.; Tiwari, V. Ecological optimization and parametric study of an irreversible regenerative modified Brayton cycle with isothermal heat addition. Entropy 2003, 5, 377–390. [Google Scholar] [CrossRef]
- Tyagi, S.K.; Chen, J.C. Performance evaluation of an irreversible regenerative modified Brayton heat engine based on the thermoeconomic criterion. Int. J. Power Energy Syst. 2006, 26, 66–74. [Google Scholar] [CrossRef]
- Kumar, R.; Kaushik, S.C.; Kumar, R. Power optimization of an irreversible regenerative Brayton cycle with isothermal heat addition. J. Therm. Eng. 2015, 1, 279–286. [Google Scholar] [CrossRef]
- Tyagi, S.K.; Chen, J.; Kaushik, S.C. Optimum criteria based on the ecological function of an irreversible intercooled regenerative modified Brayton cycle. Int. J. Exergy 2005, 2, 90–107. [Google Scholar] [CrossRef]
- Tyagi, S.K.; Wang, S.; Kaushik, S.C. Irreversible modified complex Brayton cycle under maximum economic condition. Indian J. Pure Appl. Phys. 2006, 44, 592–601. [Google Scholar]
- Tyagi, S.K.; Chen, J.; Kaushik, S.C.; Wu, C. Effects of intercooling on the performance of an irreversible regenerative modified Brayton cycle. Int. J. Power Energy Syst. 2007, 27, 256–264. [Google Scholar] [CrossRef]
- Tyagi, S.K.; Wang, S.; Park, S.R. Performance criteria on different pressure ratios of an irreversible modified complex Brayton cycle. Indian J. Pure Appl. Phys. 2008, 46, 565–574. [Google Scholar]
- Wang, J.H.; Chen, L.G.; Ge, Y.L.; Sun, F.R. Power and power density analyzes of an endoreversible modified variable-temperature reservoir Brayton cycle with isothermal heat addition. Int. J. Low-Carbon Technol. 2016, 11, 42–53. [Google Scholar] [CrossRef][Green Version]
- Wang, J.H.; Chen, L.G.; Ge, Y.L.; Sun, F.R. Ecological performance analysis of an endoreversible modified Brayton cycle. Int. J. Sustain. Energy 2014, 33, 619–634. [Google Scholar] [CrossRef]
- Tang, C.Q.; Chen, L.G.; Wang, W.H.; Feng, H.J.; Xia, S.J. Performance optimization of the endoreversible simple MCBC coupled to variable-temperature reservoirs based on NSGA-II Algorithm. Power Gener. Technol. 2020. in press (In Chinese) [Google Scholar]
- Tang, C.Q.; Feng, H.J.; Chen, L.G.; Wang, W.H. Power density analysis and multi-objective optimization for a modified endoreversible simple closed Brayton cycle with one isothermal heating process. Energy Rep. 2020, 6. in press. [Google Scholar]
- Arora, R.; Kaushik, S.C.; Kumar, R.; Arora, R. Soft computing based multi-objective optimization of Brayton cycle power plant with isothermal heat addition using evolutionary algorithm and decision making. Appl. Soft Comput. 2016, 46, 267–283. [Google Scholar] [CrossRef]
- Qi, W.; Wang, W.H.; Chen, L.G. Power and efficiency performance analyses for a closed endoreversible binary Brayton cycle with two isothermal processes. Therm. Sci. Eng. Prog. 2018, 7, 131–137. [Google Scholar] [CrossRef]
- Chen, L.G.; Zheng, J.L.; Sun, F.R.; Wu, C. Performance comparison of an irreversible closed variable-temperature heat reservoir Brayton cycle under maximum power density and maximum power conditions. Proc. IMechE Part A J. Power Energy 2005, 219, 559–566. [Google Scholar] [CrossRef]
- Chen, L.G.; Zheng, J.L.; Sun, F.R.; Wu, C. Performance comparison of an endoreversible closed variable temperature heat reservoir Brayton cycle under maximum power density and maximum power conditions. Energy Convers. Manag. 2002, 43, 33–43. [Google Scholar] [CrossRef]
- Cheng, C.Y.; Chen, C.K. Ecological optimization of an endoreversible Brayton cycle. Energy Convers. Manag. 1998, 39, 33–34. [Google Scholar] [CrossRef]
- Zheng, J.L.; Chen, L.G.; Sun, F.R. Power density analysis of an endoreversible closed Brayton cycle. Int. J. Ambient Energy 2001, 22, 95–104. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).