Standard, Point of Use, and Extended Energy Return on Energy Invested (EROI) from Comprehensive Material Requirements of Present Global Wind, Solar, and Hydro Power Technologies
Abstract
1. Introduction
- The energy surplus generated by the different energy sources available to society for discretionary uses (from growing food to family support, as well as education, health, and cultural development [13]). The most popular indicator to measure the ratio of energy surplus with relation to the required energy investments is the energy return on energy invested (EROI), i.e., the ratio of the energy delivered and the energy consumed to deliver that energy in a given time, with very abundant literature focusing both at technology and system level at different geographical scales (see e.g., [3,14,15,16,17,18,19,20,21,22,23]).
2. Overview of EROI Definitions and Their Implications for Society
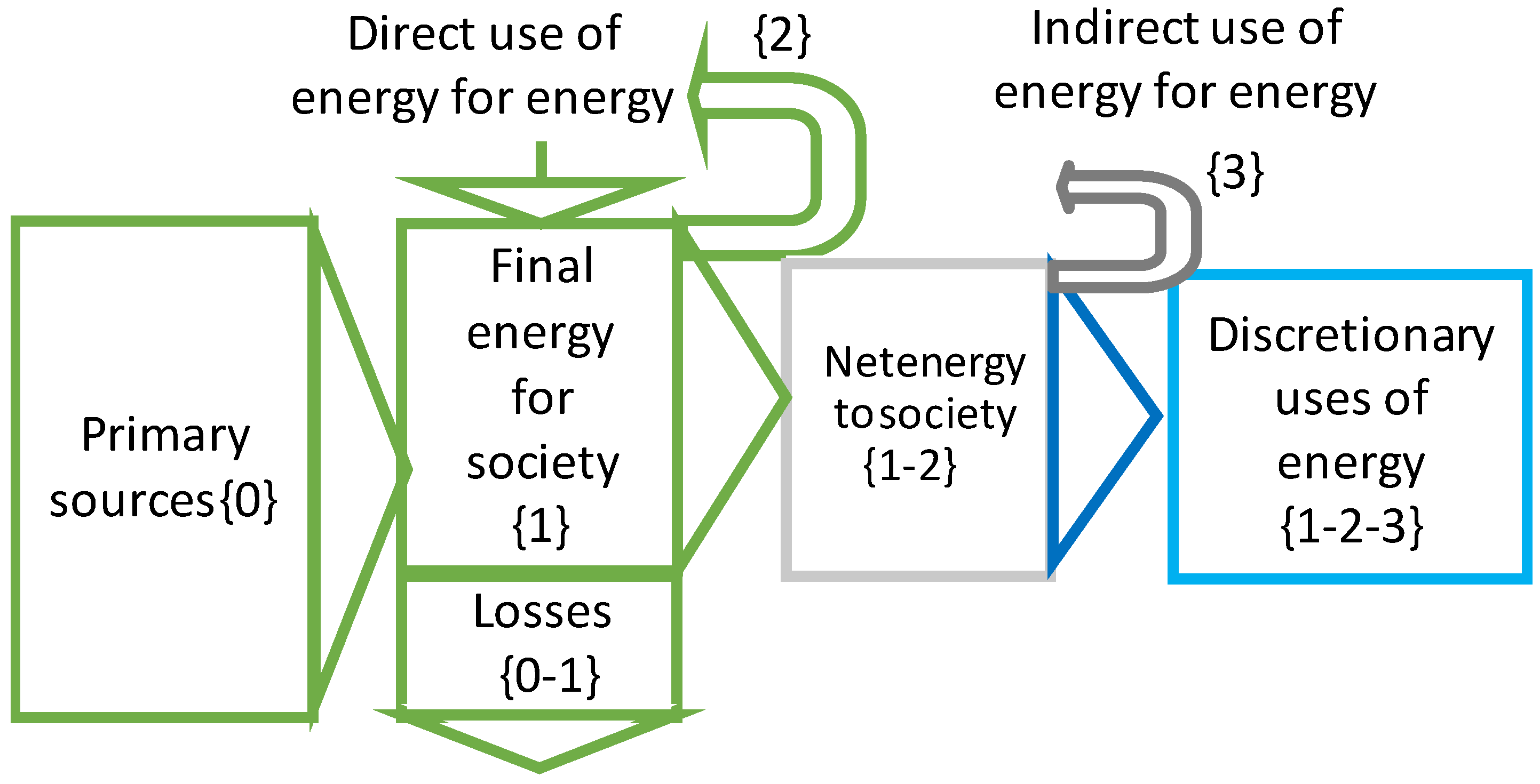
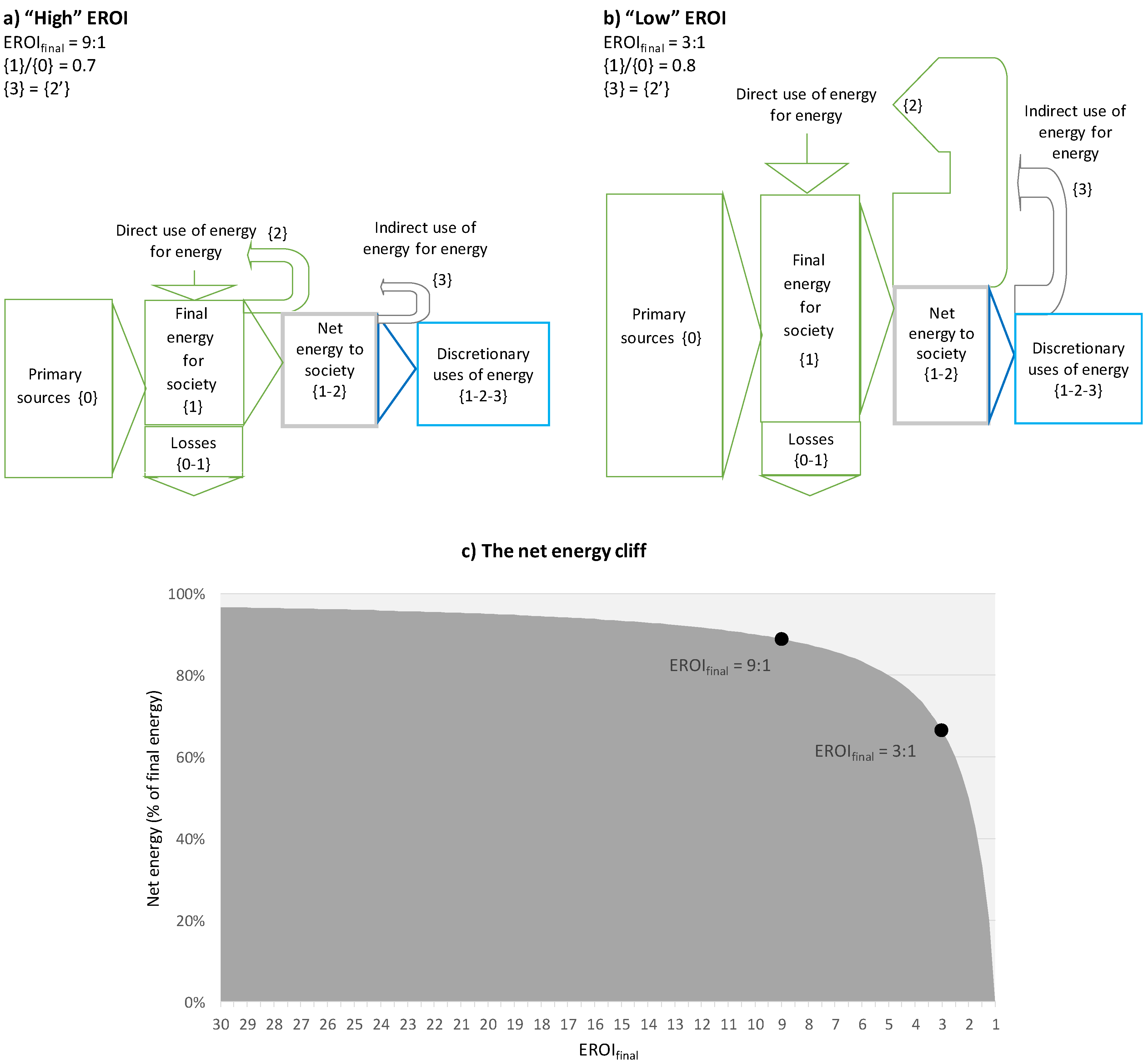
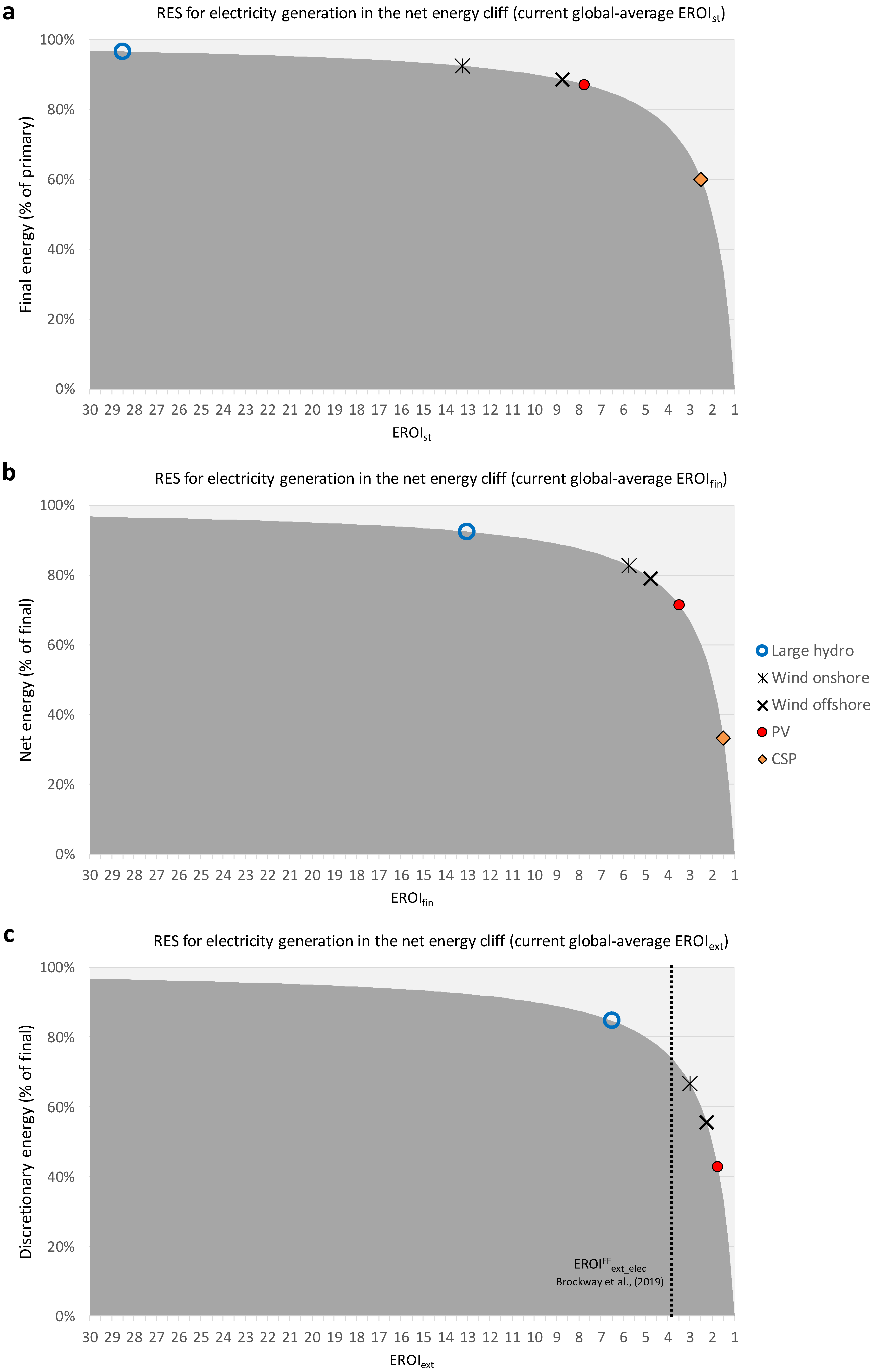
- A low EROIext means that the energy metabolism ({0}, {1}, {2}, and {3}) represents a substantial part of the economy. Since each energy flux requires capital and workers, in that case the society allocates most parts of its capital and workers to the energy system, and not the discretionary uses. Therefore, a much lower diversity of jobs and enterprises can be attained in these conditions and the result is a much simpler society (as e.g., in pre-industrial times with most workers in the primary sector and very few in the tertiary sectors). In fact, there is an “EROI minimum”, below which a complex society tends to disappear or evolve towards simpler organizational forms [38,39,58]. In fact, when the EROI approaches 1:1, the capacity installed (and, hence, the primary energy required) tends to infinity if the same level of net energy is to be maintained (see Equations (9)–(11) in Capellán-Pérez et al. [59]).
- The environmental impact depends on factors, such as the type of the energy resource (e.g., pollution and climate change caused by FFs’ combustion) and the size of the energy system (e.g., mining impacts, material residues, land-use, co-optation of fluxes of the biosphere—wind, biomass, etc.). Hence, for the same discretionary uses of energy, a lower EROI means larger environmental impacts and the need to divert a larger share of the final energy from discretionary uses to “defensive” costs [60].
- Societies require a “security buffer” (i.e., buy “insurance”), to be able to overcome unexpected events, such as accidents or natural disasters (e.g., earthquakes).
- Human inequality makes the metabolic system less efficient (in the real world, part of the discretionary energy uses will always be metabolically “useless”, such as luxuries of rich or corrupted people), so again, the supply of “useful” discretionary uses (food, domestic, education, etc.) requires an EROIext >1.
- There is a critical additional reason in the context of the energy transition given that it will require the temporary fast growth of RES sources and the dismantling of the FF they replace. In this situation, the EROI of the full system will temporarily be well below the weighted average of the static EROI of the technologies and their supporting systems (e.g., grids, storage, etc.), as shown in [3]. Noteworthy, in a society where population and energy per capita are growing, this phenomenon of “energy trap” will be aggravated.
3. Methodology
3.1. Selection of Representative Technologies
3.2. EROI Computation as a Function of the System Boundaries
3.2.1. EROI Expressions
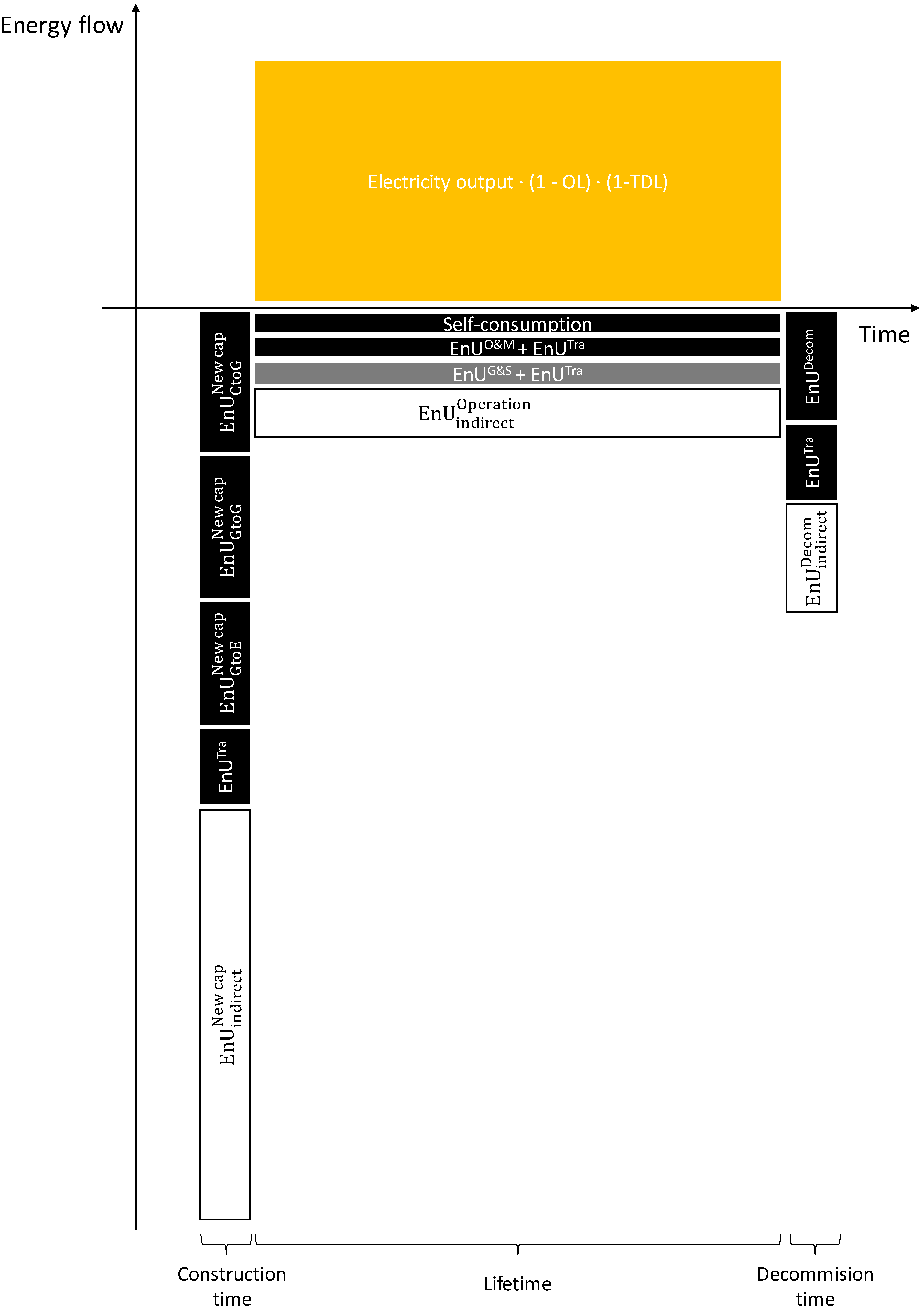
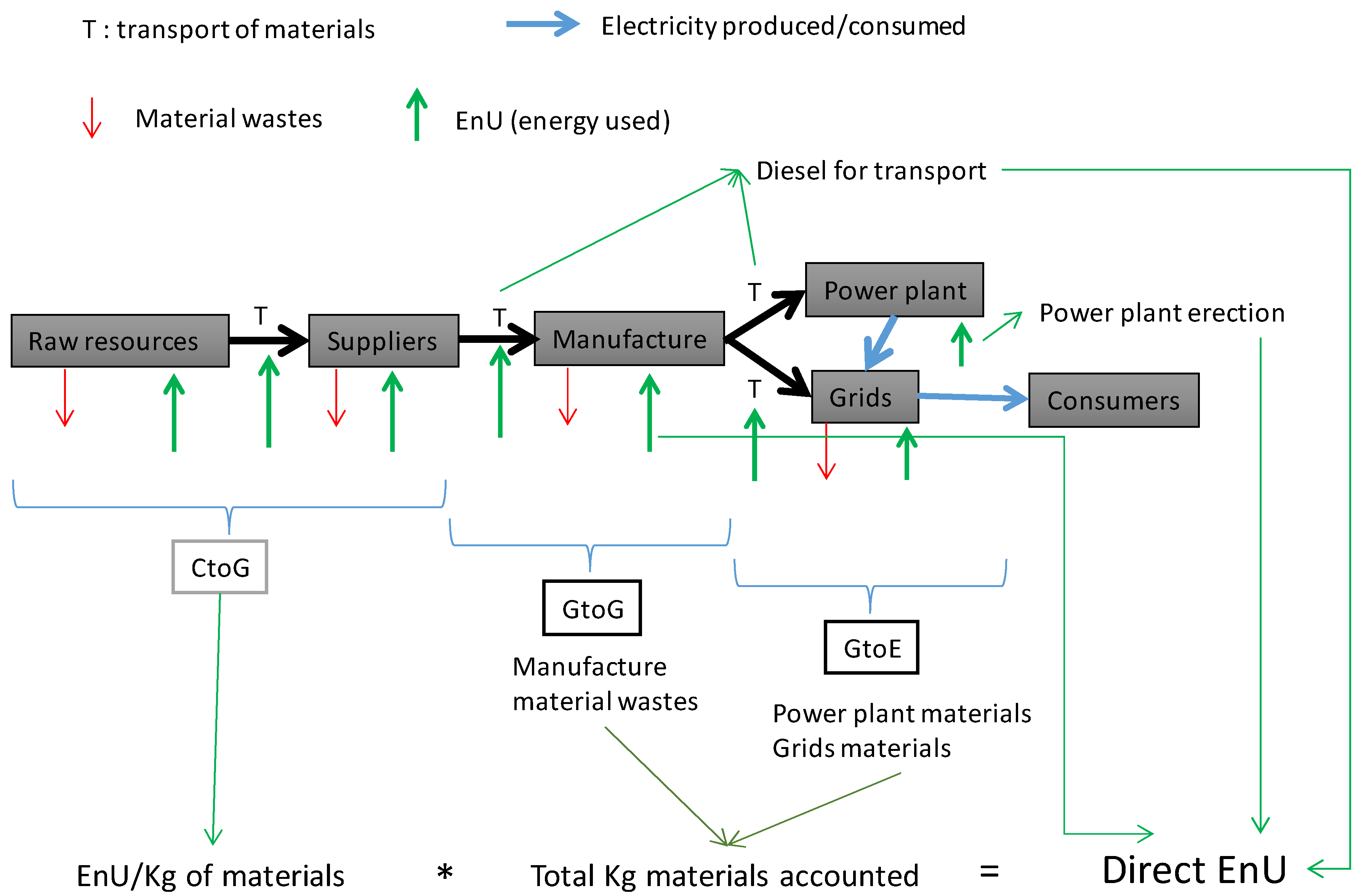
3.2.2. Computation of Direct EnUs from Material Requirements
3.2.3. Estimation of indirect EnUs for EROIext
3.3. Material Requirements and Performance Factors Per Technology
4. Results
4.1. Current Global EROI of RES Technologies
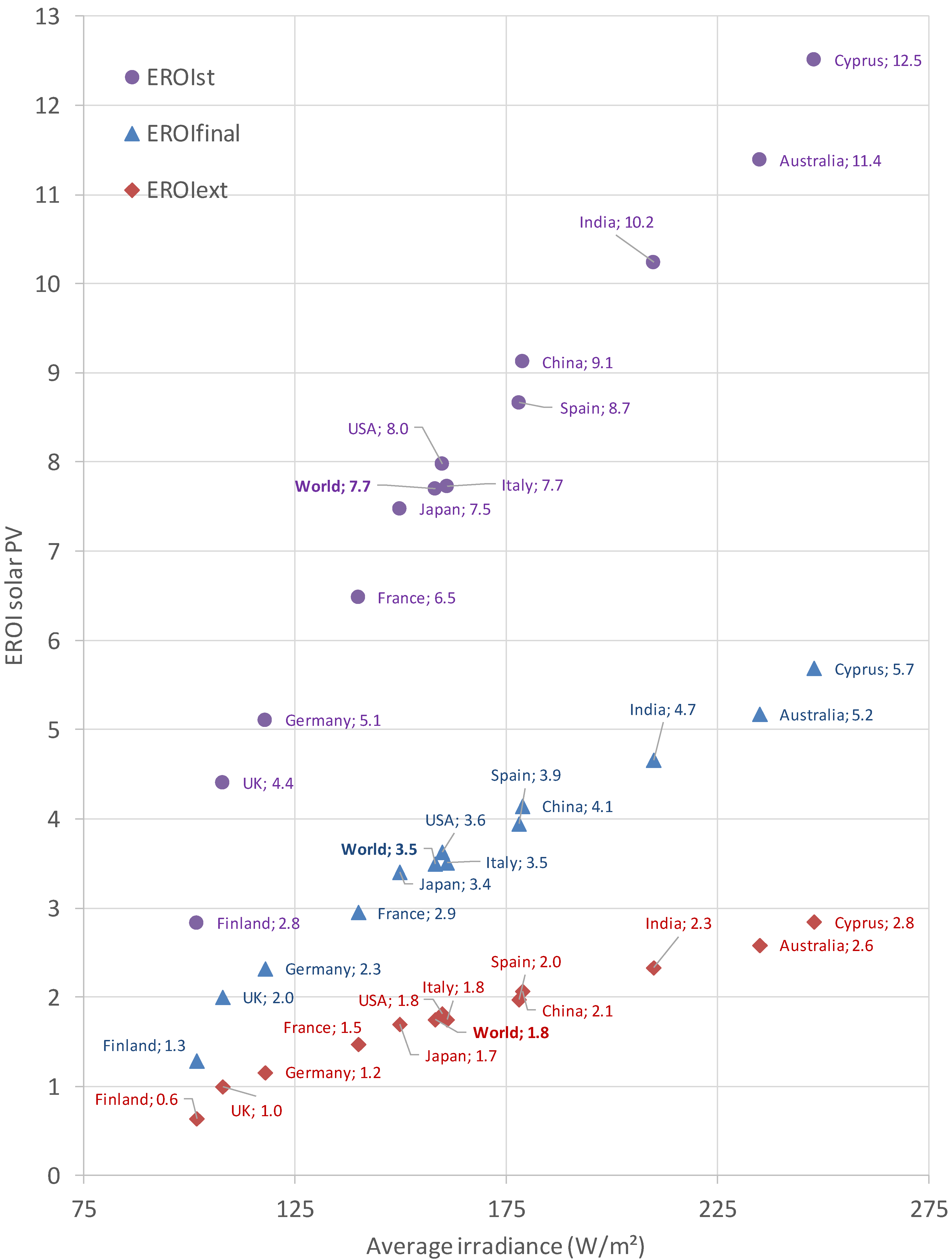
4.2. Geographically-Dependent EROI: Case Study for Solar PV
- average solar irradiance per country estimated applying a Geographical Information System (GIS);
- a reduction of the average performance ratio over the park’s life cycle due to higher temperature in the tropics;
- a more efficient use of the space in countries closer to the equator, which reduces the energy investments in the phases of cement/concrete, iron/steel low, gravel/roads, and site works (which approximately correspond to 20% of the EnUNew cap of solar PV);
- the same EROI for big solar on land and rooftop for each country (see Section 4.1).
4.3. Comparison of the EROIst of RES Technologies with the Literature
5. Discussion
5.1. On the Role of Future Technological Change
- Additional energy investments and losses related with variability management of RES such as storage capacity (PHS, electric batteries, hydrogen, etc.), power-to-X, curtailment, and additional grids. The first three factors will tend to lower the EROI of the system due to the Energy Stored On energy Invested (ESOI) of the storage device, the increase of the transformation phases with associated transformation losses, and/or the diminishing effective CF of power plant being electricity curtailed. The fourth factor includes the substantial adaptation and expansion of the existing grids to cope with connecting the new RES power plants as well as helping to evacuate power when unevenly produced and demanded.
- Thermodynamic limits to the continuous reduction of required energy investments (e.g., related with limits to substitution).
- Limits to recycling rates (other than thermodynamic): as aforementioned, most of the machining processes require some virgin or pure material because the recycled scrap cannot be fully reused [90].
- Thermodynamic limits from the side of generation. For example, the fact that there are absolute limits to the height of rotors for wind or the Benz law (modern large wind turbines already achieve peak performance coefficients in the range of 45–50%, which is pretty close to the limit of 59.26% [94])), or the limits in the conversion from sunlight to electricity, such as the Schokley–Queisser limit for single-junction solar cells. Although the latter limit could be overcome with multi-junction technologies, the key general question is how realistic it is, considering that the most sophisticated technologies—also related with the previous point—are really scalable at a significant level compared with total energy demand, or if, in the future, they will rather remain marginal.
5.2. Implications of Taking into Account the EROI for the Transition to RES
- Technological improvement of RES (and in general any factor going in the direction of EROI max in the uncertainty analysis reported in Appendix C).
- The likely large scale deployment of RES due to the enforcement of sustainability policies will (1) tend to replace FFs in the energy mix, and (2) drive an array of factors overviewed in the previous Section 5.1, which nowadays are negligible, but will become increasingly important as the renewables progressively scale-up at large levels and gain a substantial share in the energy mix. These factors will put a downward pressure on future EROI.
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. EnUs
Appendix B. Material Requirements and Performance Factors Per Technology Details
- High power lines and transformers: lifetime of 50 years (although for some specific components such as concrete, iron/steel and PVC we assume a longer lifetime of 100 years). EUROELECTRIC [149] gives a total of aerial and underground 0.32 km/MW for Europe and NREL [150] a total of 0.725 km/MW for USA. We use 0.4 km/MW of 150 KVA for aerial lines and 0.04 km/MW for underground lines. For transformers and other devices as disconnectors and circuit breakers: lifetime 30 years. We estimate the equivalence of 7 transformers of 315 KVA/MW from Bumby et al., [151] for materials and lifetimes, Jorge et al. [152,153] for lengths, lifetimes and materials, and van Tichelen and Mudgal [154] for the number of transformers and other devices such as disconnectors and circuit breakers.
- Low/medium power lines: we use data for Europe [149] to estimate the km/MW for aerial and underground lines (50% each), which gives slightly more than 5 km/MW respectively. For USA, the total km/MW are similar [155] although there are a lower relative number of underground lines (25% in 2012 [156]). Bumby et al., [151] give a lifetime of less than 50 years but conservatively we use the same lifetimes than in high power lines.
Appendix C. Sensitivity Analysis
| Technologies | - | Wind | Solar | Large Hydro | |||
|---|---|---|---|---|---|---|---|
| Parameter/ Phase | Base Case | min | max | min | max | min | max |
| CtoG + EtoG | 100% | x1.1 | x1 | x1.1 | x1 | x1.1 | x1 |
| GtoG | y% | (y + 10)% | (y − 5)% | (y + 10)% | (y − 5)% | x1.2 | x1 |
| Annual O&M | 100% | x1.2 | x1 | x1.2 | x1 | x1 | x1 |
| Decommission (Decom) | 10% of Construction phase | 15% | 5% | 15% | 5% | 15% | 5% |
| Transport of materials (Tra) | 100% | x1.25 | x.5 | x1.25 | x.5 | x1.25 | x.5 |
| Life time of the power plant (L) | y years | Y − 2.5 | y + 5 | y − 2.5 | y + 5 | y − 15 | y + 15 |
| Grids (G&S) | 100% | x1.5 | x1 | x1.5 | x1 | x1 | x1 |
| Indirect EnU | 100% | x1.5 | x1 | x1.5 | x1 | x1 | x1 |
Appendix D. Comparison with FF adjusting Brockway et al. (2019) results’
Appendix D.1. Factors Tending to Overestimate the Reported EROIext of FF in Brockway et al. (2019)
- No computation of energy investments related with the construction of energy facilities. As Brockway et al. [16] themselves point out (page 620): “our EROI estimates do not include any energy invested in the production of energy associated with the fixed capital equipment in the energy production [and transportation] industries… [our EnU estimates] are very likely to be underestimated and should be considered as lower-bound values…”.
- No computation of the decommissioning phase.
- Not fully capturing the energy investments associated to the grids.
Appendix D.2. Factors Tending to Underestimate the Reported EROIext of FF in Brockway et al. (2019)
- No computation of heat in CHP plants: when the EROI of FF power plants is computed, it should also be taken into account that FF power plants can also generate commercial heat.
- Not taking into account that the “own use” (embodied energy in the denominator of the EROI) dedicated to final “non-energy uses” of the FF primary sources (plastics, lubricants, etc.) is not attributable to the energy system because it is not energy for energy but energy for matter. Plastics, lubricants, etc., are used by the entire industry and the rest of the economy and even for the RES industry, their embodied energy use must be attributed case by case. The quantity of “non-energy uses” that reenters the FF economy is minute relative to the entire economy, and must be discounted not added. Moreover, some of this matter (e.g., plastics) could even reenter the energy system at the end of their lifetime (e.g., electricity from “waste”).
- Not all of the FF own-energy use can be attributed to producing FF energy: following Table 2 in [16], the direct EnU includes all the FF own-energy use directly used by the respective industries of coal, gas, and oil; hence, in the extraction, refining and conversion to FF-derived final fuels. However, a significant part of FF are used to produce energy that are used by other energy technologies, such as the diesel used for the construction of a RES power plant that must be attributed to the RES power plant and also their embodied energy in the refinery and the oil extraction, etc. Hence, the parameters shown in Tables 2 and 3 of [16] seem overestimated.
| Parameter/Performance Factor | Value | |
|---|---|---|
| 1 | Capacity factor (CF) | 0.45 |
| 2 | Lifetime (L) | 45 years |
| 3 | Operational Losses (OL) | 5% |
| 4 | Transmission and Distribution Losses (TDL) | 9.2% |
| 5 | Final electricity output (1 MW power plant capacity) | 55.09 × 107 MJ/MW |
| 6 | EnU in Brockway et al. (O&M direct + indirect) | 13.77 × 107 MJ/MW |
| 7 | EnU in O&M of grids (direct + indirect) | 4.14 × 107 MJ/MW |
| 8 | EnU in construction + decommissioning phases (direct + indirect) | 1.38 × 107 MJ/MW |
| 9 | Commercial heat output (corrected for quality) | 6.25 × 107 MJ/MW |
| 10 | Own use to non-energy uses (plastics, etc.) | 1.38 × 107 MJ/MW |
| 11 | Own use dedicated to non-FF energy sources | 2.18 × 107 MJ/MW |
- OL: rough own estimation based in [74] from the average losses of fossil fuel plants.
- TDL: own results, see main text.
- Final electricity output: assuming the former parameters and applying eq. 5 of the main text {= 31.54 × 106 × 0.45 × 45 × (1−0.05) × (1−0.092)} for 1 MW power plant during their lifetime.
- EnU in Brockway et al. (O&M direct and indirect): Following Brockway et al. [16] results, the EROIext of FF power plants is 4:1; therefore, assuming the final electricity output (5th point here) this translates to 13.77 × 107 MJ/MW.
- EnU in O&M of grids: in the main text we have estimated 1.15 × 107 MJ/MW for the direct O&M of grids during 25 years, as the lifetime of the FF power plants is 45 years this amounts to 45/25 times more direct costs. Following our methodology, we have assigned the same embodied costs for the indirect costs; therefore, the total EnU in O&M of grids will be: 2 × 1.15 × 107 × 45/25.
- EnU in C + D phases: we estimate for the direct costs a 5% of the total EnU accounted in Brockway et al., [16]. Kis et al. [74] results for FF power plants are less than 5% for this two phases over the total in their direct embodied energy (LCA based). Assuming another 5% for indirect costs, we arrive to a 10% of the denominator in the O&M phase accounting of Brockway et al. methodology. Then we take 10% of this number to account for this C + D phases.
- Commercial heat output: 15% is the commercial heat from power plants relative to their electricity output at plant phases (estimation based in the IEA Sankey in 2015 [72]). This output could be corrected by a quality factor, following the criteria of “final to primary” factor “g” as the “system quality of the energy mix”. We multiply this heat output by the factor g (=0.688) that we have used in our methodology (see main text). This result to 6.25 × 107 MJ/MW of “corrected” final energy output due to commercial heat (at plant phase the electricity output is 6.06 × 108 MJ/MW, then 15% of that number multiplied by “g” is the “heat” output to be added to the electricity output).
- Own use to non-energy uses: the “own use” of the power plants that is inverted to “non-energy uses” and not to the energy sector (embodied energy to fabricate materials, such as plastics, lubricants, asphalt, fertilizers, etc., which are products of the FF industry, must not be assigned to the denominator of the FF power plants, other than the plastics, lubricants, etc., that are used in this industry, which will be minute in comparison with the entire economy). We estimate that at least 9.1% of the “own use” of the denominator of the EROIext is not an embodied energy attributable to the FF because this is the proportion of the non-energy uses relative to the final energy (IEA Sankey 2017 data [72]). In fact, the fabrication of most “non-energy uses” are much more energy intensive that the oil to diesel in the refinery process (e.g., plastics, fertilizers). Moreover, some of the material outputs of FF economy at the end of their lifetime could reenter the energy economy in the form of “waste power plants”. Furthermore, the economy of FF is using, indirectly, the high-embodied energy in the chemical bonds of FF that is incorporated in the material products; a hypothetical substitution of these products (plastics, lubricants, fertilizers, etc.) will likely need more energy to fabricate alternatives, and less energy for discretionary uses of energy will have. This difficults the comparison between FF and RES power plants at this extended and system level vision. We take 10% of the denominator of Brockway et al. [16] (10% of 1.38 × 108 MJ) as a lower bound guess.
- Own use of FF dedicated to other non FF energy sources: the relative proportion of the electricity own use (Tables 2 and 3 from Brockway et al. [16]) that is used not for the FF power plants but for the EnU of the rest of the power plants (nuclear, RES). This amount must be attributable to the rest of energy sources and not to fossil fuels (in the EnU of RES of our main text are attributed to RES and not to FF). Non-FF sources of energy account for 15.8% of the primary energy (non-energy uses discounted) following the Sankey 2017 of IEA [72] (in final terms assuming only a 33% efficiency for biopower and nuclear the result is 20.1% for the contribution of non FF). This 15.8% must be attributed to these non-FF sources. Then the denominator of Brockway et al. [16] is overestimated by around 0.158 × 1.38 × 108 MJ/MW.
= (55.09 + 6.25)/(13.77 + 4.14 + 1.38 − 1.38 − 2.18) = 3.9:1.
Appendix E. Comparison of Results with Capellán-Pérez et al. (2019)
| EROIst | Wind onshore | Wind offshore | Solar PV | Solar CSP |
|---|---|---|---|---|
| From [3] | 16.0 | 9.8 | 8.2 | 3.7 |
| Adaptation of [3]’s results to the EROI definition and performance factors used in this work | 16.2 | 12.2 | 9.6 | 3.3 |
| Present work (see Table 3) | 13.2 | 8.7 | 7.8 | 2.6 |
Abbreviations
| BAU | Business as usual scenarios |
| CF | Capacity factor |
| CSP | Concentrated Solar Power |
| EnU | Energy used by the energy system to deliver energy |
| EROI | Energy Return On energy Invested |
| ESOI | Energy Stored On energy Invested |
| FF | Fossil fuels |
| g | quality correction factor of energy |
| GG | Green Growth scenarios |
| HVDCs | High-voltage, direct current |
| Hydro | Hydroelectric power plants |
| IEA | International Energy Agency |
| IO | Input–Output |
| LCA | Life-cycle analysis |
| O&M | Operation and maintenance |
| OL | Operational Losses |
| PV | Photovoltaic |
| RC | Recycled content ratio |
| RES | renewable energy sources |
| SC | Electricity self-consumption of the facility |
| TDL | Transmission and distribution losses |
References
- IPCC. Global Warming of 1.5 °C. Intergovernmental Panel on Climate Change (IPCC). Available online: http://www.ipcc.ch/report/sr15/ (accessed on 9 June 2020).
- IPCC. Climate Change 2014: Mitigation of Climate Change; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Capellán-Pérez, I.; de Castro, C.; Miguel González, L.J. Dynamic Energy Return on Energy Investment (EROI) and material requirements in scenarios of global transition to renewable energies. Energy Strategy Rev. 2019, 26, 100399. [Google Scholar] [CrossRef]
- de Koning, A.; Kleijn, R.; Huppes, G.; Sprecher, B.; van Engelen, G.; Tukker, A. Metal supply constraints for a low-carbon economy? Resour. Conserv. Recycl. 2018, 129, 202–208. [Google Scholar] [CrossRef]
- Tokimatsu, K.; Wachtmeister, H.; McLellan, B.; Davidsson, S.; Murakami, S.; Höök, M.; Yasuoka, R.; Nishio, M. Energy modeling approach to the global energy-mineral nexus: A first look at metal requirements and the 2 °C target. Appl. Energy 2017, 207, 494–509. [Google Scholar] [CrossRef]
- Valero, A.; Valero, A.; Calvo, G.; Ortego, A. Material bottlenecks in the future development of green technologies. Renew. Sustain. Energy Rev. 2018, 93, 178–200. [Google Scholar] [CrossRef]
- Campbell, C.J.; Laherrère, J. The end of cheap oil. Sci. Am. 1998, 278, 60–65. [Google Scholar] [CrossRef]
- Capellán-Pérez, I.; Mediavilla, M.; de Castro, C.; Carpintero, Ó.; Miguel, L.J. Fossil fuel depletion and socio-economic scenarios: An integrated approach. Energy 2014, 77, 641–666. [Google Scholar] [CrossRef]
- Creutzig, F.; Ravindranath, N.H.; Berndes, G.; Bolwig, S.; Bright, R.; Cherubini, F.; Chum, H.; Corbera, E.; Delucchi, M.; Faaij, A.; et al. Bioenergy and climate change mitigation: An assessment. GCB Bioenergy 2014. [Google Scholar] [CrossRef]
- Deng, Y.Y.; Haigh, M.; Pouwels, W.; Ramaekers, L.; Brandsma, R.; Schimschar, S.; Grözinger, J.; de Jager, D. Quantifying a realistic, worldwide wind and solar electricity supply. Glob. Environ. Chang. 2015, 31, 239–252. [Google Scholar] [CrossRef]
- IPCC. Special Report on Renewable Energy Sources and Climate Change Mitigation; Edenhofer, O., Pichs-Madruga, R., Sokona, Y., Seyboth, K., Matschoss, P., Kadner, S., Zwickel, T., Eickemeier, P., Hansen, G., Schlömer, S., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2011. [Google Scholar]
- Moriarty, P.; Honnery, D. What is the global potential for renewable energy? Renew. Sustain. Energy Rev. 2012, 16, 244–252. [Google Scholar] [CrossRef]
- Lambert, J.G.; Hall, C.A.S.; Balogh, S.; Gupta, A.; Arnold, M. Energy, EROI and quality of life. Energy Policy 2014, 64, 153–167. [Google Scholar] [CrossRef]
- Bhandari, K.P.; Collier, J.M.; Ellingson, R.J.; Apul, D.S. Energy payback time (EPBT) and energy return on energy invested (EROI) of solar photovoltaic systems: A systematic review and meta-analysis. Renew. Sustain. Energy Rev. 2015, 47, 133–141. [Google Scholar] [CrossRef]
- Brand-Correa, L.I.; Brockway, P.E.; Copeland, C.L.; Foxon, T.J.; Owen, A.; Taylor, P.G. Developing an Input-Output Based Method to Estimate a National-Level Energy Return on Investment (EROI). Energies 2017, 10, 534. [Google Scholar] [CrossRef]
- Brockway, P.E.; Owen, A.; Brand-Correa, L.I.; Hardt, L. Estimation of global final-stage energy-return-on-investment for fossil fuels with comparison to renewable energy sources. Nat. Energy 2019, 4, 612. [Google Scholar] [CrossRef]
- Dale, M. A Comparative Analysis of Energy Costs of Photovoltaic, Solar Thermal, and Wind Electricity Generation Technologies. Appl. Sci. 2013, 3, 325–337. [Google Scholar] [CrossRef]
- de Castro, C.; Carpintero, Ó.; Frechoso, F.; Mediavilla, M.; de Miguel, L.J. A top-down approach to assess physical and ecological limits of biofuels. Energy 2014, 64, 506–512. [Google Scholar] [CrossRef]
- Hall, C.A.S.; Lambert, J.G.; Balogh, S.B. EROI of different fuels and the implications for society. Energy Policy 2014, 64, 141–152. [Google Scholar] [CrossRef]
- Kubiszewski, I.; Cleveland, C.J.; Endres, P.K. Meta-analysis of net energy return for wind power systems. Renew. Energy 2010, 35, 218–225. [Google Scholar] [CrossRef]
- Prieto, P.A.; Hall, C.A.S. Spain’s Photovoltaic Revolution: The Energy Return on Investment, 2013th ed.; Springer: Berlin, Germany, 2013; ISBN 1-4419-9436-X. [Google Scholar]
- Raugei, M. Comments on “Energy intensities, EROIs (energy returned on invested), and energy payback times of electricity generating power plants”—Making clear of quite some confusion. Energy 2013, 59, 781–782. [Google Scholar] [CrossRef]
- Weißbach, D.; Ruprecht, G.; Huke, A.; Czerski, K.; Gottlieb, S.; Hussein, A. Energy intensities, EROIs (energy returned on invested), and energy payback times of electricity generating power plants. Energy 2013, 52, 210–221. [Google Scholar] [CrossRef]
- Carbajales-Dale, M. When is EROI Not EROI? Biophys. Econ. Resour. Qual. 2019, 4, 16. [Google Scholar] [CrossRef]
- de Castro, C.; Capellán-Pérez, I. Concentrated Solar Power: Actual Performance and Foreseeable Future in High Penetration Scenarios of Renewable Energies. Biophys. Econ. Resour. Qual. 2018, 3, 14. [Google Scholar] [CrossRef]
- Ferroni, F.; Hopkirk, R.J. Energy Return on Energy Invested (ERoEI) for photovoltaic solar systems in regions of moderate insolation. Energy Policy 2016, 94, 336–344. [Google Scholar] [CrossRef]
- Hall, C.A.S.; Klitgaard, K.A. Energy and the Wealth of Nations: Understanding the Biophysical Economy; Springer: New York, NY, USA, 2012; ISBN 978-1-4419-9398-4. [Google Scholar]
- Koppelaar, R.H.E.M. Solar-PV energy payback and net energy: Meta-assessment of study quality, reproducibility, and results harmonization. Renew. Sustain. Energy Rev. 2017, 72, 1241–1255. [Google Scholar] [CrossRef]
- Murphy, D.J.; Carbajales-Dale, M.; Moeller, D. Comparing Apples to Apples: Why the Net Energy Analysis Community Needs to Adopt the Life-Cycle Analysis Framework. Energies 2016, 9, 917. [Google Scholar] [CrossRef]
- Palmer, G.; Floyd, J. An Exploration of Divergence in EPBT and EROI for Solar Photovoltaics. Biophys. Econ. Resour. Qual. 2017, 2, 15. [Google Scholar] [CrossRef][Green Version]
- Raugei, M.; Sgouridis, S.; Murphy, D.; Fthenakis, V.; Frischknecht, R.; Breyer, C.; Bardi, U.; Barnhart, C.; Buckley, A.; Carbajales-Dale, M.; et al. Energy Return on Energy Invested (ERoEI) for photovoltaic solar systems in regions of moderate insolation: A comprehensive response. Energy Policy 2017, 102, 377–384. [Google Scholar] [CrossRef]
- Murphy, D.J.; Hall, C.A.S.; Dale, M.; Cleveland, C. Order from Chaos: A Preliminary Protocol for Determining the EROI of Fuels. Sustainability 2011, 3, 1888–1907. [Google Scholar] [CrossRef]
- Raugei, M. Net energy analysis must not compare apples and oranges. Nat. Energy 2019, 4, 86. [Google Scholar] [CrossRef]
- Carbajales-Dale, M. Chapter 21—Life Cycle Assessment: Meta-analysis of Cumulative Energy Demand for Wind Energy Technologies. In Wind Energy Engineering; Letcher, T.M., Ed.; Academic Press: Cambridge, MA, USA, 2017; pp. 439–473. ISBN 978-0-12-809451-8. [Google Scholar]
- Dale, M.; Benson, S.M. Energy Balance of the Global Photovoltaic (PV) Industry—Is the PV Industry a Net Electricity Producer? Environ. Sci. Technol. 2013, 47, 3482–3489. [Google Scholar] [CrossRef]
- Price, L.; Kendall, A. Wind Power as a Case Study. J. Ind. Ecol. 2012, 16, S22–S27. [Google Scholar] [CrossRef]
- Cottrell, F. Energy and Society: The Relation between Energy, Social Change, and Economic Development; AuthorHouse: Bloomington, IN, USA, 2009; ISBN 978-1-4490-3169-5. [Google Scholar]
- Hall, C.A.S.; Balogh, S.; Murphy, D.J.R. What is the Minimum EROI that a Sustainable Society Must Have? Energies 2009, 2, 25–47. [Google Scholar] [CrossRef]
- Hall, C.A.S.; Klitgaard, K. Energy and the Wealth of Nations: An Introduction to Biophysical Economics, 2nd ed.; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; ISBN 978-3-319-66217-6. [Google Scholar]
- White, L.A. Energy and the evolution of culture. Am. Anthropol. 1943, 45, 335–356. [Google Scholar] [CrossRef]
- Fizaine, F.; Court, V. Energy expenditure, economic growth, and the minimum EROI of society. Energy Policy 2016, 95, 172–186. [Google Scholar] [CrossRef]
- Lambert, J.; Hall, C.; Balogh, S.; Poisson, A.; Gupta, A. EROI of Global Energy Resources: Preliminary Status and Trends; College of Environmental Science and Forestry, State University of New York, United Kingdom Department for International Development: London, UK, 2012. [Google Scholar]
- Raugei, M.; Leccisi, E. A comprehensive assessment of the energy performance of the full range of electricity generation technologies deployed in the United Kingdom. Energy Policy 2016, 90, 46–59. [Google Scholar] [CrossRef]
- Gagnon, N.; Hall, C.A.S.; Brinker, L. A Preliminary Investigation of Energy Return on Energy Investment for Global Oil and Gas Production. Energies 2009, 2, 490–503. [Google Scholar] [CrossRef]
- Masnadi, M.S.; Brandt, A.R. Energetic productivity dynamics of global super-giant oilfields. Energy Environ. Sci. 2017, 10, 1493–1504. [Google Scholar] [CrossRef]
- Smil, V. Energy Transitions: History, Requirements, Prospects; Praeger: Santa Barbara, CA, USA, 2010; ISBN 0-313-38177-1. [Google Scholar]
- Arvesen, A.; Hertwich, E.G. Assessing the life cycle environmental impacts of wind power: A review of present knowledge and research needs. Renew. Sustain. Energy Rev. 2012, 16, 5994–6006. [Google Scholar] [CrossRef]
- Boccard, N. Capacity factor of wind power realized values vs. estimates. Energy Policy 2009, 37, 2679–2688. [Google Scholar] [CrossRef]
- Clack, C.T.M.; Qvist, S.A.; Apt, J.; Bazilian, M.; Brandt, A.R.; Caldeira, K.; Davis, S.J.; Diakov, V.; Handschy, M.A.; Hines, P.D.H.; et al. Evaluation of a proposal for reliable low-cost grid power with 100% wind, water, and solar. Proc. Natl. Acad. Sci. USA 2017, 114, 6722–6727. [Google Scholar] [CrossRef]
- Moriarty, P.; Honnery, D. Can renewable energy power the future? Energy Policy 2016, 93, 3–7. [Google Scholar] [CrossRef]
- Trainer, T. Some problems in storing renewable energy. Energy Policy 2017, 110, 386–393. [Google Scholar] [CrossRef]
- Trainer, T. Can Europe run on renewable energy? A negative case. Energy Policy 2013, 63, 845–850. [Google Scholar] [CrossRef]
- Trainer, T. A critique of Jacobson and Delucchi’s proposals for a world renewable energy supply. Energy Policy 2012, 44, 476–481. [Google Scholar] [CrossRef]
- Trainer, T. Can renewables etc. solve the greenhouse problem? The negative case. Energy Policy 2010, 38, 4107–4114. [Google Scholar] [CrossRef]
- Capellán-Pérez, I.; de Blas, I.; Nieto, J.; de Castro, C.; Miguel, L.J.; Carpintero, Ó.; Mediavilla, M.; Lobejón, L.F.; Ferreras-Alonso, N.; Rodrigo, P.; et al. MEDEAS: A new modeling framework integrating global biophysical and socioeconomic constraints. Energy Environ. Sci. 2020, 13, 986–1017. [Google Scholar] [CrossRef]
- Capellán-Pérez, I.; de Blas, I.; Nieto, J.; De Castro, C.; Miguel, L.J.; Mediavilla, M.; Carpintero, Ó.; Rodrigo, P.; Frechoso, F.; Cáceres, S. D4.1 MEDEAS Model and IOA Implementation at Global Geographical Level; MEDEAS Project: Barcelona, Spain, 2017. [Google Scholar]
- Brandt, A.R. How Does Energy Resource Depletion Affect Prosperity? Mathematics of a Minimum Energy Return on Investment (EROI). Biophys. Econ. Resour. Qual. 2017, 2, 2. [Google Scholar] [CrossRef]
- Murphy, D.J.; Hall, C.A.S. Energy return on investment, peak oil, and the end of economic growth. Ann. N. Y. Acad. Sci. 2011, 1219, 52–72. [Google Scholar] [CrossRef]
- Capellán-Pérez, I.; de Castro, C.; Arto, I. Assessing vulnerabilities and limits in the transition to renewable energies: Land requirements under 100% solar energy scenarios. Renew. Sustain. Energy Rev. 2017, 77, 760–782. [Google Scholar] [CrossRef]
- Moriarty, P.; Honnery, D. Ecosystem maintenance energy and the need for a green EROI. Energy Policy 2019, 131, 229–234. [Google Scholar] [CrossRef]
- UNEP. Recycling Rates of Metals. A Status Report; International Resource Panel; United Nations Environment Programme: Nairobi, Kenya, 2011. [Google Scholar]
- Valero, A.; Ortego, A.; Calvo, G.; Valero, A.; Círez, F.; Kimmich, C.; Cerny, M.; Kerschner, C.; Cernik, M.; Theofilidi, M.; et al. D2.1 Variables. Annex 9; CIRCE, MU, CRES & INSTM: Barcelona, Spain, 2016. [Google Scholar]
- de Castro, C.; Mediavilla, M.; Miguel, L.J.; Frechoso, F. Global solar electric potential: A review of their technical and sustainable limits. Renew. Sustain. Energy Rev. 2013, 28, 824–835. [Google Scholar] [CrossRef]
- Frischknecht, R.; Itten, R.; Sinha, P.; de Wild-Scholten, M.; Zhang, J.; Fthenakis, V.; Kim, H.C.; Raugei, M.; Stucki, M. Life Cycle Inventories and Life Cycle Assessment of Photovoltaic Systems; IEA PVPS Task 12, Subtask 2.0; LCA. 2015. Available online: https://www.bnl.gov/pv/files/pdf/226_Task12_LifeCycle_Inventories.pdf (accessed on 11 June 2020).
- GWEC. GWEC Webpage; Global Wind Energy Council. Available online: https://gwec.net/global-figures/wind-in-numbers/ (accessed on 3 November 2019).
- Muro Pereg, J.R.; Fernández de la Hoz, J. ECOWIND. Life Cycle Assessment of 1 kWh Generated by a GAMESA Onshore Windfarm G90 2.O MW; GAMESA: Zamudio, Spain, 2013. [Google Scholar]
- GWEC. Global Wind Report 2016; Global Wind Energy Council: Brussels, Belgium, 2017. [Google Scholar]
- LondonArray. London Array. Available online: http://www.londonarray.com/ (accessed on 28 March 2016).
- SMart Wind. Hornsea Offshore Wind Farm Project One. Chapter 3: Project Description; Smart Wind Limited: London, UK, 2013. [Google Scholar]
- Flury, K.; Frischknecht, R. Life Cycle Inventories of Hydroelectric Power Generation; ESU-Services, Fair Consulting in Sustainability: Schaffhausen, Switzerland, 2012; pp. 1–51. [Google Scholar]
- Schellenberg, G.; Donnelly, C.R.; Holder, C.; Briand, M.-H.; Ahsan, R. Sedimentation, Dam Safety and Hydropower: Issues, Impacts and Solutions 2017. In Sedimentation and Hydropower: Impacts and Solutions. p. 24. Available online: https://www.hydroreview.com/wp-content/uploads/content/dam/hydroworld/online-articles/2017/04/Sedimentation%20Dam%20Safety%20and%20Hydropower-%20Issues%20Impacts%20and%20Solutions.pdf (accessed on 11 June 2020).
- IEA. IEA Sankey Webpage; International Energy Agency. Available online: https://www.iea.org/sankey/ (accessed on 1 November 2019).
- Hertwich, E.G.; Gibon, T.; Bouman, E.A.; Arvesen, A.; Suh, S.; Heath, G.A.; Bergesen, J.D.; Ramirez, A.; Vega, M.I.; Shi, L. Integrated life-cycle assessment of electricity-supply scenarios confirms global environmental benefit of low-carbon technologies. Proc. Natl. Acad. Sci. USA 2015, 112, 6277–6282. [Google Scholar] [CrossRef]
- Kis, Z.; Pandya, N.; Koppelaar, R.H.E.M. Electricity generation technologies: Comparison of materials use, energy return on investment, jobs creation and CO2 emissions reduction. Energy Policy 2018, 120, 144–157. [Google Scholar] [CrossRef]
- Schmied, M.; Knörr, W. Calculating GHG Emissions for Freight Forwarding and Logistics Services in Accordance with EN 16258; European Association for Forwarding; Transport, Logistics and Customs Services (CLECAT): Bruxelles, Belgium, 2012. [Google Scholar]
- Hammond, G.; Jones, C. Inventory of Carbon & Energy (ICE) Version 2.0; Sustainable Energy Research Team (SERT) Department of Mechanical Engineering University of Bath: Bath, UK, 2011. [Google Scholar]
- Rankin, J. Energy use in metal production. In Proceedings of the High Temperature Processing Symposium, Melbourne, Australia, 6–7 February 2012; pp. 6–7. [Google Scholar]
- der Voet, E.V.; Oers, L.V.; Verboon, M.; Kuipers, K. Environmental Implications of Future Demand Scenarios for Metals: Methodology and Application to the Case of Seven Major Metals. J. Ind. Ecol. 2019, 23, 141–155. [Google Scholar] [CrossRef]
- Song, Y.S.; Youn, J.R.; Gutowski, T.G. Life cycle energy analysis of fiber-reinforced composites. Compos. Part A Appl. Sci. Manuf. 2009, 40, 1257–1265. [Google Scholar] [CrossRef]
- Guan, J.; Zhang, Z.; Chu, C. Quantification of building embodied energy in China using an input–output-based hybrid LCA model. Energy Build. 2016, 110, 443–452. [Google Scholar] [CrossRef]
- Wu, K.-Y.; Wu, J.-H.; Huang, Y.-H.; Fu, S.-C.; Chen, C.-Y. Estimating direct and indirect rebound effects by supply-driven input-output model: A case study of Taiwan’s industry. Energy 2016, 115, 904–913. [Google Scholar] [CrossRef]
- Nieto, J.; Carpintero, Ó.; Miguel, L.J.; de Blas, I. Macroeconomic modelling under energy constraints: Global low carbon transition scenarios. Energy Policy 2019, 111090. [Google Scholar] [CrossRef]
- Wiedmann, T.O.; Suh, S.; Feng, K.; Lenzen, M.; Acquaye, A.; Scott, K.; Barrett, J.R. Application of Hybrid Life Cycle Approaches to Emerging Energy Technologies—The Case of Wind Power in the UK. Environ. Sci. Technol. 2011, 45, 5900–5907. [Google Scholar] [CrossRef]
- European Commission. Critical Raw Materials for the UE. Report of the Ad-Hoc Working Group on Defining Critical Raw Materials; European Commission: Brussels, Belgium, 2010. [Google Scholar]
- Elshkaki, A.; Graedel, T.E. Dynamic analysis of the global metals flows and stocks in electricity generation technologies. J. Clean. Prod. 2013, 59, 260–273. [Google Scholar] [CrossRef]
- García-Olivares, A.; Ballabrera-Poy, J.; García-Ladona, E.; Turiel, A. A global renewable mix with proven technologies and common materials. Energy Policy 2012, 41, 561–574. [Google Scholar] [CrossRef]
- Prior, T.; Giurco, D.; Mudd, G.; Mason, L.; Behrisch, J. Resource depletion, peak minerals and the implications for sustainable resource management. Glob. Environ. Chang. 2012, 22, 577–587. [Google Scholar] [CrossRef]
- Trainer, T. Estimating the EROI of whole systems for 100% renewable electricity supply capable of dealing with intermittency. Energy Policy 2018, 119, 648–653. [Google Scholar] [CrossRef]
- Pihl, E.; Kushnir, D.; Sandén, B.; Johnsson, F. Material constraints for concentrating solar thermal power. Energy 2012, 44, 944–954. [Google Scholar] [CrossRef]
- Dahmus, J.B.; Gutowski, T.G. An environmental analysis of machining. In Proceedings of the ASME 2004 International Mechanical Engineering Congress and Exposition, Anaheim, CA, USA, 13–19 November 2004; American Society of Mechanical Engineers: New York, NY, USA, 2004; pp. 643–652. [Google Scholar]
- Boustani, A.; Sahni, S.; Gutowski, T.; Graves, S. Appliance Remanufacturing and Energy Savings; Sloan School of Management: Cambridge, MA, USA, 2010. [Google Scholar]
- Ciceri, N.D.; Gutowski, T.; Garetti, M. A tool to estimate materials and manufacturing energy for a product. In Proceedings of the 2010 IEEE International Symposium on Sustainable Systems and Technology, Arlington, VA, USA, 17–19 May 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1–6. [Google Scholar]
- IRENA db. IRENA Resource; International Renewable Energy Agency. Available online: http://resourceirena.irena.org (accessed on 9 June 2020).
- Dupont, E.; Koppelaar, R.; Jeanmart, H. Global available wind energy with physical and energy return on investment constraints. Appl. Energy 2018, 209, 322–338. [Google Scholar] [CrossRef]
- MTE. Estadística de la Industria de la Energía Eléctrica; Ministerio para la Transición Ecológica: Madrid, Spain, 2018. [Google Scholar]
- MTE. Estadística de la Industria de la Energía Eléctrica; Ministerio para la Transición Ecológica: Madrid, Spain, 2017. [Google Scholar]
- MTE. Estadística de la Industria de la Energía Eléctrica; Ministerio para la Transición Ecológica: Madrid, Spain, 2016. [Google Scholar]
- MTE. Estadística de la Industria de la Energía Eléctrica; Ministerio para la Transición Ecológica: Madrid, Spain, 2015. [Google Scholar]
- MTE. Estadística de la Industria de la Energía Eléctrica; Ministerio para la Transición Ecológica: Madrid, Spain, 2014. [Google Scholar]
- Ferroni, F.; Guekos, A.; Hopkirk, R.J. Further considerations to: Energy Return on Energy Invested (ERoEI) for photovoltaic solar systems in regions of moderate insolation. Energy Policy 2017, 107, 498–505. [Google Scholar] [CrossRef]
- Farthing, A.; Carbajales-Dale, M.; Mason, S.; Carbajales-Dale, P.; Matta, P. Utility-Scale Solar PV in South Carolina: Analysis of Suitable Lands and Geographical Potential. Biophys. Econ. Resour. Qual. 2016, 1, 8. [Google Scholar] [CrossRef]
- WBGU. Future Bioenergy and Sustainable Land Use; German Advisory Council on Global Change (WBGU): Berlin, Germany, 2009; ISBN 978-1-84407-841-7. [Google Scholar]
- Dupont, E.; Koppelaar, R.; Jeanmart, H. Global available solar energy under physical and energy return on investment constraints. Appl. Energy 2020, 257, 113968. [Google Scholar] [CrossRef]
- REN21. Renewables 2017. Global Status Report; REN 21: Paris, France, 2017. [Google Scholar]
- Martín-Chivelet, N. Photovoltaic potential and land-use estimation methodology. Energy 2016, 94, 233–242. [Google Scholar] [CrossRef]
- Luque, A.; Hegedus, S. Handbook of Photovoltaic Science and Engineering; John Wiley & Sons: Chichester, UK, 2011. [Google Scholar]
- Arto, I.; Capellán-Pérez, I.; Lago, R.; Bueno, G.; Bermejo, R. The energy requirements of a developed world. Energy Sustain. Dev. 2016, 33, 1–13. [Google Scholar] [CrossRef]
- Dale, M.A.J. Global Energy Modelling: A Biophysical Approach (GEMBA). Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 2010. [Google Scholar]
- Schoenberg, B.; Hall, C.A.S. The Energy Return of (Industrial) Solar—Passive Solar, PV, Wind and Hydro (#5 of 6). The Oil Drum 2008. Available online: http://theoildrum.com/node/3910 (accessed on 10 June 2020).
- Pillai, U. Drivers of cost reduction in solar photovoltaics. Energy Econ. 2015, 50, 286–293. [Google Scholar] [CrossRef]
- Dale, M.; Krumdieck, S.; Bodger, P. A Dynamic Function for Energy Return on Investment. Sustainability 2011, 3, 1972–1985. [Google Scholar] [CrossRef]
- Van de Ven, D.-J.; Capellán-Pérez, I.; Arto, I.; Cazcarro, I.; De Castro, C.; Patel, P.; González-Eguino, M. The potential land use requirements and related land use change emissions of solar energy. Nat. Sustain. 2020. under review. [Google Scholar]
- Calvo, G.; Mudd, G.; Valero, A.; Valero, A. Decreasing Ore Grades in Global Metallic Mining: A Theoretical Issue or a Global Reality? Resources 2016, 5, 36. [Google Scholar] [CrossRef]
- Harmsen, J.H.M.; Roes, A.L.; Patel, M.K. The impact of copper scarcity on the efficiency of 2050 global renewable energy scenarios. Energy 2013, 50, 62–73. [Google Scholar] [CrossRef]
- Mudd, G.M. The Environmental sustainability of mining in Australia: Key mega-trends and looming constraints. Resour. Policy 2010, 35, 98–115. [Google Scholar] [CrossRef]
- Steffen, B.; Hischier, D.; Schmidt, T.S. Historical and projected improvements in net energy performance of power generation technologies. Energy Environ. Sci. 2018, 11, 3524–3530. [Google Scholar] [CrossRef]
- Louwen, A.; van Sark, W.G.J.H.M.; Faaij, A.P.C.; Schropp, R.E.I. Re-assessment of net energy production and greenhouse gas emissions avoidance after 40 years of photovoltaics development. Nat. Commun. 2016, 7, 1–9. [Google Scholar] [CrossRef]
- Sers, M.R.; Victor, P.A. The Energy-missions Trap. Ecol. Econ. 2018, 151, 10–21. [Google Scholar] [CrossRef]
- Heun, M.K.; de Wit, M. Energy return on (energy) invested (EROI), oil prices, and energy transitions. Energy Policy 2012, 40, 147–158. [Google Scholar] [CrossRef]
- Parrique, T.; Barth, J.; Briens, F.; Kerschner, C.; Kraus-Polk, A.; Kuokkanen, A.; Spangenberg, J.H. Decoupling Debunked—Evidence and Arguments against Green Growth as a Sole Strategy for Sustainability; European Environmental Bureau (EEB): Brussels, Belgium, 2019. [Google Scholar]
- Dale, M.; Krumdieck, S.; Bodger, P. Global energy modelling—A biophysical approach (GEMBA) Part 2: Methodology. Ecol. Econ. 2012, 73, 158–167. [Google Scholar] [CrossRef]
- Sgouridis, S.; Csala, D.; Bardi, U. The sower’s way: Quantifying the narrowing net-energy pathways to a global energy transition. Environ. Res. Lett. 2016, 11, 094009. [Google Scholar] [CrossRef]
- European Commission. A Roadmap for Moving to a Competitive Low Carbon Economy in 2050; Communication from the Commission to the European Parliament, the Council, the European Economic and Social Committee and the Committee of the Regions; European Commission: Brussels, Belgium, 2011. [Google Scholar]
- Jacobs, M. Green growth: Economic theory and political discourse. Centre for Climate Change Economics and Policy Working Paper No. 108; Grantham Research Institute on Climate Change and the Environment Working Paper No. 92. 2012. Available online: http://www.lse.ac.uk/GranthamInstitute/publication/green-growth-economic-theory-and-political-discourse-working-paper-92/ (accessed on 11 June 2020).
- OECD. OECD Work on Green Growth. Available online: http://www.oecd.org/greengrowth/oecdworkongreengrowth.htm (accessed on 12 March 2018).
- OECD. Towards Green Growth; Organisation for Economic Co-operation and Development: Paris, France, 2011. [Google Scholar]
- UNEP. Towards a Green Economy: Pathways to Sustainable Development and Poverty Eradication; United Nations Environment Programme: Nairobi, Kenya, 2011. [Google Scholar]
- World Bank Inclusive Green Growth: The Pathway to Sustainable Development; World Bank Publications: Washington, DC, USA, 2012; ISBN 978-0-8213-9551-6.
- Demaria, F.; Schneider, F.; Sekulova, F.; Martinez-Alier, J. What is Degrowth? From an Activist Slogan to a Social Movement. Environ. Values 2013, 22, 191–215. [Google Scholar] [CrossRef]
- IEA; IRENA. Perspectives for the Energy Transition. Investment Needs for a Low-Carbon Energy System; International Energy Agency: Paris, France; International Renewable Energy Agency: Abu Dhabi, UAE, 2017. [Google Scholar]
- Nemet, G.F. Beyond the learning curve: Factors influencing cost reductions in photovoltaics. Energy Policy 2006, 34, 3218–3232. [Google Scholar] [CrossRef]
- Lawn, P. How well are resource prices likely to serve as indicators of natural resource scarcity? Int. J. Sustain. Dev. 2004, 7, 369–397. [Google Scholar] [CrossRef]
- Norgaard, R.B. Economic indicators of resource scarcity: A critical essay. J. Environ. Econ. Manag. 1990, 19, 19–25. [Google Scholar] [CrossRef]
- Reynolds, D.B. The mineral economy: How prices and costs can falsely signal decreasing scarcity. Ecol. Econ. 1999, 31, 155–166. [Google Scholar] [CrossRef]
- Rubin, E.S.; Azevedo, I.M.L.; Jaramillo, P.; Yeh, S. A review of learning rates for electricity supply technologies. Energy Policy 2015, 86, 198–218. [Google Scholar] [CrossRef]
- Daly, H.E. Ecological Economics and Sustainable Development; Edward Elgar Publishing: Cheltenham, UK, 2007. [Google Scholar]
- Smil, V. Power Density: A Key to Understanding Energy Sources and Uses; The MIT Press: Cambridge, MA, USA, 2015; ISBN 978-0-262-02914-8. [Google Scholar]
- Gernaat, D.E.H.J.; Bogaart, P.W.; van Vuuren, D.P.; Biemans, H.; Niessink, R. High-resolution assessment of global technical and economic hydropower potential. Nat. Energy 2017, 2, 821. [Google Scholar] [CrossRef]
- Connolly, D.; Lund, H.; Mathiesen, B.V. Smart Energy Europe: The technical and economic impact of one potential 100% renewable energy scenario for the European Union. Renew. Sustain. Energy Rev. 2016, 60, 1634–1653. [Google Scholar] [CrossRef]
- Moeller, D.; Murphy, D. Net Energy Analysis of Gas Production from the Marcellus Shale. Biophys. Econ. Resour. Qual. 2016, 1, 5. [Google Scholar] [CrossRef]
- Murphy, D.J. The implications of the declining energy return on investment of oil production. Philos. Trans. R. Soc. A 2014, 372, 20130126. [Google Scholar] [CrossRef] [PubMed]
- Ramorakane, R.J.; Dinter, F. Evaluation of parasitic consumption for a CSP plant. AIP Conf. Proc. 2016, 1734, 070027. [Google Scholar] [CrossRef]
- García-Olivares, A. Energy for a sustainable post-carbon society. Sci. Mar. 2016, 80, 257–268. [Google Scholar] [CrossRef]
- Latunussa, C.E.L.; Ardente, F.; Blengini, G.A.; Mancini, L. Life Cycle Assessment of an innovative recycling process for crystalline silicon photovoltaic panels. Sol. Energy Mater. Sol. Cells 2016, 156, 101–111. [Google Scholar] [CrossRef]
- Martinez-Alier, J. The Environmentalism of the Poor: A Study of Ecological Conflicts and Valuation; Edward Elgar Publishing: Cheltenham, UK, 2003. [Google Scholar]
- UNEP Environmental Risks and Challenges of Anthropogenic Metals Flows and Cycles; International Resource Panel; United Nations Environment Programme: Cheltenham, UK, 2013.
- Haapala, K.R.; Prempreeda, P. Comparative life cycle assessment of 2.0 MW wind turbines. Int. J. Sustain. Manuf. 2014, 3, 170–185. [Google Scholar] [CrossRef]
- Ribrant, J.; Bertling, L. Survey of failures in wind power systems with focus on Swedish wind power plants during 1997-2005. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–8. [Google Scholar]
- EUROELECTRIC. Power Distribution in Europe. Facts & Figures; Eurelectric: Brussels, Belgium, 2013. [Google Scholar]
- NREL. Renewable Electricity Futures Study (Entire Report); National Renewable Energy Laboratory: Golden, CO, USA, 2012. [Google Scholar]
- Bumby, S.; Druzhinina, E.; Feraldi, R.; Werthmann, D.; Geyer, R.; Sahl, J. Life Cycle Assessment of Overhead and Underground Primary Power Distribution. Environ. Sci. Technol. 2010, 44, 5587–5593. [Google Scholar] [CrossRef]
- Jorge, R.S.; Hawkins, T.R.; Hertwich, E.G. Life cycle assessment of electricity transmission and distribution—Part 1: Power lines and cables. Int. J. Life Cycle Assess. 2012, 17, 9–15. [Google Scholar] [CrossRef]
- Jorge, R.S.; Hawkins, T.R.; Hertwich, E.G. Life cycle assessment of electricity transmission and distribution—Part 2: Transformers and substation equipment. Int. J. Life Cycle Assess. 2012, 17, 184–191. [Google Scholar] [CrossRef]
- van Tichelen, P.; Mudgal, S. LOT 2: Distribution and Power Transformers Tasks 1–7; VITO and Bio Intelligence Service: Paris, France, 2011. [Google Scholar]
- IEA ETSAP. Electricity Transmission and Distribution; IEA ETSAP—Technology Brief; International Energy Agency: Paris, France, 2014. [Google Scholar]
- Hall, K.L. Out of Sight, Out of Mind 2012. An Updated Study on the Undergrounding of Overhead Power Lines; Edison Electric Institute: Washington, DC, USA, 2013. [Google Scholar]
- Otten, M.; Hoen, M.; Boer, E. STREAM (Study on Transport Emissions of All Modes) Freight Transport 2016. CE Delft, Deflt. Available online: www.cedelft.eu (accessed on 9 June 2020).
- Pagenkopf, J.; van den Adel, B.; Deniz, Ö.; Schmid, S. Transport Transition Concepts. In Achieving the Paris Climate Agreement Goals; Springer: Berlin/Heidelberg, Germany, 2019; pp. 131–159. [Google Scholar]
- IEA. Data and Statistics; IEA: Paris, France, 2020; Available online: https://www.iea.org/data-and-statistics (accessed on 9 June 2020).
- Cui, R.Y.; Hultman, N.; Edwards, M.R.; He, L.; Sen, A.; Surana, K.; McJeon, H.; Iyer, G.; Patel, P.; Yu, S.; et al. Quantifying operational lifetimes for coal power plants under the Paris goals. Nat. Commun. 2019, 10, 4759. [Google Scholar] [CrossRef]
- Lott, M.C. Natural Gas—Leading Retirements, New Capacity. Available online: https://blogs.scientificamerican.com/plugged-in/natural-gas-leading-the-retirements-board/ (accessed on 2 June 2020).
| Alternative Technology | Representative Technology | Main References for Material Intensities |
|---|---|---|
| Solar Concentrated Solar Power (CSP) | CSP (parabolic trough collector) with molten-salt storage without back-up: most efficient and used technology [25]. Back-up option is not considered since it is usually powered by non-renewable fuels such as natural gas. | [25,62] |
| Solar Photovoltaic (PV) | Fixed-tilt silicon PV: better performance in terms of Energy inputs and EROI [21] and subject to less mineral availability constraints [63]. A weighted average is assumed taking into account the current share of thin-film technologies in global PV mix. | [21,25,62,64] |
| Wind onshore | 2 MW onshore wind turbines, which is over the current global average wind onshore installed capacity per turbine [65]. | [62,66] |
| Wind offshore | 3.6 MW offshore wind turbines taking as reference the current average size in Europe [67]. | [62,66,68,69] |
| Large hydroelectricity (>10 MW) | Large power plant used by [70] (96 MW) (the average capacity for a large hydroelectricity power plant is ~100 MW [71]. | [70] |
| Technology | Capacity Factor (CF) (%) | Lifetime (Years) | Operational Losses (OL) (%) 2 = Expected Degradation + Availability Losses + Other | Self-Consumption (SC) (%) | ||
|---|---|---|---|---|---|---|
| Total Operational Losses (OL) (% Total over the Lifetime) | Expected Degradation (% Total over the Lifetime) | Availability Losses (% Total over the Lifetime) | ||||
| - | Own estimation from [93] | (see text for references) | (see text for references) | (see text for references) | [94] | Annual average 2014–2018 from [95,96,97,98,99] |
| CSP | 25.3 | 25 | 6.96 | 1.06 | 0 | 9.1 |
| PV | 14.2 | 25 | 4.35 | 4.35 | 0 | 1.0 |
| Wind onshore | 24.2 | 20 | 4.36 | 1.36 | 3 | 2.1 |
| Wind offshore | 40.9 | 20 | 7.24 | 2.24 | 5 | 2.1 |
| Large hydro | 41.1 | 75 | 1 1 | - | - | 1.4 |
| EROI | Large Hydropower | Wind Onshore | Wind Offshore | Solar PV | Solar CSP |
|---|---|---|---|---|---|
| EROIst | 28.4 | 13.2 | 8.7 | 7.8 | 2.6 |
| EROIfinal | 13.0 | 5.8 | 4.7 | 3.5 | 1.6 |
| EROIext | 6.5 | 2.9 | 2.3 | 1.6 | 0.8 |
| Technologies | EROIst This Work | EROIst Literature Range | Reference Literature Range Meta-Analysis and Individual Studies |
|---|---|---|---|
| Large hydro | 28.4 | 10–105 | Dale [108]; n = 16 |
| 11.2–267 | Schoenberg and Hall [109]; n = 7 | ||
| 5.9–49.6 (24.7) | Kis et al. [74] (min-max)(base) | ||
| Wind onshore | 13.2 | 12.5–66.7 | Carbajales-Dale [34] (n = 42; power rating >500 kW) |
| 4.7–125.8 | Kubiszewski et al. [20]; n > 40 | ||
| 8.9 8.1–34.5 (12.6) | Dupont et al. [94] Kis et al. [74] (min-max)(base) | ||
| Wind offshore | 8.7 | 5.4–66.7 | Carbajales-Dale [34]; n = 37 |
| 14.8–51.3 | Kubiszewski et al., [20]; n > 4 | ||
| 12 6.9–19.1 (13.5) | Dupont et al. [94] Kis et al. [74] (min-max)(base) | ||
| Solar PV | 7.8 | 8.7–34.2 | Bhandari et al., [14]; n = 23 |
| 7.2 2.7–7.5 (4.8) | Dupont et al. [94] (present) Kis et al. [74] (min-max)(base) | ||
| CSP | 2.6 | 5.2–6.7 5.4–17.9 (9.8) | Dupont et al. [94] (present) Kis et al. [74] (min-max)(base) |
| 9.6–67.6 | de Castro and Capellán-Pérez [25] n = 13 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Castro, C.; Capellán-Pérez, I. Standard, Point of Use, and Extended Energy Return on Energy Invested (EROI) from Comprehensive Material Requirements of Present Global Wind, Solar, and Hydro Power Technologies. Energies 2020, 13, 3036. https://doi.org/10.3390/en13123036
de Castro C, Capellán-Pérez I. Standard, Point of Use, and Extended Energy Return on Energy Invested (EROI) from Comprehensive Material Requirements of Present Global Wind, Solar, and Hydro Power Technologies. Energies. 2020; 13(12):3036. https://doi.org/10.3390/en13123036
Chicago/Turabian Stylede Castro, Carlos, and Iñigo Capellán-Pérez. 2020. "Standard, Point of Use, and Extended Energy Return on Energy Invested (EROI) from Comprehensive Material Requirements of Present Global Wind, Solar, and Hydro Power Technologies" Energies 13, no. 12: 3036. https://doi.org/10.3390/en13123036
APA Stylede Castro, C., & Capellán-Pérez, I. (2020). Standard, Point of Use, and Extended Energy Return on Energy Invested (EROI) from Comprehensive Material Requirements of Present Global Wind, Solar, and Hydro Power Technologies. Energies, 13(12), 3036. https://doi.org/10.3390/en13123036





