Proactive Critical Energy Infrastructure Protection via Deep Feature Learning
Abstract
1. Introduction
- The development of two challenging schemes for automatic feature learning in order to tackle the semi-supervised wind turbine fault detection problem. The proposed schemes can be extended to perform also unsupervised anomaly detection.
- The flexibility that is provided via the proposed formulations, since they can be applied to any cyber-physical system after minor modifications.
- Finally, according to the related state-of-the-art, we claim to be the first that design and develop the LSTM-SAE, and CNN-SAE architectures for the problem of wind turbine classification.
2. Related Work
2.1. Anomaly Detection
2.2. Wind Turbine Anomaly Detection
3. Proposed Methodology: Anomaly Detection in Wind Turbine Time Series Data
3.1. Stacked Sparse Autoencoders
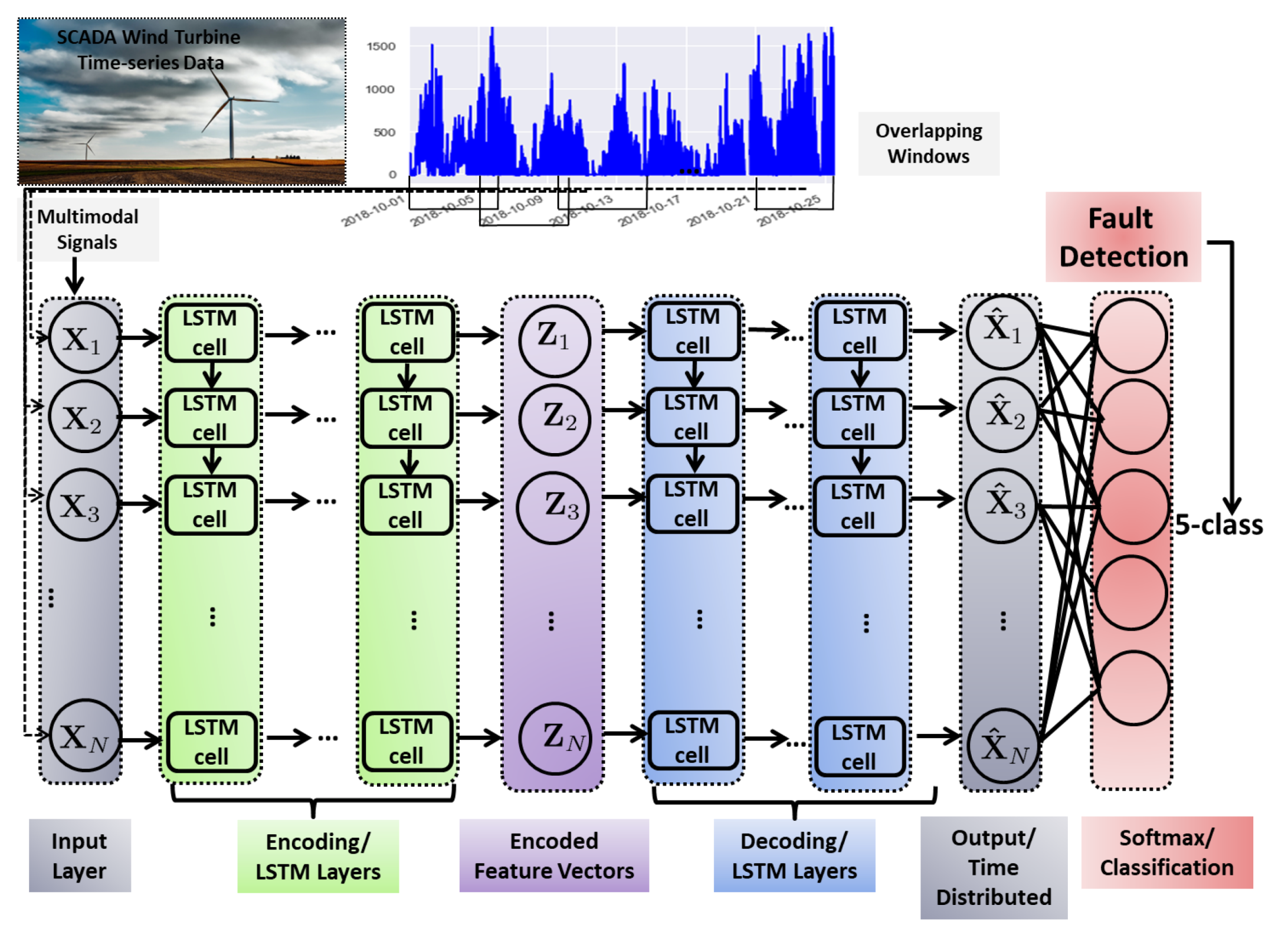
3.2. Long Short Term Memory-SAE for Wind Turbine Fault Detection
Proposed LSTM-SAE Architecture
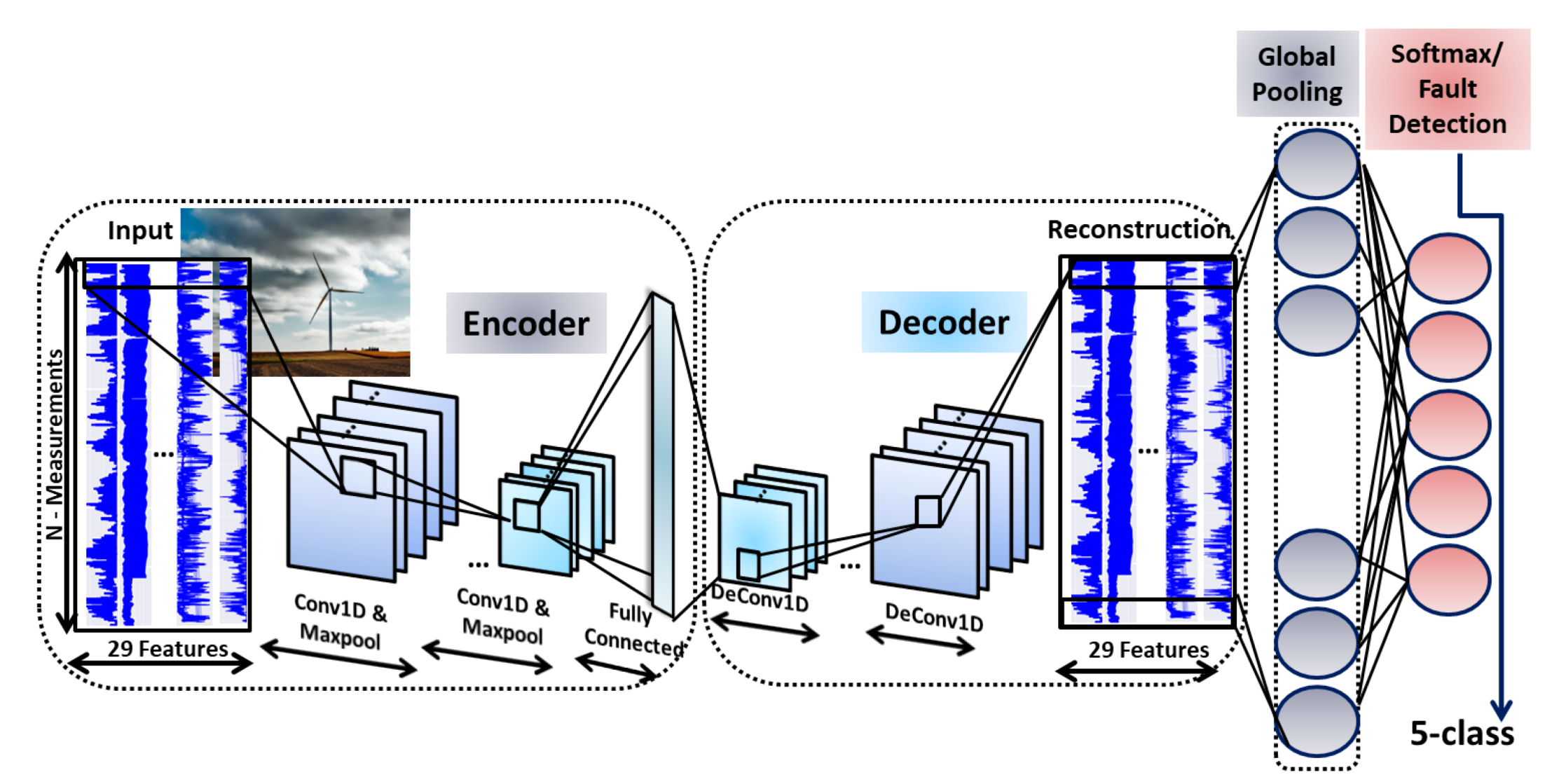
3.3. Convolutional Neural Networks-SAE for Wind Turbine Anomaly Detection
3.3.1. Convolutional Neural Networks (CNN) for 1D Signals
3.3.2. Proposed CNN-SAE Architecture
4. Experimental Evaluation
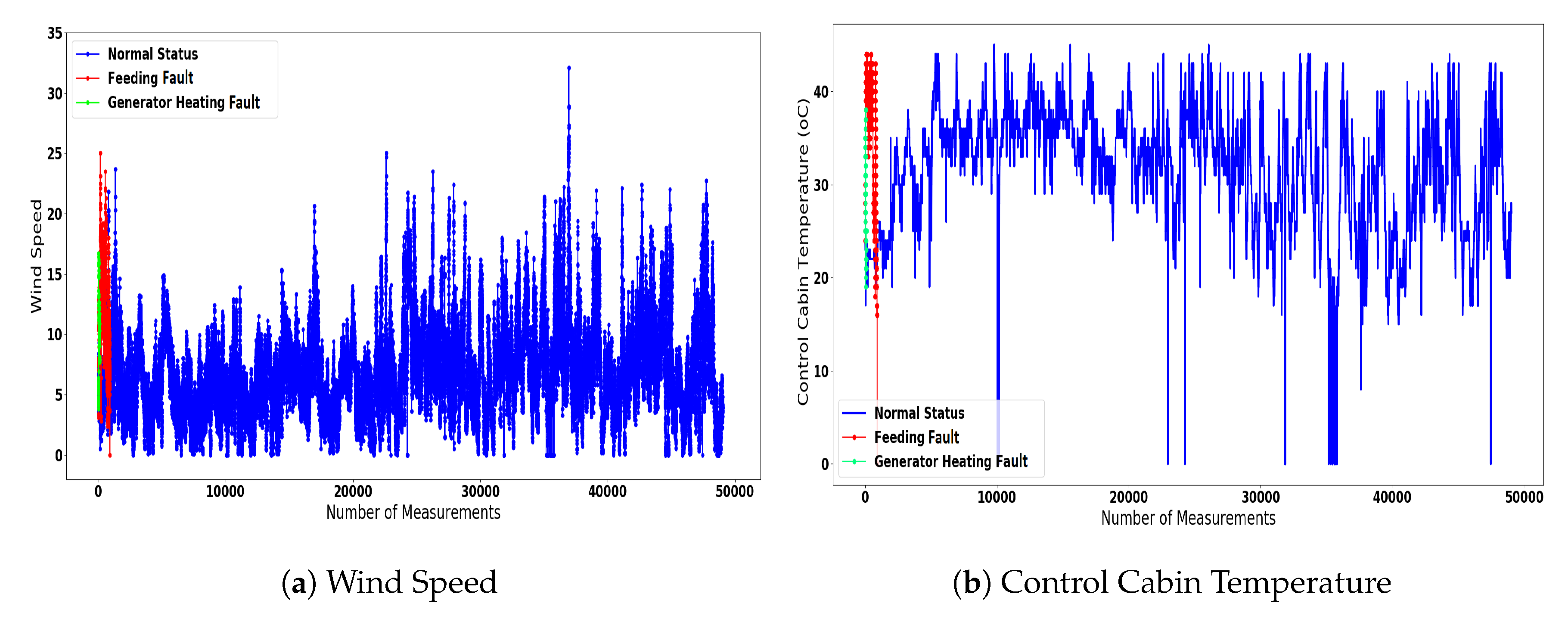
4.1. Dataset Description
- Normal State-Turbine in Operation: The turbine in normal operation;
- Feeding Fault-Load shedding: Refer to the faults that are related with the power feeding cables of the turbine;
- Excitation Fault-Overvoltage DC-link: Correspond to the malfunctions that are related with the generator excitation system of the turbine;
- Generator Heating Fault-Hygrostat Inverter: Refer to the faults that are associated with the generator’s overheating;
- Main Failure Fault-Start Delay: These faults can be either related with delays regarding the start operation of the turbine, or with the under-voltage of specific components.
4.2. Evaluation Metrics
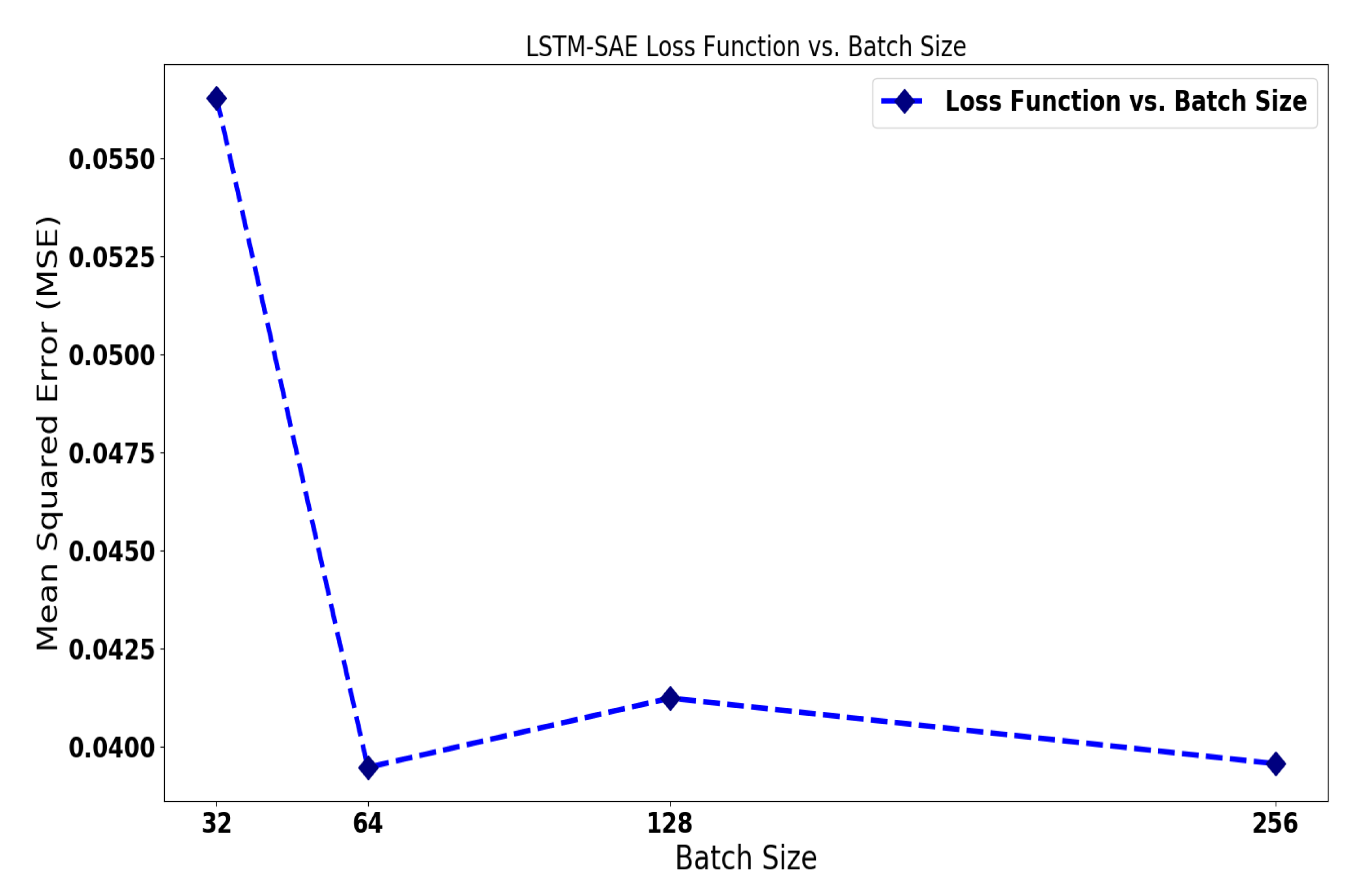
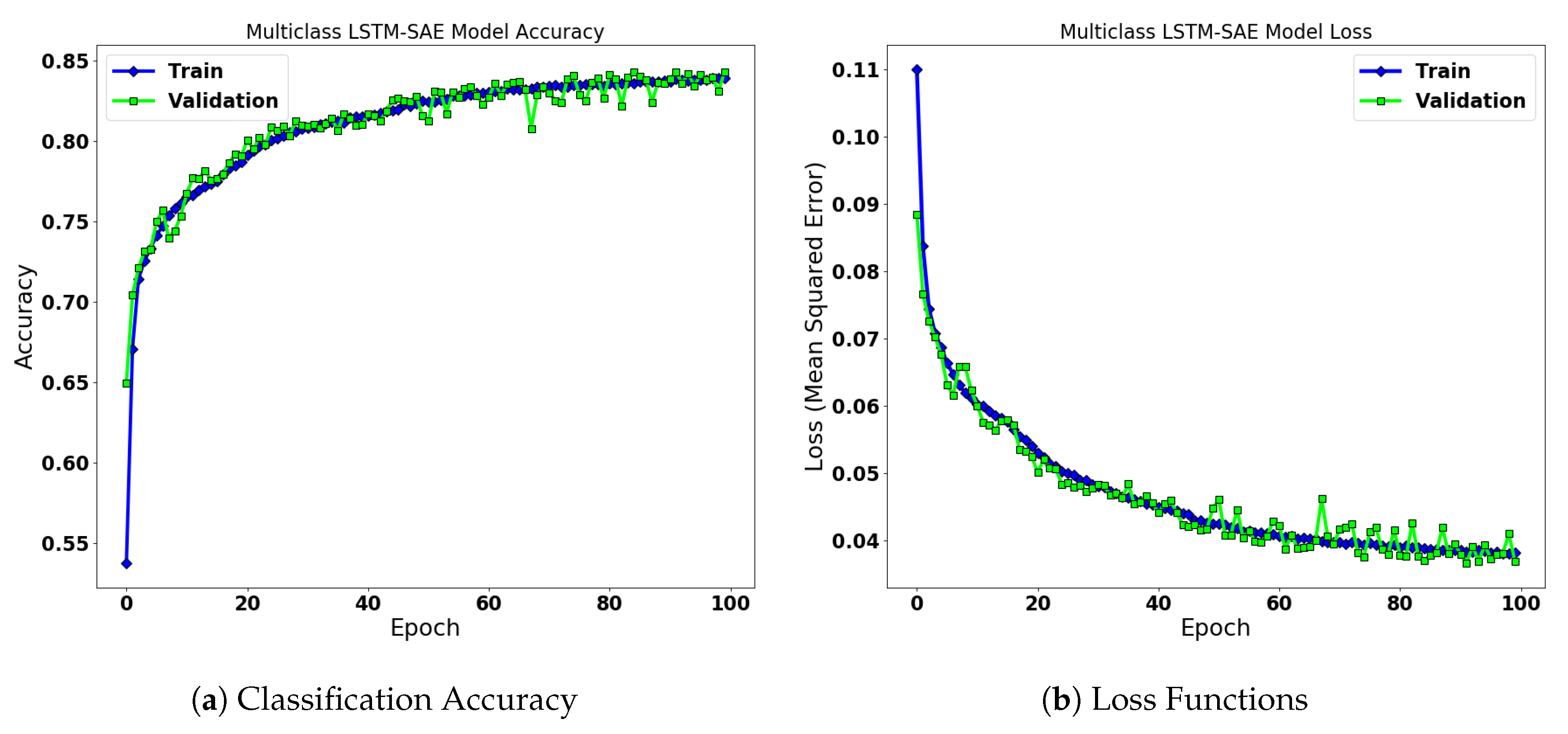
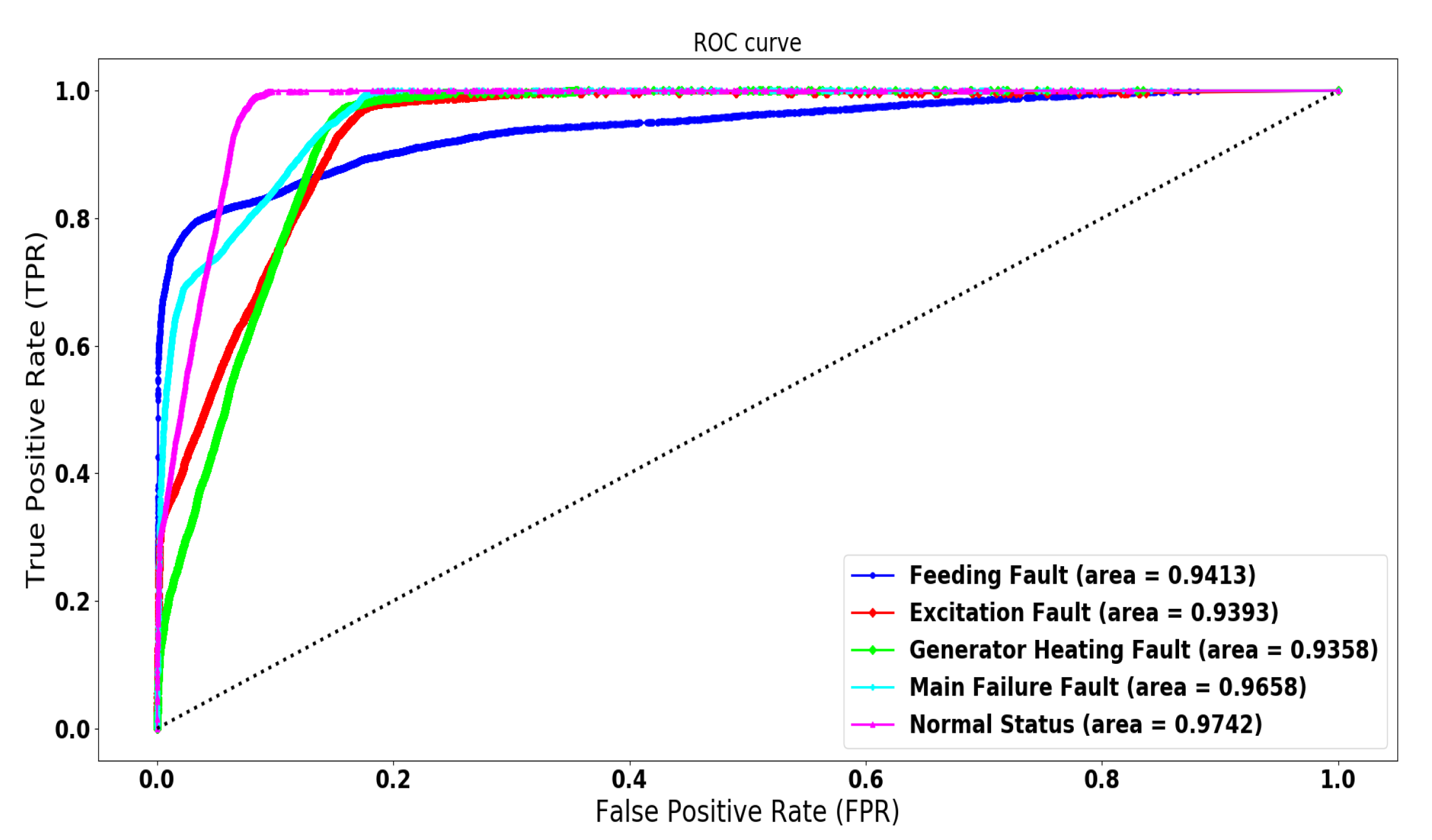
4.3. LSTM-SAE for Wind Turbine Anomaly Detection
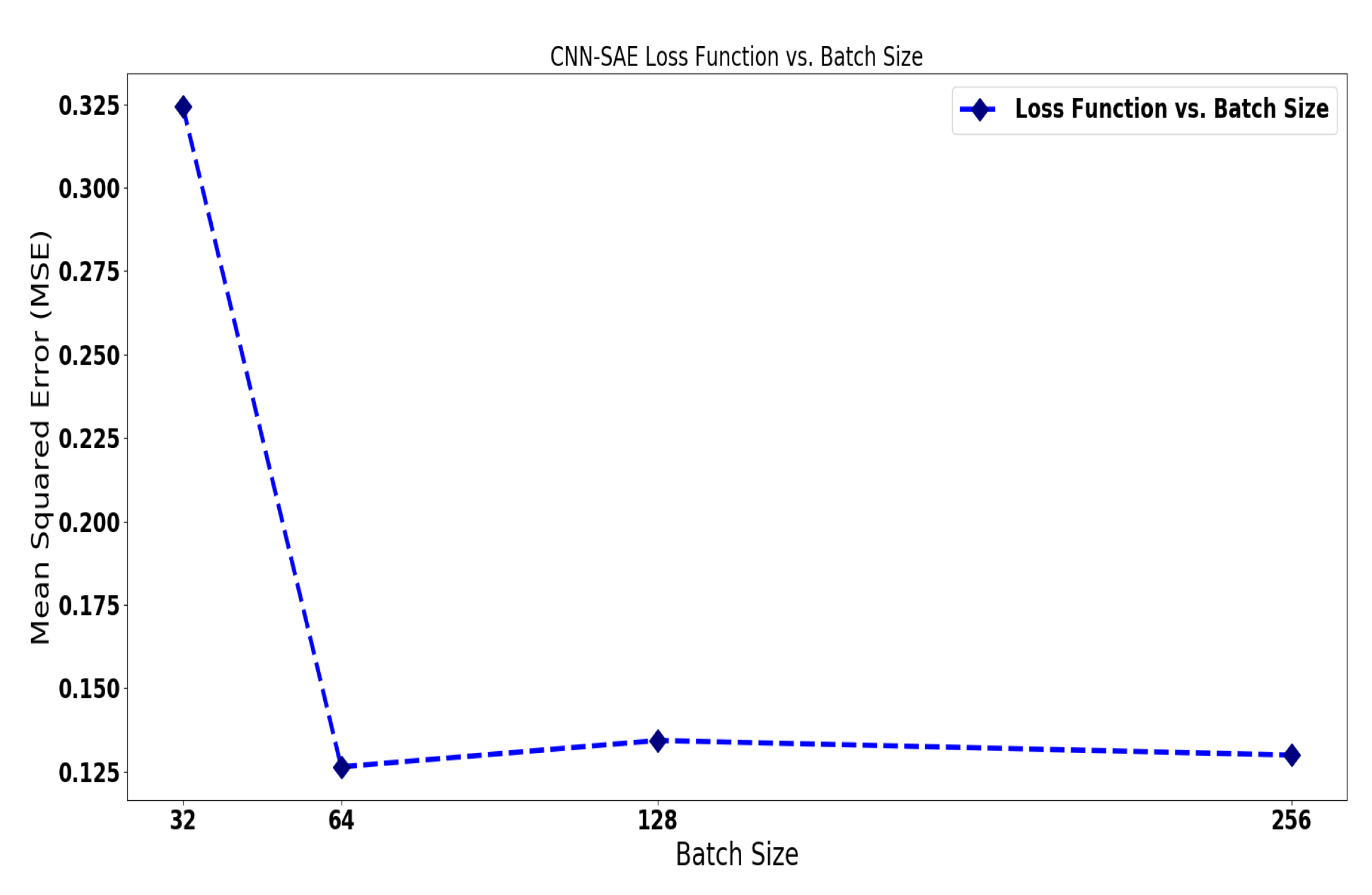
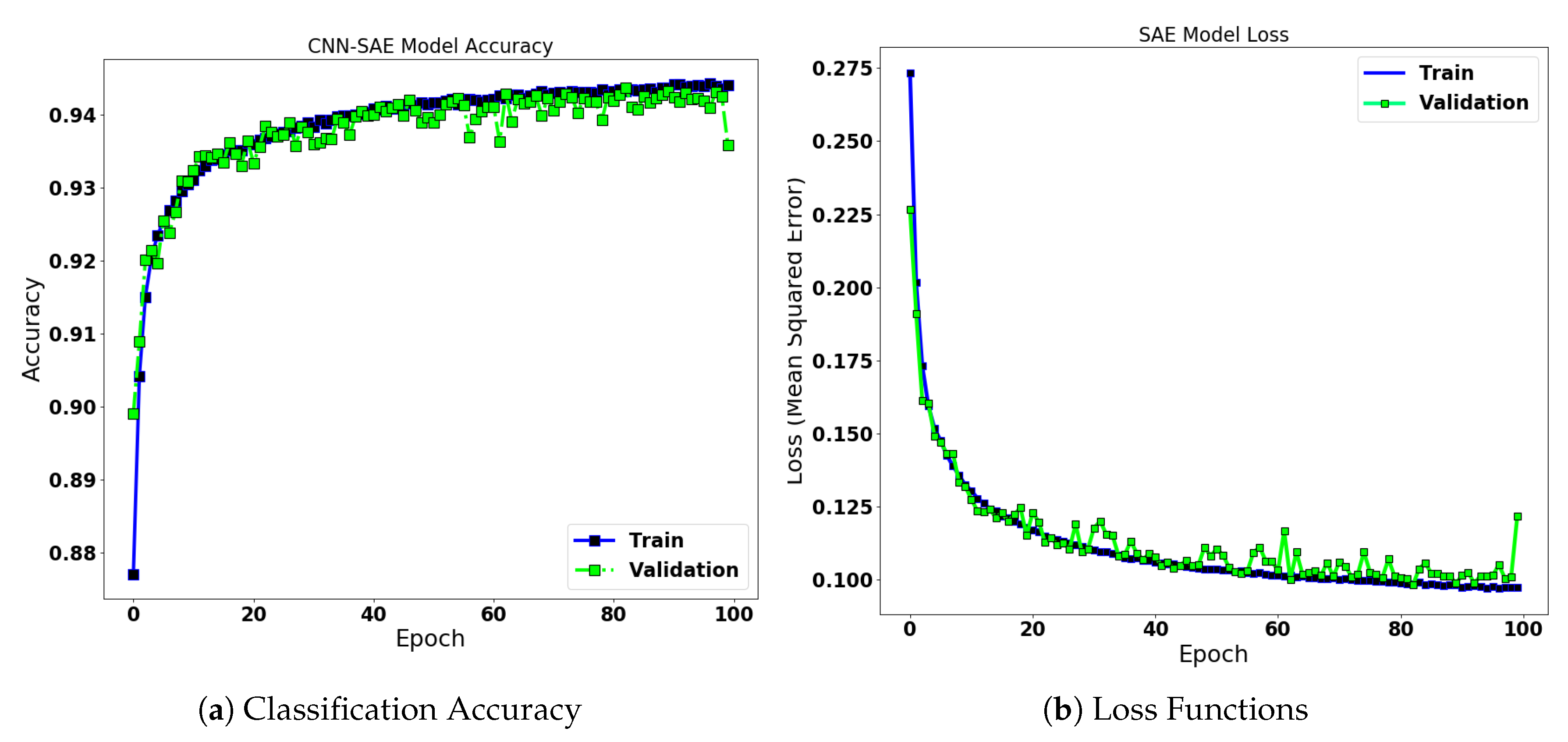
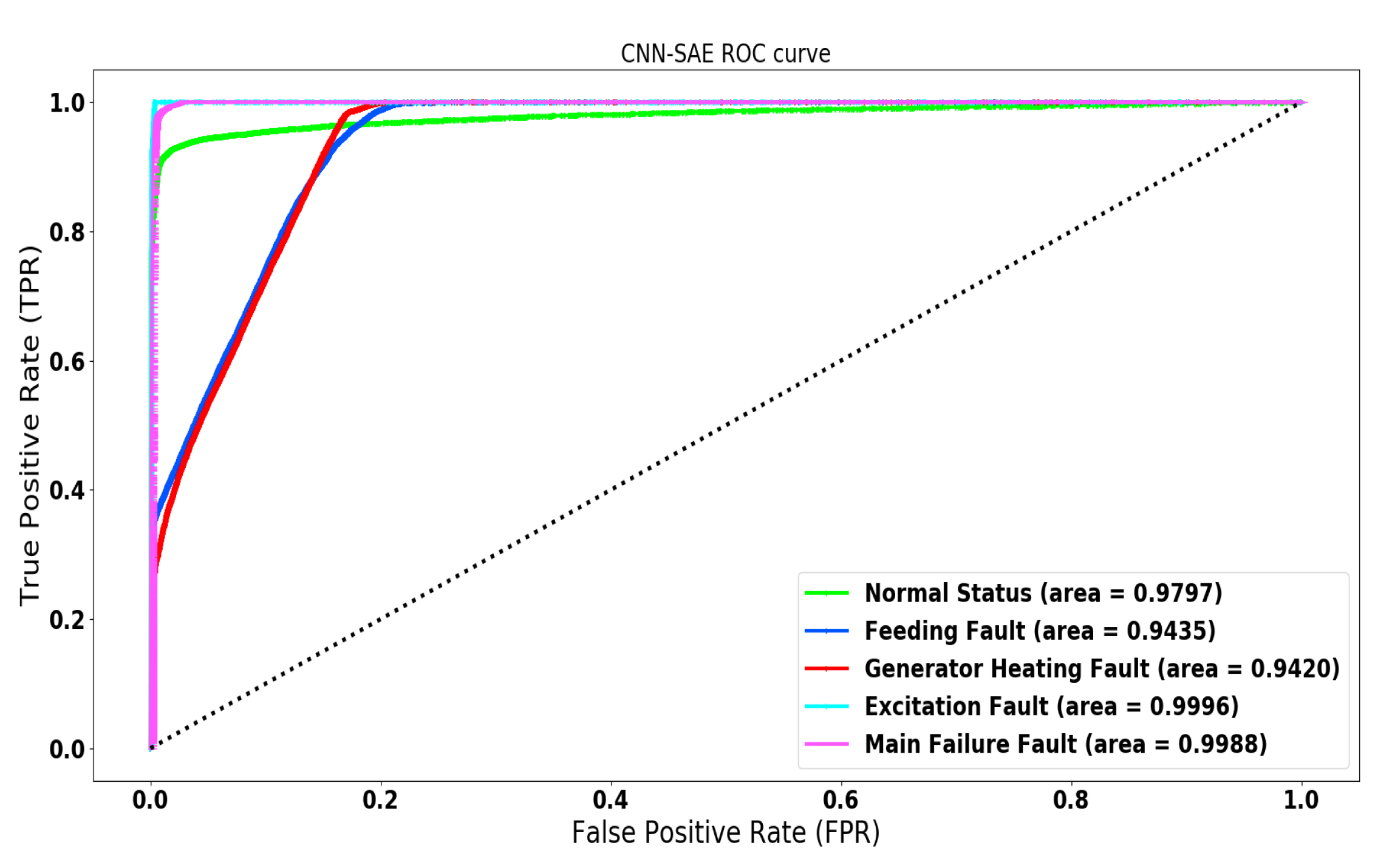
4.3.1. CNN-SAE for Wind Turbine Anomaly Detection
4.3.2. Comparison of the Developed Techniques
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, K.; Zhang, J.; Su, F. Short-Term Reliability Prediction of Key Components of Wind Turbine Based on SCADA Data. IOP Conf. Ser. Mater. Sci. Eng. 2020, 768, 062047. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, H.; Hu, W.; Yan, X. Anomaly detection and fault analysis of wind turbine components based on deep learning network. Renew. Energy 2018, 127, 825–834. [Google Scholar] [CrossRef]
- Wood, D.A. German country-wide renewable power generation from solar plus wind mined with an optimized data matching algorithm utilizing diverse variables. Energy Syst. 2019, 1–43. [Google Scholar] [CrossRef]
- Dey, S.; Pisu, P.; Ayalew, B. A comparative study of three fault diagnosis schemes for wind turbines. IEEE Trans. Control. Syst. Technol. 2015, 23, 1853–1868. [Google Scholar] [CrossRef]
- Odgaard, P.F.; Stoustrup, J.; Nielsen, R.; Damgaard, C. Observer based detection of sensor faults in wind turbines. In Proceedings of the European Wind Energy Conference, Marseille, France, 16–19 March 2009; pp. 4421–4430. [Google Scholar]
- Odgaard, P.F.; Stoustrup, J. Unknown input observer based detection of sensor faults in a wind turbine. In Proceedings of the 2010 IEEE International Conference on Control Applications, Yokohama, Japan, 8–10 September 2010; pp. 310–315. [Google Scholar]
- de Bessa, I.V.; Palhares, R.M.; D’Angelo, M.F.S.V.; Chaves Filho, J.E. Data-driven fault detection and isolation scheme for a wind turbine benchmark. Renew. Energy 2016, 87, 634–645. [Google Scholar] [CrossRef]
- Dong, J.; Verhaegen, M. Data driven fault detection and isolation of a wind turbine benchmark. In Proceedings of the IFAC World Congress, Milan, Italy, 28 August–2 September 2011; Volume 2, pp. 7086–7091. [Google Scholar]
- Tseng, J.P.V.S.; Motoda, L.C.H.; Xu, G. Advances in Knowledge Discovery and Data Mining; Lecture Notes in Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2003; Volume 8444. [Google Scholar]
- Huang, D.S.; Bevilacqua, V.; Premaratne, P. In Proceedings of the 12th International Conference Intelligent Computing Theories and Application, ICIC 2016, Lanzhou, China, 2–5 August 2016; Springer International Publishing: Cham, Switzerland, 2016; Volume 9771. [Google Scholar]
- Meng, X.; Yumoto, T.; Ma, Q.; Sun, L.; Watanabe, C. Database Systems for Advanced Applications; Springer: Berlin, Germany, 2010. [Google Scholar]
- Hao, X.; Zhang, X. Research on Abnormal Detection Based on Improved Combination of K-means and SVDD. In Proceedings of the 2017 International Conference on Power and Energy Engineering, Toronto, ON, Canada, 13–15 September 2017; Volume 114, p. 012014. [Google Scholar]
- Leahy, K.; Hu, R.L.; Konstantakopoulos, I.C.; Spanos, C.J.; Agogino, A.M. Diagnosing wind turbine faults using machine learning techniques applied to operational data. In Proceedings of the 2016 IEEE International Conference on Prognostics and Health Management (ICPHM), Ottawa, ON, Canada, 20–22 June 2016; pp. 1–8. [Google Scholar]
- Zhang, D.; Qian, L.; Mao, B.; Huang, C.; Huang, B.; Si, Y. A data-driven design for fault detection of wind turbines using random forests and XGboost. IEEE Access 2018, 6, 21020–21031. [Google Scholar] [CrossRef]
- Girshick, R. Fast r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar]
- Ng, A. Sparse autoencoder. CS294A Lect. Notes 2011, 72, 1–19. [Google Scholar]
- Ide, H.; Kurita, T. Improvement of learning for CNN with ReLU activation by sparse regularization. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 2684–2691. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Zhao, H.; Lai, Z.; Leung, H.; Zhang, X. A Gentle Introduction to Feature Learning. In Feature Learning and Understanding; Springer: Berlin, Germany, 2020; pp. 1–12. [Google Scholar]
- wt-fdd Dataset. Available online: https://wt-fdd.readthedocs.io/en/latest/ (accessed on 30 March 2020).
- Fotiadou, K.; Velivassaki, T.H.; Voulkidis, A.; Railis, K.; Trakadas, P.; Zahariadis, T. Incidents Information Sharing Platform for Distributed Attack Detection. IEEE Open J. Commun. Soc. 2020, in press. [Google Scholar] [CrossRef]
- Javaid, S.; Kaneko, M.; Tan, Y. Structural Condition for Controllable Power Flow System Containing Controllable and Fluctuating Power Devices. Energies 2020, 13, 1627. [Google Scholar] [CrossRef]
- Görnitz, N.; Kloft, M.; Rieck, K.; Brefeld, U. Toward supervised anomaly detection. J. Artif. Intell. Res. 2013, 46, 235–262. [Google Scholar] [CrossRef]
- Ahmad, S.; Lavin, A.; Purdy, S.; Agha, Z. Unsupervised real-time anomaly detection for streaming data. Neurocomputing 2017, 262, 134–147. [Google Scholar] [CrossRef]
- Filimonov, V.; Periorellis, P.; Starostin, D.; De Baynast, A.; Akchurin, E.; Klimov, A.; Minka, T.; Spengler, A. Unsupervised Anomaly Detection for Arbitrary Time Series. U.S. Patent 9,652,354, 16 May 2017. [Google Scholar]
- Akcay, S.; Atapour-Abarghouei, A.; Breckon, T.P. Ganomaly: Semi-supervised anomaly detection via adversarial training. In Proceedings of the Asian Conference on Computer Vision, Perth, Australia, 2–6 December 2018; pp. 622–637. [Google Scholar]
- Ruff, L.; Vandermeulen, R.A.; Görnitz, N.; Binder, A.; Müller, E.; Müller, K.R.; Kloft, M. Deep Semi-Supervised Anomaly Detection. arXiv 2019, arXiv:1906.02694. [Google Scholar]
- Song, H.; Jiang, Z.; Men, A.; Yang, B. A hybrid semi-supervised anomaly detection model for high-dimensional data. Comput. Intell. Neurosci. 2017, 2017, 8501683. [Google Scholar] [CrossRef] [PubMed]
- Yamanaka, Y.; Iwata, T.; Takahashi, H.; Yamada, M.; Kanai, S. Autoencoding Binary Classifiers for Supervised Anomaly Detection. In Proceedings of the Pacific Rim International Conference on Artificial Intelligence, Yanuca Island, Fiji, 26–30 August 2019; pp. 647–659. [Google Scholar]
- Ma, J.; Sun, L.; Wang, H.; Zhang, Y.; Aickelin, U. Supervised anomaly detection in uncertain pseudoperiodic data streams. ACM Trans. Internet Technol. (TOIT) 2016, 16, 1–20. [Google Scholar] [CrossRef]
- Li, Y.; Liu, S.; Shu, L. Wind turbine fault diagnosis based on Gaussian process classifiers applied to operational data. Renew. Energy 2019, 134, 357–366. [Google Scholar] [CrossRef]
- Zeng, J.; Lu, D.; Zhao, Y.; Zhang, Z.; Qiao, W.; Gong, X. Wind turbine fault detection and isolation using support vector machine and a residual-based method. In Proceedings of the 2013 American Control Conference, Washington, DC, USA, 17–19 June 2013; pp. 3661–3666. [Google Scholar]
- Schlegl, T.; Seeböck, P.; Waldstein, S.M.; Langs, G.; Schmidt-Erfurth, U. f-AnoGAN: Fast unsupervised anomaly detection with generative adversarial networks. Med Image Anal. 2019, 54, 30–44. [Google Scholar] [CrossRef]
- Zhang, C.; Song, D.; Chen, Y.; Feng, X.; Lumezanu, C.; Cheng, W.; Ni, J.; Zong, B.; Chen, H.; Chawla, N.V. A deep neural network for unsupervised anomaly detection and diagnosis in multivariate time series data. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 1409–1416. [Google Scholar]
- Gong, D.; Liu, L.; Le, V.; Saha, B.; Mansour, M.R.; Venkatesh, S.; Hengel, A.V.d. Memorizing normality to detect anomaly: Memory-augmented deep autoencoder for unsupervised anomaly detection. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27–28 October 2019; pp. 1705–1714. [Google Scholar]
- Muniyandi, A.P.; Rajeswari, R.; Rajaram, R. Network anomaly detection by cascading k-Means clustering and C4. 5 decision tree algorithm. Procedia Eng. 2012, 30, 174–182. [Google Scholar] [CrossRef]
- Aytekin, C.; Ni, X.; Cricri, F.; Aksu, E. Clustering and unsupervised anomaly detection with l 2 normalized deep auto-encoder representations. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–6. [Google Scholar]
- Papalexakis, E.E.; Beutel, A.; Steenkiste, P. Network anomaly detection using co-clustering. In Proceedings of the 2012 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining, Istanbul, Turkey, 26–29 August 2012; pp. 1054–1068. [Google Scholar]
- Huang, L.; Nguyen, X.; Garofalakis, M.; Jordan, M.I.; Joseph, A.; Taft, N. In-network PCA and anomaly detection. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 3–6 December 2007; pp. 617–624. [Google Scholar]
- Bezerra, C.G.; Costa, B.S.J.; Guedes, L.A.; Angelov, P.P. An evolving approach to unsupervised and Real-Time fault detection in industrial processes. Expert Syst. Appl. 2016, 63, 134–144. [Google Scholar] [CrossRef]
- Mahmood, S.; Rettkowski, J.; Shallufa, A.; Hübner, M.; Göhringer, D. IP Core Identification in FPGA Configuration Files using Machine Learning Techniques. In Proceedings of the 2019 IEEE 9th International Conference on Consumer Electronics (ICCE-Berlin), Berlin, Germany, 8–11 September 2019; pp. 103–108. [Google Scholar]
- Zhang, S.; Ye, F.; Wang, B.; Habetler, T.G. Semi-Supervised Learning of Bearing Anomaly Detection via Deep Variational Autoencoders. arXiv 2019, arXiv:1912.01096. [Google Scholar]
- Kalavadekar, P.N.; Sane, S.S. Building an Effective Intrusion Detection System using combined Signature and Anomaly Detection Techniques. IJITEE 2019. [Google Scholar] [CrossRef]
- Mirza, A.H.; Cosan, S. Computer network intrusion detection using sequential LSTM neural networks autoencoders. In Proceedings of the 2018 26th Signal Processing and Communications Applications Conference (SIU), Izmir, Turkey, 2–5 May 2018; pp. 1–4. [Google Scholar]
- Fink, O.; Wang, Q.; Svensén, M.; Dersin, P.; Lee, W.J.; Ducoffe, M. Potential, challenges and future directions for deep learning in prognostics and health management applications. Eng. Appl. Artif. Intell. 2020, 92, 103678. [Google Scholar] [CrossRef]
- Dienst, S.; Beseler, J. Automatic anomaly detection in offshore wind SCADA data. In Proceedings of the WindEurope Summit, Hamburg, Germany, 25–27 May 2016. [Google Scholar]
- Park, T.; Casella, G. The bayesian lasso. J. Am. Stat. Assoc. 2008, 103, 681–686. [Google Scholar] [CrossRef]
- Laouti, N.; Sheibat-Othman, N.; Othman, S. Support vector machines for fault detection in wind turbines. IFAC Proc. Vol. 2011, 44, 7067–7072. [Google Scholar] [CrossRef]
- Pandit, R.K.; Infield, D. SCADA-based wind turbine anomaly detection using Gaussian process models for wind turbine condition monitoring purposes. IET Renew. Power Gener. 2018, 12, 1249–1255. [Google Scholar] [CrossRef]
- Cui, Y.; Bangalore, P.; Tjernberg, L.B. An Anomaly Detection Approach Using Wavelet Transform and Artificial Neural Networks for Condition Monitoring of Wind Turbines’ Gearboxes. In Proceedings of the 2018 Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018; pp. 1–7. [Google Scholar]
- Hecht-Nielsen, R. Theory of the backpropagation neural network. In Neural Networks for Perception; Elesvier: Amsterdam, The Netherlands, 1992; pp. 65–93. [Google Scholar]
- Gribonval, R.; Nielsen, M. Sparse representations in unions of bases. IEEE Trans. Inf. Theory 2003, 49, 3320–3325. [Google Scholar] [CrossRef]
- Van Erven, T.; Harremos, P. Rényi divergence and Kullback-Leibler divergence. IEEE Trans. Inf. Theory 2014, 60, 3797–3820. [Google Scholar] [CrossRef]
- Malhotra, P.; Vig, L.; Shroff, G.; Agarwal, P. Long Short Term Memory Networks for Anomaly Detection in Time Series; Presses Universitaires de Louvain: New Leuven, Belgium, 2015; p. 89. [Google Scholar]
- Gong, M.; Pan, L.; Song, T.; Zhang, T. Bio-inspired Computing–Theories and Applications. In Proceedings of the International Conference on Bio-Inspired Computing: Theories and Applications, Zhengzhou, China, 22–25 November 2019. [Google Scholar] [CrossRef]
- Davis, J.; Goadrich, M. The relationship between Precision-Recall and ROC curves. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; pp. 233–240. [Google Scholar]
- Xu, B.; Wang, N.; Chen, T.; Li, M. Empirical evaluation of rectified activations in convolutional network. arXiv 2015, arXiv:1505.00853. [Google Scholar]
| Time Information | Main Status | Sub-Status | Description-Code |
|---|---|---|---|
| 13 July 2014 15:07:25 | 0 | 0 | Normal State-The Turbine is in Operational Mode |
| 14 July 2014 12:32:30 | 80 | 21 | Excitation Fault-Overvoltage DC-link |
| 17 August 2014 17:20:26 | 62 | 3 | Feeding Fault-Load shedding |
| 14 May 2014 14:41:31 | 9 | 3 | Generator Heating Fault-Hygrostat Inverter |
| 10 June 2014 00:03:10 | 60 | 2 | Main Failure Fault: Start Delay |
| Layer | Output Shape | Parameters |
|---|---|---|
| Input | (1, 29) | 0 |
| LSTM | (1, 50) | 16.000 |
| LSTM | (1, 50) | 20.200 |
| Repeat Vector | (1, 50) | 0 |
| LSTM | (1, 50) | 20.200 |
| LSTM | (1, 50) | 20.200 |
| Output (Time Distributed) | (1, 29) | 1.479 |
| Classification (Dense) | (1, 5) | 150 |
| Ground Truth vs. Prediction | Normal State | Feed. Fault | Gen. Heat. Fault | Exc. Fault | Main Failure |
|---|---|---|---|---|---|
| Normal State | 14,521 | 504 | 2407 | 280 | 1752 |
| Feed. Fault | 560 | 8185 | 10368 | 227 | 221 |
| Gen.Heat.Fault | 580 | 2484 | 16,480 | 155 | 32 |
| Exc.Fault | 192 | 182 | 591 | 18,699 | 0 |
| Main Failure Fault | 29 | 0 | 80 | 0 | 19,525 |
| Layer | Output Shape | Parameters |
|---|---|---|
| Input | (1, 29) | 0 |
| Conv1D | (27, 64) | 256 |
| Max Pooling1D | (13, 64) | 0 |
| Conv1D | (11, 32) | 6.176 |
| Max Pooling1D | (5, 32) | 0 |
| Conv1D | (3, 32) | 3.104 |
| Upsampling1D | (6, 32) | 0 |
| Conv1D | (4, 64) | 6.208 |
| Upsampling1D | (8, 64) | 0 |
| Flatten | (512) | 0 |
| Dense | (29, 1) | 14.877 |
| Classification (Dense) | (5, 1) | 150 |
| Ground Truth vs. Prediction | Normal State | Feed. Fault | Gen. Heat. Fault | Exc. Fault | Main Failure |
|---|---|---|---|---|---|
| Normal State | 296 | 801 | 43 | 202 | |
| Feed. Fault | 278 | 9.251 | 77 | 5 | |
| Gen.Heat.Fault | 390 | 2.770 | 74 | 1 | |
| Exc.Fault | 0 | 266 | 0 | 0 | |
| Main Failure Fault | 1258 | 0 | 0 | 0 |
| Methods | Stacked AE | LSTM-SAE | CNN-SAE | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Metrics | Precision | Recall | F-1 Score | Precision | Recall | F-1 Score | Precision | Recall | F-1 Score |
| Normal Status | 0.88 | 0.86 | 0.87 | 0.75 | 0.82 | 0.90 | 0.92 | ||
| Feeding Fault | 0.75 | 0.72 | 0.42 | 0.53 | 0.33 | 0.49 | |||
| Generator Fault | 0.57 | 0.84 | 0.70 | 0.65 | 0.66 | 0.84 | |||
| Excitation Fault | 0.98 | 0.98 | 0.97 | 0.95 | 0.96 | ||||
| Main Failure Fault | 0.93 | 0.91 | 0.95 | 0.94 | |||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fotiadou, K.; Velivassaki, T.H.; Voulkidis, A.; Skias, D.; De Santis, C.; Zahariadis, T. Proactive Critical Energy Infrastructure Protection via Deep Feature Learning. Energies 2020, 13, 2622. https://doi.org/10.3390/en13102622
Fotiadou K, Velivassaki TH, Voulkidis A, Skias D, De Santis C, Zahariadis T. Proactive Critical Energy Infrastructure Protection via Deep Feature Learning. Energies. 2020; 13(10):2622. https://doi.org/10.3390/en13102622
Chicago/Turabian StyleFotiadou, Konstantina, Terpsichori Helen Velivassaki, Artemis Voulkidis, Dimitrios Skias, Corrado De Santis, and Theodore Zahariadis. 2020. "Proactive Critical Energy Infrastructure Protection via Deep Feature Learning" Energies 13, no. 10: 2622. https://doi.org/10.3390/en13102622
APA StyleFotiadou, K., Velivassaki, T. H., Voulkidis, A., Skias, D., De Santis, C., & Zahariadis, T. (2020). Proactive Critical Energy Infrastructure Protection via Deep Feature Learning. Energies, 13(10), 2622. https://doi.org/10.3390/en13102622





