The Use of Generalized Gaussian Distribution in Vibroacoustic Detection of Power Transformer Core Damage
Abstract
:1. Introduction
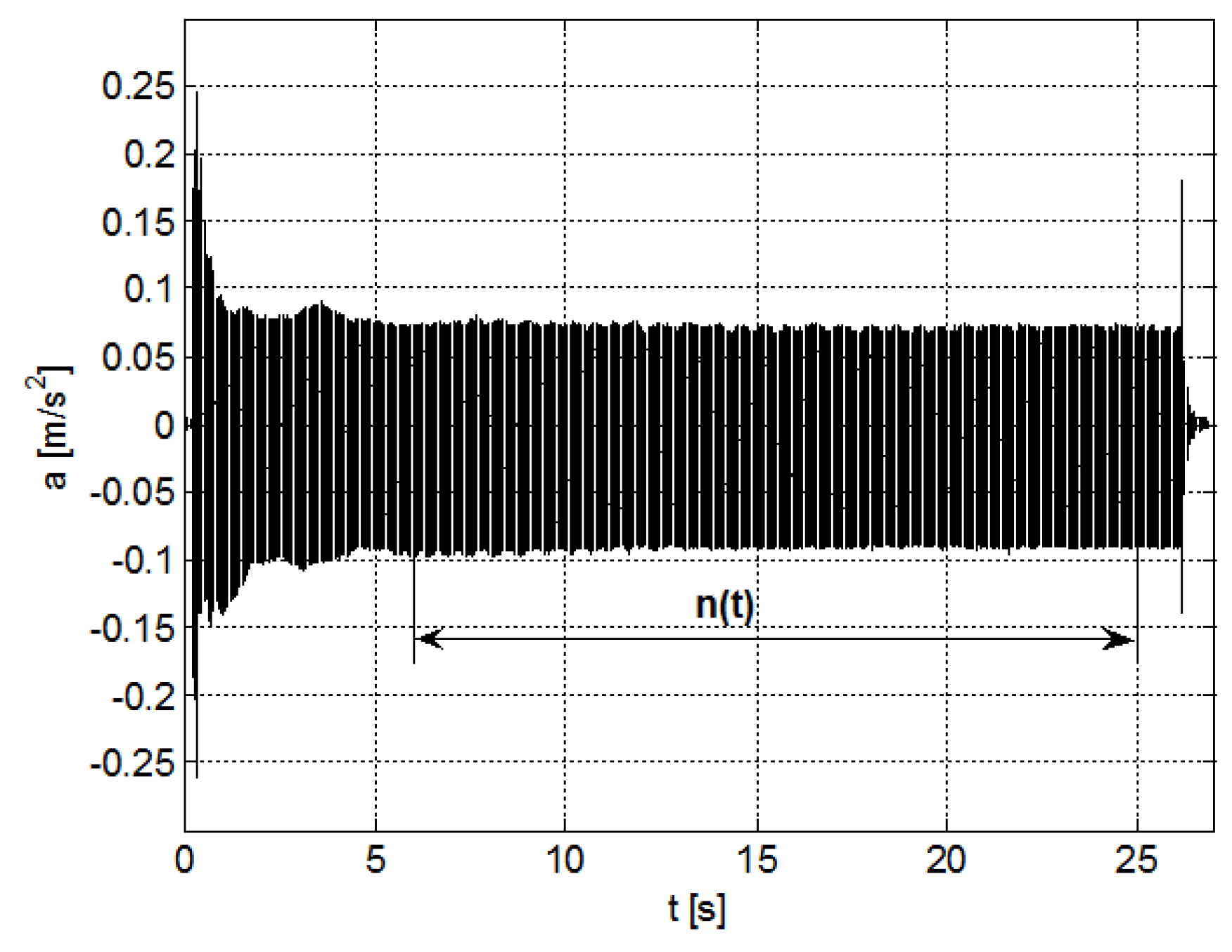
Characteristics of the Vibroacoustic Diagnostic Method
- (a)
- via transformer oil;
- (b)
- via the lid and base in direct mechanical contact with the active part.
2. Materials and Methods
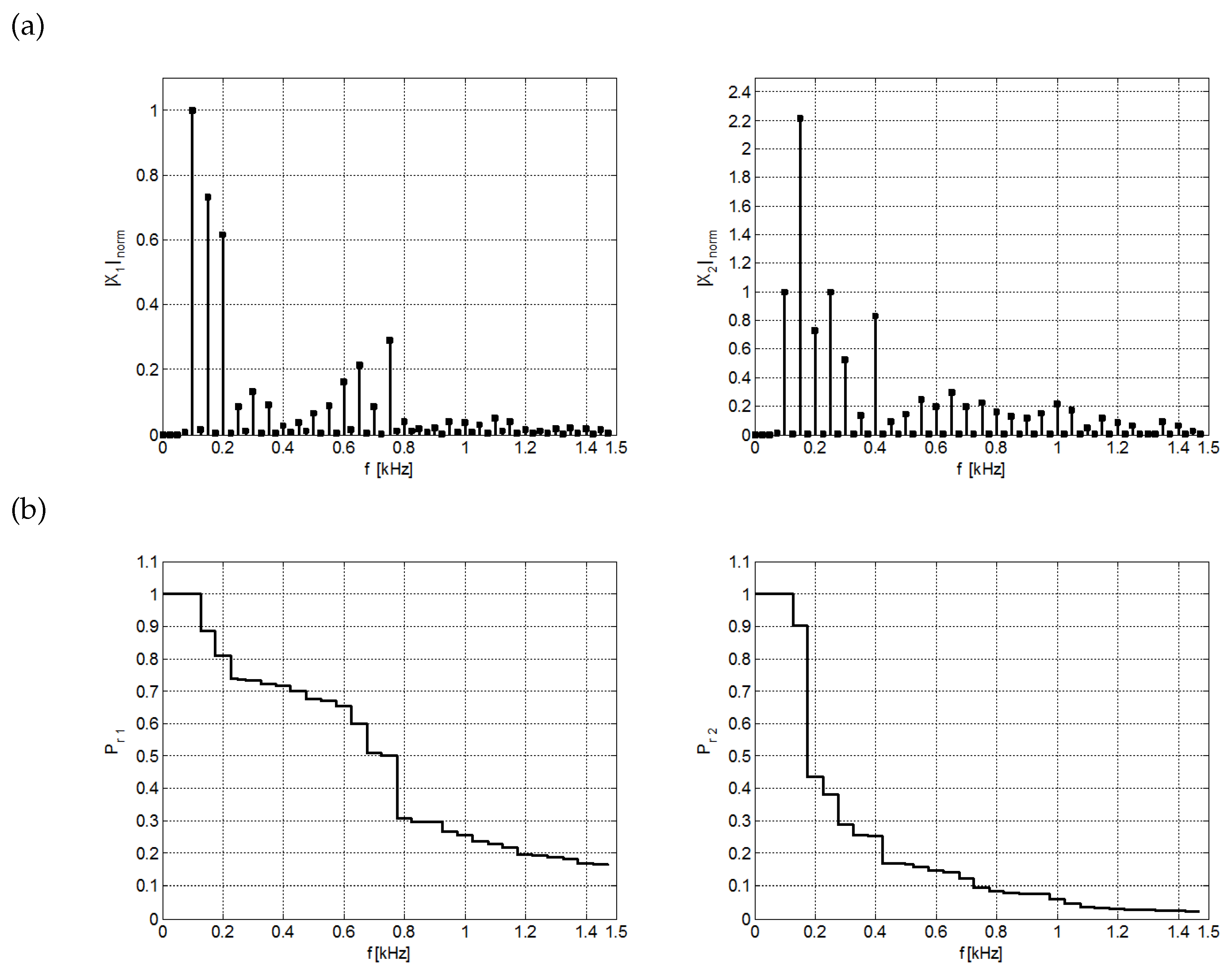
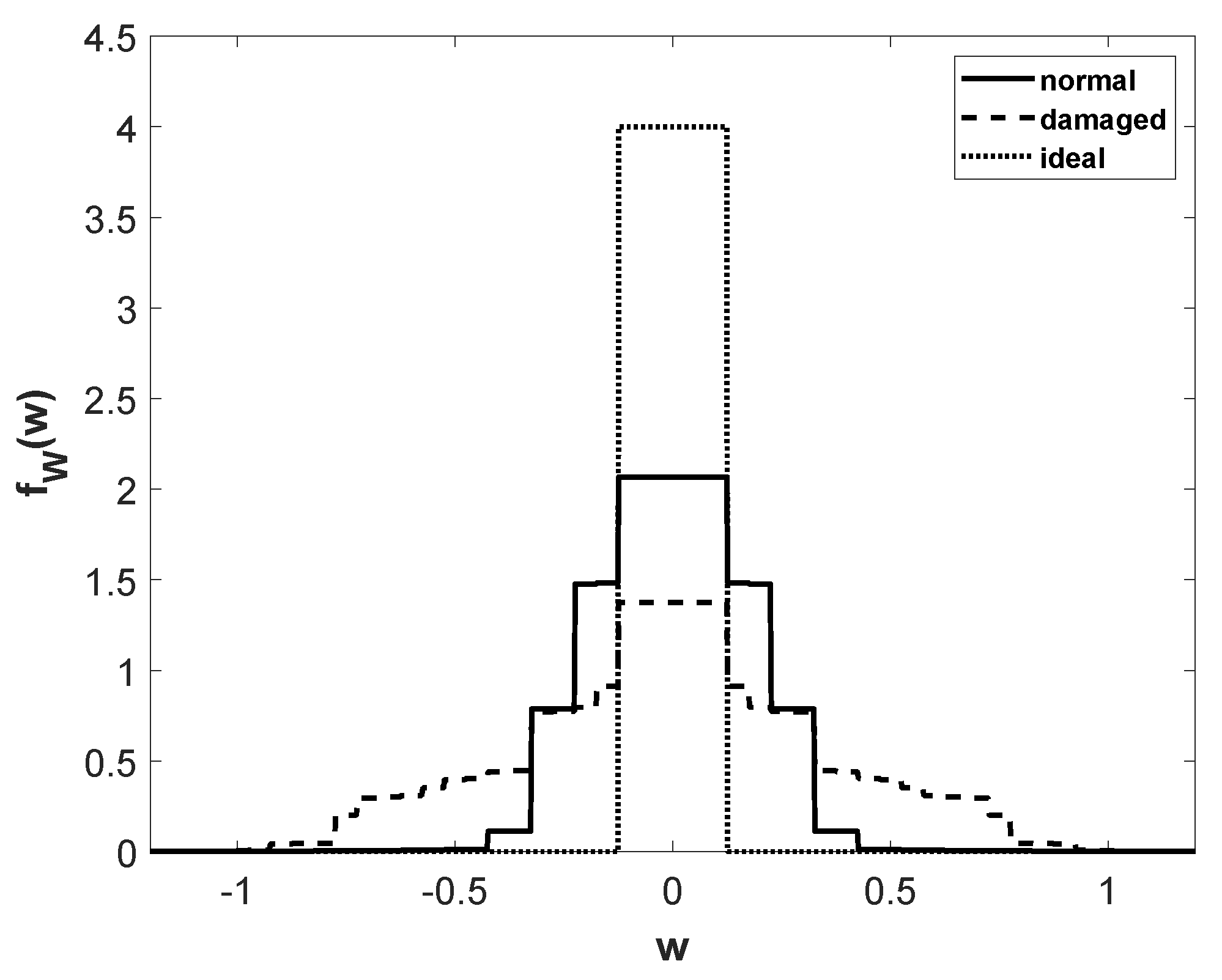
2.1. Density Function of Transformer Detector
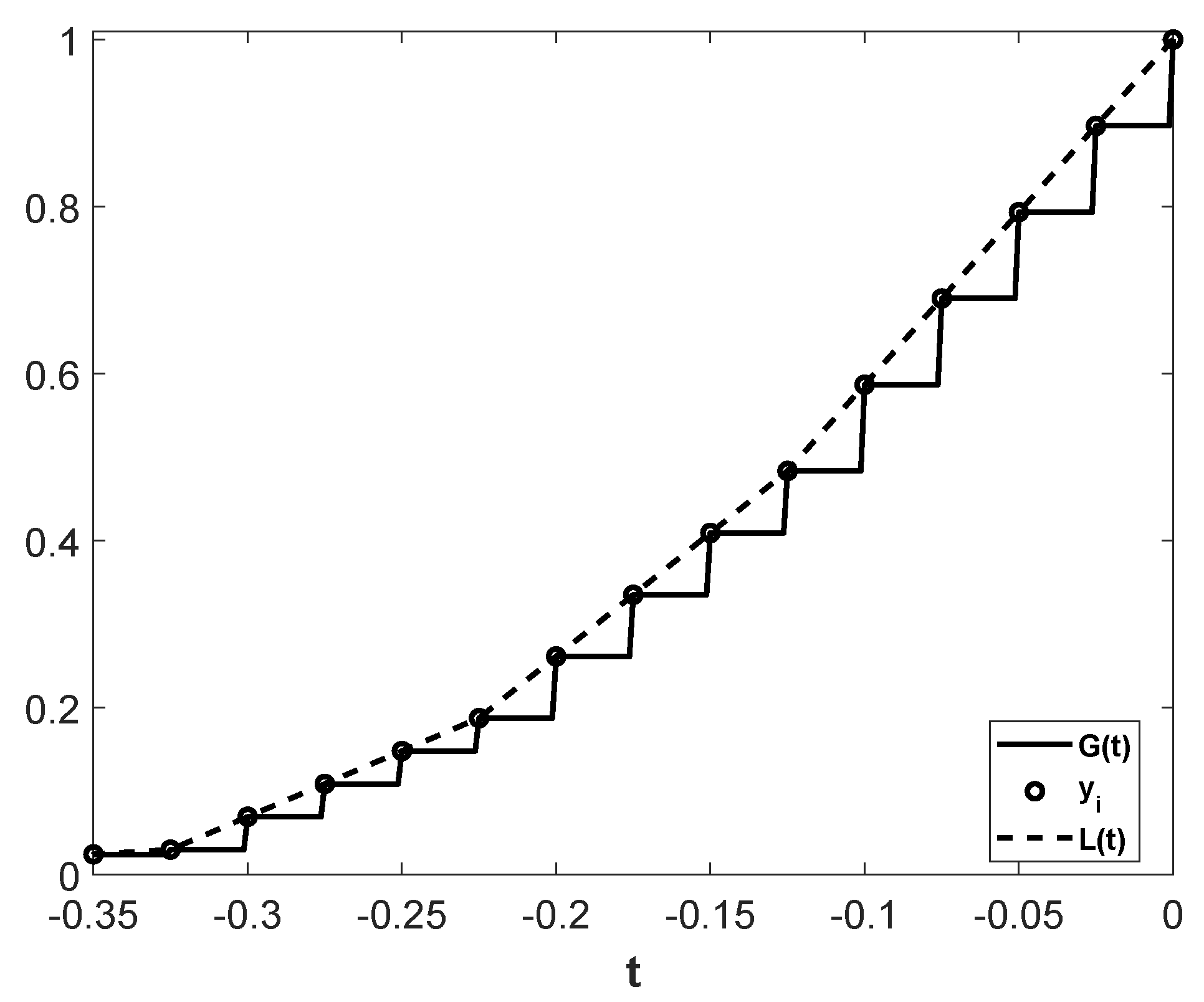
2.2. Generator for the Damaged Transformer Detector
- Generate a uniformly distributed random variable Z (16).
- Calculate a random variable T from (15).
- Generate a random variable S with (18).
- Calculate a random variable W from (21).
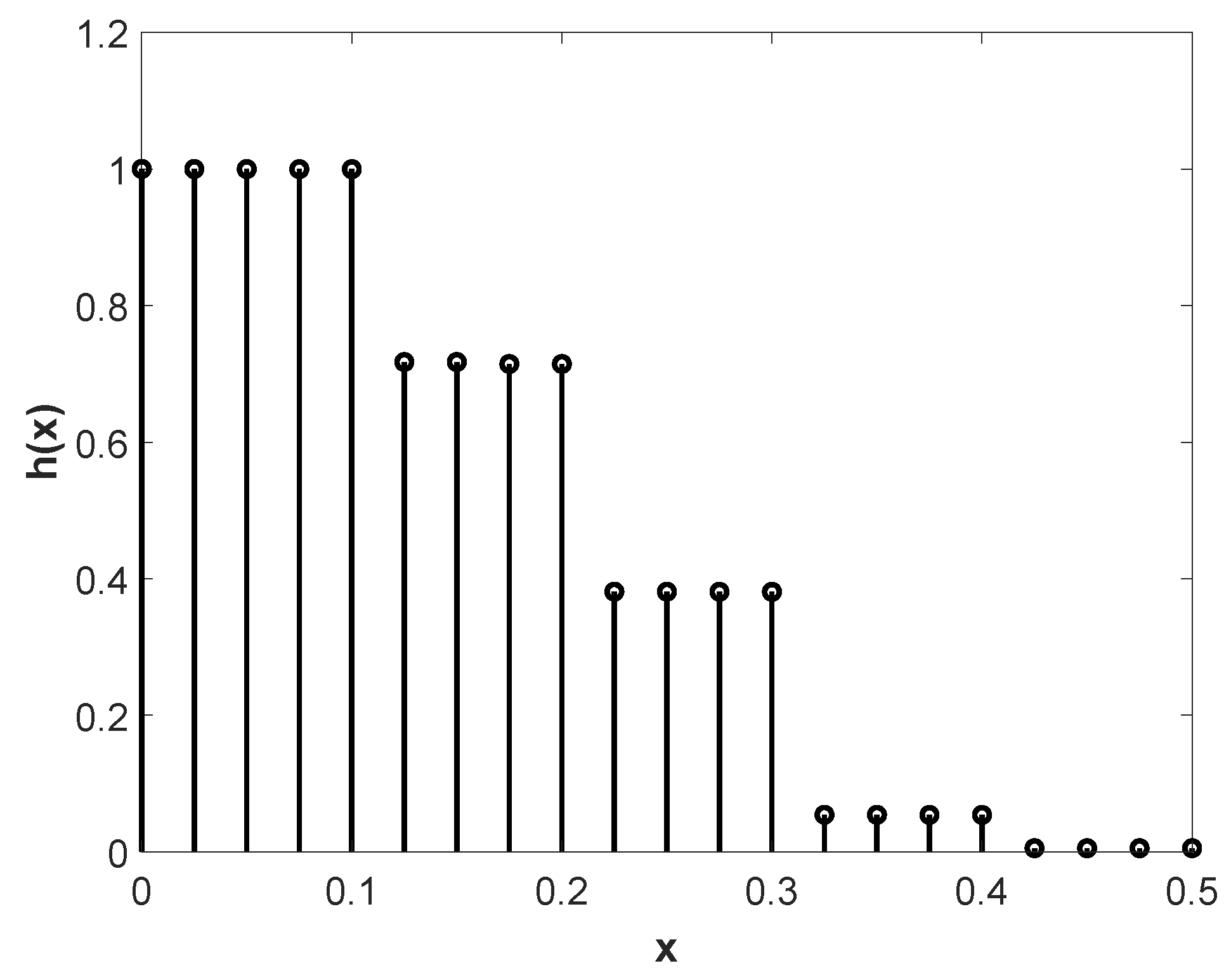
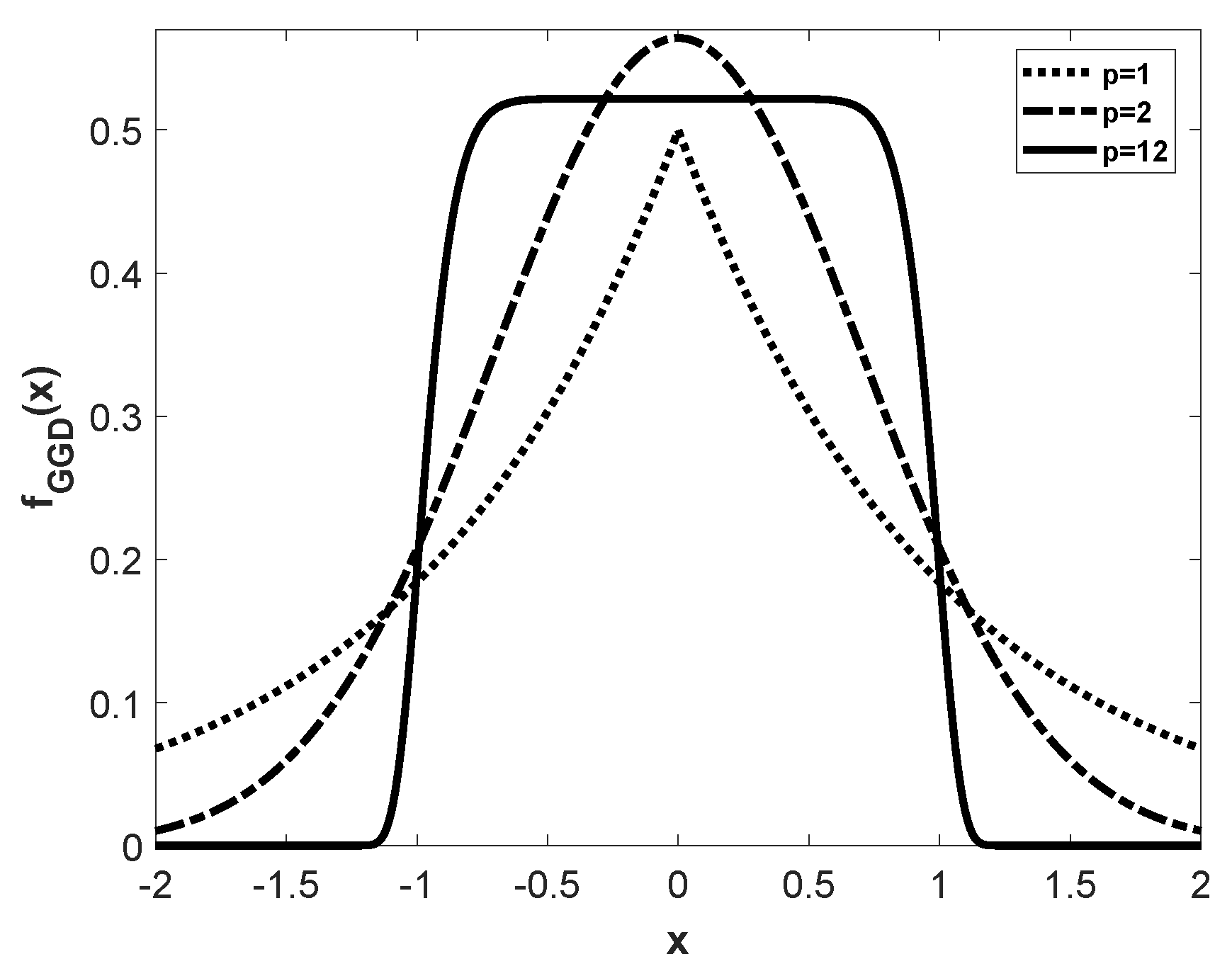
2.3. Generalized Gaussian Distribution
- corresponds to the Laplacian Distribution (LD).
- corresponds to the Gaussian Distribution (GD).
- When , the GGD density function becomes a uniform distribution.
- When , approaches an impulse function.
- was considered in [4].
- was discussed in [5].
- A more general approach for the exponents , was introduced in [6].
- The stereoscopic image quality assessment tool was designed in [10].
- More facial details in the initial image synthesis were introduced in [11].
- An efficient method to remove haze from a single image was given in [12].
- The statistical properties of natural images used to get the Natural Scene Statistics (NSS) model were modeled in [13].
- An alternative approach to the binarization of historical degraded document images was presented in [14].
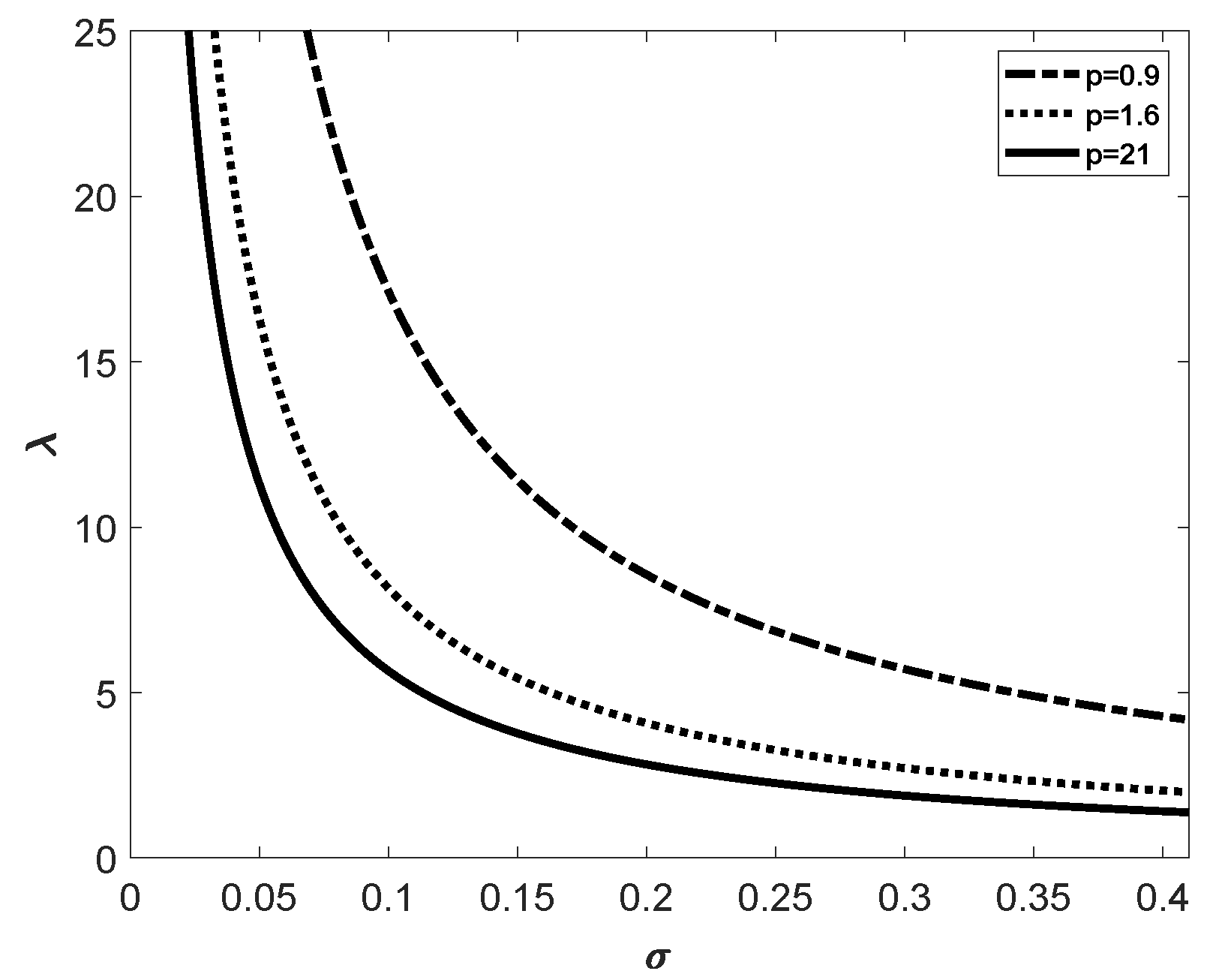
2.4. The GGD Parameters
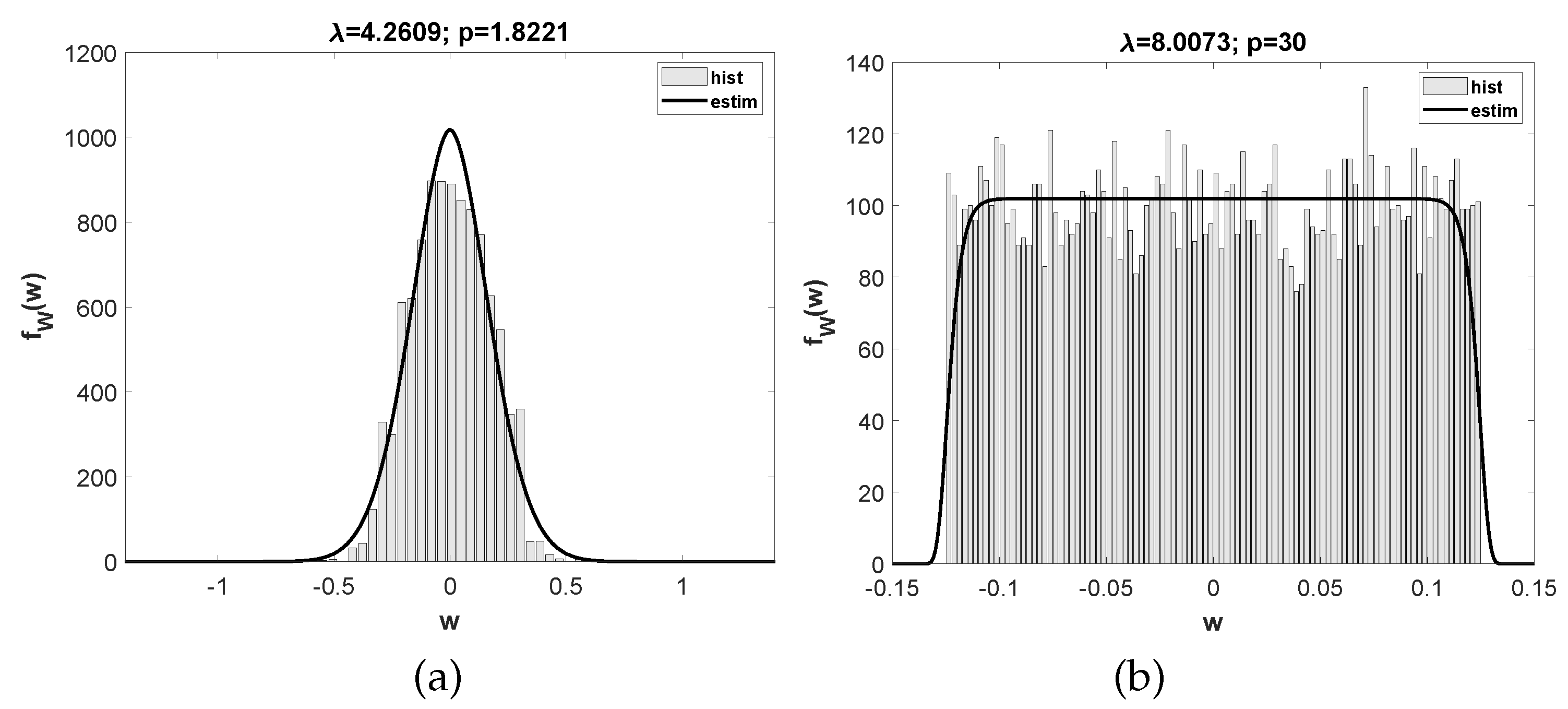
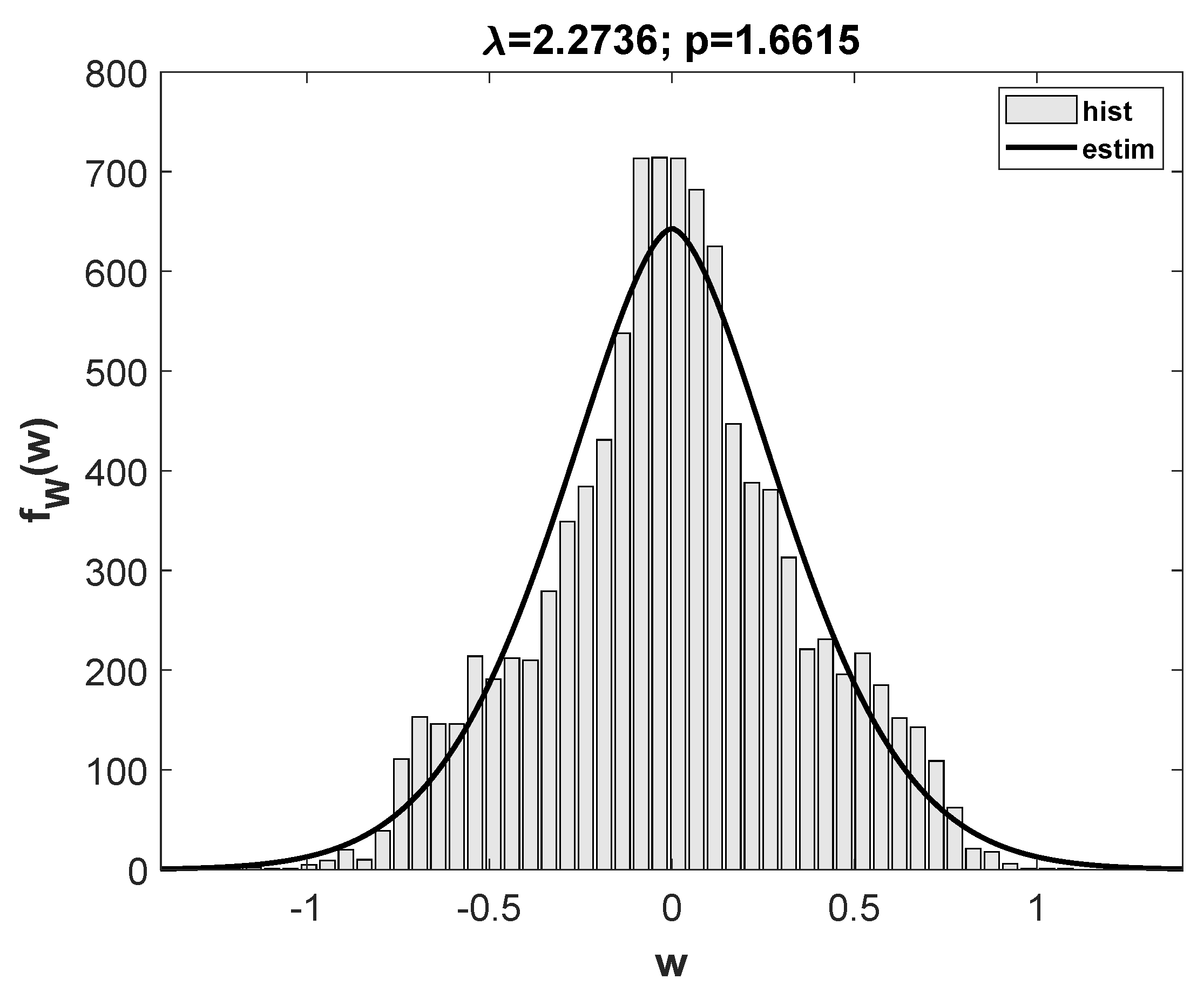
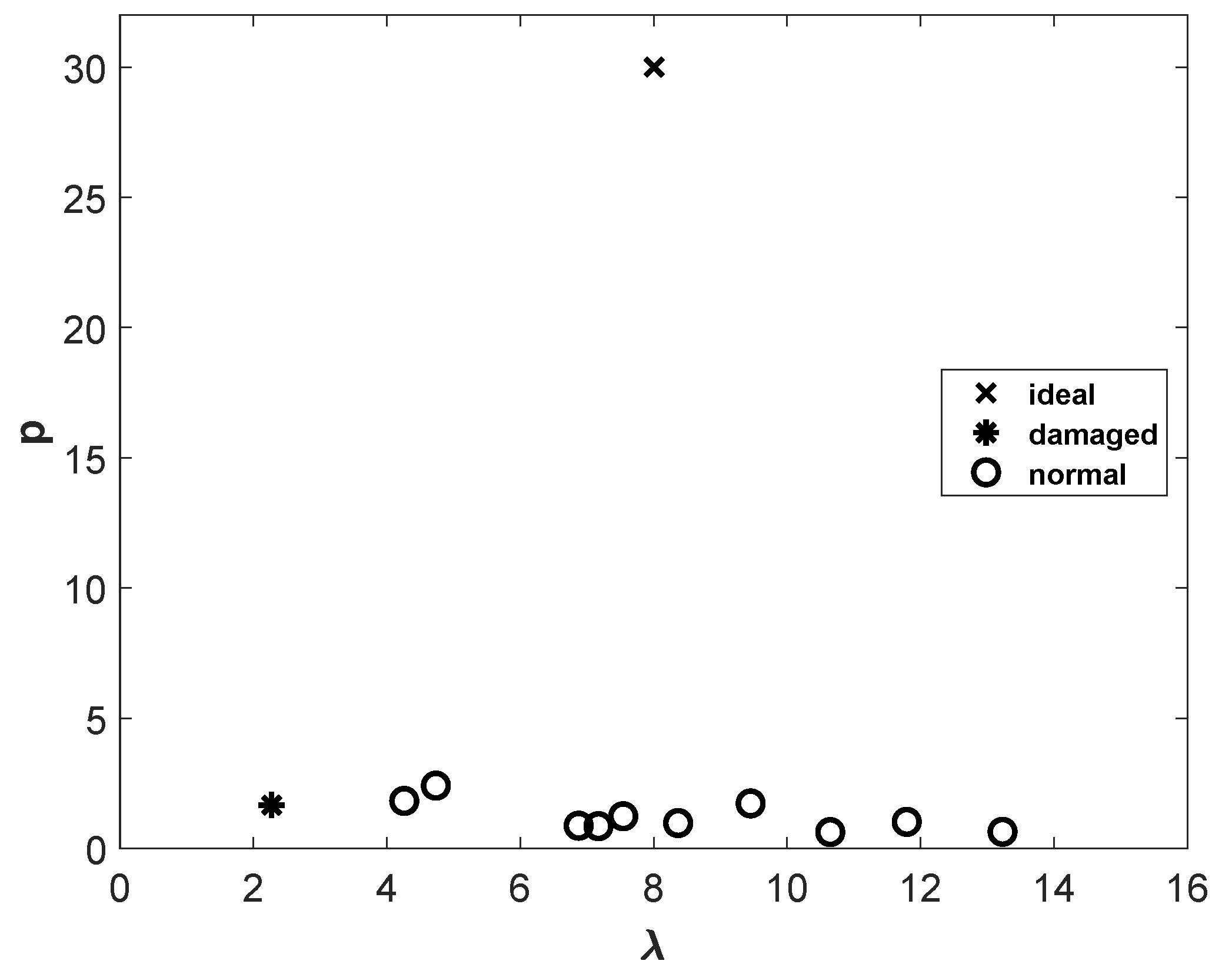
3. Results
- Frequency Response Analysis (FRA method),
- gas chromatography (DGA—Dissolved Gas Analysis),
- measurements of furans contents,
- measurements of water contents,
- tests of basic electrical properties: dielectric losses coefficient (tan ), volume resistivity, and dielectric strength.
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ji, S.; Luo, Y.; Li, Y. Research on extraction technique of transformer core fundamental frequency vibration based on OLCM. IEEE Trans. Power Deliv. 2006, 21, 1981–1988. [Google Scholar] [CrossRef]
- Kornatowski, E.; Banaszak, S. Diagnostics of a Transformer’s Active Part with Complementary FRA and VM Measurements. IEEE Trans. Power Deliv. 2014, 29, 1398–1406. [Google Scholar] [CrossRef]
- Kornatowski, E. Mechanical-Condition Assessment of Power Transformer Using Vibroacoustic Analysis. Key Eng. Mater. 2012, 500, 40–44. [Google Scholar] [CrossRef]
- Chapeau-Blondeau, F.; Monir, A. Numerical Evaluation of the Lambert W Function and Application to Generation of Generalized Gaussian Noise With Exponent 1/2. IEEE Trans. Signal Process. 2002, 50, 2160–2165. [Google Scholar] [CrossRef] [Green Version]
- Krupiński, R. Reconstructed quantized coefficients modeled with generalized Gaussian distribution with exponent 1/3. Image Process. Commun. 2016, 21, 5–12. [Google Scholar] [CrossRef] [Green Version]
- Krupiński, R. Modeling Quantized Coefficients with Generalized Gaussian Distribution with Exponent 1/m, m = 2, 3, …. In Proceedings of the Man-Machine Interactions 5: 5th International Conference on Man-Machine Interactions, ICMMI 2017, Kraków, Poland, 3–6 October 2017; Gruca, A., Czachórski, T., Harezlak, K., Kozielski, S., Piotrowska, A., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 228–237. [Google Scholar]
- Clarke, R.J. Transform Coding of Images; Academic: New York, NY, USA, 1985. [Google Scholar]
- Du, Y. Ein sphärisch invariantes Verbunddichtemodell für Bildsignale. Archiv für Elektronik und Übertragungstechnik 1991, AEÜ-45, 148–159. [Google Scholar]
- Olver, F.W.J. Asymptotics and Special Functions; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Ma, L.; Wang, X.; Liu, Q.; Ngan, K.N. Reorganized DCT-based image representation for reduced reference stereoscopic image quality assessment. Neurocomputing 2016, 215, 21–31. [Google Scholar] [CrossRef]
- Song, C.; Li, F.; Dang, Y.; Gao, H.; Yan, Z.; Zuo, W. Structured detail enhancement for cross-modality face synthesis. Neurocomputing 2016, 212, 107–120. [Google Scholar] [CrossRef]
- Wang, R.; Li, R.; Sun, H. Haze removal based on multiple scattering model with superpixel algorithm. Signal Process. 2016, 127, 24–36. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, J.; Xie, X.; Li, L.; Shi, G. Blind image quality assessment with improved natural scene statistics model. Digit. Signal Process. 2016, 57, 56–65. [Google Scholar] [CrossRef]
- Krupiński, R.; Lech, P.; Tecław, M.; Okarma, K. Binarization of Degraded Document Images with Generalized Gaussian Distribution. In Computational Science—ICCS 2019; Rodrigues, J.M.F., Cardoso, P.J.S., Monteiro, J., Lam, R., Krzhizhanovskaya, V.V., Lees, M.H., Dongarra, J.J., Sloot, P.M., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 177–190. [Google Scholar]
- Yu, S.; Zhang, A.; Li, H. A review of estimating the shape parameter of generalized Gaussian distribution. J. Comput. Inf. Syst. 2012, 21, 9055–9064. [Google Scholar]
- Krupiński, R.; Purczyński, J. Approximated fast estimator for the shape parameter of generalized Gaussian distribution. Signal Process. 2006, 86, 205–211. [Google Scholar] [CrossRef]
- Krupiński, R. Approximated fast estimator for the shape parameter of generalized Gaussian distribution for a small sample size. Bull. Polish Acad. Sci. Tech. Sci. 2015, 63, 405–411. [Google Scholar] [CrossRef] [Green Version]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krupiński, R.; Kornatowski, E. The Use of Generalized Gaussian Distribution in Vibroacoustic Detection of Power Transformer Core Damage. Energies 2020, 13, 2525. https://doi.org/10.3390/en13102525
Krupiński R, Kornatowski E. The Use of Generalized Gaussian Distribution in Vibroacoustic Detection of Power Transformer Core Damage. Energies. 2020; 13(10):2525. https://doi.org/10.3390/en13102525
Chicago/Turabian StyleKrupiński, Robert, and Eugeniusz Kornatowski. 2020. "The Use of Generalized Gaussian Distribution in Vibroacoustic Detection of Power Transformer Core Damage" Energies 13, no. 10: 2525. https://doi.org/10.3390/en13102525
APA StyleKrupiński, R., & Kornatowski, E. (2020). The Use of Generalized Gaussian Distribution in Vibroacoustic Detection of Power Transformer Core Damage. Energies, 13(10), 2525. https://doi.org/10.3390/en13102525




