Abstract
This paper optimizes opening positions on building facades to maximize the natural ventilation’s potential for ventilation and cooling purposes. The paper demonstrates how to apply computational fluid dynamics (CFD) simulation results to architectural design processes, and how the CFD-driven decisions impact ventilation and cooling: (1) background: A CFD helps predict the natural ventilation’s potential, the integration of CFD results into design decision-making has not been actively practiced; (2) methods: Pressure data on building facades were obtained from CFD simulations and mapped into the 3D modeling environment, which were then used to identify optimal positions of two openings of a zone. The effect of the selected opening positions was validated with building energy simulations; (3) results: The cross-comparison study of different window positions based on different geographical locations quantified the impact on natural ventilation effectiveness; and (4) conclusions: The optimized window position was shown to be effective, and some optimal solutions contradicted the typical cross-ventilation strategy.
1. Introduction
From visual, thermal, and aesthetic perspectives to the energy perspective, windows in architecture are the determinant of various design decisions [1,2,3]. Regarding natural ventilation, operable windows are the key component where air enters and exits; therefore, how openings are designed and placed may significantly influence the airflow. One of the few functions that have not attracted much attention is the relationship between the placement of windows and its cooling effect. If architects work on a design project with a mission to reduce cooling energy by utilizing natural ventilation as much as possible, where should they place operable windows? If there are many windows in an office and an employee wants to operate as few windows as possible, which window should be opened to cool the space?
1.1. Optimization of Opening Specifications for Natural Ventilation Performance
General design recommendations for natural ventilation include that the opening height should match the occupants’ [4], and cross ventilation should be chosen over single-sided ventilation when the depth of the room is greater than 2.5 times the height of the room [5]. In addition to these rules of thumb, researchers have studied the relationship between several specifications of windows and natural ventilation’s performance.
Some researchers paid attention to the window-to-wall ratio (WWR) and opening areas that greatly affected the thermal property of building envelops and incoming airflows. Alibaba [6] examined how thermal metrics, including the percentage of dissatisfied people (PPD) and predicted mean vote (PMV), which changed with a different WWR and opening areas in a hot and humid climate. Wang et al. [7] optimized WWR on each façade based on Singaporian weather and found out that 0.24 was the optimum WWR given that appropriate shading devices were applied. The authors also provided recommendations on the thermal properties of building materials for each building orientation for residential buildings under such a climate.
Others focused on the operation of windows for natural ventilation. Sorgato et al. [8] conducted energy simulations and found out that the daily schedule of the window operation influenced the thermal environment concerning building materials. The relationship between the thermal environment and the operation was also found in measurements done by Lai et al. [9]. The authors investigated actual residents’ behavior for a year in 14 cities in China, and suggested general operations that could be applied to different climates based on their findings from the measurements.
Besides the opening specifications mentioned above, Liu and Lee [10] tried to find the optimum window opening degrees with various window types for a residential building in Hong Kong. Lee et al. [11] devised a window system that could adapt to thermal and ventilative needs. Stavrakakis et al. [12] examined optimal height differences between openings for every 10 degrees of wind incident angles.
One of the less studied is the identification of the optimal window positions. As previous studies indicated, the optimal values vary by given conditions including climates, designs, or operations. Therefore, this paper developed a framework that optimized window positions for wind-driven natural ventilation during early design phases, identified optimal opening positions, and tested the natural ventilation performance of the optimal positions with energy simulations.
1.2. Optimization Method Integrated into the Design Process
As building simulation and multifaceted workflow are becoming frequently integrated into architectural design, the need for interactive building design and simulation is growing. As a computation method to optimize opening positions, this paper utilized existing programs and developed customized functions.
The parametrization and the optimization of our study were mostly conducted within a 3D modeling platform, Rhinoceros 3D (or Rhino [13]). Grasshopper [14] is one of the widely-adopted parametric design platforms of Rhino thanks to its ability to connect to environmental simulation engines such as EnergyPlus. Numerous architectural design and simulation studies utilized the powerful functions made available by these two tools, from lighting and thermal environment to energy simulations [15,16,17,18,19]; however, there still exists a lack of connectivity between the parametric design platform and building performance simulation particularly for natural ventilation prediction, due to the susceptibility airflow has to the surrounding environment and the complexity in interpretations. Although an airflow simulation tool, such as computational fluid dynamics (CFD), would provide useful information about natural ventilation, the communication between the software and the optimization of inputs is one of the challenges; therefore, customized add-ons in Grasshopper were created to enable data exchange from airflow simulation to energy simulation and to optimize the data, and a new way to interpret the airflow simulation results was developed.
2. Methodology
2.1. Overview
The methodology section consists of two major activities. First, we developed a methodology to identify the optimal opening positions to harness the wind-driven natural ventilation for ventilation and cooling purposes. Focusing on cross ventilation, several pairs of two window positions on building facades were examined. Second, the optimal pairs identified from the optimization were validated with building energy simulation by comparing them to the least optimal solutions.
As illustrated in Figure 1, this study used multiple software programs for simulations, visualization, optimization, and validation. Figure 1a describes the procedure for identifying the optimal opening positions, in which CFD simulation results were transferred into Python code and evaluated for optimization. A more detailed procedure is explained in Section 2.2. Figure 1b evaluates the natural ventilation performance for validation, in which optimal and non-optimal positions were tested with energy simulations. This process is explained in Section 2.3 in more detail.
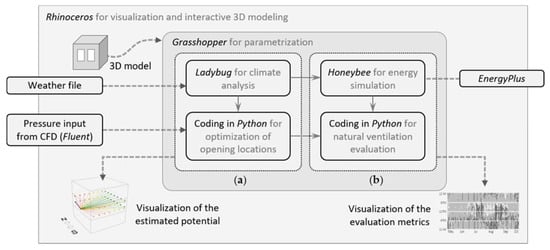
Figure 1.
Framework development: (a) optimization; (b) validation.
A three-story test building of 10 × 10 × 10 m3 was created as shown in Figure 2. The target zone to investigate was the second floor with seven windows on each façade, 28 windows per floor. Windows had identical areas of 1.43 m2, with the opening area of the 0.7 m2. In the optimization process, when a pair of two openings was investigated, the other 26 openings were assumed to be closed.
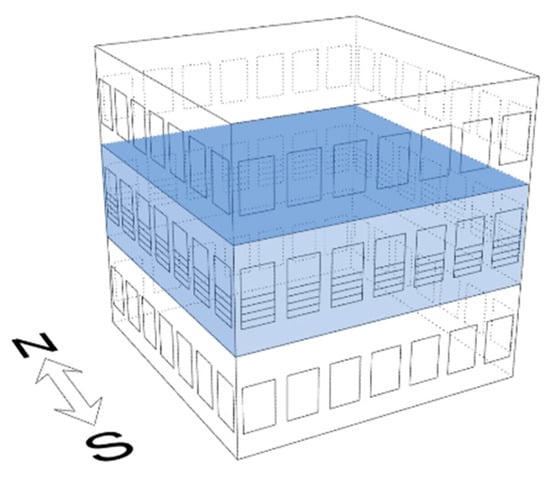
Figure 2.
Test building.
2.2. Development of a Methodology for Optimizing Opening Positions for Wind-Driven Natural Ventilation
2.2.1. Overview of the Optimization Process
This section explains how to identify and examine different pairs of opening positions for wind-driven natural ventilation from weather file and CFD simulations to quantifications of potential, as shown in Figure 1a.
Geometries were created in Rhino and parameterized in Grasshopper to connect the geometries with other software. Ladybug [20] is one of the Grasshopper plug-ins for environmental design analysis. It is a convenient tool to read, analyze, and visualize data from the EnergyPlus Weather (EPW) files. Several resources including [21,22] provide the EPW files of different places in the world. In this study, the tool was used to extract the hourly wind directions and wind speeds of a given place, which were then combined with pressure values from the CFD to create a usable dataset. Python was used for several customized functions including optimization and visualization. Fluent was used for airflow simulations, after which pressure datasets were interpreted by one of the custom programs.
2.2.2. Climate Analysis
Three locations in the USA were selected: San Francisco, CA, Nashville, TN, and Boston, MA. As shown in Table 1 and Figure 3, the selected cities showed several interesting variances in annual wind distributions. Firstly, significant differences in dominant wind directions were found among the cities. In San Francisco, more than 35% of annual wind came from the west, while in Nashville, southern and northern wind together accounted for more than 40%. Boston showed relatively even distribution compared to the other cities. Secondly, the average wind speeds of the most frequent wind direction in San Francisco and Boston exceeded 6.0 m/s, while Nashville’s dominant wind was less than 4 m/s on average. Lastly, in terms of the length of the “windy time”, Boston only had 0.5% of no-wind hours, while others had around 9%.

Table 1.
Frequency of annual wind direction and average wind speed of three different cities, San Francisco, CA; Nashville, TN; Boston, MA. Values in bold texts represent the most frequent wind direction.
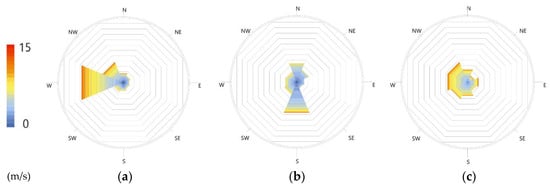
Figure 3.
Annual wind distributions in three cities categorized in eight wind directions visualized by Ladybug. Each octagonal line represents the wind direction frequency of 5%, while the color represents wind speed: (a) San Francisco, CA; (b) Nashville, TN; (c) Boston, MA.
Due to the three aspects mentioned above, investigating these cities will provide insights on how the optimum opening positions could vary from one climate to another.
For the case studies, we decided to focus on a seasonal period, May 15 to October 15. This allows the demonstration of simulations for a customized period, as well as the elimination of the times during which cooling is not of the biggest concern. The seasonal wind information is shown in Table A1 and Figure A1 in Appendix A. The original EPW file contained the wind directions resolution of 10 degrees, hence 36 directions. In Figure 3 and Figure A1, the number of directions was reduced to eight to match the number of directions used in optimization.
2.2.3. Pressure Input from CFD Simulations
The airflow available from the wind depends on opening areas of windows, wind velocity, and pressure coefficient difference, as in Equation (1):
where is the airflow rate [m3/s], is a discharge coefficient that is considered a constant (~0.61 for sliding windows), is the effective opening area [m2], is the far-field wind velocity [m2/s], and is the pressure coefficient difference between two opening positions. Assuming sliding windows, the effective area () of two operable windows is calculated by Equation (2) per [23]:
where and are the area of each opening. For other types of openings such as casement, awning, and hopper types, users have to determine the corrective values for and depending on the opening angles and window lengths [10]. The discharge coefficient () may also change by window geometry [24,25]. For our case study, the sliding window type was used.
The effective opening area can be readily calculated from the given design, and the hourly freestream wind velocity can be obtained from the weather data. The pressure coefficient difference between the two windows still needs to be determined. While other resources provide pressure coefficients on building walls, such as [26,27], this paper chose to run an external wind simulation with CFD to examine local variance on walls.
A CFD simulation calculated pressure values on the building façade, which were then converted to pressure coefficients following Equation (3):
where is the pressure [Pa] at the point on the wall, is the pressure in the freestream [Pa], is the air density [kg/m3], and is the far-field wind velocity [m2/s], all of which were obtained from the CFD simulation.
With the hourly wind speeds from the weather file, the hourly airflow rate () in Equation (1) could be generated for a given pair of two openings; however, since the pressure distribution was based on a given wind direction, users may choose to run multiple CFD simulations to consider more wind directions. We ran CFD simulations for eight wind directions: N, NE, E, SE, S, SW, W, and NW.
The case study building was set up with a commercial CFD software, Fluent [28]. Realizable k- ε (Rk–ε) turbulence model and Semi-Implicit Method for Pressure Linked Equations (SIMPLE) algorithm for pressure-velocity coupling were used, which was validated for the buildings’ application [29]. Using hexahedra mesh with an expansion ratio of 1.2, the mesh size of 0.5 m was applied near the test building per [30] which recommends 0.5–1.0 m for the vicinity of buildings. For a more realistic building, grid resolutions should be determined with mesh dependency studies as they may directly influence the accuracy of the results. More refined grid sizes may be required depending on building specifications (with detailed geometry) and simulation purposes (with or without indoors) [30,31]. The computational domain was determined based on the building height, H = 10 m. The domain was extended from the test building by 6 H in the upstream and vertical directions, 5 H in lateral directions, and 15 H in the downstream direction in compliance with the suggestions from the European Cooperation in Science and Technology [31]. The wind speed at the reference height of 10 m from the ground was set 2 m/s, and the power law was used to create a vertical profile of the wind speed. The wind speed at the height H () followed the Equation (4):
where is the reference wind speed, an exponent determined by the terrain, and is the height at which was measured. The pressure results from the CFD simulation were then converted to pressure coefficients per Equation (3), and the distributions on building facades are shown in Figure 4.
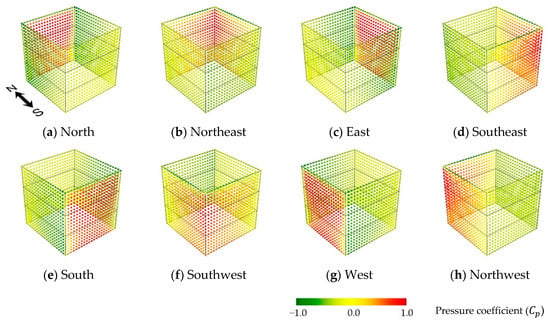
Figure 4.
Pressure coefficient distribution on building façades when the wind comes from eight directions: (a) North wind; (b) Northeast wind; (c) East wind; (d) Southeast wind; (e) South wind; (f) Southwest wind; (g) West wind; (h) Northwest wind.
In this Step, two Important things should be Noted. First, any CFD programs validated for urban flow applications may be used. However, the accuracy of the pressure results could depend on the experience of the user in addition to the validity of a program. Since inappropriate settings and human-related errors could compromise the accuracy of the optimization, users must ensure the reliability of their CFD results. Second, for a more realistic setting, including a building with more details and neighboring buildings, this CFD phase would be more challenging and critical. The pressure coefficients will directly affect the optimization, which is discussed in the following sections.
2.2.4. Mapping the Pressure Data
The pressure results obtained from CFD simulations were mapped into the Grasshopper domain. Written in Python, three major functions were created: a data reading function, a grouping function, and a data interpretation function. First, the pressure data from CFD with their coordinates in the comma-separated values (CSV) format were read (Figure 5a). Pressure values were converted into pressure coefficients during this process; therefore, at the end of this process, an individual data point had been assigned to its coordinates, pressure, and pressure coefficient.
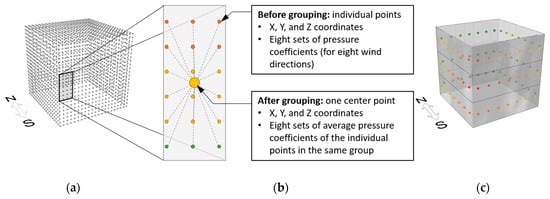
Figure 5.
Pressure data mapping process from computational fluid dynamics (CFD) to 3D environment: (a) data reading from CFD; (b) data grouping; (c) data interpretation based on one wind direction.
Next, the resolution of the surface grids to represent the actual openings were determined, and the nearby pressure points were grouped per the grid resolution (Figure 5b). The walls on each floor were divided by seven surfaces to match the building design shown in Figure 2, creating a total of 28 candidate positions.
The pressure coefficients of each grid were interpolated as an averaged value. For example, Figure 5c visualized pressure coefficients of south-west wind. These Python functions used object-oriented programming, which enabled the codes to keep track of the manipulated values.
2.2.5. Finding the Optimal Pair of Two Openings
Once the pressure coefficients were mapped, the optimization went through three major processes: pairing, evaluation, and optimization.
For pairing, one position needed to be fixed to connect with other positions. With a fixed window position selected, the Python program made n-1 pairs with neighboring positions out of the total n positions. In the codes, the “pair i” consisted of a fixed opening position and the other opening location, i. A set of pressure coefficient differences () of each wind direction was then assigned to each pair: that is, eight sets of for eight wind directions were stored in our tests.
In this study, we searched for two optimal pairs, one with a fixed position on the north wall and the other with a fixed position on the east wall. The pairs created with these fixed openings are shown in Figure 6, where dots represent the opening positions and lines connect the pairs.
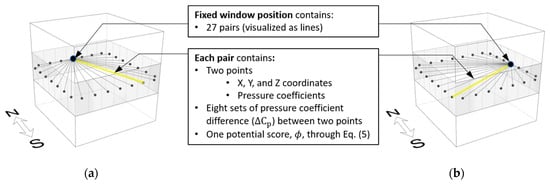
Figure 6.
Opening pairs created: (a) when a fixed opening was on the north wall; (b) when a fixed opening was on the east wall.
To evaluate the potential of a pair, the sets of stored in the pair are the key factors to look at. In an unlikely case in which only one dominant wind direction presents, the optimal pair among n pairs could be found by directly searching for the greatest pressure coefficient differences as inferred from Equation (1); however, to consider multiple wind directions at various speeds, which is true in reality, a few more factors need to be examined for a better evaluation of potential. First, the frequencies of the wind directions were examined. For example, there may be a case in which the pressure difference of a pair could be greater with the north wind than with the west wind. It is possible that the west wind happens to be more frequent than the north wind. In this case, a pair’s potential should be weighted to consider the west wind’s higher frequency, as well as the north wind’s greater driving force. Second, the hourly average wind speeds, as a direct factor for the amount of airflow, were considered in combination with hourly directions. Finally, the integrated potential score of the pair i () was calculated by Equation (5):
where is the pressure coefficient difference of the ith pair when the wind is coming from the jth wind direction, is the annual average wind speed of the jth wind direction, and is the normalized frequency of the jth wind direction. Mathematically speaking, the sum of is the average wind speed of the given climate. Since is the sum of , the magnitude of depends on the pressure coefficient differences and the average wind speed. With the minimum value being zero, there is no specific upper boundary in . The scores made the evaluation convenient because each pair no longer had to carry eight sets of pressure coefficient differences corresponding to eight wind directions, but only one comprehensive score. In the codes, the scores were assigned to their pairs and were visualized in different colors. With eight wind directions and 27 pairs applied to Equation (5), the integrated score was calculated by Equation (6):
where are the score of the 27 pairs based on the fixed opening position. The wind speeds used in Equation (6) were obtained from weather data of each city.
Once the evaluation of pairs was finished, the optimization process identified the optimal pair. For this process, Equation (6) was used as the objective function to look for the maximum score, . The search was simplified as the number of search points were reduced from the original CFD points to only 28 points. We used the general brute-force algorithm, which probed the entire pool of points and found the maximum value. For example, Figure 7 visualizes the evaluation and the optimization for San Francisco, CA. Evaluated pairs are displayed in different colors to represent the relativity and optimal pairs are visualized as thick lines. The entire results including the other cities are discussed in Section 3.
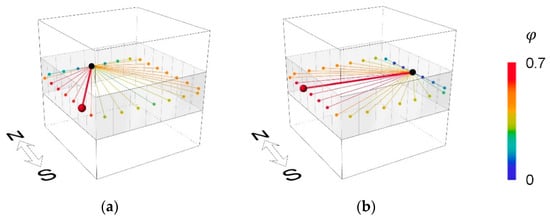
Figure 7.
Evaluation and optimization of pairs of a case in San Francisco, CA: (a) when a fixed opening was on the north wall; (b) when a fixed opening was on the east wall.
2.3. Simulations for Validation
2.3.1. Overview of Simulations for Validation
The optimization program developed in Section 2.2 identified optimal pairs based on Equation (6). To check whether the methodology worked, building performance simulations were conducted, particularly to answer the following questions:
- Does the optimal pair perform better than the other pairs?
- How is the decision made differently in various cities with different wind profiles?
To answer the first question, we selected the least optimal pair (with the lowest ) in addition to the optimal pair. When selecting the least optimal pair, only non-coplanar pairs were considered, to remain in the cross-ventilation regime. This excluded six coplanar opening positions that were on the same wall as the fixed position. Cross comparison of different climates was conducted to answer the second question.
As was in the optimization program, the validation was also conducted within the Rhino and Grasshopper domains. This was convenient because the annual pressure coefficients information yielded in Figure 1a could be directly translated to the validation task in Figure 1b. A Grasshopper plug-in for energy simulation, Honeybee [32], was used to simulate with EnergyPlus [33], an open-source building energy simulation engine. Honeybee converted Rhino geometries into simulation components including walls, roofs, floors, and windows. It then simulated the cooling energy that would be needed when there were no operable windows for natural ventilation. The reason why the simulations were done without operable windows was that the mechanical cooling demand became the reference cooling power that the room needed from natural ventilation. The cooling demand was needed to evaluate a performance metric, natural ventilation effectiveness (NVE) proposed by [16]. Detailed calculation is explained in the following section. Python was used to calculate natural ventilation performance metrics to evaluate various window positions.
Since the validation was to check the impact of opening positions for a given building, the identical building energy simulation (BES) settings listed in Table 2 were applied to all cases. A seasonal period of May 15 to Oct 15 was examined following the methodology laid out in Section 2.2.

Table 2.
Input setting used for energy simulation.
2.3.2. Evaluation Metric: Natural Ventilation Effectiveness (NVE)
Natural ventilation potential can be evaluated by a performance metric called natural ventilation effectiveness (NVE) [16]. This metric measures the capability of natural ventilation to cool and ventilate the given space; therefore, NVE is a proper metric to evaluate different performances of window pairs selected from the optimization program.
To yield the metric, another customized function calculated the hourly ratios () of “available air changes per hour (ACH)” to “required ACH”. The available ACH () is the ACH that a room can achieve by natural ventilation, and the required ACH () is the hypothetical ACH with which the mechanical ventilation and cooling demands become zero. These hourly ratios are averaged to compute NVE of a specific duration of a year, as in Equation (7):
where is the number of hours in the given duration and we used 3680 for our simulation period. For convenience, we will call the hourly ratio of the hourly NVE.
To focus on wind-driven natural ventilation, we obtained from Equation (8):
where is the airflow rate (m3/s) calculated in Equation (1), and is the volume of the room (m2).
The required ACH () considers two purposes of natural ventilation: ventilation and cooling. The required ACH for the ventilation purpose () is calculated by Equations (9) and (10):
where is the minimum outdoor airflow (m3/s) for ventilation, is the outdoor airflow required per person (m3/s-ppl), is the number of people in the room (ppl), is the outdoor airflow required per unit area (m3/s-m2), and is the floor area of the room (m2). The values for and in Equation (9) are provided in [34].
The required ACH for the cooling purpose () is determined by cooling demands and outdoor air temperature as in Equations (11) and (12):
where is the required airflow for cooling (m3/s), is the cooling energy needed when natural ventilation was not used (kW), is air density (kg/m3), is the specific heat of air (kJ/kg-K), is the indoor setpoint temperature (K), and is the outdoor temperature (K). When , and are set to infinite as natural ventilation cannot provide cooling, hence the “+” sign in Equation (11). In this paper, was obtained from running energy simulations in Honeybee.
The required ACH () for the NVE calculation is finally determined by Equation (13):
In addition to NVE, we yielded a modified NVE that considered only the minimum ventilation requirement to help understand the validation results more clearly. The NVE for ventilation only was simply calculated by substituting for in Equation (7) without the process of Equations (11)–(13). We named it for convenience, which can be expressed in Equation (14):
From Equations (1), (8)–(10), and (14), we can infer that an hourly is zero only when there is no wind at all. Excluding the cooling aspect makes it easier to achieve a high value of than a high value of NVE. For example, the minimum ventilation rate, in Equation (9), may be achieved by natural ventilation even when the outdoor air is warmer than the setpoint temperature since cooling was not a concern in calculating ; therefore, calculating provided an initial idea of wind’s availability of a given site, and thus it was informative to examine how the metric evolved as more aspects were added, such as cooling demand and outdoor air temperature.
3. Results
3.1. Results of Optimization
Optimal pairs identified in Section 2.2 are illustrated in Figure 8 and Figure 9 with solid lines. The least optimal pairs are connected through dotted lines. Figure 8 shows the results when there was a fixed window on the north wall, and Figure 9 shows the results with the fixed position on the east wall. More results with various fixed opening positions are appended in Appendix B, Table A2. For convenience, the optimal pairs were denoted with a subscript 1 as in and , and the least optimal pairs (with the lowest ) were denoted with a subscript 0 as in and . These are also as noted in the legends of Figure 8 and Figure 9. Results of the optimization include:
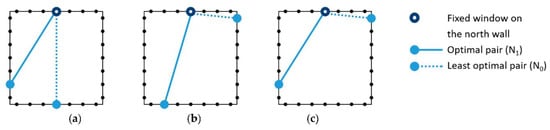
Figure 8.
The optimal pairs and the least optimal pairs identified by Equation (6), when a fixed window on the north wall: (a) San Francisco, CA; (b) Nashville, TN; (c) Boston, NA.
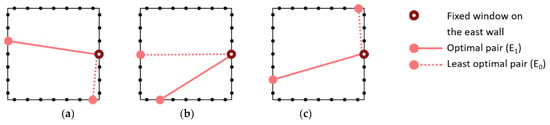
Figure 9.
The optimal pairs and the least optimal pairs identified by Equation (6), when a fixed window on the east wall: (a) San Francisco, CA; (b) Nashville, TN; (c) Boston, NA.
- In San Francisco, the optimization identified openings on the west wall as and (optimal), and openings on the south wall as and (least optimal).
- In Nashville, the optimization identified openings on the south as and , an opening on the east wall as , and the opening on the west wall as .
- In Boston, the optimization identified openings on the west wall as and , an opening on the east wall for , and an opening on the north wall for .
In addition to the results shown in Figure 8 and Figure 9, results with various fixed window positions are appended in Table A2 in Appendix B.
3.2. Validation
As discussed in Section 2.3.2, two metrics were examined. One is a partial NVE for the ventilation purpose only () from Equation (14), and the other is the original NVE for both ventilation and cooling purposes from Equation (7).
3.2.1. Natural Ventilation Effectiveness for Ventilation only ()
Figure 10 and Table 3 show the results of three cities with the four selected pairs, , , and . In all cities, the optimal pairs ( and ) showed the improvement from their counterparts ( and ), as much as 1.73 times (San Francisco) and as little as 1.05 times (Boston). Among the three cities, Boston appeared to have the greatest . This could be explained by Boston’s wind condition, in which the number of “no-wind” hours was significantly less than in other cities and the average speed was relatively high (Table A1 in Appendix A). Since the purpose of was to have a sense of wind’s availability on site, the next section examines how these values change when cooling is considered.
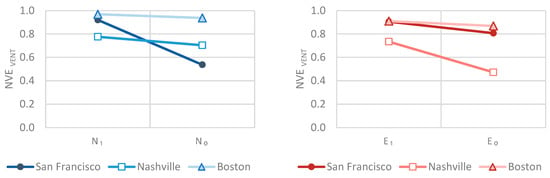
Figure 10.
Validation result: of San Francisco, Nashville, and Boston with the selected pairs.

Table 3.
Validation result: of San Francisco, Nashville, and Boston with the selected pairs. NVE: natural ventilation effectiveness.
3.2.2. Natural Ventilation Effectiveness for both Ventilation and Cooling (NVE).
The NVE results are shown in Figure 11 and Table 4. The results once again confirmed the advantage of choosing the optimal pairs ( and ) over the pairs identified as the least optimal ( and ). The greatest difference between the pairs was found between and of San Francisco. This implies that a strategic placement (or operation) of operable windows helps provide 84% of the cooling demands by natural ventilation during the simulation period (May 15 to October 15), while uninformed window placement could only provide 48% of cooling power.
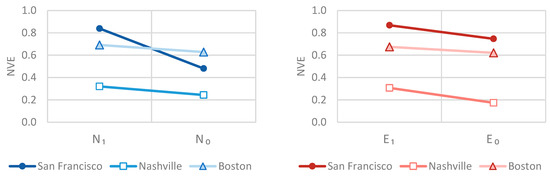
Figure 11.
Validation result: of San Francisco, Nashville, and Boston with the selected pairs.

Table 4.
Validation result: of San Francisco, Nashville, and Boston with the selected pairs.
Compared to the results in Section 3.2.1, the effectiveness has been considerably reduced in some cases when cooing effect was considered in addition to ventilation. The graphs of Figure 12 show these changes. The reason for such reduction can be explained through Equation (11). NVE depends on two additional conditions: these are cooling demand and outdoor air temperature. Particularly, Nashville showed the greatest reduction from to . This is because summer in Nashville is warmer than the other cities, rendering natural ventilation less effective for cooling. In contrast, San Francisco showed the least reduction from to .
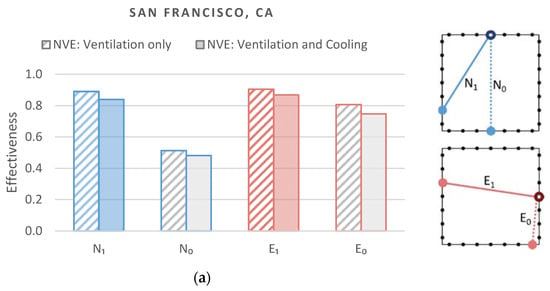
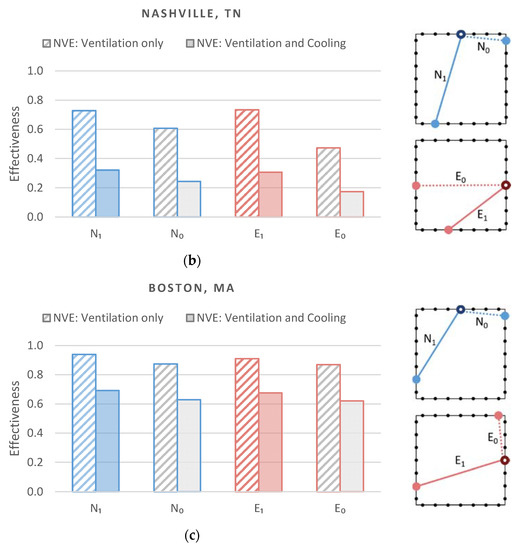
Figure 12.
Validation results of compared to : (a) San Francisco, CA; (b) Nashville, TN; (c) Boston, MA.
3.3. Sensitivity Analysis
The opening area was 0.7 m2 in the validation, which was about 50% of the glazing area. For sensitivity analysis, various opening-to-glazing ratios were tested from 17%, 33%, 50%, 67%, 83%, to 100%, and the results are shown in Figure 13, In some cases, the performance is less sensitive with a greater opening area. For example, and of San Francisco, and of Nashville, and all cases of Boston had less than two percentage point difference when the opening-to-glazing ratio was 100%. However, in other cases, the performance difference between the optimal and non-optimal solutions was greater with an enlarged opening area. Such cases are and of San Francisco, and and of Nashville. The result data are appended to Table A3, Table A4 and Table A5.
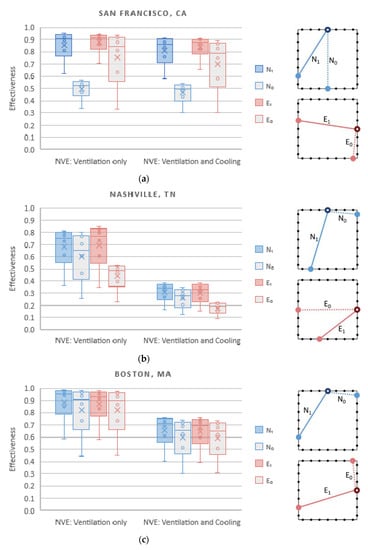
Figure 13.
Natural ventilation effectiveness of with opening-to-glazing ratios of 12.5%, 25%, 37.5%, 50%, 62.5%, 75%, 87.5%, and 100%: (a) San Francisco, CA; (b) Nashville, TN; (c) Boston, MA.
4. Discussion
4.1. Finding the Optimal Opening Positions
The results shown in Section 3.1 suggested that a typical cross-ventilation configuration, which is assumed to have two windows placed on the opposite walls, was effective in some cases. San Francisco’s Nashville’s , and Boston’s are the examples. Other results immediately implied that this may not be the case. For example, San Francisco’s least optimal pairs () in Figure 8a and Nashville’s least optimal pair () in Figure 9b indicated that the typical window placement could even result in the least utilization of natural ventilation. This can be explained by looking at the dominant wind directions of the cities. In San Francisco, the dominant wind direction was the west wind. A north–south window pair in such condition will have relatively less pressure differences, as the pair is placed on the sideward walls instead of windward and leeward walls. In Nashville, in contrast, the dominant wind direction was the south wind, so the least pressure difference would occur at the east–west window pair.
Another finding to address is that the optimal pairs were the result of the considerations of multiple wind directions and speeds. For example, of San Francisco was not the due east–west position, but slightly towards the north direction. This was because the second dominant wind direction of San Francisco was the northwest as shown in Figure A1 (Appendix A).
Also, the optimal pairs selected from different fixed positions under the three test climates (Table A2) indicated that placing one opening on the windward wall would be the best choice in most cases.
In summary, key findings include:
- The optimal pairs identified by the proposed methodology significantly varied by climates.
- Placing two openings on the opposite walls, which is typical for cross ventilation, may not always offer the best performance, and may even present the least performance depending on climate conditions.
- The determination of the optimal positions is influenced by multiple wind directions and speed, in addition to the dominant wind direction.
- If a simulation is not available, the safest guess is to place one opening on the windward wall.
4.2. The Impact of the Optimal Opening Positions on Natural Ventilation Effectiveness
In all cases, the optimal pairs outperformed their counterparts as shown in Section 3.2. The results supported the hypothesis that the strategy of placing the openings through the optimization had a meaningful impact on the ventilation’s effectiveness. The impact of the optimal positions versus non-optimal positions varied by several factors. First and foremost, climate conditions play a critical role in determining the effectiveness of natural ventilation. Under warmer climates like Nashville, the performance of the optimal pairs still suffered despite the improvement it showed over the least optimal pairs. Ranging between NVE of 0.22 and 0.38 even with the greatest opening area, decisionmakers might opt for mechanical cooling at all times. On the other hand, a climate with a cooler summer as San Francisco, NVE can vary significantly. For example, the performance of a pair that could provide 91% (NVE = 0.91) of the required cooling power could substantially drop to 54% depending on the opening positions. The opening area was another contributing factor to NVE. The smaller the opening area, the more prominent NVE differences shown between optimal and non-optimal cases. Some cases still showed significant differences even with a greater opening area.
The optimal and non-optimal pairs did not show a critical difference when two conditions were met: when opening areas were large enough and when wind direction distribution was less skewed. For example, the least optimal pairs of Boston still showed comparable performance although slightly reduced compared to the optimal pairs, as shown in Figure 10 and Figure 11. The reason is that Boston’s wind directions are relatively evenly distributed, unlike the other two climates, so the natural ventilation performance is less subject to different positionings. However, Figure 13c indicates that when the opening area is relatively small, the impact of optimization can increase. Therefore, even though the wind distribution has less variation, the optimization can be still helpful.
4.3. Expandatility to a more Complex Building in an Urban Setting
The proposed methodology can be adapted for a more realistic building in several ways. First, to reflect the better representation of a site and a building, more advanced CFD simulations should be conducted. The geometries should not only include significant features of a building of interest but also neighboring buildings and large objects, such as trees. Grid resolutions and computational domain sizes should also be modified. Users may follow references for CFD simulation settings including [31,35,36,37]. Once multiple sets of pressure data are obtained with the urban airflow, the optimization function (Equation (5)) can then be directly used with general weather data even with such complex urban setting. This is one of the strongest advantages of using pressure coefficients instead of pressure, because the pressure coefficients calculated from Equation (3) have already inherited the effect of surrounding buildings in their values. Therefore, regardless of a city center or a suburb, the same wind data can be used in Equations (1), (3) and (5).
Secondly, one may select fewer wind directions during Section 2.2.2, as it can be impractical to conduct realistic urban flow simulations for eight wind directions. For example, Green Mark, the Singaporean green building guidelines, suggest that users use four prevailing wind directions in CFD simulations, including north, northeast, south, and southeast winds, which represent their climate [30].
4.4. Expandability to an Existing Buildings
In addition to assisting in an early design phase, there are largely two ways to apply the proposed methodology to an existing building, for which owners may want to add an operation strategy. The first option, similar to what we described in this paper, is to run CFD simulations of the real building and surrounding conditions. For practical reasons, the expert may choose eight or fewer prevailing wind directions, and follow the rest of the steps described in Section 2.2.4 and Section 2.2.5. In this case, the challenge is to run the CFD simulations correctly as mentioned in Section 4.4. The other option is to measure pressure directly on the existing window locations using sensors. When logging pressure values, performers have to record corresponding wind speeds and directions from the weather station at the same time. After enough data are measured and pressure coefficients are calculated in a CSV files, they may skip the grouping process shown in Figure 5b as the measured data points are of real windows. The rest of the steps in Section 2.2.4 and Section 2.2.5 can be conducted. In addition to these two major options, one may conduct wind-tunnel experiments, which could be more costly.
4.5. BES-Integrated Design Workflow
The workflow we used (Figure 1) consisted of two parts: optimization and validation. Combining the two parts, this methodology can be used for natural ventilation analysis integrated with a building energy simulation (BES). With a more accessible and/or faster airflow simulation resources, such as [35,36,37], this workflow is feasible for an early architectural building design.
When a fluid simulation is not available, users may seek secondary recourses for obtaining pressure coefficient values. For example, from databases or empirical data, although they generally assign one values on each facade based on the orientation of the surface and wind directions.
4.6. Limitation and Future Development
4.6.1. Limitation
- As the title of this paper clarified, the opening pairs were examined based on the given wind conditions. To consider buoyancy-driven ventilation, the optimization function needs to be modified.
- The optimization function was based on a steady-state condition and does not explain the effect of thermal mass. Further research is needed to consider the relationship between opening positions and the transient behavior of buildings.
- The optimization assumed that the maximum airflow would lead to the greatest cooling energy savings; however, the optimal solution might miss a ‘better’ solution due to the indoor air distribution or flow pattern. There might be a pair that might have less potential score () but would distribute the air more efficiently thus improving the air circulation.
- In the CFD simulations, no surrounding condition was considered. For a local-specific analysis, immediate surrounding conditions including buildings and large trees should be modeled in CFD simulations.
- The test cases used eight wind directions. The number of directions is adjustable that one can use fewer or more directions if desired; however, this paper did not test on the minimum number of wind directions to be considered for the optimization.
- Natural ventilation’s availability is not solely determined by wind and temperature. Realistic constraints that were not examined in this paper include noise, pollution, and pollen.
4.6.2. Future Development
- Validation with experimental measurements with fluctuating wind directions will enhance the methodology and help better understand the performance of the optimal solutions.
- Tool development to make the optimization program available to the public will encourage architects and BES professionals to consider natural ventilation in their practice.
5. Conclusions
This paper developed a framework to identify optimal opening positions to best utilize wind-driven natural ventilation. We conducted CFD simulations to obtain local pressure on building facades for eight wind directions, imported and mapped the pressure values in 3D programs, and calculated an integrated potential score to find the optimum. The optimization solutions were compared with non-optimal solutions by conducting building energy simulations and investigating in NVE as an evaluation metric, which led to the following conclusions:
- The effectiveness of wind-driven natural ventilation is greatly influenced by how windows are positioned in addition to outdoors conditions.
- The optimized window positions were shown to be effective, and some optimal solutions contradicted the typical cross-ventilation strategy.
The proposed optimization methodology was developed based on the frequency and the average wind speed of each direction, as well as pressure distributions on building façades under each wind direction. The proposed optimal solutions were proven to be more effective than the other solutions identified to have the least potential. The benefits of the optimization process include that:
- The proposed optimization methodology helps designers utilize outsourced pressure data during the preliminary design phase.
- The optimized solutions reduced the need for iterating design alternatives to maximize the natural ventilation’s cooling effect.
- The connectivity of the proposed framework to the existing airflow analysis method in CFD enables the comprehensive interpretation of the CFD results to be used in a seasonal analysis as opposed to a point-in-time analysis.
- With further examination of surrounding buildings and operation schedules, this optimization method can also be expanded to existing buildings with multiple windows.
Author Contributions
Conceptualization, N.Y.; data curation, N.Y.; formal analysis, N.Y.; funding acquisition, N.Y.; investigation, N.Y.; methodology, N.Y., J.M.H., and W.W.; resources, M.A.P. and A.M.; software, N.Y. and J.M.H.; supervision, M.A.P., and A.M.; validation, N.Y.; visualization, N.Y.; Writing—original draft, N.Y.; writing—review and editing, N.Y., M.A.P., J.M.H., W.W., and A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Assistant Secretary for Energy Efficiency and Renewable Energy, Building Technologies Office of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A. Seasonal Wind Profiles of Three Cities

Table A1.
Frequency of seasonal (May 15–Oct 15) wind direction and average wind speed extracted from EnergyPlus Weather (EPW) files of three different cities, San Francisco, CA; Nashville, TN; Boston, MA. Values in bold text represent the most frequent wind direction.
Table A1.
Frequency of seasonal (May 15–Oct 15) wind direction and average wind speed extracted from EnergyPlus Weather (EPW) files of three different cities, San Francisco, CA; Nashville, TN; Boston, MA. Values in bold text represent the most frequent wind direction.
| Wind Angle θ* | San Francisco, CA | Nashville, TN | Boston, MA | |||
|---|---|---|---|---|---|---|
| Frequency | Average Wind Speed | Frequency | Average Wind Speed | Frequency | Average Wind Speed | |
| N | 4.38% | 3.99 m/s | 14.83% | 3.16 m/s | 7.93% | 4.30 m/s |
| NE | 3.17% | 2.82 m/s | 13.50% | 3.28 m/s | 7.71% | 5.21 m/s |
| E | 1.27% | 2.83 m/s | 5.74% | 2.46 m/s | 9.50% | 4.28 m/s |
| SE | 1.33% | 3.06 m/s | 4.79% | 2.62 m/s | 8.63% | 3.92 m/s |
| S | 3.71% | 4.31 m/s | 23.19% | 3.01 m/s | 15.04% | 4.65 m/s |
| SW | 8.41% | 4.89 m/s | 10.63% | 3.42 m/s | 21.46% | 5.04 m/s |
| W | 47.48% | 6.60 m/s | 8.98% | 3.38 m/s | 17.56% | 5.23 m/s |
| NW | 26.46% | 6.10 m/s | 5.76% | 3.22 m/s | 11.69% | 4.96 m/s |
| No wind | 3.79% | 0 m/s | 12.58% | 0 m/s | 0.49% | 0 m/s |
| Total | 100% | 5.66 m/s | 100% | 2.73 m/s | 100% | 4.77 m/s |
* North wind (N): 0 ≤ θ < 22.5 or 337.5 ≤ θ ≤ 0; northeast wind (NE): 22.5 ≤ θ < 67.5; east wind (E): 67.5 ≤ θ < 112.5; southeast wind (SE): 112.5 ≤ θ < 157.5; south wind (S): 157.5 ≤ θ < 202.5; southwest wind (SW): 202.5 ≤ θ < 247.5; west wind (W): 247.5 ≤ θ < 292.5; northwest wind (NW): 292.5 ≤ θ < 337.5, where θ is the wind direction.
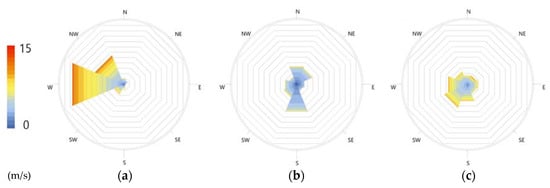
Figure A1.
Seasonal (May 15–Oct 15) wind distributions in three cities categorized in eight wind directions visualized by Ladybug. Each octagonal line represents the wind direction frequency of 5%, while the color represents wind speed: (a) San Francisco, CA; (b) Nashville, TN; (c) Boston, MA.
Appendix B. Result of Optimal Pairs

Table A2.
The integrated potential score of pairs () with various fixed opening positions in three different cities. Optimal and the least optimal pairs are displayed as thick lines. Other candidate pairs are displayed as thin lines.
Table A2.
The integrated potential score of pairs () with various fixed opening positions in three different cities. Optimal and the least optimal pairs are displayed as thick lines. Other candidate pairs are displayed as thin lines.
| San Francisco | Nashville | Boston |
|---|---|---|
 | 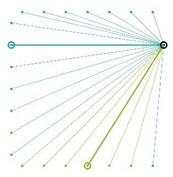 | 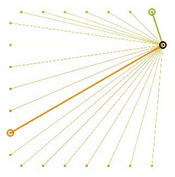 |
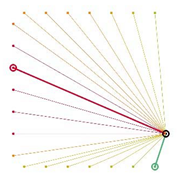 | 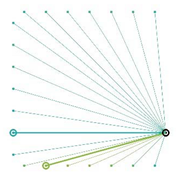 |  |
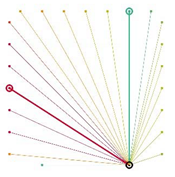 | 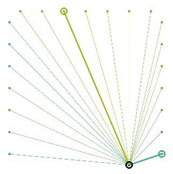 | 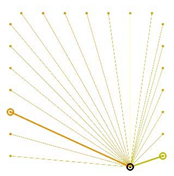 |
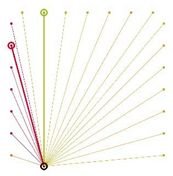 | 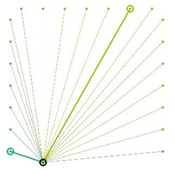 | 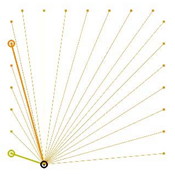 |
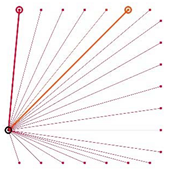 | 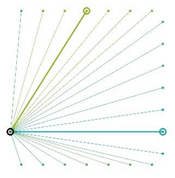 | 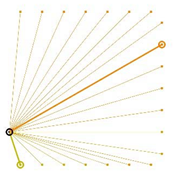 |
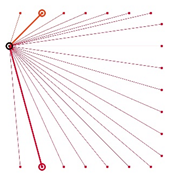 | 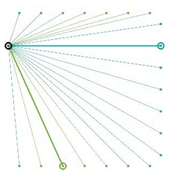 | 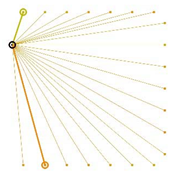 |
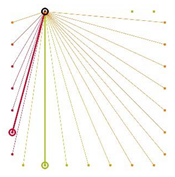 | 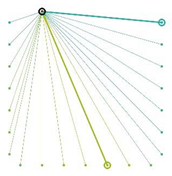 | 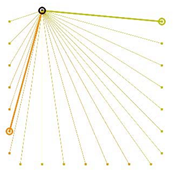 |
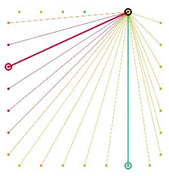 | 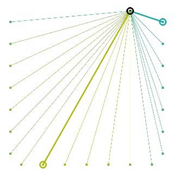 | 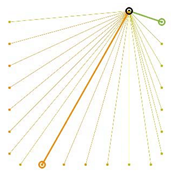 |
Appendix C. Validation Results

Table A3.
Sensitivity analysis results for San Francisco, CA.
Table A3.
Sensitivity analysis results for San Francisco, CA.
| Opening-to-Glazing Ratio | N1 | N0 | E1 | E0 | |
|---|---|---|---|---|---|
| NVEvent | 16.7% | 0.62 | 0.34 | 0.71 | 0.33 |
| 33.3% | 0.81 | 0.47 | 0.86 | 0.63 | |
| 50.0% | 0.89 | 0.51 | 0.91 | 0.81 | |
| 66.7% | 0.92 | 0.54 | 0.92 | 0.88 | |
| 83.3% | 0.94 | 0.56 | 0.94 | 0.92 | |
| 100.0% | 0.95 | 0.57 | 0.94 | 0.94 | |
| NVE | 16.7% | 0.58 | 0.30 | 0.66 | 0.30 |
| 33.3% | 0.76 | 0.43 | 0.82 | 0.58 | |
| 50.0% | 0.841 | 0.481 | 0.87 | 0.75 | |
| 66.7% | 0.88 | 0.51 | 0.89 | 0.83 | |
| 83.3% | 0.90 | 0.53 | 0.90 | 0.87 | |
| 100.0% | 0.91 | 0.54 | 0.91 | 0.89 |
1 Pairs with the bold text: NVE plots of these pairs are appended in Appendix C, Figure A2.

Table A4.
Sensitivity analysis results for Nashville, TN.
Table A4.
Sensitivity analysis results for Nashville, TN.
| Opening-to-Glazing Ratio | N1 | N0 | E1 | E0 | |
|---|---|---|---|---|---|
| NVEvent | 16.7% | 0.36 | 0.26 | 0.35 | 0.23 |
| 33.3% | 0.61 | 0.46 | 0.61 | 0.39 | |
| 50.0% | 0.73 | 0.61 | 0.73 | 0.47 | |
| 66.7% | 0.78 | 0.70 | 0.80 | 0.51 | |
| 83.3% | 0.80 | 0.77 | 0.83 | 0.52 | |
| 100.0% | 0.82 | 0.81 | 0.85 | 0.53 | |
| NVE | 16.7% | 0.14 | 0.10 | 0.13 | 0.08 |
| 33.3% | 0.26 | 0.19 | 0.24 | 0.14 | |
| 50.0% | 0.32 | 0.24 | 0.311 | 0.171 | |
| 66.7% | 0.35 | 0.29 | 0.34 | 0.19 | |
| 83.3% | 0.37 | 0.32 | 0.37 | 0.21 | |
| 100.0% | 0.38 | 0.34 | 0.38 | 0.21 |
1 Pairs with the bold text: NVE plots of these pairs are appended in Appendix C, Figure A3.

Table A5.
Sensitivity analysis results for Boston, MA.
Table A5.
Sensitivity analysis results for Boston, MA.
| Opening-to-Glazing Ratio | N1 | N0 | E1 | E0 | |
|---|---|---|---|---|---|
| NVEvent | 16.7% | 0.59 | 0.44 | 0.58 | 0.45 |
| 33.3% | 0.85 | 0.73 | 0.83 | 0.73 | |
| 50.0% | 0.94 | 0.87 | 0.91 | 0.87 | |
| 66.7% | 0.97 | 0.94 | 0.95 | 0.93 | |
| 83.3% | 0.98 | 0.97 | 0.97 | 0.96 | |
| 100.0% | 0.99 | 0.98 | 0.98 | 0.98 | |
| NVE | 16.7% | 0.41 | 0.30 | 0.39 | 0.31 |
| 33.3% | 0.61 | 0.51 | 0.60 | 0.51 | |
| 50.0% | 0.691 | 0.631 | 0.68 | 0.62 | |
| 66.7% | 0.73 | 0.69 | 0.72 | 0.68 | |
| 83.3% | 0.75 | 0.72 | 0.74 | 0.71 | |
| 100.0% | 0.76 | 0.74 | 0.76 | 0.74 |
1 Pairs with the bold text: NVE plots of these pairs are appended in Appendix C, Figure A4.
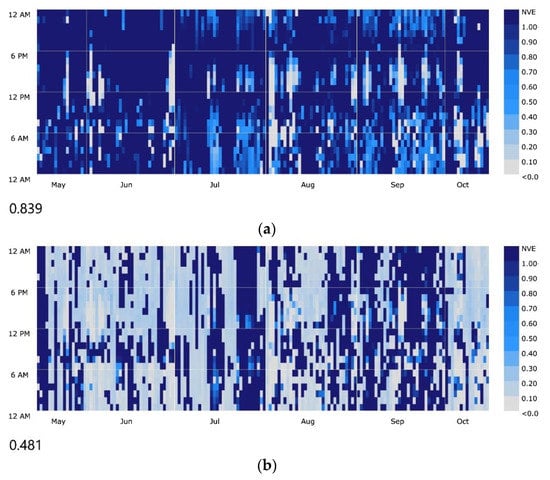
Figure A2.
Seasonal NVE plot with an opening-to-glazing ratio of 50% in San Francisco: (a) pair N1; (b) pair N0.
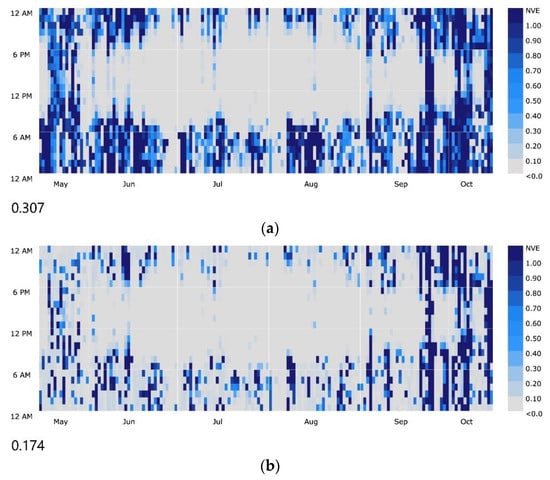
Figure A3.
Seasonal NVE plot with an opening-to-glazing ratio of 50% in Nashville: (a) pair E1; (b) pair E0.
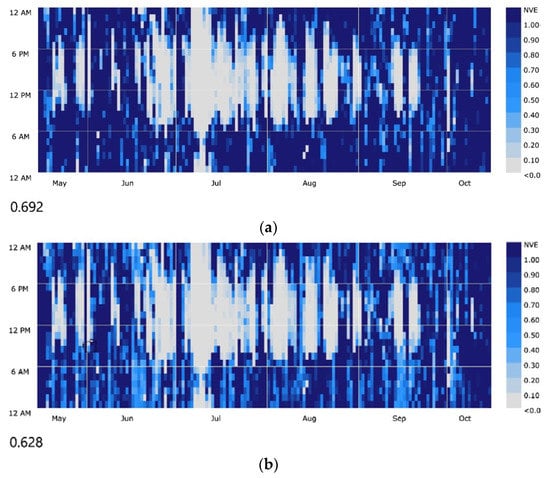
Figure A4.
Seasonal NVE plot with an opening-to-glazing ratio of 50% in Boston: (a) pair N1; (b) pair N0.
References
- Kaasalainen, T.; Mäkinen, A.; Lehtinen, T.; Moisio, M.; Vinha, J. Architectural window design and energy efficiency: Impacts on heating, cooling and lighting needs in Finnish climates. J. Build. Eng. 2020, 27, 100996. [Google Scholar] [CrossRef]
- Liu, M.; Heiselberg, P.K.; Antonov, Y.I.; Mikkelsen, F.S. Parametric analysis on the heat transfer, daylight and thermal comfort for a sustainable roof window with triple glazing and external shutter. Energy Build. 2019, 183, 209–221. [Google Scholar] [CrossRef]
- Pilechiha, P.; Mahdavinejad, M.; Pour Rahimian, F.; Carnemolla, P.; Seyedzadeh, S. Multi-objective optimisation framework for designing office windows: Quality of view, daylight and energy efficiency. Appl. Energy 2020, 261, 114356. [Google Scholar] [CrossRef]
- Natural Ventilation in Buildings: A Design Handbook; Allard, F., Ed.; James and James Science Publishers Ltd: London, UK, 1998; ISBN 978-1-873936-72-6. [Google Scholar]
- CIBSE. Application Manual 10: Natural Ventilation in Non-Domestic Buildings; Chartered Institution of Building Services Engineers: Norwich, UK, 2005. [Google Scholar]
- Alibaba, H. Determination of Optimum Window to External Wall Ratio for Offices in a Hot and Humid Climate. Sustainability 2016, 8, 187. [Google Scholar] [CrossRef]
- Wang, L.; Wong, N.H.; Shuo, L. Facade design optimization for naturally ventilated residential buildings in Singapore. Energy Build 2007, 39, 954–961. [Google Scholar] [CrossRef]
- Sorgato, M.J.; Melo, A.P.; Lamberts, R. The effect of window opening ventilation control on residential building energy consumption. Energy Build. 2016, 133, 1–13. [Google Scholar] [CrossRef]
- Lai, D.; Jia, S.; Qi, Y.; Liu, J. Window-opening behavior in Chinese residential buildings across different climate zones. Build. Environ. 2018, 142, 234–243. [Google Scholar] [CrossRef]
- Liu, T.; Lee, W.L. Influence of window opening degree on natural ventilation performance of residential buildings in Hong Kong. Sci. Technol. Built Environ. 2020, 26, 28–41. [Google Scholar] [CrossRef]
- Lee, S.-W.; Leigh, S.-B.; Kim, T.; Cheong, C.H.; Cho, S. Cooling energy reduction effect of parallel double-window system operation in residential buildings in South Korea. Indoor Built Environ. 2019, 28, 636–658. [Google Scholar] [CrossRef]
- Stavrakakis, G.M.; Zervas, P.L.; Sarimveis, H.; Markatos, N.C. Optimization of window-openings design for thermal comfort in naturally ventilated buildings. Appl. Math. Model. 2012, 36, 193–211. [Google Scholar] [CrossRef]
- Robert McNeel & Associates Rhino 6 for Windows and Mac. Available online: https://www.rhino3d.com/ (accessed on 4 December 2019).
- Davidson, S. Grasshopper. Available online: https://www.grasshopper3d.com/ (accessed on 4 December 2019).
- Srisamranrungruang, T.; Hiyama, K. Balancing of natural ventilation, daylight, thermal effect for a building with double-skin perforated facade (DSPF). Energy Build. 2020, 210, 109765. [Google Scholar] [CrossRef]
- Yoon, N.; Malkawi, A. Predicting the effectiveness of wind-driven natural ventilation strategy for interactive building design. In Proceedings of the 15th International Building Simulation Conference, San Francisco, CA, USA, 7–9 August 2017; pp. 2163–2170. [Google Scholar]
- Konis, K.; Gamas, A.; Kensek, K. Passive performance and building form: An optimization framework for early-stage design support. Sol. Energy 2016, 125, 161–179. [Google Scholar] [CrossRef]
- Caldas, L.; Santos, L. Painting with light: An interactive evolutionary system for daylighting design. Build Environ. 2016, 109, 154–174. [Google Scholar] [CrossRef]
- Lee, K.S.; Han, K.J.; Lee, J.W. Feasibility Study on Parametric Optimization of Daylighting in Building Shading Design. Sustainability 2016, 8, 1220. [Google Scholar] [CrossRef]
- Ladybug Tools Ladybug. Available online: https://www.ladybug.tools/ladybug.html (accessed on 4 December 2019).
- Ladybug Tools Epwmap. Available online: https://www.ladybug.tools/epwmap/ (accessed on 13 March 2020).
- EnergyPlus Weather Data. Available online: https://energyplus.net/weather (accessed on 13 March 2020).
- BSI. BS 5925-1991: Code of Practice for Ventilation Principles and Designing for Natural Ventilation; British Standards Institution: London, UK, 1991; ISBN 0 580 19285 7. [Google Scholar]
- Cruz, H.; Viegas, J.C. On-site assessment of the discharge coefficient of open windows. Energy Build. 2016, 126, 463–476. [Google Scholar] [CrossRef]
- Heiselberg, P.; Sandberg, M. Evaluation of discharge coefficients for window openings in wind driven natural ventilation. Int. J. Vent. 2006, 5, 43–52. [Google Scholar] [CrossRef]
- Orme, M.; Liddament, M.W.; Wilson, A. Numerical Data for Air Infiltration and Natural Ventilation Calculations; Air Infiltration and Ventilation Centre: Coventry, UK, 1998; p. 100. [Google Scholar]
- Swami, M.V.; Chandra, S. Correlations for pressure distribution on buildings and calculation of natural-ventilation airflow. Ashrae Trans. 1988, 94, 243–266. [Google Scholar]
- ANSYS Ansys Fluent Software: Flow Modeling & CFD Simulation Software. Available online: https://www.ansys.com/products/fluids/ansys-fluent (accessed on 3 January 2020).
- Montazeri, H.; Blocken, B.; Derome, D.; Carmeliet, J.; Hensen, J.L.M. CFD analysis of forced convective heat transfer coefficients at windward building facades: Influence of building geometry. J. Wind Eng. Ind. Aerodyn. 2015, 146, 102–116. [Google Scholar] [CrossRef]
- Building and Construction Authority, Ministry of National Development of the Singapore Government. GM RB: 2016 Green Mark For Residential Buildings: Technical Guide and Requirements; BCA: Singapore, 2017.
- COST. Best Practice Guideline for The CFD Simulation of Flows in the Urban Environment: COST Action 732 Quality Assurance and Improvement of Microscale Meteorological Models; Meteorological Inst.: Hamburg, Germany, 2007. [Google Scholar]
- Ladybug Tools Honeybee. Available online: https://www.ladybug.tools/honeybee.html (accessed on 4 December 2019).
- National Renewable Energy Laboratory EnergyPlus. Available online: https://energyplus.net/ (accessed on 14 March 2020).
- ASHRAE. ANSI/ASHRAE Standard 62.1-2016: Ventilation for Acceptable Indoor Air Quality; American Society of Heating, American Society of Heating, Refrigerating and Air-Conditioning Engineers: Atlanta, GA, USA, 2016. [Google Scholar]
- Ladybug Tools Butterfly. Available online: https://www.ladybug.tools/butterfly.html (accessed on 14 January 2019).
- Mortezazadeh Dorostkar, M. CityFFD—City Fast Fluid Dynamics Model for Urban Microclimate Simulations. Ph.D. Thesis, Concordia University, Montreal, QC, Canada, 2019. [Google Scholar]
- Tian, W.; VanGilder, J.; Condor, M.; Han, X.; Zuo, W. An Accurate Fast Fluid Dynamics Model for Data Center Applications. In Proceedings of the 2019 18th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), Las Vegas, NV, USA, 29–31 May 2019; pp. 1275–1281. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).