Direct Shear Experimental Study on the Mobilized Dilation Behavior of Granite in Alxa Candidate Area for High-Level Radioactive Waste Disposal

Abstract

Dilation behavior is of great importance for reasonable modeling of the stability of the host rock of the repository for high-level radioactive waste disposal. It is a suitable method for carrying out direct shear experiments to analyze the dilation behavior of rock with well understood physical meanings. Based on a series of direct shear experiments on granite samples from the Alxa candidate area under different normal stresses, the shear stress‒shear strain and shear stress‒normal strain relations have been studied in detail. Five typical stages have been divided associated with the fracturing process and deformation behaviors of the granite samples during the experimental process, and the method to determine the typical stress thresholds has been proposed. It has also been found that the increasing normal stress may reduce the maximum dilation angle, and when the normal stress is relatively lower, the negative dilation angle may occur during the post-peak stage. According to the data collected from the direct shear tests, an empirical model of the mobilized dilation angle dependent on normal stress and plastic shear strain is proposed. This mobilized dilation angle has clear physical meanings and can be used in plastic constitutive models of the host rock of the repository, and this analysis can also be put forward to other types of geomechanical problems, including the deformation behaviors related to landslide, earthquake, and so on.

1. Introduction

Extensive studies on the geological disposal of high-level radioactive waste (HLW) have been carried out for several decades [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28]. Alxa area is one of the three candidate areas with a large volume of granitic intrusions in China [22,23,25,29]. Geomechanical properties of the host rock are of paramount importance for evaluating the stability of the repository during the periods of construction and operation.

Owing to the effects of far field in-situ stresses or redistributed stresses induced by excavation, the shearing load may play an important role in the stability of underground opening [30,31,32,33]. Dilation behavior is considered as an important factor for better modeling of the deformation behavior of the surrounding rock mass [34,35,36]. Many previous researches have been carried out based on conventional tri-axial compression experiments on cylindrical rock samples. According to these experimental studies, different stages of stress-strain relations have been divided, and dilation behaviors have been studied associated with the process of crack propagation and acoustic emission events during the compression [1,35,37,38]. These studies are mainly on the phenomenological and mechanism researches. However, a quantified estimation of the rock dilation behavior is required. As a parameter controlling the plastic volume changes [34], the dilation angle is always used in the plastic constitutive model for rock. For example, for the flow rule:

$${\dot{\epsilon }}_{ij}^p= \dot{\lambda }\frac{\partial g}{\partial {\sigma }_{ij}}$$

(1)

where ${\dot{\epsilon }}_{ij}^p$ is the incremental plastic strain tensor, ${\sigma }_{ij}$ is the stress tensor, $\dot{\lambda }$ is a non-negative multiplier, and $g$ is the plastic potential function. For rock and soil material, we always use the non-associated flow rule, and the plastic potential function $g$ usually takes the form of

$$g= \frac{1}{2}\left({\sigma }_1-{\sigma }_3\right)+\frac{1}{2}\left({\sigma }_1+{\sigma }_3\right)\sin \psi +c$$

(2)

where ${\sigma }_1$ and ${\sigma }_3$ are the maximum and minimum principal stresses, $c$ is a constant, and $\psi$ is the dilation angle [34].

The dilation angle of rock has been widely studied in many published references [34,35,36]. In the early stage, the dilation angle was considered to be constant, and suggestions for determining the constant dilation angle for rock masses were also provided [34,39]. However, the researchers later found that the assumption of constant dilation angle should not be realistic, and different methods for describing the dilation angle have been provided considering the varying confining pressures and plastic parameters [40,41,42]. More recently, Zhao and Cai [35] proposed a mobilized dilation angle model dependent on confining pressures and plastic shear strain; thereafter, this model was put forward for analyses of rock masses [43]. Walton and Diederichs [36] argued that this model has too many parameters that are difficult for determination, and a new dilation angle was proposed with a piecewise style [36,44,45].

These studies were mainly based on conventional tri-axial compression experiments with the stress state of σ₁ > σ₂ = σ₃ (σ₁, σ₂, and σ₃ are the maximum, intermediate, and minimum principal stress, respectively). By a series of deductions based on the theory of plasticity, the dilation angle $\psi$ is determined as [34]:

$$\sin \psi = \frac{{\dot{\epsilon }}_{\mathrm{v}}^{\mathrm{p}}}{-2{\dot{\epsilon }}_1^{\mathrm{p}}+{\dot{\epsilon }}_{\mathrm{v}}^{\mathrm{p}}}$$

(3)

where, ${\dot{\epsilon }}_{\mathrm{v}}^{\mathrm{p}}$ and ${\dot{\epsilon }}_1^{\mathrm{p}}$ is the volumetric and axial plastic strain increments, respectively. For the conventional tri-axial compression test, the lateral plastic strain increment (${\dot{\epsilon }}_2^{\mathrm{p}}={\dot{\epsilon }}_3^{\mathrm{p}}$) should be measured carefully to calculate ${\dot{\epsilon }}_{\mathrm{v}}^{\mathrm{p}}={\dot{\epsilon }}_1^{\mathrm{p}}-2{\dot{\epsilon }}_2^{\mathrm{p}}$. In fact, the lateral deformation is not uniform during the post-peak period, so it is not easy to measure the lateral and volumetric strain accurately.

Comparatively, the dilation angle defined according to the direct shear experiment has a very clear physical meaning, which can be better understood by the sketch presented in Figure 1a. A sketch of the direct shear experiment on a cubic sample is presented in Figure 1b. Under the effect of shear loading, a shear zone may be formed with the evolution of the fractures. In Figure 1c, an element is selected in the shear zone to illustrate the physical meaning of shear strain ${\gamma }_{xy}$ and dilation angle $\psi$. The dashed line shows the original element, and solid line shows the sheared element. The shear strain ${\gamma }_{xy}$ arises from the distortion of the element, and the normal strain ${\epsilon }_{yy}$ is determined the normal deformation Δy divided by the original y-length of the element. By conducting the direct shear tests, the dilation angle $\psi$ can be described as [34]:

$$\tan \psi = -{\dot{\epsilon }}_{yy}^{\mathrm{p}}/{\dot{\gamma }}_{xy}^{\mathrm{p}}$$

(4)

where, ${\dot{\epsilon }}_{yy}^{\mathrm{p}}$ and ${\dot{\gamma }}_{xy}^{\mathrm{p}}$ are the plastic normal strain increment and plastic shear strain increment, respectively. The symbols x and y here follow the coordinate system shown in Figure 1.

Consequently, it may be a considerable choice to study the dilation behavior of rock by carrying out a series of direct shear tests under different normal stresses. In addition to the stability analyses on underground excavation, this method can also be used to study the deformation behavior related to landslide and earthquake.

Direct shear experiments have been widely used for analyzing the mechanical properties of geomaterials. For soil and sand samples, a direct shear test is usually used for studying the shear strength and deformation behaviors [46,47,48,49,50]. For rock samples, on the one hand, a direct shear test is often applied to research the strength and deformation behaviors of rock discontinuities [51,52,53,54,55,56,57,58,59,60,61]; on the other hand, a direct shear test has been carried out for studying the fracturing patterns inside the rock [31,62]. There are still very few studies discussing the deformation behavior of rock, or associating the fracturing process with the stress-strain relations under direct shear experiments [31]. The dilation behavior has been analyzed in some references by conducting direct shear tests considering various normal stresses; however, these studies are mainly focused on the descriptions based on observation, and a detailed, quantified analysis on the dilation angle is still required to be conducted.

In the Alxa candidate area, field investigations have been carried out in two sub-areas (TMS and NRG sub-areas), and four 600 m deep boreholes have been drilled in these two sub-areas. For more detailed information about the Alxa candidate area, readers are referred to [22]. Rock structures have been studied, and cored samples have been tested in the laboratory for analyzing their strength and deformation properties, seepage behaviors, and thermal effect on mechanical characteristics [22,23,25]. Nonetheless, the dilation behavior has not been studied. The mobilization of the dilation angle is still required to study for a reasonable plastic model of the underground repository.

Consequently, based on a series of direct shear experiments on the granite samples from Alxa candidate areas, the stress-strain relations will be studied in detail, and the dilation behavior will be investigated considering both the normal stress and the plastic shear strain. This paper is organized as follows: In Section 2, the granite samples, as well as the experimental setup and methods, are introduced. Thereafter, the experimental results are provided in Section 3, with a detailed characterization of both shear stress—shear strain and shear stress—normal strain relations. Section 4 provides a systematic discussion on the mobilization of dilation angle dependent on the normal stress and plastic shear strain. With collected data from the experiments, a fitted empirical model of dilation angle will be proposed.

2. Samples and Experimental Methods

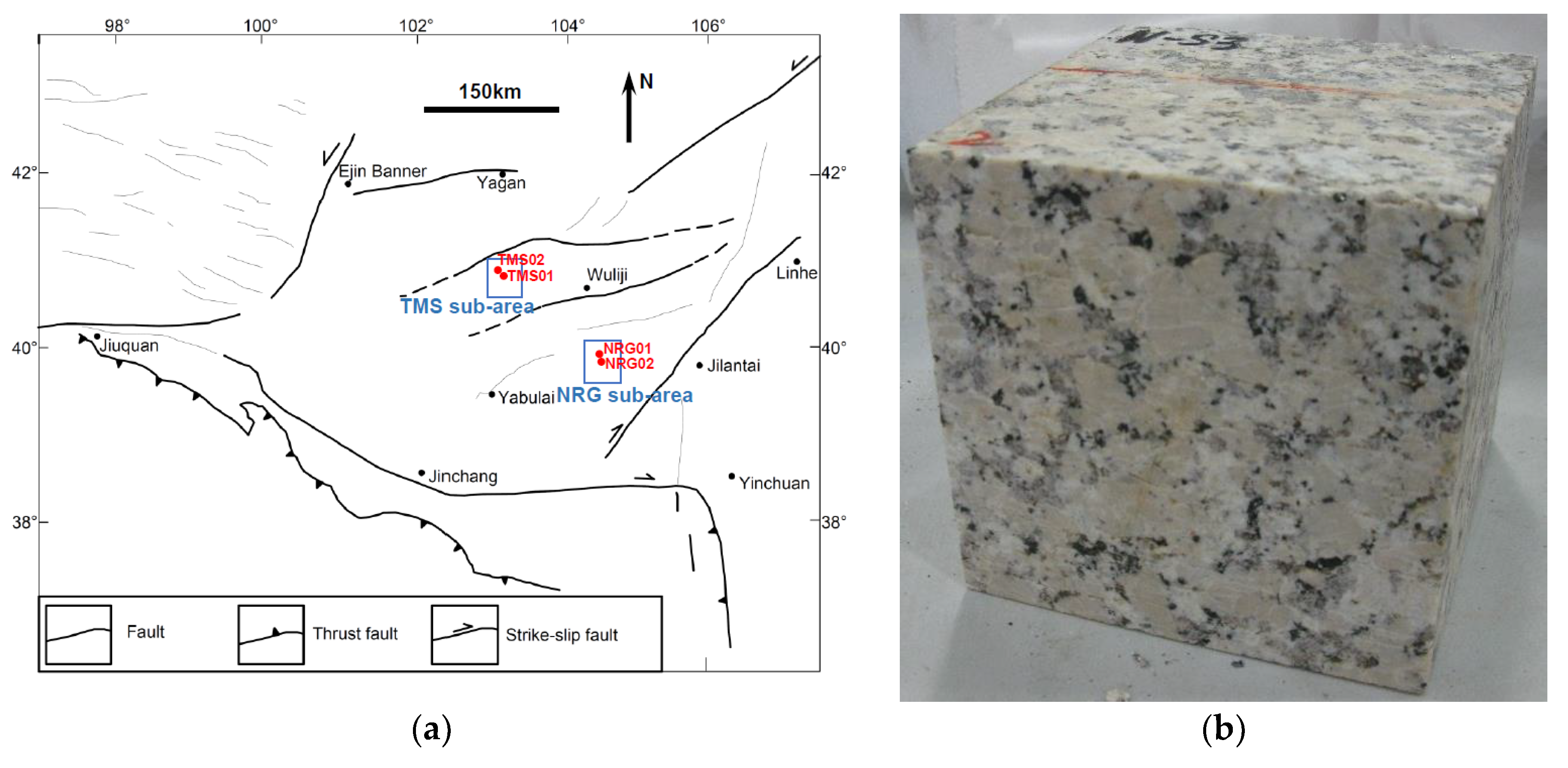
2.1. Samples

According to the previous field investigation and experimental studies on the Alxa candidate area, the granite around NRG01 borehole in NRG sub-area shows the best rock mass quality and strength behaviors in this candidate area [22]. Therefore, it is an optimal selection to use the granite samples from this site for further geomechanical studies. A schematic map of the main geological structures around the Alxa area, as well as the locations of four boreholes, are presented in Figure 2a.

As the drilled cores have a very limited diameter (about 63.5 mm), it is not easy to use the cored samples to prepare the cubic specimens suitable for the direct shear box. In this study, the granite samples are taken from a quarry near the NRG01 borehole in the Alxa candidate area. Cubic samples are well prepared with the size of 100 × 100 × 100 mm, as shown in Figure 2b. It can be seen that the samples show pink color and have heterogeneously distributed coarse grains, and they have almost the same mineral components (alkali feldspar, plagioclase, quartz, and biotite) as the cored samples. The samples have an average density of 2.61 g/mm³. Although the quarry samples are closer to the surface, it can be observed that they are only slightly weathered. These samples are still very intact, and no obvious joints or fractures are found in the specimens, so they can be used to conduct a series of analyses of the dilation behaviors in the current period when we cannot obtain the suitable specimens at depth. The detailed sizes of each of the specimens are listed in

Table 1. Sizes of the cubic granite samples and the applied normal stresses for direct shear tests.

NO.	Sample Size (mm × mm × mm)	Normal Stress (MPa)
N-S1	98.91 × 99.07 × 99.05	5
N-S2	99.12 × 99.16 × 99.15	3
N-S3	98.87 × 98.90 × 99.06	7
N-S4	99.02 × 99.33 × 99.14	11
N-S5	99.01 × 99.28 × 98.83	9
N-S6	99.16 × 98.97 × 99.11	13
N-S7	99.26 × 98.98 × 99.07	15
N-S8	99.22 × 98.88 × 99.13	17
N-S9	99.03 × 99.11 × 99.09	15
N-S10	99.08 × 99.13 ×98.77	15
N-S11	98.83 × 98.94 × 98.94	9
N-S12	98.99 × 99.07 × 98.87	9
N-S13	99.22 × 99.09 × 99.18	3
N-S14	99.09 × 99.08 × 99.20	3

.

2.2. Experimental Methods

A series of direct shear experiments under different normal stresses have been carried out with a DSC-800 direct shear experimental system (Figure 3) developed by Key Laboratory of Shale Gas and Geoengineering, Chinese Academy of Sciences. The tests are conducted according to the following steps:

(1)

Each cubic granite sample is placed in the shear box. Thereafter, the normal stress is applied to the specimens to the target value. In this study, considering the loading capacity of the test machine, the normal stresses ranging from 3 to 17 MPa are applied. Actually, the results presented in the following sections show that this range of normal stresses is suitable enough to conduct a systematic analysis of the dilation behavior of these granite samples. The applied normal stress value for each specimen has been listed in Table 1.

(2)

When the normal stress reaches the designed value, shear stress is applied to each sample with a shear strain rate of 1.0 × 10⁻⁵ s⁻¹. Each experiment continues until the shear stress reaches a residual value or the shearing failure of the specimen occurs.

(3)

During the experiment, two force transducers are installed to measure the shear and normal loads, and a pair of LVDT (linear variable differential transformer) type extensometers [36,45,63,64] are used to measure the strain values at both normal and shear directions. The data are recorded with a sampling interval of 0.02 s. With these recorded data, the shear stress‒normal strain curve and shear stress‒shear strain curve are drawn for each of the tests.

The physical process of the direct shear test on cubic samples is also illustrated in the sketch presented in Figure 1b.

3. Experimental Results

A series of peak strength values can be obtained from the direct shear tests on the granite samples under different normal stresses (Figure 4). It should be noted that only the tests under the normal stresses of 3, 9, and 15 MPa were repeated three times considering the limited numbers of the samples, and each of the tests under the other normal stresses was carried out on just one single sample. It is found that these strength values can be well fitted by the linear Coulomb criterion. The fitting result shows that the granite samples have a cohesion of 6.6 MPa and internal friction angle of 65.7°.

The obtained stress–strain curves are presented in Figure 5. The shear stress–shear strain curves have been obtained for each of the tests under different normal stresses. In Figure 5, only eight shear stress–shear strain curves under the eight different normal stresses (without the curves obtained from the repeated tests) are presented for clear observation. Unfortunately, the shear stress–normal strain curves have only been recorded successfully for the experiments under the normal stresses σ_n = 7, 11, 13, 15, and 17 MPa. Nonetheless, these curves provided enough data for the analyses in this study. It should be noted that the negative value of the normal strain means the expansion of the specimen at the direction of normal stress, and the positive value of the shear strain means the decrease of the angle ∠xoy under the effect of shear loading (according to the coordinate system, as shown in Figure 1).

According to the shear stress–shear strain curves and shear stress–normal strain curves presented in Figure 5, several characteristics can be observed as follows:

(1)

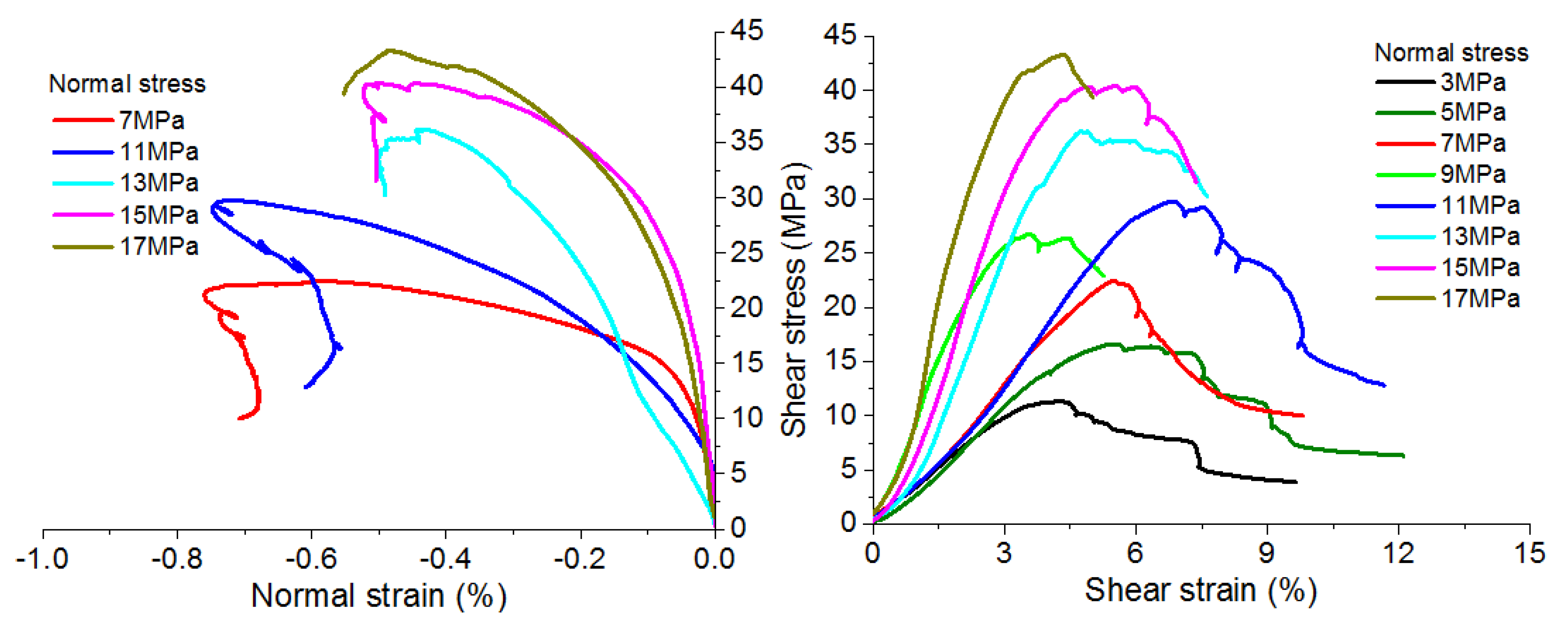
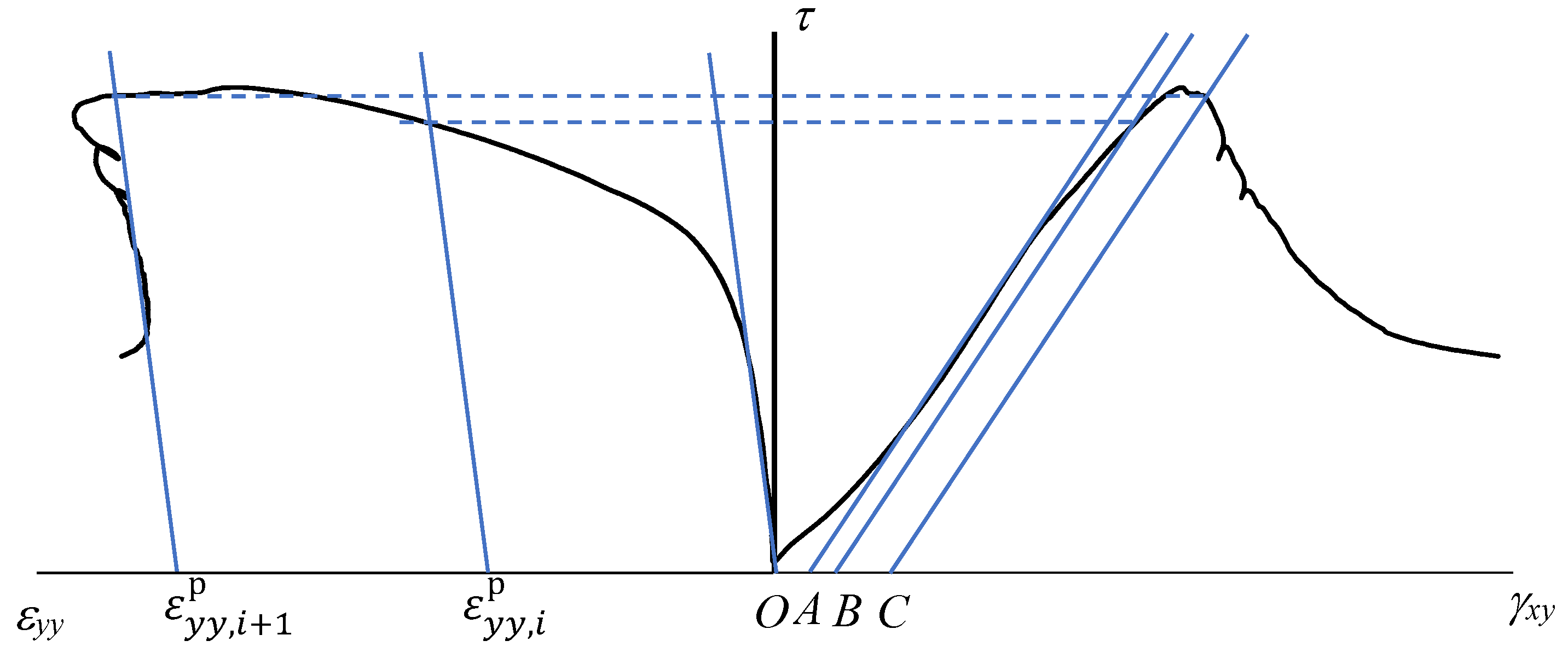
The shear stress–shear strain curves and shear stress–normal strain curves can be divided into five different stages: (I) Crack closure stage. In this stage, the slope of the shear stress–shear strain curve keeps growing to reach a constant value, showing the closure of the pre-existing cracks inside the specimen. This process may also be mixed with the effect of seating and sample adjustment. It should be noted that the normal strain curves show a slight expansion instead of crack closure induced by compaction because the crack closure process at the normal direction has occurred during the preparation process of applying a normal load, which is prior to the shear loading, so it cannot be shown in this curve. (II) Linear elastic stage. In this stage, both the shear stress–shear strain curve and the shear stress–normal strain curve behave in an almost linear style. (III) Stable crack growth stage. Although the shear stress–shear strain curve still appears linear, the normal strain shows an apparent depart from linearity. Scattered distributed cracks begin to develop in a stable way, and the onset of crack initiation also means the beginning of dilation. (IV) Unstable crack propagation stage. Both the shear strain and normal strain increase in an apparently non-linear style, meaning that crack coalescence and the unstable crack propagation occurs. (V) Post-peak stage. The shear stress decreases with the increasing shear strain, meaning that the shear zone is forming, and the shear load cannot be maintained. The detailed division of the different stages is demonstrated in Figure 6, with a typical stress-strain curve from this group of experiments. It should be noted that the information of the cracking process has not been monitored in this study, but the above-mentioned analyses are believed to be reasonable because they are based on the features of the stress-strain curves, as well as a comparison with the stage division of conventional tri-axial compression experiments [1,35,37,38].

(2)

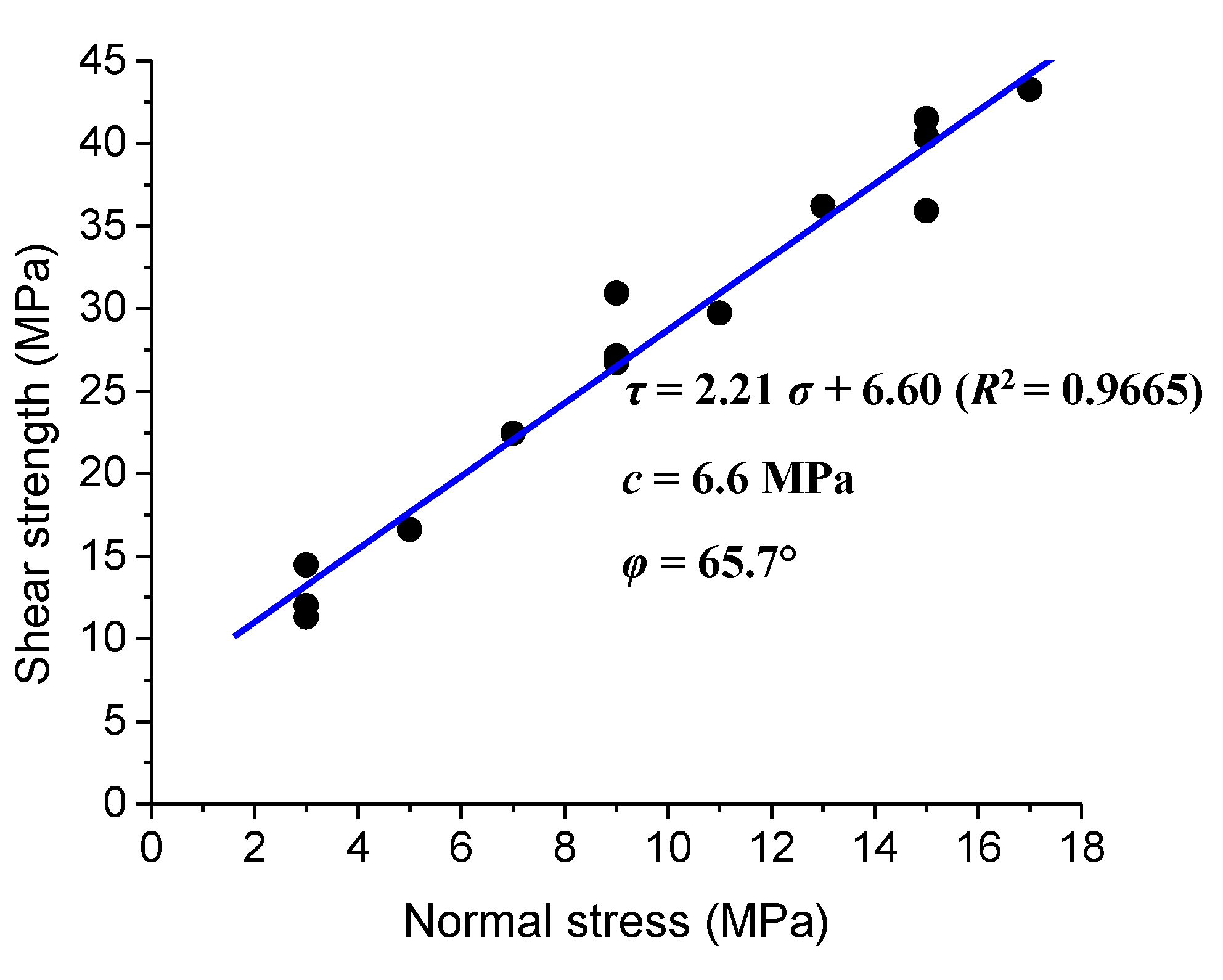
When the normal stress is relatively low (e.g., σ_n = 3 and 5 MPa), the shear stress drops in a gradual manner after the failure of the specimen, showing relatively ductile post-peak behavior; with increasing normal stress, the post-peak behavior turns to be more brittle. Under the normal stress σ_n = 13 MPa to 17 MPa, it seems that the granite samples are prone to fail before reaching the residual shear strength. It appears that the direct shear test results show a ductile–brittle transition behavior, instead of the brittle–ductile transition behavior usually found in the conventional tri-axial compression experiments [35]. This study tries to provide an explanation as follows: For the cases under lower normal stresses, the peak shear strength is lower, so the strain energy stored in the test system is also lower. Consequently, lower strain energy will be released when failure occurs; therefore, the shear stress drops in a more stable manner. On the other hand, the higher normal stress may result in higher peak shear strength, and higher strain energy will be released during the post-peak stage, leading to a more violent failure of the specimen. It should be noted that the post-peak behavior should also be closely related to the fracturing patterns under different normal stresses, which requires a more systematic research.

(3)

When the failure occurs, the normal strain is apparently higher under relatively lower normal stresses (e.g., σ_n = 7 MPa and 11 MPa) than that under higher stresses (e.g., σ_n = 13, 15, and 17 MPa). It is interesting to find that the normal strain may decrease during the post-failure stage. This decrease is more obvious for the samples under lower normal stresses (e.g., σ_n = 7 and 11 MPa). This phenomenon is related to the dilation behavior and will be discussed in detail in the next section.

4. Data Analyses and Discussion

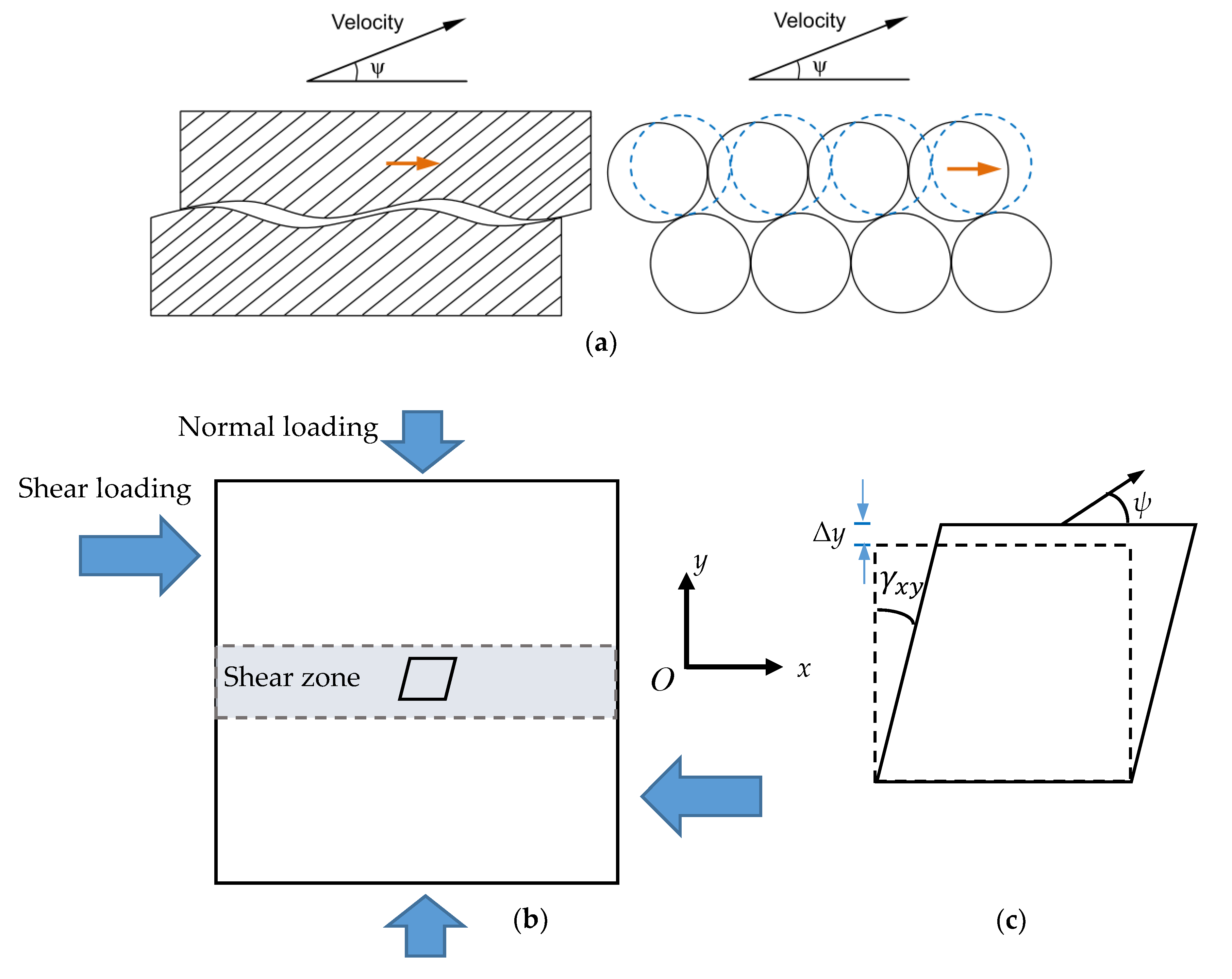
4.1. Methods

Based on the results obtained from the direct shear experiments on the granite samples under different normal stresses, the dilation angle can be calculated according to Equation (4) presented in Section 1. It should be noted that there is a negative sign in this equation, as the normal strain ${\epsilon }_{yy}$ is defined as negative when the specimen has an expansion at the direction of normal stress in this study.

Based on the definition in Equation (4), a series of plastic normal strain and plastic shear strain values should be obtained in order to analyze the dilation behavior of the granite samples under the direct shear experiments. The cyclic loading and unloading test is an ideal method to differentiate the elastic and plastic components of the normal and shear strains at each cycle. However, it is not easy to control this type of test, especially during the post-peak stage, when the fractures always propagate in an unstable manner. Furthermore, the data will be limited by the number of cycles. Therefore, another method is used, assuming that the unloading modulus is the same as the initial deformation modulus, and this method has been widely accepted in many studies [35,36,44]. In this way, a series of assumed loading-unloading cycles can be obtained by carrying out the common direct shear experiments. Thereafter, a series of plastic normal strain and shear strain values can be collected. A sketch of this method is provided in Figure 7. A series of lines parallel with the tangent lines at the linear elastic stage of the τ–ε_yy curves and τ–γ_xy curves are drawn to determine the plastic normal strain ${\epsilon }_{yy,i}^{\mathrm{p}}$ and plastic shear strain ${\gamma }_{xy,i}^{\mathrm{p}}$, respectively. The symbol i here means a series of positive integers, showing that a series of plastic strain values can be collected with this method. It should be noted that there is a gap $\left|OA\right|$ owing to the crack closure stage of σ₁–ε₁ curves, so this gap should be removed when determining the plastic shear strain ${\gamma }_{xy,i}^{\mathrm{p}}$:

$${\gamma }_{xy,i}^{\mathrm{p}}= \left|OB\right|-\left|OA\right|, {\gamma }_{xy,i+1}^{\mathrm{p}}= \left|OC\right|-\left|OA\right|.$$

(5)

According to the plastic normal and shear strain values, the dilation angle can be calculated by the following Equation:

$$\tan \psi = -{\dot{\epsilon }}_{yy}^{\mathrm{p}}/{\dot{\gamma }}_{xy}^{\mathrm{p}}=-\frac{{\epsilon }_{yy,i+1}^{\mathrm{p}}-{\epsilon }_{yy,i}^{\mathrm{p}}}{{\gamma }_{xy,i+1}^{\mathrm{p}}-{\gamma }_{xy,i}^{\mathrm{p}}}.$$

(6)

With this method, the dilation angles of the granite samples under different normal stresses can be obtained, and the dilation behaviors of the specimens will be discussed.

4.2. Mobilized Dilation Angle of the Granite Samples Dependent on Normal Stress and Plastic Shear Strain

With the obtained plastic normal and shear strain values under various normal stresses, their relations are illustrated as the curves in Figure 8. It can be found that the plastic normal strain values are negative for all the cases, showing a plastic expanding deformation during the tests. The plastic normal strain expands significantly at the beginning stage with increasing plastic shear strain; thereafter, it turns flat and reaches a peak value. For the cases under lower normal stress (e.g., σ_n = 7 and 11 MPa), the expanding of plastic normal strain has a slight decrease after the peak value, while this phenomenon has not been observed for the cases with higher normal stresses (e.g., σ_n = 13, 15, and 17 MPa).

The calculated dilation angle values are presented in Figure 9. It can be found that the dilation angle is mobilized depending on the normal stress and plastic shear strain. According to the mobilization of the dilation angles, several features can be observed as follows:

(1)

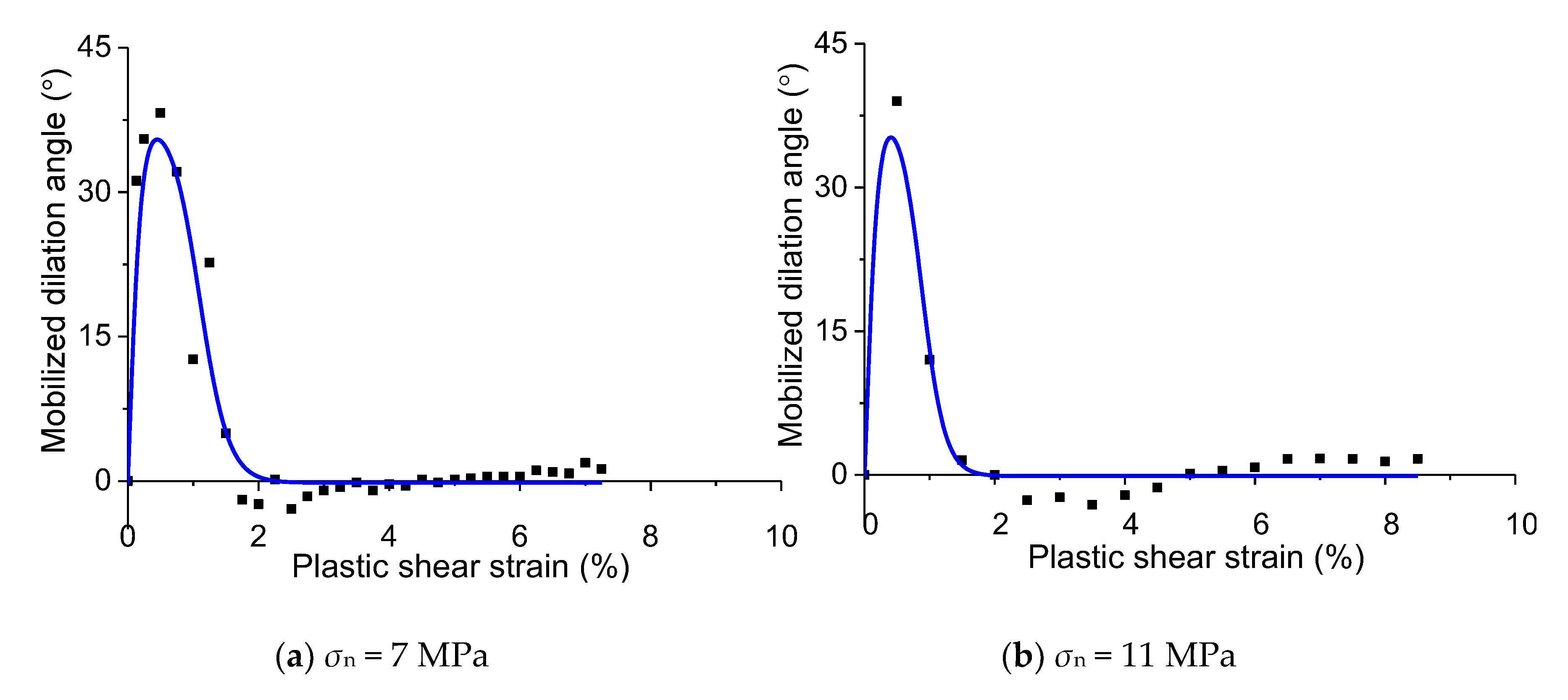
For all the tests under different normal stresses, the dilation angle increases significantly to the peak value firstly with the increasing plastic shear strain; thereafter, it drops to a residual value.

(2)

For the cases under higher normal stresses (e.g., σ_n = 13, 15, and 17 MPa), the dilation angles are all positive. The peak value of the dilation angle is lower than that under the lower normal stresses; however, the residual value is relatively higher.

(3)

When the normal stress is relatively lower (e.g., σ_n = 7 and 11 MPa), the maximum dilation angle is higher, and it drops in a more significant manner. The dilation angle can even drop to a negative value, meaning the behavior of “contraction” occurs. However, the absolute value of the negative dilation angle is not very high.

The mobilized dilation angle can be well fitted by the following equation:

$$\psi = {\psi }_{\max }\left[\frac{2}{1+\exp (-5\frac{{\gamma }^{\mathrm{p}}}{{\gamma }_{\phi ,\max }^{\mathrm{p}}})}-1\right]-({\psi }_{\max }-{\psi }_{\mathrm{r}})\left[\frac{1}{1+\exp (-5\frac{2{\gamma }^{\mathrm{p}}-{\gamma }_{\phi ,\mathrm{r}}^{\mathrm{p}}}{{\gamma }_{\phi ,\mathrm{r}}^{\mathrm{p}}})}\right]$$

(7)

where, ${\psi }_{\max }$ and ${\psi }_{\mathrm{r}}$ are the maximum and residual values of the dilation angle, respectively; ${\gamma }_{\phi ,\max }^{\mathrm{p}}$ is the plastic shear strain when the dilation angle reaches the peak value; ${\gamma }_{\phi ,\mathrm{r}}^{\mathrm{p}}$ is the plastic shear strain when the dilation angle approaches the residual value.

The fitted parameters are presented in

Table 2. Fitted parameters for the dilation angle–plastic shear strain curves under different normal stresses.

Normal Stress (MPa)	${\mathit{\psi }}_{\mathbf{max}} (°)$	${\mathit{\psi }}_{\mathbf{r}} (°)$	${\mathit{\gamma }}_{\mathit{\phi },\mathbf{max}}^{\mathbf{p}} (\%)$	${\mathit{\gamma }}_{\mathit{\phi },\mathbf{r}}^{\mathbf{p}} (\%)$	R2
7	38.20	−0.18	0.50	2.20	0.9150
11	39.01	−0.12	0.50	1.76	0.9565
13	16.81	1.48	0.50	1.83	0.8517
15	23.66	1.98	0.50	2.00	0.9236
17	15.45	5.36	0.50	2.58	0.9008

.

According to Table 2, the four parameters are dependent on the normal stress values. With the fitted data in Table 2, the four parameters can be further fitted with Equations (8)–(11). The fitted curves and equations are presented in Figure 10.

$${\psi }_{\max }=a_1{\sigma }_{\mathrm{n}}^{b_1}$$

(8)

$${\psi }_{\mathrm{r}}=a_2{\sigma }_{\mathrm{n}}^{b_2}$$

(9)

$${\gamma }_{\phi ,\max }^{\mathrm{p}}=a_3$$

(10)

$${\gamma }_{\phi ,\mathrm{r}}^{\mathrm{p}}=a_4{\sigma }_{\mathrm{n}}+b_4$$

(11)

This empirical mobilized dilation angle has clear physical meanings, and the parameters can be easily determined by conducting a series of direct shear tests. This model can be used in the plastic constitutive models (as shown in Equations (1) and (2) for an example) for describing the deformation behavior of the host rock of the repository for HLW disposal. It may also be extended to other types of rock engineering. In future studies, we should conduct more experiments on different types of rock to extend the applicability of this model.

5. Conclusions

Based on a series of direct shear experiments on the granite samples from the Alxa candidate area in China for HLW disposal, this paper supplied a systematic analysis of the shear stress–shear strain and shear stress–normal strain relations. The dilation behaviors of the granite samples were especially studied in detail, and an empirical model on the mobilization of dilation angle dependent on the normal stress and plastic shear strain was proposed. The main contributions are as follows:

(1)

The shear stress–shear strain curves and shear stress–normal strain curves are divided into five typical stages, which are associated with the deformation and fracturing process. The typical stress thresholds were proposed to divide the different stages.

(2)

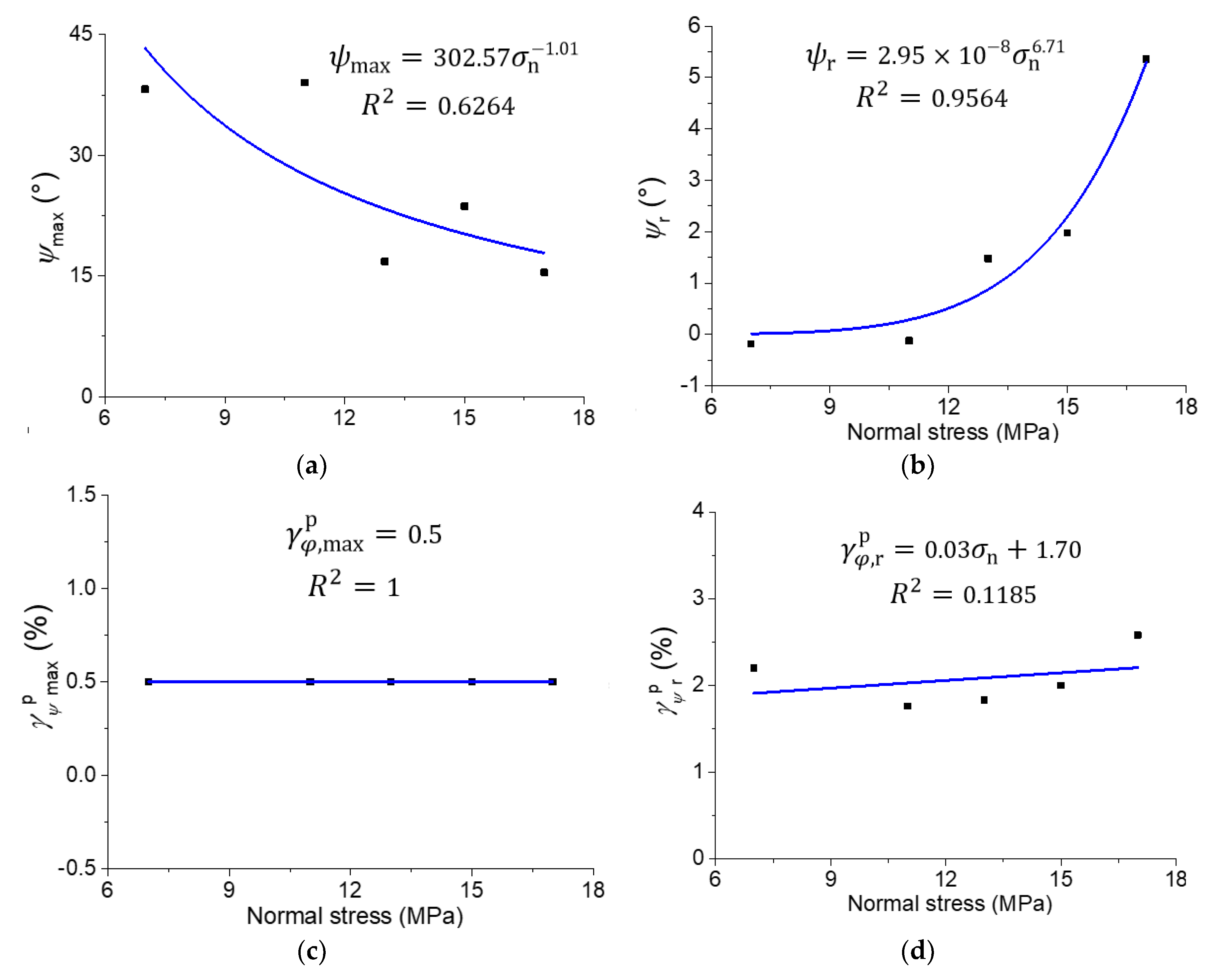
It is found that the increasing normal stress may reduce the maximum dilation angle. When the normal stress is lower, the negative dilation angle may occur; however, this phenomenon has not been observed in the cases under higher normal stresses.

(3)

An empirical model of the mobilized dilation angle dependent on normal stress and plastic shear strain is proposed based on the fitting of the data collected from the direct shear tests. This model can be used in further studies on the constitutive modeling of the host rock.

This study provided a method to analyze the mobilization angle of rock under direct shear test. The proposed model has well understood physical meanings, and it is easy to determine the values of the parameters. This study can be used for better modeling on the stability of the repository for HLW disposal, and this method can also be put forward to analyze the stability of other geomechanical problems, including the deformation behaviors related to landslides, earthquakes, and so on.

It should also be noted that the effect of temperature induced by the nuclear waste cannot be ignored when considering the mechanical behavior of the host rock, so more studies are required considering the effect of heat on the dilation behavior of the granite samples. In addition, more systematic experimental studies on more types of rock associated with the monitoring of the fracturing process will be conducted to extend the applicability of the dilation angle model supplied in this study.