A Mixing Behavior Study of Biomass Particles and Sands in Fluidized Bed Based on CFD-DEM Simulation
Abstract
1. Introduction
2. Methodology
2.1. Particle Model
2.2. Governing Equations of Fluid Phase
2.3. Particle Mixing Index
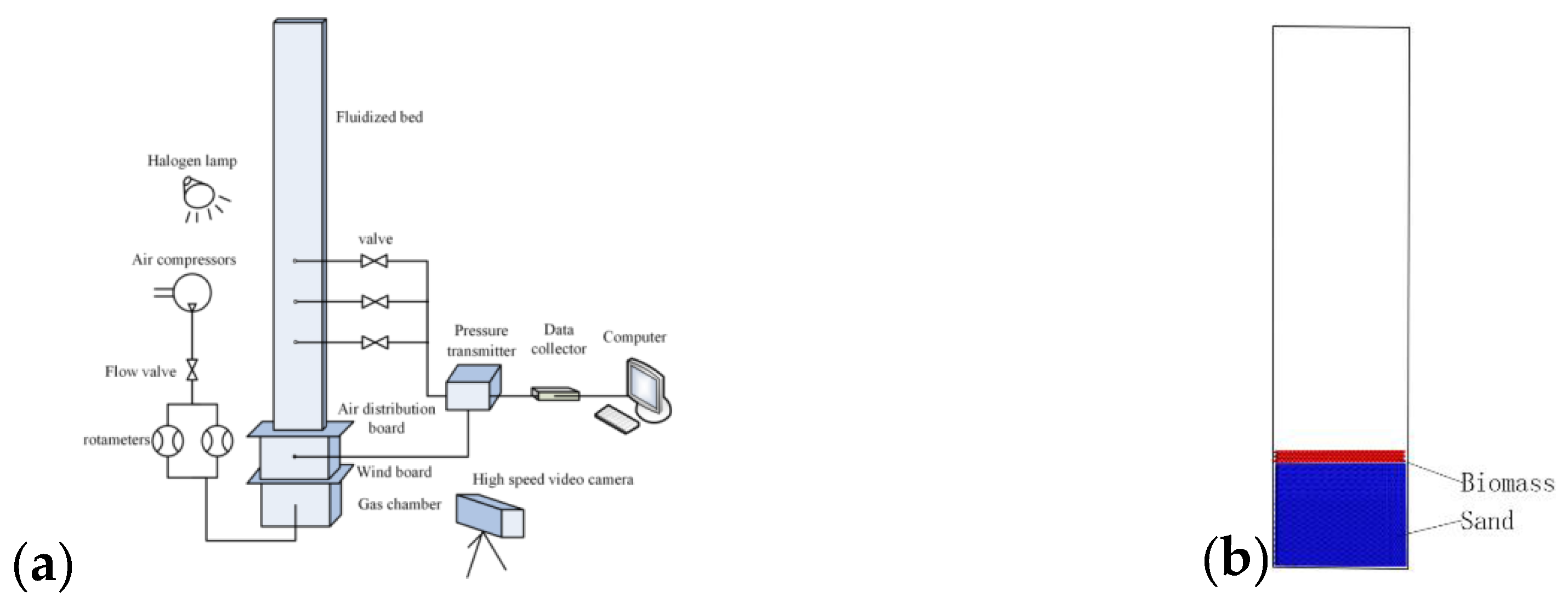
3. Experiment and Simulation Conditions
3.1. Experiment Details
3.2. Simulation Conditions
4. Results and Discussion
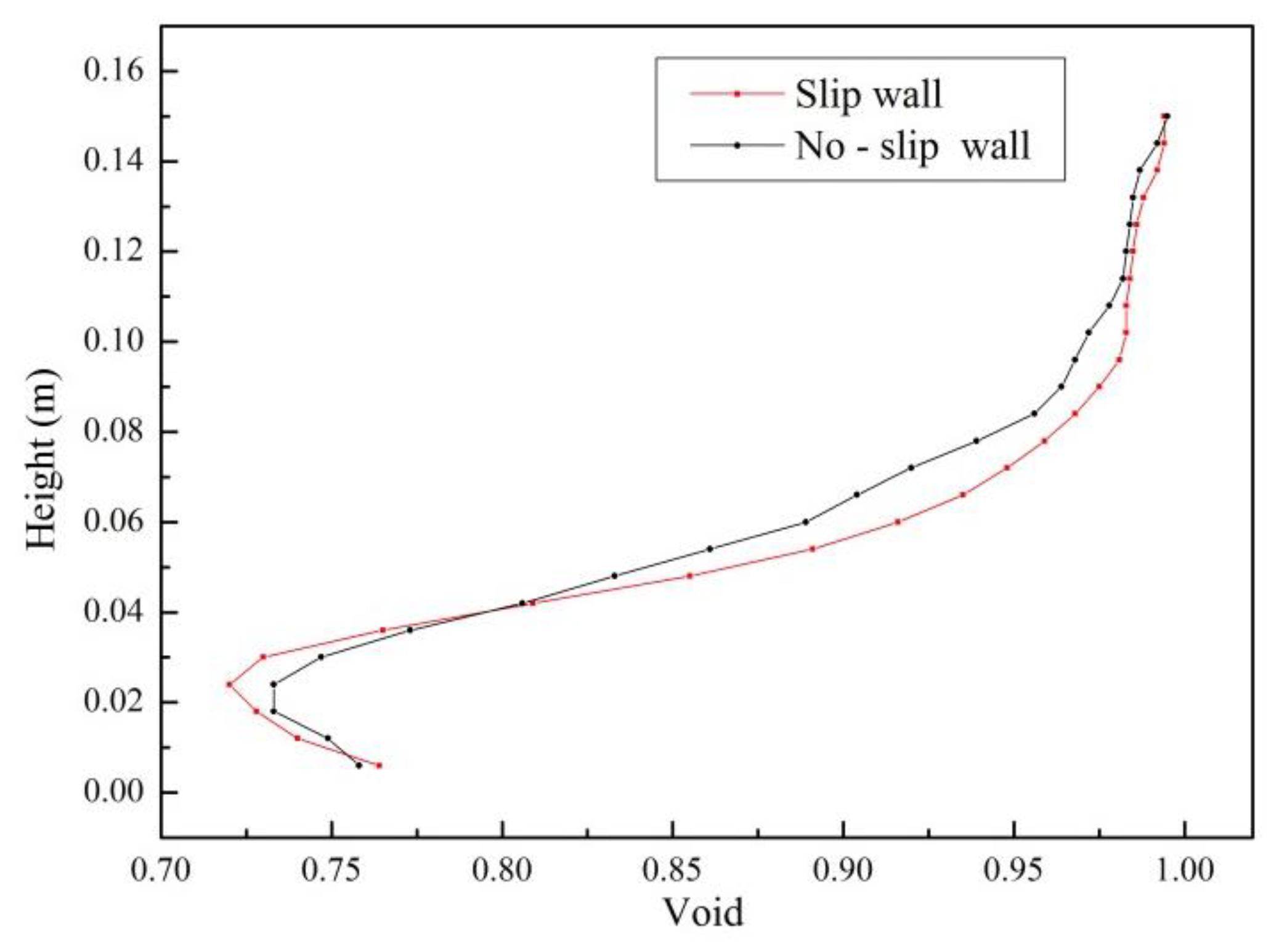
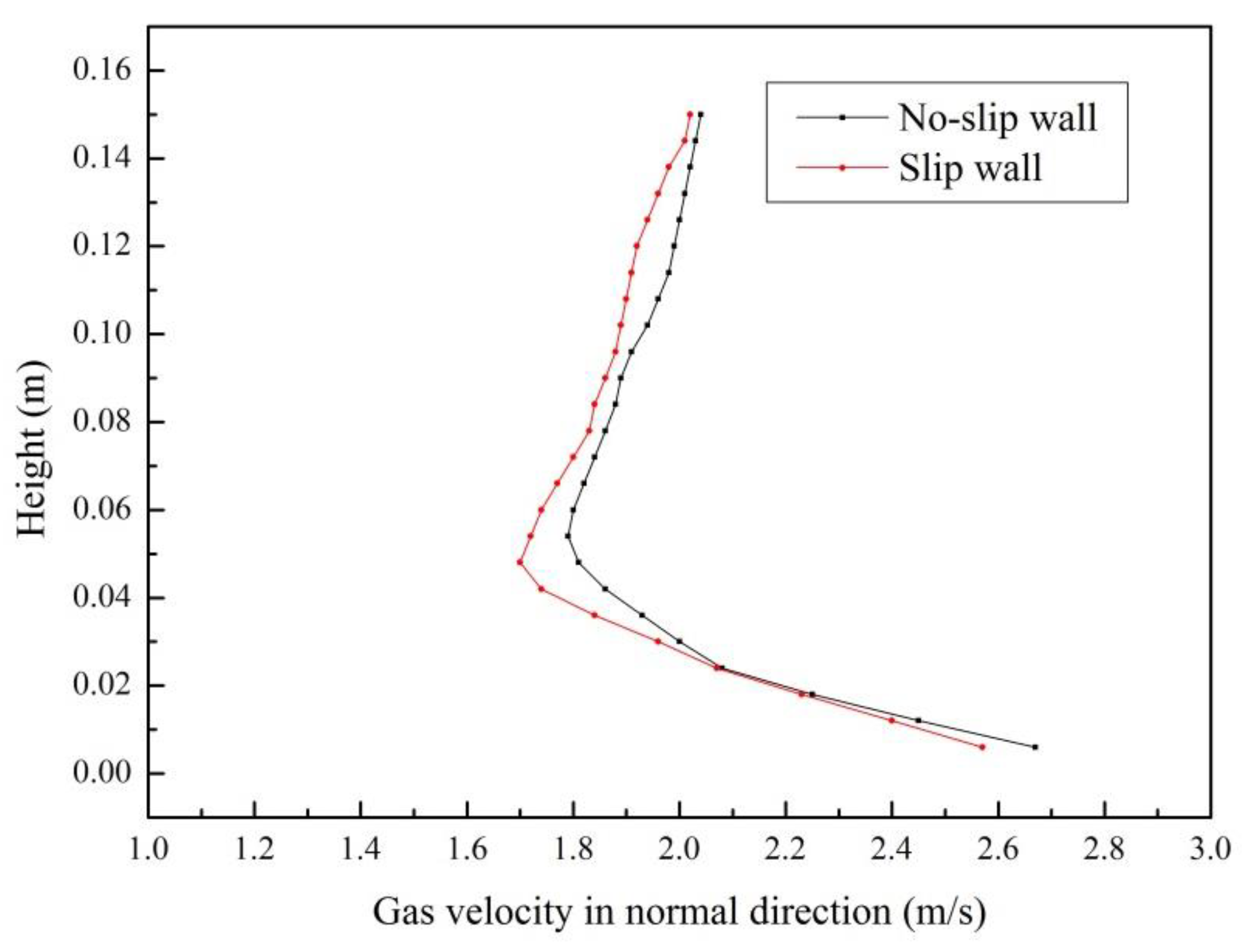
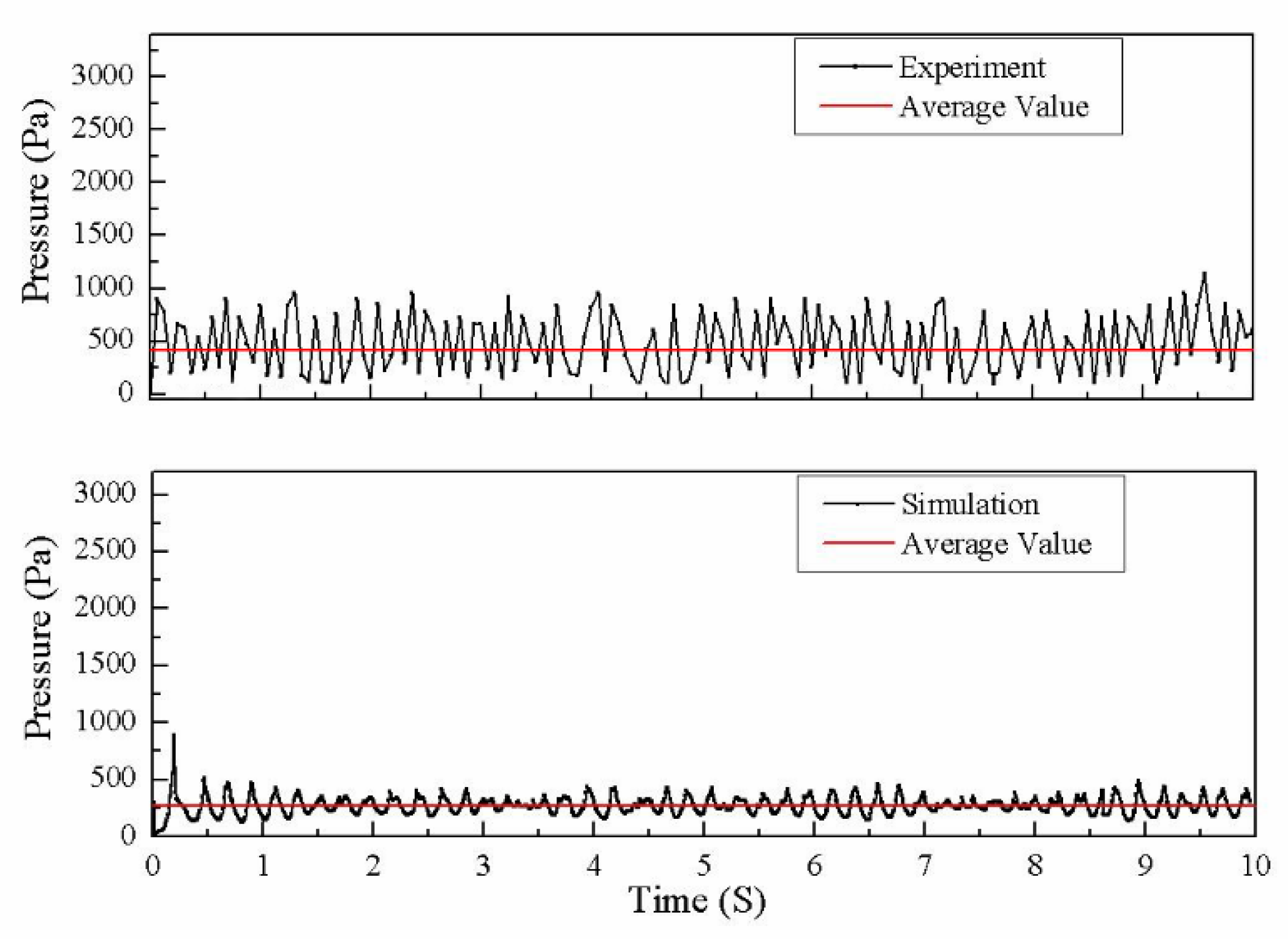
4.1. Validity of Simulation Results
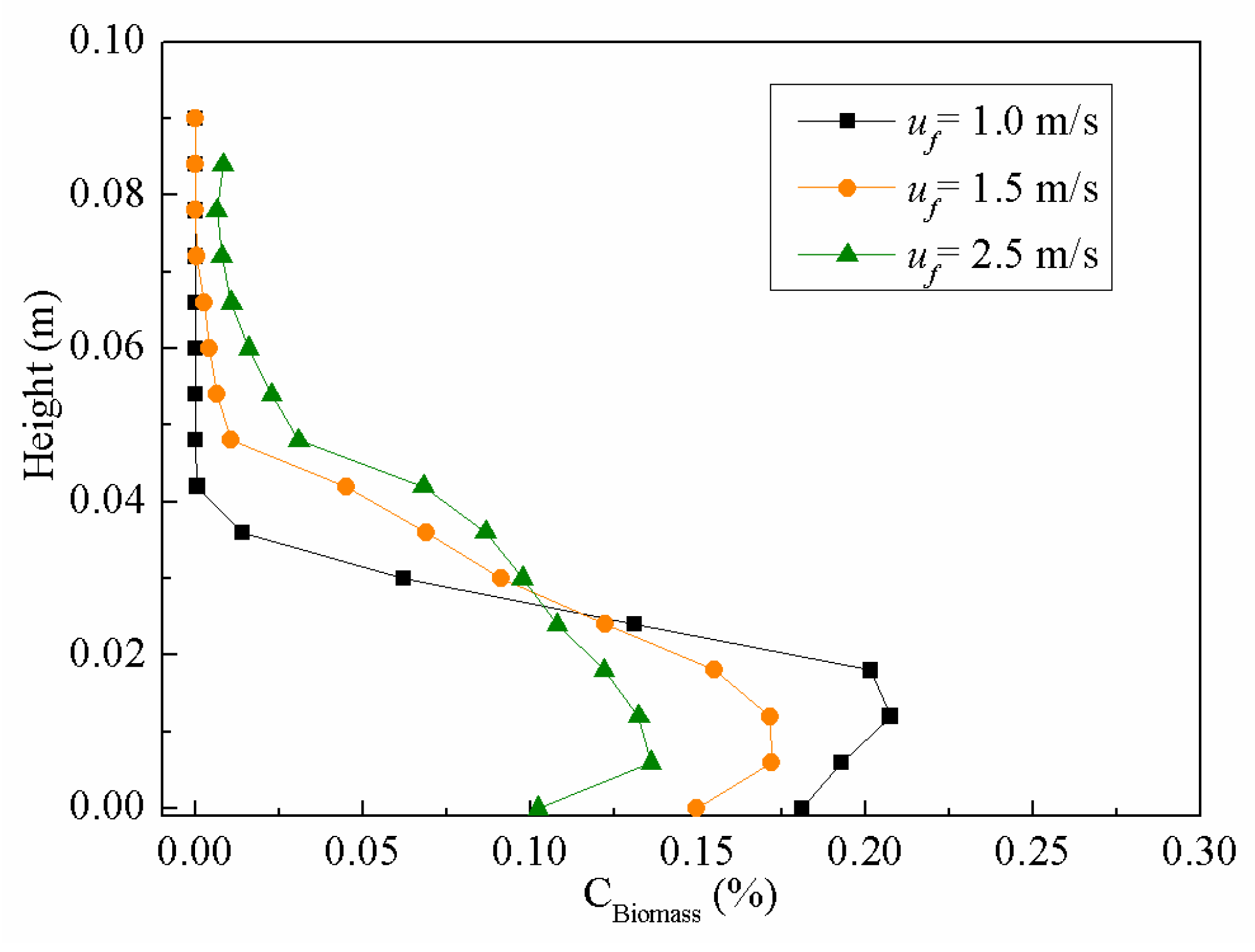
4.2. Particle Mixing Characteristics at Different Gas Velocities
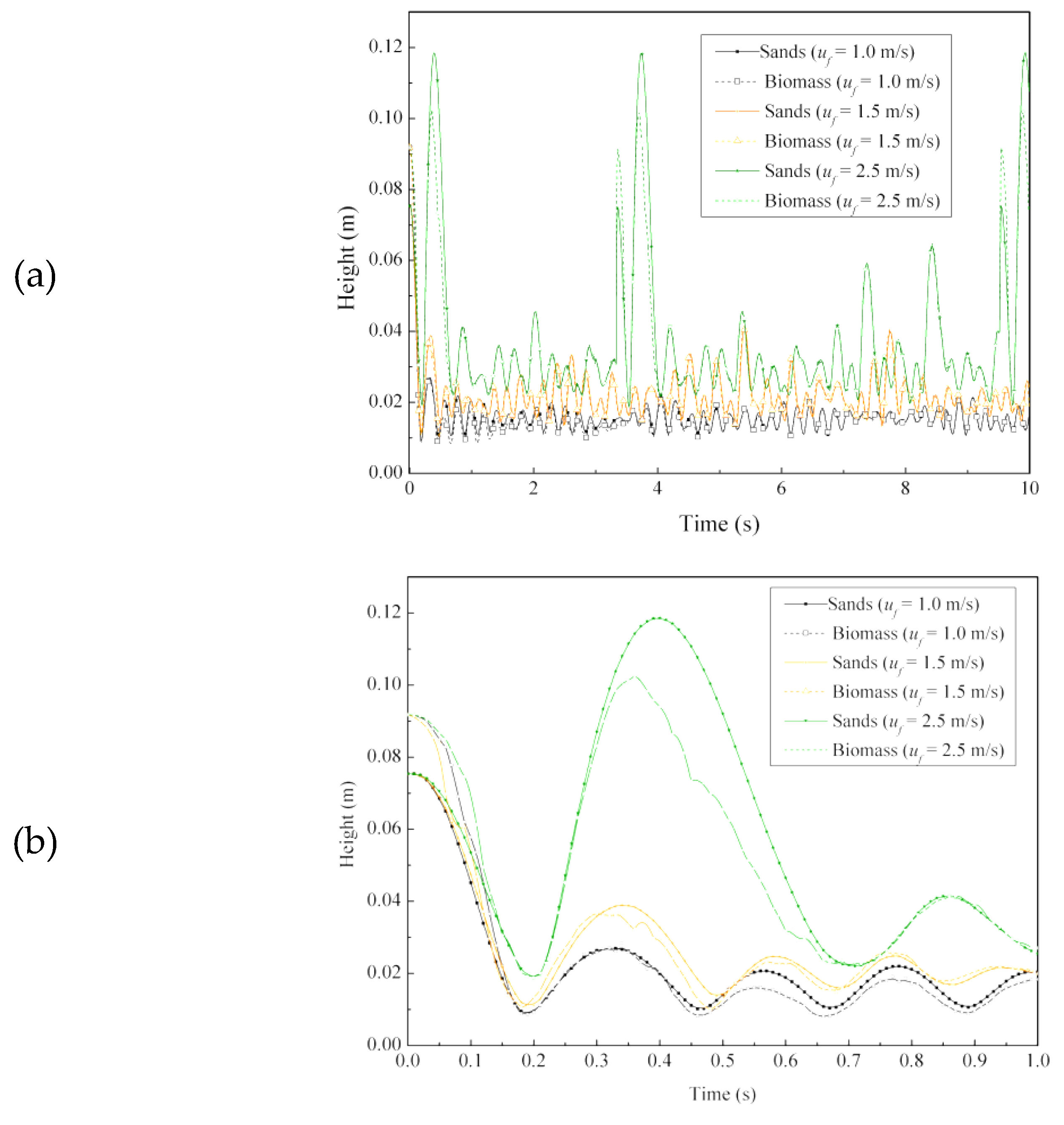
4.2.1. Instantaneous Particle Height
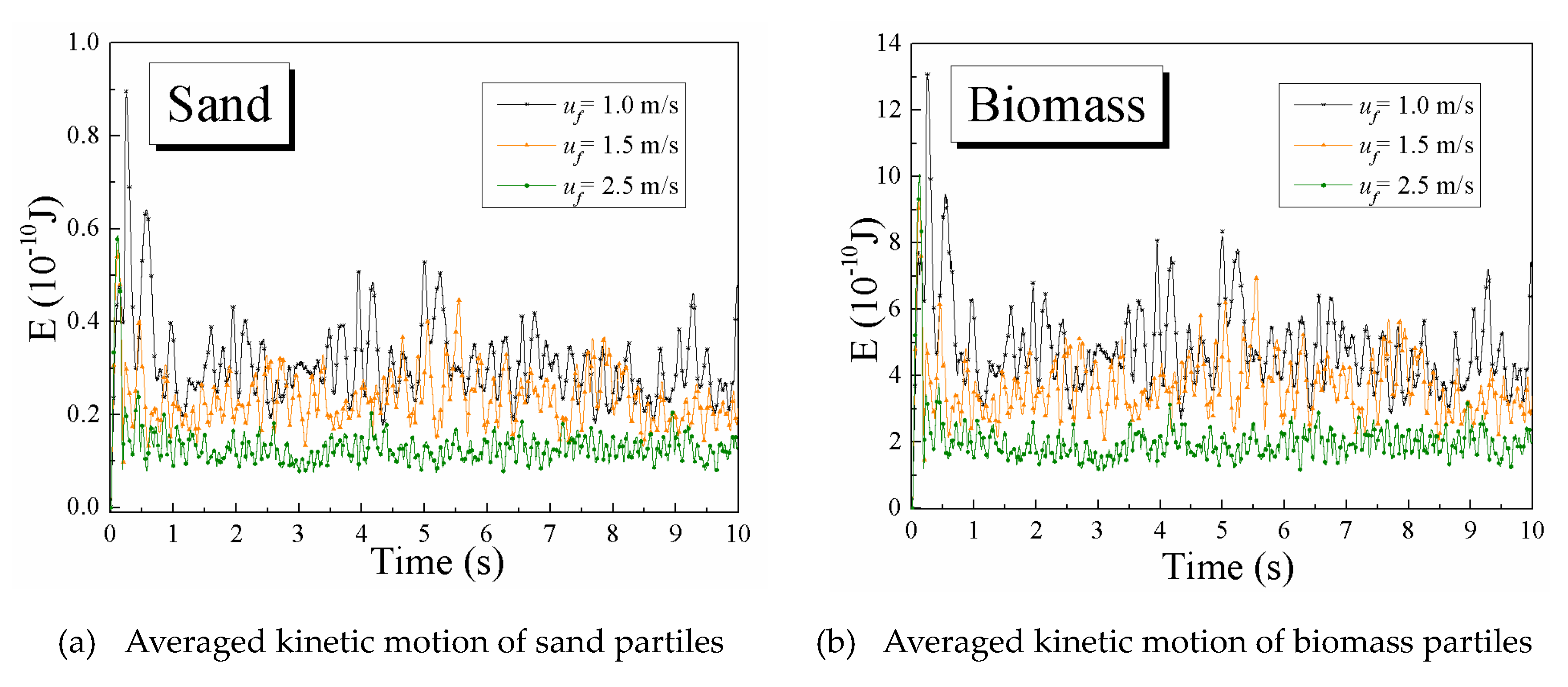
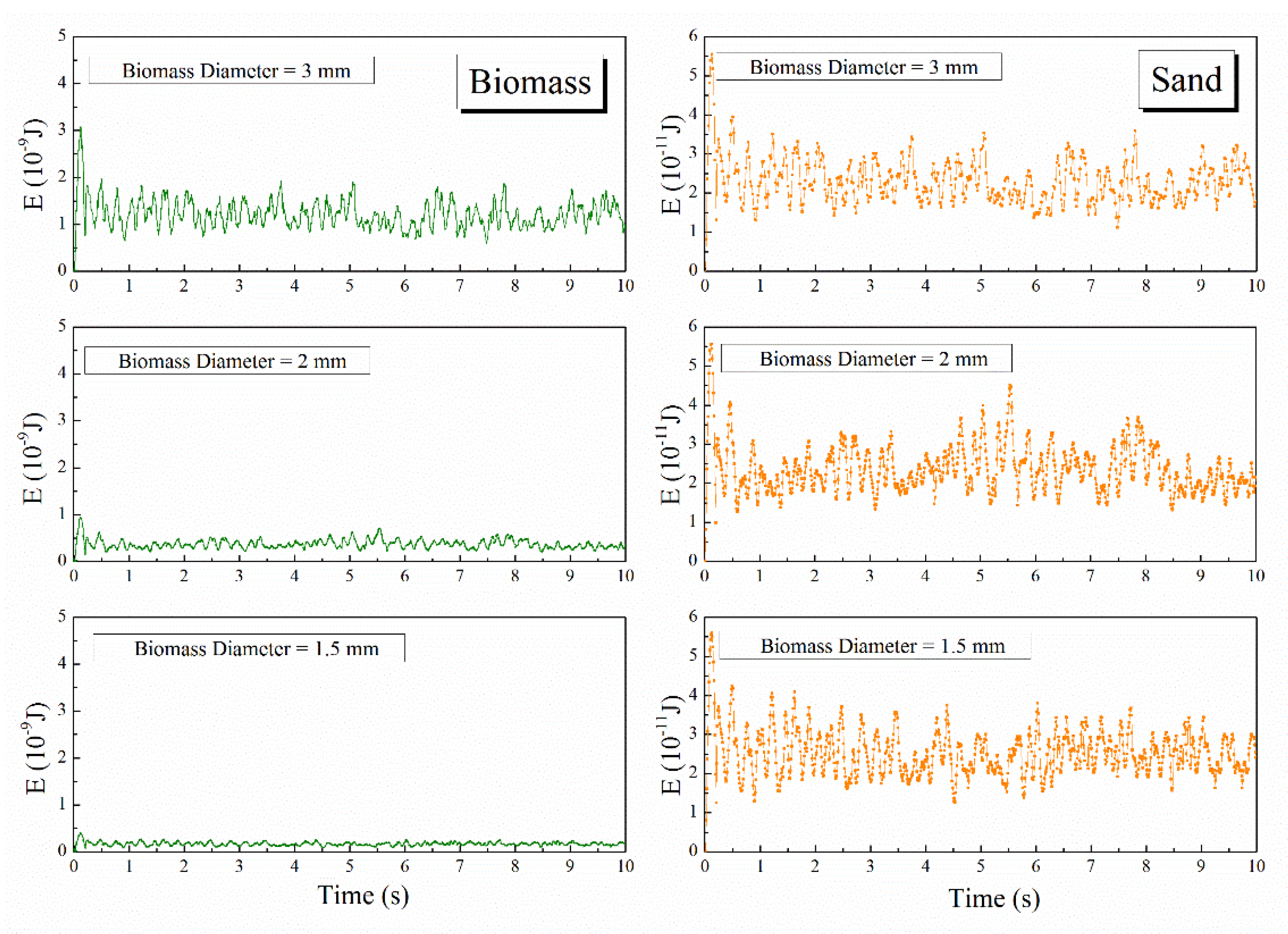
4.2.2. Particle Averaged Kinetic Energy
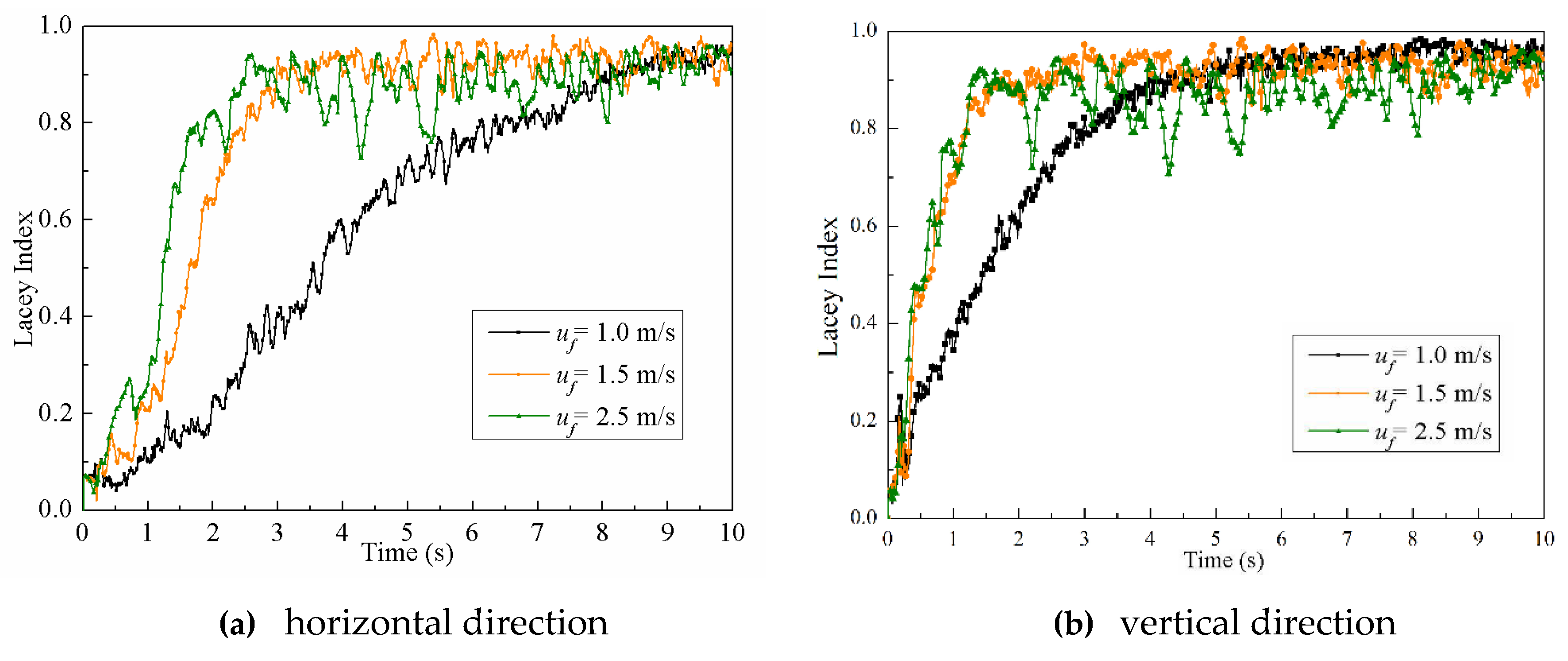
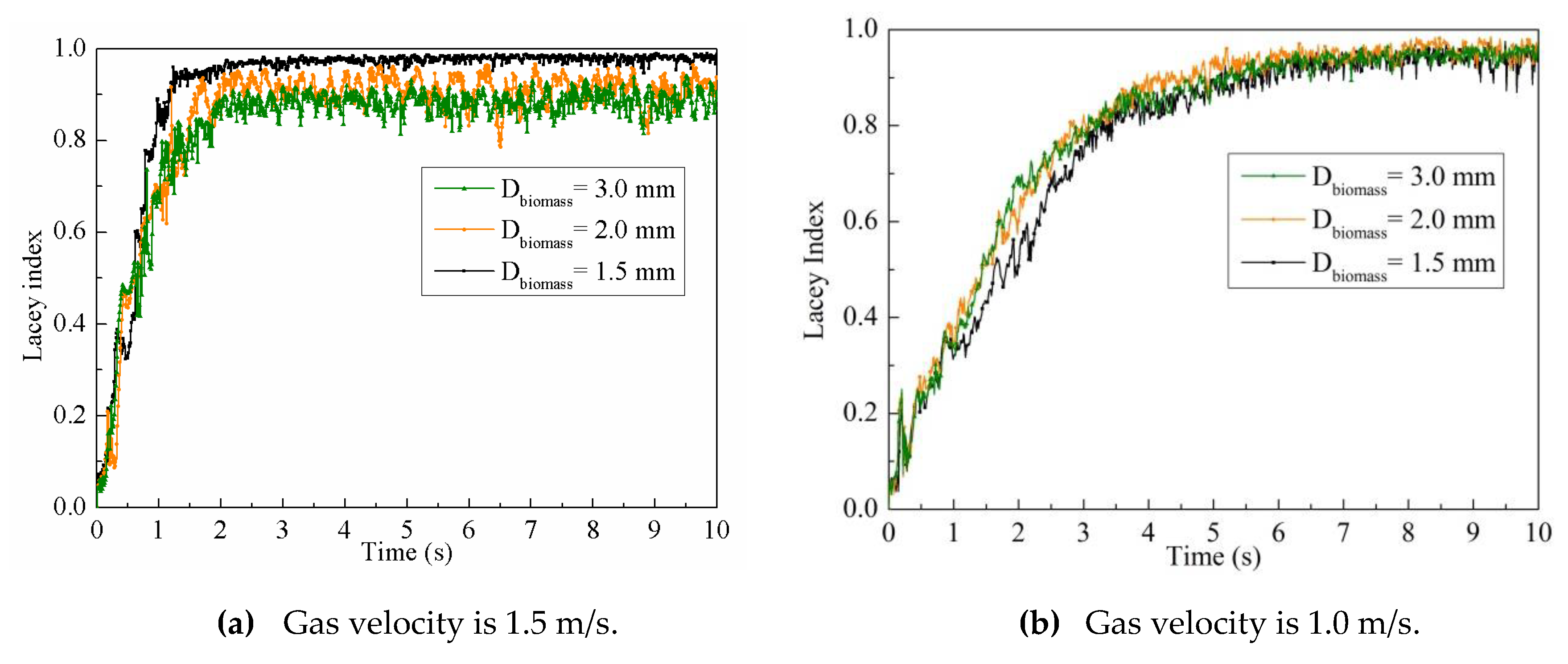
4.2.3. Particle Mixing Index
4.2.4. Time Averaged Biomass Distribution
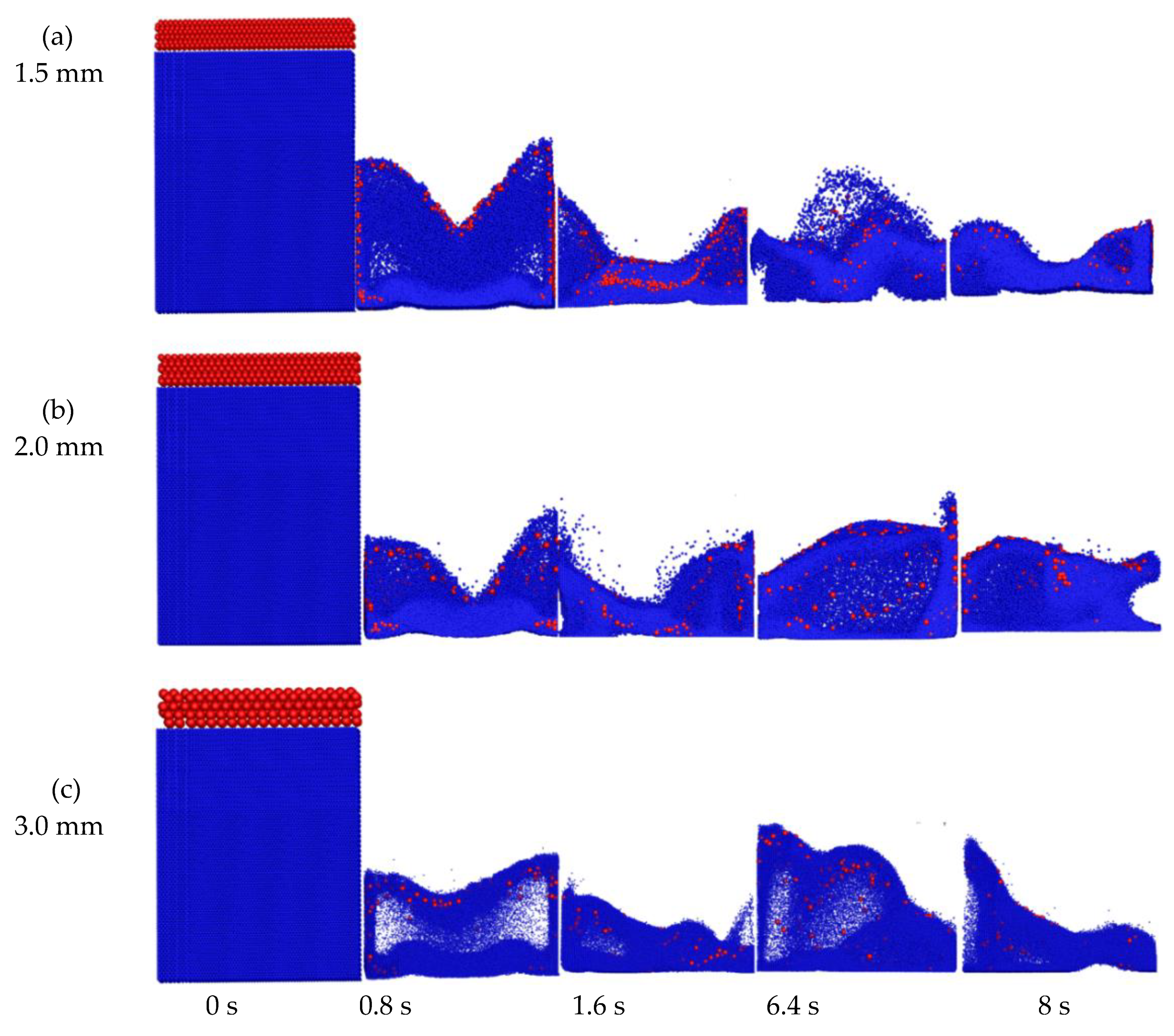
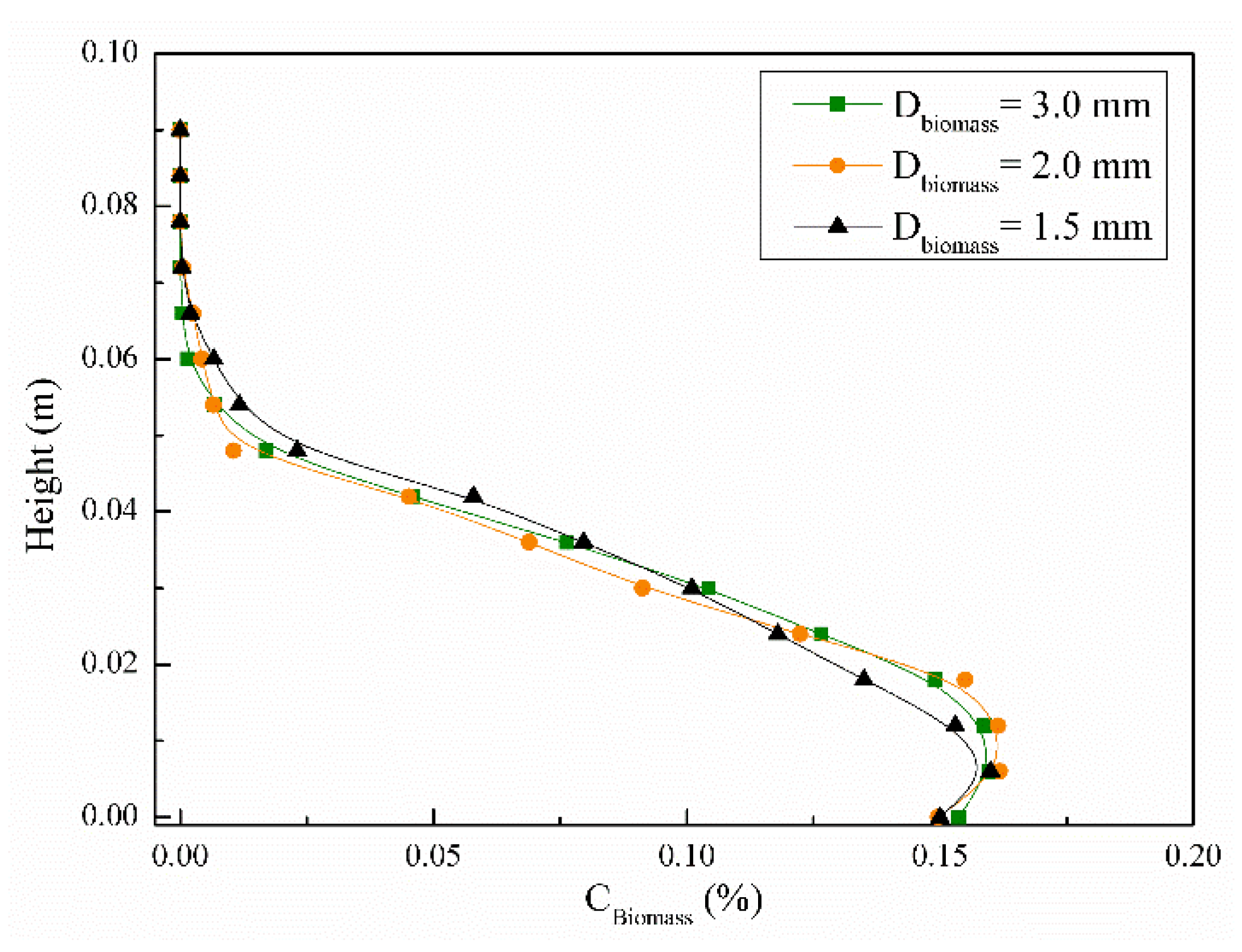
4.3. Particle Mixing Characteristics with Different Biomass Particle Sizes
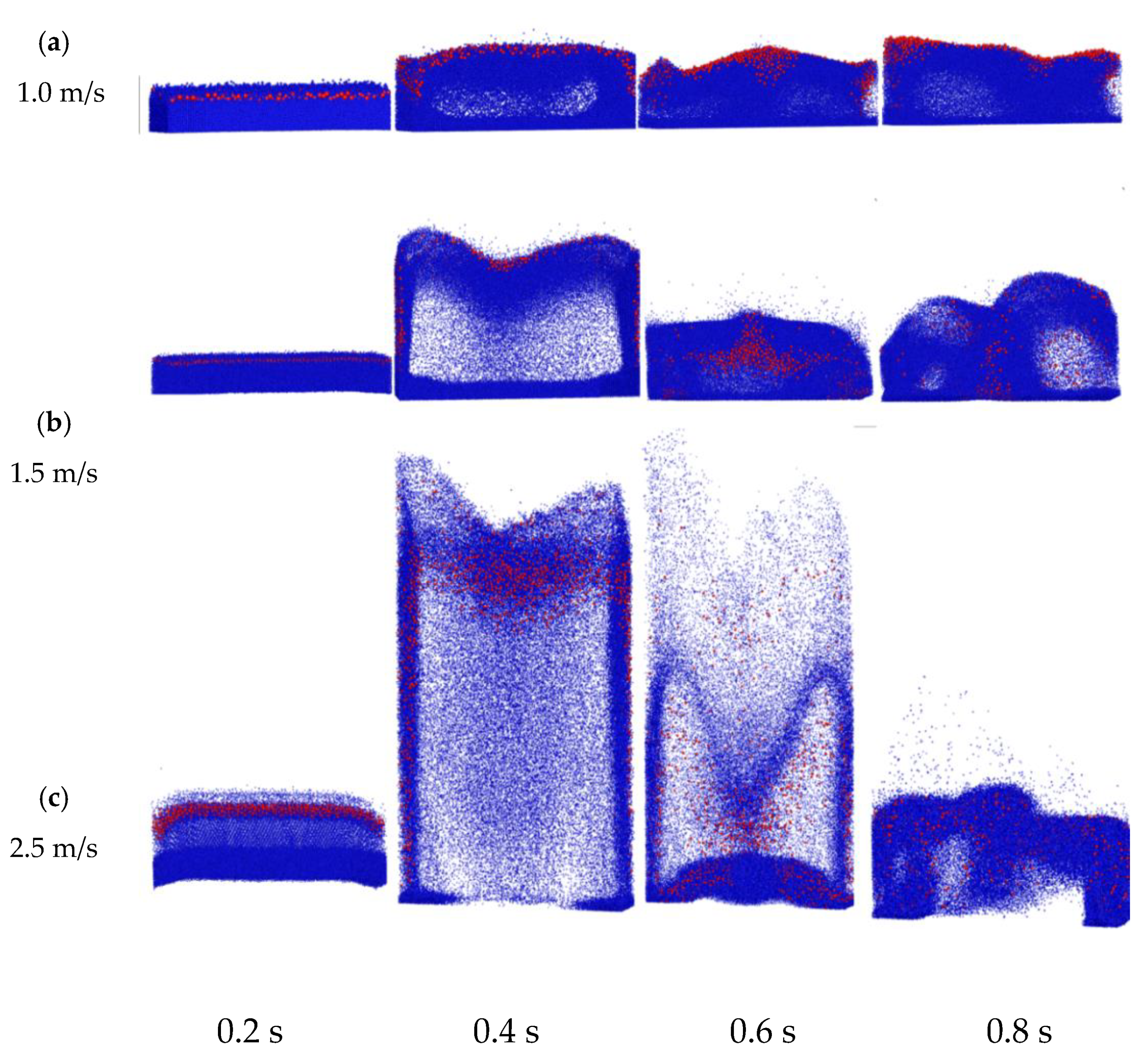
4.3.1. Instantaneous Particle Mixing Behavior
4.3.2. Particle Averaged Kinetic Energy
4.3.3. Time Averaged Biomass Distribution
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| drag force coefficient of singe particle | |
| mean of sampled concentration | |
| ci | local concentration |
| Db | biomass particle distribution |
| Dij | strain tensor |
| dp | diameter of particle p |
| fc | contact force |
| fd | gas-solid drag force |
| fpg | pressure gradient force |
| G | acceleration of gravity |
| Gp | particle gravity |
| Hb | instantaneous height of biomass particles |
| Hs | instantaneous height of sand |
| Is | particle momentum of rotation inertia |
| M | number of sand |
| mp | particle mass |
| Nbiomass | total number of biomass particles in the case |
| Nsand | total number of sand in the case |
| P | gas phase pressure |
| Re | Reynolds number |
| Ts | particle torque |
| uf | fluid velocity |
| up | particle velocity |
| up,i | velocity of particle i |
| vcell | volume of cell |
| Vp | volume of particle p |
| vp,i | volume of particle i |
| ρf | gas phase density |
| µf | gas dynamic viscosity |
| α | void fraction |
| β | interphase momentum transfer coefficient |
| δij | Kronecker delta function |
| κ | tensor of stress |
| σ02 | variance of complete separated particles in statistical grids |
| σr2 | concentration variation of particles when fully mixed |
References
- Sher, F.; Pans, M.A.; Afilaka, D.T.; Sun, C.; Liu, H. Experimental investigation of woody and non-woody biomass combustion in a bubbling fluidised bed combustor focusing on gaseous emissions and temperature profiles. Energy 2017, 141, 2069–2080. [Google Scholar] [CrossRef]
- Sher, F.; Pans, M.A.; Sun, C.; Snape, C.; Liu, H. Oxy-fuel combustion study of biomass fuels in a 20 kW(th) fluidized bed combustor. Fuel 2018, 215, 778–786. [Google Scholar] [CrossRef]
- Ku, X.; Li, T.; Lovas, T. CFD-DEM simulation of biomass gasification with steam in a fluidized bed reactor. Chem. Eng. Sci. 2015, 122, 270–283. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, B.S.; Zhong, W.Q.; Ren, B.; Xiao, R. Characterization of Fluidization and Segregation of Biomass Particles by Combining Image Processing and Pressure Fluctuations Analysis. Int. J. Chem. React. Eng. 2009, 7. [Google Scholar] [CrossRef]
- Sun, Q.Q.; Lu, H.L.; Liu, W.T.; He, Y.R.; Yang, L.D.; Gidaspow, D. Simulation and experiment of segregating/mixing of rice husk-sand mixture in a bubbling fluidized bed. Fuel 2005, 84, 1739–1748. [Google Scholar]
- Madhlyanon, T.; Piriyarungroj, N.; Soponronnarit, S. Cold flow behavior study in novel cyclonic fluidized bed combustor (psi-FBC). Energy Convers. Manag. 2008, 49, 1202–1210. [Google Scholar] [CrossRef]
- Formisani, B.; Girimonte, R.; Vivacqua, V. Fluidization of Mixtures of Two Solids Differing in Density or Size. AIChE J. 2011, 57, 2325–2333. [Google Scholar] [CrossRef]
- Leon, M.A.; Dutta, A. Fluidization Characteristics of Rice Husk in A Bubbling Fluidized Bed. Can. J. Chem. Eng. 2010, 88, 18–22. [Google Scholar] [CrossRef]
- Zhong, W.Q.; Jin, B.S.; Zhang, Y.; Wang, X.F.; Xiao, R. Fluidization of Biomass Particles in a Gas-Solid Fluidized Bed. Energy Fuel 2008, 22, 4170–4176. [Google Scholar] [CrossRef]
- Si, C.D.; Guo, Q.J. Fluidization Characteristics of Binary Mixtures of Biomass and Quartz Sand in an Acoustic Fluidized Bed. Ind. Eng. Chem. Res. 2008, 47, 9773–9782. [Google Scholar] [CrossRef]
- Rao, K.; Reddy, G.V. Cold Flow Studies of Rice Husk, Saw Dust, and Groundnut Shell Fuels in a Fluidized Bed. Energy Sources Part A—Recovery Util. Environ. Eff. 2010, 32, 1701–1711. [Google Scholar] [CrossRef]
- Palappan, K.G.; Sai, P.S.T. Studies on segregation of binary mixture of solids in continuous fast fluidized bed. Chem. Eng. J. 2008, 139, 330–338. [Google Scholar] [CrossRef]
- Zhong, W.Q.; Xiong, Y.Q.; Yuan, Z.L.; Zhang, M.Y. DEM simulation of gas-solid flow behaviors in spout-fluid bed. Chem. Eng. Sci. 2006, 61, 1571–1584. [Google Scholar] [CrossRef]
- Zhao, X.J.; Eri, Q.T.; Wang, Q. An Investigation of the Restitution Coefficient Impact on Simulating Sand-Char Mixing in a Bubbling Fluidized Bed. Energies 2017, 10, 617. [Google Scholar] [CrossRef]
- Zhuang, Y.Q.; Chen, X.M.; Luo, Z.H.; Xiao, J. CFD-DEM modeling of gas-solid flow and catalytic MTO reaction in a fluidized bed reactor. Comput. Chem. Eng. 2014, 60, 1–16. [Google Scholar] [CrossRef]
- Amiri, Z.; Movahedirad, S. Bubble-induced particle mixing in a 2-D gas-solid fluidized bed with different bed aspect ratios: A CFD-DPM study. Powder Technol. 2017, 320 (Suppl. C), 637–645. [Google Scholar] [CrossRef]
- Saidi, M.; Tabrizi, H.B.; Grace, J.R.; Lim, C.J.; Ahmad, G. Hydrodynamic and Mixing Characteristics of Gas-Solid Flow in a Pulsed Spouted Bed. Ind. Eng. Chem. Res. 2015, 54, 7933–7941. [Google Scholar] [CrossRef]
- Xu, H.B.; Zhong, W.Q.; Yuan, Z.L.; Yu, A.B. CFD-DEM study on cohesive particles in a spouted bed. Powder Technol. 2017, 314, 377–386. [Google Scholar] [CrossRef]
- Xu, Y.; Musser, J.; Li, T.; Gopalan, B.; Panday, R.; Tucker, J.; Breault, G.; Clarke, M.A.; Rogers, W.A. Numerical Simulation and Experimental Study of the Gas-Solid Flow Behavior Inside a Full-Loop Circulating Fluidized Bed: Evaluation of Different Drag Models. Ind. Eng. Chem. Res. 2018, 57, 740–750. [Google Scholar] [CrossRef]
- Wang, J. A Review of Eulerian Simulation of Geldart a Particles in Gas-Fluidized Beds. Ind. Eng. Chem. Res. 2009, 48, 5567–5577. [Google Scholar] [CrossRef]
- Oke, O.; Van Wachem, B.; Mazzei, L. Lateral solid mixing in gas-fluidized beds: CFD and DEM studies. Chem. Eng. Res. Des. 2016, 114 (Suppl. C), 148–161. [Google Scholar] [CrossRef][Green Version]
- Liu, D.; Chen, X. Quantifying lateral solids mixing in a fluidized bed by modeling the thermal tracing method. AIChE J. 2012, 58, 745–755. [Google Scholar] [CrossRef]
- Pantaleev, S.; Yordanova, S.; Janda, A.; Marigo, M.; Ooi, J.Y. An experimentally validated DEM study of powder mixing in a paddle blade mixer. Powder Technol. 2017, 311, 287–302. [Google Scholar] [CrossRef]
- Luo, K.; Wu, F.; Yang, S.L.; Fan, J.R. CFD-DEM study of mixing and dispersion behaviors of solid phase in a bubbling fluidized bed. Powder Technol. 2015, 274, 482–493. [Google Scholar] [CrossRef]
- Ma, H.Q.; Zhao, Y.Z. CFD-DEM investigation of the fluidization of binary mixtures containing rod-like particles and spherical particles in a fluidized bed. Powder Technol. 2018, 336, 533–545. [Google Scholar] [CrossRef]
- Feng, Y.Q.; Xu, B.H.; Zhang, S.J.; Yu, A.B.; Zulli, P. Discrete particle simulation of gas fluidization of particle mixtures. AIChE J. 2004, 50, 1713–1728. [Google Scholar] [CrossRef]
- Deb, S.; Tafti, D.K. Two and three dimensional modeling of fluidized bed with multiple jets in a DEM–CFD framework. Particuology 2014, 16, 19–28. [Google Scholar] [CrossRef]
- Njobuenwu, D.O.; Fairweather, M. Dynamics of single, non-spherical ellipsoidal particles in a turbulent channel flow. Chem. Eng. Sci. 2015, 123, 265–282. [Google Scholar] [CrossRef]
- Van Wachem, B.; Zastawny, M.; Zhao, F.; Mallouppas, G. Modelling of gas-solid turbulent channel flow with non-spherical particles with large Stokes numbers. Int. J. Multiph. Flow 2015, 68, 80–92. [Google Scholar] [CrossRef]
- Wang, X.; Zhong, Z.; Wang, H.; Wang, Z. Application of Hilbert-Huang transformation in fluidized bed with two-component (biomass particles and quartz sands) mixing flow. Korean J. Chem. Eng. 2014, 32, 43–50. [Google Scholar] [CrossRef]
- Zhu, L.L.; Zhong, Z.P.; Wang, H.; Wang, Z.Y. Simulation of large biomass pellets in fluidized bed by DEM-CFD. Korean J. Chem. Eng. 2016, 33, 3021–3028. [Google Scholar] [CrossRef]
- Ergun, S. Fluid flow through oached columns. Chem. Eng. Prog. 1952, 48, 89–94. [Google Scholar]
- Wen, C.Y.; Yu, Y.H. A Generalized Method for Predicting Minimum Fluidization Velocity. AIChE J. 1966, 12, 610–612. [Google Scholar] [CrossRef]
- Rowe, P.N.; Henwood, G.A.; United Kingdom Atomic Energy Authority. Drag Forces in a Hydraulic Model of a Fluidised Bed—Part I; UKAEA: London, UK, 1960.
- Cundall, P.A.; Strack, O.D.L. Discrete Numerical-Model for Granular Assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Tsuji, Y.; Kawaguchi, T.; Tanaka, T. Discrete particle simulation of two-dimensional fluidized bed. Powder Technol. 1993, 77, 79–87. [Google Scholar] [CrossRef]
- Bruchmüller, J.; van Wachem, B.; Gu, S.; Luo, K.; Brown, R. Modeling the thermochemical degradation of biomass inside a fast pyrolysis fluidized bed reactor. AIChE J. 2012, 58, 3030–3042. [Google Scholar] [CrossRef]
- Lacey, P.M.C. Developments in The Theory of Particle Mixing. J. Appl. Chem. 1954, 4, 257–268. [Google Scholar] [CrossRef]
- Wang, H.; Zhong, Z.; Wang, X.; Guo, F. Intelligent identification of the flow regimes of two-component particles in a fluidized bed with the optimized fuzzy c-means clustering algorithm. Korean J. Chem. Eng. 2016, 33, 1674–1680. [Google Scholar] [CrossRef]
- Zhao, F.; George, W.K.; van Wachem, B.G.M. Four-way coupled simulations of small particles in turbulent channel flow: The effects of particle shape and Stokes number. Phys. Fluids 2015, 27, 083301. [Google Scholar] [CrossRef]
- Chung, Y.C.; Ooi, J.Y. A study of influence of gravity on bulk behavior of particulate solid. Particuology 2008, 6, 467–474. [Google Scholar] [CrossRef]
- Zhong, W.Q.; Zhang, Y.; Jin, B.S.; Zhang, M.Y. Discrete Element Method Simulation of Cylinder-Shaped Particle Flow in a Gas-Solid Fluidized Bed. Chem. Eng. Technol. 2009, 32, 386–391. [Google Scholar] [CrossRef]
- Norouzi, H.R.; Mostoufi, N.; Mansourpour, Z.; Sotudeh-Gharebagh, R.; Chaouki, J. Characterization of solids mixing patterns in bubbling fluidized beds. Chem. Eng. Res. Des. 2011, 89, 817–826. [Google Scholar] [CrossRef]

| Force | Equation |
|---|---|
| Normal elastic force | |
| Normal damping force | |
| Tangential elastic force | |
| Tangential damping force | |
| *where, , , , , in which, E* is the reduced elastic modulus, Ei and Ej is the Elastic modulus of particle i and j; r* is the reduced radius, ri and rj is the radius of particle i and j; Gi and Gj is the shear modulus of particle i and j, vi and vj is poisson ratio of particle i and j [37]. | |
| Parameters | Unit | Value |
|---|---|---|
| Diameter of sand | mm | 0.8 |
| Diameter of biomass particle | mm | 1.5, 2, 3 |
| Density of sand | kg/m3 | 2650 |
| Density of biomass | kg/m3 | 1300 |
| Density of gas | kg/m3 | 1.28 |
| Velocity of gas | m/s | 1.0 m/s, 1.5 m/s, 2.5 m/s |
| Viscosity of gas | Pa∙s | 1.75 × 10−5 |
| Wall young’s modulus | MPa | 1 × 106 |
| Wall friction coefficient | 0.35 | |
| Wall restitution coefficient | 0.9 | |
| Biomass Young’s modulus | Mpa | 1.6 × 103 |
| Biomass Possion ratio | 0.4 | |
| Biomass friction coefficient | 0.34 | |
| Biomass restitution coefficient | 0.59 | |
| Biomass mass fraction | 2%, 4%, 6% | |
| Sand Young’s modulus | Mpa | 1 × 106 |
| Sand Possion ratio | 0.33 | |
| Sand friction coefficient | 0.35 | |
| Sand restitution coefficient | 0.9 | |
| CFD Mesh size | mm | 6 × 6 × 6 |
| vmf | m/s | 0.36, 0.4, 0.54 |
| Biomass Diameter | Mass Ratio | ||
|---|---|---|---|
| 2% | 4% | 6% | |
| 1.5 mm | 903 | 1806 | 2708 |
| 2 mm | 381 | 762 | 1143 |
| 3 mm | 113 | 226 | 339 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zhong, Z. A Mixing Behavior Study of Biomass Particles and Sands in Fluidized Bed Based on CFD-DEM Simulation. Energies 2019, 12, 1801. https://doi.org/10.3390/en12091801
Wang H, Zhong Z. A Mixing Behavior Study of Biomass Particles and Sands in Fluidized Bed Based on CFD-DEM Simulation. Energies. 2019; 12(9):1801. https://doi.org/10.3390/en12091801
Chicago/Turabian StyleWang, Heng, and Zhaoping Zhong. 2019. "A Mixing Behavior Study of Biomass Particles and Sands in Fluidized Bed Based on CFD-DEM Simulation" Energies 12, no. 9: 1801. https://doi.org/10.3390/en12091801
APA StyleWang, H., & Zhong, Z. (2019). A Mixing Behavior Study of Biomass Particles and Sands in Fluidized Bed Based on CFD-DEM Simulation. Energies, 12(9), 1801. https://doi.org/10.3390/en12091801





