Finite-Volume High-Fidelity Simulation Combined with Finite-Element-Based Reduced-Order Modeling of Incompressible Flow Problems
Abstract
:1. Introduction
2. Theory
2.1. Governing Equations
2.1.1. FE Discretization
2.1.2. FV Discretization
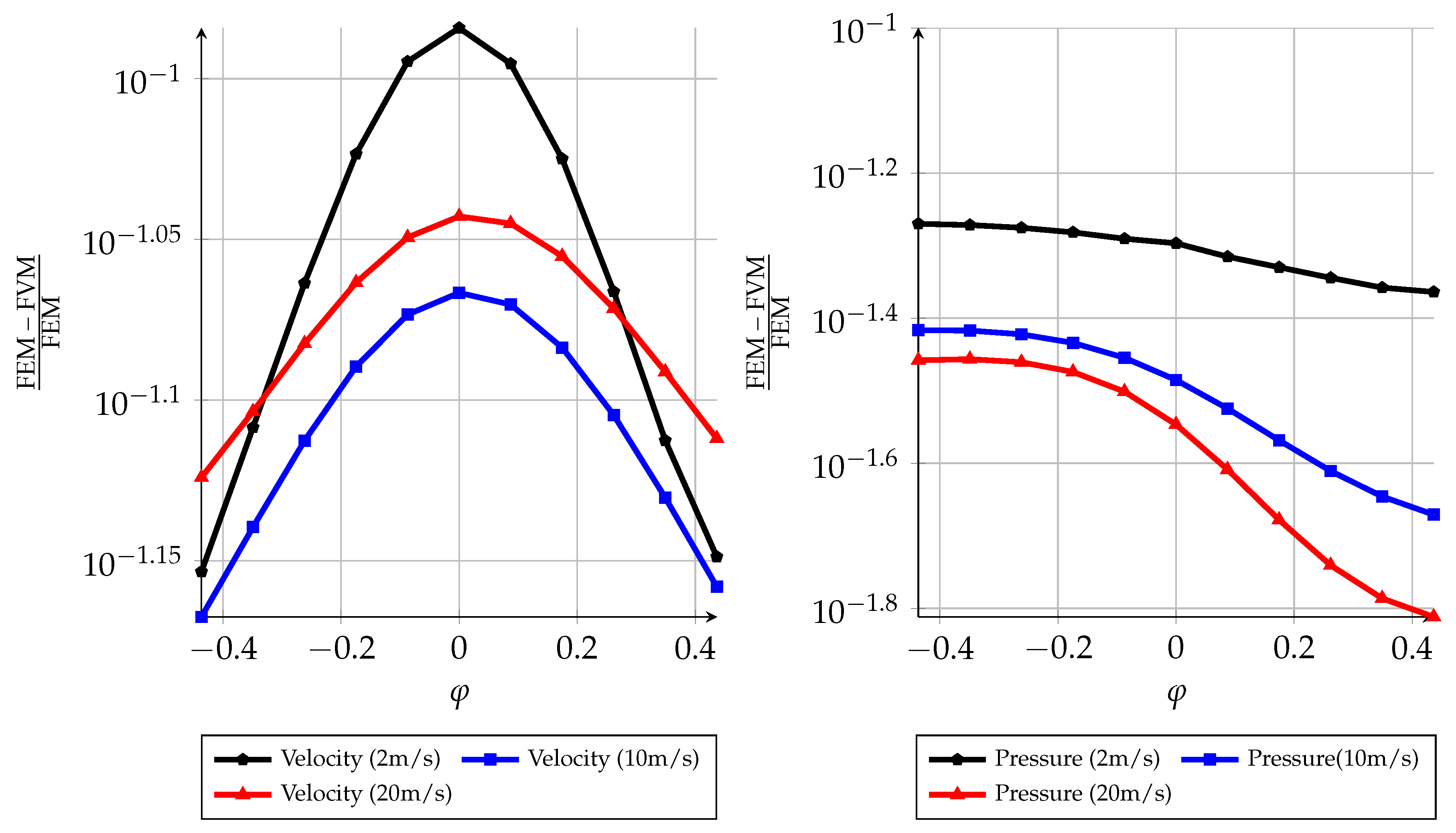
2.2. Projection of FV Results to FE Space
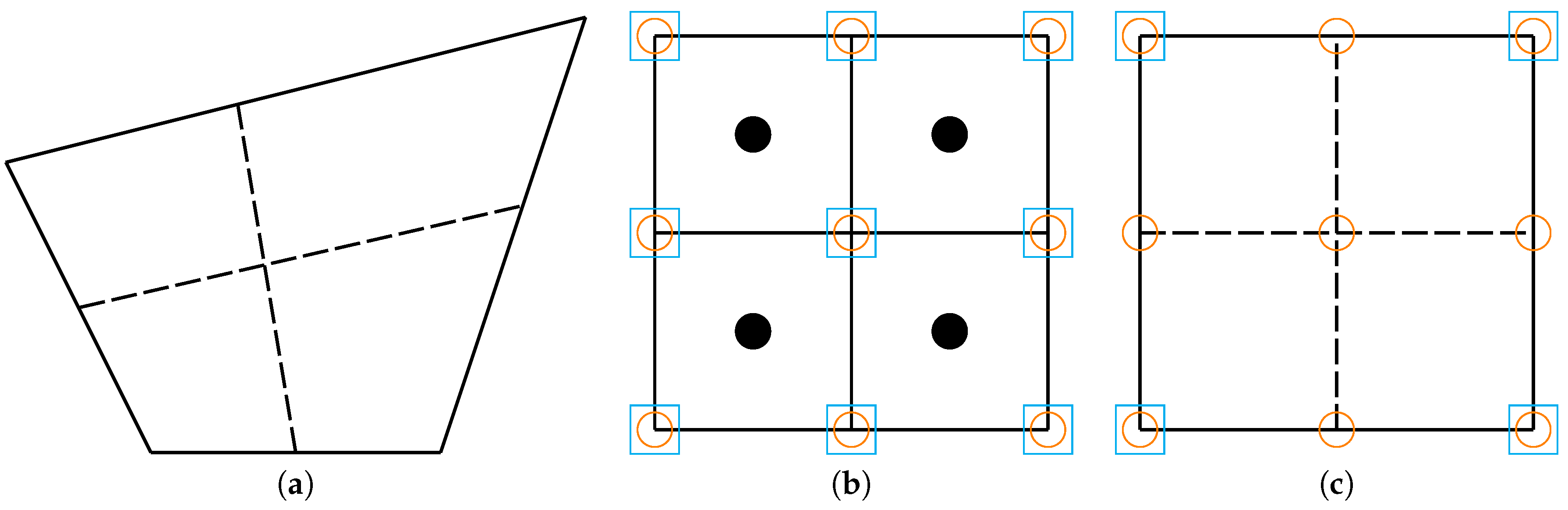
- Cell centers to cell nodes interpolation:In the first stage, the velocity and pressure fields that are calculated by OpenFOAM at the center of the control volumes are interpolated onto the control volume vertices using Inverse Distance Weighting (IDW) interpolation before they are stored at VTK-files. Thus, the stored velocity and pressure results on the VTK-files are implicitly assumed to be interpolated as bilinear fields.
- Projection to taylor hood FE space:In the second stage, the velocity and pressure results stored on the VTK-files are projected onto the Taylor–Hood FE space. Herein, we have used -projection for both velocities and pressure.
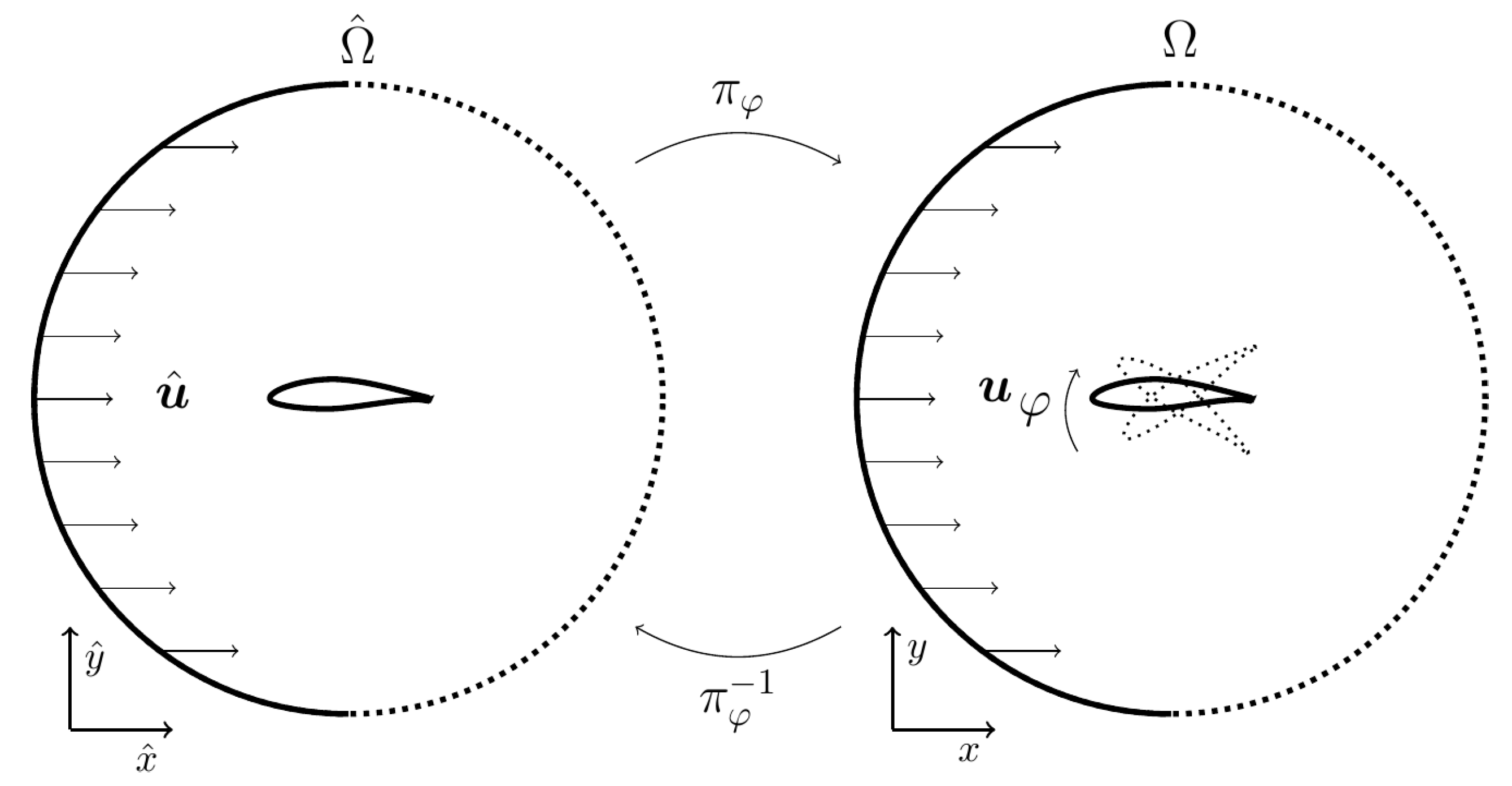
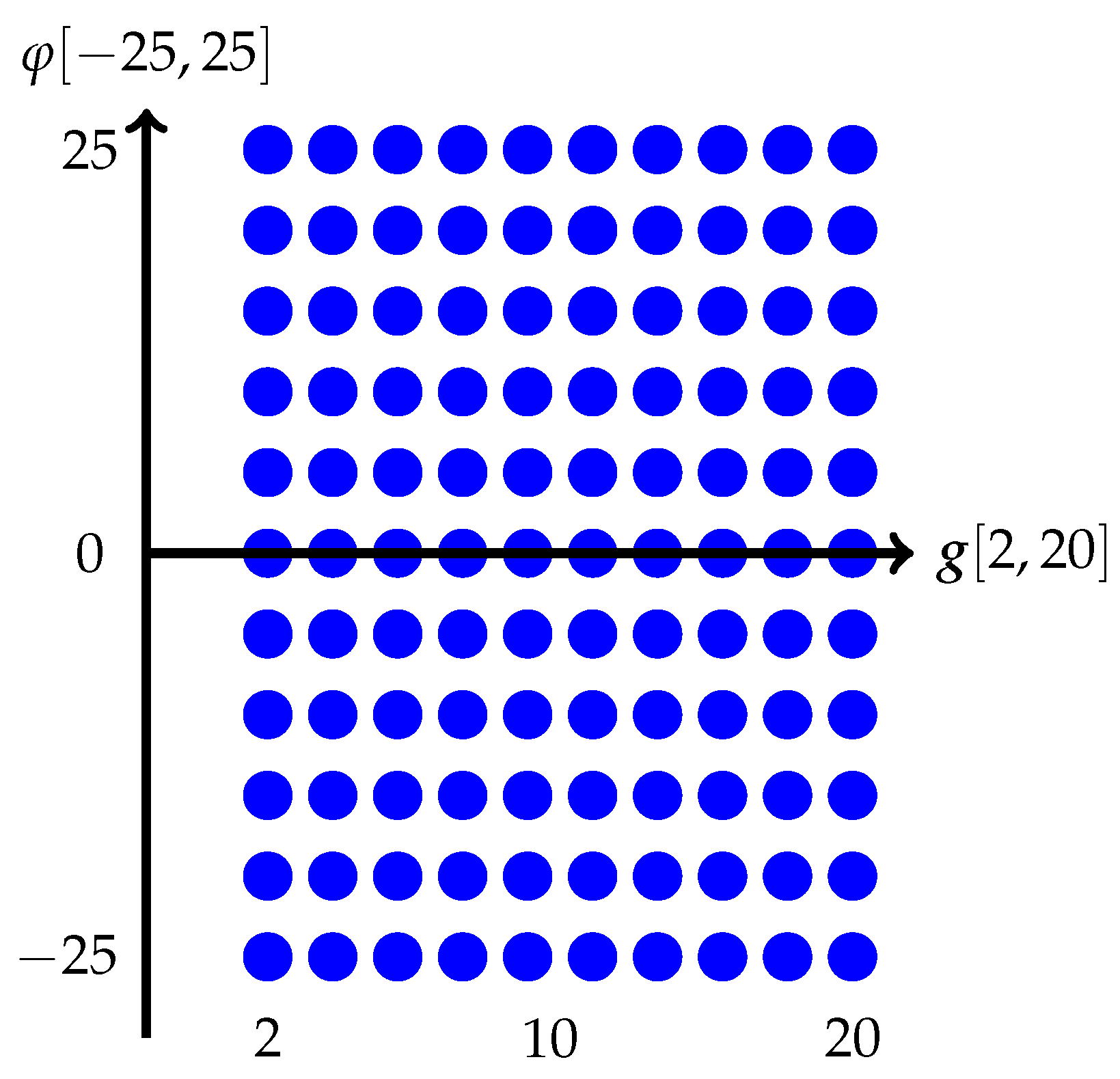
2.3. Parametric Dependency
2.4. ROM Using POD
2.5. Mixed and Uniform Methods
3. Development of the Solver
ROM Solver
4. Results and Discussion
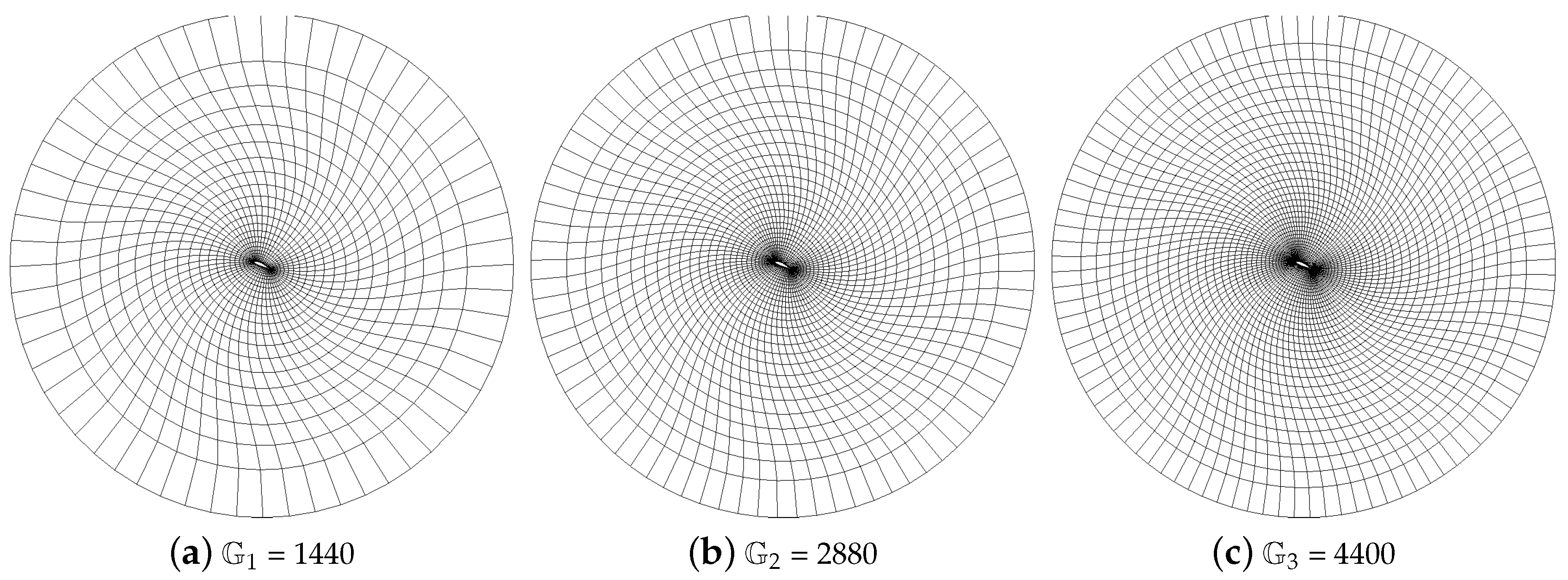
4.1. High-Fidelity Simulation Setup
4.2. Snapshots Creation
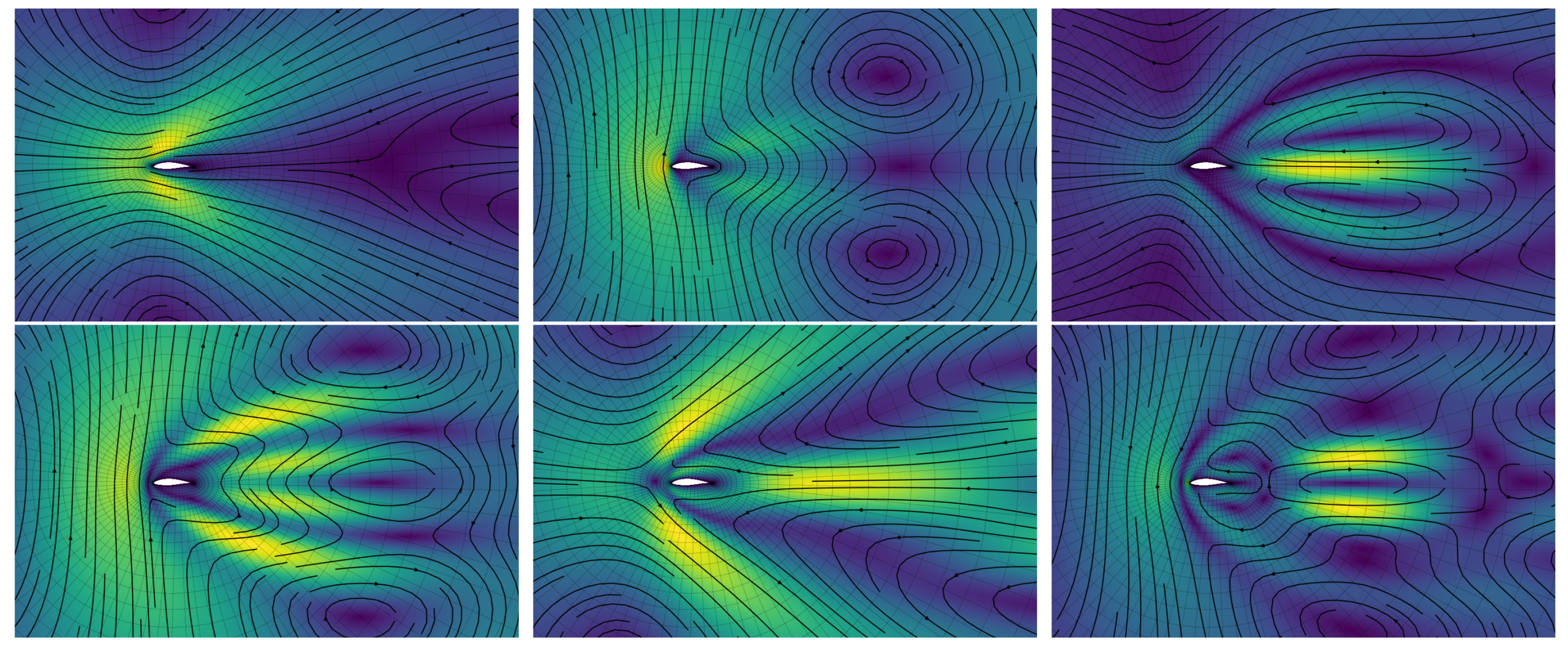
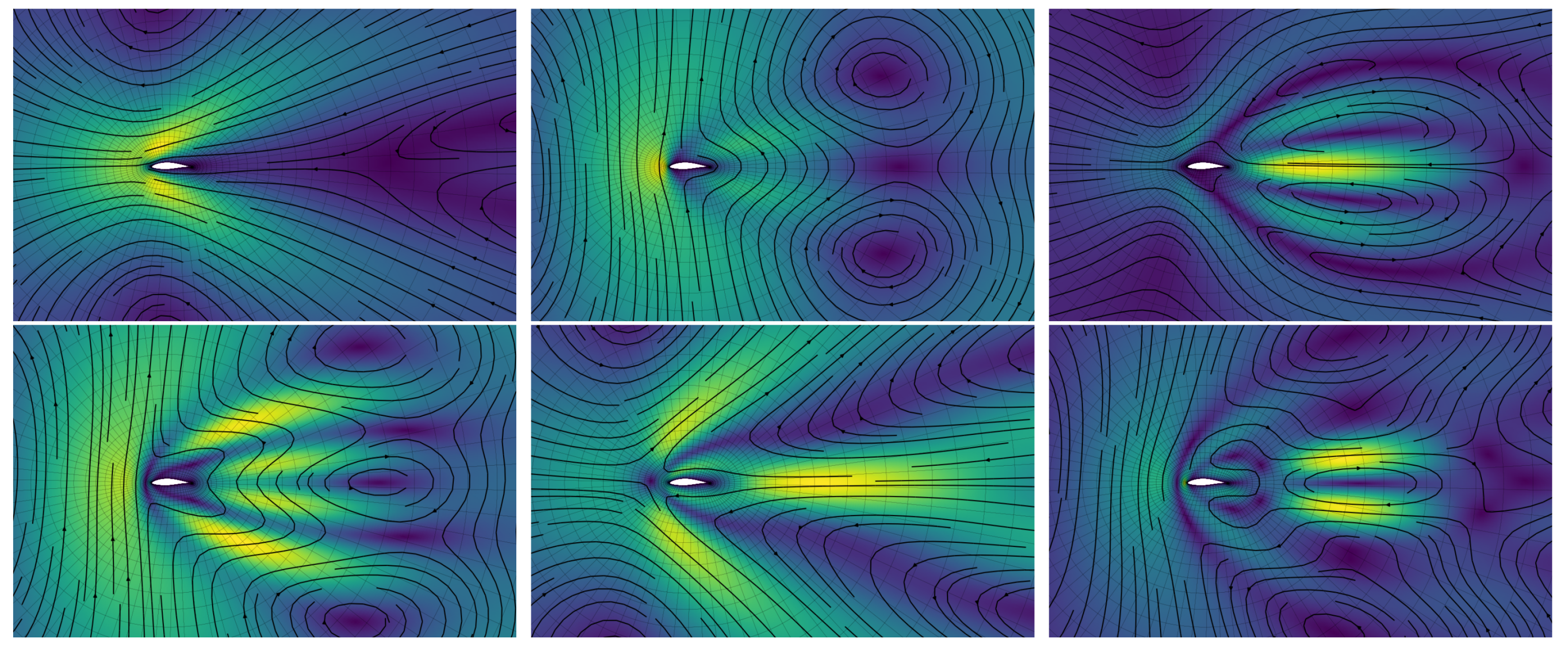
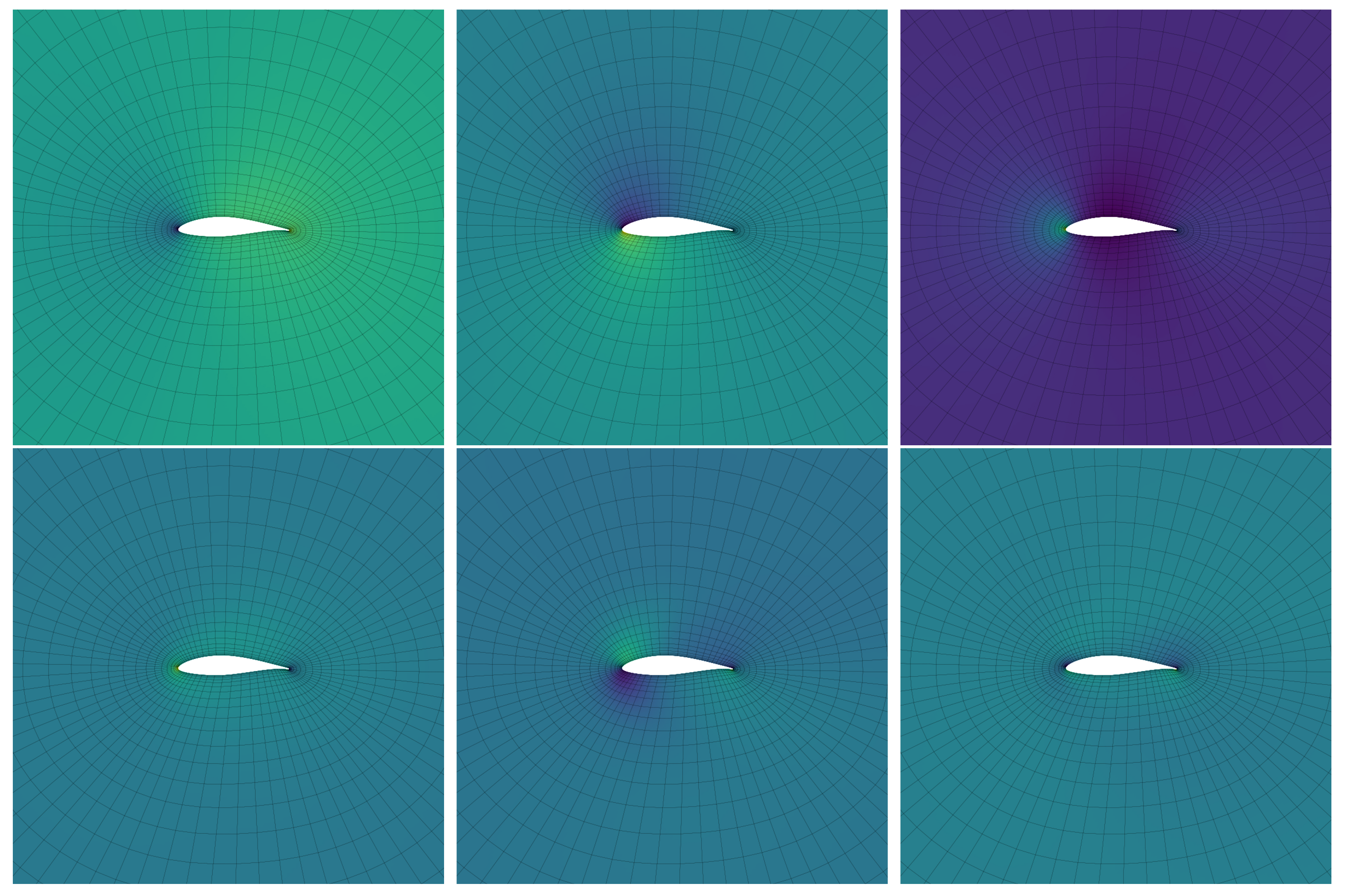
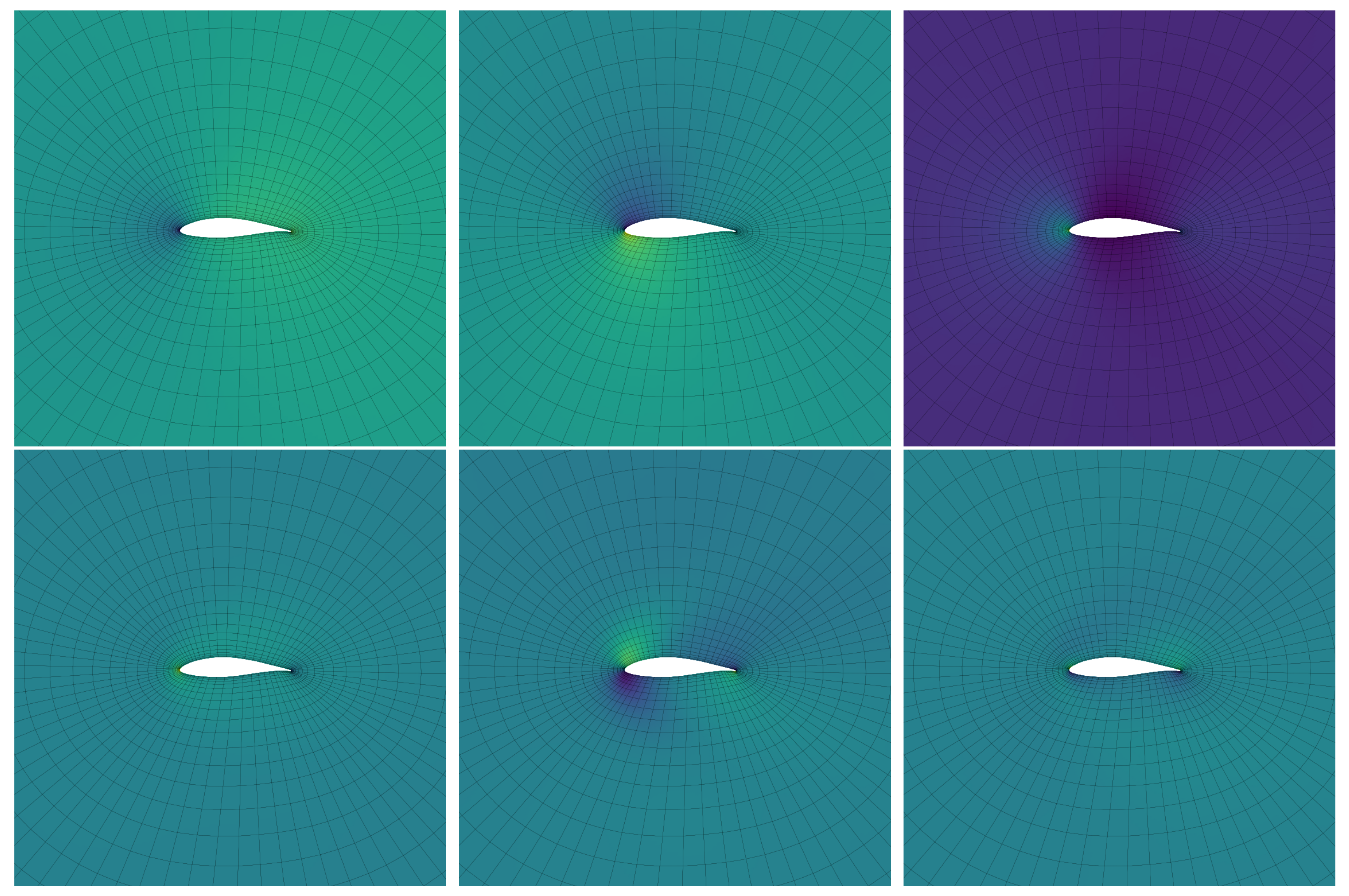
4.3. Spatial Development of Modes/Reduced Basis
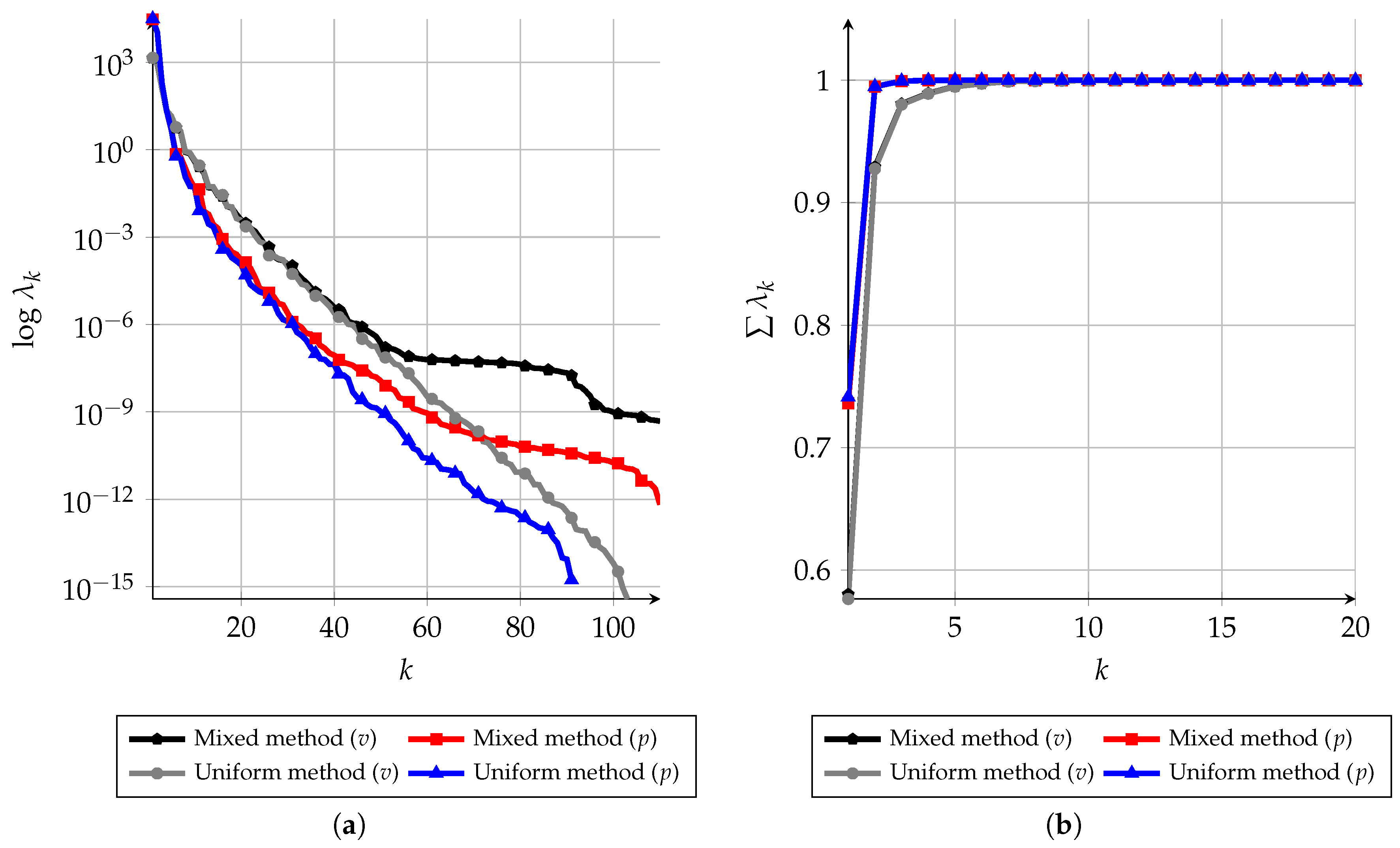
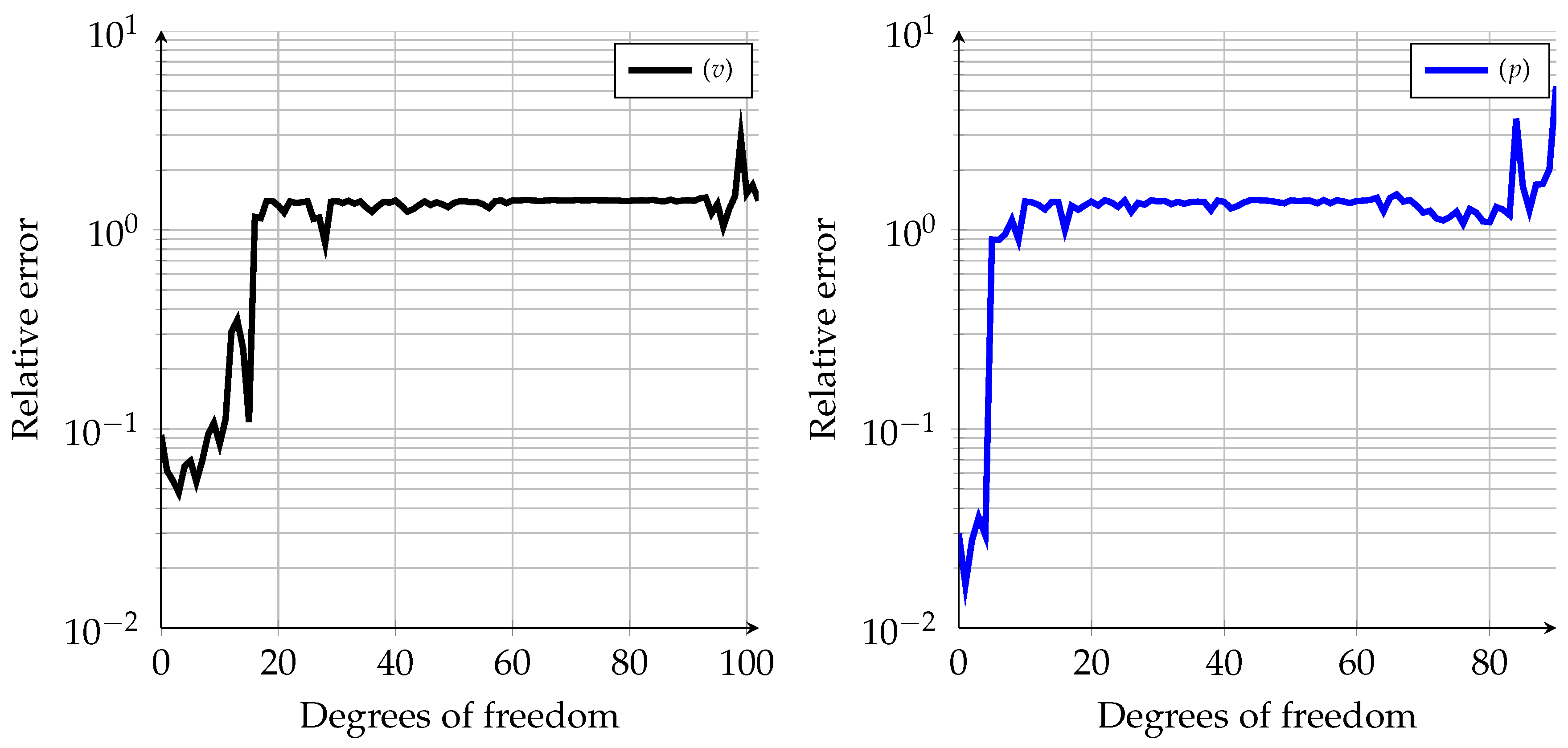
4.4. Spectrum and Related Error
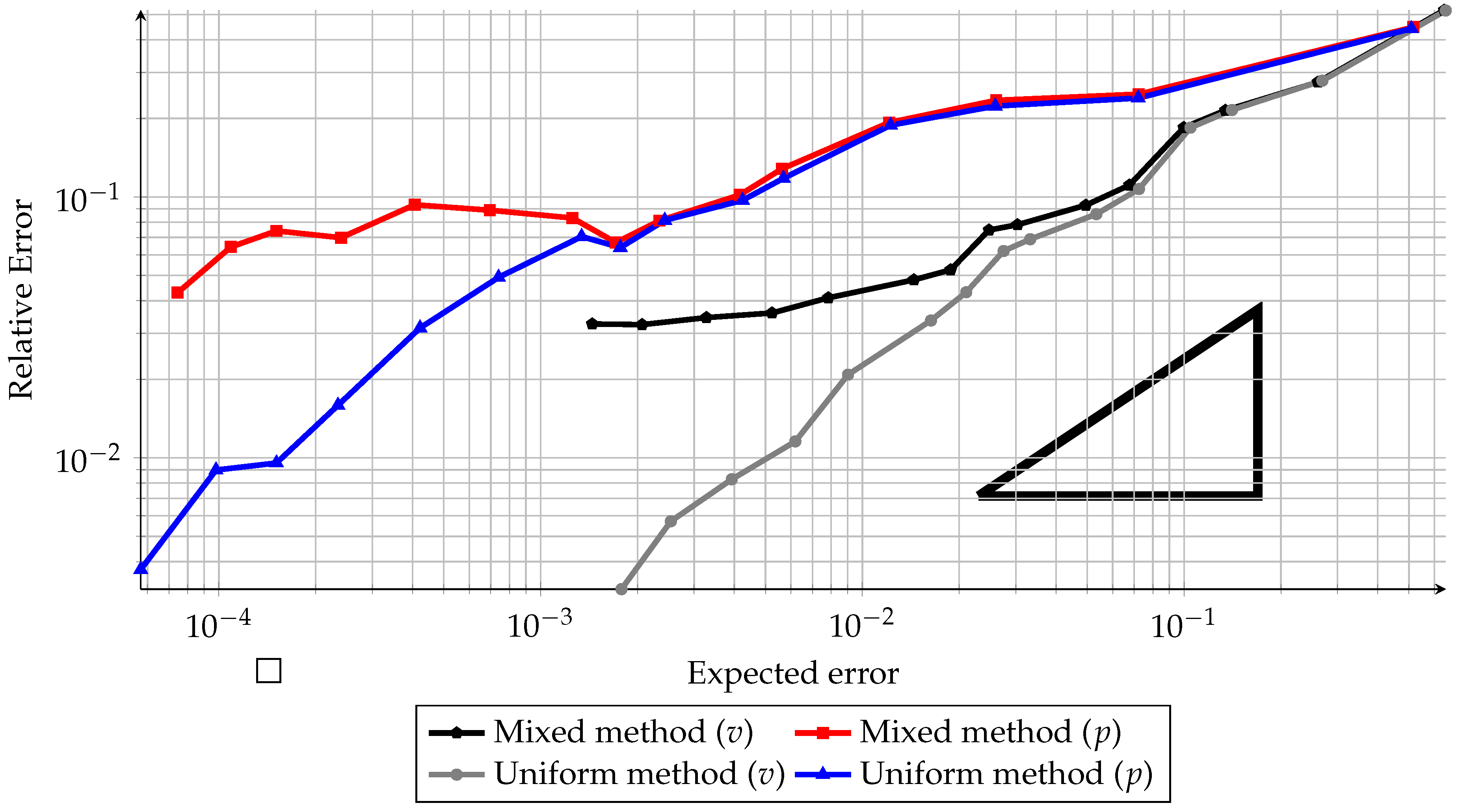
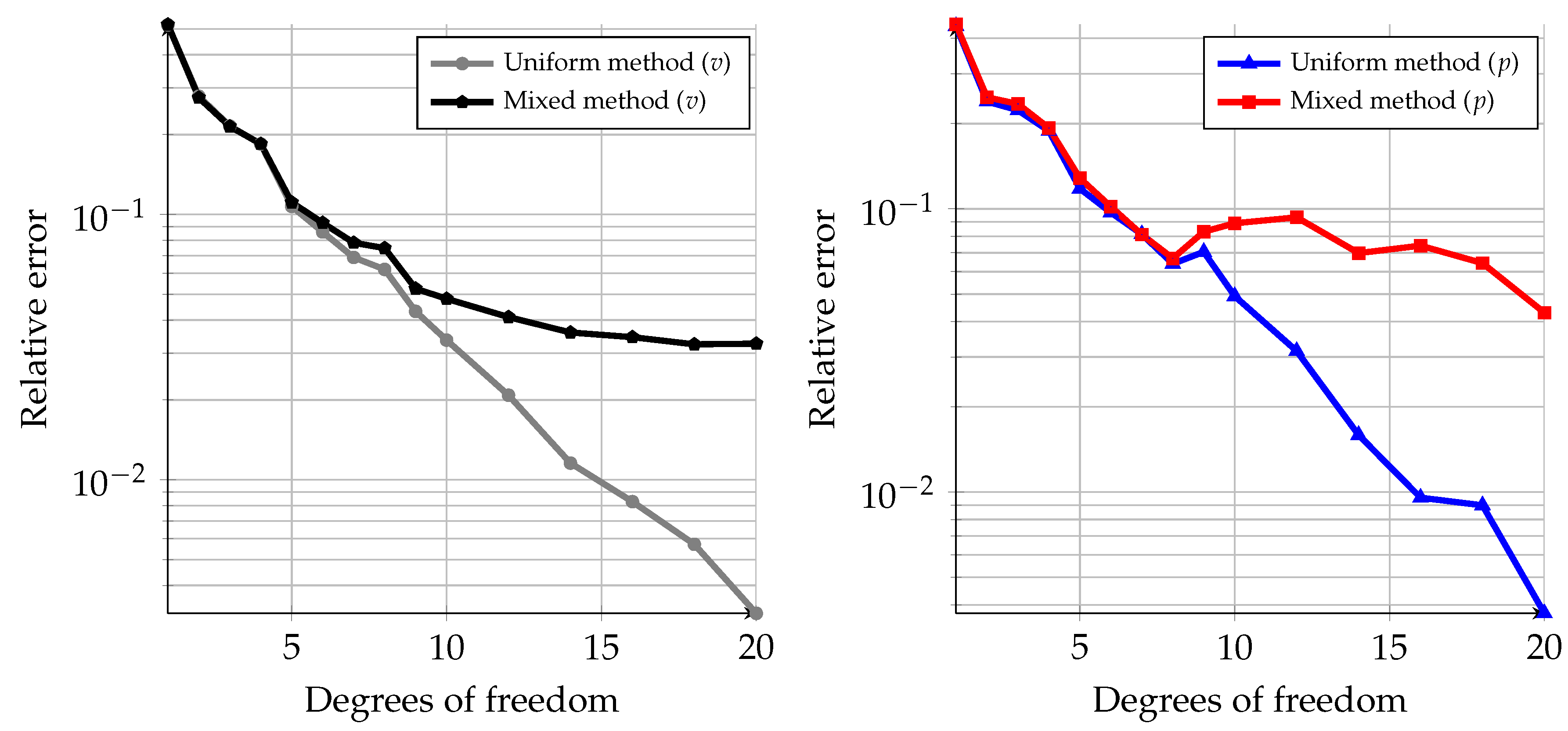
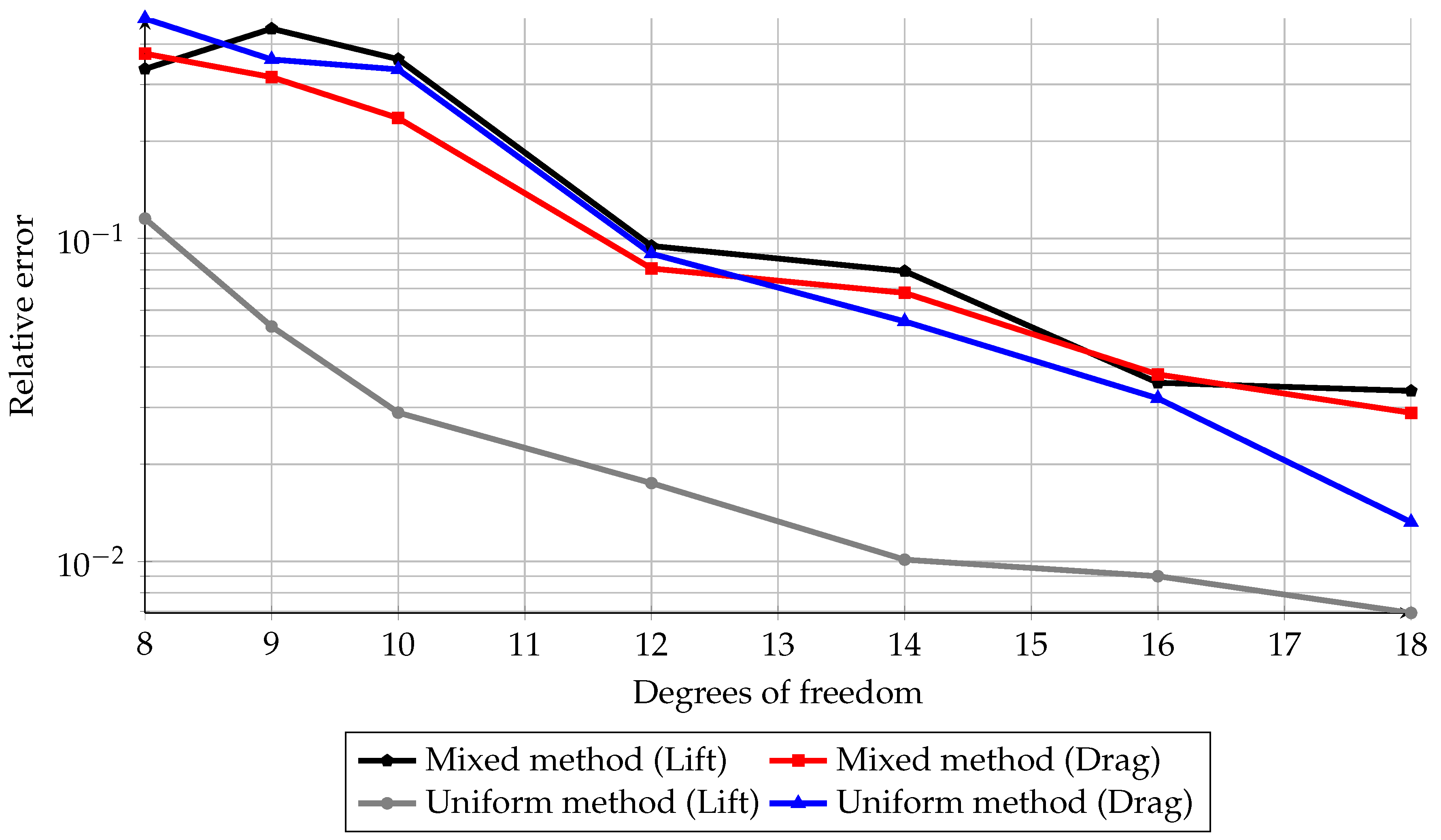
4.5. Accuracy of the Mixed and Uniform Methods
4.6. Computational Speedup
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rui, H. Analysis on a Finite Volume Element Method for Stokes Problems. Acta Math. Appl. Sin. 2005, 21, 359–372. [Google Scholar] [CrossRef]
- Luan, S.; Lian, Y.; Ying, Y.; Tang, S.; Wagner, G.J.; Liu, W.K. An enriched finite element method to fractional advection–diffusion equation. Comput. Mech. 2017, 60, 181–201. [Google Scholar] [CrossRef]
- Bruger, A.; Nilsson, J.; Kress, W. A Compact Higher Order Finite Difference Method for the Incompressible Navier–Stokes Equations. J. Sci. Comput. 2002, 17, 551–560. [Google Scholar] [CrossRef]
- Takizawa, K. Computational engineering analysis with the new-generation space–time methods. Comput. Mech. 2014, 54, 193–211. [Google Scholar] [CrossRef]
- Tezduyar, T.E.; Takizawa, K.; Moorman, C.; Wright, S.; Christopher, J. Space time finite element computation of complex fluid structure interactions. Int. J. Numer. Methods Fluids 2010, 64, 1201–1218. [Google Scholar] [CrossRef]
- Abbaspour, M.; Radmanesh, A.R.; Soltani, M.R. Unsteady flow over offshore wind turbine airfoils and aerodynamic loads with computational fluid dynamic simulations. Int. J. Environ. Sci. Technol. 2016, 13, 1525–1540. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Hsu, M.C.; Akkerman, I.; Wright, S.; Takizawa, K.; Henicke, B.; Spielman, T.; Tezduyar, T.E. 3D simulation of wind turbine rotors at full scale. Part I: Geometry modeling and aerodynamics. Int. J. Numer. Methods Fluids 2011, 65, 207–235. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Hsu, M.C.; Takizawa, K.; Tezduyar, T.E. ALE-VMS and ST-VMS methods for computer modeling of wind turbine rotor aerodynamics and fluid-structure interaction. Math. Model. Methods Appl. Sci. 2012, 22, 1230002. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; Wiley Classic Library Edition: Hoboken, NJ, USA, 1995. [Google Scholar]
- Akhtar, I.; Marzouk, O.A.; Nayfeh, A.H. A van der Pol-Duffing oscillator model of hydrodynamic forces on canonical structures. J. Comput. Nonlinear Dyn. 2009, 4, 041006. [Google Scholar] [CrossRef]
- Ballarin, F.; Manzoni, A.; Quarteroni, A.; Rozza, G. Supremizer stabilization of POD-Galerkin approximation of parametrized steady incompressible Navier-Stokes equations. Int. J. Numer. Methods Eng. 2015, 102, 1136–1161. [Google Scholar] [CrossRef]
- Fonn, E.; Tabib, M.; Siddiqui, M.S.; Rasheed, A.; Kvamsdal, T. A step towards reduced order modelling of flow characterized by wakes using proper orthogonal decomposition. Energy Procedia 2017, 137, 452–459. [Google Scholar] [CrossRef]
- Tabib, M.; Rasheed, A.; Siddiqui, M.S.; Kvamsdal, T. A full-scale 3D vs 2.5D vs 2D analysis of flow pattern and forces for an industrial-scale 5MW NREL reference wind-turbine. Energy Procedia 2017, 137, 477–486. [Google Scholar] [CrossRef]
- Quarteroni, A.; Manzoni, A.; Negri, F. Reduced Basis Methods for Partial Differential Equations; Springer International Publishing: Berlin, Germany, 2016. [Google Scholar]
- Rozza, G. Fundamentals of reduced basis method for problems governed by parametrized PDEs and applications. In Separated Representations and PGD-Based Model Reduction: Fundamentals and Applications; CISM International Centre for Mechanical Sciences; Springer: Berlin, Germany, 2014; Volume 554, Chapter 4. [Google Scholar]
- Stabile, G.; Hijazi, S.N.; Lorenzi, S.; Mola, A.; Rozza, G. Advances in reduced order modelling for CFD: Vortex shedding around a circular cylinder using a POD-Galerkin method. arXiv, 2017; arXiv:1701.03424. [Google Scholar]
- Hsu, M.C.; Bazilevs, Y. Fluid structure interaction modeling of wind turbines: Simulating the full machine. Comput. Mech. 2012, 50, 821–833. [Google Scholar] [CrossRef]
- Soldner, D.; Brands, B.; Zabihyan, R.; Steinmann, P.; Mergheim, J. A numerical study of different projection-based model reduction techniques applied to computational homogenisation. Comput. Mech. 2017, 60, 613–625. [Google Scholar] [CrossRef]
- Peng, L.; Mohseni, K. Nonlinear model reduction via a locally weighted POD method. Int. J. Numer. Methods Eng. 2016, 106, 372–396. [Google Scholar] [CrossRef]
- Aubry, N. On the hidden beauty of the proper orthogonal decomposition. Theor. Comput. Fluid Dyn. 1991, 2, 339–352. [Google Scholar] [CrossRef]
- Ly, H.V.; Tran, H.T. Modeling and control of physical processes using proper orthogonal decomposition. Math. Comput. Model. 2001, 33, 223–236. [Google Scholar] [CrossRef]
- Bergmann, M.; Bruneau, C.H.; Iollo, A. Enablers for robust POD models. J. Comput. Phys. 2009, 228, 516–538. [Google Scholar] [CrossRef]
- Sirisup, S.; Karniadakis, G. Stability and accuracy of periodic flow solutions obtained by a POD-penalty method. Phys. D Nonlinear Phenom. 2005, 202, 218–237. [Google Scholar] [CrossRef]
- Lorenzi, S.; Cammi, A.; Luzzi, L.; Rozza, G. POD-Galerkin method for finite volume approximation of Navier-Stokes and RANS equations. Comput. Methods Appl. Mech. Eng. 2016, 311, 151–179. [Google Scholar] [CrossRef]
- Rowley, C. Model reduction for fluids, using balanced proper orthogonal decomposition. Int. J. Bifurc. Chaos Appl. Sci. Eng. 2005, 15, 997–1013. [Google Scholar] [CrossRef]
- Bakewell, H.P., Jr.; Lumley, J.L. Viscous sublayer and adjacent wall region in turbulent pipe flow. Phys. Fluids 1967, 10, 1880–1889. [Google Scholar] [CrossRef]
- Berkooz, G.; Holmes, P.; Lumley, J.L. The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 1993, 25, 539–575. [Google Scholar] [CrossRef]
- Sirovich, L. Turbulence and the dyanmics of coherent structures. Q. Appl. Math. 1987, 45, 561–590. [Google Scholar] [CrossRef]
- Noack, B.R.; Eckelmann, H. A low-dimensional Galerkin method for the three-dimensional flow around a circular cylinder. Phys. Fluids 1994, 6, 124–143. [Google Scholar] [CrossRef]
- Sirisup, S.; Karniadakis, G.E.; Xiu, D.; Kevrekidis, I.G. Equation-free/Galerkin-free POD-assisted computation of incompressible flows. J. Comput. Phys. 2005, 207, 568–587. [Google Scholar] [CrossRef]
- Tallet, A.; Allery, C.; Leblond, C.; Liberge, E. A minimum residual projection to build coupled velocity-pressure POD-ROM for incompressible Navier-Stokes equations. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 909–932. [Google Scholar] [CrossRef]
- Løvgren, A.E.; Maday, Y.; Rønquist, E.M. A reduced basis element method for the steady Stokes problem. ESAIM: M2AN 2006, 40, 529–552. [Google Scholar] [CrossRef]
- Jasak, H. Error Analysis and Estimation in the Finite Volume Method with Applications to Fluid Flows; Imperial College, University of London: London, UK, 1996. [Google Scholar]
- Prenter, F.; Verhoosel, C.; Zwieten, G.; Brummelen, E. Condition number analysis and preconditioning of the finite cell method. Comput. Methods Appl. Mech. Eng. 2017, 316, 297–327. [Google Scholar] [CrossRef]
- Rambo, J.; Joshi, Y. Reduced-order modeling of turbulent forced convection with parametric conditions. Int. J. Heat Mass Transf. 2007, 50, 539–551. [Google Scholar] [CrossRef]
- Tezduyar, T. Stabilized Finite Element Formulations for Incompressible Flow Computations; Advances in Applied Mechanics; Elsevier: Amsterdam, The Netherlands, 1991; Volume 28, pp. 1–44. [Google Scholar]
- Jain, S.; Bhatt, V.D.; Mittal, S. Shape optimization of corrugated airfoils. Comput. Mech. 2015, 56, 917–930. [Google Scholar] [CrossRef]
- Tezduyar, T.; Mittal, S.; Ray, S.; Shih, R. Incompressible flow computations with stabilized bilinear and linear equal-order-interpolation velocity-pressure elements. Comput. Methods Appl. Mech. Eng. 1992, 95, 221–242. [Google Scholar] [CrossRef]
- Evans, J.A.; Hughes, T.J.R. Discrete spectrum analyses for various mixed discretizations of the Stokes eigenproblem. Comput. Mech. 2012, 50, 667–674. [Google Scholar] [CrossRef]
- Broeckhoven, T.; Smirnov, S.; Ramboer, J.; Lacor, C. Finite volume formulation of compact upwind and central schemes with artificial selective damping. J. Sci. Comput. 2004, 21, 341–367. [Google Scholar] [CrossRef]
- Fonn, E.; van Brummelen, H.; Kvamsdal, T.; Rasheed, A. Fast divergence-conforming reduced basis methods for steady Navier–Stokes flow. Comput. Methods Appl. Mech. Eng. 2019, 346, 486–512. [Google Scholar] [CrossRef]
- Weller, J.; Lombardi, E.; Bergmann, M.; Iollo, A. Numerical methods for low-order modeling of fluid flows based on POD. Int. J. Numer. Methods Fluids 2010, 63, 249–268. [Google Scholar] [CrossRef]
- Couplet, M.; Basdevant, C.; Sagaut, P. Calibrated reduced-order POD-Galerkin system for fluid flow modelling. J. Comput. Phys. 2005, 207, 192–220. [Google Scholar] [CrossRef]
- Takizawa, K.; Henicke, B.; Tezduyar, T.E.; Hsu, M.C.; Bazilevs, Y. Stabilized space–time computation of wind-turbine rotor aerodynamics. Comput. Mech. 2011, 48, 333–344. [Google Scholar] [CrossRef]
- Takizawa, K.; Tezduyar, T.E. Multiscale space–time fluid–structure interaction techniques. Comput. Mech. 2011, 48, 247–267. [Google Scholar] [CrossRef]
- Citriniti, J.H. Reconstruction of the global velocity field in the axisymmetric mixing layer utilizing the proper orthogonal decomposition. J. Fluid Mech. 2000, 418, 137. [Google Scholar] [CrossRef]
- Gamard, S.; Jung, D.; Woodward, S.; George, W.K. Application of a slice proper orthogonal decomposition to the far field of an axisymmetric turbulent jet. Phys. Fluids 2002, 14, 2515. [Google Scholar] [CrossRef]
- Younis, B.A.; Przulj, V.P. Computation of turbulent vortex shedding. Comput. Mech. 2005, 37, 408. [Google Scholar] [CrossRef]
| Mixed-Velocity | Uniform-Velocity | Mixed-Pressure | Uniform-Pressure | |
|---|---|---|---|---|
| DoFs | ||||
| 1 | 0.5855145451 | 0.5764554385 | 0.7334786512 | 0.7413536071 |
| 2 | 0.9320673270 | 0.9276187838 | 0.9947750576 | 0.9948088692 |
| 3 | 0.9819303885 | 0.9801400555 | 0.9993205450 | 0.9993294807 |
| 4 | 0.9900400584 | 0.9890380980 | 0.9998532791 | 0.9998502524 |
| 5 | 0.9954221934 | 0.9947546689 | 0.9999682922 | 0.9999676828 |
| 6 | 0.9975491011 | 0.9971518139 | 0.9999827134 | 0.9999820036 |
| 7 | 0.9990781402 | 0.9988937420 | 0.9999945064 | 0.9999940851 |
| 8 | 0.9993870184 | 0.9992443210 | 0.9999970640 | 0.9999968682 |
| 9 | 0.9996459298 | 0.9995575066 | 0.9999984249 | 0.9999982012 |
| 10 | 0.9997908626 | 0.9997329171 | 0.9999995168 | 0.9999994521 |
| 11 | 0.9998805961 | 0.9998491443 | 0.9999996861 | 0.9999996457 |
| 12 | 0.9999385575 | 0.9999185397 | 0.9999998352 | 0.9999998220 |
| 13 | 0.9999560220 | 0.9999403728 | 0.9999998957 | 0.9999998900 |
| 14 | 0.9999725492 | 0.9999616808 | 0.9999999427 | 0.9999999450 |
| 15 | 0.9999810290 | 0.9999733205 | 0.9999999688 | 0.9999999681 |
| 16 | 0.9999892611 | 0.9999845707 | 0.9999999772 | 0.9999999772 |
| 17 | 0.9999926070 | 0.9999891758 | 0.9999999843 | 0.9999999857 |
| 18 | 0.9999957257 | 0.9999935479 | 0.9999999881 | 0.9999999904 |
| 19 | 0.9999969535 | 0.9999953122 | 0.9999999918 | 0.9999999940 |
| 20 | 0.9999979067 | 0.9999968180 | 0.9999999945 | 0.9999999967 |
| ♯ DoFs | Speedup | Relative Error (Velocity) | Relative Error (Pressure) | |
|---|---|---|---|---|
| High-fidelity | 110 | 1 | 0 | 0 |
| Uniform method | 5 | 15,370 | ||
| 10 | 4122 | |||
| 15 | 1972 | |||
| 20 | 1011 | |||
| Mixed method | 5 | 25,981 | ||
| 10 | 6902 | |||
| 15 | 2936 | |||
| 20 | 1764 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siddiqui, M.S.; Fonn, E.; Kvamsdal, T.; Rasheed, A. Finite-Volume High-Fidelity Simulation Combined with Finite-Element-Based Reduced-Order Modeling of Incompressible Flow Problems. Energies 2019, 12, 1271. https://doi.org/10.3390/en12071271
Siddiqui MS, Fonn E, Kvamsdal T, Rasheed A. Finite-Volume High-Fidelity Simulation Combined with Finite-Element-Based Reduced-Order Modeling of Incompressible Flow Problems. Energies. 2019; 12(7):1271. https://doi.org/10.3390/en12071271
Chicago/Turabian StyleSiddiqui, M. Salman, Eivind Fonn, Trond Kvamsdal, and Adil Rasheed. 2019. "Finite-Volume High-Fidelity Simulation Combined with Finite-Element-Based Reduced-Order Modeling of Incompressible Flow Problems" Energies 12, no. 7: 1271. https://doi.org/10.3390/en12071271
APA StyleSiddiqui, M. S., Fonn, E., Kvamsdal, T., & Rasheed, A. (2019). Finite-Volume High-Fidelity Simulation Combined with Finite-Element-Based Reduced-Order Modeling of Incompressible Flow Problems. Energies, 12(7), 1271. https://doi.org/10.3390/en12071271





