Flow Conditions for PATs Operating in Parallel: Experimental and Numerical Analyses
Abstract
1. Introduction
2. Head Losses within PATs
3. Experimental Set-Up
4. Numerical Simulations
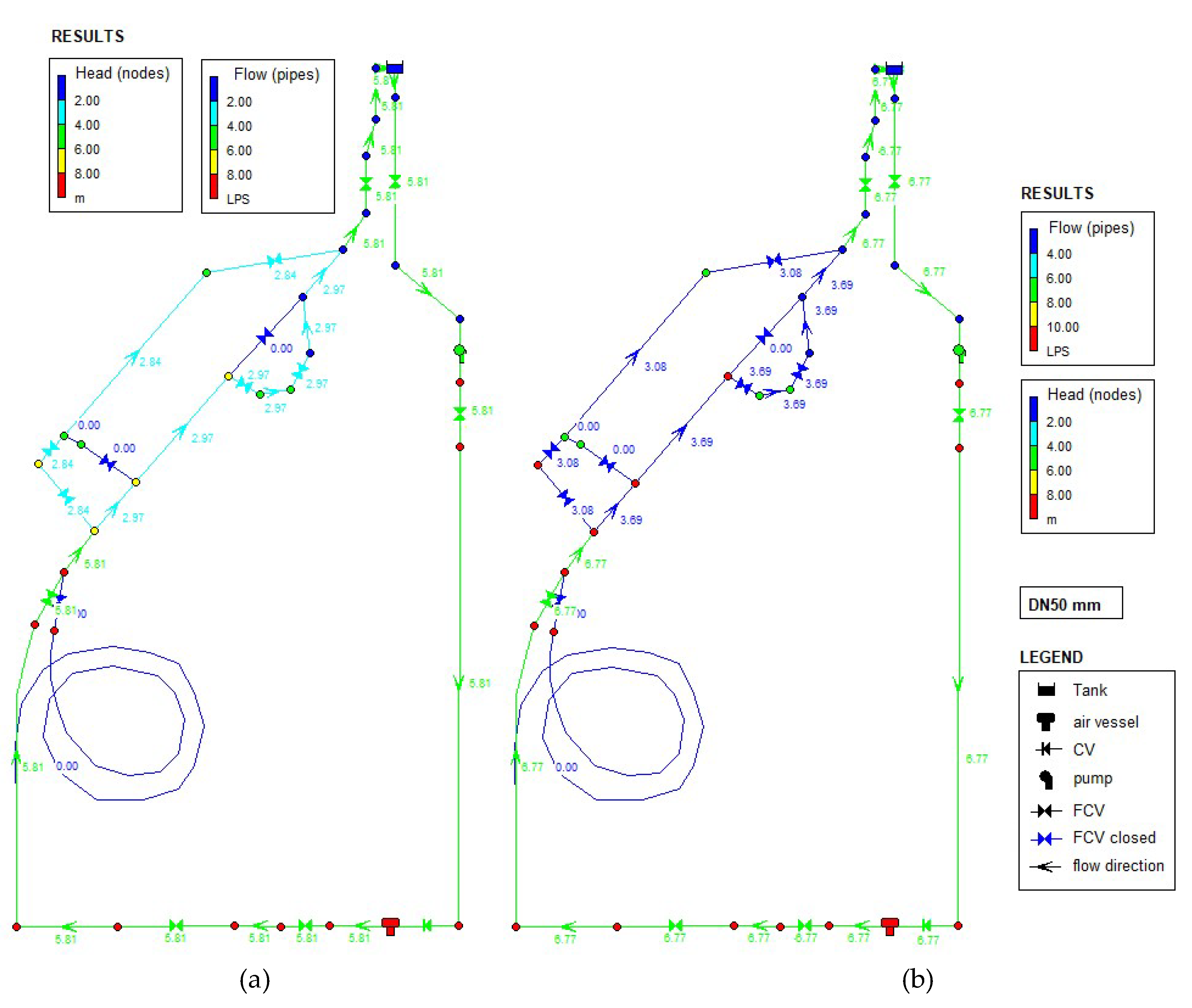
4.1. EPANET Model
4.2. CFD Model
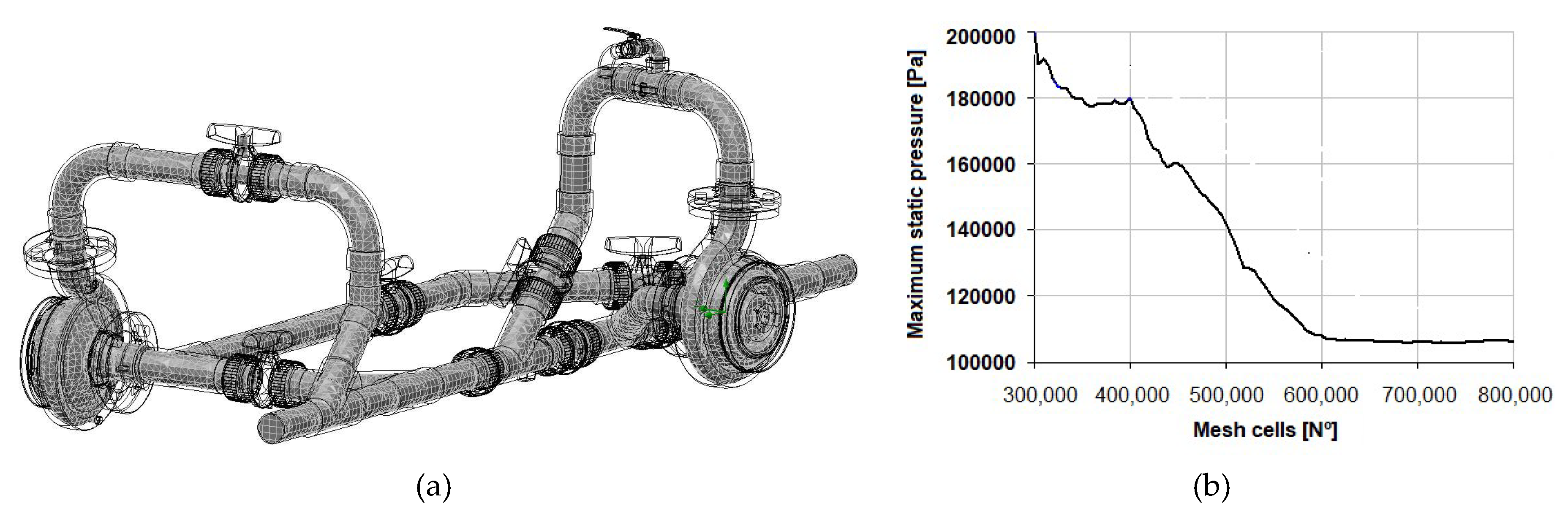
4.2.1. PAT Geometry and Mesh
4.2.2. Boundary Conditions
5. Results and Discussion
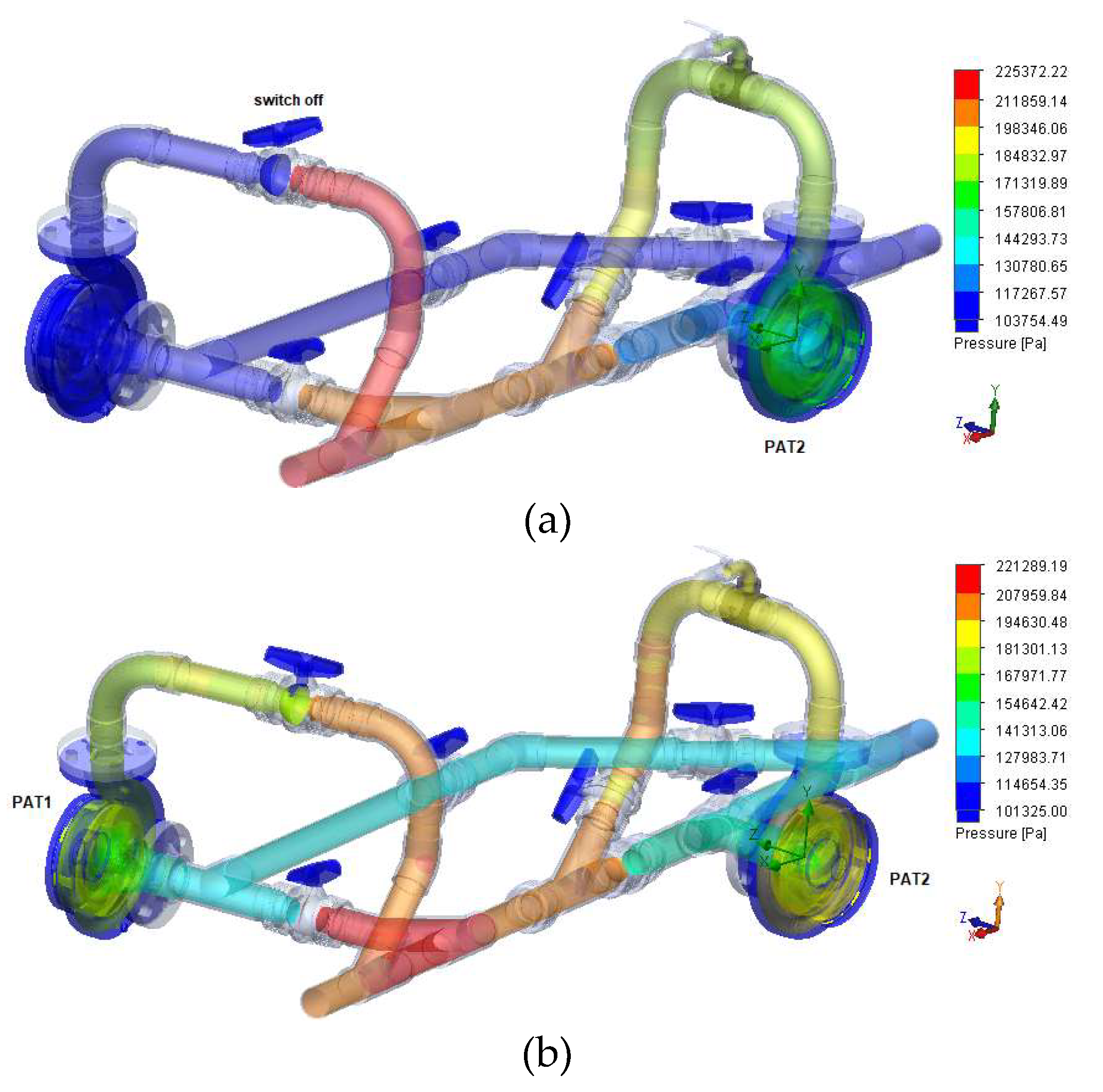
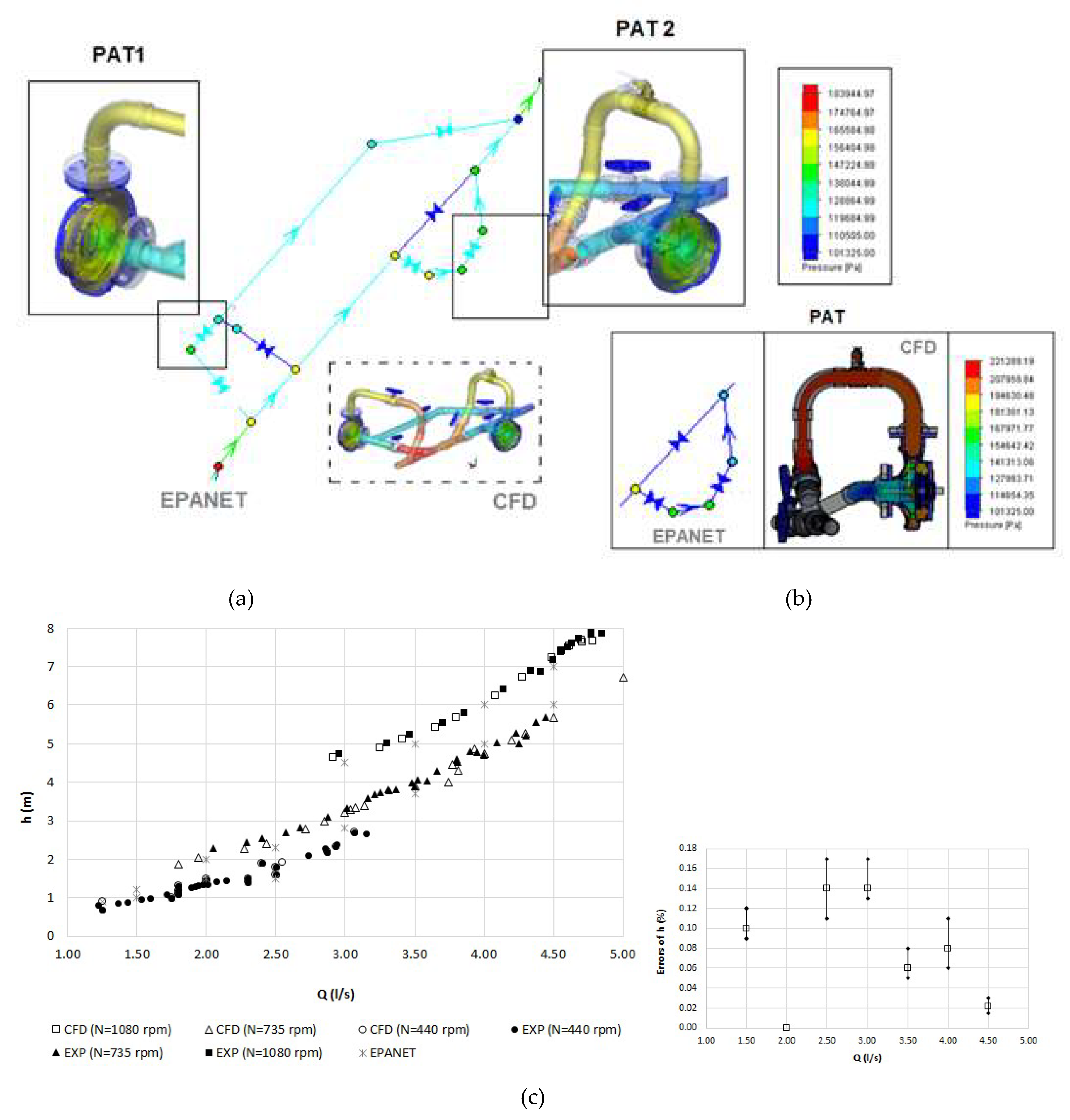
5.1. Pressure Variation and Velocity Streamlines Distribution
5.2. Analysis of the Head Losses of the PATs System
5.3. Comparisons
6. Conclusions
- (1)
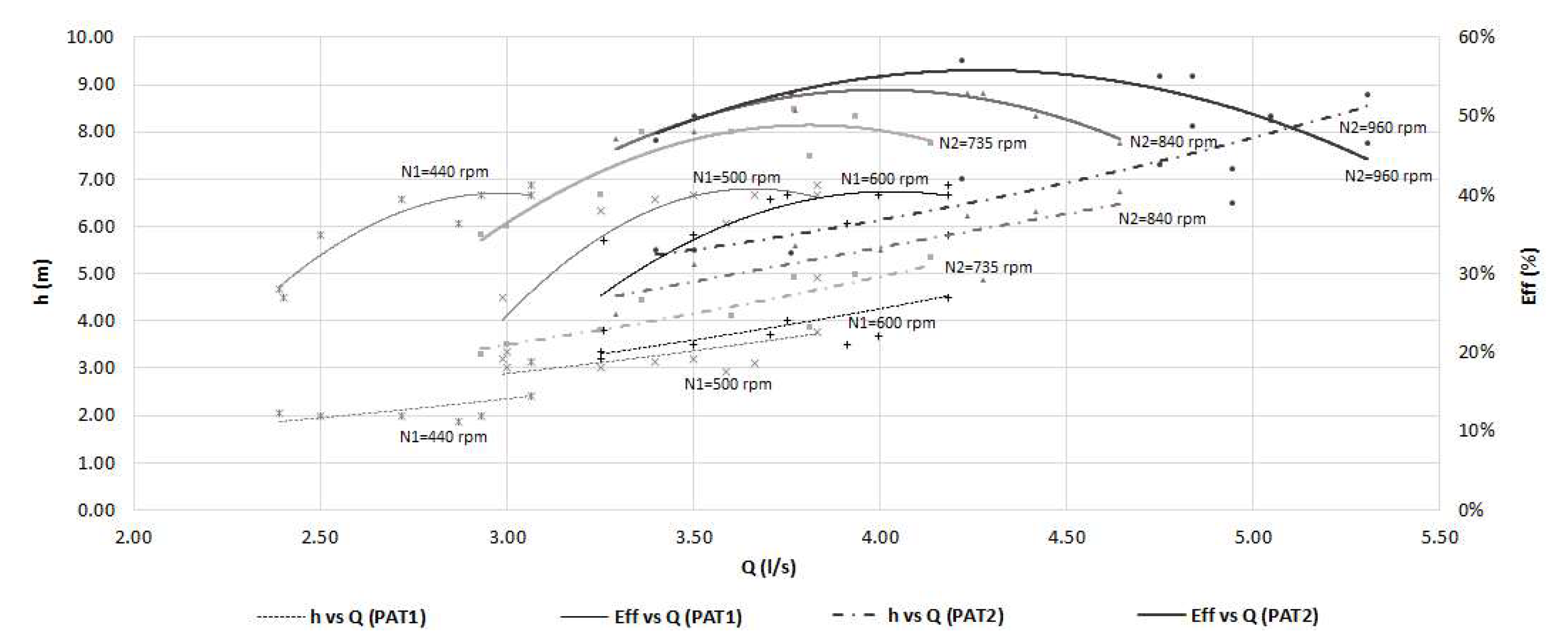
- The characteristic curves were rather different from PAT1 to PAT2 due to different rotational speeds and flow rates, associated to each PAT, even for equal machines working in parallel mode;
- (2)
- During the steady state operating condition, in the parallel configuration, the optimal point was obtained for a total flow of Q =7.50 L/s and H = 4 m; corresponding to Q = 4.00 L/s for PAT1 and Q = 3.53 L/s for PAT2, associated to N1 = 440 rpm and N2 = 735 rpm, respectively;
- (3)
- Although parallel operation increases the total flow rate, it also causes greater head losses, with a reduction in the flow rate in each PAT, and consequentially, alterations in the efficiency of each PAT;
- (4)
- In the CFD model, the head losses can be estimated in accordance with empirical formulations, with acceptable errors, allowing a better comprehension of the flow pattern inside the PAT system;
- (5)
- The benefits of PATs working in parallel are the possibility for covering higher flow range conditions than for a single PAT.
- (6)
- Comparing the CFD model with experimental tests, the optimal point for total flow during numerical simulations was achieved for Q = 7.6 L/s and H = 4 m. Also, the predicted flow rates were in good agreement with the measured data, presenting an average error of 10%.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ismail, M.A.; Othman, A.K.; Islam, S.; Zen, H. End suction centrifugal pump operating in turbine mode for microhydro applications. Adv. Mech. Eng. 2015, 7. [Google Scholar] [CrossRef]
- Jain, S.V.; Patel, R.N. Investigations on pump running in turbine mode: A review of the state-of-the-art. Renew. Sustain. Energy Rev. 2014, 30, 841–868. [Google Scholar] [CrossRef]
- Darmawi, R.; Sipahutar, S.M.; Bernas, M.S.; Imanuddin, M.S. Renewable energy and hydropower utilization tendency worldwide. Renew. Sustain. Energy Rev. 2013, 17, 213–215. [Google Scholar] [CrossRef]
- García, I.F.; Ferras, D.; Mc Nabola, A. Potential of energy recovery and water saving using micro-hydropower in rural water distribution networks. J. Water Resour. Plann. Manag. 2019, 145, 05019001. [Google Scholar] [CrossRef]
- Ramos, H.; Borga, A. Pumps as turbines: An unconventional solution to energy production. Urban Water 1999, 1, 261–263. [Google Scholar] [CrossRef]
- Williams, A.A. Pumps as turbines for low cost micro hydropower. Renew. Energy 1996, 9, 1227–1234. [Google Scholar] [CrossRef]
- Motwani, K.H.; Jain, S.V.; Patel, R.N. Cost analysis of pump as turbine for pico hydropower plants—A case study. Procedia Eng. 2013, 51, 721–726. [Google Scholar] [CrossRef]
- Orchard, B.; Klos, S. Pumps as turbines for water industry. World Pumps 2009, 2009, 22–23. [Google Scholar] [CrossRef]
- Yang, S.S.; Derakhshan, S.; Kong, F.Y. Theoretical, numerical and experimental prediction of pump as turbine performance. Renew. Energy 2012, 48, 507–513. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; López-Jiménez, P.; Ramos, H.M. Modified affinity laws in hydraulic machines towards the best efficiency line. Water Resour. Manag. 2018, 3, 829–844. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; Sánchez-Romero, F.J.; López-Jiménez, P.; Ramos, H.M. PATs selection towards sustainability in irrigation networks: Simulated annealing as a water management tool. Renew. Energy 2018, 116, 234–249. [Google Scholar] [CrossRef]
- Alatorre-Frenk, C. Cost Minimisation in Micro-Hydro Systems Using Pumps-as-Turbines; University of Warwick: Coventry, UK, 1994. [Google Scholar]
- Carravetta, A.; Derakhshan, S.; Ramos, H.M. Pumps as Turbines, Fundamentals and Applications; Springer International Publishing: New York, NY, USA, 2018; ISSN 2195-9862. [Google Scholar]
- Spangler, D. Centrifugal pumps in reverse. An alternative to conventional turbines. Water Wastewater Int. 1988, 3, 13–17. [Google Scholar]
- Ramos, H. Guidelines for Design of Small Hydropower Plants; Western Regional Energy Agency & Network: Belfast, UK, 2000; ISBN 972 96346 4 5. [Google Scholar]
- Pérez-Sánchez, M.; Simão, M.; López-Jiménez, P.; Ramos, H.M. CFD analyses and experiments in a PAT modeling: Pressure variation and system efficiency. Fluids 2017, 2, 51. [Google Scholar] [CrossRef]
- Chapallaz, G.; Eichenberger, J.M.; Fischer, P. Manual on Pumps Used as Turbines; Vieweg: Braunschweig, Germany, 1992. [Google Scholar]
- Ramos, H.M.; Almeida, A.B. Dynamic orifice model on waterhammer analysis of high and medium heads of small hydropower schemes. J. Hydraul. Res. 2001, 39, 429–436. [Google Scholar] [CrossRef]
- Derakhshan, S.; Nourbakhsh, A. Experimental study of characteristic curves of centrifugal pumps working as turbines in different specific speeds. Exp. Therm. Fluid Sci. 2008, 32, 800–807. [Google Scholar] [CrossRef]
- Simão, M.; Pérez-Sánchez, M.; Carravetta, A.; López-Jiménez, P.; Ramos, H.M. Velocities in a centrifugal PAT operation: Experiments and CFD analyses. Fluids 2017, 3, 3. [Google Scholar] [CrossRef]
- Vieira, T.S.; Siqueira, J.R.; Bueno, A.D.; Morales, R.; Estevam, V. Analytical study of pressure losses and fluid viscosity effects on pump performance during monophase flow inside an ESP stage. J. Pet. Sci. Eng. 2015, 127, 245–258. [Google Scholar] [CrossRef]
- Fecarotta, O.; Aricò, C.; Carravetta, A.; Martino, R.; Ramos, H.M. Hydropower potential in water distribution networks: Pressure control by PATs. Water Resour. Manag. 2015, 29, 699–714. [Google Scholar] [CrossRef]
- Carravetta, A.; Giudice, G.; Fecarotta, O.; Ramos, H.M. Pump as turbine (PAT) design in water distribution network by system effectiveness. Water 2013, 5, 1211–1225. [Google Scholar] [CrossRef]
- Agarwal, T. Review of pump as turbine (PAT) for micro-hydropower. Int. J. Emerg. Technol. Adv. Eng. 2012, 2, 163–169. [Google Scholar]
- Derakhshan, S.; Mohammadi, B.; Nourbakhsh, A. Efficiency improvement of centrifugal reverse pumps. J. Fluids Eng. 2009, 131, 211039. [Google Scholar] [CrossRef]
- Rossman, L.A. EPANET 2 User’s Manual; U.S. Environmental Protection Agency (EPA): Cincinnati, OH, USA, 2000.
- Fecarotta, O.; Carravetta, A.; Ramos, H.M.; Martino, R. An improved affinity model to enhance variable operating strategy for pumps used as turbines. J. Hydraul. Res. 2016, 54, 332–341. [Google Scholar] [CrossRef]
- Buono, D.; Frosina, E.; Mazzone, A.; Cesaro, U.; Senatore, A. Study of a pump as turbine for a hydraulic urban network using a tridimensional CFD modeling methodology. Energy Procedia 2015, 82, 201–208. [Google Scholar] [CrossRef]
- Mentor Graphics Corporation. FloEFD Technical Reference; Mentor Graphics Corporation: Wilsonville, OR, USA, 2011. [Google Scholar]
- Abilgaziyev, A.; Nogerbek, N.; Rojas-Solórzano, L. Design optimization of an oil-air catch can separation system. J. Transp. Technol. 2015, 5, 15. [Google Scholar] [CrossRef]
- Ramos, H.M.; Almeida, A.B. Dynamic effects in micro-hydro modelling. Int. Water Power Dam Constr. 2003, 55, 22–25. [Google Scholar]
- Frosina, E.; Dario, B.; Senatore, A. A Performance prediction method for Pumps as Turbines (PAT) using a Computational Fluid Dynamics (CFD) modeling approach. Energies 2017, 10, 103. [Google Scholar] [CrossRef]
- Sun, D.; Prado, M.G. Single-phase model for ESP’s performance. In Proceedings of the TUALP Annual Advisory Board Meeting, Tulsa/Oklahoma, Oklahoma City, OK, USA, 23‒26 March 2002; p. 42. [Google Scholar]
- Thin, K.C.; Khaing, M.; Aye, K.M. Design and performance analysis of centrifugal pump. World Acad. Sci. Eng. Technol. China 2008, 46, 422–429. [Google Scholar]
- Bing, H.; Tan, L.; Cao, S.L.; Lu, L. Prediction method of impeller performance and analysis of loss mechanism for mixed-flow pump. Sci. China Technol. Sci. 2012, 55, 1988–1998. [Google Scholar] [CrossRef]


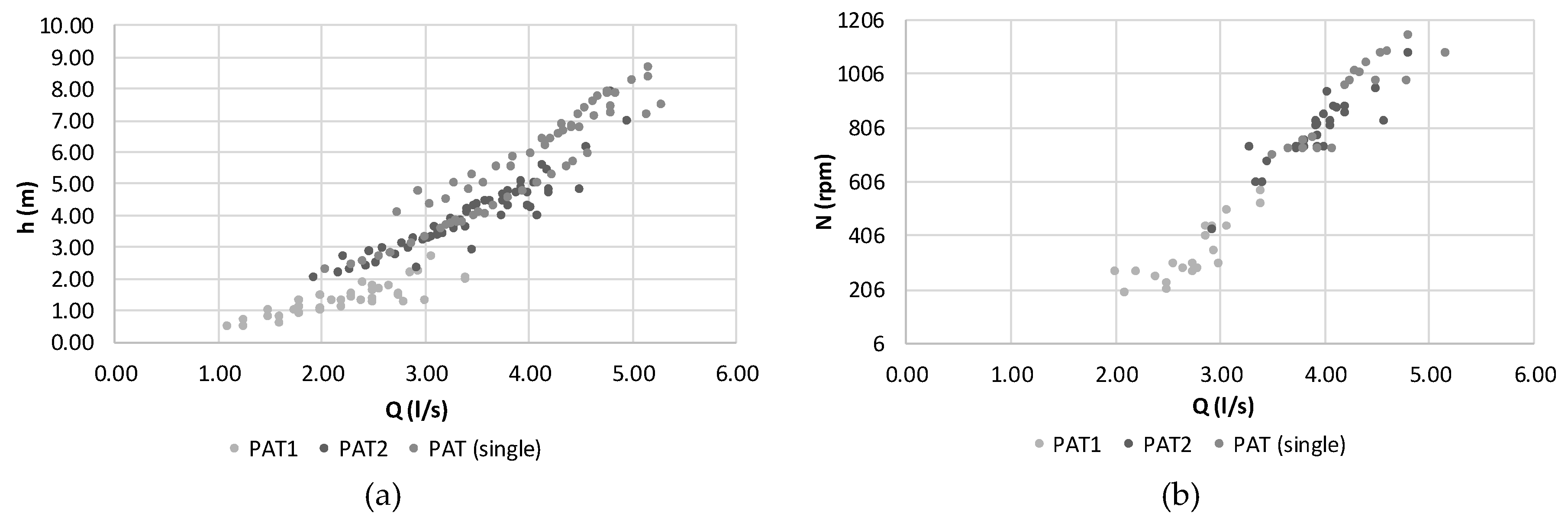
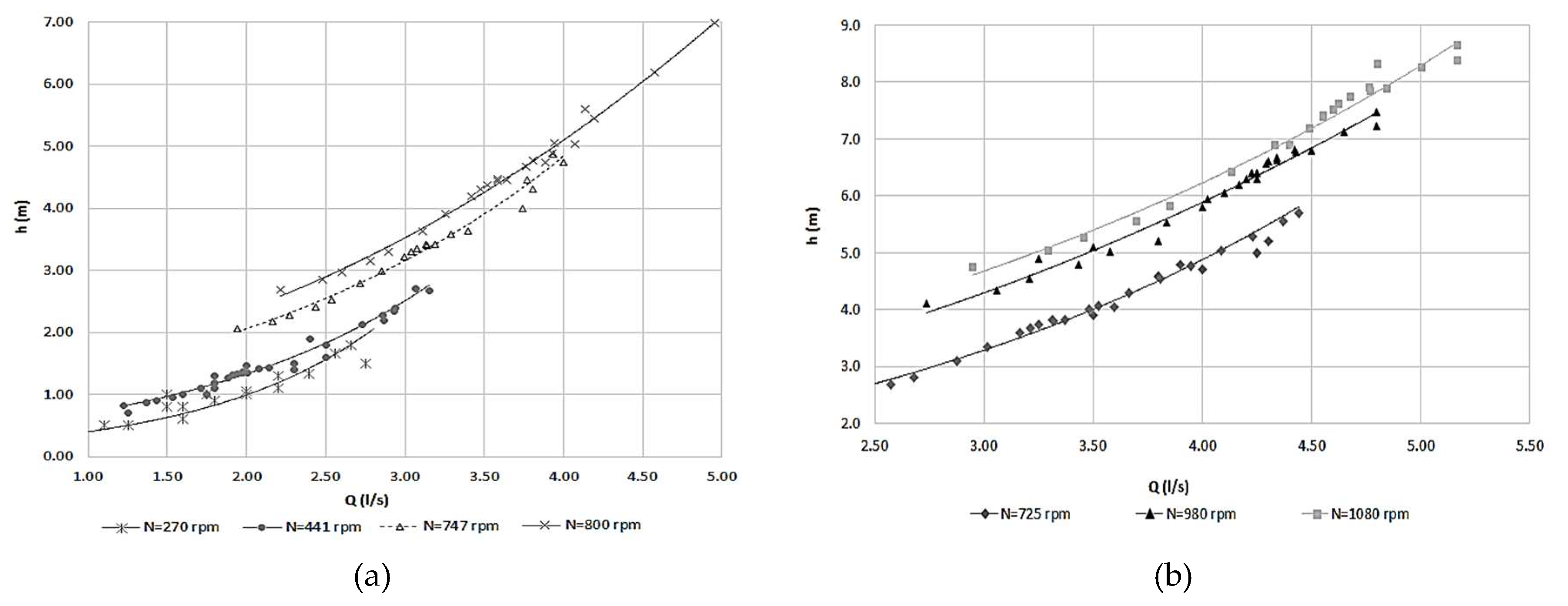
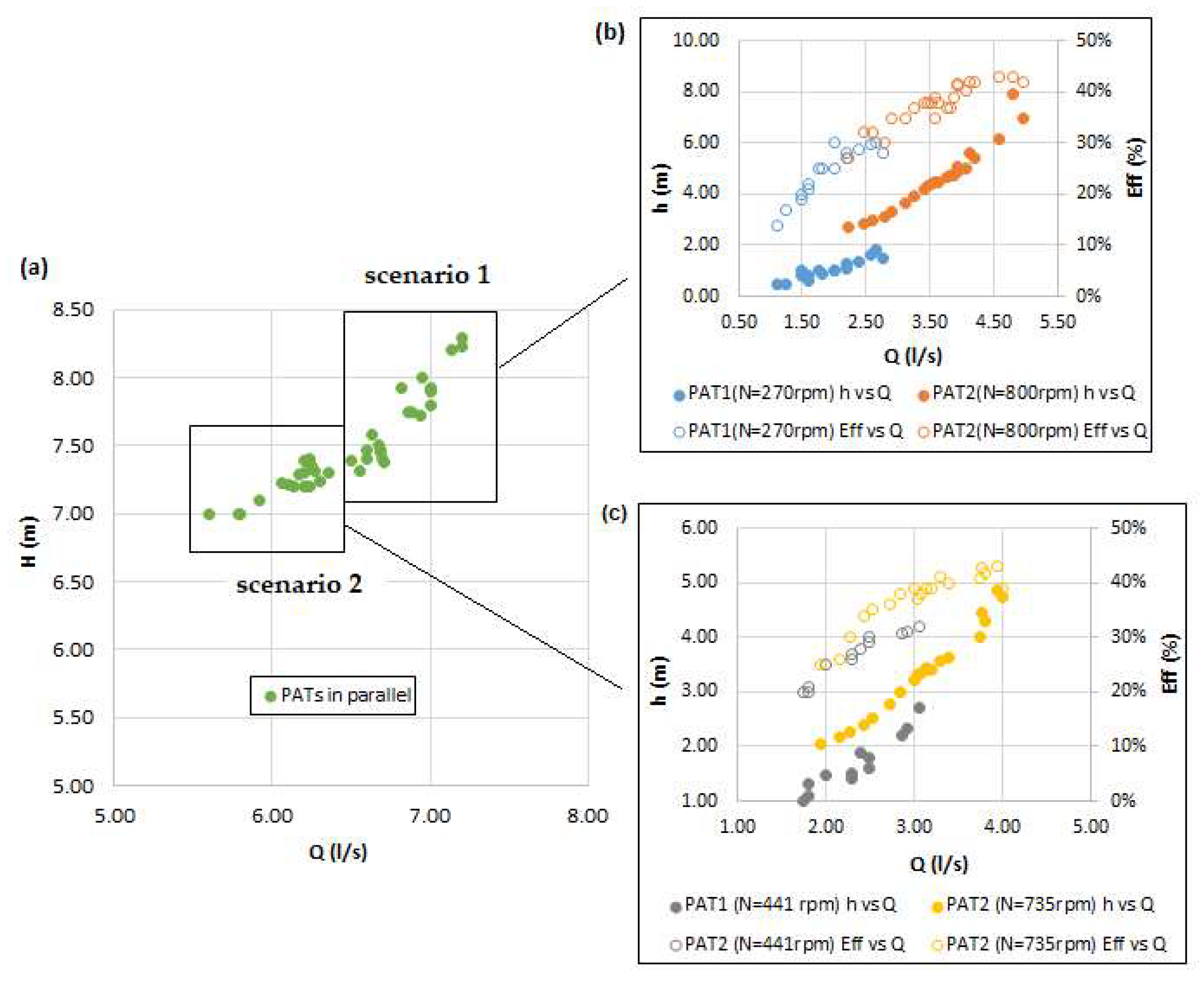

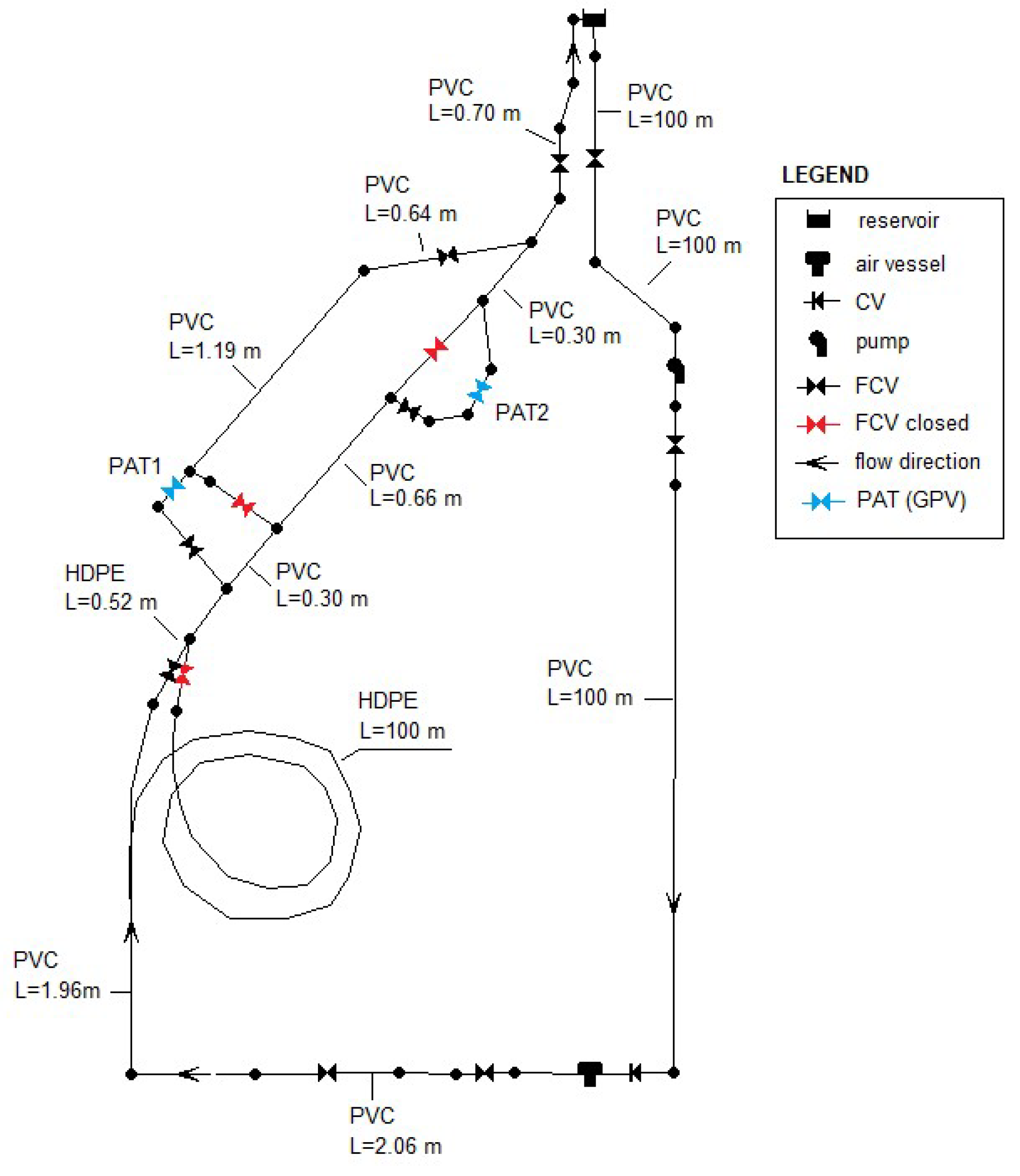

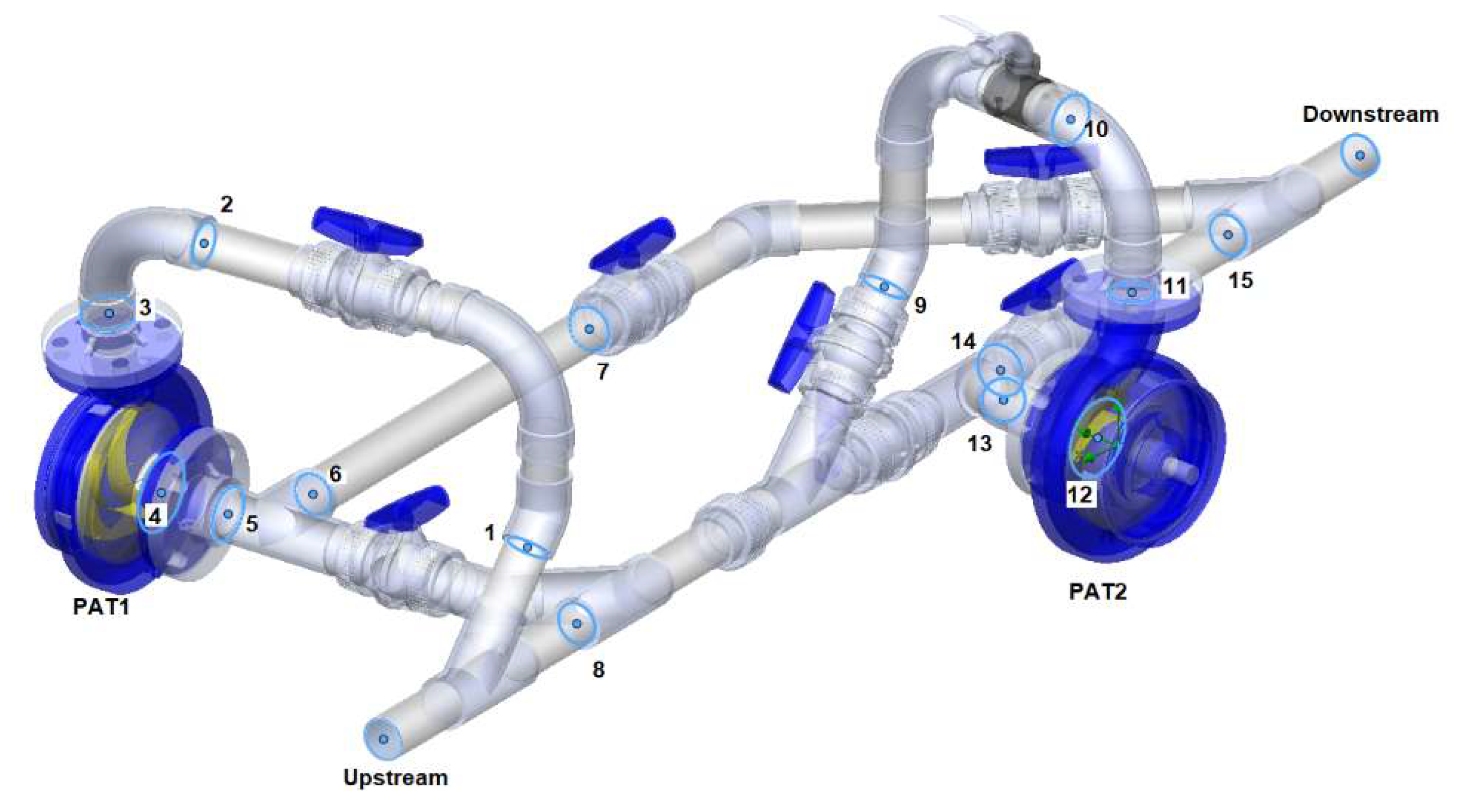
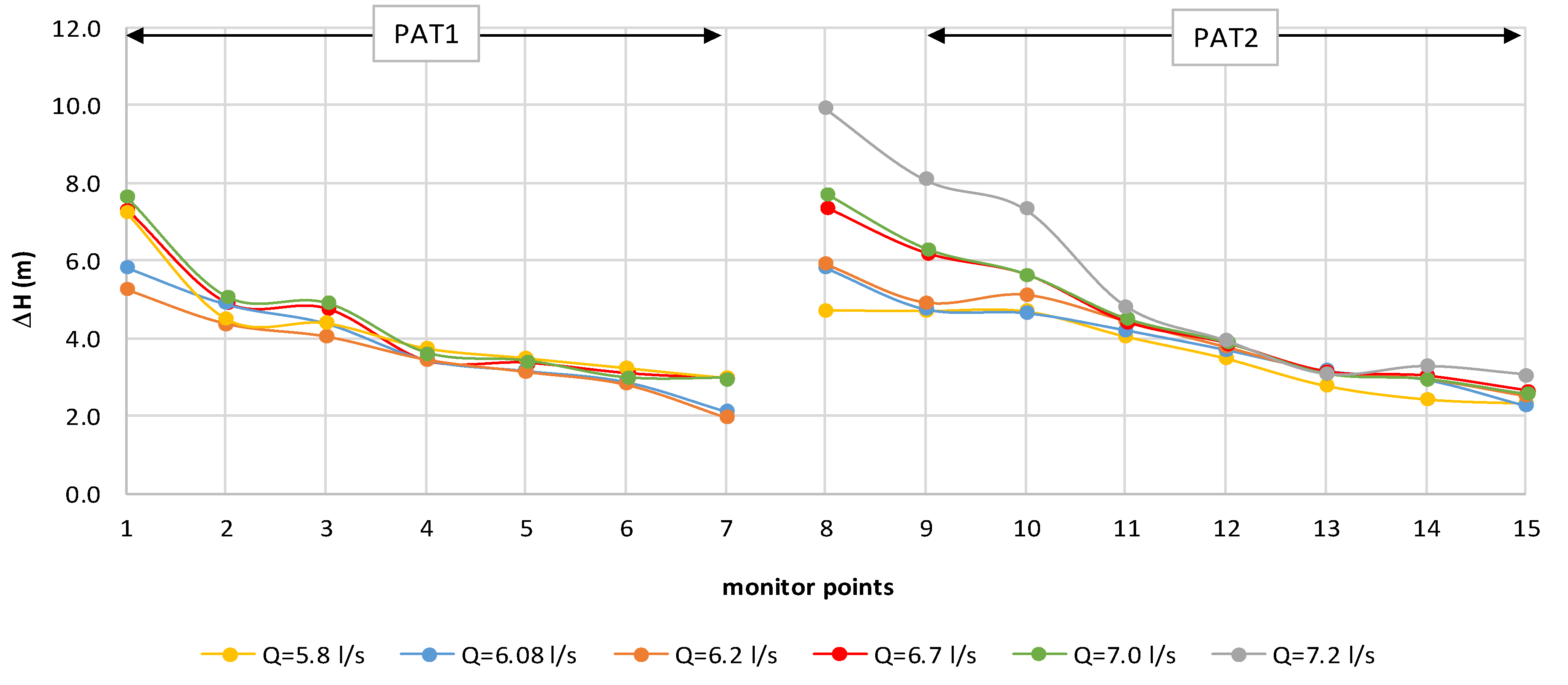
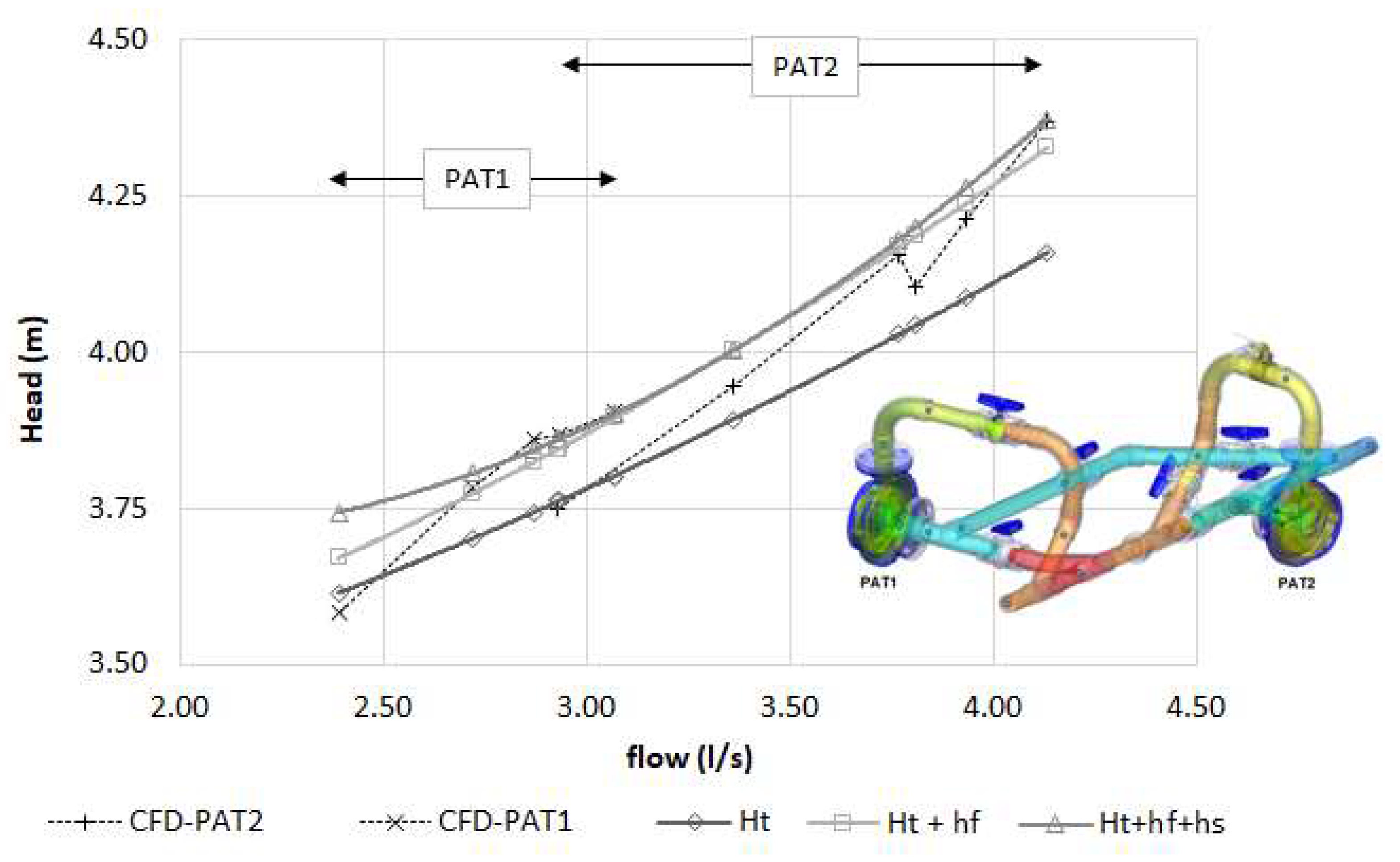

| Condition | QPAT1 (L/s) | QPAT2 (L/s) | NPAT1 (rpm) | NPAT2 (rpm) | h PAT1 (m) | h PAT2 (m) |
|---|---|---|---|---|---|---|
| PATs in Parallel | 2.66 | 3.94 | 284 | 816 | 1.80 | 5.05 |
| 2.93 | 3.93 | 427 | 812 | 2.34 | 4.88 | |
| 2.56 | 3.74 | 300 | 725 | 1.66 | 4.00 | |
| 2.39 | 4.81 | 250 | 1083 | 1.34 | 7.93 | |
| 2.93 | 4.07 | 427 | 813 | 2.34 | 5.04 | |
| 2.39 | 3.81 | 250 | 754 | 1.34 | 4.30 | |
| 3.07 | 3.93 | 497 | 772 | 2.70 | 4.87 | |
| 2.93 | 3.77 | 427 | 735 | 2.34 | 4.45 | |
| 3.07 | 4.13 | 497 | 875 | 2.70 | 5.59 | |
| 2.87 | 2.93 | 400 | 427 | 2.19 | 2.34 | |
| 3.40 | 4.20 | 520 | 860 | 2.04 | 4.80 | |
| 3.00 | 4.10 | 300 | 880 | 1.31 | 4.01 | |
| 2.80 | 3.46 | 280 | 680 | 1.26 | 2.90 | |
| 3.40 | 4.50 | 570 | 950 | 1.98 | 4.82 | |
| 2.50 | 4.20 | 230 | 880 | 1.37 | 4.70 | |
| 2.75 | 4.00 | 300 | 850 | 1.47 | 4.30 | |
| 2.10 | 4.03 | 190 | 935 | 1.33 | 4.23 | |
| 2.50 | 3.42 | 205 | 600 | 1.29 | 4.10 | |
| 2.95 | 3.35 | 350 | 600 | 2.26 | 3.85 | |
| 2.05 | 1.14 | 440 | 735 | 1.40 | ||
| 2.16 | 1.31 | 1.50 | ||||
| 2.45 | 1.73 | 1.80 | ||||
| 2.63 | 1.96 | 2.00 | ||||
| 2.95 | 2.36 | 2.40 | ||||
| 3.24 | 2.71 | 2.80 | ||||
| 3.38 | 2.87 | 3.00 | ||||
| 3.52 | 3.02 | 3.20 | ||||
| 3.64 | 3.16 | 3.40 | ||||
| 3.77 | 3.30 | 3.60 | ||||
| 3.89 | 3.43 | 3.80 | ||||
| 4.00 | 3.56 | 4.00 | ||||
| 4.12 | 3.69 | 4.20 | ||||
| 4.23 | 3.81 | 4.40 | ||||
| 2.39 | 3.26 | 270 | 830 | 1.34 | 3.90 | |
| 2.66 | 3.11 | 1.80 | 3.63 | |||
| 2.56 | 2.78 | 1.66 | 3.14 | |||
| 2.00 | 2.60 | 1.00 | 2.97 | |||
| 1.80 | 2.22 | 0.90 | 2.69 | |||
| 2.00 | 2.90 | 1.05 | 3.29 | |||
| 2.20 | 2.48 | 1.50 | 2.85 | |||
| 2.75 | 3.42 | 1.50 | 4.19 | |||
| Single PAT | 3.81 | 725 | 4.54 | |||
| 3.95 | 724 | 4.78 | ||||
| 4.09 | 725 | 5.03 | ||||
| 4.23 | 726 | 5.29 | ||||
| 4.80 | 980 | 7.22 | ||||
| 4.42 | 980 | 6.82 | ||||
| 4.80 | 979 | 7.46 | ||||
| 4.17 | 980 | 6.20 | ||||
| 4.34 | 1080 | 8.26 | ||||
| 4.80 | 1080 | 8.38 | ||||
| 4.76 | 1081 | 7.91 | ||||
| 4.95 | 1150 | 8.66 | ||||
| 4.49 | 1079 | 7.19 | ||||
| Ref. | Parameter | Formula | Complement |
|---|---|---|---|
| [31,32,33,34] | net theoretical head (Ht) | ||
| [31,33] | friction loss (hf) | ||
| [34] | shock loss (hs) | kshock = 0.2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simão, M.; Pérez-Sánchez, M.; Carravetta, A.; Ramos, H.M. Flow Conditions for PATs Operating in Parallel: Experimental and Numerical Analyses. Energies 2019, 12, 901. https://doi.org/10.3390/en12050901
Simão M, Pérez-Sánchez M, Carravetta A, Ramos HM. Flow Conditions for PATs Operating in Parallel: Experimental and Numerical Analyses. Energies. 2019; 12(5):901. https://doi.org/10.3390/en12050901
Chicago/Turabian StyleSimão, Mariana, Modesto Pérez-Sánchez, Armando Carravetta, and Helena M. Ramos. 2019. "Flow Conditions for PATs Operating in Parallel: Experimental and Numerical Analyses" Energies 12, no. 5: 901. https://doi.org/10.3390/en12050901
APA StyleSimão, M., Pérez-Sánchez, M., Carravetta, A., & Ramos, H. M. (2019). Flow Conditions for PATs Operating in Parallel: Experimental and Numerical Analyses. Energies, 12(5), 901. https://doi.org/10.3390/en12050901








