Determining Soil-Water Characteristic Curves from Mercury Intrusion Porosimeter Test Data Using Fractal Theory
Abstract
1. Introduction
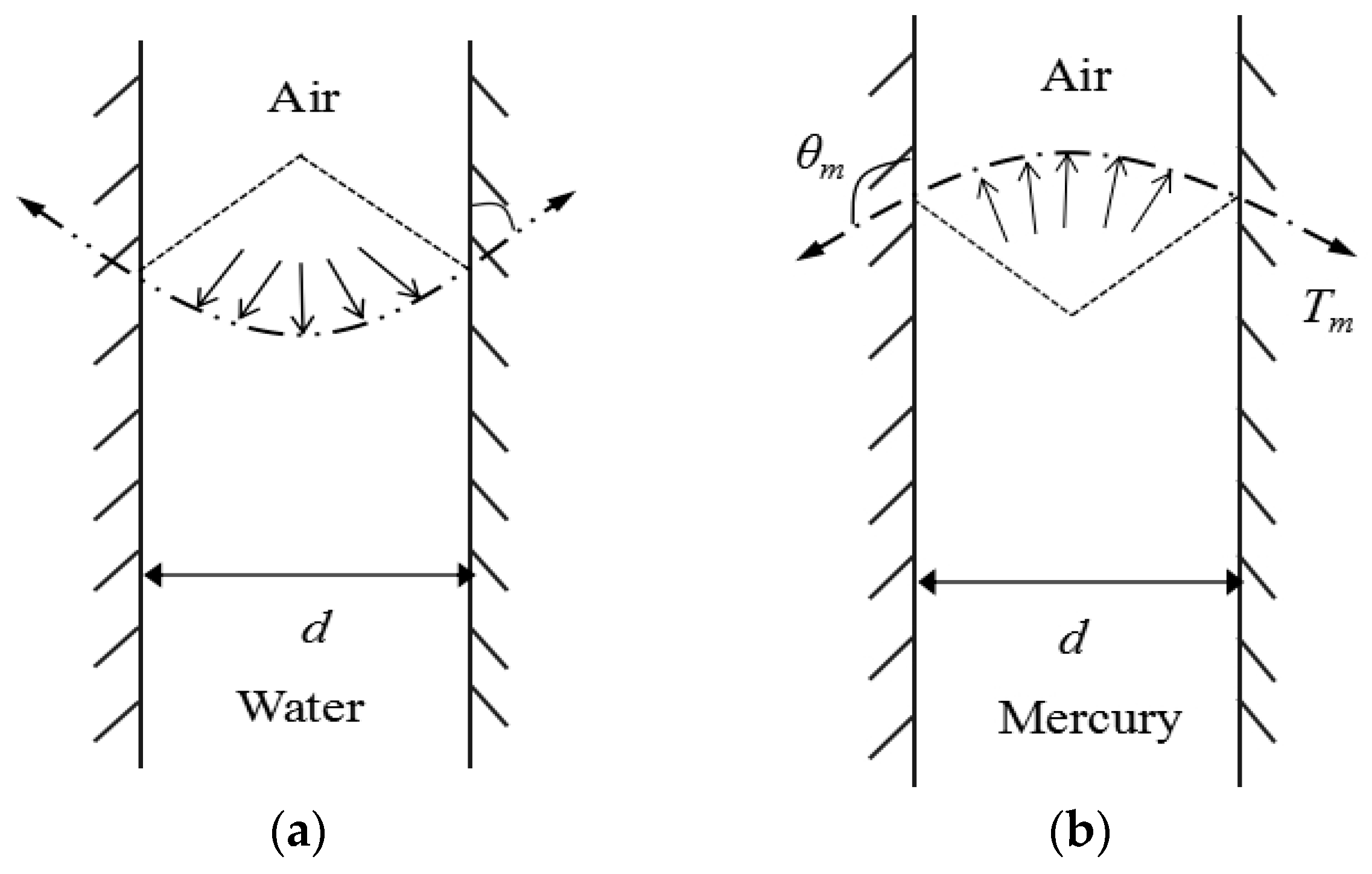
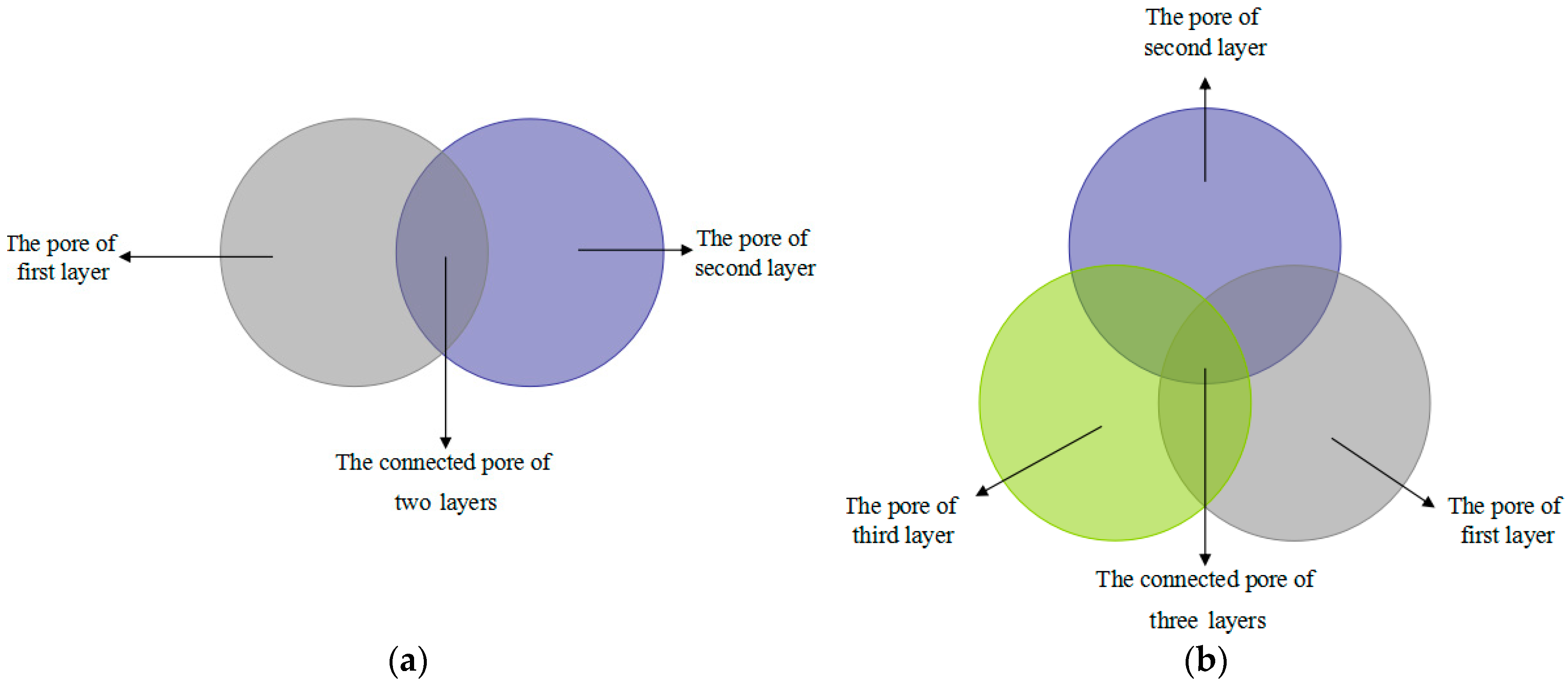
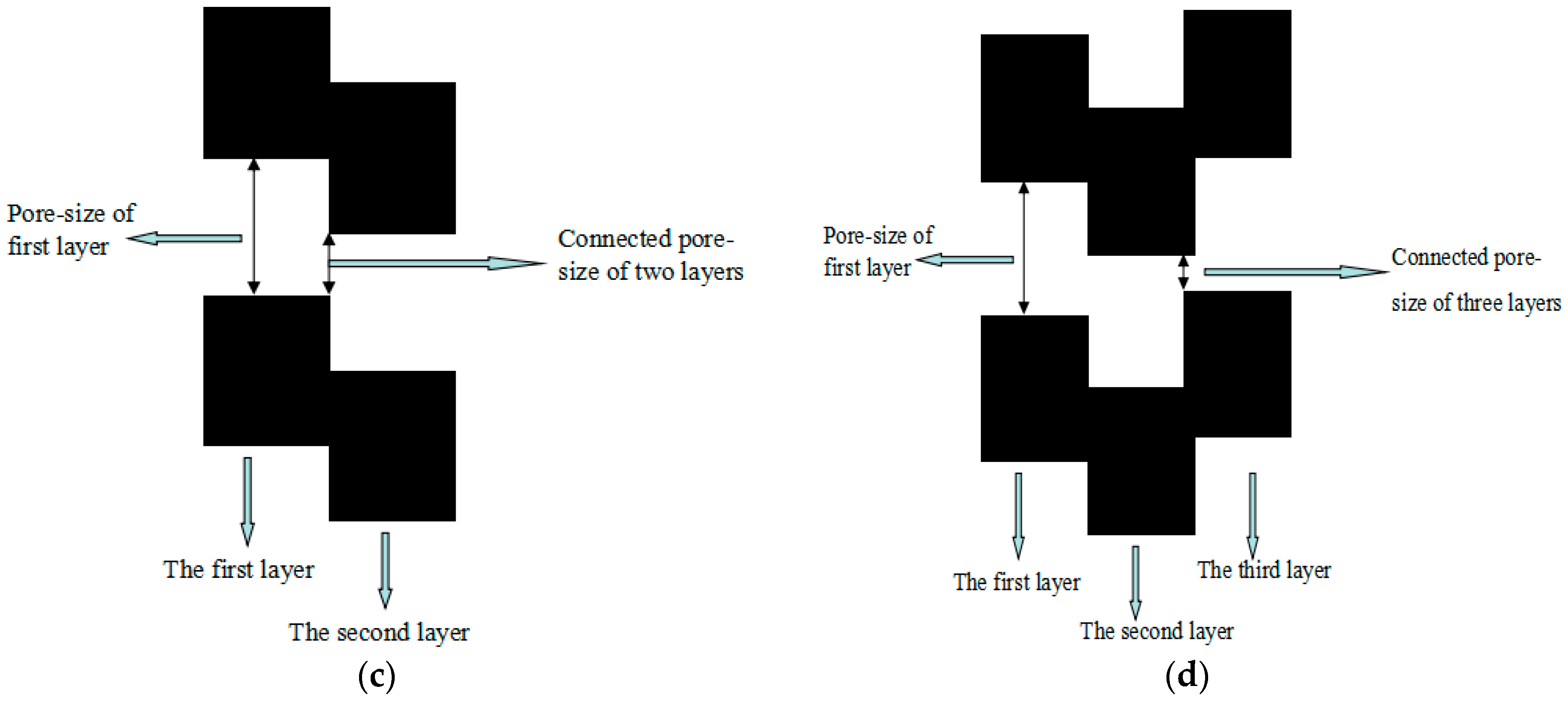
2. MIP Theory
3. SWCC Fractal Model
4. Parameter Determination from MIP Test Results
4.1. Fractal Dimension
4.2. Air-Entry Value
4.2.1. Sample Scale Effect
4.2.2. Determining the Air-Entry Value Ψa by Considering the Sample Scale Effect
5. Materials and Tests
5.1. MIP Tests
5.2. SWCC Tests
6. Results and Discussion
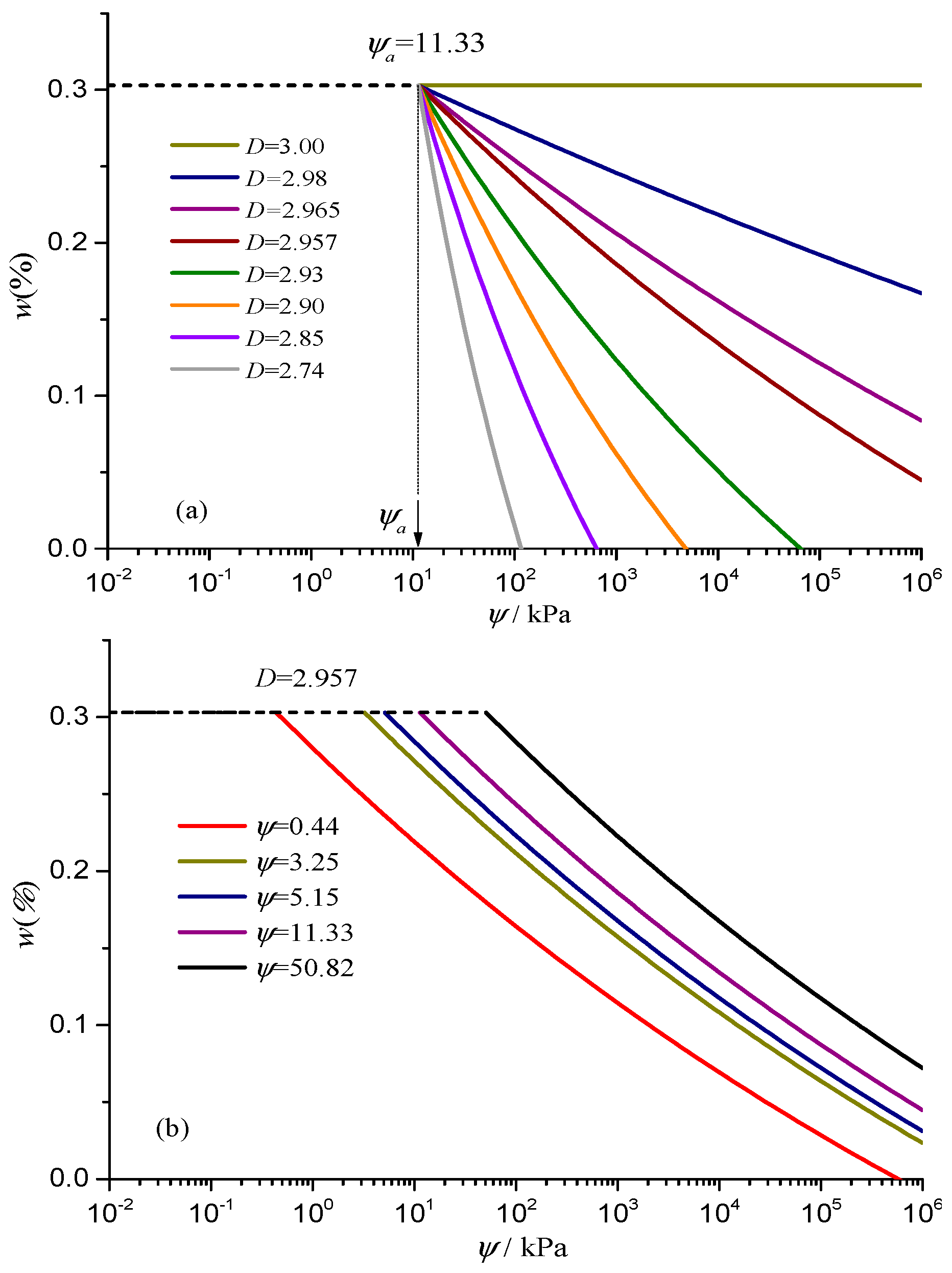
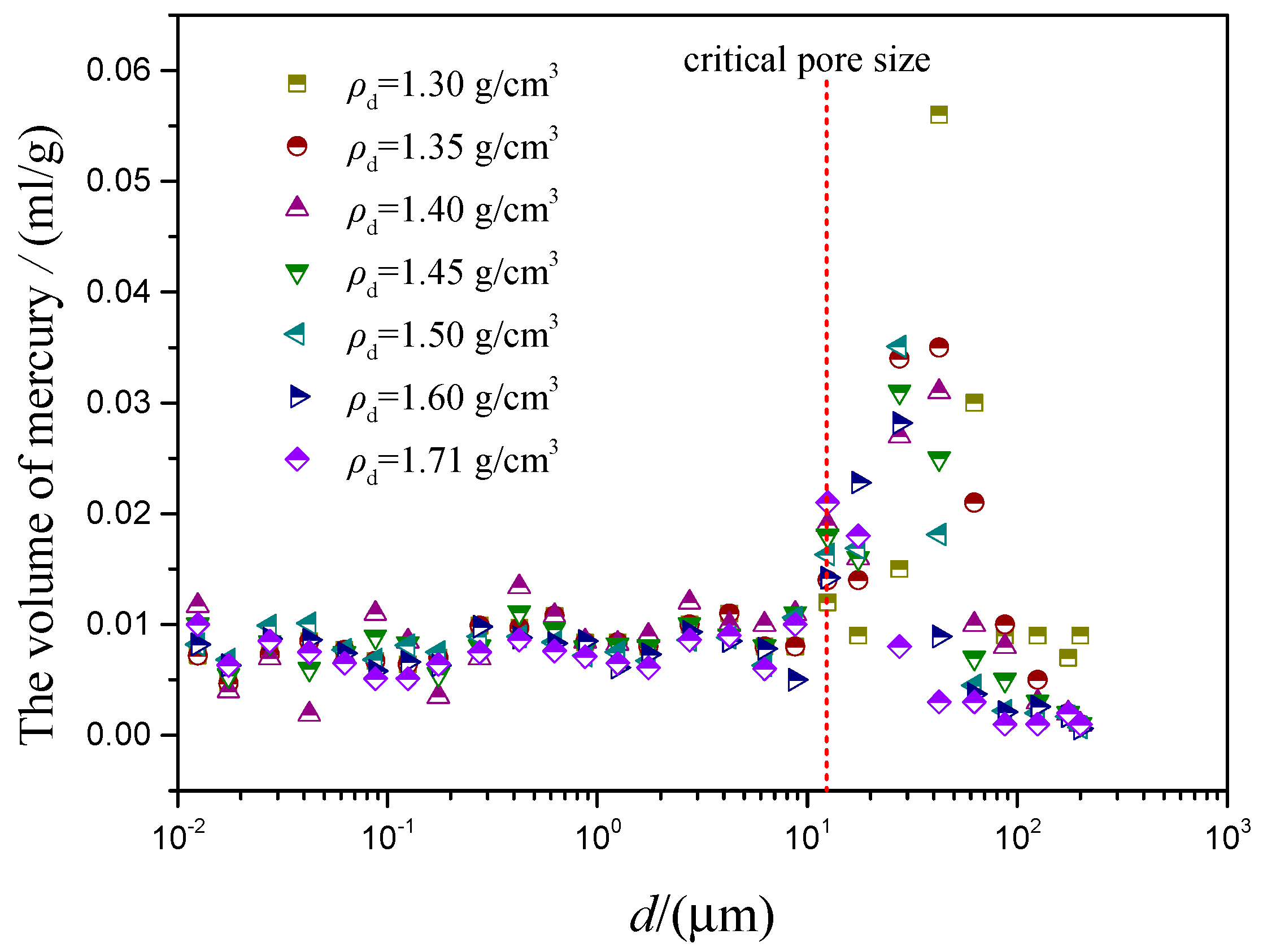
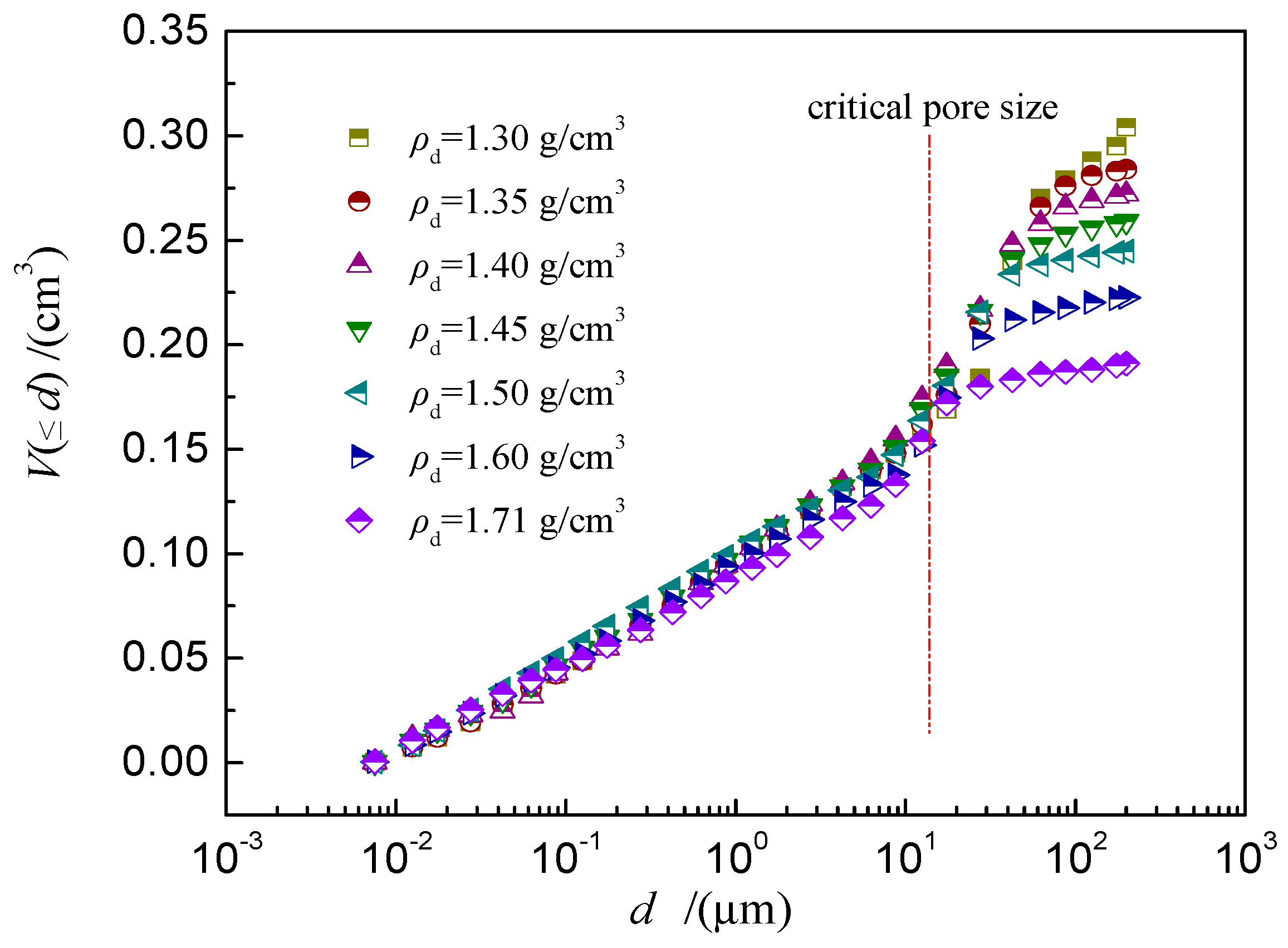
6.1. Critical Pore Size and Fractal Dimension
6.2. Air-Entry Value
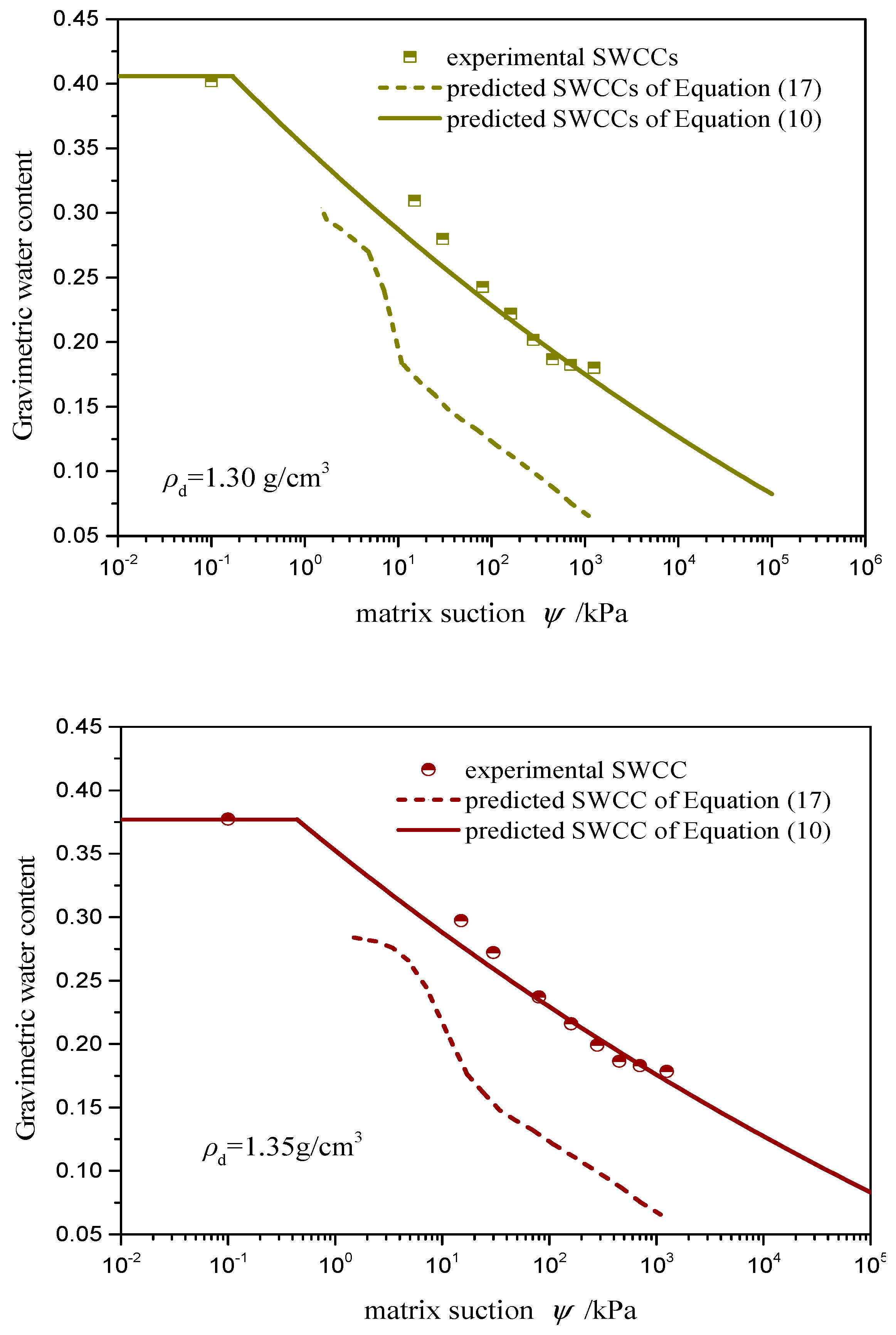
6.3. Validation with SWCC Data
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Noh, J.H.; Lee, S.R.; Park, H. Prediction of Cryo-SWCC during Freezing Based on Pore-Size Distribution. Int. J. Geomech. 2012, 12, 428–438. [Google Scholar] [CrossRef]
- Christopher, B. Prediction of soil water retention properties using pore-size distribution and porosity. Can. J. Soil Sci. 2013, 50, 435–450. [Google Scholar]
- Hu, R.; Chen, Y.F.; Liu, H.H.; Zhou, C.B. A water retention curve and unsaturated hydraulic conductivity model for deformable soils: Consideration of the change in pore-size distribution. Geotechnique 2013, 63, 1389–1405. [Google Scholar] [CrossRef]
- Arroyo, H.; Rojas, E.; Pérez-Rea, M.D.L.L.; Horta, J. A porous model to simulate the evolution of the soil-water characteristic curve with volumetric strains. C. R. Mécanique 2015, 343, 264–274. [Google Scholar] [CrossRef]
- Ghanbarian-Alavijeh, B.; Liaghat, A.M. Evaluation of soil texture data for estimating soil water retention curve. Can. J. Soil Sci. 2009, 89, 461–471. [Google Scholar] [CrossRef]
- Della Vecchia, G.; Dieudonné, A.; Jommi, C.; Charlier, R. Accounting for evolving pore size distribution in water retention models for compacted clays. Int. J. Numer. Anal. Methods Geomech. 2015, 39, 702–723. [Google Scholar] [CrossRef]
- Mandelbrot, B. The Fractal Geometry of Nature: Updated and Augmented; W. H. Freeman Co.: New York, NY, USA, 1983. [Google Scholar]
- Perfect, E. Modeling the primary drainage curve of prefractal porous media. Vadose Zone J. 2005, 4, 959–966. [Google Scholar] [CrossRef]
- Bayat, H.; Neyshaburi, M.R.; Mohammadi, K.; Nariman-Zadeh, N.; Iranneiad, M.; Gregory, A.S. Combination of artificial neural networks and fractal theory to predict soil water retention curve. Comput. Electron. Agric. 2013, 92, 92–103. [Google Scholar] [CrossRef]
- Tao, G.L.; Wu, X.K.; Xiao, H.L.; Chen, Q.S.; Cai, J.C. A unified fractal model for permeability coefficient of unsaturated soil. Fractals 2019, 27. [Google Scholar] [CrossRef]
- Li, K.J.; Zeng, F.G.; Cai, J.C.; Sheng, G.L.; Xia, P.; Zhang, K. Fractal characteristics of pores in talyuan formation shale from Hedong goal field, China. Fractals 2018, 26, 1840006. [Google Scholar] [CrossRef]
- Ghanbarian, B.; Hunt, A.G. Fractals: Concepts and Applications in Geosciences. Available online: https://www.crcpress.com/Fractals-Concepts-and-Applications-in-Geosciences/Ghanbarian-Hunt/p/book/9781498748711 (accessed on 14 November 2017).
- Tyler, S.W.; Wheatcraft, S.W. Fractal processes in soil water retention. Water Resour. Res. 1990, 26, 1047–1056. [Google Scholar] [CrossRef]
- Perrier, E.; Rieu, M.; Sposito, G.; Marsily, D.G. Models of the water retention curve for soils with a fractal pore size distribution. Water Resour. Res. 1996, 32, 3025–3031. [Google Scholar] [CrossRef]
- Xu, Y.F.; Dong, P. Fractal models for the soil-water characteristic of unsaturated soils. Rock Soil Mech. 2002, 23, 400–405. [Google Scholar]
- Xu, Y.F. Calculation of unsaturated hydraulic conductivity using a fractal model for the pore-size distribution. Comput. Geotech. 2004, 31, 549–557. [Google Scholar] [CrossRef]
- Perrier, E.; Bird, N.; Rieu, M. Generalizing the fractal model of soil structure: The pore-solid fractal approach. Geoderma 1999, 88, 137–164. [Google Scholar] [CrossRef]
- Bird, N.; Perrier, E.; Rieu, M. The water retention function for a model of soil structure with pore and solid fractal distributions. Eur. J. Soil Sci. 2000, 51, 55–63. [Google Scholar] [CrossRef]
- Huang, G.H.; Zhang, R.D. Evaluation of soil water retention curve with the pore-solid fractal model. Geoderma 2005, 127, 52–61. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, R.D. Estimation of soil water retention curve: An asymmetrical Pore-Solid fractal model. Wuhan Univ. J. Nat. Sci. 2011, 16, 171–178. [Google Scholar] [CrossRef]
- Ghanbarian-Alavijeh, B.; Millán, H. The relationship between surface fractal dimension and soil water content at permanent wilting point. Geoderma 2009, 151, 224–232. [Google Scholar] [CrossRef]
- Ghanbarian-Alavijeh, B.; Millán, H.; Huang, G. A review of fractal, prefractal and pore-solid-fractal models for parameterizing the soil water retention curve. Can. J. Soil Sci. 2011, 91, 1–14. [Google Scholar] [CrossRef]
- Tao, G.L.; Chen, Y.; Yuan, B.; Gan, S.C.; Wu, X.K.; Zhu, X.L. Predicting soil-water retention curve based on NMR technique and fractal theory. J. Geotech. Eng. 2018, 40, 1466–1472. [Google Scholar]
- Ninjgarav, E.; Chung, S.G.; Jang, W.Y.; Ryu, C.K. Pore size distribution of Pusan clay measured by mercury intrusion porosimetry. KSCE J. Civ. Eng. 2007, 11, 133–139. [Google Scholar] [CrossRef]
- Lubelli, B.; Winter, D.A.M.; Post, J.A.; van Hees, R.P.J.; Drury, M.R. Cryo-FIB-SEM and MIP study of porosity and pore size distribution of bentonite and kaolin at different moisture contents. Appl. Clay Sci. 2013, 81, 358–365. [Google Scholar] [CrossRef]
- Wei, X.; Hattab, M.; Fleureau, J.M.; Hu, R. Micro-macro-experimental study of two clayey materials on drying paths. Bull. Eng. Geol. Environ. 2013, 72, 495–508. [Google Scholar] [CrossRef]
- Zong, Y.T.; Yu, X.L.; Zhu, M.X.; Lu, S. Characterizing soil pore structure using nitrogen adsorption, mercury intrusion porosimetry, and synchrotron-radiation-based X-ray computed microtomography techniques. J. Soils Sediment. 2015, 15, 302–312. [Google Scholar] [CrossRef]
- Regab, R.; Feyen, J.; Hillel, D. Effect of the method for determining pore size distribution on prediction of the hydraulic conductivity function and of infiltration. Soil Sci. Soc. Am. J. 1982, 134, 141–145. [Google Scholar] [CrossRef]
- Prapaharan, S.; Altschaeffl, A.G.; Dempsey, B.J. Moisture curve of comp actedclay: Mercury intrusion method. J. Geotech. Eng. 1985, 111, 1139–1142. [Google Scholar] [CrossRef]
- Kong, L.W.; Tan, L.R. A simple method of determining the soil-water characteristic curve indirectly. In Proceedings of the Asian Conference on Unsaturated Soils, Singapore, 18–19 May 2000. [Google Scholar]
- Simms, P.H.; Yanful, E.K. Predicting soil-water characteristic curves of compacted plastic soils from measured pore size distributions. Géotechnique 2002, 52, 269–278. [Google Scholar] [CrossRef]
- Zhang, L.M.; Li, X. MicroPorosity Structure of Coarse Granular Soils. J. Geotech. Geoenviron. Eng. 2010, 136, 1425–1436. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Cui, Z.D. Effects of freezing-thawing and cyclic loading on pore size distribution of silty clay by mercury intrusion porosimetry. Cold Reg. Sci. Technol. 2018, 145, 185–196. [Google Scholar] [CrossRef]
- Zhang, J.R.; Tao, G.L.; Huang, L.; Yuan, L. Porosity models for determining the pore-size distribution of rocks and soils and their applications. Chin. Sci. Bull. 2010, 55, 3960–3970. [Google Scholar] [CrossRef]
- Tao, G.L.; Zhang, J.R. Two categories of fractal models of rock and soil expressing volume and size- distribution of pores and grains. Chin. Sci. Bull. 2009, 54, 4458–4467. [Google Scholar] [CrossRef]
- Tan, L.R.; Kong, L.W. Special Geotechnical Soil Science, 1st ed.; Science Press: Beijing, China, 2006. [Google Scholar]
- Zhao, M.H. Soil Mechanics and Foundation Engineering, 3rd ed.; Wuhan University Technology Press: Wuhan, China, 2009. [Google Scholar]
- Tao, G.L.; Zhu, X.L.; Hu, Q.Z.; Zhuang, X.S.; He, J.; Chen, Y. Critical pore-size phenomenon and intrinsic fractal characteristic of clay in the process of compression. Rock Soil Mech. 2019, 40, 81–90. [Google Scholar]
- Ghanbarian, B.; Hunt, A.G. Improving unsaturated hydraulic conductivity estimation in soils via percolation theory. Geoderma 2017, 303, 9–18. [Google Scholar] [CrossRef]
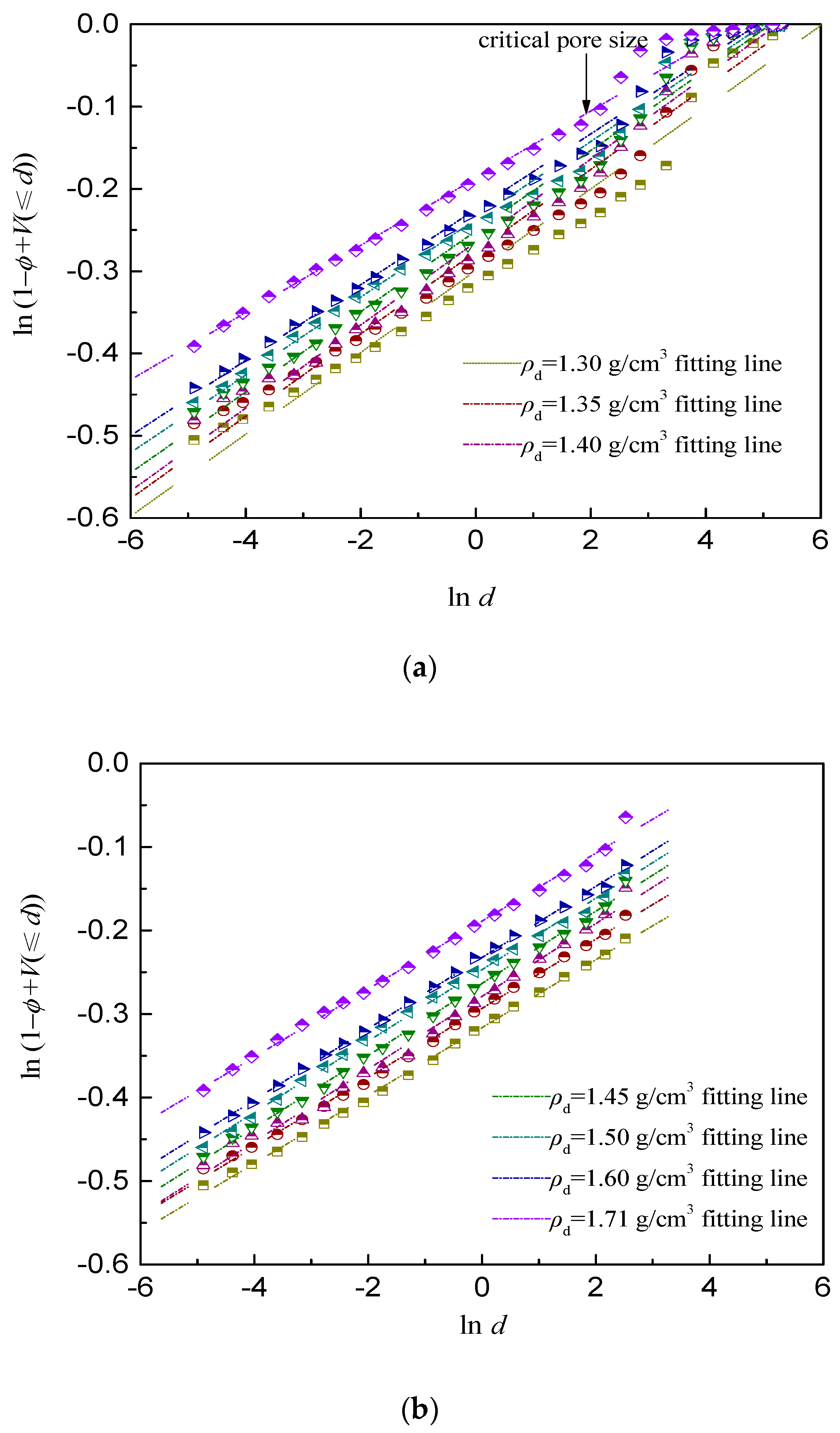
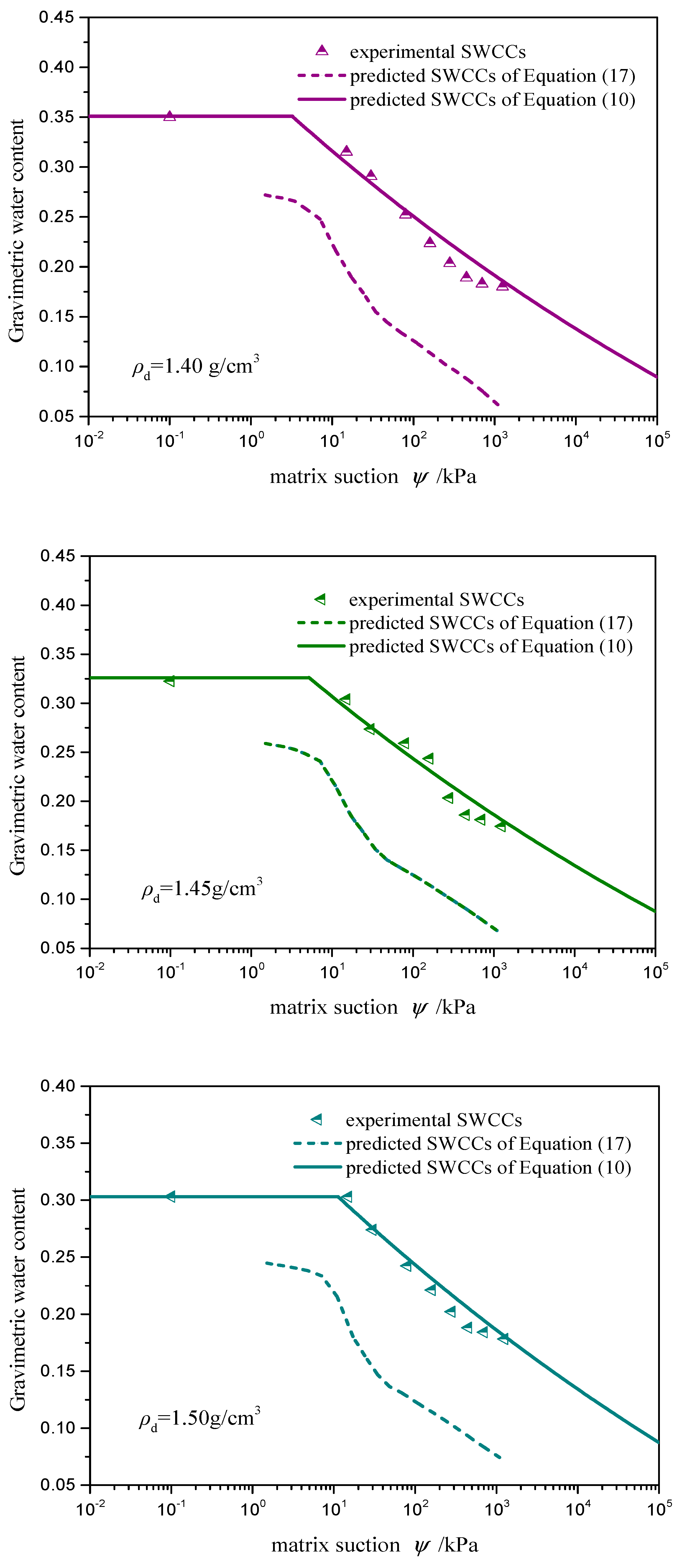
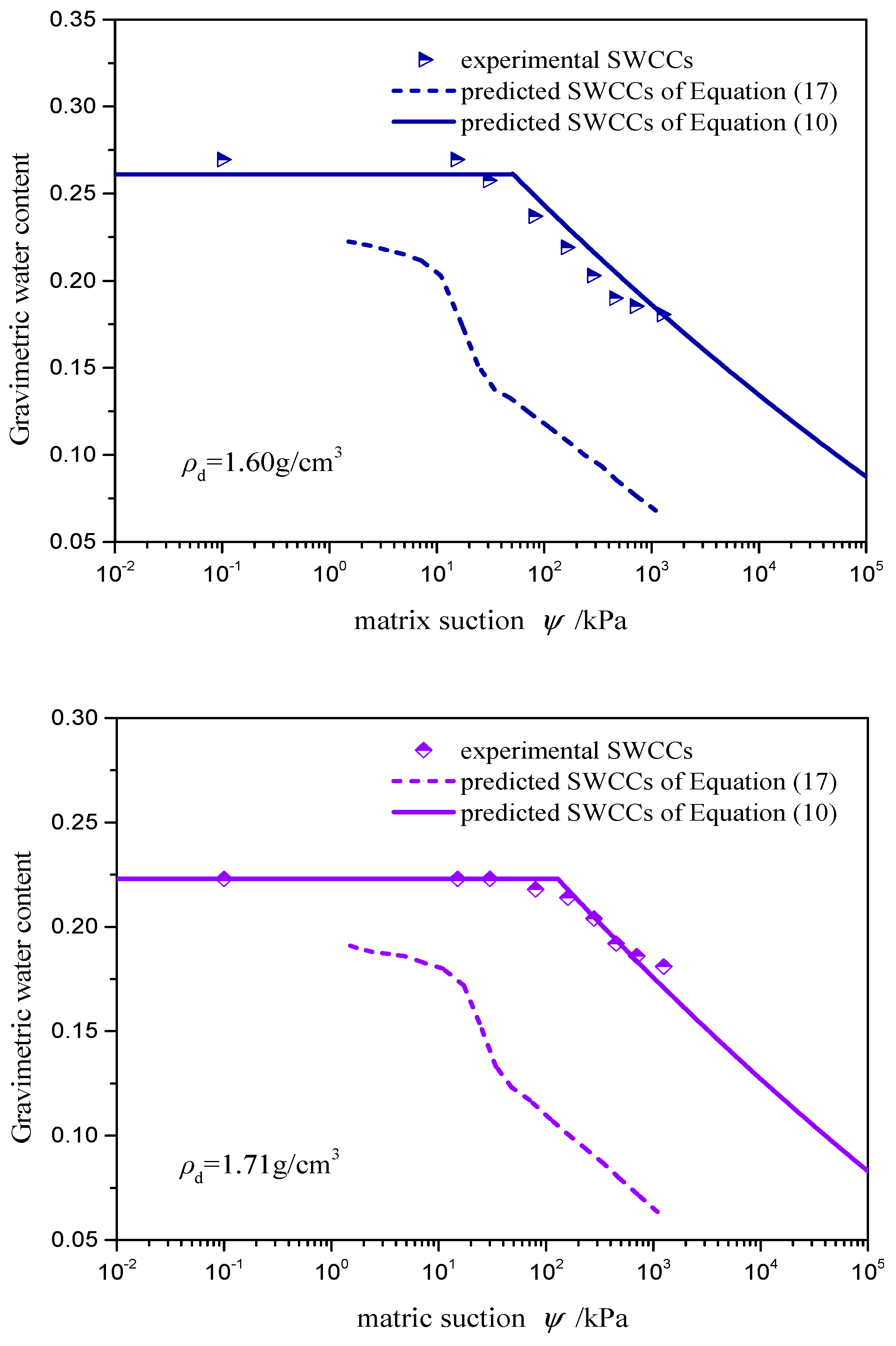
| Dry Density (g/cm3) | Expression of Fitting Line | Correlation Coefficient R2 | Fractal Dimension D |
|---|---|---|---|
| 1.30 | y = 0.050x − 0.299 | 0.985 | 2.950 |
| 1.35 | y = 0.050x − 0.276 | 0.989 | 2.950 |
| 1.40 | y = 0.050x − 0.265 | 0.991 | 2.950 |
| 1.45 | y = 0.049x − 0.251 | 0.994 | 2.951 |
| 1.50 | y = 0.047x − 0.237 | 0.994 | 2.953 |
| 1.60 | y = 0.046x − 0.225 | 0.995 | 2.954 |
| 1.71 | y = 0.041x − 0.187 | 0.994 | 2.959 |
| Dry Density (g/cm3) | Expression of Fitting Line | Correlation Coefficient R2 | Fractal Dimension D |
|---|---|---|---|
| 1.30 | y = 0.041x − 0.316 | 0.998 | 2.959 |
| 1.35 | y = 0.041x − 0.293 | 0.998 | 2.959 |
| 1.40 | y = 0.044x − 0.279 | 0.992 | 2.956 |
| 1.45 | y = 0.043x − 0.263 | 0.998 | 2.957 |
| 1.50 | y = 0.043x − 0.247 | 0.998 | 2.957 |
| 1.60 | y = 0.043x − 0.232 | 1 | 2.957 |
| 1.71 | y = 0.041x − 0.189 | 0.996 | 2.959 |
| Dry Density (g/cm3) | φ | dmax/(μm) | Ψa/(kPa) |
|---|---|---|---|
| 1.30 | 0.53 | 172,73 | 0.17 |
| 1.35 | 0.51 | 6880 | 0.44 |
| 1.40 | 0.49 | 922 | 3.25 |
| 1.45 | 0.47 | 583 | 5.15 |
| 1.50 | 0.45 | 265 | 11.33 |
| 1.60 | 0.42 | 59 | 50.82 |
| 1.71 | 0.38 | 23 | 129.56 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, G.; Chen, Y.; Xiao, H.; Chen, Q.; Wan, J. Determining Soil-Water Characteristic Curves from Mercury Intrusion Porosimeter Test Data Using Fractal Theory. Energies 2019, 12, 752. https://doi.org/10.3390/en12040752
Tao G, Chen Y, Xiao H, Chen Q, Wan J. Determining Soil-Water Characteristic Curves from Mercury Intrusion Porosimeter Test Data Using Fractal Theory. Energies. 2019; 12(4):752. https://doi.org/10.3390/en12040752
Chicago/Turabian StyleTao, Gaoliang, Yin Chen, Henglin Xiao, Qingsheng Chen, and Juan Wan. 2019. "Determining Soil-Water Characteristic Curves from Mercury Intrusion Porosimeter Test Data Using Fractal Theory" Energies 12, no. 4: 752. https://doi.org/10.3390/en12040752
APA StyleTao, G., Chen, Y., Xiao, H., Chen, Q., & Wan, J. (2019). Determining Soil-Water Characteristic Curves from Mercury Intrusion Porosimeter Test Data Using Fractal Theory. Energies, 12(4), 752. https://doi.org/10.3390/en12040752






