Effect of Salts on Interfacial Tension and CO2 Mass Transfer in Carbonated Water Injection
Abstract
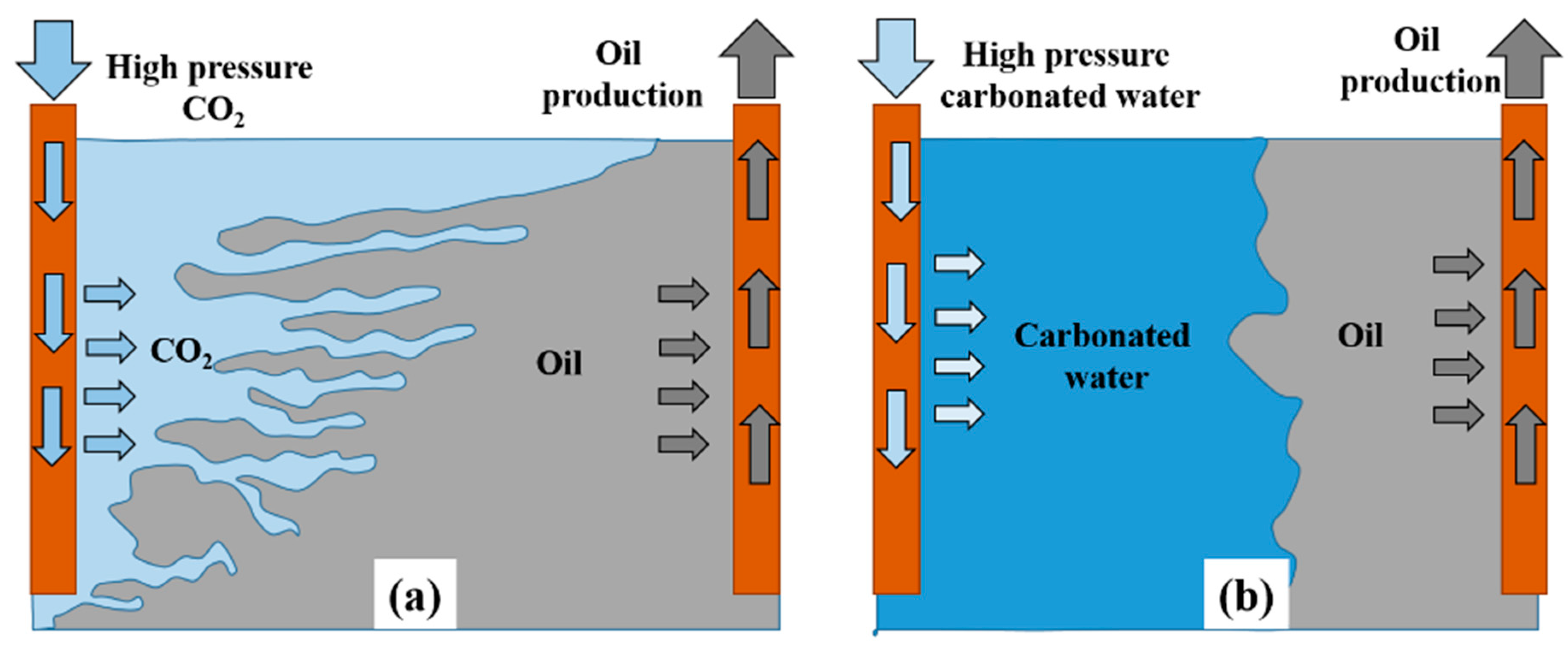
1. Introduction
2. Experimental and Numerical Study
2.1. Materials
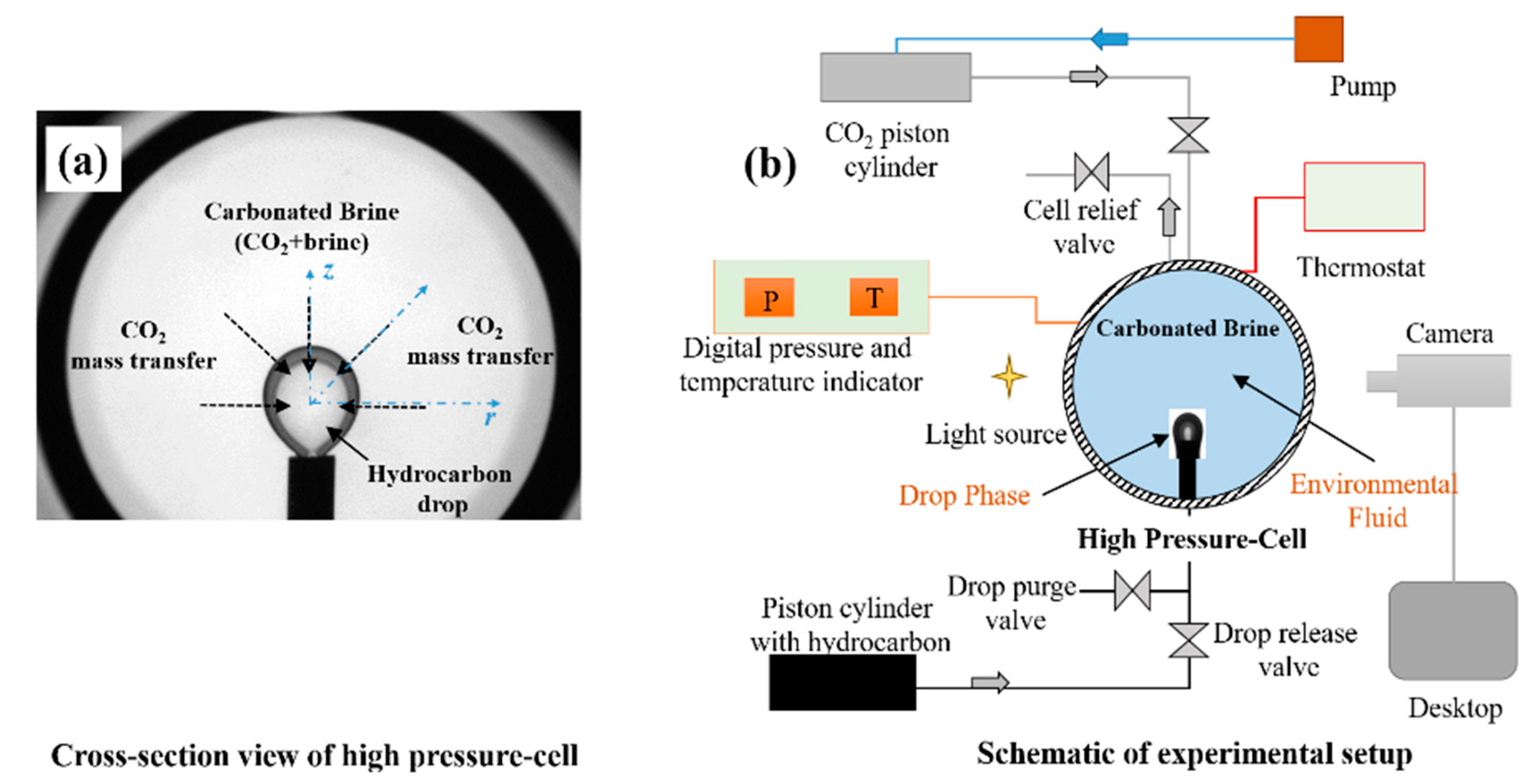
2.2. Experimental Setup and Procedure
2.3. IFT Measurement
2.4. Diffusion Coefficient Measurement
2.4.1. Mathematical Model
3.4.2. Numerical Model
2.4.3. Dynamic Interface (Boundary) Method
3. Results and Conclusions
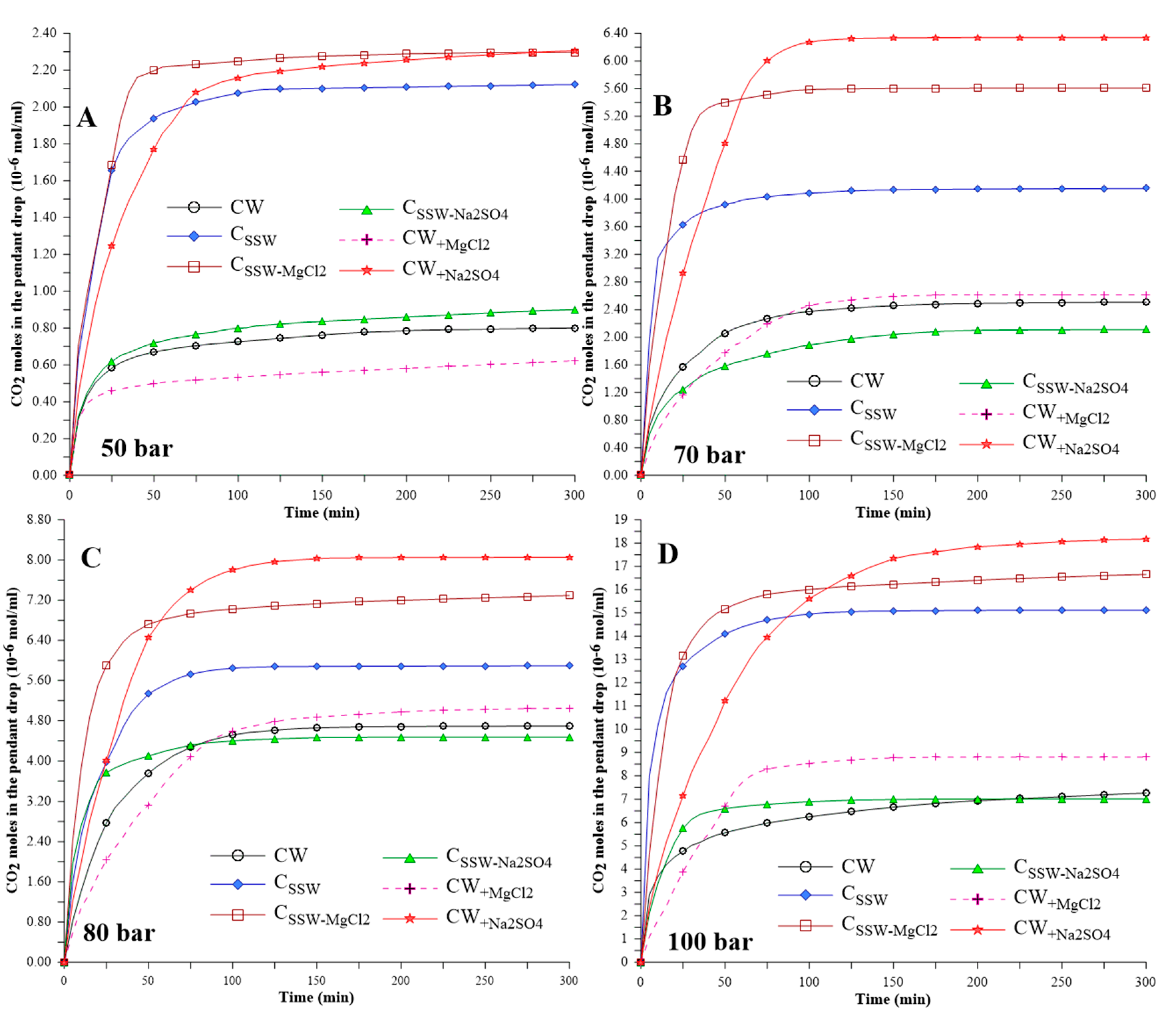
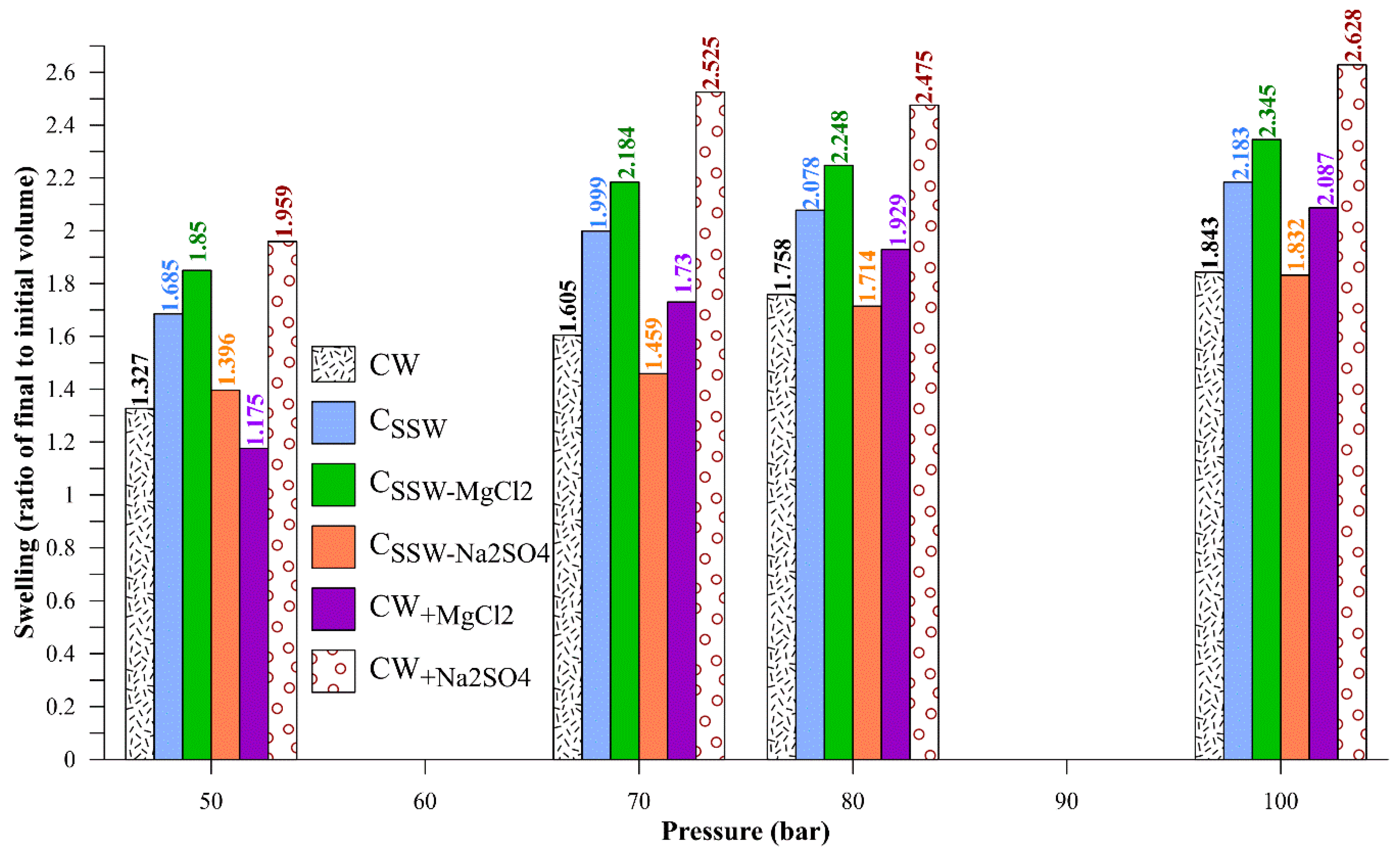
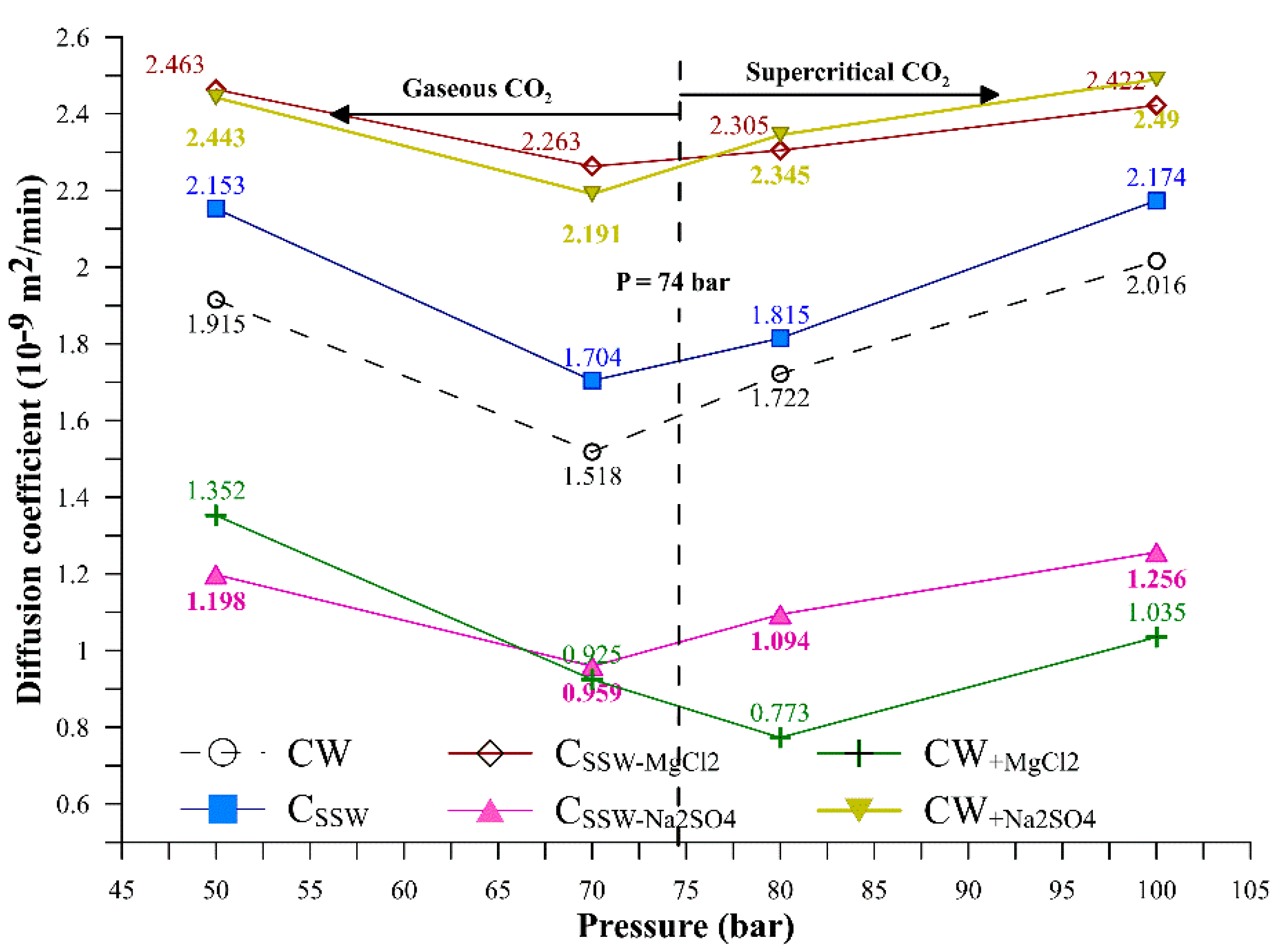
3.1. Swelling and Diffusion Coefficient
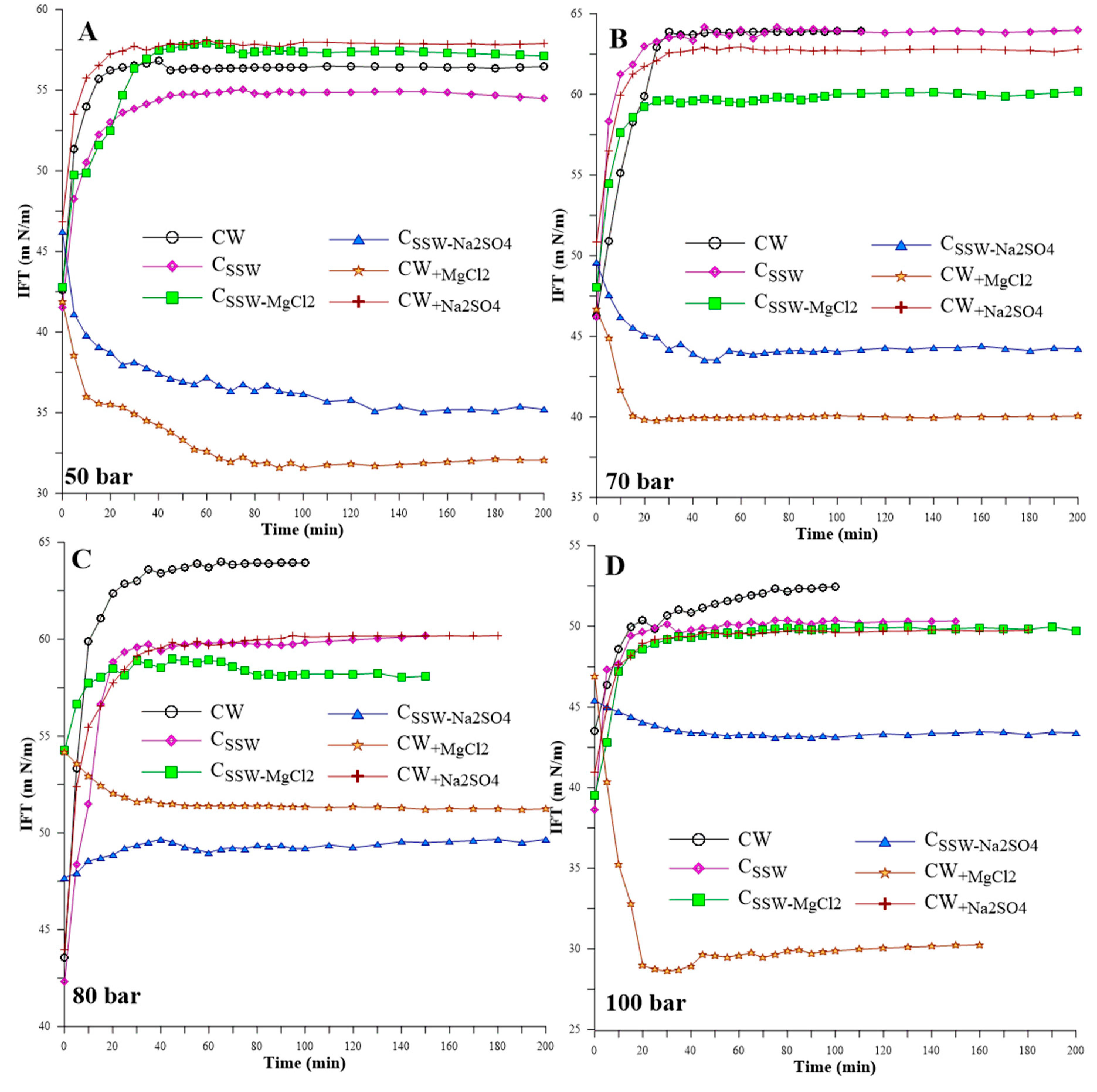
3.2. IFT
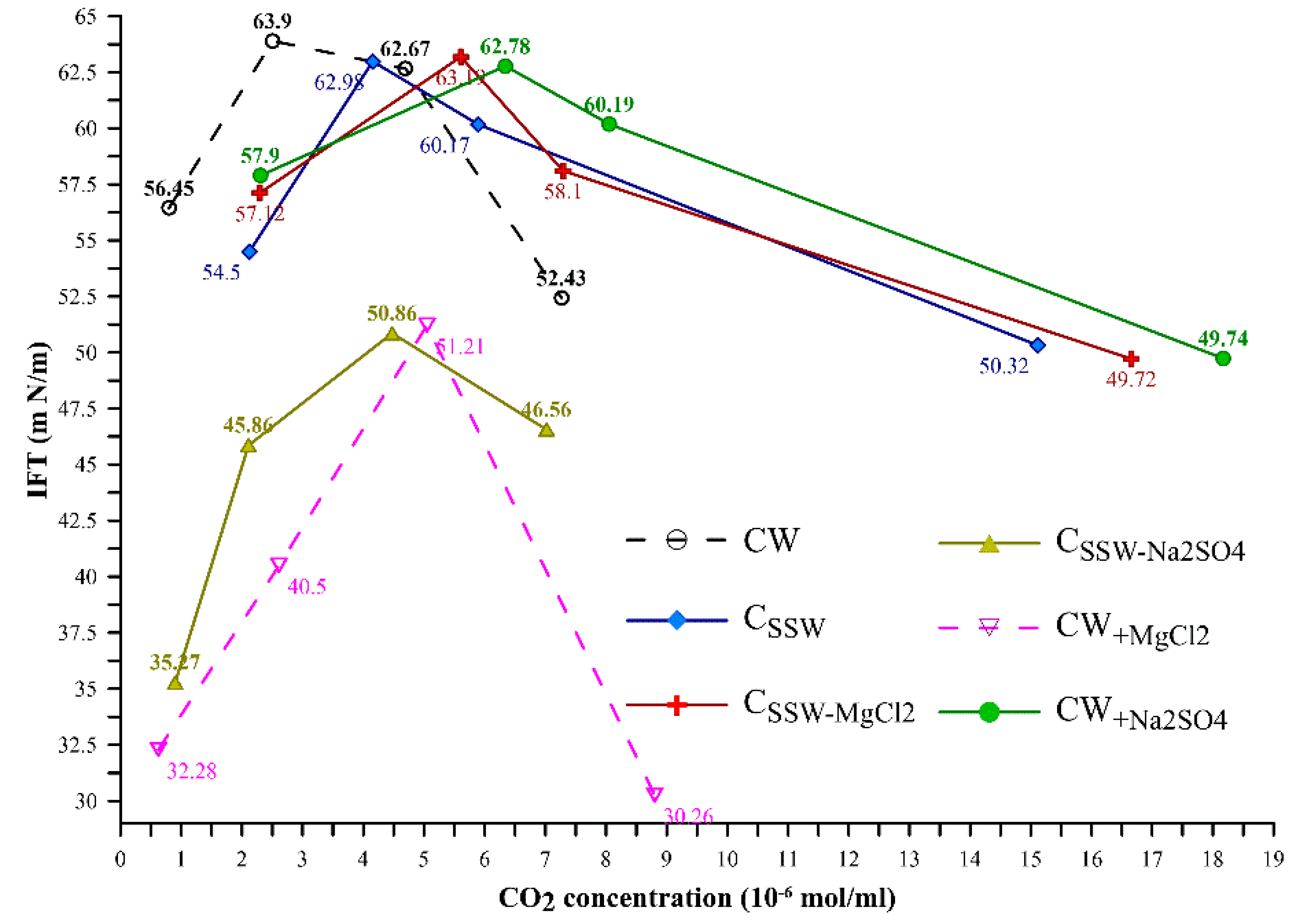
3.3. IFT and Concentration of Transferred CO2 into n-Decane
3.4. Interfacial Adsorption Isotherm (Surface Excess)
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Riazi, M.; Sohrabi, M.; Jamiolahmady, M.; Ireland, S. Oil recovery improvement using CO2-enriched water injection. In Proceedings of the 2009 EUROPEC/EAGE Conference and Exhibition, Amsterdam, The Netherlands, 8–11 June 2009. [Google Scholar]
- Esene, C.; Rezaei, N.; Aborig, A.; Zendehboudi, S. Comprehensive review of carbonated water injection for enhanced oil recovery. Fuel 2019, 237, 1086–1107. [Google Scholar] [CrossRef]
- Kechut, N.I.; Sohrabi, M.; Jamiolahmady, M. Experimental and numerical evaluation of carbonated water injection (cwi) for improved oil recovery and CO2 storage. In Proceedings of the 2011 SPE EUROPEC/EAGE Annual Conference and Exhibition, Vienna, Austria, 23–26 May 2011. [Google Scholar]
- Riazi, M.; Sohrabi, M.; Jamiolahmady, M. Experimental study of pore-scale mechanisms of carbonated water injection. Transp. Porous Media 2011, 86, 73–86. [Google Scholar] [CrossRef]
- Dejam, M.; Hassanzadeh, H. Diffusive leakage of brine from aquifers during CO2 geological storage. Adv. Water Resour. 2018, 111, 36–57. [Google Scholar] [CrossRef]
- Dejam, M.; Hassanzadeh, H. The role of natural fractures of finite double-porosity aquifers on diffusive leakage of brine during geological storage of CO2. Int. J. Greenh. Gas Control 2018, 78, 177–197. [Google Scholar] [CrossRef]
- Nowrouzi, I.; Manshad, A.K.; Mohammadi, A.H. Effects of dissolved binary ionic compounds and different densities of brine on interfacial tension (ift), wettability alteration, and contact angle in smart water and carbonated smart water injection processes in carbonate oil reservoirs. J. Mol. Liquids 2018, 254, 83–92. [Google Scholar] [CrossRef]
- Mashayekhizadeh, V.; Kord, S.; Dejam, M. Eor potential within iran. Spec. Top. Rev. Porous Media Int. J. 2014, 5, 325–354. [Google Scholar] [CrossRef]
- Gomari, K.R.; Hamouda, A. Effect of fatty acids, water composition and ph on the wettability alteration of calcite surface. J. Pet. Sci. Eng. 2006, 50, 140–150. [Google Scholar] [CrossRef]
- Zhang, P.; Tweheyo, M.T.; Austad, T. Wettability alteration and improved oil recovery by spontaneous imbibition of seawater into chalk: Impact of the potential determining ions Ca2+, Mg2+, and SO42−. Colloids Surf. A Physicochem. Eng. Asp. 2007, 301, 199–208. [Google Scholar] [CrossRef]
- Manshad, A.K.; Nowrouzi, I.; Mohammadi, A.H. Effects of water soluble ions on wettability alteration and contact angle in smart and carbonated smart water injection process in oil reservoirs. J. Mol. Liquids 2017, 244, 440–452. [Google Scholar] [CrossRef]
- Hamouda, A.A.; Rezaei Gomari, K.A. Influence of temperature on wettability alteration of carbonate reservoirs. In Proceedings of the 2006 SPE/DOE Symposium on Improved Oil Recovery, Tulsa, OK, USA, 22–26 April 2006. [Google Scholar]
- Cai, B.-Y.; Yang, J.-T.; Guo, T.-M. Interfacial tension of hydrocarbon+ water/brine systems under high pressure. J. Chem. Eng. Data 1996, 41, 493–496. [Google Scholar] [CrossRef]
- Lashkarbolooki, M.; Ayatollahi, S. Investigation of ionic liquids based on pyridinium and imidazolium as interfacial tension reducer of crude oil-water and their synergism with mgcl2. J. Pet. Sci. Eng. 2018, 171, 414–421. [Google Scholar] [CrossRef]
- Manshad, A.K.; Olad, M.; Taghipour, S.A.; Nowrouzi, I.; Mohammadi, A.H. Effects of water soluble ions on interfacial tension (ift) between oil and brine in smart and carbonated smart water injection process in oil reservoirs. J. Mol. Liquids 2016, 223, 987–993. [Google Scholar] [CrossRef]
- Serrano-Saldaña, E.; Domínguez-Ortiz, A.; Pérez-Aguilar, H.; Kornhauser-Strauss, I.; Rojas-González, F. Wettability of solid/brine/n-dodecane systems: Experimental study of the effects of ionic strength and surfactant concentration. Colloids Surf. A Physicochem. Eng. Asp. 2004, 241, 343–349. [Google Scholar] [CrossRef]
- Ikeda, N.; Aratono, M.; Motomura, K. Thermodynamic study on the adsorption of sodium chloride at the water/hexane interface. J. Colloid Interface Sci. 1992, 149, 208–215. [Google Scholar] [CrossRef]
- Aveyard, R.; Saleem, S.M. Interfacial tensions at alkane-aqueous electrolyte interfaces. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases 1976, 72, 1609–1617. [Google Scholar] [CrossRef]
- Lashkarbolooki, M.; Ayatollahi, S.; Riazi, M. The impacts of aqueous ions on interfacial tension and wettability of an asphaltenic–acidic crude oil reservoir during smart water injection. J. Chem. Eng. Data 2014, 59, 3624–3634. [Google Scholar] [CrossRef]
- Hosseini, S.; Shuker, M.; Hosseini, Z.; Tomocene, T.J.; Shabib-Asl, A.; Sabet, M. The role of salinity and brine ions in interfacial tension reduction while using surfactant for enhanced oil recovery. Res. J. Appl. Sci. Eng. Technol. 2015, 9, 722–726. [Google Scholar] [CrossRef]
- Badakshan, A.; Bakes, P. The Influence of Temperature and Surfactant Concentration on Interfacial Tension of Saline Water and Hydrocarbon Systems in Relation to Enhanced Oil Recovery by Chemical Flooding; Society of Petroleum Engineers: Richardson, TX, USA, 1990. [Google Scholar]
- Isdahl, O.M. Influence of Silica Based Nanofluid on the Physical Properties, Ift, and CO2 Diffusion in a Carbonated Water-n-Decane System: An Experimental and Numerical Study; University of Stavanger: Stavanger, Norway, 2017. [Google Scholar]
- Perera, M.; Gamage, R.; Rathnaweera, T.; Ranathunga, A.; Koay, A.; Choi, X. A review of CO2-enhanced oil recovery with a simulated sensitivity analysis. Energies 2016, 9, 481. [Google Scholar] [CrossRef]
- Shi, Y.; Zheng, S.; Yang, D. Determination of individual diffusion coefficients of alkane solvent (s)–CO2–heavy oil systems with consideration of natural convection induced by swelling effect. Int. J. Heat Mass Transf. 2017, 107, 572–585. [Google Scholar] [CrossRef]
- Yang, D.; Gu, Y. Determination of diffusion coefficients and interface mass-transfer coefficients of the crude oil−CO2 system by analysis of the dynamic and equilibrium interfacial tensions. Ind. Eng. Chem. Res. 2008, 47, 5447–5455. [Google Scholar] [CrossRef]
- Yang, C.; Gu, Y. New experimental method for measuring gas diffusivity in heavy oil by the dynamic pendant drop volume analysis (dpdva). Ind. Eng. Chem. Res. 2005, 44, 4474–4483. [Google Scholar] [CrossRef]
- Yang, D.; Tontiwachwuthikul, P.; Gu, Y. Dynamic interfacial tension method for measuring gas diffusion coefficient and interface mass transfer coefficient in a liquid. Ind. Eng. Chem. Res. 2006, 45, 4999–5008. [Google Scholar] [CrossRef]
- Bagalkot, N.; Hamouda, A.A. Diffusion coefficient of CO2 into light hydrocarbons and interfacial tension of carbonated water–hydrocarbon system. J. Geophys. Eng. 2018, 15, 2516. [Google Scholar] [CrossRef]
- Zhu, H.; Shanks, B.H.; Heindel, T.J. Effect of electrolytes on co−water mass transfer. Ind. Eng. Chem. Res. 2009, 48, 3206–3210. [Google Scholar] [CrossRef]
- Collins, K.D. Charge density-dependent strength of hydration and biological structure. Biophys. J. 1997, 72, 65–76. [Google Scholar] [CrossRef]
- Nguyen, T.; Ali, S. Effect of nitrogen on the solubility and diffusivity of carbon dioxide into oil and oil recovery by the immiscible wag process. J. Can. Pet. Technol. 1998, 37. [Google Scholar] [CrossRef]
- Sigmund, P.M. Prediction of molecular diffusion at reservoir conditions. Part 1-measurement and prediction of binary dense gas diffusion coefficients. J. Can. Pet. Technol. 1976, 15. [Google Scholar] [CrossRef]
- Upreti, S.R.; Mehrotra, A.K. Diffusivity of CO2, CH4, C2H6 and N2 in athabasca bitumen. Can. J. Chem. Eng. 2002, 80, 116–125. [Google Scholar] [CrossRef]
- Sheikha, H.; Pooladi-Darvish, M.; Mehrotra, A.K. Development of graphical methods for estimating the diffusivity coefficient of gases in bitumen from pressure-decay data. Energy Fuels 2005, 19, 2041–2049. [Google Scholar] [CrossRef]
- Riazi, M.R. A new method for experimental measurement of diffusion coefficients in reservoir fluids. J. Pet. Sci. Eng. 1996, 14, 235–250. [Google Scholar] [CrossRef]
- Bagalkot, N.; Hamouda, A.A. Experimental and numerical method for estimating diffusion coefficient of the carbon dioxide into light components. Ind. Eng. Chem. Res. 2017, 56, 2359–2374. [Google Scholar] [CrossRef]
- Yang, D.; Tontiwachwuthikul, P.; Gu, Y. Interfacial tensions of the crude oil+ reservoir brine+ CO2 systems at pressures up to 31 MPa and temperatures of 27 °C and 58 °C. J. Chem. Eng. Data 2005, 50, 1242–1249. [Google Scholar] [CrossRef]
- Ghorbani, M.; Mohammadi, A.H. Effects of temperature, pressure and fluid composition on hydrocarbon gas-oil interfacial tension (ift): An experimental study using adsa image analysis of pendant drop test method. J. Mol. Liquids 2017, 227, 318–323. [Google Scholar] [CrossRef]
- Hamouda, A.A.; Maevskiy, E. Oil recovery mechanism (s) by low salinity brines and their interaction with chalk. Energy Fuels 2014, 28, 6860–6868. [Google Scholar] [CrossRef]
- Lemmon, E.; McLinden, M.; Friend, D.; Linstrom, P.; Mallard, W. Nist Chemistry Webbook, Nist Standard Reference Database Number 69; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2011.
- Duan, Z.; Sun, R. An improved model calculating CO2 solubility in pure water and aqueous nacl solutions from 273 to 533 k and from 0 to 2000 bar. Chem. Geol. 2003, 193, 257–271. [Google Scholar] [CrossRef]
- Bagalkot, N.; Hamouda, A.A.; Isdahl, O.M. Dynamic interfacial tension measurement method using axisymmetric drop shape analysis. MethodsX 2018, 5, 676–683. [Google Scholar] [CrossRef] [PubMed]
- Gmb, K. Drop Shape Analyzer—dsa100 hp. Available online: https://www.kruss-scientific.com/fileadmin/user_upload/website/brochures/kruss-techdata-dsa100hp-en.pdf (accessed on 29 May 2018).
- Jaeger, P.T.; Eggers, R. Interfacial properties at elevated pressures in reservoir systems containing compressed or supercritical carbon dioxide. J. Supercrit. Fluids 2012, 66, 80–85. [Google Scholar] [CrossRef]
- Bagalkot, N.; Hamouda, A.A. Interfacial tension and CO2 diffusion coefficients for a CO2+ water and n-decane system at pressures of 10 to 160 bar. RSC Adv. 2018, 8, 38351–38362. [Google Scholar] [CrossRef]
- Jamialahmadi, M.; Emadi, M.; Müller-Steinhagen, H. Diffusion coefficients of methane in liquid hydrocarbons at high pressure and temperature. J. Pet. Sci. Eng. 2006, 53, 47–60. [Google Scholar] [CrossRef]
- Yang, C.; Gu, Y. Diffusion coefficients and oil swelling factors of carbon dioxide, methane, ethane, propane, and their mixtures in heavy oil. Fluid Phase Equilib. 2006, 243, 64–73. [Google Scholar] [CrossRef]
- Zeppieri, S.; Rodríguez, J.; López de Ramos, A. Interfacial tension of alkane+ water systems. J. Chem. Eng. Data 2001, 46, 1086–1088. [Google Scholar] [CrossRef]
- Brandal, Ø.; Sjöblom, J.; Øye, G. Interfacial behavior of naphthenic acids and multivalent cations in systems with oil and water. I. A pendant drop study of interactions between n-dodecyl benzoic acid and divalent cations. J. Dispers. Sci. Technol. 2004, 25, 367–374. [Google Scholar] [CrossRef]
- Garrels, R.; Thompson, M. A chemical model for sea water at 25 °C and one atmosphere total pressure. Am. J. Sci. 1962, 260, 57–66. [Google Scholar] [CrossRef]
- O’Brien, J.T.; Prell, J.S.; Bush, M.F.; Williams, E.R. Sulfate ion patterns water at long distance. J. Am. Chem. Soc. 2010, 132, 8248–8249. [Google Scholar] [CrossRef] [PubMed]
| References | Type of Aqueous Systems | Experimental Conditions | Observations |
|---|---|---|---|
| Reduction in IFT | |||
| Gomari and Hamouda [9] | n-decane/brine with MgCl2 and Na2SO4 | 82.4 to 158 °C, atmospheric pressure | IFT reduction in the presence of MgCl2 and Na2SO4 compared to distilled water |
| Serrano-Saldaña, et al. [16] | n-dodecane/brine with sodium dodecyl sulfate (SDS) and NaCl | 25 °C, atmospheric pressure | The presence and rising surfactant concentration leads to a reduction in the IFT |
| Hosseini, et al. [20] | Crude oil/brine with Na+, K+, Cl, Mg2+, and Ca2+ ions | 25 °C, atmospheric pressure | The presence of divalent ions (Ca2+ and Mg2+) decreases the oil/brine IFT. At a given concentration Mg2+ shows a lower oil/brine IFT than Ca2+ |
| Increment in IFT | |||
| Ikeda, et al. [17] | n-hexane/water with NaCl | 25 °C, 0 to 100 Mpa | Increment in IFT due to the presence of NaCl in water |
| Cai, et al. [13] | normal alkane + water/brine with NaCl, CaCl2, MgCl2 | 25 to 80 °C,1 to 300 bar | Increase in IFT due to the presence of salt. Weakly dependent on pressure and salt species |
| Badakshan and Bakes [21] | Toluene, n-hexane and cyclohexane/brine with NaCl, NaHCO3, Na2SO4 | 20 °C to 75 °C, atmospheric pressure | For all the salts an increment in IFT was observed |
| Salt-dependent IFT variation | |||
| Lashkarbolooki, et al. [19] | Crude oil/brine with NaCl, KCl, Na2SO4, MgSO4, CaSO4, CaCl2, and MgCl2 | Ambient temperature and pressure | Reduction in IFT at high salinity conditions especially for MgCl2. The increment in IFT for monovalent salts such as NaCl and KCl is used |
| Aveyard and Saleem [18] | n-dodecane-decane/brine with LiCl, NaCl, KCl, KBr, NaBr, KI, and Na2SO4 | 20 °C, atmospheric pressure | Reduction in IFT in the presence of KI. An increment in IFT for rest of the salts |
| IFT of carbonated brine/hydrocarbon system | |||
| Manshad, et al. [15] | Crude oil/carbonated water with NaCl, CaCl2, MgCl2, KCl, and Na2SO4 | 75 °C, pressure up to 137 bar | Presence of salt reduces the IFT and is a function of the type of salt |
| Nowrouzi, et al. [7] | Crude oil/ carbonated brine with NaCl, CaCl2, MgCl2, KCl, MgSO4, K2SO4, and Na2SO4 | 75 °C, up to 140 bar | Salts are able to reduce the IFT. Addition of CO2 further enhances the reduction in IFT. Minimum IFT was obtained for MgCl2+K2SO4 combination |
| Isdahl [21] | n-decane/ carbonated synthetic sea water with silica nanofluid | 25 °C and 45 °C, 10 to 90 bar | Marginal reduction in IFT for the combination of salt and CO2 in water |
| Brine | Composition (g/L) | Purpose | |||||
|---|---|---|---|---|---|---|---|
| NaCl | MgCl2 *6H2O | Na2SO4 | CaCl2 *2H2O | KCl | NaHCO3 | ||
| SSW | 23.38 | 9.05 | 3.41 | 1.91 | 0.75 | 0.17 | Combination of salts on CO2 mass transfer and IFT |
| SSW-MgCl2 | 23.38 | 0 | 3.41 | 1.91 | 0.75 | 0.17 | Combination of salts in the absence of Magnesium on IFT and CO2 mass transfer |
| SSW-Na2SO4 | 23.38 | 9.05 | 0 | 1.91 | 0.75 | 0.17 | Combination of salts in the absence of Sulfate on IFT and CO2 mass transfer |
| DIW+MgCl2 | 0 | 9.05 | 0 | 0 | 0 | 0 | Magnesium on CO2 mass transfer and IFT |
| DIW+NaSO4 | 0 | 0 | 3.41 | 0 | 0 | 0 | Sulfate on CO2 mass transfer and IFT |
| Pressure (bar) | IFT (mN/m) | |||||
| CW | CSSW | CSSW-MgCl2 | CSSW-Na2SO4 | CW+MgCl2 | CW+Na2SO4 | |
| 1 | 50.13 | 43.18 | 51.19 | 31.09 | 31.82 | 52.58 |
| 50 | 56.45 | 54.35 | 57.31 | 35.26 | 32.28 | 57.95 |
| 70 | 63.90 | 63.80 | 67.50 | 47.85 | 40.5 | 62.75 |
| 80 | 62.67 | 60.49 | 58.14 | 50.85 | 51.97 | 60.18 |
| 100 | 52.43 | 50.46 | 49.56 | 46.56 | 30.26 | 49.73 |
| Pressure (bar) | pH | |||||
| CW | CSSW | CSSW-MgCl2 | CSSW-Na2SO4 | CW+MgCl2 | CW+Na2SO4 | |
| 1 | 7.00 | 6.97 | 7.02 | 6.61 | 6.57 | 7.13 |
| 50 | 3.24 | 3.27 | 3.25 | 3.15 | 3.19 | 3.37 |
| 70 | 3.2 | 3.22 | 3.21 | 3.1 | 3.14 | 3.33 |
| 80 | 3.18 | 3.21 | 3.19 | 3.09 | 3.13 | 3.31 |
| 100 | 3.17 | 3.19 | 3.18 | 3.07 | 3.11 | 3.30 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamouda, A.A.; Bagalkot, N. Effect of Salts on Interfacial Tension and CO2 Mass Transfer in Carbonated Water Injection. Energies 2019, 12, 748. https://doi.org/10.3390/en12040748
Hamouda AA, Bagalkot N. Effect of Salts on Interfacial Tension and CO2 Mass Transfer in Carbonated Water Injection. Energies. 2019; 12(4):748. https://doi.org/10.3390/en12040748
Chicago/Turabian StyleHamouda, Aly A, and Nikhil Bagalkot. 2019. "Effect of Salts on Interfacial Tension and CO2 Mass Transfer in Carbonated Water Injection" Energies 12, no. 4: 748. https://doi.org/10.3390/en12040748
APA StyleHamouda, A. A., & Bagalkot, N. (2019). Effect of Salts on Interfacial Tension and CO2 Mass Transfer in Carbonated Water Injection. Energies, 12(4), 748. https://doi.org/10.3390/en12040748






