Implementation of Open Boundaries within a Two-Way Coupled SPH Model to Simulate Nonlinear Wave–Structure Interactions
Abstract
1. Introduction
- Accurate wave generation and wave absorption through coupling an SPH solver to an FNPF solver using the open boundary formulation by Tafuni et al. [24],
- Having an online exchange of information in two directions between the SPH solver and the FNPF solver.
2. Smoothed Particle Hydrodynamics
2.1. SPH Fundamentals
2.2. Governing Equations
2.3. Delta-SPH Formulation
3. Boundary Conditions in DualSPHysics
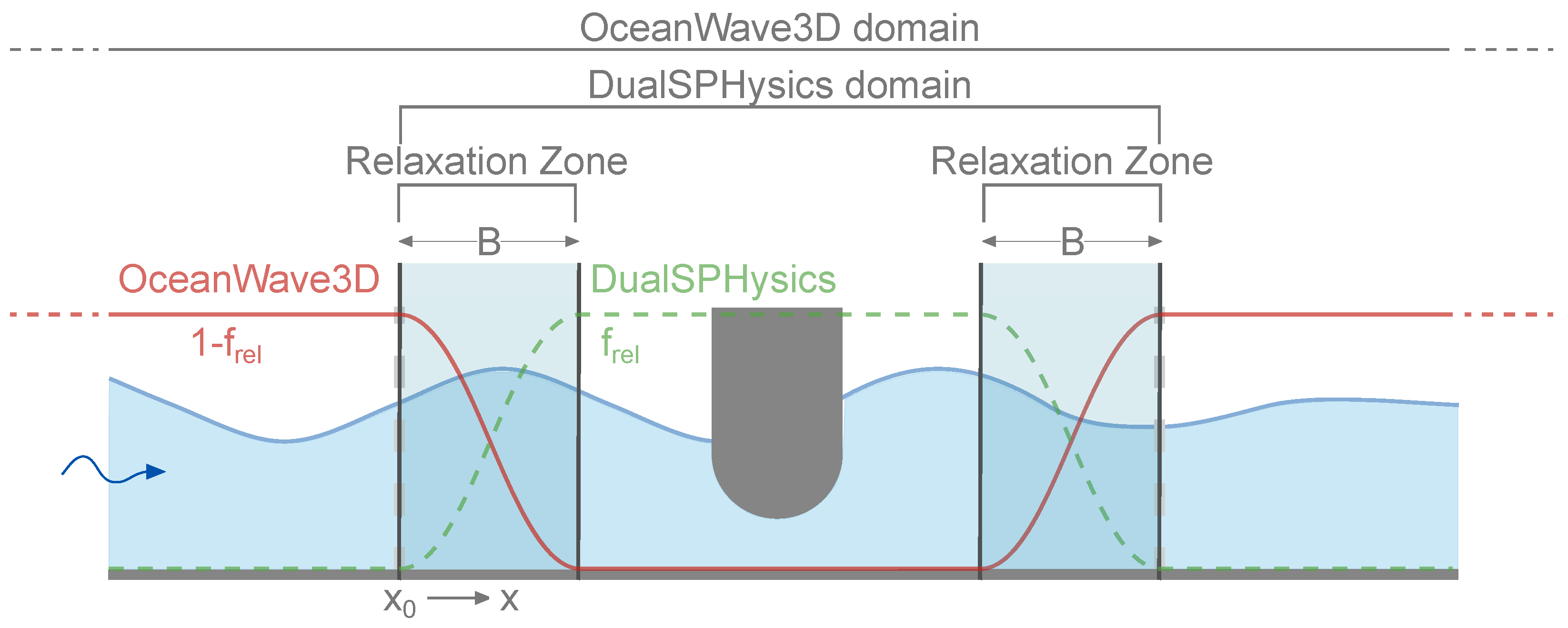
3.1. Open Boundary Conditions
3.2. Fixed Boundary Condition with Pressure Correction
3.3. Comparison to the State-of-the-Art
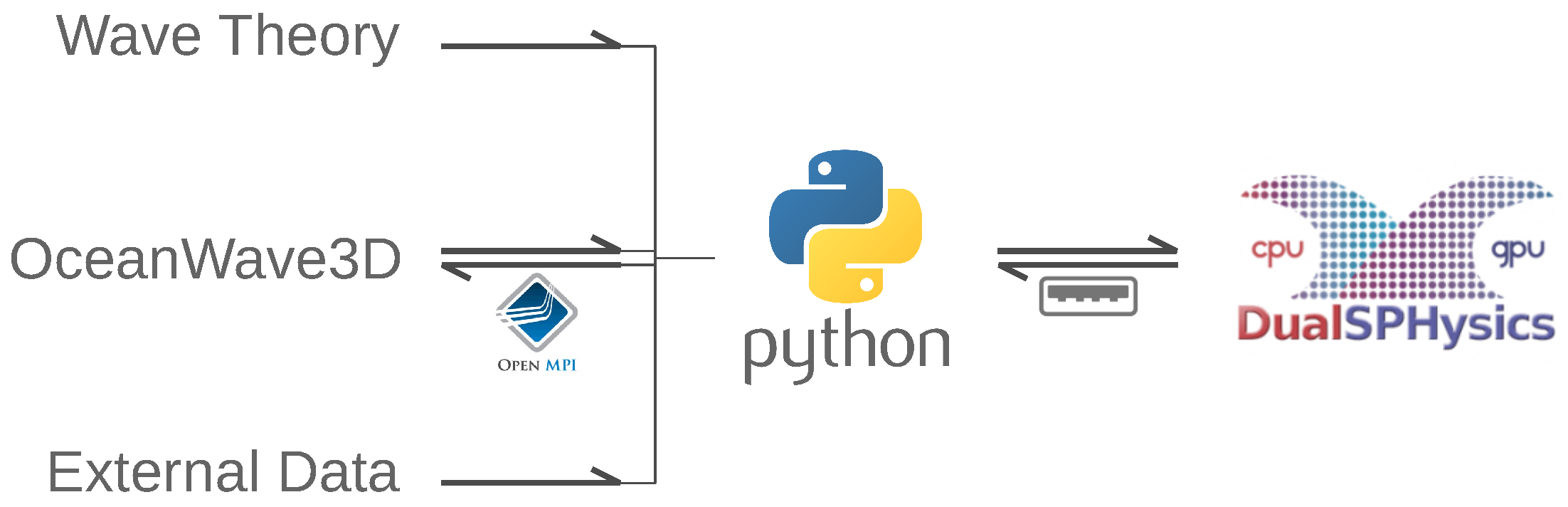
4. Coupling Methodology Using DualSPHysics and OceanWave3D
4.1. Inlet Velocity Correction
4.2. Outlet Velocity Correction
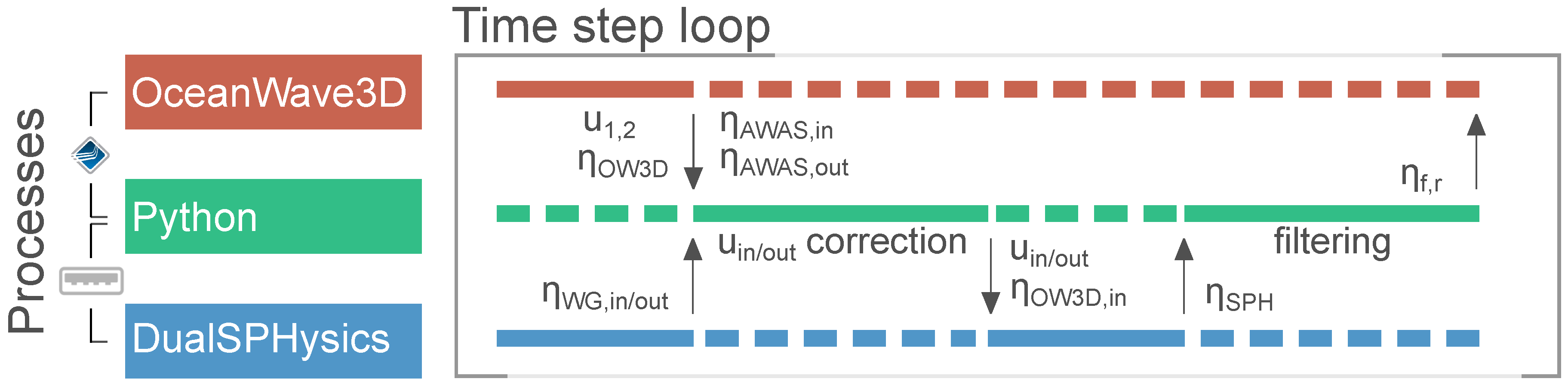
4.3. Coupling Algorithm
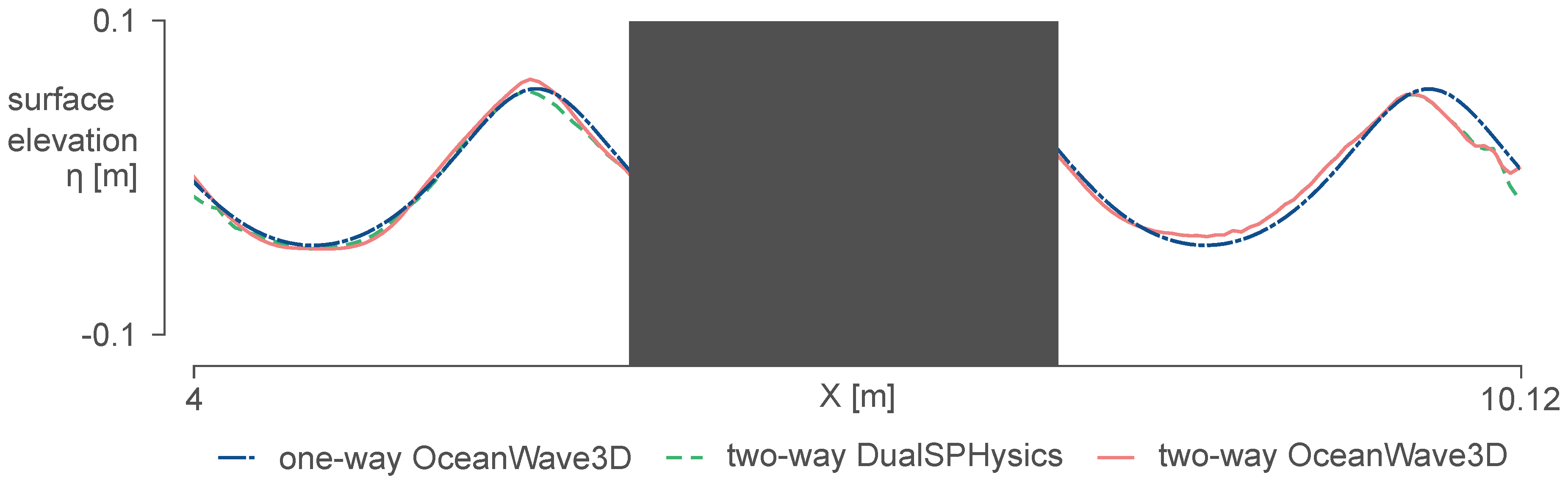
5. 2D Coupled Model: Validation
5.1. DualSPHysics Solver Options
5.2. Results and Discussion
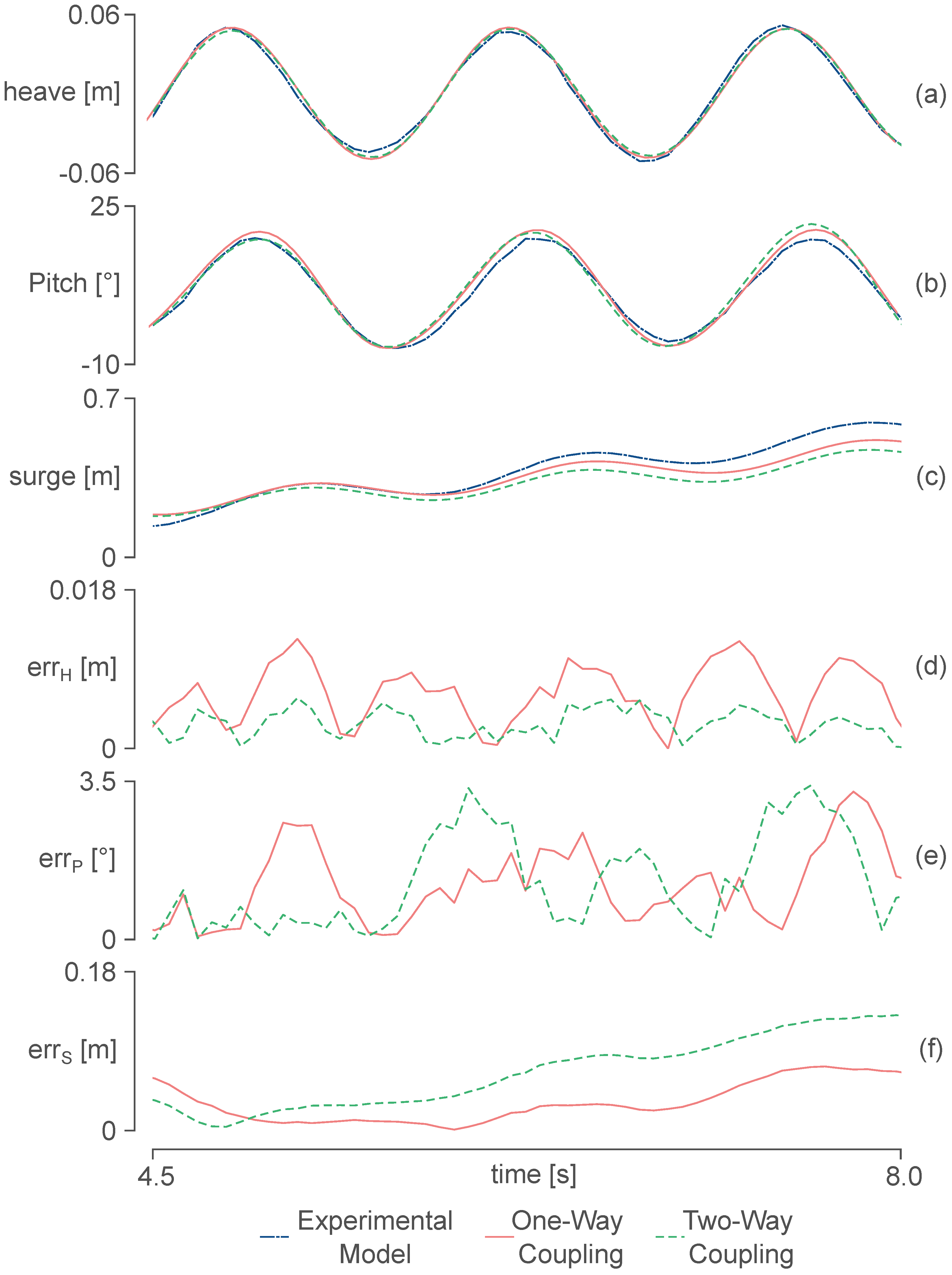
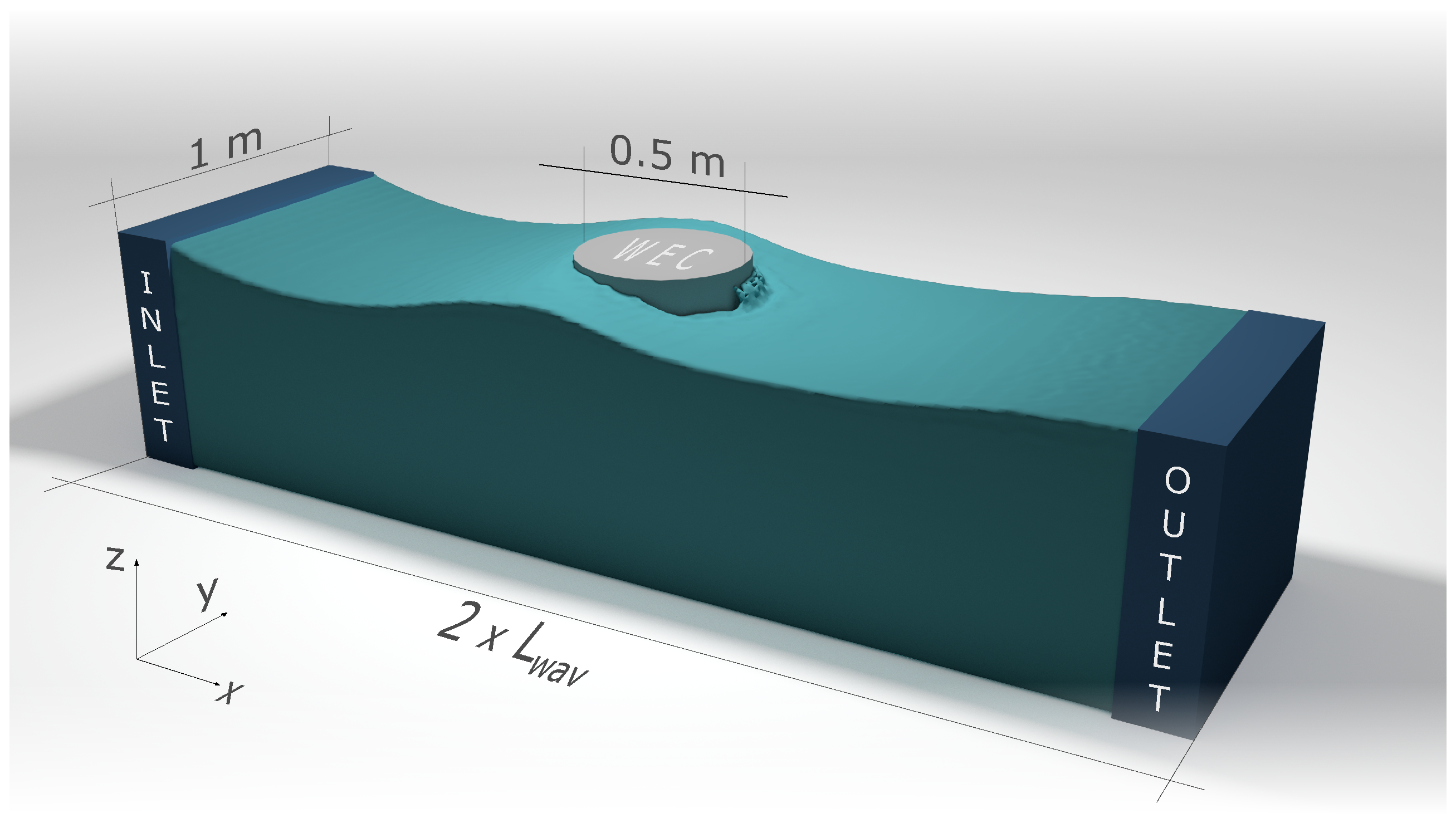
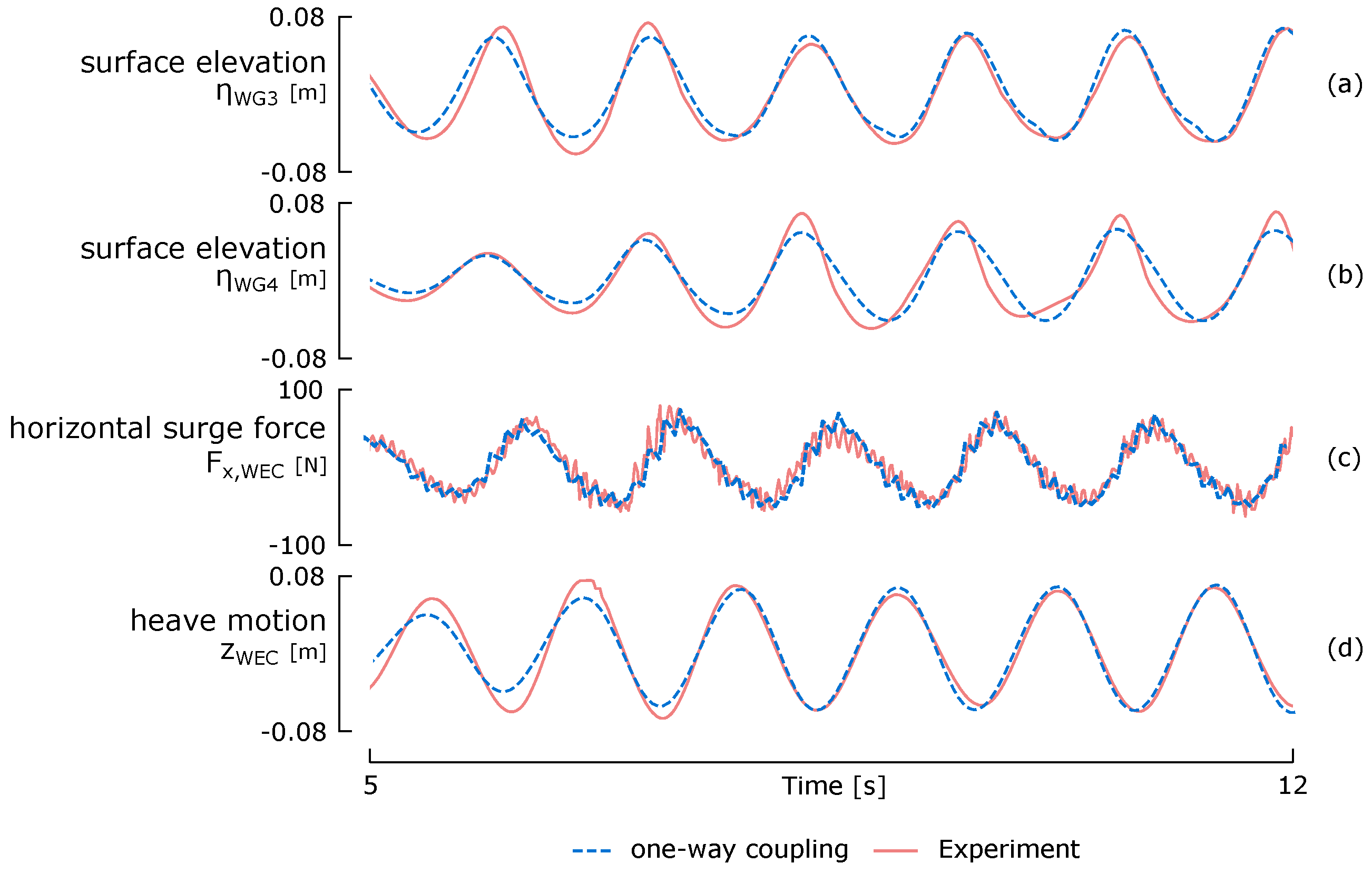
6. 3D Coupled Model: Proof-of-Concept
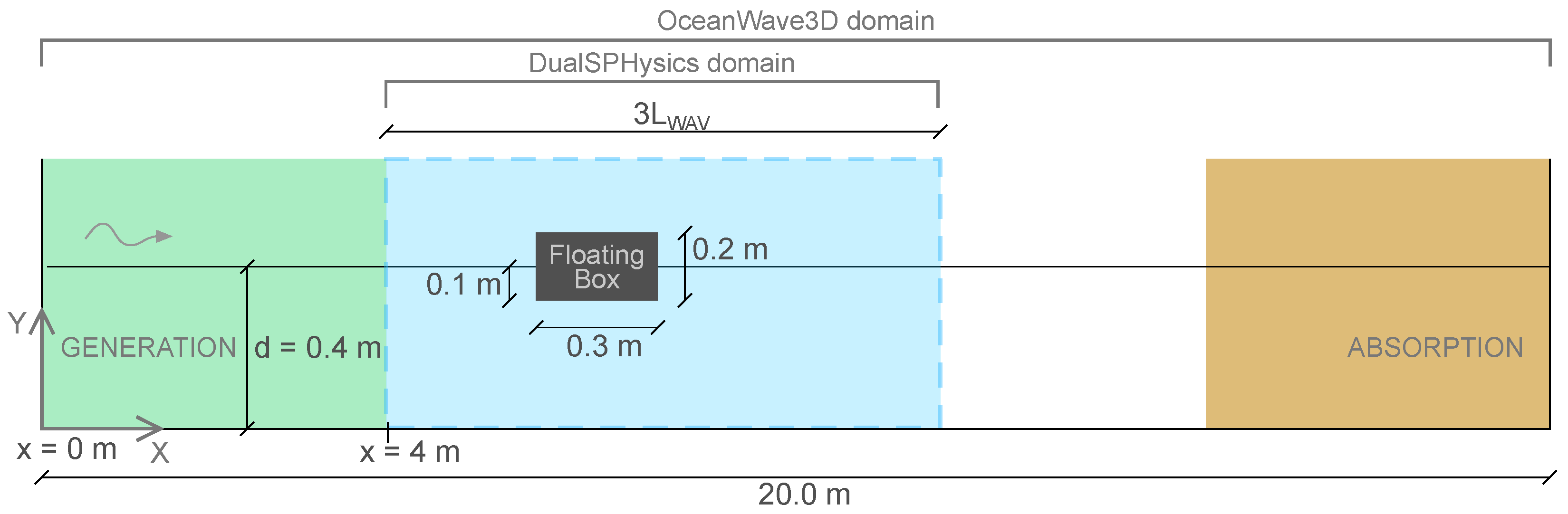
6.1. Experimental Set-up
6.2. Numerical Set-up
6.3. Results and Discussion
6.4. Computational Speed-up
6.5. Visual Comparison of Overtopping
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gotoh, H.; Khayyer, A. On the state-of-the-art of particle methods for coastal and ocean engineering. Coast. Eng. J. 2018, 60, 79–103. [Google Scholar] [CrossRef]
- SPH Numerical Development Working Group. Available online: http://spheric-sph.org/grand-challenges (accessed on 20 February 2019).
- Bouscasse, B.; Marrone, S.; Colagrossi, A.; Di Mascio, A. Multi-purpose interfaces for coupling SPH with other solvers. In Proceedings of the 8th International SPHERIC Workshop, Trondheim, Norway, 4–6 June 2013. [Google Scholar]
- Fourtakas, G.; Stansby, P.; Rogers, B.; Lind, S. An Eulerian-Lagrangian incompressible SPH formulation (ELI-SPH) connected with a sharp interface. Comput. Methods Appl. Mech. Eng. Comput. Methods Appl. Mech. Eng. 2018, 329, 532–552. [Google Scholar] [CrossRef]
- Altomare, C.; Domínguez, J.M.; Crespo, A.J.C.; Suzuki, T.; Caceres, I.; Gómez-Gesteira, M. Hybridisation of the wave propagation model SWASH and the meshfree particle method SPH for real coastal applications. Coast. Eng. J. 2016, 57, 1–34. [Google Scholar]
- Altomare, C.; Tagliafierro, B.; Domínguez, J.; Suzuki, T.; Viccione, G. Improved relaxation zone method in SPH-based model for coastal engineering applications. Appl. Ocean Res. 2018, 81, 15–33. [Google Scholar] [CrossRef]
- Zijlema, M.; Stelling, G.; Smit, P. SWASH: An operational public domain code for simulating wave fields and rapidly varied flows in coastal waters. Coast. Eng. 2011, 58, 992–1012. [Google Scholar] [CrossRef]
- Kassiotis, C.; Ferrand, M.; Violeau, D.; Rogers, B.; Stansby, P.; Benoit, M.; Rogers, B.D.; Stansby, P.K. Coupling SPH with a 1D Boussinesq-type wave model. In Proceedings of the 6th International SPHERIC Workshop, Hamburg, Germany, 8–10 June 2011; pp. 241–247. [Google Scholar]
- Narayanaswamy, M.; Crespo, A.J.C.; Gómez-Gesteira, M.; Dalrymple, R.A. SPHysics-FUNWAVE hybrid model for coastal wave propagation. J. Hydraul. Res. 2010, 48, 85–93. [Google Scholar] [CrossRef]
- Kirby, J.T.; Wei, G.; Chen, Q.; Kennedy, A.B.; Dalrymple, R.A. FUNWAVE 1.0: Fully Nonlinear Boussinesq Wave Model-Documentation And User’s Manual; Research Report NO. CACR-98-06; University of Delaware: Delaware, NJ, USA, 1998. [Google Scholar]
- Ma, Q.; Yan, S. QALE-FEM for numerical modelling of nonlinear interaction between 3D moored floating bodies and steep waves. Int. J. Numer. Methods Eng. 2009, 78, 713–756. [Google Scholar] [CrossRef]
- Fourtakas, G.; Stansby, P.K.; Rogers, B.D.; Lind, S.J.; Yan, S.; Ma, Q.W. On the coupling of Incompressible SPH with a Finite Element potential flow solver for nonlinear free surface flows. In Proceedings of the 27th International Ocean and Polar Engineering Conference. International Society of Offshore and Polar Engineers, San Francisco, CA, USA, 25–30 June 2017. [Google Scholar]
- Chicheportiche, J.; Hergault, V.; Yates, M.; Raoult, C.; Leroy, A.; Joly, A.; Violeau, D. Coupling SPH with a potential Eulerian model for wave propagation problems. In Proceedings of the 11th SPHERIC International Workshop, Munich, Germany, 14–16 June 2016; pp. 246–252. [Google Scholar]
- Didier, E.; Neves, D.; Teixeira, P.R.F.; Neves, M.G.; Viegas, M.; Soares, H. Coupling of FLUINCO mesh-based and SPH mesh-free numerical codes for the modeling of wave overtopping over a porous breakwater. In Proceedings of the International Short Course on Applied Coastal Research, Lisbon, Portugal, 4–7 June 2013. [Google Scholar]
- Teixeira, P.R.D.F.; Awruch, A.M. Numerical simulation of fluid–structure interaction using the finite element method. Comput. Fluids 2005, 34, 249–273. [Google Scholar] [CrossRef]
- Kumar, P.; Yang, Q.; Jones, V.; Mccue-Weil, L. Coupled SPH-FVM simulation within the OpenFOAM framework. Procedia IUTAM 2015, 18, 76–84. [Google Scholar] [CrossRef]
- Marrone, S.; Di Mascio, A.; Le Touzé, D. Coupling of Smoothed Particle Hydrodynamics with Finite Volume method for free-surface flows. J. Comput. Phys. 2016, 310, 161–180. [Google Scholar] [CrossRef]
- Napoli, E.; De Marchis, M.; Gianguzzi, C.; Milici, B.; Monteleone, A. A coupled Finite Volume–Smoothed Particle Hydrodynamics method for incompressible flows. Comput. Methods Appl. Mech. Eng. 2016, 310, 674–693. [Google Scholar] [CrossRef]
- Engsig-Karup, A.P.; Bingham, H.B.; Lindberg, O. An efficient flexible-order model for 3D nonlinear water waves. J. Comput. Phys. 2009, 228, 2100–2118. [Google Scholar] [CrossRef]
- Crespo, A.; Domínguez, J.; Rogers, B.; Gómez-Gesteira, M.; Longshaw, S.; Canelas, R.; Vacondio, R.; Barreiro, A.; García-Feal, O. DualSPHysics: Open-source parallel CFD solver based on Smoothed Particle Hydrodynamics (SPH). Comput. Phys. Commun. 2015, 187, 204–216. [Google Scholar] [CrossRef]
- Verbrugghe, T.; Domínguez, J.M.; Crespo, A.J.; Altomare, C.; Stratigaki, V.; Troch, P.; Kortenhaus, A. Coupling methodology for smoothed particle hydrodynamics modelling of nonlinear wave–structure interactions. Coast. Eng. 2018, 138, 184–198. [Google Scholar] [CrossRef]
- Tafuni, A.; Domínguez, J.; Vacondio, R.; Sahin, I.; Crespo, A. Open boundary conditions for large-scale SPH simulations. In Proceedings of the 11th SPHERIC International Workshop, Munich, Germany, 14–16 June 2016. [Google Scholar]
- Tafuni, A.; Domínguez, J.M.; Vacondio, R.; Crespo, A. Accurate and efficient SPH open boundary conditions for real 3D engineering problems. In Proceedings of the 12th International SPHERIC Workshop, Ourense, Spain, 13–15 June 2017; pp. 1–12. [Google Scholar]
- Tafuni, A.; Domínguez, J.; Vacondio, R.; Crespo, A. A versatile algorithm for the treatment of open boundary conditions in Smoothed particle hydrodynamics GPU models. Comput. Methods Appl. Mech. Eng. 2018, 342, 604–624. [Google Scholar] [CrossRef]
- Ni, X.; Feng, W.; Huang, S.; Zhang, Y.; Feng, X. A SPH numerical wave flume with non-reflective open boundary conditions. Ocean Eng. 2018, 163, 483–501. [Google Scholar] [CrossRef]
- Crespo, A.; Domínguez, J.; Gómez-Gesteira, M.; Barreiro, A.; Rogers, B. User Guide for DualSPHysics Code; The University of Manchester and Johns Hopkins University, University of Vigo: Vigo, Spain, 2018. [Google Scholar]
- Wendland, H. Piecewise polynomial, positive definite and compactly supported radial functions of minimal degree. Adv. Comput. Math. 1995, 4, 389–396. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed particle hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Altomare, C.; Crespo, A.J.; Domínguez, J.M.; Gómez-Gesteira, M.; Suzuki, T.; Verwaest, T. Applicability of Smoothed Particle Hydrodynamics for estimation of sea wave impact on coastal structures. Coast. Eng. 2015, 96, 1–12. [Google Scholar] [CrossRef]
- Shao, S.; Lo, E.Y. Incompressible SPH method for simulating Newtonian and non-Newtonian flows with a free surface. Adv. Water Resour. 2003, 26, 787–800. [Google Scholar] [CrossRef]
- Lo, E.Y.; Shao, S. Simulation of near-shore solitary wave mechanics by an incompressible SPH method. Appl. Ocean Res. 2002, 24, 275–286. [Google Scholar]
- Monaghan, J.J. Simulating free surface flows with SPH. J. Comput. Phys. 1994, 110, 399–406. [Google Scholar] [CrossRef]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Leimkuhler, B.J.; Reich, S.; Skeel, R.D. Integration methods for molecular dynamics. IMA Vol. Math. Appl. 1996, 82, 161–186. [Google Scholar]
- Monaghan, J.; Kos, A. Solitary waves on a Cretan beach. J. Waterw. Port Coast. Ocean Eng. 1999, 125, 145–155. [Google Scholar] [CrossRef]
- Molteni, D.; Colagrossi, A. A simple procedure to improve the pressure evaluation in hydrodynamic context using the SPH. Comput. Phys. Commun. 2009, 180, 861–872. [Google Scholar] [CrossRef]
- Antuono, M.; Colagrossi, A.; Marrone, S. Numerical diffusive terms in weakly-compressible SPH schemes. Comput. Phys. Commun. 2012, 183, 2570–2580. [Google Scholar] [CrossRef]
- Liu, M.; Liu, G. Restoring particle consistency in smoothed particle hydrodynamics. Appl. Numer. Math. 2006, 56, 19–36. [Google Scholar] [CrossRef]
- Crespo, A.; Gómez-Gesteira, M.; Dalrymple, R.A. Boundary Conditions Generated by Dynamic Particles in SPH Methods; CMC-Tech Science Press: Henderson, NV, USA, 2007; Volume 5, p. 173. [Google Scholar]
- Marrone, S.; Antuono, M.; Colagrossi, A.; Colicchio, G.; Touzé, D.L.; Graziani, G. Delta-SPH model for simulating violent impact flows. Comput. Methods Appl. Mech. Eng. 2011, 200, 1526–1542. [Google Scholar] [CrossRef]
- Dean, R.G.; Dalrymple, R.A. Wavemaker Theory. In Water Wave Mechanics for Engineers and Scientists; World Scientific: Singapore, 1991; pp. 170–186. [Google Scholar]
- Altomare, C.; Domínguez, J.; Crespo, A.; González-Cao, J.; Suzuki, T.; Gómez-Gesteira, M.; Troch, P. Long-crested wave generation and absorption for SPH-based DualSPHysics model. Coast. Eng. 2017, 127, 37–54. [Google Scholar] [CrossRef]
- Rossum, G. Python Reference Manual; Technical Report; CWI: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Ren, B.; He, M.; Dong, P.; Wen, H. Nonlinear simulations of wave-induced motions of a freely floating body using WCSPH method. Appl. Ocean Res. 2015, 50, 1–12. [Google Scholar] [CrossRef]
- Altomare, C.; Suzuki, T.; Domínguez, J.; Barreiro, A.; Crespo, A.; Gómez-Gesteira, M. Numerical wave dynamics using Lagrangian approach: Wave generation and passive & active wave absorption. In Proceedings of the 10th SPHERIC International Workshop, Parma, Italy, 16–18 June 2015. [Google Scholar]
- Verbrugghe, T. Coupling Methodologies for Numerical Modelling of Floating Wave Energy Converters. Ph.D. Thesis, Ghent University, Ghent, Belgium, 2018. [Google Scholar]
- Learn About Your New HERO5 Black. Available online: https://gopro.com/yourhero5/black (accessed on 20 February 2019).
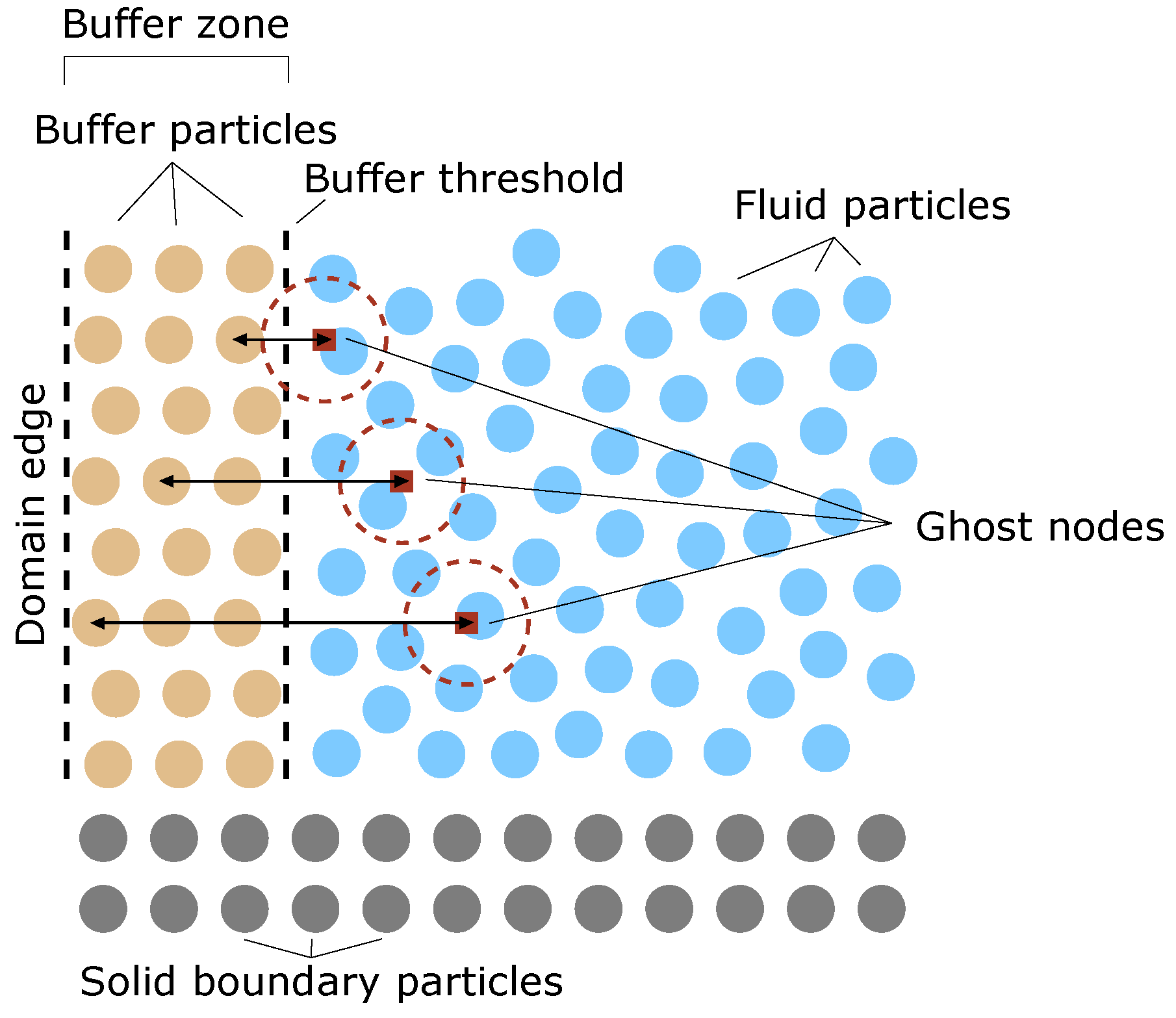
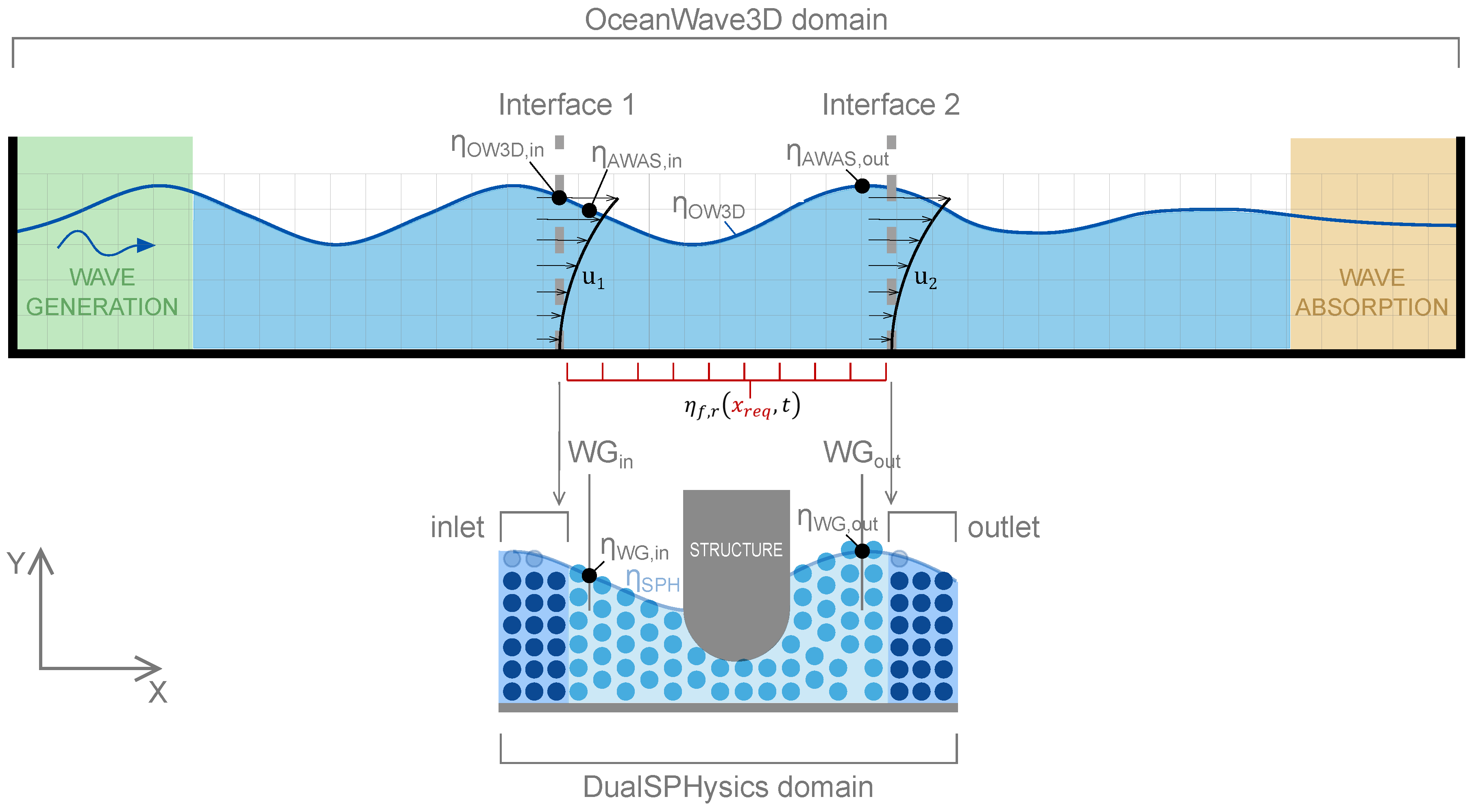
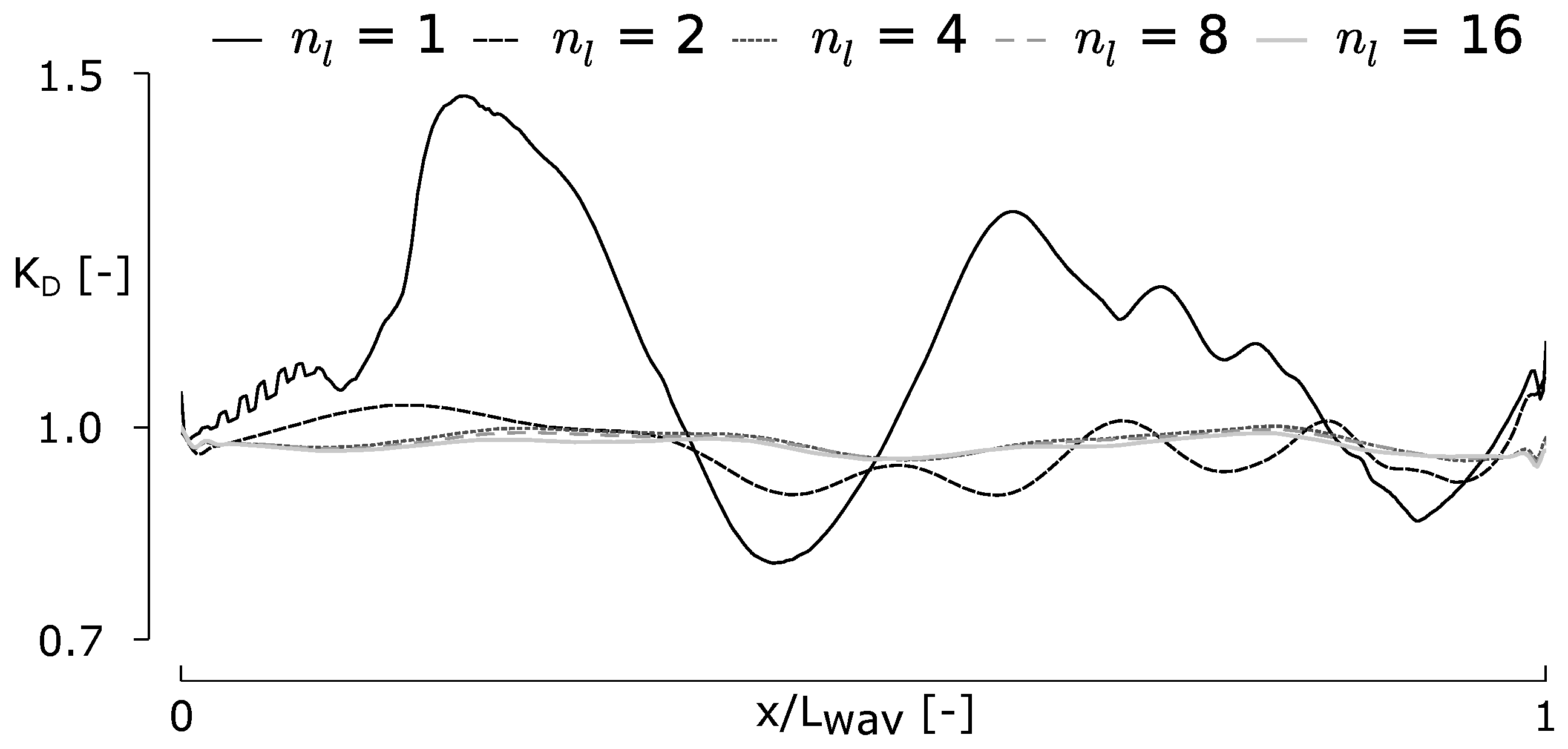
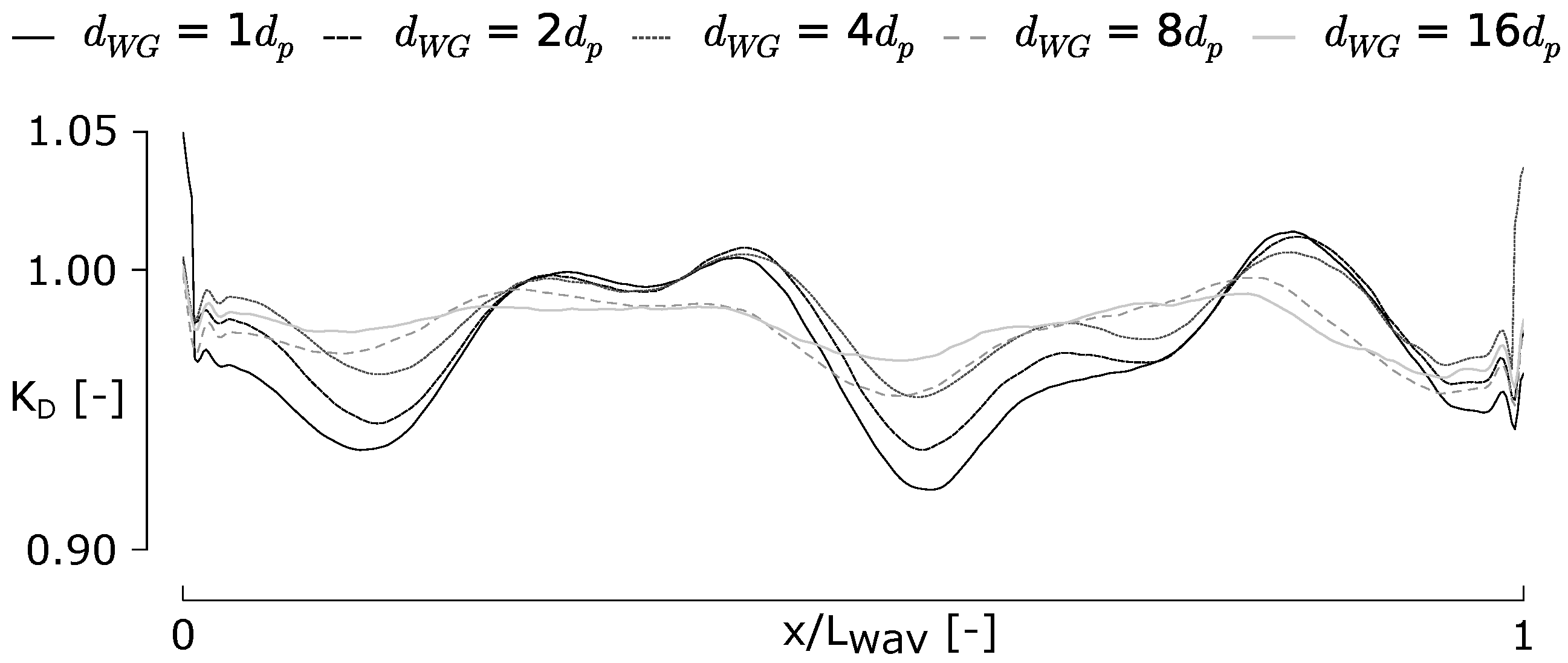


| Quantity | Horizontal Velocity u | Vertical Velocity w | Surface Elevation η | Pressure p |
|---|---|---|---|---|
| inlet | Imp | No | Imp | Hyd |
| outlet | Imp | No | Ext | Ext |
| Time Integration Scheme | Verlet |
|---|---|
| Time Step | Variable (including CFL and viscosity) |
| Kernel | Wendland |
| Smoothing Length | |
| Viscosity Treatment | Artificial () |
| Equation of State | Tait equation |
| Boundary Conditions | Open Boundary Conditions |
| -SPH | Yes (-SPH = 0.1) |
| Wave Height H [m] | 0.12 |
| Wave Period T [s] | 1.2 |
| Water Depth d [m] | 0.7 |
| Wave Length L [m] | 2.17 |
| Particle Size d [m] | 0.01 |
| Domain Length [m] | 4.34 |
| Domain Width W [m] | 1.0 |
| WEC Diameter D [m] | 0.5 |
| WEC Draft q [m] | 0.113 |
| Wave Theory | Stokes 5th |
| Time Step Algorithm | Verlet |
| Artificial Viscosity | 0.01 |
| -SPH | 0.1 |
| One-Way Coupling | Full Model | Difference | |
|---|---|---|---|
| # Particles | 5,010,954 | 25,473,152 | 508% |
| # Fluid Particles | 2,949,433 | 21,165,100 | 718% |
| GPU Memory [MB] | 780 | 3941 | 505% |
| Estimated Runtime [hr] | 35 | 144 | 411% |
| Real Runtime [hr] | 91 | 375 | 411% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Verbrugghe, T.; Stratigaki, V.; Altomare, C.; Domínguez, J.M.; Troch, P.; Kortenhaus, A. Implementation of Open Boundaries within a Two-Way Coupled SPH Model to Simulate Nonlinear Wave–Structure Interactions. Energies 2019, 12, 697. https://doi.org/10.3390/en12040697
Verbrugghe T, Stratigaki V, Altomare C, Domínguez JM, Troch P, Kortenhaus A. Implementation of Open Boundaries within a Two-Way Coupled SPH Model to Simulate Nonlinear Wave–Structure Interactions. Energies. 2019; 12(4):697. https://doi.org/10.3390/en12040697
Chicago/Turabian StyleVerbrugghe, Tim, Vasiliki Stratigaki, Corrado Altomare, J. M. Domínguez, Peter Troch, and Andreas Kortenhaus. 2019. "Implementation of Open Boundaries within a Two-Way Coupled SPH Model to Simulate Nonlinear Wave–Structure Interactions" Energies 12, no. 4: 697. https://doi.org/10.3390/en12040697
APA StyleVerbrugghe, T., Stratigaki, V., Altomare, C., Domínguez, J. M., Troch, P., & Kortenhaus, A. (2019). Implementation of Open Boundaries within a Two-Way Coupled SPH Model to Simulate Nonlinear Wave–Structure Interactions. Energies, 12(4), 697. https://doi.org/10.3390/en12040697








