Equivalent Circuit Model Construction and Dynamic Flow Optimization Based on Zinc–Nickel Single-Flow Battery
Abstract
1. Introduction
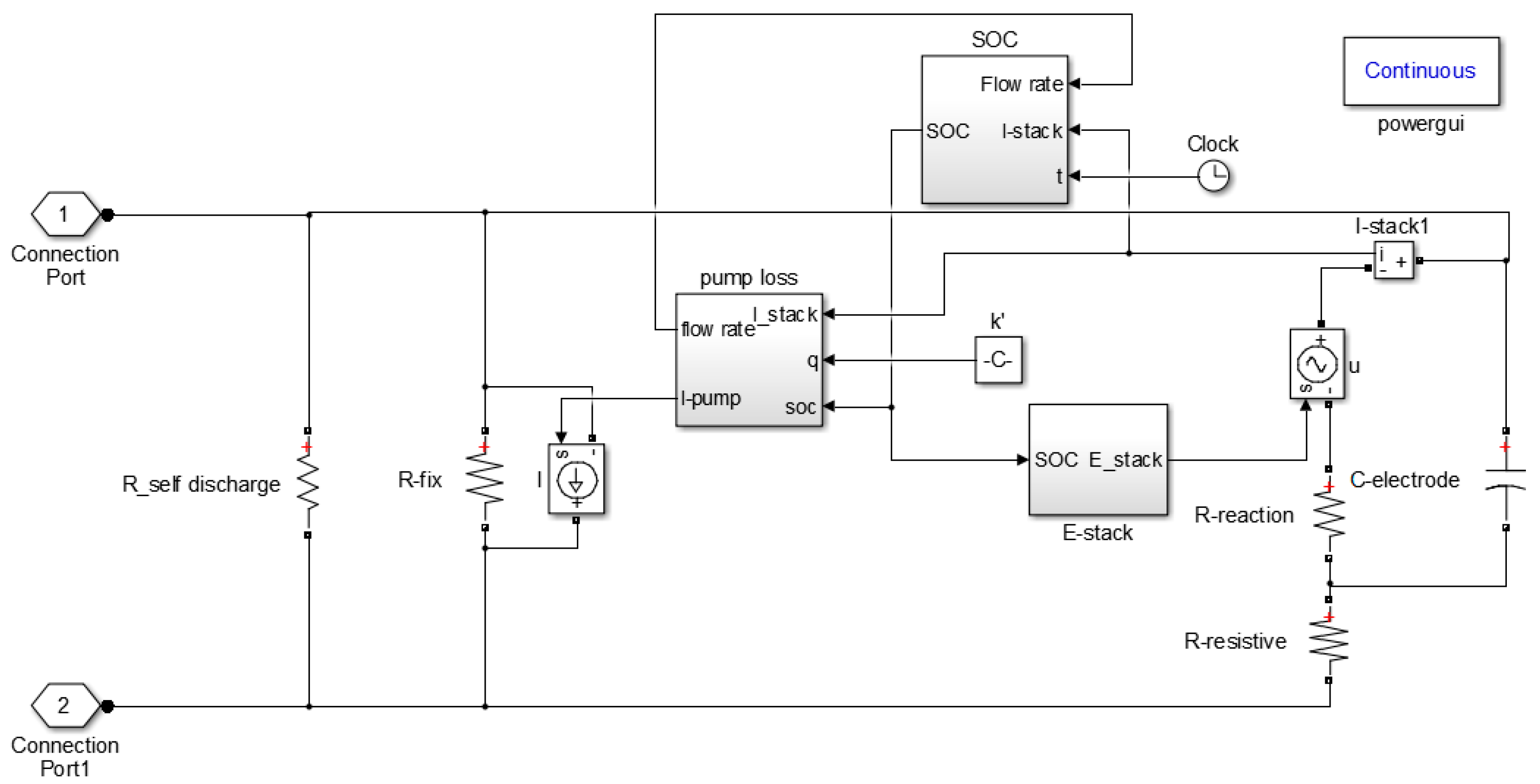
2. Equivalent Circuit Model
2.1. Internal Loss
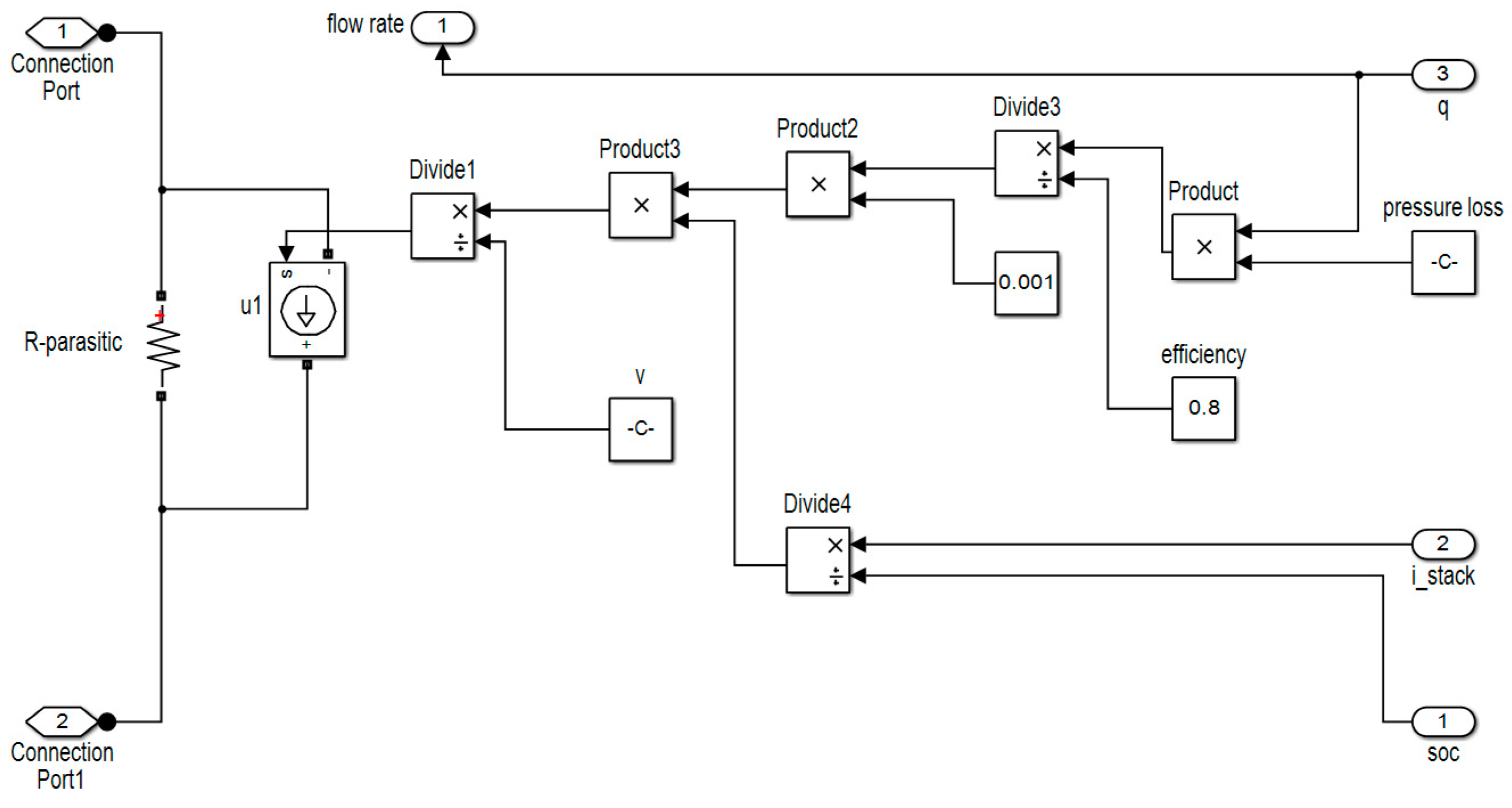
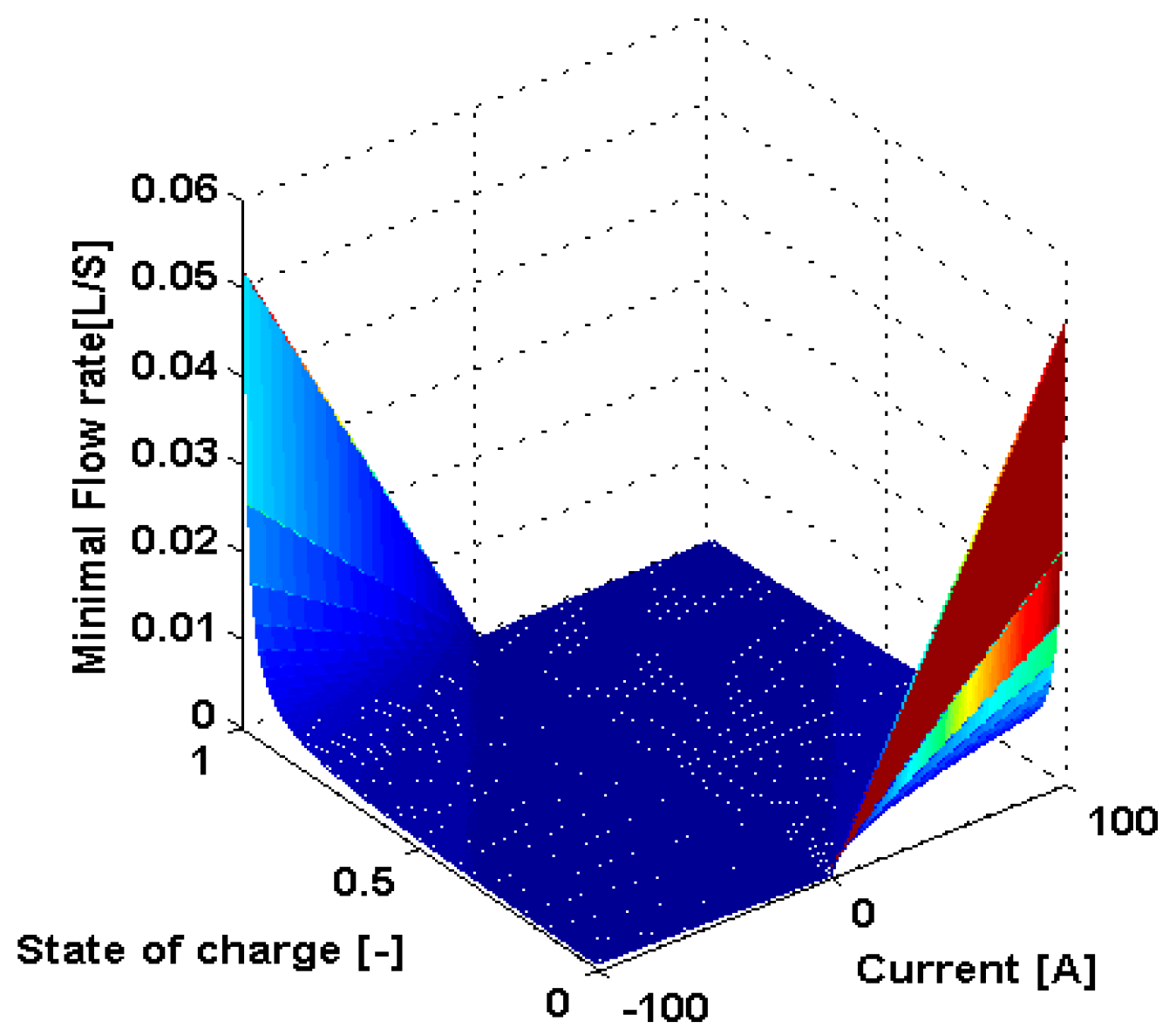
2.2. Pump Loss Model
2.3. Self-Discharge Loss
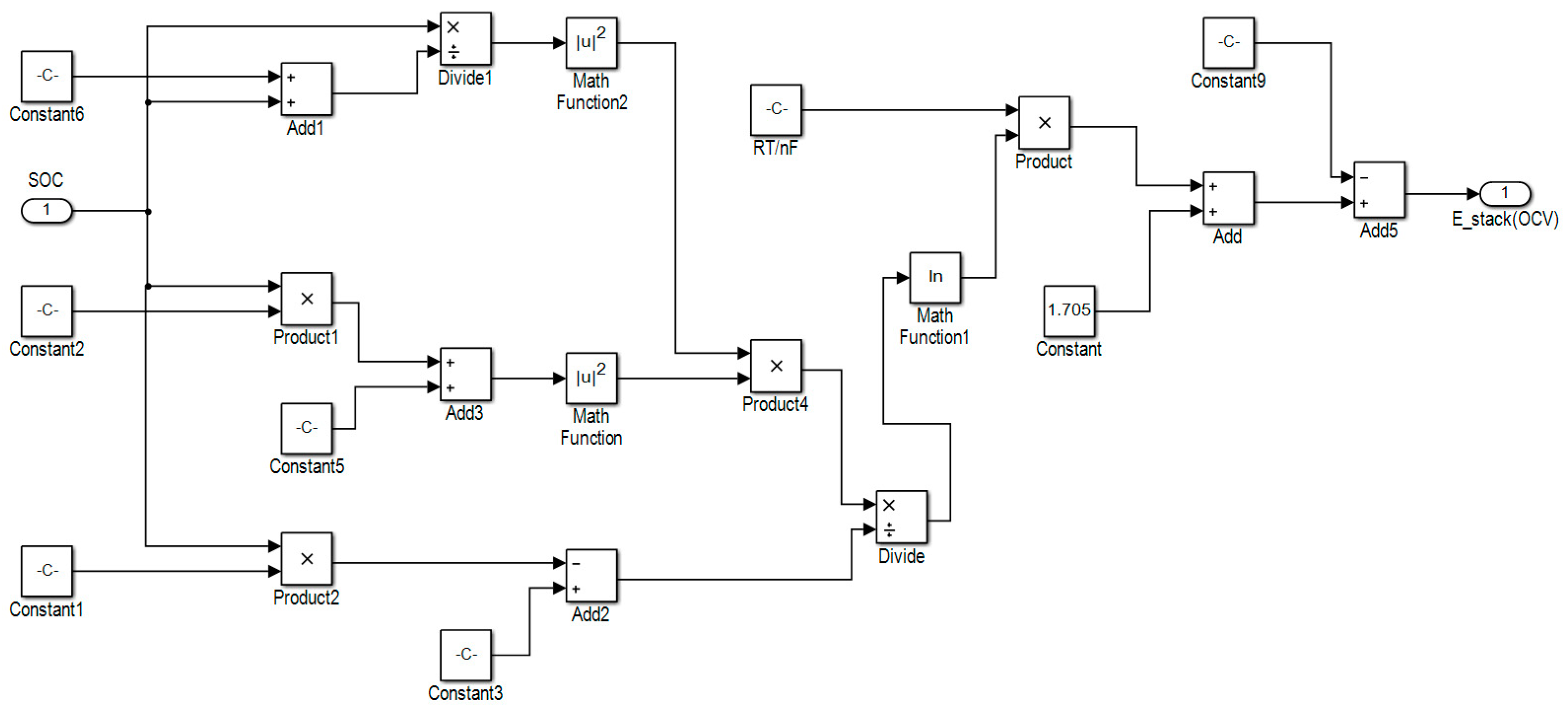
2.4. Voltage Estimation Model
2.5. SOC Estimation Model
3. Results and Discussions
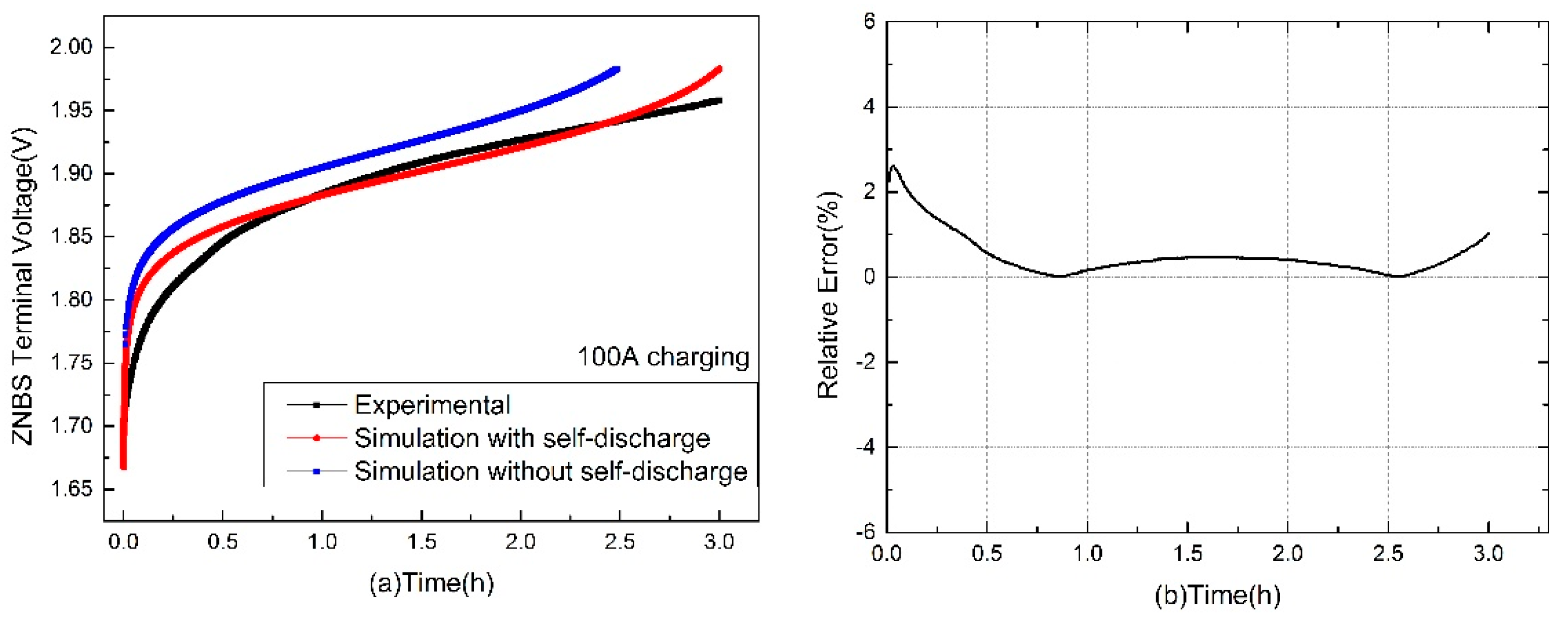
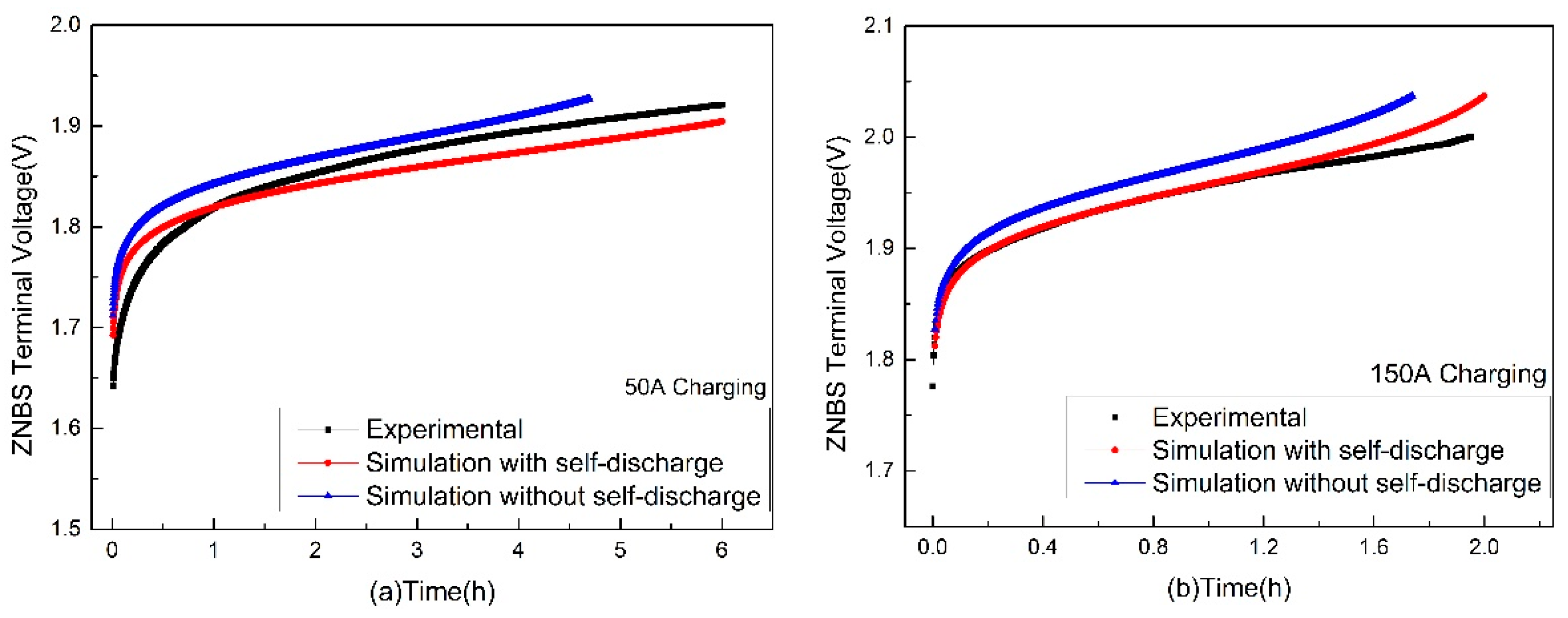
3.1. Terminal Voltage Estimation and Error Analysis of the Charging
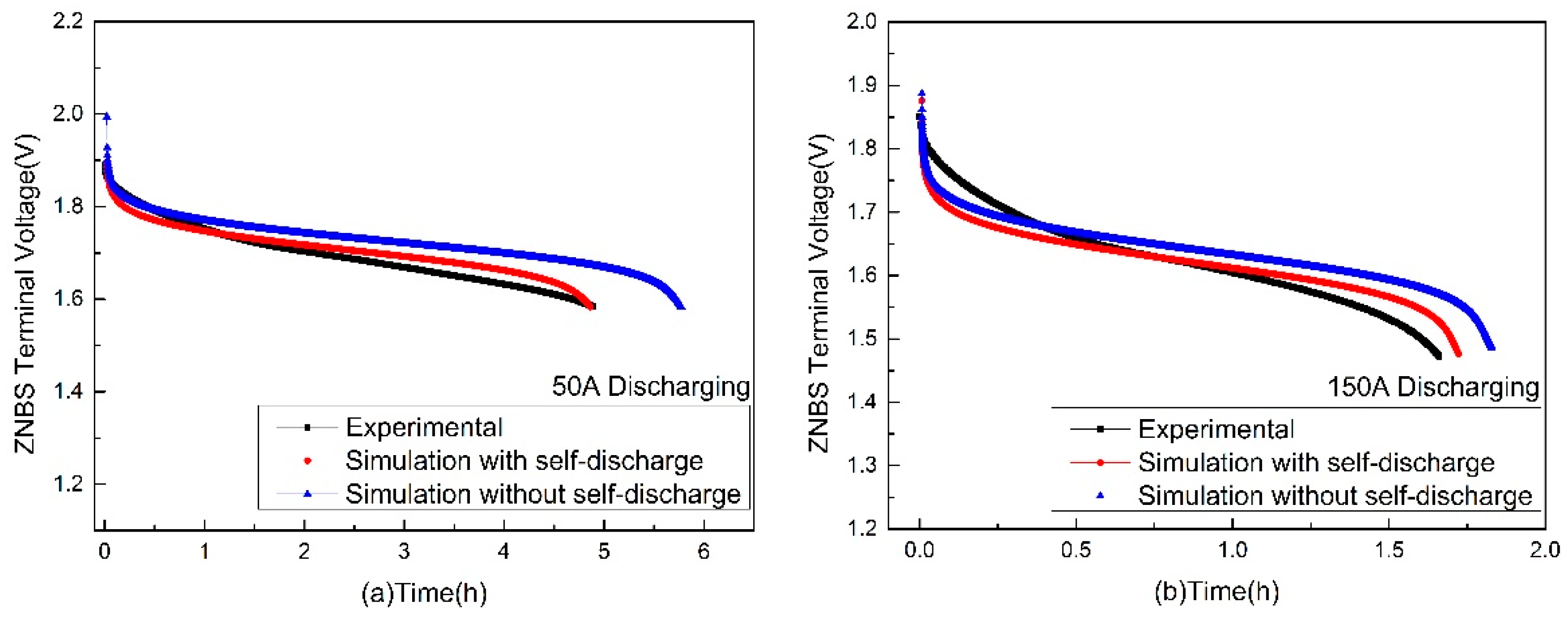
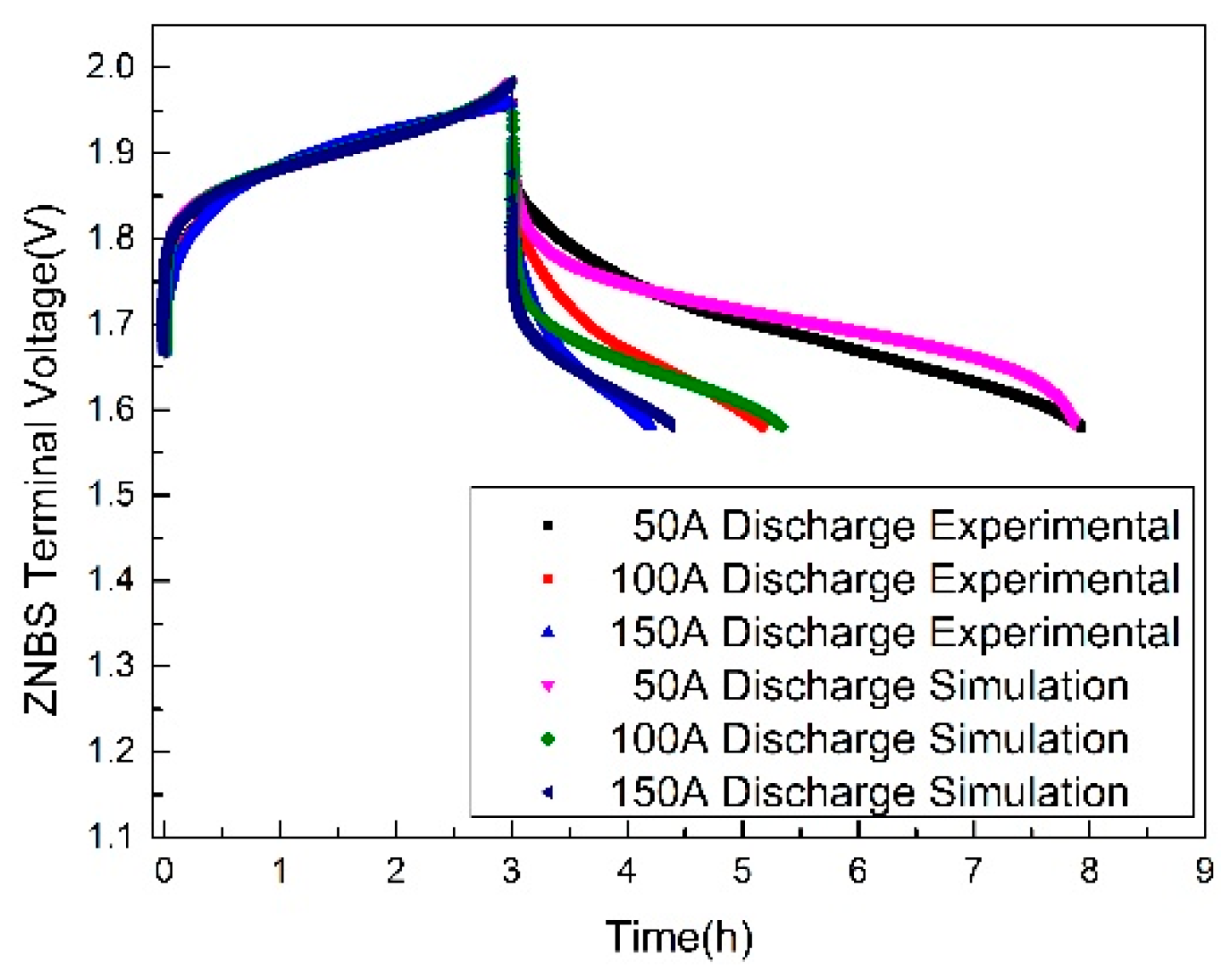
3.2. Terminal Voltage Estimation and Error Analysis of the Discharging
3.3. Coulomb Efficiency Analysis
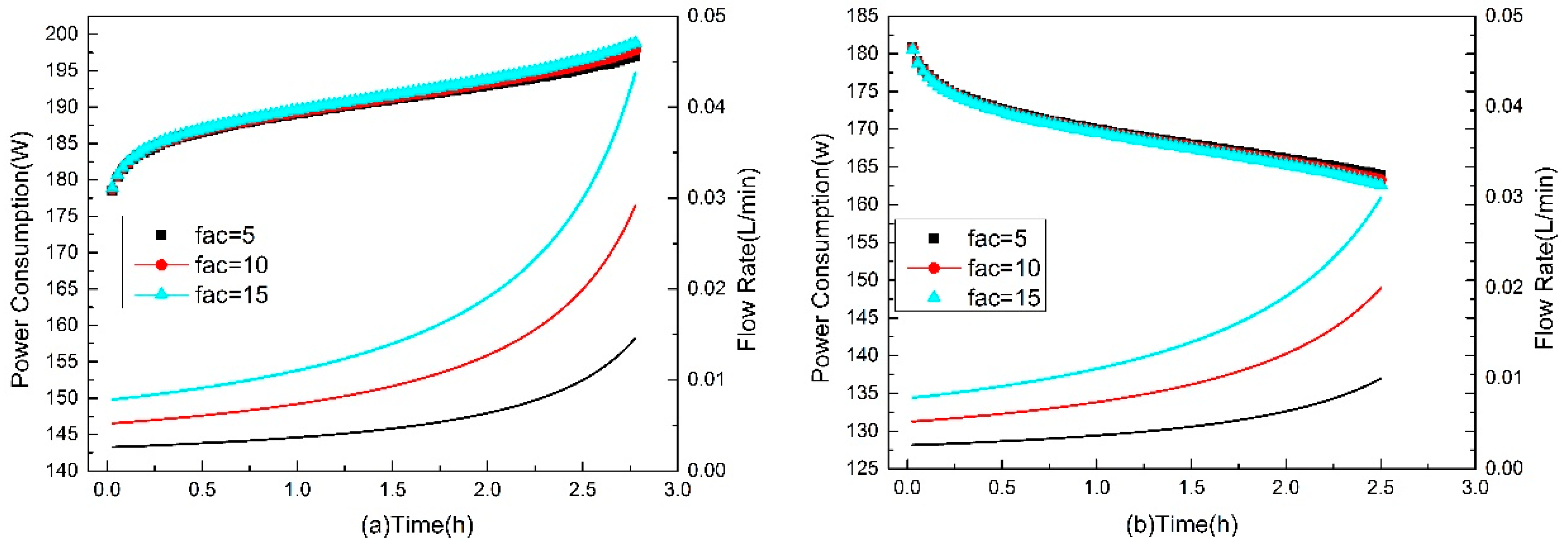
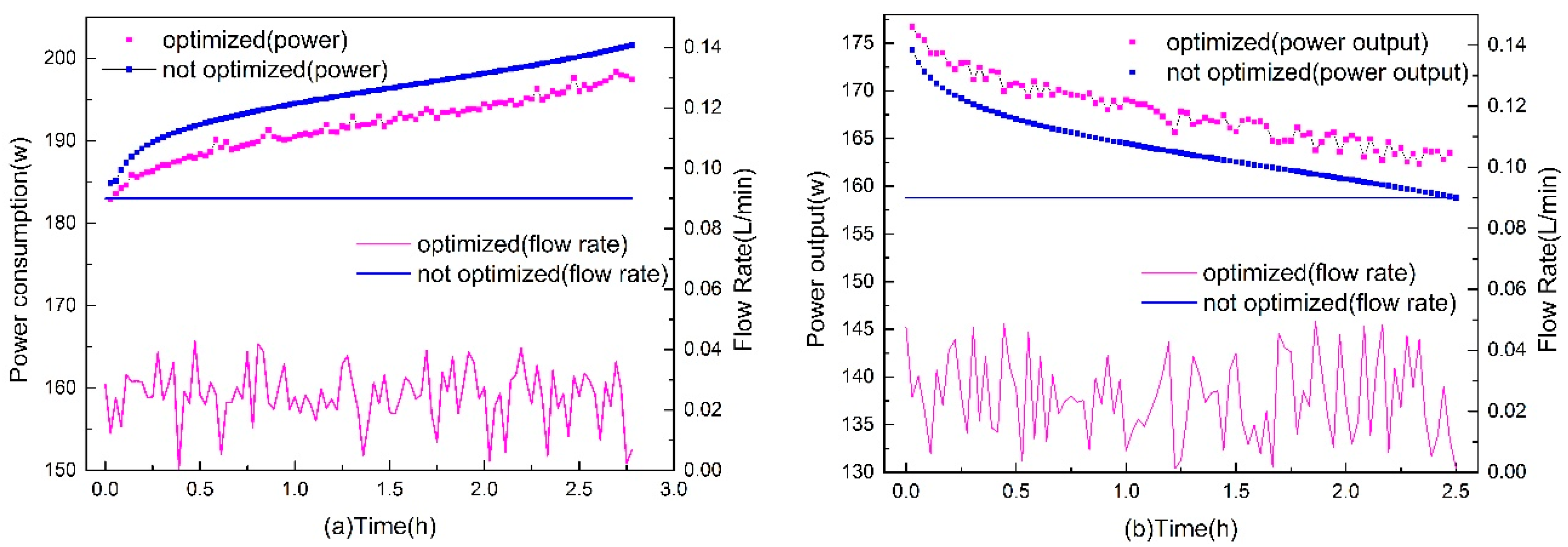
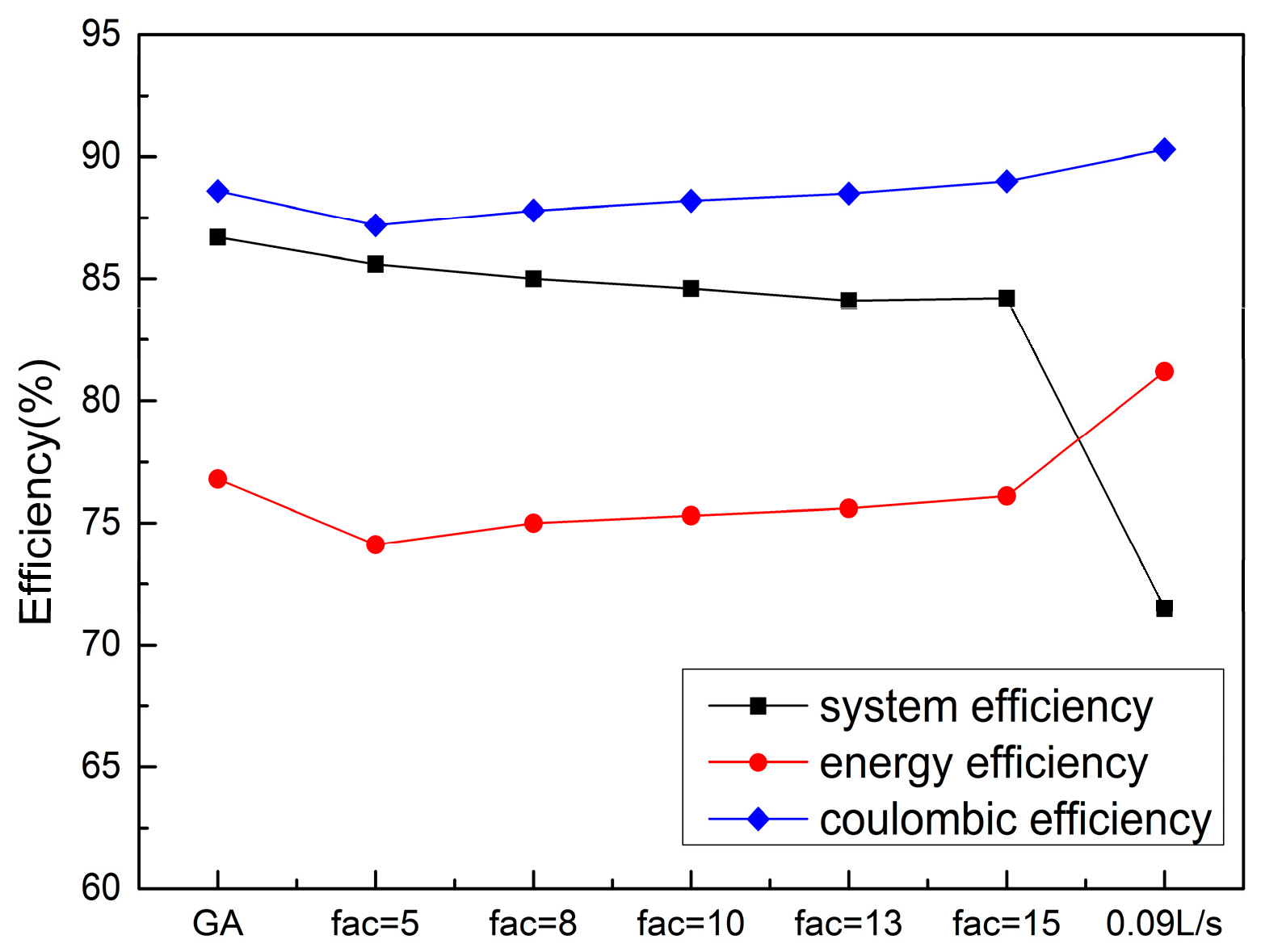
3.4. Dynamic Flow Rate Optimization
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Stack power | Localized loss | ||
| Stack power rating | Self-discharge power loss | ||
| K | Power loss coefficient | Self-discharge resistance | |
| Maximum charge and discharge current | Vstack | Stack terminal voltage | |
| R | Internal loss resistance | Estack | Stack potential |
| Vmin | Stack minimum voltage | Stack stage of charge | |
| Fixed loss power | Tank stage of charge | ||
| Fixed loss resistor | n | No. of electrons transferred per mole | |
| Mechanical loss | Q | Electrolyte flow rate | |
| Internal mechanical loss of stack | F | Faraday constant | |
| Mechanical loss in the pipe | factor | Flow rate factor | |
| Velocity of the electrolyte inside the pipe | Coulombic efficiency | ||
| Z | Height of the pipe | Energy efficiency | |
| Pipeline loss | System efficiency | ||
| Hydraulic resistance | Pump efficiency |
References
- Xie, X.; Zheng, Q.; Li, X.; Zhang, H. Current advances in the flow battery technology. Energy Storage Sci. Technol. 2017, 6, 1050–1057. [Google Scholar]
- Ding, M.; Chen, Z.; Su, J.; Chen, Z.; Zhu, C. Optimal Control of Battery Energy Storage Based on Variables Smoothing Time Constant. Autom. Electr. Syst. 2013, 01, 19–25. [Google Scholar]
- Zhao, P.; Zhang, H.; Zhou, H. Research outline of redox flow cells for energy storage in china. Chin. Battery Ind. 2005, 10, 96–99. [Google Scholar]
- Jia, Z.; Song, S.; Wang, B. A critical review on redox flow batteries for electrical energy storage. Energy Storage Sci. Technol. 2012, 01, 50–57. [Google Scholar]
- Hazza, A.; Pletcher, D.; Wills, R. A novel flow battery: A lead acid battery based on an electrolyte with soluble lead (II) Part I. Chem. Phys. 2004, 6, 1773–1778. [Google Scholar] [CrossRef]
- Pletcher, D.; Wills, R. A novel flow battery: A lead acid battery based on an electrolyte with soluble lead (II) Part II. Chem. Phys. 2004, 6, 1779–1785. [Google Scholar]
- Pletcher, D.; Wills, R. A novel flow battery—A lead acid battery based on an electrolyte with soluble lead (II) III. J. Power Sour. 2005, 149, 96–102. [Google Scholar] [CrossRef]
- Hazza, A.; Pletcher, D.; Wills, R. A novel flow battery—A lead acid battery based on an electrolyte with soluble lead (II) IV. J. Power Sour. 2005, 149, 103–111. [Google Scholar] [CrossRef]
- Cheng, J.; Zhang, L.; Yang, Y.; Wen, Y.; Cao, G.; Wang, X. Preliminary study of single flow zinc–Nickel battery. Electrochem. Commun. 2007, 9, 2639–2642. [Google Scholar] [CrossRef]
- Pan, J.; Sun, Y.; Cheng, J.; Wen, Y.; Yang, Y.; Wan, P. Study on a new single flow acid Cu-Pb O2battery. Electrochem. Commun. 2008, 10, 1226–1229. [Google Scholar] [CrossRef]
- Xu, Y.; Wen, Y.; Cheng, J.; Cao, G.; Yang, Y. Study on a single flow acid Cd-chloranil battery. Electrochem. Commun. 2009, 11, 1422–1424. [Google Scholar] [CrossRef]
- Zhang, L.; Cheng, J.; Yang, Y.; Wen, Y.; Xie, Z. Preliminary Study of Single Flow Zinc-Nickel Battery. Electrochemistry 2008, 14, 248–252. [Google Scholar]
- Zhang, L.; Cheng, J.; Yang, Y.; Wen, Y.; Wang, X.; Cao, G. Study of zinc electrodes for single flow zinc/nickel battery application. J. Power Sour. 2008, 179, 381–387. [Google Scholar] [CrossRef]
- Cheng, J.; Wen, Y.; Xu, Y.; Cao, G.; Yang, Y. Effects of Substrates on Deposition of Zinc from flowing Alkaline Zincate Solutions. Chem. J. Chin. Univ.-Chin. 2011, 32, 2640–2644. [Google Scholar]
- Wang, J.; Zhang, L.; Zhang, C.; Xiao, Q.; Zhang, J.; Cao, C. The Influence of Bi3+ and Tetrabutylammonium Bromide on the Dendritic Growth Behavior of Alkaline Rechargeable Zinc Electrode. Funct. Mater. 2001, 32, 45–47. [Google Scholar]
- Wen, Y.; Cheng, J. The inhibition of the spongy electrocry stallization of zinc from dopedflowing alkaline zincate solutions. J. Power Sour. 2009, 193, 890–894. [Google Scholar] [CrossRef]
- Wen, Y.; Wang, T.; Cheng, J.; Pan, J.; Cao, G.; Yang, Y. Lead ion and tetrabutylammonium bromide as inhibitors of the growth of spongy zinc in single flow zinc/nickel batteries. Electrochim. Acta 2012, 59, 64–68. [Google Scholar] [CrossRef]
- Song, S. Study on Electrolyte of Zinc/Nickel Single Flow Battery. Ph.D. Thesis, Beijing University of Chemical Technology, Beijing, China, 2014. [Google Scholar]
- Cheng, Y.; Zhang, H. A high power density single flow zinc-nickel battery with three-dimensional porous negative electrode. J. Power Sour. 2013, 241, 196–202. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhang, H. Performance gains in single flow zinc-nickel batteries through novel cell configuration. Electrochim. Acta 2013, 105, 618–621. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhang, H. Effect of temperature on the performances and in situ polarization analysis of zinc-nickel single flow batteries. J. Power Sour. 2014, 249, 435–439. [Google Scholar] [CrossRef]
- Yao, S.; Ji, Y.; Wang, Y.; Song, Y.; Xiao, M.; Cheng, J. Optimization Analysis for the Internal Flow Field of Nickel-zinc Single Flow Energy Storage Battery with 32-Cell. Oxid. Commun. 2016, 39, 3223–3234. [Google Scholar]
- Zhao, P.; Cheng, J.; Xu, Y.; Wen, Y.; He, K.; Cao, G. Pilot Scale Development of Zn/Ni single flow redox battery. In Summary of the 29th Annual Academic Meeting of the Chinese Chemical Society—Chapter 24: Chemical Power; Peking University: Beijing, China, 2014. [Google Scholar]
- Barote, L.; Marinescu, C.; Georgescu, M. VRB modeling for storage in stand-alone wind energy systems. IEEE Powertech. Conf. 2009. [Google Scholar] [CrossRef]
- Barote, L.; Marinescu, C. A new control method for VRB SOC estimation in stand-alone wind energy systems. Intern. Conf. Clean Electr. Power. 2009, 253–257. [Google Scholar]
- Chahwan, J.; Abbey, C.; Joos, G. VRB modelling for the study of output terminal voltages, internal losses and performance. Electr. Power Conf. 2008. [Google Scholar] [CrossRef]
- Bhattacharjee, A.; Saha, H. Design and experimental validation of a generalised electrical equivalent model of Vanadium Redox Flow Battery for interfacing with renewable energy sources. J. Energy Storage 2017, 13, 220–232. [Google Scholar] [CrossRef]
- Bhattacharjee, A.; Roy, A.; Banerjee, N.; Patra, S.; Saha, H. Precision dynamic equivalent circuit model of a Vanadium Redox Flow Battery and determination of circuit parameters for its optimal performance in renewable energy applications. J. Power Sour. 2018, 396, 506–518. [Google Scholar] [CrossRef]
- Yao, S.; Liao, P.; Xiao, M.; Cheng, J.; He, K. Equivalent circuit modeling and simulation of the zinc-nickel single flow batteries. AIP Adv. 2017, 7, 1–10. [Google Scholar] [CrossRef]
- Xiao, M.; Liao, P.; Yao, S.; Cheng, J. Experimental study on charge/discharge characteristics of zinc-nickel single-flow battery. J. Renew. Sustain. Energy 2017, 9. [Google Scholar] [CrossRef]
- Yao, S.; Liao, P.; Xiao, M.; Cheng, J.; He, K. Modeling and simulation of the zinc-nickel single flow batteries based on MATLAB/Simulink. AIP Adv. 2016, 6. [Google Scholar] [CrossRef]
- Chi, X.; Zhu, M.; Wu, Q. Research on optimal operation control based on the equivalent model of VRFB system. Energy Storage Sci. Technol. 2018, 7, 530–538. [Google Scholar]
- Yao, S.; Liao, P.; Xiao, M.; Cheng, J.; Cai, W. Study on Electrode Potential of Zinc-nickel Single-Flow Battery during Charge. Energies 2017, 10, 1101. [Google Scholar] [CrossRef]
- Blanc, C. Modelling of Vanadium Redox Flow Battery Electricity Storage System. Ph.D. Thesis, Echole Polytechnique Federale De Lausanne, Lausanne, Switzerland, 2017. [Google Scholar]
- Ma, X.; Zhang, H.; Sun, C.; Zou, Y.; Zhang, T. An optimal strategy of electrolyte flow rate for vanadium redox flow battery. J. Power Sour. 2012, 203, 153–158. [Google Scholar] [CrossRef]
- Fu, J.; Zheng, M.; Wang, X.; Sun, J.; Wang, T. Flow-Rate Optimization and Economic Analysis of Vanadium Redox Flow Batteries in a Load-Shifting Application. J. Energy Eng. 2017, 143, 1–13. [Google Scholar] [CrossRef]
- Tang, A.; Bao, J.; Skyllaskazacos, M. Studies on pressure losses and flow rate optimization in vanadium redox flow battery. J. Power Sour. 2014, 248, 154–162. [Google Scholar] [CrossRef]
- Wang, T.; Fu, J.; Zheng, M.; Yu, Z. Dynamic control strategy for the electrolyte flow rate of vanadium redox flow batteries. Appl. Energy 2018, 227, 613–623. [Google Scholar] [CrossRef]
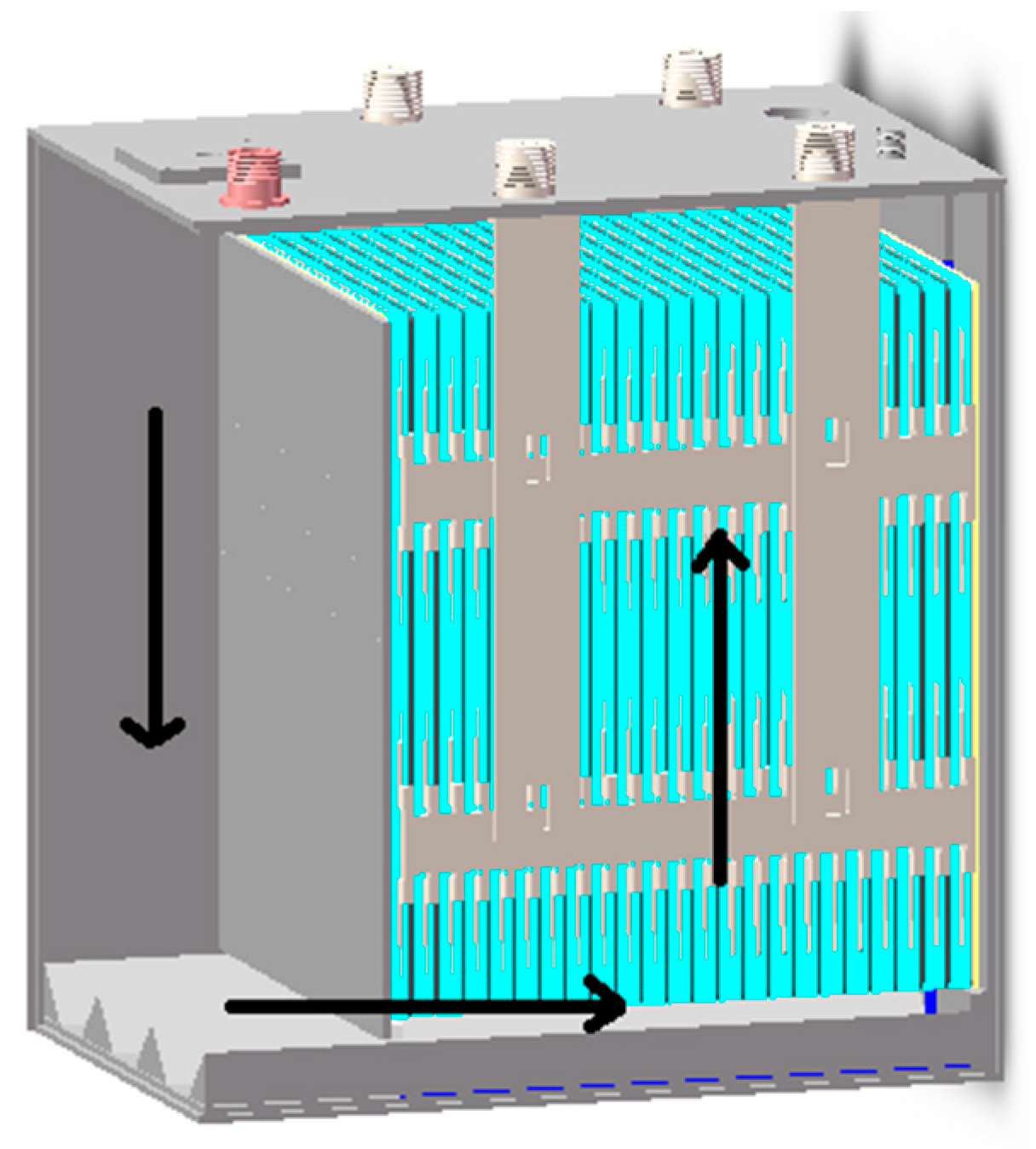
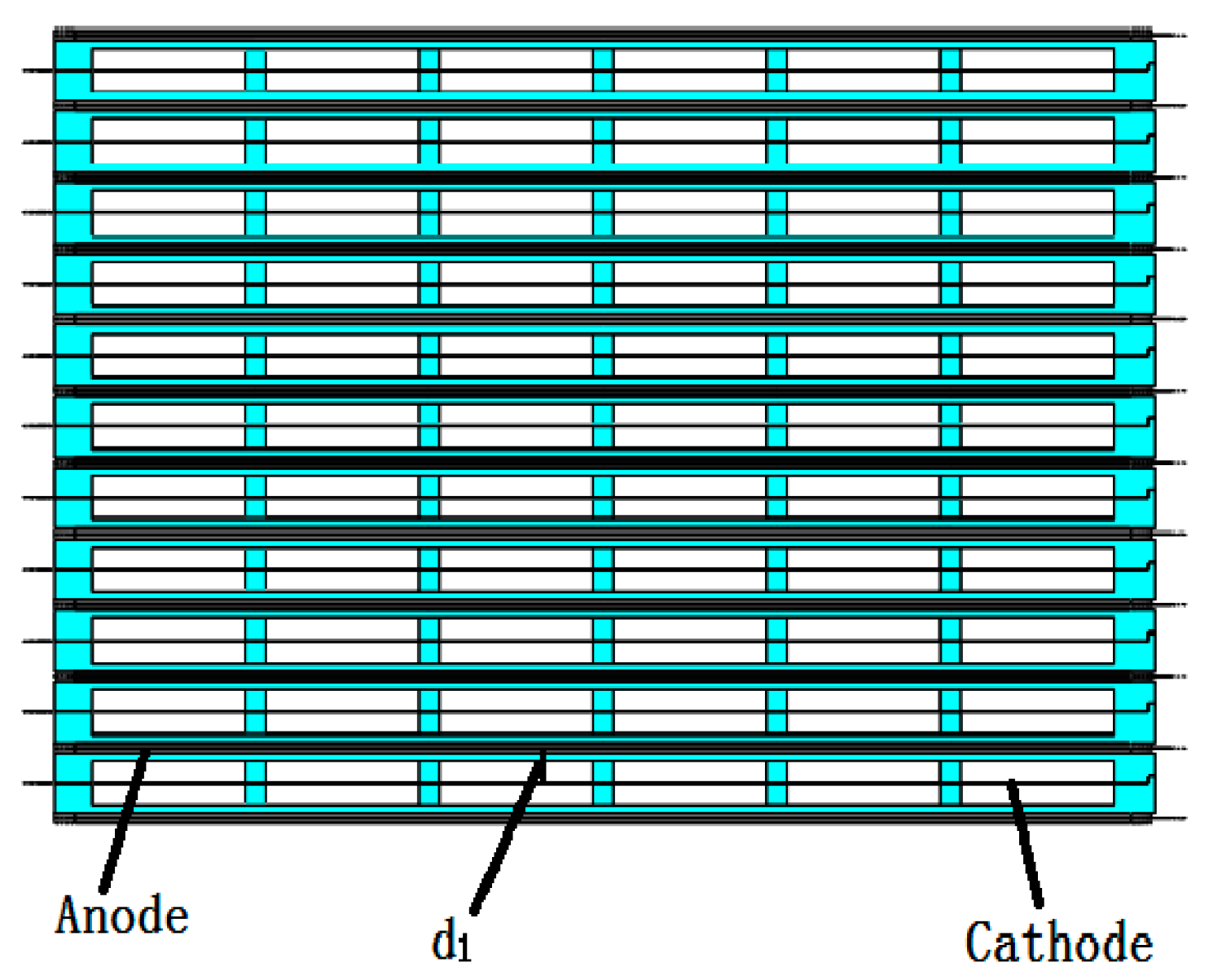


| Main Components | Size Parameters |
|---|---|
| Height of porous nickel electrode (mm) | 240 |
| Width of porous nickel electrode (mm) | 186 |
| Thickness of porous nickel electrode (mm) | 0.64 |
| Height of negative pole (mm) | 240 |
| Width of negative pole (mm) | 186 |
| Thickness of negative pole (mm) | 0.08 |
| Distance between anode and cathode(d1/mm) | 160 |
| Electrolyte density (kg·m−3) | 1456.1 |
| Electrolyte viscosity (kg·m−1·s−1) | 0.003139 |
| No. of parallel cells in stack | 23 |
| Inner diameter of the pipeline (mm) | 15 |
| Length of pipeline (cm) | 40 |
| Pipeline import and export height difference (cm) | 5 |
| Number of bends | 3 |
| Parameters | Unit | Range |
|---|---|---|
| mol·m−3 | 0–35,300 | |
| mol·m−3 | 9600–11,000 | |
| mol·m−3 | 300–1000 | |
| mol·m−3 | 35,300 |
| Parameters | Unit | Value |
|---|---|---|
| Rated voltage | V | 1.6 |
| A | 200 | |
| V | 1.2 | |
| W | 160 | |
| Stack capacity | Ah | 300 |
| Number of parallel cells | - | 23 |
| Operating temperature range | °C | −40~40 |
| Volume of electrolyte | L | 8.5 |
| Ω | 0.00064 | |
| Ω | 0.00036 | |
| - | 10.8% | |
| - | 4.35% | |
| Ω | 0.313 | |
| F | 138 | |
| Ω | 0.16 | |
| f | - | 0.039 |
| - | 0.8 | |
| F | C/mol−1 | 96485 |
| - | 0.2 | |
| Pa/m3 | 14186843 | |
| n | - | 2 |
| T | K | 298 |
| C | mol/L | 1 |
| Charging Current (A) | Maximum Relative Error (%) | Minimum Relative Error (%) | Charging Completion Time (h) |
|---|---|---|---|
| 50 | 1.1 | 0.02 | 6 |
| 100 | 2.61 | 0.001 | 3 |
| 150 | 1.44 | 0 | 2 |
| Discharging Current (A) | Maximum Relative Error (%) | Minimum Relative Error (%) | Discharging Completion Time (h) |
|---|---|---|---|
| 50 | 1.8 | 0.002 | 5.3 |
| 100 | 3.75 | 0.004 | 2.48 |
| 150 | 3.85 | 0.02 | 1.78 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, S.; Sun, X.; Xiao, M.; Cheng, J.; Shen, Y. Equivalent Circuit Model Construction and Dynamic Flow Optimization Based on Zinc–Nickel Single-Flow Battery. Energies 2019, 12, 582. https://doi.org/10.3390/en12040582
Yao S, Sun X, Xiao M, Cheng J, Shen Y. Equivalent Circuit Model Construction and Dynamic Flow Optimization Based on Zinc–Nickel Single-Flow Battery. Energies. 2019; 12(4):582. https://doi.org/10.3390/en12040582
Chicago/Turabian StyleYao, Shouguang, Xiaofei Sun, Min Xiao, Jie Cheng, and Yaju Shen. 2019. "Equivalent Circuit Model Construction and Dynamic Flow Optimization Based on Zinc–Nickel Single-Flow Battery" Energies 12, no. 4: 582. https://doi.org/10.3390/en12040582
APA StyleYao, S., Sun, X., Xiao, M., Cheng, J., & Shen, Y. (2019). Equivalent Circuit Model Construction and Dynamic Flow Optimization Based on Zinc–Nickel Single-Flow Battery. Energies, 12(4), 582. https://doi.org/10.3390/en12040582





