Dynamic Carbon-Constrained EPEC Model for Strategic Generation Investment Incentives with the Aim of Reducing CO2 Emissions
Abstract
1. Introduction
- The suggested model is dynamic. The dynamic nature of investment decisions has not been considered in the generation capacity expansion problem in [5,8,21,23,36,37,39,40,41,44,45,46,50]. This is critical for a multi-period stochastic mathematical programming with an equilibrium constraints (MPEC) model consisting of transmission network constraints.
- The GEP model for each strategic producer in this paper is bi-level, but this problem in [4,14,23], and Refs. [50,51,52] is not bi-level as typical applications of bi-level approach in operational planning. Reference [53] presents bi-level models defined as a mathematical optimization problem constrained by another optimization problem, as this approach is increasingly applied to electricity markets [8,54].
- The hybrid market including both capacity payment and firm contract is considered, as simultaneous existence of these two investment incentives has not been considered in [5,6,8,9,14,19,21,23,36,37,38,39,40,41,43,44,45,46,50,52,54]. Therefore, our method uses the EPEC model for investigating impacts of the both investment incentives on power generation sector.
- √
- Integrating the impact of carbon emissions as well as incentive investments into the Dynamic carbon-constrained Equilibrium programming equilibrium constraints (DCC-EPEC) model.
- √
- The effect of different markets is studied in the investment performance of strategic producers in multi-stage planning by the DCC-EPEC model.
- √
- Implementing a multi-stage stochastic framework for a generation expansion model for strategic investors considering non-anticipativity constraints to make the proposed problem computationally expensive, and likely intractable, especially in the case of large-scale case studies;
- √
- calculating dynamic reliability indices for investment incentive policies;
2. Modelling EO, CP, FC, and Hybrid Markets
2.1. Modeling Behaviour of the Market and Competitors
2.1.1. Market Clearing Model for the Impact of Investment Incentives
2.1.2. Dynamic Model for the Impact of Investment Incentives
2.1.3. The Bi-Level Model for Each Strategic Producer Incorporating Market-Clearing and Dynamic Models
2.2. Modeling Uncertainty in the Market
2.2.1. Modeling Existing Uncertainties
2.2.2. Issue of Non-Anticipativity
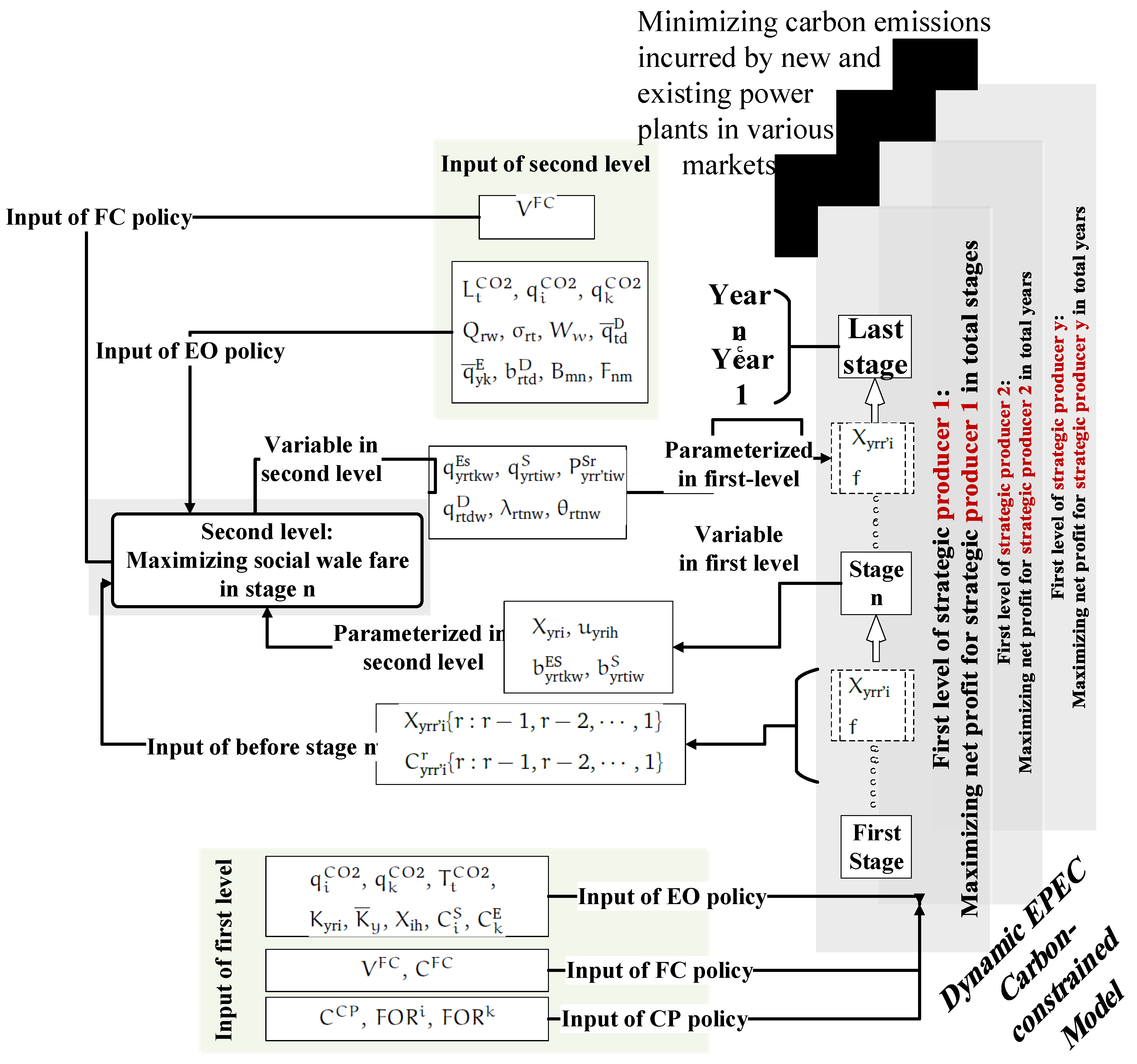
3. Problem Formulation
The Proposed Carbon-Constrained EPEC Model
4. Inputs and Outputs of Each Level for Different Markets
4.1. Inputs and Outputs of Each Stage
4.2. Stage to Stage Inputs and Outputs
5. The Pseudo-Code of Algorithm for Solutions for Investment Problems in Different Markets
| Algorithm 1 The algorithm for solving the suggested DCC-EPEC Model |
Require: Input data ▹ uncertainty related to non-strategic producer s investments and demand growth, as well as network information, Market features, elastic demands
|
6. Case Study
6.1. Inputs of Case Study
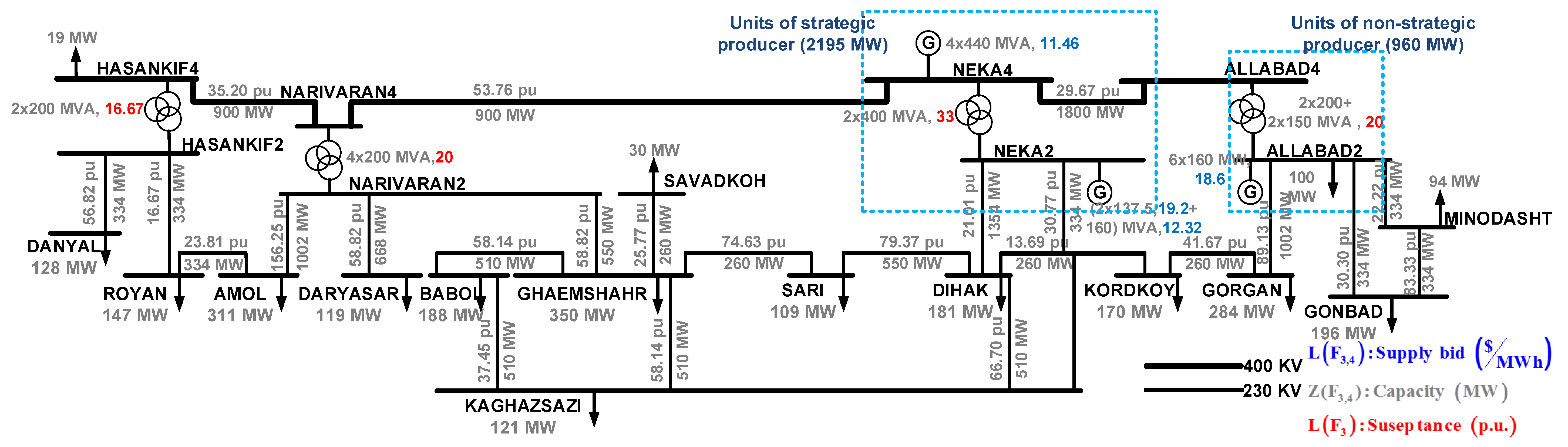
6.1.1. Introduction of the MREC Transmission Network
6.1.2. Inputs of Investment Incentives for CP and FC
6.2. Analysis of EO, CP, FC, and Hybrid Markets on MREC Power Transmission Network for Competition between One Strategic Producer and Non-Strategic Producers
6.2.1. EO Market
6.2.2. CP Market
6.2.3. FC Market
6.2.4. Hybrid Market
- √
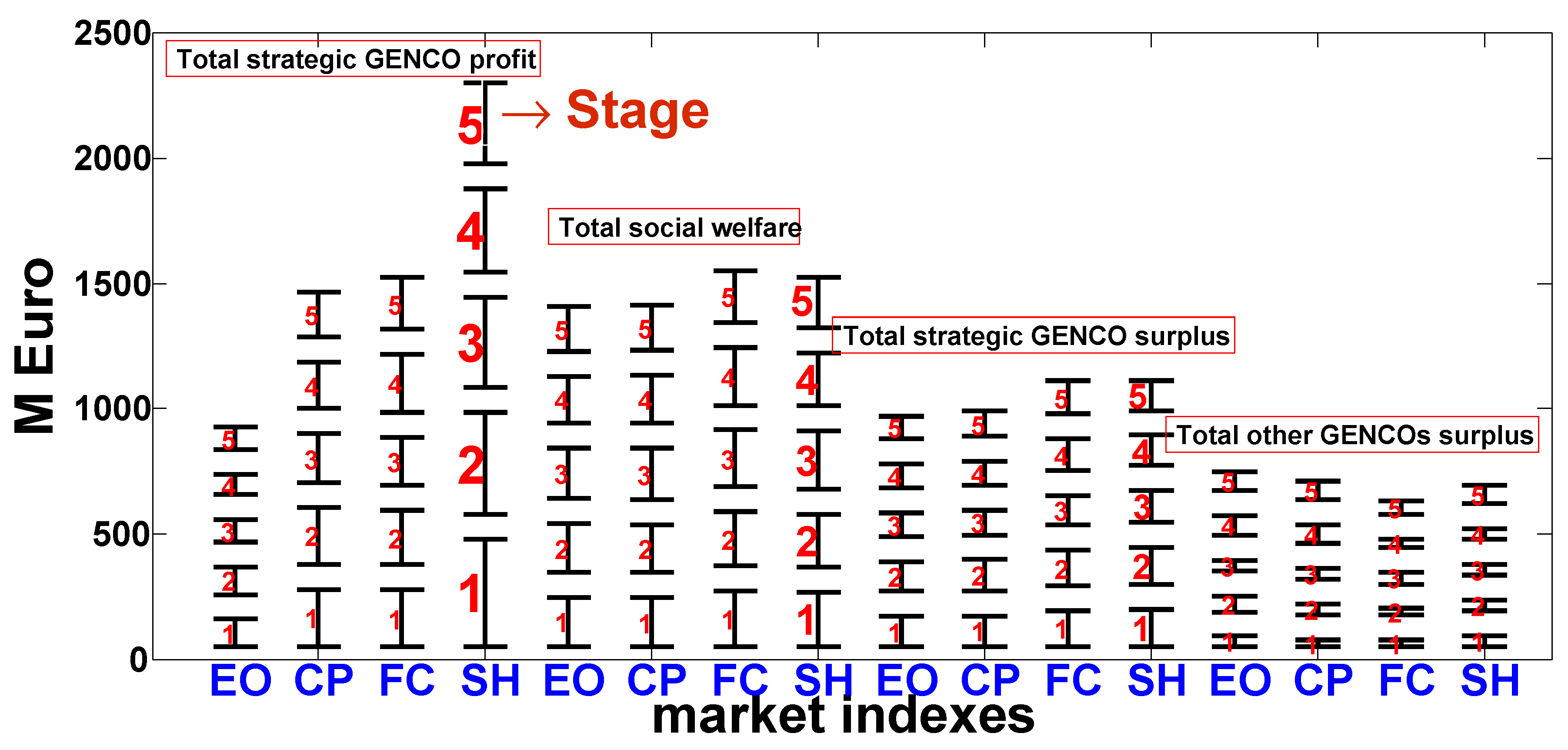
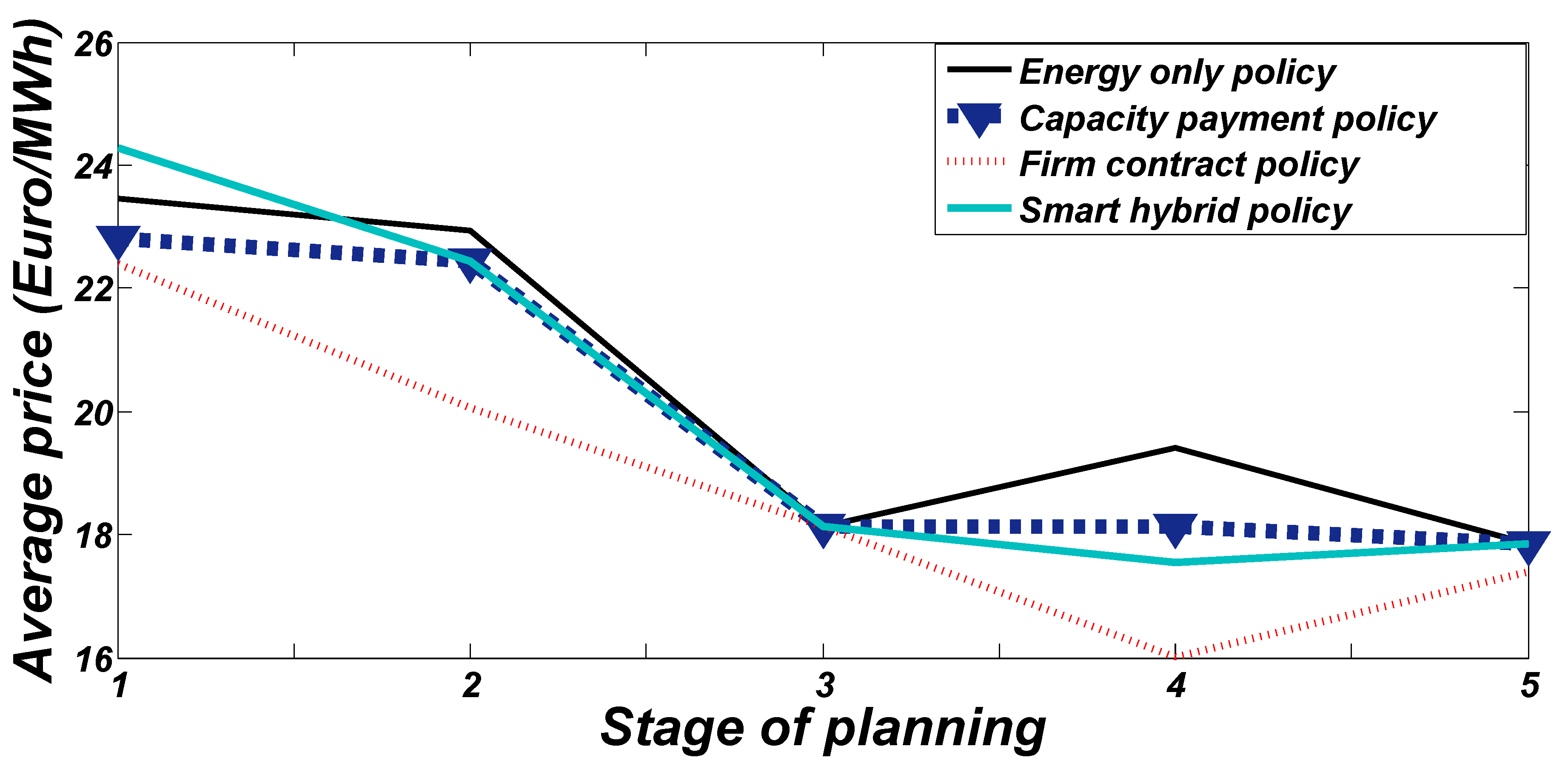
- The total profit of the strategic company in the hybrid market increases by 76% compared to the FC market despite a 1500 MW decline in the strategic company’s investment. The strategic company’s profit in the hybrid market is 3.89 and 1.82 times as much as that in the EO and CP markets. The net surplus of the strategic company in this market increased by 74%, 22.73%, and 0.29% compared to its value on the EO, CP, and FC markets, respectively.
- √
- Social welfare on the hybrid market increases by 11.95% and 11.19%, respectively, compared to its values on the EO and CP markets. Net consumer surplus in the hybrid market decreases by 34.97% due to an increase of 7.66% in the market price. Therefore, social welfare in this market decreases by 2.65% compared to its value in the FC market.
- √
- The total consumer surplus is 138.39 M€, 166.03 M€, 258.63 M€, and 168.17 M€ for the EO, CP, FC, and H designs accordingly. As a result, FC market is assumed as the most appropriate policy for consumers.
- √
- Net surplus of non-strategic companies on the EO market increases by 14.49%, 61.77%, and 22.37% respectively compared to the EO, CP, and FC policies. Therefore, the EO market is better for non-strategic companies in the long run.
- √
- Strategic company’s profit in the hybrid policy is 3.89, 1.82, and 1.76 times higher than that in the EO, CP, and FC policies. Therefore, the hybrid market is better for the strategic company.
- √
- Table 1 provides the reliability indices of GEP planning for different markets during the planning period. Investment incentives improve network reliability significantly. In the absence of investment in one stage, indices of reliability increase over the previous stage due to the growth in load. In the case of the same investments in different policies, reliability depends on a potential investment, and power consumption, and the number of new units.
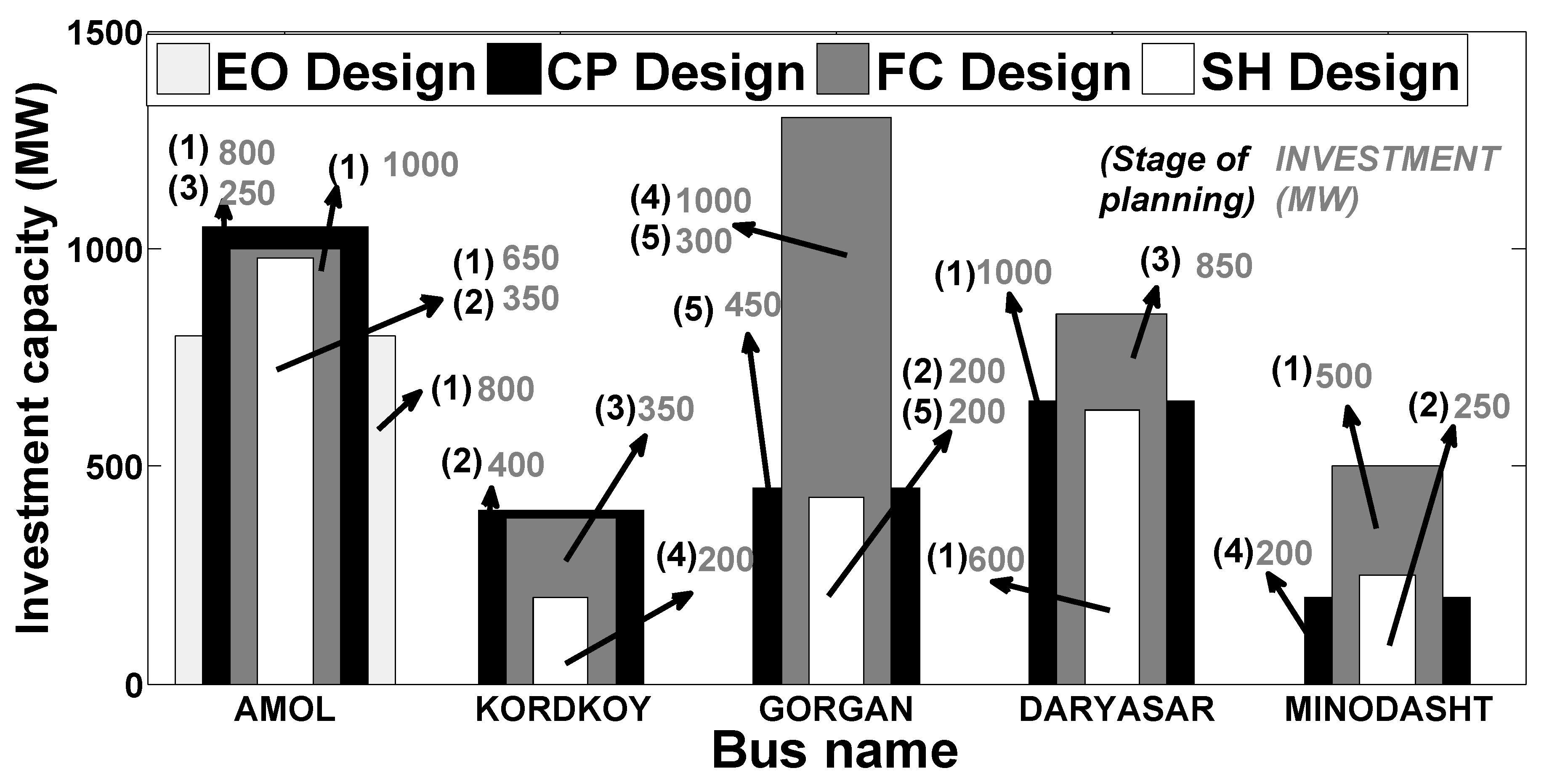
6.3. Results of Competition between Strategic Producers
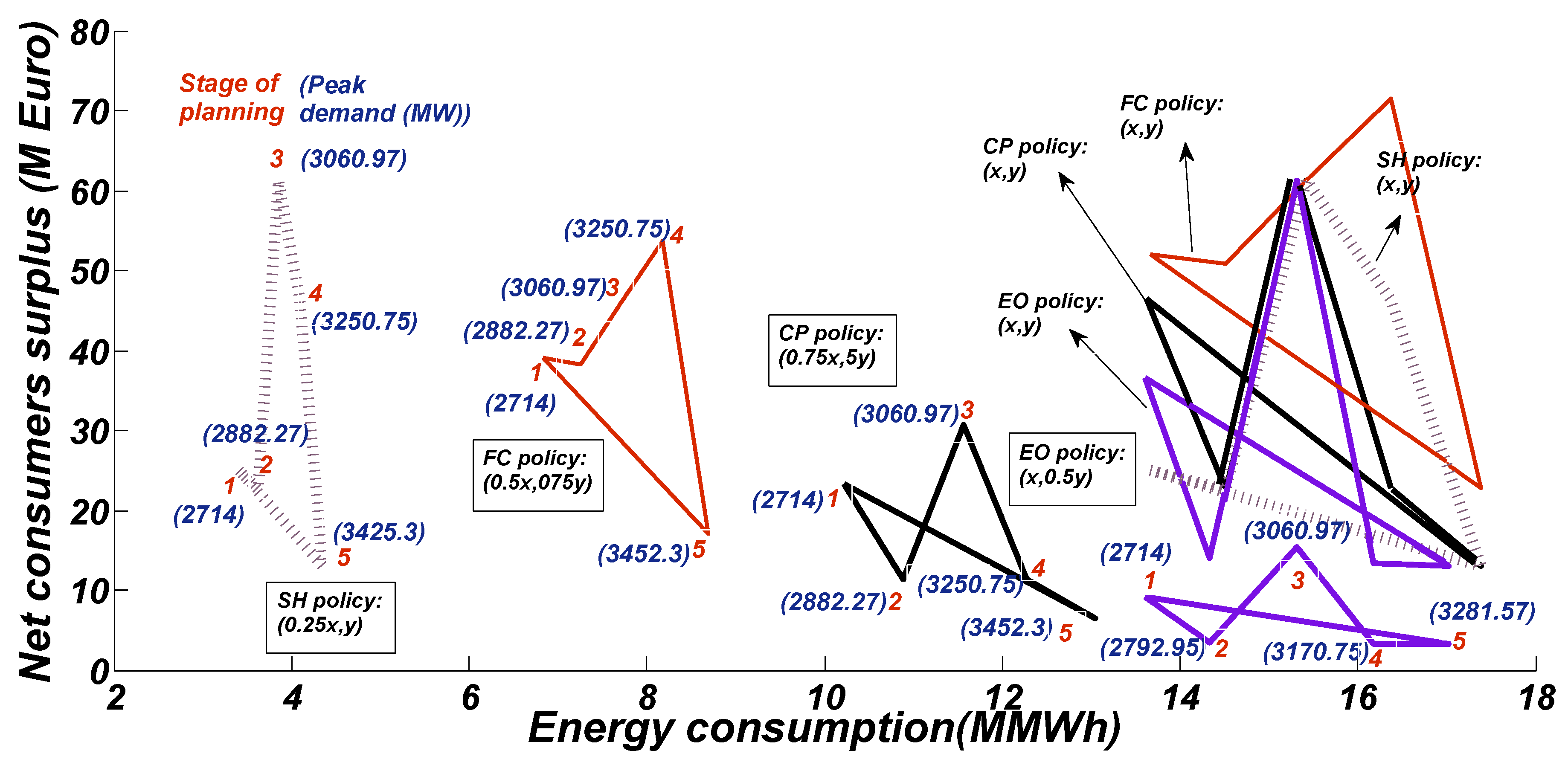
- Energy only: For EO strategy, only strategic producer 2 invests in new peak power plants to build 200 MW in the fourth year of planning in Sari and 300 MW in the fifth year of planning in Aliabad. In this case, the carbon emission for the whole year is 52,000 tons, which is equal to the highest level allowed. Social welfare and total productions are 74.3 M€ and 3.57 MWh, respectively, with a capital cost of 7.09 M€. It is also noted that the average market clearing price is 33,551 €/MWh.
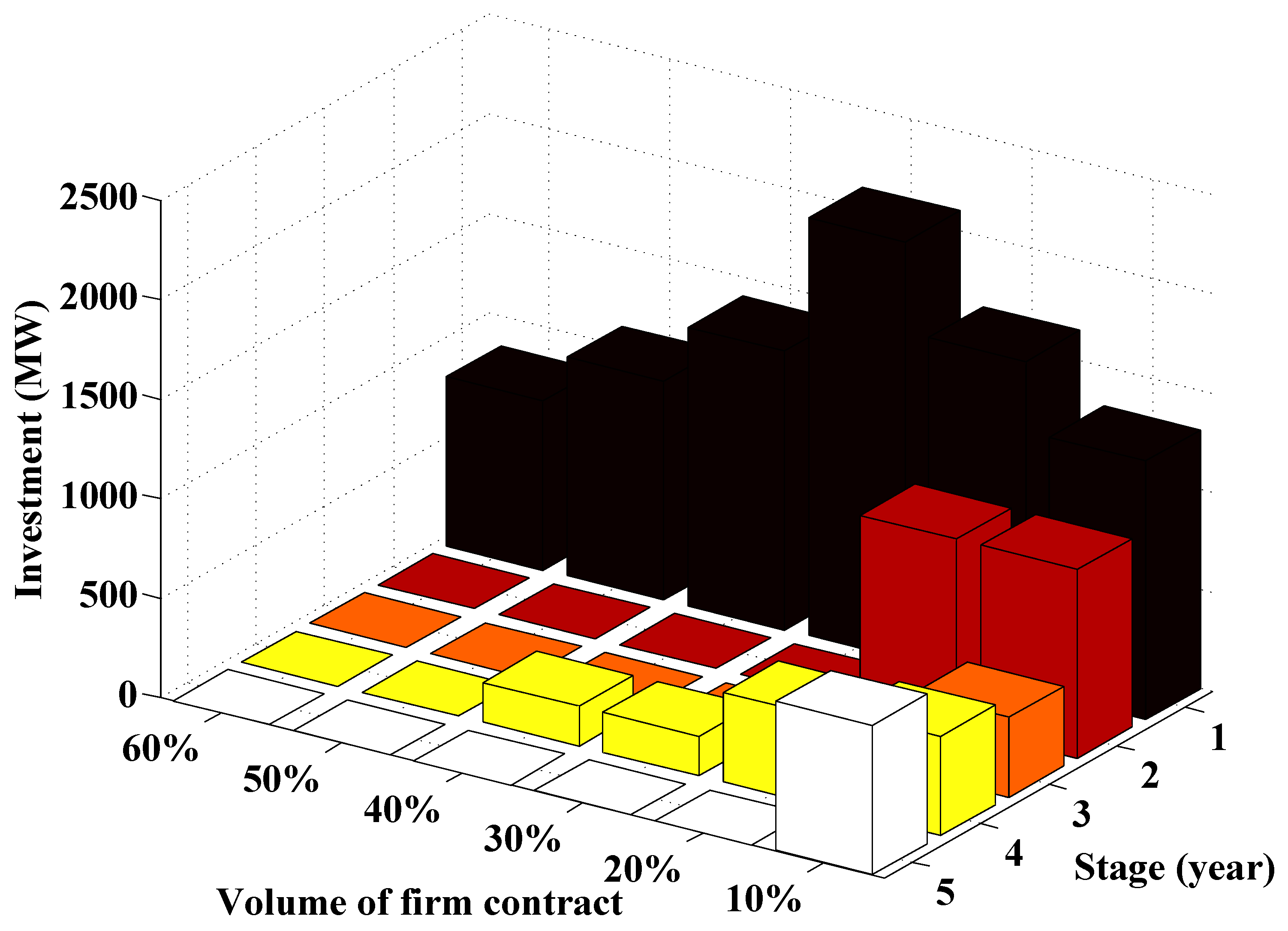
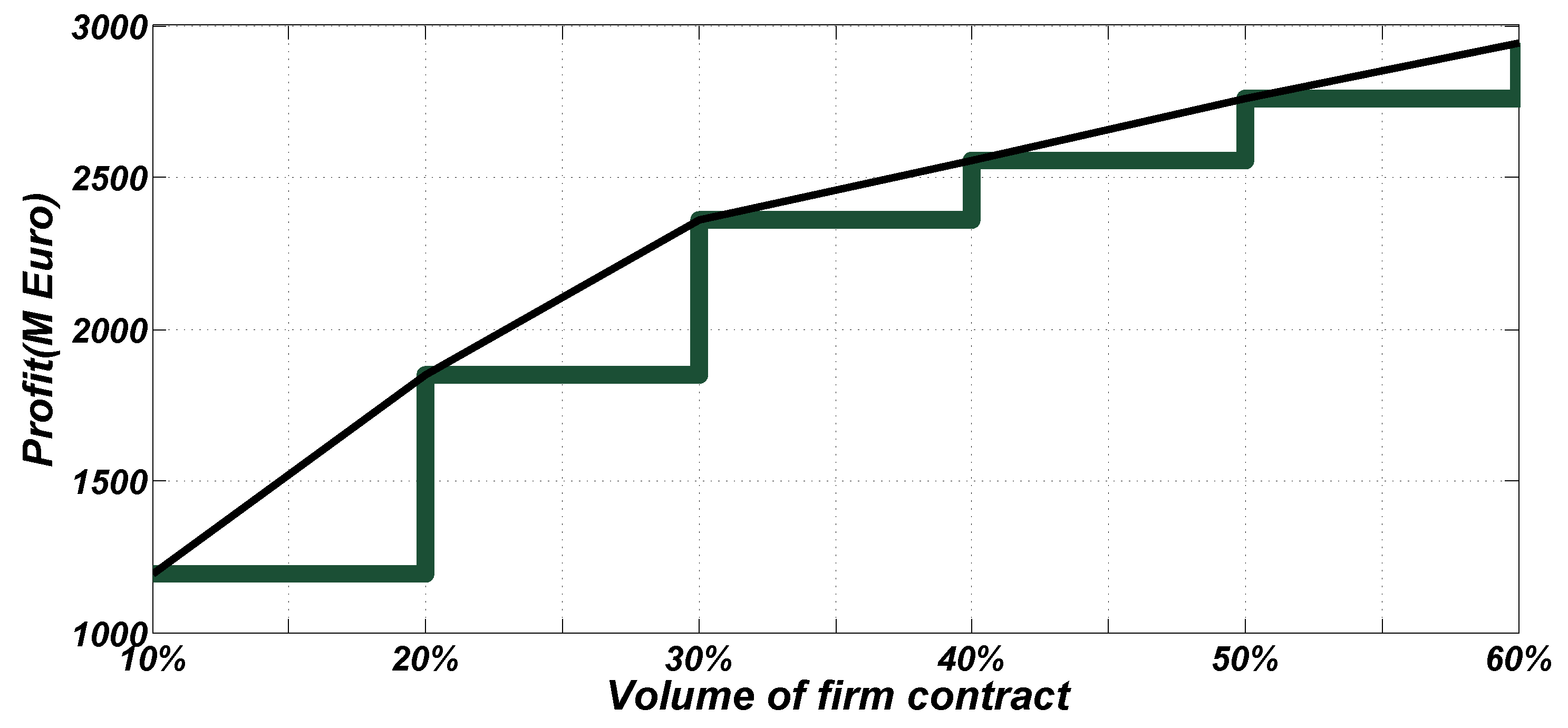
- Firm contact: In the context of FC strategy, where the volume of the firm contract is to be 10%, strategic producer 1 is encouraged to invest in 800 MW of peak units in Neka in year 5. On the other hand, strategic producer 2 invests in 300 MW of peak power in the first year in Sari and 200 MW in the fourth year in Aliabad. Thus, the total investment of producers in the FC policy is increased by 160% compared to that of the EO policy due to the firm contract; accordingly, the investment expense in the FC policy is increased by 317%. Social welfare is also improved by 299%. In addition, the Available Capacity In Planning Duration (ACIPD) [55] in the FC policy is 2700 MW; that of the EO strategy, on the other hand, is equivalent to 700 MW.When the volume of the firm contract is increased by 20%, strategic producer 2 invests 200 MW of peak units 1 year as compared to the previous year. In this situation, social welfare is boosted by 41.54 percent. In addition, social welfare improves by 37.1% when the amount of the agreement is increased by 10%. There is a carbon emission restriction when the quantity of the firm contract exceeds 30%. The carbon emission limits have therefore risen to 4, 2, and 1 Mton for peak, shoulder, and off-peak time blocks, respectively. In this case, when the volume of firm contract policy is 30%, strategic producer 1 is encouraged to invest 700 MW in Sari and 1000 MW in Neka, all in the fifth year. Investment cost for volumes of firm contract 30%, 40%, 50%, 60%, 70%, 80%, 90%, and 100% is equal to 29.83 M€, 29.83, 29.83, 26.86, 29.18, 29.55, 28.54, and 29.27 M€ accordingly. As a consequence of the budget restriction, it is clear that there is no special change in investment costs. In addition, the social welfare connected with each of these volumes is 235.24, 288.53, 341.82, 363.32, 440.34, 499.21, 534.24, and 598.80 M€, respectively. Social welfare is observed to improve as the volume of the firm contract rises. In addition, the total carbon emission for each volume is 2.41, 2.96, 3.51, 3.73, 4.48, 4.82, 5.39, 5.9 Mton, respectively. Understandably, the quantity of total carbon emissions rises with a rise in the volume of the firm contract. For each case, ACIPD is equal to 3000 MW, 3000 MW, 3000 MW, 2700 MW, 2900 MW, 2800 MW, 2800 MW, and 2800 MW, respectively. It is noted that there is no particular shift to the ACIPD caused by a budget restriction. With an increase in the budget, it is observed that the ACIPD has risen.
- Capacity payment: In CP policy, strategic producer 1 invests 1900 MW of peak units in Sari and Neka so that the amount of ACIPD, in this case, is 2900 MW. As a result, CP policy ACIPD rises by 2200 MW compared to EO policy. As peak units have reduced carbon emissions, strategic producers are encouraged to invest in this type of technology. Social welfare in CP policy is equivalent to 74.39 M€, while carbon emissions are equivalent to 0.75 Mton.
- Hybrid market: In the hybrid market, strategic producer 1 invests 200 MW in Neka in the first year and 200 MW in Sari in the third year. Strategic producer 2 also invests 200 MW of peak units in the first year. As a consequence, ACIPD is 2600 MW in the Hybrid market. The amount of carbon emissions and social welfare is 1.2 MTon and 130.38 M€, respectively; following that, it is observed that the amounts of carbon emission and social welfare are increased by 63%, and 75%, compared to those of the CP market, As a result, these amounts have risen compared to those of the EO policy. It is observed that no particular change in ACIPD, social welfare, and carbon emissions has occurred with a rise in the carbon emission restriction as a result of the lack of a budget to spend. When the budget is expanded to 150 M€, the social welfare and carbon emissions are equivalent to 342.2 M€ and 3.42 MTon, respectively.
7. Conclusions
- The results illustrated that the FC, CP, and hybrid markets encouraged investment in the peak unit. Constructing units with maximum capacities according to the available investments are recommended for the considered markets to improve the reliability indices.
- The energy the new strategic units produce in the FC market is increased compared to the CP market.
- With the increase in the volume of the FC, total investment capacity by the strategic company is reduced. It is emphasized that the technology of all units reaches its peak to maximize the sharing capabilities of non-strategic companies.
- The amount of total carbon emission increases with an increase in the volume of the firm contract.
- No specific change in ACIPD, social welfare, and carbon emissions occur with an increase in carbon emission limitation if there is no more budget to invest. In fact, there is a connection between budget, carbon limitation, and volume of firm contracts in the planning.
- The strategic company’s profit can be increased by optimal volume and rate of FC, which in turn increases the strategic company’s profit. In summary, the FC market policies are observed to lead and to be the most optimal in terms of social welfare for consumers and non-strategic companies in the long run as well as hybrid market and also being better suited for the strategic counterparts.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| r/r | stage index |
| t | demand blocks index |
| y | strategic company index |
| i/k | index of new/existing power plants owned by strategic company |
| d | index for demand |
| w/w | scenario index |
| h | new unit capacity index |
| n/m | bus index |
| weight of demand block t in stage r | |
| weight of scenario w | |
| demand growth in year r and scenario w | |
| annual investment cost of the new generating unit (€/MW) | |
| total budget of strategic generation company y for investment (M€) | |
| option h for investment capacity of new unit i (MW) | |
| capacity of existing generation unit k of strategic generation company y (MW) | |
| maximum load of demand d in block t (MW) | |
| marginal cost of new/existing unit of strategic GENCO (€/MWh) | |
| price bid of demand d in demand block t and year r (M€Wh) | |
| susceptance of line n–m (p.u.) | |
| transmission capacity of line n–m (MW) | |
| f | discount rate |
| firm contract volume/price (Percent)/(€) | |
| capacity payment price (€) | |
| forced outage rate of new/existing unit (Percent) | |
| coefficient of existing/new units (Ton/MWh) | |
| limit of emission (Ton) | |
| amount of tax of emission (€/Ton) | |
| capacity investment of new unit i of the strategic generation company y in stage r (MW) | |
| binary variable that is equal to 1 if the hth investment option of technology i is selected in stage r, otherwise it is equal to 0 | |
| power produced by existing/new unit k/i of strategic generation company y (MW) | |
| available Capacity/Power produced of new unit i of strategic generation company y in year r, in years after the installation in year r (MW) | |
| demand d, in stage r (MW) | |
| offer of strategic GENCO y in market-clearing for its existing/new unit k/i (€/MWh) | |
| offer of strategic GENCO y for its new unit i, in market-clearing related to the stage r, in the stages after the Construction in stage r (€/MWh) | |
| market-clearing price (€/MWh) | |
| marginal cost of new unit of GENCO i, in stage r, in the stages after the installation in stage r (€/MWh) | |
| voltage angle | |
Appendix A
Appendix A.1. Converting the DCC-EPEC Market Model into Equivalent Single-Level Models
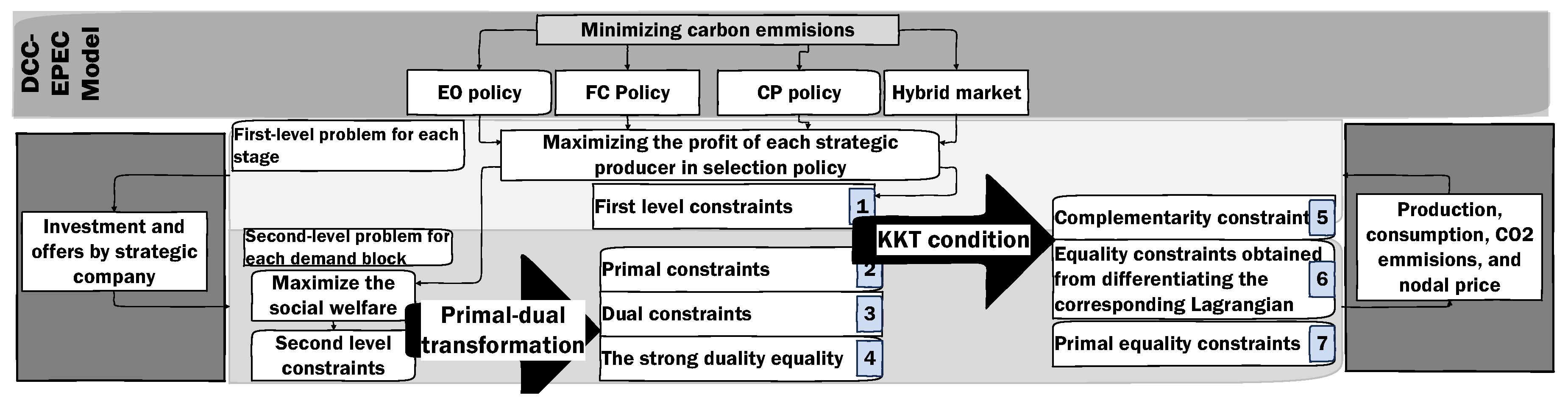
Appendix A.2. Implementing Primal-Dual Transformation to the Second Level
Appendix A.2.1. Dual Constraints
Appendix A.2.2. The Strong Duality Equality of the Second Level Problem
Appendix A.2.3. Primal Constraints
Appendix A.3. Enforcing Karush–Kuhn–Tucker (KKT) Conditions to the New First Level Model
Appendix A.3.1. Primal Equality Constraints
Appendix A.3.2. Constraints Obtained from the Derivative of the Related Lagrangian Term to Decision Variables
Appendix A.3.3. Complementary Constraints
Appendix A.4. Linearization Related to Equivalent MINLP Problem of the DCC-EPEC Model
- For linearizing the obtained complementary constraint, a different approach can be used. The first approach frequently used in recent research is big-M reformulation. This approach is used to linearize without approximation [65]. Choosing the amount of M is such a challenging issue that the authors in [66] pay attention to overcoming this problem. In this approach, the obtained complementary constraint in the form of 0 ≤ x ⊥ y ≥ 0 is equivalent to x ≥ 0, y ≥ 0, x ≤ MO and y ≤ M(1-O) so that O and M are binary variables and a constant big amount. Another approach without approximation is an SOS1-based one. In this approach, x + y = and x − y = so that and are SOS1 variables [67]. This solution is so costly for large scale models that another approach which uses approximation has emerged. In this approach, SOS1 variables are relaxed to non-negative ones, leading to considering the term in an objective function to be penalized [67]. However, choosing the amount of b is also assumed to be an issue. In this paper, big-M reformulation is used to linearize.
- Dual theory constraint (Equation (A6)): The dual theory constraint obtained from primal-dual transform is nonlinear due to multiplication of continuous variables. On the other hand, owing to the fact that this equation is equivalent to the set of complimentary constraints using KKT conditions, dual theory constraints are replaced with equivalent constraints. Afterwards, the equivalent complementary constraints are linearized using the explanations of the previous part:
- Equations that have :Due to the fact that MPEC obtained is not convex, the amount of dual variables is not unique; consequently, dual variable () can be parameterized to a specific value.
References
- Ghalebani, A.; Das, T.K. Design of Financial Incentive Programs to Promote Net Zero Energy Buildings. IEEE Trans. Power Syst. 2017, 32, 75–84. [Google Scholar] [CrossRef]
- Movahednasab, A.; Rashidinejad, M.; Abdollahi, A. A system dynamics analysis of the long run investment in market based electric generation expansion with renewable resources. Int. Trans. Electr. Energy Syst. 2017, 27, e2338. [Google Scholar] [CrossRef]
- Marzband, M.; Azarinejadian, F.; Savaghebi, M.; Pouresmaeil, E.; Guerrero, J.M.; Lightbody, G. Smart transactive energy framework in grid-connected multiple home microgrids under independent and coalition operations. Renew. Energy 2018, 126, 95–106. [Google Scholar] [CrossRef]
- Qiu, J.; Yang, H.; Dong, Z.Y.; Zhao, J.H.; Meng, K.; Luo, F.J.; Wong, K.P. A Linear Programming Approach to Expansion Co-Planning in Gas and Electricity Markets. IEEE Trans. Power Syst. 2016, 31, 3594–3606. [Google Scholar] [CrossRef]
- Dehghan, S.; Amjady, N.; Conejo, A.J. Reliability-Constrained Robust Power System Expansion Planning. IEEE Trans. Power Syst. 2016, 31, 2383–2392. [Google Scholar] [CrossRef]
- Noz Delgado, G.M.; Contreras, J.; Arroyo, J.M. Multistage Generation and Network Expansion Planning in Distribution Systems Considering Uncertainty and Reliability. IEEE Trans. Power Syst. 2016, 31, 3715–3728. [Google Scholar] [CrossRef]
- Valinejad, J.; Barforoshi, T.; Marzband, M.; Pouresmaeil, E.; Godina, R.; Catalão, J.P.S. Investment Incentives in Competitive Electricity Markets. Appl. Sci. 2018, 8, 1978. [Google Scholar] [CrossRef]
- Park, H.; Baldick, R. Stochastic Generation Capacity Expansion Planning Reducing Greenhouse Gas Emissions. IEEE Trans. Power Syst. 2015, 30, 1026–1034. [Google Scholar] [CrossRef]
- Shu, J.; Wu, L.; Zhang, L.; Han, B. Spatial Power Network Expansion Planning Considering Generation Expansion. IEEE Trans. Power Syst. 2015, 30, 1815–1824. [Google Scholar] [CrossRef]
- Tavakoli, M.; Shokridehaki, F.; Akorede, M.F.; Marzband, M.; Vechiu, I.; Pouresmaeil, E. CVaR-based energy management scheme for optimal resilience and operational cost in commercial building microgrids. Int. J. Electr. Power Energy Syst. 2018, 100, 1–9. [Google Scholar] [CrossRef]
- Xu, Y.; Huang, C.; Chen, X.; Mili, L.; Tong, C.H.; Korkali, M.; Min, L. Response-Surface-Based Bayesian Inference for Power System Dynamic Parameter Estimation. IEEE Trans. Smart Grid 2018, 10, 5899–5909. [Google Scholar] [CrossRef]
- Ameli, A.; Farrokhifard, M.; Ahmadifar, A.; Haghifam, M. Distributed generation planning based on the distribution company’s and the DG owner’s profit maximization. Int. Trans. Electr. Energy Syst. 2013, 25, 216–232. [Google Scholar] [CrossRef]
- Valinejad, J.; Marzband, M.; Korkali, M.; Xu, Y.; Sumaiti, A.S.A. Hierarchical Interactive Architecture based on Coalition Formation for Neighborhood System Decision Making. arXiv 2019, arXiv:1910.07039. [Google Scholar]
- Barati, F.; Seifi, H.; Sepasian, M.S.; Nateghi, A.; Shafie-khah, M.; Catalão, J.P.S. Multi-Period Integrated Framework of Generation, Transmission, and Natural Gas Grid Expansion Planning for Large-Scale Systems. IEEE Trans. Power Syst. 2015, 30, 2527–2537. [Google Scholar] [CrossRef]
- Valinejad, J.; Oladi, Z.; Barforoushi, T.; Parvaniac, M. Stochastic Unit Commitment in the Presence of Demand Response Program under Uncertainties. Int. J. Eng. 2017, 30, 1134–1143. [Google Scholar]
- Marzband, M.; Fouladfar, M.H.; Akorede, M.F.; Lightbody, G.; Pouresmaeil, E. Framework for smart transactive energy in home-microgrids considering coalition formation and demand side management. Sustain. Cities Soc. 2018, 40, 136–154. [Google Scholar] [CrossRef]
- Marzband, M.; Javadi, M.; Pourmousavi, S.A.; Lightbody, G. An advanced retail electricity market for active distribution systems and home microgrid interoperability based on game theory. Electr. Power Syst. Res. 2018, 157, 187–199. [Google Scholar] [CrossRef]
- Liu, G.; Wen, F.; MacGill, I. Optimal timing for generation investment with uncertain emission mitigation policy. Eur. Trans. Electr. Power 2010, 21, 1015–1027. [Google Scholar] [CrossRef]
- Gil, E.; Aravena, I.; Cárdenas, R. Generation Capacity Expansion Planning Under Hydro Uncertainty Using Stochastic Mixed Integer Programming and Scenario Reduction. IEEE Trans. Power Syst. 2015, 30, 1838–1847. [Google Scholar] [CrossRef]
- Quintero, J.; Zhang, H.; Chakhchoukh, Y.; Vittal, V.; Heydt, G.T. Next, Generation Transmission Expansion Planning Framework: Models, Tools, and Educational Opportunities. IEEE Trans. Power Syst. 2014, 29, 1911–1918. [Google Scholar] [CrossRef]
- Jabr, R.A. Robust Transmission Network Expansion Planning With Uncertain Renewable Generation and Loads. IEEE Trans. Power Syst. 2013, 28, 4558–4567. [Google Scholar] [CrossRef]
- Han, C.; Hur, D.; Sohn, J.; Park, J. Assessing impacts of capacity mechanism on long term market equilibrium. Eur. Trans. Electr. Power 2009, 20, 218–230. [Google Scholar] [CrossRef]
- Han, C.K.; Hur, D.; Sohn, J.M.; Park, J.K. Assessing the Impacts of Capacity Mechanisms on Generation Adequacy With Dynamic Simulations. IEEE Trans. Power Syst. 2011, 26, 1788–1797. [Google Scholar] [CrossRef]
- Dent, C.J.; Bialek, J.W.; Hobbs, B.F. Opportunity Cost Bidding by Wind Generators in Forward Markets: Analytical Results. IEEE Trans. Power Syst. 2011, 26, 1600–1608. [Google Scholar] [CrossRef]
- Doorman, G.L.; Botterud, A. Analysis of Generation Investment Under Different Market Designs. IEEE Trans. Power Syst. 2008, 23, 859–867. [Google Scholar] [CrossRef]
- Lee, Y.Y.; Baldick, R.; Hur, J. Firm-Based Measurements of Market Power in Transmission-Constrained Electricity Markets. IEEE Trans. Power Syst. 2011, 26, 1962–1970. [Google Scholar] [CrossRef]
- Alvarez, F.; Rudnick, H. Impact of Energy Efficiency Incentives on Electricity Distribution Companies. IEEE Trans. Power Syst. 2010, 25, 1865–1872. [Google Scholar] [CrossRef]
- Tavakoli, M.; Shokridehaki, F.; Mousa Marzband, R.G.; Pouresmaeil, E. A two stage hierarchical control approach for the optimal energy management in commercial building microgrids based on local wind power and PEVs. Sustain. Cities Soc. 2018, 41, 332–340. [Google Scholar] [CrossRef]
- Soder, L. Analysis of Pricing and Volumes in Selective Capacity Markets. IEEE Trans. Power Syst. 2010, 25, 1415–1422. [Google Scholar] [CrossRef]
- Vazquez, C.; Rivier, M.; Perez-Arriaga, I.J. A market approach to long-term security of supply. IEEE Trans. Power Syst. 2002, 17, 349–357. [Google Scholar] [CrossRef]
- Li, F.; Tolley, D.; Padhy, N.P.; Wang, J. Framework for Assessing the Economic Efficiencies of Long-Run Network Pricing Models. IEEE Trans. Power Syst. 2009, 24, 1641–1648. [Google Scholar] [CrossRef]
- Kockar, I.; Galiana, F.D. Combined pool/bilateral dispatch. II. Curtailment of firm and nonfirm contracts. IEEE Trans. Power Syst. 2002, 17, 1184–1190. [Google Scholar] [CrossRef]
- Careri, F.; Genesi, C.; Marannino, P.; Montagna, M.; Rossi, S.; Siviero, I. Generation Expansion Planning in the Age of Green Economy. IEEE Trans. Power Syst. 2011, 26, 2214–2223. [Google Scholar] [CrossRef]
- Saboori, H.; Hemmati, R. Considering Carbon Capture and Storage in Electricity Generation Expansion Planning. IEEE Trans. Sustain. Energy 2016, 7, 1371. [Google Scholar] [CrossRef]
- Valinejad, J.; Firouzifar, S.; Marzband, M.; Al-Sumaiti, A.S. Reconsidering insulation coordination and simulation under the effect of pollution due to climate change. Int. Trans. Electr. Energy Syst. 2018, 28, e2595. [Google Scholar] [CrossRef]
- Kazempour, S.J.; Conejo, A.J.; Ruiz, C. Strategic Generation Investment Using a Complementarity Approach. IEEE Trans. Power Syst. 2011, 26, 940–948. [Google Scholar] [CrossRef]
- Kazempour, S.J.; Conejo, A.J. Strategic Generation Investment Under Uncertainty Via Benders Decomposition. IEEE Trans. Power Syst. 2012, 27, 424–432. [Google Scholar] [CrossRef]
- Valinejad, J.; Marzband, M.; Akorede, M.F.; Elliott, I.D.; Godina, R.; Matias, J.; Pouresmaeil, E. Long-term decision on wind investment with considering different load ranges of power plant for sustainable electricity energy market. Sustainability 2018, 10, 3811. [Google Scholar] [CrossRef]
- Kazempour, S.J.; Conejo, A.J.; Ruiz, C. Generation investment equilibria with strategic producer—Part I. IEEE Trans. Power Syst. 2013, 28, 2613–2622. [Google Scholar] [CrossRef]
- Kazempour, S.J.; Conejo, A.J.; Ruiz, C. Generation Investment Equilibria With Strategic Producers—Part II: Case Studies. IEEE Trans. Power Syst. 2013, 28, 2623–2631. [Google Scholar] [CrossRef]
- Wogrin, S.; Barquín, J.; Centeno, E. Capacity Expansion Equilibria in Liberalized Electricity Markets: An EPEC Approach. IEEE Trans. Power Syst. 2013, 28, 1531–1539. [Google Scholar] [CrossRef]
- Valinejad, J.; Marzband, M.; Barforoushi, T.; Kyyrä, J.; Pouresmaeil, E. Dynamic stochastic EPEC model for Competition of Dominant Producers in Generation Expansion Planning. In Proceedings of the 5th International Symposium on Environment Friendly Energies and Applications (EFEA), Rome, Italy, 24–26 September 2018. [Google Scholar]
- Valinejad, J.; Marzband, M.; Akorede, M.F.; Barforoshi, T.; Jovanović, M. Generation expansion planning in electricity market considering uncertainty in load demand and presence of strategic GENCOs. Electr. Power Syst. Res. 2017, 152, 92–104. [Google Scholar] [CrossRef]
- Taheri, S.S.; Kazempour, J.; Seyedshenava, S. Transmission expansion in an oligopoly considering generation investment equilibrium. Energy Econ. 2017, 64, 55–62. [Google Scholar] [CrossRef]
- Pozo, D.; Sauma, E.E.; Contreras, J. A Three-Level Static MILP Model for Generation and Transmission Expansion Planning. IEEE Trans. Power Syst. 2013, 28, 202–210. [Google Scholar] [CrossRef]
- Hesamzadeh, M.R.; Yazdani, M. Transmission Capacity Expansion in Imperfectly Competitive Power Markets. IEEE Trans. Power Syst. 2014, 29, 62–71. [Google Scholar] [CrossRef]
- Jin, S.; Ryan, S.M. A Tri-Level Model of Centralized Transmission and Decentralized Generation Expansion Planning for an Electricity Market—Part I: Formulation. IEEE Trans. Power Syst. 2014, 29, 132–141. [Google Scholar] [CrossRef]
- Jin, S.; Ryan, S.M. A Tri-Level Model of Centralized Transmission and Decentralized Generation Expansion Planning for an Electricity Market—Part II: Case Studies. IEEE Trans. Power Syst. 2014, 29, 142–168. [Google Scholar] [CrossRef]
- Valinejad, J.; Marzband, M.; Xu, Y.; Uppal, H.; Al-Sumaiti, A.S.; Barforoshi, T. Dynamic behavior of multi-carrier energy market in view of investment incentives. Electr. Eng. 2019, 101, 1033–1051. [Google Scholar] [CrossRef]
- Barforoushi, T.; Moghaddam, M.P.; Javidi, M.H.; Sheikh-El-Eslami, M.K. Evaluation of Regulatory Impacts on Dynamic Behavior of Investments in Electricity Markets: A New Hybrid DP/GAME Framework. IEEE Trans. Power Syst. 2010, 25, 1978–1986. [Google Scholar] [CrossRef]
- Niu, H.; Baldick, R.; Zhu, G. Supply function equilibrium bidding strategies with fixed forward contracts. IEEE Trans. Power Syst. 2005, 20, 1859–1867. [Google Scholar] [CrossRef]
- van Stiphout, A.; Vos, K.D.; Deconinck, G. The Impact of Operating Reserves on Investment Planning of Renewable Power Systems. IEEE Trans. Power Syst. 2017, 32, 378–388. [Google Scholar] [CrossRef]
- Zhao, F.; Luh, P.B.; Yan, J.H.; Stern, G.A.; Chang, S.C. Payment Cost Minimization Auction for Deregulated Electricity Markets With Transmission Capacity Constraints. IEEE Trans. Power Syst. 2008, 23, 532–544. [Google Scholar] [CrossRef]
- Valinejad, J.; Barforoushi, T. Generation expansion planning in electricity markets: A novel framework based on dynamic stochastic MPEC. Int. J. Electr. Power Energy Syst. 2015, 70, 108–117. [Google Scholar] [CrossRef]
- Valinejad, J.; Marzband, M.; Busawona, K.; Kyyrä, J.; Pouresmaeil, E. Investigating Wind Generation Investment Indices in Multi-Stage Planning. In Proceedings of the 5th International Symposium on Environment Friendly Energies and Applications (EFEA), Rome, Italy, 24–26 September 2018. [Google Scholar]
- Vasquez, J.; Guerrero, J.; Savaghebi, M.; Eloy-Garcia, J.; Teodorescu, R. Modeling, Analysis, and Design of Stationary-Reference-Frame Droop-Controlled Parallel Three-Phase Voltage Source Inverters. IEEE Trans. Ind. Electron. 2013, 60, 1271–1280. [Google Scholar] [CrossRef]
- Bauso, D. Game Theory: Models, Numerical Methods and Applications; Now Publishers: Delft, The Netherlands, 2014. [Google Scholar]
- Birge, J.R.; Louveaux, F. Introduction to Stochastic Programming; Springer: Cham, Switzerland, 2011. [Google Scholar]
- Xu, Y.; Mili, L.; Sandu, A.; von Spakovsky, M.R.; Zhao, J. Propagating Uncertainty in Power System Dynamic Simulations Using Polynomial Chaos. IEEE Trans. Power Syst. 2018, 34, 338–348. [Google Scholar] [CrossRef]
- Conejo, A.J.; Morales, M.C.J.M. Decision Making under Uncertainty in Electricity Markets; Springer: Cham, Switzerland, 2010. [Google Scholar]
- Shabani, A.; Hosseini, H.; Karegar, H.K.; Jalilzadeh, S. Optimal generation expansion planning in IPP presence with HCGA. In Proceedings of the 2008 IEEE 2nd International Power and Energy Conference, Johor Bahru, Malaysia, 1–3 December 2008; pp. 143–147. [Google Scholar]
- Nualhong, D.; Chusanapiputt, S.; Jantarang, S.; Pungprasert, V. Generation Expansion Planning Including Biomass Energy Sources with Global Environmental Consideration Using Improved Tabu Search. In Proceedings of the TENCON 2005—2005 IEEE Region 10 Conference, Melbourne, Australia, 21–24 November 2005; pp. 1–5. [Google Scholar]
- Xu, Y.; Mili, L. Probabilistic Power Flow Analysis based on the Adaptive Polynomial Chaos-ANOVA Method. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018. [Google Scholar]
- Xu, Y.; Mili, L.; Zhao, J. Probabilistic Power Flow Calculation and Variance Analysis based on Hierarchical Adaptive Polynomial Chaos-ANOVA Method. IEEE Trans. Power Syst. 2019, 34, 3316–3325. [Google Scholar] [CrossRef]
- Fortuny-Amat, J.; McCarl, B. A representation and economic interpretation of a two-level programming problem. J. Oper. Res. Soc. 1981, 32, 783–792. [Google Scholar] [CrossRef]
- Moiseeva, E.; Hesamzadeh, M.R. Strategic Bidding of a Hydropower Producer under Uncertainty: Modified Benders Approach. IEEE Trans. Power Syst. 2018, 33, 861–873. [Google Scholar] [CrossRef]
- Siddiqui, S.; Gabriel, S.A. An SOS1-based approach for solving MPECs with a natural gas market application. Netw. Spat. Econ. 2013, 13, 205–227. [Google Scholar] [CrossRef]




| Year | Market Design | LOLP (%) | LOLE (day/year) | LOEE (MMWh) |
|---|---|---|---|---|
| 1 | Energy | 1.02 | 3.71 | 0.0244 |
| Capacity payment | 0.00239 | 0.0087 | 0.0000618 | |
| Firm contract | 0.0318 | 0.116 | 0.000908 | |
| Hybrid | 0.00176 | 0.0064 | 0.0000779 | |
| 2 | Energy | 1.03 | 3.77 | 0.0321 |
| Capacity payment | 0.00118 | 0.0043 | 0.0000346 | |
| Firm contract | 0.0338 | 0.123 | 0.000893 | |
| Hybrid | 0.00374 | 0.0137 | 0.0000779 | |
| 3 | Energy | 1.1 | 4.02 | 0.0579 |
| Capacity payment | 0.003147 | 0.0115 | 0.0000880 | |
| Firm contract | 0.0419 | 0.153 | 0.00168 | |
| Hybrid | 0.00563 | 0.0206 | 0.000204 | |
| 4 | Energy | 1.18 | 4.30 | 0.0697 |
| Capacity payment | 0.00326 | 0.0119 | 0.0000889 | |
| Firm contract | 0.00133 | 0.005 | 0.0000381 | |
| Hybrid | 0.0119 | 0.0435 | 0.000411 | |
| 5 | Energy | 1.22 | 4.44 | 0.0818 |
| Capacity payment | 0.0137 | 0.005 | 0.0000389 | |
| Firm contract | 0.0003627 | 0.00048 | 0.0000032 | |
| Hybrid | 0.00318 | 0.134 | 0.000962 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valinejad, J.; Marzband, M.; Elsdon, M.; Saad Al-Sumaiti, A.; Barforoushi, T. Dynamic Carbon-Constrained EPEC Model for Strategic Generation Investment Incentives with the Aim of Reducing CO2 Emissions. Energies 2019, 12, 4813. https://doi.org/10.3390/en12244813
Valinejad J, Marzband M, Elsdon M, Saad Al-Sumaiti A, Barforoushi T. Dynamic Carbon-Constrained EPEC Model for Strategic Generation Investment Incentives with the Aim of Reducing CO2 Emissions. Energies. 2019; 12(24):4813. https://doi.org/10.3390/en12244813
Chicago/Turabian StyleValinejad, Jaber, Mousa Marzband, Michael Elsdon, Ameena Saad Al-Sumaiti, and Taghi Barforoushi. 2019. "Dynamic Carbon-Constrained EPEC Model for Strategic Generation Investment Incentives with the Aim of Reducing CO2 Emissions" Energies 12, no. 24: 4813. https://doi.org/10.3390/en12244813
APA StyleValinejad, J., Marzband, M., Elsdon, M., Saad Al-Sumaiti, A., & Barforoushi, T. (2019). Dynamic Carbon-Constrained EPEC Model for Strategic Generation Investment Incentives with the Aim of Reducing CO2 Emissions. Energies, 12(24), 4813. https://doi.org/10.3390/en12244813





