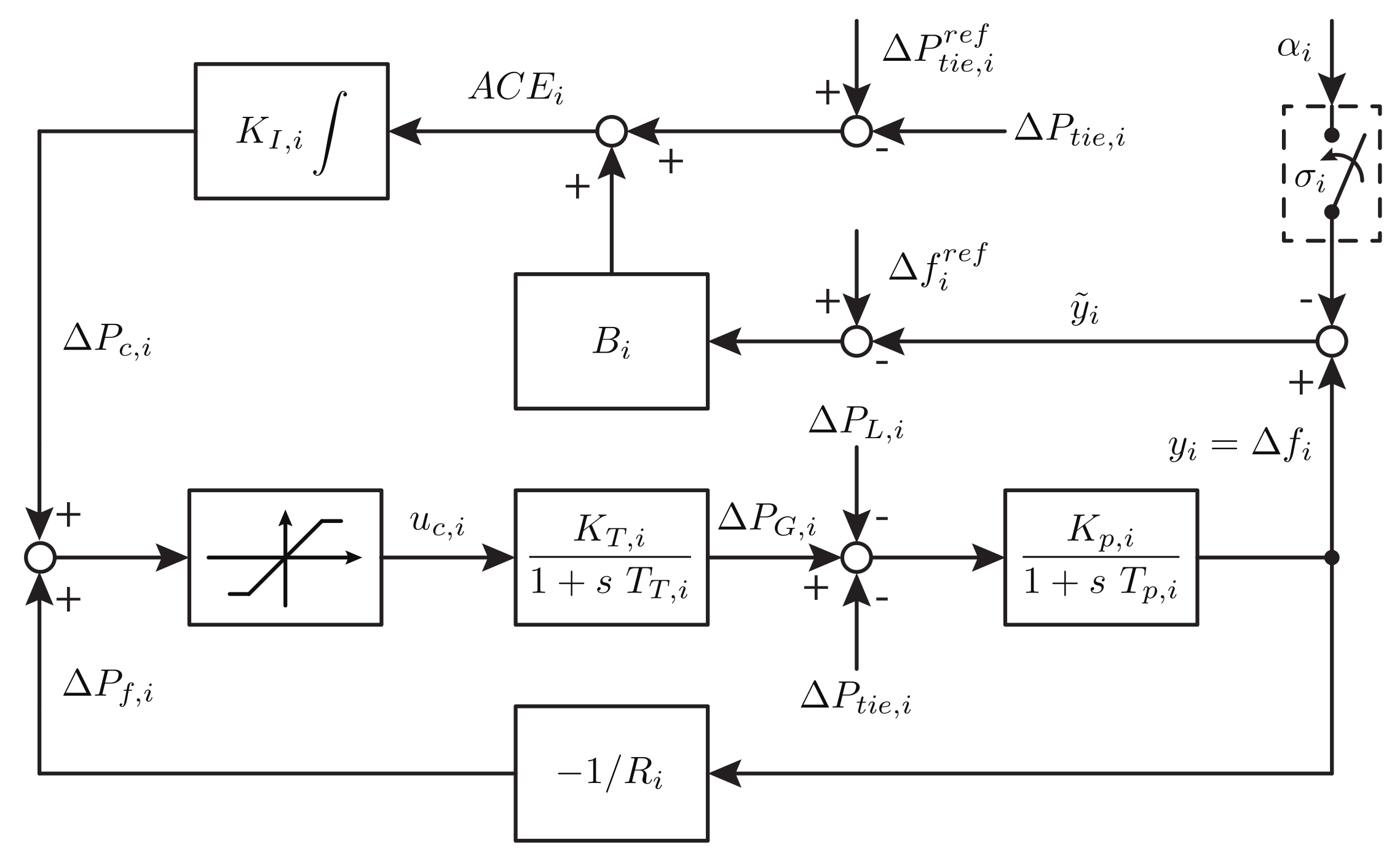
In this section, we investigate the security enhancing capabilities of the previously developed estimation-based and set-theoretic attack detectors, considering the load-frequency control loop of the test case two-area power system, subject to an intermittent data corruption cyber-attack on the frequency measurements. The efficiency of the proposed hybrid detection scheme is also commented and verified in each attack scenario studied.
In contrast, intermittent attacks, that affect only some control areas, are much more realistic, since they require less resources for their implementation. From an impact point of view, the intermittent attacks are equally potent, since they can create oscillations on the power exchanged between the connected areas. In this way, they stress the tie lines to their thermal limits, forcing them to transmit on average more power than they are scheduled to, and they also compromise the synchronized operation of the coupled generators. Finally, their effect on the response of the power system is only temporary, something that makes them hard to detect during the nominal operation of the grid and even harder in the presence of load changes.
The parameters of the two-area power network used in the simulations are provided in the
Table 1. The formulas of
and
are given as
where
[Hz] is the nominal network frequency. The simulations start at
, the initial condition is set to be
and we have a global sampling frequency
[Hz]. The tie line is assumed to be lossless, the nominal exchanged power between the areas is scheduled to be
[MW] and the synchronization coefficients are
[MW/rad]. The bounds
are selected as small percentages of the power bases
and the bounds
are selected through simulations. Specifically, we observed that even in the presence of the maximum admissible step load changes
, the deviations
remain always bounded by
. The bounds
service the maximum admissible load changes and they also ensure the existence of a nonempty robust invariant set
. The design parameters of the set-theoretic detector that was used here are taken directly from [
27].
The performance of both the estimation-based and the set-theoretic attack detectors is assessed in the case of an intermittent attack that affects only the first control area. The switching signal is given by the Equation (26), the switching bounds are given as [Hz] and [Hz], whereas the tolerance is selected as . For the second area we have an attack signal and for all . We remark that the value of is meaningful only if it is smaller than the frequency measurement error .
The remainder of this section is split into three parts. In the first part, we calculate the steady-state and transient critical thresholds of the output-based and the full state-based estimators, verifying their values via simulations. In the second part, we perform a comparative study on the behavior of the output-based, the full state-based and the set-theoretic attack detectors, for indicative values of the attack signal . It is shown that the two detectors complement each other and that we can achieve better results if we use the three-modal system operation proposed in the Equation (70). Finally, in the third part, we address certain limitations of the above detection mechanisms.
5.1. Estimator Thresholds Verification
For the extraction of the steady-state thresholds, we have to consider that each control area is affected by its maximum admissible step load change. Since the bounds of all are symmetric for all , the maximum admissible step load changes for the overall networked system can be described by any vertex of the polyhedral set . Consequently, we can select and then apply the disturbance for all . We highlight that for the extraction of the estimator thresholds, we must assume that the system evolves in the absence of an attacker, that is when for all and for all .
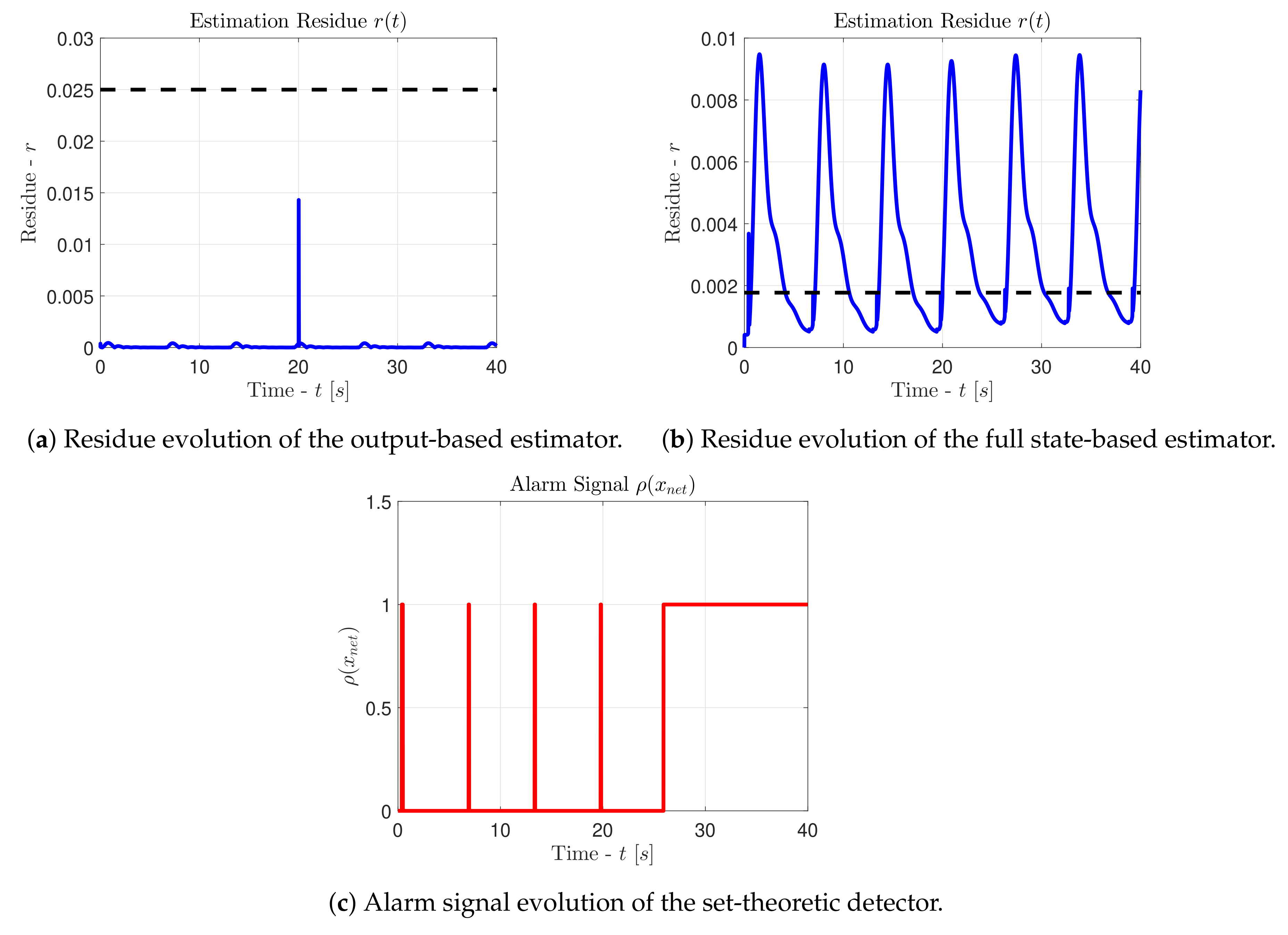
For the output-based estimator we have explained that the steady-state threshold must always be selected as
. Hence, the transient threshold cannot be explicitly derived by the Equation (69) and needs to be decided arbitrarily. We select
and based on the
Figure 2a the values of both thresholds are meaningful. For the full state-based estimator the steady-state threshold is given by the Equations (59)–(61) as
and this value is verified by the
Figure 2b. Based on the Equation (69) for
, we can obtain the transient bound as
.
We highlight that for a two-area power system, and only then, we encounter the degenerate case . Therefore, the equation used to describe in the network dynamics (28) and (29) can be neglected as redundant during the design of the estimators.
5.2. Case Study of an Intermittent Attack
The detection capabilities of the proposed detectors are assessed in the presence of unknown load changes. We assume that the power network is subject to the following step load changes:
Let us observe the
Figure 3, where we depict with solid blue lines (
•) the response of the estimation residue and with dashed black lines (•) the transient threshold
. It is evident that an output estimator is unable to disclose an attack with
, when it is driven by the switching signal of the Equation (26). In addition, if we consider the transient threshold
and the hybrid detection scheme (70), then it is obvious that the output estimator will never put the system in alert mode, since
for all
. Furthermore, the intense spike observed in the
Figure 3a occurs not due to the attack but due to the load change that happens at
[s]. On the other hand, the improved full state estimator is able to put the system into alert mode every time the attacker affects the automatic generation control unit and is always able to discern between an attack and a load change. Indeed, the normalization of the state variables with their maximum safety values smooths the spike at
[s], and creates overshoots in the response of the residue only when an actual attacker affects the networked system. Finally, the set-theoretic detector will never trigger an alarm, unless the state vector exits the set
at
[s]. In this case, the hybrid scheme (70) allows us to react faster in comparison to the case where we would depend only on the use of a set-theoretic detector.
Let us now perform an analysis regarding the detection and the early detection of the attack, in terms of absolute time units. For
, the
Figure 3b reveals that the first activation of an alert occurs at
[s]. Considering that the set-theoretic detector will trigger an alarm at
[s], we infer that the hybrid detection scheme hints the abnormal system behavior
[s] faster than the set-theoretic detector, offering a significant improvement.
Accordingly, in the
Figure 4, we consider the case of an attack with
. Again, the output estimator is unable to detect an attack during the transient response and decides that the system operates normally. Once more, the spike observed in the
Figure 4a at
[s] is caused by the load change and not by the attack. On the other hand, the improved full state estimator is again able to smooth the load change spike and can put the system into alert mode at the correct time instances. Lastly, for
, we observe that the set-theoretic detector can trigger an alarm whenever the attacker affects the system, ensuring its disclosure even from the very first activation.
Next, we address again the matter of the detection and the early detection of the attack, in terms of absolute time units. For
, the
Figure 4b reveals that the first activation of an alert occurs at
[s] and occurs faster than the first activation of an alert when
, because now we have an attack signal with a larger value. On the other hand, the
Figure 4c reveals that the set-theoretic detector activates an alarm for the first time at
[s]. In this case, an alarm is triggered almost immediately after the activation of the attacker, therefore the hybrid detection scheme does not offer further advantages in the faster detection of the adversary.
In conclusion, we infer that the hybrid detection scheme (70) encapsulates successfully the best traits of the two detection methods. Whenever the set-theoretic detector triggers an alarm, we know with certainty that the state vector has exited the robust invariant set , thus we can guarantee the existence of an attacker. Accordingly, whenever the residue of the full state estimator exceeds a transient threshold, while the alarm signal is inactive, the existence of an attacker is hinted, and the system is put in alert state. In this way, we can deploy countermeasures faster than we would if we relied only on the outcome of the set-theoretic detection mechanism.
We close this part by providing a set of figures that depict the response of the state variables in the case of an intermittent attack with . These figures will be helpful in order to understand the differences between the two modeling approaches for and , and will also clarify how the set-theoretic oriented modeling approach works for the detection of an intermittent attack pattern. The results obtained for an attack signal with are similar to those obtained for an attack signal with , so the latter ones are omitted.
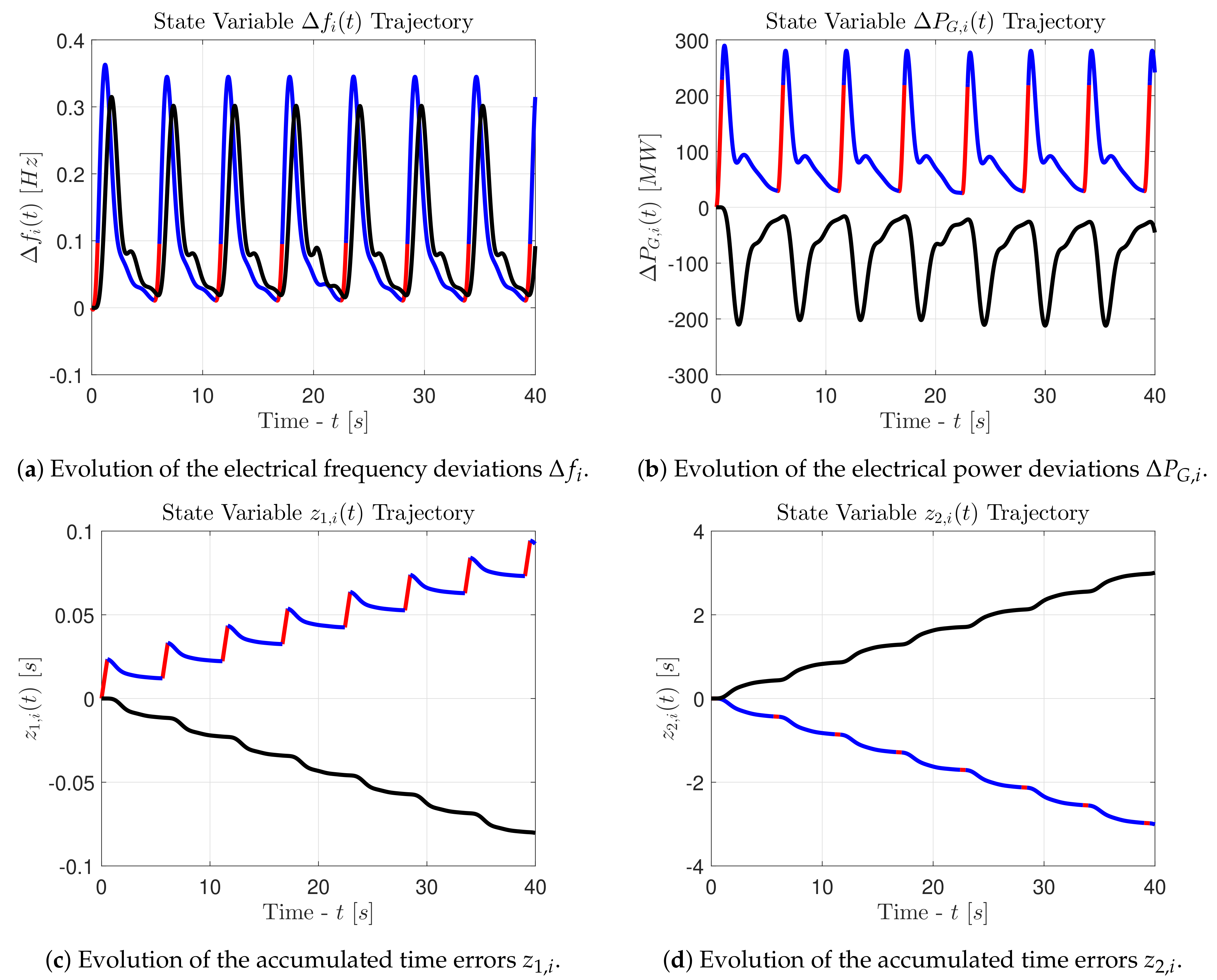
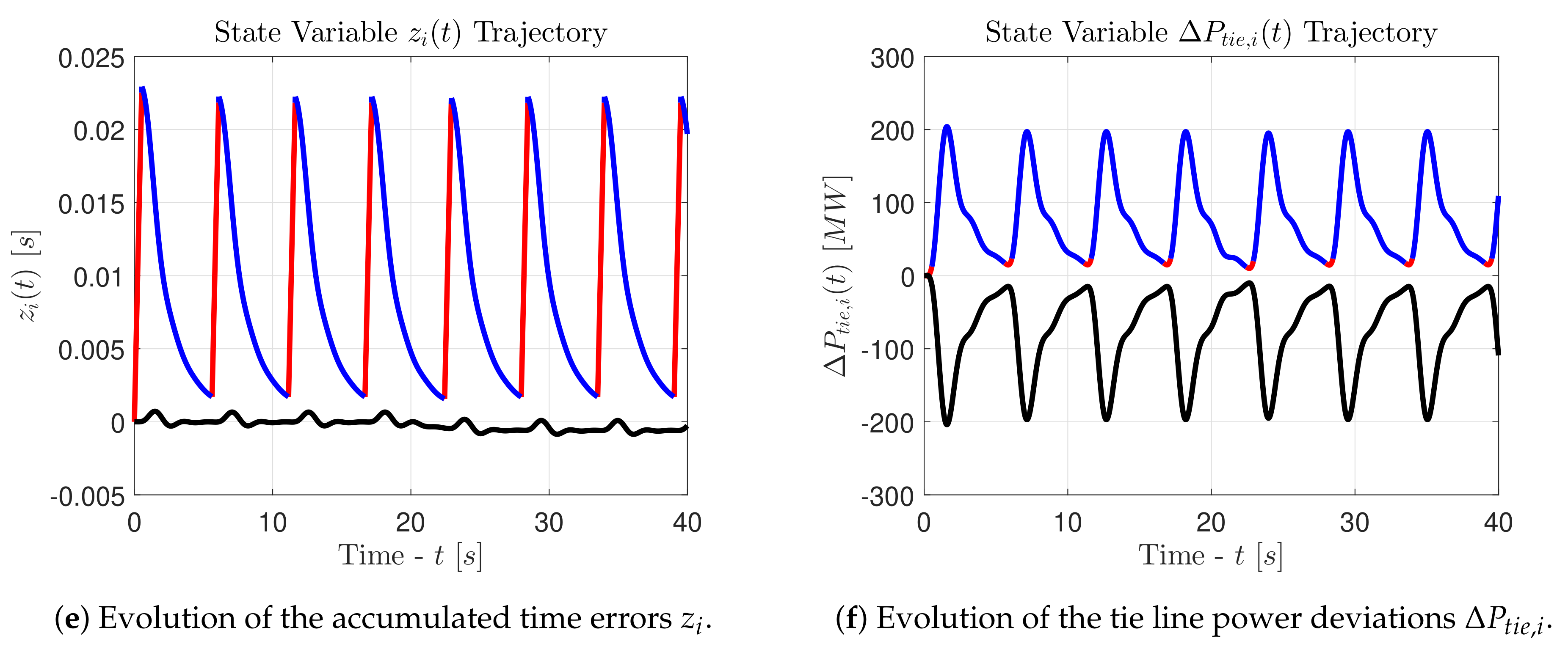
Let us observe the graphs in the
Figure 5. The state variables associated with the first control area are printed in red (
•) and blue (
•) lines, whereas the state variables associated with the second control area are printed in black (•) lines. The red color indicates an active attacker, whereas the blue color indicates an inactive attacker. It is evident that the intermittent pattern forces the electrical frequency to oscillate, according to the hysteresis-based switching signal (26). The frequency oscillations remain within the bounds of the inequality (50). However, these oscillations cause fluctuations on the power which is exchanged between the two areas through the connecting tie line. As we can see, the state variables
have an oscillatory behavior and the average power that flows through the connecting tie line is increased. This leads to problems associated with the synchronization of the generators and with the thermal limits of the tie line. Finally, the state variables
obtained for
are always stable, while the state variables
and
obtained for
have an unstable behavior. Indeed, after every new activation of the attacker, the state variables
and
begin to diverge linearly towards infinity. This behavior is essential for a set-theoretic detector, since it ensures that at some point the state vector will exit the set
, ultimately triggering an alarm. This last remark is visible in the
Figure 3c after
[s], when
, and in the
Figure 4c after
[s], when
.
Finally, it is worth mentioning that we cannot use the networked system dynamics (28)–(37) for
to develop both a set-theoretic detector and a full state estimator, because the Equation (60), which is necessary for the extraction of the steady-state estimation threshold
, involves the matrix
. Indeed, the latter matrix does not exist when the matrix
is Lyapunov stable with unit eigenvalues, something that happens when we select the modeling approach that depends on the Equations (28)–(37) for
[
27].
5.3. Limitations of the Proposed Detectors
The limitations of the proposed detection mechanisms are presented based on the occurrences of false positive or false negative activations of the alarm condition and the alert state. For the remainder of our analysis, the term false positive refers to an activation of the alarm condition or the alert state of the hybrid detection scheme (70), when the system is not affected by an attacker. Accordingly, the term false negative refers to the case where an attacker affects the system but neither the alarm condition nor the alert state are ever activated. We address the occurrences of false positives and false negatives considering the cases of the set-theoretic detectors and the estimation-based detectors separately.
First, we examine the false positives and the false negatives of the set-theoretic detectors. The set-theoretic detector triggers an alarm signal only when the state trajectory exits the robust invariant set . The robust invariance property ensures that if the state vector begins to evolve from an initial condition that belongs to the set , then the emanating state trajectory will remain within the set for all future time instances and for all admissible disturbances sequences . In addition, the set has been calculated in the absence of an attacker. This implies that, it is impossible for the state trajectory to exit the set in the absence of an attacker, and therefore it is impossible for the set-theoretic detector to yield a false positive.
On the other hand, the stability analysis that was established in our previous work [
27] and was briefly reviewed in the current article, indicates that the set-theoretic detector may be unable to disclose an attack, only when the adversary affects all the control areas of the network with the same persistent attack signals, that is when
and
for all
and for all
. In this case, a false negative may occur, because the response of the system is proven to be asymptotically stable. Indeed, if the attack signals remain small, then the attained steady-state equilibrium may still belong to the set
and respect the alarm constraints. For further details on this scenario, the reader is referred to [
27]. However, if the attacker affects only some control areas of the network, but not all of them, as is the case in this work, then the integral variables
and
will always demonstrate an unstable behavior. In other words, it is only a matter of time until the state trajectory exits the convex and compact set
, whereupon an alarm will be triggered. In conclusion, it is impossible for the set-theoretic detector to yield a false negative, unless
and
for all
and for all
and for relatively small values of the attack signals
.
We proceed with the analysis of the false positives and the false negatives of the estimation-based detectors. Out of the two estimation-based detectors, the output-based estimators perform poorly and unreliably in every scenario that we presented. They yield constantly false negatives and are unable to disclose an attacker. Therefore, we focus on the full state-based estimators. We have to address the false positives and the false negatives associated both with the alarm condition and the alert state condition .
First, we address the false positives and the false negatives of the alarm condition
. The full state-based estimator triggers an alarm signal only when the estimation residue reaches a steady-state value larger than the critical threshold
. As long as the estimation residue oscillates, something that occurs in an intermittent attack, the alarm condition
can never be used to activate an alarm, either correct or false. Persistent attacks can lead to false negatives, as shown in [
27], but never to false positives, since
is calculated for
and
for all
.
Let us now address the false positives and the false negatives of the alert state condition
. In the case of an intermittent attack, the full state-based estimator can help with the timely disclosure of the attacker by putting the system into alert mode, whenever
. Clearly, since the value of the design parameter
has to be selected ad hoc, it is possible for this detector to fail to trigger an alert state, thus yielding a false negative. This scenario is presented in the following simulation, where the responses of the state variables are again similar to the ones given in the
Figure 5 and, therefore, are omitted for brevity. We consider that the attack signal becomes
and that the system is now subject to a different disturbance sequence, which is described by the equations
The output-based estimator and the set-theoretic detector remain the same but we consider two different transient thresholds for the full state-based estimator. Specifically, in the
Figure 6b, we depict with black (•) dashed line the standard transient threshold
, with
, whereas we use the green (
●) dashed line to depict a different transient threshold with
. It is evident that for
the full state-based estimator is able to put the system in alert state whenever the attacker actually affects it and the first activation of the alert state occurs at
[s]. However, if we select
, then the full state-based estimator yields constantly false negatives.
The
Figure 6c also reveals that the set-theoretic detector is able to disclose the attack only when the state vector exits the robust invariant set
, something that happens at
[s]. Finally, we remark that the hybrid detection scheme for
improves the behavior of the set-theoretic detector, since it is able to hint the existence of an attack
[s] faster than the set-theoretic detector alone. However, the hybrid detection scheme for
is unable to trigger an alert state and can only activate an alarm at
[s] due to the set-theoretic detector.
Lastly, we address the false positives regarding the condition . As we have already explained, since the parameter is selected ad hoc, the transient threshold does not offer any detection guarantees. Consequently, it is possible for the full state-based estimator to yield a false positive, when an attacker is absent and the system is affected by a more elaborate disturbance sequence . However, typical disturbance sequences assume the form of step load changes, in which case a sufficiently large value of the parameter reduces the occurrence of false positives.
To sum up, the set-theoretic detectors can never yield a false positive and they can yield a false negative only when and for all and for all and for small attack signals. Thus, they can never yield a false negative during intermittent attacks. The output-based detectors yield constantly false negatives and are not suitable for the disclosure of intermittent attacks. Finally, the full state-based estimators cannot rely on their alarm condition to disclose intermittent attacks but they can help inprove the security of the system through the alert condition , which can be activated during the transients. The activation of this condition depends on the value of the ad hoc selected parameter and can either lead to false negatives, for small-valued attack signals paired with small-valued disturbance sequences and a poorly chosen value of , or to false positives, for elaborately constructed disturbance sequences and a poorly chosen value of . However, the latter case is rare, since usually we are mostly concerned with step load changes.
In conclusion, the above analysis along with the overall simulation results demonstrate that a hybrid detection scheme that combines a set-theoretic detector and a full state-based estimator is particularly robust, regarding the matter of false positives and false negatives. A false positive simply cannot occur, whereas a false negative may occur only under certain circumstances and can be avoided with the proper selection of the design parameters of the detectors.