Experimental and Numerical Analysis of the Effect of Vortex Generator Installation Angle on Flow Separation Control
Abstract
1. Introduction
2. Methods
2.1. Numerical Conditions
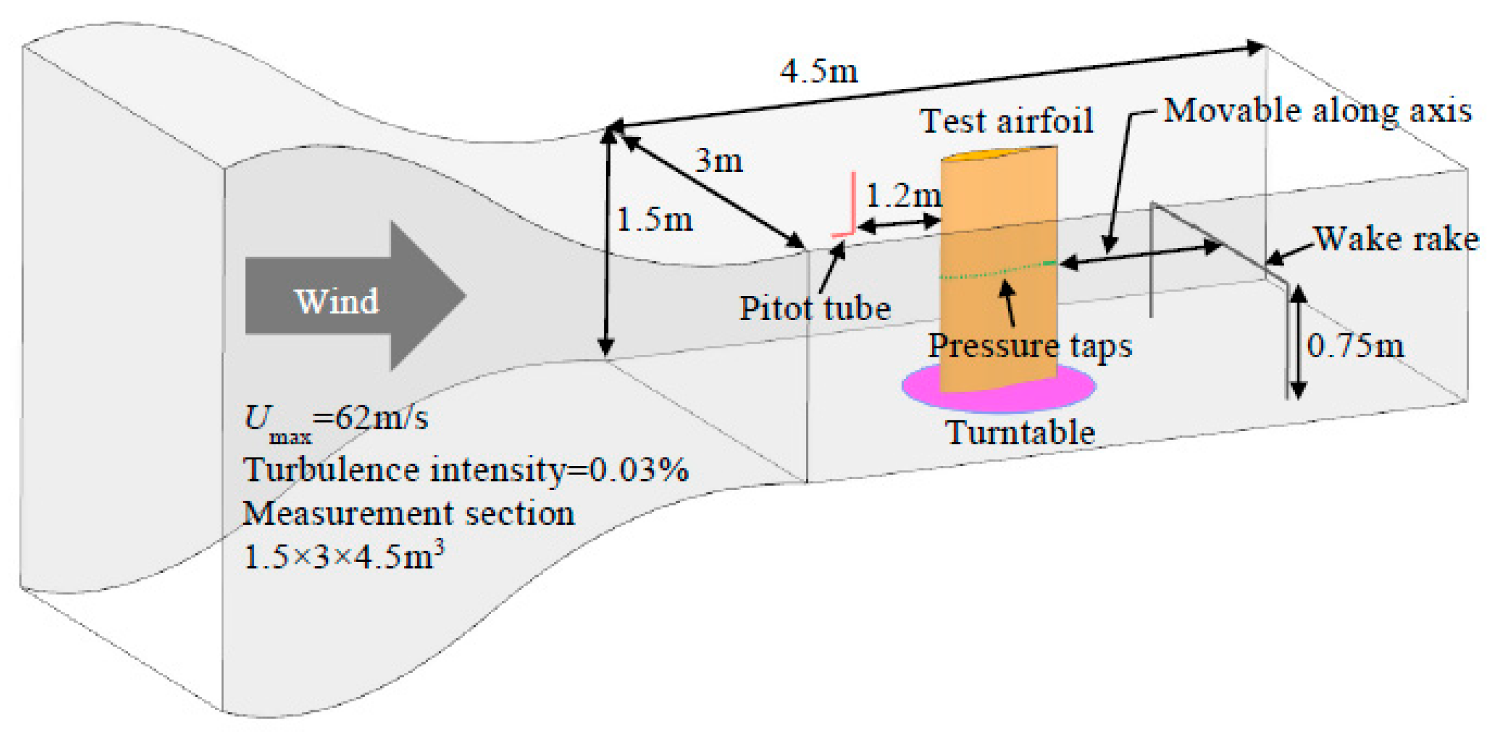
2.2. Experimental Setup
3. Results and Discussion
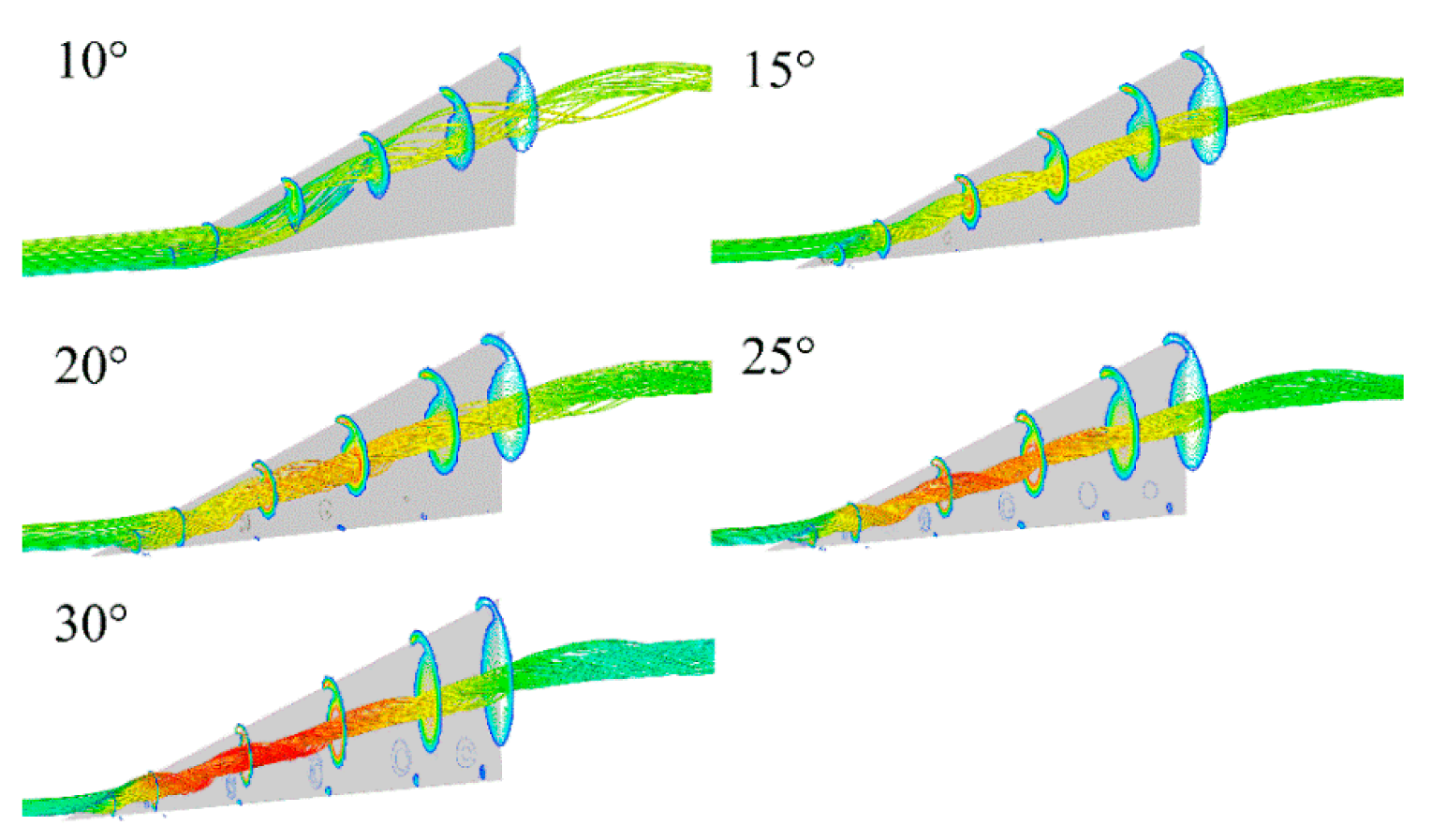
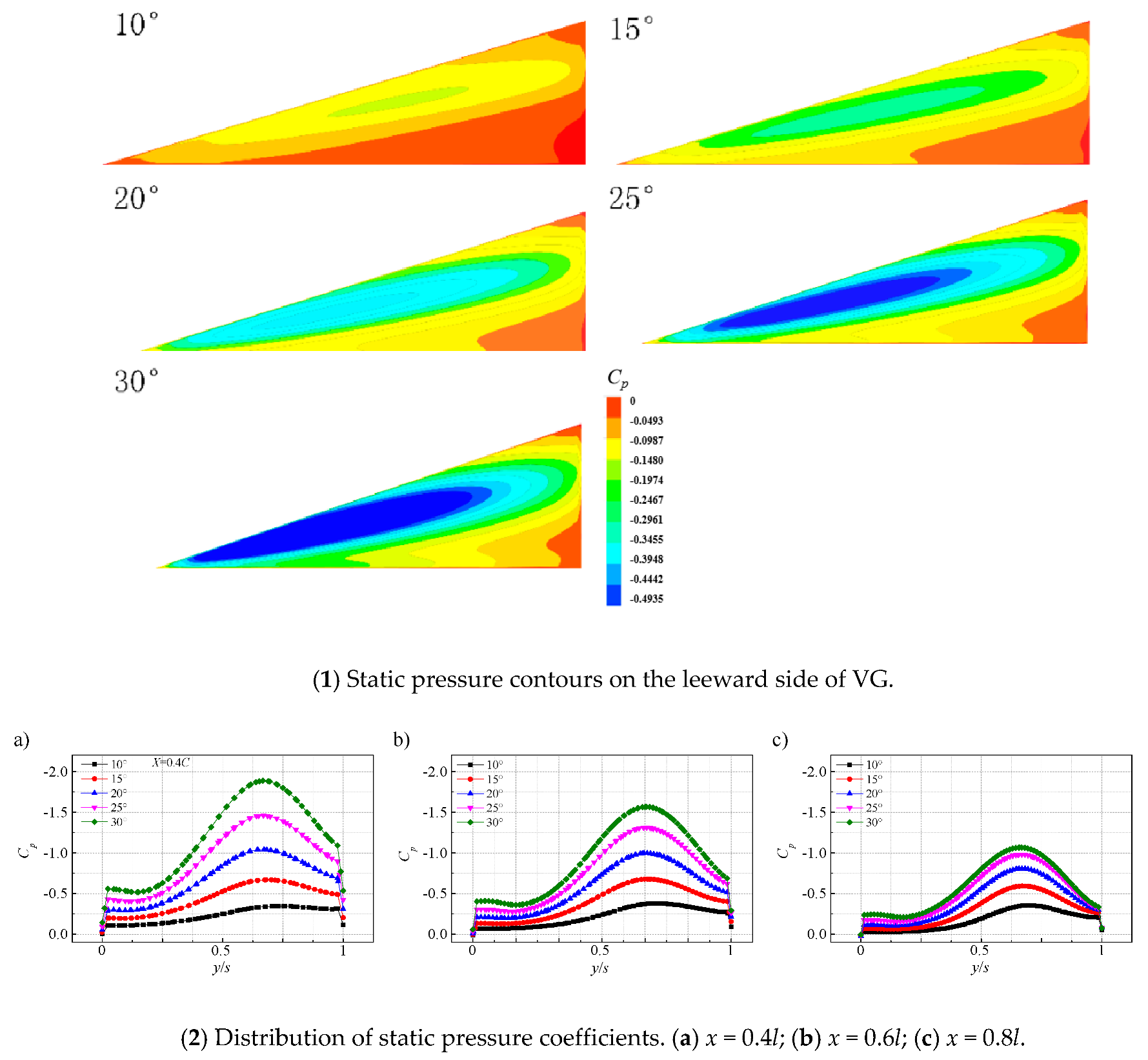
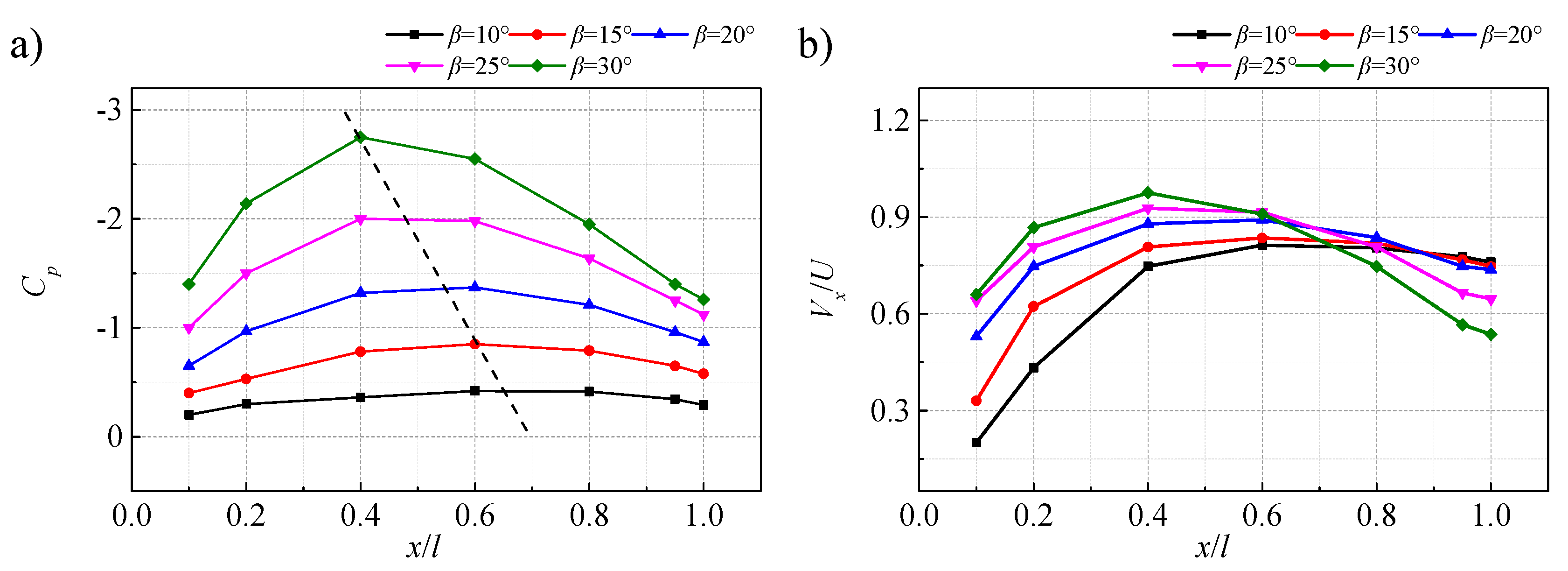
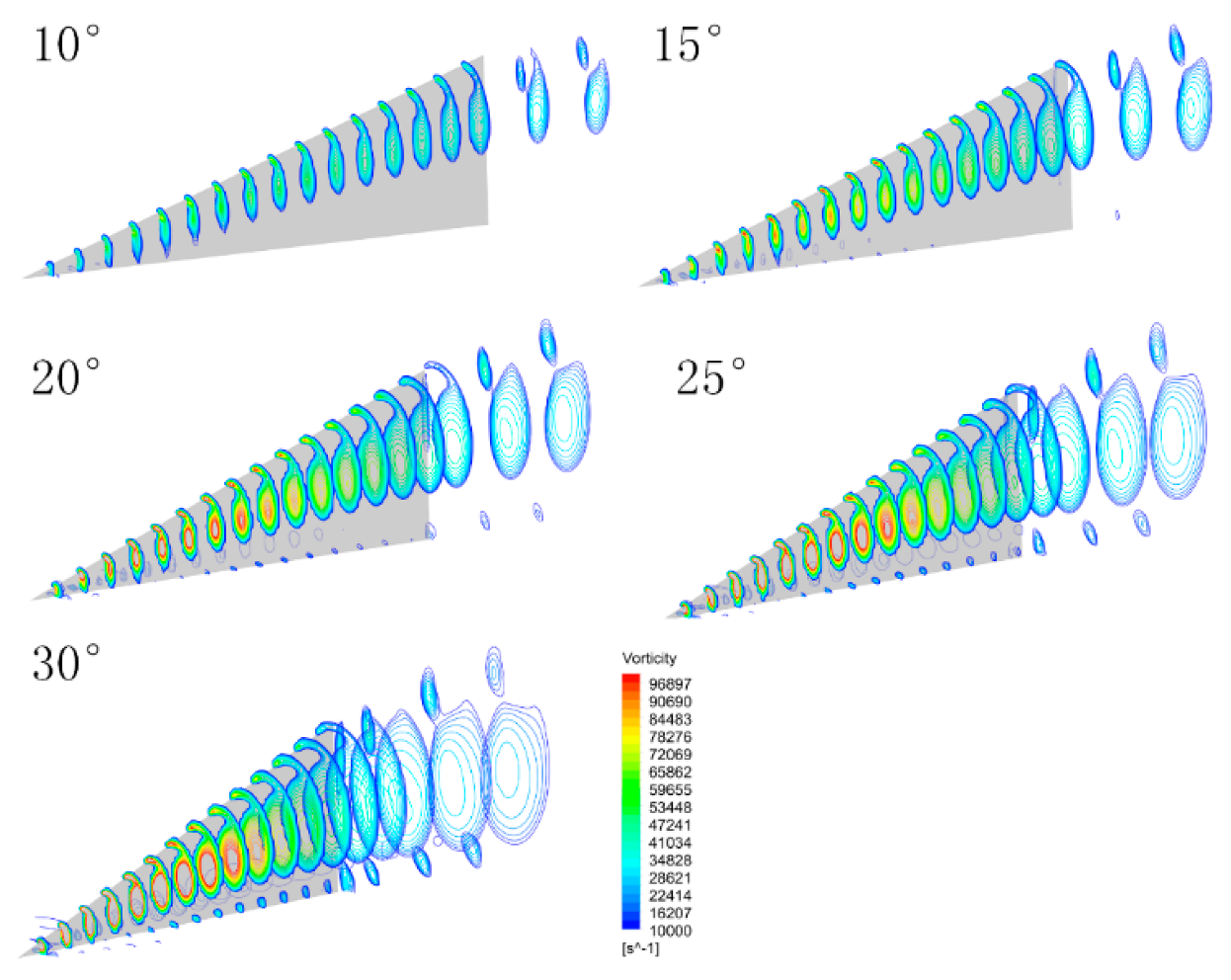
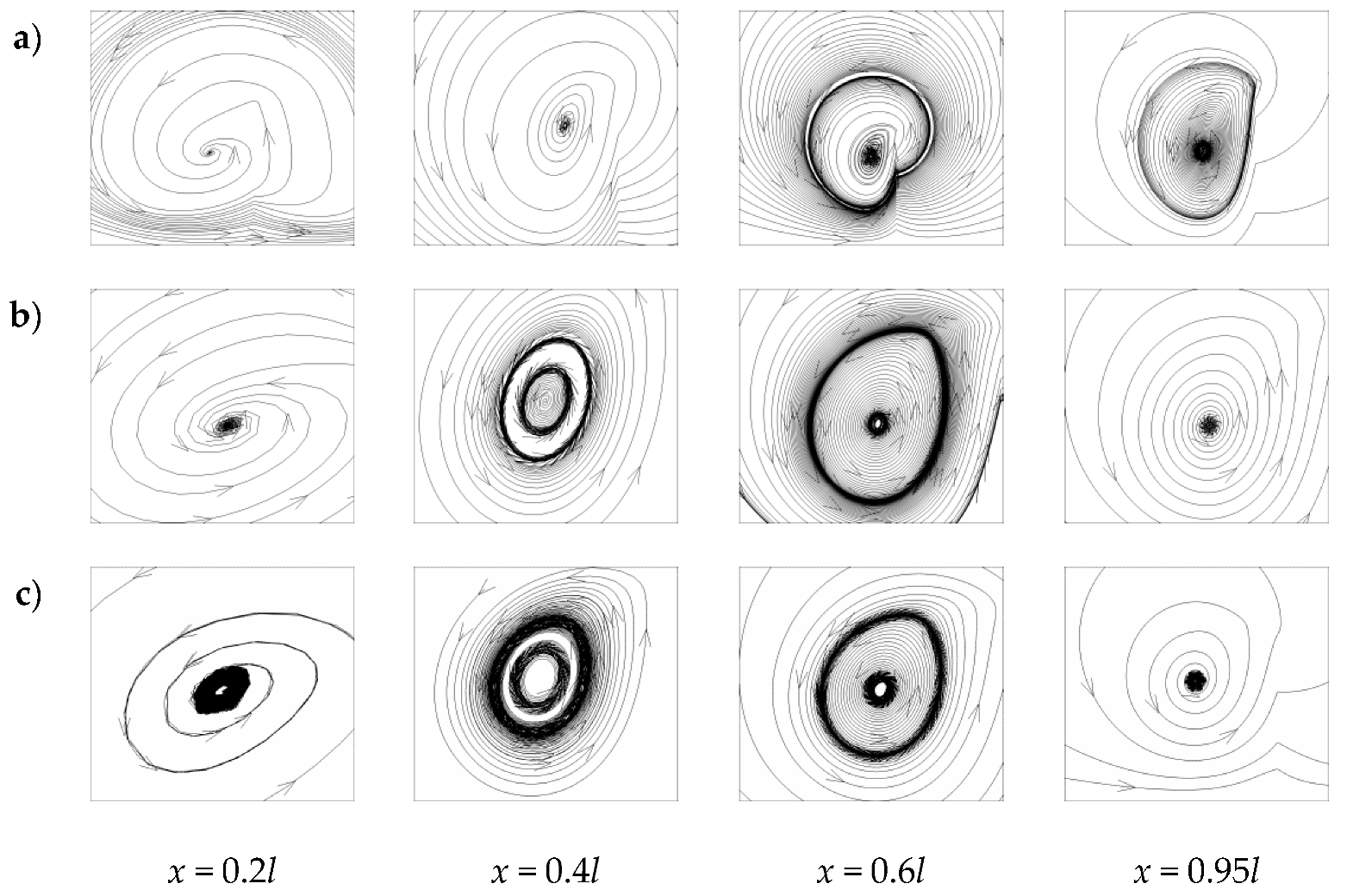
3.1. Analysis of Numerical Results
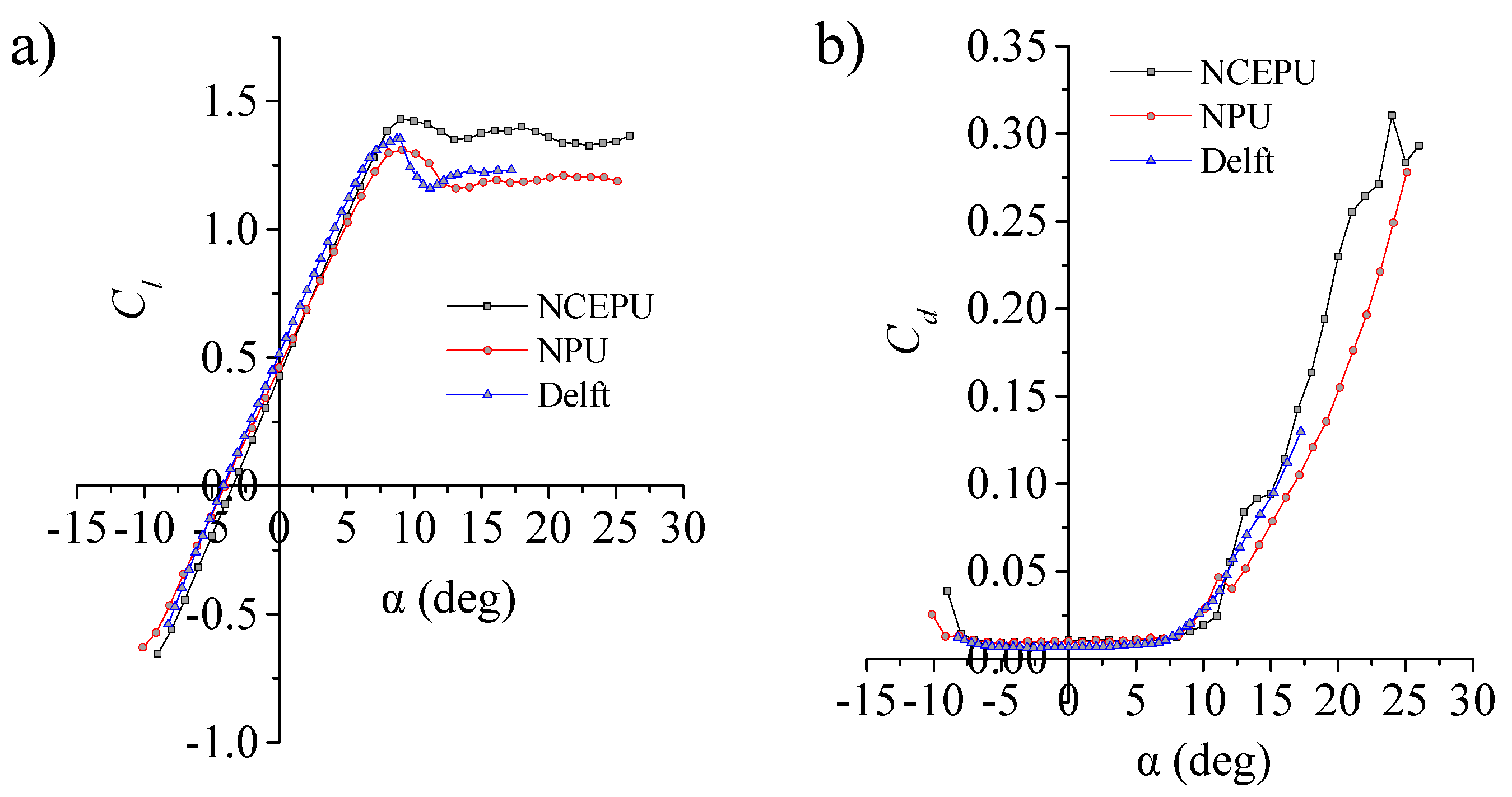
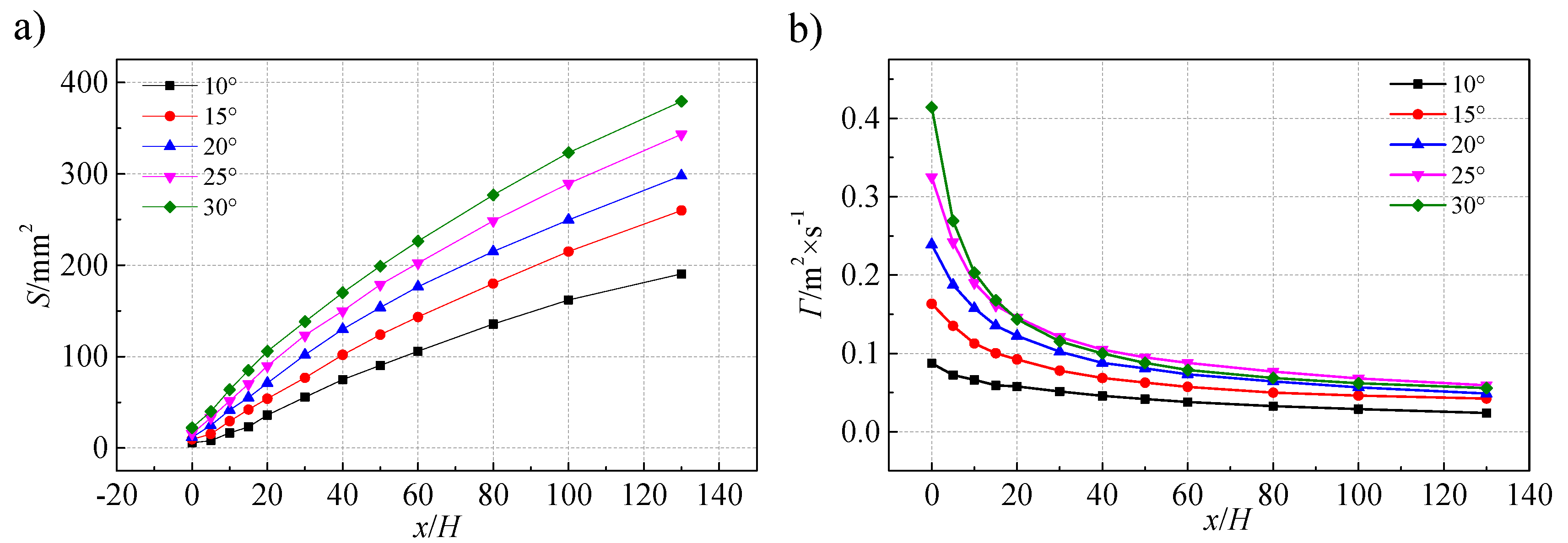
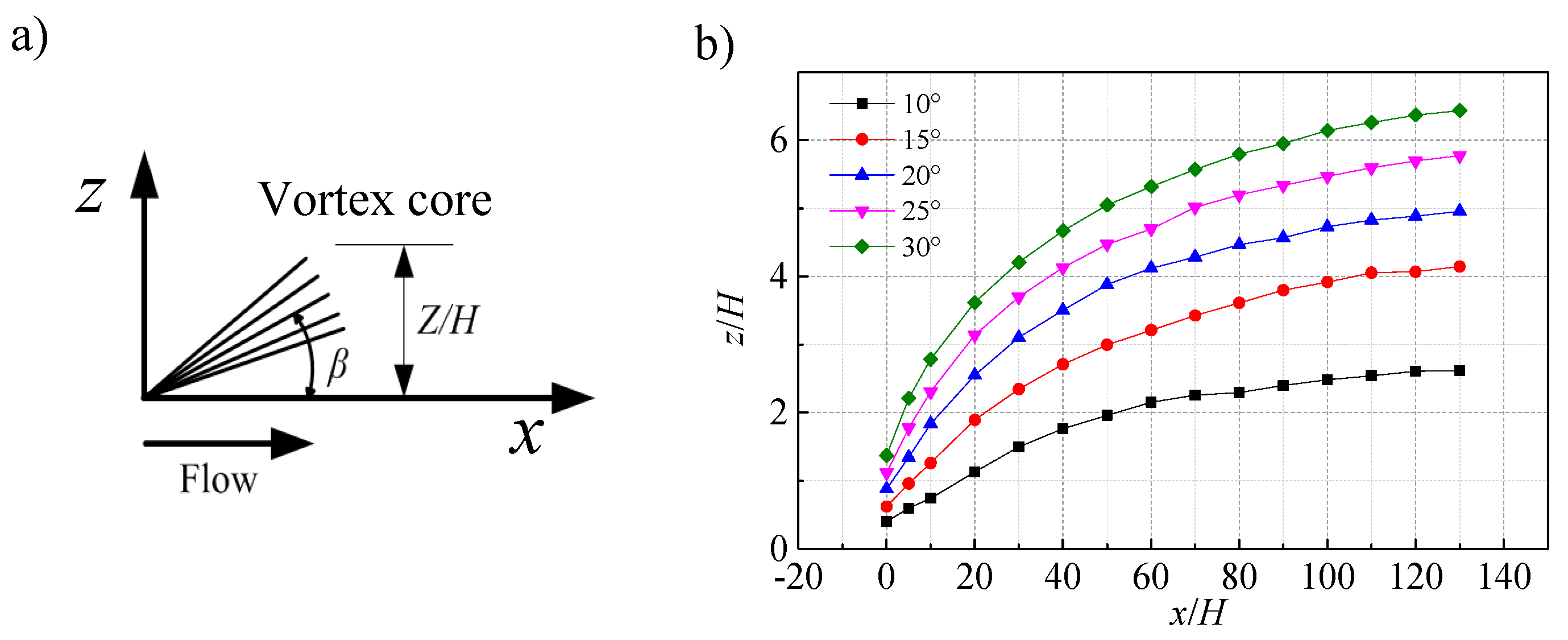
3.2. Analysis of Experimental Results.
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, X.; Ye, Z.; Kang, S.; Hu, H. Investigations on the Unsteady Aerodynamic Characteristics of a Horizontal-Axis Wind Turbine during Dynamic Yaw Processes. Energies 2019, 12, 3124. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Y.; Wang, L.; Ding, L.; Hu, H. Numerical Study of Nacelle Wind Speed Characteristics of a Horizontal Axis Wind Turbine under Time-Varying Flow. Energies 2019, 12, 3993. [Google Scholar] [CrossRef]
- Macquart, T.; Maheri, A.; Busawon, K. Microtab dynamic modelling for wind turbine blade load rejection. Renew. Energy 2014, 64, 144–152. [Google Scholar] [CrossRef]
- Kametani, Y.; Fukagata, K.; Orlu, R.; Schlatter, P. Effect of uniform blowing/suction in a turbulent boundary layer at moderate Reynolds number. Int. J. Heat Fluid Flow 2015, 55, 132–142. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Movahhedi, M. Wind turbine power improvement utilizing passive flow control with microtab. Energy 2018, 150, 575–582. [Google Scholar] [CrossRef]
- Yang, H.; Jiang, L.-Y.; Hu, K.-X.; Peng, J. Numerical study of the surfactant-covered falling film flowing down a flexible wall. Eur. J. Mech. Fluids 2018, 72, 422–431. [Google Scholar] [CrossRef]
- Ziadé, P.; Feero, M.A.; Sullivan, P.E. A numerical study on the influence of cavity shape on synthetic jet performance. Int. J. Heat Fluid Flow 2018, 74, 187–197. [Google Scholar] [CrossRef]
- Matteo, C.; Andrea, P.; Luigi de, L. Design approach to predict synthetic jet formation and resonance amplifications. Exp. Ther. Fluid Sci. 2019, 107, 79–87. [Google Scholar]
- Ma, L.; Wang, X.; Zhu, J.; Kang, S. Dynamic Stall of a Vertical-Axis Wind Turbine and Its Control Using Plasma Actuation. Energies 2019, 12, 3738. [Google Scholar] [CrossRef]
- Zong, H.; Chiatto, M.; Kotsonis, M.; De Luca, L. Plasma Synthetic Jet Actuators for Active Flow Control. Actuators 2018, 7, 77. [Google Scholar] [CrossRef]
- Lin, J.C. Review of research on low-profile vortex generators to control boundary-layer separation. Prog. Aerosp. Sci. 2002, 38, 389–420. [Google Scholar] [CrossRef]
- Hansen, M.O.L.; Velte, C.M.; Øye, S. Aerodynamically shaped vortex generator. Wind Energy 2015, 19, 563–567. [Google Scholar] [CrossRef]
- Barlas, T.K.; van Kuik, G.A.M. Review of state of the art in smart rotor control research for wind turbines. Prog. Aerosp. Sci. 2010, 46, 1–27. [Google Scholar] [CrossRef]
- Johnson, S.J.; Baker, J.P.; Dam, C.P.V. An overview of active load control techniques for wind turbines with an emphasis on microtabs. Wind Energy 2010, 13, 239–253. [Google Scholar] [CrossRef]
- Manolesos, M.; Voutsinas, S.G. Experimental investigation of the flow past passive vortex generators on an airfoil experiencing three-dimensional separation. J. Wind Eng. Ind. Aerodyn. 2015, 142, 130–148. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, B.; Qiu, Q.; Xu, X. Flow control on the NREL S809 wind turbine airfoil using vortex generators. Energy 2017, 118, 1210–1221. [Google Scholar] [CrossRef]
- Taylor, H.D. The Elimination of Diffuser Separation by Vortex Generators; United Aircraft Corporation Report No. R-4012-3; United Aircraft Corporation: Moscow, Russia, June 1947. [Google Scholar]
- Godard, G.; Stanislas, M. Control of a decelerating boundary layer. Part 1: Optimization of passive vortex generators. Aerosp. Technol. 2006, 10, 181–191. [Google Scholar] [CrossRef]
- Godard, G.; Stanislas, M. Control of a decelerating boundary layer. Part 2: Optimization of slotted jets vortex generators. Aerosp. Sci. Technol. 2006, 10, 394–400. [Google Scholar] [CrossRef]
- Godard, G.; Stanislas, M. Control of a decelerating boundary layer. Part 3: Optimization of round jets vortex generators. Aerosp. Sci. Technol. 2006, 10, 455–464. [Google Scholar] [CrossRef]
- Gao, L.; Zhang, H.; Liu, Y.; Han, S. Effects of vortex generators on a blunt trailing-edge airfoil for wind turbines. Renew. Energy 2015, 76, 303–311. [Google Scholar] [CrossRef]
- Martínez-Filgueira, P.; Fernandez-Gamiz, U.; Zulueta, E.; Errasti, I.; Fernandez-Gauna, B. Parametric study of low-profile vortex generators. Int. J. Hydrog. Energy 2017, 42, 17700–17712. [Google Scholar] [CrossRef]
- Zhen, T.K.; Zubair, M.; Ahmad, K.A. Experimental and Numerical Investigation of the Effects of Passive Vortex Generators on Aludra UAV Performance. Chin. J. Aeronaut. 2011, 24, 577–583. [Google Scholar] [CrossRef]
- Kundu, P.; Sarkar, A.; Nagarajan, V. Improvement of performance of S1210 hydrofoil with vortex generators and modified trailing edge. Renew. Energy 2019, 142, 643–657. [Google Scholar] [CrossRef]
- Gageik, M.; Nies, J.; Klioutchnikov, I.; Olivier, H. Pressure wave damping in transonic airfoil flow by means of micro vortex generators. Aerosp. Sci. Technol. 2018, 81, 65–77. [Google Scholar] [CrossRef]
- Mereu, R.; Passoni, S.; Inzoli, F. Scale-resolving CFD modeling of a thick wind turbine airfoil with application of vortex generators: Validation and sensitivity analyses. Energy 2019, 187, 115969. [Google Scholar] [CrossRef]
- Manolesos, M.; Papadakis, G.; Voutsinas, S.G. Revisiting the assumptions and implementation details of the BAY model for vortex generator flows. Renew. Energy 2020, 146, 1249–1261. [Google Scholar] [CrossRef]
- Brüderlin, M.; Zimmer, M.; Hosters, N.; Behr, M. Numerical simulation of vortex generators on a winglet control surface. Aerosp. Sci. Technol. 2017, 71, 651–660. [Google Scholar] [CrossRef]
- Yang, K.; Zhang, L.; Xu, J.Z. Simulation of aerodynamic performance affected by vortex generators on blunt trailing-edge airfoils. Sci. China Ser. E Technol. Sci. 2010, 53, 1–7. [Google Scholar] [CrossRef]
- Sørensen, N.N.; Zahle, F.; Bak, C.; Vronsky, T. Prediction of the Effect of Vortex Generators on Airfoil Performance. J. Phys. Conf. Ser. 2014, 524, 12019. [Google Scholar] [CrossRef]
- Fouatih, O.M.; Medale, M.; Imine, O.; Imine, B. Design optimization of the aerodynamic passive flow control on NACA 4415 airfoil using vortex generators. Eur. J. Mech. B Fluids 2016, 56, 82–96. [Google Scholar] [CrossRef]
- Zhang, L.; Li, X.; Yang, K.; Xue, D. Effects of vortex generators on aerodynamic performance of thick wind turbine airfoils. J. Wind Eng. Ind. Aerodyn. 2016, 156, 84–92. [Google Scholar] [CrossRef]
- Lishu, H.; Zhide, Q. Experimental Research on Control Flow over Airfoil Based on Vortex Generator and Gurney Flap. Acta Aeronaut. Astronaut. Sin. 2011, 32, 1429–1434. [Google Scholar]
- Reuss, R.L.; Hoffman, M.J.; Gregorek, G.M. Effects of Surface Roughness and Vortex Generators on the NACA 4415 Airfoil; Vortex Augmented Turbines; The Ohio State University: Columbus, OH, USA, 1995; p. 12. [Google Scholar]
- Velte, C.M.; Hansen, M.O.L. Investigation of flow behind vortex generators by stereo particle image velocimetry on a thick airfoil near stall. Wind Energy 2013, 16, 775–785. [Google Scholar] [CrossRef]
- Delnero, J.S.; Di Leo, J.M.; Camocardi, M.E.; Martínez, M.A.; Lerner, J.L.C.; Delnero, J.S.; Di Leo, J.M. Experimental study of vortex generators effects on low Reynolds number airfoils in turbulent flow. Int. J. Aerodyn. 2012, 2, 50. [Google Scholar] [CrossRef]
- Lishu, H.; Zhide, Q.; Wenping, S. Experimentally Studying Effects of Different Layouts of Vortex Generator on Controlling Stall Flow over Airfoil. J. Northwestern Polytech. Univ. 2011, 29, 524–528. [Google Scholar]
- Baldacchino, D.; Ferreira, C.; Tavernier, D.D.; Timmer, W.A.; van Bussel, G.J.W. Experimental parameter study for passive vortex generators on a 30% thick airfoil. Wind Energy 2018, 21, 745–765. [Google Scholar] [CrossRef]
- Lin, J.C.; Robinson, S.K.; McGhee, R.J.; Valarezo, W.O. Separation control on high-lift airfoils via micro-vortex generators. J. Aircr. 2015, 31, 1317–1323. [Google Scholar] [CrossRef]
- Li, X.; Yang, K.; Wang, X. Experimental and Numerical Analysis of the Effect of Vortex Generator Height on Vortex Characteristics and Airfoil Aerodynamic Performance. Energies 2019, 12, 959. [Google Scholar] [CrossRef]
- Li, X.; Yang, K.; Hu, H.; Wang, X.; Kang, S. Effect of Tailing-Edge Thickness on Aerodynamic Noise for Wind Turbine Airfoil. Energies 2019, 12, 270. [Google Scholar] [CrossRef]
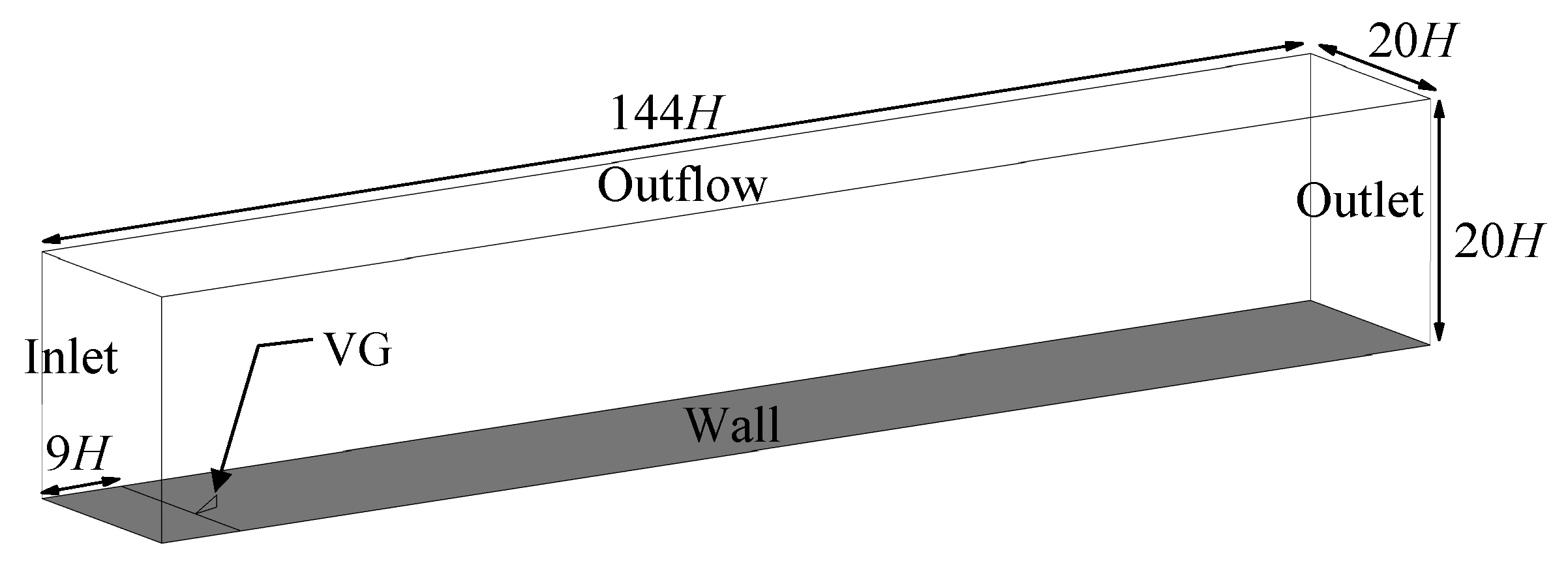
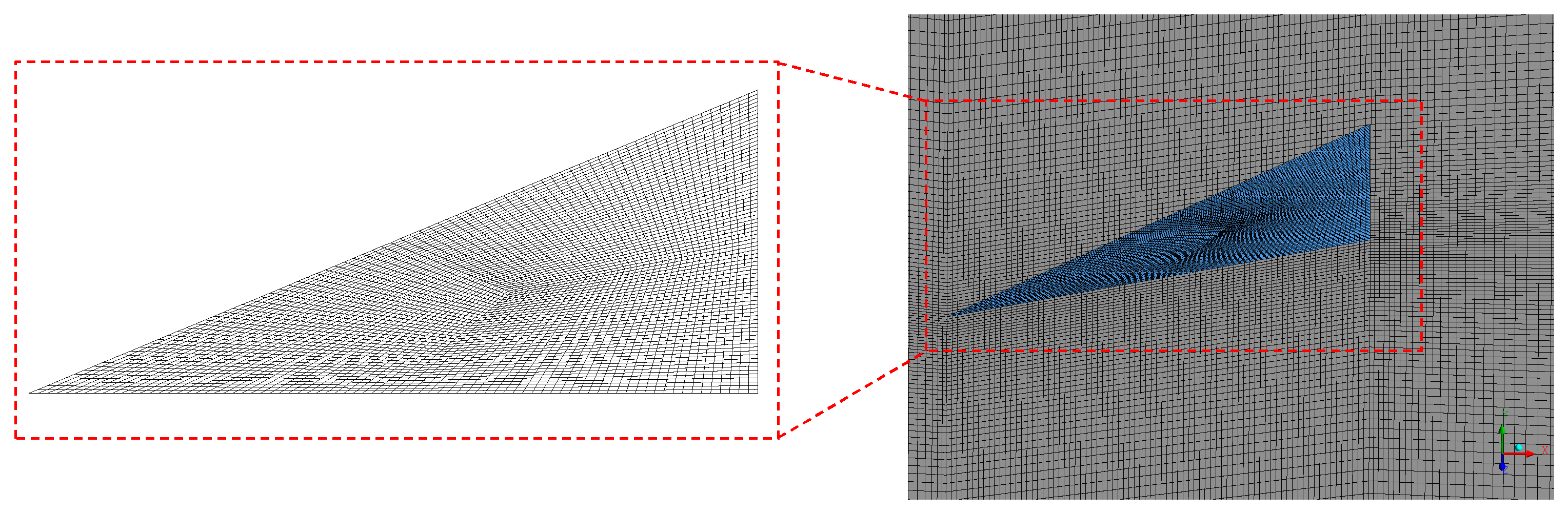
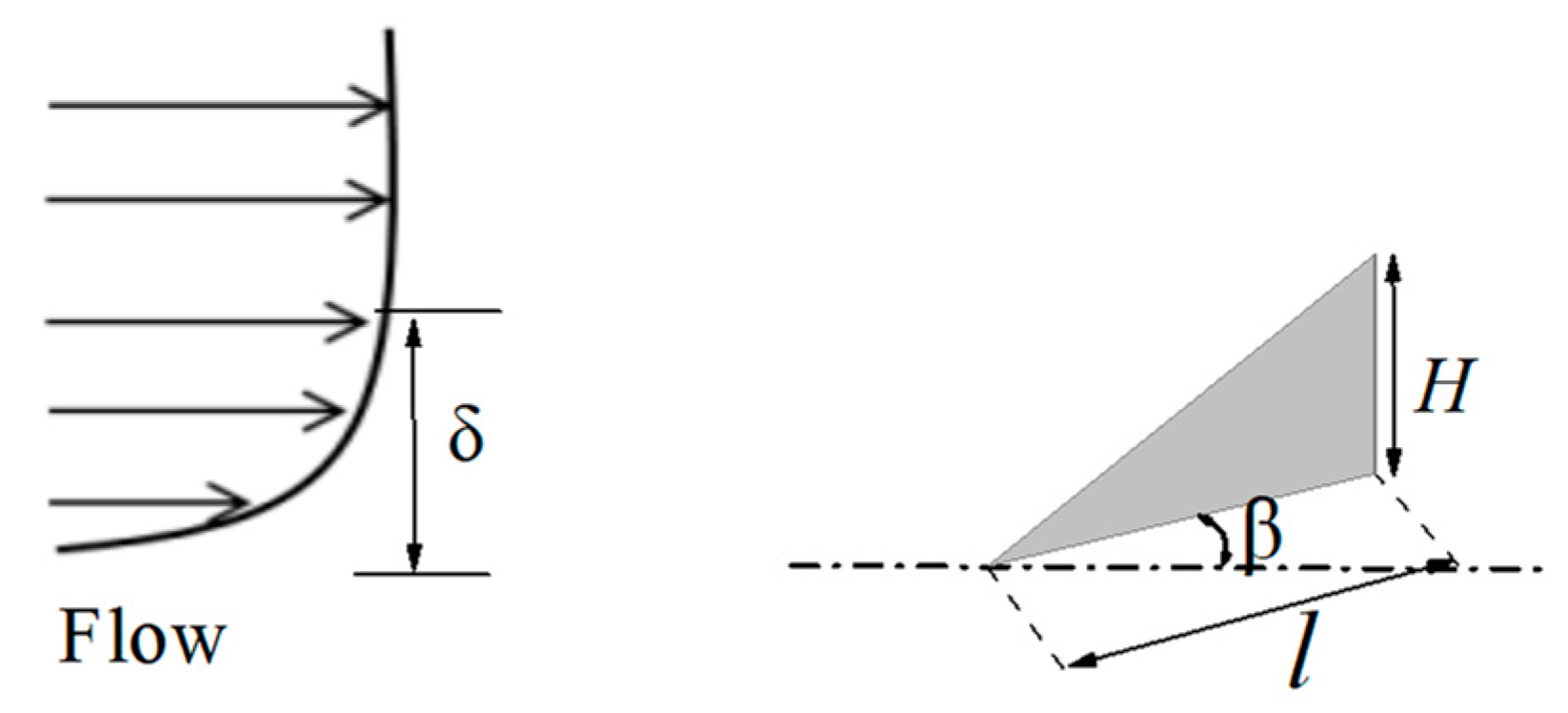


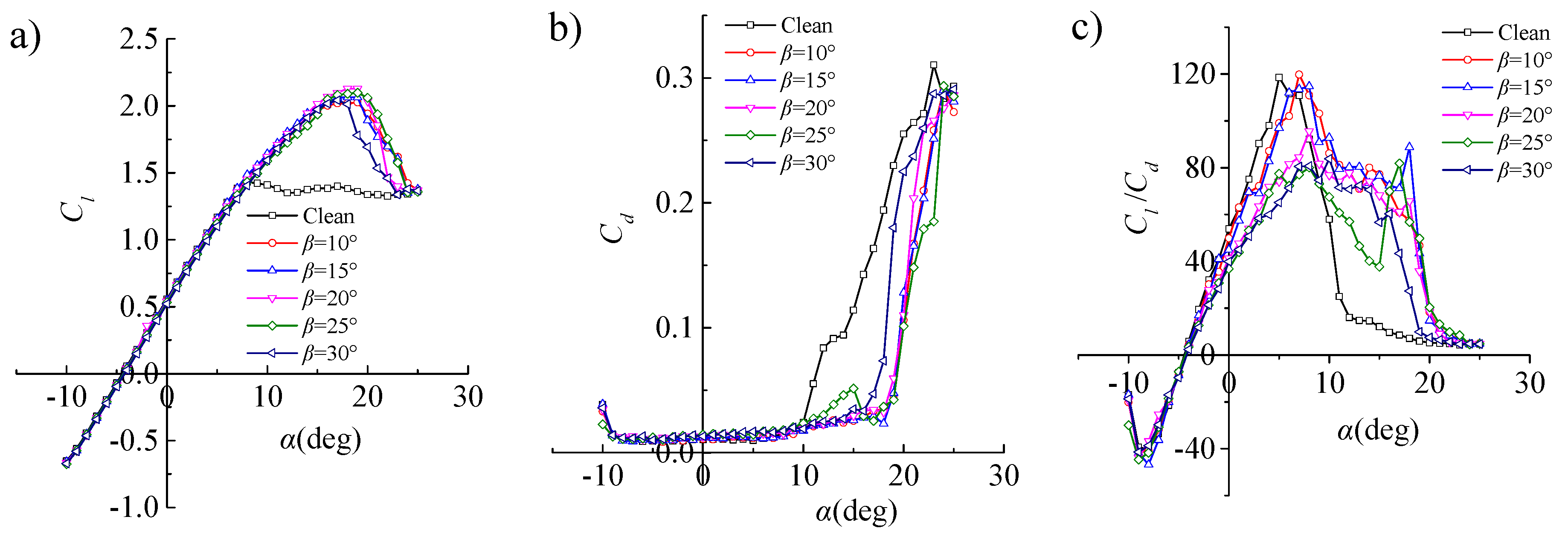
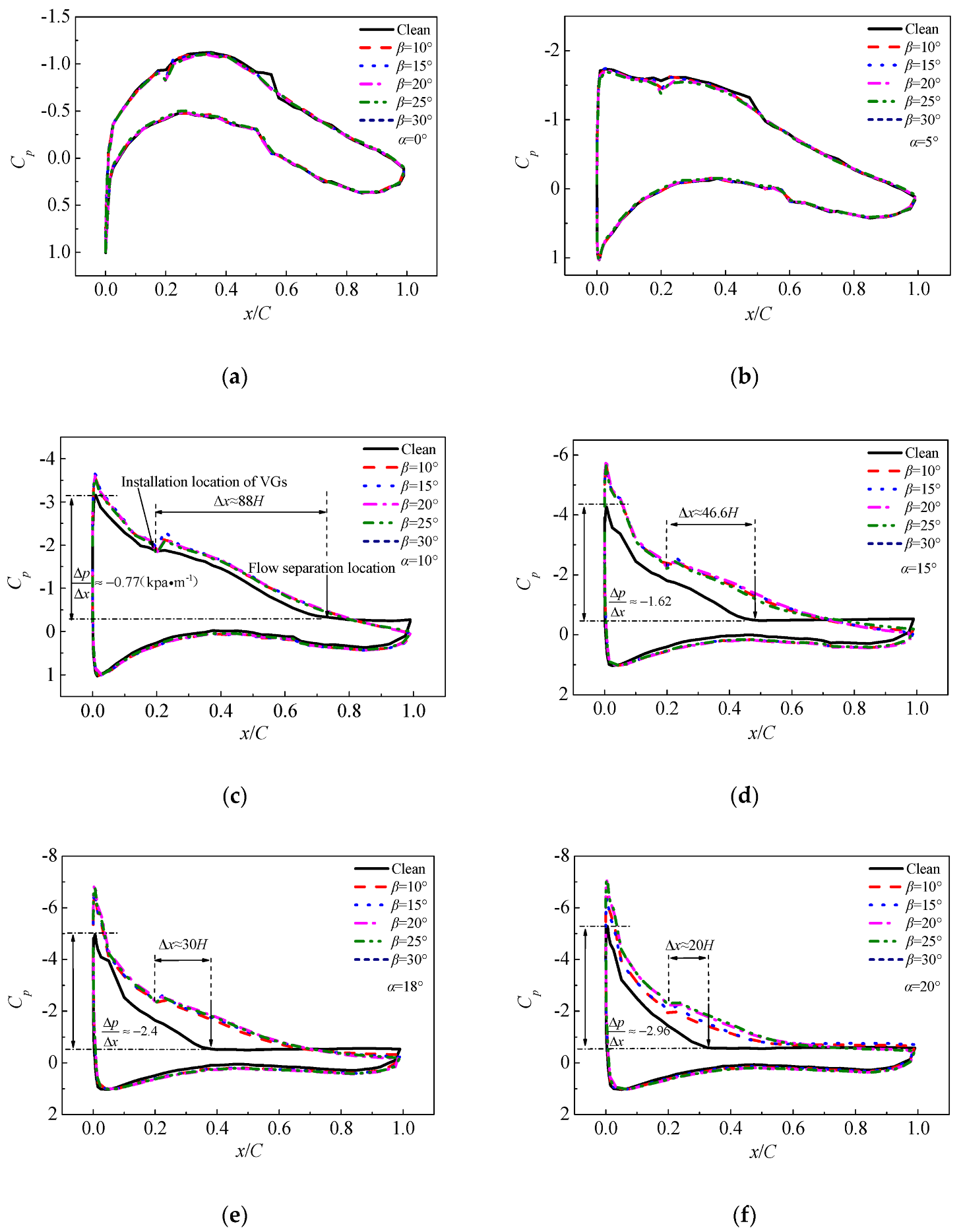
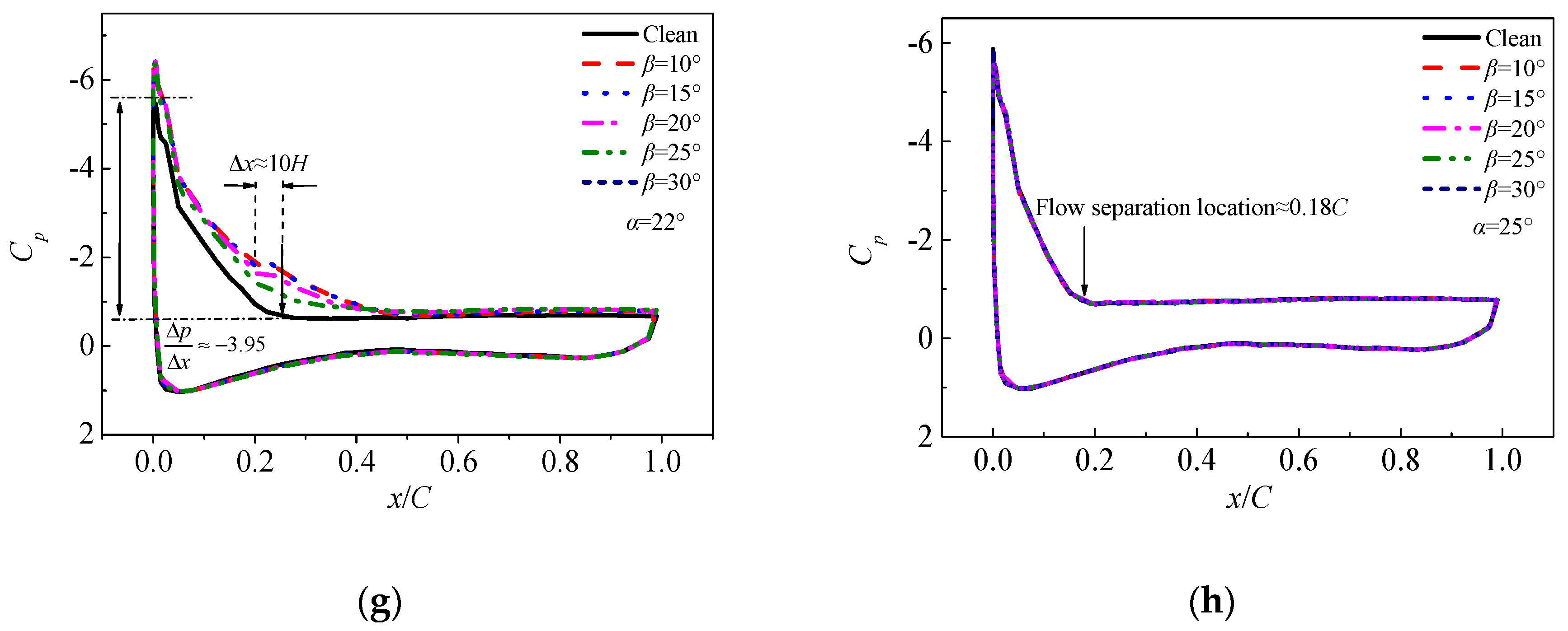
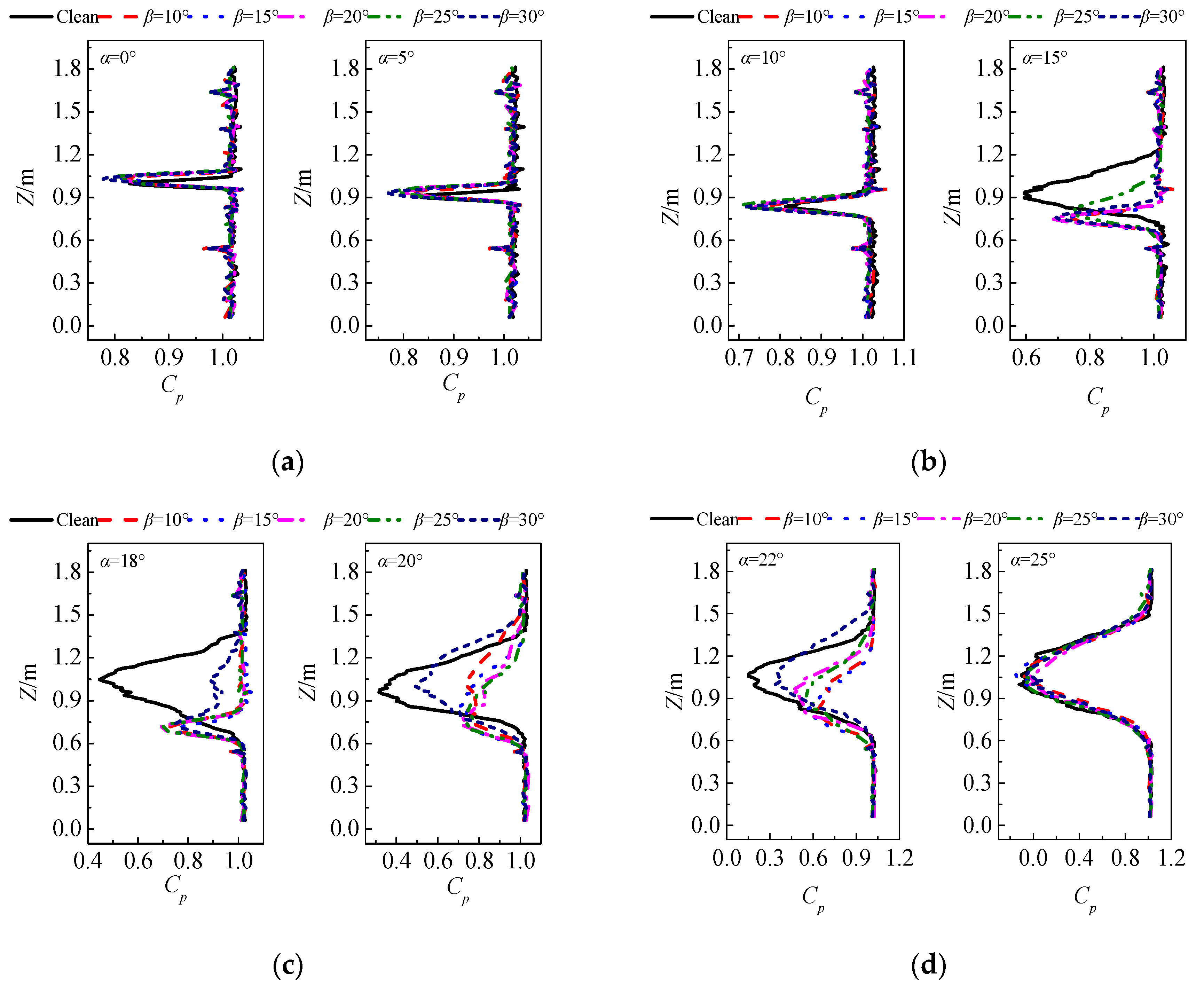
| Installation Angle β (°) | Height H (mm) | Height Ratio (H/δ) | Chord Length l |
|---|---|---|---|
| 10, 15, 20, 25, 30 | 5 | 1.0 | 2.5 |
| Variables | Mesh | Richardson Extrapolation | ||||
|---|---|---|---|---|---|---|
| Coarse | Medium | Fine | RE | p | R | |
| Cl | 0.5893 | 0.5918 | 0.5921 | 0.5922 | 3.05 | 0.12 |
| Cd | 0.2237 | 0.225 | 0.2251 | 0.2251 | 3.70 | 0.07 |
| Cl/Cd | 2.6211 | 2.6219 | 2.6221 | 2.6222 | 2.0 | 0.25 |
| Installation Angle β (°) | Length l (mm) | Height H (mm) | Spacing S/H | Pitch Distance λ/H |
|---|---|---|---|---|
| 10, 15, 20, 25, 30 | 17 | 5 | 5 | 5 |
| Case | Stall Attack Angle | Increment of Maximum Cl | Variations of Cd at 18° | Variations of Maximum Lift-Drag Ratio | Increment of Lift-Drag Ratio at 18° |
|---|---|---|---|---|---|
| Clean | 8° | 0% | 0% | 0% | 0% |
| β = 10° | 18° | 41.58% | −81.93% | −1.03% | 708.83% |
| β = 15° | 18° | 44.297% | −88.00% | −3.20% | 1146.04% |
| β = 20° | 18° | 48.77% | −83.28% | −19.35% | 821.86% |
| β = 25° | 18° | 46.69% | −81.01% | −32.47% | 696.77% |
| β = 30° | 18° | 42.69% | −62.13% | −31.89% | 284.56% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.-K.; Liu, W.; Zhang, T.-J.; Wang, P.-M.; Wang, X.-D. Experimental and Numerical Analysis of the Effect of Vortex Generator Installation Angle on Flow Separation Control. Energies 2019, 12, 4583. https://doi.org/10.3390/en12234583
Li X-K, Liu W, Zhang T-J, Wang P-M, Wang X-D. Experimental and Numerical Analysis of the Effect of Vortex Generator Installation Angle on Flow Separation Control. Energies. 2019; 12(23):4583. https://doi.org/10.3390/en12234583
Chicago/Turabian StyleLi, Xin-Kai, Wei Liu, Ting-Jun Zhang, Pei-Ming Wang, and Xiao-Dong Wang. 2019. "Experimental and Numerical Analysis of the Effect of Vortex Generator Installation Angle on Flow Separation Control" Energies 12, no. 23: 4583. https://doi.org/10.3390/en12234583
APA StyleLi, X.-K., Liu, W., Zhang, T.-J., Wang, P.-M., & Wang, X.-D. (2019). Experimental and Numerical Analysis of the Effect of Vortex Generator Installation Angle on Flow Separation Control. Energies, 12(23), 4583. https://doi.org/10.3390/en12234583





