Threshold Pore Pressure Gradients in Water-Bearing Tight Sandstone Gas Reservoirs
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Characterizations of Tight Cores
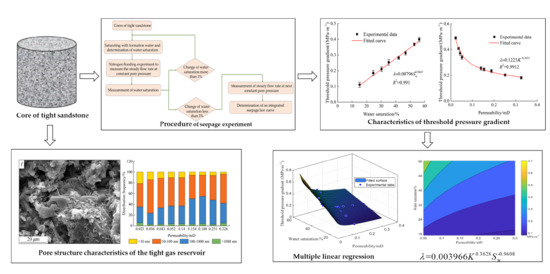
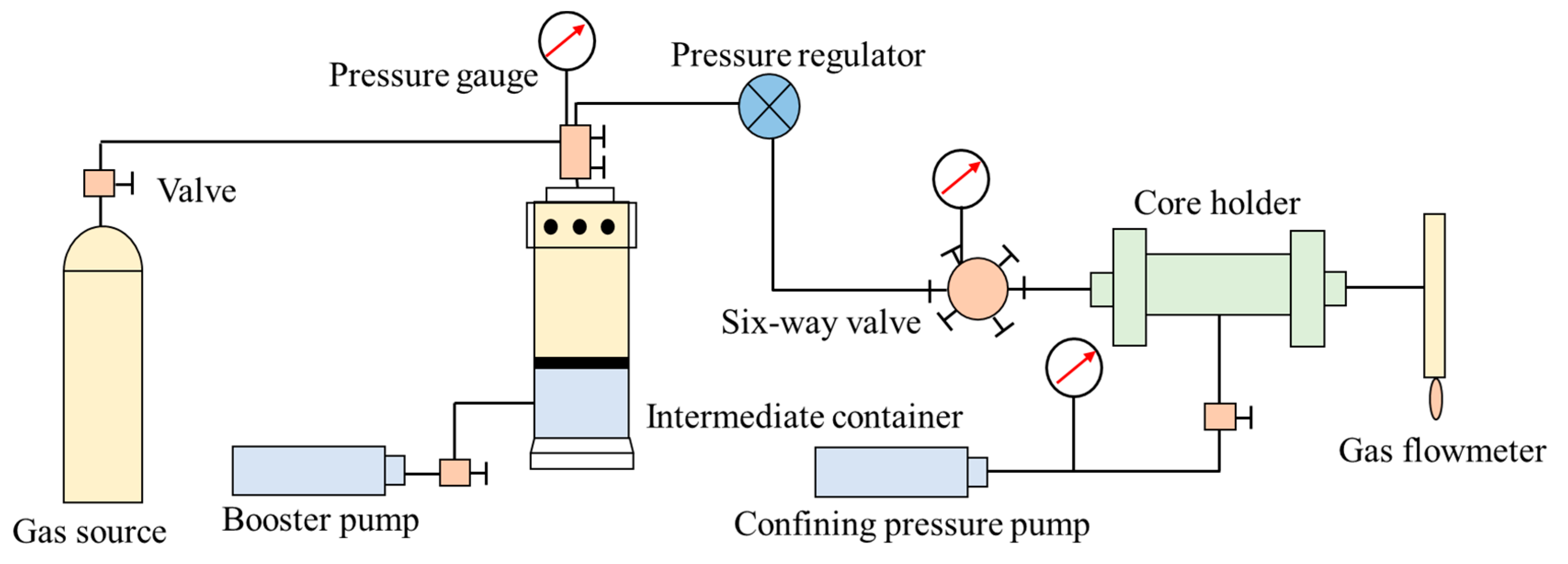
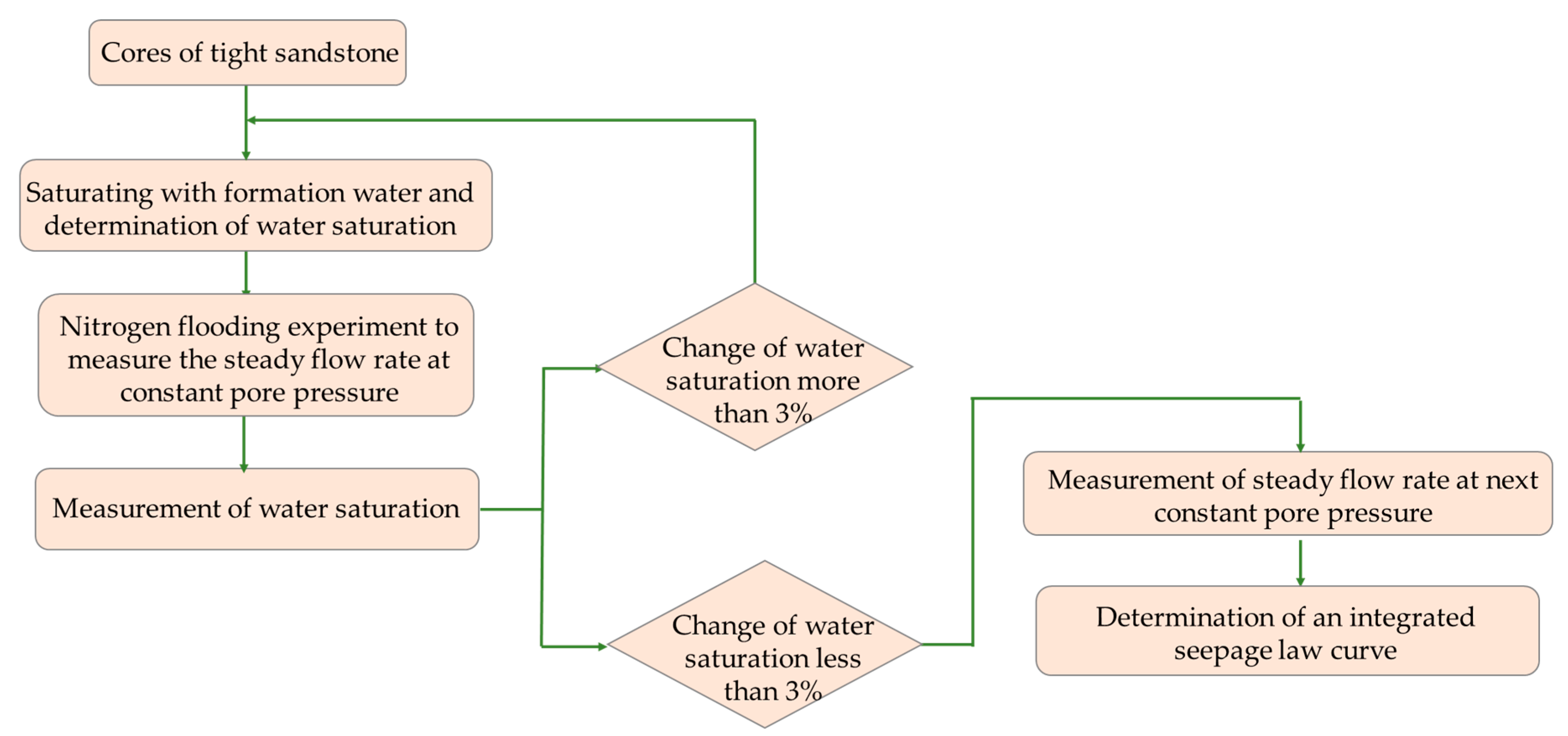
2.3. Seepage Experiments of Gas in Tight Cores
2.4. TPG Calculation Method
3. Pore Structure of Tight Gas Reservoirs
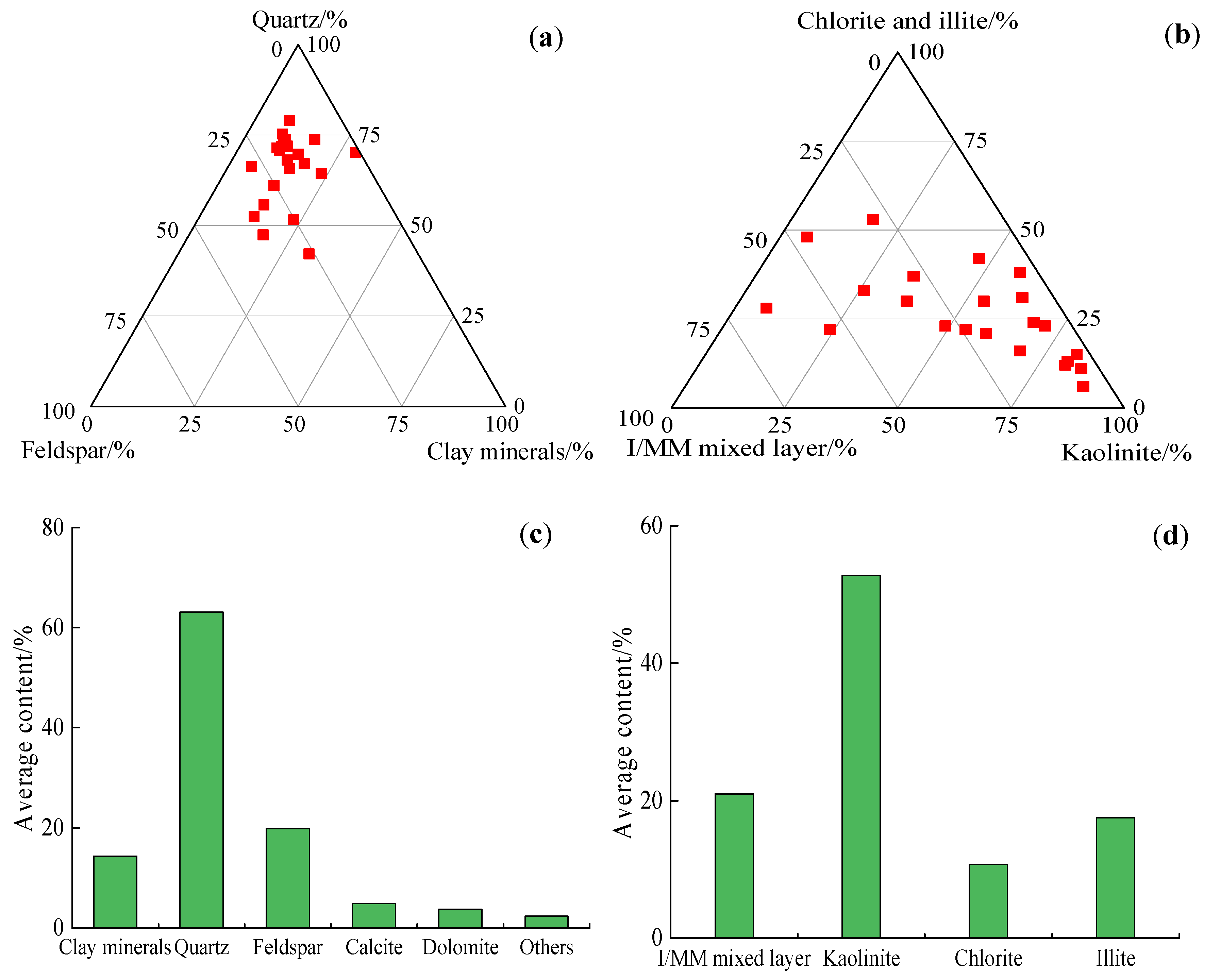
3.1. Mineral Compositions
3.2. Microscopic Morphologies
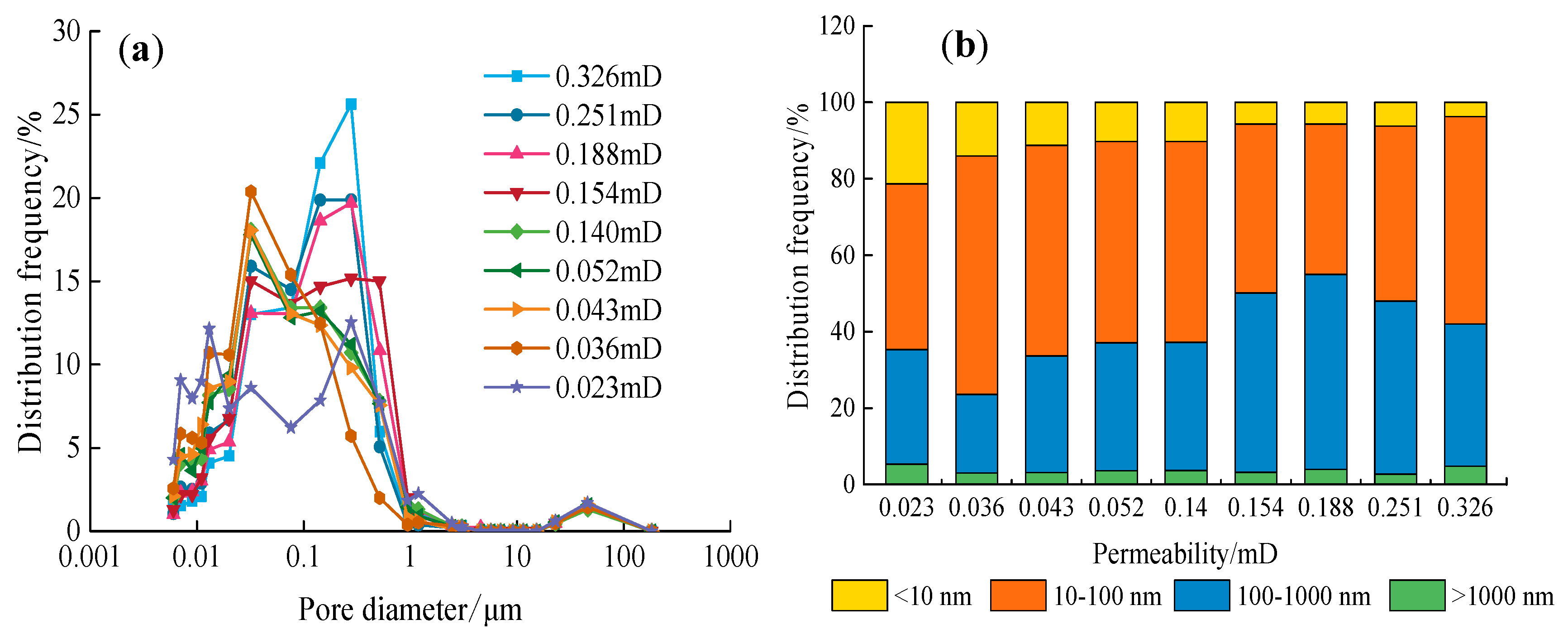
3.3. Pore Distributions
4. Characteristics of the TPG in Tight Gas Reservoirs
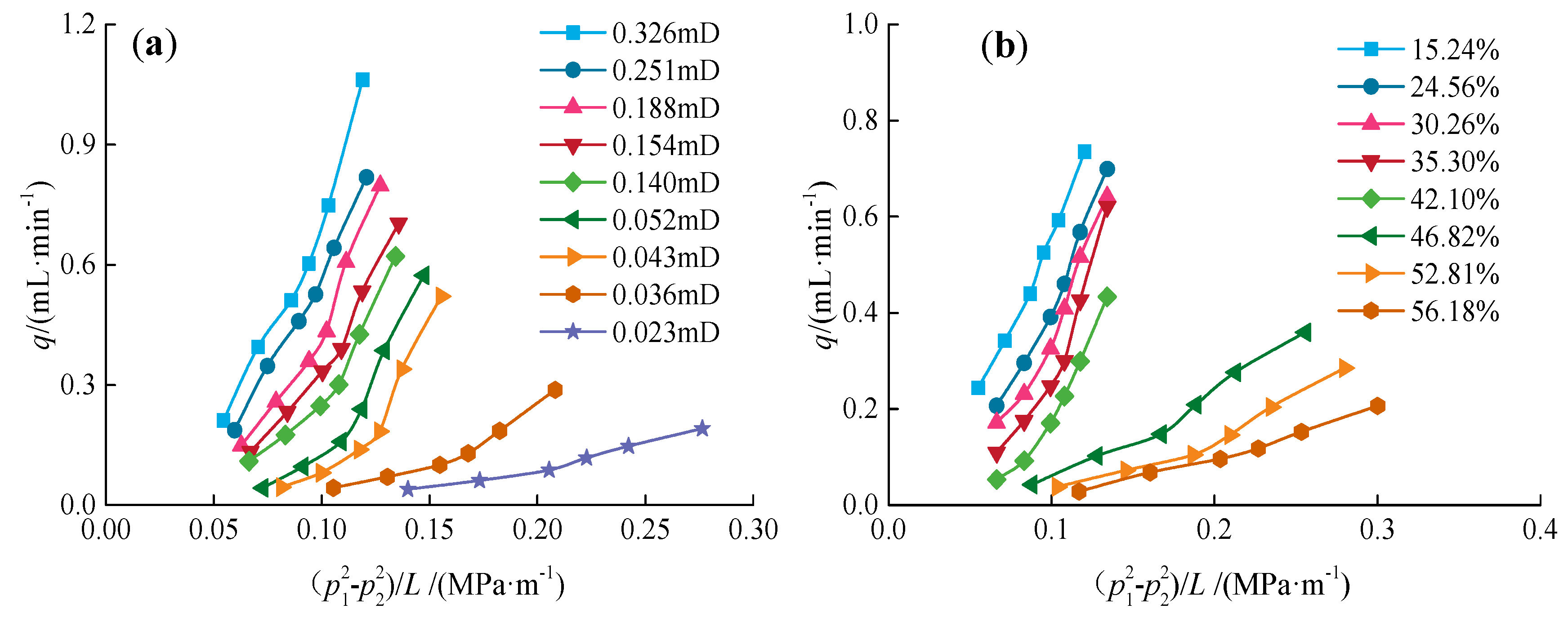
4.1. Nonlinear Seepage Characteristics of Gas in Tight Gas Reservoirs
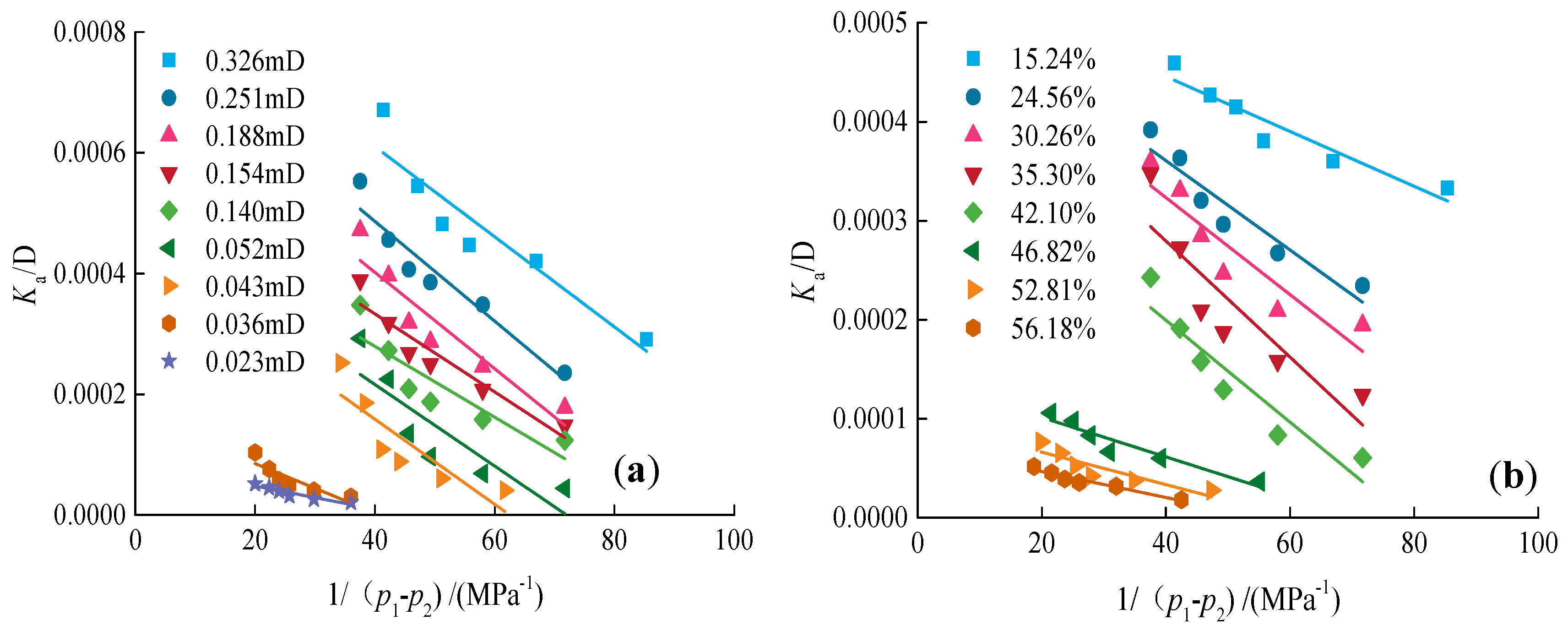
4.2. TPG Analysis
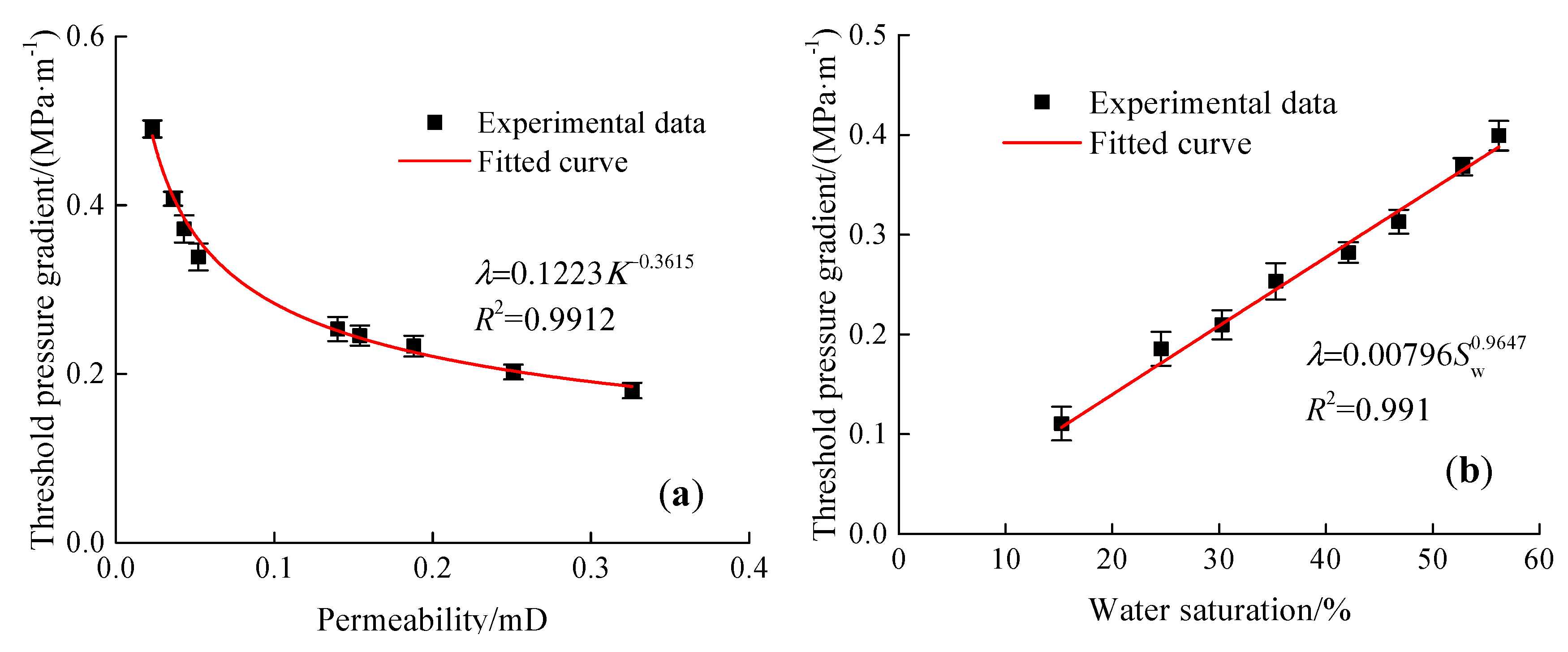
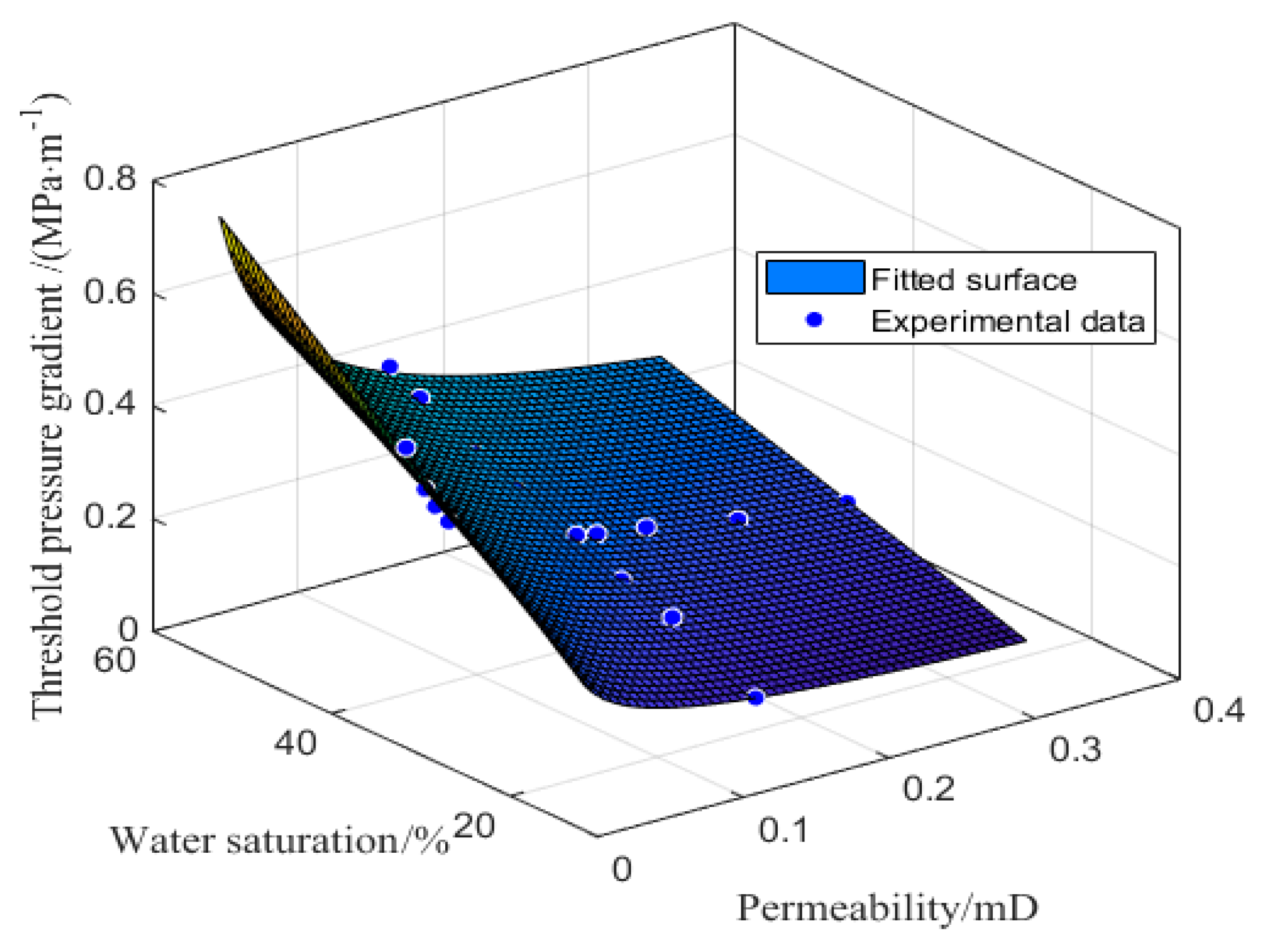
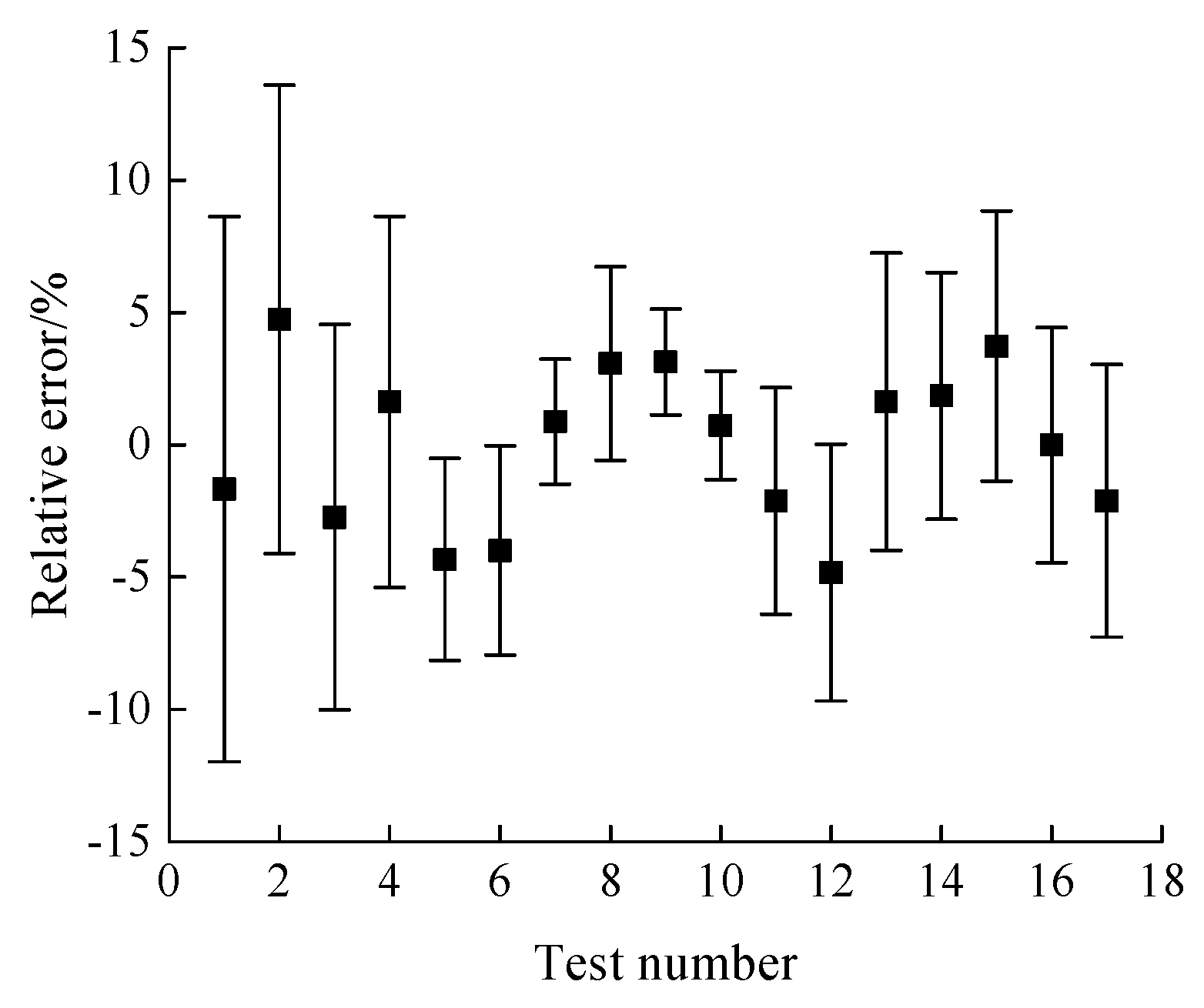
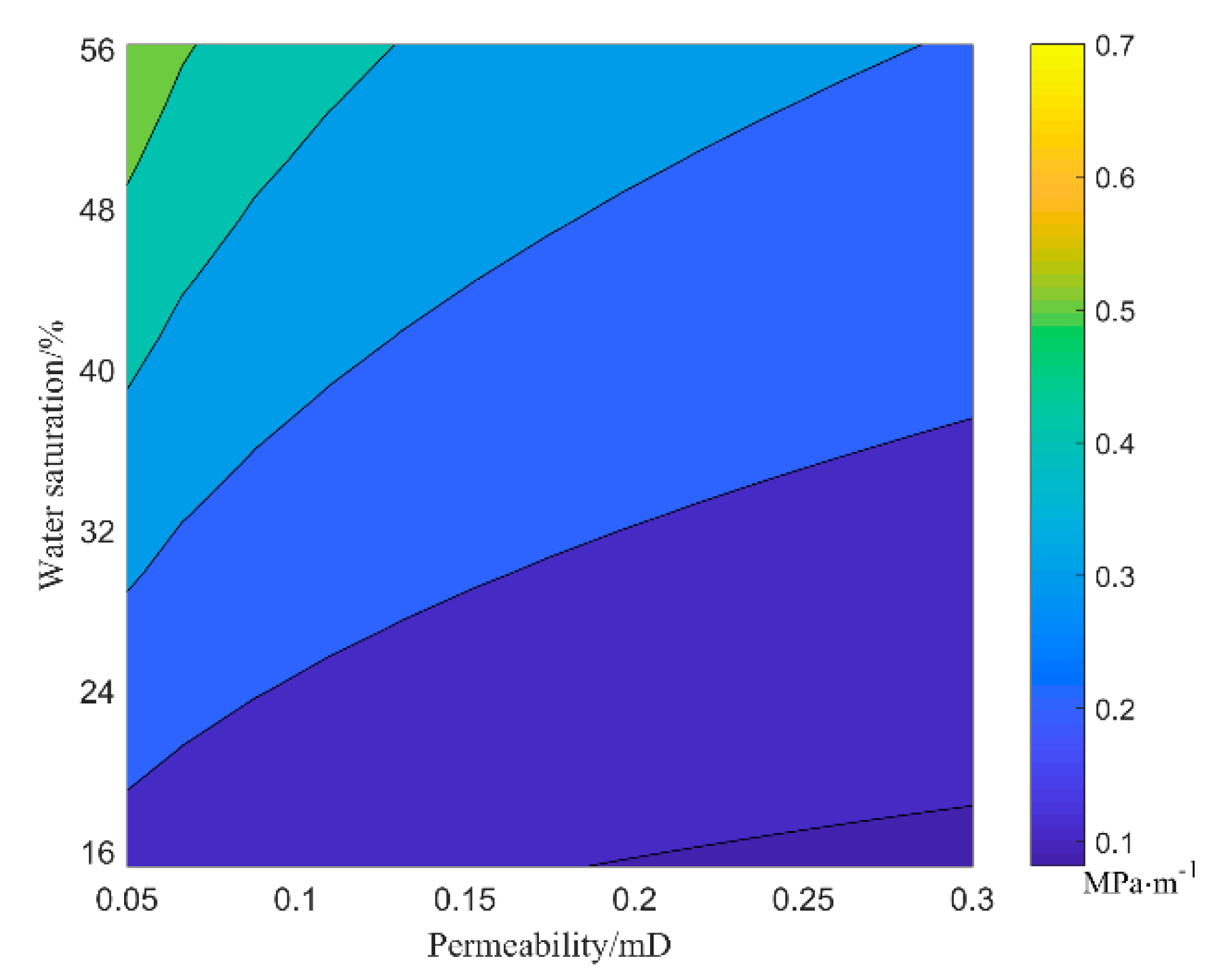
4.3. Mathematical TPG Model and Its Verification
5. Conclusions
- (1)
- The pore development in the tight gas reservoir is mainly related to clastic minerals such as quartz and feldspar, and small pores formed by various clay minerals are widely developed. The diameter of pores in the tight gas reservoir mainly is distributed below 1 micron, comprising mostly mesopores (100–1000 nm in diameter) and small pores (10–100 nm in diameter). The proportion of micropores (less than 10 nm in diameter) increases with a decrease of permeability in the tight gas reservoir. The water-sensitive mineral (I/MM mixed layer) and the complex pore structure will both make gas seepage in the tight gas reservoir more difficult under water-bearing conditions.
- (2)
- The gas seepage in the tight gas reservoir under water-bearing conditions shows a non-linear seepage characteristic, resulting in a TPG. The TPG of gas in the tight gas reservoir increases either with a decrease of core permeability or with an increase of water saturation. The TPG of gas has a power function of high correlation with core permeability or water saturation. The mathematical TPG model, paying special attention to the impact of core permeability and water saturation, reveals that permeability has a greater effect on TPG at high water saturation, while water saturation has a greater effect on TPG at low permeability.
Author Contributions
Funding
Conflicts of Interest
References
- Ji, G.; Jia, A.L.; Meng, D.W.; Guo, Z.; Wang, G.T.; Cheng, L.H.; Zhao, X. Technical strategies for effective development and gas recovery enhancement of a large tight gas field: A case study of Sulige gas field, Ordos Basin, NW China. Petrol. Explor. Dev. 2019, 46, 629–641. [Google Scholar] [CrossRef]
- Zhang, H.; Zhong, Y.; Kuru, E.; Kuang, J.C.; She, J.P. Impacts of permeability stress sensitivity and aqueous phase trapping on the tight sandstone gas well productivity-A case study of the Daniudi gas field. J. Petrol. Sci. Eng. 2019, 177, 261–269. [Google Scholar] [CrossRef]
- Huang, H.X.; Sun, W.; Ji, W.M.; Zhang, R.H.; Du, K.; Zhang, S.H.; Ren, D.Z.; Wang, Y.W.; Chen, L.; Zhang, X. Effects of pore-throat structure on gas permeability in the tight sandstone reservoirs of the Upper Triassic Yanchang formation in the Western Ordos Basin, China. J. Petrol. Sci. Eng. 2018, 162, 602–616. [Google Scholar] [CrossRef]
- Sun, L.D.; Fang, C.L.; Li, F.; Zhu, R.K.; He, D.B. Petroleum exploration and development practices of sedimentary basins in China and research progress of sedimentology. Petrol. Explor. Dev. 2010, 37, 385–396. [Google Scholar]
- Zhang, L.F.; Zhou, F.J.; Zhang, S.C.; Li, Z.; Wang, J.; Wang, Y.C. Evaluation of permeability damage caused by drilling and fracturing fluids in tight low permeability sandstone reservoirs. J. Petrol. Sci. Eng. 2019, 175, 1122–1135. [Google Scholar]
- Zhang, D.J.; Kang, Y.L.; Selvadurai, A.P.S.; You, L.J.; Tian, J. The role of phase trapping on permeability reduction in an ultra-deep tight sandstone gas reservoirs. J. Petrol. Sci. Eng. 2019, 178, 311–323. [Google Scholar] [CrossRef]
- Shen, J.; Qin, Y.; Li, Y.P.; Wang, G. Experimental investigation into the relative permeability of gas and water in low-rank coal. J. Petrol. Sci. Eng. 2019, 175, 303–316. [Google Scholar] [CrossRef]
- Fan, X.Q.; Wang, G.W.; Dai, Q.Q.; Li, Y.F.; Zhang, F.S.; He, Z.B.; Li, Q.B. Using image logs to identify fluid types in tight carbonate reservoirs via apparent formation water resistivity spectrum. J. Petrol. Sci. Eng. 2019, 178, 937–947. [Google Scholar] [CrossRef]
- Song, H.Q.; Liu, Q.P.; Yang, D.W.; Yu, M.X.; Lou, Y.; Zhu, W.Y. Productivity equation of fractured horizontal well in a water-bearing tight gas reservoir with low-velocity non-Darcy flow. J. Nat. Gas Sci. Eng. 2014, 18, 467–473. [Google Scholar] [CrossRef]
- Qin, S.F.; Li, F.; Li, W.; Zhou, Z.; Zhou, G.X. Formation mechanism of tight coal-derived-gas reservoirs with medium-low abundance in Xujiahe Formation, central Sichuan Basin, China. Mar. Petrol. Geol. 2018, 89, 144–154. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhang, C.; Zhu, L.Q. A fractal irreducible water saturation model for capillary tubes and its application in tight gas reservoir. J. Petrol. Sci. Eng. 2017, 159, 731–739. [Google Scholar] [CrossRef]
- Yang, X.; Meng, Y.F.; Shi, X.C.; Li, G. Influence of porosity and permeability heterogeneity on liquid invasion in tight gas reservoirs. J. Nat. Gas Sci. Eng. 2017, 37, 169–177. [Google Scholar] [CrossRef]
- Wojnarowski, P.; Czarnota, R.; Janiga, D.; Stopa, J. Novel liquid-gas corrected permeability correlation for dolomite formation. Int. J. Rock. Mech. Min. 2018, 112, 11–15. [Google Scholar] [CrossRef]
- Tanikawa, W.; Shimamoto, T. Comparison of Klinkenberg-corrected gas permeability and water permeability in sedimentary rocks. Int. J. Rock. Mech. Min 2009, 46, 229–238. [Google Scholar] [CrossRef]
- Song, H.Q.; Cao, Y.; Yu, M.X.; Wang, Y.H.; Killough, J.E.; Leung, J. Impact of permeability heterogeneity on production characteristics in water-bearing tight gas reservoirs with threshold pressure gradient. J. Nat. Gas Sci. Eng. 2015, 22, 172–181. [Google Scholar] [CrossRef]
- Zeng, J.; Wang, X.Z.; Guo, J.C.; Zeng, F.H.; Zhang, Q.S. Composite linear flow model for multi-fractured horizontal wells in tight sand reservoirs with the threshold pressure gradient. J. Petrol. Sci. Eng. 2018, 165, 890–912. [Google Scholar] [CrossRef]
- Tian, W.B.; Li, A.F.; Ren, X.X.; Josephine, Y. The threshold pressure gradient effect in the tight sandstone gas reservoirs with high water saturation. Fuel 2018, 226, 221–229. [Google Scholar] [CrossRef]
- Ding, J.C.; Yang, S.L.; Nie, X.R.; Wang, Z.L. Dynamic threshold pressure gradient in tight gas reservoir. J. Nat. Gas Sci. Eng. 2014, 20, 155–160. [Google Scholar] [CrossRef]
- Feng, X.; Zhong, B.; Liu, X.X. Diagnosing and parsing techniques on nonlinear effects of gas seepage. Nat. Gas Ind. 2008, 28, 127–129. [Google Scholar]
- Zhang, F.; Jiang, Z.X.; Sun, W.; Li, Y.H.; Zhang, X.; Zhu, L.; Wen, M. A multiscale comprehensive study on pore structure of tight sandstone reservoir realized by nuclear magnetic resonance, high pressure mercury injection and constant-rate mercury injection penetration test. Mar. Petrol. Geol. 2019, 109, 208–222. [Google Scholar] [CrossRef]
- Guo, X.B.; Huang, Z.L.; Zhao, L.B.; Han, W.; Ding, C.; Sun, X.W.; Yan, R.T.; Zhang, T.H.; Yang, X.J.; Wang, R.M. Pore structure and multi-fractal analysis of tight sandstone using MIP, NMR and NMRC methods: A case study from the Kuqa depression, China. J. Petrol. Sci. Eng. 2019, 178, 544–558. [Google Scholar] [CrossRef]
- Xi, K.L.; Cao, Y.C.; Haile, B.G.; Zhu, R.K.; Jahren, J.; Bjørlykke, K.; Zhang, X.X.; Hellevang, H. How does the pore-throat size control the reservoir quality and oiliness of tight sandstones? The case of the Lower Cretaceous Quantou Formation in the southern Songliao Basin, China. Mar. Petrol. Geol. 2016, 76, 1–15. [Google Scholar] [CrossRef]
- Lu, S.F.; Li, J.Q.; Zhang, P.F.; Xue, H.T.; Wang, G.L.; Zhang, J.; Liu, H.M.; Li, Z. Classification of microscopic pore-throats and the grading evaluation on shale oil reservoirs. Petrol. Explor. Dev. 2018, 45, 452–460. [Google Scholar] [CrossRef]
- Mosavat, N.; Hasanidarabadi, B.; Pourafshary, P. Gaseous slip flow simulation in a micro/nano pore-throat structure using the lattice Boltzmann model. J. Petrol. Sci. Eng. 2019, 177, 93–103. [Google Scholar] [CrossRef]
- Sakhaee-Pour, A.; Agrawal, A. Integrating acoustic emission into percolation theory to predict permeability enhancement. J. Petrol. Sci. Eng. 2018, 160, 152–159. [Google Scholar] [CrossRef]
- Awadh, S.M.; Ali, K.K.; Alazzawi, A.T. Geochemical exploration using surveys of spring water, hydrocarbon and gas seepage, and geobotany for determining the surface extension of Abu-Jir Fault Zone in Iraq: A new way for determining geometrical shapes of computational simulation models. J. Geochem. Explor. 2013, 124, 218–229. [Google Scholar] [CrossRef]
- Sakran, S.; Nabih, M.; Henaish, A.; Ziko, A. Structural regime and its impact on the mechanism and migration pathways of hydrocarbon seepage in the southern Gulf of Suez rift: An approach for finding new unexplored fault blocks. Mar. Petrol. Geol. 2016, 71, 55–75. [Google Scholar] [CrossRef]

| Core Number | Length (cm) | Diameter (cm) | Porosity (%) | Permeability (mD) |
|---|---|---|---|---|
| 1 | 4.75 | 2.52 | 5.91 | 0.188 |
| 2 | 4.45 | 2.50 | 7.60 | 0.154 |
| 3 | 4.52 | 2.50 | 4.30 | 0.023 |
| 4 | 4.50 | 2.52 | 5.92 | 0.140 |
| 5 | 4.30 | 2.52 | 6.32 | 0.043 |
| 6 | 4.10 | 2.52 | 6.82 | 0.052 |
| 7 | 6.00 | 2.52 | 7.81 | 0.036 |
| 8 | 4.55 | 2.50 | 7.52 | 0.326 |
| 9 | 5.00 | 2.50 | 5.70 | 0.251 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Long, Y.; Sun, Y.; Zhang, S.; Song, F.; Wang, X. Threshold Pore Pressure Gradients in Water-Bearing Tight Sandstone Gas Reservoirs. Energies 2019, 12, 4578. https://doi.org/10.3390/en12234578
Wang Y, Long Y, Sun Y, Zhang S, Song F, Wang X. Threshold Pore Pressure Gradients in Water-Bearing Tight Sandstone Gas Reservoirs. Energies. 2019; 12(23):4578. https://doi.org/10.3390/en12234578
Chicago/Turabian StyleWang, Yong, Yunqian Long, Yeheng Sun, Shiming Zhang, Fuquan Song, and Xiaohong Wang. 2019. "Threshold Pore Pressure Gradients in Water-Bearing Tight Sandstone Gas Reservoirs" Energies 12, no. 23: 4578. https://doi.org/10.3390/en12234578
APA StyleWang, Y., Long, Y., Sun, Y., Zhang, S., Song, F., & Wang, X. (2019). Threshold Pore Pressure Gradients in Water-Bearing Tight Sandstone Gas Reservoirs. Energies, 12(23), 4578. https://doi.org/10.3390/en12234578