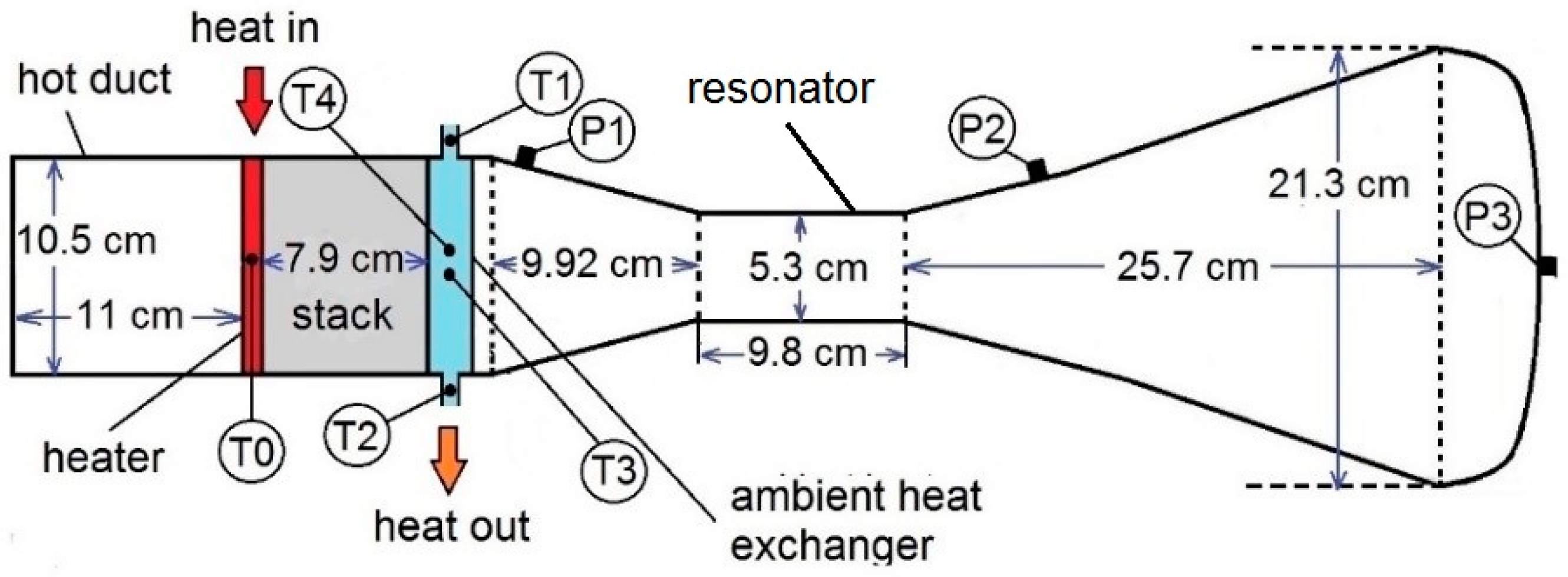
1. Introduction
Thermoacoustic (TA) engines are energy conversion devices whose operation relies on the cyclic heat transfer experienced by an acoustically oscillating gas with the solid walls of a porous medium. This technology, including prime movers, refrigerators, and heat pumps, has recently received increasing attention for having high potential to be a reliable, low-cost, and environmentally friendly technology, with remarkable applications in the renewable energy and waste heat recovery sectors.
Although the theoretical basis of TA systems is well established (the so-called linear theory of thermoacoustics [
1,
2,
3,
4]), the behavior of some components has not yet received proper mathematical modelling. The major of these components is the heat exchanger (HX) for which well-established design methodologies are still not available. This lack of knowledge derives from the TA HXs being subjected to oscillatory flows. This means that the fluid particles periodically reverse their direction of flow over a distance equal to the peak-to-peak particle displacement amplitude. Therefore, an arbitrary increase in the HX length could not automatically lead to an increase of the heat transfer area but, eventually, only to an increase of the thermoviscous dissipation [
4]. Therefore, when designing efficient HXs, the HX length must be simultaneously optimized with the pore hydraulic diameter and the fin thickness (or, equivalently, the HX blockage ratio) in order for the target heat load to be transferred under a small gas-solid temperature difference in conjunction with low pressure drop [
5,
6].
This type of calculation, however, requires the knowledge of the gas-side heat transfer coefficient as a necessary prerequisite, which, due to the oscillatory character of the flow, cannot be derived from conventional correlation laws for compact HXs generally referring to steady fluid flows.
There are only a few studies in the literature concerned with the experimental determination of heat transfer correlations for oscillatory flows and that could serve as a basis for theoretical modelling.
Paek et al. [
7] carried out an experimental investigation of the thermal performance of a parallel-plate HX acting as the cold HX of a TA cooler. A heat transfer correlation in terms of Colburn-j factor was proposed.
Thermoacoustic coolers were also used by Nsofor et al. [
8] and Tang et al. [
9] to investigate the gas side heat transfer coefficient of HXs of the parallel-plate type.
Experiments involving standing wave devices with two identical HXs and no stack in between were conducted by Kamsanam et al. [
10] and Ilori et al. [
11] to investigate the thermal performance of HXs of the parallel-plate type and parallel tube type. The derived correlation laws were expressed in terms of Nusselt numbers.
All the above studies indicate that steady flow heat transfer correlations for compact HXs could be not applicable for TA applications, since they may introduce significant errors in predicting the gas-side convection coefficient. Deviations between experimental data and model predictions as high as 71.3% were found in [
10], although Paek et al. [
7] found deviations of about 38% that further decreased by making improvements in the correlation model. As for the “boundary layer heat transfer model”, currently integrated in DeltaEC [
12] (the main simulation code of TA devices), deviations as high as 114% were found in [
7] and as low as 21.5% were found in [
9]. The results reported in these studies are therefore not univocal and need further validation. Therefore, additional experimental investigations could be useful to expand the range of operative conditions and geometrical configurations.
With this aim, in this paper, an experimental study of the thermal performance of a TA HX is carried out. The work involves the determination of the heat fluxes sustained by a HX of the finned-tube type through standard heat balance measurements. This HX functions as an ambient HX of a prime mover of the standing wave type, a configuration not considered in the above cited investigations and that needs a specific data reduction. From the experimental data, the gas-side heat transfer coefficient over a wide range of velocity amplitudes is calculated. A new correlation law expressed in terms of dimensionless Nusselt number is then derived and compared to a number of theoretical models currently applied in thermoacoustics. This new proposed correlation could be usefully applied in the design of practical TA HXs.
3. Calculation Methodology
To estimate the heat transfer rates sustained by the ambient HX and the related gas-side heat transfer coefficient, a procedure based on standard energy balance calculations was applied. The heat flux transferred by the HX was estimated from the measured values of the inlet and outlet water temperatures and of the water volume flow rate,
Va, as
where
ca and
ρa are the specific heat and density of water, respectively. This heat flux comprises the heat flux
Q transported hydrodynamically by the acoustic wave along the stack, the heat flux
QK1 transported by thermal conduction in the stack (both by the gas and the solid), the heat flux
QK2 transported by thermal conduction by the stack-holder walls and thermal insulating sleeve, and the heat flux
QK3 originating from dissipation of acoustic power and transported by thermal conduction in the resonator walls to the ambient HX where it is extracted. Therefore, to estimate
Q (which enters in the calculation of the gas-side heat transfer coefficient), the conduction contribution
QK =
QK1 +
QK2+
QK3 has to be subtracted from
QA:
With this aim, the heat flux (
QK1 +
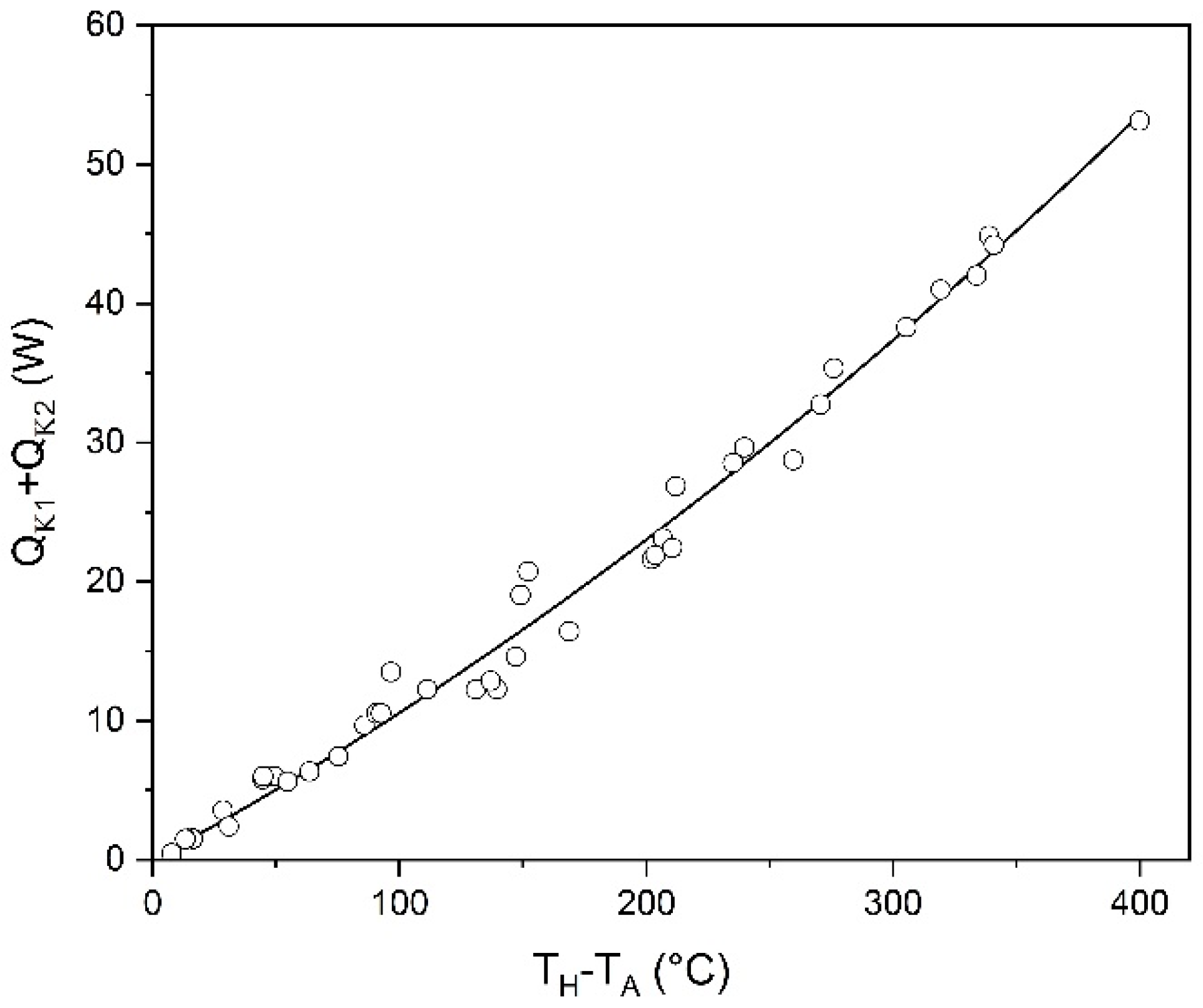
QK2) was experimentally determined once for all by powering the heater below the onset temperature of the engine and measuring the thermal load on the AHX. Results are shown in
Figure 6 where (
QK1 +
QK2) is plotted against the temperature difference between the heater,
TH, and the ambient heat exchanger,
TA = (
Ts +
Tg)/2. As for the
QK3 contribution, it was estimated by simulating the energy fluxes in the engine by the DeltaEC code where the experimental values recorded by the dynamic pressure sensors P1, P2, and P3 were used as inputs for model refinements. By this procedure, the
Q values resulted about 25% lower than the measured
QA values.
To make the calculated
Q consistent with the inlet and outlet temperatures of water, the
QK contribution to the inlet—outlet temperature difference was subtracted from the measured values of
T2 as follows
where
T2′ is the outlet temperature of water that would be measured if the
QK contribution was absent, i.e., if the HX was uniquely loaded by the convection heat flux. By this procedure, the
T2 values decreased by about 2.5%.
According to Paek et al. [
7] and Kamsanam et al. [
10], HXs found in thermoacoustic devices are typically of the crossflow type so the log-mean-temperature-difference (LMTD) method can be conveniently applied for the calculation of the heat transfer rates. In this method, the overall heat transfer coefficient,
UA, is defined as
where
θml, the log-mean temperature difference, is defined as
Note that in Equation (6), the inlet and outlet temperatures of the primary fluid (the gas) are the same (
Tg), being the flow oscillatory. Once
Q and
θml are calculated from the experimental data through Equations (2)–(4) and (6), they can be substituted in Equation (5) to determine the overall heat transfer coefficient
UA. The estimation of the gas-side heat transfer coefficient is then done, considering that for the geometry of the investigated HX,
UA has the following expression [
16]:
where
Ai,
Kt, and
d are the total inner surface, the thermal conductivity, and the wall thickness of the copper tube, respectively;
ha and
h are the water-side and gas-side heat transfer coefficients, respectively; Π and
Lfi are the cross section perimeter and half the length of the
i-th fin, respectively;
Ab is the total area of the un-finned surface of the tubes; and
ηfi, the efficiency of the
i-th fin, has the following expression
Kf and Af are the thermal conductivity and cross-section area and of the fin, respectively.
The application of Equation (7) requires preliminary the determination of the water-side heat transfer coefficient
ha. With this purpose, the HX was immersed in a water bath with temperature controlled at 50 °C by a refrigerator/heating circulator. This served to maintain the HX in isothermal conditions while a flow of water at 25 °C was sent to the inlet section of the HX. Taking into account that the temperature drop across the copper wall of the water tube is negligible (being that the wall is thin,
d ≈ 1 mm, and of high thermal conductivity,
Kt ≈ 400 W/mK), the measured temperature of the fin base
Ts is assumed to be equal to the temperature of the internal surfaces of the water tube. Recalling now the energy balance equations for the case of internal flow with constant surface temperature [
16], the measured values of
T1,
T2, and
Ts allow one to estimate
ha through the equation
For a water flow rate of 60 l/h, for example, the method furnished the value ha = 2495 ± 21 W/m2K (the indicated accuracy being the standard deviation of measurements).
The measurement uncertainty is estimated on the basis of standard formulas for error propagation [
17]. To increase the accuracy in the measurement of temperature differences (Δ
T), the thermocouples have been previously calibrated in situ by an environmental test chamber. This reduced the error in Δ
T to ±0.2 °C. The accuracy in the measurement of the flow rate of water was 0.0048 L/min. The uncertainty on Nusselt number is estimated to be around 20%.
4. Results and Discussion
The heat transfer coefficients estimated as previously described and expressed in terms of dimensionless Nusselt numbers
(
Dh being the hydraulic diameter of the HX pores and
K the gas thermal conductivity) are correlated to the local peak acoustic Reynolds number
ρ0 being the mean gas density,
η the dynamic viscosity, and
v1 the acoustic velocity amplitude calculated by simulating the standing-wave engine by the DeltaEC code [
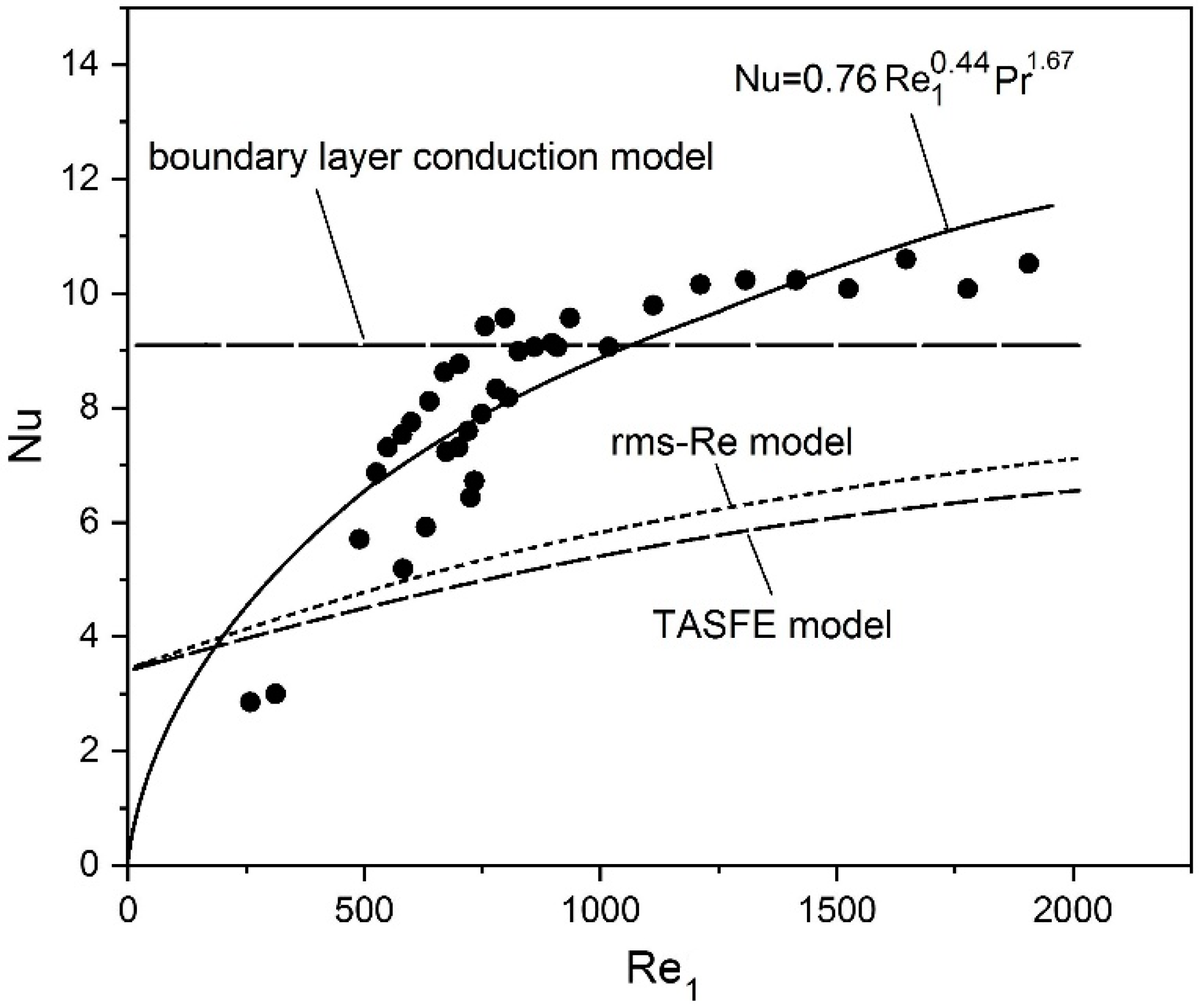
12] (where the pressure values measured by P1, P2, and P3 were used for iterative refinements of the model). The experimental results are shown in
Figure 7 (full circles) together with the regression curve (continuous line) obtained by fitting the data by the function
where the values obtained for parameters
a,
b, and c were 0.76, 0.44, and 1.67, respectively. Other correlation laws, derived by heat transfer models currently applied in thermoacoustics, are also shown.
The long dashed line refers to the “boundary layer conduction heat transfer” model proposed by Swift [
3]. The model (implemented in DeltaEC) calculates the heat transfer coefficient
h by the relation
where
yeff = min {
y0,
δκ}.
The short dashed line refers to the “time-average steady-flow equivalent” (TASFE) model [
18]. This model derives proper heat transfer correlation laws for the oscillatory flow regime by taking the time average over an acoustic cycle of classical steady flow correlations for compact HX. The Hausen correlation [
16] for laminar flow is considered in the present work:
D being the diameter of the duct,
LT the thermal entry length, and Re
D the Reynolds number. The TASFE correlation resulting from taking the time-average of Equation (14) over half the acoustic period is
The dotted line refers to the “root mean square Reynolds number” (rms-Re) [
18]. In this model, the Reynolds numbers, figuring in conventional steady flow correlations, are substituted by their rms values. Application of the model to the Hausen correlation provides:
Note that in Equations (15) and (16), the heat exchanger fin length (LHX = 2 cm) has been arbitrarily identified with the thermal entry length, LT, of Equation (14).
An inspection of the figure reveals that the boundary layer conduction heat transfer model predicts a constant Nusselt number, independent of the amplitude of the oscillation velocity. The model overestimates the experimental data at low Reynolds numbers (Re < 600) and slightly underestimates them at high Reynolds numbers (Re > 600).
The TASFE and rms-Re models are able to predict the increase of Nu with Re1 but, analogously to the previous model, overestimate the experimental data at low Reynolds numbers (Re < 300) and underestimates them at high Reynolds numbers (Re > 300). Furthermore, the Nu number provided by the rms-Re results slightly higher than that provided by the TASFE model.
For Re1 > 300, the relative difference between the model predictions and the experimental data amounts to 19%, 38%k and 41% for the boundary layer, rms-Re, and TASFE models, respectively. Therefore, the results of the present study indicate that the boundary layer model performs better than the rms-Re and TASFE models in predicting the heat transfer coefficients in oscillating flows.
Adapting steady flow correlation laws to oscillating flows by simply taking their time average an acoustic cycle is probably too crude of an approximation that does not capture the mechanism of heat transfer under oscillating flows.