An Improved Bare Bone Multi-Objective Particle Swarm Optimization Algorithm for Solar Thermal Power Plants
Abstract
:1. Introduction
2. Mathematical Model of Solar Power Generation System
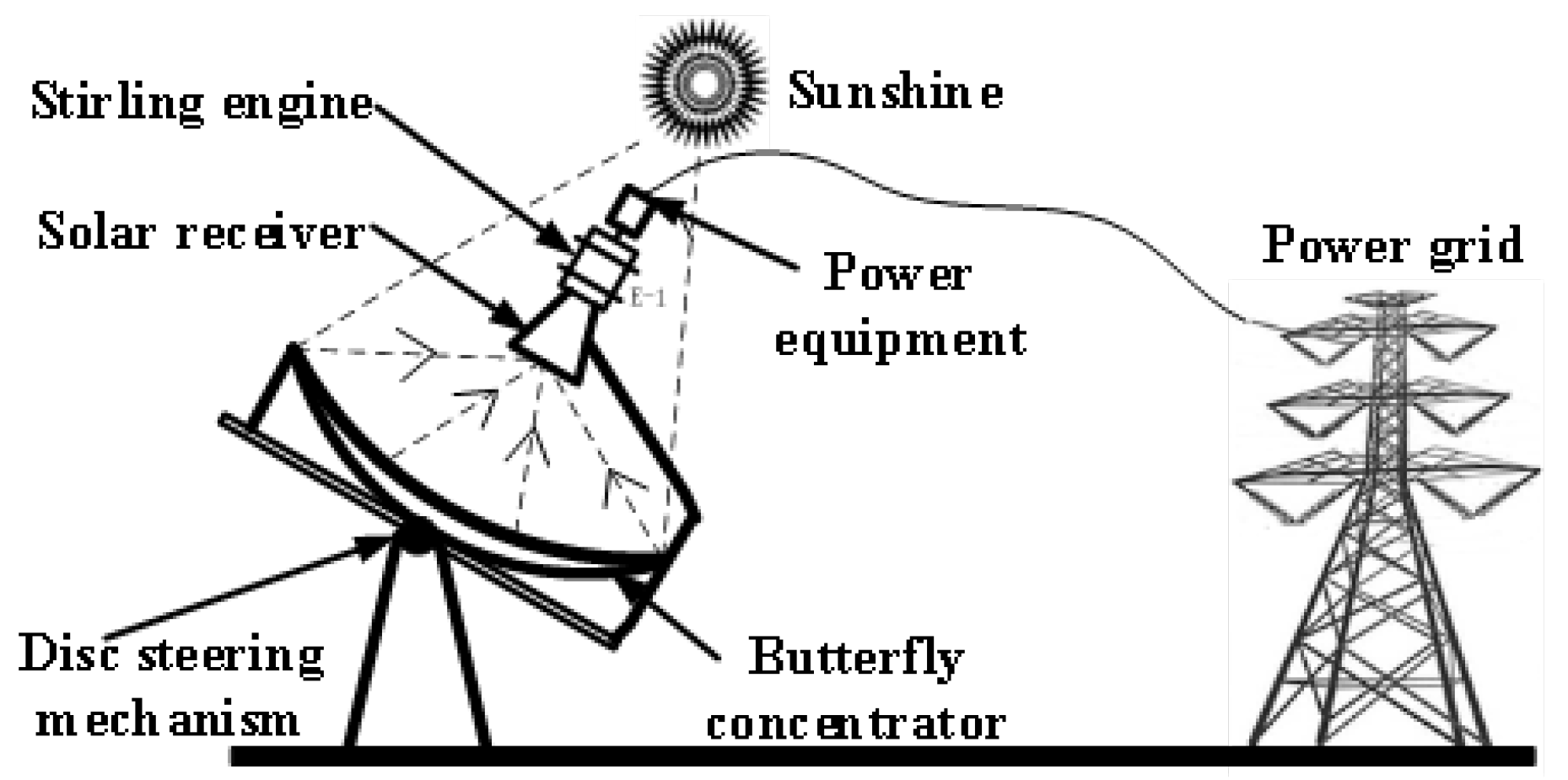
2.1. Mathematical Model of Solar Stirling Power Generation System
2.1.1. Decision Variables
2.1.2. Constants
2.1.3. Objective Function
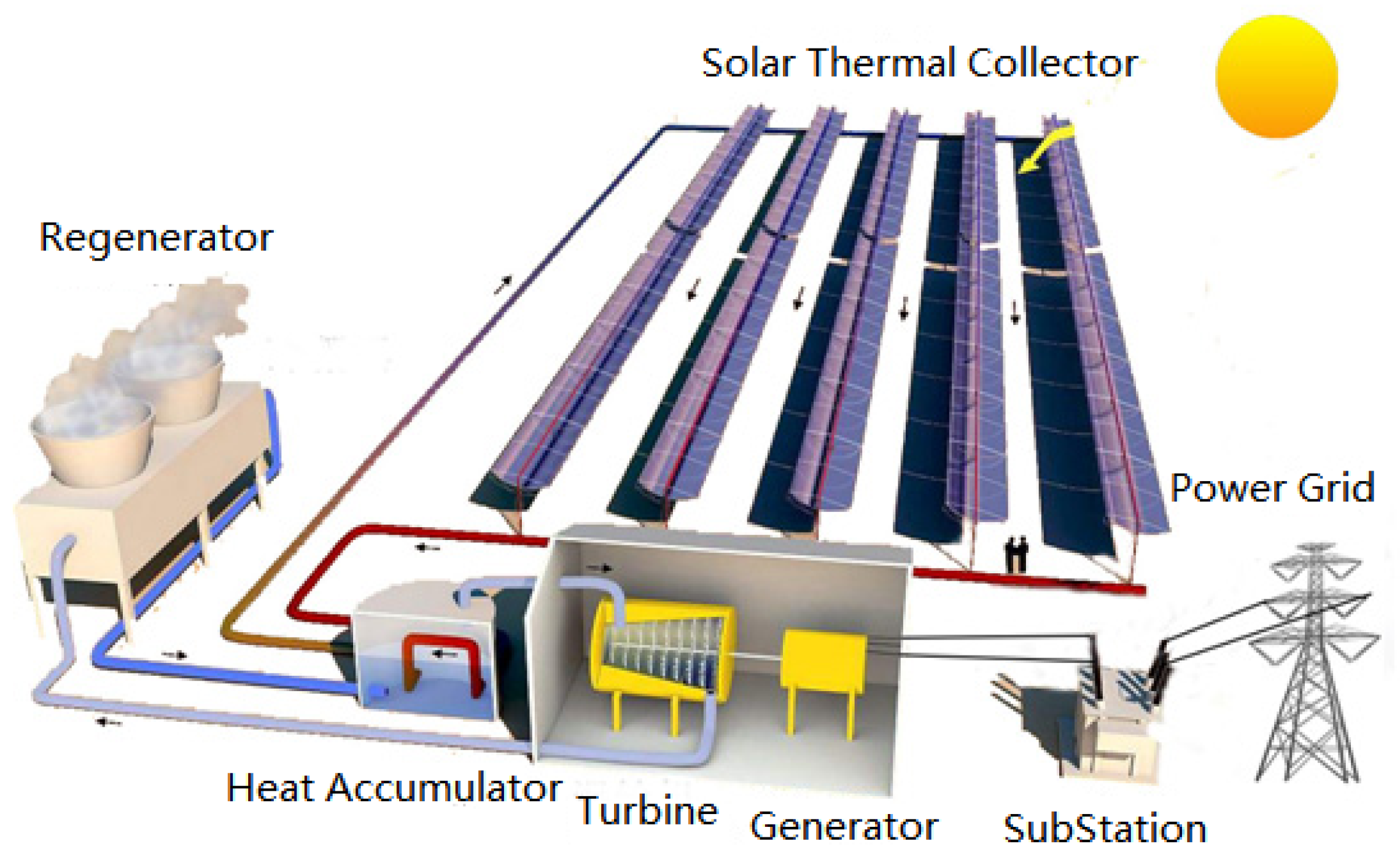
2.2. Mathematical Model of Solar Brayton Power Generation System
2.2.1. Decision Variables and Their Range of Values
2.2.2. Constants
2.2.3. Objective Function
2.2.4. Restrictions
3. Improved Multi-Objective Particle Swarm Optimization Algorithm
3.1. Traditional Backbone Particle Swarm Optimization Algorithm(BBPSO)
3.2. Improved Backbone Particle Swarm Optimization Algorithm
- (1)
- Initialization
- (2)
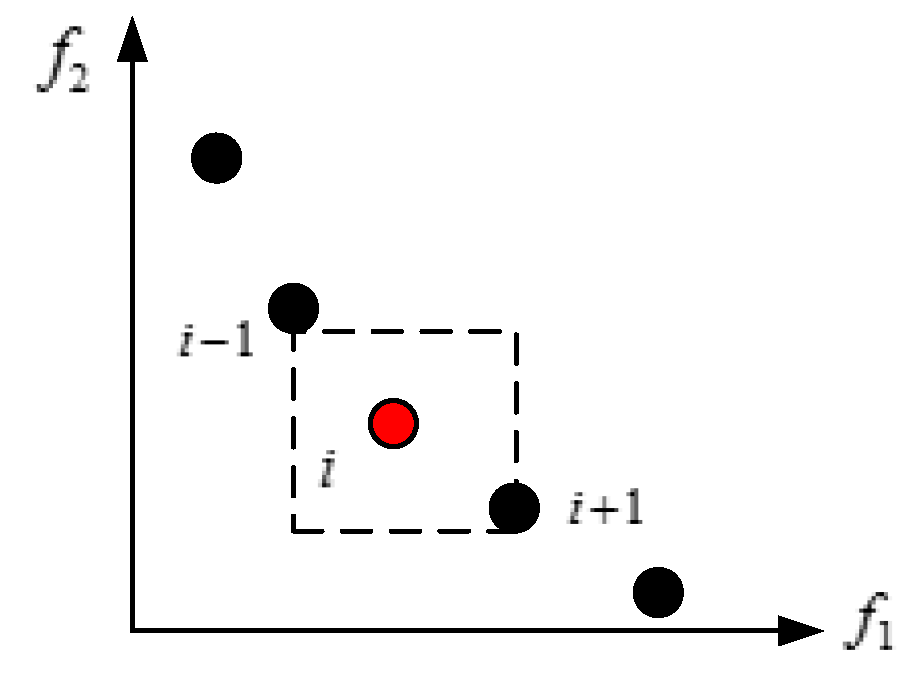
- Update of particle individual leader
- (3)
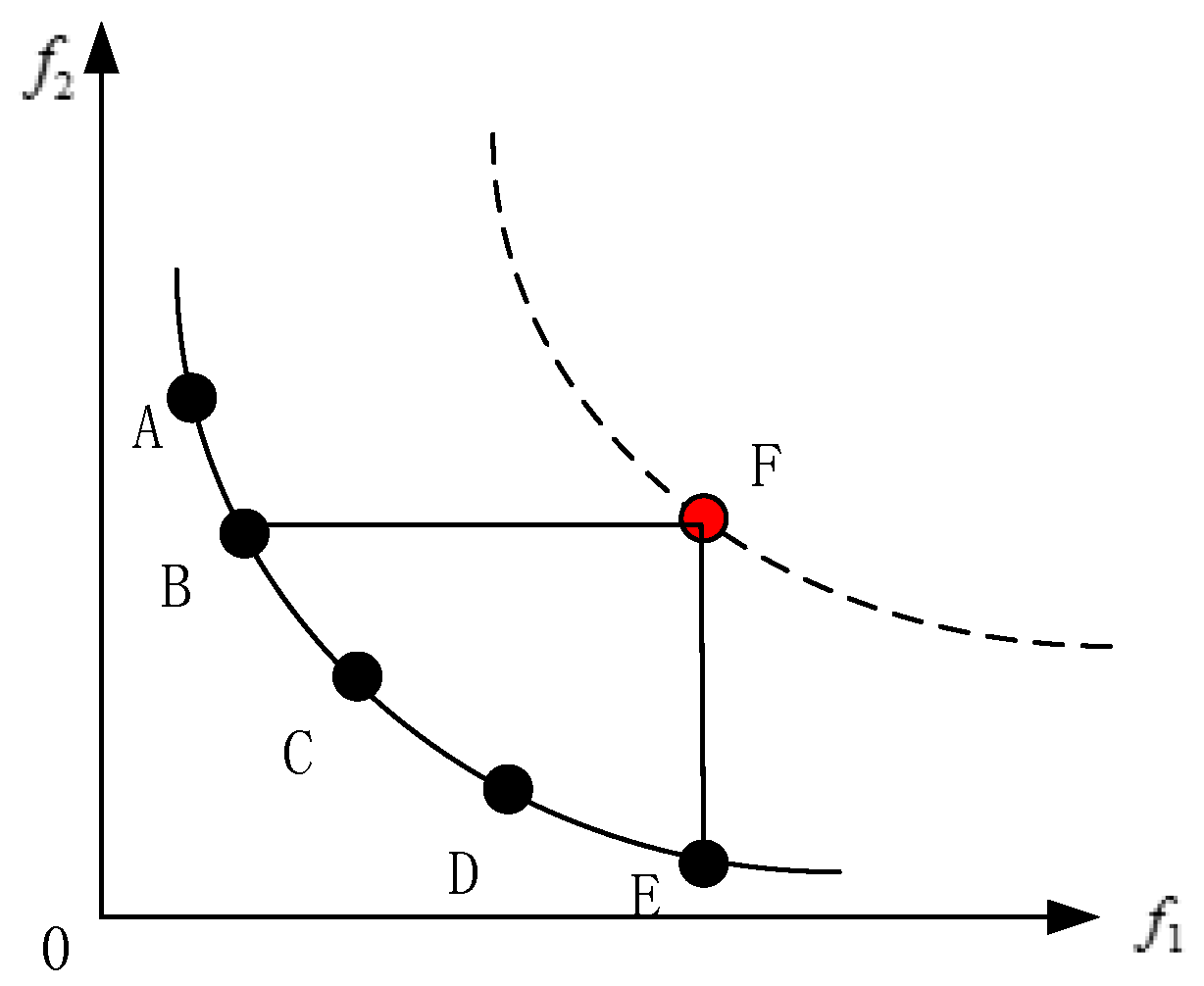
- Selection of Particle global leader
- (4)
- Update formula for particle position
- (5)
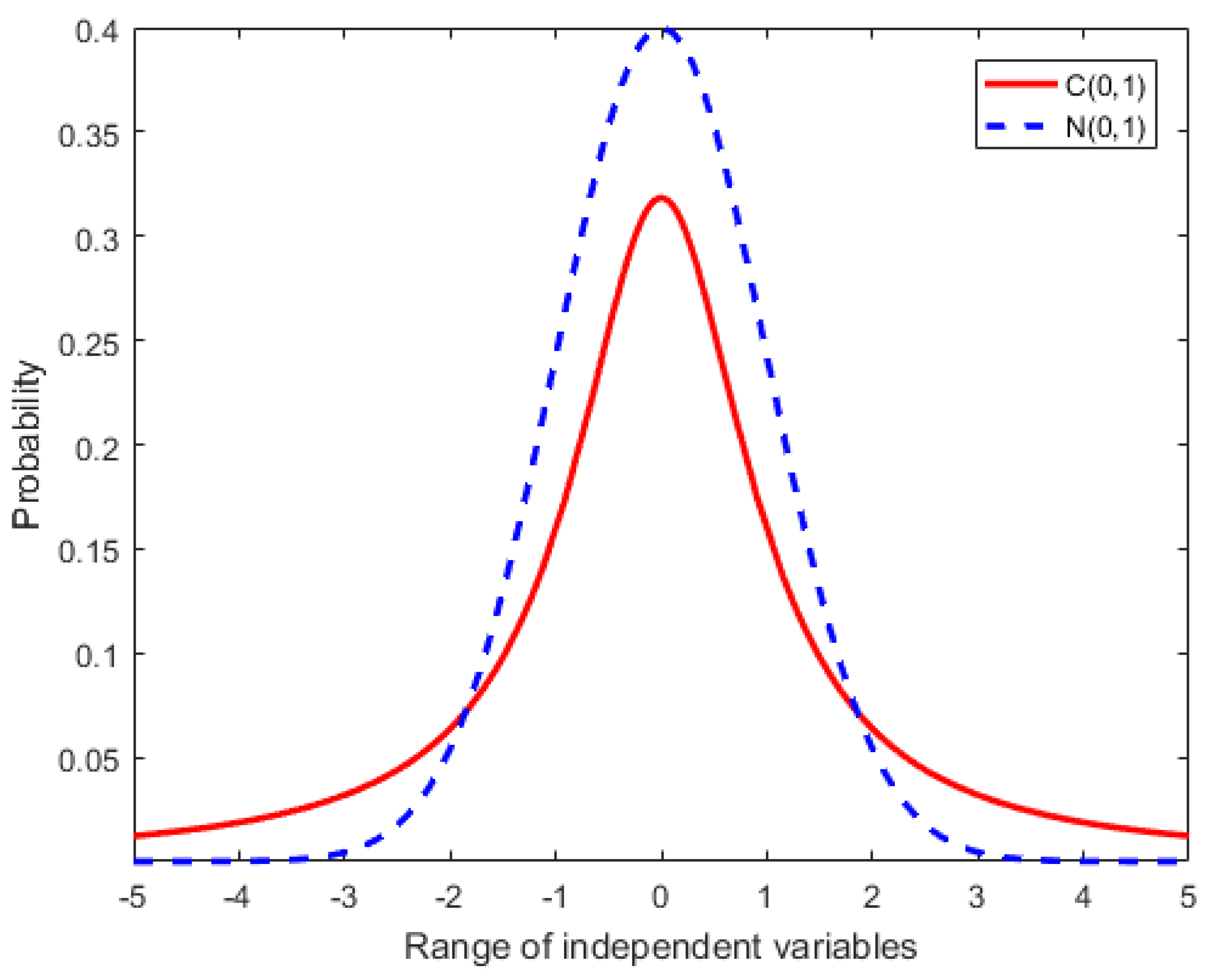
- Mutation operator based on Cauchy time-varying mutation mechanism
| Algorithm 1: Gaussian time varying mutation operation |
|
| Algorithm 2: Cauthy time varying mutation operation |
|
- (6)
- Particle out of bounds processing mechanism
- (7)
- Update of the reserve set
4. Simulation Experiment Analysis
4.1. Multi-Objective Test Environment
4.1.1. Multi-Objective Test Function
4.1.2. Multi-Objective Evaluation Index
- (1)
- Inverted General Distance (IGD)
- (2)
- Hyper Volume (HV)
- (3)
- Multi-objective comparison algorithm
4.2. Simulation Results and Performance Analysis
5. Application of IBBMOPSO to the Optimization of Solar Power Systems
5.1. Multi-Objective Optimization Methods
5.1.1. Fuzzy Optimization
5.1.2. Linear Programming Method for Multidimensional Analysis of Preference(LINMAP)
5.1.3. Technique for Order Preference by Similarity to an Ideal Solution(TOPSIS)
5.2. Simulation Experiments
5.2.1. Algorithm Implementation of Multi-objective Engineering Design Problem
5.2.2. Simulation Results for Solar Stirling Power Generation System
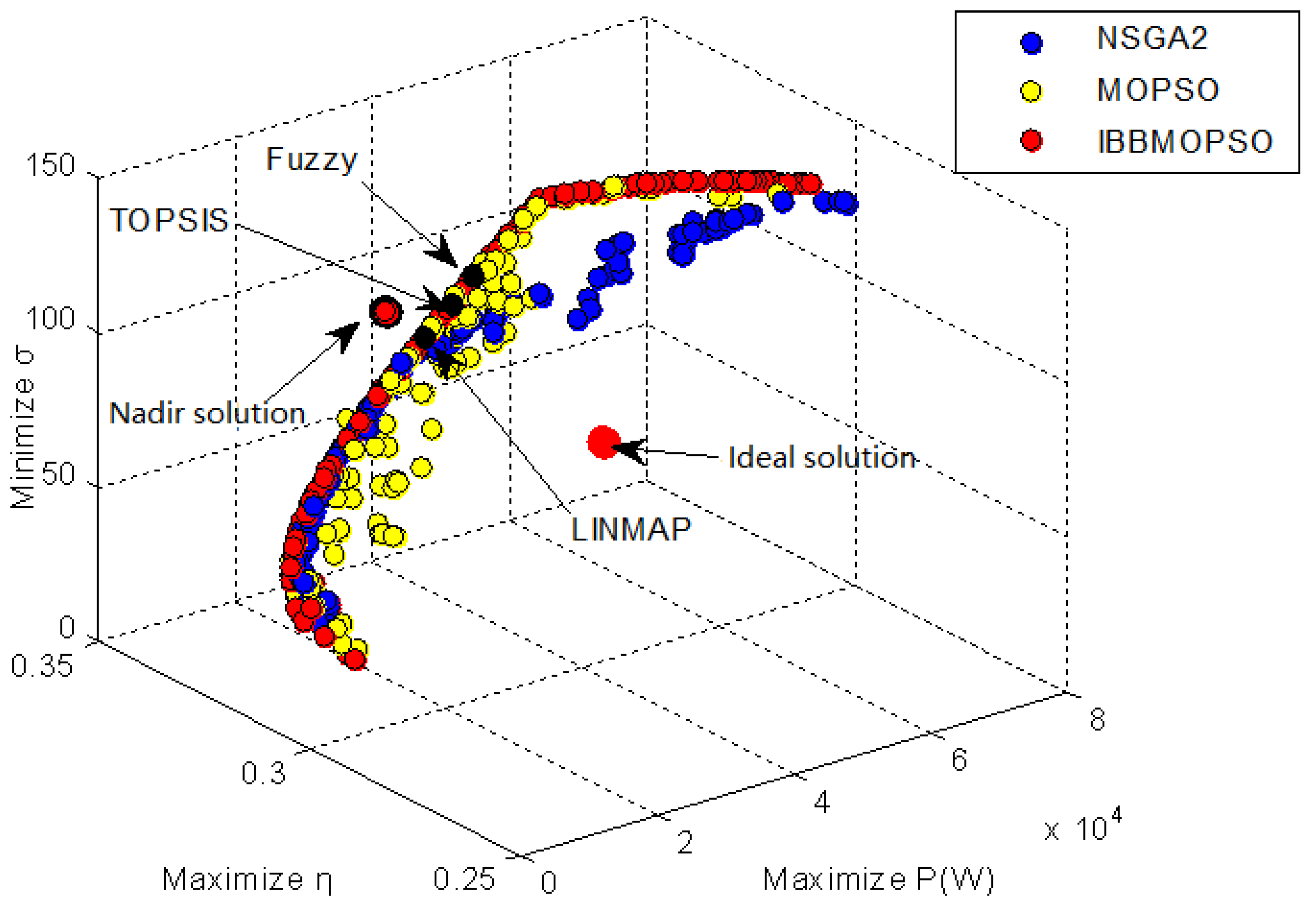
5.2.3. Simulation Results of Solar Brayton Power Generation System
6. Conclusions and Future Work
- Multi-objective optimization algorithms play an increasingly important role in optimizing the power generation systems from solar energy.
- The IBBMOPSO is proposed based on the BBMOPSO. The experimental results show that IBBMOPSO has better performance than other multi-objective intelligent optimization algorithms.
- IBBMOPSO can provide more options for multi-objective engineering optimization problems than other multi-objective intelligent optimization algorithms.
Author Contributions
Funding
Conflicts of Interest
References
- ExxonMobil. 2018 Outlook for Energy: A View to 2040. Available online: https://corporate.exxonmobil.com (accessed on 25 March 2019).
- Li, G.Q.; Wang, H.Z.; Zhang, S.L.; Xin, J.T.; Liu, H.C. Recurrent neural networks based photovoltaic power forecasting approach. Energies 2019, 12, 2538. [Google Scholar] [CrossRef]
- Divina, F.; Torres, M.G.; Vela, F.A.G.; Noguera, J.L.V. A comparative study of time series forecasting methods for short term electric energy consumption prediction in smart buildings. Energies 2019, 12, 1934. [Google Scholar] [CrossRef]
- UN. United Nations Decade of Sustainable Energy for all 2014–2024. Available online: https://www.un.org/en/sections/observances/international-decades (accessed on 19 July 2018).
- Vrinceanu, A.; Grigorescu, L.; Dumitrascu, M.; Mocanu, L.; Dumitrica, C.; Micu, D.; Kucsicsa, G.; Mitrica, B.; Vrinceanu. Impacts of photovoltaic farms on the environment in the romanian plain. Energies 2019, 12, 2533. [Google Scholar] [CrossRef]
- NREL. Assessment of Parabolic trough and Power Tower Solar Technology Cost and Performance Forecast; Report No. NREL/SR-550-34440; NREL: Golden, Co, USA, 2003; pp. 24–28.
- Leon, L.J. Optimization of Dish Solar Collectors. Energy 1983, 7, 684–694. [Google Scholar]
- Francisco, N.; Alain, F. Thermal model of a dish Stirling systems. Sol. Energy 2009, 83, 81–89. [Google Scholar]
- Hafez, A.Z.; Ahmed, S.; Ismail, I.M. Solar parabolic dish Stirling engine system design, simulation and thermal analysis. Energy Convers. Manag. 2016, 15, 60–75. [Google Scholar] [CrossRef]
- Caballero, G.E.C.; Mendoza, L.S.; Martinez, A.M. Optimization of a dish Stirling system working with DIR-type receiver using multi-objective techiniques. Appl. Energy 2017, 204, 271–286. [Google Scholar] [CrossRef]
- Li, Y.; Xiong, B.Y.; Su, Y.X.; Tang, J.R.; Leng, Z.W. Particle swarm optimization-based power and temperature control scheme for grid-connected DFIG-based dish-Stirling solar-thermal system. Energies 2019, 12, 1300. [Google Scholar] [CrossRef]
- Anthony, P. Solar Brayton-cycle power system development. Prog. Aerosp. Sci. 1966, 16, 759–793. [Google Scholar]
- Springer, T.; Fridfdld, J. Space station freedom solar dynamic power generation. In Technology for Space Station Evolution. Volume 4: Power Systems/Propulsion/Robotics; NASA: Washington DC, USA, 1990; Volume 4, pp. 65–81. [Google Scholar]
- Meas, M.R.; Bello-Ochende, T. Thermodynamic design optimization of an open air recuperative twin-shaft solar therjal Brayton cycle with combined or exclusive reheating and intercooling. Energy Convers. Manag. 2017, 148, 770–784. [Google Scholar] [CrossRef]
- Malali, P.D.; Chaturvedi, S.K.; Abdel-Salam, T. Performance optimization of a regenerative Brayton heat engine coupled with a parabolic dish solar collector. Energy Convers. Manag. 2017, 143, 85–95. [Google Scholar] [CrossRef]
- Khan, M.S.; Abid, M.; Ali, H.M.; Amber, K.P. Comparative performance assessment of solar dish assisted s-CO2 Brayton cycle using nanofluids. Appl. Therm. Eng. 2019, 148, 295–306. [Google Scholar] [CrossRef]
- Marler, M.T.; Arora, J.S. The weighted method for multi-objetive optimization: New insights. Struct. Multidiscip. Optim. 2010, 41, 853–862. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W. Management models and industrial applications of linear programming. Math. Comput. 1962, 16, 401. [Google Scholar] [CrossRef]
- Ignizio, J.P.; Cavalier, T.M. Linear Programming in Single and Multiple-Objective Systems; Prentice Hall: Upper Saddle River, NJ, USA, 1982. [Google Scholar]
- Romero, C. Handbook of critical issuues in goal programming. Eur. J. Oper. Res. 1992, 62, 252. [Google Scholar]
- Yu, P.L. A class of solutions for group decision problems. Manag. Sci. 1973, 19, 936–946. [Google Scholar] [CrossRef]
- Zeleny, M. Multi-Criteria Decision Making; MCGraw-Hill: New York, NY, USA, 1982. [Google Scholar]
- Konak, A.; Colt, D.W.; Smith, A.E. Multi-objective optimization using genetic algorithms: A tutorial. Reliab. Eng. Syst. Saf. 2006, 91, 992–1007. [Google Scholar] [CrossRef]
- Mostaghim, S.; Teich, J. Strategies for finding good local guides in multi-objective particle swarm optimization (MOPSO). In Proceedings of the 2003 IEEE Swarm Intelligence Symposium(SIS 03), Indianapolis, IN, USA, 24–26 April 2003; pp. 26–33. [Google Scholar]
- Basu, M. Economic environmental dispatch using multi-objective differential evolution. Appl. Soft Comput. 2011, 11, 2845–2853. [Google Scholar] [CrossRef]
- Zhang, Q.F.; Li, H. MOEA/D: A Multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Nazemzadegan, M.R.; Kasaeian, A.; Toghyani, S.; Ahmadi, M.H.; Saidur, R.; Ming, T. Multi-objetive optimization in a finite time thermodynamic method for dish-Stirling by branch and bound method and MOPSO algorithm. Front. Energy 2017, 8, 1701–2095. [Google Scholar]
- Li, Y.Q.; Liao, S.M.; Liu, G. Thermo-economic multi-objective optimization for a solar-dish Brayton system using NSGA-II and decision making. Int. J. Electr. Power Energy Syst. 2015, 64, 167–175. [Google Scholar] [CrossRef]
- Li, Y.Q.; Liu, G.; Liu, X.P. Thermodynamic multi-objetive optimization of a solar-dish Brayton system based on the maximum power output, thermal efficiency and ecological performance. Renew. Energy 2016, 95, 465–473. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the International Conference on Neural Networks(ICNN’95), Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Tripathi, P.K.; Bandyopadhyay, S.; Pal, S.K. Adaptive multi-objective particle swarm optimization algorithm. In Proceedings of the IEEE Congress on Evolutionary Compytation, Singapore, 25–28 September 2007. [Google Scholar]
- Praven, K.T.; Sanghamitra, B.; Sankar, K.P. Multi-Objective Particle Swarm Optimization and Multi-Swarm Concepts and Constraint Handing; Oklahoma State Unversity: Stillwater, OK, USA, 2008. [Google Scholar]
- Zhang, Y.; Gong, D.W.; Ding, Z.H. A bare-bones multi-objetive particle swarm optimization algorithm for environmental/economic dispatch. Inf. Sci. 2012, 192, 213–227. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Mohammadi, A.H.; Dehghani, S.; Barranco-Jimenez, M.A. Multi-objective thermodynamic-based optimization of output power of Solar Dish-Stirling engine by implementing an evolutionary algorithm. Energy Convers. Manag. 2013, 75, 438–445. [Google Scholar] [CrossRef]
- Punnathanam, V.; Kotecha, P. Multi-objective optimization of Stirling engine systems using Front-based Yin-Yang-Pair Optimization. Energy Convers. Manag. 2017, 133, 332–348. [Google Scholar] [CrossRef]
- Li, Y.Q.; He, Y.L.; Wang, W.W. Optimization of solar-powered Stirling heat engine with finite-time thermodynamics. Renew. Energy 2011, 36, 421–427. [Google Scholar]
- Sharma, A.; Shulka, S.K.; Rai, A.K. Finite time thermodynamic analysis and optimization of solar-dish Stirling heat engine with regenerative losses. J. Therm. Sci. 2011, 15, 995–1009. [Google Scholar] [CrossRef]
- Kennedy, J. Bare bones particle swarms. In Proceedings of the 2003 IEEE Swarm Intelligence Symposium, Indianapolis, IN, USA, 24–26 April 2003. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A.M.T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Raquel, C.R.; Naval, P.C. An effective use of crowding distance in multiobjective particle swarm optimization. In Proceedings of the IEEE Congress on Evolutionary Computation, Edinburgh, UK, 2–4 September 2005. [Google Scholar]
- Zitzler, E.; Deb, K.; Thiele, L. Comparsion of multi-objective evolutionary algorithms: Empirical results. IEEE Trans. Evol. Comput. 2000, 8, 173–195. [Google Scholar]
- Carlos, A.; Coello, C.; Margarita, R.S. A Study of the parallelization of a coevolutionary multi-objective evolutionary algorithm. In MICAI 2004: Advances in Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Zitzler, E.; Thiele, L. Multi objective evolutionary algorithms:a comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Lopez-lbanez, M.; Prasad, T.D.; Paechter, B. Multi-objective optimisation of the pump scheduling problem using SPEA2. In Proceedings of the IEEE Congress on Evolutionary Computation, Edinburgh, UK, 2–5 September 2005; pp. 435–442. [Google Scholar]
- Saha, S.; Bandyopadhyay, S. A generalized automatic clustering algorithm in a multiobjective framework. Appl. Soft Comput. 2013, 13, 89–108. [Google Scholar] [CrossRef]
- Van den Bergh, F.; Engelbrecht, A.P. A Cooperative Approach to Particle Swarm Optimization. IEEE Trans. Evol. Comput. 2004, 8, 225–239. [Google Scholar] [CrossRef]
- Wang, H.O.; Tanaka, K.; Griffin, M.F. An approach to fuzzy control of nonlinear systems: Stability and design issues. IEEE Trans. Fuzzy Syst. 1996, 4, 14–23. [Google Scholar] [CrossRef]
- Srinivasan, V.; Shocker, A.D. Linear programming techniquer for multidimensional analysis of preference. Psychometrica 1973, 38, 337–369. [Google Scholar] [CrossRef]
- Bellman, R.; Zadeh, L.A. Decision making in a fuzzy environment. Manag. Sci. 1970, 17, 141–164. [Google Scholar] [CrossRef]

| Variable Name | Symbol | Minimum Value | Maximum Value |
|---|---|---|---|
| Effectiveness’s of regenerator | 0.4 | 0.8 | |
| Effectiveness’s of the low temperature heat exchanger | 0.4 | 0.9 | |
| Effectiveness’s of thehigh temperature heat exchanger | 0.4 | 0.9 | |
| Heat capacitance rate of the heat sink | 300 | 1800 | |
| Heat capacitance rate of the heat source | 300 | 1800 | |
| Working temperature in high temperature isothermal process | 800 | 1000 | |
| Working temperature in low temperature isothermal process | 400 | 510 |
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| 1000 | 20 | 290 | |||
| 15 | 0.9 | ||||
| 1300 | n | 1 | |||
| 1300 | 2 | 288 | |||
| 4.3 | 2.5 |
| Parameter | Explanation |
|---|---|
| maximize output power of the Stirling model | |
| the net heat released from the heat source | |
| the net heat absorbed by the radiator | |
| the cycle period of the system | |
| the heat released from the heat source to the working fluid | |
| the heat absorbed by the cooling radiator from the working fluid | |
| the heat transfer loss from the heat source to the heat sink | |
| the overall efficiency of the system | |
| the product of the collector efficiency | |
| the Stirling engine efficiency | |
| minimize entropy production rate | |
| the average temperature of heat source | |
| the average temperature of heat sink |
| Variable Name | Symbol | Minimum Value | Maximum Value |
|---|---|---|---|
| High temperature heat exchanger efficiency | 0.5 | 0.7 | |
| Low temperature heat exchanger efficiency | 0.5 | 0.7 | |
| Accumulator efficiency | 0.5 | 0.8 | |
| Heat accumulator high temperature | 700 | 1000 | |
| Heat accumulator low temperature | 400 | 500 | |
| The temperature of the working fluid in the Brayton cycle 1 |
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| 0.85 | 0.02 | ||||
| 1000 | 20 | 2000 | |||
| 1300 | 300 | 2000 | |||
| 1300 | k | 4 | 1050 |
| Parameter | Explanation |
|---|---|
| maximize output power of the Brayton model | |
| the total heat absorption rate in the heat reserve | |
| the total heat release rate released into the cold reserve | |
| maximize thermal efficiency | |
| the Brayton heat engine efficiency | |
| the product of the dish concentrator efficiency | |
| the heat transfer loss from the heat source to the heat sink | |
| F | maximize thermal economics |
| annual investment costs | |
| fuel consumption costs | |
| a | minimize entropy production rateXX |
| b | the annual operating hours per unit of heat input |
| the hot end of the heat exchange area | |
| the cold end of the heat exchange area |
| Algorithm | Parameter |
|---|---|
| NSGA2 | The variation coefficient of variation is set to 20 |
| The probability of variation is 3 | |
| The probability of crossover is 0.9 | |
| Bidding selection | |
| SPEA2 | The exchange probability is set to 0.5 |
| The two mutation probabilities are 0.2 | |
| The two crossover probabilities are 0.8 | |
| Bidding selection | |
| PESA2 | The number of grids is 7 |
| The probability of crossover is 0.5 | |
| The probability of mutation is 0.5 | |
| MOPSO | The number of grids is 7 |
| The probability of mutation is 0.1 | |
| Both the individual and the global learning factors are 1 and 2 | |
| The inertia weight is = 0.5 | |
| BBMOPSO | Mutation parameter = 10 |
| IBBMOPSO | Mutation parameter = 10 |
| Point adjustment factor = 0.01 |
| test function | NAGA2 | SPEA2 | PESA2 | MOPSO | BBMOPSO | IBBMOPSO |
|---|---|---|---|---|---|---|
| DEB | 1.7490 × 10 | 1.8600 × 10 | 1.5721×10 | 1.8470 × 10 | 1.5404 × 10 | 1.4061 × 10 |
| FON | 2.4048 × 10 | 1.8560 × 10 | 3.1648 × 10 | 0.0029 | 1.8636 × 10 | 1.3385 × 10 |
| ZDT1 | 0.0833 | 8.5192 × 10 | 0.0055 | 0.0057 | 8.9124 × 10 | 8.5016 × 10 |
| ZDT2 | 0.2426 | 9.3335 × 10 | 0.0151 | 0.1074 | 1.4219 × 10 | 8.4975 × 10 |
| ZDT3 | 0.0757 | 1.8114 × 10 | 0.0108 | 0.0172 | 1.5631 × 10 | 1.4031 × 10 |
| ZDT4 | 2.7766 | 0.0953 | 1.0983 | 7.5984 | 2.2880 × 10 | 6.0598 × 10 |
| ZDT6 | 0.1006 | 2.2246 × 10 | 0.0366 | 0.1510 | 7.2898 × 10 | 8.0147 × 10 |
| Test Function | NAGA2 | SPEA2 | PESA2 | MOPSO | BBMOPSO | IBBMOPSO |
|---|---|---|---|---|---|---|
| DEB | 0.4584 | 0.4600 | 0.4647 | 0.4626 | 0.4708 | 0.4721 |
| FON | 0.3086 | 0.2400 | 0.2490 | 0.2807 | 0.3048 | 0.3102 |
| ZDT1 | 0.4321 | 0.6200 | 0.5740 | 0.6301 | 0.6580 | 0.6595 |
| ZDT2 | 0.0571 | 0.3200 | 0.2480 | 0.1720 | 0.3050 | 0.3261 |
| ZDT3 | 0.4403 | 0.7000 | 0.6840 | 0.7610 | 0.7500 | 0.7612 |
| ZDT4 | 0.1204 | 0.5500 | 0.7700 | 0.0080 | 0.0730 | 0.1228 |
| ZDT6 | 0.6370 | 0.2400 | 0.5220 | 0.6910 | 0.2823 | 0.2840 |
| Stanard | Algorithm | Variable | Objective Function | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Max | NSGA-II | 0.9 | 0.6888 | 0.8 | 1800 | 1800 | 995 | 503 | 68,128.6 | 136.9749 | 0.29560 |
| MOPSO | 0.9 | 0.7966 | 0.8 | 1800 | 1800 | 1000 | 510 | 70,286.9 | 139.2471 | 0.29554 | |
| IBBMOPSO | 0.9 | 0.8000 | 0.8 | 1800 | 1800 | 1000 | 510 | 70,341.7 | 139.2852 | 0.29559 | |
| Max | NSGA-II | 0.9 | 0.7582 | 0.4 | 1155 | 300 | 924 | 400 | 9374.07 | 24.86587 | 0.30632 |
| MOPSO | 0.9 | 0.7859 | 0.7 | 300 | 300 | 989 | 402 | 14,021.0 | 29.39113 | 0.32472 | |
| IBBMOPSO | 0.9 | 0.4000 | 0.4 | 300 | 300 | 1000 | 400 | 8177.84 | 21.91929 | 0.30274 | |
| Max | NSGA-II | 0.9 | 0.7980 | 0.8 | 458 | 1512 | 991 | 400 | 40,562.1 | 73.54372 | 0.34102 |
| MOPSO | 0.9 | 0.8000 | 0.8 | 1800 | 1800 | 999 | 400 | 61,184.0 | 106.4823 | 0.34479 | |
| IBBMOPSO | 0.9 | 0.8000 | 0.8 | 1800 | 1800 | 1000 | 400 | 61,195.2 | 106.3605 | 0.34495 | |
| Algorithm | Decision Makings | Variable | Objective Function | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| IBBMOPSO | Fuzzy | 0.9 | 0.8000 | 0.8 | 957 | 1522 | 1000 | 400 | 50,818.9 | 89.12639 | 0.34385 |
| TOPSIS | 0.9 | 0.8000 | 0.8 | 984 | 1291 | 1000 | 400 | 47,353.7 | 83.33009 | 0.34338 | |
| LINMAP | 0.9 | 0.8000 | 0.8 | 729 | 1189 | 1000 | 400 | 42,668.9 | 75.53539 | 0.34262 | |
| Stanard | Algorithm | Variable | Objective Function | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| F | ||||||||||
| NSGA-II | 0.7 | 0.7 | 0.8 | 1000 | 408 | 596 | 68.4118 | 0.30428 | 0.23076 | |
| MOPSO | 0.7 | 0.7 | 0.8 | 1000 | 400 | 600 | 71.3588 | 0.30562 | 0.23206 | |
| IBBMOPSO | 0.7 | 0.7 | 0.8 | 1000 | 400 | 600 | 71.3588 | 0.30562 | 0.23206 | |
| Max | NSGA-II | 0.7 | 0.7 | 0.8 | 1000 | 408 | 596 | 68.3864 | 0.30433 | 0.23079 |
| MOPSO | 0.7 | 0.7 | 0.8 | 1000 | 400 | 567 | 67.9143 | 0.31441 | 0.23776 | |
| IBBMOPSO | 0.7 | 0.7 | 0.8 | 1000 | 400 | 566 | 67.8689 | 0.31443 | 0.23776 | |
| Max | NSGA-II | 0.7 | 0.7 | 0.8 | 1000 | 408 | 596 | 68.3918 | 0.30433 | 0.23079 |
| MOPSO | 0.7 | 0.7 | 0.8 | 1000 | 400 | 564 | 67.3770 | 0.31450 | 0.23772 | |
| IBBMOPSO | 0.7 | 0.7 | 0.8 | 1000 | 400 | 563 | 67.3226 | 0.31450 | 0.23771 | |
| Algorithm | Decision Makings | Variable | Objective Function | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| F | ||||||||||
| IBBMOPSO | Fuzzy | 0.7 | 0.7 | 0.8 | 1000 | 400 | 574 | 69.1006 | 0.31360 | 0.23740 |
| TOPSIS | 0.7 | 0.7 | 0.8 | 1000 | 400 | 586 | 70.4810 | 0.31074 | 0.23560 | |
| LINMAP | 0.7 | 0.7 | 0.8 | 1000 | 400 | 586 | 70.4194 | 0.31095 | 0.23574 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, Q.; Wang, H.; Sun, Z.; Yang, Z. An Improved Bare Bone Multi-Objective Particle Swarm Optimization Algorithm for Solar Thermal Power Plants. Energies 2019, 12, 4480. https://doi.org/10.3390/en12234480
Niu Q, Wang H, Sun Z, Yang Z. An Improved Bare Bone Multi-Objective Particle Swarm Optimization Algorithm for Solar Thermal Power Plants. Energies. 2019; 12(23):4480. https://doi.org/10.3390/en12234480
Chicago/Turabian StyleNiu, Qun, Han Wang, Ziyuan Sun, and Zhile Yang. 2019. "An Improved Bare Bone Multi-Objective Particle Swarm Optimization Algorithm for Solar Thermal Power Plants" Energies 12, no. 23: 4480. https://doi.org/10.3390/en12234480
APA StyleNiu, Q., Wang, H., Sun, Z., & Yang, Z. (2019). An Improved Bare Bone Multi-Objective Particle Swarm Optimization Algorithm for Solar Thermal Power Plants. Energies, 12(23), 4480. https://doi.org/10.3390/en12234480





