Looking for Energy Losses of a Rotary Permanent Magnet Magnetic Refrigerator to Optimize Its Performances
Abstract
1. Introduction
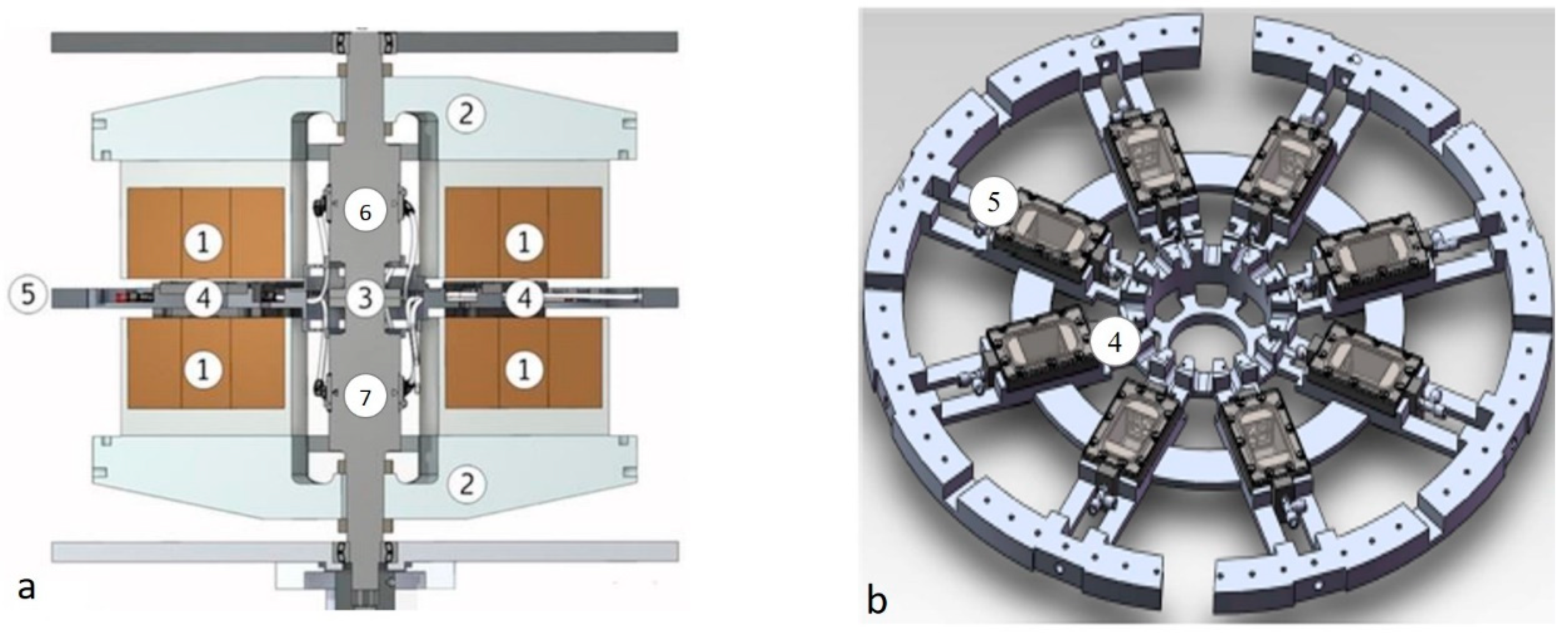
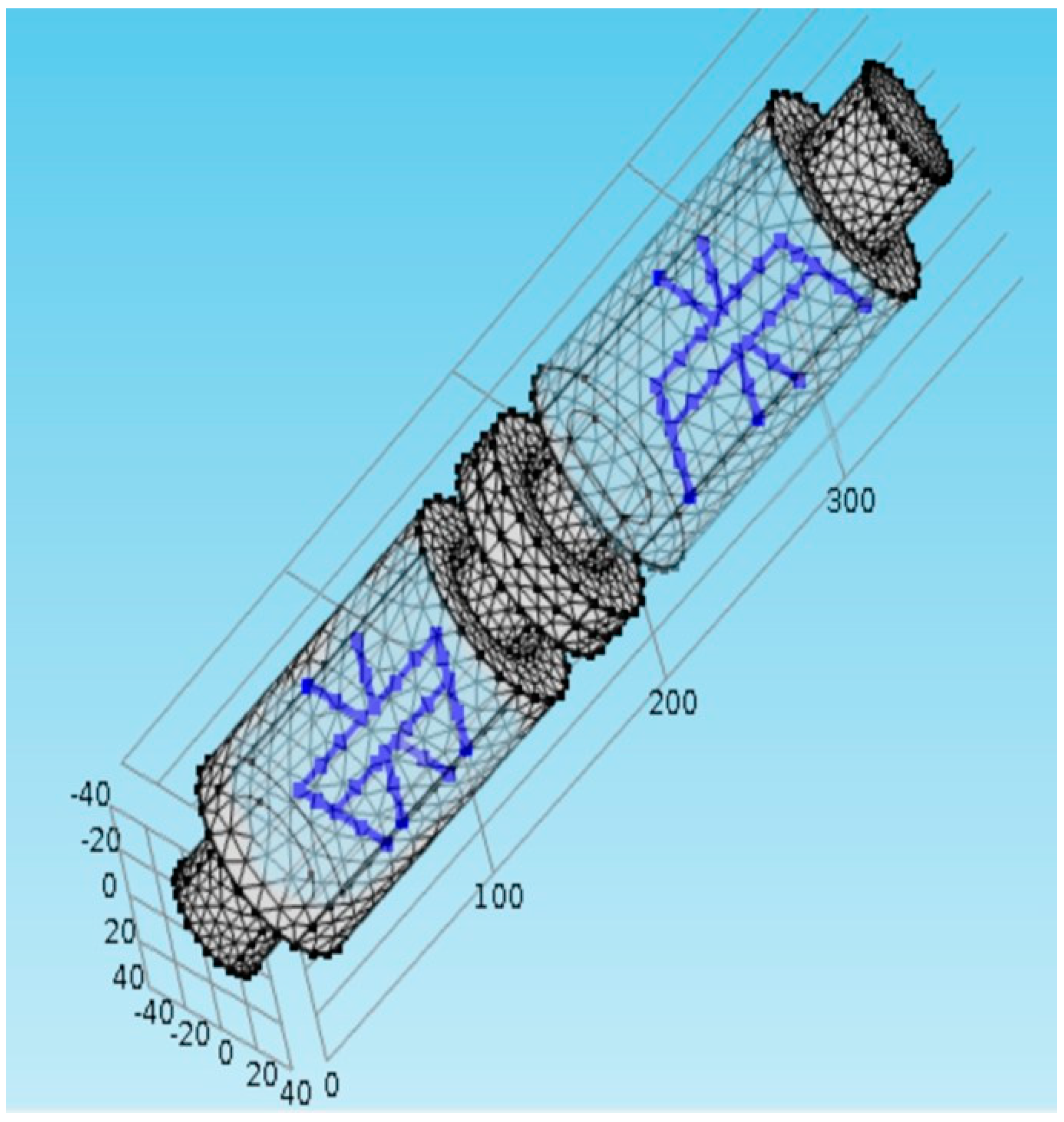
2. The Prototype and the Experimental Measurement System
3. Energy Losses Model
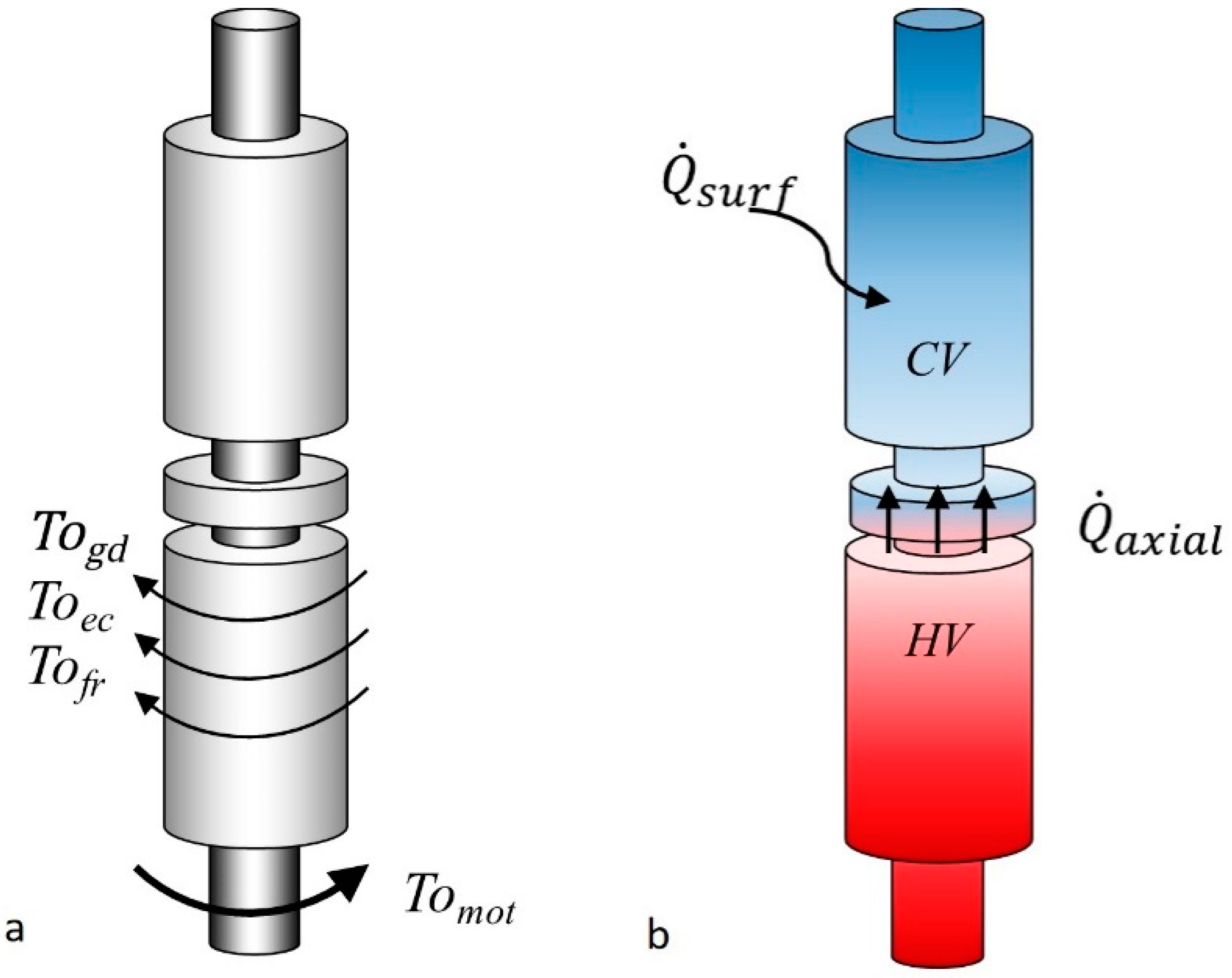
3.1. Mechanical Model
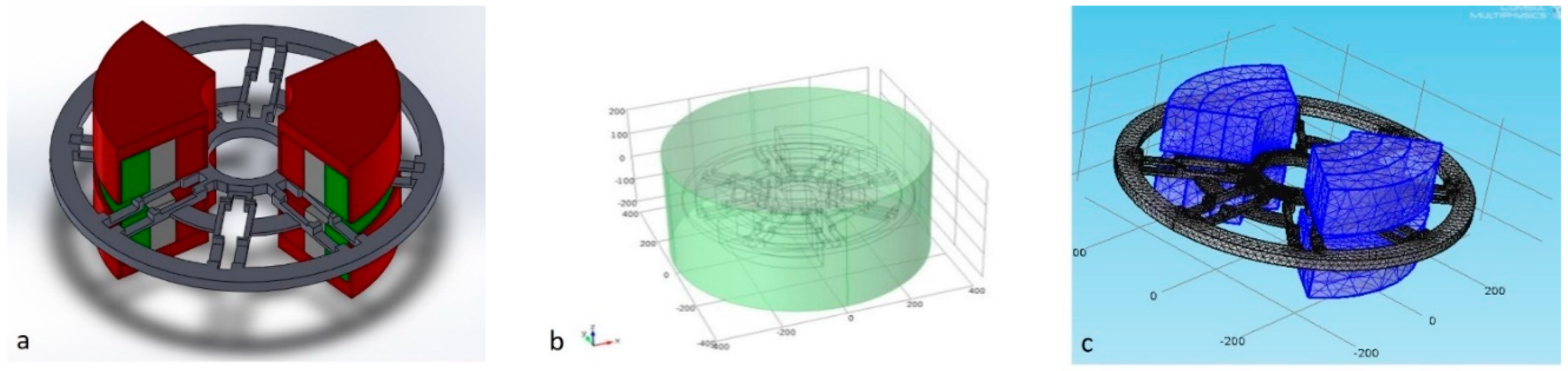
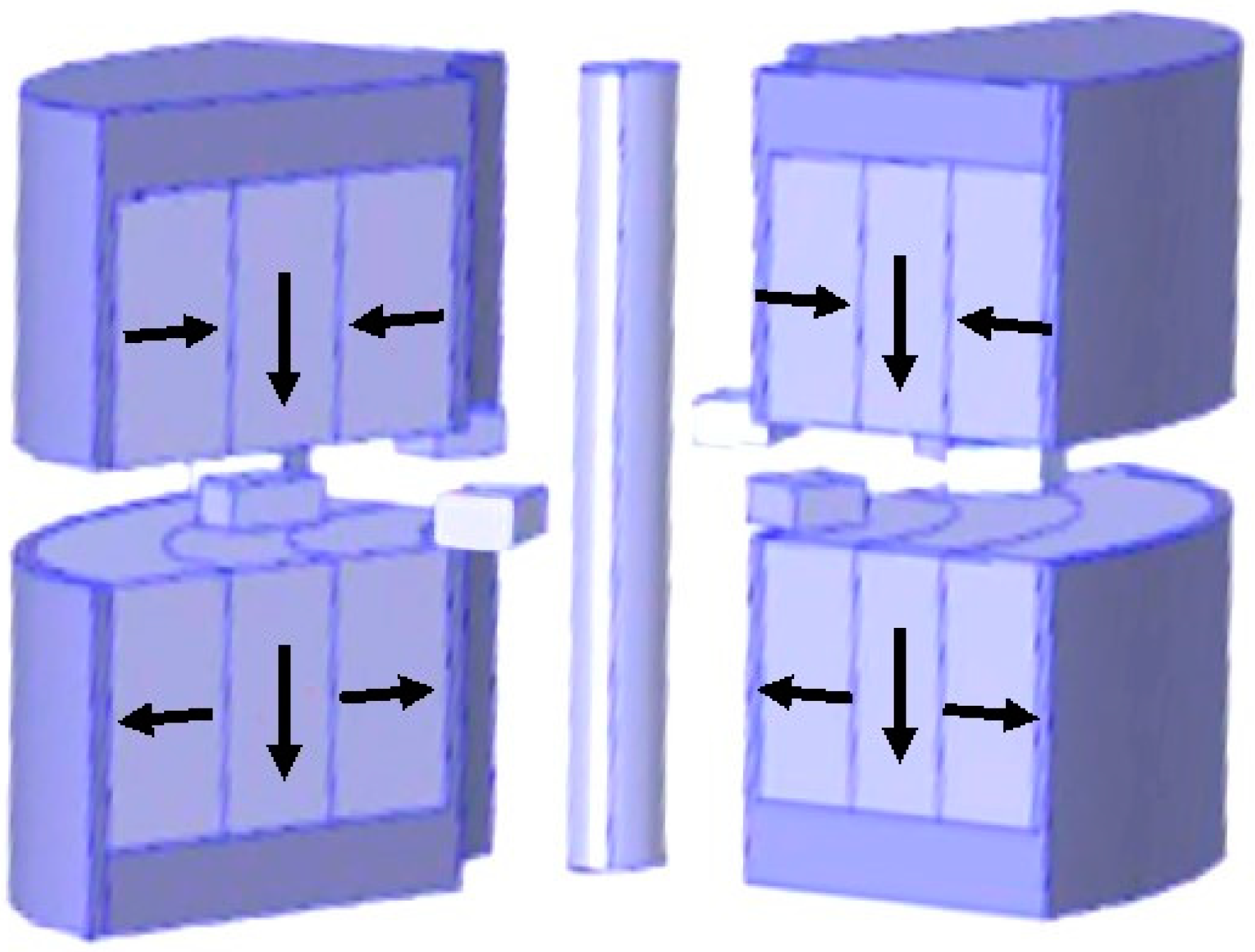
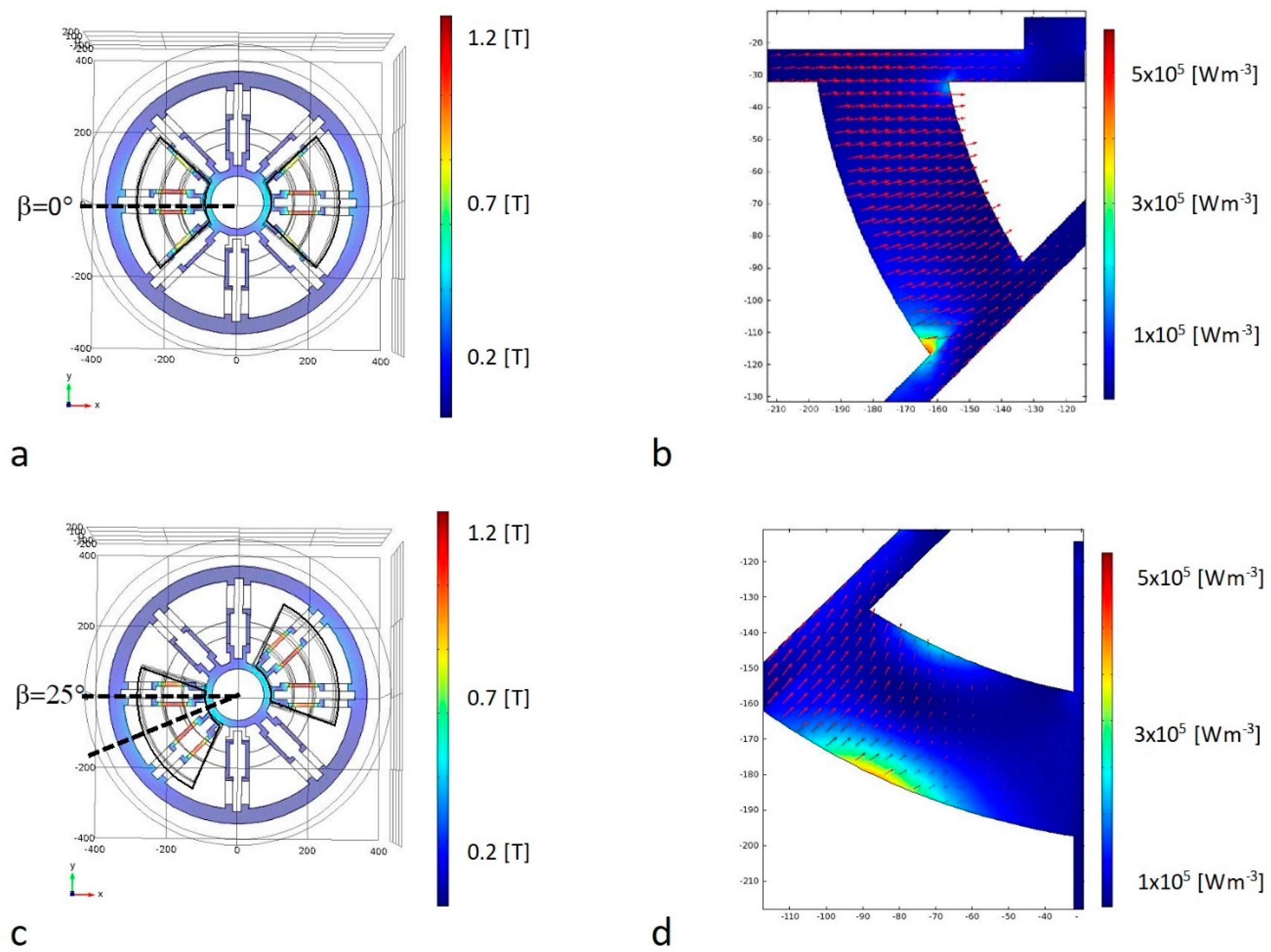
3.1.1. Static Magnetic Field Model
3.1.2. Stationary Eddy Currents Power Dissipation Model
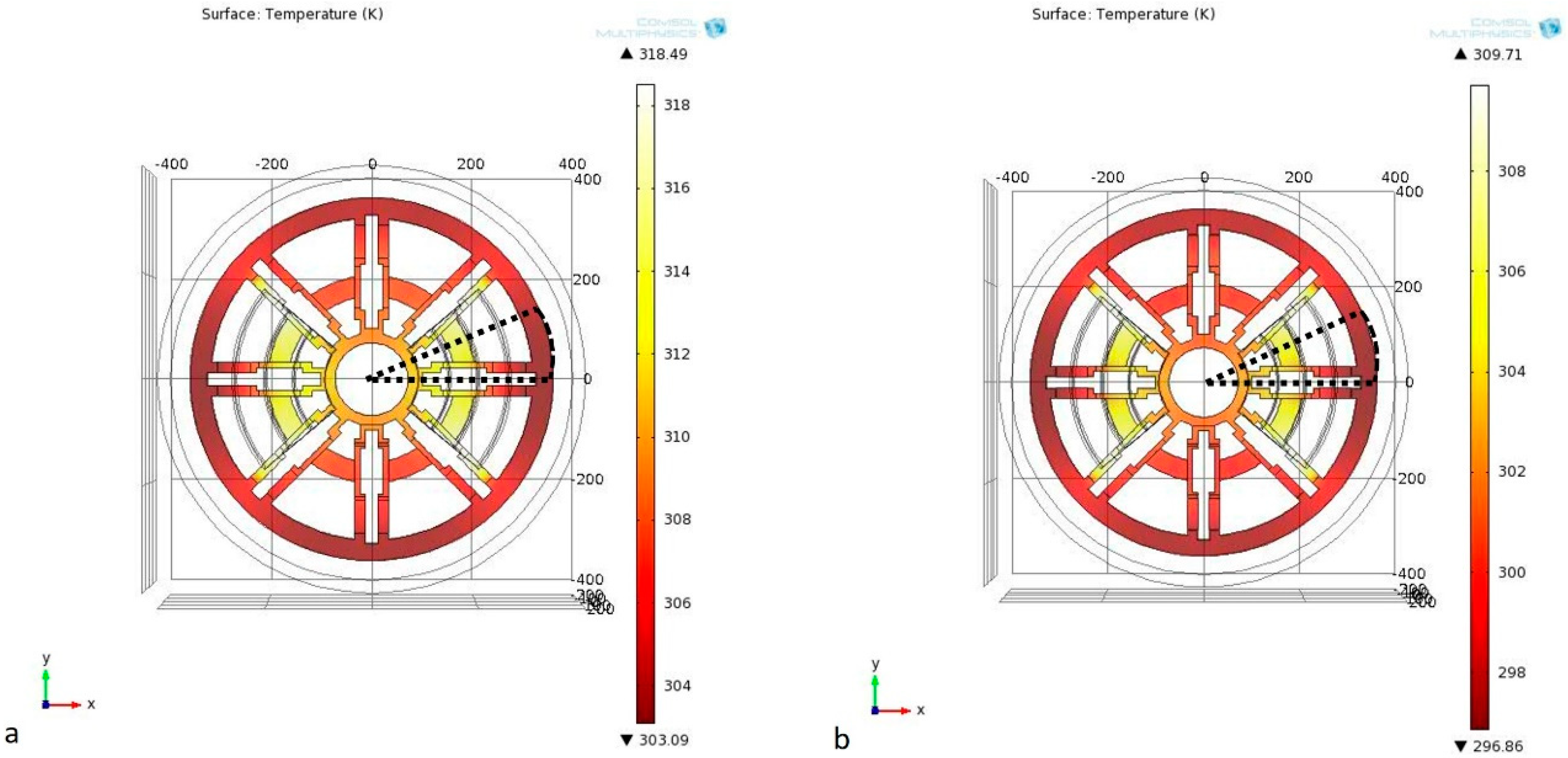
3.1.3. Stationary Thermal Model
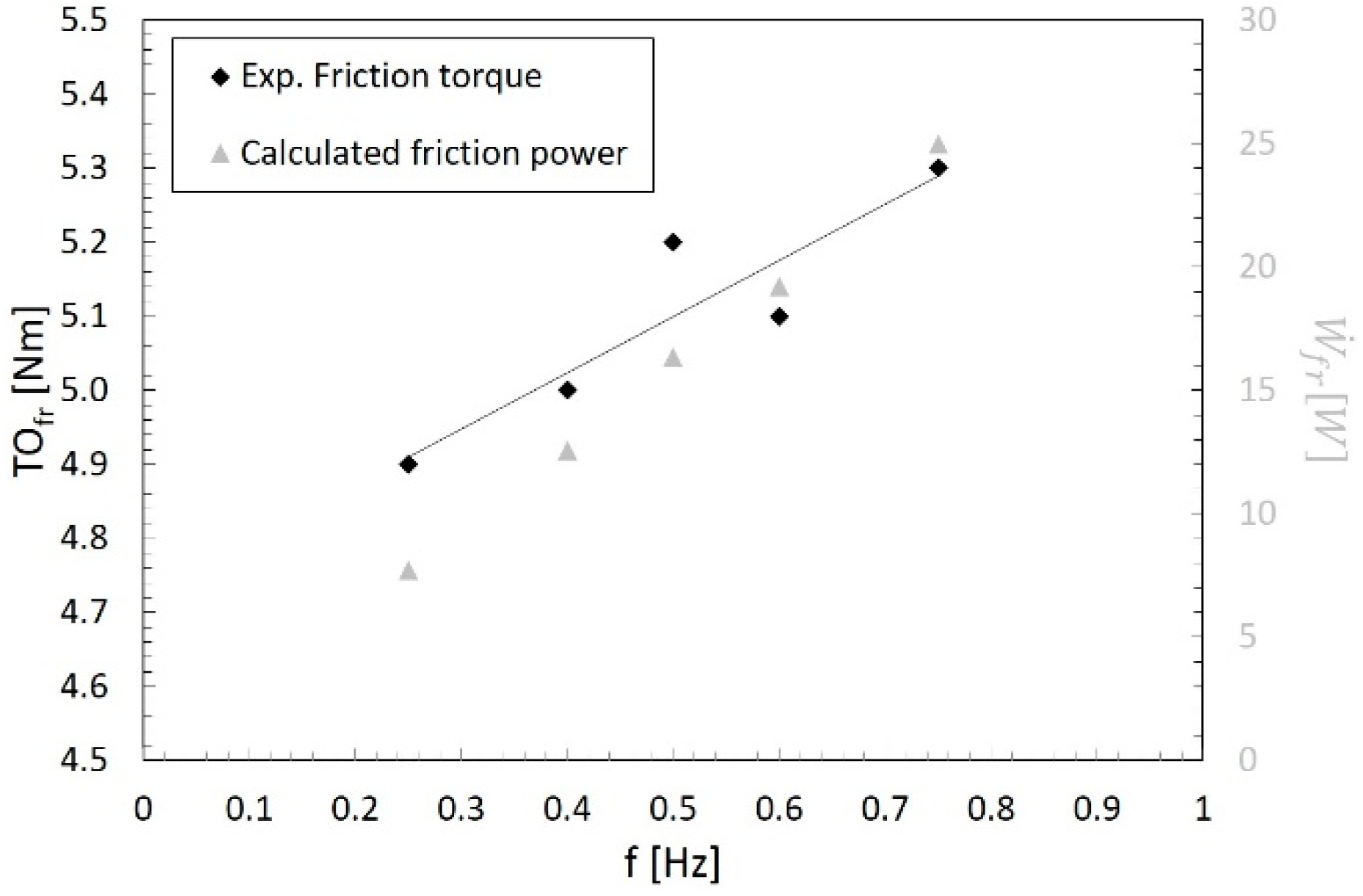
3.1.4. Semi-Empirical Evaluation of Friction Losses
3.2. Thermal Model
4. Model Validation
4.1. Mechanical Model Validation
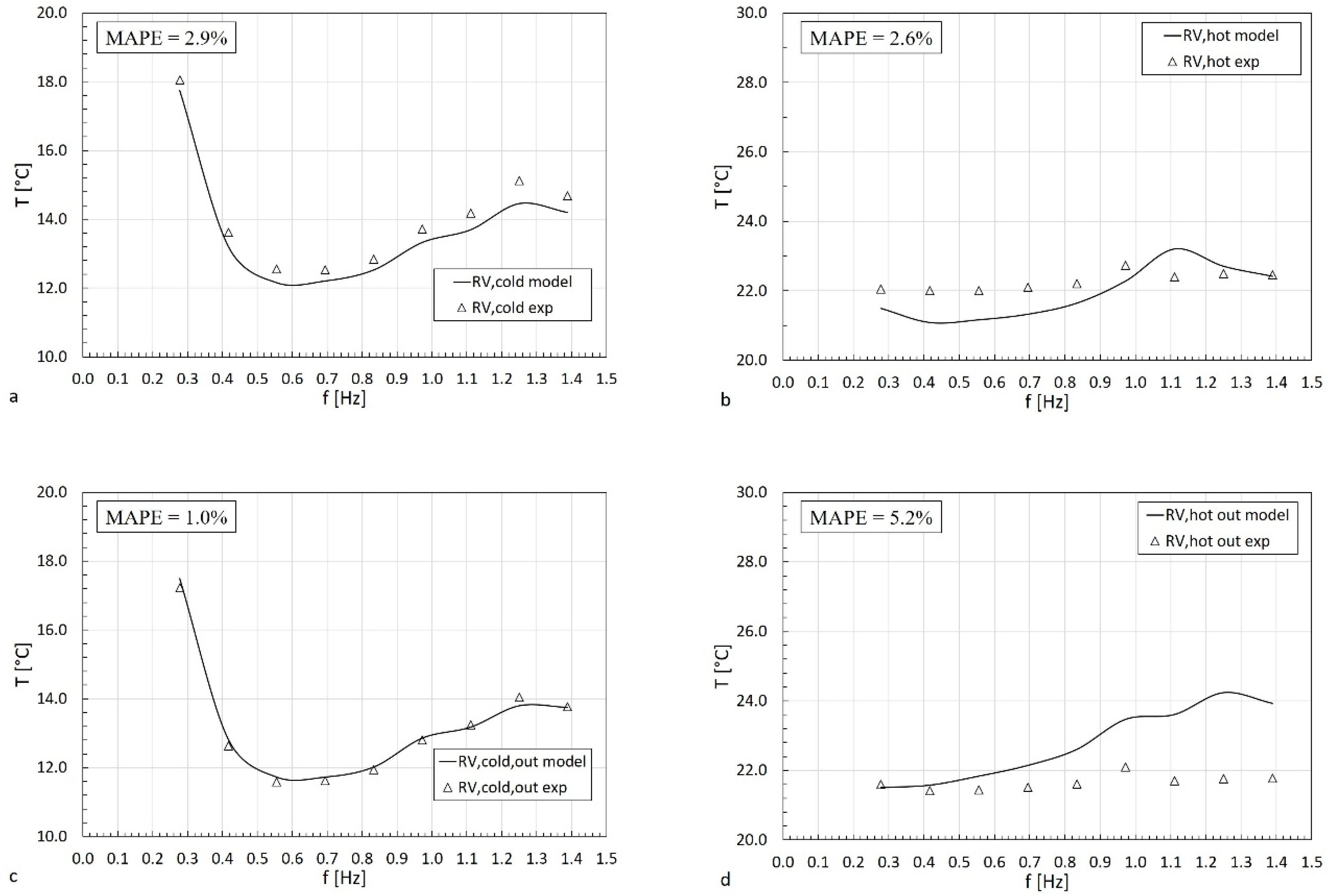
4.2. Thermal Model Validation
5. Results and Discussion
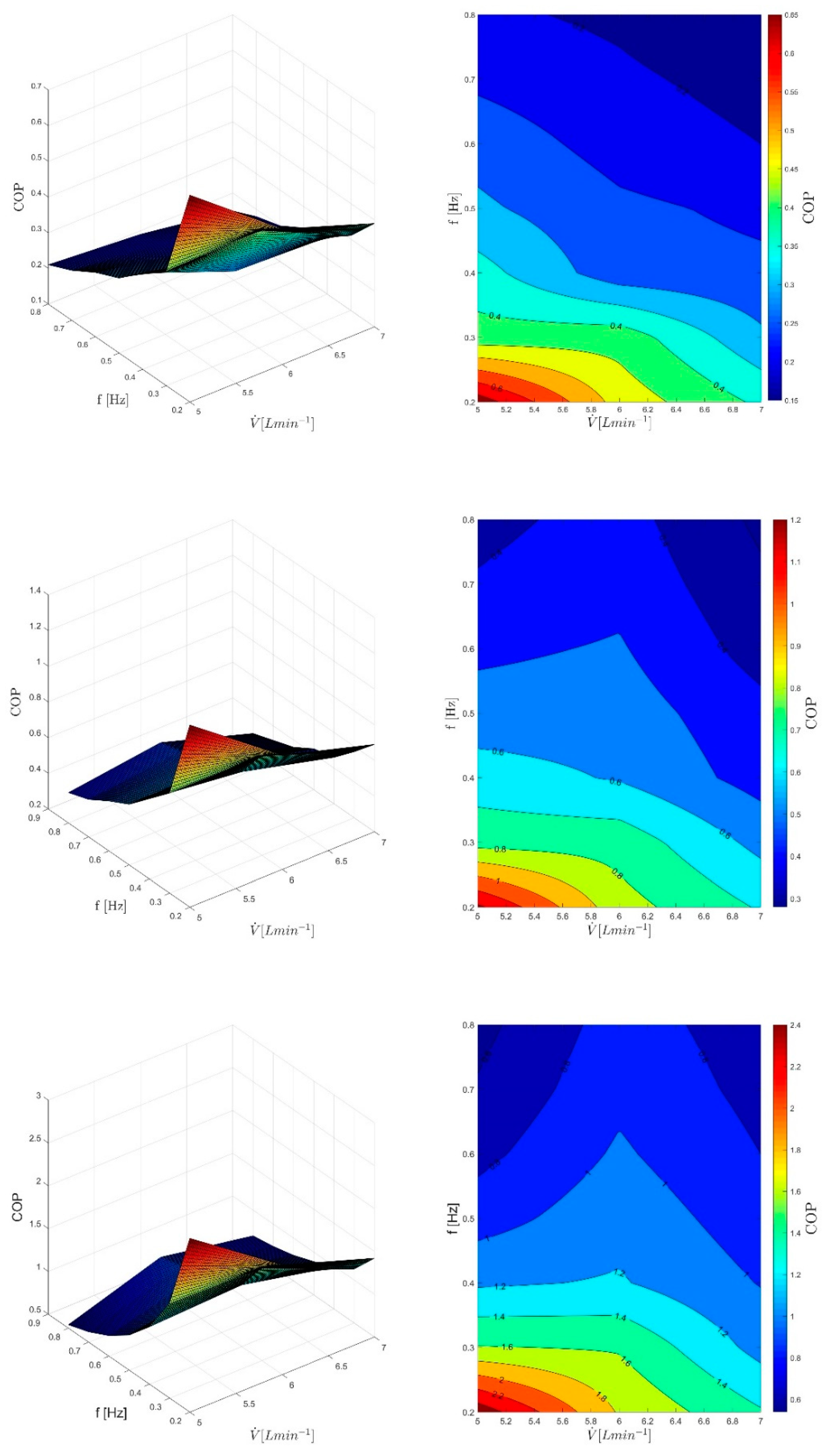
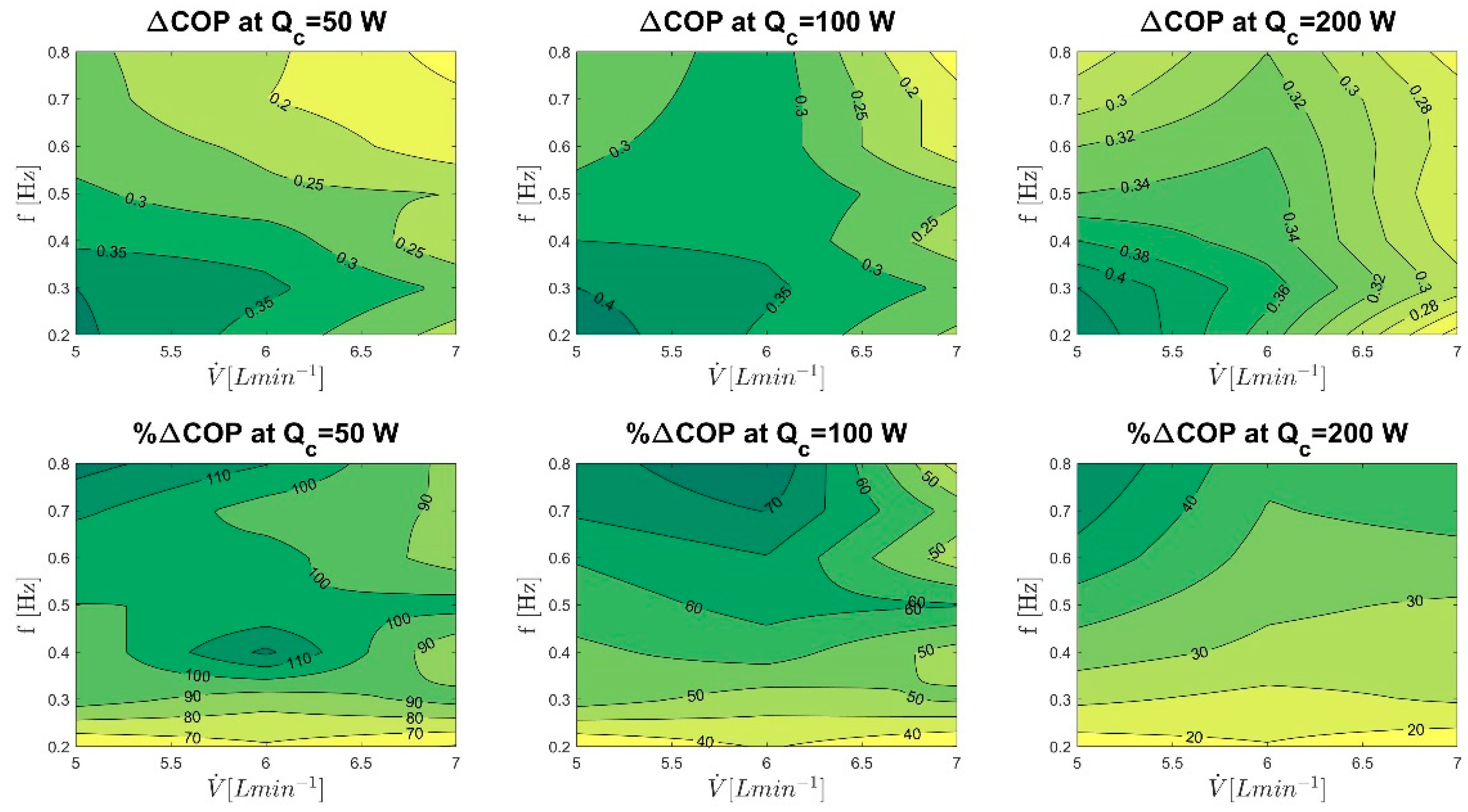
5.1. COP Improvement by Reducing Eddy Currents
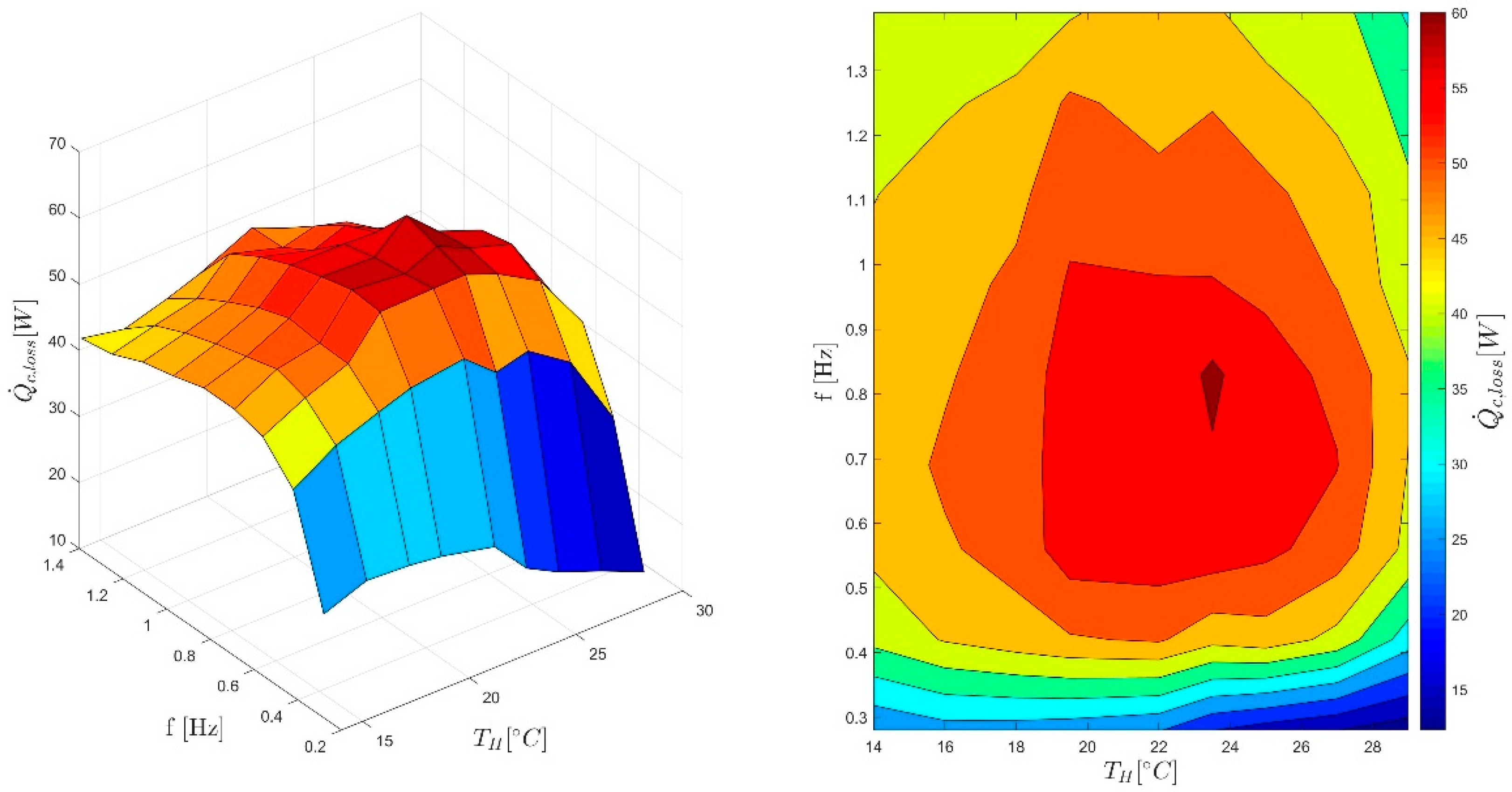
5.2. COP Improvement by Reducing Parasitic Thermal Load
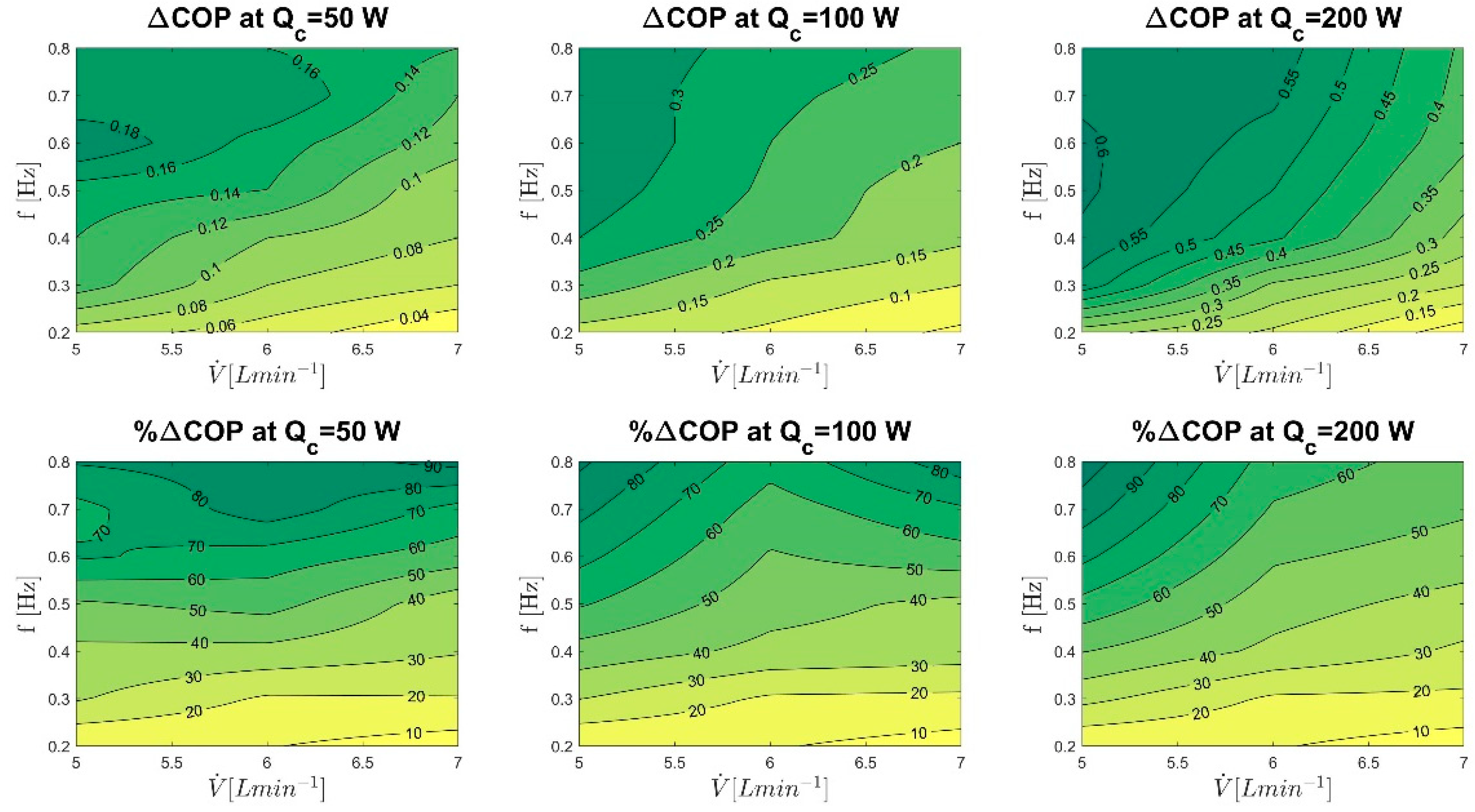
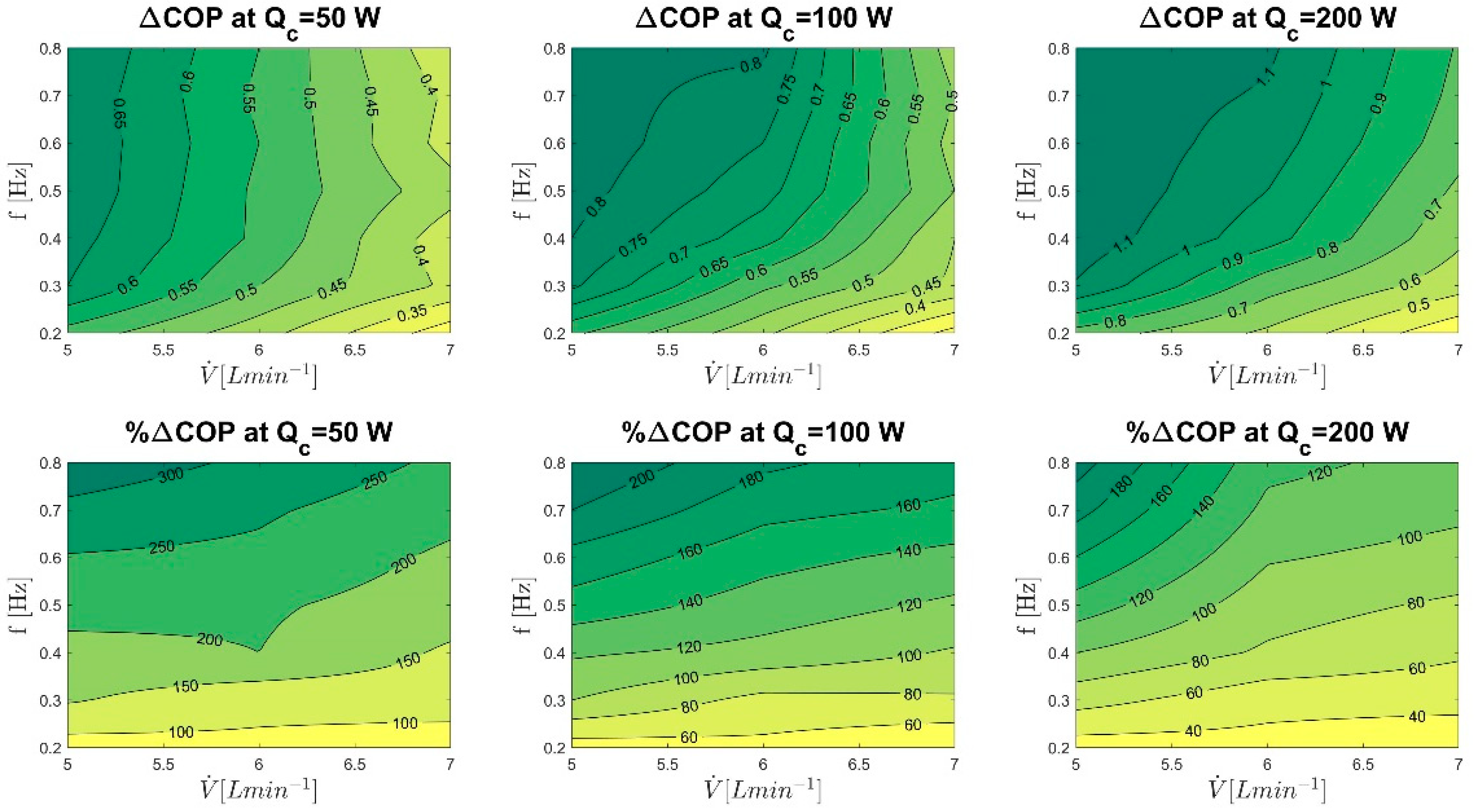
5.3. Overall Achievable COP Improvement
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Barclay, J.A. Theory of an Active Magnetic Regenerative Refrigerator. United States. Available online: https://www.osti.gov/servlets/purl/6224820 (accessed on 26 July 2019).
- Steven Brown, J.; Domanski, P.A. Review of alternative cooling technologies. Appl. Therm. Eng. 2014, 64, 252–262. [Google Scholar] [CrossRef]
- Rowe, A. Thermodynamics of active magnetic regenerators: Part I. Cryogenics 2012, 52, 111–118. [Google Scholar] [CrossRef]
- Rowe, A. Thermodynamics of active magnetic regenerators: Part II. Cryogenics 2012, 52, 119–128. [Google Scholar] [CrossRef]
- Aprea, C.; Greco, A.; Maiorino, A.; Masselli, C. The environmental impact of solid-state materials working in an active caloric refrigerator compared to a vapor compression cooler. Int. J. Heat Technol. 2018, 36, 1155–1162. [Google Scholar] [CrossRef]
- Aprea, C.; Greco, A.; Maiorino, A.; Masselli, C. Magnetic refrigeration: An eco-friendly technology for the refrigeration at room temperature. J. Phys. Conf. Ser. 2015, 655, 012026. [Google Scholar] [CrossRef]
- Greco, A.; Aprea, C.; Maiorino, A.; Masselli, C. A review of the state of the art of solid-state caloric cooling processes at room-temperature before 2019. Int. J. Refrig. 2019, 106, 66–88. [Google Scholar] [CrossRef]
- Yu, B.; Liu, M.; Egolf, P.W.; Kitanovski, A. A review of magnetic refrigerator and heat pump prototypes built before the year 2010. Int. J. Refrig. 2010, 33, 1029–1060. [Google Scholar] [CrossRef]
- Engelbrecht, K.; Pryds, N. Progress in magnetic refrigeration and future challenges. In Proceedings of the 6th IIF-IIR International Conference on Magnetic Refrigeration. International Institute of Refrigeration, Victoria, BC, Canada, 7–10 September2014. [Google Scholar]
- Lozano, J.A.; Engelbrecht, K.; Bahl, C.R.H.; Nielsen, K.K.; Eriksen, D.; Olsen, U.L.; Barbosa, J.R.; Smith, A.; Prata, A.T.; Pryds, N. Performance analysis of a rotary active magnetic refrigerator. Appl. Energy 2013, 111, 669–680. [Google Scholar] [CrossRef]
- Rowe, A. Configuration and performance analysis of magnetic refrigerators. Int. J. Refrig. 2011, 34, 168–177. [Google Scholar] [CrossRef]
- Rosario, L.; Rahman, M.M. Analysis of a magnetic refrigerator. Appl. Therm. Eng. 2011, 31, 1082–1090. [Google Scholar] [CrossRef]
- Romero Gómez, J.; Ferreiro Garcia, R.; Carbia Carril, J.; Romero Gómez, M. Experimental analysis of a reciprocating magnetic refrigeration prototype. Int. J. Refrig. 2013, 36, 1388–1398. [Google Scholar] [CrossRef]
- Lozano, J.A.; Engelbrecht, K.; Bahl, C.R.H.; Nielsen, K.K.; Barbosa, J.R.; Prata, A.T.; Pryds, N. Experimental and numerical results of a high frequency rotating active magnetic refrigerator. Int. J. Refrig. 2014, 37, 92–98. [Google Scholar] [CrossRef]
- Aprea, C.; Greco, A.; Maiorino, A.; Masselli, C. The energy performances of a rotary permanent magnet magnetic refrigerator. Int. J. Refrig. 2016, 61, 1–11. [Google Scholar] [CrossRef]
- Aprea, C.; Greco, A.; Maiorino, A.; Mastrullo, R.; Tura, A. Initial experimental results from a rotary permanent magnet magnetic refrigerator. Int. J. Refrig. 2014, 43, 111–122. [Google Scholar] [CrossRef]
- Lozano, J.A.; Capovilla, M.S.; Trevizoli, P.V.; Engelbrecht, K.; Bahl, C.R.H.; Barbosa, J.R. Development of a novel rotary magnetic refrigerator. Int. J. Refrig. 2016, 68, 187–197. [Google Scholar] [CrossRef]
- Eriksen, D.; Engelbrecht, K.; Bahl, C.R.H.; Bjørk, R.; Nielsen, K.K.; Insinga, A.R.; Pryds, N. Design and experimental tests of a rotary active magnetic regenerator prototype. Int. J. Refrig. 2015, 58, 14–21. [Google Scholar] [CrossRef]
- Huang, B.; Lai, J.W.; Zeng, D.C.; Zheng, Z.G.; Harrison, B.; Oort, A.; van Dijk, N.H.; Brück, E. Development of an experimental rotary magnetic refrigerator prototype. Int. J. Refrig. 2019, 104, 42–50. [Google Scholar] [CrossRef]
- Albertini, F.; Bennati, C.; Bianchi, M.; Branchini, L.; Cugini, F.; De Pascale, A.; Fabbrici, S.; Melino, F.; Ottaviano, S.; Peretto, A.; et al. Preliminary Investigation on a Rotary Magnetocaloric Refrigerator Prototype. Energy Procedia 2017, 142, 1288–1293. [Google Scholar] [CrossRef]
- Gimaev, R.; Spichkin, Y.; Kovalev, B.; Kamilov, K.; Zverev, V.; Tishin, A. Review on magnetic refrigeration devices based on HTSC materials. Int. J. Refrig. 2019, 100, 1–12. [Google Scholar] [CrossRef]
- Plaznik, U.; Tušek, J.; Kitanovski, A.; Poredoš, A. Numerical and experimental analyses of different magnetic thermodynamic cycles with an active magnetic regenerator. Appl. Therm. Eng. 2013, 59, 52–59. [Google Scholar] [CrossRef]
- Kitanovski, A.; Plaznik, U.; Tušek, J.; Poredoš, A. New thermodynamic cycles for magnetic refrigeration. Int. J. Refrig. 2014, 37, 28–35. [Google Scholar] [CrossRef]
- Lucia, U. General approach to obtain the magnetic refrigeretion ideal coefficient of performance. Phys. A Stat. Mech. Its Appl. 2008, 387, 3477–3479. [Google Scholar] [CrossRef]
- Trevizoli, P.V.; Nakashima, A.T.; Peixer, G.F.; Barbosa, J.R. Évaluation de la performance d’un régénérateur magnétique actif pour les applications de refroidissement—Partie I: Analyse expérimentale et performance thermodynamique. Int. J. Refrig. 2016, 72, 192–205. [Google Scholar] [CrossRef]
- Aprea, C.; Greco, A.; Maiorino, A.; Masselli, C. A comparison between rare earth and transition metals working as magnetic materials in an AMR refrigerator in the room temperature range. Appl. Therm. Eng. 2015, 91, 767–777. [Google Scholar] [CrossRef]
- Aprea, C.; Greco, A.; Maiorino, A. A dimensionless numerical analysis for the optimization of an active magnetic regenerative refrigerant cycle. Int. J. Energy Res. 2013, 37, 1475–1487. [Google Scholar] [CrossRef]
- Gao, X.Q.; Shen, J.; He, X.N.; Tang, C.C.; Li, K.; Dai, W.; Li, Z.X.; Jia, J.C.; Gong, M.Q.; Wu, J.F. Improvements of a room-temperature magnetic refrigerator combined with Stirling cycle refrigeration effect. Int. J. Refrig. 2016, 67, 330–335. [Google Scholar] [CrossRef]
- He, X.N.; Gong, M.Q.; Zhang, H.; Dai, W.; Shen, J.; Wu, J.F. Design and performance of a room-temperature hybrid magnetic refrigerator combined with Stirling gas refrigeration effect. Int. J. Refrig. 2013, 36, 1465–1471. [Google Scholar] [CrossRef]
- Aprea, C.; Greco, A.; Maiorino, A. GeoThermag: A geothermal magnetic refrigerator. Int. J. Refrig. 2015, 59, 75–83. [Google Scholar] [CrossRef]
- Lucas, C.; Koehler, J. Experimental investigation of the COP improvement of a refrigeration cycle by use of an ejector. Int. J. Refrig. 2012, 35, 1595–1603. [Google Scholar] [CrossRef]
- Aprea, C.; Greco, A.; Maiorino, A. An application of the artificial neural network to optimise the energy performances of a magnetic refrigerator. Int. J. Refrig. 2017, 82, 238–251. [Google Scholar] [CrossRef]
- Qian, S.; Yuan, L.; Yu, J.; Yan, G. Variable load control strategy for room-temperature magnetocaloric cooling applications. Energy 2018, 153, 763–775. [Google Scholar] [CrossRef]
- Qian, S.; Yuan, L.; Yu, J. An online optimum control method for magnetic cooling systems under variable load operation. Int. J. Refrig. 2019, 97, 97–107. [Google Scholar] [CrossRef]
- Aprea, C.; Cardillo, G.; Greco, A.; Maiorino, A.; Masselli, C. A rotary permanent magnet magnetic refrigerator based on AMR cycle. Appl. Therm. Eng. 2016, 101, 699–703. [Google Scholar] [CrossRef]
- Lei, T.; Engelbrecht, K.; Nielsen, K.K.; Veje, C.T. Study of geometries of active magnetic regenerators for room temperature magnetocaloric refrigeration. Appl. Therm. Eng. 2017, 111, 1232–1243. [Google Scholar] [CrossRef]
- Arnold, D.S.; Tura, A.; Ruebsaat-Trott, A.; Rowe, A. Design improvements of a permanent magnet active magnetic refrigerator. Int. J. Refrig. 2014, 37, 99–105. [Google Scholar] [CrossRef]
- Monfared, B. Design and optimization of regenerators of a rotary magnetic refrigeration device using a detailed simulation model. Int. J. Refrig. 2018, 88, 260–274. [Google Scholar] [CrossRef]
- Li, Z.; Shen, J.; Li, K.; Gao, X.; Guo, X.; Dai, W. Assessment of three different gadolinium-based regenerators in a rotary-type magnetic refrigerator. Appl. Therm. Eng. 2019, 153, 159–167. [Google Scholar] [CrossRef]
- Klinar, K.; Tomc, U.; Jelenc, B.; Nosan, S.; Kitanovski, A. New frontiers in magnetic refrigeration with high oscillation energy-efficient electromagnets. Appl. Energy 2019, 236, 1062–1077. [Google Scholar] [CrossRef]
- Czernuszewicz, A.; Kaleta, J.; Kołosowski, D.; Lewandowski, D. Experimental study of the effect of regenerator bed length on the performance of a magnetic cooling system. Int. J. Refrig. 2019, 97, 49–55. [Google Scholar] [CrossRef]
- Capovilla, M.S.; Lozano, J.A.; Trevizoli, P.V.; Barbosa, J.R. Performance evaluation of a magnetic refrigeration system. Sci. Technol. Built Environ. 2016, 22, 534–543. [Google Scholar] [CrossRef]
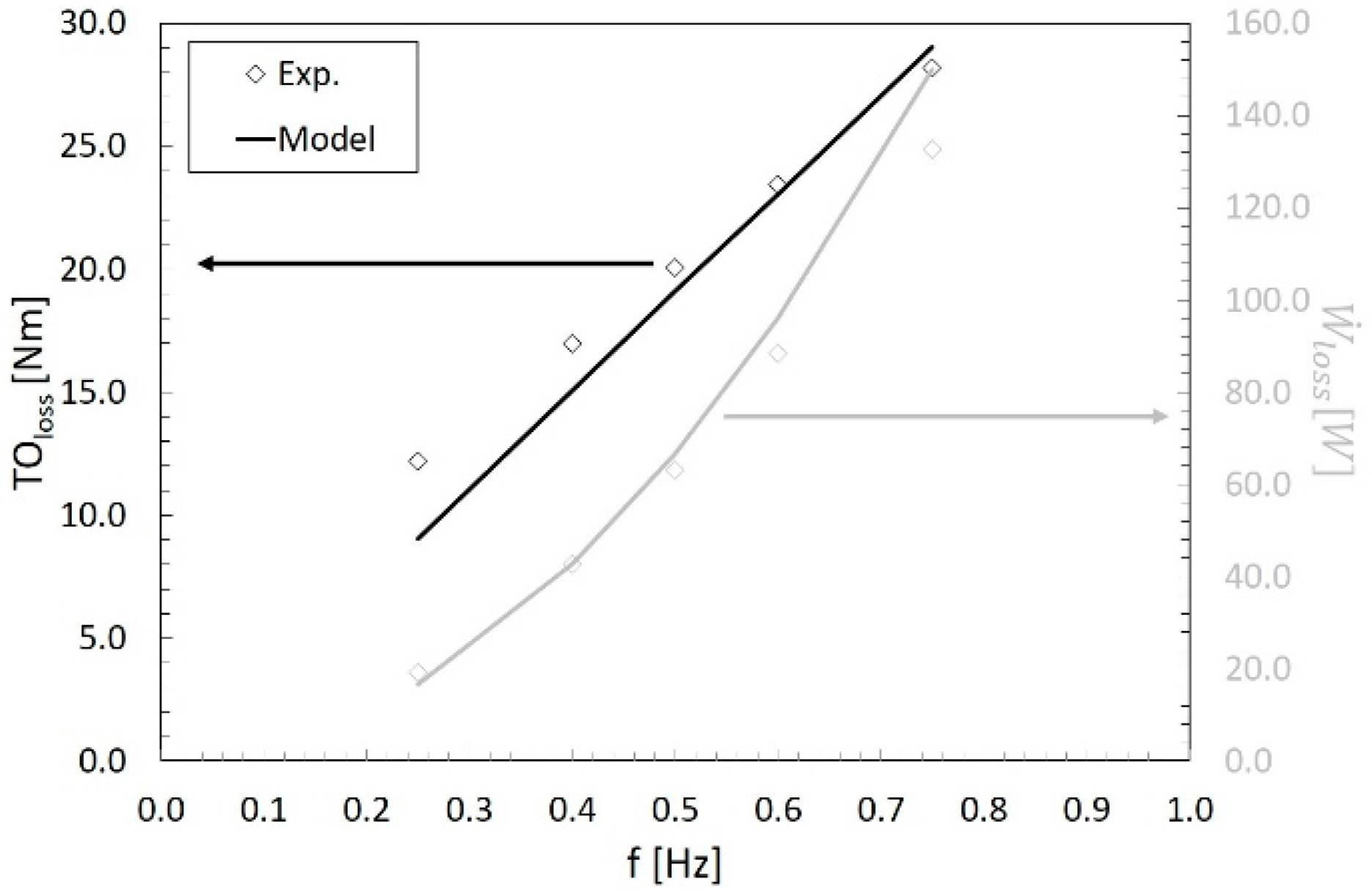
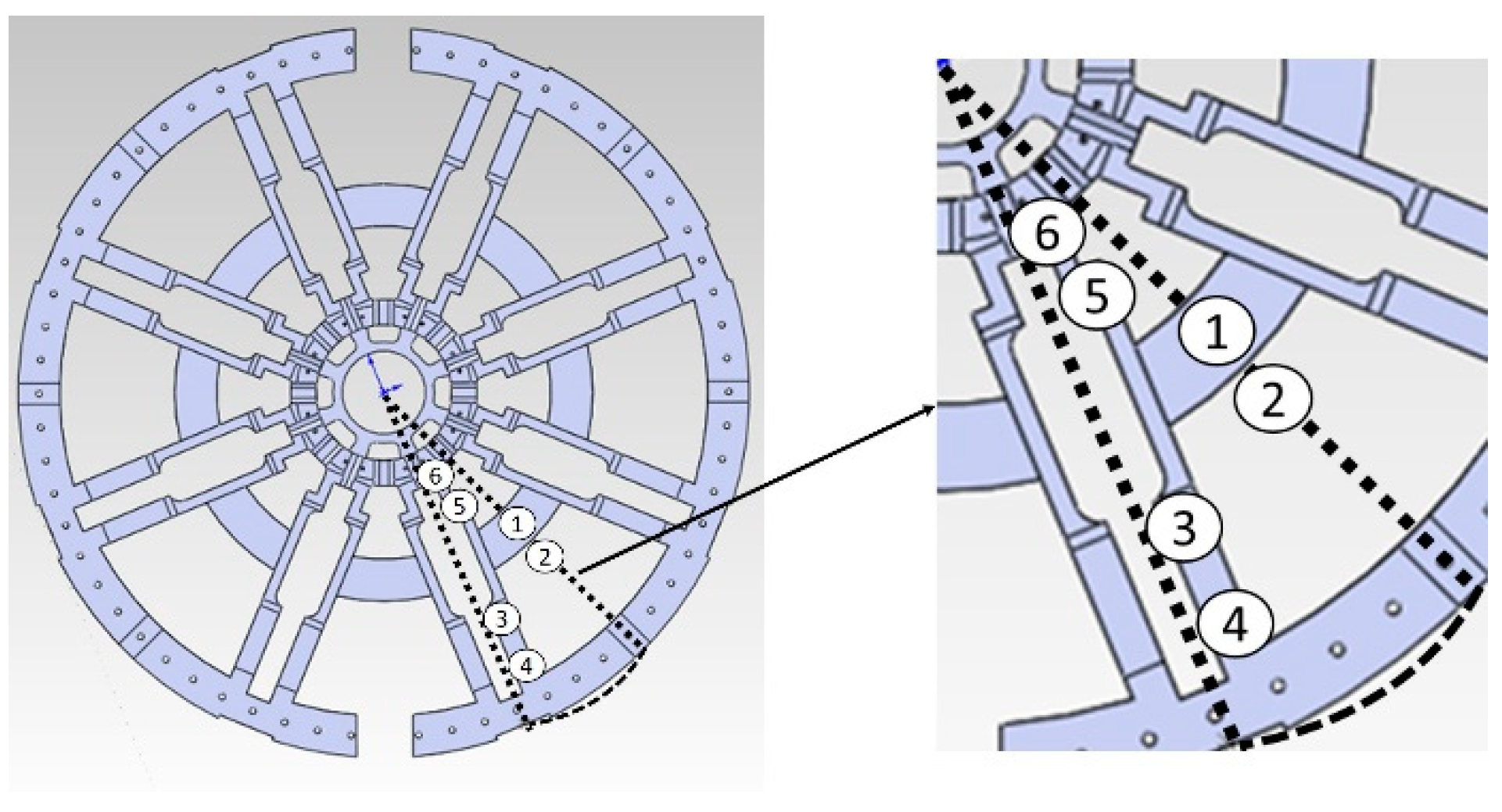
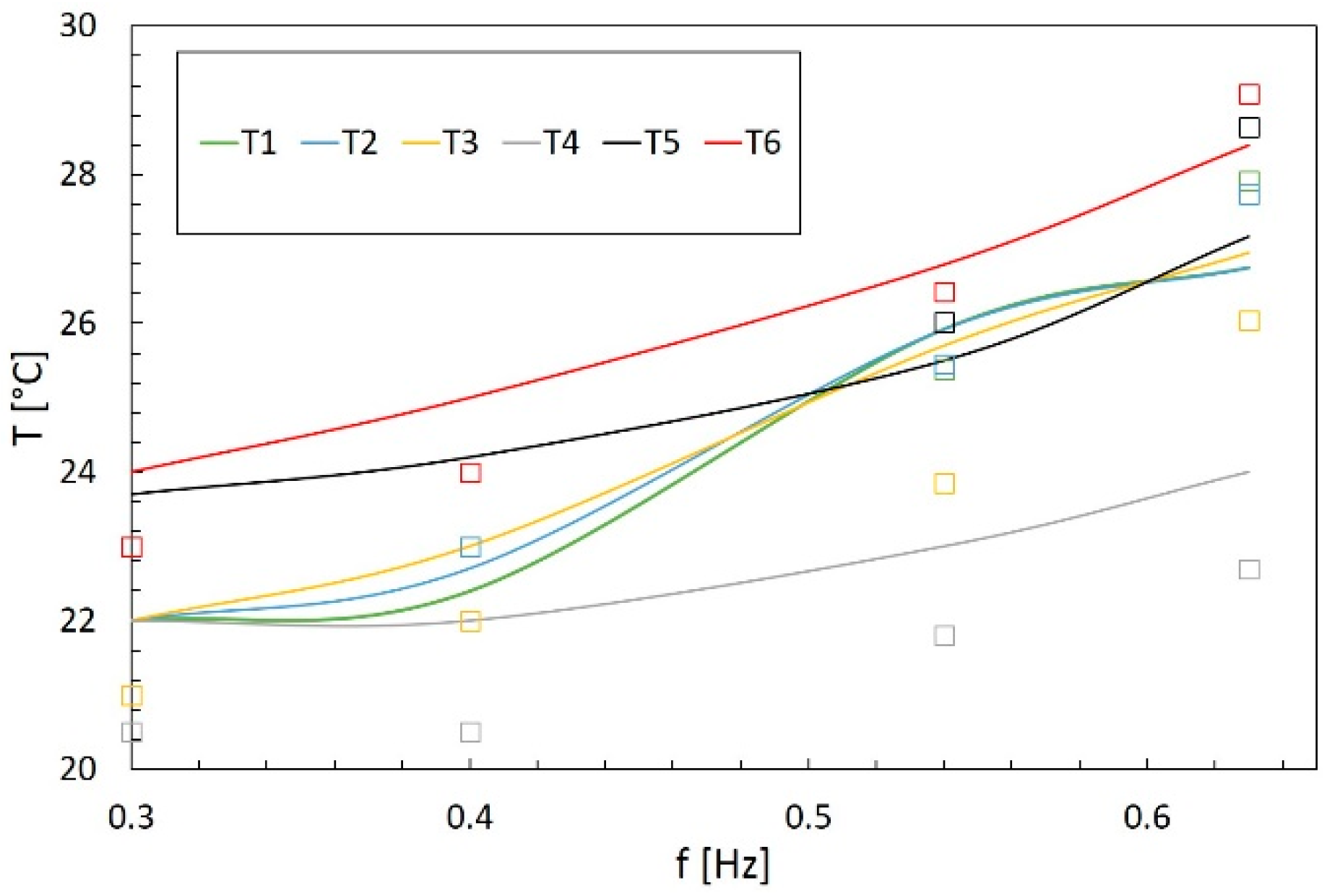
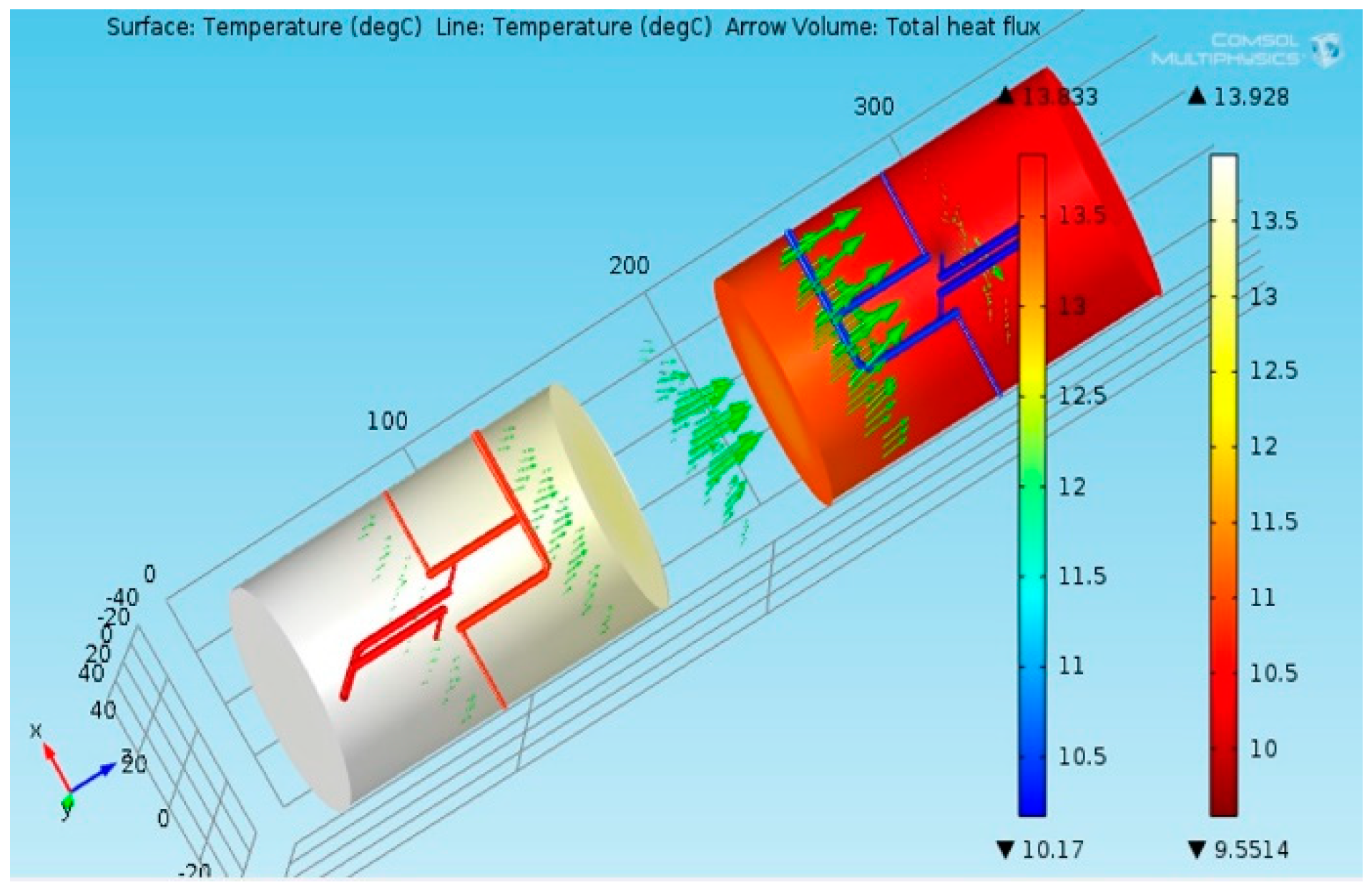
| Measurement | Instrument Type | Accuracy |
|---|---|---|
| Temperature | RTD 4 wires | 0.1 K |
| Torque | Torque transducer | 0.5% |
| Angular velocity | Optical encoder | 0.01° s−1 |
| Magnetic field | Hall probe | 0.4% |
| Water flow | Electromagnetic flowmeter | 0.5% |
| Electrical power | Electromagnetic wattmeter | 0.2% |
| X (cm) | y (cm) | Bz_sim (T) | Bz_exp (T) | Absolute Error (T) | Relative Error (%) |
|---|---|---|---|---|---|
| 0 | 100 | 0.297 | 0.350 | −0.053 | −15.1 |
| 0 | −180 | −1.270 | −1.180 | −0.090 | 7.5 |
| 0 | −200 | −1.069 | −1.085 | 0.020 | −1.5 |
| −100 | −180 | −0.827 | −0.800 | −0.030 | 3.4 |
| −150 | 0 | 0.085 | 0.075 | 0.010 | 12.8 |
| Relative error range (%) | 1.7–4.4 | 0.2–4.2 | 0.1–1.6 | 0.4–11.4 |
| Absolute max error (°C) | 0.7 | 0.9 | 0.3 | 2.5 |
| COPref | COPec | COPQc,loss | COPec+Qc,loss | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TH [°C] | Ave | Max | Min | Ave | Max | Min | Ave | Max | Min | Ave | Max | Min | |
| 16 | 0.35 | 0.68 | 0.15 | 0.45 | 0.75 | 0.29 | 0.61 | 1.08 | 0.25 | 0.79 | 1.19 | 0.46 | |
| 28.6% | 10.3% | 93.3% | 74.3% | 58.8% | 66.7% | 125.7% | 75.0% | 206.7% | |||||
| 22 | 0.35 | 0.68 | 0.15 | 0.45 | 0.75 | 0.29 | 0.64 | 1.09 | 0.28 | 0.83 | 1.21 | 0.51 | |
| 28.6% | 10.3% | 93.3% | 82.9% | 60.3% | 86.7% | 137.1% | 77.9% | 240.0% | |||||
| 32 | 0.38 | 0.69 | 0.15 | 0.49 | 0.79 | 0.28 | 0.64 | 1.04 | 0.26 | 0.85 | 1.25 | 0.48 | |
| 28.9% | 14.5% | 86.7% | 68.4% | 50.7% | 73.3% | 123.7% | 81.2% | 220.0% | |||||
| 16 | 0.66 | 1.22 | 0.28 | 0.83 | 1.35 | 0.52 | 0.94 | 1.64 | 0.37 | 1.18 | 1.82 | 0.70 | |
| 25.8% | 10.7% | 85.7% | 42.4% | 34.4% | 32.1% | 78.8% | 49.2% | 150.0% | |||||
| 22 | 0.66 | 1.22 | 0.28 | 0.83 | 1.35 | 0.52 | 0.97 | 1.65 | 0.40 | 1.22 | 1.83 | 0.75 | |
| 25.8% | 10.7% | 85.7% | 47.0% | 35.2% | 42.9% | 84.8% | 50.0% | 167.9% | |||||
| 32 | 0.75 | 1.35 | 0.37 | 0.95 | 1.51 | 0.64 | 1.02 | 1.66 | 0.56 | 1.33 | 1.87 | 0.99 | |
| 26.7% | 11.9% | 73.0% | 36.0% | 23.0% | 51.4% | 77.3% | 38.5% | 167.6% | |||||
| 16 | 1.52 | 2.53 | 0.89 | 1.81 | 2.80 | 1.21 | 1.83 | 2.96 | 1.11 | 2.18 | 3.28 | 1.51 | |
| 19.1% | 10.7% | 36.0% | 20.4% | 17.0% | 24.7% | 43.4% | 29.6% | 69.7% | |||||
| 22 | 1.52 | 2.53 | 0.89 | 1.81 | 2.80 | 1.21 | 1.86 | 2.97 | 1.15 | 2.23 | 3.29 | 1.57 | |
| 19.1% | 10.7% | 36.0% | 22.4% | 17.4% | 29.2% | 46.7% | 30.0% | 76.4% | |||||
| 32 | 1.58 | 1.97 | 1.21 | 1.83 | 2.22 | 1.44 | 1.86 | 2.26 | 1.47 | 2.16 | 2.54 | 1.76 | |
| 15.8% | 12.7% | 19.0% | 17.7% | 14.7% | 21.5% | 36.7% | 28.9% | 45.5% | |||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maiorino, A.; Mauro, A.; Del Duca, M.G.; Mota-Babiloni, A.; Aprea, C. Looking for Energy Losses of a Rotary Permanent Magnet Magnetic Refrigerator to Optimize Its Performances. Energies 2019, 12, 4388. https://doi.org/10.3390/en12224388
Maiorino A, Mauro A, Del Duca MG, Mota-Babiloni A, Aprea C. Looking for Energy Losses of a Rotary Permanent Magnet Magnetic Refrigerator to Optimize Its Performances. Energies. 2019; 12(22):4388. https://doi.org/10.3390/en12224388
Chicago/Turabian StyleMaiorino, Angelo, Antongiulio Mauro, Manuel Gesù Del Duca, Adrián Mota-Babiloni, and Ciro Aprea. 2019. "Looking for Energy Losses of a Rotary Permanent Magnet Magnetic Refrigerator to Optimize Its Performances" Energies 12, no. 22: 4388. https://doi.org/10.3390/en12224388
APA StyleMaiorino, A., Mauro, A., Del Duca, M. G., Mota-Babiloni, A., & Aprea, C. (2019). Looking for Energy Losses of a Rotary Permanent Magnet Magnetic Refrigerator to Optimize Its Performances. Energies, 12(22), 4388. https://doi.org/10.3390/en12224388








