A Hybrid Multi-Objective Crisscross Optimization for Dynamic Economic/Emission Dispatch Considering Plug-In Electric Vehicles Penetration †
Abstract
1. Introduction
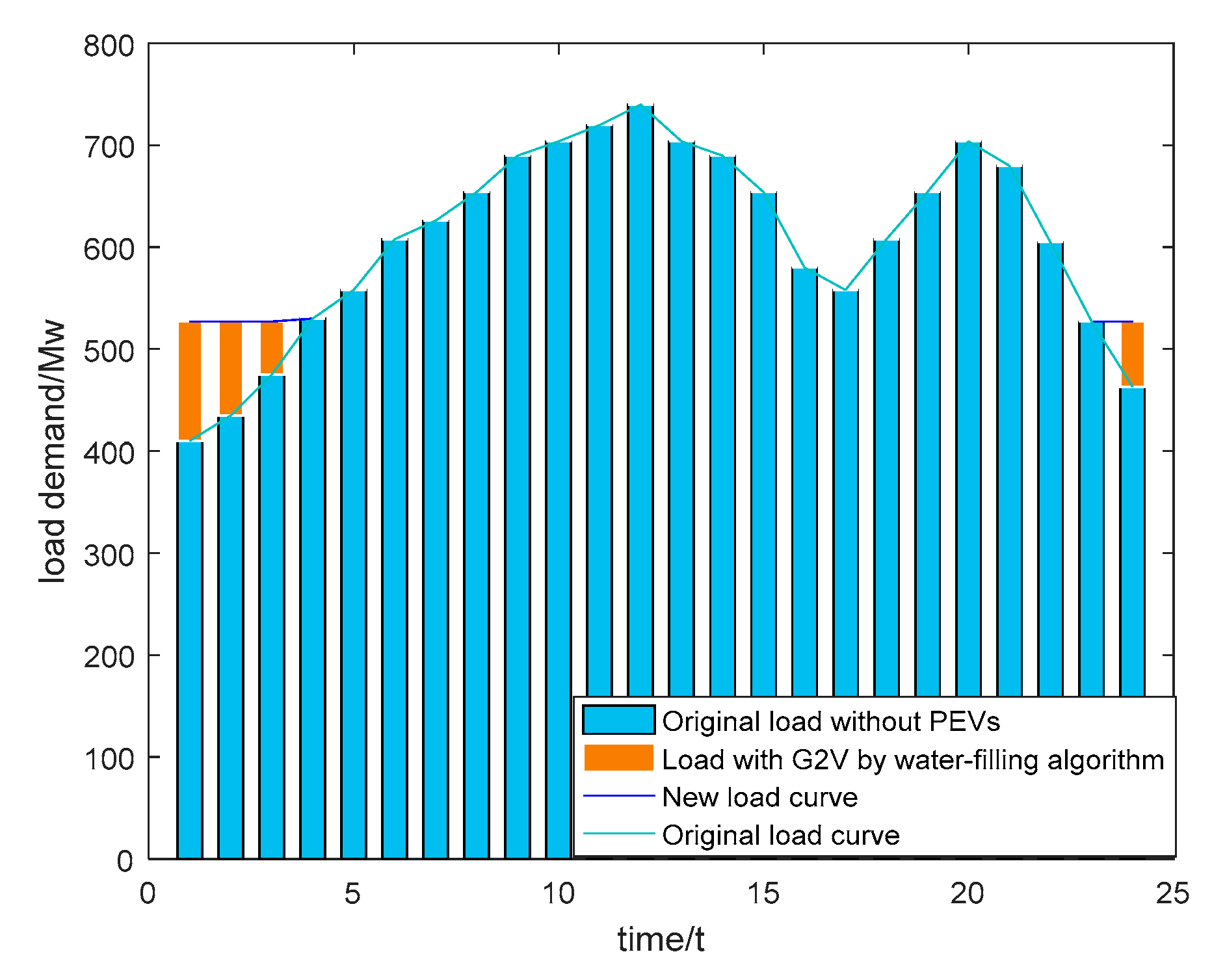
- In optimization model of the dynamic economic/emission multi-objective dispatching problem, the PEVs are considered for the purpose to achieve peak shaving and valley filling. According to the put forward model, DEED problem with consideration of PEVs is surveyed. Currently, there is very limited work being done for solving the DEED problem considering PEVs to shave peak and fill valley, particularly on the research of influence on DEED problem brought from different G2V and V2G demands. This is a multi-peak and nonlinear multi-objective optimization problem. In existing work, DEED considered with PEVs only studies the scheduling of PEVs, the effect of G2V and V2G technologies do not need to be considered. The load shaved during peak period is distributed to each PEV, and in order to implement valley filling, a water-filling algorithm [36] has been employed. As a result, a new 24-h load curve would be produced for the DEED problem.
- A new application of the hybrid heuristic algorithm integrating CSO and DE is presented for robust, efficient, and accurate optimization of the DEED involving PEVs. A new multi-objective differential evolution and crisscross optimization (MODECSO) is put forward. MODECSO has the following properties. (1) The elitist reservation strategy and crowding entropy and fuzzy-based mechanism are employed to generate the Pareto optimal front (POF) that overcomes the shortcomings of the weighted sum strategy. (2) For the purpose to make convergence rate accelerated, the global optimal quantity is introduced to improve the horizontal crossover operator. (3) A new adaptive parameter method with self-learning ability is put forward. By using this strategy, there is no need to try out appropriate mutation and crossover constant for each optimization problem, and the algorithm can evolve to suitable control parameter values automatically according to the evolution process.
- Some infeasible solutions may carry important information that is useful for finding the optimal solutions. To ensure the diversity of the offspring, a repair technique is proposed to deal with the constraints to avoid discarding useful infeasible solutions. During the optimizing process, instead of penalty function, the heuristic constraint handling method is used in solving various constrains effectively. Moreover, it does not need to select penalty factors as well as any other parameters, besides it also could direct these infeasible solutions into the feasible domain.
2. The Dynamic Economic/Emission Dispatch Model with Consideration of Plug-In Electric Vehicles
2.1. Objective Functions
2.2. Constraints
2.3. Problem Formulation
2.4. Constraints Handling
3. The Proposed Approach
3.1. The Proposed Algorithm
3.1.1. Crisscross Optimization Algorithm
3.1.2. Differential Evolution Algorithm
3.2. Optimization Strategy
3.2.1. The Elitist Reservation Strategy
3.2.2. Crowding Entropy-Based Diversity Measure
3.2.3. Fuzzy Theory
3.3. Multi-Objective Differential Evolution and Crisscross Optimization Algorithm
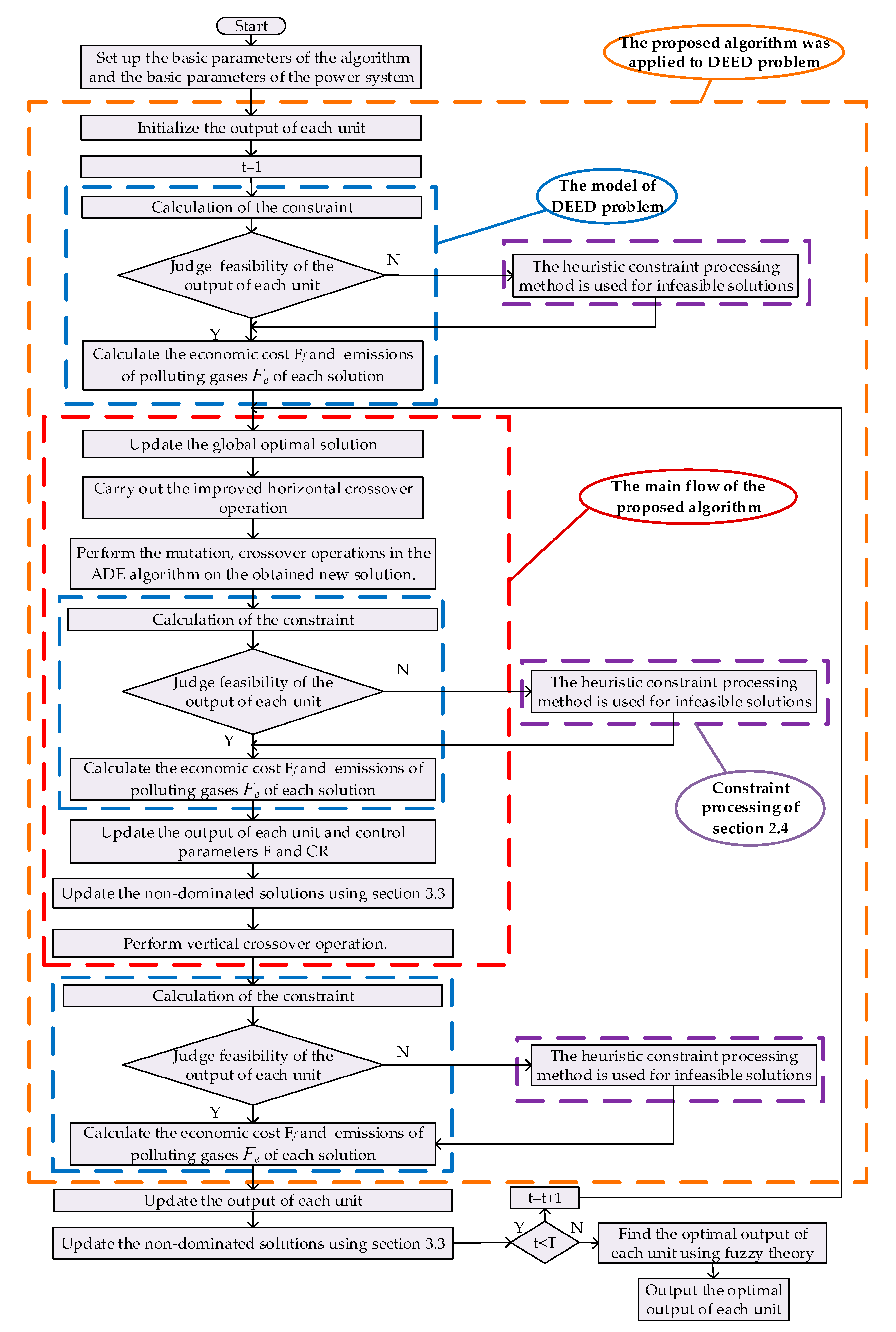
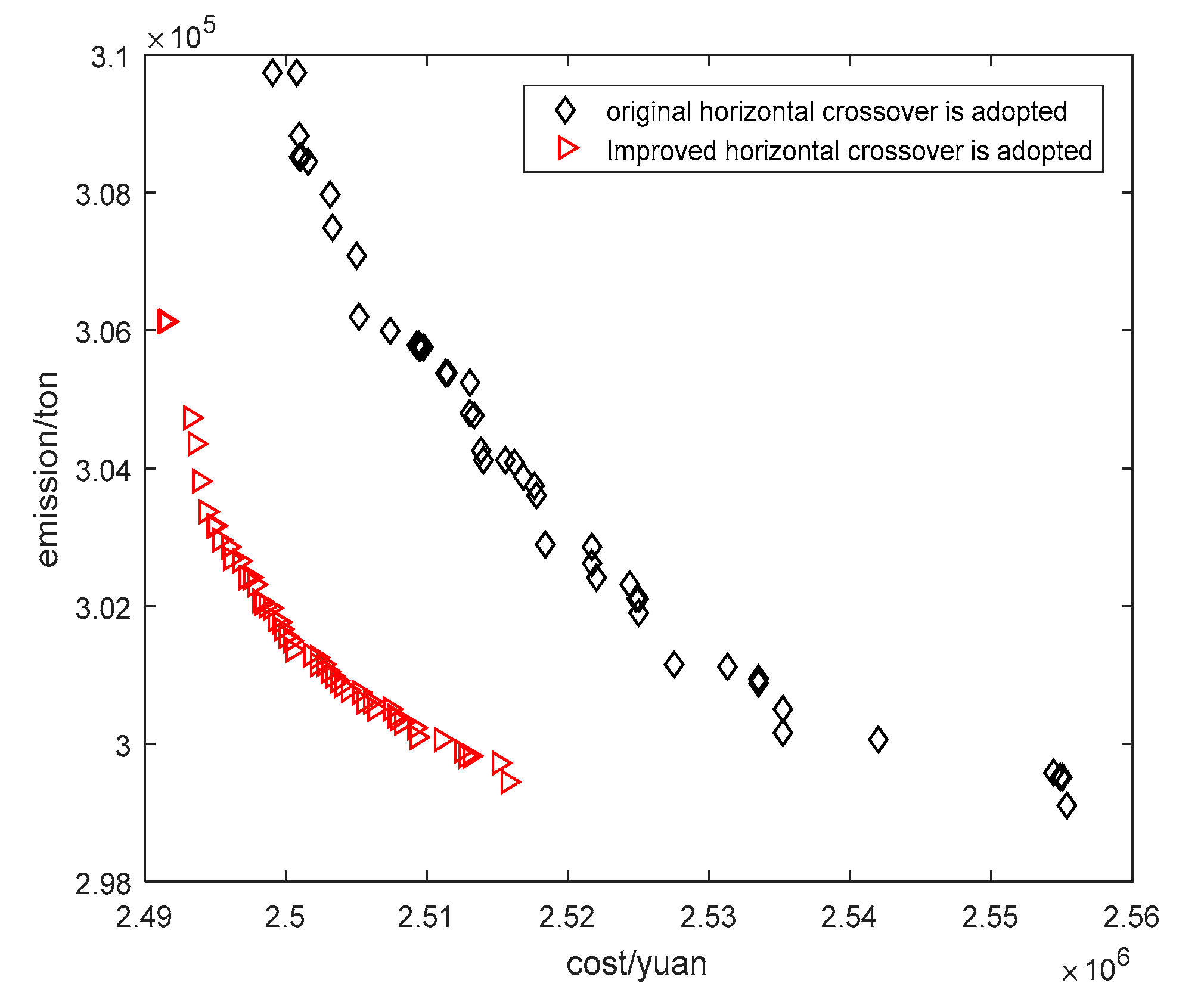
- Step 1: Initialize the population and set the parameters of the algorithm.Step 2: Compute the fitness function.Step 3: Create an empty external archive.Step 4: While iter < Maxiter do.Step 5: Select a solution in the external archive as global optimal solution randomly.Step 6: Perform improved horizontal crossover operation.Step 7: Carry out three operations in the ADE algorithm.Step 8: Compute the fitness function.Step 9: Update the whole population and control parameters.Step 11: Carry out vertical crossover operation.Step 12: Compute the fitness function.Step 13: Update the population.Step 15: End while.
4. Simulation and Analysis
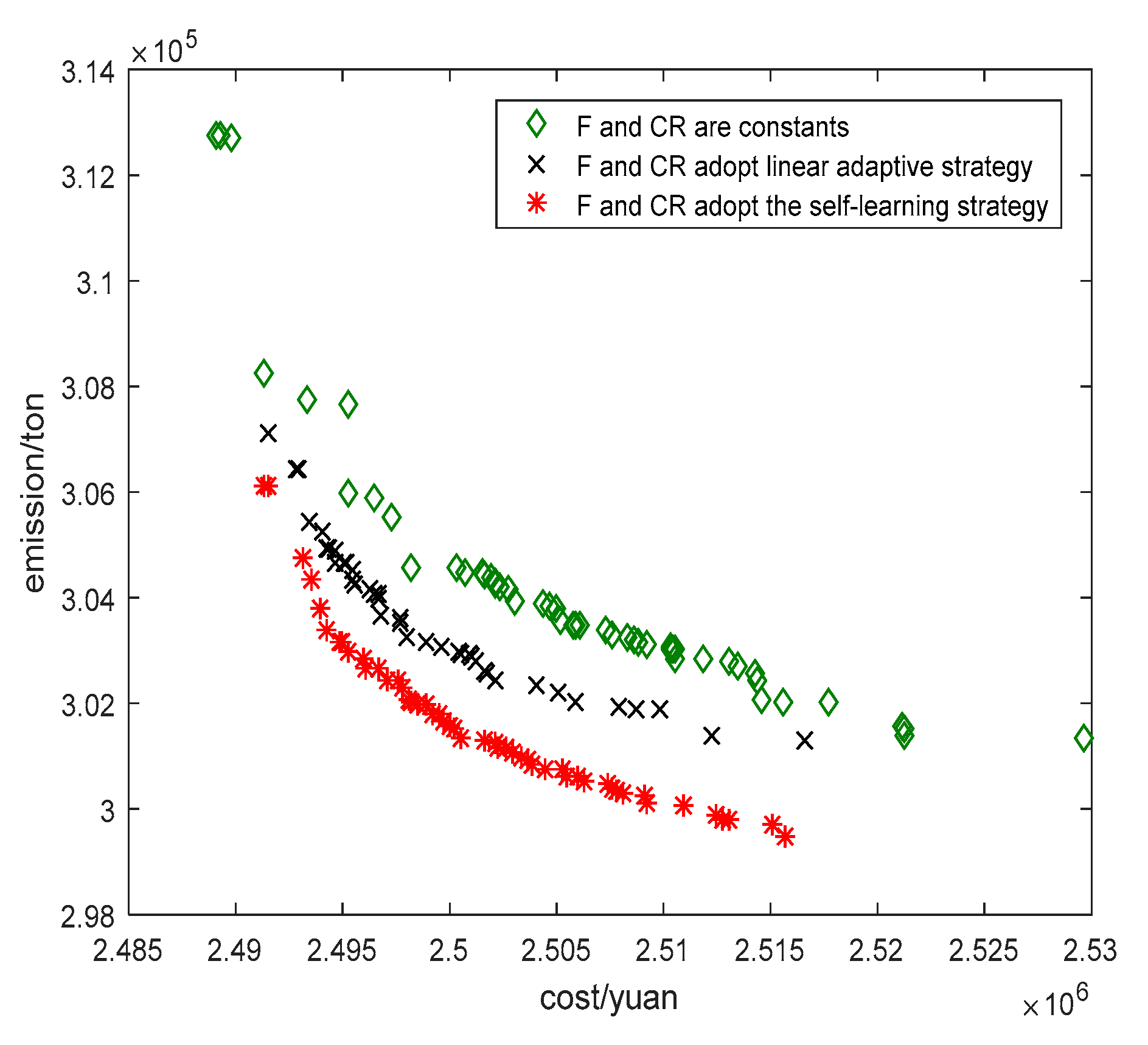
- F and CR are constants and remain the same throughout the iteration.
- F and CR adopt linear adaptive strategy. During the whole iteration process, the control parameter F decreases with the iterations, and CR increases with the iterations.
- F and CR adopt the self-learning strategy of parameters proposed in this paper.
- F and CR adopt the self-learning strategy of parameters, but the improved horizontal crossover operations do not be performed.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Naderi, E.; Azizivahed, A.; Narimani, H.; Fathi, M.; Narimani, M.R. A Comprehensive Study of Practical Economic Dispatch Problems by a New Hybrid Evolutionary Algorithm. Appl. Soft Comput. 2017, 61, 1186–1206. [Google Scholar] [CrossRef]
- Qu, B.Y.; Zhu, Y.S.; Jiao, Y.C.; Wu, M.Y.; Suganthan, P.N.; Liang, J.J. A Survey on Multi-objective Evolutionary Algorithms for the Solution of the Environmental/Economic Dispatch Problems. Swarm Evol. Comput. 2018, 38, 1–11. [Google Scholar] [CrossRef]
- Chouhdry, Z.R.; Hasan, K.M.; Raja, M.A.Z. Design of reduced search space strategy based on integration of Nelder–Mead method and pattern search algorithm with application to economic load dispatch problem. Neural. Comput. Appl. 2018, 30, 3693–3705. [Google Scholar] [CrossRef]
- Li, Z.Y.; Zou, D.X.; Zhi, K. A harmony search variant and a useful constraint handling method for the dynamic economic emission dispatch problems considering transmission loss. Eng. Appl. Artif. Intell. 2019, 84, 18–40. [Google Scholar] [CrossRef]
- Jabr, R.A.; Coonick, A.H.; Cory, B.J. A homogeneous linear programming algorithm for the security constrained economic dispatch problem. IEEE Trans. Power Syst. 2000, 15, 930–936. [Google Scholar] [CrossRef]
- Travers, D.L.; Kaye, R. Dynamic dispatch by constructive dynamic programming. IEEE Trans. Power Syst. 1998, 13, 72–78. [Google Scholar] [CrossRef]
- Papageorgiou, L.G.; Fraga, E.S. A mixed integer quadratic programming formulation for the economic dispatch of generators with prohibited operating zones. Electr. Power Syst. Res. 2007, 77, 1292–1296. [Google Scholar] [CrossRef]
- Chen, C.L. Non-convex economic dispatch: A direct search approach. Energy Convers. Manag. 2007, 48, 219–225. [Google Scholar] [CrossRef]
- Hindi, K.; Ab Ghani, M. Dynamic economic dispatch for large scale power systems: A Lagrangian relaxation approach. Int. J. Electr. Power Energy Syst. 1991, 13, 51–56. [Google Scholar] [CrossRef]
- Zaman, M.F.; Elsayed, S.M.; Ray, T. Evolutionary Algorithms for Dynamic Economic Dispatch Problems. IEEE Trans. Power Syst. 2016, 31, 1486–1495. [Google Scholar] [CrossRef]
- Liang, H.; Liu, Y.; Li, F.; Shen, Y.L. A Hybrid Bat Algorithm for Economic Dispatch with Random Wind Power. IEEE Trans. Power Syst. 2018, 33, 5052–5061. [Google Scholar] [CrossRef]
- Niu, Q.; Zhang, H.; Li, K.; Irwin, G.W. An efficient harmony search with new pitch adjustment for dynamic economic dispatch. Energy 2014, 65, 25–43. [Google Scholar] [CrossRef]
- Das, D.B.; Patvardhan, C. New multi-objective stochastic search technique for economic load dispatch. IEE Proc. Gener. Trans. Distrib. 1998, 145, 747–752. [Google Scholar] [CrossRef]
- Sayah, S.; Hamouda, A. A hybrid differential evolution algorithm based on particle swarm optimization for non-convex economic dispatch problems. Appl. Soft Comput. 2013, 13, 1608–1619. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, D.W.; Geng, N.; Sun, X.Y. Hybrid bare-bones PSO for dynamic economic dispatch with valve-point effects. Appl. Soft Comput. 2014, 18, 248–260. [Google Scholar] [CrossRef]
- Basu, M. Hybridization of bee colony optimization and sequential quadratic programming for dynamic economic dispatch. Int. J. Electr. Power Energy Syst. 2013, 44, 591–596. [Google Scholar] [CrossRef]
- Wang, S.K.; Chiou, P.J.; Liu, C.W. Non-smooth/non-convex economic dispatch by a novel hybrid differential evolution algorithm. Gener. Trans. Distrib. IET 2007, 1, 793–803. [Google Scholar] [CrossRef]
- Soares, A.; Rabelo, R.; Delbem, A. Optimization based on phylogram analysis. Expert Syst. Appl. 2017, 78, 32–50. [Google Scholar] [CrossRef]
- Shams, M.; Rashedi, E.; Dashti, S.M.; Hakimi, A. Ideal gas optimization algorithm. Int. J. Artif. Intell. 2017, 15, 116–130. [Google Scholar]
- Abed-Alguni, B.H. Island-based cuckoo search with highly disruptive polynomial mutation. Int. J. Artif. Intell. 2019, 17, 57–82. [Google Scholar]
- Precup, R.E.; David, R.C. Nature-Inspired Optimization Algorithms for Fuzzy Controlled Servo Systems. In Butterworth-Heinemann; Butterworth-Heinemann: Oxford, UK, 2019. [Google Scholar]
- Fernandez, L.P.; San Román, T.C.; Cossent, R.; Domingo, C.M.; Frias, P. Assessment of the impact of plug-in electric vehicles on distribution networks. IEEE Trans. Power Syst. 2010, 26, 206–213. [Google Scholar] [CrossRef]
- Ansari, J.; Gholami, A.; Kazemi, A.; Jamei, M. Environmental/economic dispatch incorporating renewable energy sources and plug-in vehicles. IET Gener. Trans. Distrib. 2014, 8, 2183–2198. [Google Scholar]
- Ma, H.P.; Yang, Z.L.; You, P.C.; Fei, M.R. Multi-objective biogeography-based optimization for dynamic economic emission load dispatch considering plug-in electric vehicles charging. Energy 2017, 135, 101–111. [Google Scholar] [CrossRef]
- Zhao, J.H.; Wen, F.S.; Dong, Z.Y.; Xue, Y.S.; Wong, K.P. Optimal dispatch of electric vehicles and wind power using enhanced particle swarm optimization. IEEE Trans. Ind. Inf. 2012, 8, 889–898. [Google Scholar] [CrossRef]
- Kempton, W.; Tomic, J. Vehicle-to-grid implementation: From stabilizing the grid to supporting large-scale renewable energy. J. Power Sources 2005, 144, 280–294. [Google Scholar] [CrossRef]
- Kempton, W.; Tomic, J. Vehicle-to-grid power fundamentals: Calculating capacity and net revenue. J. Power Sources 2005, 144, 268–279. [Google Scholar] [CrossRef]
- Andervazh, M.R.; Javadi, S. Emission-economic dispatch of thermal power generation units in the presence of hybrid electric vehicles and correlated wind power plants. IET Gener. Trans. Distrib. 2017, 11, 2232–2243. [Google Scholar] [CrossRef]
- Yang, Z.; Li, K.; Foley, A. Computational scheduling methods for integrating plug-in electric vehicles with power systems: A review. Renew. Sustain. Energy Rev. 2015, 51, 396–416. [Google Scholar] [CrossRef]
- Yang, Z.; Sun, L.; Ke, M. Optimal Charging Strategy for Plug-In Electric Taxi with Time-Varying Profits. IEEE Trans. Smart Grid 2014, 5, 2787–2797. [Google Scholar] [CrossRef]
- Kang, M.T.; Ramachandaramurthy, V.K.; Jia, Y.Y. Integration of electric vehicles in smart grid: A review on vehicle to grid technologies and optimization techniques. Renew. Sustain. Energy Rev. 2016, 53, 720–732. [Google Scholar]
- Qiu, W.; Zhang, J.H.; Liu, N. Multi-objective optimal generation dispatching with large-scale plug-in hybrid electric vehicles penetration. Trans. China Electrotech. Soc. 2013, 28, 160–167. [Google Scholar]
- Yang, Z.; Kang, L.I.; Niu, Q. A self-learning TLBO based dynamic economic/environmental dispatch considering multiple plug-in electric vehicle loads. J. Mod. Power Syst. Clean Energy 2014, 2, 298–307. [Google Scholar] [CrossRef]
- Qu, B.Y.; Qiao, B.H.; Zhu, Y.S.; Jiao, Y.C.; Xiao, J.M. Using multi-objective evolutionary algorithm to solve dynamic environment and economic dispatch with EVs. Int. Conf. Swarm Intell. 2017, 10386, 31–39. [Google Scholar]
- Mou, Y.; Xing, H.; Lin, Z.; Fu, M. A new approach to distributed charging control for plug-in hybrid electric vehicles. In Proceedings of the 33rd Chinese Control Conference, Nanjing, China, 28–30 July 2014; pp. 8118–8123. [Google Scholar]
- Mou, Y.; Xing, H.; Fu, M. Decentralized PWM-based charging control for plug-in electric vehicles. In Proceedings of the 2015 European Control Conference, Linz, Austria, 15–17 July 2015. [Google Scholar]
- Debnath, U.K.; Ahmad, I.; Habibi, D. Energy storage model with gridable vehicles for economic load dispatch in the smart grid. Int. J. Electr. Power Energy Syst. 2015, 64, 1017–1024. [Google Scholar] [CrossRef]
- Hao, X.; Fu, M.; Lin, Z. Decentralized Optimal scheduling for charging and discharging of plug-in electric vehicles in smart grids. IEEE Trans. Power Syst. 2016, 31, 4118–4127. [Google Scholar]
- Alham, M.H.; Elshahed, M.; Ibrahim, D.K.; EI Zahab, E.E.D.A. A dynamic economic emission dispatch considering wind power uncertainty incorporating energy storage system and demand side management. Renew. Energy 2016, 96, 800–811. [Google Scholar] [CrossRef]
- Jiang, X.W.; Zhou, J.Z.; Wang, H.; Zhang, Y.C. Modeling and Solving for Dynamic Economic Emission Dispatch of Power System. Power Syst. Technol. 2013, 37, 385–391. [Google Scholar]
- Basu, M. Fuel constrained economic emission dispatch using non-dominated sorting genetic algorithm-II. Energy 2014, 78, 649–664. [Google Scholar] [CrossRef]
- Ozyon, S.; Temurtas, H.; Durrmus, B.; Kuvat, G. Charged system search algorithm for emission constrained economic power dispatch problem. Energy 2012, 46, 420–430. [Google Scholar] [CrossRef]
- Alsumait, J.S.; Qasem, M.; Sykulski, J.K. An improved Pattern Search based algorithm to solve the Dynamic Economic Dispatch problem with valve-point effect. Energy Convers. Manag. 2010, 51, 2062–2067. [Google Scholar] [CrossRef]
- Neto, J.X.V.; Reynoso-Meza, G.; Ruppel, T.H. Solving non-smooth economic dispatch by a new combination of continuous GRASP algorithm and differential evolution. Int. J. Electr. Power Energy Syst. 2017, 84, 13–24. [Google Scholar] [CrossRef]
- Meng, A.B.; Chen, Y.C.; Yin, H.; Chen, S. Crisscross optimization algorithm and its application. Knowl. Based Syst. 2014, 67, 218–229. [Google Scholar] [CrossRef]
- Rainer, S.; Price, K. Difference evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar]
- Wu, L.H.; Wang, Y.N.; Yuan, X.F. Environmental/economic power dispatch problem using multi-objective differential evolution algorithm. Electr. Power Syst. Res. 2010, 80, 1171–1181. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multi-objective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Cheng, S. Study on Multi-objective Optimization of Distribution Network with Distributed Generation. Ph.D. Thesis, Chongqing University, Chongqing, China, 2013. [Google Scholar]
- Liang, H.; Liu, Y.; Li, F. A multi-objective hybrid bat algorithm for combined economic/emission dispatch. Int. J. Electr. Power Energy Syst. 2018, 101, 103–115. [Google Scholar] [CrossRef]
- Wang, L.; Singh, C. Environmental/economic power dispatch using a fuzzified multi-objective particle swarm optimization algorithm. Electr. Power Syst. Res. 2007, 77, 1654–1664. [Google Scholar] [CrossRef]
- Liang, H.J.; Liu, Y.G.; Liu, F.Z. Dynamic Economic/Emission Dispatch Including PEVs for Peak Shaving and Valley Filling. IEEE Trans. Ind. Electron. 2018, 66, 2880–2890. [Google Scholar] [CrossRef]
- Basu, M. Dynamic economic emission dispatch using non-dominated sorting genetic algorithm-II. Electr. Power Energy Syst. 2008, 30, 140–149. [Google Scholar] [CrossRef]
- Meng, A.; Zhuan, L.I. Dynamic environmental economic dispatch of power system adopting multi-objective crisscross optimization algorithm. Power Syst. Prot. Control 2016, 44, 109–115. [Google Scholar]
- Zhu, Z.; Wang, J.; Baloch, M.H. Dynamic economic emission dispatch using modified NSGA-II. Int. Trans. Electr. Energy Syst. 2016, 26, 2684–2698. [Google Scholar] [CrossRef]
- Niknam, T.; Golestaneh, F.; Sadeghi, M.S. Multi-objective-Teaching-Learning-Based Optimization for Dynamic Economic Emission Dispatch. IEEE Syst. J. 2012, 6, 341–352. [Google Scholar] [CrossRef]
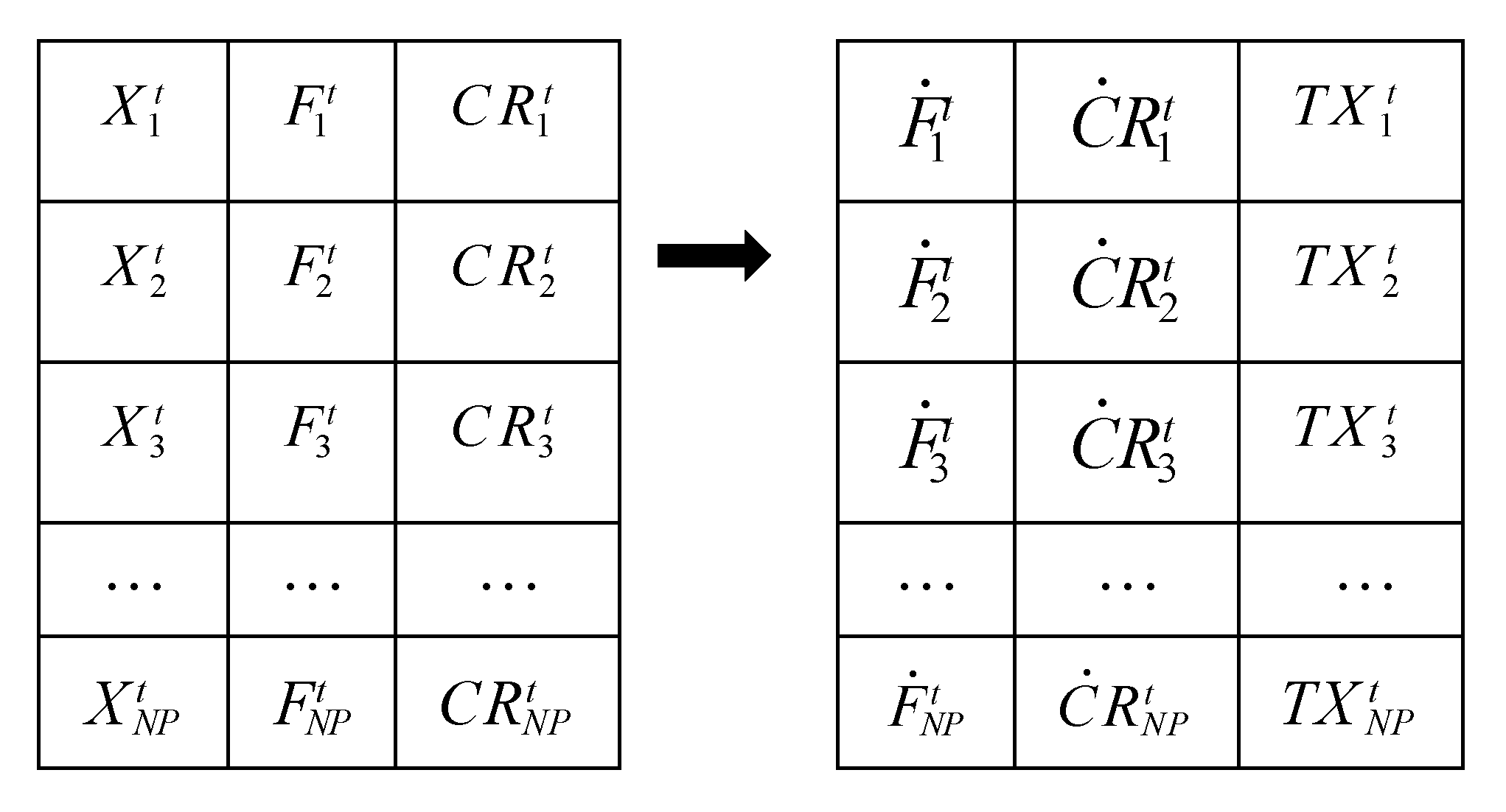
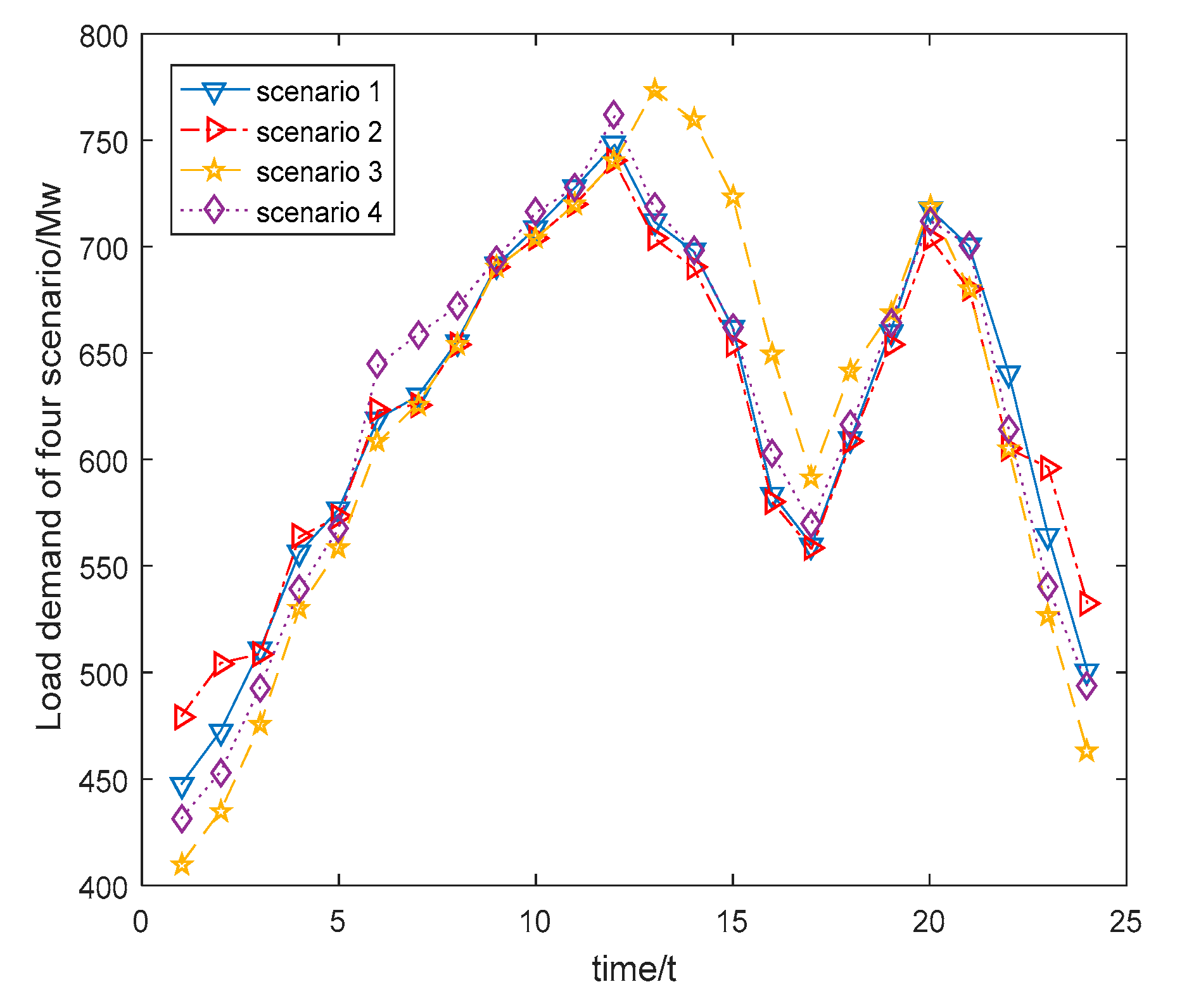


| Hour/h | Load/Mw | Hour/h | Load/Mw | Hour/h | Load/Mw | Hour/h | Load/Mw |
|---|---|---|---|---|---|---|---|
| 1 | 410 | 7 | 626 | 13 | 704 | 19 | 654 |
| 2 | 435 | 8 | 654 | 14 | 690 | 20 | 704 |
| 3 | 475 | 9 | 690 | 15 | 654 | 21 | 680 |
| 4 | 530 | 10 | 704 | 16 | 580 | 22 | 605 |
| 5 | 558 | 11 | 720 | 17 | 558 | 23 | 527 |
| 6 | 608 | 12 | 740 | 18 | 608 | 24 | 463 |
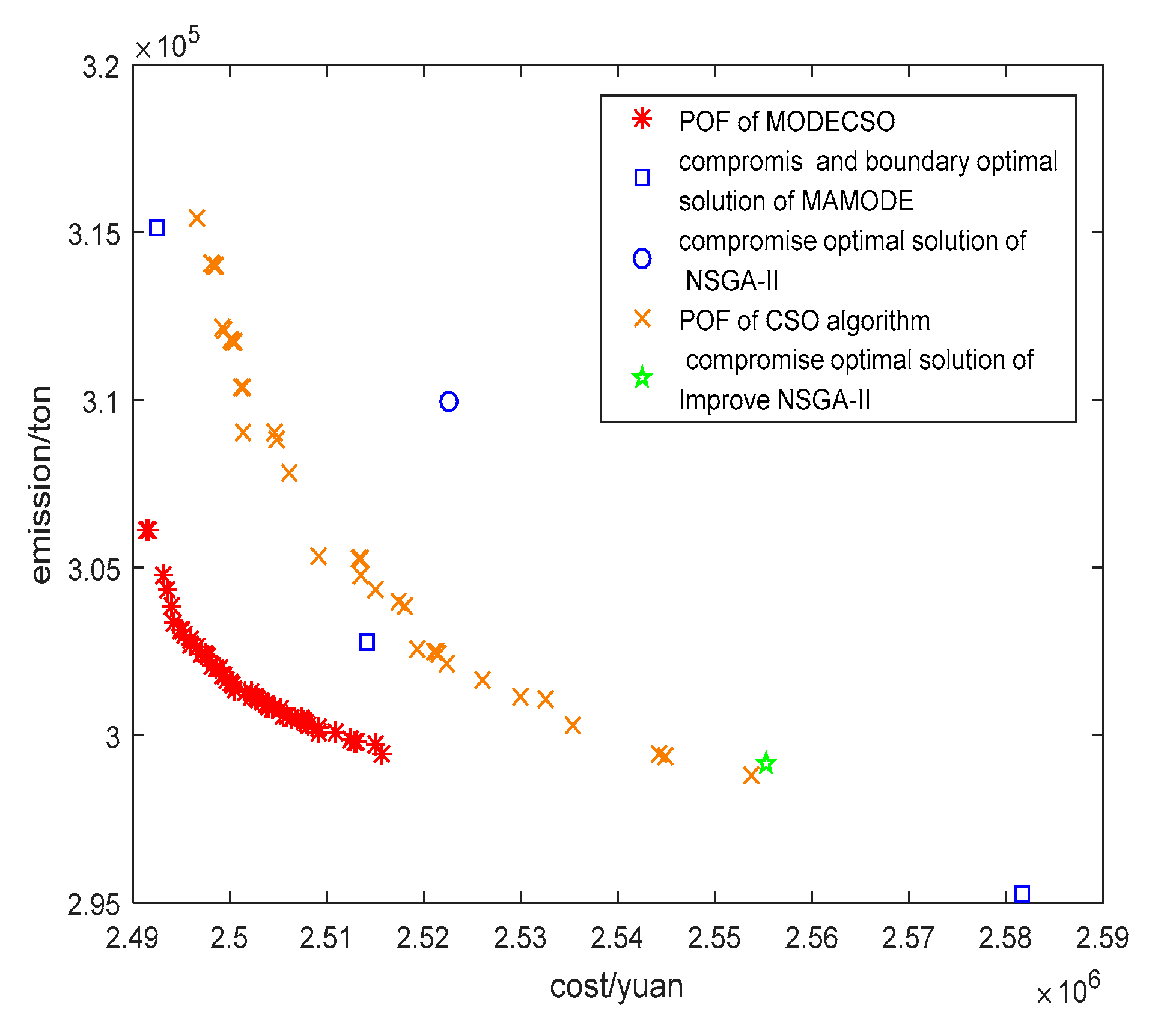
| Algorithm | Selected Target | Cost/Yuan (106) | Emission/Ton (105) | The Satisfaction of the Compromise Solution | CPU Time (min) |
|---|---|---|---|---|---|
| NSGA-II [53] | Best cost Best emission Compromise | — — 2.5226 | — — 3.0994 | — — 0.18137 | - |
| CSO [54] | Best cost Best emission Compromise | — — 2.5013 | — — 3.0905 | — — 0.19086 | 3.89 |
| Improved NSGA-II [55] | Best cost Best emission Compromise | — — 2.5552 | — — 2.9924 | — — 0.20476 | 3.47 |
| MAMODE [56] | Best cost Best emission Compromise | 2.4925 2.5817 2.5141 | 3.1512 2.9524 3.0274 | — — 0.20667 | 3.15 |
| MODECSO | Best cost Best emission Compromise | 2.4712 — 2.4882 | — 2.9214 3.0226 | — — 0.21633 | 3.42 |
| Scenario 1: EPRI charging scenario | Scenario 2: Off-peak charging scenario | ||||||||||||
| Time | Charging probability (%) | Time | Charging probability (%) | ||||||||||
| 1:00–6:00 | 10 | 10 | 9.5 | 7 | 5 | 3 | 1:00–6:00 | 18.5 | 18.5 | 9 | 9 | 4 | 4 |
| 7:00–12:00 | 1 | 0.3 | 0.3 | 1.3 | 2.1 | 2.1 | 7:00–12:00 | 0 | 0 | 0 | 0 | 0 | 0 |
| 13:00–18:00 | 2.1 | 2.1 | 2.1 | 1 | 0.5 | 0.5 | 13:00–18:00 | 0 | 0 | 0 | 0 | 0 | 0 |
| 19:00–24:00 | 1.6 | 3.6 | 5.4 | 9.5 | 10 | 10 | 19:00–24:00 | 0 | 0 | 0 | 0 | 18.5 | 18.5 |
| Scenario 3: Peak charging scenario | Scenario 4: Random charging scenario | ||||||||||||
| Time | Charging probability (%) | Time | Charging probability (%) | ||||||||||
| 1:00–6:00 | 0 | 0 | 0 | 0 | 0 | 0 | 1:00–6:00 | 5.7 | 4.9 | 4.8 | 2.4 | 2.6 | 9.7 |
| 7:00–12:00 | 0 | 0 | 0 | 0 | 0 | 0 | 7:00–12:00 | 8.7 | 4.8 | 1.1 | 3.2 | 2.1 | 5.7 |
| 13:00–18:00 | 18.5 | 18.5 | 18.5 | 18.5 | 9 | 9 | 13:00–18:00 | 3.8 | 2.2 | 2.1 | 6.1 | 3.2 | 2.2 |
| 19:00–24:00 | 4 | 4 | 0 | 0 | 0 | 0 | 19:00–24:00 | 2.8 | 2.2 | 5.5 | 2.5 | 3.5 | 8.2 |
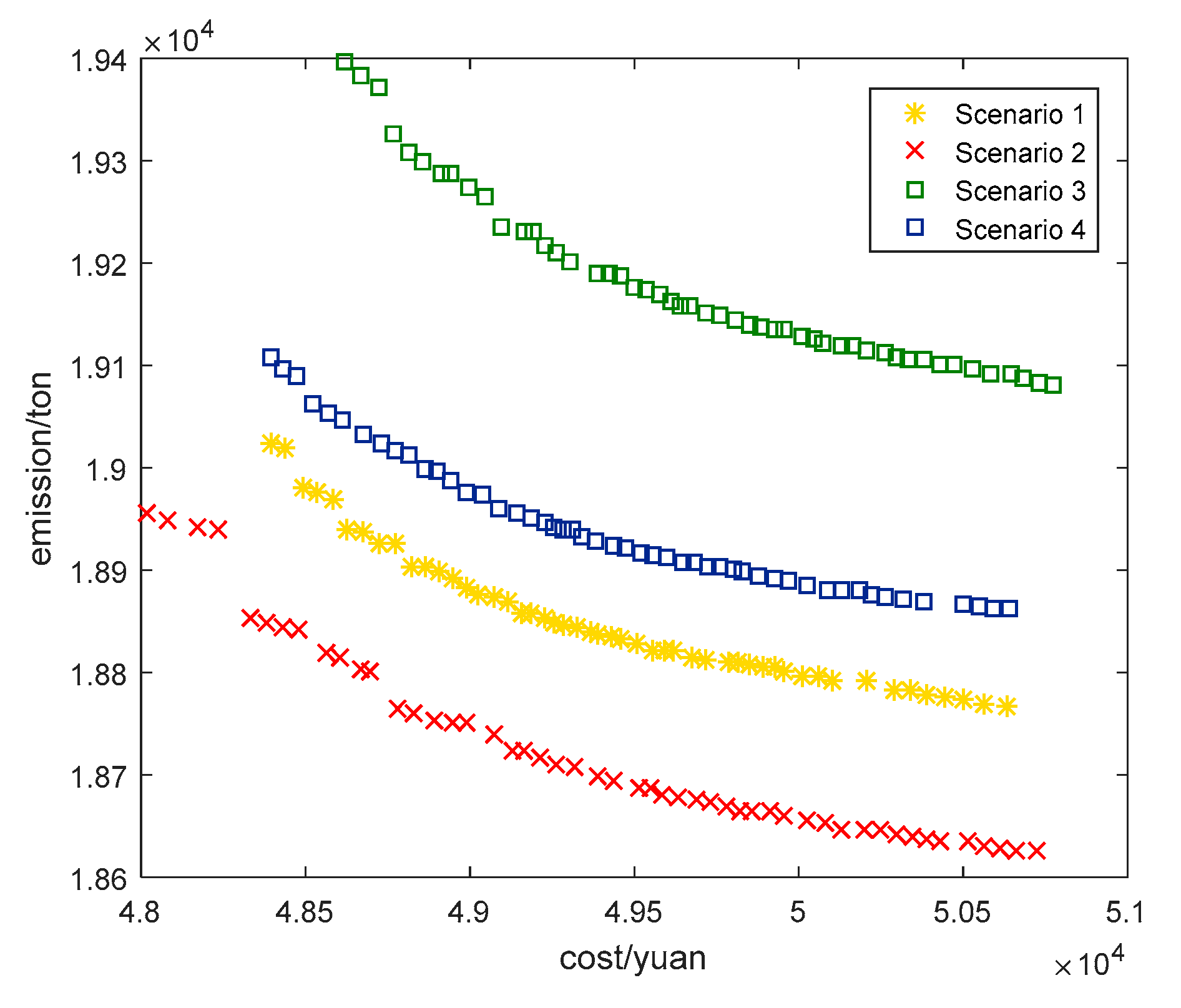
| Scenarios | Cost/Yuan/104 | Emission/Ton/104 | Peak Load/Valley Load |
|---|---|---|---|
| Scenario 1 | 4.8392 | 1.9107 | 1.6712 |
| Scenario 2 | 4.8017 | 1.8955 | 1.5437 |
| Scenario 3 | 4.8616 | 1.9398 | 1.8863 |
| Scenario 4 | 4.8393 | 1.9108 | 1.7650 |
| Hour/h | P1/Mw | P2/Mw | P3/Mw | P4/Mw | P5/Mw | PEV/Mw |
|---|---|---|---|---|---|---|
| 1 | 72.41 | 94.12 | 112.26 | 125.60 | 137.57 | −126 |
| 2 | 72.38 | 97.01 | 122.68 | 124.46 | 125.42 | −101 |
| 3 | 70.15 | 101.26 | 112.12 | 129.41 | 128.97 | −61 |
| 4 | 70.22 | 93.87 | 115.04 | 127.79 | 134.93 | −6 |
| 5 | 72.19 | 89.73 | 126.56 | 147.17 | 128.78 | 0 |
| 6 | 75.00 | 91.88 | 135.25 | 178.07 | 135.41 | 0 |
| 7 | 73.89 | 98.08 | 135.57 | 192.34 | 134.31 | 0 |
| 8 | 75.00 | 96.25 | 152.41 | 199.49 | 139.70 | 0 |
| 9 | 74.25 | 102.99 | 172.26 | 209.36 | 141.05 | 0 |
| 10 | 74.38 | 110.00 | 175.00 | 213.79 | 141.13 | 0 |
| 11 | 74.36 | 120.04 | 173.89 | 214.11 | 148.39 | 0 |
| 12 | 75.00 | 122.00 | 175.00 | 216.21 | 163.24 | 0 |
| 13 | 74.47 | 115.12 | 172.90 | 210.28 | 141.59 | 0 |
| 14 | 74.06 | 103.00 | 173.60 | 209.16 | 140.11 | 0 |
| 15 | 72.62 | 98.33 | 161.14 | 196.33 | 134.54 | 0 |
| 16 | 74.04 | 95.15 | 127.15 | 154.71 | 135.89 | 0 |
| 17 | 70.89 | 97.87 | 132.19 | 129.66 | 133.79 | 0 |
| 18 | 71.03 | 96.16 | 154.13 | 163.11 | 131.22 | 0 |
| 19 | 73.58 | 96.13 | 156.40 | 197.40 | 139.34 | 0 |
| 20 | 72.69 | 114.86 | 174.16 | 211.48 | 141.13 | 0 |
| 21 | 73.45 | 96.43 | 175.00 | 206.68 | 138.05 | 0 |
| 22 | 71.14 | 97.08 | 138.53 | 170.86 | 134.98 | 0 |
| 23 | 67.24 | 94.32 | 113.76 | 127.78 | 138.78 | -9 |
| 24 | 70.95 | 92.14 | 117.49 | 131.12 | 130.24 | -73 |
| Cost: 4.7837 × 104; emissions: 1.8896 × 104 | ||||||
| Hour/h | P1/Mw | P2/Mw | P3/Mw | P4/Mw | P5/Mw | PEV/Mw |
|---|---|---|---|---|---|---|
| 1 | 69.84 | 96.85 | 117.84 | 125.69 | 140.50 | −134.5 |
| 2 | 71.06 | 98.15 | 122.53 | 129.03 | 129.86 | −109.5 |
| 3 | 69.59 | 94.27 | 122.17 | 129.33 | 135.30 | −69.5 |
| 4 | 70.64 | 95.45 | 120.04 | 127.41 | 137.11 | −14.5 |
| 5 | 74.10 | 95.87 | 121.61 | 132.77 | 140.16 | 0 |
| 6 | 74.06 | 98.51 | 137.85 | 167.54 | 137.71 | 0 |
| 7 | 75.00 | 97.25 | 124.91 | 197.37 | 139.70 | 0 |
| 8 | 72.89 | 96.61 | 149.27 | 206.38 | 137.68 | 0 |
| 9 | 75.00 | 103.37 | 174.42 | 205.95 | 141.15 | 0 |
| 10 | 74.37 | 109.35 | 175.00 | 211.89 | 143.79 | 0 |
| 11 | 74.47 | 111.98 | 173.51 | 210.15 | 144.27 | 16 |
| 12 | 73.37 | 111.77 | 172.91 | 211.62 | 144.71 | 36 |
| 13 | 74.89 | 110.74 | 174.80 | 210.31 | 143.56 | 0 |
| 14 | 74.41 | 103.08 | 171.09 | 207.15 | 144.18 | 0 |
| 15 | 74.15 | 99.24 | 160.17 | 194.40 | 134.88 | 0 |
| 16 | 71.27 | 98.06 | 120.17 | 160.14 | 137.45 | 0 |
| 17 | 71.92 | 95.46 | 124.33 | 133.52 | 139.22 | 0 |
| 18 | 74.16 | 97.01 | 131.93 | 175.88 | 136.69 | 0 |
| 19 | 73.75 | 97.75 | 153.38 | 200.72 | 137.29 | 0 |
| 20 | 74.18 | 109.13 | 173.76 | 215.98 | 141.30 | 0 |
| 21 | 74.34 | 99.59 | 174.24 | 209.97 | 131.44 | 0 |
| 22 | 71.21 | 96.46 | 140.77 | 172.02 | 132.07 | 0 |
| 23 | 70.28 | 91.49 | 123.54 | 131.98 | 133.34 | −17.5 |
| 24 | 72.17 | 95.44 | 129.06 | 127.08 | 126.81 | −81.5 |
| Cost: 4.7676 × 104; emissions: 1.8797 × 104 | ||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mei, P.; Wu, L.; Zhang, H.; Liu, Z. A Hybrid Multi-Objective Crisscross Optimization for Dynamic Economic/Emission Dispatch Considering Plug-In Electric Vehicles Penetration. Energies 2019, 12, 3847. https://doi.org/10.3390/en12203847
Mei P, Wu L, Zhang H, Liu Z. A Hybrid Multi-Objective Crisscross Optimization for Dynamic Economic/Emission Dispatch Considering Plug-In Electric Vehicles Penetration. Energies. 2019; 12(20):3847. https://doi.org/10.3390/en12203847
Chicago/Turabian StyleMei, Panpan, Lianghong Wu, Hongqiang Zhang, and Zhenzu Liu. 2019. "A Hybrid Multi-Objective Crisscross Optimization for Dynamic Economic/Emission Dispatch Considering Plug-In Electric Vehicles Penetration" Energies 12, no. 20: 3847. https://doi.org/10.3390/en12203847
APA StyleMei, P., Wu, L., Zhang, H., & Liu, Z. (2019). A Hybrid Multi-Objective Crisscross Optimization for Dynamic Economic/Emission Dispatch Considering Plug-In Electric Vehicles Penetration. Energies, 12(20), 3847. https://doi.org/10.3390/en12203847




