A Hybrid Compensation Topology for Battery Charging System Based on IPT Technology
Abstract
1. Introduction
2. Analysis of Circuits
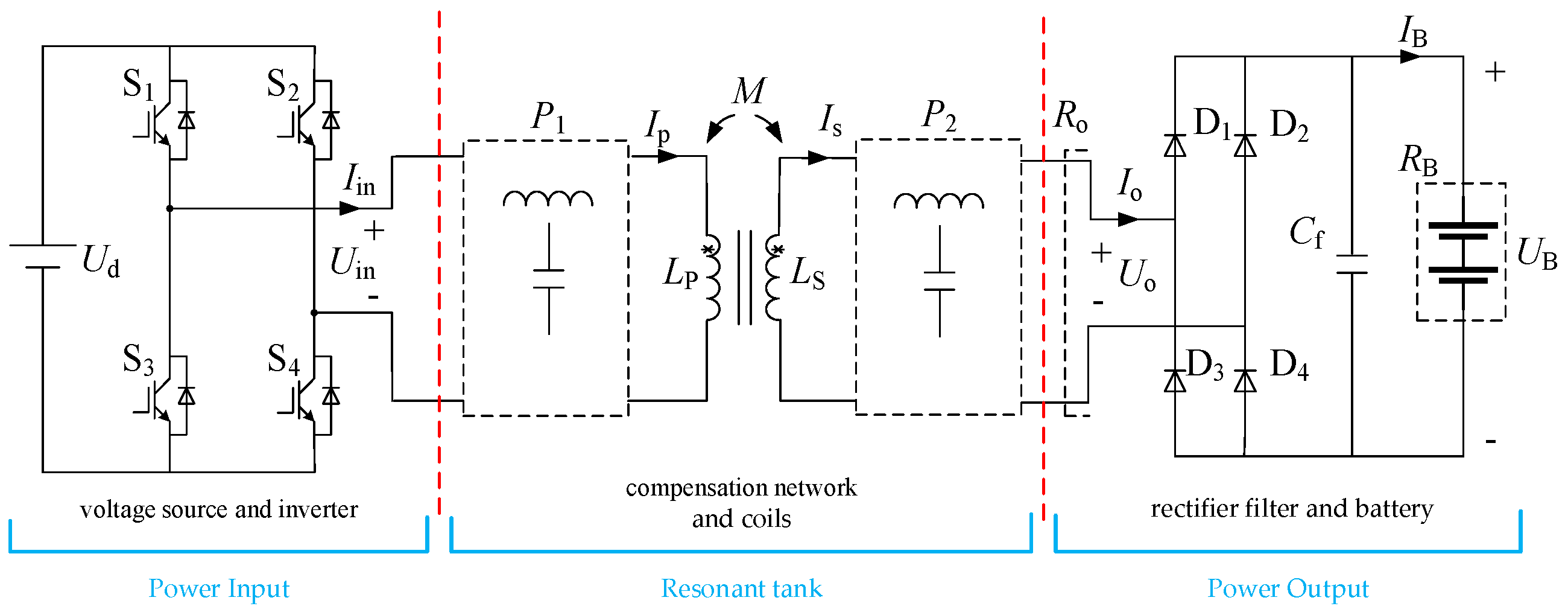
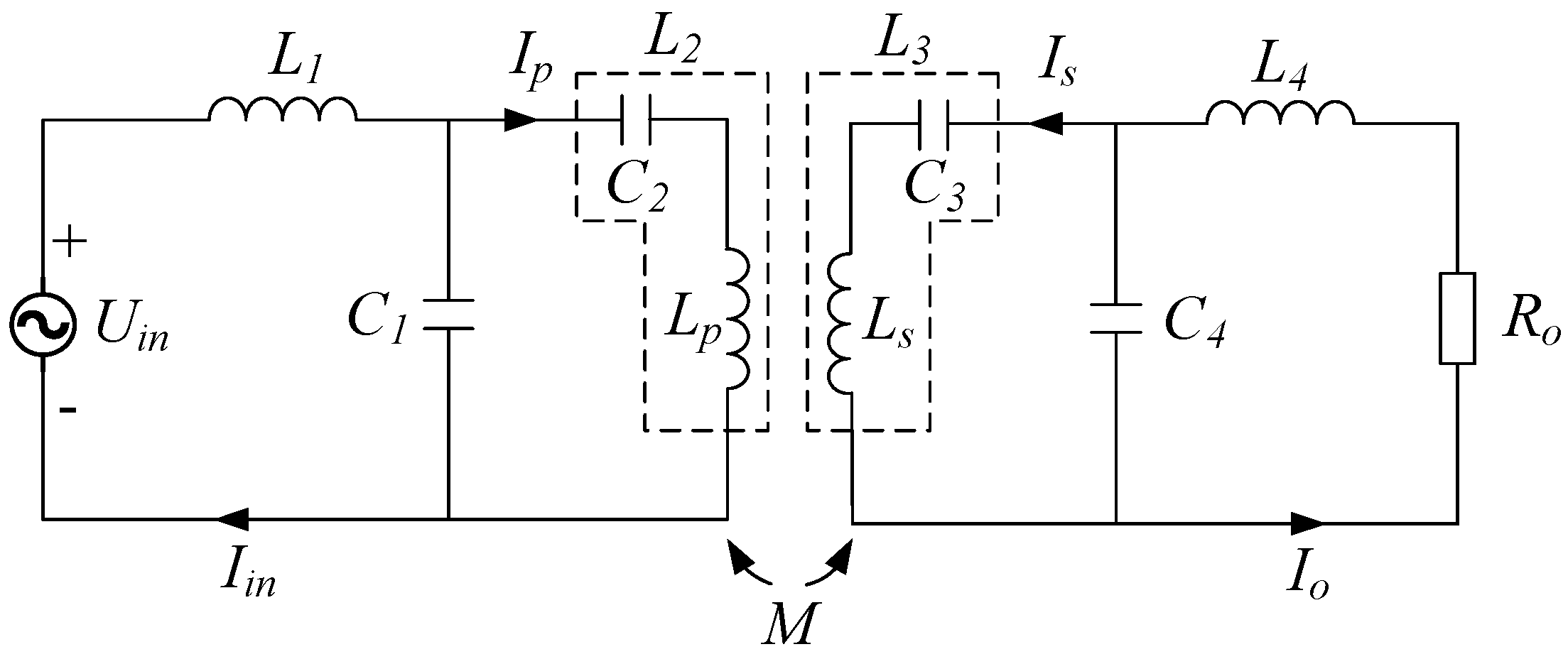
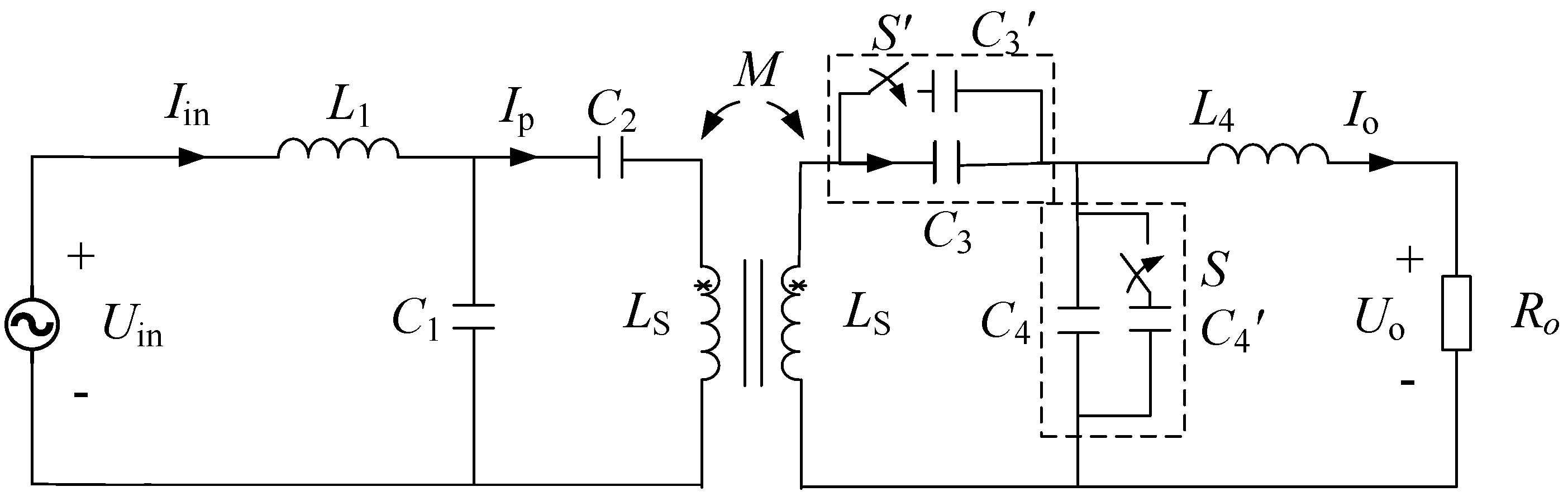
2.1. System Topology
2.2. Realization of CC Mode and CV Mode
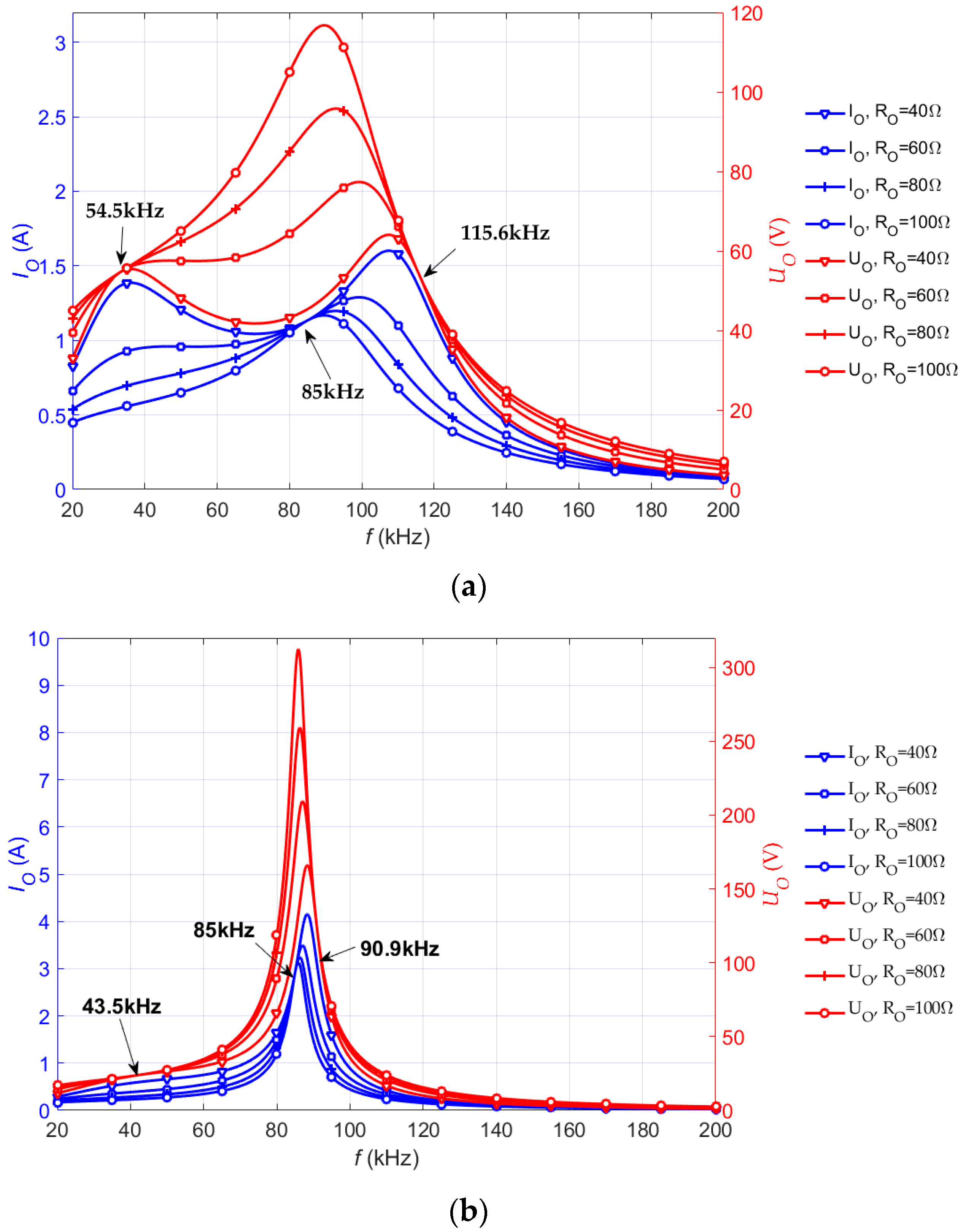
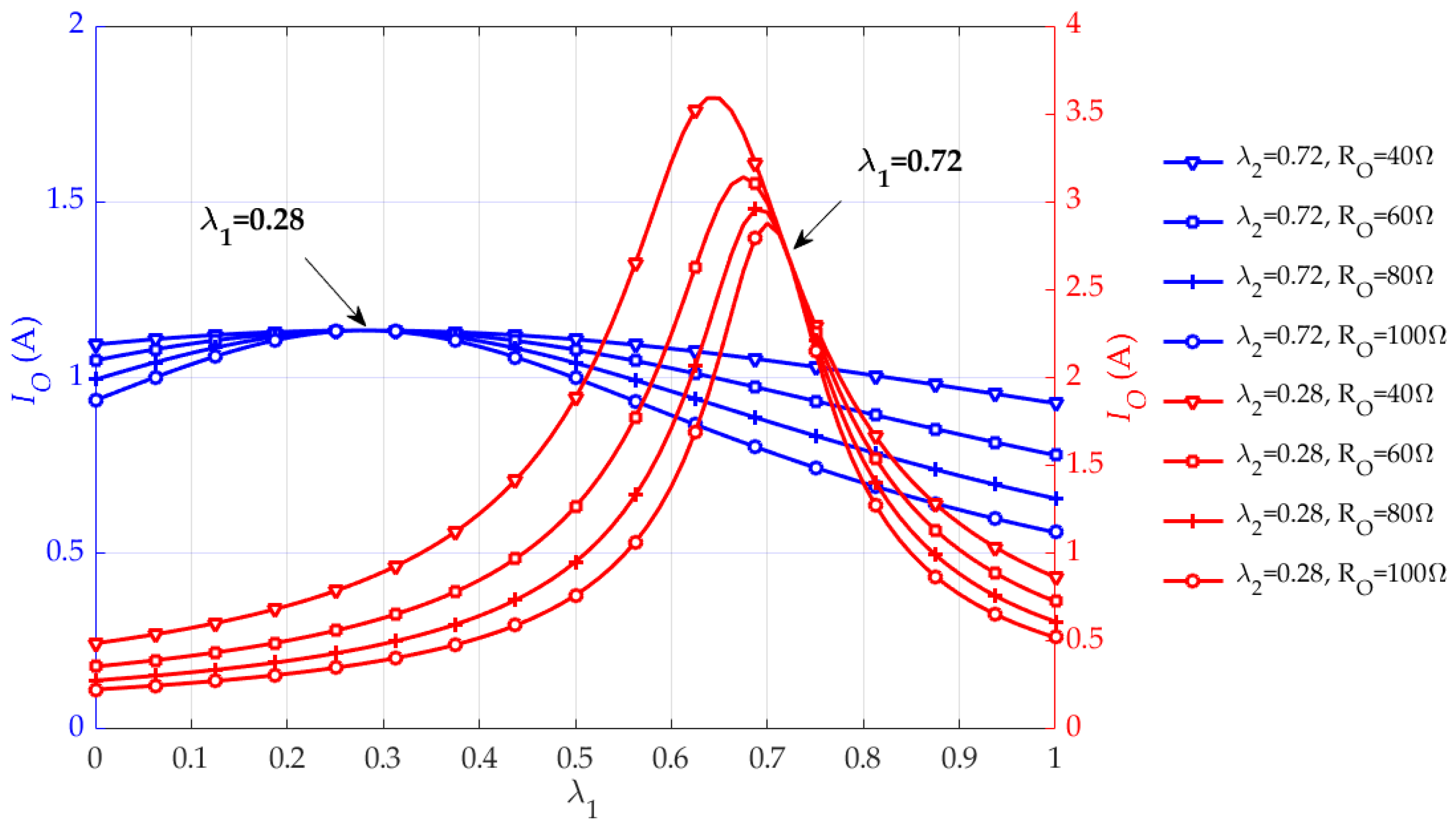
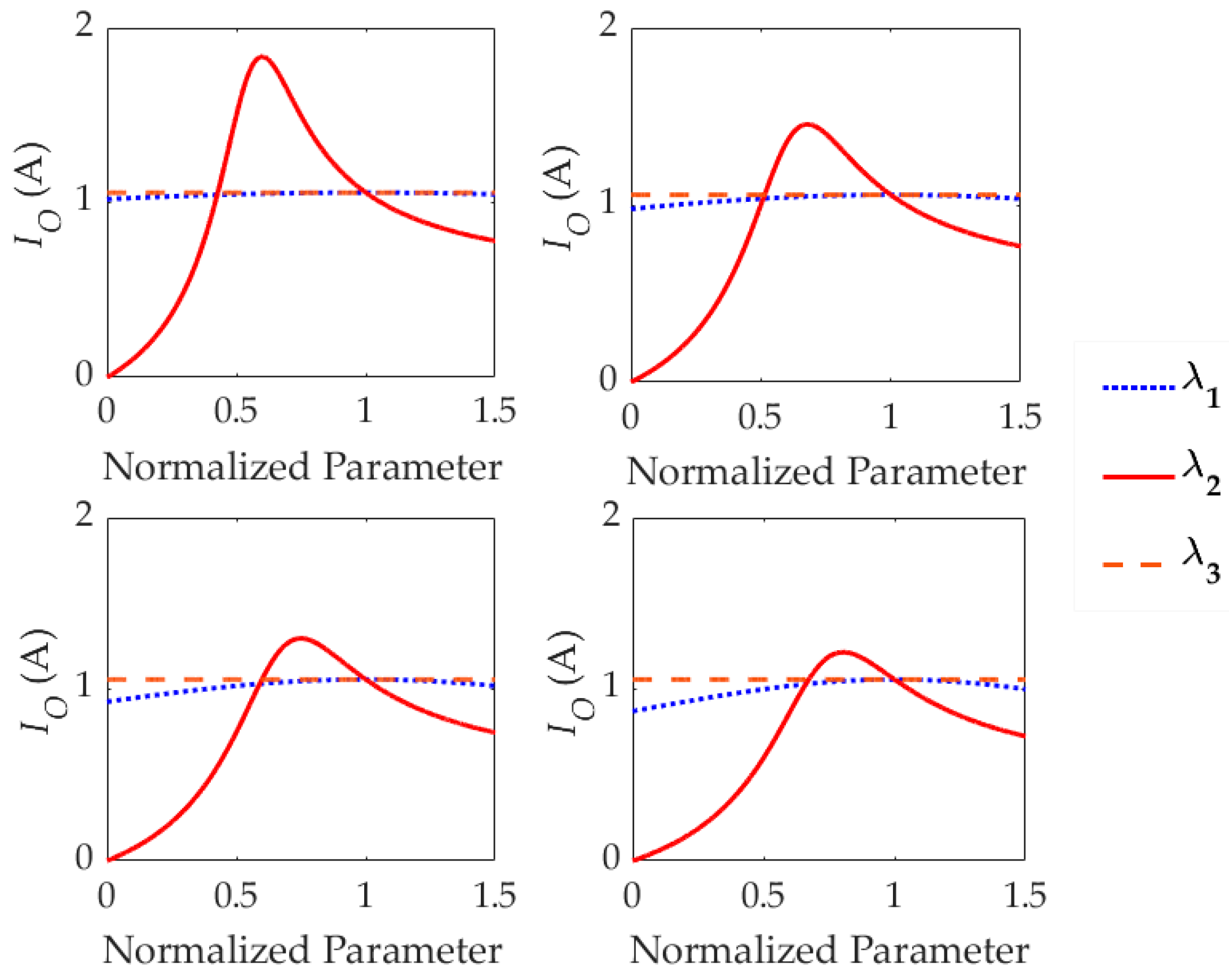
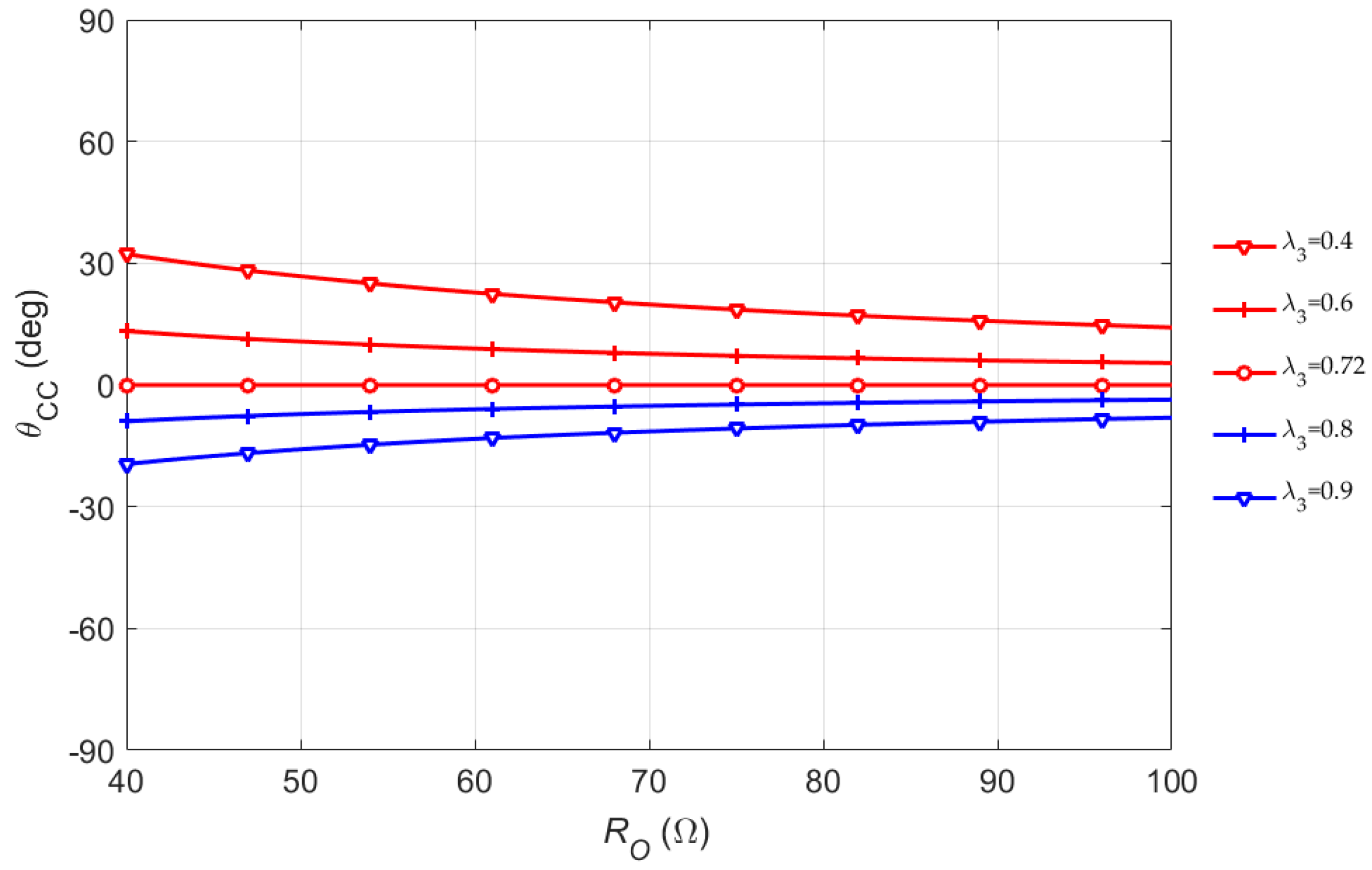
2.3. Parameters Analysis
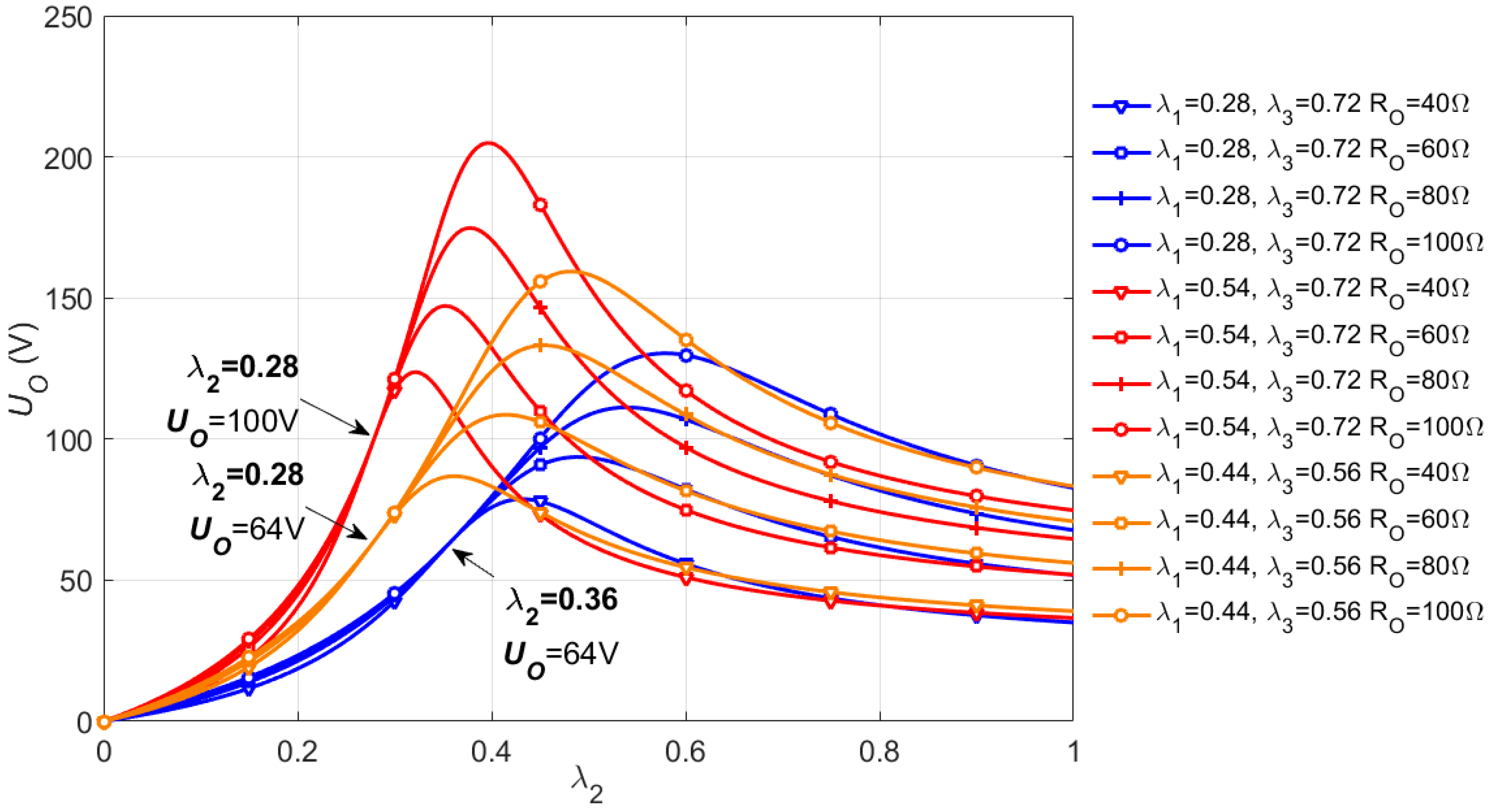
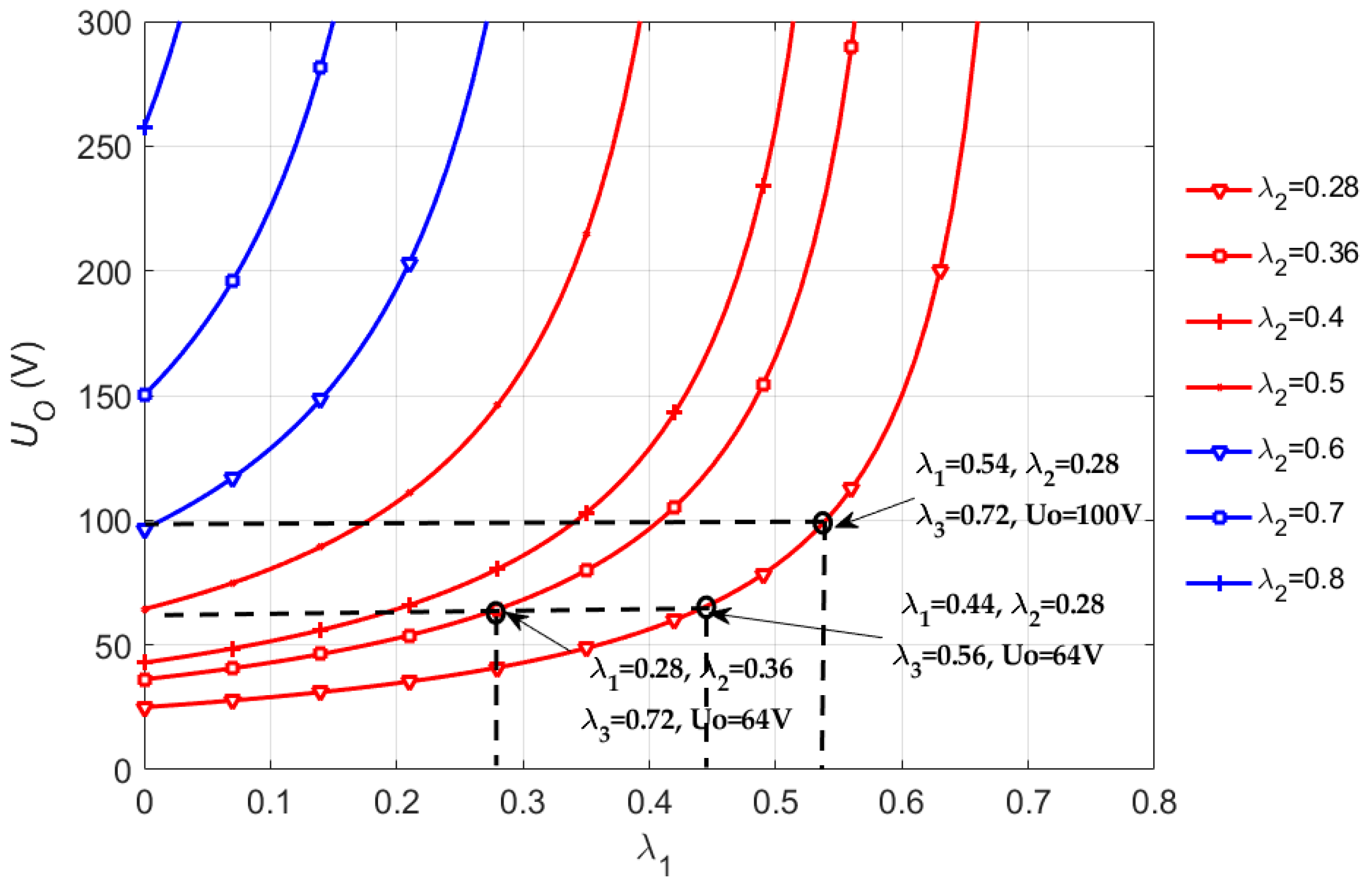
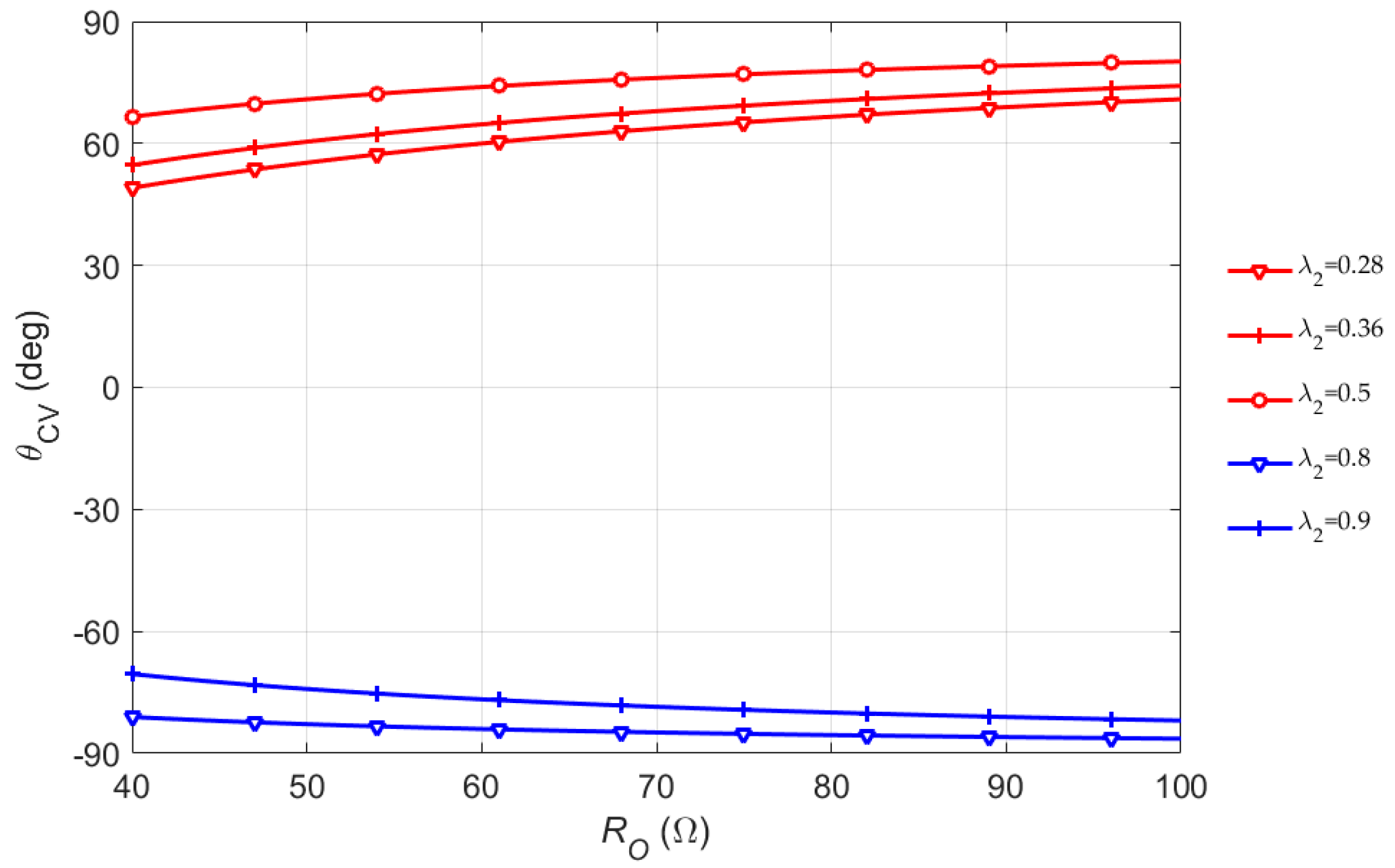
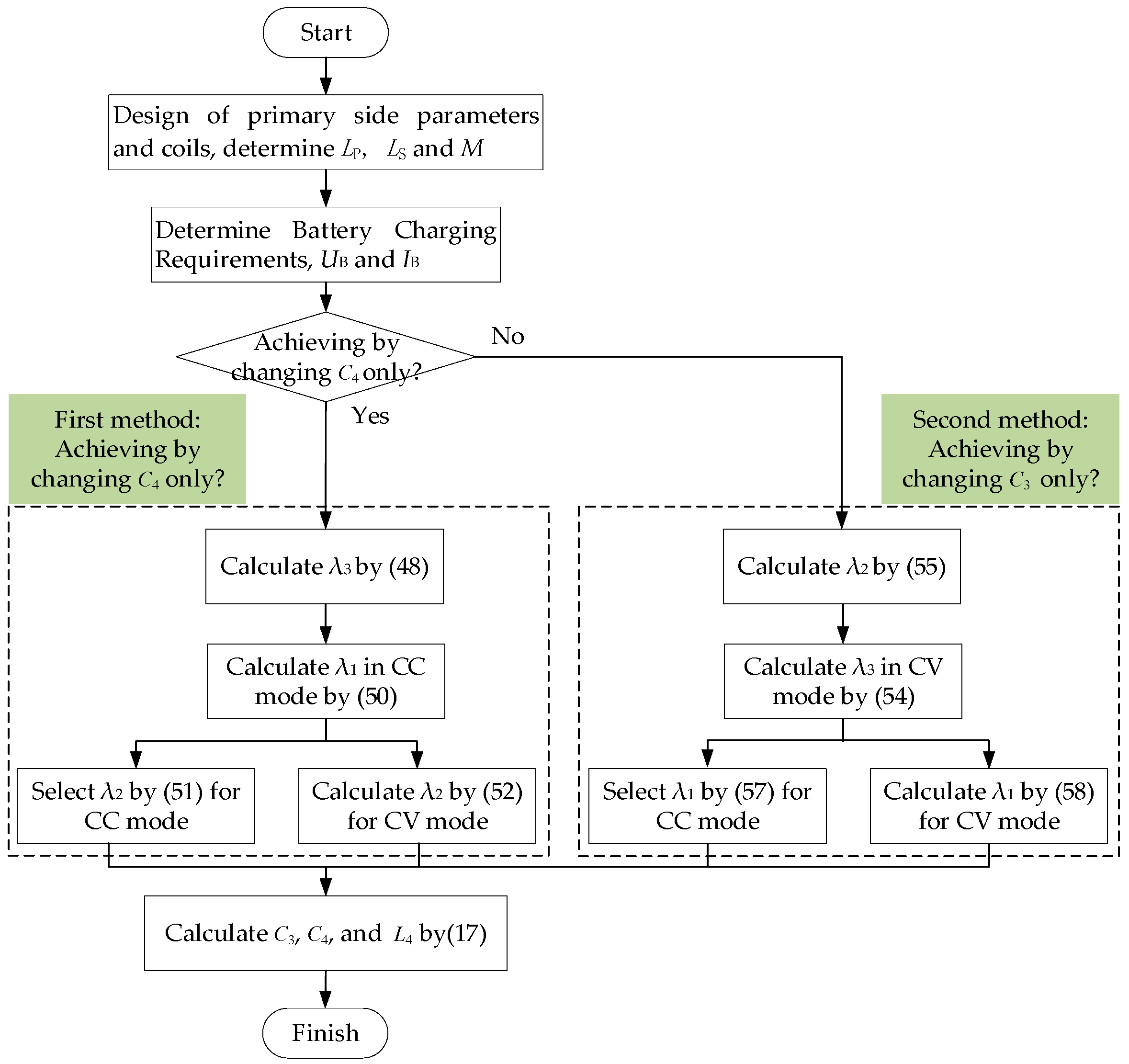
3. Parameters Design
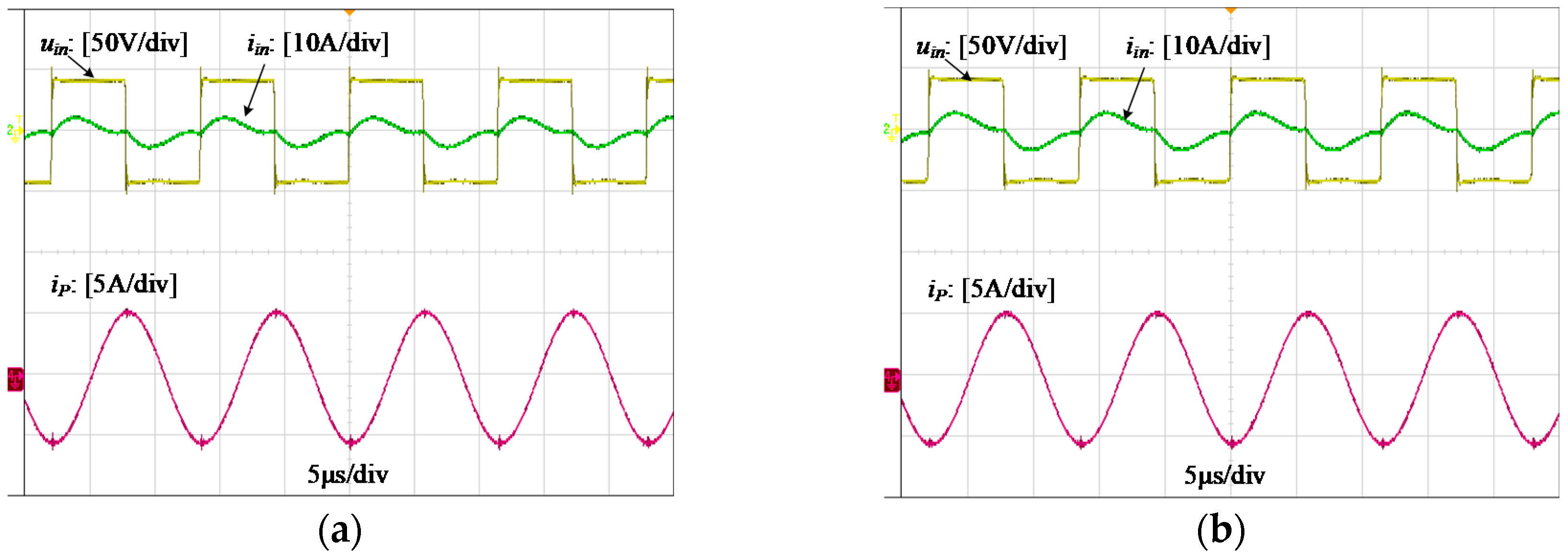
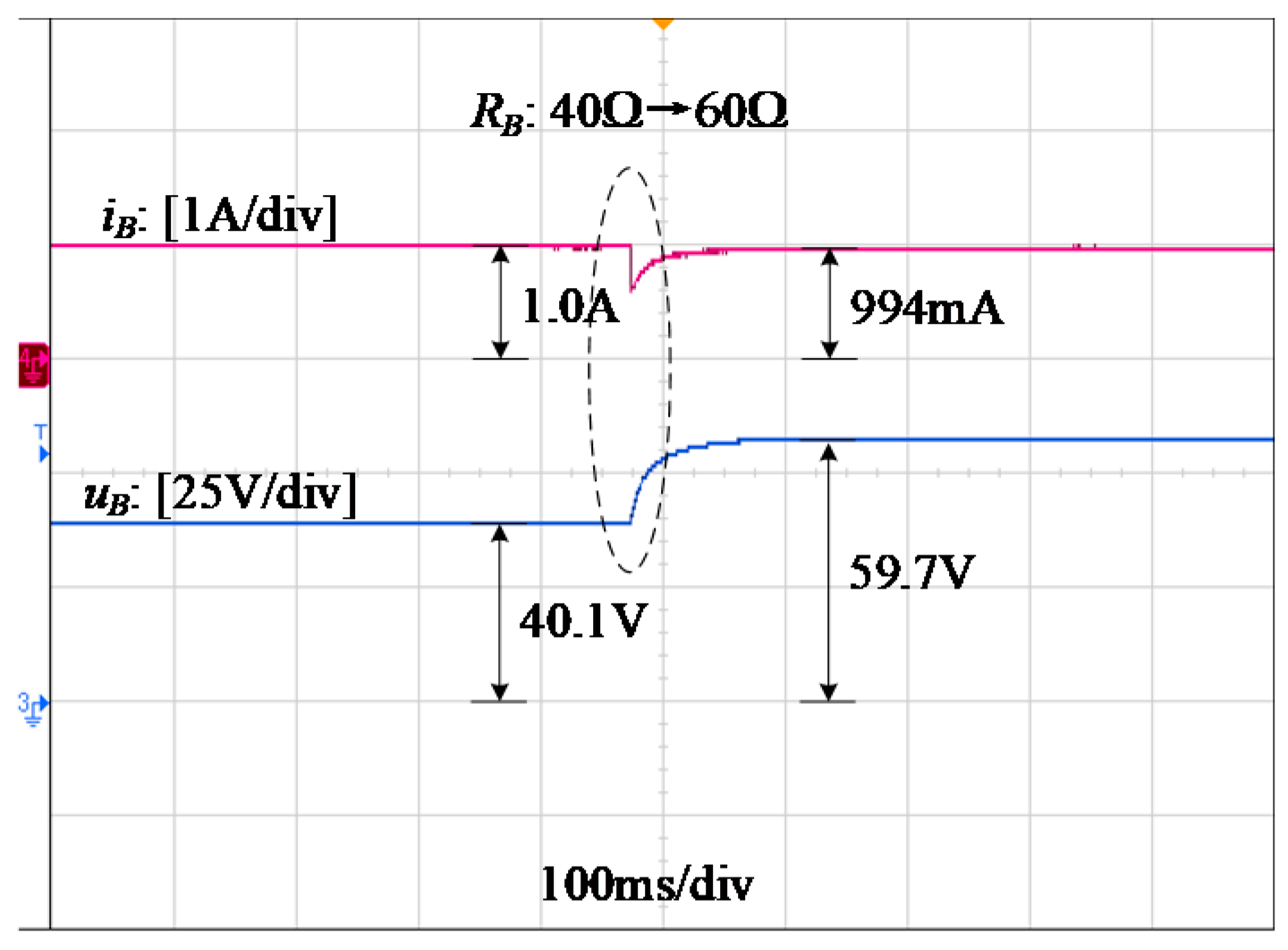
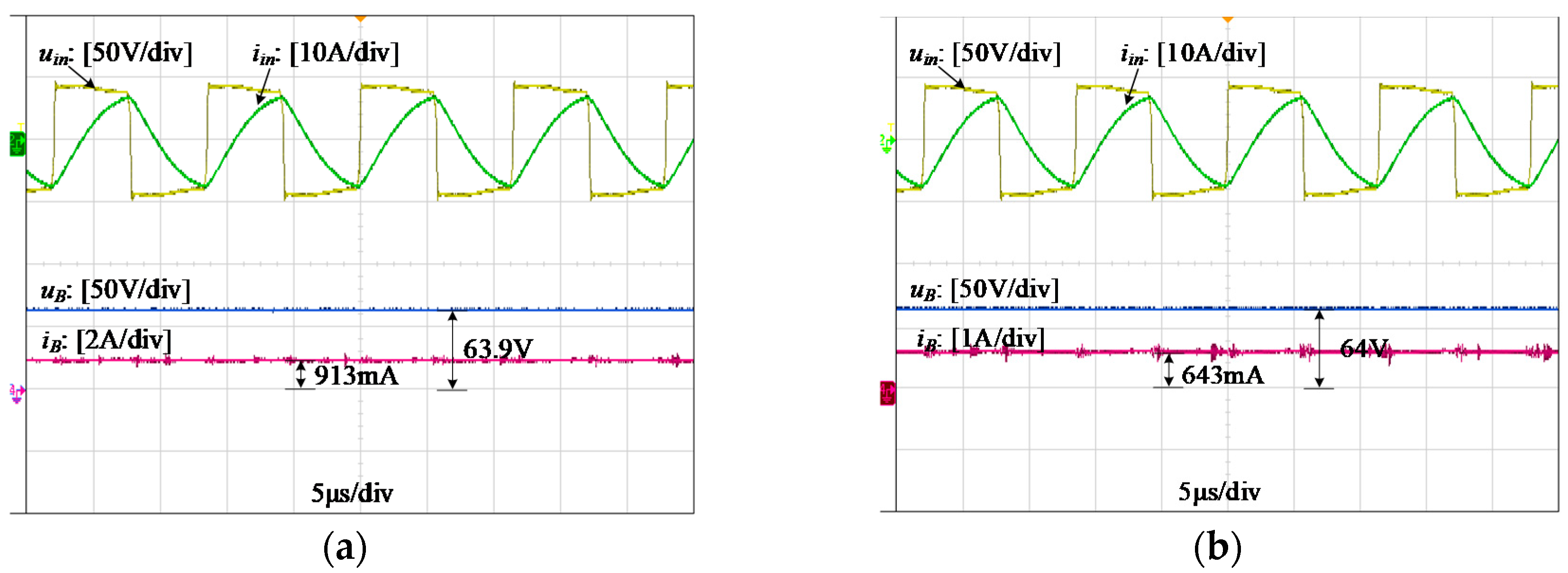
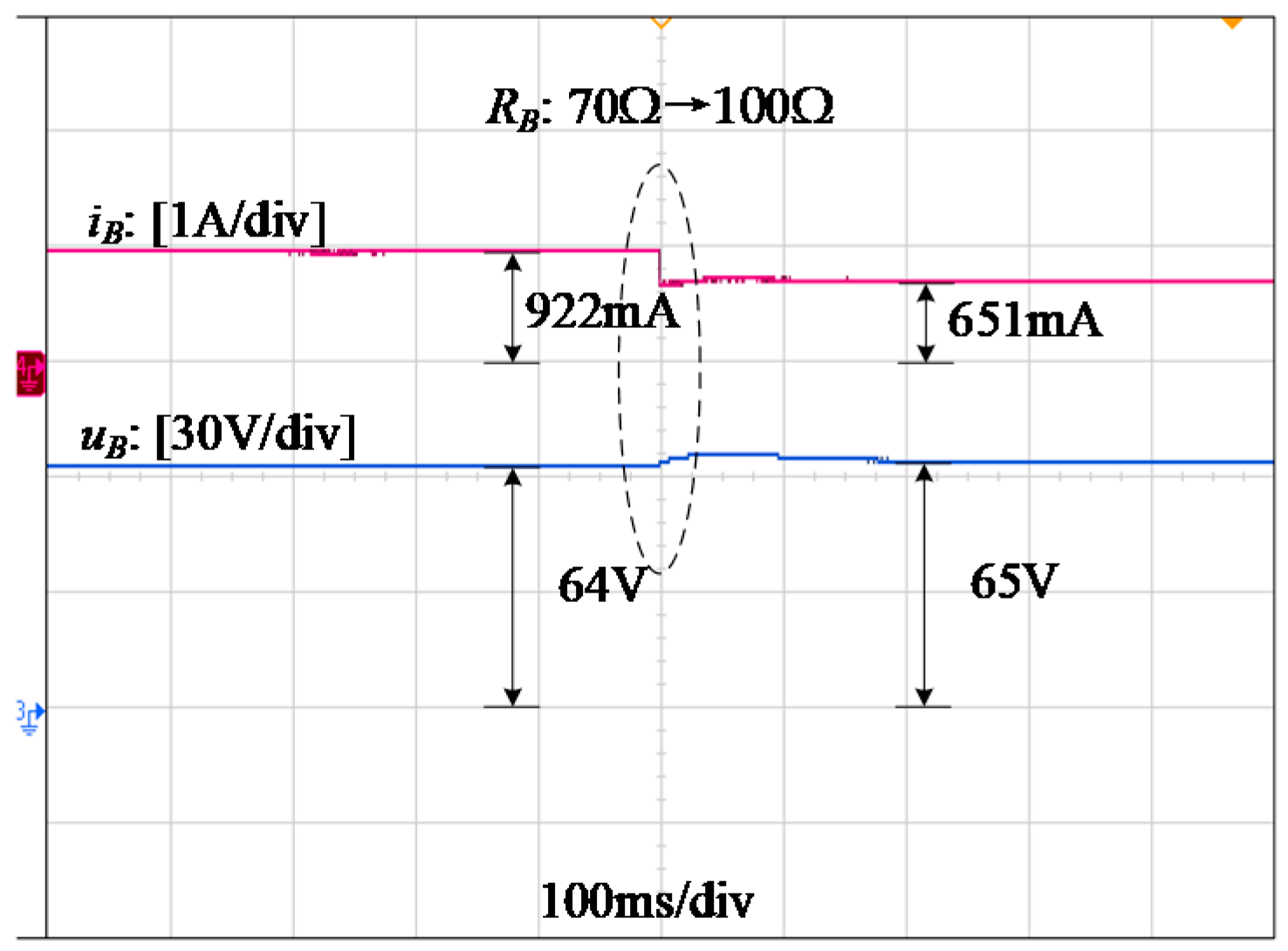
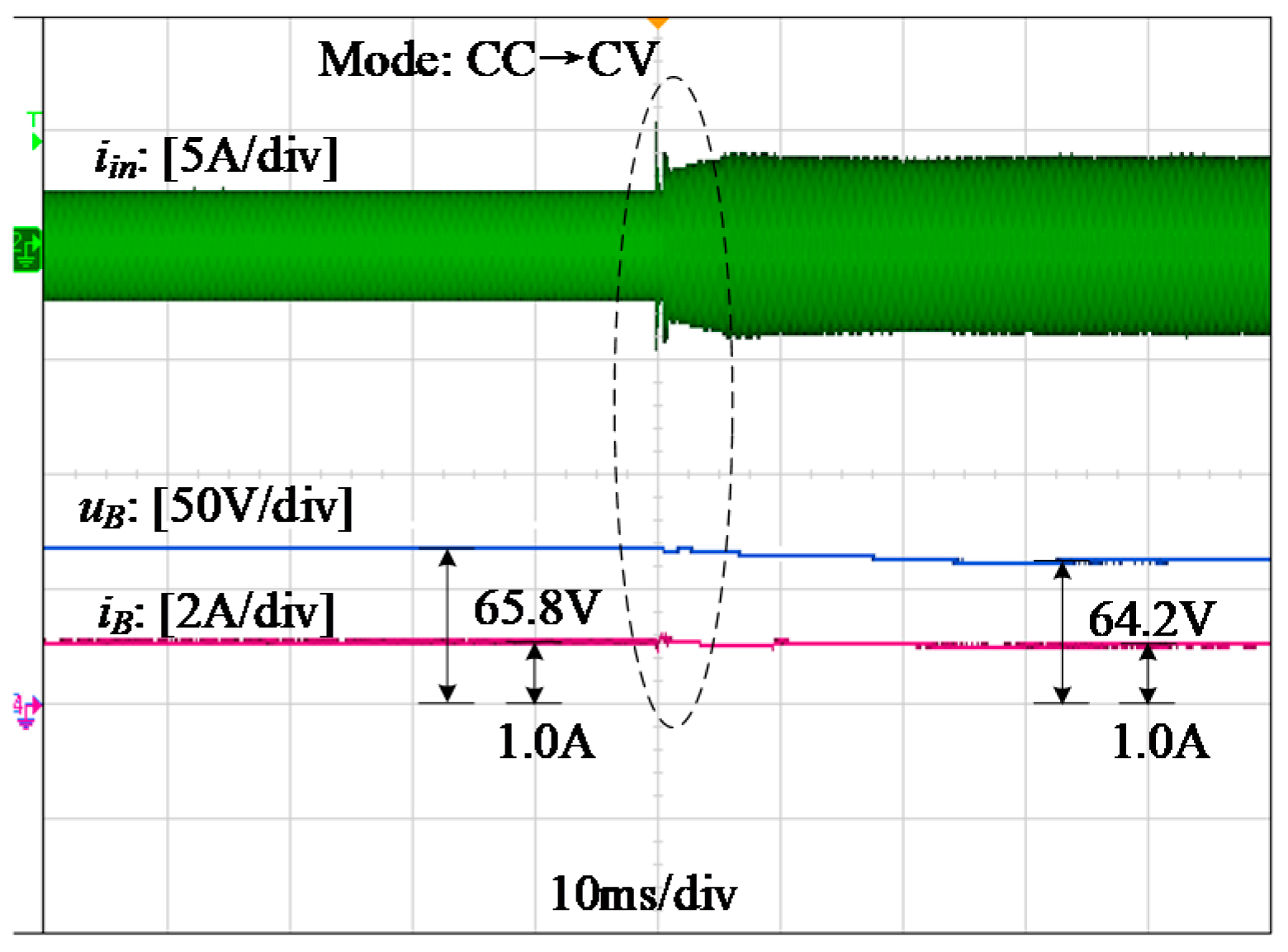
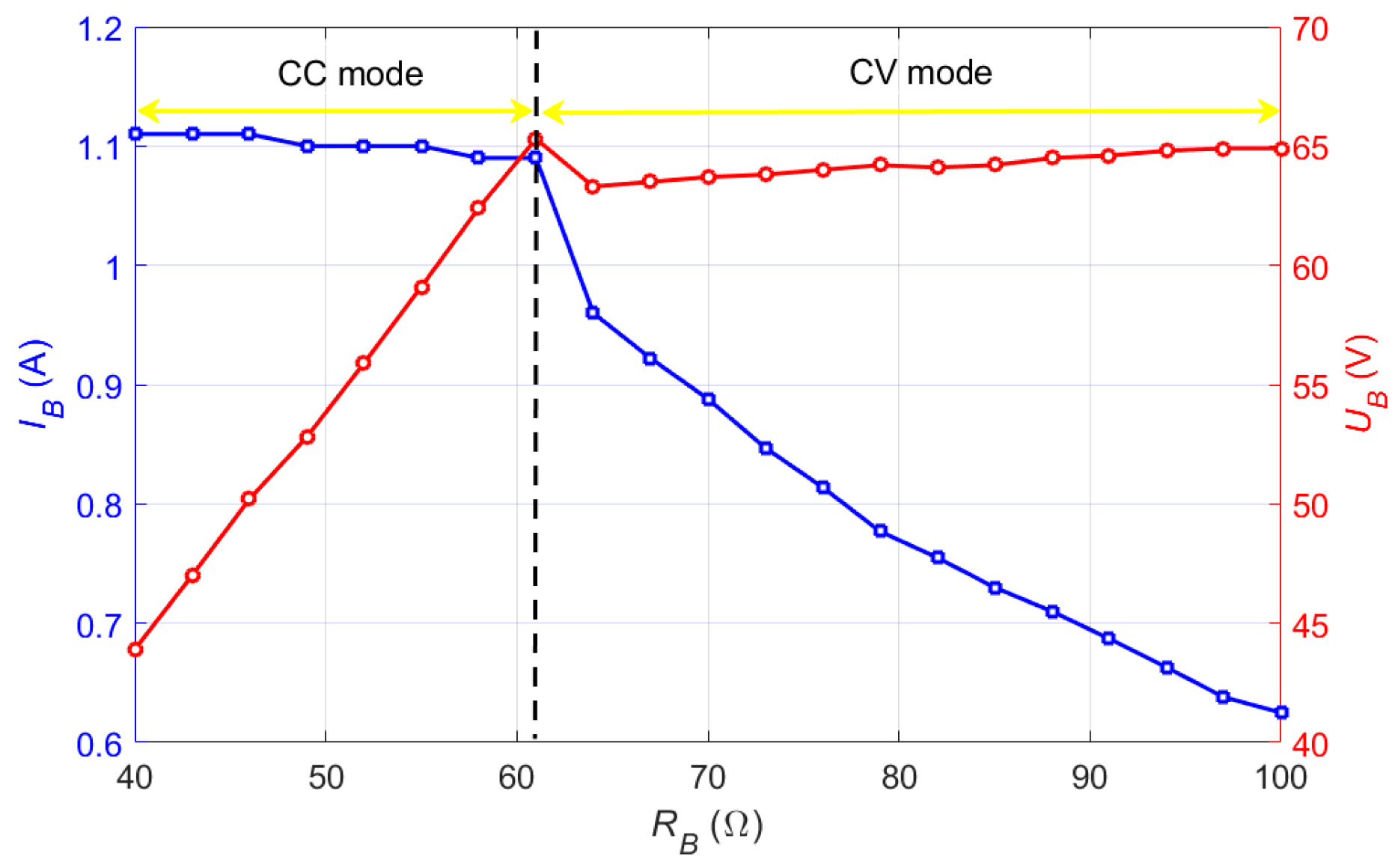
4. Experimental Verification
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- RamRakhyani, A.K.; Mirabbasi, S.; Chiao, M. Design and optimization of resonance-based efficient wireless power delivery systems for biomedical implants. IEEE Trans. Biomed. Circuits Syst. 2011, 5, 48–63. [Google Scholar] [CrossRef] [PubMed]
- Wu, R.; Li, W.; Luo, H.; Sin, J.K.; Yue, C.P. Design and characterization of wireless power links for brain–machine interface applications. IEEE Trans. Power Electron. 2014, 29, 5462–5471. [Google Scholar] [CrossRef]
- Patil, D.; Mcdonough, M.K.; Miller, M.; Fahimi, B.; Balsara, P.T. Wireless Power Transfer for Vehicular Applications: Overview and Challenges. IEEE Trans. Transp. Electrifi. 2018, 4, 3–37. [Google Scholar] [CrossRef]
- Li, S.; Mi, C.C. Wireless Power Transfer for Electric Vehicle Applications. IEEE J. Emerg. Sel. Topics Power Electron. 2015, 3, 4–17. [Google Scholar]
- Buja, G.; Bertoluzzo, M.; Mude, K.N. Design and Experimentation of WPT Charger for Electric City Car. IEEE Trans. Ind. Electron. 2015, 62, 7436–7447. [Google Scholar] [CrossRef]
- Han, W.; Chau, K.T.; Zhang, Z. Flexible induction heating using magnetic resonant coupling. IEEE Trans. Ind. Electron. 2016, 64, 1982–1992. [Google Scholar] [CrossRef]
- Han, H.; Mao, Z.; Zhu, Q.; Su, M.; Hu, A.P. A 3D Wireless Charging Cylinder with Stable Rotating Magnetic Field for Multi-Load Application. IEEE Access. 2019, 7, 35981–35997. [Google Scholar] [CrossRef]
- Kang, X.U.; Chen, X.; Liu, D. Electrical Impedance Transformation Techniques for an Ultrasonic Coupling Wireless Power Transfer System under Sea Water. Proc. CSEE 2015, 35, 4461–4467. [Google Scholar]
- Qu, X.; Chu, H.; Wong, S.C.; Chi, K.T. An IPT Battery Charger with Near Unity Power Factor and Load-independent Constant Output Combating Design Constraints of Input Voltage and Transformer Parameters. IEEE Trans. Power Electron. 2019, 34, 7719–7727. [Google Scholar] [CrossRef]
- Yilmaz, M.; Krein, P.T. Review of Battery Charger Topologies, Charging Power Levels, and Infrastructure for Plug-In Electric and Hybrid Vehicles. IEEE Trans. Power Electron. 2013, 28, 2151–2169. [Google Scholar] [CrossRef]
- Khaligh, A.; Li, Z. Battery, Ultracapacitor, Fuel Cell, and Hybrid Energy Storage Systems for Electric, Hybrid Electric, Fuel Cell, and Plug-In Hybrid Electric Vehicles: State of the Art. IEEE Trans. Veh. Technol. 2010, 59, 2806–2814. [Google Scholar] [CrossRef]
- Li, T.; Wang, X.; Zheng, S.; Liu, C. An Efficient Topology for Wireless Power Transfer over a Wide Range of Loading Conditions. Energies 2018, 11, 141. [Google Scholar] [CrossRef]
- Li, H.; Li, J.; Wang, K.; Chen, W.; Yang, X. A Maximum Efficiency Point Tracking Control Scheme for Wireless Power Transfer Systems Using Magnetic Resonant Coupling. IEEE Trans. Power Electron. 2015, 30, 3998–4008. [Google Scholar] [CrossRef]
- Wu, H.H.; Gilchrist, A.; Sealy, K.D.; Bronson, D. A High Efficiency 5 kW Inductive Charger for EVs Using Dual Side Control. IEEE Trans. Ind. Electron. 2012, 8, 585–595. [Google Scholar] [CrossRef]
- Li, Z.; Zhu, C.; Jiang, J.; Song, K. A 3 kW Wireless Power Transfer System for Sightseeing Car Supercapacitor Charge. IEEE Trans. Power Electron. 2017, 32, 3301–3316. [Google Scholar] [CrossRef]
- Liu, N.; Habetler, T.G. Design of a Universal Inductive Charger for Multiple Electric Vehicle Models. IEEE Trans. Power Electron. 2015, 30, 6378–6390. [Google Scholar] [CrossRef]
- Wang, C.S.; Covic, G.A.; Stielau, O.H. Power Transfer Capability and Bifurcation Phenomena of Loosely Coupled Inductive Power Transfer Systems. IEEE Trans. Ind. Electron. 2004, 51, 148–157. [Google Scholar] [CrossRef]
- Auvigne, C.; Germano, P.; Ladas, D.; Perriard, Y. A Dual-topology ICPT Applied to an Electric Vehicle Battery Charger. In Proceedings of the 2012 International Conference on Electrical Machines, Marseille, France, 2–5 September 2012; pp. 2287–2292. [Google Scholar]
- Sun, Y.; Zhang, H.; Tao, W.; Ma, J.; Li, L.; Xia, J. Constant-Voltage Inductively Coupled Power Transfer System with Wide Load Range Based on Variable Structure Mode. Autom. Electr. Power Syst. 2016, 40, 109–114. [Google Scholar]
- Qu, X.; Han, H.; Wong, S.C.; Tse, C.K.; Chen, W. Hybrid IPT topologies with constant current or constant voltage output for battery charging applications. IEEE Trans. Power Electron. 2015, 30, 6329–6337. [Google Scholar] [CrossRef]
- Mai, R.; Chen, Y.; Zhang, Y.; Yang, N.; Cao, G.; He, Z. Optimization of the Passive Components for an S-LCC Topology-Based WPT System for Charging Massive Electric Bicycles. IEEE Trans. Ind. Electron. 2018, 65, 5497–5508. [Google Scholar] [CrossRef]
- Ji, L.; Wang, L.; Liao, C.; Li, S. Design of Electric Vehicle Wireless Charging System with Automatic Charging Mode Alteration at Secondary Side. Autom. Electr. Power Syst. 2017, 23, 143–148. [Google Scholar]
- Liu, G.; Bai, J.; Cui, Y.; Li, Z.; Yue, C. Double-Sided LCL Compensation Alteration Based on MCR-WPT Charging System. Trans. China Electrotech. Soc. 2019, 34, 1569–1579. [Google Scholar]
- Qu, X.; Jing, Y.; Han, H.; Wang, S.; Tes, C.K. Higher Order Compensation for Inductive-Power-Transfer Converters with Constant-Voltage or Constant-Current Output Combating Transformer Parameter Constraints. IEEE Trans. Power Electron. 2017, 32, 394–405. [Google Scholar] [CrossRef]
- Li, S.; Li, W.; Deng, J.; Nguyen, T.D.; Mi, C. A double-sided LCC compensation network and its tuning method for wireless power transfer. IEEE Trans. Veh. Technol. 2015, 64, 2261–2273. [Google Scholar] [CrossRef]
- Kan, T.; Nguyen, T.D.; White, J.C.; Malhan, R.K.; Mi, C. A New Integration Method for an Electric Vehicle Wireless Charging System Using LCC Compensation Topology: Analysis and Design. IEEE Trans. Power Electron. 2017, 32, 1638–1650. [Google Scholar] [CrossRef]

| Symbol | Value | Symbol | Value |
|---|---|---|---|
| L1 | 19.95 μH | LS | 147.6 μH |
| LP | 603.8 μH | L4 | 106.24 μH |
| C1 | 183.02 nF | C3 | 80.94 nF |
| C2 | 5.94 nF | C4 | 33 nF |
| Ui | 40 V | RO | 40–100 Ω |
| M | 34.21 μH | f | 85 kHz |
| λ1 | λ2 for CC Mode | λ2 for CV Mode | λ3 |
|---|---|---|---|
| 0.28 | 0.72 | 0.36 | 0.72 |
| C3 | C4 | C4 | L4 |
| 80.94 nF | 33 nF | 66 nF | 106.24 μH |
| λ1 for CC Mode | λ1 for CV Mode | λ2 | λ3 |
|---|---|---|---|
| 0.72 | 0.44 | 0.28 | 0.56 |
| C3 | C3 | C4 | L4 |
| 33 nF | 51.51 nF | 80.94 nF | 82.63 μH |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Zhang, X.; Yang, X.; Liu, Q.; Sun, Y. A Hybrid Compensation Topology for Battery Charging System Based on IPT Technology. Energies 2019, 12, 3818. https://doi.org/10.3390/en12203818
Yang J, Zhang X, Yang X, Liu Q, Sun Y. A Hybrid Compensation Topology for Battery Charging System Based on IPT Technology. Energies. 2019; 12(20):3818. https://doi.org/10.3390/en12203818
Chicago/Turabian StyleYang, Junfeng, Xiaodong Zhang, Xu Yang, Qiujiang Liu, and Yi Sun. 2019. "A Hybrid Compensation Topology for Battery Charging System Based on IPT Technology" Energies 12, no. 20: 3818. https://doi.org/10.3390/en12203818
APA StyleYang, J., Zhang, X., Yang, X., Liu, Q., & Sun, Y. (2019). A Hybrid Compensation Topology for Battery Charging System Based on IPT Technology. Energies, 12(20), 3818. https://doi.org/10.3390/en12203818




