Separation Flow Control of a Generic Ground Vehicle Using an SDBD Plasma Actuator
Abstract
1. Introduction
2. Experimental Equipment
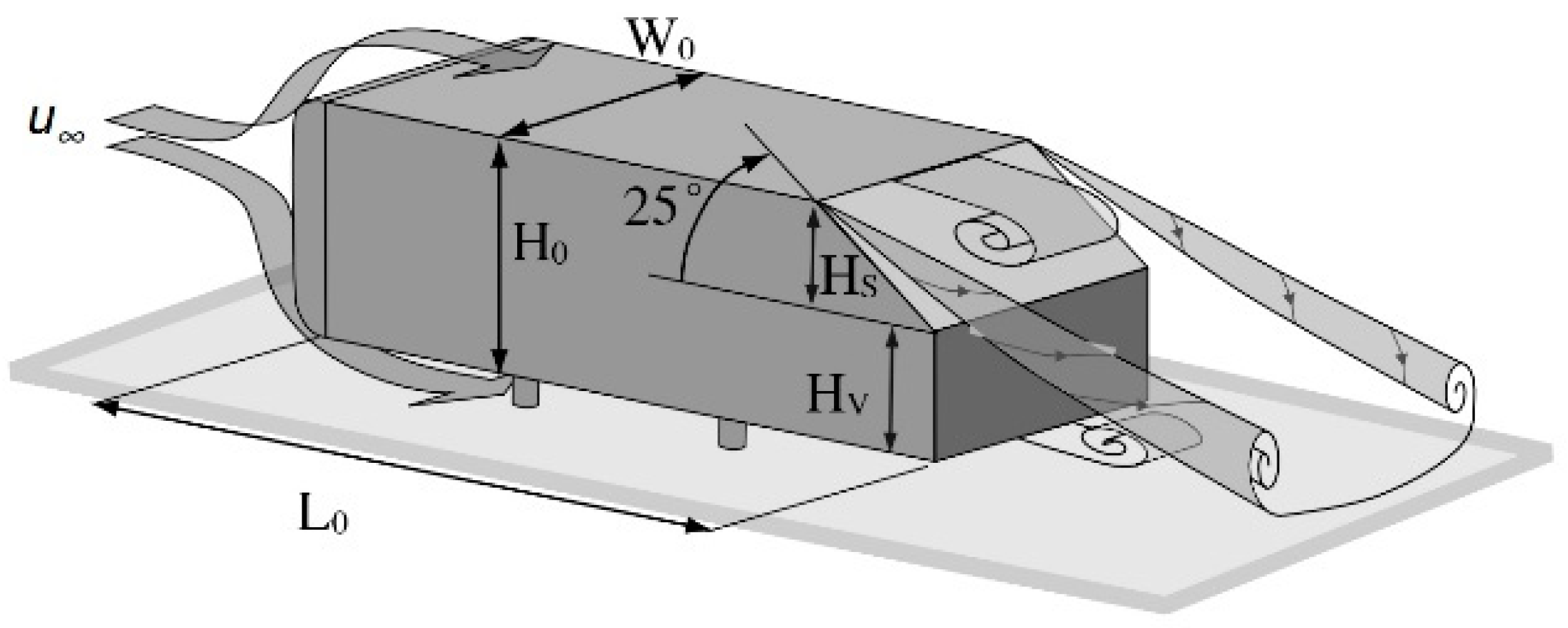
2.1. Vehicle Geometry
2.2. Wind Tunnel and Measuring Instrument
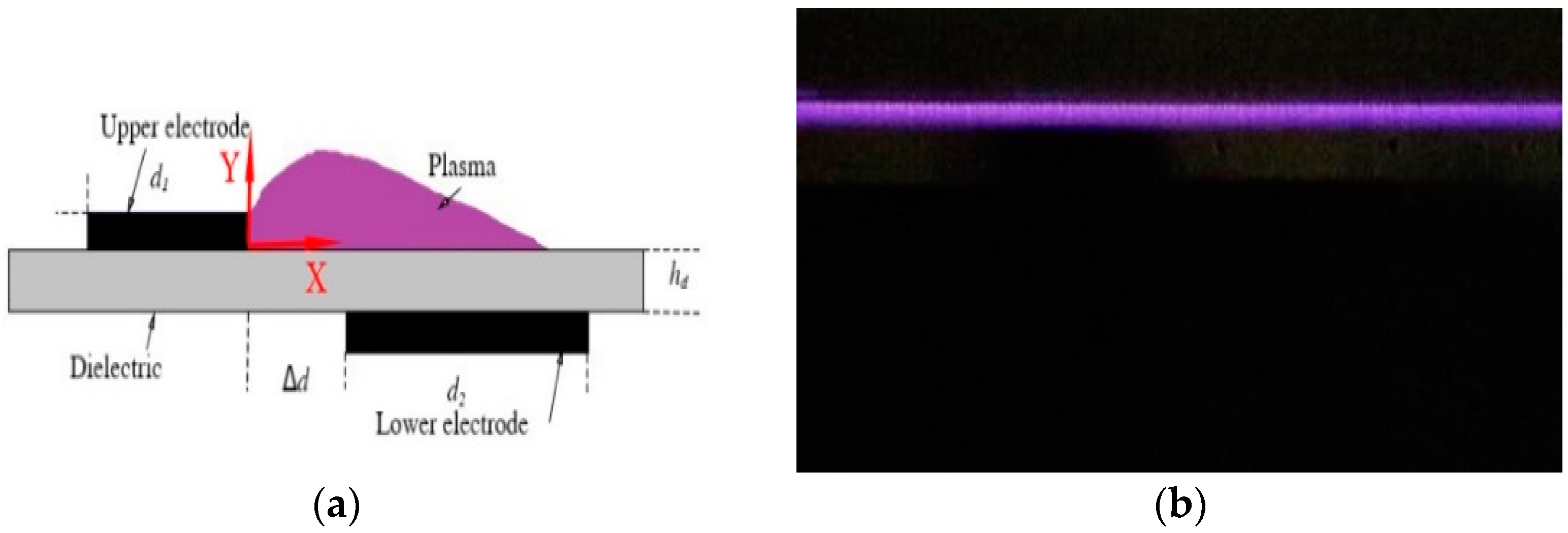
2.3. SDBD Plasma Actuator
3. Aerodynamic Characteristics of the Ionic Wind Induced by the SDBD Actuator
3.1. Arrangement of the Quiescent Flow Test
3.2. Velocity Measurement
4. Wake Flow Control of the Ahmed Body
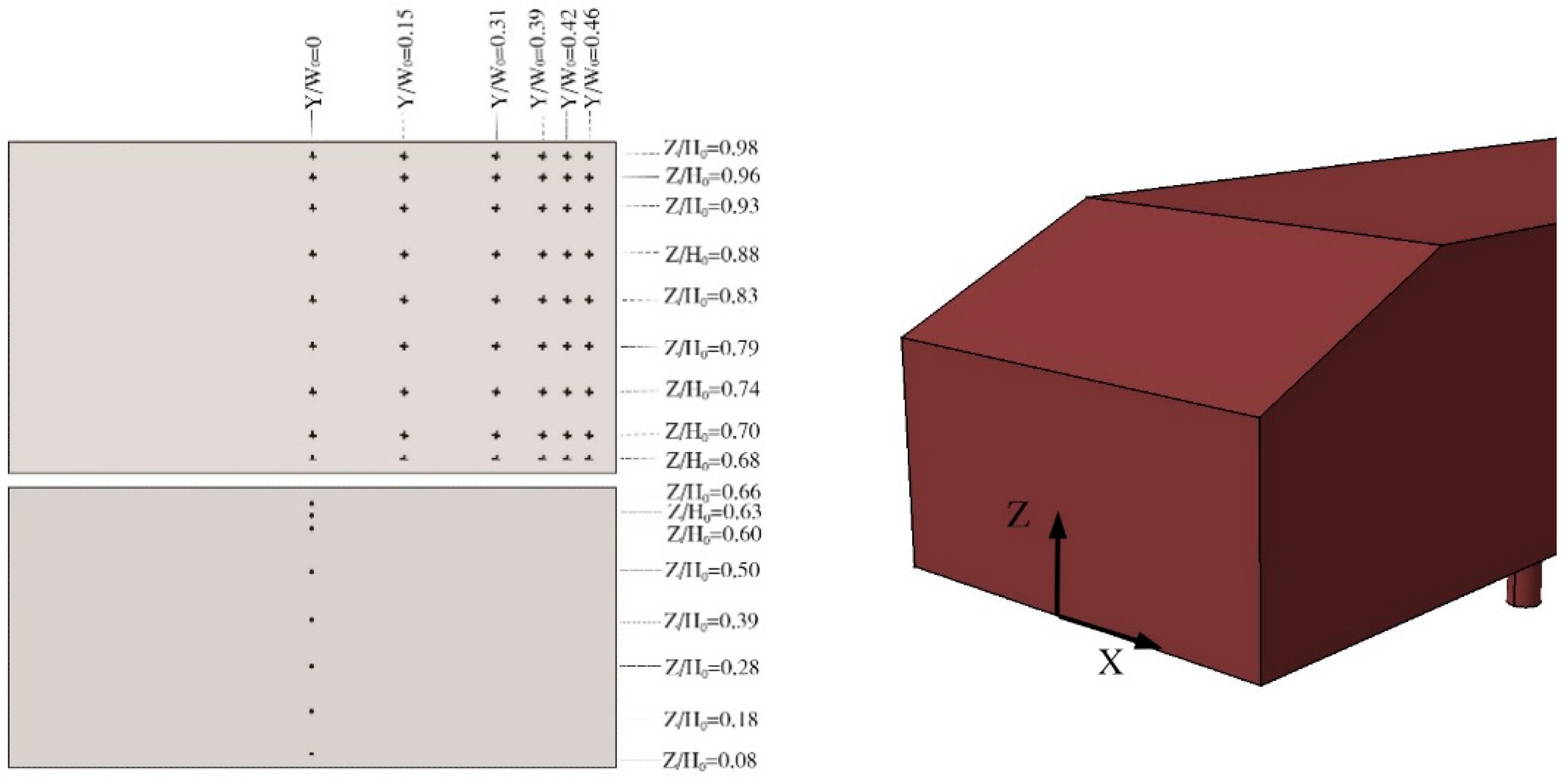
4.1. Arrangement of the Wind Tunnel Experiment
4.2. Control Effect under Different Positions of the Actuator
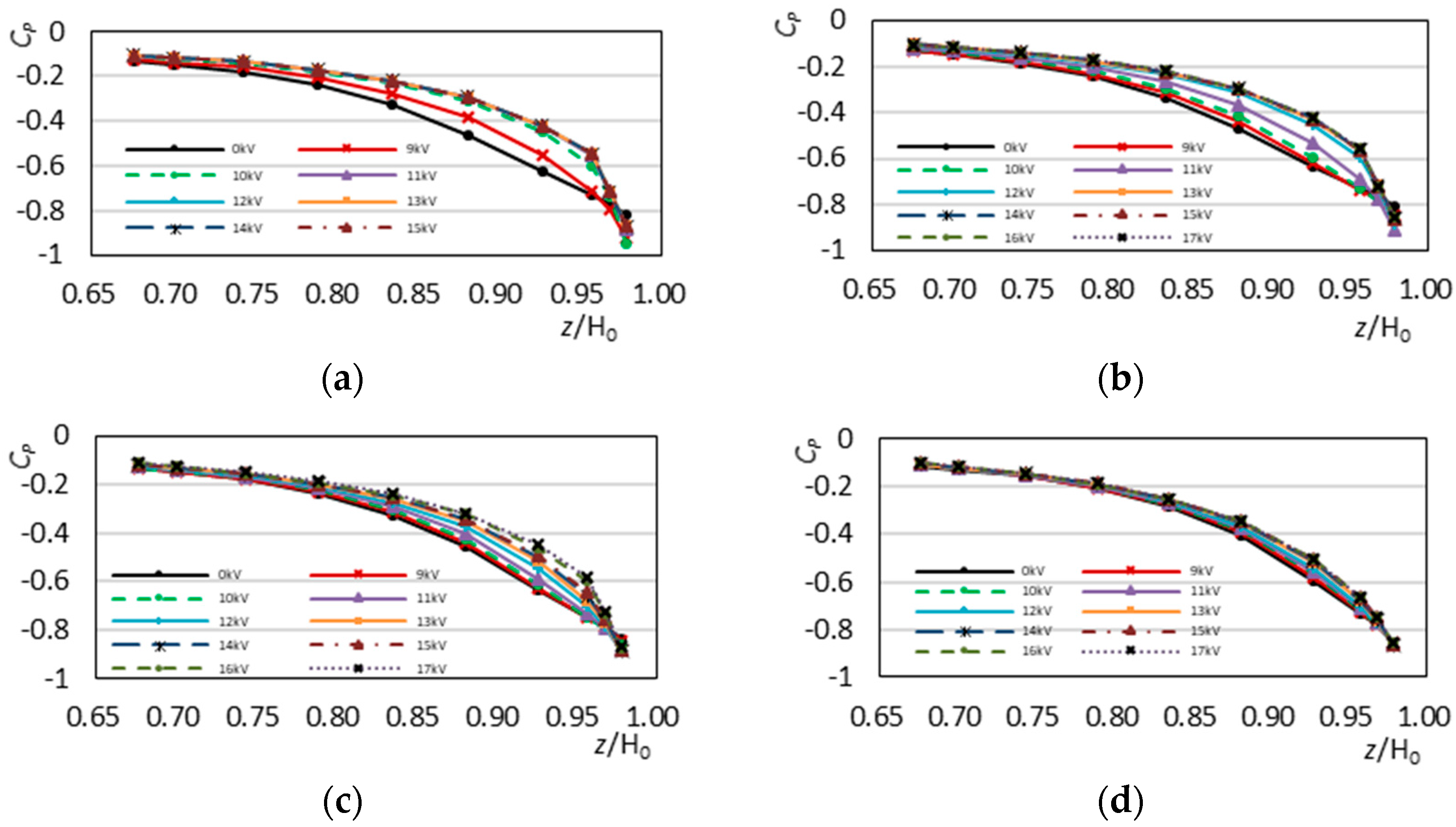
4.3. Control Effect under Different Excitation Voltages
4.4. Control Effect at Different Wind Speeds
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hu, X.; Yang, B.; Lei, Y.; Wang, J.; Li, X.; Liao, L.; Xu, T. Automotive shape optimization using the radial basis function model based on a parametric surface grid. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2016, 230, 1808–1821. [Google Scholar] [CrossRef]
- Fourrie, G.; Keirsbulck, L.; Labraga, L.; Gilliéron, P. Bluff-body drag reduction using a deflector. Exp. Fluids 2011, 50, 385–395. [Google Scholar] [CrossRef]
- Kourta, A.; Leclerc, C. Characterization of synthetic jet actuation with application to Ahmed body wake. Sens. Actuators A Phys. 2013, 192, 13–26. [Google Scholar] [CrossRef]
- Barros, D.; Borée, J.; Noack, B.R.; Spohn, A.; Ruiz, T. Bluff body drag manipulation using pulsed jets and coanda effect. J. Fluid Mech. 2016, 805, 422–459. [Google Scholar] [CrossRef]
- Lu, W.; Huang, G.; Wang, J.; Yang, Y. Interpretation of Four Unique Phenomena and the Mechanism in Unsteady Flow Separation Controls. Energies 2019, 12, 587. [Google Scholar] [CrossRef]
- Metka, M.; Gregory, J.W. Drag Reduction on the 25-deg Ahmed Model Using Fluidic Oscillators. J. Fluids Eng. 2015, 137, 051108. [Google Scholar] [CrossRef]
- Benard, N.; Moreau, E. Electrical and mechanical characteristics of surface AC dielectric barrier discharge plasma actuators applied to airflow control. Exp. Fluids 2014, 55, 1846. [Google Scholar] [CrossRef]
- Moreau, E.; Debien, A.; Breux, J.M.; Benard, N. Control of a turbulent flow separated at mid-chord along an airfoil with DBD plasma actuators. J. Electrost. 2016, 83, 78–87. [Google Scholar] [CrossRef]
- Moreau, E. Airflow control by non-thermal plasma actuators. J. Phys. D (Appl. Phys.) 2007, 40, 605–636. [Google Scholar] [CrossRef]
- Rodrigues, F.; Mushyam, A.; Pascoa, J.; Trancossi, M. A new plasma actuator configuration for improved efficiency: The stair-shaped dielectric barrier discharge actuator. J. Phys. D Appl. Phys. 2019, 52, 385201. [Google Scholar] [CrossRef]
- Suzen, Y.B.; Huang, P.G.; Jacob, J.D.; Ashpis, D.E. Numerical simulations of plasma based flow control applications. In Proceedings of the 35th Fluid Dynamics Conference and Exhibit, AIAA 2005–4633, Toronto, ON, Canada, 6–9 June 2005. [Google Scholar]
- Kriegseis, J.; Duchmann, A.; Tropea, C.; Grundmann, S. On the classification of dielectric barrier discharge plasma actuators: A comprehensive performance evaluation study. J. Appl. Phys. 2013, 114, 053301. [Google Scholar] [CrossRef]
- He, C.; Corke, T.C.; Patel, M.P. Numerical and Experimental Analysis of Plasma Flow Control over a Hump Model. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, AIAA 2007–0935, Reno, NV, USA, 8–11 January 2007. [Google Scholar]
- Boeuf, J.P.; Lagmich, Y.; Pitchford, L.C. Contribution of positive and negative ions to the electrohydrodynamic force in a dielectric barrier discharge plasma actuator operating in air. J. Appl. Phys. 2009, 106, 023115. [Google Scholar] [CrossRef]
- Magnier, P.; Hong, D.; Leroy-Chesneau, A.; Bauchire, J.M.; Hureau, J. Control of separated flows with the ionic wind generated by a DC corona discharge. Exp. Fluids 2007, 42, 815–825. [Google Scholar] [CrossRef][Green Version]
- Boucinha, V.; Magnier, P.; Régine, W.; Leroy-Chesneau, A.; Joussot, R. Characterization of the Ionic Wind Induced by a Sine DBD Actuator Used for Laminar-to-Turbulent Transition Delay. In Proceedings of the 4th Flow Control Conference, AIAA 2008–4210, Seattle, WA, USA, 23–26 June 2008. [Google Scholar]
- Komuro, A.; Takashima, K.; Suzuki, K.; Kanno, S.; Nonomura, T.; Kaneko, T.; Ando, A.; Asai, K. Influence of discharge energy on the lift and drag forces induced by a nanosecond-pulse-driven plasma actuator. Plasma Sources Sci. Technol. 2019, 28, 065006. [Google Scholar] [CrossRef]
- Fukumoto, H.; Aono, H.; Watanabe, T.; Tanaka, M.; Matsuda, H.; Osako, T.; Nonomura, T.; Oyama, A.; Fujii, K. Control of dynamic flowfield around a pitching NACA633−618 airfoil by a DBD plasma actuator. Int. J. Heat Fluid Flow 2016, 62, 10–23. [Google Scholar] [CrossRef]
- Abdollahzadeh, M.; Pascoa, J.C.; Oliveir, P.J. Comparison of DBD plasma actuators flow control authority in different modes of actuation. Aerosp. Sci. Technol. 2018, 78, 183–196. [Google Scholar] [CrossRef]
- Al-Sadawi, L.; Chong, T.P.; Kim, J.H. Aerodynamic noise reduction by plasma actuators for a flat plate with blunt trailing edge. J. Sound Vib. 2019, 439, 173–193. [Google Scholar] [CrossRef]
- Cai, J.; Tian, Y.; Meng, X.; Han, X.; Zhang, D.; Hu, H. An experimental study of icing control using DBD plasma actuator. Exp. Fluids 2017, 58, 102. [Google Scholar] [CrossRef]
- Kim, T.; Yun, S. Aerodynamic drag reduction of 3D train model using dielectric barrier discharge plasma actuators. In Proceedings of the 21th International Symposium on Plasma Chemistry (ISPC 21), Cairns Convention Centre, Queensland, Australia, 4–9 August 2013. [Google Scholar]
- Vernet, J.A.; Örlü, R.; Söderblom, D.; Elofsson, P.; Alfredsson, P.H. Plasma streamwise vortex generators for flow separation control on trucks. Flow Turbul. Combust 2018, 100, 1101–1109. [Google Scholar] [CrossRef]
- Roy, S.; Zhao, P.; Dasgupta, A.; Soni, J. Dielectric barrier discharge actuator for vehicle drag reduction at highway speeds. AIP Adv. 2016, 6, 025322. [Google Scholar] [CrossRef]
- Krajnovic, S.; Basara, B. LES of the flow around Ahmed body with active flow control. Turbul. Interact. 2010, 110, 247–254. [Google Scholar]
- Boucinha, V.; Weber, R.; Kourta, A. Drag reduction of a 3D bluff body using plasma actuators. Int. J. Aerodyn. 2011, 1, 262–281. [Google Scholar] [CrossRef]
- Shadmani, S.; Mojtaba, M.; Mojtaba Mousavi Nainiyan, S.; Mirzaei, M.; Ghasemiasl, R.; Pouryoussefi, S.G. Experimental Investigation of Flow Control Over an Ahmed Body Using DBD Plasma Actuator. J. Appl. Fluid Mech. 2018, 11, 1267–1276. [Google Scholar] [CrossRef]
- Ahmed, S.R.; Ramm, G.; Faltin, G. Some salient features of the time-averaged ground vehicle wake. In Proceedings of the SAE Technical Paper Series, International Congress and Exposition, Detroit, MI, USA, 27 February–2 March 1984. [Google Scholar]
- Hucho, W.H. Aerodynamics of Road Vehicles; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Brunn, A.; Wassen, E.; Sperber, D.; Nitsche, W.; Thiele, F. Active drag control for a generic car model. Notes Numer. Fluid Mech. Multidiscip. Des. 2007, 95, 247–259. [Google Scholar]
- Qi, X.; Yang, L.; Yan, H.; Jin, Y.; Hua, Y.; Ren, C. Experimental study on surface dielectric barrier discharge plasma actuator with different encapsulated electrode widths for airflow control at atmospheric pressure. Plasma Sci. Technol. 2016, 18, 1005–1011. [Google Scholar] [CrossRef]
- Gao, G.; Dong, L.; Peng, K.; Wei, W.; Li, C.; Wu, G. Comparison of the surface dielectric barrier discharge characteristics under different electrode gaps. Phys. Plasmas 2017, 24, 013510. [Google Scholar] [CrossRef]
- Forte, M.; Jolibois, J.; Pons, J.; Moreau, E.; Touchard, G.; Cazalens, M. Optimization of a dielectric barrier discharge actuator by stationary and non-stationary measurements of the induced flow velocity: Application to airflow control. Exp. Fluids 2007, 43, 917–928. [Google Scholar] [CrossRef]
- Li, Z.; Hu, B.; Lan, S.; Zhang, J.; Huang, J. Control of turbulent channel flow using a plasma-based body force. Comput. Fluids 2015, 119, 26–36. [Google Scholar] [CrossRef]
- Dalvand, E.; Ebrahimi, S.M.; Pouryoussefi, S.G. Experimental investigation, modeling and prediction of transition from uniform discharge to filamentary discharge in DBD plasma actuators using artificial neural network. Appl. Therm. Eng. 2018, 129, 50–61. [Google Scholar] [CrossRef]
- Sato, M.; Aono, H.; Yakeno, A.; Nonomura, T.; Fujii, K. Multifactorial Effects of Operating Conditions of Dielectric-Barrier-Discharge Plasma Actuator on Laminar-Separated-Flow Control. AIAA J. 2015, 1–16. [Google Scholar] [CrossRef]
- Joseph, P.; Amandolese, X.; Aider, J. Drag reduction on the 25° slant angle Ahmed reference body using pulsed jets. Exp. Fluids 2012, 52, 1169–1185. [Google Scholar] [CrossRef]
- Aubrun, S.; Mcnally, J.; Alvi, F.; Kourta, A. Separation flow control on a generic ground vehicle using steady microjet arrays. Exp. Fluids 2011, 51, 1177–1187. [Google Scholar] [CrossRef]

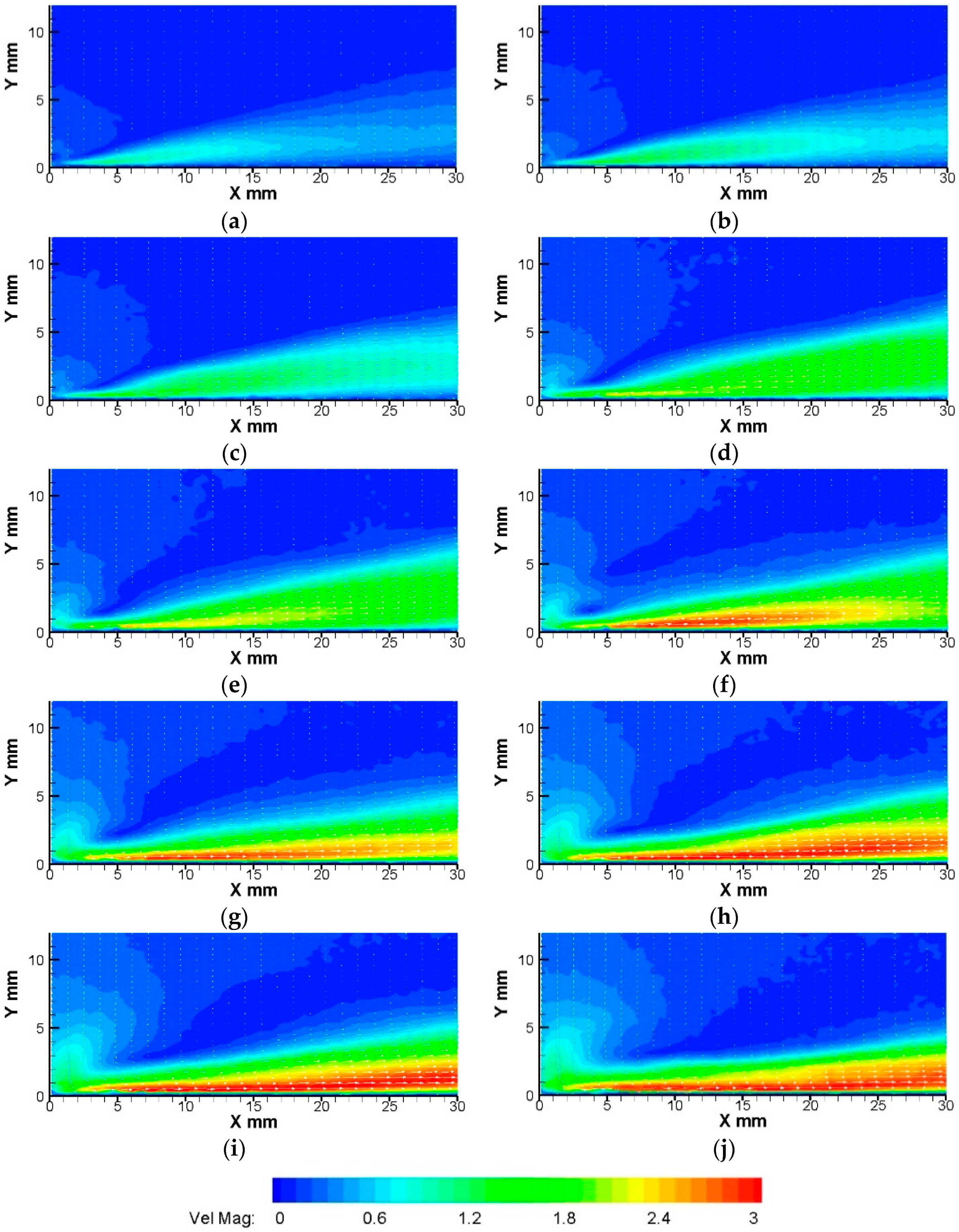


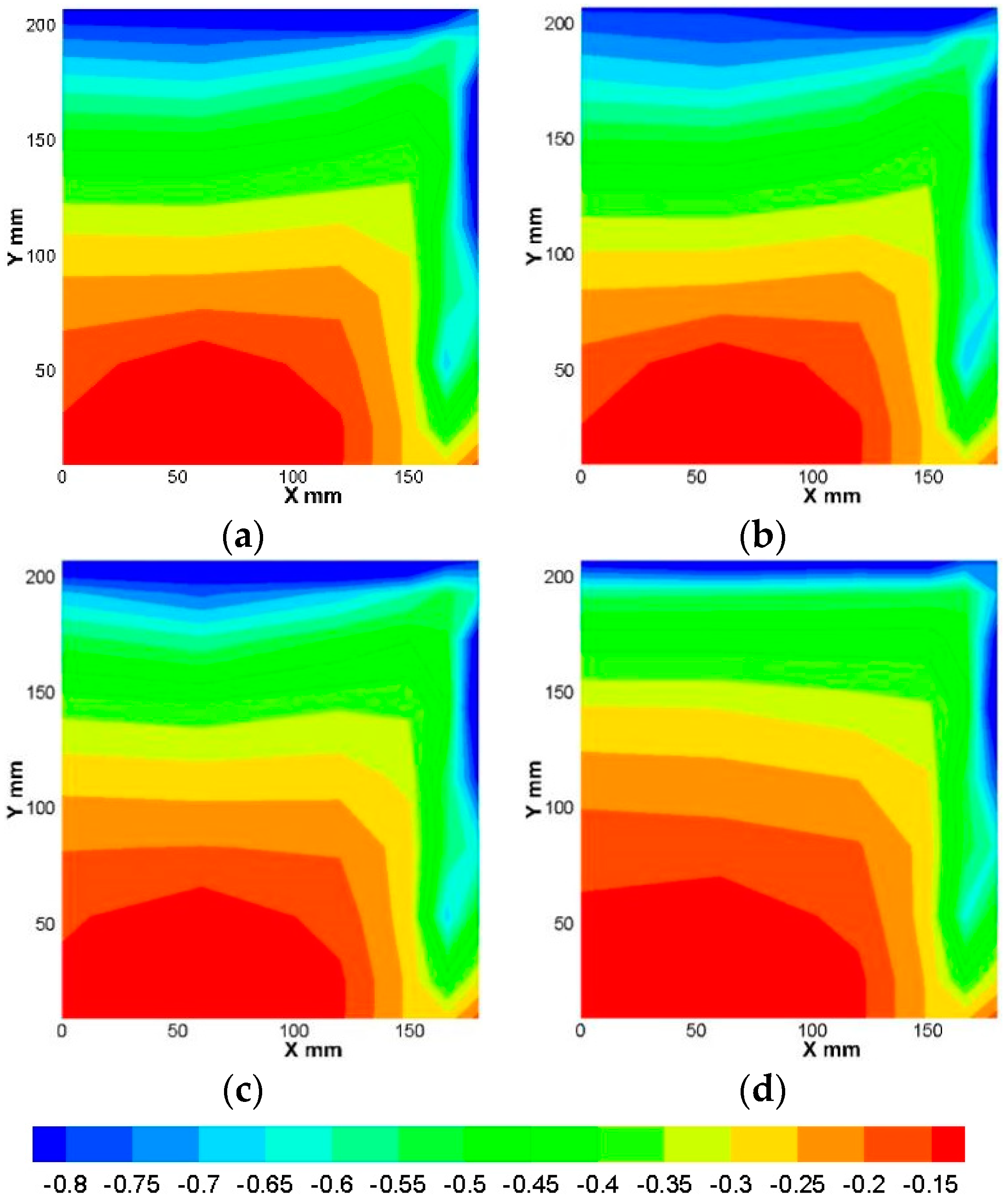
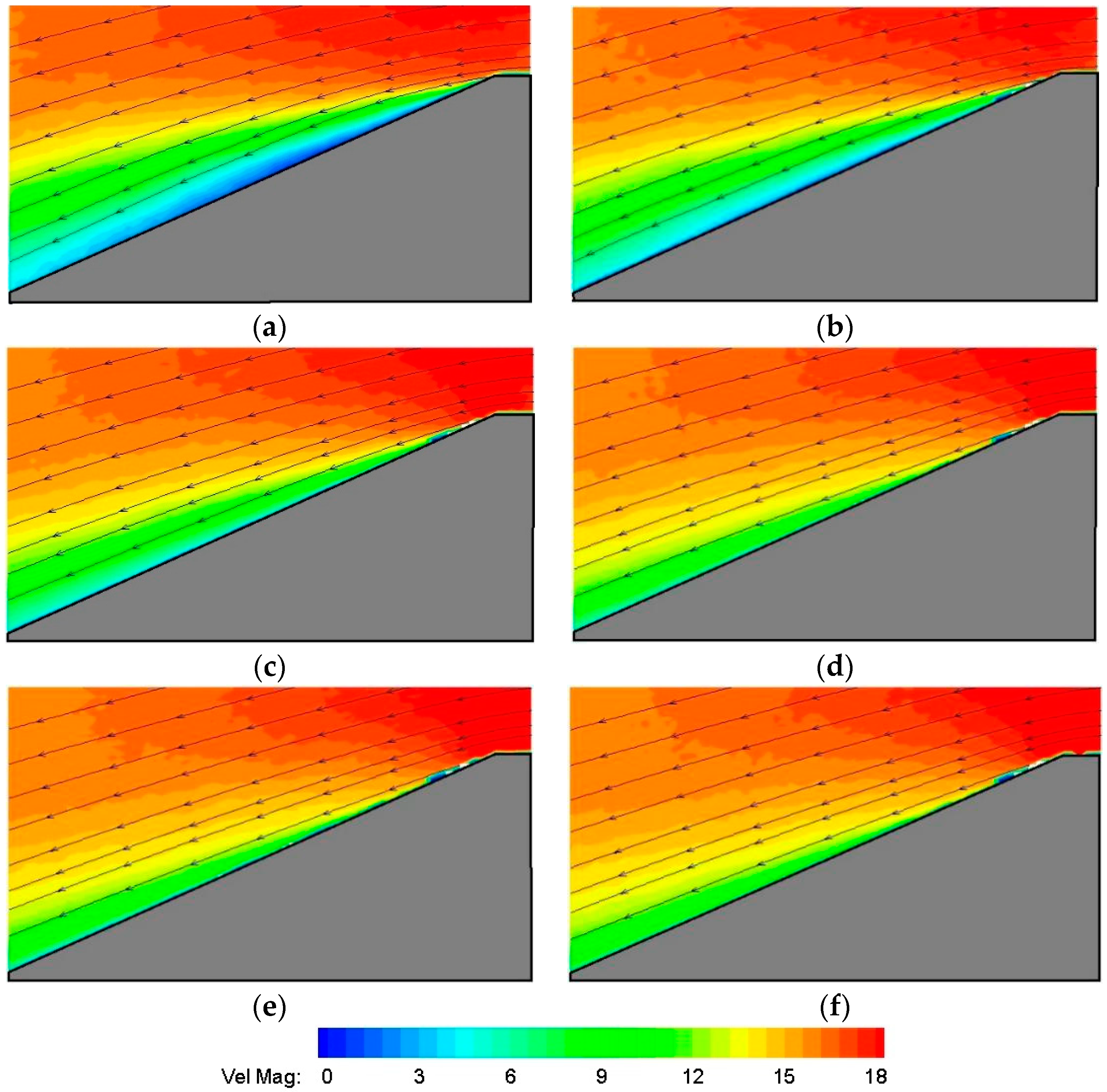
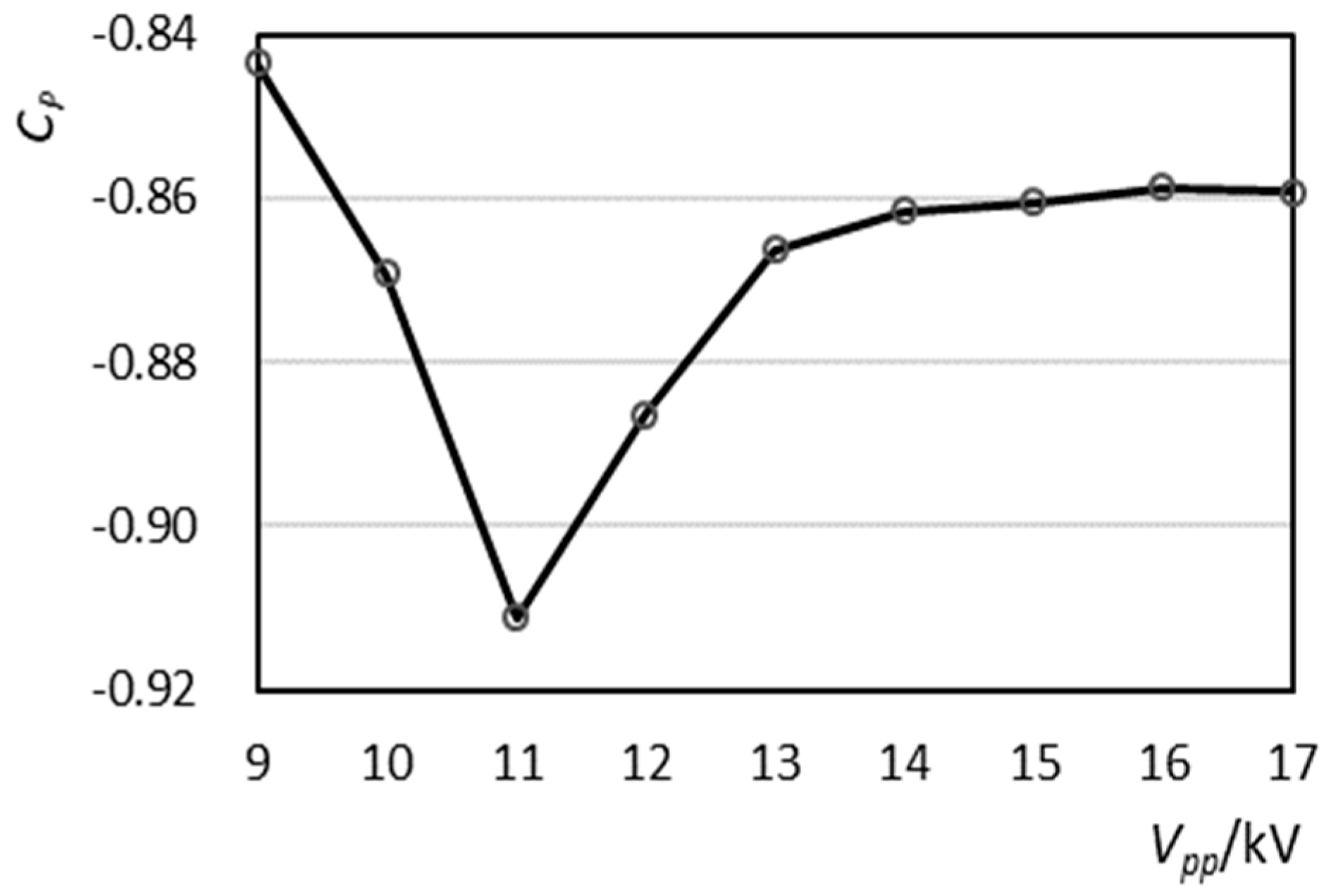
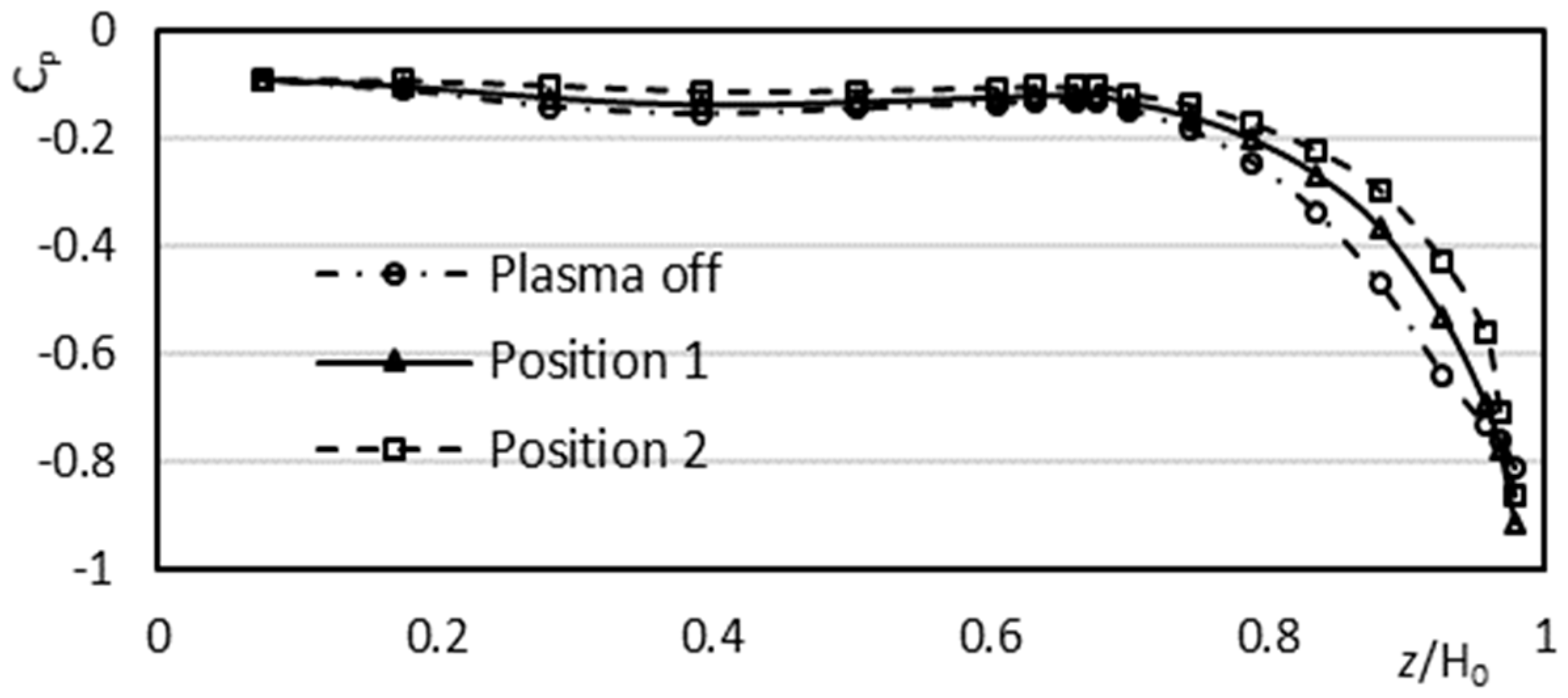
| Vpp (kV) | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| Umax (m/s) | 1.32 | 1.56 | 1.71 | 2.40 | 2.54 | 3.01 | 3.10 | 3.16 | 3.30 | 3.22 |
| U∞ (m/s) | 10 | 15 | 20 | 25 |
| ∆Cdmax (%) | −7.92 | −7.87 | −6.20 | −2.91 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hui, Z.; Hu, X.; Guo, P.; Wang, Z.; Wang, J. Separation Flow Control of a Generic Ground Vehicle Using an SDBD Plasma Actuator. Energies 2019, 12, 3805. https://doi.org/10.3390/en12203805
Hui Z, Hu X, Guo P, Wang Z, Wang J. Separation Flow Control of a Generic Ground Vehicle Using an SDBD Plasma Actuator. Energies. 2019; 12(20):3805. https://doi.org/10.3390/en12203805
Chicago/Turabian StyleHui, Zheng, Xingjun Hu, Peng Guo, Zewei Wang, and Jingyu Wang. 2019. "Separation Flow Control of a Generic Ground Vehicle Using an SDBD Plasma Actuator" Energies 12, no. 20: 3805. https://doi.org/10.3390/en12203805
APA StyleHui, Z., Hu, X., Guo, P., Wang, Z., & Wang, J. (2019). Separation Flow Control of a Generic Ground Vehicle Using an SDBD Plasma Actuator. Energies, 12(20), 3805. https://doi.org/10.3390/en12203805





