Abstract
In this paper, the discrete phase model (DPM) was introduced to study the fuel injector cavitations process and the macro spray characteristic of three different types of nozzle spray shape with diesel and hybrid biofuel blend for several injection pressures and backpressures. The three types of nozzle spray shapes used were circle, elliptical A type, and elliptical B type. The cavitations’ flows inside the injector nozzles were simulated with Computer Fluid Dynamics (CFD) simulations using the cavitations mixture approach. The effect of nozzle spray shape towards the spray characteristic of hybrid biofuel blends is analyzed and compared with the standard diesel. Furthermore, a verification and validation from both the experimental results and numerical results are also presented. The nozzle flow simulation results indicated that the fuel type did not affect the cavitation area vastly, but were more dependent on the nozzle spray shape. In addition, the spray width of the elliptical nozzle shape was higher as compared to the circular spray. Moreover, as the backpressure increased, the spray width downstream increased as well. The spray tip penetration for the elliptical nozzle shape was shorter than the circular nozzle shape due to circular nozzles having smaller nozzle widths and lesser spray cone angles. Thus, this resulted in smaller aerodynamic drag.
1. Introduction
The atomization and fuel spray characteristics play a vital part in direct injection diesel engines especially for gas emissions and combustion efficiency [1]. In recent years, the fuel injection system shows development toward high injection pressure with a small hole injector in order to follow the requirements of Europe 6 and the regulations of low emissions. Hence, the turbulence intensity and velocity of the fuel injection system becomes greater and the fuel and air interaction is more complicated when compared with traditional system. Furthermore, straight vegetable oils (SVOs) have received considerable attention as alternative energy sources for engines. This popularity is based on its identical material characteristics to diesel fuel and it is also biodegradable, non-toxic, renewable, and has lower sulphur production [2]. The biodiesel is usually used as a renewable clean source due to its promising ability to reduce the soot emission in diesel engines. Thus, it is crucial to investigate the fuel injector nozzle effect and the mechanism of spray characteristics with different types of fuel. Furthermore, the fuel injector experiences energy loss and leakage under extreme high injection pressure [3]. In another preliminary study, Hussain et al. [4] proposed that the elliptic jets of different aspect ratios changed the entrainment and other turbulence phenomena, which is useful in increasing the diesel engine performance. The biodiesel can be used as an alternative fuel due to it having lower volatility, a higher oxygen percentage, and a narrow boiling point [5,6].
There are several techniques that are used to produce biodiesel, such as preheating, blending, micro-emulsion, and trans-esterification. Currently, the trans-esterification is the most widely utilized method due to its capability to decrease the viscosity and change the triglycerides into glycerol and fatty acid methyl ester [7,8,9]. However, the trans-esterification method is very costly and is coupled with a complex process that requires specific instruments and equipment. Moreover, crude glycerol also produces by-products during the process. Hence, a costly purification mechanism is required to yield pure glycerol, which has superior product properties than the crude glycerol [10]. Furthermore, the viscosity of SVO can be reduced effectively and economically by blending the SVO with other lower viscosity fuels. In general, biodiesel has a greater viscosity and density than fossil diesel [11]. Furthermore, the cavitations and evaporation properties of biodiesel are dissimilar as compared to diesel due to its high molecular mass properties [10,12,13]. It was found that the mixed fuel has nearly the same operation qualities with diesel fuel but a high consumption of brake-specific fuel. They have claimed that this is mainly caused by low calorific value (CV) of the blend, which leads to a drop in engine performance. However, the emission of NOx was identified to be smaller compared to the diesel.
Various studies have been reported on emissions and combustion when biodiesel is used, especially from the experimental perspective. Desantes et al. [14] provided an in-depth analysis of the influence of using biodiesel blended fuels in a standard injection system using experimental work. The long injection test results showed that the biodiesel spray pattern was affected by longer spray tip penetration and a smaller spray cone angle. For short injection periods, they observed a decrease in fuel mass injection because of the high fuel viscosity. Nearly identical results were also reported by Priesching et al. [15] in their study of the influence of biodiesel blends on the mixture formation. They identified that the same mass flow was produced by the temperatures of diesel and biodiesel at high engine loads. Allocca et al. [16] studied various biofuel performance characteristics, which focused on the temperature effect. The experimental results indicated that a lower cone angle and tip penetration were achieved at ambient temperature; meanwhile, the respective simulation results showed better performances compared to the experimental observations. Thomas [17] conducted a study on the effect of a biodiesel fuel injector to the tip deposits on transport refrigeration units (TRU). He found that the injector tip deposit of biodiesel was not affected by the conventional fuel detergent additive. Furthermore, Ramadhas et al. [18] carried out engine tests with biodiesel and highlighted the modification on diesel engine is not needed to operate biodiesel-blended fuels.
Numerical studies on the nozzle spray behaviors of biofuel are rarely found in previous research, which focuses on the experimental works. Mohan et al. [19] reported the spray characteristics of ether fuels by using a new hybrid spray model in KIVA4 CFD code. They found that ether fuels required more fuel amount to attain similar power output compared to diesel fuel. The simulation result shows that the atomization’s of ether fuels are greater than diesel due to a high Reynolds number and low Ohnesorge number of ether fuel. Another report on a numerical study of spray and combustion characteristics of diesel was conducted by Lee and Huh [20], who have been using a Conditional Moment Closure Incompletely Stirred Reactor (CMC-ISR) model to capture the chemistry coupling between with turbulence flow. The analysis of hydro grinding effects and hole shapes on biodiesel spray using experiments and simulation was studied by Som et al. [21]. The study provides readers some understanding on the turbulence levels inside the nozzle orifice when the orifice geometry is changed. The fuel primary breakup, spray penetration, and dispersion are strongly influenced by hydro grinding and conicity behaviors. Similarly, Mohan et al. [22] investigated the spray characteristics of dimethyl ether (DME) and diethyl ether (DEE) by using KIVA-4 CFD software. The study proved that the spray tip penetration of ether fuel was shorter than diesel due to the low viscosity and density of ether fuel. However, the diesel fuel characterized by a high Ohnesorge number and low Reynolds number exhibited poor atomization behavior compared to the ether fuel. Recently, Zhou et al. [23] performed a numerical study on the spray of R404A by using the OPENFOAM software. Their results showed that the droplet diameter and spray morphology were nearly identical with those done in the experiment. Furthermore, the spray profile, penetration distance, and velocity were significantly affected by the ambient pressure. In addition, a study on characteristic of diesel and biodiesel with effect on spray angle had been undertaken by Kegl et al. [24]. Their results demonstrated that cavitations in the nozzle hole and chamber pressures affected the fuel spray properties.
Numerous numerical methods have been utilized to simulate fuel spray characteristics, for example, the finite volume method (FVM) [19,22,25] and finite element method (FEM) [26,27]. In this study, the discrete phase method (DPM) with FVM was utilized to capture the motion of the fuel droplet particle. By using the DPM, this study will offer a powerful tool for upcoming investigations that establishes simulations of spray characteristics regarding the effect of nozzle spray shape and fuel properties. Recent studies by researchers [28,29,30,31] suggest that DPM has the potential to simulate particle trajectory in a continuous phase.
Generally, it can be observed that the fuel spray characteristics of hybrid biofuel and elliptical orifice jets have still not been fully explored, particularly for spray behavior and performance as stated in this brief literature review. The elliptical nozzle is promising and beneficial in enhancing the performance of sprays. Moreover, there is less literature on the comparative investigation of the mechanism of injector and spray atomization behavior with a standard diesel and hybrid biofuel under realistic diesel engine and high-pressure conditions. Furthermore, previous studies used the nozzle shape size with diameters (0.3–3 mm) that were relatively larger from the standard diesel nozzle (0.1–0.2 mm). This research aims to analyze and compare the fuel injector and spray characteristics of three different types of nozzle spray shape, which are circle, elliptical A type, and elliptical B type using diesel and hybrid biofuel under various injection pressures (50 MPa, 1000 MPa, 180 MPa) and backpressures (1 MPa, 3 MPa). Both numerical and experimental studies will be compared in order to enhance the validity of the current research work.
2. Mathematical Model
2.1. Injector Flow Phase
The numerical calculations in this research were performed using Fluent version 18 CFD software. The bidirectional interactions among multi-phase flow and particle are used for the 3-D simulation of spray characteristics. The multiphase flow was described using the mixture model, which considered that vapor and liquid phases were mixed uniformly. The governing equations for the continuous flow of the fuel in the injector consist of the continuity, momentum, and energy equation that solved the Navier–Stokes equations. The equations are listed as follow:
Continuity equation:
The conservation of momentum is described using:
The conservation of energy can be expressed as:
Where ρ is the fluid density, ui is the fluid velocity, is the shear stress, and gi = −9.81 m/s is the gravitational acceleration at the earth’s surface.
The shear–stress transport (SST) k-ω solver was utilized for the entire turbulence model investigations described in this work. The model was chosen because it has advantages for boundary layer problems, plus it is more accurate and robust compared to other turbulence models [32]. The shear–stress transport (SST) k-ω model solves the turbulence kinetic energy (k) and the dissipation rate (ω), respectively. They are obtained from the transport equation and given as follows:
In this study, the enhanced wall treatment model approach was used to capture the behavior of flow near the wall, which had a no-slip condition. This effect had a significant impact on the fidelity of the numerical simulation.
2.2. Discrete Particle Phase
For the spray development simulation, DPM was used to capture the flow of vapour formation and the atomization phase. The Navier–Stokes equations and continuity equation were solved to compute the continuous phase, whereas the force balance on the particle was integrated into the solver to calculate the trajectories of particles. For a two-way interaction, the continuous phase was calculated based on the Eulerian model, whereas the particle trajectories were calculated based on the result of the continuous flow. The two-way coupling of process scheme is shown in Figure 1.
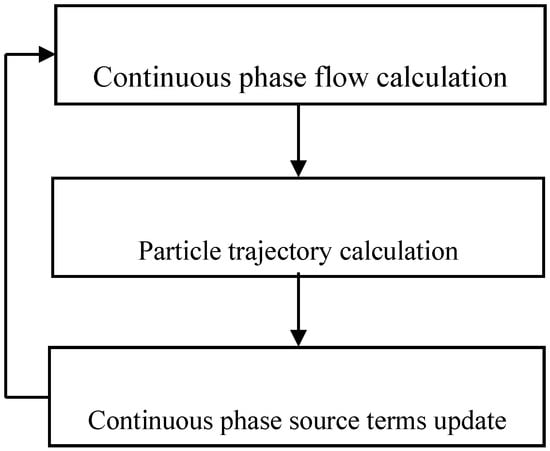
Figure 1.
Coupling scheme.
The particle force balance, which is related to inertia and additional forces, can be expressed as:
Particle force balance:
where, p is the particle density and pp is the fluid density; u is the velocity of the particle and up is the velocity of the fluid phase; Fx is the other forces that interact with the particles due to mass, acceleration, and pressure; and FD (u − up) is the drag force that equates to each of the particles, where FD is defined as:
where µ is the fluid molecular viscosity, ρp is the particle density, CD is the particles drag coefficient, Re is the Reynolds number, and dp is the particle diameter of the droplets that are assumed as spheres in this study. The equation for CD is given as:
where α1, α2, and α3 are constants based on the ranges of Reynolds number.
In the two-way coupling, the momentum, heat, and mass can be transferred during continuous and discrete phase. The momentum exchanged from the continuous phase to the discrete phase is calculated by computing the momentum difference when the particle enters the control volume. The change in momentum equation can be expressed as:
where Fother is the additional interaction forces, Δt is the time step, and ṁp is the particle mass flow rates. The particle trajectory can be calculated using:
The droplet experiences the thermophoresis force when it is heated. Thermophoresis is the phenomena where a small particle of gas experiences a force in the direction opposite to temperature gradient. Equation (8), using the change of temperature, is given as:
where DT is the thermophoric coefficient, which use the form suggested by Talbot [33]:
Where Kn is the Knudsen number, Tc is the fluid thermal conductivity based on translational energy only, kp is the particle thermal conductivity, mp is the particle mass, µ is the fluid viscosity, Cs = 1.17, Ct = 2.18, and Cm = 1.14.
2.3. Spray Simulations
The spray behaviour is simulated by the DPM where droplets were grouped into packages where individual droplets were defined by same velocity, diameter, pressure, etc. The momentum exchange between continuous flow and DPM was allowed to track each parcel trajectory tracking. A majority of the studies on spray development were focused on evaporation and droplet collision only, whereas the breakup process is acknowledged as one of the important factors. However, it has not been fully solved until today.
The whole breakup process is divided into two processes, which are primary breakup and the secondary breakup. The whole breakup process is handled in two processes due to the diesel engine having a high injection pressure. The primary breakup model is accounted for when the breakup phenomena happens at the nozzle exit where the initial fuel is falling apart into small droplets. Meanwhile, the secondary breakup model is handled from the initial drops until the further breakup process [34]. The whole breakup process is shown in Figure 2. The whole breakup model was calculated using three breakup models. For the primary area, the Kelvin–Helmholtz (KH) model is utilized at the nozzle exit area where the liquid breakup happened, whereas the Taylor analogy breakup (TAB) model is applied to the area beyond the initial primary breakup area. In this study we suggested a third model to be used that combines both KH and TAB model which is called the KH-TAB model.
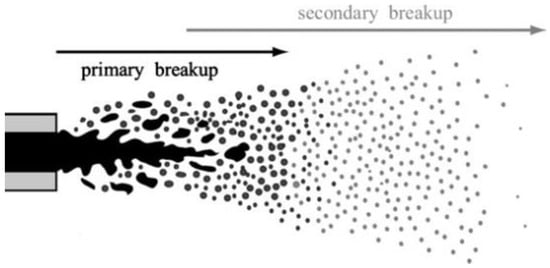
Figure 2.
Primary and secondary breakup processes.
2.3.1. Primary Breakup Modeling
The model for the primary breakup is established according to the combination effects of Kelvin–Helmholtz (KH) waves directed by aerodynamic forces with Rayleigh–Taylor (RT) instabilities that caused secondary breakup [35], as shown in Figure 3. In region A, the KH instability caused the droplet to break from the liquid phase; meanwhile, in region B, the RT instability caused the secondary breakup to happen.
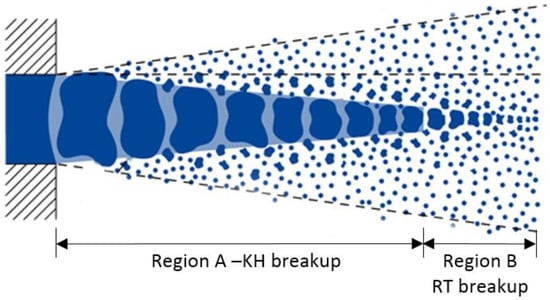
Figure 3.
KHRT breakup model concept.
In the KH breakup model, the frequency (ΩKH) and corresponding wavelength (Λ KH) according to Reitz [36] is calculated using:
where
with ρg denoting the gas density, ρl is the liquid density, σ is surface tension, Ur is the magnitude of velocity between two phases, and vl is the liquid viscosity.
During the breakup process, the critical droplet radius rKH occurred due to a decrease in the droplet radius. Hence, the breakup time τKH and the critical droplet radius rKH are calculated by:
with B0 = 0.61 and Bl = 20.
In the RT model, the frequency of the fastest growing wave (ΩRT) is given by:
where gt is the droplet acceleration. The wave number is computed using:
When the RT waves were propagating, the time becoming larger than the breakup time τRT breakup will occur. The τRT is calculated using:
where Cτ is the Rayleigh–Taylor breakup time constant. Then, the radius of the smaller droplets is given using:
where CRT is the breakup radius constant.
2.3.2. Secondary Breakup Modeling
The model for the secondary breakup is established for the purposes of capturing the mixture of the aerodynamic mechanism during a spray process. In a continuous–phase medium, one of the influential parameters that influences the discrete particles’ behaviour is the Stokes number. The Stokes number is a dimensionless number that indicates the behaviour of discrete particles. The Stokes number equation is defined as:
where u0 is the initial flow velocity, l0 is the characteristic diameter of the obstacle, and t0 is the particle relaxation time.
The discrete particles were kept on track using the fluid streamlines when the Stokes number was low, whereas the discrete particles followed along their initial trajectories when the Stokes number was high. Thus, more particles will be generated with lower Stokes numbers during the breakup process. In this study, the widely used Taylor analogy breakup (TAB) model was used to account for these breakup forces. The TAB model is based upon Taylor’s [37] analogy between an oscillating and distorting droplet and a spring mass system, as seen in Figure 4.
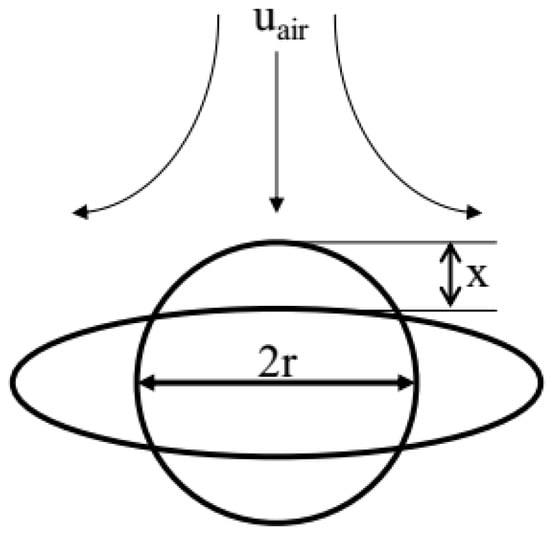
Figure 4.
TAB model analogy [38].
In this model, the equation of droplet motion is given using:
where y is defined using the following:
where:
The mean size of the product droplet is calculated based on the energy conversation of a parent and child droplet analysis. The equation is derived to be:
where the constant z is 10/3.
3. Experimental Procedures
3.1. Fuel Preparation
A blend at mixing ratios of 68% (RP032MC068) of refined palm oil (RPO) with Melaleuca cajuput oil (MCO) was prepared. The emulsifier or surfactant was not used during the blending process. Each mix of RPO with MCO was blended with a stirrer to ensure homogeneity between RPO and MCO. The blends were kept in a glass bottle, stored at ambient temperature and monitored for a phase separation. A Brookfield DV-III Rheometer was used to measure the dynamic viscosity of RPO-MCO blend. The test was done at a maintained temperature of 40 °C. The measured value was taken five times and the mean was calculated. The spray performance, volatility, and quality of fuel atomization were determined using the viscosity properties. A Gay-Lussac pycnometer was used to determine the density of fuel samples. The reading was taken at room temperature (≈27 °C).
3.2. Fuel Properties
For the aim of investigating the effects of nozzle shape on the spray characteristics of diesel and hybrid biofuel, the hybrid biofuel was blended between Melaleuca cajuput oil (MCO) and refined palm oil (RPO) in order to reduce its viscosity, hence improving the atomization of the fuels. The material properties of the diesel and RP032MC068 blends (hybrid biofuel) are listed in Table 1. These results were obtained from tests done at the Faculty of Chemical Engineering, Universiti Sains Malaysia.

Table 1.
Material properties of the diesel and RP032MC068 blends.
3.3. Experiment Setup
The spray visualization system experiment was done to prove the feasibility of the simulation results. The current experimental work was executed with a circular nozzle of diameter equal to 0.16 mm under 50 MPa of pressure and 3 MPa of backpressure. Ambient temperature was established as 27 °C in this study.
Figure 5 depicts the spray test platform diagram for investigating the diesel and hybrid biofuel spray characteristics. The spray test platform consisted of Chevrolet Captiva common rail injection system and an Olympus high speed video camera system. The common rail injection system consisted of a high-pressure pump, pipes, electromotor, and a solenoid type six-hole nozzle (Siemens A2C2002584). Different high injection pressures were achieved at the pump by using the electromotor. A solenoid type six-hole nozzle was mounted at the middle of the injection chamber with a dimension of 30 cm × 30 cm. The images of the spraying moment were recorded using Olympus i-SPEED 2 high speed video camera.
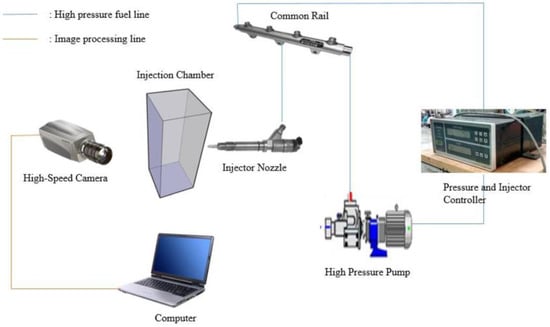
Figure 5.
Visualization spray test platform.
The injection duration or time and the injection pressure were set on the controller unit. In this research, the injection time was fixed at 1 ms and the injection pressure was set at 50 MPa. The motor was turned on and then the spraying of hybrid biofuel started by passing through the injector. Images of the spraying moment were recorded using a high-speed video camera system. The experiment was repeated 10 times for each injection pressure to reduce the fluctuation error. The measurement of the average spray’s penetration length, spray width, and spray angle were obtained and calculated using ImageJ software. Certain images presented in the experiment works were processed with MATLAB to acquire the spray boundary images.
4. Simulation Methodology
A six-hole diesel fuel injector (Siemens A2C2002584) was chosen with nozzle angle of 150°. In order to save computation time, only a single nozzle out of six nozzles was modeled from the evenly distributed injector. The injector diagram and geometry of the nozzle model is shown in Figure 6. In this study, three types of nozzle shape—circle, elliptical A, and elliptical B—were evaluated. The type of injector spray nozzle shape used in this study and the dimensions are summarized in Table 2.

Figure 6.
Injector geometry.

Table 2.
Injector hole geometric characteristics.
In the present study the aspect ratio 1.2 and 1.4 is chosen based on recommendations and works by Lee and Baek [39]. They suggested that the elliptic jets with a small aspect ratio of 2 and lower can be used effectively as a passive control device in engineering applications that need strong mixing and thrust augmentation. The comparison of injector nozzle hole diameters for a commercial diesel engine is shown in Table 3.

Table 3.
Comparison of injector nozzle hole diameter of commercial diesel engine.
The injector model was meshed using a path-conforming meshing method in all the simulation works presented here. This method was selected because of its capability to capture structural complexity with relative ease and creates a very fine mesh to reduce discrete errors. Figure 6 presents the whole mesh produced from the injector model. The hole was meshed with 1,000,000 elements based on the optimum grid independence test result. An interface was created between the mesh hole and the domain volume in order to reduce discrete errors.
The interaction between two phases (air and fuel) was modelled using the DPM. The Euler method was utilized to study the flow field factors such as temperature, pressure, density, and velocity. The shape of spray chosen was the cone model due to its similarity with the real shape of spray in the nozzle. The drag and collision of the particle effect was described via selection of the wave model as the secondary atomization model and was embedded with the O’Rourke collision model and dynamic drag model.
In the analysis, the fuel and air were considered as a different phase. The volume of fluid (VOF) method was used to track the fuel interface during the liquid/vapor phase transition. The SST k-ε turbulence model was chosen because it has been found to provide accurate outcomes for the nozzle cavitations flow and spray characteristics [40]. Moreover, a continuum surface force (CSF) model was utilized to incorporate surface tension in the interaction between fuel and air phases. The surface tension was fixed to a first-degree polynomial that depended on the temperature. An implicit solver was applied for solving the momentum and pressure equations together with the phase continuity equation. The second-order upwind discretization and SIMPLE scheme were used for pressure-velocity coupling. A time-dependent formula was implemented for the phase transition in each time step. The residual error and convergence ratio were set to be in the order of 10−3 to 10−4. The range of time step was set between 1.0 × 10−6 s to 1.0 × 10−8 s. The fuels used for this study are listed in Table 1.
The boundary condition for the injector wall was set as reflective and the domain inside the injector was selected as a no-slip boundary condition. Table 4 shows the additional boundary conditions used during the simulations.

Table 4.
Operating boundary conditions.
Grid Independence Tests
A grid independence test was carried out to examine the stability of the mesh resolution used in the simulation and recognize the optimum mesh condition for a precise computational result. This test is typically performed for the simulation analysis in order to find the adequate number of mesh elements. The simulation was evaluated through the range of meshes from low to extra fine. From the data analysis, the optimum mesh was the mesh resolution that was comprised of an error within a 5% limit. As Figure 7 shows, the optimum mesh utilized during the simulation was the mesh that contains a total number of 1,010,836 cells. Furthermore, the graph illustrates that when the mesh size increased from 1 million to 3.19 million, the discrete error was 1.56%, which was small and well within the 5% standard limit. This 3.19 million mesh grid was chosen in all simulations due to the optimal simulation’s accuracy and low execution time.
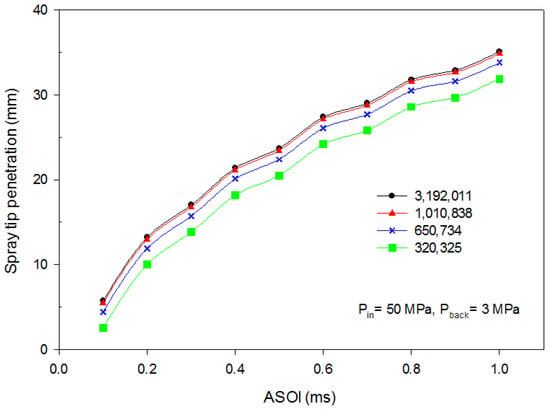
Figure 7.
Summary of grid independence test.
5. Result and Discussion
5.1. Model Validation
The experimental data obtained from the 3-D injector flow and spray simulation were limited due to the cover inside the injector and dense spray cloud formations. Hence, based on the method presented above, a simulation system was developed with ANSYS Fluent. For verification purposes, the experimental results of Yu et al. [41], which used diesel fuel with the same material properties and operating conditions as in the present numerical study, were compared with the simulation results. Furthermore, our experimental results were also included in the results. The operating conditions for the setup were 50 MPa and a backpressure of 3 MPa with 0.16 mm of circular nozzle shape. In this research, the method to calculate spray cone angle was proposed by Pastor et al. [42]. The MATLAB software was used to process the captured spray images from both experiment and simulation and the images were converted into boundary lines as shown in Figure 8, where θ is the spray cone angle, L is the spray tip penetration, and Ws is the widths of the spray cloud, which were denoted as a length between the spray cloud borders.
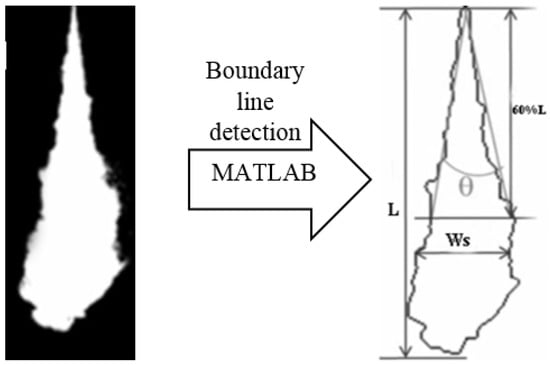
Figure 8.
Spray boundary detection using MATLAB software.
Figure 9 presents the simulation and experimental spray characteristic of a 50 MPa injection pressure and 3 MPa backpressure with a 0.16 mm circular nozzle shape. As shown in Figure 9, the spray characteristic between experiment and simulation were nearly identical at the same ASOI. However, our experimental work has a small deviation between simulation and the experiment from Yu et al. [41] due to the poor resolution of the high-speed camera. Furthermore, it can be found that the experimental spray characteristic shows a coarse pattern at the nozzle exit due to difficulty for the experimental work to capture the small structure in the spray. Nevertheless, the numerical technique was useful to replicate the macro scale characteristics of the spray. Additionally, the quantitative results of spray performances are analyzed in the next section.
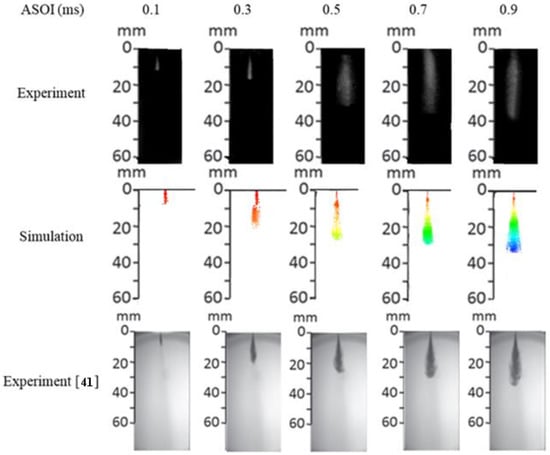
Figure 9.
Comparison of the spray characteristic between simulation and experimental results.
Figure 10 presents the spray tip penetration for a circular nozzle shape with 50 MPa of pressure and 3 MPa of backpressure for both the experiment and simulation. Based on the comparison results displayed in Figure 10, the result shows that almost identical results were obtained between the experiment and numerical simulations for spray tip penetration. Furthermore, the spray tip penetration average error between the experiment by Yu et al. [41], and current experiment and simulations, were 5.16% and 6.33%, respectively.
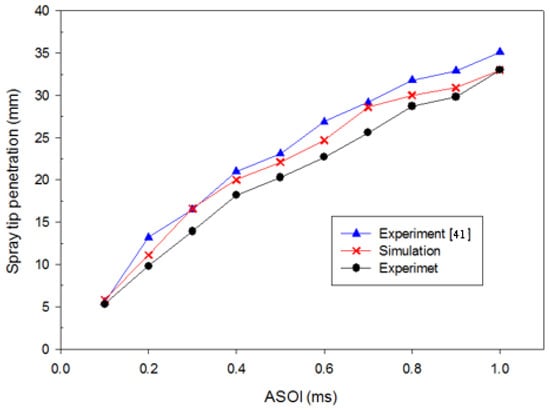
Figure 10.
Spray tip penetration growth for a circular nozzle shape with 50 MPa of pressure and 3 MPa of backpressure for the experiments and simulation.
Figure 11 depicts the spray cone angle for a circular nozzle shape with 50 MPa of pressure and 3 MPa of backpressure for the experiments and simulation. It can be seen from the graph in Figure 11 that the simulation results are quantitatively consistent with the experimental results, and the average discrepancy between experiment by Yu et al. [41], and the current experiment and simulations was within about 3.8% and 7.1%, respectively. Based on the assessment, the advantage of the simulation with Fluent was verified for sufficiently handling the spray formation behaviour. Thus, the present modelling methodology gave reliable predictions for the spray formation behaviour.
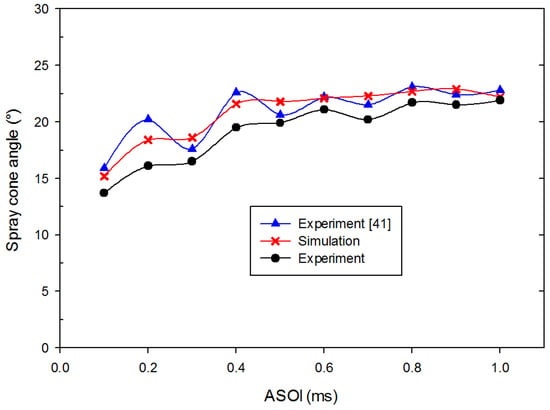
Figure 11.
Evolution of spray cone angle for a circular nozzle shape with 50 MPa of pressure and 3 MPa of backpressure for experiments and simulation.
5.2. Nozzle Flow Simulations
Figure 12 shows the cavitations flow in the diesel nozzle for three different nozzle shapes (circle, elliptical A, elliptical B) and two different fuel (diesel, hybrid biofuel) with the same injection pressure (180 MPa) over a different time. In the figure, the red regions contain 100% of liquid fuel and the blue regions contain pure gaseous fuel. It is apparent from Figure 12 that the cavitations intensity was more intensive for elliptical A and elliptical B as compared to the circle nozzle shape at the same injection time. Furthermore, the volume fraction of gas was comparatively bigger for elliptical A and elliptical B at the same injection time as compared to the circle nozzle shape. In this study, the aspect ratio of the elliptical nozzle shape was found to affect the cavitations flow. The elliptical B cavitations intensity was more intensive than the elliptical A nozzle shape. This discrepancy could be attributed to the cavitations region that developed near the zone where the fuel flowed back into the nozzle bore. The elliptical nozzle shape decreased significantly compared to the initial vapor production due to aerodynamic effects and greater local pressure, thus leading to greater cavitations flow. From the data in Figure 12, it can also be seen that diesel gave only marginally wider regions of vapour formation. The cavitations zones were small because of the injector experiencing a very high range of pressure. Generally, in terms of the cavitations flow perspectives, the diesel and hybrid biofuel acted in the same way.
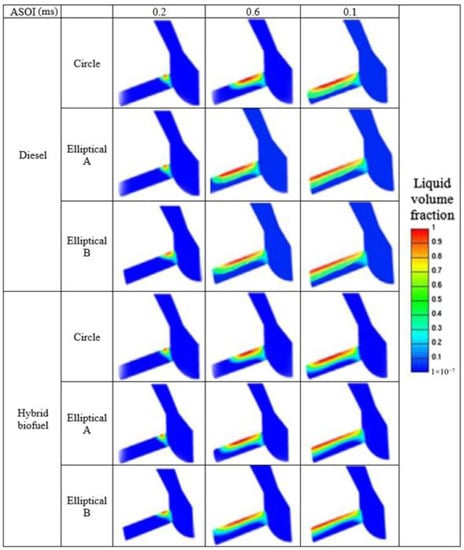
Figure 12.
Cavitation in diesel nozzle for different nozzle spray shape with an injection pressure of 180 MPa.
In order to compare and get a better understanding of the injection cavitations evolution, the transient average liquid velocity in the nozzle for the two fuels and the three nozzle shapes at the outlet plane is shown in Figure 13. From the graph in Figure 13, it can be seen that the average velocity for both elliptical A and elliptical B were higher than that of a circular. This is because the elliptical nozzle shape can hold larger droplets, which contributes to the higher starting momentum when compared to circular nozzle shape. In addition, the average velocity was increased as the aspect ratio of the elliptical nozzle shape increased. Despite that, the average velocity for diesel was higher than that of hybrid biofuel under the same nozzle shape. It seems possible that these results were obtained due to diesel having much lower viscosity as compared to the hybrid biofuel. Thus, this increased the coefficient of discharge, and consequently the exit velocity.
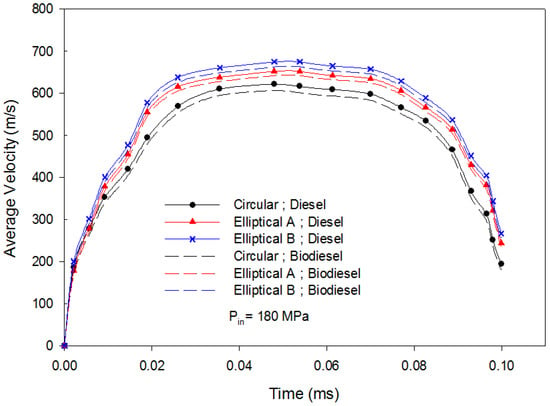
Figure 13.
Outlet Average liquid velocity under 180 MPa pressure for different type of nozzle shape and fuel.
5.3. Spray Simulation Results
5.3.1. Spray Images Growth
Figure 14 illustrates the spray images for circular, elliptical A, and elliptical B nozzle types at different injection pressures (50 MPa, 100 MPa, 180 MPa) and a backpressure of 3 MPa at 0.9 ms ASOI for diesel and hybrid biofuel (RP032MC068). Based on the obtained results, it was shown that diesel produced smaller cone angles compared to the hybrid biofuel blend, which yielded a bigger cloud after the secondary breakup for both the circular and elliptical nozzle shape. Smaller droplets and increased spray angles were discovered when the elliptical nozzle shape was utilized compared to the circular shape. This was mainly due to higher aerodynamic effects for the elliptical B nozzle shape, which could reduce the droplets size and thus lead to a bigger cloud after the secondary breakup. The droplets became smaller when the pressure was increased for both diesel and hybrid biofuel. From the observation of the spray characteristic result, the elliptical A and elliptical B nozzle shape yielded a larger cloud and slower spray characteristics for the hybrid biofuel blend, whereas a thicker and faster spray was produced for diesel fuel. Furthermore, the droplets became smaller when the pressure was increased for both diesel and the hybrid biofuel. The capability of the simulation to anticipate such occurrences was caused by the comprehensive modelling in the thick main area where the primary breakup happened.
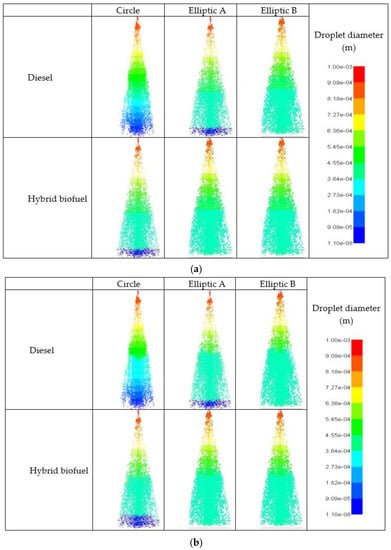
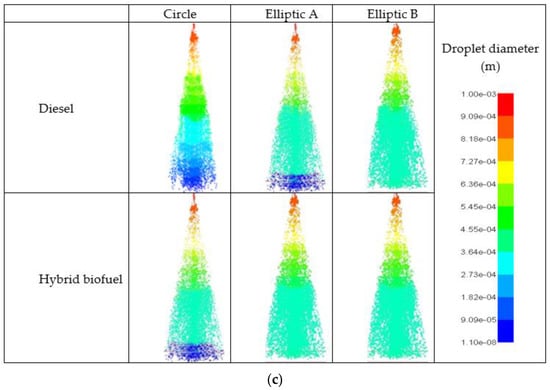
Figure 14.
Fuel spray images at 0.9 ms ASOI for elliptical and circular nozzle types: (a) 50 MPa pressure injection, (b) 100 MPa pressure injection, and (c) 180 MPa pressure injection.
5.3.2. Spray Tip Penetration
Figure 15 provides the spray tip penetration under different injection conditions for the different types of nozzle shapes at a 3 MPa backpressure. It can be seen from the data in Figure 15 that the spray tip penetration for the elliptical A and elliptical B was always shorter than that of the circular nozzle shape. This was due to circular sprays having both smaller spray cloud widths and spray cone angles. The circular nozzle shape experienced lower aerodynamic drag as compared to the elliptical nozzle shape and consequently it produced longer penetration. As the injection pressure was increased, the spray tip penetration turned out to be longer for the similar nozzle shape and backpressure. Further analysis showed that the type of fuel had a small effect on the different nozzle shape with regard to the spray tip penetration, although the diesel fuel gave a slightly higher spray tip penetration as compared to hybrid biofuel blends. Although the nozzle shape had different spray tip penetration values, the trend was clearly similar for all the curves, where all of them kept increasing.
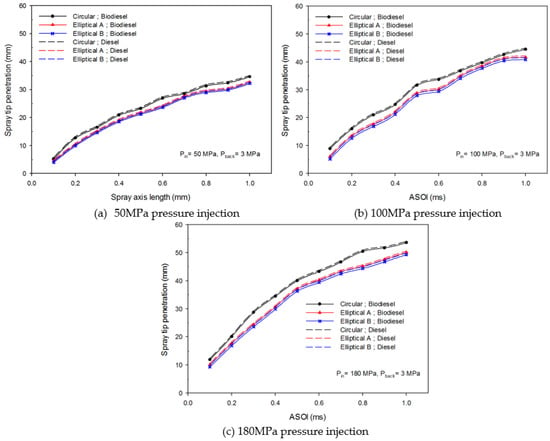
Figure 15.
Spray tip penetration under different pressures: (a) 50 MPa pressure injection, (b) 100 MPa pressure injection, and (c) 180 MPa pressure injection.
5.3.3. Spray Cone Angle
The spray cone angles were plotted versus ASOI in Figure 16 in order to give a better understanding and compare the performance of different nozzle geometry on spray cone angle under real engine conditions and high-pressure circumstances. Figure 16 illustrates that when the backpressure was increased, the spray cone angle also increased for all nozzle spray shapes. For the elliptical nozzle shape, the aspect ratio of the elliptical nozzle shape was found to influence the spray cone angle. The spray cone angle for elliptical B was found to be much higher than that of the elliptical A. However, the elliptical A spray cone angle was greater than that of elliptical B for the initial process. Later, the spray cone angle for elliptical B increased to be identical or lower for the end process of the spray. From these results, it appears that the elliptical nozzle shape experienced an axis-switching phenomenon in a diesel engine with high pressure conditions. These results obtained from the current investigation are consistent with the spray width results below. Furthermore, it can be seen in Figure 16 that the spray cone angle of the circular nozzle shape was smaller than that of the elliptical nozzle shape. This discrepancy could be attributed to aerodynamic effects of the elliptical nozzle shape, which had a bigger cross section and spray surface area than the circular nozzle shape. Another possible explanation for this is that the elliptical nozzle shape experienced an axis-switching phenomenon, which is crucial to boost the ratio of the air entrainment [43] and consequently leading to larger spray cone angle. In addition, the type of fuel on the different nozzle shape has a small effect to the spray cone angle although the diesel fuel gives a slightly higher spray cone angle than of hybrid biofuel blends. Based from the obtained results, it was shown that diesel produced smaller cone angles as compared to a hybrid biofuel blend, which yielded a bigger cloud after the secondary breakup than all the nozzle shapes. This happened due to the larger viscosity of hybrid biofuel as compared to diesel, which caused unstable spray and droplets that effects the production of the spray characteristic.
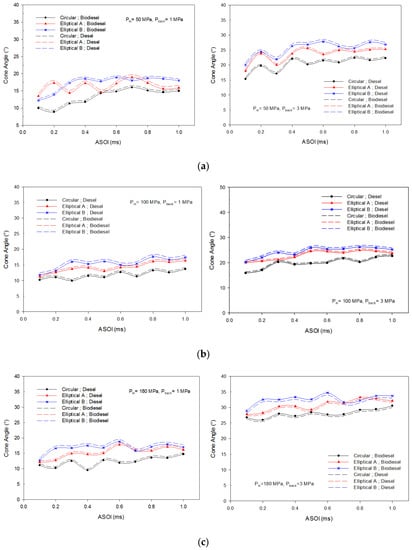
Figure 16.
Spray cone angle for different types of nozzle shape and fuel: (a) 50 MPa pressure injection, (b) 100 MPa pressure injection, and (c) 180 MPa pressure injection.
5.3.4. Spray Width
The ratio of spray width (WS) over the nozzle hydraulic diameters (D) has been used to compare the data of spray width. The spray widths were taken into account to compare the spray characteristics of different nozzle shapes under the real diesel engine and high-pressure conditions. Figure 17 displays the results of spray width (WS/D) along the spray axis length. As can be seen from Figure 17, the spray width of the elliptical A and elliptical B nozzle shapes was much larger than that of the circle shape for all pressure conditions. Furthermore, the spray width of elliptical B was much bigger than the elliptical A nozzle shape. These results showed that the superior spray atomization and bigger spray cone angle could be achieved by using elliptical A and elliptical B nozzle shape compared to a circular nozzle shape. From the graph in Figure 17, it is apparent that the elliptical A and B spray widths were fluctuating along the spray axis length. This investigation shows that elliptical A and elliptical B experienced an axis-switching phenomenon under the real diesel engine and high-pressure conditions. What is interesting in this data is that as the backpressure was increased with the same injection pressure, the axis-switching phenomenon of the spray width decreased. The current study found that the aerodynamic effects could be boosted by increasing the backpressure. Another important finding was that the high-pressure conditions were useful to reduce the axis-switching phenomenon. All the nozzle shapes demonstrated higher spray width when the injection pressure was increased. It seems possible that these results were due to a higher difference between inlet and outlet velocity and steady air and fuel interaction were achieved when the spray velocity became greater under a higher injection pressure. These findings of the current study were consistent with those of Abramovich [44] who found that axis-switching was due to pressure differentials in the plane of the vortex ring.
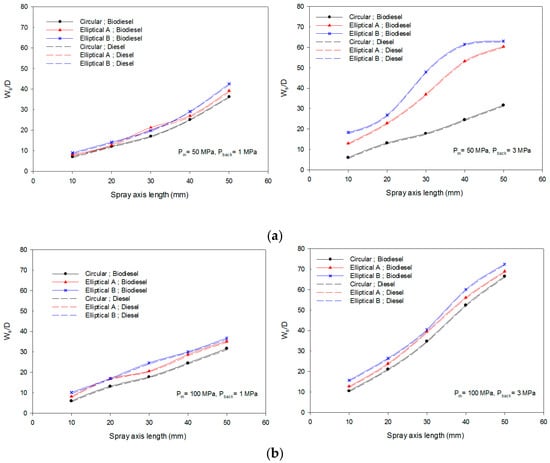
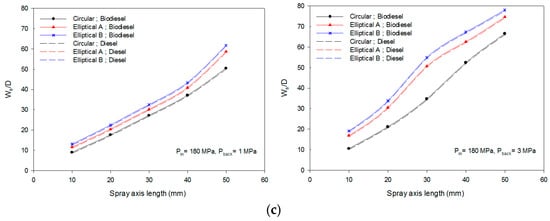
Figure 17.
Ratio of spray width over nozzle hydraulic diameters (a) 50 MPa pressure injection; (b) 100 MPa pressure injection; (c) 180 MPa pressure injection.
In this study, the aspect ratio of the elliptical nozzle shape was found to affect the spray width. The spray width for elliptical B was found to be higher than that of elliptical A. This result may have been caused by the higher inertia, viscous forces, and rapid changes in pressure for elliptical B as compared to elliptical A. In addition, the type of fuel in the different nozzle shape had a small effect on the spray width, although the diesel fuel gave a slightly higher spray width than that of the hybrid biofuel blends.
6. Conclusions
This study presented a numerical investigation about flow in the nozzle and spray performances in a standard diesel injector, drawing comparison between the usage of diesel and hybrid biofuel blends with three different nozzle geometries, which were circle, elliptical A, and elliptical B under different pressures and backpressures. Some of the most critical findings are summarized below:
- The nozzle flow simulation results indicated that the fuel type had little effect on the cavitation area and it is dependence on the nozzle spray shape. The diesel delivered slightly a higher average velocity than hybrid biofuel under high injection pressure (180 MPa). These behaviors were generally caused by viscosity and density properties. The cavitations intensity was more intensive for elliptical A and elliptical B as compared to the circle nozzle shape for the same injection time. The aspect ratio of the elliptical nozzle shape was found to affect the cavitations flow, where the elliptical B cavitations intensity was more intensive than the elliptical A nozzle shape.
- The droplet size of the elliptical nozzle shape was smaller compared to the circular shape due to higher aerodynamic effects found in the elliptical nozzle shape that could reduce the droplets size, and thus leading to a bigger cloud formation after the secondary breakup. The evidence from this study suggests that the droplet size became smaller when the pressure was increased for both diesel and hybrid biofuel
- The spray tip penetration of the elliptical nozzle shape was smaller than the circular nozzle shape. This was due to the circular nozzle having smaller spray widths and cone angles. Further analysis showed that the type of fuel on the different nozzle shape had a small effect towards the spray tip penetration, although diesel fuel gave a slightly higher spray tip penetration compared to hybrid biofuel blends. In addition, the spray tip penetration was affected by the aspect ratio of the elliptical nozzle shape.
- The elliptical nozzle shape was larger compared to the circular nozzle shape in terms of spray cone angles. The spray cone angle for elliptical B was found to be much higher than that of elliptical A. This indicated that the aspect ratio of the elliptical nozzle shape was found to affect the spray cone angles. Moreover, the type of fuel on the different nozzle shape had a minor influence to the spray cone angles. The results show that diesel produced smaller cone angles compared to the biofuel blend.
- The spray widths of the circular nozzle shape were smaller than those of the elliptical A and elliptical B under all injection pressures and backpressures. However, the fuel type had little effect on the spray widths for all the nozzle shape. Furthermore, the aspect ratio of the elliptical nozzle shape was found to affect the spray width.
Further work needs to be done to establish whether the length of the orifice under an ultra-high injection pressure may contribute to affect the cavitations flow and thus affecting the spray performance of the diesel injector.
Author Contributions
Conceptualization, M.H.H.I., F.I., and M.Y.I.; methodology, M.H.H.I., S.C.M., and M.Y.I.; software, M.H.H.I., M.Z.A., and M.S.A.A.; validation, M.H.H.I., F.I., M.Z.A., and M.S.A.A.; resources, S.C.M. and M.Y.I.; writing—original draft preparation, M.H.H.I.; writing—review and editing, M.H.H.I. and F.I.; administration, M.Y.I.; funding acquisition, M.Y.I.
Funding
This research was funded by Universiti Sains Malaysia for the postdoctoral program and under the Fundamental Research Grant Scheme (FRGS/1/2016/TK07/USM/02/2; 203.PMEKANIK.6071356).
Acknowledgments
We would like to acknowledge the financial support from Ministry of Higher Education Malaysia and Universiti Sains Malaysia for the postdoctoral program and the Fundamental Research Grant Scheme (FRGS/1/2016/TK07/USM/02/2; 203.PMEKANIK.6071356).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shervani-Tabar, M.T.; Sheykhvazayefi, M.; Ghorbani, M. Numerical study on the effect of the injection pressure on spray penetration length. Appl. Math. Model. 2013, 37, 7778–7788. [Google Scholar] [CrossRef]
- Sidibé, S.S.; Blin, J.; Vaitilingom, G.; Azoumah, Y. Use of crude filtered vegetable oil as a fuel in diesel engines state of the art: Literature review. Renew. Sustain. Energy Rev. 2010, 14, 2748–2759. [Google Scholar] [CrossRef]
- Qian, D.; Liao, R. A Nonisothermal Fluid-Structure Interaction Analysis on the Piston/Cylinder Interface Leakage of High-Pressure Fuel Pump. J. Tribol. 2014, 136, 21704–21708. [Google Scholar] [CrossRef]
- Hussain, F.; Husain, H.S. Elliptic jets. Part 1. Characteristics of unexcited and excited jets. J. Fluid Mech. 1989, 208, 257–320. [Google Scholar] [CrossRef]
- Ge, C.J.; Yoon, K.S.; Choi, J.N. Using Canola Oil Biodiesel as an Alternative Fuel in Diesel Engines: A Review. Appl. Sci. 2017, 7, 881. [Google Scholar] [CrossRef]
- Suresh, M.; Jawahar, C.P.; Richard, A. A review on biodiesel production, combustion, performance, and emission characteristics of non-edible oils in variable compression ratio diesel engine using biodiesel and its blends. Renew. Sustain. Energy Rev. 2018, 92, 38–49. [Google Scholar] [CrossRef]
- Shi, S.; Valle-Rodríguez, J.O.; Siewers, V.; Nielsen, J. Prospects for microbial biodiesel production. Biotechnol. J. 2011, 6, 277–285. [Google Scholar] [CrossRef] [PubMed]
- Rahman, Z.; Nawab, J.; Sung, H.B.; Kim, C.S. A Critical Analysis of Bio-Hydrocarbon Production in Bacteria: Current Challenges and Future Directions. Energies 2018, 11, 2663. [Google Scholar] [CrossRef]
- Yellapu, S.K.; Bharti; Kaur, R.; Kumar, L.R.; Tiwari, B.; Zhang, X.; Tyagi, R.D. Recent developments of downstream processing for microbial lipids and conversion to biodiesel. Bioresour. Technol. 2018, 256, 515–528. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Wu, H. Effect of major impurities in crude glycerol on solubility and properties of glycerol/methanol/bio-oil blends. Fuel 2015, 159, 118–127. [Google Scholar] [CrossRef]
- Meher, L.C.; Vidya Sagar, D.; Naik, S.N. Technical aspects of biodiesel production by transesterification—A review. Renew. Sustain. Energy Rev. 2006, 10, 248–268. [Google Scholar] [CrossRef]
- Rakopoulos, C.D.; Antonopoulos, K.A.; Rakopoulos, D.C.; Hountalas, D.T.; Giakoumis, E.G. Comparative performance and emissions study of a direct injection Diesel engine using blends of Diesel fuel with vegetable oils or bio-diesels of various origins. Energy Convers. Manag. 2006, 47, 3272–3287. [Google Scholar] [CrossRef]
- Channapattana, S.V.; Kantharaj, C.; Shinde, V.S.; Pawar, A.A.; Kamble, P.G. Emissions and Performance Evaluation of DI CI—VCR Engine Fuelled with Honne oil Methyl Ester/Diesel Blends. Energy Procedia 2015, 74, 281–288. [Google Scholar] [CrossRef]
- Desantes, J.M.; Payri, R.; Salvador, F.J.; Manin, J. Influence on Diesel Injection Characteristics and Behavior Using Biodiesel Fuels; SAE International: Warrendale, PA, USA, 2009. [Google Scholar]
- Priesching, P.; Pavlovic, Z.; Ertl, P.; Del Giacomo, N.; Beatrice, C.; Mancaruso, E.; Vaglieco, B.M. Numerical and Experimental Investigation of the Influence of Bio-Diesel Blends on the Mixture Formation, Combustion and Emission Behavior of a Modern HSDI Diesel Engine; SAE International: Warrendale, PA, USA, 2009. [Google Scholar]
- Allocca, L.; Mancaruso, E.; Montanaro, A.; Vaglieco, B.M.; Vassallo, A. Renewable Biodiesel/Reference Diesel Fuel Mixtures Distribution in Non-Evaporating and Evaporating Conditions for Diesel Engines; SAE International: Warrendale, PA, USA, 2009. [Google Scholar]
- Sem, T.R. Investigation of Injector Tip Deposits on Transport Refrigeration Units Running on Biodiesel Fuel; SAE International: Warrendale, PA, USA, 2004. [Google Scholar]
- Ramadhas, A.S.; Jayaraj, S.; Muraleedharan, C. Characterization and effect of using rubber seed oil as fuel in the compression ignition engines. Renew. Energy 2005, 30, 795–803. [Google Scholar] [CrossRef]
- Mohan, B.; Yang, W.; Yu, W.; Tay, K.L.; Chou, S.K. Numerical Simulation on Spray Characteristics of Ether Fuels. Energy Procedia 2015, 75, 919–924. [Google Scholar] [CrossRef]
- Lee, Y.; Huh, K.Y. Numerical study on spray and combustion characteristics of diesel and soy-based biodiesel in a CI engine. Fuel 2013, 113, 537–545. [Google Scholar] [CrossRef]
- Som, S.; Ramirez, A.I.; Longman, D.E.; Aggarwal, S.K. Effect of nozzle orifice geometry on spray, combustion, and emission characteristics under diesel engine conditions. Fuel 2011, 90, 1267–1276. [Google Scholar] [CrossRef]
- Mohan, B.; Yang, W.; Yu, W.; Tay, K.L. Numerical analysis of spray characteristics of dimethyl ether and diethyl ether fuel. Appl. Energy 2017, 185, 1403–1410. [Google Scholar] [CrossRef]
- Zhou, Z.-F.; Lu, G.-Y.; Chen, B. Numerical study on the spray and thermal characteristics of R404A flashing spray using OpenFOAM. Int. J. Heat Mass Transf. 2018, 117, 1312–1321. [Google Scholar] [CrossRef]
- Kegl, B.; Lešnik, L. Modeling of macroscopic mineral diesel and biodiesel spray characteristics. Fuel 2018, 222, 810–820. [Google Scholar] [CrossRef]
- Pairan, M.R.; Asmuin, N.; Isa, N.M.; Sies, F. Characteristic study of flat spray nozzle by using particle image velocimetry (PIV) and ANSYS simulation method. AIP Conf. Proc. 2017, 1831, 20009. [Google Scholar] [CrossRef]
- Kuleshov, A.S. Use of Multi-Zone DI Diesel Spray Combustion Model for Simulation and Optimization of Performance and Emissions of Engines with Multiple Injection; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2006; Volume 1385. [Google Scholar]
- Battistoni, M.; Grimaldi, C.N. Numerical analysis of injector flow and spray characteristics from diesel injectors using fossil and biodiesel fuels. Appl. Energy 2012, 97, 656–666. [Google Scholar] [CrossRef]
- Lin, S.; Ding, L.; Zhou, Z.; Yu, G. Discrete model for simulation of char particle gasification with structure evolution. Fuel 2016, 186, 656–664. [Google Scholar] [CrossRef]
- Rashidi, S.; Bovand, M.; Abolfazli Esfahani, J.; Ahmadi, G. Discrete particle model for convective AL2O3–water nanofluid around a triangular obstacle. Appl. Therm. Eng. 2016, 100, 39–54. [Google Scholar] [CrossRef]
- Thiruvengadam, M.; Zheng, Y.; Tien, J.C. DPM simulation in an underground entry: Comparison between particle and species models. Int. J. Min. Sci. Technol. 2016, 26, 487–494. [Google Scholar] [CrossRef]
- Di Sarli, V.; Russo, P.; Sanchirico, R.; Di Benedetto, A. CFD simulations of the effect of dust diameter on the dispersion in the 20L bomb. Chem. Eng. Trans. 2013, 31, 727–732. [Google Scholar]
- Song, X.; Park, Y.C. Numerical Analysis of Butterfly Valve-Prediction of Flow Coefficient and Hydrodynamic Torque Coefficient. In Proceedings of the World Congress on Engineering and Computer Science, San Francisco, CA, USA, 24–26 October 2007; pp. 2–6, ISBN 978-988-98671-6-4. [Google Scholar]
- Talbot, L.; Cheng, R.K.; Schefer, R.W.; Willis, D.R. Thermophoresis of particles in a heated boundary layer. J. Fluid Mech. 1980, 101, 737–758. [Google Scholar] [CrossRef]
- Turner, M.R.; Sazhin, S.S.; Healey, J.J.; Crua, C.; Martynov, S.B. A breakup model for transient Diesel fuel sprays. Fuel 2012, 97, 288–305. [Google Scholar] [CrossRef]
- Reitz, R.D.; Beale, J.C. Modeling Spray Atomization with The Kelvin-Helmholtzrayleigh-Taylor Hybrid Model. At. Sprays 1996, 9, 623–650. [Google Scholar] [CrossRef]
- Reitz, R. Modeling atomization processes in high-pressure vaporizing sprays. At. Spray Technol. 1987, 3, 309–337. [Google Scholar]
- Taylor, G.I. The shape and acceleration of a drop in a high speed air stream. Sci. Pap. G I Taylor 1963, 3, 457–464. [Google Scholar]
- O’Rourke, P.J.; Amsden, A.A. The Tab Method for Numerical Calculation of Spray Droplet Breakup; SAE International: Warrendale, PA, USA, 1987. [Google Scholar]
- Lee, S.-J.; Baek, S.-J. The effect of aspect ratio on the near-field turbulent structure of elliptic jets. Flow Meas. Instrum. 1994, 5, 170–180. [Google Scholar] [CrossRef]
- Salvador, F.J.; Gimeno, J.; Pastor, J.M.; Martí-Aldaraví, P. Effect of turbulence model and inlet boundary condition on the Diesel spray behavior simulated by an Eulerian Spray Atomization (ESA) model. Int. J. Multiph. Flow 2014, 65, 108–116. [Google Scholar] [CrossRef]
- Yu, S.; Yin, B.; Deng, W.; Jia, H.; Ye, Z.; Xu, B.; Xu, H. Experimental study on the spray characteristics discharging from elliptical diesel nozzle at typical diesel engine conditions. Fuel 2018, 221, 28–34. [Google Scholar] [CrossRef]
- Pastor, J.V.; Arrègle, J.; Palomares, A. Diesel spray image segmentation with a likelihood ratio test. Appl. Opt. 2001, 40, 2876–2885. [Google Scholar] [CrossRef] [PubMed]
- Chen, N.; Yu, H. Mechanism of axis switching in low aspect-ratio rectangular jets. Comput. Math. Appl. 2014, 67, 437–444. [Google Scholar] [CrossRef]
- Abramovich, G.N. On the deformation of the rectangular turbulent jet cross-section. Int. J. Heat Mass Transf. 1982, 25, 1885–1894. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).