Performance Analysis of Hydrofoil Shaped and Bi-Directional Diffusers for Cross Flow Tidal Turbines in Single and Double-Rotor Configurations
Abstract
1. Introduction
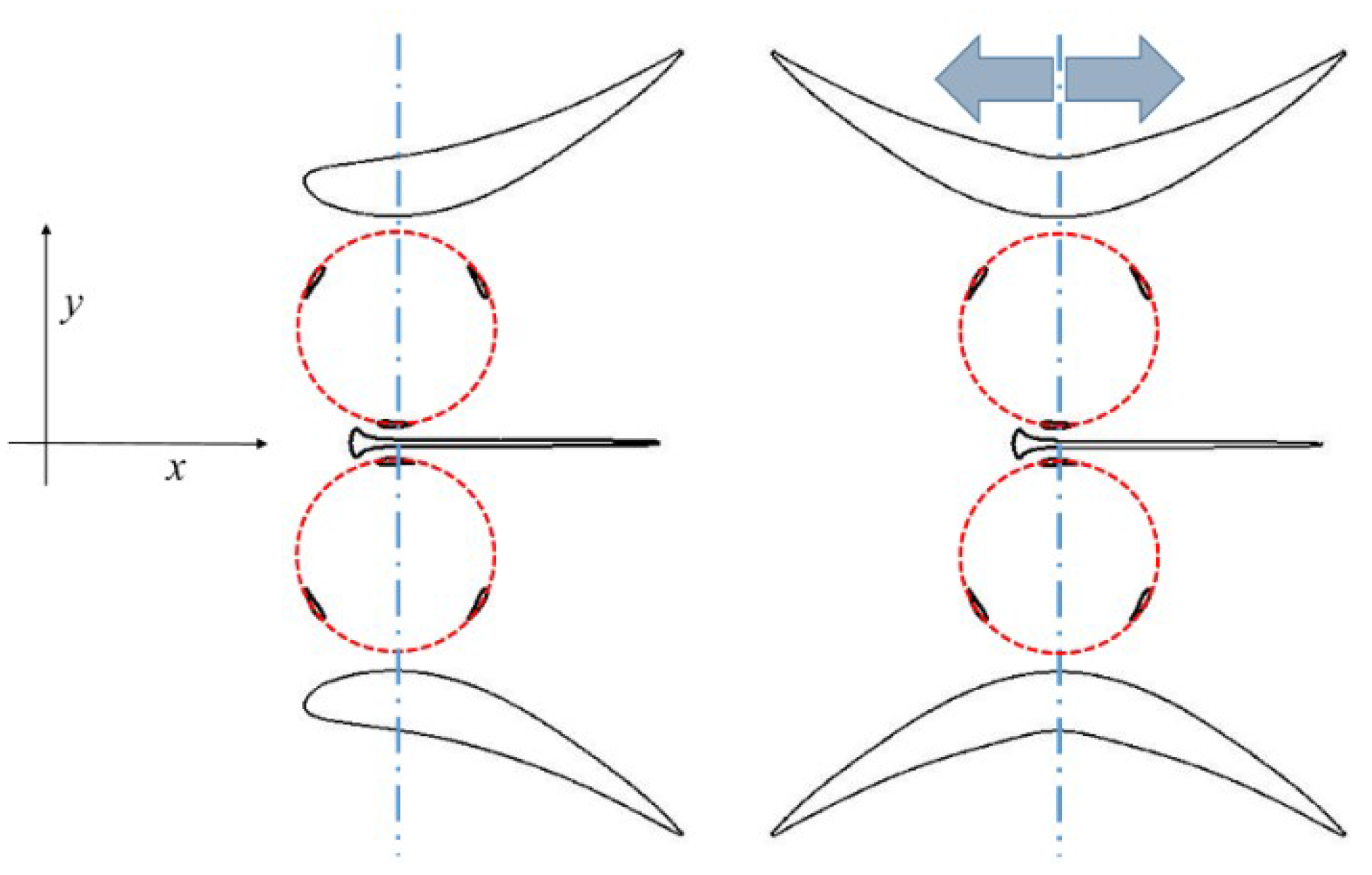
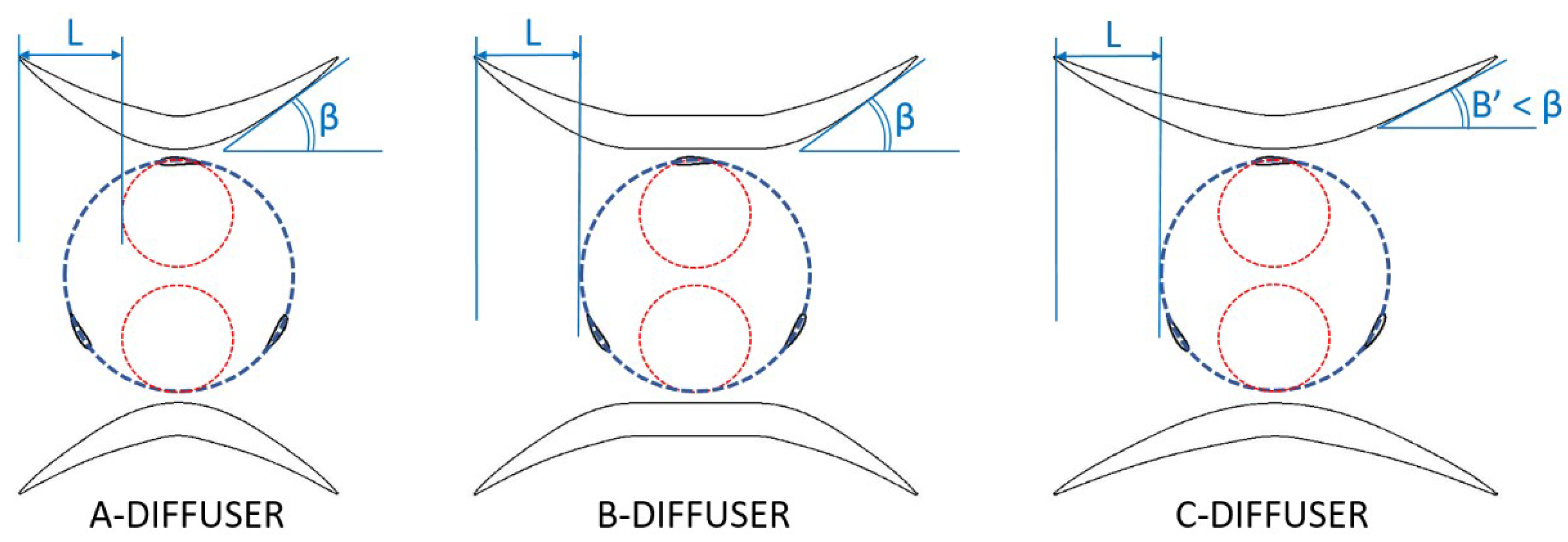
2. Aims and Case Studies
3. Model Set-Up and Validation
3.1. Grids and Solution Method
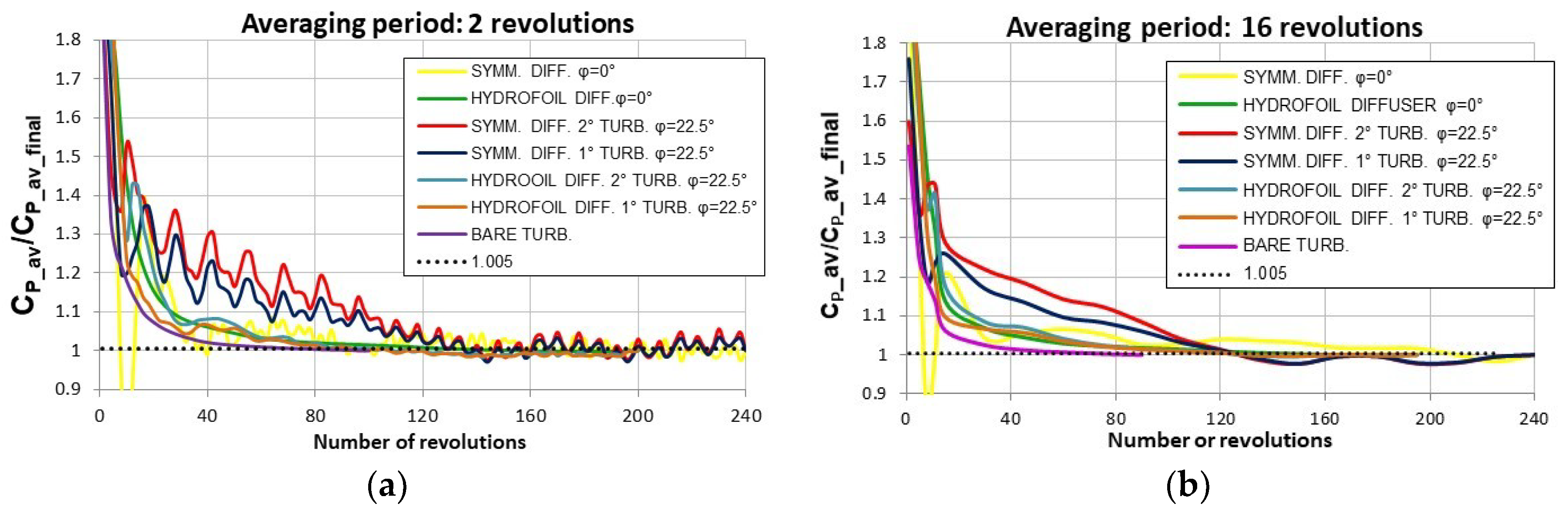
3.2. Validation and Sensitivities
4. Results and Discussion
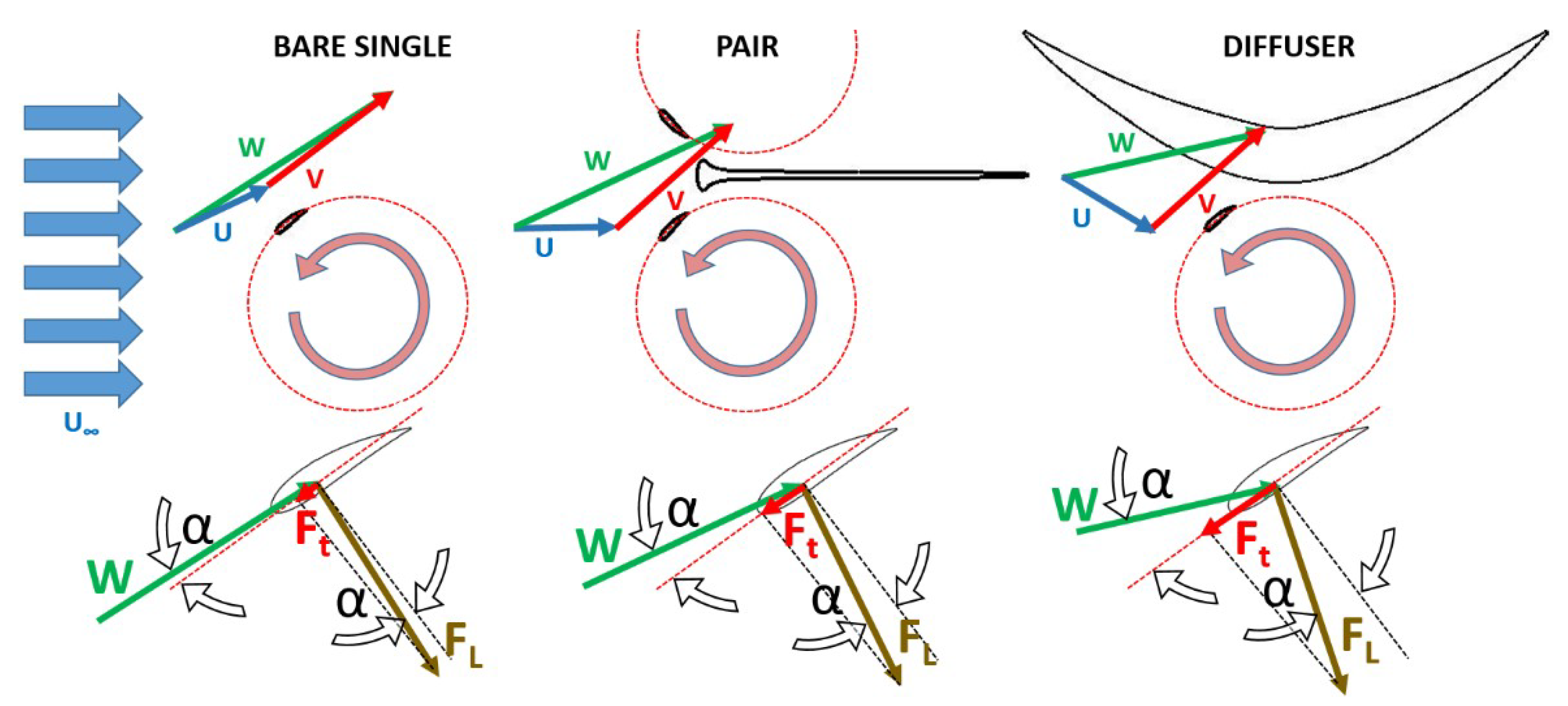
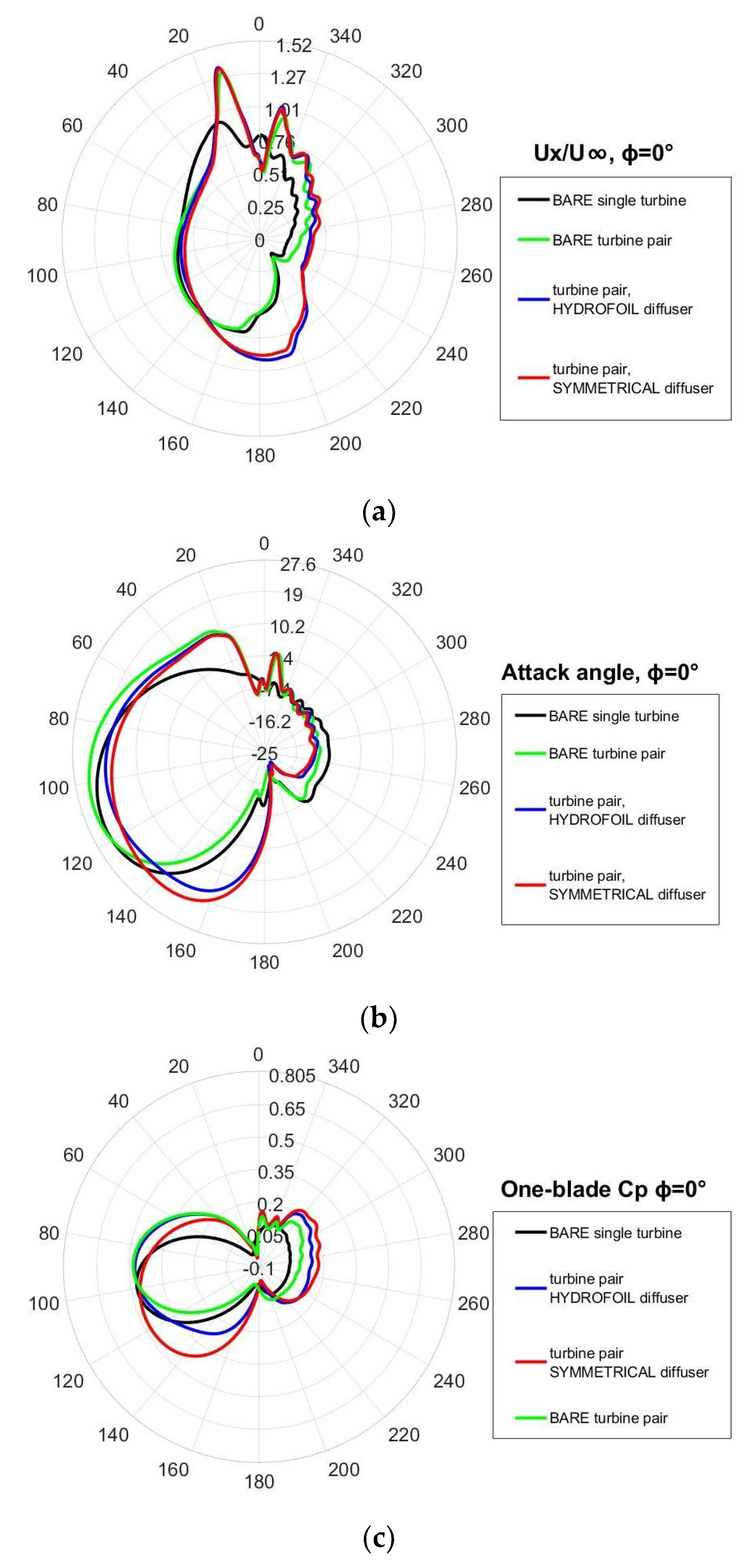
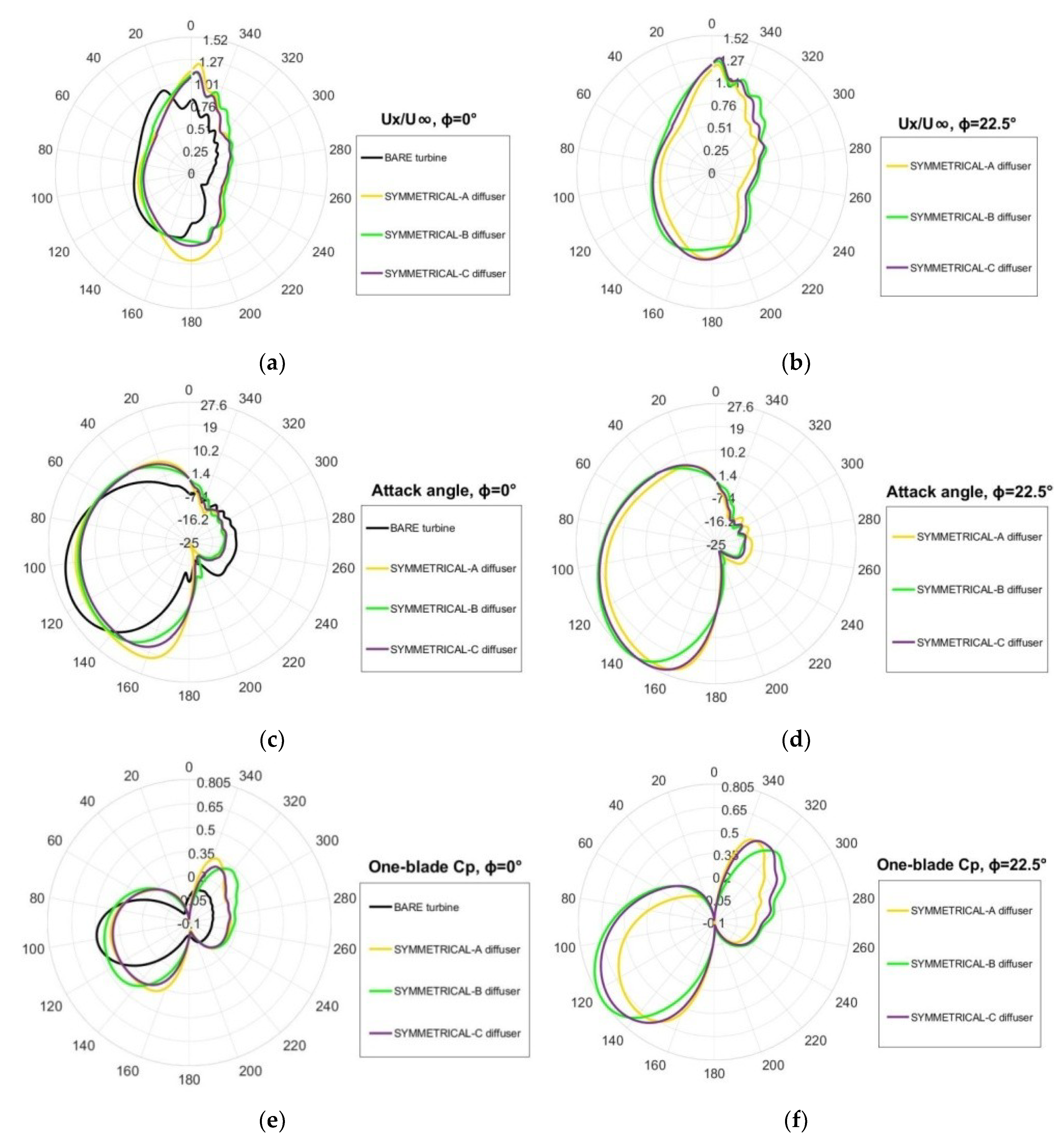
4.1. Importance of the Attack Angle
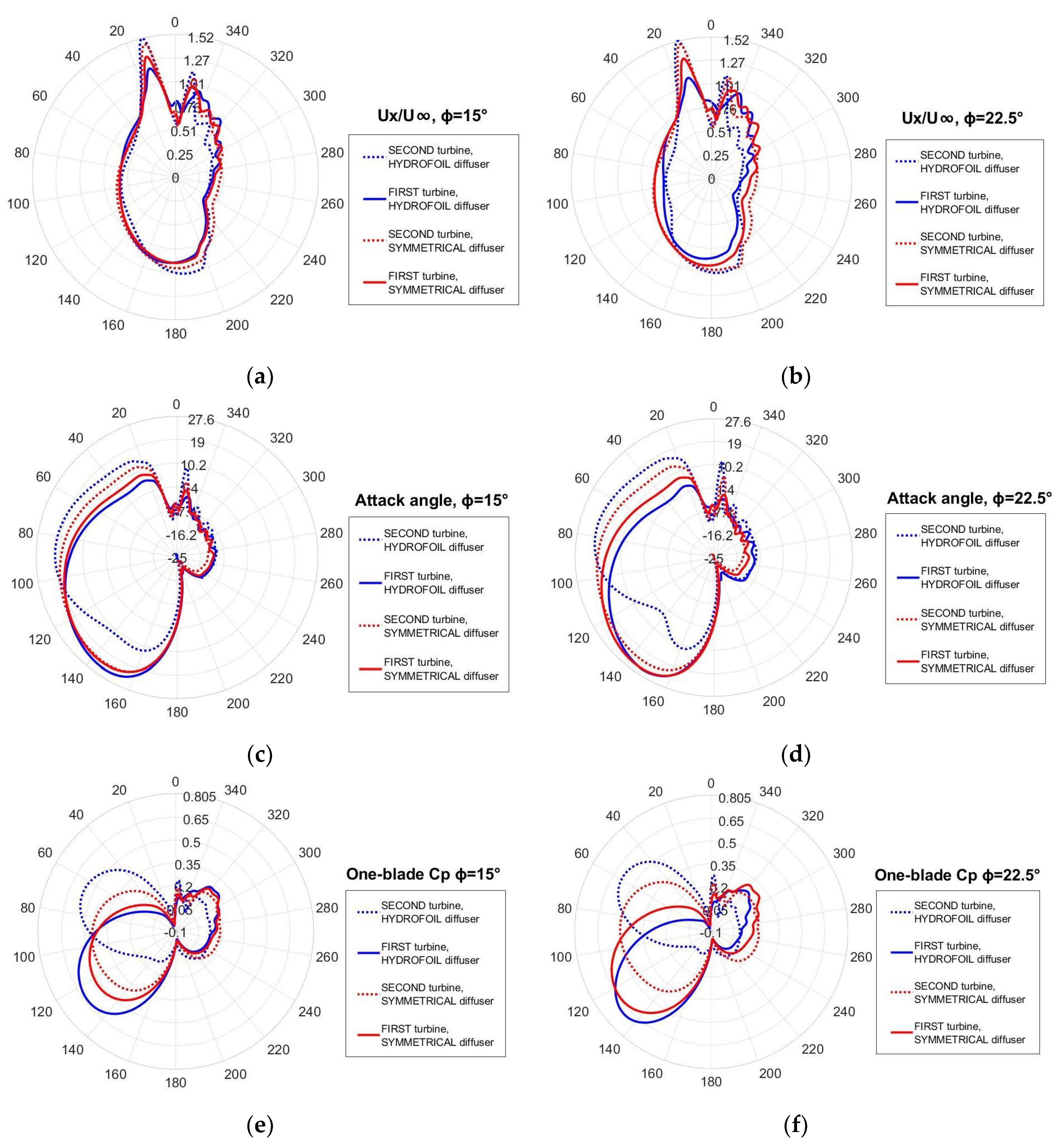
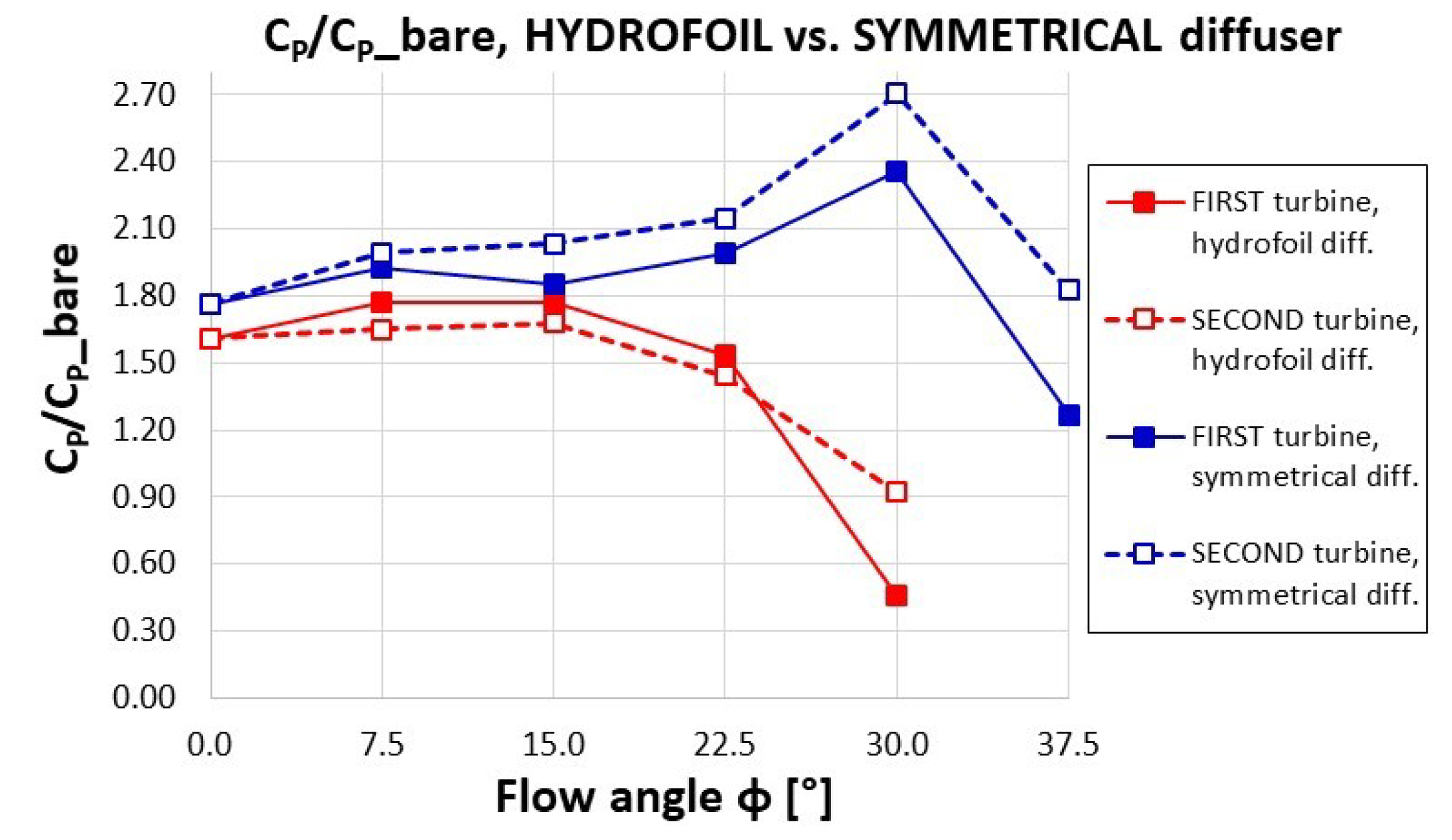
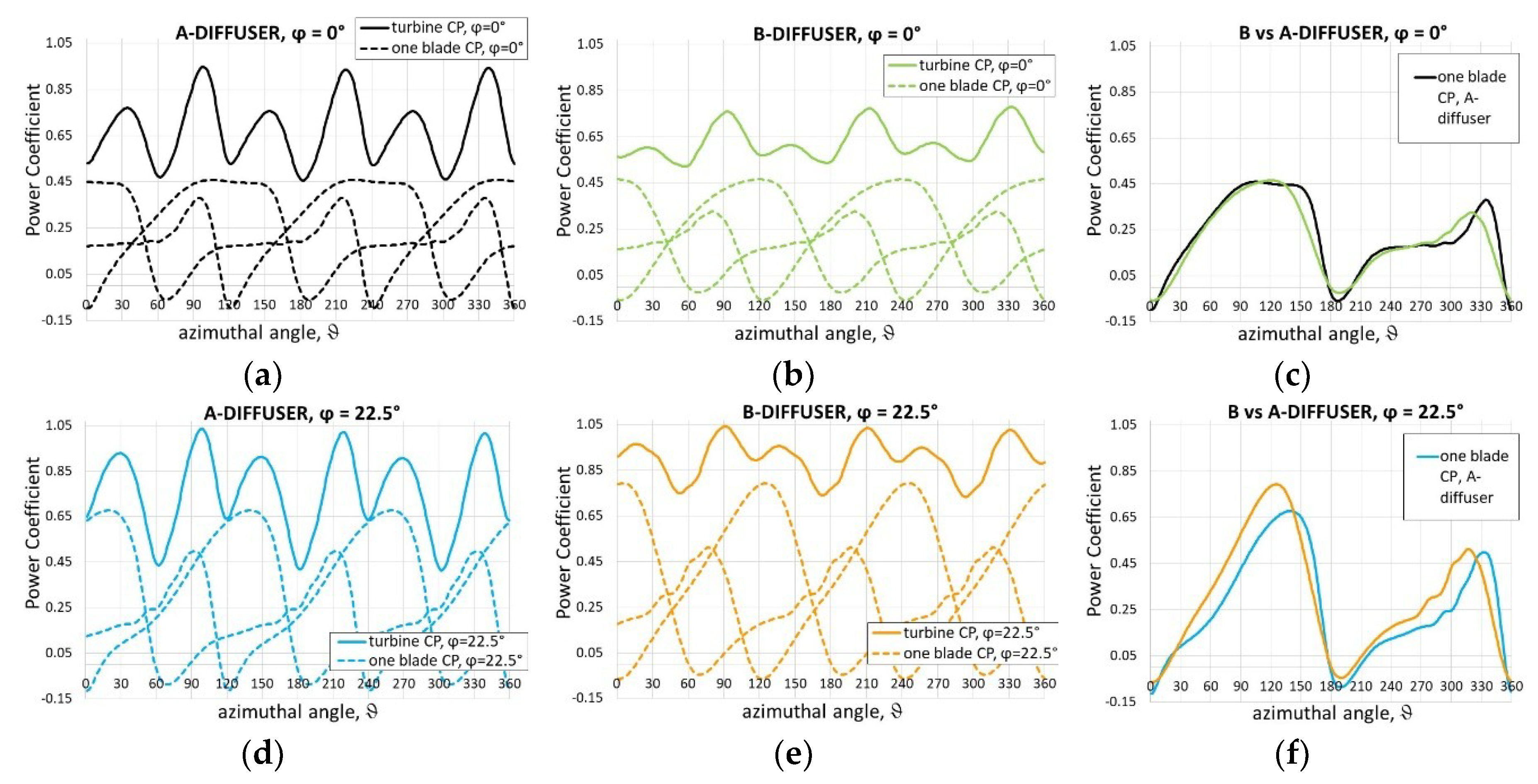
4.2. CP of the Turbine Pairs
- (1)
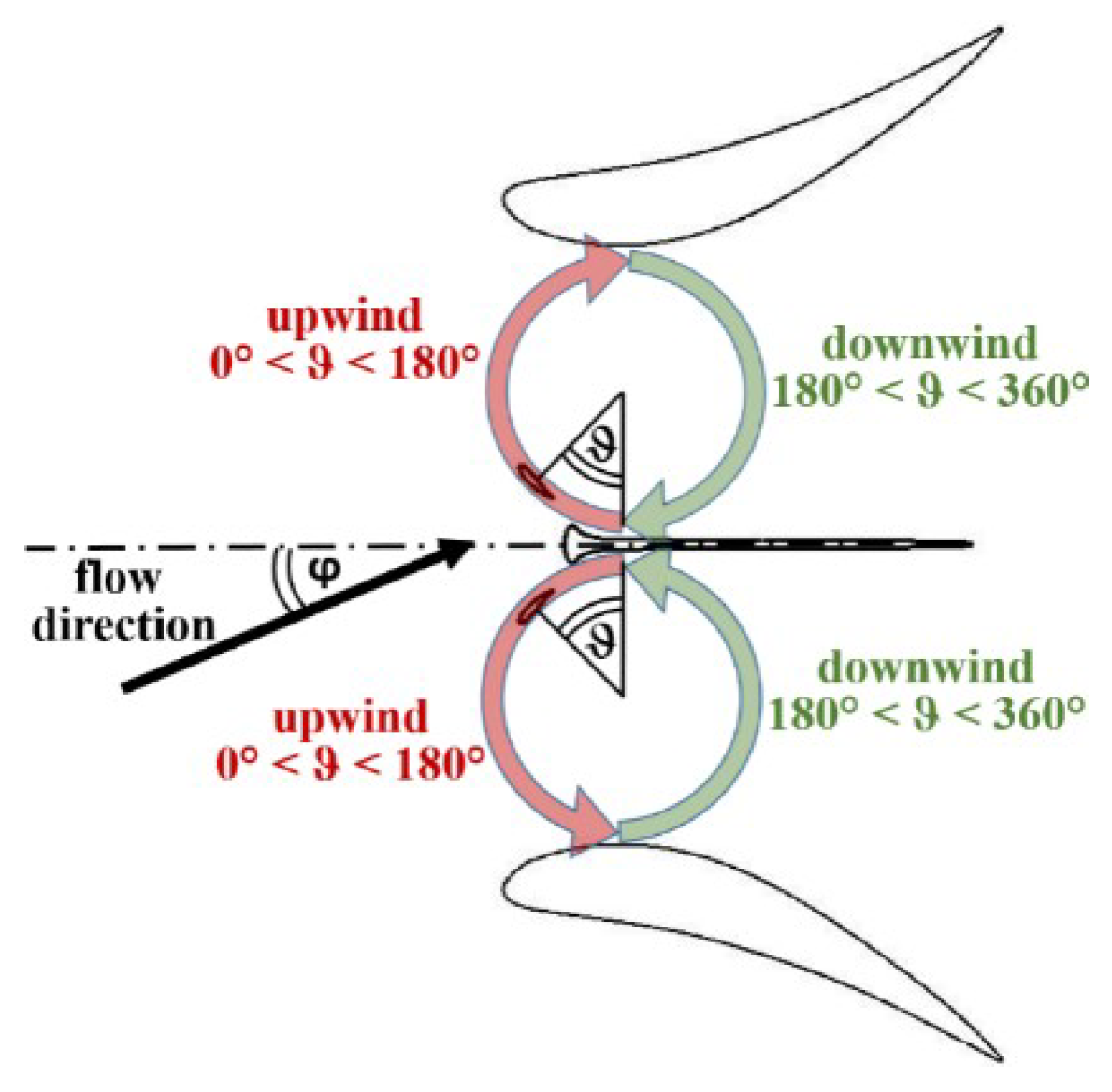
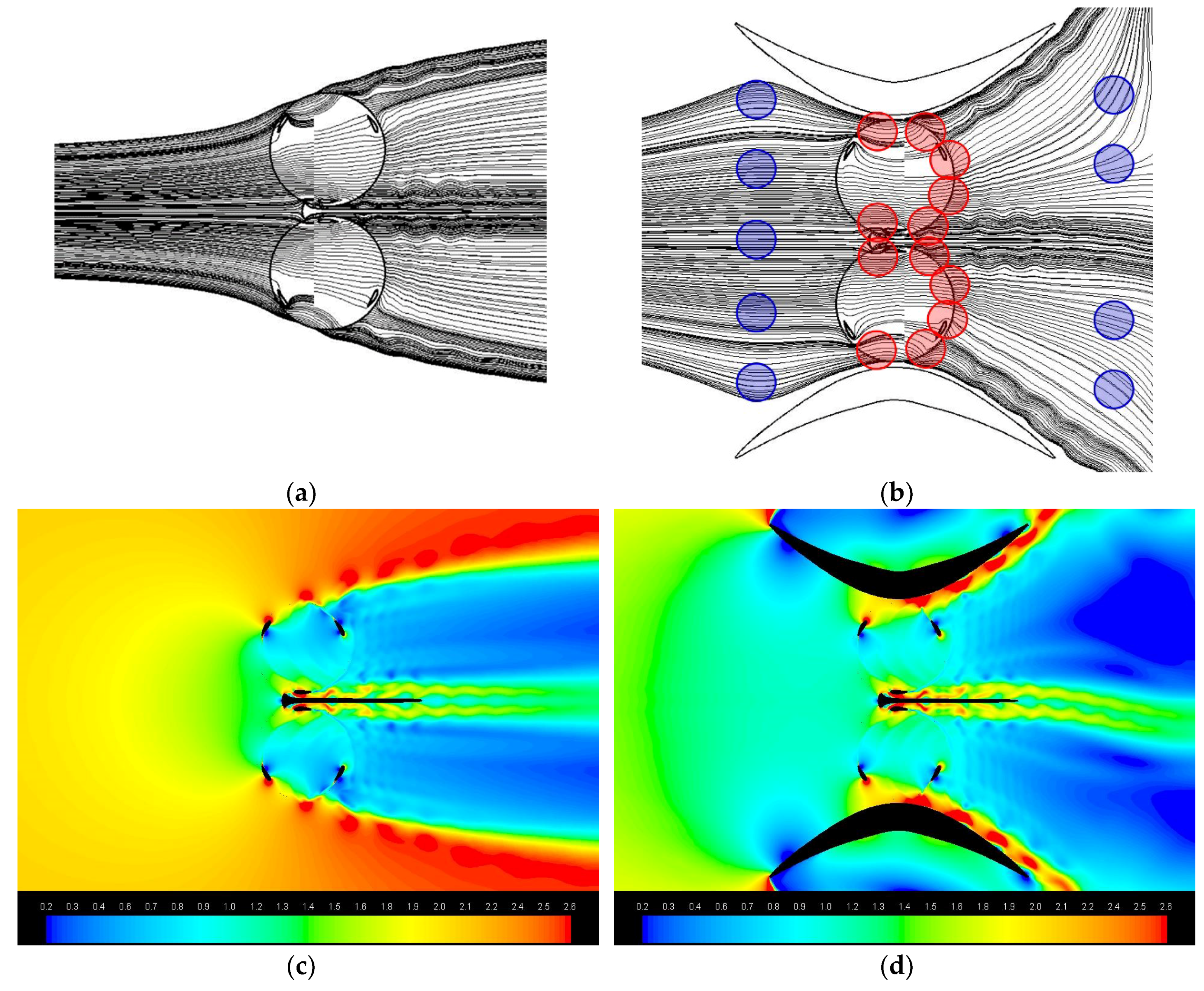
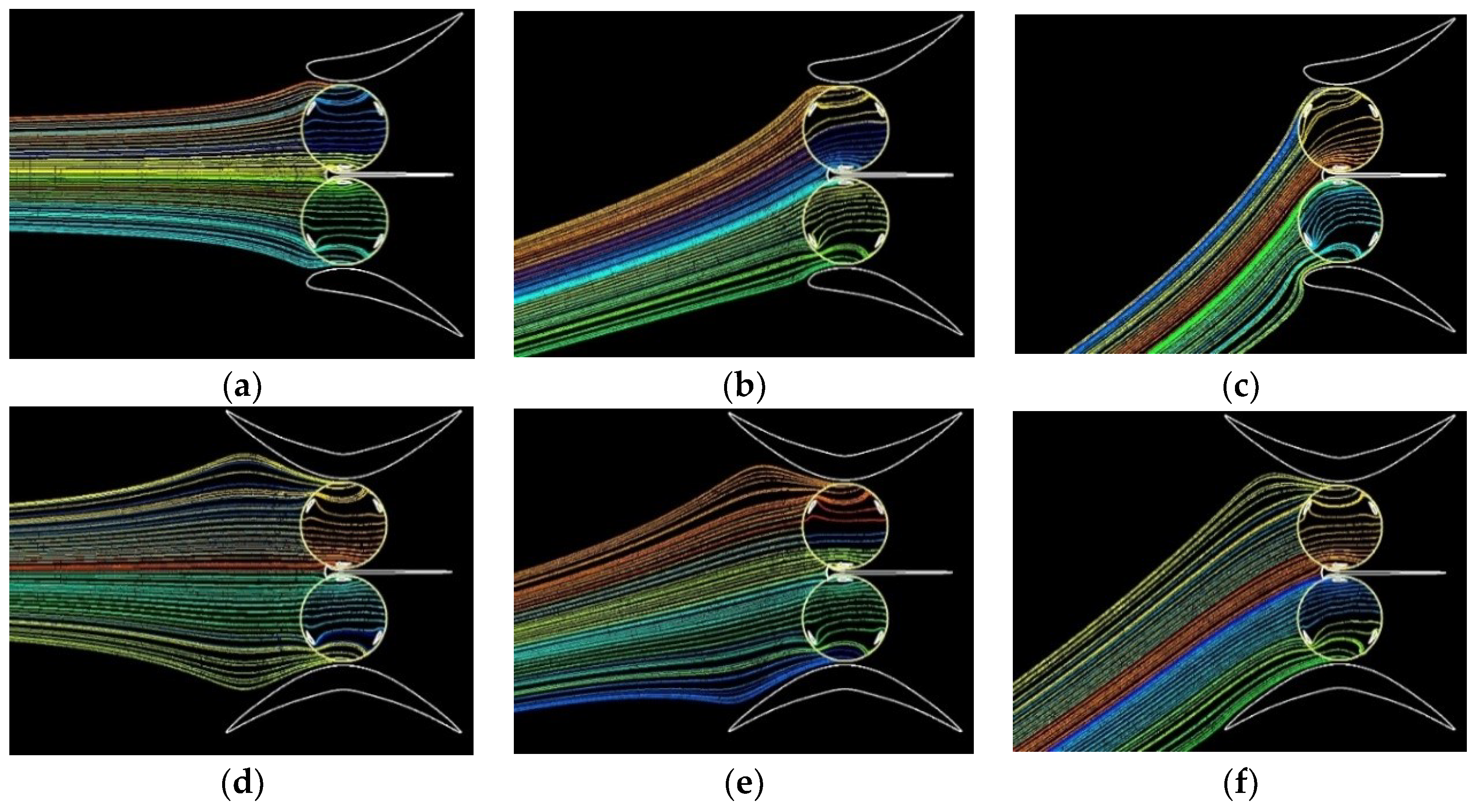
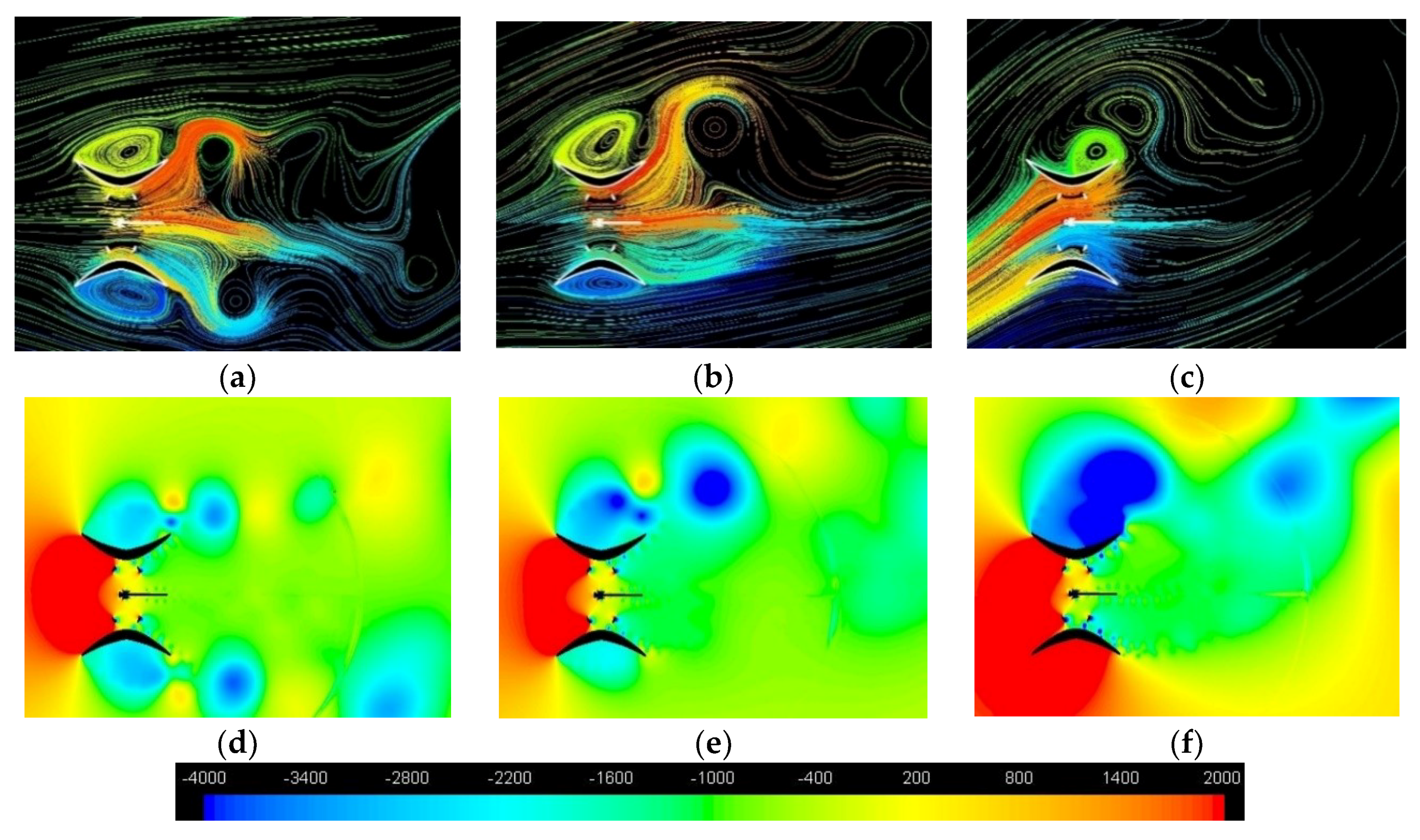
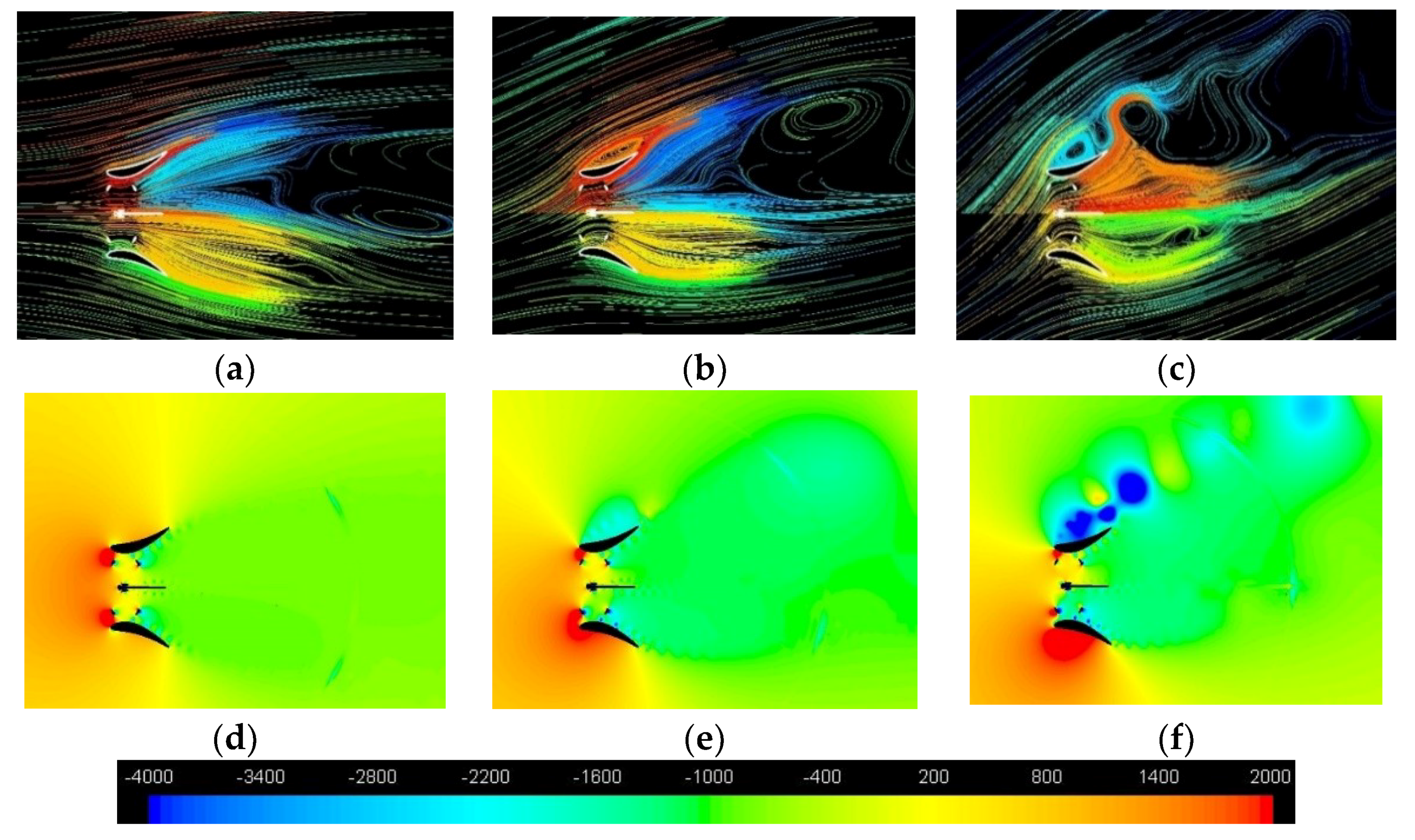
- Taking into account the rotation direction of each turbine (shown in Figure 6) it is evident that the effect of the converging walls of the symmetrical diffuser occurs mainly during the final part of the blade upwind path. As demonstrated by the direction of the path-lines, this effect consists of an increase in the attack angle, whose consequences on lifting and torque have already been illustrated in Figure 7. It happens for both the rotors if φ = 0°, only for the “second turbine” (that is the upper one) if φ > 0°. The relative extent of this favourable effect (i.e., in comparison to what happens in the original diffuser) is greater the greater the yaw angle is.
- (2)
- For φ = 0°, the stream tube of the symmetrical diffuser appears larger (a measurement done at the domain inlet boundary revealed +3.5% respect to the original diffuser) indicating a better flow concentration capability.
- (3)
- For the hydrofoil shaped diffuser the stream tube width slightly increases at φ = 15° but appears drastically narrowed at φ = 30°, while for the symmetrical diffuser the width continues surprisingly to grow up to φ = 30°.
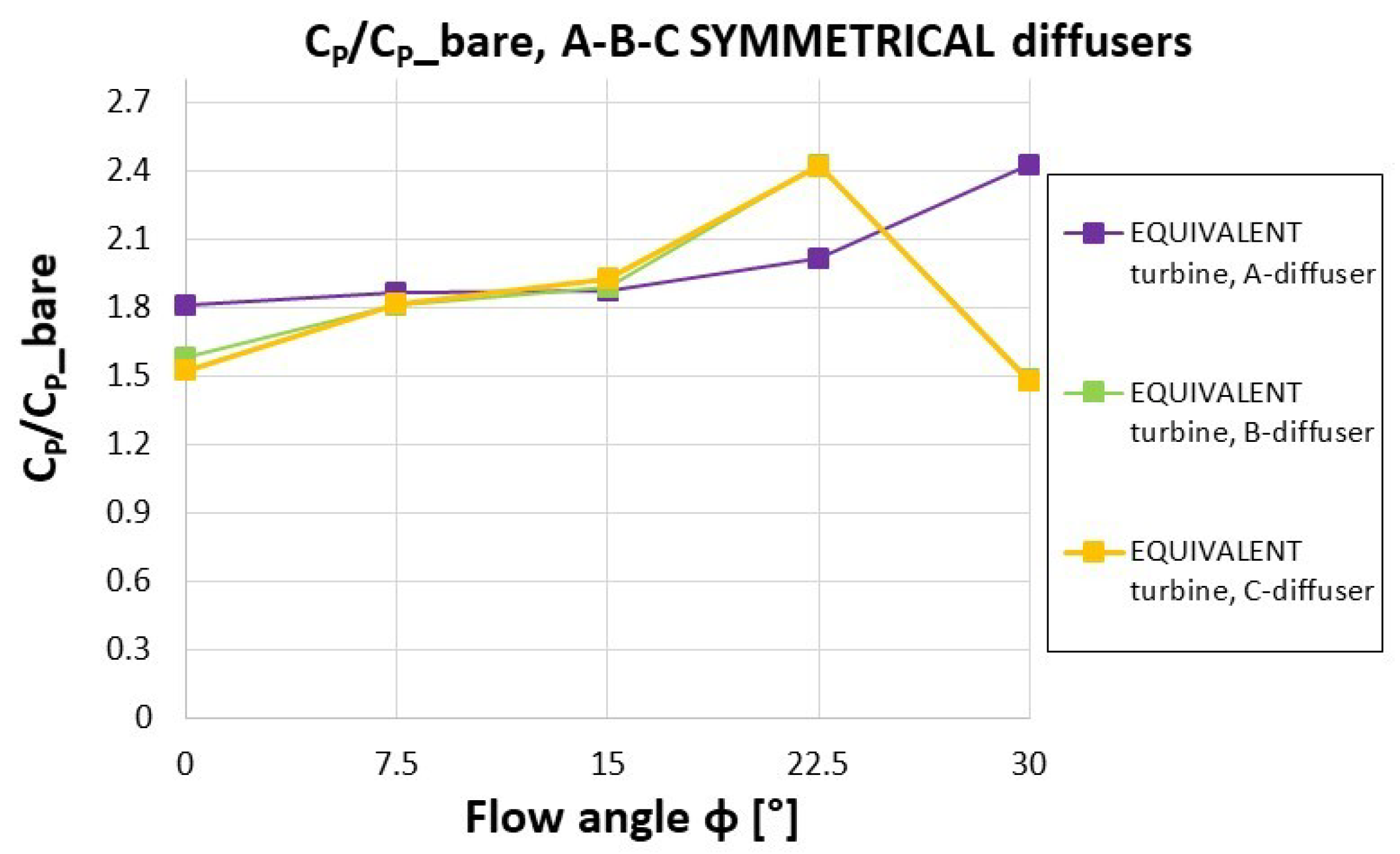
4.3. CP of the Equivalent Turbine
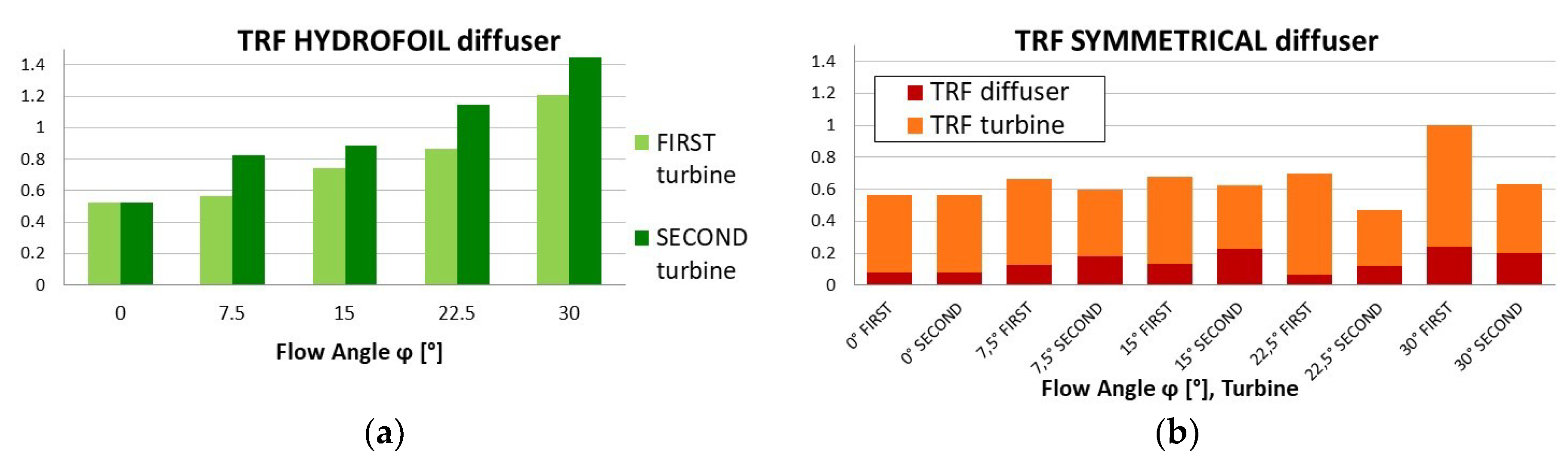
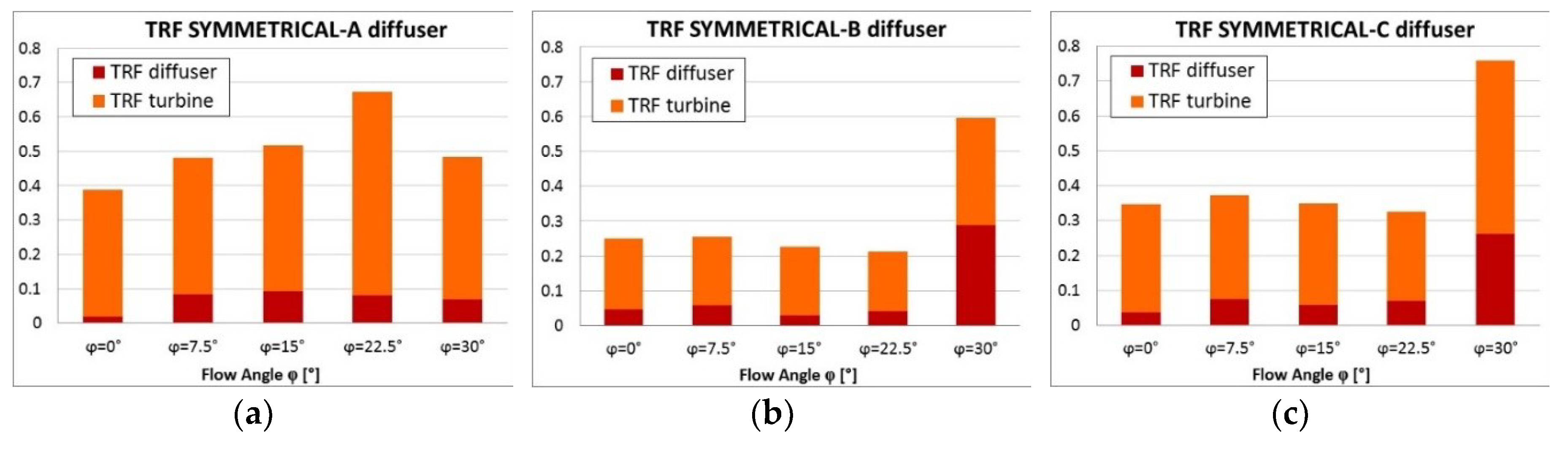
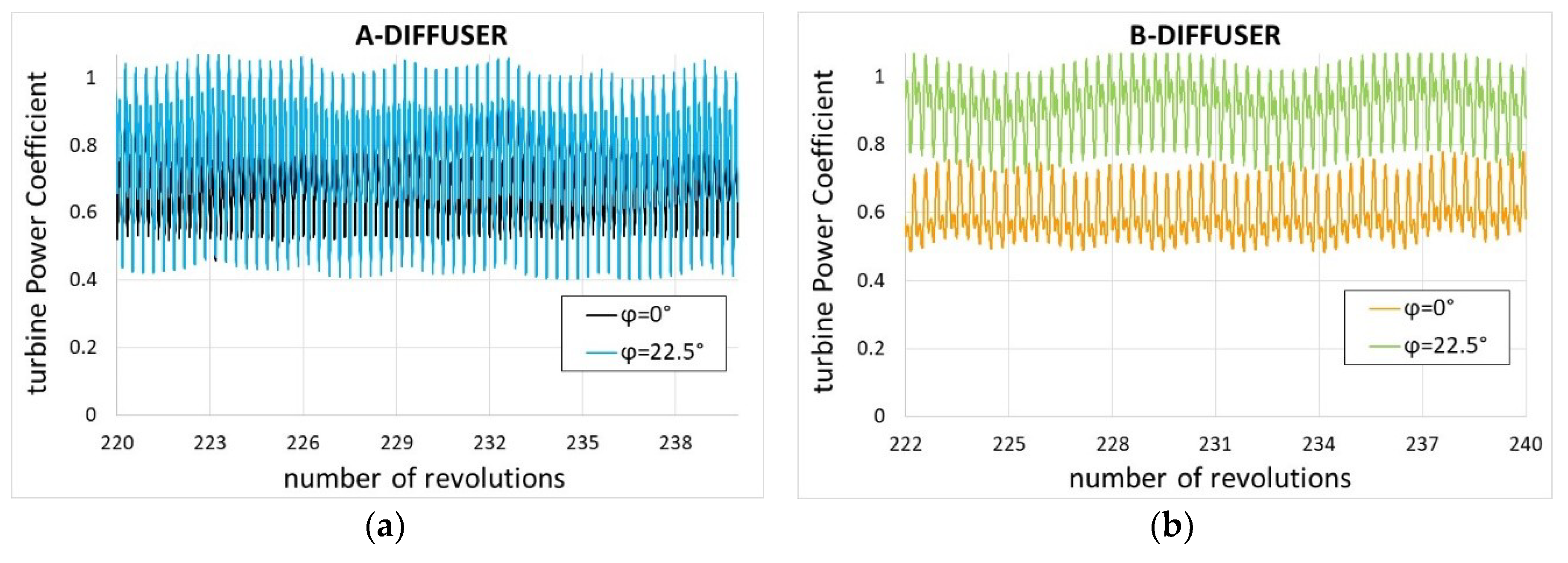
4.4. Torque Ripple
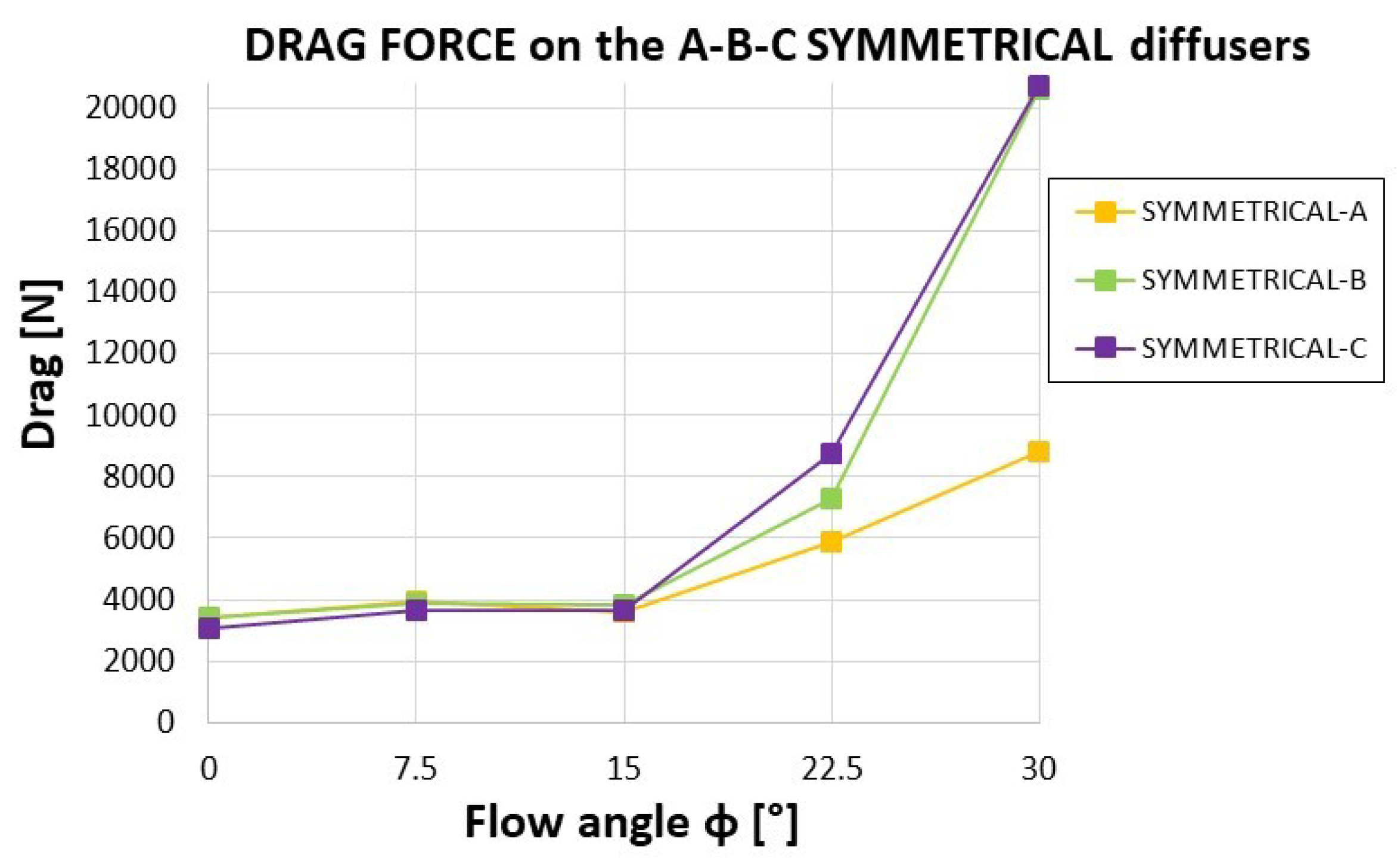
4.5. Drag on the Diffuser
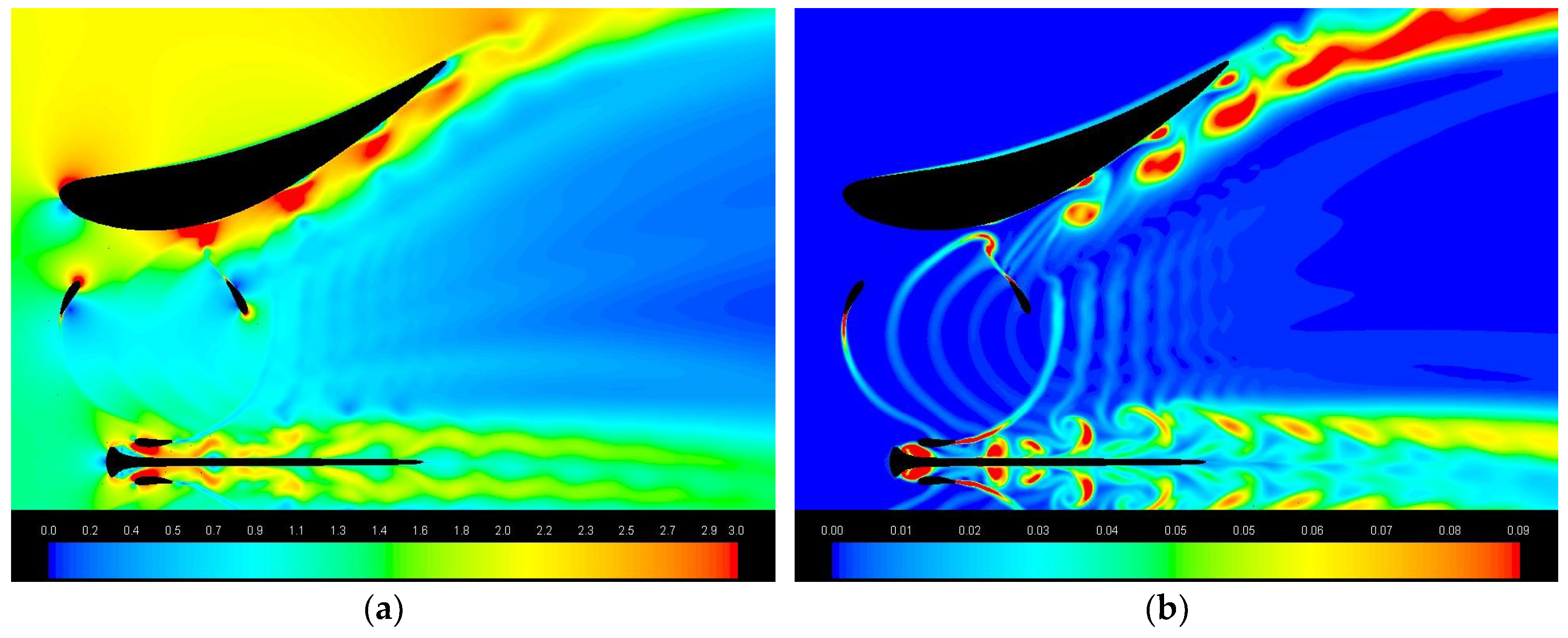
4.6. Wakes
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Latin symbols | |
| AR | turbine aspect ratio [-] |
| B | number of blades [-] |
| CFT | cross flow turbine |
| CP | power coefficient [-] |
| D | turbine diameter [m] |
| D* | equivalent turbine diameter [m] |
| H | blade length [m] |
| R | turbine radius [m] |
| T | torque [Nm] |
| TSR | tip speed ratio [-] |
| TRF | torque ripple factor [-] |
| U∞ | free stream velocity magnitude [m/s] |
| Ux | absolute x-velocity at blade position [m/s] |
| Uy | absolute y-velocity at blade position [m/s] |
| W | flow apparent velocity [m] |
| y+ | dimensionless wall distance [-] |
| Greek symbols | |
| α | angle of attack [°] |
| ϑ | blade azimuthal angle [°] |
| ρ | air density [kg/m3] |
| σ | blade solidity [-] |
| φ | yaw angle of the current [°] |
| Ω | turbine angular velocity [rad/s] |
References
- Scheurich, F.; Brown, R. Vertical-axis wind turbines in oblique flow: Sensitivity to rotor geometry. In Proceedings of the EWEA Annual Event, Brussels, Belgium, 14–17 March 2011. [Google Scholar]
- Bedon, G.; De Betta, S.; Benini, E. A computational assessment of the aerodynamic performance of a tilted Darrieus wind turbine. Wind Eng. Ind. Aerodyn. 2015, 145, 263–269. [Google Scholar] [CrossRef]
- Chowdury, A.M.; Akimoto, H.; Hara, Y. Comparative CFD analysis of Vertical Axis Wind Turbine in upright and tilted configuration. Renew. Energy 2016, 85, 327–337. [Google Scholar] [CrossRef]
- Dabiri, J.O. Potential order-of-magnitude enhancement of wind farm power density via counter-rotating vertical-axis wind turbine arrays. J. Renew. Sustain. Energy 2011, 3, 043104. [Google Scholar] [CrossRef]
- Kinzel, M.; Mulligan, Q.; Dabiri, J.O. Energy exchange in an array of vertical-axis wind turbines. J. Turbul. 2012, 13, 1–13. [Google Scholar] [CrossRef]
- Vergaerde, A.; De Troyer, T.; Kluczewska-Bordier, J.; Parneix, N.; Silvert, F.; Runacres, M.C. Wind tunnel experiments of a pair of interacting vertical-axis wind turbines. In IOP Conf. Series: Journal of Physics; IOP Publishing: Bristol, UK, 2018; Volume 1037, p. 072049. [Google Scholar]
- Foreman, K.M.; Gilbert, B.; Oman, R.A. Diffuser augmentation of wind turbines. Sol. Energy 1977, 20, 305–311. [Google Scholar] [CrossRef]
- Igra, O. Research and development for shrouded wind turbines. Energy Convers. Manag. 1981, 21, 13–48. [Google Scholar] [CrossRef]
- Flay, R.; Nash, T.; Phillips, D. Aerodynamic Analysis and Monitoring of the Vortec7 Diffuser Augmented Wind Turbine; Institution of Professional Engineers New Zealand: Wellington, New Zealand, 1998. [Google Scholar]
- Van Bussel, G.J.W. An assessment of the performance of diffuser augmented wind turbines (DAWTs). In Proceedings of the ASME Joint Engineering Fluid Conference, San Francisco, CA, USA, 18–23 July 1999. [Google Scholar]
- Hansen, M.O.L.; Sørensen, N.N.; Flay, R.G.J. Effect of Placing a Diffuser around a Wind Turbine. Wind Energy 2000, 3, 207–213. [Google Scholar] [CrossRef]
- Ohya, Y.; Uchida, T.; Karasudani, T.; Hasegawa, M.; Kume, H. Numerical studies of flow around a wind turbine equipped with a flanged-diffuser shroud using an actuator-disc model. Wind Eng. 2012, 36, 455–472. [Google Scholar] [CrossRef]
- Goltembott, U.; Ohya, Y.; Yoshida, S.; Jamieson, P. Aerodynamic interaction of diffuser augmented wind turbines in multi-rotor systems. Renew. Energy 2017, 112, 25–34. [Google Scholar] [CrossRef]
- OpenHydro Group Ltd. Available online: www.openhydro.com (accessed on 19 December 2014).
- Lunar Energy. Available online: www.lunarenergy.co.uk (accessed on 19 December 2014).
- Atlantis Resources. Available online: http://atlantisresourcesltd.com (accessed on 21 December 2014).
- Clean Current Power Systems Inc. Available online: www.cleancurrent.com (accessed on 22 December 2014).
- Fleming, C.F.; Willden, R.H.J. Analysis of bi-directional ducted tidal turbine performance. Int. J. Mar. Energy 2016, 16, 162–173. [Google Scholar] [CrossRef]
- Allsop, S.; Peyrard, C.; Thies, P.R.; Boulougouris, E.; Harrison, G.P. Hydrodynamic analysis of a ducted open centre tidal stream turbine using blade element momentum theory. Ocean Eng. 2017, 141, 531–542. [Google Scholar] [CrossRef]
- Blunden, L.S.; Batten, W.M.J.; Bahaj, A.S. Comparing Energy Yields from Fixed and Yawing Horizontal Axis Marine Current Turbines in the English Channel. In Proceedings of the ASME 27th International Conference on Offshore Mechanics and Arctic Engineering, Esturil, Portugal, 15–20 June 2008. [Google Scholar]
- Frost, C.H.; Evans, P.S.; Harrold, M.J.; Mason-Jones, A.; O’Doherty, T.; O’Doherty, D.M. The impact of axial flow misalignment on a tidal turbine. Renew. Energy 2017, 113, 1333–1344. [Google Scholar] [CrossRef]
- Cresswell, N.W.; Ingram, G.L.; Dominy, R.G. The impact of diffuser augmentation on a tidal stream turbine. Ocean Eng. 2015, 108, 155–163. [Google Scholar] [CrossRef]
- Phillips, D.G. An Investigation on Diffuser Augmented Wind Turbine Design. Ph.D. Thesis, University of Auckland, Auckland, New Zealand, 2003. [Google Scholar]
- Foreman, K.M.; Gilbert, B.L. Further Investigations of Diffuser Augmented Wind Turbines Parts I and II; Grumman Research Department: New York, NY, USA, 1979. [Google Scholar]
- Münch-Alligné, C.; Schmid, J.; Richard, S.; Gaspoz, A.; Brunner, N.; Hasmatuchi, V. Experimental Assessment of a New Kinetic Turbine Performance for Artificial Channels. Water 2018, 10, 311. [Google Scholar] [CrossRef]
- Ponta, F.; Dutt, G.S. An improved vertical-axis water-current turbine incorporating a channeling device. Renew. Energy 2000, 20, 223–241. [Google Scholar] [CrossRef]
- Malipeddi, A.R.; Chatterjee, D. Influence of duct geometry on the performance of Darrieus hydroturbine. Renew. Energy 2012, 43, 292–300. [Google Scholar] [CrossRef]
- Geurts, B.; Simão Ferreira, C.J.; Van Zuijlen, A.; Van Bussel, H. Aerodynamic Analysis of a Vertical Axis Wind Turbine in a Diffuser. In Proceedings of the 3rd EWEA Conference—Torque 2010: The Science of making Torque from Wind, Heraklion, Greece, 28–30 June 2010. [Google Scholar]
- Letizia, S.; Zanforlin, S. Hybrid CFD-source Terms Modelling of a Diffuser-augmented Vertical Axis Wind Turbine. Energy Procedia 2016, 10, 1280–1287. [Google Scholar] [CrossRef]
- Dominguez, F.; Achard, J.-L.; Zanette, J.; Corre, C. Fast power output prediction for a single row of ducted cross-flow water turbines using a BEM-RANS approach. Renew. Energy 2016, 8, 658–670. [Google Scholar] [CrossRef]
- Achard, J.L.; Imbault, D.; Tourabi, A. Turbine Engine with Transverse-Flow Hydraulic Turbine Having Reduced Total Lift Force. U.S. Patent US8,827,631 (B2), 9 September 2014. [Google Scholar]
- Zanforlin, S.; Burchi, F.; Bitossi, N. Hydrodynamic interactions between three closely-spaced vertical Axis tidal turbines. Energy Procedia 2016, 101, 520–527. [Google Scholar] [CrossRef]
- Zanforlin, S. Advantages of vertical axis tidal turbines set in close proximity: A comparative CFD investigation in the English Channel. Ocean Eng. 2018, 156, 358–372. [Google Scholar] [CrossRef]
- Maître, T.; Amet, E.; Pellone, C. Modeling of the flow in a Darrieus water turbine: Wall grid refinement analysis and comparison with experiments. Renew. Energy 2013, 51, 497–512. [Google Scholar] [CrossRef]
- Marsh, P.; Ranmuthugala, D.; Penesis, I.; Thomas, G. Three-dimensional numerical simulations of straight-bladed vertical axis tidal turbines investigating power output, torque ripple and mounting forces. Renew. Energy 2015, 83, 67–77. [Google Scholar] [CrossRef]
- Li, C.; Zhu, S.; Xu, Y.; Xiao, Y. 2.5D large eddy simulation of vertical axis wind turbine in consideration of high angle of attack flow. Renew. Energy 2013, 51, 317–330. [Google Scholar] [CrossRef]
- Castelli, M.R.; Monte, A.D.; Quaresimin, M.; Benini, E. Numerical evaluation of aerodynamic and inertial contributions to Darrieus wind turbine blade deformation. Renew. Energy 2013, 51, 101–112. [Google Scholar] [CrossRef]
- Lain, S.; Osorio, C. Simulation and evaluation of a straight-bladed Darrieus-type cross flow marine turbine. J. Sci. Ind. Res. 2010, 69, 906–912. [Google Scholar]
- Menter, F.R. Zonal two equation k-ω turbulence models for aerodynamic flows. In Proceedings of the 24th Fluid Dynamics Conference, Orlando, FL, USA, 6–9 July 1993. AIAA Paper 93-2906. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Wilcox, D.C. Formulation of the k-ω turbulence model revisited. AIAA J. 2008, 46, 2823–2838. [Google Scholar] [CrossRef]
- Bachant, P.; Wosnik, M. Modeling the near-wake of a vertical-axis cross-flow turbine with 2-D and 3-D RANS. J. Renew. Sustain. Energy 2016, 8, 053311. [Google Scholar] [CrossRef]
- FLUENT Training Material—ANSYS Release Version 14.5, Lecture Transient Flow Modeling, Introduction to ANSYS Fluent; ANSYS Inc.: Canonsburg, PA, USA, 2012.
- Balduzzi, F.; Bianchini, A.; Maleci, R.; Ferrara, G.; Ferrari, L. Critical issues in the CFD simulation of Darrieus wind turbines. Renew. Energy 2016, 85, 419–435. [Google Scholar] [CrossRef]
- Ferreira, C.J.S.; Bijl, H.; van Bussel, G.; van Kuik, G. Simulating Dynamic Stall in a 2D VAWT: Modeling strategy, verification and validation with Particle Image Velocimetry data. J. Phys. Conf. Ser. 2007, 75, 12023. [Google Scholar] [CrossRef]
- Zanforlin, S.; Deluca, S. Effects of the Reynolds number and the tip losses on the optimal aspect ratio of straight-bladed Vertical Axis Wind Turbines. Energy 2018, 148, 179–195. [Google Scholar] [CrossRef]
- Almohammadi, K.M.; Ingham, D.B.; Ma, L.; Pourkashan, M. Computational fluid dynamics (CFD) mesh independency techniques for a straight blade vertical axis wind turbine. Energy 2013, 58, 483–493. [Google Scholar] [CrossRef]
- Zanforlin, S.; Nishino, T. Fluid dynamic mechanisms of enhanced power generation by closely spaced vertical axis wind turbines. Renew. Energy 2016, 99, 1213–1226. [Google Scholar] [CrossRef]
- Zanforlin, S.; Letizia, S. Effects of upstream buildings on the performance of a synergistic roof-and-diffuser augmentation system for cross flow wind turbines. J Wind Eng. Ind. Aerodyn. 2019, 184, 329–341. [Google Scholar] [CrossRef]
- Shives, M.; Crawford, C. Developing an empirical model for ducted tidal turbine performance using numerical simulation results. Proc. Inst. Mech. Eng. Part A J. Power Energy 2011, 226, 112–125. [Google Scholar] [CrossRef]
- Sanz, W.; Kelterer, M.; Pecnik, R.; Marn, A.; Göttlich, E. Numerical Investigation of the Effect of Tip Leakage Flow on an Aggressive S-Shaped Intermediate Turbine Duct. In Proceedings of the ASME Turbo Expo 2009: Power for Land, Sea, and Air, Volume 7: Turbomachinery, Parts A and B, Orland, FL, USA, 8–12 June 2009. [Google Scholar]
- Kwong, A.H.M.; Dowling, A.P. Active boundary-layer control in diffusers. AIAA J. 1994, 32, 2409–2414. [Google Scholar] [CrossRef]
- Castelli, M.R.; Pavesi, G.; Battisti, L.; Benini, E.; Ardizzon, G. Modeling Strategy and Numerical Validation for a Darrieus Vertical Axis Micro-Wind Turbine. In Proceedings of the International Mechanical Engineering Congress & Exposition, Vancouver, BC, Canada, 12–18 November 2010. [Google Scholar]
- Setoguchi, T.; Shiomi, N.; Kanedo, K. Development of Two-Way Diffuser for Tidal Energy Conversion System. Renew. Energy 2004, 29, 1757–1771. [Google Scholar] [CrossRef]
- Ohya, Y.; Karasudani, T.; Sakurai, A.; Abe, K.; Inoue, M. Development of a shrouded wind turbine with a flanged diffuser. J. Wind Eng. Ind. Aerodyn. 2008, 96, 524–539. [Google Scholar] [CrossRef]


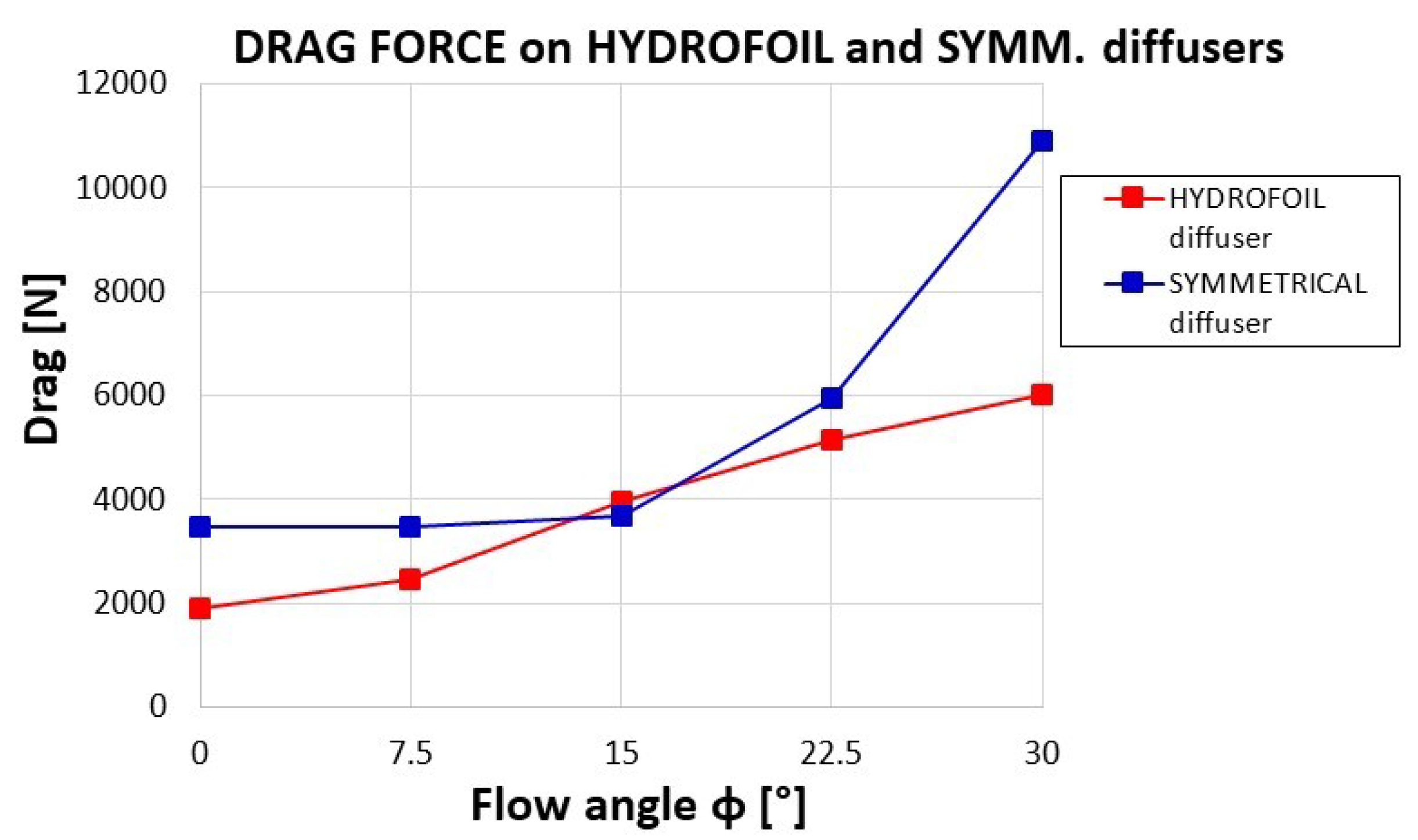
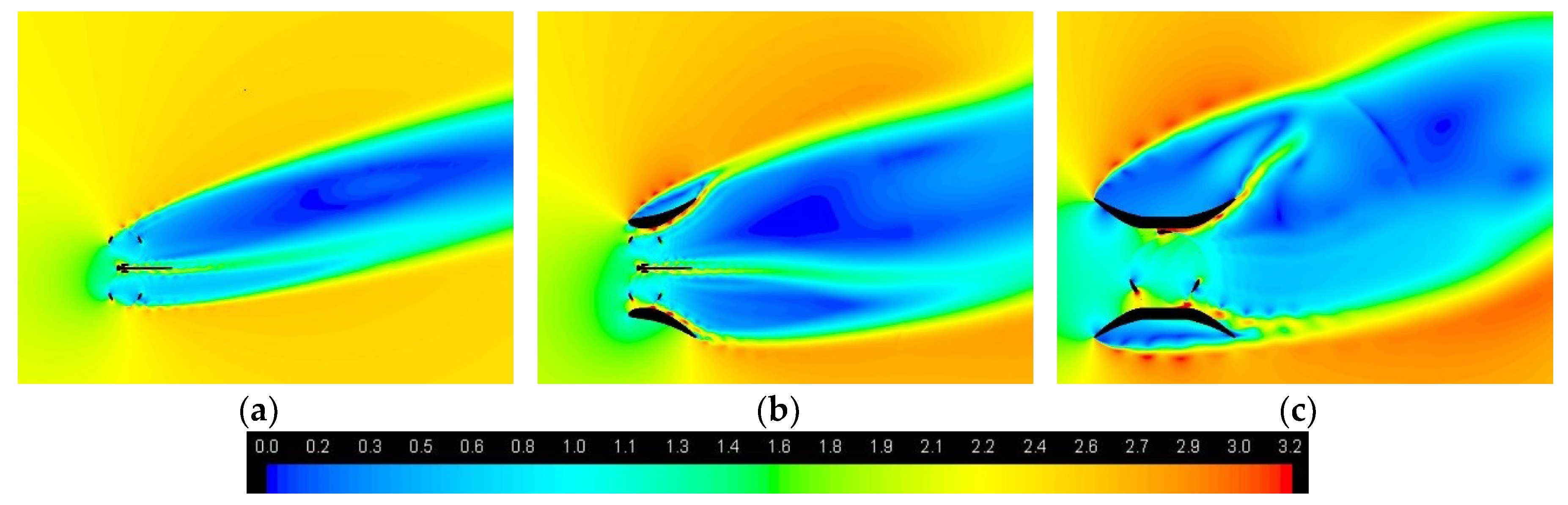
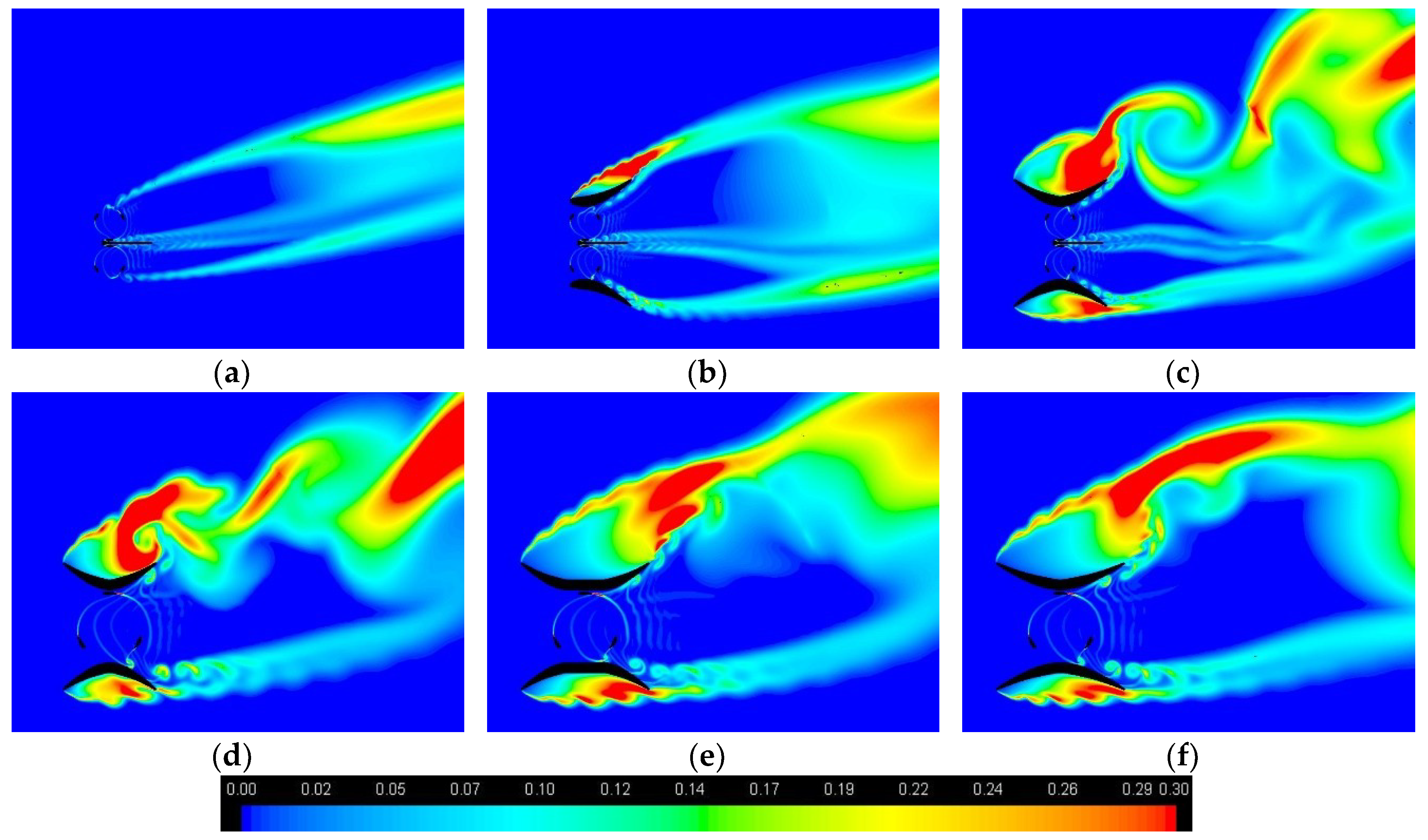
| Diffuser Type | Yaw, ϕ | CP Bare | CP First | CP Second | CP Averaged | Overall TRF First | Overall TRF Second | Drag [N] |
|---|---|---|---|---|---|---|---|---|
| Hydrofoil shaped | 0° | 0.350 | 0.572 | 0.572 | 0.572 | 0.528 | 0.528 | 1884 |
| 7.5° | 0.350 | 0.618 | 0.577 | 0.598 | 0.568 | 0.823 | 2467 | |
| 15° | 0.350 | 0.619 | 0.587 | 0.603 | 0.743 | 0.887 | 3951 | |
| 22.5° | 0.350 | 0.536 | 0.503 | 0.520 | 0.867 | 1.145 | 5144 | |
| 30° | 0.350 | 0.505 | 0.484 | 0.495 | 1.206 | 1.445 | 6009 | |
| Symmetrical | 0° | 0.350 | 0.614 | 0.614 | 0.614 | 0.567 | 0.567 | 3483 |
| 7.5° | 0.350 | 0.670 | 0.695 | 0.683 | 0.617 | 0.533 | 3451 | |
| 15° | 0.350 | 0.653 | 0.712 | 0.683 | 0.682 | 0.624 | 3664 | |
| 22.5° | 0.350 | 0.695 | 0.751 | 0.723 | 0.672 | 0.471 | 5943 | |
| 30° | 0.350 | 0.824 | 0.946 | 0.885 | 0.930 | 0.630 | 10,893 |
| Symmetrical Diffuser Type | Yaw Angle, ϕ | CP Bare | CP Ducted | Overall TRF | Drag Force [N] |
|---|---|---|---|---|---|
| A | 0° | 0.378 | 0.683 | 0.388 | 3425 |
| 7.5° | 0.378 | 0.728 | 0.482 | 3925 | |
| 15° | 0.378 | 0.707 | 0.517 | 3609 | |
| 22.5° | 0.378 | 0.761 | 0.484 | 5899 | |
| 30° | 0.378 | 0.918 | 0.672 | 8809 | |
| B | 0° | 0.378 | 0.598 | 0.251 | 3428 |
| 7.5° | 0.378 | 0.683 | 0.255 | 3865 | |
| 15° | 0.378 | 0.715 | 0.227 | 3846 | |
| 22.5° | 0.378 | 0.916 | 0.212 | 7292 | |
| 30° | 0.378 | 0.562 | 0.596 | 20636 | |
| C | 0° | 0.378 | 0.576 | 0.347 | 3053 |
| 7.5° | 0.378 | 0.686 | 0.372 | 3675 | |
| 15° | 0.378 | 0.729 | 0.349 | 3678 | |
| 22.5° | 0.378 | 0.915 | 0.326 | 8734 | |
| 30° | 0.378 | 0.558 | 0.759 | 20709 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zanforlin, S.; Buzzi, F.; Francesconi, M. Performance Analysis of Hydrofoil Shaped and Bi-Directional Diffusers for Cross Flow Tidal Turbines in Single and Double-Rotor Configurations. Energies 2019, 12, 272. https://doi.org/10.3390/en12020272
Zanforlin S, Buzzi F, Francesconi M. Performance Analysis of Hydrofoil Shaped and Bi-Directional Diffusers for Cross Flow Tidal Turbines in Single and Double-Rotor Configurations. Energies. 2019; 12(2):272. https://doi.org/10.3390/en12020272
Chicago/Turabian StyleZanforlin, Stefania, Fulvio Buzzi, and Marika Francesconi. 2019. "Performance Analysis of Hydrofoil Shaped and Bi-Directional Diffusers for Cross Flow Tidal Turbines in Single and Double-Rotor Configurations" Energies 12, no. 2: 272. https://doi.org/10.3390/en12020272
APA StyleZanforlin, S., Buzzi, F., & Francesconi, M. (2019). Performance Analysis of Hydrofoil Shaped and Bi-Directional Diffusers for Cross Flow Tidal Turbines in Single and Double-Rotor Configurations. Energies, 12(2), 272. https://doi.org/10.3390/en12020272






