Flow and Fast Fourier Transform Analyses for Tip Clearance Effect in an Operating Kaplan Turbine
Abstract
1. Introduction
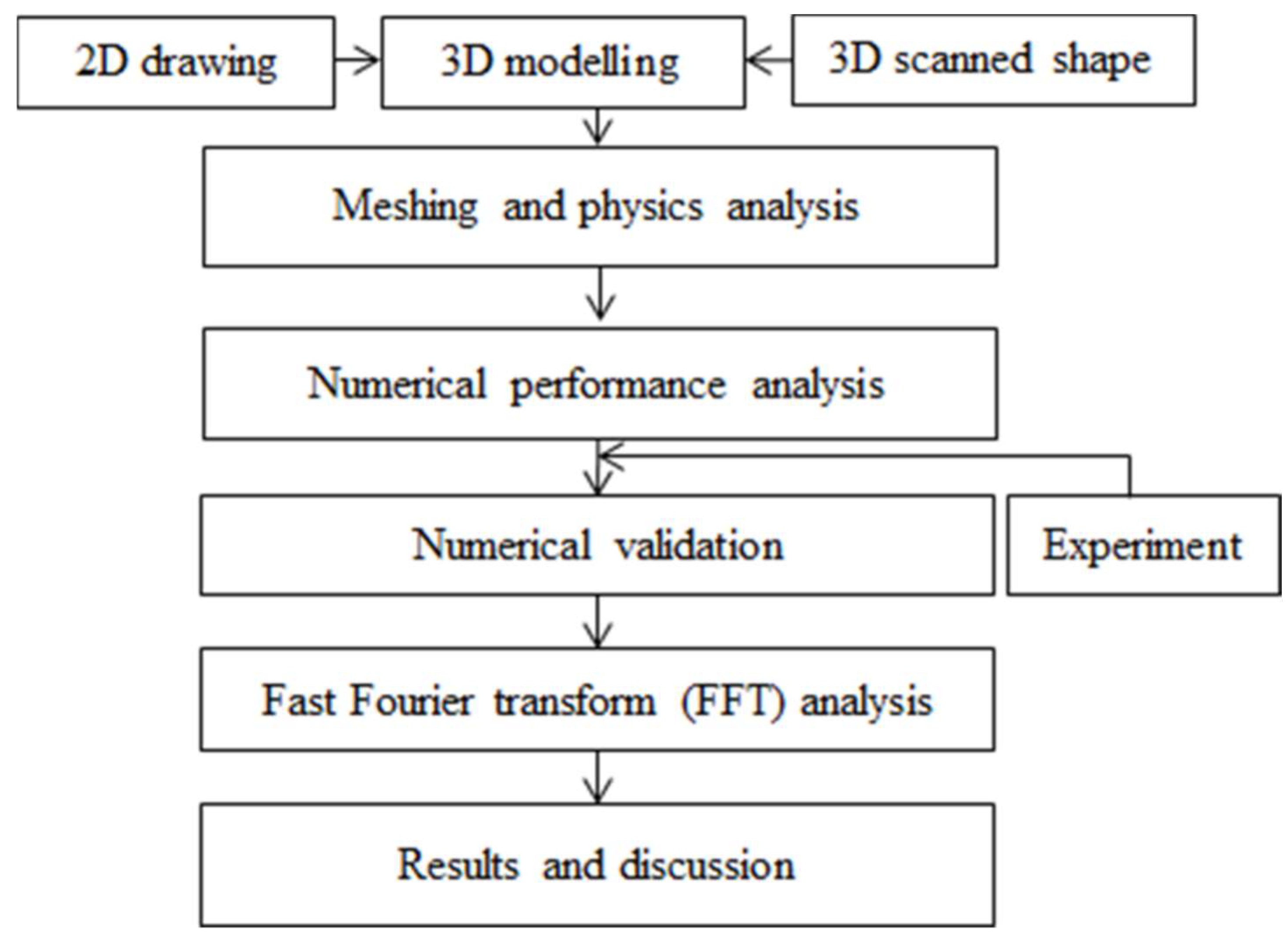
2. Numerical Analysis
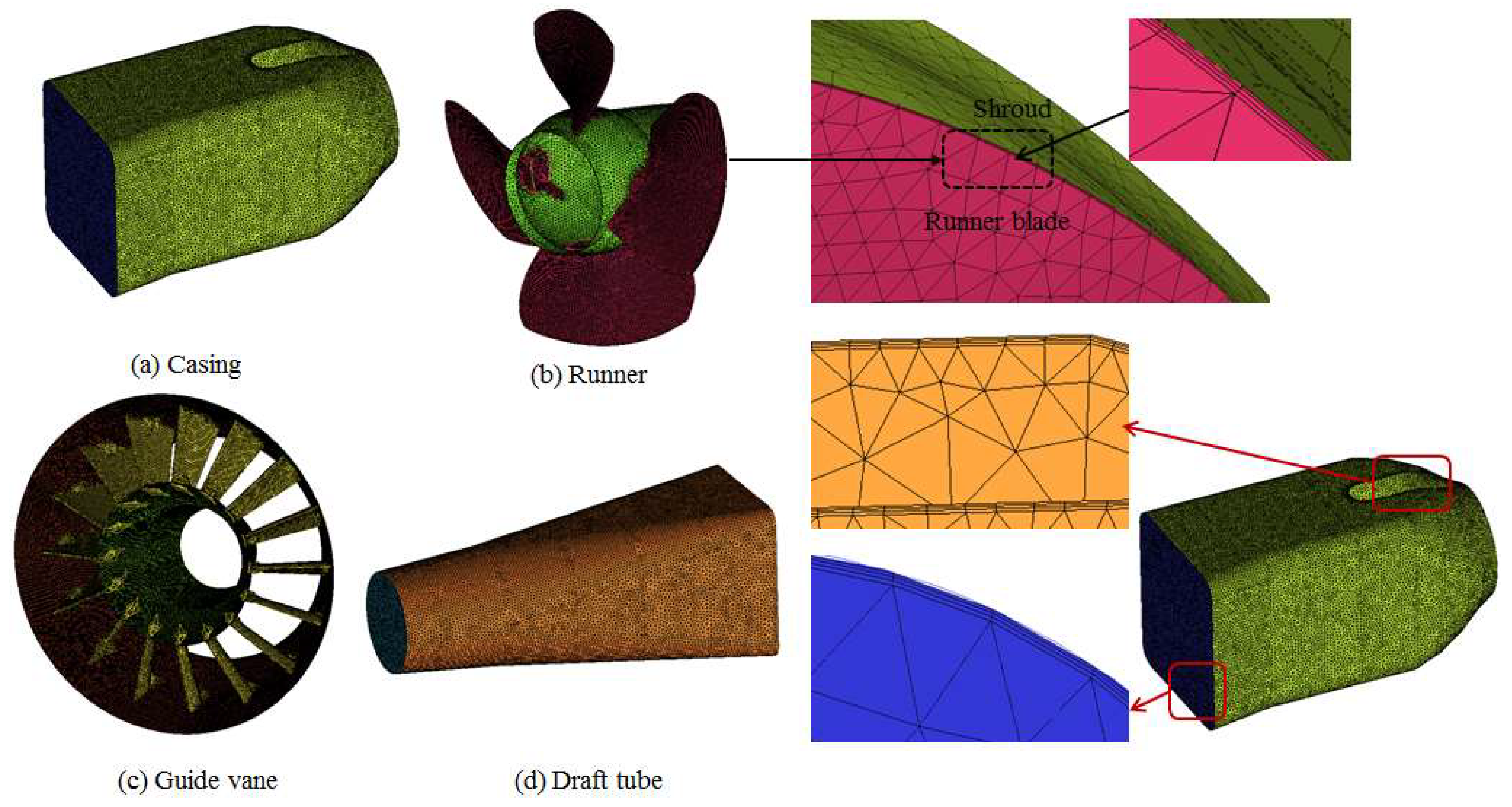
2.1. Geometrical Model and Meshing
2.2. Governing Equations
2.3. Calculation of Hydraulic Performance
3. Results and Discussion
3.1. Validation of Numerical Results
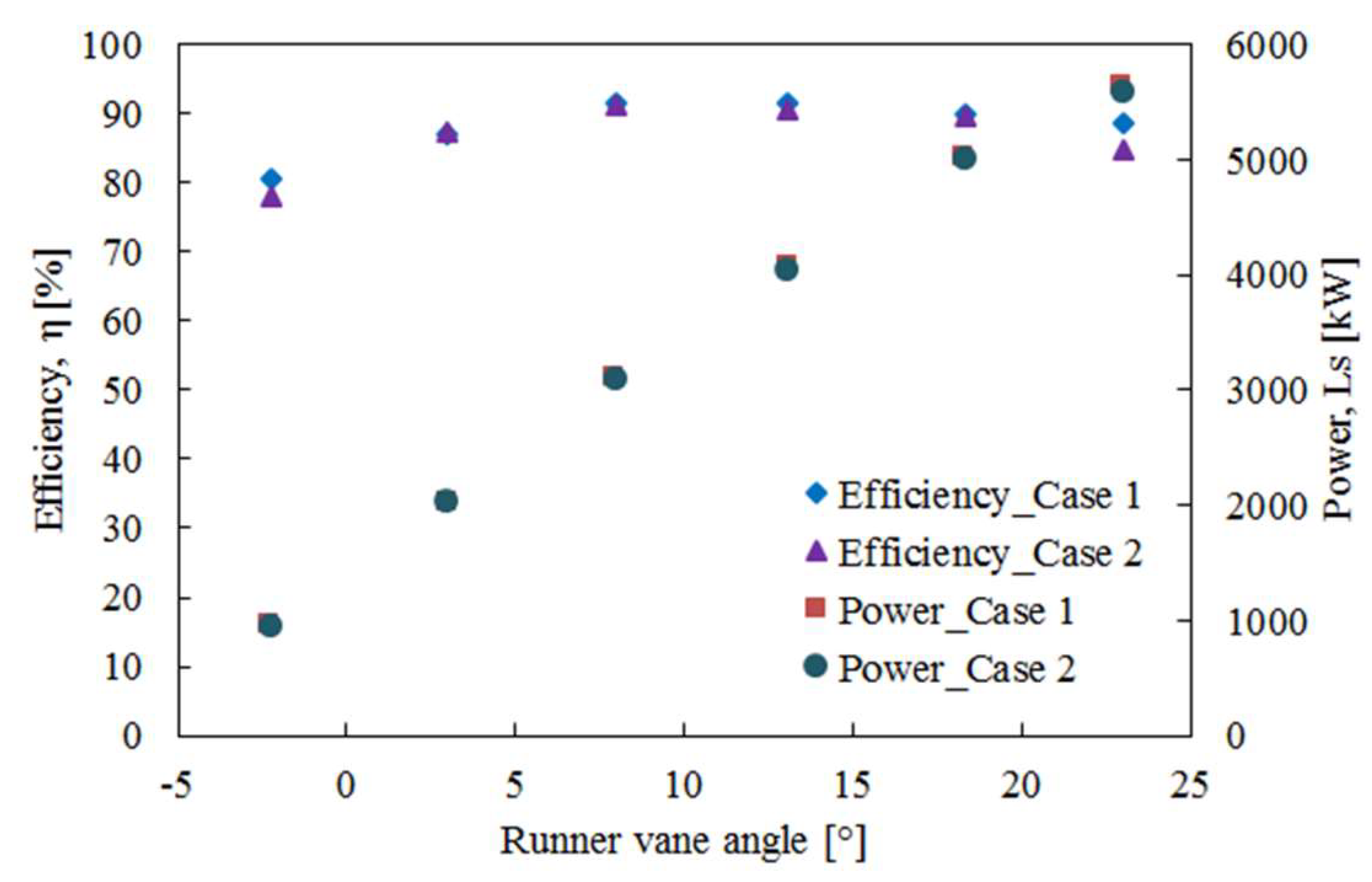
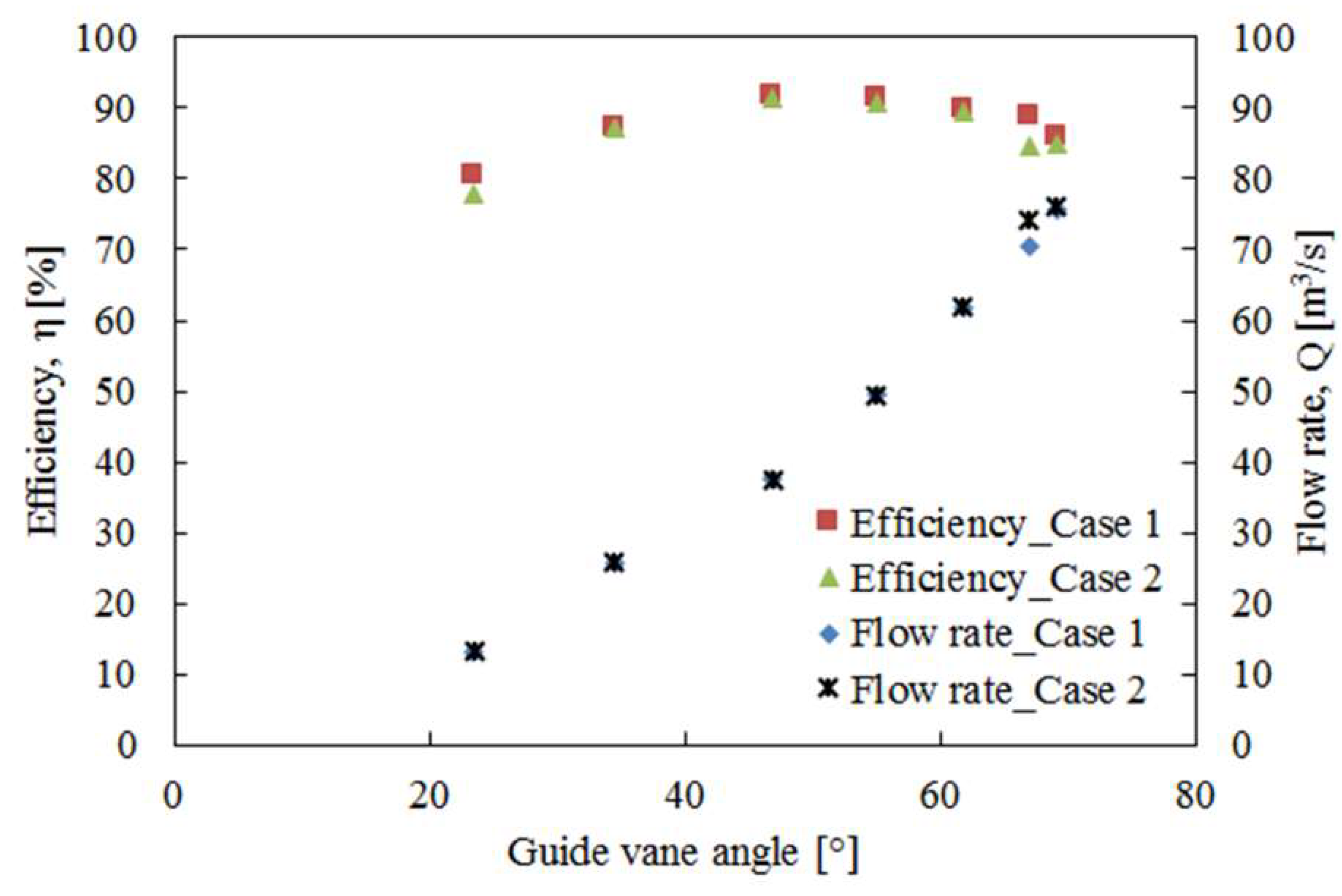
3.2. Performance Characteristics
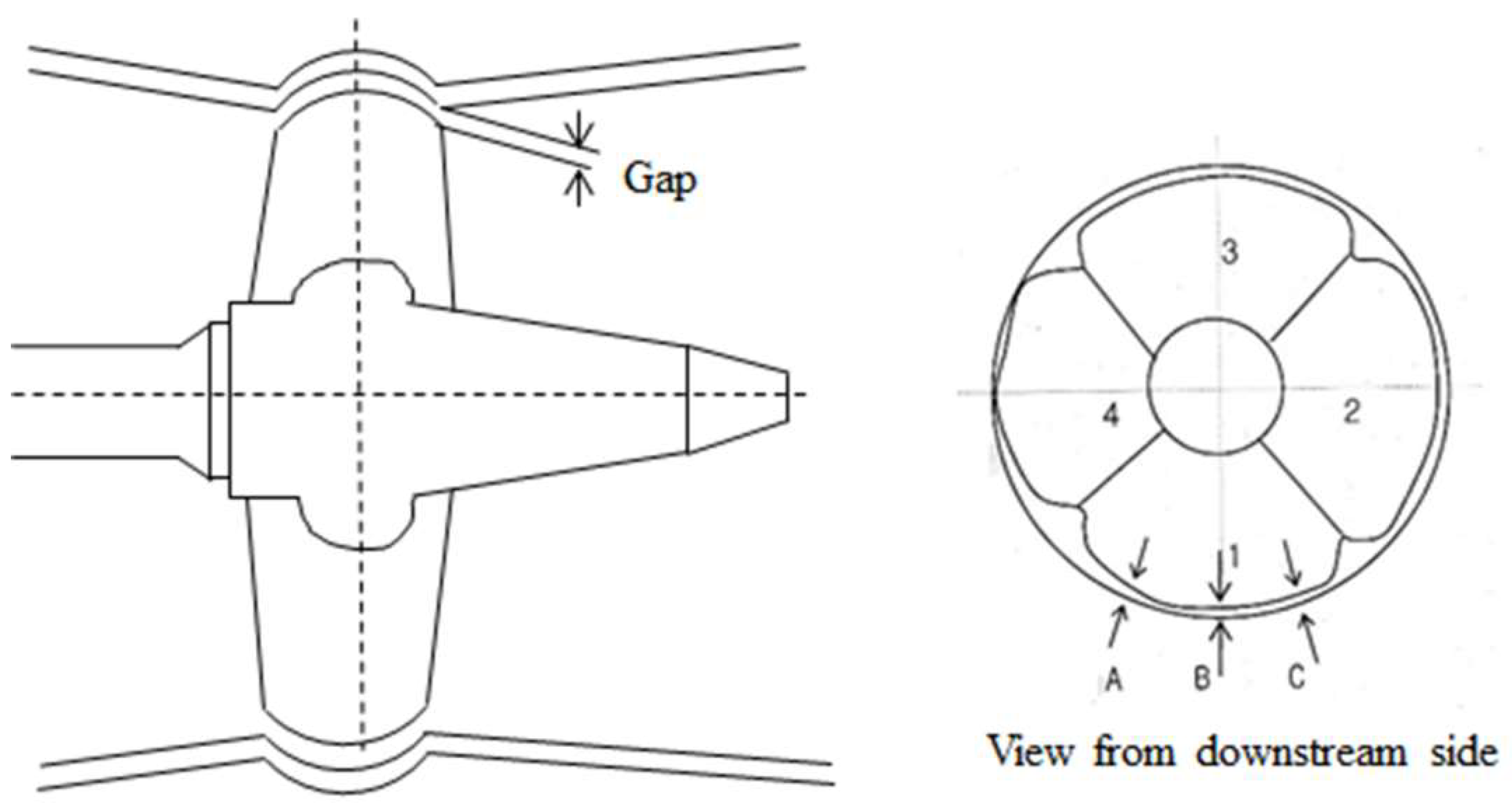
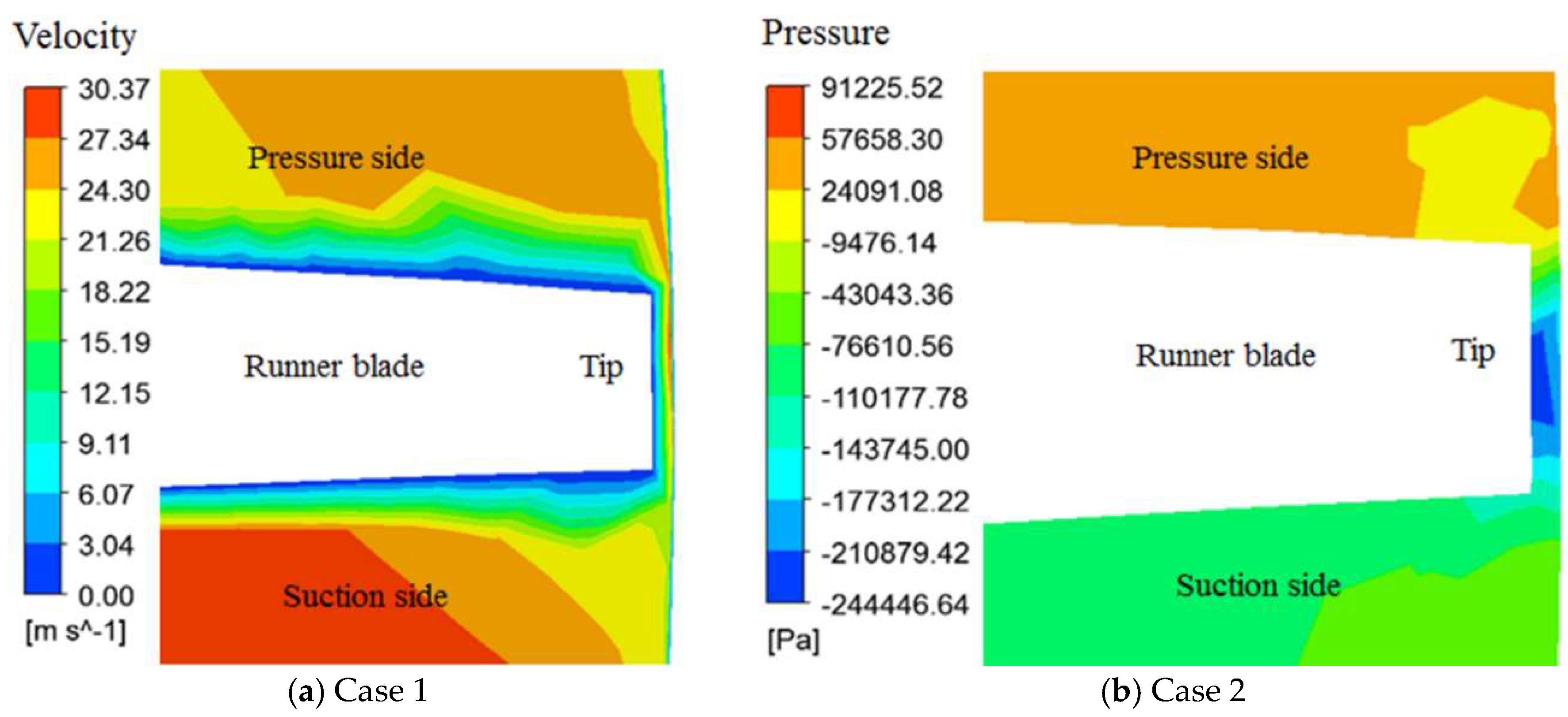
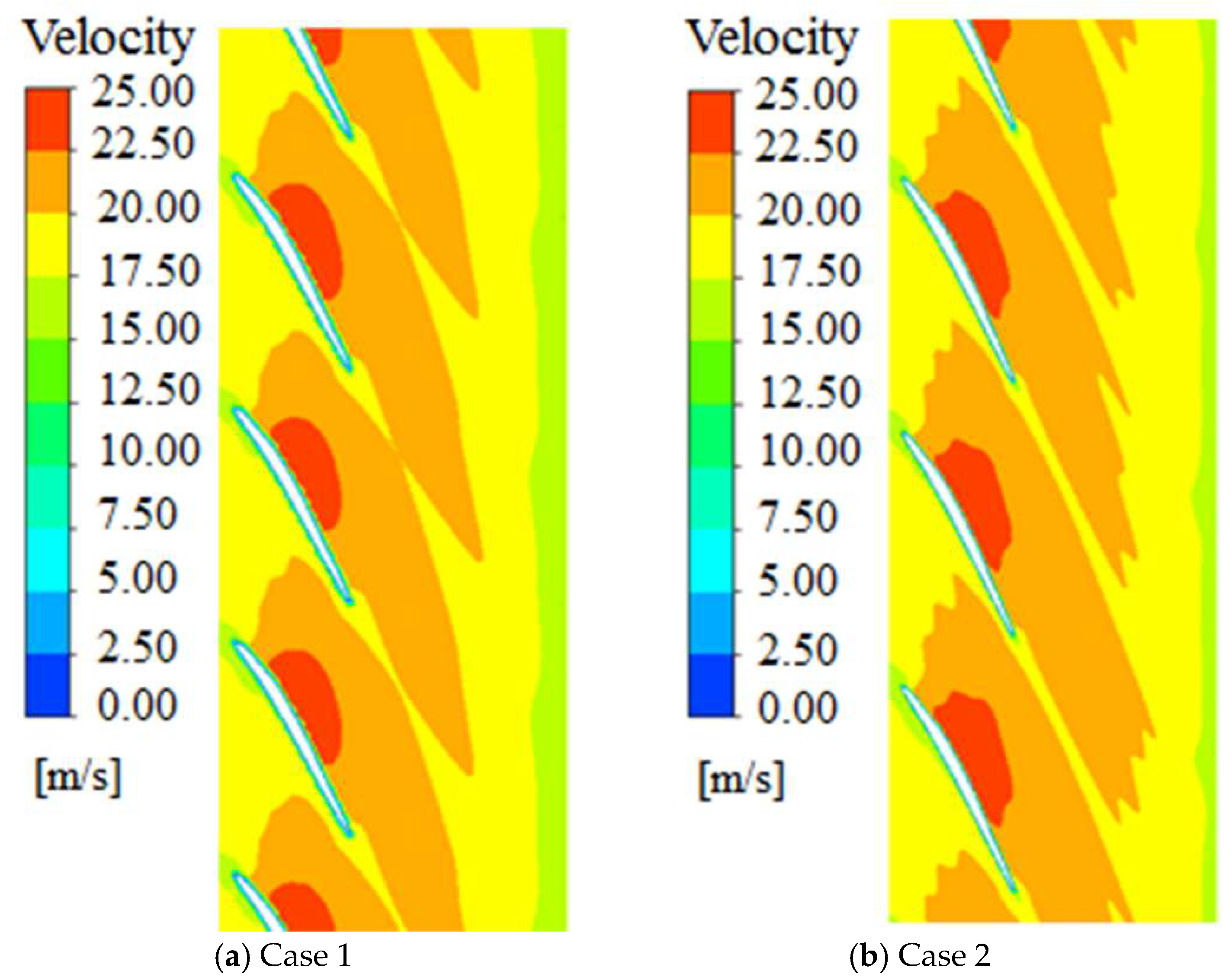
3.3. Effect of Tip Clearance
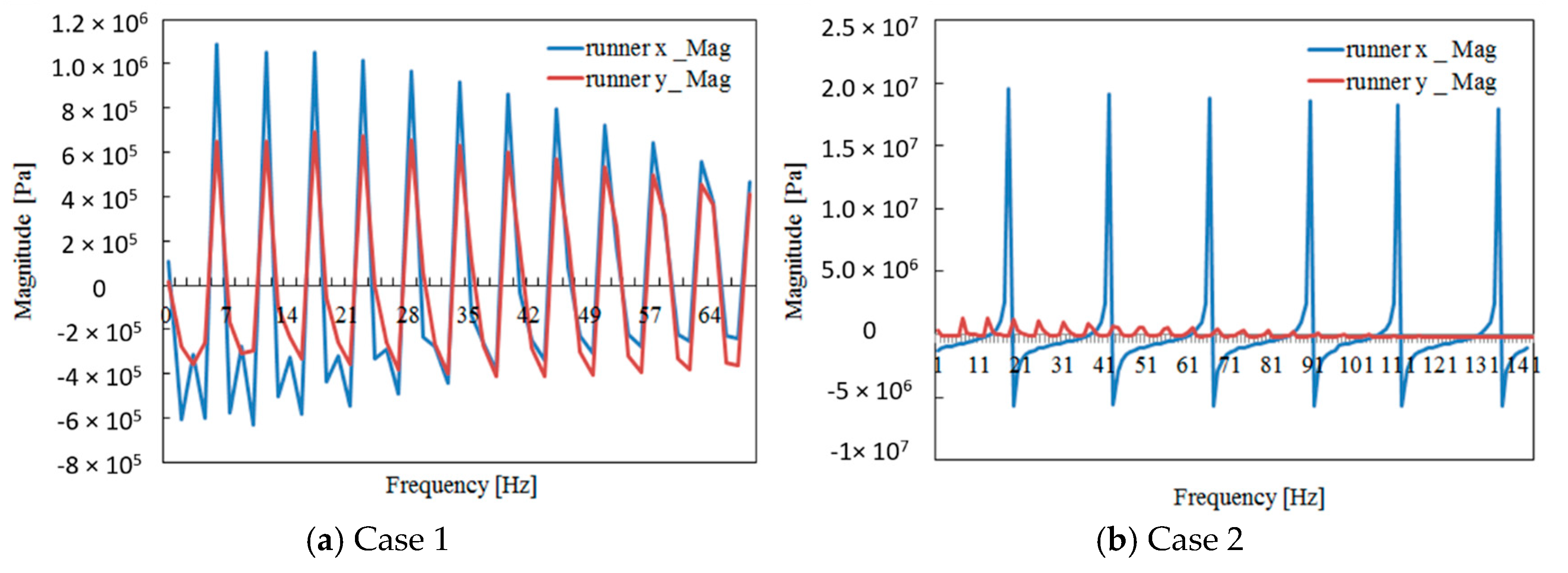
3.4. Pressure Pulsation Analysis
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| CFD | Computational Fluid dynamics |
| FFT | Fast Fourier Transformation |
| GCI | Grid convergence index |
| g | Acceleration due to gravity, m/s2 |
| H | Head, m |
| Ls | Shaft power, kW |
| p | Pressure, Pa |
| Q | Flow rate, m3/s |
| r | Mesh ratio |
| Si | Area of a face cell |
| Tshaft | Torque, N·m |
| t | Time, s |
| Velocity vector, m/s | |
| v | Velocity of fluid, m/s |
| Vni | Velocity along the face normal vector |
| x | Component of position vector, m |
| z | Elevation of water level, m |
| Greek Symbols | |
| ρ | Density, kg/m3 |
| Turbine efficiency, % | |
| ω | Angular velocity, rad/s |
| μ | Viscosity, Pa·s |
| Subscript | |
| i, j | Tensor indices |
| 1, 2 | Inlet, outlet |
References
- Fox, R.W.; Mcdonald, A.T.; Pritchard, P.J.; Leylegain, J.C. Fluid Mechanics, 8th ed.; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Wu, H.; Feng, J.J.; Wu, G.K.; Luo, X.Q. Numerical investigation of hub clearance flow in a Kaplan turbine. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 072026. [Google Scholar] [CrossRef]
- Roussopoulos, K.; Monkewitz, P.A. Measurements of Tip Vortex Characteristics and the Effect of an Anti-Cavitation Lip on a Model Kaplan Turbine Blade. Flow Turbul. Combust. 2000, 64, 119–144. [Google Scholar] [CrossRef]
- Chen, G.T.; Greitzer, E.M.; Tan, C.S.; Marble, F.E. Similarity analysis of compressor tip clearance flow structure. ASME J. Turbomach. 1991, 113, 260–269. [Google Scholar] [CrossRef]
- Song, S.J.; Martinez-Sanchez, M. Rotordynamic effects due to turbine leakage flow: Part I, Blade scale effects. ASME J. Turbomach. 1997, 119, 695–703. [Google Scholar]
- Storer, J.A.; Cumpsty, N.A. Tip leakage flow in axial compressors. ASME J. Turbomach. 1991, 113, 252–259. [Google Scholar] [CrossRef]
- Heyes, F.J.G.; Hodson, H.P. Measurement and prediction of tip clearance flow in linear turbine cascades. ASME J. Turbomach. 1993, 115, 376–382, 698. [Google Scholar] [CrossRef]
- Murayama, M.; Yoshida, Y.; Tsujimoto, Y. Unsteady Tip Leakage Vortex Cavitation Originating From the Tip Clearance of an Oscillating Hydrofoil. ASME J. Fluids Eng. 2006, 128, 421–429. [Google Scholar] [CrossRef]
- Cojocaru, V.; Balint, D.; Campian, C.V.; Nedelcu, D.; Jianu, C. Numerical Investigations of Flow on the Kaplan Turbine Runner Blade Anticavitation Lip with Modified Cross Section, Recent Researches in Mechanics. In Proceedings of the 2nd International Conference on Theoretical and Applied Mechanics 2011 (TAM ‘11), Corfu Island, Greece, 14–16 July 2011; pp. 215–218. [Google Scholar]
- Hutton, S.P. Component Losses in Kaplan Turbines and the Prediction of Efficiency from Model Tests. Proc. Inst. Mech. Eng. 1954, 168, 743–762. [Google Scholar] [CrossRef]
- Laborde, R.; Chantrel, P.; Mory, M. Tip Clearance and Tip Vortex Cavitation in Axial Flow Pump. ASME J. Fluids Eng. 1997, 119, 680–685. [Google Scholar] [CrossRef]
- Tallman, J.J.; Lakshminarayana, B.B. Numerical Simulation of Tip Leakage Flows in Axial Flow Turbines, With Emphasis on Flow Physics: Part I—Effect of Tip Clearance Height. ASME J. Turbomach. 2000, 123, 314–323. [Google Scholar] [CrossRef]
- Nilsson, H.; Davidson, L. Validations of CFD against detailed velocity and pressure measurements in water turbine runner flow. Int. J. Numer. Methods Fluids 2003, 41, 863–879. [Google Scholar] [CrossRef]
- Gehrer, A.; Schmidl, R.; Sadnik, D. Kaplan turbine runner optimization by numerical flow simulation (CFD) and an evolutionary algorithm. In Proceedings of the 23rd IAHR Symposium on Hydraulic Machinery and Systems, Yokohama, Japan, 17–21 October 2006. [Google Scholar]
- Bodkhe, R.G.; Nandurkar, Y.Y.; Akant, S.S.; Banker, S.L. Experimental analysis on Kaplan turbine to determine performance characteristics curve at part load conditions. Int. J. Res. Eng. Applied Sci. 2015, 3, 37–41. [Google Scholar]
- Anup, K.C.; Thapa, B.; Lee, Y.-H. Transient numerical analysis of rotor–stator interaction in a Francis turbine. Renew. Energy 2014, 65, 227–235. [Google Scholar]
- Wang, F.J.; Li, X.Q.; MA, J.M.; Yang, M. Experimental investigation of characteristic frequency in unsteady hydraulic behaviour of a large hydraulic turbine. J. Hydrodyn. 2009, 21, 12–19. [Google Scholar] [CrossRef]
- Su, W.T.; Li, X.B.; Lan, C.F.; Ah, S.; Wang, J.S.; Li, F.C. Chaotic dynamic characteristics of pressure fluctuation signals in hydro-turbine. J. Mech. Sci. Technol. 2016, 30, 5009–5017. [Google Scholar] [CrossRef]
- Glowacz, A. Fault diagnosis of single-phase induction motor based on acoustic signals. Mech. Syst. Signal Process. 2018, 117, 65–80. [Google Scholar] [CrossRef]
- Glowacz, A. Acoustic-based fault diagnosis of commutator motor. Electronics 2018, 7, 299. [Google Scholar] [CrossRef]
- Fei, S.-W. Fault Diagnosis of Bearing by Utilizing LWT-SPSR-SVD-Based RVM with Binary Gravitational Search Algorithm. Shock Vib. 2018, 2018, 1–8. [Google Scholar] [CrossRef]
- Caesarendra, W.; Tjahjowidodo, T. A Review of Feature Extraction Methods in Vibration-Based Condition Monitoring and Its Application for Degradation Trend Estimation of Low-Speed Slew Bearing. Machines 2017, 5, 21. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, S.; Dou, H.-S.; Wu, S.; Chen, T. Numerical prediction and similarity study of pressure fluctuation in a prototype Kaplan turbine and the model turbine. Comput. Fluids 2012, 56, 128–142. [Google Scholar] [CrossRef]
- Rivetti, A.; Lucino, C.; Liscia, S.; Muguerza, D.; Avellan, F. Pressure pulsation in Kaplan turbines: Prototype- CFD comparison. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 062035. [Google Scholar] [CrossRef]
- Drtina, P.; Sallaberger, M. Hydraulic turbines—Basic principles and state-of-the art computational fluid dynamics applications. Proc. Inst. Mech. Eng. Part C. 1999, 213, 85–102. [Google Scholar] [CrossRef]
- Zhou, L.J.; Wang, Z.; Xiao, R.; Luo, Y. Analysis of dynamic stresses in Kaplan turbine blades. Eng. Comput. 2007, 24, 753–762. [Google Scholar] [CrossRef]
- Onoda, T.; Ito, N.; Hironobu, Y. Unusual condition monitoring based on support vector machines for hydroelectric power plants. In Proceedings of the IEEE Congress on Evolutionary Computation, Hong Kong, China, 1–6 June 2008. [Google Scholar]
- Vázquez, J.A.; Cloud, C.H.; Eizember, R.J. Simplified modal analysis for the plant machinery engineer. In Proceedings of the Asia Turbomachinery and Pump Symp., Marina Bay Sands, Singapore, 22–25 February 2016. [Google Scholar]
- Ansys Inc. ANSYS-CFX (CFX Introduction, CFX Reference Guide, CFX Tutorials, CFX-Pre User’s Guide, CFX-Solver Manager User’s Guide, Theory Guide); Release 16.00; Ansys Inc.: Cannonsburg, PA, USA, 2016. [Google Scholar]
- Trivedi, C.; Cervantes, M.J.; Gandhi, B.K.; Dahlhaug, O.G. Experimental and Numerical Studies for a High Head Francis Turbine at Several Operating Points. ASME J. Fluids Eng. 2013, 135, 111102. [Google Scholar] [CrossRef]
- Bergstrom, J.; Gebart, R. Estimation of Numerical Accuracy for the Flow Field in a Draft Tube. Int. J. Num. Meth. Heat Fluid Flow 1999, 9, 472–486. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure for Estimation and Reporting of Uncertainty due to Discretization in CFD Applications. ASME J. Fluids Eng. 2008, 130, 078001. [Google Scholar]
- Friziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics, 3rd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Choi, H.J.; Zullah, M.A.; Roh, H.W.; Ha, P.S.; Oh, S.Y.; Lee, Y.H. CFD validation of performance improvement of a 500 kW Francis turbine. Renew. Energy 2013, 54, 111–123. [Google Scholar] [CrossRef]
- Georgiadis, N.J.; Yoder, D.A.; Engblorn, W.B. Evaluation of modified two-equation turbulence models for jet flow predictions. AIAA J. 2006, 44, 3107–3114. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD, 1st ed.; DCW Industries, Inc.: La Cañada Flintridge, CA, USA, 1994. [Google Scholar]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]



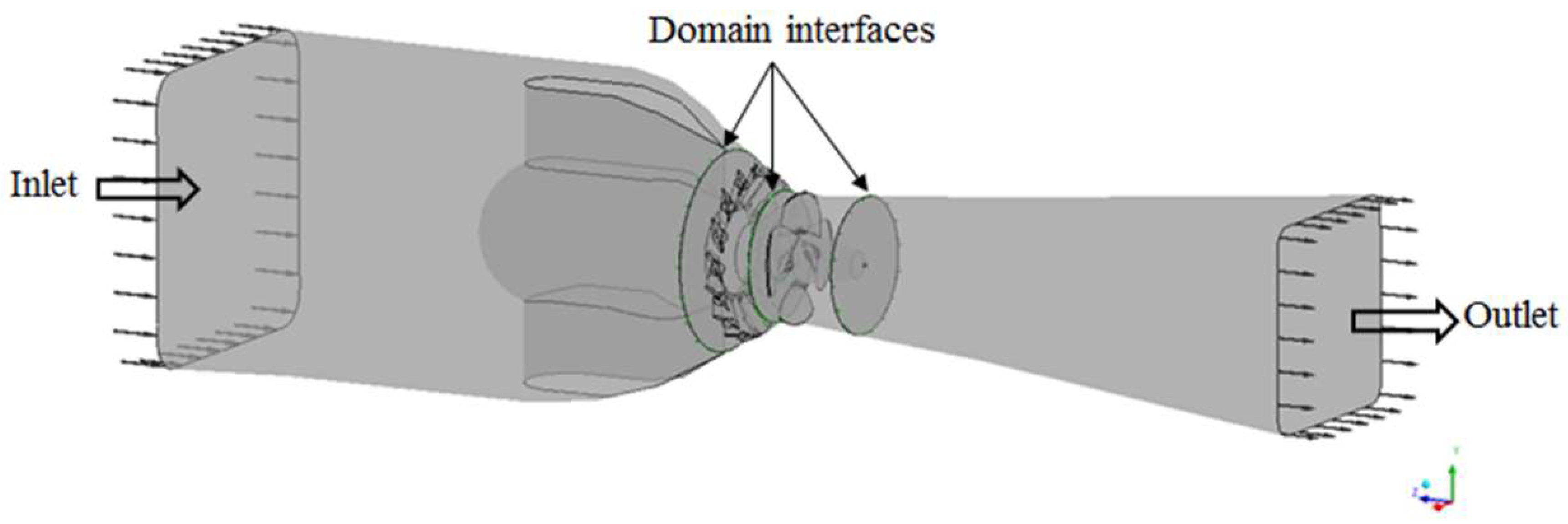




| Description | Dimension |
|---|---|
| Runner outlet diameter | 1648.25 mm |
| Head | 9.2 m |
| Flow rate | 75.3 m3/s |
| Max. Power | 6000 kW |
| Rotational speed | 171.4 rpm |
| Runner blade | 4 |
| Guide vane | 16 |
| Description | Elements | Nodes | Y+ |
|---|---|---|---|
| Casing | 3,495,838 | 694,056 | ~478 |
| Guide vane | 2,744,459 | 520,788 | ~276 |
| Runner | 7,054,423 | 1,313,645 | ~597 |
| Draft tube | 3,212,250 | 638,744 | ~121 |
| Total | 1,6506,970 | 3,167,233 |
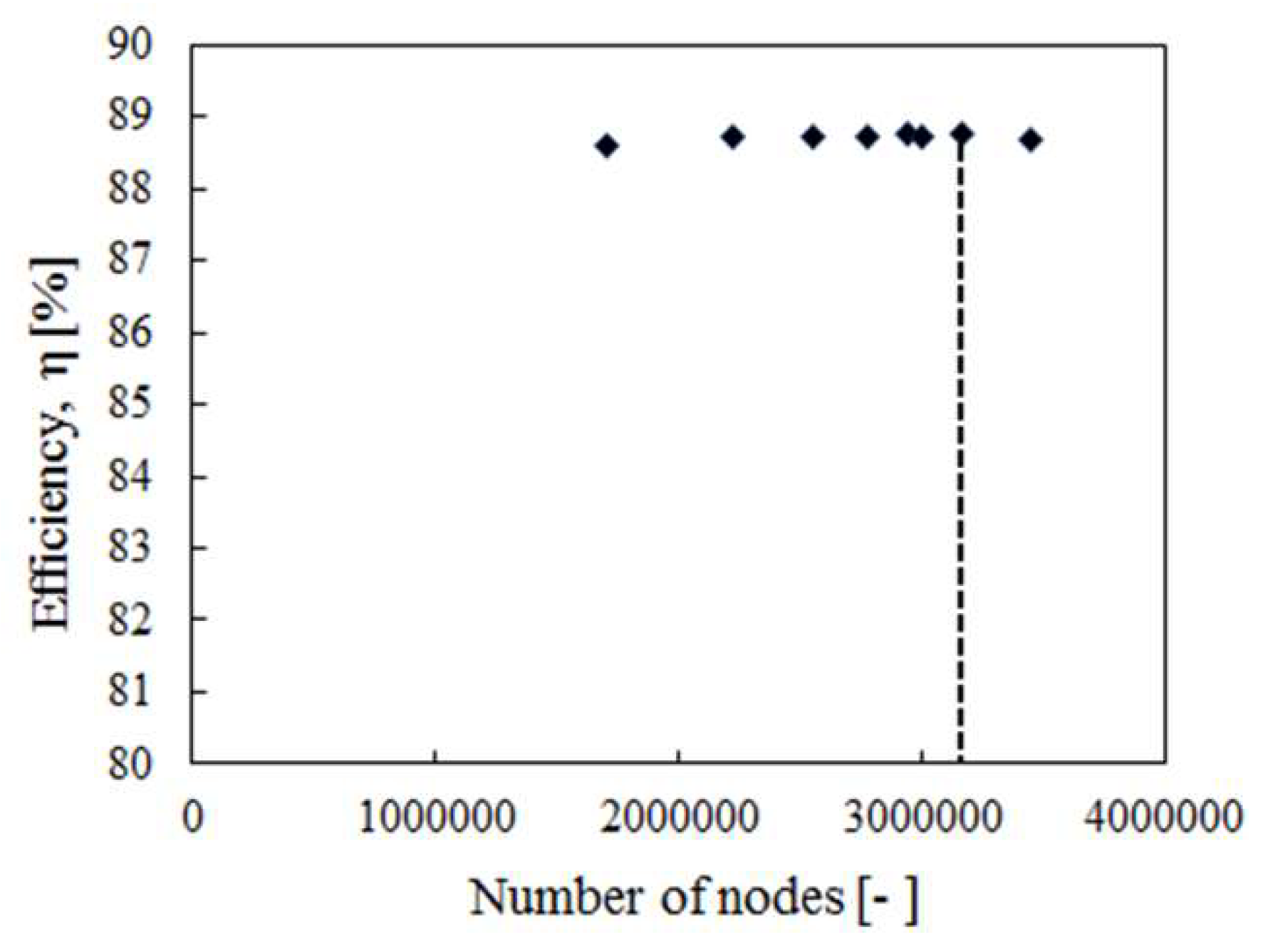
| No. | Nodes | Grid Ratio, r | Efficiency (%) | Error, εa | GCI |
|---|---|---|---|---|---|
| 1 | 1698866 | 1.31 | 88.602 | 0.11738 | 0.2047 |
| 2 | 2225771 | 1.14 | 88.706 | 0.00676 | 0.0269 |
| 3 | 2551448 | 1.08 | 88.712 | 0.03382 | 0.2359 |
| 4 | 2770562 | 1.14 | 88.742 | 0.00789 | 0.0321 |
| 5 | 3167233 | 1.07 | 88.749 | 0.00225 | 0.0171 |
| 6 | 2935178 | 0.97 | 88.747 | 0.02028 | 0.5708 |
| 7 | 3002617 | 0.86 | 88.729 | 0.03156 | 0.1619 |
| No. | Guide Vane Angle (°) | Runner Vane Angle (°) | Elements | Nodes |
|---|---|---|---|---|
| 1 | 23.5 | −2.25 | 6,292,574 | 1,213,316 |
| 2 | 34.5 | 3 | 11,690,834 | 2,142,607 |
| 3 | 46.87 | 7.95 | 8,418,222 | 1,576,519 |
| 4 | 55 | 13.07 | 6,119,611 | 1,185,878 |
| 5 | 61.82 | 18.3 | 6,118,300 | 1,185,676 |
| 6 | 67 | 23 | 16,506,970 | 3,167,233 |
| 7 | 68.5 | 23 | 11,685,688 | 2,141,639 |
| 8 | 69.1 | 25 | 12,626,332 | 2,305,743 |
| 9 | 72 | 25 | 12,628,024 | 2,306,005 |
| No. | Guide Vane Angle (°) | Runner Vane Angle (°) | Elements | Nodes |
|---|---|---|---|---|
| 1 | 23.5 | −2.25 | 11,109,862 | 2,007,133 |
| 2 | 34.5 | 3 | 42,082,030 | 7,466,191 |
| 3 | 46.87 | 7.95 | 8,783,048 | 1,643,035 |
| 4 | 55 | 13.07 | 6,647,494 | 1,281,519 |
| 5 | 61.82 | 18.3 | 14,069,184 | 2,603,090 |
| 6 | 67 | 23 | 27,291,793 | 4,937,129 |
| 7 | 68.5 | 23 | 12,210,473 | 2,236,618 |
| 8 | 69.1 | 25 | 18,238,111 | 3,309,172 |
| 9 | 72 | 25 | 18,239,803 | 3,309,434 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.-H.; Rakibuzzaman, M.; Kim, K.; Suh, S.-H. Flow and Fast Fourier Transform Analyses for Tip Clearance Effect in an Operating Kaplan Turbine. Energies 2019, 12, 264. https://doi.org/10.3390/en12020264
Kim H-H, Rakibuzzaman M, Kim K, Suh S-H. Flow and Fast Fourier Transform Analyses for Tip Clearance Effect in an Operating Kaplan Turbine. Energies. 2019; 12(2):264. https://doi.org/10.3390/en12020264
Chicago/Turabian StyleKim, Hyoung-Ho, Md Rakibuzzaman, Kyungwuk Kim, and Sang-Ho Suh. 2019. "Flow and Fast Fourier Transform Analyses for Tip Clearance Effect in an Operating Kaplan Turbine" Energies 12, no. 2: 264. https://doi.org/10.3390/en12020264
APA StyleKim, H.-H., Rakibuzzaman, M., Kim, K., & Suh, S.-H. (2019). Flow and Fast Fourier Transform Analyses for Tip Clearance Effect in an Operating Kaplan Turbine. Energies, 12(2), 264. https://doi.org/10.3390/en12020264







