Wind Speed and Power Ultra Short-Term Robust Forecasting Based on Takagi–Sugeno Fuzzy Model
Abstract
1. Introduction
2. Methodology
2.1. The Approach of Takagi–Sugeno (T–S) Fuzzy Model
2.2. Fuzzy C-Means (FCM) Algorithm
- Step (1)
- Give an initial membership matrix U0; Set ε a small positive number; Input data set Z to be clustered; Set the number of cluster set C, the fuzzy index m and the iteration l = 0;
- Step (2)
- Obtain the updated clustering center vi according to (1);
- Step (3)
- Obtain the updated distance norm and the objective function according to (2) and (3);
- Step (4)
- Obtain the update membership matrix according to (4);
- Step (5)
- Stop the iteration when ‖Ji+1 − Ji‖<ε, otherwise, set l = l + 1, return to Step 2;
2.3. Recursive Least Squares (RLS) Algorithm
- Step (1)
- Determine the input and the output data sequence according to the measured data;
- Step (2)
- Set the initial values for θ(k) and P(k);
- Step (3)
- Compute θ(k), P(k), w(k) as shown in (5);
- Step (4)
- Set k = k + 1, go to Step 3;
3. Proposed Forecasting Model for Wind Speed and Wind Power
3.1. Flow Work of Forecasting Model Based on T–S Fuzzy Model
3.2. Error Index
3.3. Parameters
3.4. Input Variables
4. Case Study
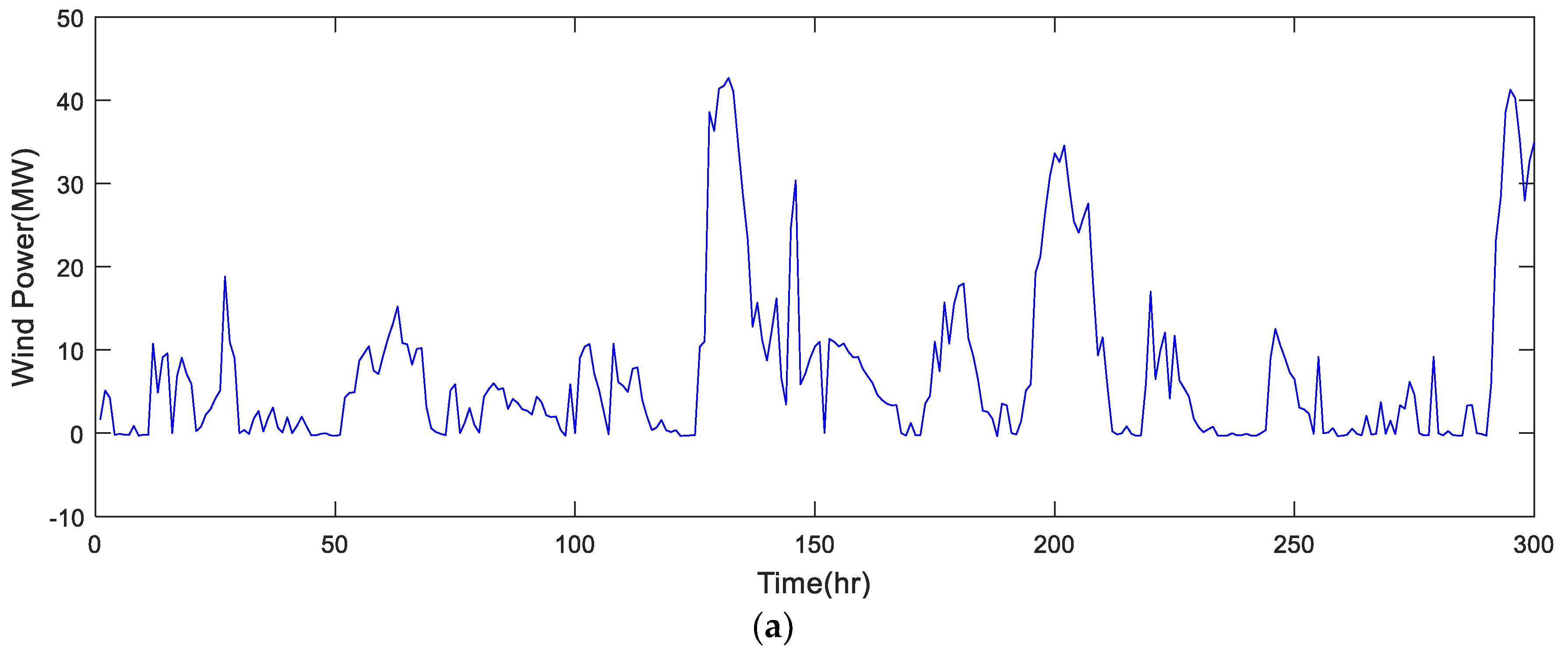
4.1. Data Sets
4.2. Data Processing
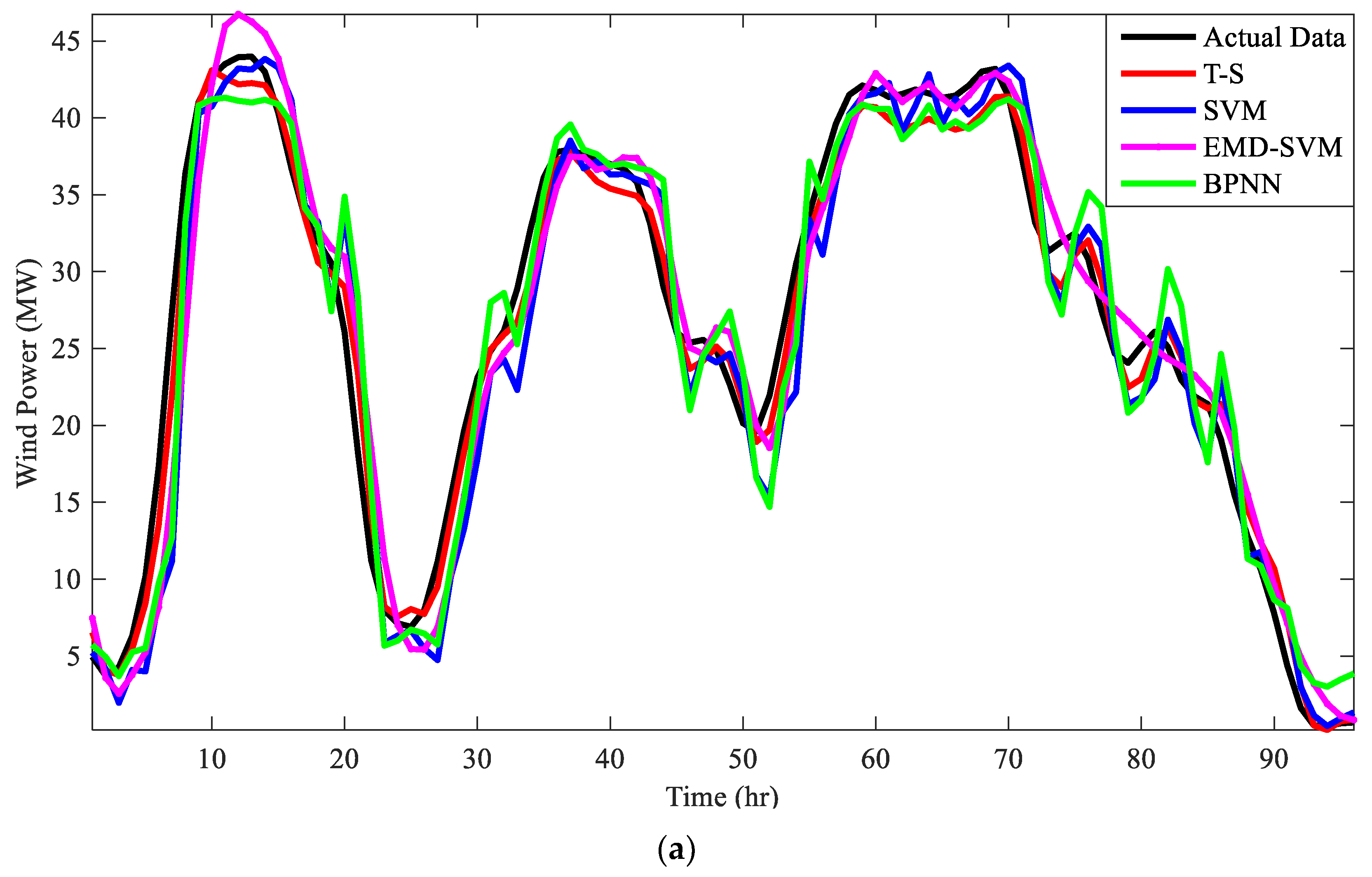
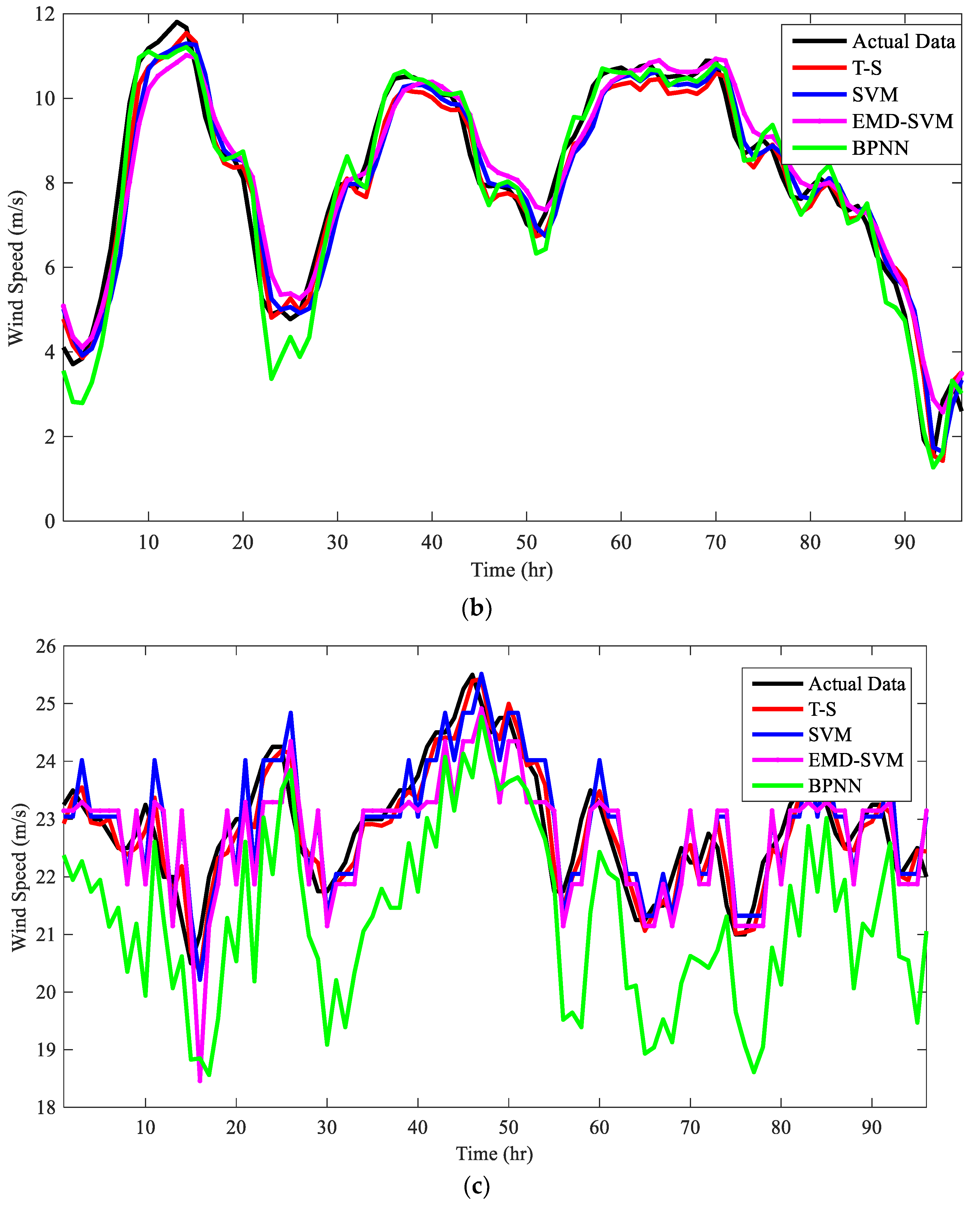
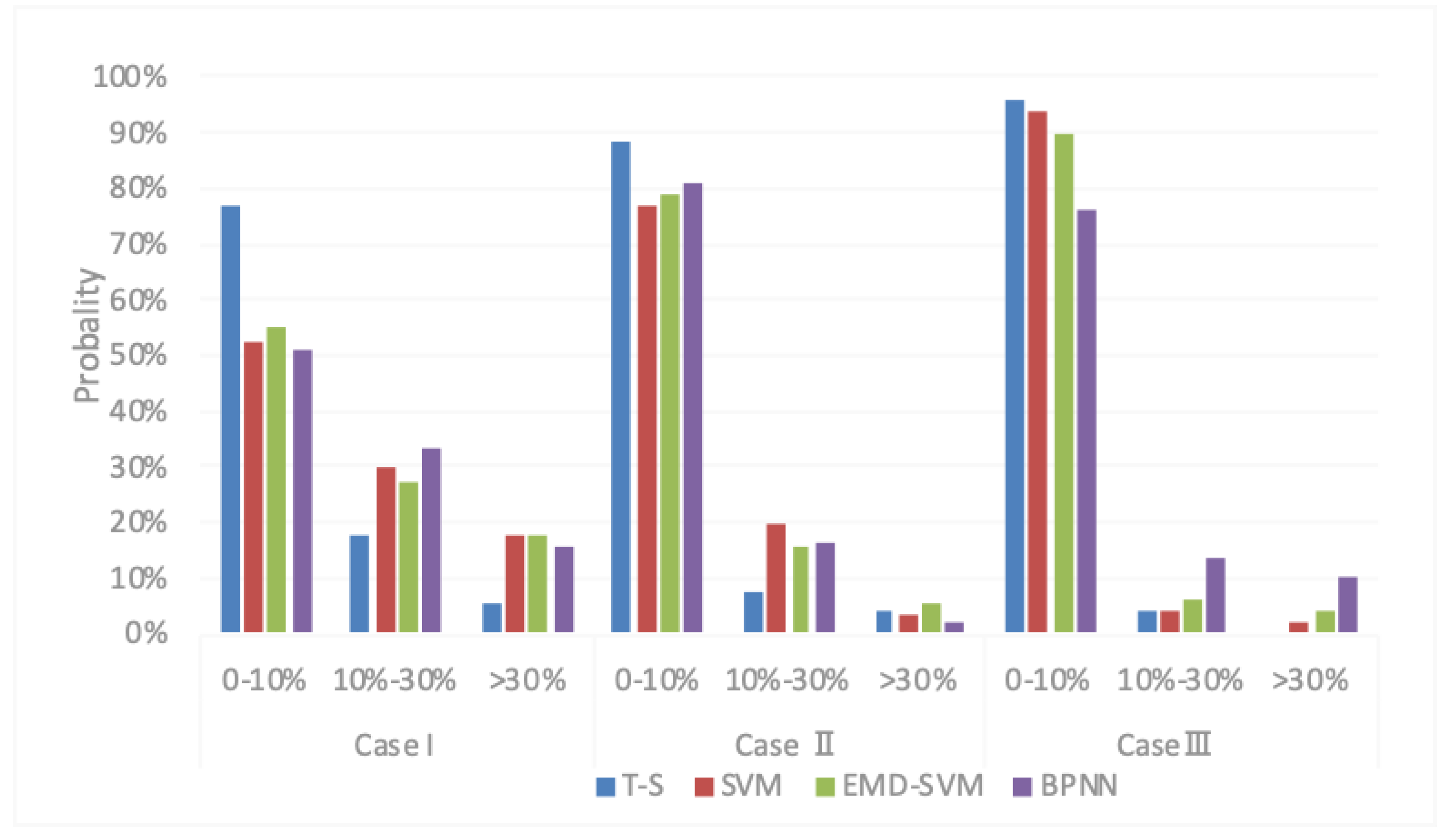
4.3. Study in Wind Power and Wind Speed Forecasting
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| xi | Input of the model |
| Sn | n-th sub system |
| μn | Membership degree for input variable to Sn |
| Rule n | Fuzzy rule for Sn |
| yn | Output of the n-th subsystem |
| wn | Weight for the n-th subsystem to total output |
| y | Output of the model |
| Z | Finite dataset to be clustered |
| U | Membership matrix of Z |
| V | Vector of the clusters’ center |
| C | Number of clusters |
| n | Number of samples |
| m | Fuzzy exponential |
| Dik2 | Square inner product distance norm |
| θ(k) | Parameter matrix |
| P(k) | Covariance matrix |
| w(k) | Gain matrix |
| m(k) | Input matrix |
| ywind power | Final output of wind power forecasting |
| ywind speed | Final output of wind speed forecasting |
| Wwpi | Weight of the output of the i-th wind power forecasting submodel |
| Wwsi | Weight of the output of the i-th wind speed forecasting submodel |
| WPi | Wind power i hour before the predicted point |
| WSi | Wind speed i hours before the predicted point. |
| T-S | Takagi-Sugeno fuzzy model |
| FCM | Fuzzy c-means clustering algorithm |
| RLS | Recursive least squares method |
| SVM | Support vector machine |
| EMD-SVM | Combined model of SVM and empirical mode decomposition |
| BPNN | Back propagation neural network methods |
| RMSE | Error indexes are the root mean squares of the errors |
| MAE | Mean absolute error |
| MAPE | Mean percentage absolute error |
| ML | Machine learning |
| RE | Relative error |
| IA | Index of agreement |
References
- Steve, S.; Klaus, R.; Kenneth, H. Global Wind Report Annual Market Update 2017. Available online: http://files.gwec.net/register?file=/files/GWR2017.pdf (accessed on 25 April 2018).
- Bokde, N.; Feijóo, A. A Review on Hybrid Empirical Mode Decomposition Models for Wind Speed and Wind Power Prediction. Energies 2019, 12, 254. [Google Scholar] [CrossRef]
- Yan, J.; Liu, Y.; Li, F.; Gu, C. Novel Cost Model for Balancing Wind Power Forecasting Uncertainty. IEEE Trans. Energy Convers. 2017, 32, 318–329. [Google Scholar] [CrossRef]
- Chang, W.; Ming, Y.; Chang, P.; Ke, Y.-C.; Chung, V. Forecasting wind power in the Mai Liao Wind Farm based on the multi-layer perceptron artificial neural network model with improved simplified swarm optimization. Int. J. Electr. Power Energy Syst. 2014, 55, 741–748. [Google Scholar]
- Nguyen, H.T.; Nguyen, T.H.; Dreglea, A.I. Robust approach to detection of bubbles based on images analysis. Int. J. Artif. Intell. 2018, 16, 167–177. [Google Scholar]
- Tokarev, M.P.; Abdurakipov, S.S.; Gobyzov, O.A.; Seredkin, A.V.; Dulin, V.M. Monitoring of combustion regimes based on the visualization of the flame and machine learning. J. Phys. Conf. Ser. 2018, 1128, 012138. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Nguyen, T.H.; Sidorov, D.; Dreglea, A. Machine learning algorithms application to road defects classification. Intell. Decis. Technol. 2018, 12, 59–66. [Google Scholar] [CrossRef]
- . Liu, F.; Li, R.R.; Li, Y.; Yan, R.F.; Saha, T. Takagi–Sugeno fuzzy model-based approach considering multiple weather factors for the photovoltaic power short-term forecasting. IET Renew. Power Gener. 2017, 10, 1281–1287. [Google Scholar] [CrossRef]
- Liu, Q.; Li, Y.; Luo, L.; Peng, Y.; Cao, Y. Power Quality Management of PV Power Plant with Transformer Integrated Filtering Method. IEEE Trans. Power Deliv. 2019, 34, 941–949. [Google Scholar] [CrossRef]
- Tomin, N.V.; Kurbatsky, V.G.; Sidorov, D.N.; Zhukov, A.V. Machine Learning Techniques for Power System Security Assessment. IFAC PapersOnLine 2016, 49, 445–450. [Google Scholar] [CrossRef]
- Voropai, N.I.; Tomin, N.V.; Sidorov, D.N.; Kurbatsky, V.G.; Panasetsky, D.A.; Zhukov, A.V.; Efimov, D.N.; Osak, A.B. A Suite of Intelligent Tools for Early Detection and Prevention of Blackouts in Power Interconnections. Autom. Remote Control 2018, 79, 1741. [Google Scholar] [CrossRef]
- Tao, Q.; Liu, F.; Li, Y.; Sidorov, D. Air Pollution Forecasting using a Deep Learning Model based on 1D Convnets and Bidirectional GRU. IEEE Access 2019, 7, 76690–76698. [Google Scholar] [CrossRef]
- Sidorov, D.N.; Muftahov, I.R.; Tomin, N.; Karamov, D.N.; Panasetsky, D.A.; Dreglea, A.; Liu, F.; Foley, A. A Dynamic Analysis of Energy Storage with Renewable and Diesel Generation using Volterra Equations. IEEE Trans. Ind. Inf. 2019. [Google Scholar] [CrossRef]
- Wang, J.; Qin, S.; Zhou, Q.; Jiang, H. Medium-term wind speeds forecasting utilizing hybrid models for three different sites in Xinjiang, China. Renew. Energy 2014, 76, 91–101. [Google Scholar] [CrossRef]
- Babu, C.N.; Reddy, B.E. A moving-average filter based hybrid ARIMA–ANN model for forecasting time series data. Appl. Soft Comput. J. 2014, 23, 27–38. [Google Scholar] [CrossRef]
- Moustris, K.P.; Zafirakis, D.; Kavvadias, K.A.; Kaldellis, J.K. Wind power forecasting using historical data and artificial neural networks modeling. In Proceedings of the Mediterranean Conference on Power Generation, Belgrade, Serbia, 6–9 November 2017. [Google Scholar]
- Zhao, Y.; Lin, Y.; Zhi, L.; Song, X.; Lang, Y.; Su, J. A novel bidirectional mechanism based on time series model for wind power forecasting. Appl. Energy 2016, 177, 793–803. [Google Scholar] [CrossRef]
- Gong, L.; Jing, S. On comparing three artificial neural networks for wind speed forecasting. Appl. Energy 2010, 87, 2313–2320. [Google Scholar]
- Li, Y.; Wen, Z.; Cao, Y.; Tan, Y.; Sidorov, D.; Panasetsky, D. A combined forecasting approach with model self-adjustment for renewable generations and energy loads in smart community. Energy 2017, 129, 216–227. [Google Scholar] [CrossRef]
- Kurbatsky, V.G.; Sidorov, D.N.; Spiryaev, V.A.; Tomin, N.V. The hybrid model based on Hilbert-Huang Transform and neural networks for forecasting of short-term operation conditions of power system. In Proceedings of the 2011 IEEE Trondheim Power Tech, Trondheim, Norway, 19–23 June 2011; pp. 1–7. [Google Scholar]
- Yan, J.; Liu, Q.; Han, S.; Wang, Y.; Feng, S. Reviews on uncertainty analysis of wind power forecasting. Renew. Sustain Energy Rev 2015, 52, 1322–1330. [Google Scholar] [CrossRef]
- Men, Z.; Yee, E.; Lien, F.S.; Wen, D.; Chen, Y. Short-term wind speed and power forecasting using an ensemble of mixture density neural networks. Renew. Energy 2016, 87, 203–211. [Google Scholar] [CrossRef]
- Mahmoud, T.; Dong, Z.; Ma, J. An advanced approach for optimal wind power generation prediction intervals by using self-adaptive evolutionary extreme learning machine. Renew. Energy 2018, 126, 254–269. [Google Scholar] [CrossRef]
- Liang, Z.; Liang, J.; Wang, C.; Dong, X.; Miao, X. Short-term wind power combined forecasting based on error forecast correction. Energy Convers. Manag. 2016, 119, 215–226. [Google Scholar] [CrossRef]
- Chitsaz, H.; Amjady, N.; Zareipour, H. Wind power forecast using wavelet neural network trained by improved Clonal selection algorithm. Energy Convers. Manag. 2015, 89, 588–598. [Google Scholar] [CrossRef]
- Vapnik, V.N.; Chervonenkis, A.Y. On the uniform convergence of relative frequencies of events to their probabilities. In Measures of Complexity; Vovk, V., Papadopoulos, H., Gammerman, A., Eds.; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 27, 1–27. [Google Scholar] [CrossRef]
- Fu, Y.; Wang, H.; Wu, G. Realization of EMD signal processing method in LabVIEW and MATLAB. J. Beijing Inst. Mach. 2008, 23, 23–27. [Google Scholar]
- Liu, F.; Li, R.; Li, Y.; Cao, Y.; Panasetsky, D.; Sidorov, D. Short-term wind power forecasting based on T–S fuzzy model. In Proceedings of the 2016 IEEE Pes Asia-Pacific Power and Energy Engineering Conference (APPEEC), Xi’an, China, 25–28 October 2016; pp. 414–418. [Google Scholar]
- Osório, G.J.; Matias, J.C.O.; Catalão, J.P.S. Short-term wind power forecasting using adaptive neuro-fuzzy inference system combined with evolutionary particle swarm optimization, wavelet transform and mutual information. Renew. Energy 2015, 75, 301–307. [Google Scholar] [CrossRef]
- Tomin, N.; Zhukov, A.; Sidorov, D.; Kurbatsky, V.; Panasetsky, D.; Spiryaev, V. Random forest based model for preventing large-scale emergencies in power systems. Int. J. Artif. Intell. 2015, 13, 211–228. [Google Scholar]
- Li, Q.; Peng, C. A Least Squares Support Vector Machine Optimized by Cloud-Based Evolutionary Algorithm for Wind Power Generation Prediction. Energies 2016, 9, 585. [Google Scholar]





| Error Indexes | RMSE | MAE | MAPE | IA | |
|---|---|---|---|---|---|
| Input Variable | |||||
| [WP1] | 3.3347 | 2.4245 | 0.8611 | 0.9871 | |
| [WP1 WP2] | 1.9922 | 1.4526 | 0.5020 | 0.9955 | |
| [WP1 WP2 WP3] | 1.9102 | 1.3911 | 0.3111 | 0.9959 | |
| [WP1 WP2 WP3 WP4] | 1.8837 | 1.3902 | 0.3386 | 0.9960 | |
| [WP1 WP2 WP3 WP4 WP5] | 1.9469 | 1.4488 | 0.4641 | 0.9957 | |
| Error Indexes | RMSE | MAE | MAPE | IA | |
|---|---|---|---|---|---|
| Input Variable | |||||
| [WS1] | 1.0332 | 0.6519 | 0.1077 | 0.9665 | |
| [WS1 WS2] | 0.8452 | 0.5161 | 0.0925 | 0.9740 | |
| [WS1 WS2 WS3] | 0.7520 | 0.4610 | 0.0760 | 0.9830 | |
| [WS1 WS2 WS3 WS4] | 0.7654 | 0.4660 | 0.0778 | 0.9823 | |
| [WS1 WS2 WS3 WS4 WS5] | 0.7754 | 0.4666 | 0.0777 | 0.9821 | |
| Case I | Case II | Case II | |
|---|---|---|---|
| RMSE | |||
| t-s | 1.8104 | 0.4503 | 0.3427 |
| svm | 3.8018 | 0.6376 | 0.6768 |
| emd-svm | 3.2462 | 0.6579 | 0.7735 |
| bpnn | 3.6529 | 0.5316 | 1.7974 |
| MAPE (%) | |||
| t-s | 9.3551 | 6.1542 | 1.2265 |
| svm | 17.3577 | 7.9282 | 2.4060 |
| emd-svm | 24.8647 | 8.6377 | 2.6926 |
| bpnn | 36.3843 | 6.5766 | 6.9218 |
| MAE | |||
| t-s | 1.4760 | 0.3598 | 0.1550 |
| svm | 2.7301 | 0.4847 | 0.3069 |
| emd-svm | 2.4386 | 0.5082 | 0.3501 |
| bpnn | 2.8029 | 0.3939 | 0.8117 |
| IA | |||
| t-s | 0.9949 | 0.9912 | 0.9713 |
| svm | 0.9789 | 0.9817 | 0.8873 |
| emd-svm | 0.9844 | 0.9796 | 0.8420 |
| bpnn | 0.9797 | 0.9891 | 0.6307 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, F.; Li, R.; Dreglea, A. Wind Speed and Power Ultra Short-Term Robust Forecasting Based on Takagi–Sugeno Fuzzy Model. Energies 2019, 12, 3551. https://doi.org/10.3390/en12183551
Liu F, Li R, Dreglea A. Wind Speed and Power Ultra Short-Term Robust Forecasting Based on Takagi–Sugeno Fuzzy Model. Energies. 2019; 12(18):3551. https://doi.org/10.3390/en12183551
Chicago/Turabian StyleLiu, Fang, Ranran Li, and Aliona Dreglea. 2019. "Wind Speed and Power Ultra Short-Term Robust Forecasting Based on Takagi–Sugeno Fuzzy Model" Energies 12, no. 18: 3551. https://doi.org/10.3390/en12183551
APA StyleLiu, F., Li, R., & Dreglea, A. (2019). Wind Speed and Power Ultra Short-Term Robust Forecasting Based on Takagi–Sugeno Fuzzy Model. Energies, 12(18), 3551. https://doi.org/10.3390/en12183551







