Abstract
The three-step rule of distributed photovoltaic (DPVs) connecting to a distribution network in the planning of practical photovoltaic projects is modeled in this paper. On this basis, a method based on large sample historical generation-load data is proposed to comprehensively evaluate the DPV limit penetration level of the low voltage–medium voltage (LV-MV) distribution network, which is the premise of DPV connection planning. Considering the fluctuations of generation-load data in time and space, the DPV limit penetration level of the LV network is evaluated based on kernel density estimation. On this basis, considering the uncertainties of DPVs connecting node schemes and connection capacity, the limit penetration level of DPVs continuously connecting to the MV network is evaluated based on the dichotomy method and stochastic simulation. Finally, the feasibility of evaluating the DPV limit penetration level by the proposed method is verified based on an example of a real distribution network, which is of great importance for the planning of a distribution network with high DPV permeability to continuously connect to DPVs.
1. Introduction
The gradual depletion of global primary energy has prompted people to pay more attention to renewable and clean energy [1,2], and new energy-based power generation has become the focus of energy development in various countries. Among them, the gradual maturity of photovoltaic technology in recent years has led to the continuous reduction of its power generation cost [3]. To increase people’s income and promote local development, the Chinese government has special subsidy policies for the construction of a distributed photovoltaic (DPV) system, and grid companies have also provided certain policy incentives for grid-connected DPVs on the user side. As a result, there is a growing demand for DPVs connecting to the distribution network, which would bring great challenges to the safe operation of the grid, and this mainly includes the influence on power quality, network loss, grid reliability and so on [4,5]. Considering that voltage deviation is the most prominent influence [6,7], it is necessary to carry out related research on the DPV limit penetration level of distribution networks under the constraint of voltage deviation. Meanwhile, in actual projects, DPVs are preferentially connected to low-voltage (LV) distribution networks, and then to medium-voltage (MV) distribution networks. Due to their different connecting abilities, the DPV limit penetration level of low voltage–medium voltage (LV-MV) distribution networks should be evaluated comprehensively rather than separately.
In terms of problems regarding the connection of distributed generation (DG) to the distribution network, several scholars have conducted research on the location and capacity of the connection of DG in the LV or MV distribution network. The calculation model for the connection of DG to the distribution network with different electrical constraint targets has been established by relevant documents, and analyses and solutions are proposed based on different solving methods: analytic method, intelligent optimization method or random simulation. Khoa, T.H. et al. [8] proposed a method based on multi-objective constraints to calculate the optimal location and maximum capacity of the DG grid connected through a cuckoo search algorithm. Alturki, M. et al. [9] proposed a method to determine the absorption capacity of a distribution network DG based on linear programming optimization. Moradi, M.H. et al. [10] adopted a joint algorithm based on Genetic Algorithm (GA) and Intelligent Water Drops (IWD) to obtain the optimal location and capacity of DG in a micro grid. Li, B. et al. [11] proposed a calculation model of DPV limit peak capacity on multiple power quality indexes using a current injection method. Torquato, R. et al. [12] adopted a simplified Monte Carlo method to analyze the absorption capacity of LV distribution networks to DPVs under the background of high permeability based on the overvoltage constraint. Zhang, S.X. et al. [13] established statistical models of DG and load, and the model of DG location and capacity planning was built. Dubey, A. et al. [14] calculated the DPV penetration level based on voltage drop constraint through a matrix description method. Zhou, L.X. et al. [15] calculated the DPV digesting and absorbing capacity of a distribution network when node voltage and power flow are the main constraints by using a forward-backward generation power flow algorithm and an annealing algorithm. Zhang, H. et al. [16] proposed the DPV optimal penetration level calculation model under different load distributions, and verified the solution based on an ant colony algorithm. Xu, Z.C. et al. [17] evaluated the photovoltaic digesting and absorbing capacity of a distribution network based on voltage sensitivity by means of stochastic scene simulation. Yao, H.M. et al. [18] used the Monte Carlo random method to simulate a large-scale photovoltaic (PV) connecting scenario, and a voltage control strategy was proposed. Zhao, B. et al. [19] proposed a stochastic analysis method to determine PV accommodation capacity of an actual feeder. Rylander, M. et al. [20] introduced a simplified stochastic simulation, and the DPV limit penetration level can be quickly determined by calculating the contour boundary of the scatter diagram. The above literatures covered analytical methods, intelligent optimization methods and stochastic simulation. Compared to the stochastic simulation, the former two usually solve models according to the optimal configuration and cannot reflect the real connecting ability of a network. In a case analysis of the literature, the Institute of Electrical and Electronics Engineers (IEEE) standard system as an example for simulation verification is taken to calculate the DPV limit penetration level, however, the large sample data of actual grid operation and the actual photovoltaic output data of different regions have not been fully considered. At the same time, most existing references evaluate the dynamic consumption ability of DPVs connected to the distribution network at the level of real-time operation, which does not reflect well the connection potential of DPVs at the level of LV-MV network planning.
In view of the three-step rule of DPVs connecting to the distribution network, this paper proposes a method to comprehensively evaluate the DPV limit penetration level of an LV-MV distribution network based on large sample historical generation-load data. Considering the fluctuations of load data in LV networks, the DPV limit penetration level of LV distribution network is calculated based on kernel density estimation. On the basis of a large number of DPVs connecting to an LV distribution network, the limit penetration level of DPVs connecting to a single MV node and the moment of maximum connecting restrictions are evaluated based on large sample generation-load data and the dichotomy method. Then, considering the uncertainties of DPV connecting node schemes and connecting capacity, the limit penetration level of DPV connection via multiple MV nodes is evaluated based on stochastic simulation. The DPV maximum penetration level across voltage-grade is achieved via a comprehensive evaluation of the LV-MV distribution network, providing a basis for DPV connection planning. Thus, a variety of connecting schemes for DPVs with a certain capacity can be provided on the basis of the three-step rule and the limit penetration level evaluation.
2. Problem Statement
There are two ways to connect DPVs to a power grid: (a) connecting to the transmission network, or (b) connecting to the distribution network. As shown in Figure 1, when DPVs are connected to the distribution network, it can be connected to the MV distribution network or the LV distribution network. First, the actual photovoltaic power generation is grid connected according to the unit power factor based on policy implications of grid companies on DPV projects. Thus, the model of DPVs in this paper only injects active power, and its apparent power is approximately equal to its active power.

Figure 1.
Schematic diagram of distributed photovoltaics (DPVs) connecting to medium voltage (MV) and low voltage (LV) distribution networks.
In Figure 1, there are n 10 kV nodes in the distribution network, corresponding to n 10/0.4 kV LV courts, and each court has m users. The rated transmission capacity of the kth court is SN.k, and the total apparent power of the kth court in kVA is Sk = Pk + jQk = ∑(Pk.i + jQk.i) (1 ≤ k ≤ n, 1 ≤ i ≤ m), where Sk.i = Pk.i + jQk.i is the apparent power of the ith user in the LV court k. U0 is the head voltage of the line, Uk is the voltage of the kth 10 kV node. Zk = Rk + jXk = Lk(r + jx), which is the impedance between the (k−1)th bus and the kth bus. Lk is the line length between the two bus lines, and r and x are the resistance and reactance of the unit-length line, respectively. Pvmid.k is the active power injected by DPVs to node k of the MV distribution network, and Pvlow.k is the active power injected by DPVs to LV court k.
When planning DPV connection to a distribution network, DPV connecting rules under the premise of network security should be determined first. In practical projects, DPV power is considered to be locally consumed in LV networks first, and then to be transmitted to the superior MV distribution network. Therefore, DPV connection to an LV-MV distribution network is subject to the three-step rule according to actual DPV projects, as shown in Equation (1).
where PDPV is the DPV capacity to connect, Pvlow is the DPV limit penetration level of the LV distribution network, and Pvmid is the limit penetration level of the MV distribution network to continuously connect to DPVs.
Mode = −1 means DPVs with the capacity of PDPV are not allowed to connect to the LV-MV network. Mode = 0 means DPVs with the capacity of PDPV need to connect to the LV-MV network. Mode = 1 means all the DPVs are connected to the LV network.
Under the three-step rule of DPV connection, DPVs are preferentially connected to the LV distribution network in practical projects. However, in the case of insufficient residual capacity in LV distribution networks due to the large number of DPV connections, the MV distribution network may continue to connect DPVs of a certain capacity. Therefore, to connect more DPVs under the premise of the grid security, the connection capacity planning of DPVs in the LV-MV distribution networks needs to be evaluated comprehensively rather than separately.
Before planning DPV connection to a distribution network, comprehensive evaluation of DPV limit penetration levels of an LV-MV distribution network is required. In general, priority should be given to calculating the DPV limit penetration level (Pvlow) of the LV distribution network. Then, evaluate the ability (Pvmid) of the MV distribution network to absorb more DPVs with a large number of DPVs connecting to the LV distribution network.
However, due to the fluctuations in both the LV and MV distribution networks, there are still some problems in evaluating Pvlow and Pvmid of LV-MV distribution networks:
- (1)
- The temporal characteristics of the DPV output and load fluctuation have a great impact on the evaluation of DPV limit penetration level. Whether this kind of stochastic probability problem is properly handled will directly affect the accuracy of the evaluation results [15,21,22].
- (2)
- DPV location and capacity planning is another crucial stochastic probability problem to be solved. The key is to deal with the uncertainties about the specific location and number of DPVs connecting nodes [8,10,21].
To support the comprehensive evaluation of LV-MV distribution networks, this article improves the traditional methods [11,17] in solving the fluctuations of both DPVs and loads. Also, stochastic simulation with improved sampling methods and probability analysis are used to replace the original maximum and minimum capacity determination method:
- (1)
- The DPV limit penetration level of the LV distribution network is calculated based on the method of kernel density estimation analyzing large sample data. The minimum load at a certain confidence level can make good use of transformer overloading ability.
- (2)
- The DPV limit penetration level of the MV distribution network is calculated based on large sample data and stochastic simulation. The simulation efficiency of DPVs connecting schemes can be improved based on the reasonable selection of two-phase sampling methods.
Finally, a solution to the DPV planning problem can be obtained:
- (1)
- Determine the three-step rule of DPVs connecting to LV-MV distribution network.
- (2)
- Comprehensively evaluate the DPV limit penetration level of LV-MV distribution network by solving the stochastic probability problems of generation-load data fluctuations and DPV connecting uncertainties.
- (3)
- For DPVs of a certain capacity, specific connecting schemes are given depending on three different mode values: connection to LV distribution networks, connection to the LV-MV distribution network, and connection is not allowed.
3. Calculation Model of DPV Limit Penetration Level for an LV Distribution Network
3.1. Basic Calculation Model for an LV Distribution Network
When DPVs are connected to an LV network, if the DPV power cannot be completely consumed on the spot, the power flow will be sent back to the superior MV distribution network. The overload capacity of distribution transformers is shown in Table A1 of Appendix A. Considering the overload capacity (i.e., the allowable time of continuous overload operation) of a distribution transformer, it should not be operated in overload mode for a long time. This paper takes the rated capacity of a transformer as the upper limit of its continuous power transmission. And the capacity of a transformer to operate under short-term overload can be used by the load with a certain confidence level based on kernel density estimation.
According to Figure 1, the limit value of Pvlow.k is the limit penetration level of the LV court k, as shown in Equation (2). The rated transmission capacity of a distribution transformer SN.k is generally a fixed value. Therefore, the DPV limit penetration level is available when the total load Sk is the minimum. It should be pointed out that the minimum apparent power of load mentioned in this section is the minimum apparent power in the time range when DPVs have power injection.
where Pvlow(k) is the DPV limit penetration level of the LV court k.
3.2. DPV Limit Penetration Level Evaluation of an LV Distribution Network Based on Kernel Density Estimation
When connected to the LV distribution network, the DPV limit penetration level depends on the minimum apparent power of the load. However, the data values at each time point may not be completely reliable due to the periodic sampling of load data. Therefore, the minimum apparent power at a certain confidence level should be evaluated.
According to the central limit theorem and the law of large numbers, as a large sample random variable, load data can be approximately reflected by a normal distribution. This paper estimates load data with unknown density function based on kernel density, that is, Gaussian kernel function is used to normally fit large sample load data. So, the probability density of the annual apparent power for the LV courts can be obtained. Then, the load data at a certain confidence level can be evaluated. The kernel density calculation is shown in Equation (3):
where Si refers to the apparent power data of the distribution of large samples, ntime is the data dimension, K(S*) is the kernel function, and h is the window width.
The optimal window width HMISE is selected by the Gaussian method, as shown in Equations (4) and (5):
where MISE(h) refers to the mean square integral error, fh(s) refers to the probability density function, f(s) refers to the true probability density function, and HMISE refers to the best window width.
After obtaining the probability density of load data in each LV court by kernel density estimation, the load power confidence interval at a certain confidence level can be determined, and the value of its left boundary is the minimum apparent power of the load at this confidence level. Therefore, the DPV limit penetration level of the LV court k is given by Equation (6). The minimum value of the confidence level can be obtained from Equation (7), and in practice, it can be set to a larger value than the minimum value.
where Sβ,k is the minimum apparent power of the LV court k at the confidence level βk (%) and βk is the confidence level of the LV court k.
4. Calculation Model of DPV Limit Penetration Level for a MV Distribution Network
When evaluating the ability of the superior MV distribution network to continuously connect to DPVs on the basis of a large number of DPV connections in the LV distribution network, voltage deviation has become the primary factor limiting the integration of DG into the MV distribution network [23]. The connection of large-scale DPVs will increase the system voltage. This paper evaluates the DPV limit penetration level of a MV distribution network with ±7% voltage deviation constraint.
4.1. Basic DPV Limit Penetration Level Calculation Model for a MV Distribution Network
When all 10 kV nodes of the MV distribution network are not connected to DPVs and the LV distribution network is connected to DPVs with the limit penetration level, the voltage calculation equation of node k is shown in Equation (8):
In capacity analysis and calculation, the distribution network voltage can be approximately equivalent to the rated voltage UN, i.e., Ui ≈ UN (1 ≤ i ≤ n). When a 10 kV node c connects to DPVs alone in the MV distribution network, the voltage value (pu) of node k is calculated as shown in Equations (9) and (10). Equation (9) calculates the voltage of node c and the previous nodes (1 ≤ i ≤ c), and Equation (10) calculates the voltage of nodes (c < i ≤ n) after node c. When the MV distribution network has multiple nodes connecting to DPVs, the voltage value (pu) of node k is calculated as shown in Equation (11). When DPVs are not connected to 10 kV node k or LV court k, the corresponding values of Pvmid.k and Pvlow.k in the equations are set to 0.
where Uk(pu) is the voltage value (pu) of 10 kV node k after DPVs are connected. The physical significance of other symbols has been described previously and will not be described again.
Equations (9)–(11) can be used to calculate the voltage value (pu) of any 10 kV node at any time after the DPVs are connected to the LV-MV distribution network. The DPV limit penetration level of the MV distribution network can be obtained when the voltage value (pu) of one or more nodes in the MV distribution network reaches 1.07, as shown in Equation (12):
where Pvmid(i) is the limit penetration level of 10-kV, node i continuously connects to DPVs alone, max(Pvmid.i) is the limit injected power to node i, and PV1kW is the actual output of 1-kW DPV at the corresponding moment. Pv.total denotes the total limit penetration level of continuous DPV connection to the MV distribution network via multiple nodes, npv is the total number of nodes connected to DPVs in the limit. ∃Uk(pu) = 1.07 means that the voltage value (pu) of one or more nodes in the grid reaches 1.07.
4.2. DPV Limit Penetration Level Evaluation Based on Dichotomy Method and Stochastic Simulation
Timing sequence characteristics of load and photovoltaic output data in distribution network have a great impact on the DPV limit penetration level evaluation [24]. In this paper, Pvmid(i) of different nodes is evaluated based on the spatio-temporal characteristics of generation-load data and the dichotomy method. Moreover, the day with the maximum DPV connecting restriction throughout the year can be obtained. Therefore, Pv.total can be evaluated based on stochastic simulation, without considering the timing sequence characteristics of the whole year.
4.2.1. Limit Penetration Level Evaluation for DPVs Connected to MV Distribution Network via Single Node
For the solution method based on dichotomy, the value interval of the DPV limit penetration level of node i is shown in Equation (13). Each time the connection capacity is changed, the voltage of each node is calculated. If there is no node voltage exceeding the limit, lower boundary of the interval is bisected, as shown in Equation (14). Otherwise, upper boundary of the interval is bisected, as shown in Equation (15). As the difference between the upper and lower boundaries of the interval shrinks and approximates to the optimal value, Pvmid(i) is determined.
Here, Pdown(i) is the lower boundary of the interval, and Pup(i) is the upper boundary of the interval, given in kW.
According to the generation-load data for each time in the year, the DPV limit penetration level for each node at different times in the year can be calculated after a certain number of binary iterations. The minimum value at a certain time is taken as the DPV limit penetration level for the day, and the minimum value of DPV limit penetration level of all days in the year is taken as Pvmid(i).
4.2.2. Limit Penetration Level Evaluation for DPVs Connected to MV Distribution Network Via Multiple Nodes
After evaluating the annual DPV limit penetration level of single-node connection, the problem about the fluctuations of generation-load data is solved. Therefore, when DPVs continuously connected via multiple MV nodes, handling the uncertainties of the location, number of connection points, and their respective DPV connection capacity are critical.
If the problem of DPV installation space is not taken into account, six typical connection scenarios are possible, such as DPV beginning, medium, and end-centralized connection [25]. The stochastic simulation method is adopted in this paper to analyze the fluctuations of DPV multi-node connection. Stochastic simulation includes two-phase sampling and capacity simulation. The basic steps in a stochastic simulation are as follows:
● Step 1: Determination of all nodes that can connect to DPVs.
There are many contact nodes without users in the distribution network, only the load nodes are considered to connect to DPVs when evaluating the limit penetration level. N nodes that can connect to DPVs in an LV-MV network can be determined according to the DPV connecting scenario.
● Step 2: Two-phase sampling of location and quantity of DPV connecting points.
To reduce the repetition of DPV connection schemes based on stochastic sampling, the method of two-phase sampling is adopted. The number of connection points is determined in the first sampling, the specific multiple connected positions are determined in the second sampling. Thus, a DPV connecting location scheme can be obtained through two-phase sampling.
Firstly, sampling and rounding is introduced, as shown in Figure A1 of Appendix A. The value interval of the sampling function f(x) is [0,N]. A random value in [0,N] can be extracted (if it is negative, take the absolute value). Define M as the number of connection points. M can be obtained after stochastic sampling and rounding up. The probability of each integer being sampled varies from μ1 to μN, as shown in Equation (16).
where μk is the probability of integer k being sampled.
According to the priority ordering of nodes connecting to DPVs, DPV connecting location schemes can be obtained via a second sampling of N nodes. The specific process is as follows:
- (1)
- The N nodes are numbered by 1~N and projected onto the sampling function f(x).
- (2)
- Priority ordering is performed: stochastic integers are generated by the sampling function. DPVs are given priority to the node extracted first, and the extracted numbers will not be extracted again until all nodes are extracted.
- (3)
- The first M nodes of the sampling result are selected to connect to DPVs, which means a kind of DPV connection location scheme.
● Step 3: Limit penetration level evaluation based on capacity simulation.
When calculating Pv.total, only the day with the maximum DPV connecting restriction determined in Section 4.2.1 is taken into account. Combined with the positive correlation between DPV penetration level and load level, the capacity simulation method proposed in this paper is presented as Equation (17).
where and PQdata are M ∗ 1 matrices corresponding to M nodes connecting to DPVs in the network. Pr(z) is the total DPV penetration level of the z-th capacity simulation. (z) is the DPV injection power to each node in the z-th capacity simulation. PQdata is the apparent power of the load of each node and g is the accumulation coefficient of capacity.
The whole process of stochastic simulation is shown in Figure 2.

Figure 2.
Stochastic simulation flow chart.
Explanations of the steps of stochastic simulation are in Figure 2:
In step 1, how to extract a DPV connection location scheme via two-phase sampling is described in detail in the previous parts of this article.
In step 2, ‘Set k1 = −1, k2 = 0’ is to calculate the voltage of the distribution network when there is no DPV connected. Subsequently, the maximum node voltage is tested every 20 times the capacity simulation. If the maximum node voltage exceeds the limit, the capacity simulation is stopped. Otherwise, continue for 20 times.
In step 3, the data to be recorded includes the location of DPV connection points for each simulation, the capacity of each connection, and the maximum value of node voltage in this simulation.
After evaluating the DPV limit penetration level of the LV-MV distribution network based on the methods mentioned, the boundary parameters Pvlow and Pvmid of the mode can be obtained, as shown in Equation (18). Then, DPVs of a certain connecting capacity can be precisely planned to connect to the distribution network under the three-step rule.
5. Analysis of Examples
The example is based on an 85-node 10-kV power distribution network in a rural area. The electrical topology is shown in Figure A2 of Appendix B. There are 35 load nodes in the whole distribution network. The time span of both load and photovoltaic output data is 1 h (i.e., there are 8760 time points in the whole year). Taking DPV terminal centralized connection as an example, 12 load nodes of the 23 nodes at the end are determined to be able to connect to DPVs. The topology is shown in Figure A3 of Appendix B. The model of transformers and lines are shown in Table A2 of Appendix B.
5.1. DPV Limit Penetration Level Evaluation for LV Distribution Network
Firstly, the confidence level βk of each LV court can be calculated according to Equation (7). To simplify calculation, the maximum value of all min(βk) is used as the confidence level of all LV courts. The annual load data of each LV distribution network are evaluated at a confidence level of β = 95% based on kernel density estimation. Taking LV court 63 as an example for visualization, the rated transmission capacity of the transformer is 100 kVA. The probability density of the annual load data is shown in Figure 3, where the width of each straight is 0.2 kVA.
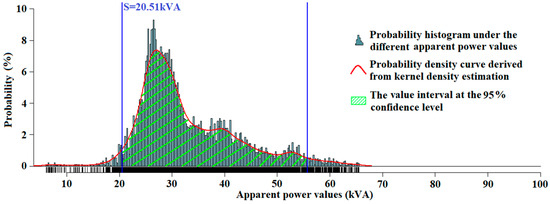
Figure 3.
Power kernel density estimation of court 63.
As shown in Figure 3, in LV court 63, min(S63) = 6.09 kVA, S95%,63 = 20.51 kVA. S95%,63 is more than three times better than 3.6 times min(S63), increasing by 14.42 kVA. Correspondingly, Pvlow,95%(63) = 120.51 kW, increased by 13.59% over Pvlow(63).
In the same way, the S95%,k and min(Sk) of other LV courts can be evaluated based on kernel density estimation and the minimum rule, respectively. The DPV limit penetration level Pvlow(k) and Pvlow,95%(k) of each LV court can be calculated respectively according to Equation (1) and Equation (5). Compared with the rated capacity of the distribution transformer of each LV court, the result is shown in Figure 4.
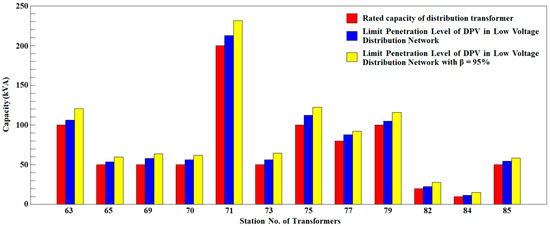
Figure 4.
Comparison of DPV limit penetration level in each LV court.
As shown in Figure 4, the DPV limit penetration level in every LV court based on kernel density estimation is significantly higher than that based on the minimum rule. In particular, both the DPV limit penetration level of court 71 and its increase were the largest, respectively, valuing 231.38 kVA and 18.69 kVA. The DPV limit penetration level of court 84 was the minimum, with the smallest increase of 3.65 kVA. In general, the total DPV limit penetration level of all the 12 LV courts based on kernel density estimation is 1033.49 kVA, which increased by 10.37% over that based on the minimum rule. It can be concluded that the DPV limit penetration level determined based on kernel density estimation evaluating load data can better reflect the DPV connection ability of an LV distribution network compared to the conventional minimum rule. If studying on a distribution network with higher load levels, the difference between S95%,k and min(Sk) can be more considerable.
Considering extreme conditions, each LV distribution network is connected to DPVs at the limit penetration level (with a total connection of 1033.49 kVA). On this basis, the limit penetration level of the MV distribution network continuously connected to DPVs is evaluated via a single-node and multi-node connect to DPVs respectively, as shown in Section 5.2 and Section 5.3, respectively.
5.2. Evaluation of DPV Limit Penetration Level for MV Distribution Networks with Single Node Connection
Take the 85th 10 kV node at the end of the line as an example. Considering calculation speed and accuracy, take the binary number as 15, the initial condition as Pdown(85) = 0 and Pup(85) = 10 MW. The daily DPV limit penetration level for the entire year is evaluated, as shown in Figure 5.
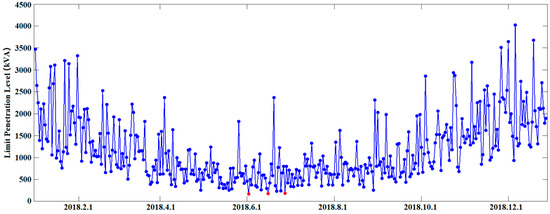
Figure 5.
DPV limit penetration level for each day of the year at the 85th node.
Figure 5 shows that the overall DPV limit penetration level is lower in spring and summer than that in autumn and winter. The DPV limit penetration level in autumn and winter is more than 1000 kVA. On some days in the winter, the level can be more than 2000 kVA. The DPV limit penetration levels in spring and summer are mostly less than 1000 kVA, or even lower. It may be concluded from these results that the DPV limit penetration level is directly related to the actual output of DPVs (i.e., the irradiation intensity).
Specifically, the maximum DPV limit penetration level of the 85th node occurs on 9 December 2018, up to 4019.47 kVA. From June to July, there were three days that the limit was less than 200 kVA, which was significantly lower than other days. The minimum value appeared on June 2, and the ultimate DPV limit penetration level of node 85 is Pvmid(85) = 169.98 kVA. Results indicate that the final Pdown(85) = 169.97 kVA and Pup(85) = 169.99 kVA, with an accuracy of 0.01 kVA.
Relatively, the comparison of the DPV limit penetration level based on different methods of generation-load uncertainty analysis is shown in Table 1. Here, the large sample data based method of this paper, the method of load prediction [13], the method of DPV output prediction [15] and the method of typical moment (with the maximum DPV permeability) [17] are adopted.

Table 1.
Comparison of different analysis methods of generation-load uncertainty.
As shown in Table 1, the results calculated by the method based on the predicted photovoltaic output slightly deviate from the real value because of prediction errors. The results based on load forecasting have a larger deviation than those based on DPV output prediction; this is because actual load distribution (similar to Figure 3) is not the adopted standard normal distribution. Additionally, the results obtained by the typical time method have the most serious deviation due to its large contingency. In this paper, the large sample data-based evaluation method ensured that the results are more reliable compared to the other three mentioned methods. At the same time, the moment of maximum DPV connecting restrictions can be obtained, and then, only the uncertainties of the location and number of connecting nodes need to be considered when evaluating the limit penetration level of DPV multi-node connection.
Further, by comparing and calculating the daily DPV limit penetration level in the entire year, the DPV limit penetration level of each node can be evaluated when a node connects to DPVs alone, as shown in Figure 6. There, the red points are the load nodes and the blue points are the connecting nodes with no users.
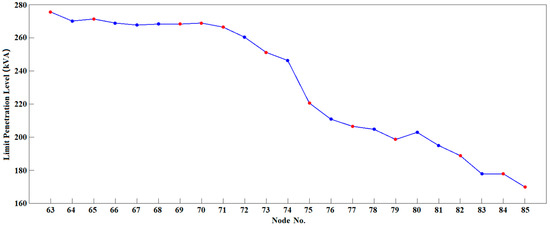
Figure 6.
DPV limit penetration level of the 23 nodes at the end of the line.
As shown in Figure 6, nodes of the MV distribution network can continue to connect to DPVs for a certain capacity after a large capacity of DPVs are connected to the LV courts. The limit penetration level of a single node connecting to DPVs ranges from 169.98 to 275.57 kVA. Among all nodes, Pvmid(63) = 275.57 kVA, which is the maximum value of DPV for each node. Additionally, the DPV limit penetration level of the 63rd node is 105.59 kVA higher than that of the 85th node. It can be seen that the closer the node is to the end, the lower the limit penetration level.
Finally, the results show that the total time required for calculating the DPV limit penetration level for 23 nodes based on the dichotomy method is 5117.25 s, and the calculation time for a single node is approximately 222.49 s.
5.3. Evaluation of DPV Limit Penetration Level for MV Distribution Network with Multi-Node Connection
Sampling functions such as ① beta distribution β(2,5), ② gamma distribution γ(2,3), ③ pseudo-normal distribution [17], and ④ uniform distribution [18,19] were selected as the optional functions according to sample M (the number of connection points) and nodes connected to DPVs.
First, the sampling method of two-phase sampling should be determined. Combined with this example, the total number of schemes corresponding to different values from 2 to 12 for M is 4083. Take 5000 as the number of sampling to compare different sampling methods, as shown in Table 2. (to avoid randomness, each value of the ‘number of schemes sampled’ in the table is the minimum of 1000 repetitions).

Table 2.
Comparison of two-phase sampling methods.
As shown in Table 1, it can be found that reasonable selection of the sampling method can effectively reduce the sampling repetition rate of the DPV connection location schemes while improving the efficiency of stochastic simulation. In 5000 times repetition of two-phase sampling, it is obvious that the two-phase sampling methods that contain ‘③’ are far less efficient than those that do not. Specially, the method ‘① + ④’ sampled the largest number of schemes, a total of 2756 schemes, which covered 26.65% more schemes than method ‘④ + ④’ [18,19] and nearly three times more than method ‘④ + ③’ [17]. Up to 67.50% of all the schemes were covered based on method ‘① + ④’. Method ‘③ + ③’ only covered 10.51% of all the schemes, which was the lowest. All the mentioned methods take less than a minute to calculate so that the selection of sampling method mainly considers the sampling efficiency.
In general, two-phase sampling can sample more schemes than single-sampling. When uniform distribution is taken as the second sampling, the maximum number of schemes can be sampled. It means that the sampling probability of each node during the second sampling should be as equal as possible. When β(2,5) is taken as the first sampling, more schemes can be sampled than γ(2,3) and pseudo-normal sampling. It can be found that the closer the probability density distribution of the first sampling function is to the distribution characteristic of "big in the middle and small at both ends" of combinatorial function, the higher the scheme coverage.
After comparative analysis, method ‘① + ④’ is selected: β(2,5) was identified as the first sampling function, and uniform sampling as the second sampling function. Considering the repetition rate of sampling results, the number of stochastic simulations is 20,000. The two-phase sampling results are shown in Table 3.

Table 3.
Results of 20,000 two-phase sampling.
As shown in Table 2, 4028 different DPV connection location schemes were extracted from 20,000 times two-phase sampling, which covered 98.65% of all the schemes. Compared to traditional stochastic simulation, this article optimizes the sampling method to cover more DPV connection schemes, which effectively improves the evaluation accuracy and reliability of the DPV limit penetration level.
When capacity simulation is carried out for the location scheme of DPV connection points determined by 20,000 two-phase sampling according to Equation (15), the value selection of the accumulation coefficient g affects the calculation accuracy of the power flow. When g ≥ 8, the matrix is close to the singular value, and when g ≤ 7, the convergence of the power flow calculation can be guaranteed.
The day of the year with the maximum DPV connection limit was June 2 according to the calculation results presented in Section 5.2. To improve the calculation accuracy, let g = 0.2. Capacity simulations of 20,000 sample results were conducted based on the generation-load data on June 2. The minimum value in the day is taken as the limit penetration level of the distribution network when multiple nodes are connected to DPVs. The simulation results at the corresponding time are shown in Figure 7. The running time is 1500.34 s, and the total time to calculate the DPV limit penetration level of this LV-MV distribution network is about 6617.59 s.
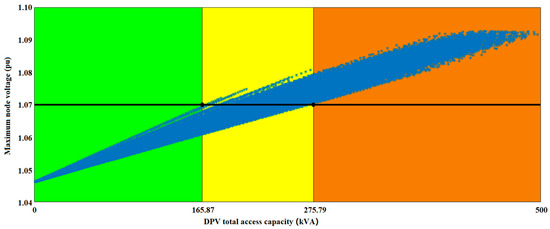
Figure 7.
The limited penetration level of DPV multi-node connection.
As shown in Figure 7, the maximum value of system node voltage (pu) reached 1.046 after DPVs were connected in each LV court at the limit penetration level. Based on this, the limit penetration level of the MV distribution network when multiple nodes are connected to DPVs was calculated. Pv.total = 165.87 kVA can be determined according to the minimum rule, however, connection capacity can be further improved by optimizing connection schemes because of the need for mass connection of users. Pv.total = 275.79 kVA can be determined according to the maximum rule, but the voltage may exceed the limit if improper planning for the DPV connection location scheme.
Obviously, continuous connection of DPVs from 165.87 kVA to 275.79 kVA may cause potential safety hazards in the LV-MV network. In this paper, each scatter point in the figure represents a specific DPV connection scheme, and schemes that meet the requirements can be screened out. Therefore, the proposed stochastic simulation can solve the two mentioned problems by giving specific DPV connection schemes, which can not only guarantee the safety of the power grid, but also improve DPV connecting capacity to meet the needs of users.
Therefore, it can be calculated that the DPV limit penetration level under the premise of grid safety is 1309.28 kVA in total based on the comprehensive evaluation of the LV-MV distribution network. Pvlow = 1033.49 kVA is increased by more than 10% on the basis of the minimum rule. Pvmid = 275.79 kVA increased by 26.69% over the LV courts based on the improved stochastic simulation.
For the planning of DPVs with a certain capacity in this distribution network, all DPVs can be distributed to each LV distribution network when connecting capacity is less than 1033.49 kVA (mode = 1) based on the three-step rule of DPV connection. When DPV connecting capacity is larger than 1033.49 kVA but no more than 1309.28 kVA (mode = 0), the 275.79 kVA DPVs beyond the limit penetration level of the LV distribution network can be connected to the MV distribution network. When DPV connecting capacity is larger than 1309.28 kVA (mode = −1), it will not be allowed to connect to this distribution network due to network security issues.
Finally, compare the connection schemes of a certain DPV capacity: when the DPV capacity is larger than 1293.49 kVA but not more than 1309.28 kVA, DPVs exceeding 260 kVA shall be connected to the MV distribution network. It was found that the MV distribution network allows DPVs to connect to five single nodes (the 63rd, 65th, 69th, 70th, or 71th node), as well as many multi-node connection schemes through the 20,000 stochastic simulations. Due to space limitation. This paper only lists six schemes corresponding to 2~7 connection points, as shown in Table 4.

Table 4.
Comparison of limited penetration schemes with multi-node connection.
The results show that the number of nodes that continue to connect to DPVs is less than seven when total connecting capacity exceeds 1293.49 kW. Especially, the 75th, 77th, 79th, and 85th nodes are not allowed to continuously connect to DPVs due to grid security constraints. As shown in Table 3, there is only one connecting scheme when connecting to DPVs at the limit penetration level, including the 63th and 65th node. In general, the method proposed in this paper can provide a variety of connecting schemes for DPVs of a certain capacity. In terms of practical applications, power grid companies can provide corresponding connection schemes combined with specific reporting installation requirements based on strictly limited DPV penetration levels.
6. Conclusions
This paper proposed a comprehensive evaluation method of LV-MV distribution networks based on large sample data of generation-load. The following conclusions can be drawn from the calculation results:
- The model of the three-step rule of DPV connection planning is set up according to practical projects.
- The stochastic probability of load data is solved based on kernel density estimation, which improved the DPV limit penetration level of LV distribution network by more than 10%.
- A method to estimate the DPV limit penetration level of each point was proposed considering both the topology of distribution network and the characteristics of load fluctuation.
- The original method of determining the maximum and minimum capacity was replaced by stochastic simulation and probability analysis where the total DPV limit penetration level of LV-MV distribution network can be increased by 10%~30%.
- Aiming at a specific DPV reporting capacity, the methods mentioned can provide more DPVs connecting schemes by improving the two-phase sampling method than traditional stochastic simulation, which is helpful for solving practical problems.
Distribution network with DPVs connected mainly includes the assessment of the limit penetration level at the planning level and the dynamic absorption ability at the real-time operation level. With the increasing penetration rate of distributed generation supply in the distribution network, based on the large-scale connection of the existing distribution network to distributed generation, accurately evaluating the ability of distributed photovoltaic to continue to connect, coordinating and optimizing the effective absorption of distributed generation still needs to be further studied.
Author Contributions
Conceptualization, J.L., T.J., J.W., K.W. and L.W.; methodology, J.L. and T.J.; software, T.J. and J.W.; validation, J.L., K.W. and L.W.; formal analysis, J.L. and J.W.; investigation, K.W. and L.W.; resources, K.W. and L.W.; data curation, J.L. and T.J.; writing—original draft preparation, J.L.; writing—review and editing, J.L. and T.J.; visualization, J.L.; supervision, T.J.; project administration, J.W.; funding acquisition, K.W. and L.W.
Funding
This research was funded by the Science and Technology Project of State Grid Corporation of China, grant number 522722180003.
Acknowledgments
We would like to thank Editage for English language editing.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Overload capacity of distribution transformers.
Table A1.
Overload capacity of distribution transformers.
| Overload Factor | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.8 | 2.0 |
| Allowable Overload Time (hours:minutes) | 19:00 | 5:50 | 3:00 | 1:45 | 1:10 | 0:13 | 0:06 |
When the ambient temperature is 30 °C.

Figure A1.
Schematic diagram of node sampling by numbered projection.
Appendix B
The electrical topology and the topology of the last 12 load nodes connecting to DPVs is shown respectively from Figure A2 to Figure A3. The model of the LV-MV distribution network adopted in the case analysis is shown in Table A2.
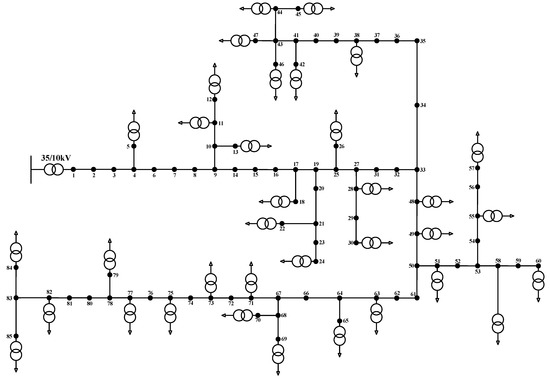
Figure A2.
The electrical topology of the 85-node LV-MV distribution network.
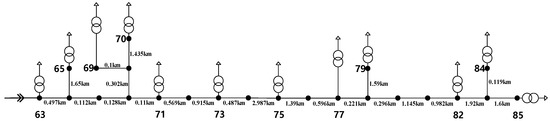
Figure A3.
The topology of the last 12 load nodes connecting to DPVs.

Table A2.
Electrical models of simulated network.
Table A2.
Electrical models of simulated network.
| Node Number of LV Courts | Distribution Transformer Model | Rated Capacity/kVA | Node Number of LV Courts | Distribution Transformer Model | Rated Capacity/kVA |
|---|---|---|---|---|---|
| 5 | S7 | 100 | 51 | S11 | 400 |
| 11 | S7 | 20 | 55 | S11 | 100 |
| 12 | S9 | 20 | 57 | S7 | 20 |
| 13 | SZ11 | 100 | 58 | S7 | 30 |
| 18 | S11 | 400 | 60 | S7 | 20 |
| 22 | S11 | 200 | 63 | S11 | 100 |
| 24 | S7 | 30 | 65 | S7 | 50 |
| 26 | S7 | 50 | 69 | S9 | 50 |
| 28 | S7 | 30 | 70 | S11 | 50 |
| 30 | S7 | 100 | 71 | S11 | 200 |
| 38 | S7 | 50 | 73 | S7 | 50 |
| 42 | S9 | 50 | 75 | S11 | 100 |
| 44 | S7 | 20 | 77 | S7 | 80 |
| 45 | S7 | 20 | 79 | S7 | 100 |
| 46 | S11 | 250 | 82 | S7 | 20 |
| 47 | S11 | 400 | 84 | S7 | 10 |
| 48 | S11 | 400 | 85 | S11 | 50 |
| 49 | S11 | 400 | Number of transformers | 35 | |
All lines are ‘LGJ-70’: r = 0.45 Ohm/km, x = 0.368 Ohm/km.
References
- UNEP. Global Trends in Renewable Energy Investment 2016; Frankfurt School, UNEP Centre: Frankfurt, Germany, 2016. [Google Scholar]
- IRENA. Remap: Roadmap for a Renewable Energy Future, 2016th ed.; IRENA: Abu Dhabi, UAE, 2016. [Google Scholar]
- Yuan, Y.; Yang, C.A.; Zhang, X.; Chun, L.I.; Huang, Y.; Peng, L.I.; Kejun, Q.I. Optimal proportion of wind and PV capacity in provincial power systems based on bilevel optimization algorithm under low-carbon economy. J. Mod. Power Syst. Clean Energy 2015, 3, 33–40. [Google Scholar] [CrossRef]
- Al Kaabi, S.S.; Zeineldin, H.H.; Khadkikar, V. Planning active distribution networks considering multi-DG configurations. IEEE Trans. Power Syst. 2014, 29, 785–793. [Google Scholar] [CrossRef]
- Wang, J.; Gao, H.; Zou, G.; Wu, Z. Comprehensive evaluation of impacts of distributed generation on voltage and line loss in distribution network. Presented at the 2015 5th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Changsha, China, 26–29 November 2015. [Google Scholar]
- Haque, M.M.; Wolfs, P. A review of high PV penetrations in LV distribution networks: Present status, impacts and mitigation measures. Renew. Sust. Energy Rev. 2016, 62, 1195–1208. [Google Scholar] [CrossRef]
- Chamana, M.; Chowdhury, B.H.; Jahanbakhsh, F. Distributed control of voltage regulating devices in the presence of high PV penetration to mitigate ramp-rate issues. IEEE Trans. Smart Grid 2018, 9, 1086–1095. [Google Scholar] [CrossRef]
- Khoa, T.H.; Nallagownden, P.; Baharudin, Z.; Dieu, V.N. One Rank Cuckoo Search Algorithm for Optimal Placement of Multiple Distributed Generators in Distribution Networks. Presented at the TENCON 2017—2017 IEEE Region 10 Conference, Penang, Malaysia, 5–8 November 2017. [Google Scholar]
- Alturki, M.; Khodaei, A.; Paaso, A.; Bahramirad, S. Optimization-based Distribution network Hosting Capacity Calculations. Appl. Energy 2018, 219, 350–360. [Google Scholar] [CrossRef]
- Moradi, M.H.; Abedini, M. A Novel Method for Optimal DG Units Capacity and Location in Microgrids. Int. J. Electr. Power Energy Syst. 2016, 75, 236–244. [Google Scholar] [CrossRef]
- Li, B.; Pan, G.C.; Chen, B.Y.; Li, P.J. Limit Peak Capacity Calculation of Distributed Photovoltaic with Power Quality Constraints. Autom. Electr. Power Syst. 2016, 40, 43–50. [Google Scholar] [CrossRef]
- Torquato, R.; Salles, D.; Pereira, C.O.; Meira, P.C.; Freitas, W. A Comprehensive Assessment of PV Hosting Capacity on Low-Voltage Distribution Systems. IEEE Trans. Power Deliv. 2018, 33, 1002–1012. [Google Scholar] [CrossRef]
- Zhang, S.X.; Chen, K.; Long, Y.; Cheng, H.; Li, K. Distributed Wind Generator Planning Based on Shuffled Frog Leaping Algorithm. Autom. Electr. Power Syst. 2013, 37, 76–82. [Google Scholar]
- Dubey, A.; Santoso, S. On Estimation and Sensitivity Analysis of Distribution Circuit’s Photovoltaic Hosting Capacity. IEEE Trans. Power Syst. 2017, 32, 2779–2789. [Google Scholar] [CrossRef]
- Zhou, L.X.; Zhang, D.; Li, C.; Li, H.; Huo, W. Access Capacity Analysis Considering Correlation of Distributed Photovoltaic Power and Load. Autom. Electr. Power Syst. 2017, 41, 56–61. [Google Scholar]
- Zhang, H.; Tong, X.Q.; Yin, J. Influence of distributed photovoltaic power generation on distribution network and the design of optimal access scheme. J. Eng. 2019, 16, 1361–1367. [Google Scholar] [CrossRef]
- Xu, Z.C.; Zhao, B.; Ding, M. Photovoltaic Hosting Capacity Evaluation of Distribution Networks and Inverter Parameters Optimization Based on Node Voltage Sensitivity. Proc. CSEE 2016, 36, 1578–1587. [Google Scholar]
- Yao, H.M.; Du, X.H.; Li, T.J.; Jia, C. Simulation of Consumption Capacity and Voltage Control Strategy of Distribution Network with High Penetration of Photovoltaics. Power Syst. Technol. 2019, 43, 462–469. [Google Scholar]
- Zhao, B.; Wei, L.; Xu, Z.; Zhou, J.; Ge, X.H. Photovoltaic accommodation capacity determination of actual feeder based on stochastic scenarios analysis with storage system considered. Autom. Electr. Power Syst. 2015, 39, 34–40. [Google Scholar] [CrossRef]
- Rylander, M.; Smith, J.; Sunderman, W. Streamlined method for determining distribution system hosting capacity. IEEE Trans. Ind. Appl. 2016, 52, 105–111. [Google Scholar] [CrossRef]
- Li, R.H.; Gao, Y.J.; Cheng, H.X. Two step optimal dispatch based on multiple scenarios technique for active distribution system with the uncertainties of intermittent distributed generation and load considered. Presented at the 2014 International Conference on Power System Technology, Chengdu, China, 20–22 October 2014; pp. 3303–3308. [Google Scholar]
- Aghaei, J.; Niknam, T.; Azizipanah-Abarghooee, R.; Arroyo, J.M. Scenario-based dynamic economic emission dispatch considering load and wind power uncertainties. Int. J. Electr. Power Energy Syst. 2013, 47, 351–367. [Google Scholar] [CrossRef]
- Zou, H.L.; Han, X.Y.; Liao, Q.F.; Liu, D. Penetration Capacity Calculation for Distributed Generation Considering Voltage Quality and Short Circuit Capacity Constraints. Power Syst. Technol. 2016, 40, 2273–2280. [Google Scholar] [CrossRef]
- Bai, X.Q.; Zhao, Z.; Bao, H.B. DG planning based on CLARA algorithm with consideration of timing characteristics. Electr. Power Autom. Equip. 2016, 36, 14–22, 29. [Google Scholar] [CrossRef]
- Liu, J.; Huang, W. Analysis on Grid-Connectible Capacity of Distributed PV Generation in Case of PV Generation Distribution Close to Load Distribution. Power Syst. Technol. 2015, 39, 299–306. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).