1. Introduction
With resource exhaustion and environment deterioration, more and more renewable energy generation is being incorporated into the power grid [
1,
2,
3]. However, renewable energy generation, such as wind and solar energy, has the inherent characteristics of randomness and intermittence [
4,
5,
6]. The direct integration of distributed renewable energy into the grid will cause the mismatch of power and finally result in instability. This motivates the development of the microgrid. Actually, the microgrid [
7,
8,
9,
10] is a small-scale power distribution system, which is composed of distributed power sources and neighbor loads. When compared with the traditional power grid, the microgrid has several advantages. First, the microgrid can be virtually self-sufficient, which will reduce the long-distance transmission loss. Second, these distributed renewable energy generations can be well used and managed in microgrid. However, in the traditional centralized scheduling of power grid, the renewable energies cannot be fully utilized. Thus, the study of microgrid operation is necessary.
In the microgrid, there are operations for different time periods, namely, the real-time, short-term, mid-term, and long-term [
11]. Especially, the hour-ahead operation, which belongs to the short-term operation, may affect the unit commitment [
12,
13], economic dispatch [
14], demand side management [
15], spinning reserve scheduling [
16], and so on. In the microgrid hour-ahead operation, the demand forecasting plays an important role. Actually, there are various demand forecasting approaches [
17], including the multiple regression, fuzzy logic, expert systems, artificial neural networks (ANNs), and so on. Among these demand forecasting methods, the ANN [
18,
19,
20] is preferred because of its higher prediction accuracy, shorter processing time, and stronger adaptation. The development of ANN has entailed three stages until now. The ANN now possesses a larger set of data, a more powerful computer, and a more deeply trained network. When compared to some newly artificial intelligent algorithms, the ANN is fundamental, mature, and easy to perform.
The demand forecasted by ANN [
18] can be used as the desired demand in hour-ahead scheduling of microgrid. However, on the one hand, with the increasing application of controllable loads, the demand side has the flexibility to adjust the electricity consumption. On the other hand, the microgrid tends to operate in a market-oriented mode. Thus, an energy trading can happen among electricity suppliers and retailers. The final trading electricity will be decided by the suppliers and retailers rather than the supplier monopoly. To design a new energy trading management framework for the microgrid, two challenges need to be tackled: the utility optimization and the market participants’ privacy protection.
The utility optimization of the microgrid has been discussed in lists of publications [
21,
22,
23]. Reference [
21] has studied the electricity cost minimization problem for the residential microgrid with distributed energy resources. References [
22,
23] both have formulated the operation cost minimization schemes in the droop-controlled microgrid. However, the papers mentioned above only consider the supplier cost. In this paper, the operators of buses take the responsibility of purchasing electricity from the upstream supplier and selling electricity to the local users or downstream buses. These operators can be called retailers in microgrid. The profit earned by these retailers is also considered in the microgrid utility optimization.
In the microgrid utility optimization, most papers only consider the active power, and other power flow parameters, such as reactive power, voltage, and current and so on, are ignored; therefore, the schedule results may violate the stable operation conditions of the microgrid. Therefore, power flow constraints play an important role in the scheduling of the microgrid. Meanwhile, if the power flow equations are added as constraints, the power loss can be calculated. Then, besides the cost and profit, the power loss of transmission is also considered in the objective function.
There exist different kinds of approaches to solve optimization problems. Evolutionary algorithms, such as a hybrid evolutionary method combining particle swarm optimization (PSO) and genetic algorithms (GAs) using fuzzy logic [
24], Grey Wolf Optimizer-based algorithms [
25], island-based Cuckoo search [
26], ideal gas optimization algorithm [
27], and so on, can be applied to various optimization systems and proved to be successful. Other than evolutionary algorithms, an exact approach can also solve optimization problems. The radial power flow model in [
28,
29] can be solved using the convex optimization method. Therefore, in this paper, the microgrid energy trading problem with power flow constraints will be proved to be convex. Convex optimization problems are relatively easy to solve. However, the centralized solution method needs a control center to acquire global information of the microgrid, which causes an invasion of market participants’ privacy and obstructs the process of marketization. Therefore, a distributed energy trading management needs to be designed. References [
30,
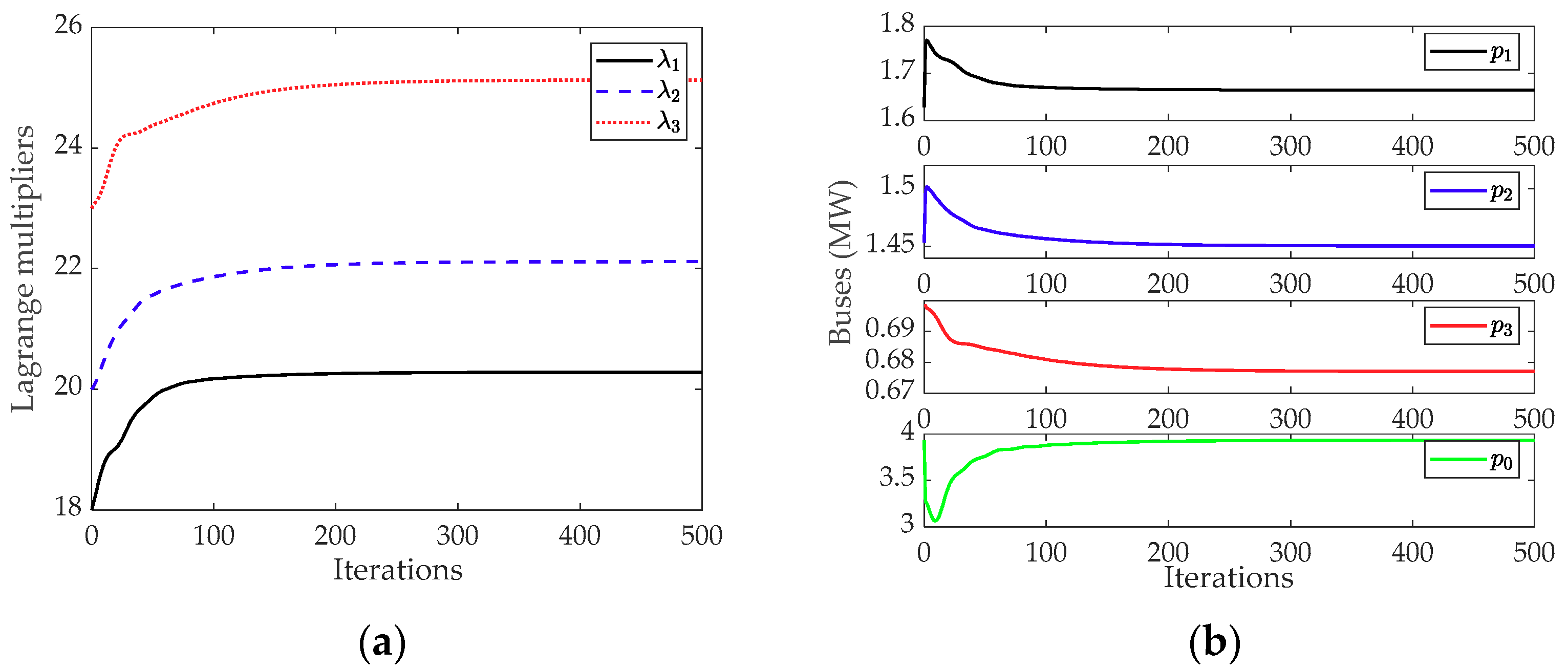
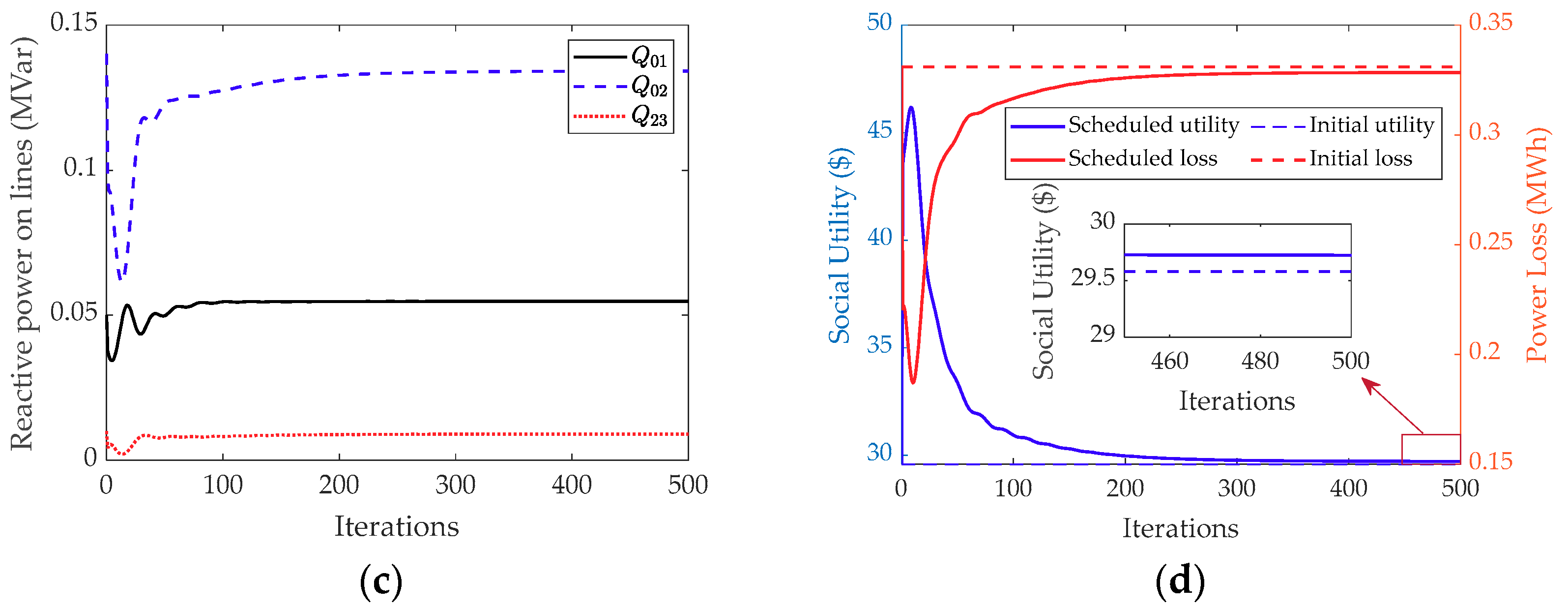
31] introduce a distributed optimization method, the predictor corrector proximal multiplier (PCPM) method. Lagrange multipliers are used to decouple the variables in the objective function. Then, the supplier and retailers of the microgrid can solve their local optimization by negotiating only with neighbors. After the optimization, the social utility of the microgrid is maximized by considering the minimization of power loss.
The main contributions of this paper are summarized as follows.
The ANN method is used to forecast the demand of LV distribution networks. The hourly forecast results participate in the energy trading as the desired reference demand. This ensures that the final trading decision will not deviate too far from the forecasted demand;
The power loss minimization is added to the objective function. Additionally, the power flow constraints are also added to the optimization problem. Therefore, in the iteration of optimization, the microgrid operation is guaranteed to be within the allowable range;
The energy trading optimization problem is solved by decomposing it into local benefit optimization sub problems of the supplier and buses. The local sub problems can be solved by negotiation of operators only with their neighbors. The privacy of market participants is protected.
The paper is organized as follows. In
Section 2, the microgrid system framework is introduced. Additionally, the power flow, demand forecasting, and optimization problems of the micro-grid are formulated.
Section 3 applies the PCPM algorithm to solving the distributed energy trading management. Numerical examples to complement the theoretical analysis are provided in
Section 4. Finally, the conclusion is stated in
Section 5.
2. Proposed Microgrid System
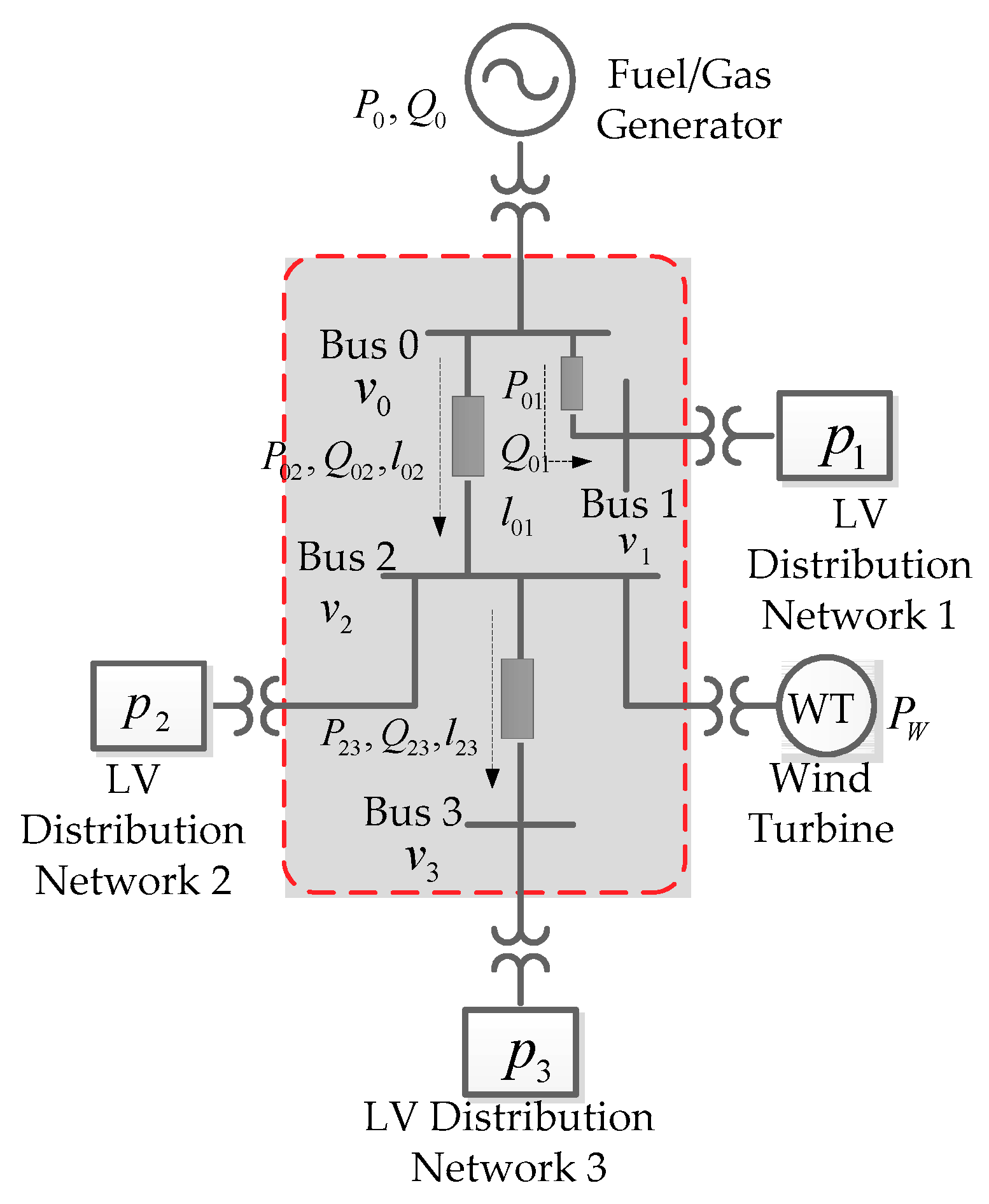
In an islanded electricity supply network, multiple small-scale low voltage (LV) distribution networks can be connected in a radial pattern to form a multi-bus medium voltage microgrid, which is shown in
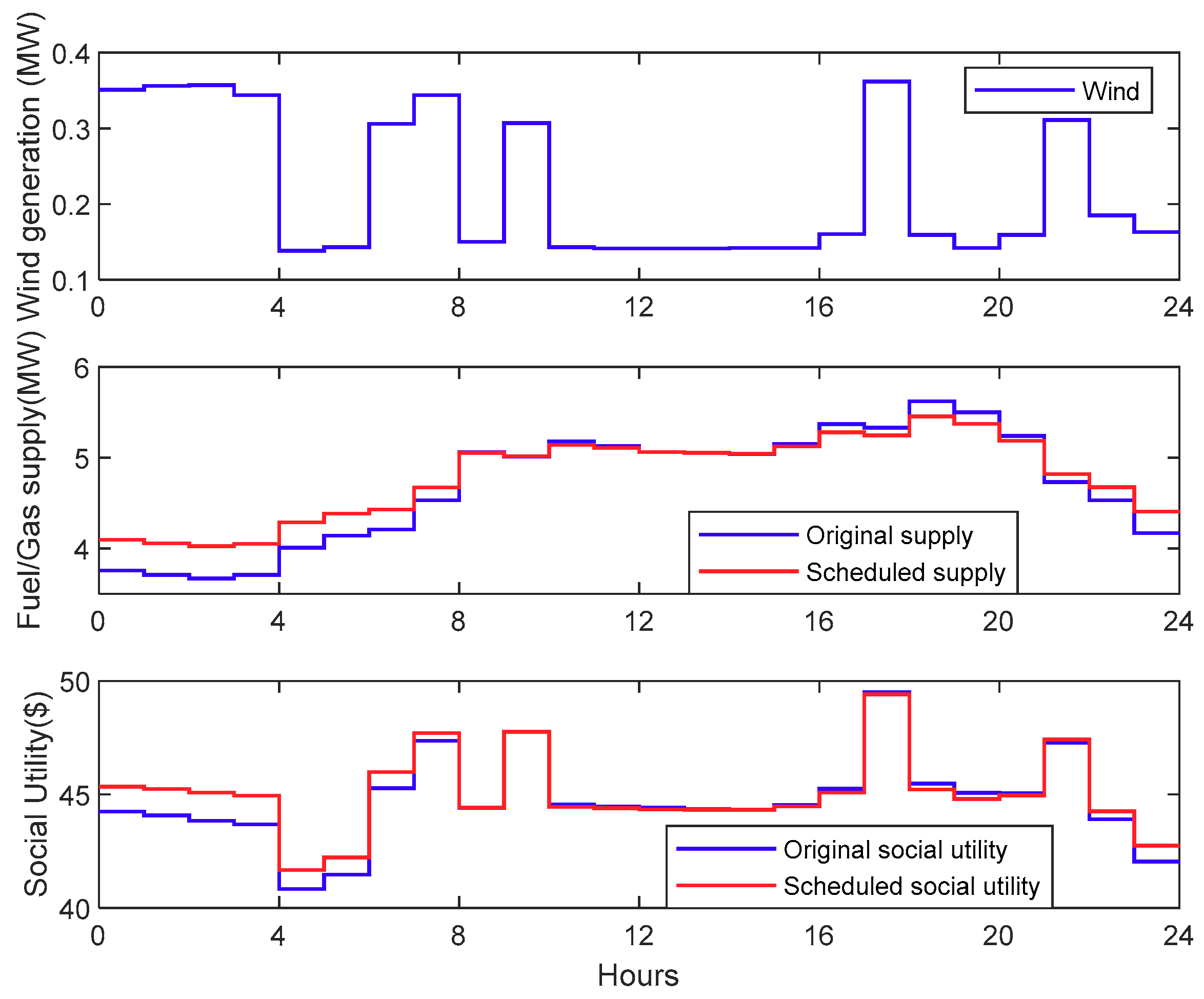
Figure 1. Each bus has an independent operator that can manage its power supply and demand. The operators are equipped with an advanced metering infrastructure that enables bidirectional communication among buses. In this radial microgrid, the fuel/gas generator is the main supplier. The renewable generators, such as wind power generators and solar power generators, can only supply local demand. The operators of buses take the responsibility of purchasing electricity from upstream suppliers and selling electricity to local users or downstream buses. These operators can be called retailers in microgrid.
2.1. Power Flow Constraints
If only active power is considered in the scheduling of the microgrid, and other power flow parameters, such as reactive power, voltage, current, and so on, are ignored, the schedule results may violate the stable operation conditions of the microgrid. Therefore, power flow constraints play an important role in scheduling of the microgrid.
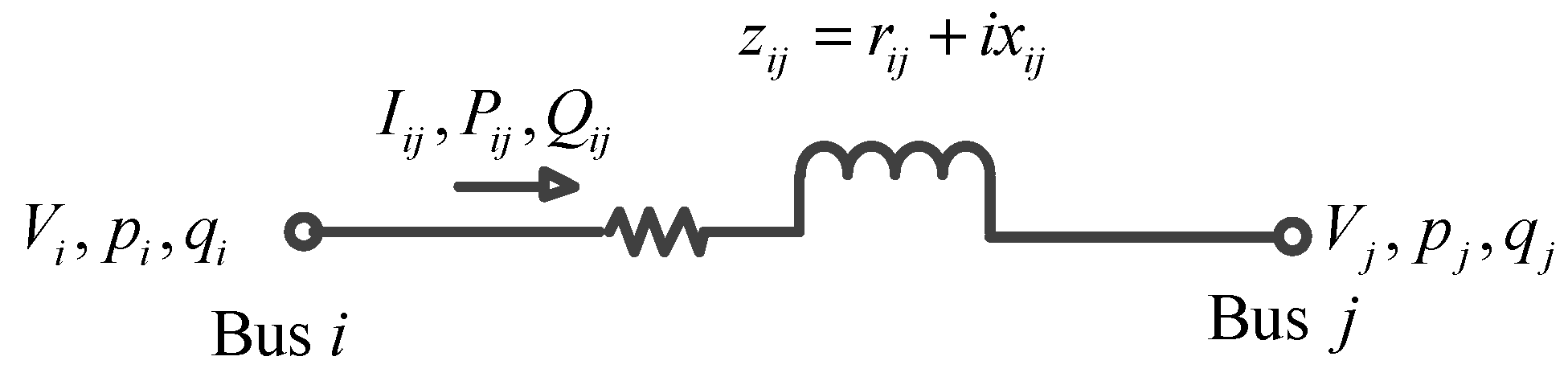
The radial distribution network of the microgrid is modeled as a directed tree graph
. The buses in set
are indexed by
. Additionally, the distribution line, which connects bus
i and bus
j, is denoted as
. The main supplier, the fuel/gas generator, is indexed as bus 0. It is the slack bus, which means its voltage is fixed as
and it will supply active and reactive power (
) to balance the electricity demand. For each bus
,
is its complex voltage and
is its complex power injection. If the bus has renewable generators,
is the demand minus generation. For each line,
,
is the complex current from bus
i to bus
j.
is the impedance, and
is the complex power that flows on the distribution line
. These notations are illustrated in
Figure 2.
Given a radial distribution microgrid, the branch flow model [
28,
29] is as follows:
In order to simplify the notations,
,
.
can be derived from Equations (2) and (3). If it is squared, then we can get the branch flow model without phase angle of voltage and current
Reference [
28] verifies that if
is given, the unique phase angle of the radial network can be determined.
2.2. Demand Forecasting Using Artificial Neural Network Method
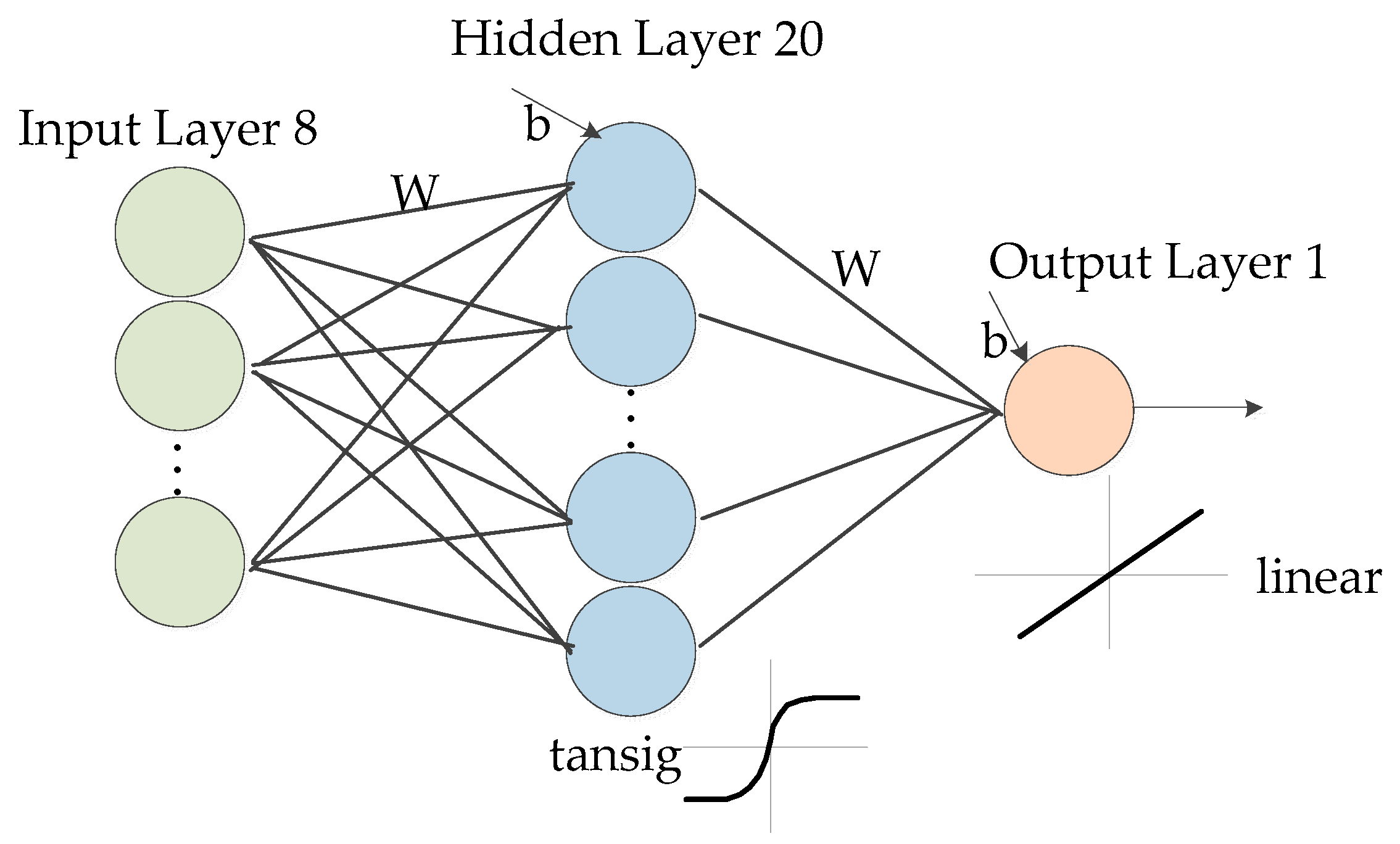
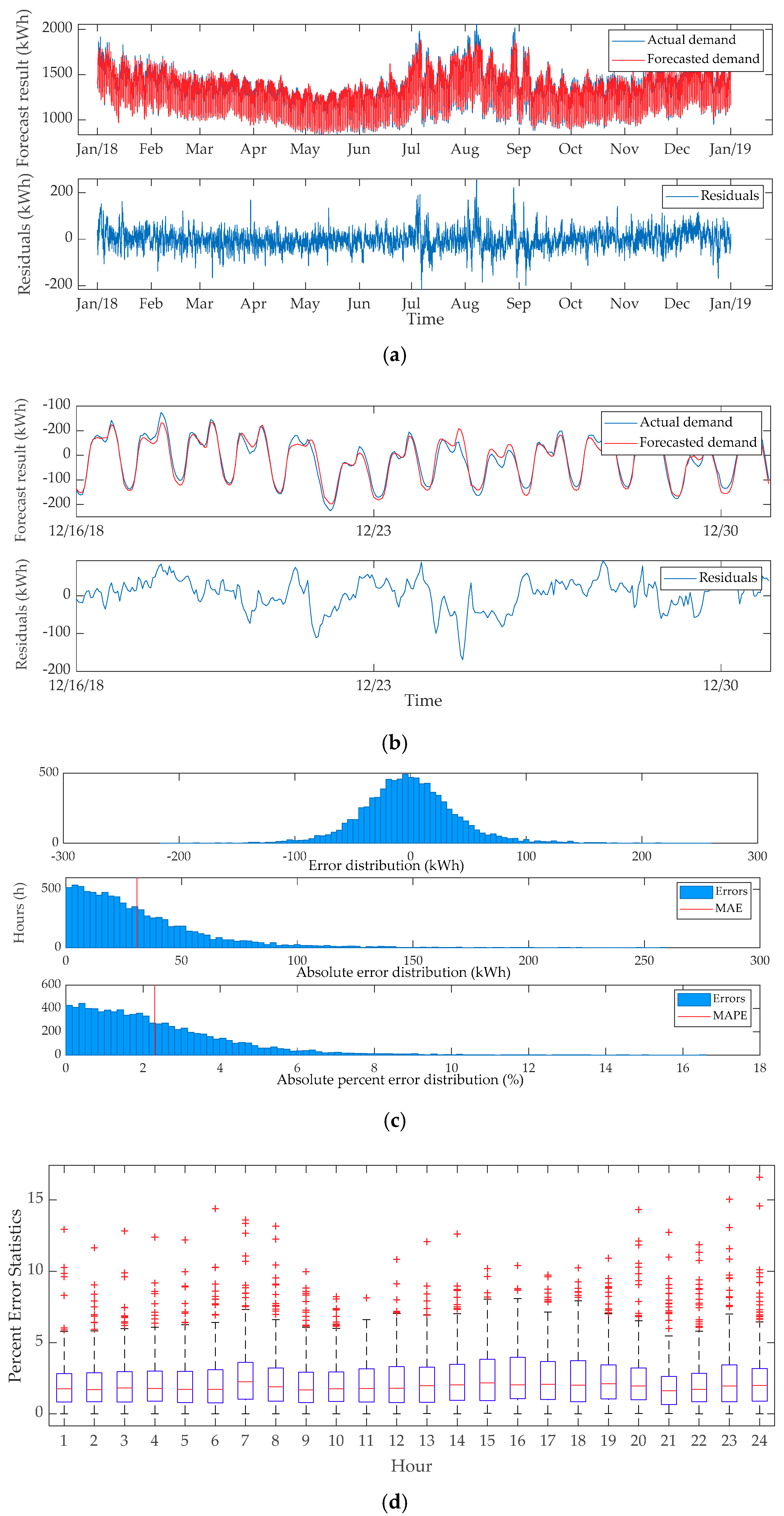
In the energy trading, the accurate forecast of the demand can decrease the waste and maintain stable operation of the power grid. Compared with conventional methods, artificial neural network (ANN) can forecast the demand with higher accuracy. In this paper, the ANN structure is shown in
Figure 3. It is a single hidden layer network. In the hidden layer, there are 20 neurons and the activation function is a tansig function. In the output layer, the activation function is a linear function. The training method is Levenberg–Marquardt algorithm. The ANN is trained and tested on a publicly available set of real electricity demand data from the ISO-NE [
32]. We extract historical hourly electricity demand data of three zones from 1 January 2016 to 31 December 2018. The hourly weather data of these zones can also be acquired from the ISO-NE. After the preparation of data, the inputs of the training include:
The dry bulb and dew point temperature;
The hour and the day;
The label of holiday/weekend;
The average demand of previous day;
The demand from the same hour the previous day;
The load from the same hour and same day from the previous week.
The data set of years 2016 and 2017 is used to train the ANN. The training set is used for building the model (estimating its parameters). Once the neural network model is built, we can use it to forecast the next hour demand with the eight inputs. The forecasted output result can be compared with the real data from 2018. Then, we can test the performance of the model on out-of-sample data. The performance will be shown in the simulation part. The final hour-ahead forecast output is used as the reference demand of bus i, .
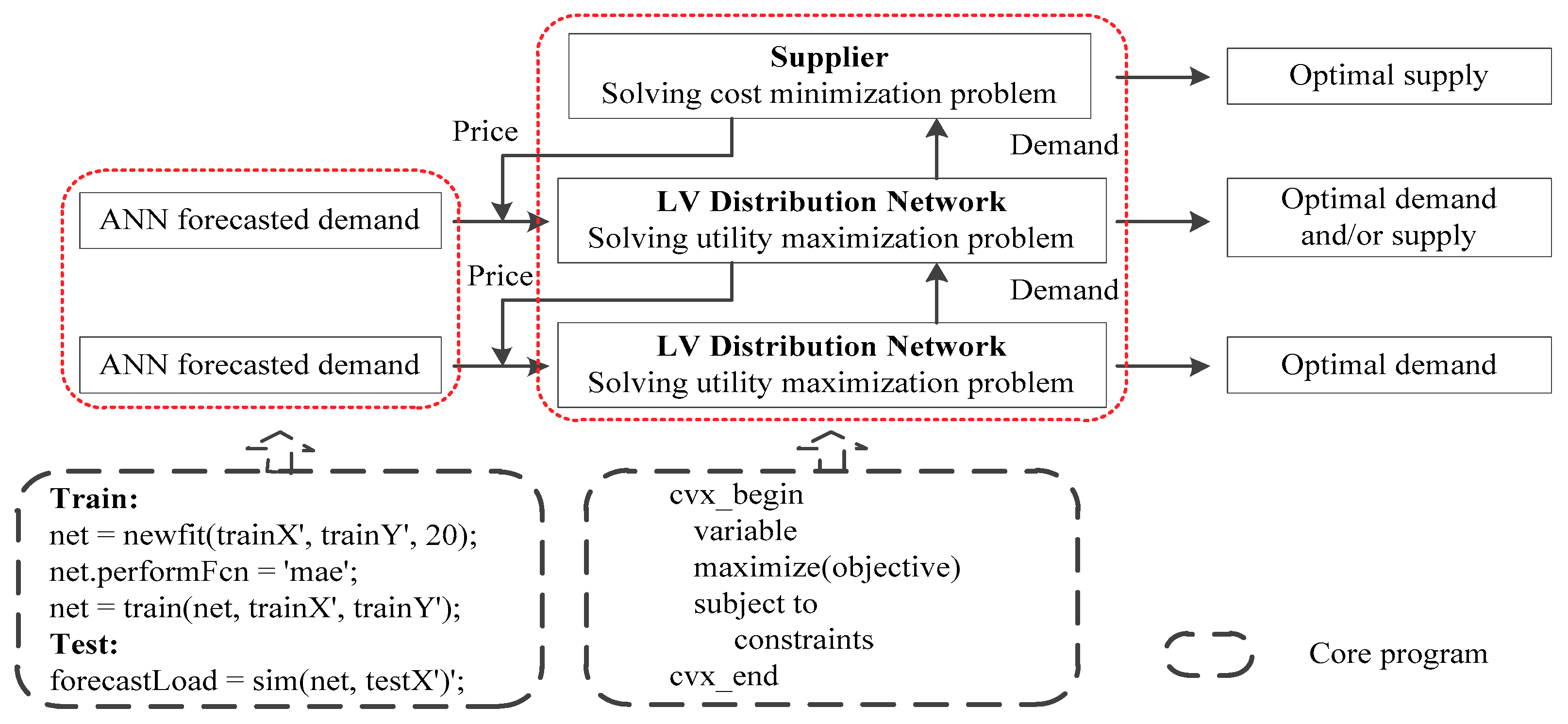
2.3. Social Utility Maximization
The social utility of the MV microgrid is defined as the profit of LV distribution networks minus the cost of generation. The objective of the microgrid is to maximize the social utility, which is shown in Equation (8). In (8), the power flow constraints are also considered. Therefore, minimization of the power loss of transmission lines can be added to the objective.
In the Equation (8),
is the retail electricity price of bus
i. Even if consumers of buses own controllable applications,
is penalty coefficient of the difference between reference demand
and final supply
. The initial reference demand
can be obtained by the ANN method.
is the cost function of the fuel/gas generator. It is indicated by a quadratic function [
33]
, where
are varying fuel/gas coefficients. The parameter
is used to represent the fixed hourly cost of renewable generators at bus
j. The coefficient
can adjust the weight of the power loss term.
The quadratic Equation (7) is a constraint in (8). Because it is non-affine, (8) is not convex. Reference [
28] relaxes it into an inequality constraint, which can convex the power flow constraints.
(9) can be converted to a second-order cone constraint as follows:
Then, the convex optimization function of microgrid utility maximization is function (8) with substitutional constraint (9).
The validity conditions for the relaxation is proposed in [
28]. In the paper, it is easy to satisfy the conditions considering the structure of the microgrid.
After the second-order cone relaxation, the objective function becomes convex, which can be solved centrally. However, a control center is needed to take the responsibility of global control; it requires detailed information of the microgrid, which causes privacy issues. With market-oriented reform, operators of buses aim to maximize their own benefits and expect to protect their privacy during trading. Therefore, the microgrid social utility maximization problem needs to be solved using distributed mechanisms.