An Asymptotic Numerical Continuation Power Flow to Cope with Non-Smooth Issue
Abstract
:1. Introduction
- (1)
- In this paper, a new CPF calculation method based on asymptotic numerical method (ANM) is proposed, which can only cope with quadratic functions. PV-PQ bus type switch is reformulated by Fischer-Burmeister (FB) functions. FB function is also transformed into quadratic equation to meet the requirements of ANM. Then, ANM is used to calculate the continuous power flow and more robust than predictor-corrector based method to cope with constraints exchange issue. Conventional buses type switch logic methods in CPF, as the number of PV buses changing to PQ increases, the use of logical judgment inevitably increases the burden of calculation, even causing the power flow calculation failed.
- (2)
- Compared with the conventional predictor-corrector method, ANM can quickly approach the voltage collapse point by self-adaptive step size adjustment and constant Jacobian matrix used for power series expansion, thus greatly improving the CPF calculation efficiency.
2. Establishment and Solution of ANM-CPF
2.1. Semi-Smooth Quadratic Power Flow Equations
2.2. Algorithm of ANM-CPF
3. Case Study
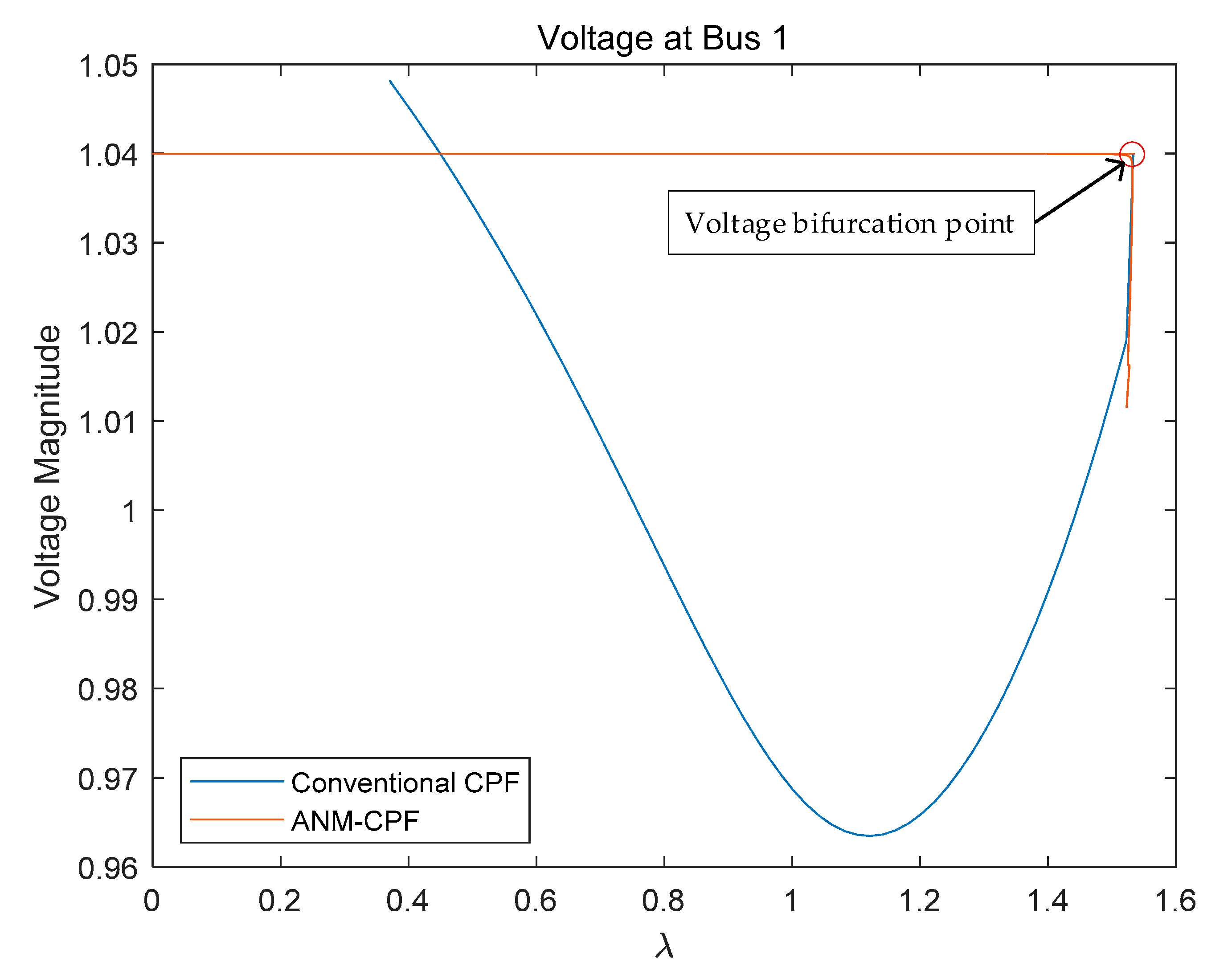
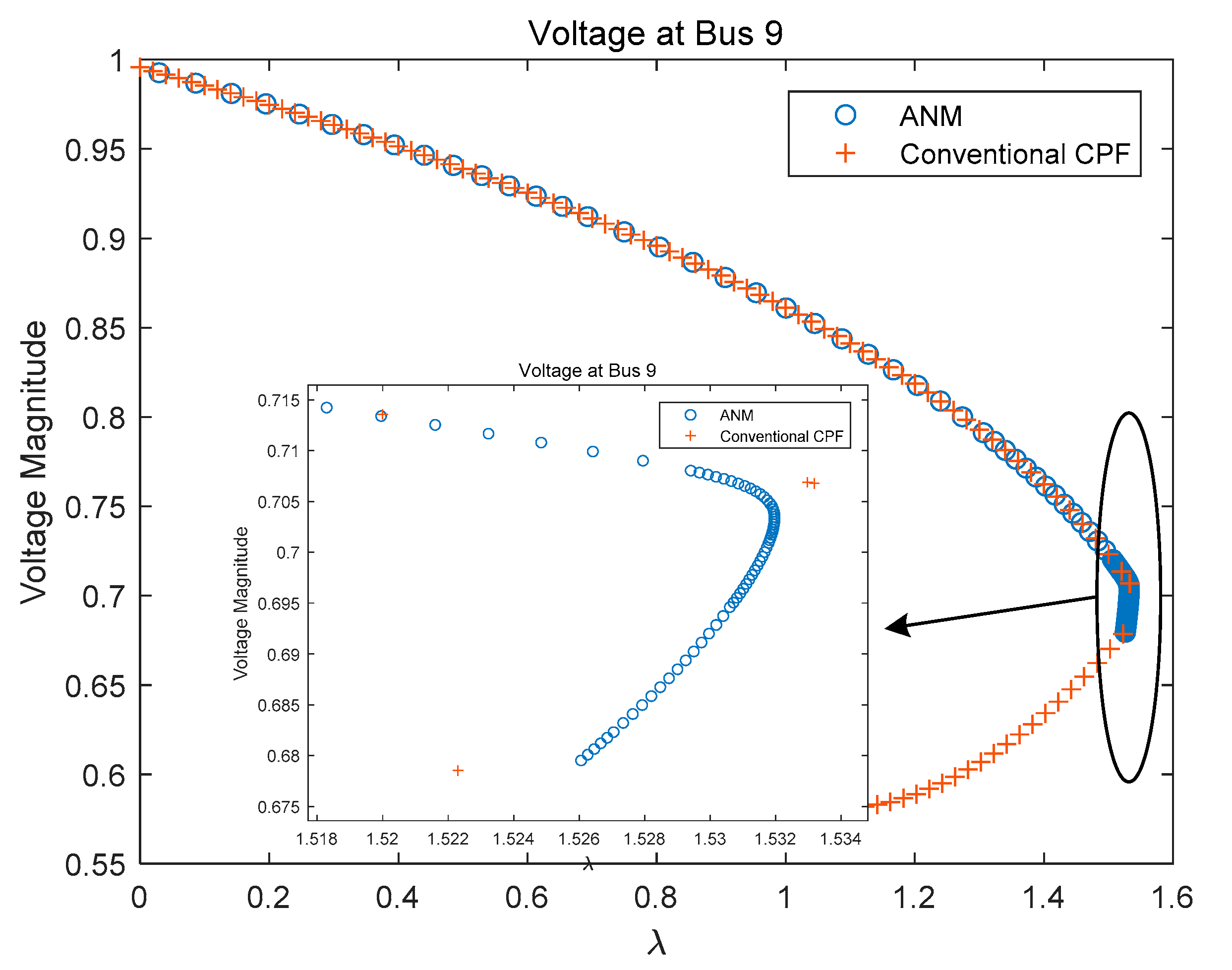
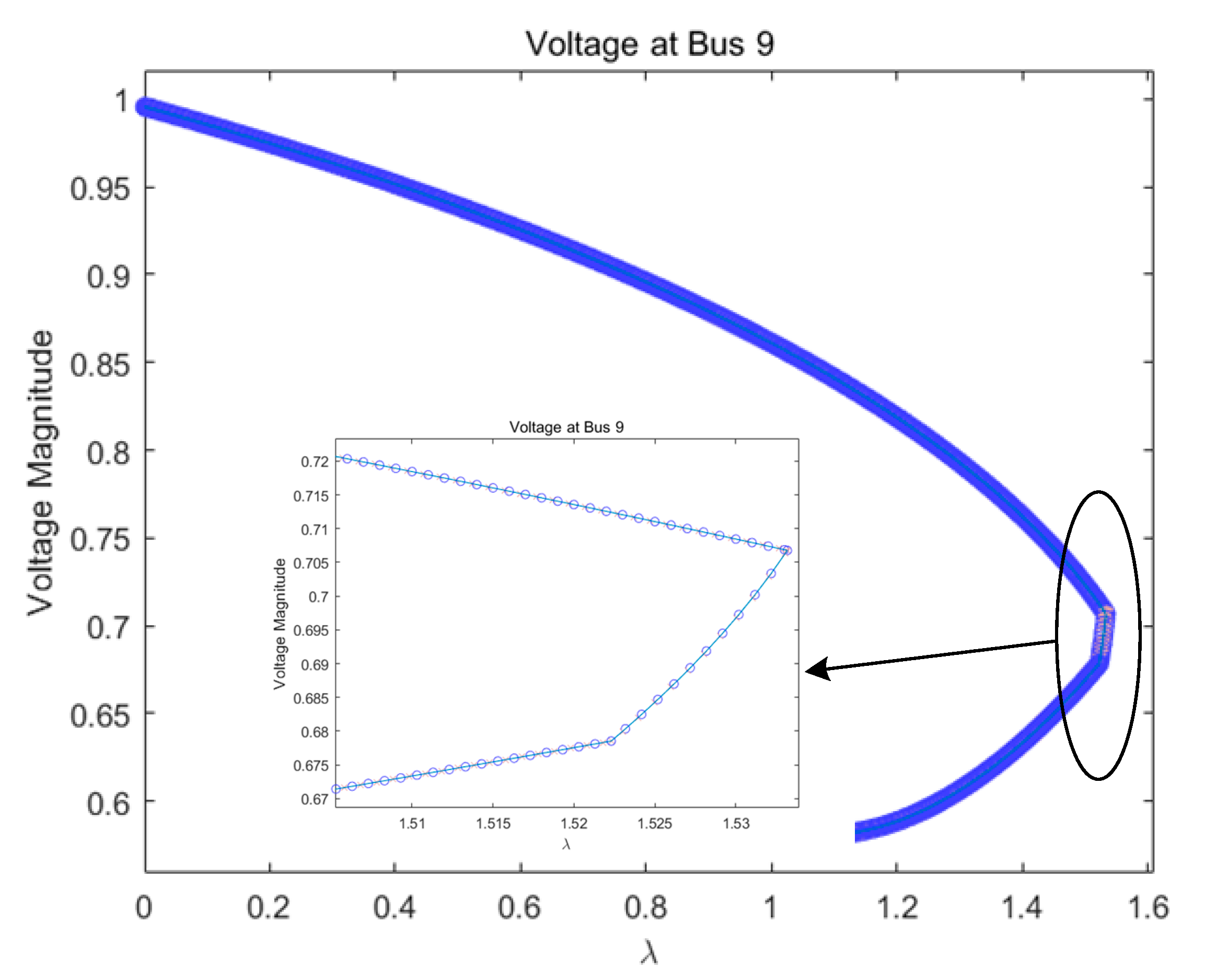
3.1. Example 1: IEEE Nine-Bus Network
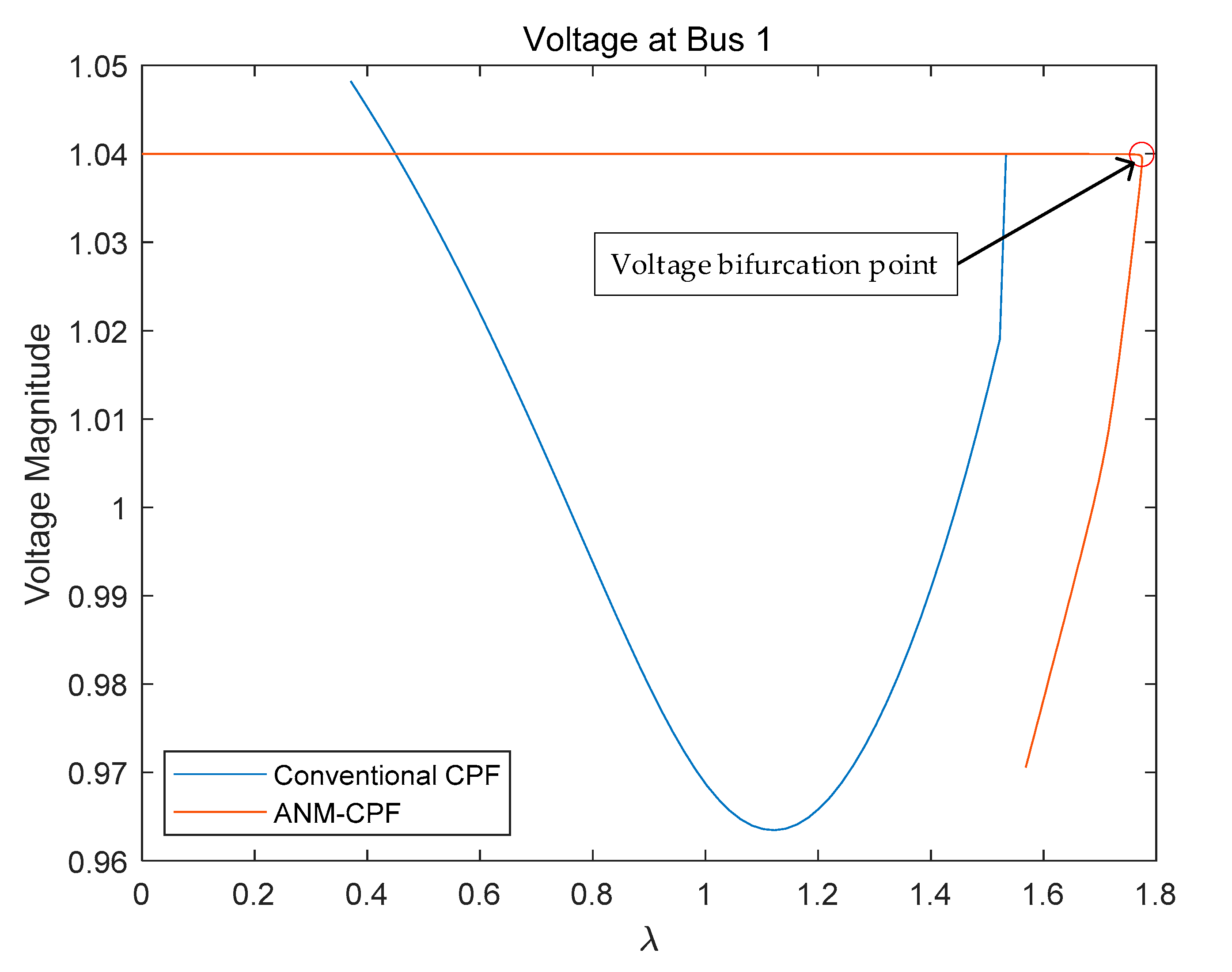
3.1.1. Without the Consideration of Reactive Power Limit in CPF
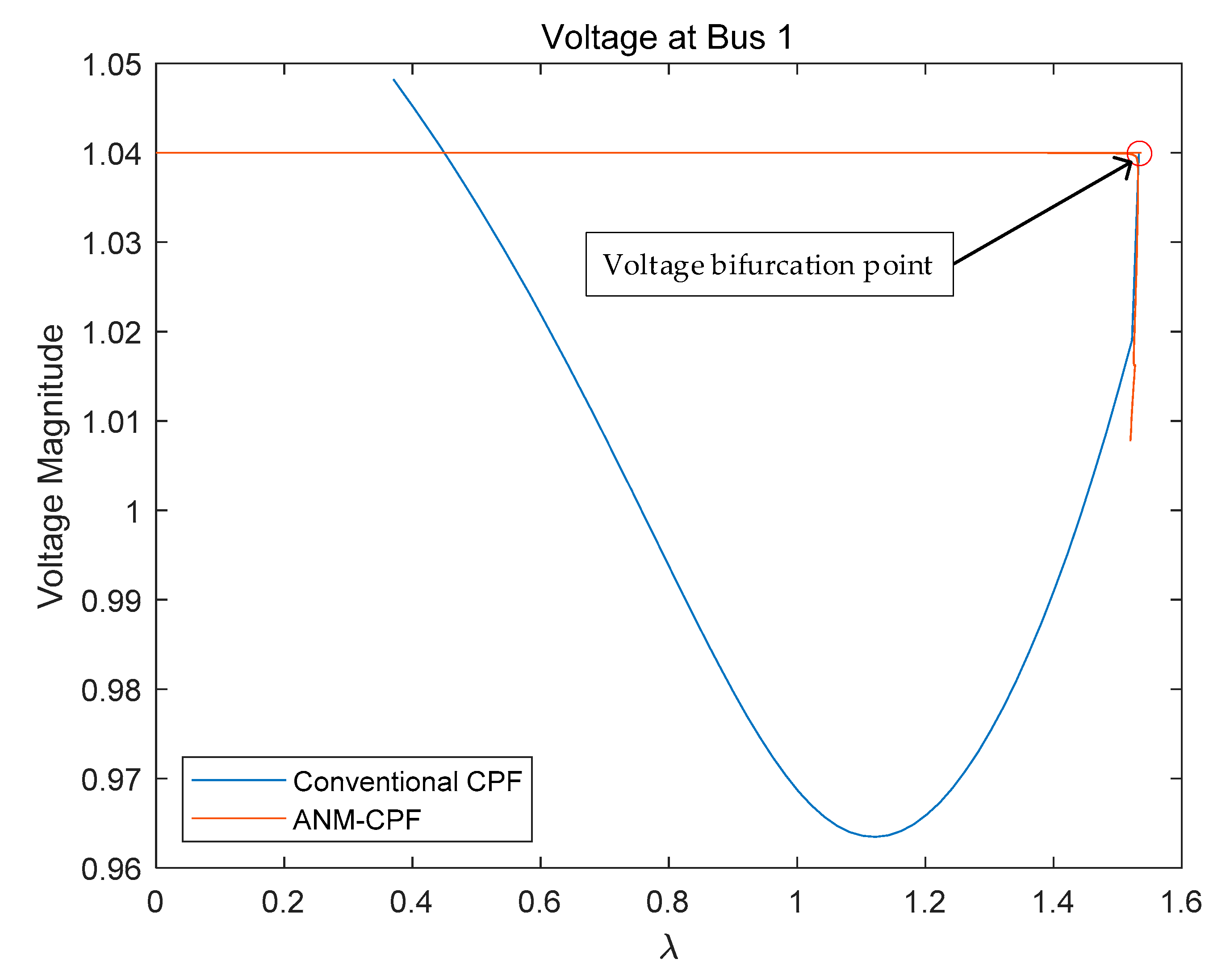
3.1.2. Consideration of Reactive Power Limit in CPF
3.1.3. Impact of Slack Variable on CPF
3.2. Example 2: A Large 182-Bus Network
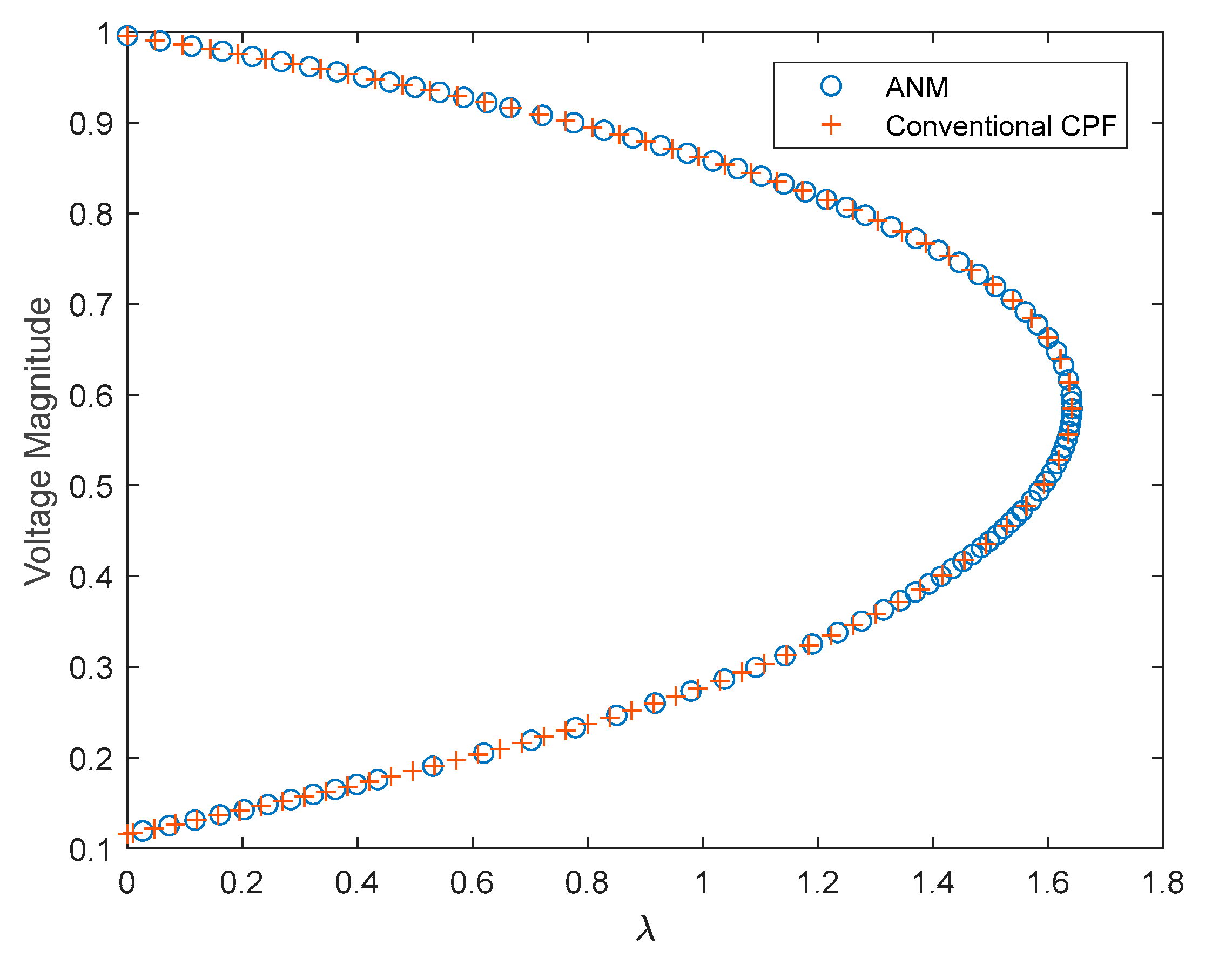
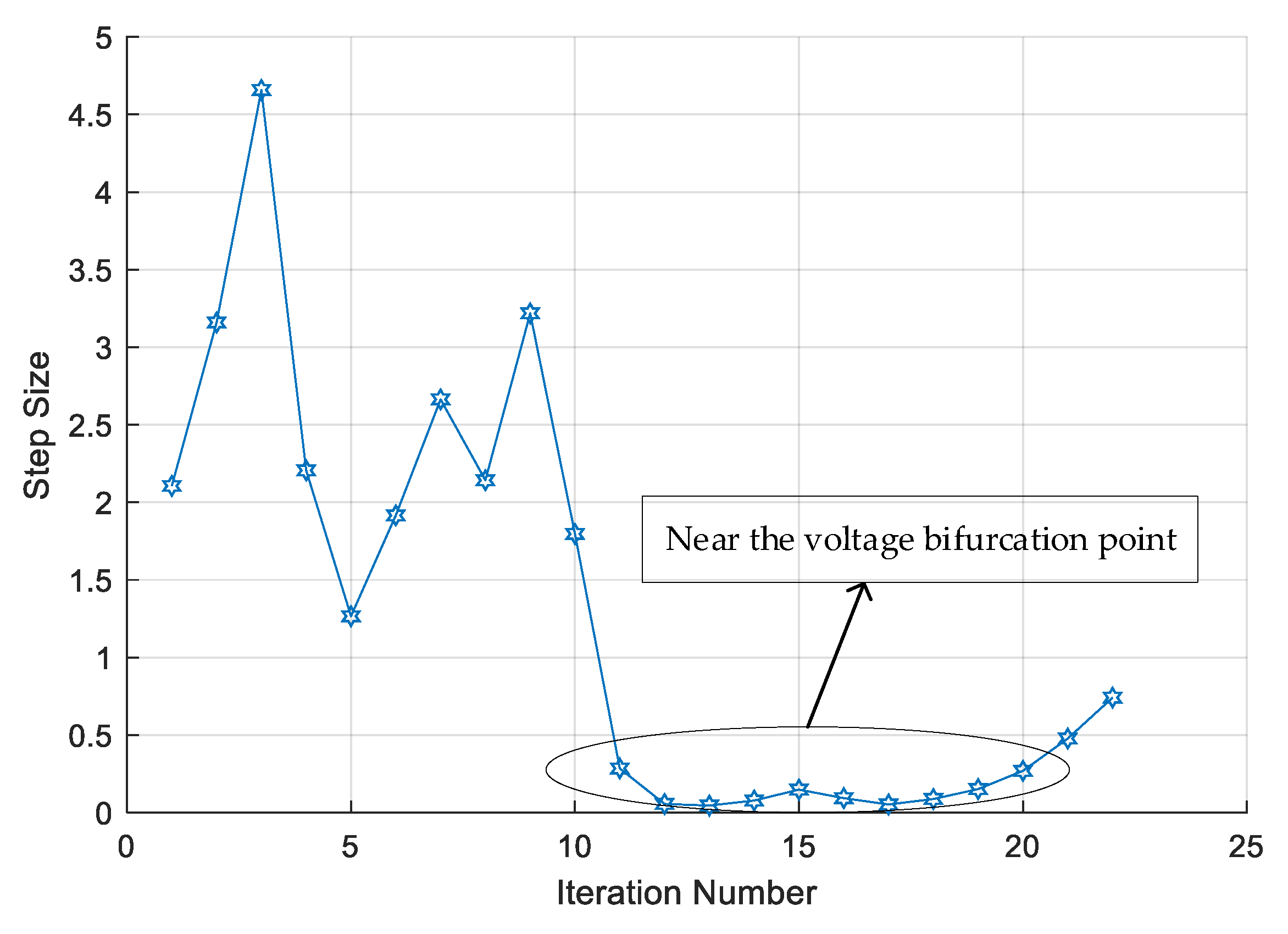
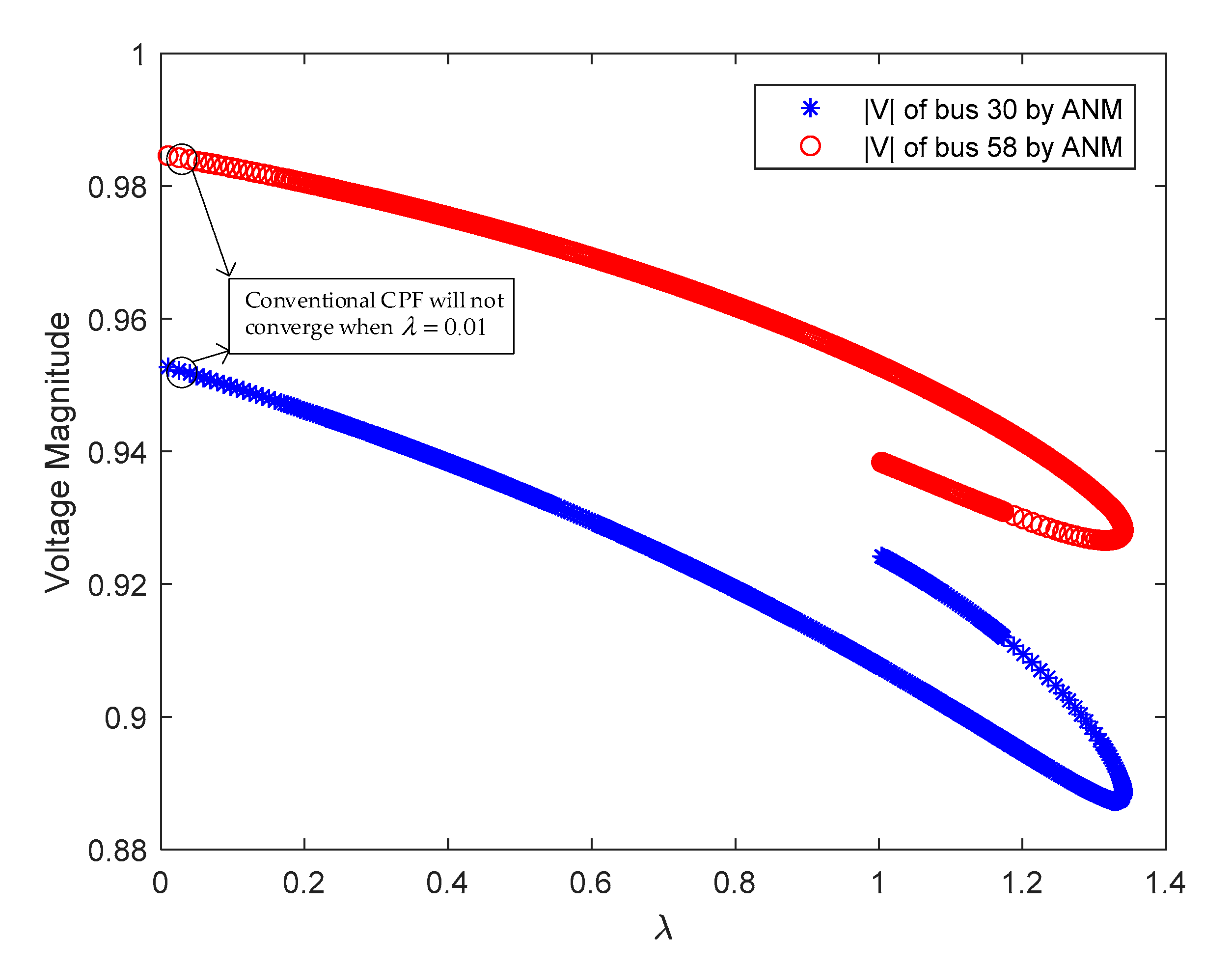
3.2.1. Computation of ANM-CPF
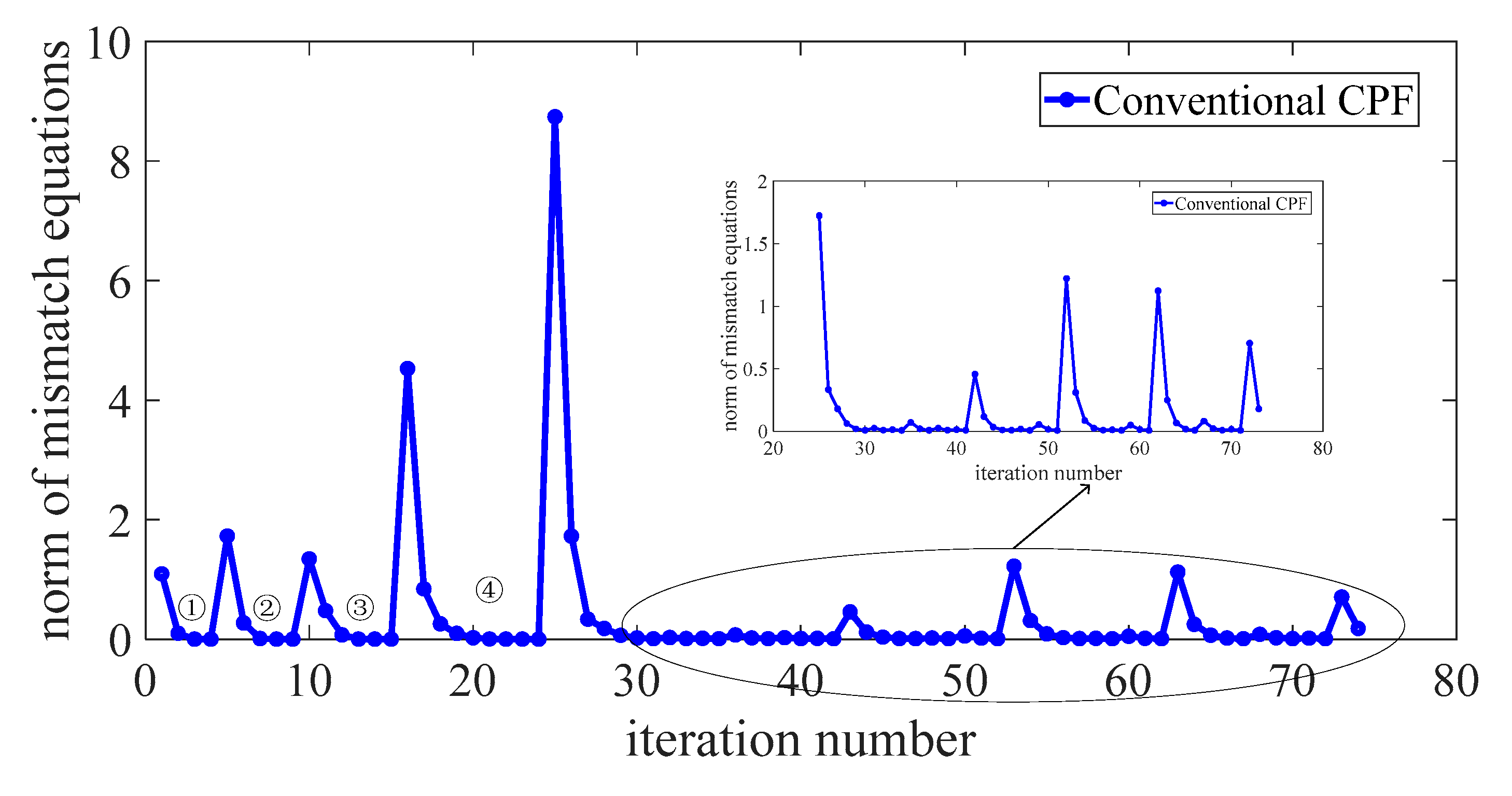
3.2.2. Computation Failures of Conventional CPF
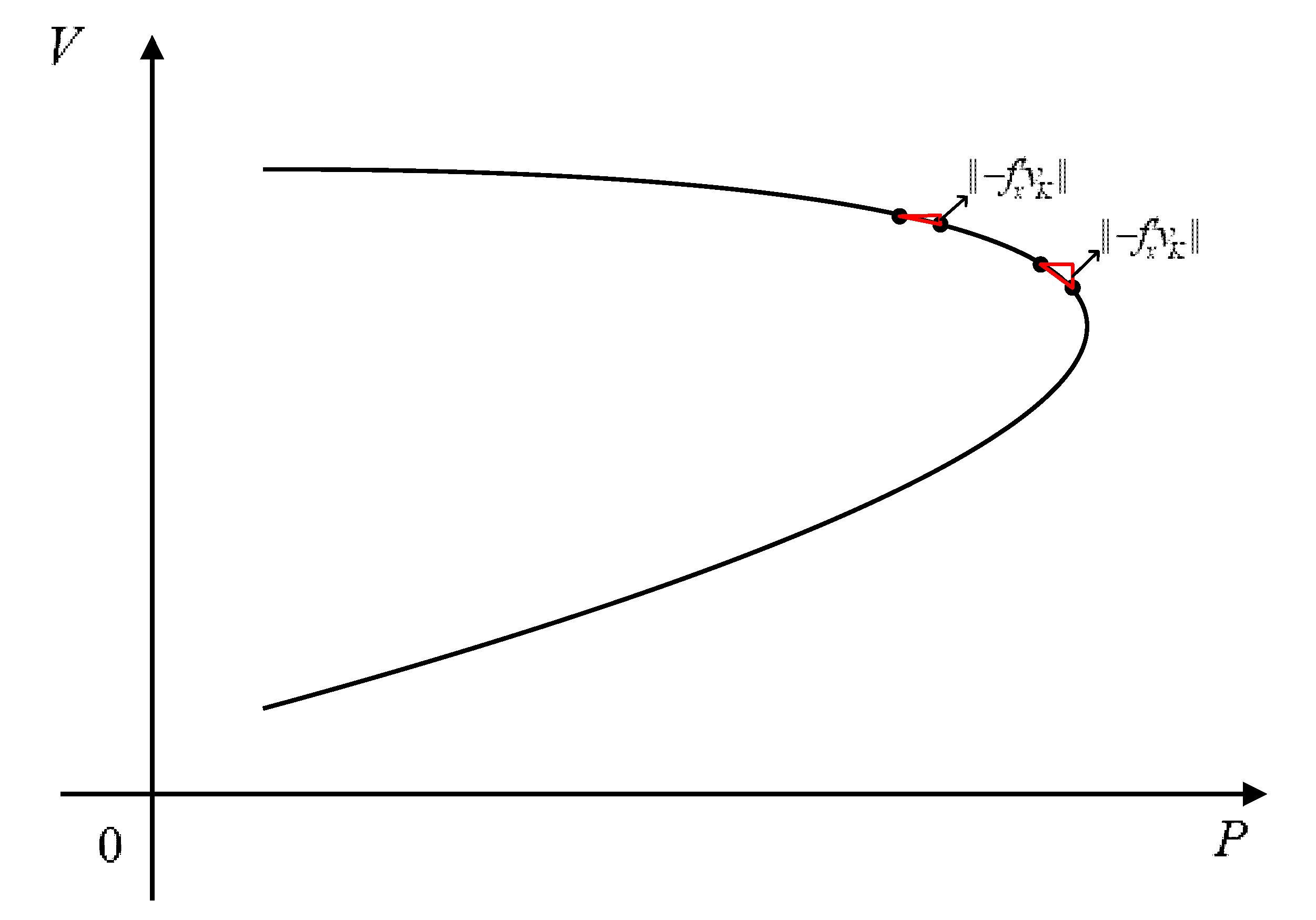
3.2.3. The Reason for the Proposed Method Working
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CPF | continuation power flow |
| ANM | asymptotic numerical method |
| PF | power flow |
| FB | Fischer-Burmeister |
| CPU | Central processing unit |
| PV | PV is used to describe bus types, which means that the active power and voltage of the bus are known. |
| PQ | PQ is used to describe bus types, which means that the active and reactive power of bus are known. |
| Q | Q is used to describe bus types, which means that the reactive power and phase angle of the bus are known |
Appendix A
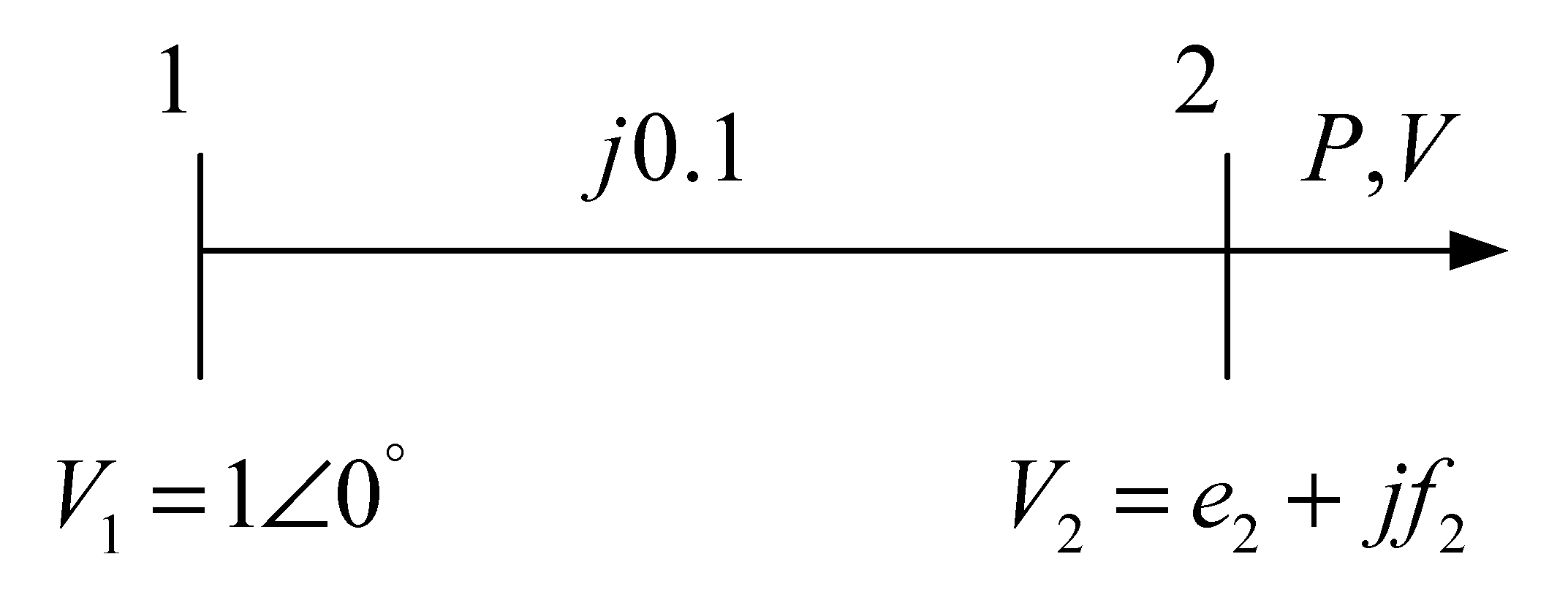
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
| Iteration Number | Step Size |
|---|---|
| 1 | 0 |
| 2 | 0.3799978 |
| 3 | 0.7599956 |
| 4 | 1.1399935 |
| 5 | 1.5199913 |
| 6 | 1.8999891 |
| 7 | 2.2799869 |
| 8 | 2.6599847 |
| 9 | 3.0399826 |
| 10 | 3.4199804 |
| 11 | 3.7999782 |
| 12 | 4.1799760 |
| 13 | 4.5599739 |
| 14 | 4.9399717 |
| 15 | 5.3199695 |
References
- Wang, X.-F.; Song, Y.-H.; Irving, M. Modern Power Systems Analysis; Springer: New York, NY, USA, 2008; ISBN 978-0-387-72852-0. [Google Scholar]
- Feng, Z.; Ajjarapu, V.; Long, B. Identification of voltage collapse through direct equilibrium tracing. IEEE Trans. Power Syst. 2000, 15, 342–349. [Google Scholar] [CrossRef]
- Fnaiech, N.; Jendoubi, A.; Zoghlami, M.; Bacha, F. Continuation power flow of voltage stability limits and a three dimensional visualization approach. In Proceedings of the 2015 16th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Monastir, Tunisia, 21–23 December 2015; pp. 163–168. [Google Scholar]
- Kumar, S.; Kumar, A.; Sharma, N.K. Analysis of power flow, continuous power flow and transient stability of IEEE-14 bus integrated wind farm using PSAT. In Proceedings of the 2015 International Conference on Energy Economics and Environment (ICEEE), Greater Noida, India, 27–28 March 2015; pp. 1–6. [Google Scholar]
- Garcia, P.A.N.; Vinagre, M.P.; Oliveira, E.J. Fault analysis using continuation power flow and phase coordinates. In Proceedings of the IEEE Power Engineering Society General Meeting, Denver, CO, USA, 6–10 June 2004; Volume 2, pp. 872–874. [Google Scholar]
- Wang, M.; Xia, Y.; Chen, Y.; Huang, S. GPU-based power flow analysis with continuous Newton’s method. In Proceedings of the 2017 IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 26–28 November 2017; pp. 1–5. [Google Scholar]
- Cao, B.; Bo, M.; Pan, J.; Liu, Y. Static Voltage Stability Analysis Based on the Combination of Dynamic Continuous Power Flow and Adaptive Chaotic Particle Swarm Optimization. In Proceedings of the 2018 IEEE 3rd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 12–14 October 2018; pp. 2217–2221. [Google Scholar]
- Canizares, C.A.; Alvarado, F.L. Point of collapse and continuation methods for large AC/DC systems. IEEE Trans. Power Syst. 1993, 8, 1–8. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, B. Reasons and countermeasures for computation failures of continuation power flow. In Proceedings of the 2006 IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006; p. 6. [Google Scholar]
- Zhao, J.; Zhou, C.; Chen, G. A novel bus-type extended Continuation Power Flow considering remote voltage control. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar]
- Zhu, P.; Taylor, G.; Irving, M. A novel Q-Limit guided Continuation Power Flow method. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–7. [Google Scholar]
- Yue, X.; Venkatasubramanian, V.M. Complementary limit induced bifurcation theorem and analysis of Q limits in power-flow studies. In Proceedings of the 2007 iREP Symposium—Bulk Power System Dynamics and Control—VII. Revitalizing Operational Reliability, Charleston, SC, USA, 19–24 August 2007; pp. 1–8. [Google Scholar]
- Avalos, R.J.; Canizares, C.A.; Milano, F.; Conejo, A.J. Equivalency of Continuation and Optimization Methods to Determine Saddle-Node and Limit-Induced Bifurcations in Power Systems. IEEE Trans. Circuits Syst. I Regul. Pap. 2009, 56, 210–223. [Google Scholar] [CrossRef]
- Pirnia, M.; Cañizares, C.A.; Bhattacharya, K. Revisiting the power flow problem based on a mixed complementarity formulation approach. IET Gener. Transm. Distrib. 2013, 7, 1194–1201. [Google Scholar] [CrossRef]
- De Rubira, T.T.; Wigington, A. Extending complementarity-based approach for handling voltage band regulation in power flow. In Proceedings of the 2016 Power Systems Computation Conference (PSCC), Genoa, Italy, 20–24 June 2016; pp. 1–6. [Google Scholar]
- Lin, Y.; Ju, Y. A Robust Three-Phase Power Flow for Active Distribution Network Embedded Autonomous Voltage Regulating Strategies. In Proceedings of the 2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 20–22 October 2018; pp. 1–8. [Google Scholar]
- Chiang, H.-D.; Flueck, A.J.; Shah, K.S.; Balu, N. CPFLOW: A practical tool for tracing power system steady-state stationary behavior due to load and generation variations. IEEE Trans. Power Syst. 1995, 10, 623–634. [Google Scholar] [CrossRef]
- Li, S.-H.; Chiang, H.-D. Nonlinear predictors and hybrid corrector for fast continuation power flow. IET Gener. Transm. Distrib. 2008, 2, 341. [Google Scholar] [CrossRef]
- Fischer, A. A special newton-type optimization method. Optimization 1992, 24, 269–284. [Google Scholar] [CrossRef]
- Yang, X.; Zhou, X. Application of asymptotic numerical method with homotopy techniques to power flow problems. Int. J. Electr. Power Energy Syst. 2014, 57, 375–383. [Google Scholar] [CrossRef]
- Zimmerman, R.D.; Murillo-Sanchez, C.E.; Thomas, R.J. MATPOWER: Steady-State Operations, Planning, and Analysis Tools for Power Systems Research and Education. IEEE Trans. Power Syst. 2011, 26, 12–19. [Google Scholar] [CrossRef]
- Ju, Y. Constraints Exchange Data. Available online: https://gitee.com/cieeyodaju/Constraints-Exchange-Data (accessed on 6 August 2019).
- Ruan, C.; Wang, X.; Wang, X.; Gao, F.; Li, Y. Improved Continuation Power Flow Calculation Method Based on Coordinated Combination of Parameterization. In Proceedings of the 2018 IEEE 2nd International Electrical and Energy Conference (CIEEC), Beijing, China, 4–6 November 2018; pp. 207–211. [Google Scholar]
- Alam, M.M.; Moreira, C.; Islam, M.R.; Mehedi, I.M. Continuous Power Flow Analysis for Micro-Generation Integration at Low Voltage Grid. In Proceedings of the 2019 International Conference on Electrical, Computer and Communication Engineering (ECCE), Cox’sBazar, Bangladesh, 7–9 February 2019; pp. 1–5. [Google Scholar]
| Method | ANM-CPF | Conventional CPF |
|---|---|---|
| Average CPU time for each point/s |
| Slack Variable | ||
|---|---|---|
| Average CPU time for each point/s |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Ju, Y.; Zhu, Z. An Asymptotic Numerical Continuation Power Flow to Cope with Non-Smooth Issue. Energies 2019, 12, 3493. https://doi.org/10.3390/en12183493
Huang Y, Ju Y, Zhu Z. An Asymptotic Numerical Continuation Power Flow to Cope with Non-Smooth Issue. Energies. 2019; 12(18):3493. https://doi.org/10.3390/en12183493
Chicago/Turabian StyleHuang, Yan, Yuntao Ju, and Zeping Zhu. 2019. "An Asymptotic Numerical Continuation Power Flow to Cope with Non-Smooth Issue" Energies 12, no. 18: 3493. https://doi.org/10.3390/en12183493
APA StyleHuang, Y., Ju, Y., & Zhu, Z. (2019). An Asymptotic Numerical Continuation Power Flow to Cope with Non-Smooth Issue. Energies, 12(18), 3493. https://doi.org/10.3390/en12183493




