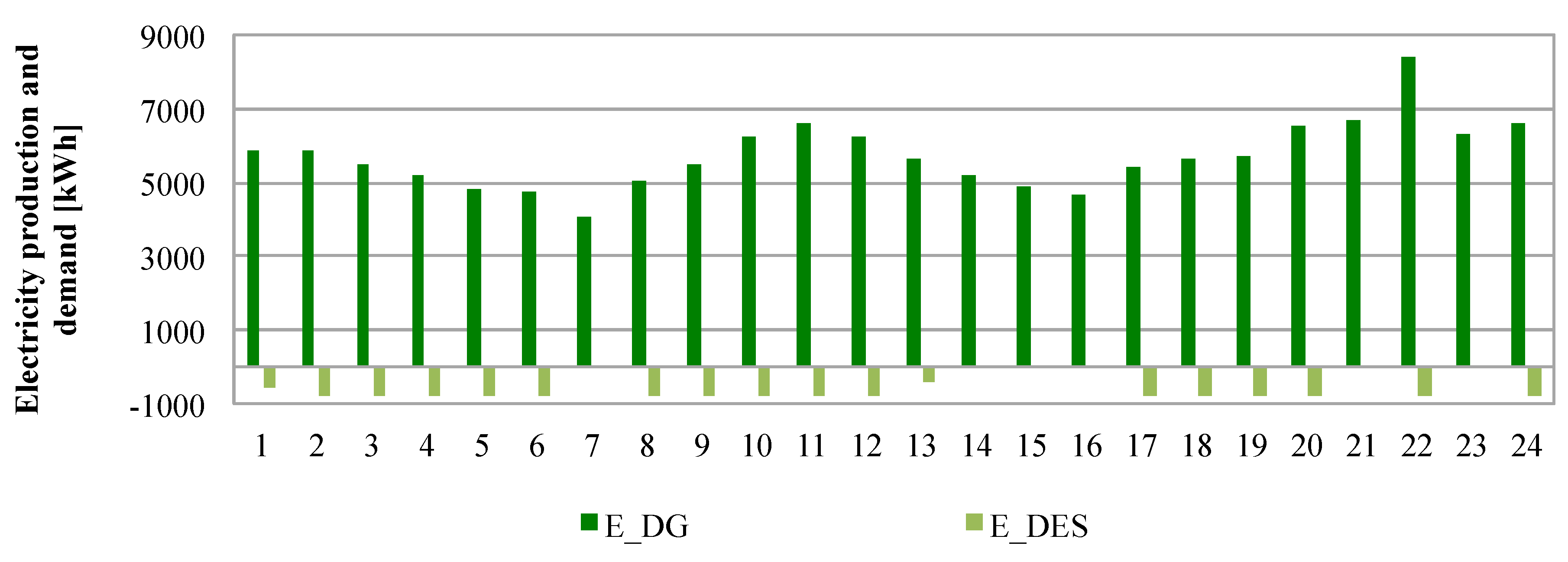
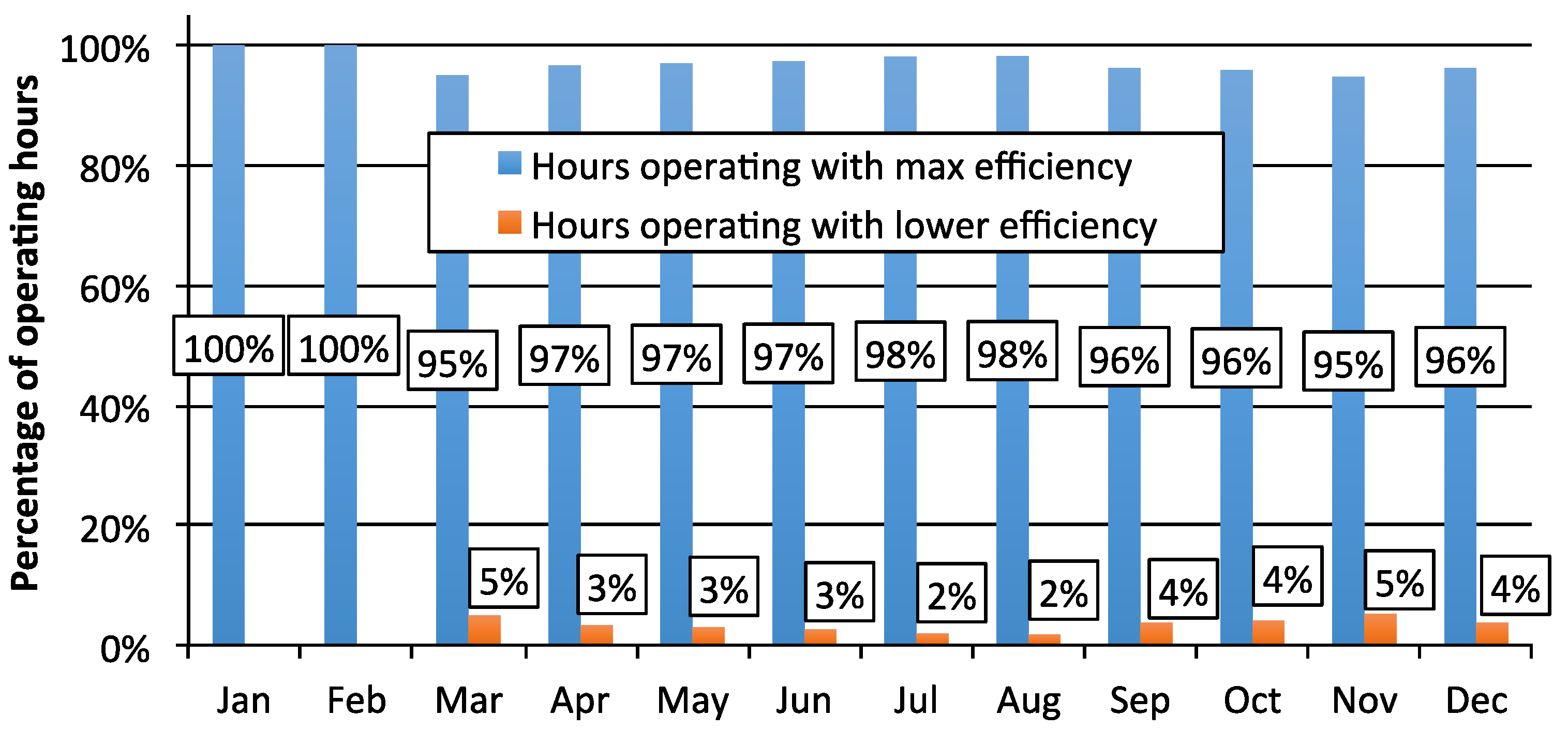
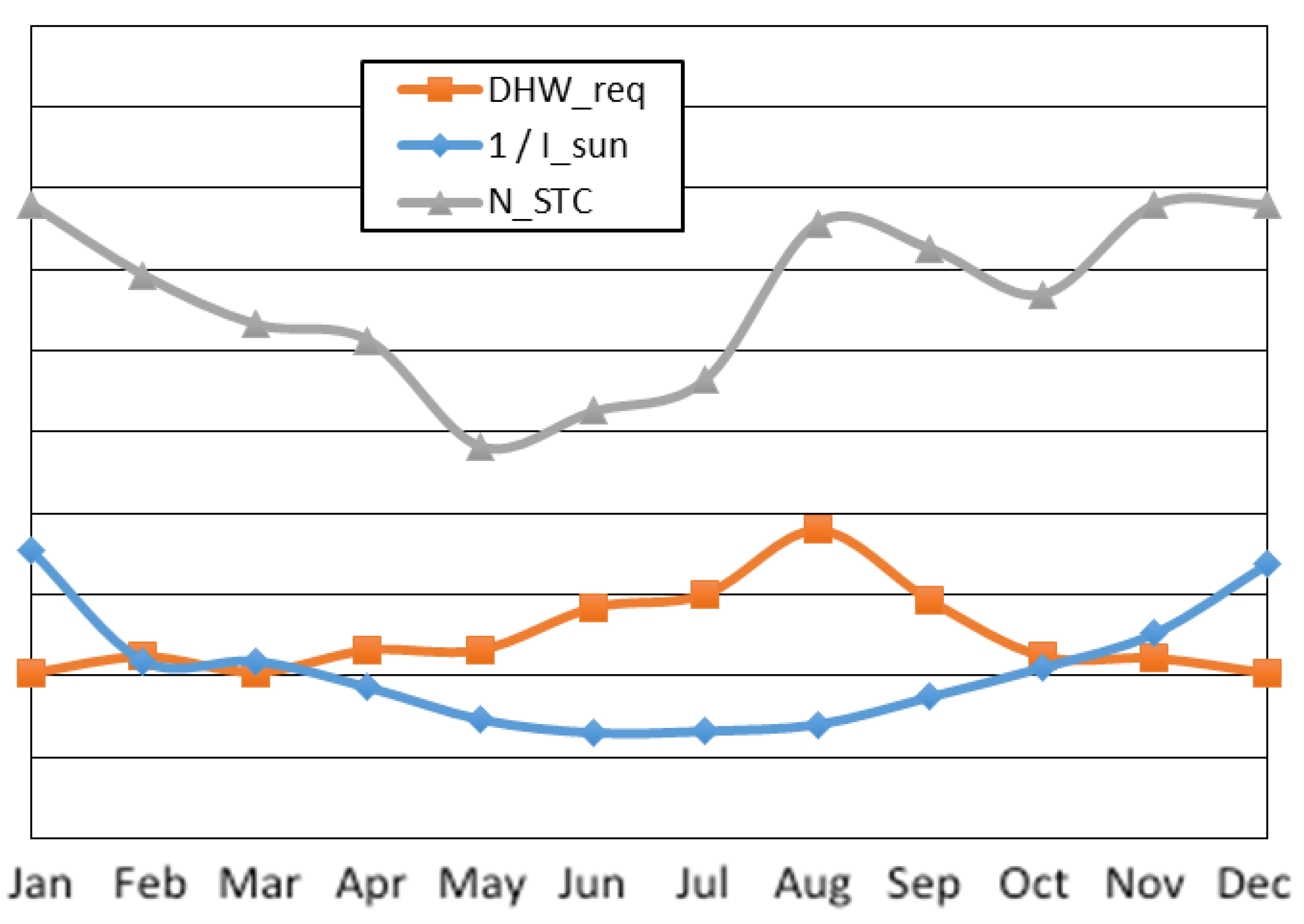
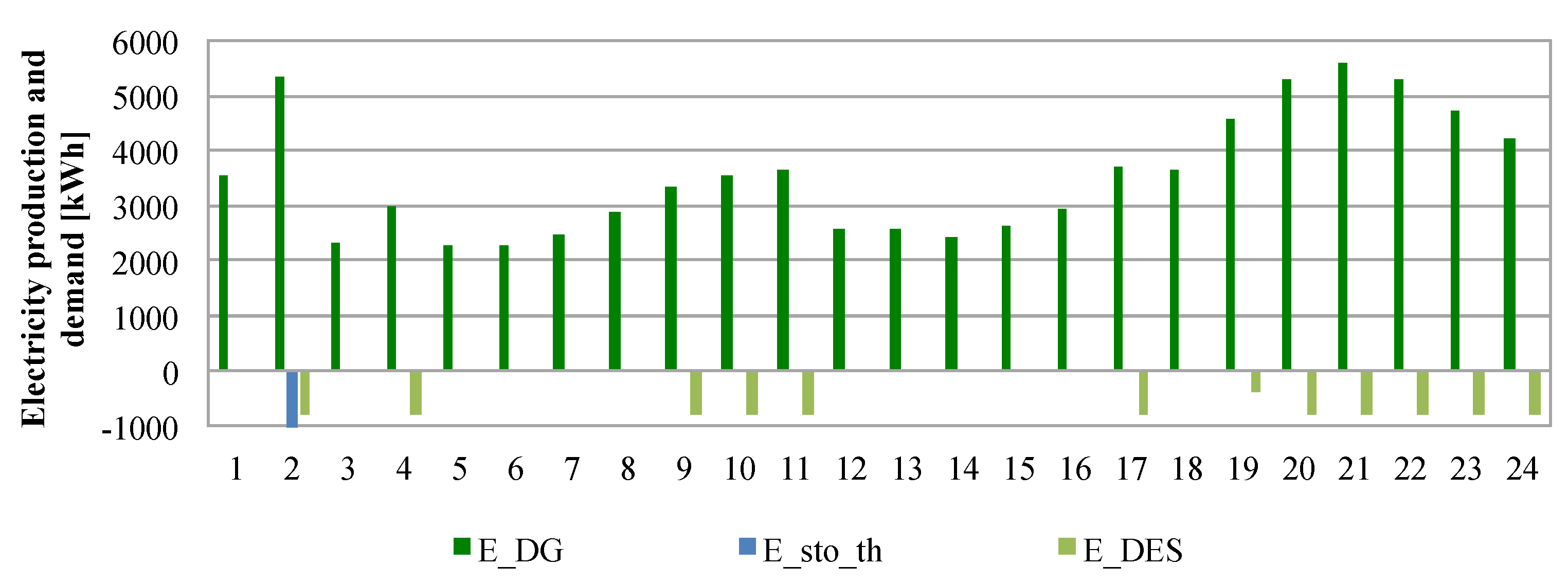
2.1. Literature Review on Energy Hubs
Differently from the past, where each energy carrier was operated independently (e.g., electricity [
6], natural gas [
7], and district heating [
8]), recently an increasing number of publications started focusing on MESs, where electricity, heating, cooling, water, transport, and others interact at various levels, in order to get an optimized operation [
9].
Moslehi et al. [
10] developed a methodology to optimally coordinate the operation of a large industrial cogeneration system, including both electric and thermal systems, with the purpose to minimize the overall costs while satisfying electric and steam constraints. The thermal system is modeled as a linear steady-state model, and the electric system as a standard Newton’s power flow model.
Groscurth et al. [
11] developed a general model framework aimed at supporting decision-making during the development and realization of regional and municipal energy systems, with the purpose to minimize non-renewable primary energy, air pollutant emissions, and monetary cost. The optimal solution is obtained looking for Pareto-optimal combinations of conventional energy-supply techniques, allowing for an increasing use of RESs and ESSs. The model also includes heat exchangers, cogeneration, heat pumps (HP), demand-side measures and dwelling insulation.
In [
12], Bakken et al. presented, among others, a new model designed to analyze complex energy transport systems with multiple energy carriers. The transport system consists of different energy sources (oil, coal, electricity, gas, liquefied natural gas), conversion between different energy carriers, and different energy storages (hydro, liquefied natural gas storage, and gas caverns). The optimization is carried out using MATLAB linear programming algorithms, considering both equality and inequality constraints.
Hecq et al. [
13] developed a linear programming model (PRELE), allowing the analysis of combined electricity and gas markets of several interconnected networks, minimizing the total investment and operating system costs.
Bakken et al. [
14] outlined a new methodology for analyzing complex energy systems with multiple energy carriers, including technological, economic, and environmental aspects. To better generalize their study, they use a combination of stochastic dynamic programming and deterministic short-term optimization. Available sources are gas (from landfills), biomass (from forestry and farming), and waste (from companies and offices).
In [
15], An et al. presented a combined optimal power flow method, considering both electricity and natural gas networks, aiming at maximizing social welfare. First, the electric load flow problem is solved, and the results are used to solve the gas load flow problem.
In [
16], Gil et al. developed a single mathematical framework of electricity, gas, coal, and water, using a network flow optimization model. The proposed model, based on the actual US national electricity grid, is able to ensure the economic and physical integrity of the electricity network, taking into account the strong coupling within different energy subsystems.
Nazar and Haghifam [
17] developed a three-stage optimization procedure to achieve the optimal expansion planning of a system, minimizing the investment and operational costs and maximizing the system reliability, using the energy hub to take into account the impact of multiple energy carriers. The algorithm allows to determine the optimal allocations, to select optimal capacities and replacement alternatives of system devices, and finally to ensure the optimal restoration in contingency conditions.
Quelhas et al. [
18] presented a network flow programming model to evaluate how nodal prices in the electric network are influenced by the dynamics of integrated energy systems and of the various fossil fuel networks (assumed to be similar to that of the USA), with the purpose to find the most economically efficient use of electricity generation, demand, and fuel supply and delivery. The proposed algorithm can be solved by applying the generalized network simplex algorithm.
Soderman and Pettersson [
19] proposed a MILP model, with the objective to minimize the overall cost of a distributed energy system, consisting of electricity production and demand, heat production and consumption, power transmission, fuel transport, water transport, and heat storage. The developed algorithm is able to identify the location and the type of production units, heat transport lines, and storages, according to the selected objective function.
In [
20,
21], Geidl and Andersson presented an approach to manage energy flows in MESs, including gas, electricity, and district heat, based on the idea of energy hubs. In [
20], the optimization of energy flows is elaborated using a single entity containing all storages and conversion devices, with a multi-input and multi-output coupling. The problem is defined as a topological optimization, and addressed as a nonlinear constrained optimization problem defined by an objective function under different constraints. In [
21], the MES is represented as the sum of several interconnected energy hubs, coupled between them using power conversion devices. A general dispatch rule for linear energy hubs is also derived.
A real case study addressing the energy hub approach was shown by Schulze et al. In [
22] the energy hub concept was used to solve optimal power flow problems with a high number of RESs. The objective function is a combination of cost minimization and benefit maximization of each energy hub, considering different energy sources such as natural gas, electricity, fuel oil, and district heating. The model is implemented using MATLAB under linear and non-linear constraints.
Almassalkhi and Hiskens [
23] developed a novel method for analyzing interconnected multi-carrier energy hub systems, supporting natural gas, electricity, wind capacity and district heat. The model is implemented using MATLAB and demonstrated on a set of more than 100 hubs, using binary variables to avoid non-linearity.
La Scala et al. [
24] analyzed a system composed by several interconnected energy hubs with multiple energy carriers, in order to obtain the optimal energy flow management. The problem is addressed exploiting a non-linear multi-objective optimization procedure, able to minimize several cost functions (technical, economic, and environmental), ensuring a reliable operation of the multi-carrier energy system (electricity and natural gas), also in presence of volatile energy prices and high load demands.
Pazouki et al. [
25] proposed an optimal operation method to analyze an energy hub as a super node in an electrical distribution network, where gas, electricity, and wind at the input port cover the required demands in the form of electricity, heat, gas, and water, taking into account storage, direct connections, or demand shifting. A MILP model is used to identify the optimal solution, minimizing the operation cost and maximizing the system reliability in nine different case studies.
Proietto et al. [
26] developed a heuristic and non-linear programming-based algorithm in order to get the optimal energy flows dispatch, maximizing the profit for the plant owner. The optimal energy flows dispatch is obtained controlling an energy management system (EMS) as an energy-hub connected to electricity, gas, and hydrogen networks.
Brahman et al. [
27] proposed optimal operation methods to analyze a residential energy hub model, where natural gas, electricity, and solar radiation at the input port provide the required demands in the form of electricity, heating, and cooling. The authors also consider demand response (DR) programs, including load curtailment, load shifting, and flexible thermal load of major household appliances, in order to increase the operational flexibility of the model. The results are tested for three different case studies, using both a minimum cost objective function and a multi-objective function, taking also into account pollutant emissions.
Arnone et al. [
28] proposed an innovative MES involving both electrical energy and hydrogen power sources. An EMS is able to optimally manage a system composed by a water electrolyzer, a fuel cell, and two different storage systems (INGRID project), exploiting a multi-object optimization algorithm, implemented using MATLAB.
Ma et al. [
29] developed an optimal dispatch strategy for a MES, considered as a whole micro energy grid. To enhance the reliability and flexibility of the energy hub, the classic combined cooling, heating, and power (CCHP) is expanded considering a generic energy hub, including RESs, EESs, and CCHP. The generic optimal dispatch model aims to minimize the daily operation cost and the environmental costs, using a MILP optimization algorithm, also considering DR.
Timothée et al. [
30] developed an optimal dispatch model of a multi-energy hub, including RESs (PV and wind energy), combined heat and power (CHP), internal combustion generator (ICG), heat, and thermal storages. The optimal dispatch solution is obtained using an evolutionary algorithm, and the flexibility of load demand is obtained using vehicle-to-grid technology.
In Attardo et al. [
31], the economic assessment of energy systems aimed at covering electricity and heating demands of an urban district was performed, and comparing results in Italian and Vietnamese scenarios. The study was deepened in [
32], where also the cooling demand was evaluated and a multi-objective optimization approach was adopted, considering both economic and environmental objective functions.
As shown in the previous literature works, most of the papers, especially at the beginning, focused on the integration of electric and thermal systems (gas and oil markets) [
7,
10,
13,
15]. Only in later years, with the progress of the research, MESs started to focus on other energy sources, such as renewable energies [
22,
23,
25,
27,
29,
30,
31,
32], biomass and waste [
14], district heat, energy storages [
12,
19,
20,
25,
28,
29,
30,
31,
32], water transport [
16,
19,
25], district heat [
20,
22,
23,
26], demand-side measures [
11,
25,
27,
28,
30,
31,
32], and so on. The optimization is carried out using linear but also non-linear programming methods, with the aim to minimize mainly technological, economic or environmental aspects. Sometimes, a MILP algorithm is used to minimize more than one function at a time [
19,
25,
29].
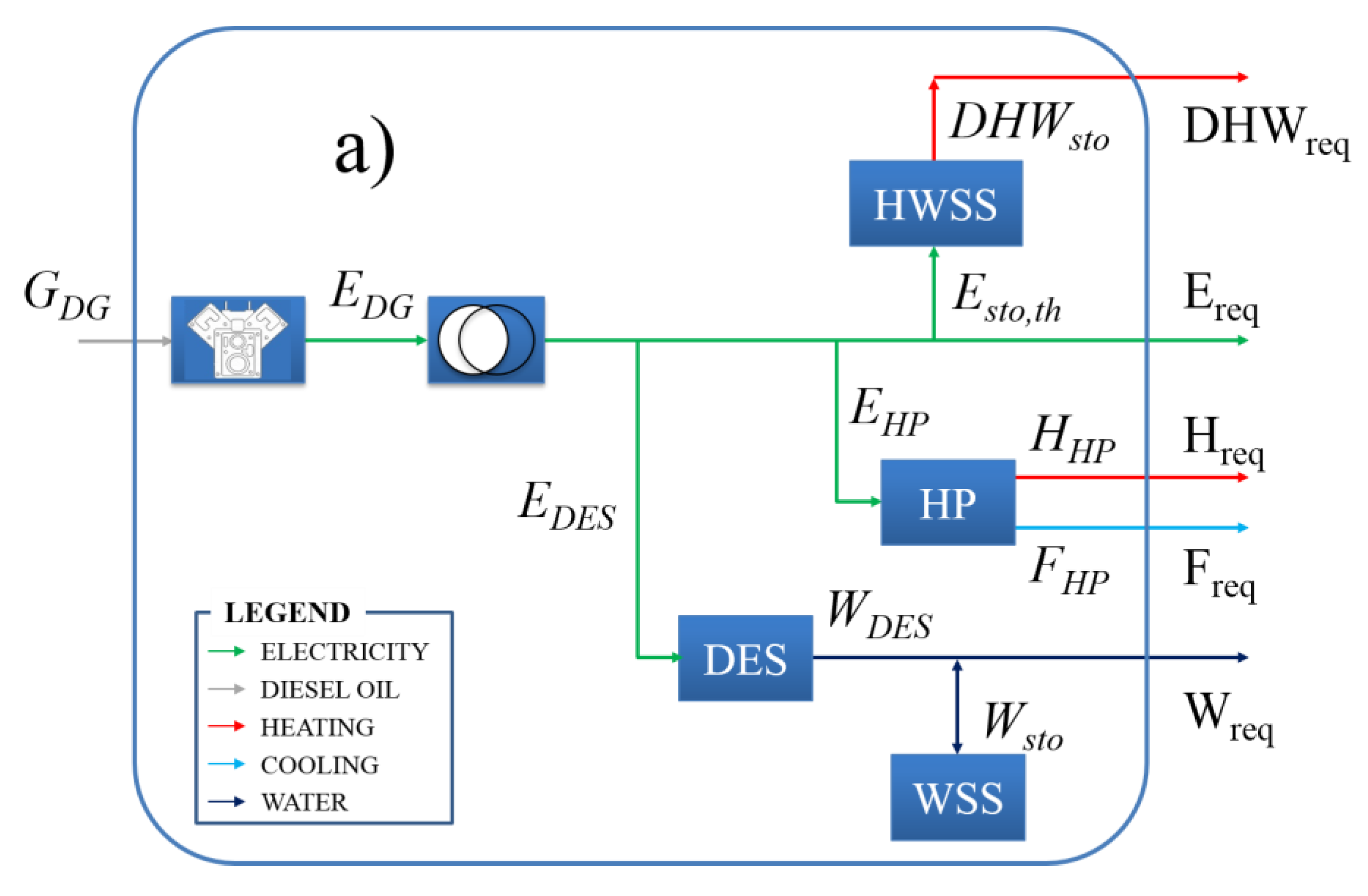
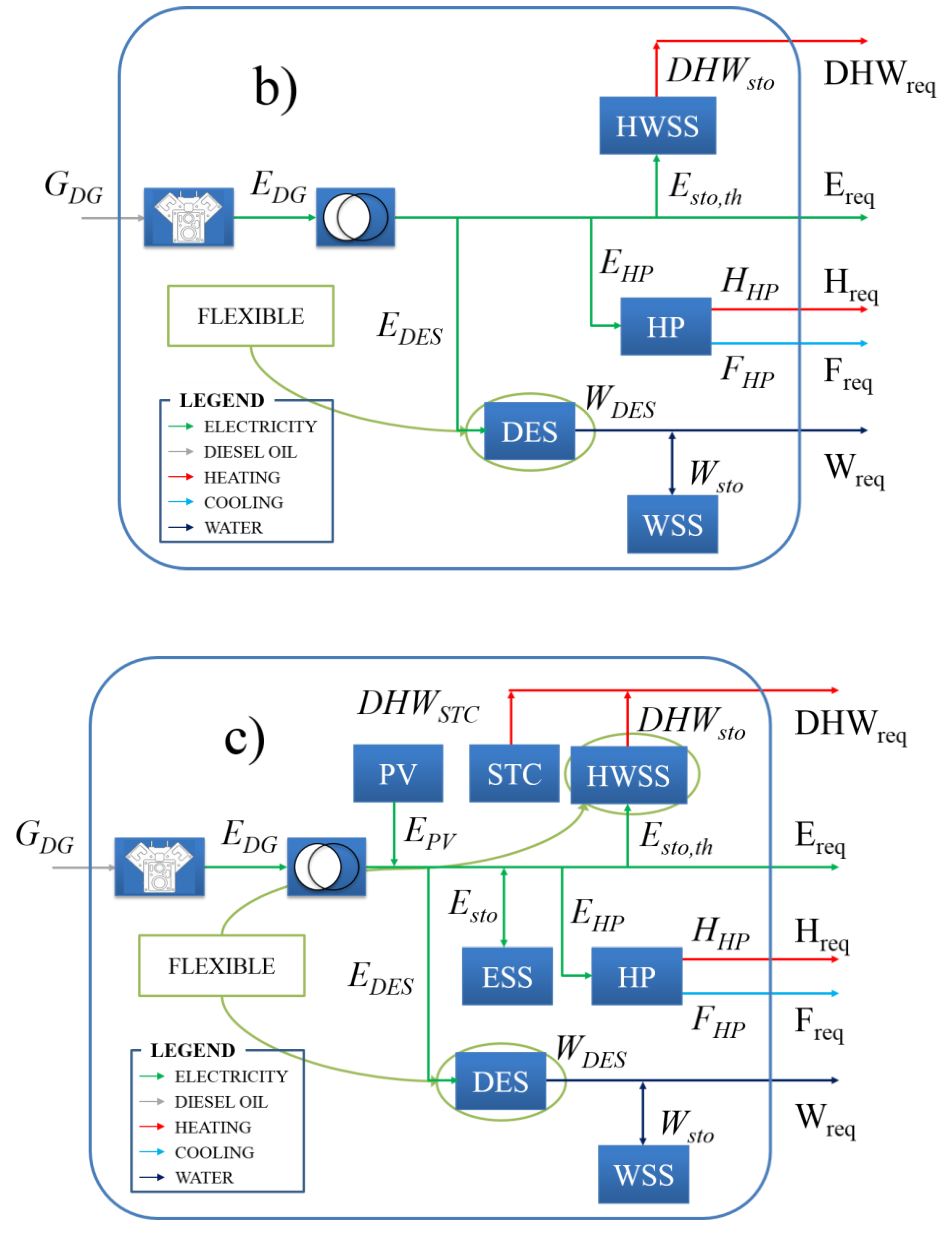
According to this brief literature analysis, the original contribution of this paper is the employment of the energy hub scheme for the synthesis, design and scheduling of new equipment, taking also into account flexibility services offered by the loads. Both medium and small flexible loads are considered in the analysis, specifically electricity to supply the desalination units and DHW storages installed in residential houses, operated as a unique entity through a main controller.
2.2. Energy Efficiency Measures in Small Islands
With the ratification of the Paris Agreement, 174 Countries (and the European Union) are obliged to introduce specific energy policies in order to limit the CO
2 emissions and, consequently, global warming. As reported in the Second Article of the Paris Agreement, the common goal is the limitation of global warming to “well below 2 °C”, in comparison with the preindustrial levels [
33]. To achieve this ambitious target, two kinds of solutions can be adopted [
34]:
Replacement of the existing power plants supplied by fossil fuels with new technologies supplied by RESs;
Improvement of innovative solutions to reduce the energy demand from the final energy consumers, such as the installation of more efficient technologies or the adoption of smart controlling systems.
The application of both techniques is necessary to maximize the environmental benefits, as the different effects produced [
35]. In the energy sector, the investments for the installation of RESs have grown in the last decades. It is estimated that all countries invested annually 47 billion USD in 2004 to 286 billion USD in 2015 [
36].
Despite the diffusion of plants supplied by RESs, several areas continue to be strongly energy-dependent from fossil fuels. This condition is quite common in the numerous small islands around the world. Some of them are classified as Small Islands Developing States (SIDSs), an acronym introduced in 1994 by the United Nations. The upgraded list of SIDSs is composed by 58 countries, divided in Caribbean (29 countries), Pacific (20 countries), and AIMS (acronym of Africa, Indian Ocean, Mediterranean, and South China Sea, including nine countries) [
37].
Considering the energy sector, both SIDSs and small islands belonging to developed countries show several common peculiarities, as [
38]:
Major energy dependence on imported fossil fuels;
Small-scale generation systems to produce electricity;
High costs for the energy production, infrastructure, transportation, communication and servicing;
Under-utilization of the local available RESs;
In many cases the installation of RESs is an economically feasible solution.
In addition, SIDSs are directly exposed to the international markets of oil, influencing the local economy. Population and local economy show a growing trend. SIDSs are characterized also by a little resilience to natural disasters and a fragile environment [
39,
40]. It is estimated that about 21 million people live in 2056 small islands, each one having between 1000 and 100,000 inhabitants. These communities require an electrical energy demand equal to 52,690 GWh/y, of which 22,770 GWh/y are concentrated in the Pacific Oceans [
41]. In this context, fossil fuel is the main (or in several case the only) source to supply the local energy demand, with Fiji being the only exception. Indeed, thanks to the copious precipitation, this country was able to satisfy 48.74% of the annual energy demand in 2017 [
42] through hydro power plants. Small islands usually import fossil fuels from mainland or foreign territories. Papua New Guinea, Trinidad, and Tobago are the only exceptions, as these countries produce and export fossil fuels [
43].
About the electrical energy sector, small islands are usually equipped with stand-alone electrical grids, supplied by local diesel power stations [
44]. The electrical network is underdeveloped, especially in SIDSs, where it is possible to find small villages disconnected from the main electrical grid. In this case the electricity production is entrusted to very small generators. In case of developed countries, small islands sometimes are interconnected each other or linked to mainland [
43,
45]. To reduce the dependence from fossil fuels and the emission of greenhouse gases, many islands are adopting specific policies to increase their energy sustainability. As introduced before, two kinds of projects can be implemented: the introduction of RESs and the improvement of energy efficiency for final users. The first approach is quite popular in the literature. As an example, the installation of renewable energy mixes has been proposed in numerous small islands around the world, such as Samsø (Denmark) [
46], Faroe Islands [
47], Canary Islands (Spain) [
48,
49], Azores (Portugal) [
50], Maldives [
51], and Reunion Island (France) [
52].
Samsø is a famous example of an islanded community totally powered by RESs. This island is located at the east of Denmark, with a population of 3700 inhabitants. The local electrical network is linked to the mainland one, but the local energy production is enough to cover the local demand, thanks to the utilization of wind turbines and the realization of a heating district network supplied by biomass, produced locally [
46]. The case of archipelagos located in remote areas is more complex [
53].
As an example, Faroe Islands form an autonomous country (belonging to the Kingdom of Denmark), composed by 18 islands and located in the North Atlantic Ocean between Scotland, Norway, and Iceland. About 50,000 inhabitants live in this archipelago, requiring annually about 335 GWh. The electricity production is entrusted to fossil fuels (49%), hydropower (33%), and wind source (18%) (2017 data) [
47]. To reduce the dependence from fossil fuels, Katsaprakakis et al. [
47] investigated the possibility to install a wind park to cover 60% of the local energy demand, adding also PV panels and a pumping hydro plant to regularize the electricity production during the year and produce the remaining part of the energy demand.
Canary Islands is a Spanish archipelago located 100 km west from Morocco, in the Atlantic Ocean. About 2.2 million people live in this archipelago, of which 0.85 million live in Gran Canaria and 0.89 million in Tenerife. Gils and Simon [
48] investigated the adoption of concentrated solar panels, wind turbines, and pumping hydro plants to improve the RESs share in the islands. The proposed energy scenario suggests also the installation of electrical links to interconnect each other the small islands [
48]. To supply the Canary Islands, Rusu investigated also the potential exploitation of sea-wave energy source, considering the current prototypal technologies [
49].
Stenzel et al. analyzed the environmental implications of a RESs mix to supply the Graciosa Island, belonging to the Azores, that are a Portuguese archipelago located in the North Atlantic Ocean [
50]. The G.R.A.C.I.O.S.A Project suggests the installation of a wind park (4.5 MW), PV panels (1 MW), and the utilization of the existing oil-based power generators to balance the electrical network [
50].
Maldives is an autonomous country located to the south of Sri Lanka and India (about 1000 km from Asia) in the Indian Ocean. To supply this archipelago, Liu et al. realized a feasibility study, proposing the installation of a RESs mix based on solar, wind, and biomass sources. The energy balance of the local network could be entrusted to the local desalination and to the diesel power plants, modulating the active units [
51].
Selosse et al. investigated different energy scenarios, considering Reunion as a case study. This French island is located in the Indian Ocean, to the east of Madagascar. Several energy sources are considered: biomass, hydropower, wind, solar, geothermal, sea-wave, and the ocean thermal energy conversion (OTEC; i.e., the exploitation of the thermal gradient at different depths of the sea) [
52].
As shown in the previous examples, the literature is currently focused on the proposal of renewable energy mixes, considering, normally, wind and solar as energy sources. Geothermal, hydropower and biomass are sometimes taken into account, if they are available. More exotic RESs are occasionally evaluated (sea-wave and OTEC) being this technology at a prototypal stage. An important contribution to the reduction of CO
2 emissions can be given by the improvement of the energy efficiency at final users premises, as introduced by the Kyoto protocol and following environmental agreements [
54,
55].
In this context, Italy recently published two important decrees to promote the introduction of RESs and the improvement of energy efficiency in small islands. In detail, the decree 14 February 2017 emitted by the Italian Ministry of Economic Development establishes specific targets for 20 small Italian islands, indicating the minimal power to install from RESs (as regards the electricity consumption) and the minimal surface of solar thermal collectors (STCs) to install (as regards the energy demand for DHW) [
56]. It is important to underline that the greatest part of Italian small islands is inserted in programs to preserve the natural landscape, so the installation of extensive RES plants (e.g., wind turbines) may not be easily implemented [
57].
The decree n. 340 of 14 July 2017 issued by the Italian Ministry of Environment, Land, and Sea provides a funding of 15 million euros to implement specific projects in 21 Italian small islands to improve the energy efficiency at final users premises [
58].
Considering the Italian framework and the review of the literature above reported, the authors are interested in investigating the potential energy savings that is achievable in small islands equipped with desalination plants (DESs). Indeed, most of the islands in the Mediterranean Sea is equipped with a DES, including Lampedusa, Linosa, Ustica and Pantelleria [
57].
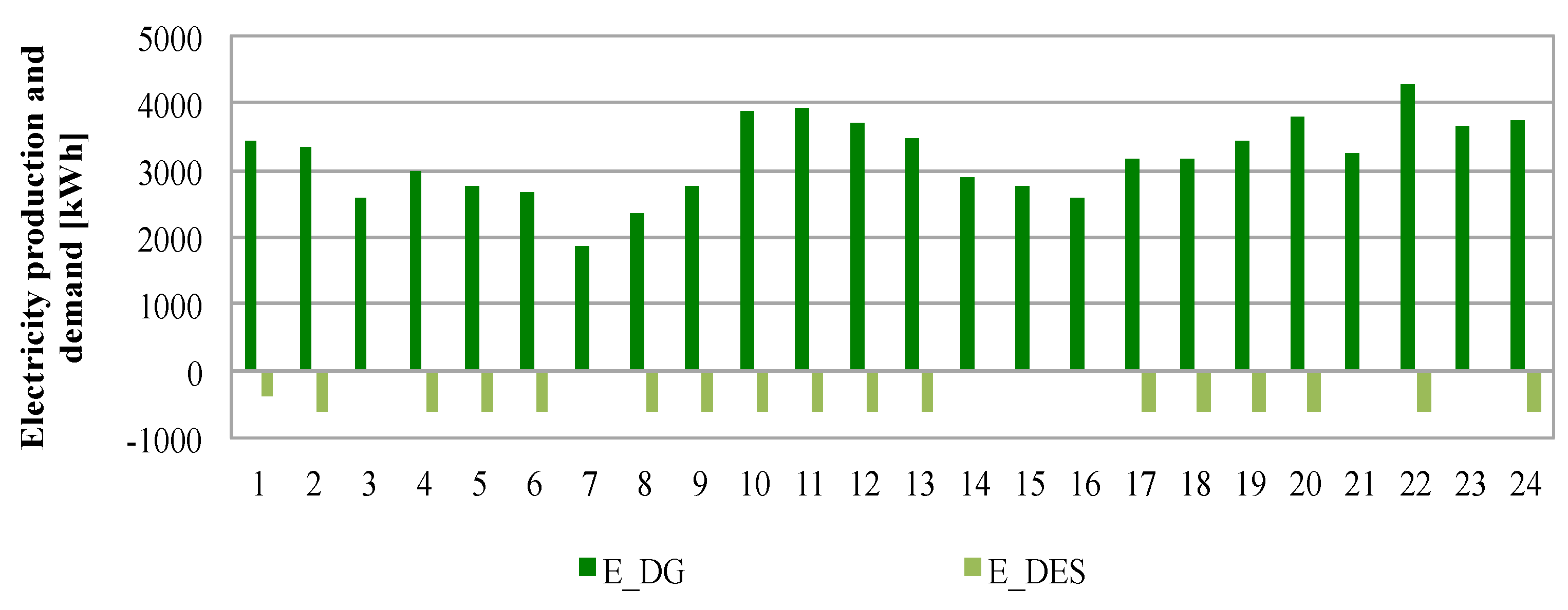
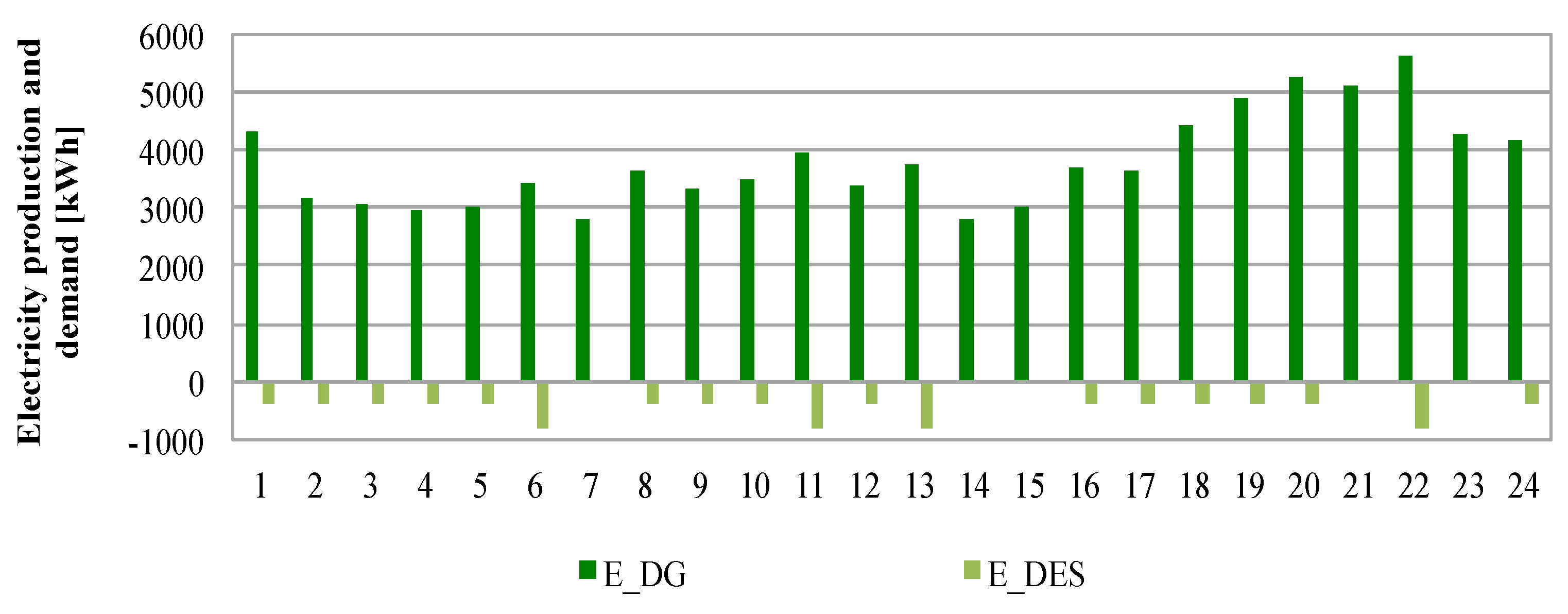
Using a multi-carrier energy hub approach to model small islands, it is possible to modulate the electricity demand from the DES in order to maximize the energy efficiency of the existing power plants, decoupling the freshwater demand thanks to the installation of a water reserve (in most cases already existing). The second step is the modulation of electricity consumption to produce DHW. Indeed, as shown in a recent report produced by RSE (Italian acronym of “Ricerca sul Sistema Energetico”, Research on Energy Systems), electric resistance water heaters (ERWHs) are commonly used in Italian small islands to produce DHW [
59]. As this technology requires only electricity and it is equipped with a hot water reserve, it is also possible to decouple the DHW demand from the electricity production.
2.3. Grid-Interactive Water Heaters for Energy Storage
As demand response (DR) can push customers to rationalize their energy consumption, playing a vital role in peak-load shifting or load-leveling strategies, more attentions are paid to it nowadays. However, the researches on DR implemented in MESs are rare, and the DR models or strategies are far from full investigation. Customer-side flexibility is the ability of electricity users to reduce their consumption in peak-load hours, shifting part of the load to low-cost hours. The customer-side flexibility has been widely studied by many authors in several works [
60,
61,
62]. Some of them focus on the heating system models [
63,
64], others on the estimation of the heating demand [
65]. Many of the DR programs aim at minimizing customer energy costs [
66,
67,
68], while others help to improve the power system operation [
69]. Among different solutions to increase flexibility of electricity systems, grid interactive water heaters (GIWHs) can make a significant contribution, against a relatively low cost. As a result, several flexibility programs have already been implemented in the USA, aiming to coordinate several million GIWHs with the electricity network [
70,
71]. A GIWH can be considered as a thermal storage medium, able to store thermal energy in a tank, in the form of hot water, when the price of electricity is low, while using it during high-price hours, or when a peak in the power diagram occurs. In most cases, the operation of GIWH does not impact on the end-user comfort, due to the large size of the water tanks.
Large-tank electric resistance water heaters (ERWHs) have been identified as the ideal technology to offer DR services to the power network, mainly thanks to the large storage capacity and the high power consumption (able to offset a significant part of the daily power diagram). Furthermore, the ERWH power profiles are often consistent to the utility needs, since the highest consumption occurs during the peak power periods. In terms of cost efficiency, the GIWH is the most cost-effective energy storage technology, being an order of magnitude cheaper than the other technologies [
70]. According to the ES-Select Tool of Sandia National Laboratories [
72], compared to other storage technologies GIWHs appear the cheapest. GIWHs differ from traditional water heaters since they can be controlled through a bi-directional equipment, able to rapidly turn on/off the GIWH, or increase/decrease the load in just a few seconds. For example, in presence of a capacity shortage in the power network (due to an under-generation condition), GIWHs can be rapidly turned off or partialized. Conversely, in presence of an over-generation condition, GIWHs can be turned-on, to help alleviate the excess of power generation, allowing the load to follow generation. Since the development of the GIWH is quite a mature technology [
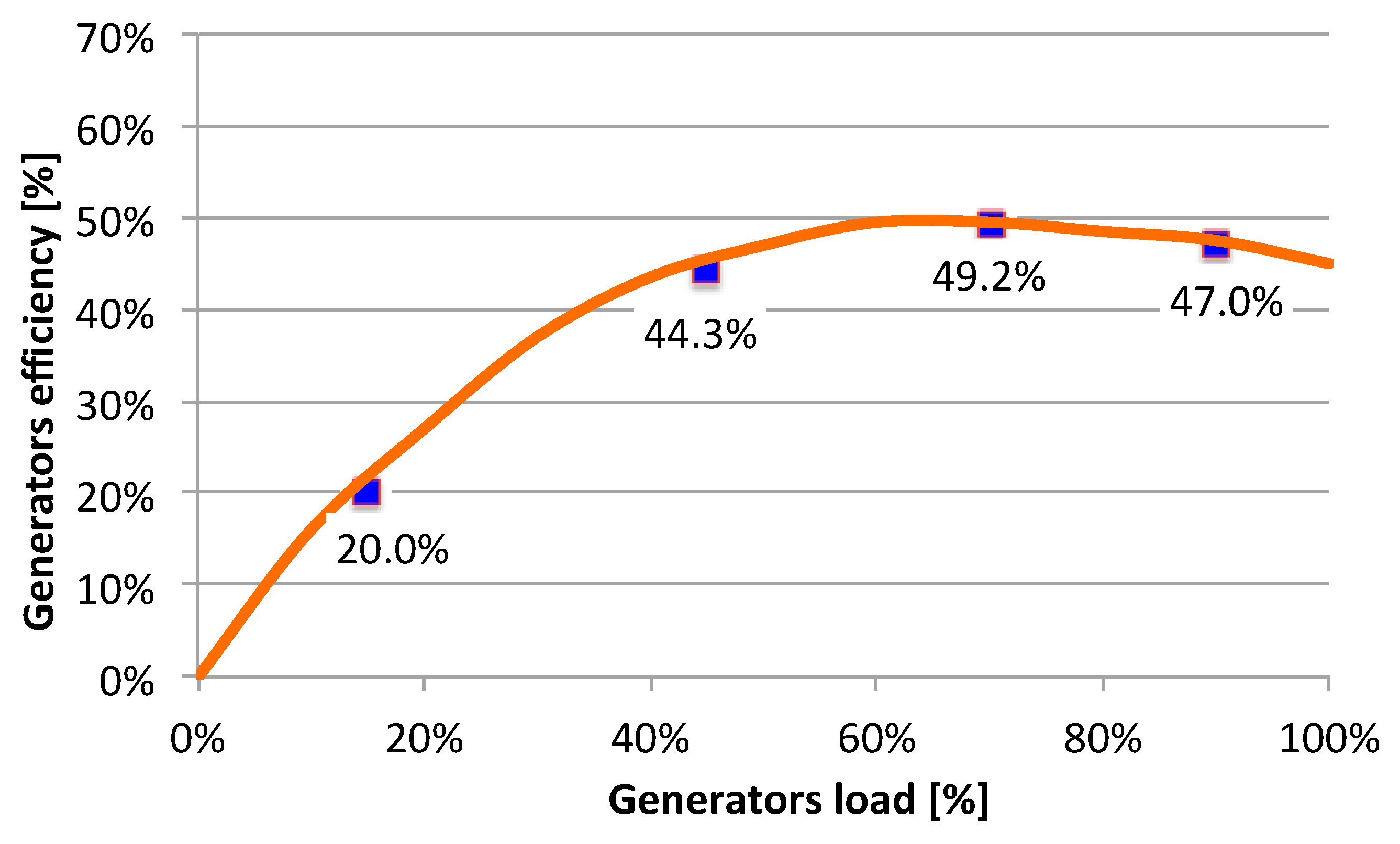
73], and it provided very profitable results in previous experiences with low installation costs, in this study the possibility of providing flexibility services in Pantelleria from ERWH systems for load modulation is analyzed. Furthermore, since one of the highest electrical loads in Pantelleria is the DES, this research also investigated the potential benefit deriving from the cooperated scheduling of these loads to reduce the consumption of the local diesel generators.