Remaining Useful Life Prediction of Rolling Element Bearings Using Supervised Machine Learning
Abstract
1. Introduction
- Avoiding catastrophic failure, unscheduled maintenance and production loss.
- Reducing maintenance costs by minimizing the number of unnecessary interventions and machine overhauls.
- Increasing the lifespan of components by providing advance information on the severity of the fault to be maintained.
2. Methodology
Contributions
- It improves the fitting of the features extracted from vibration measurements through the use of appropriate regression models.
- It explores the possibility of combining regression models with ANNs to improve the predictive accuracy of regression models.
- A test rig was designed and experimental tests were conducted to generate bearing failure data in order to validate the proposed prognostic model. The model was also validated through industrial data provided by a commercial company.
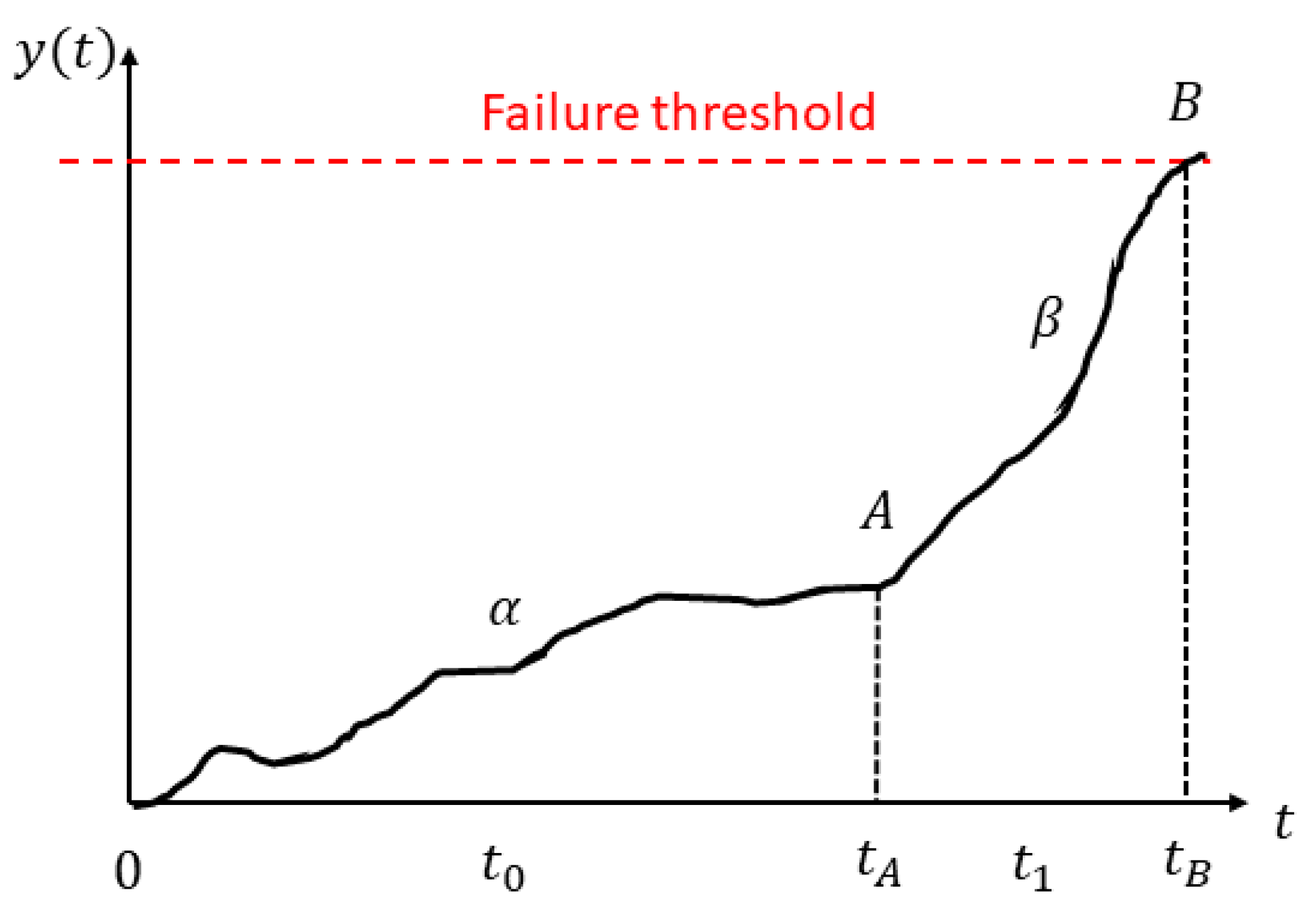
3. Statistical Condition Indicators
3.1. Kurtosis
3.2. Root Mean Square
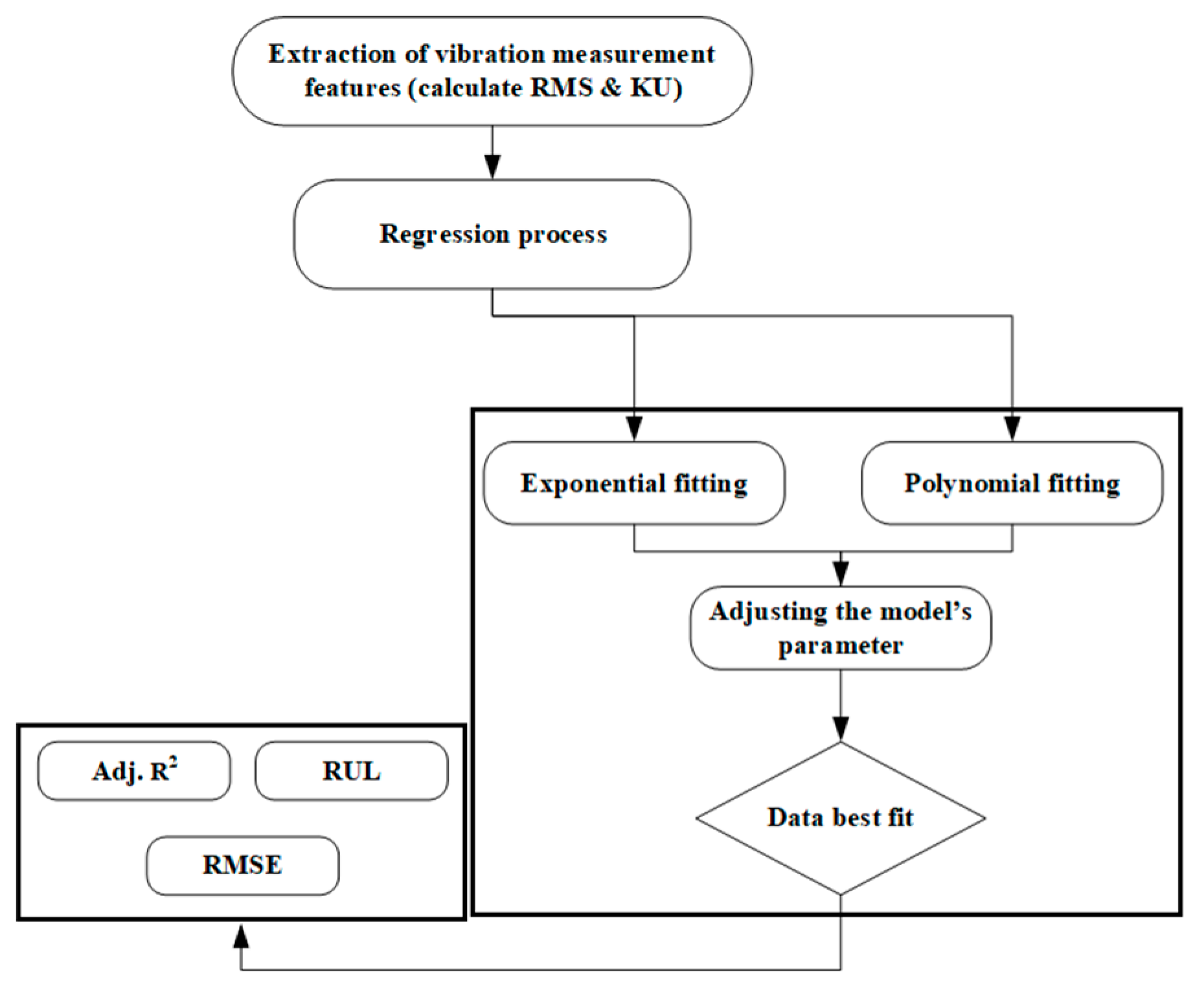
4. Regression Analysis
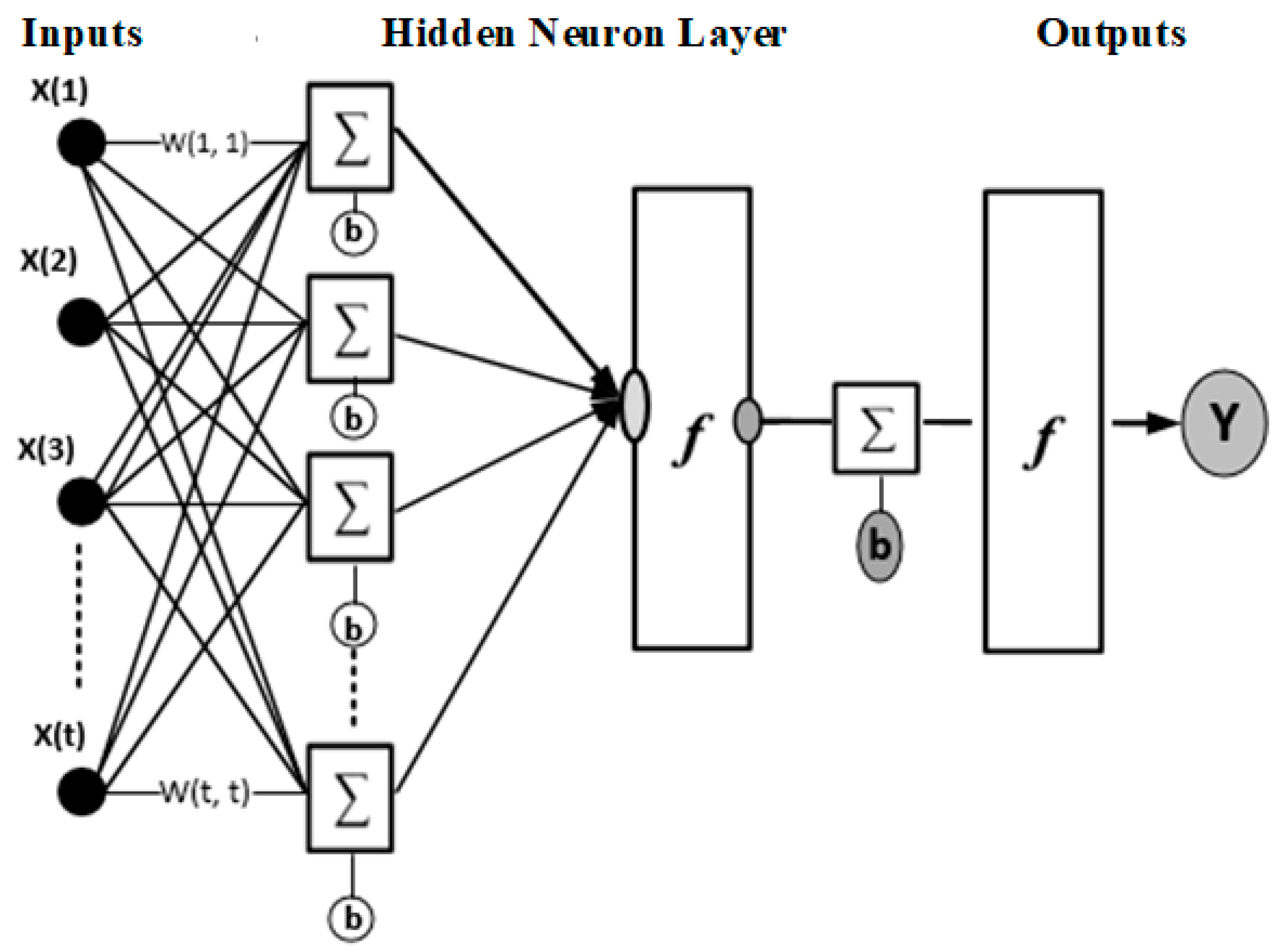
5. Multilayer Artificial Neural Network
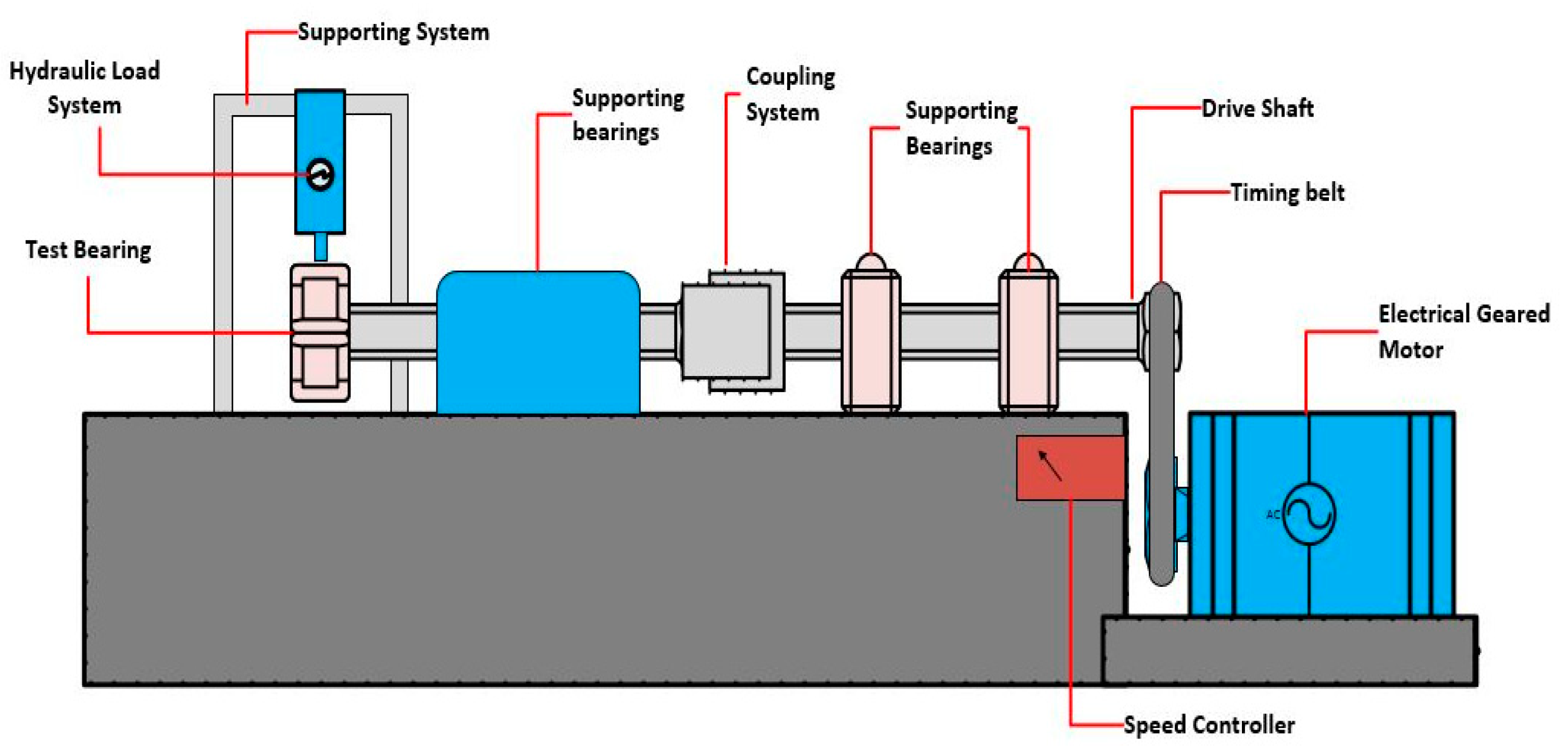
6. Data Collection
6.1. Dataset 1
6.2. Dataset 2
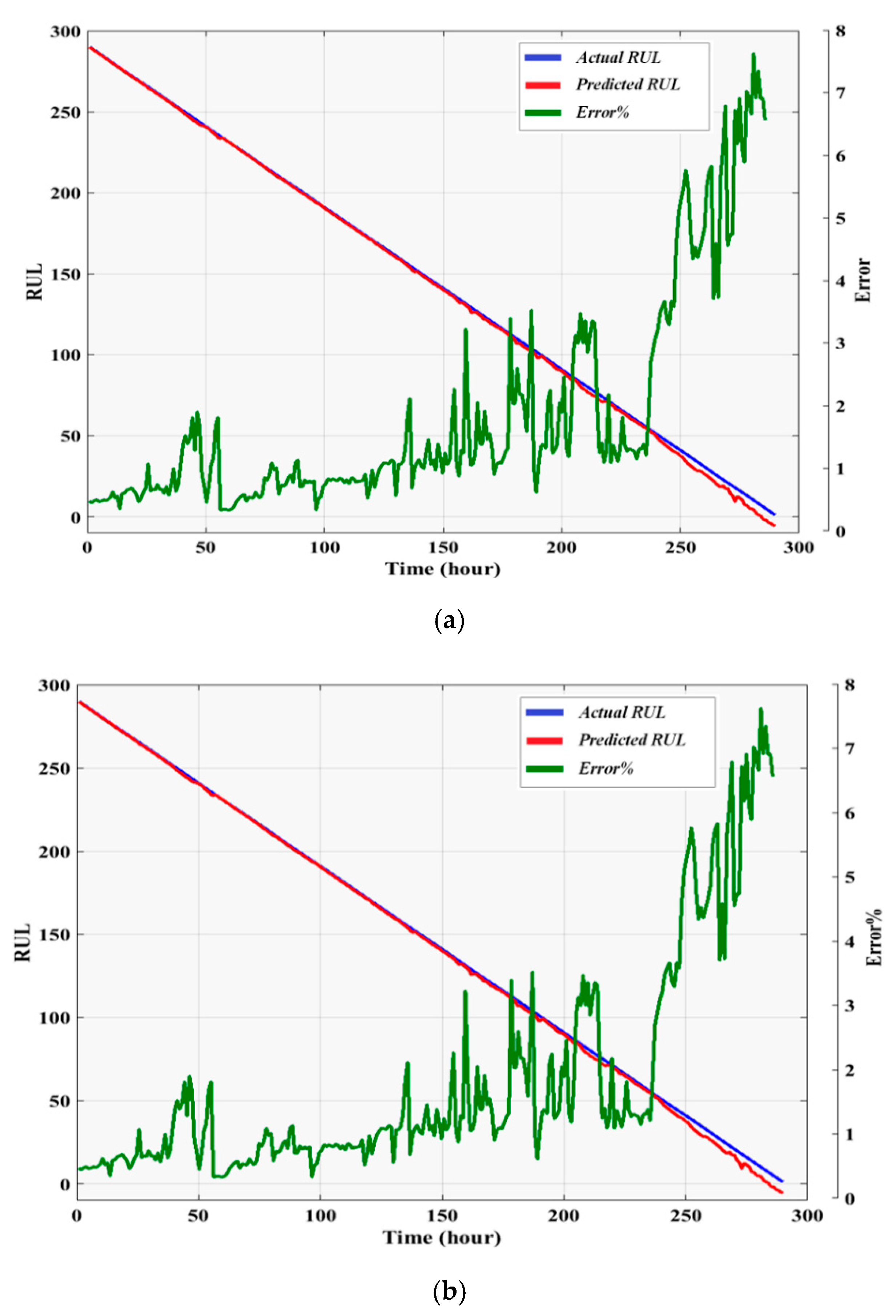
7. Results
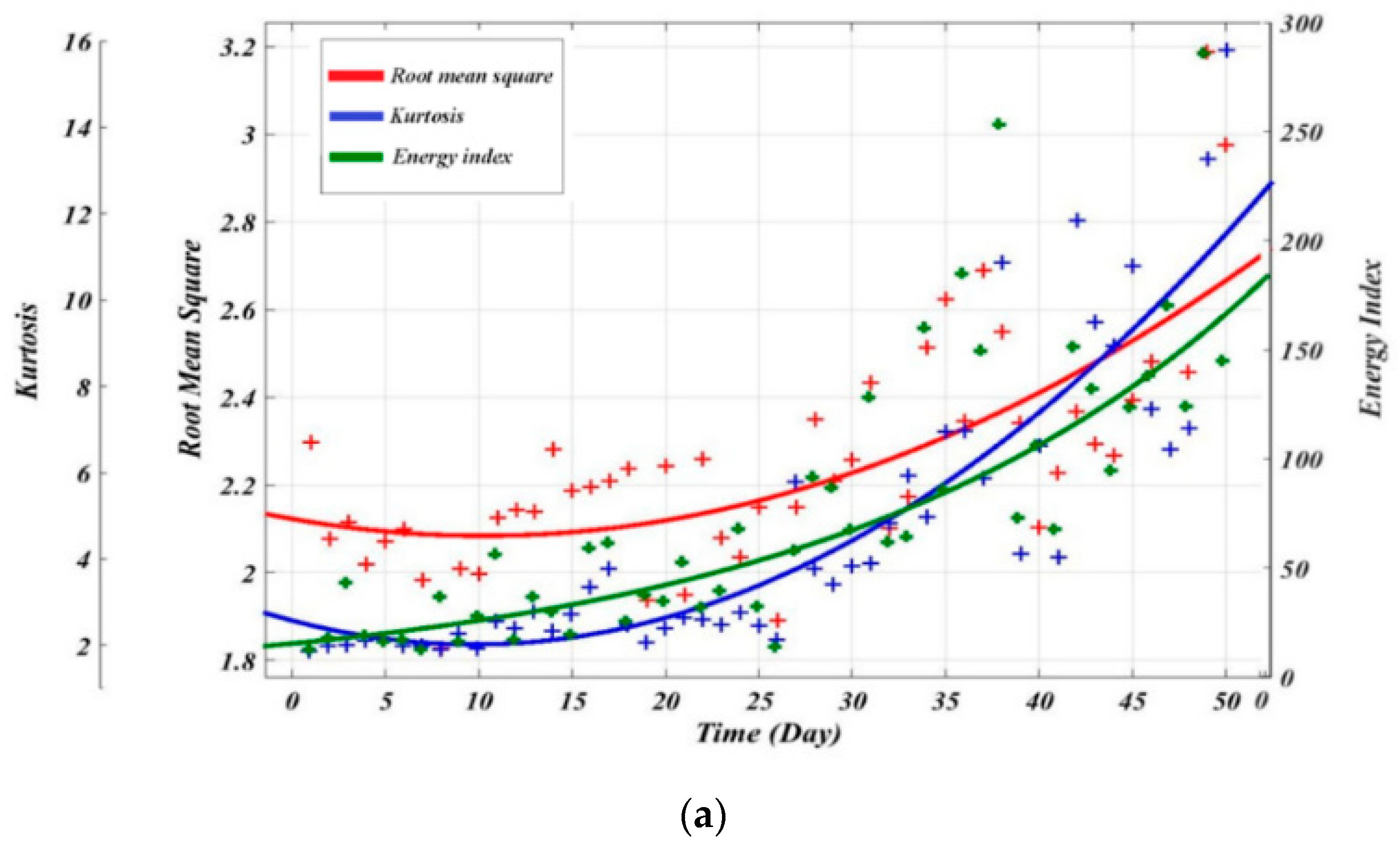
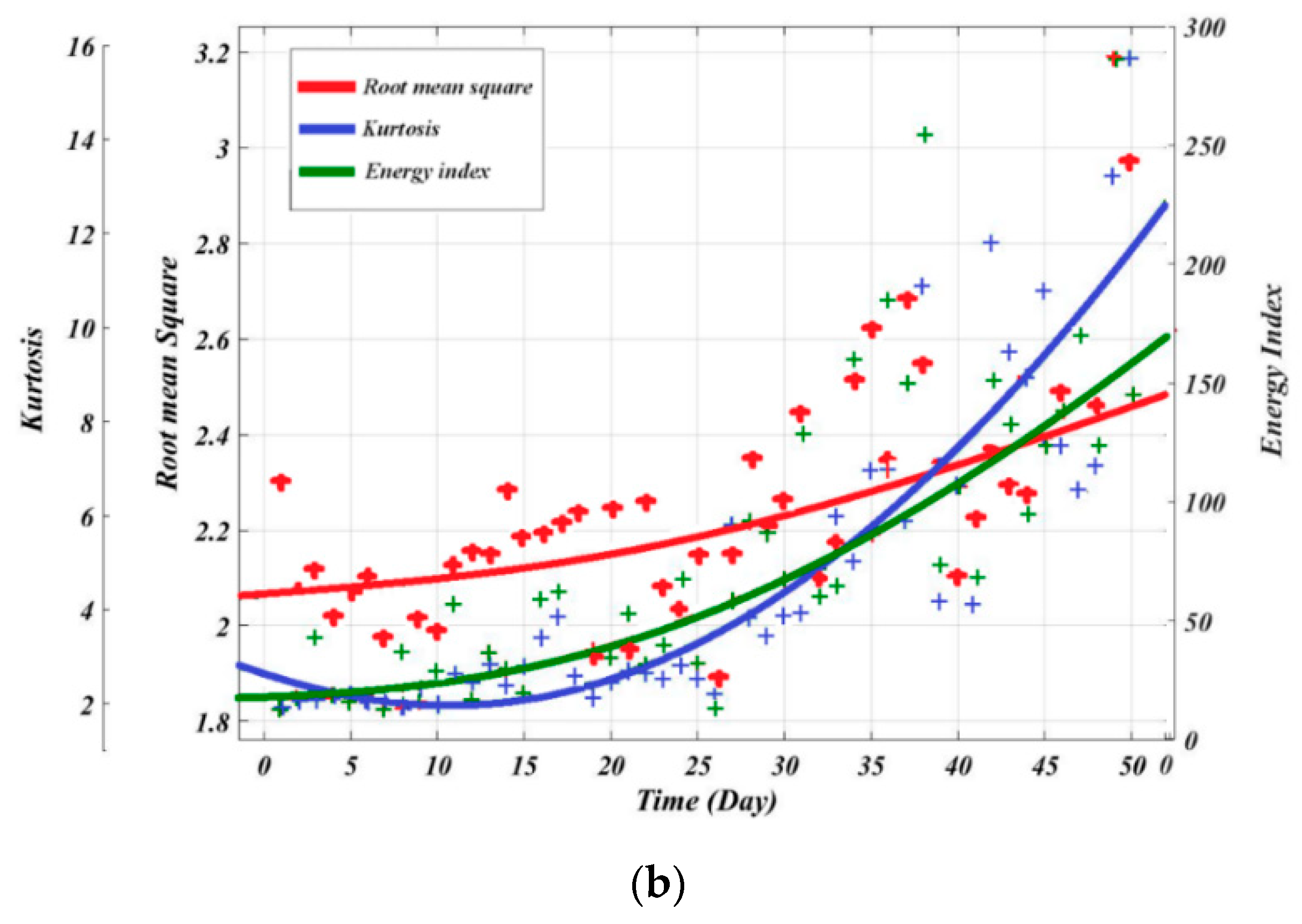
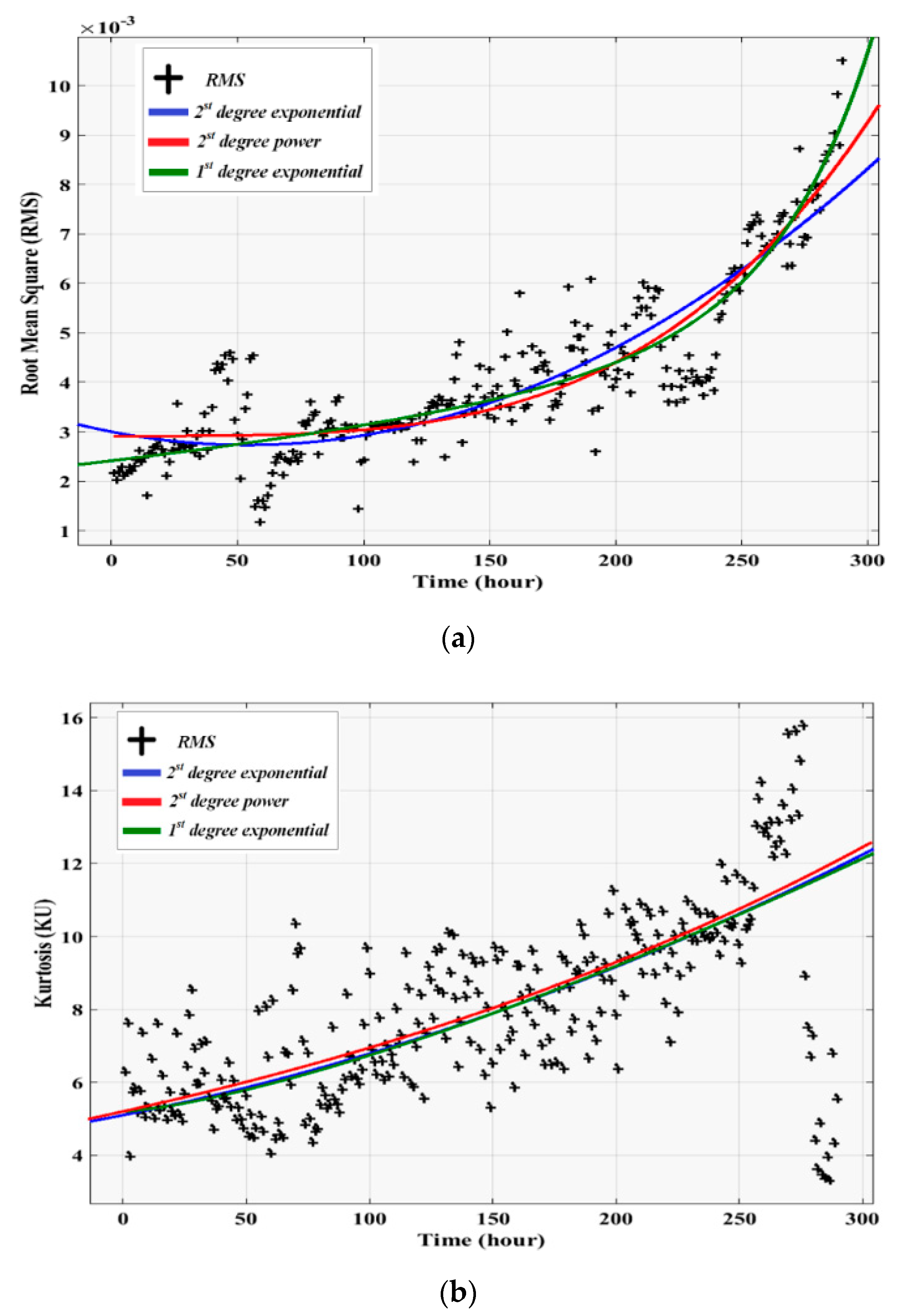
7.1. Signal Features Regression
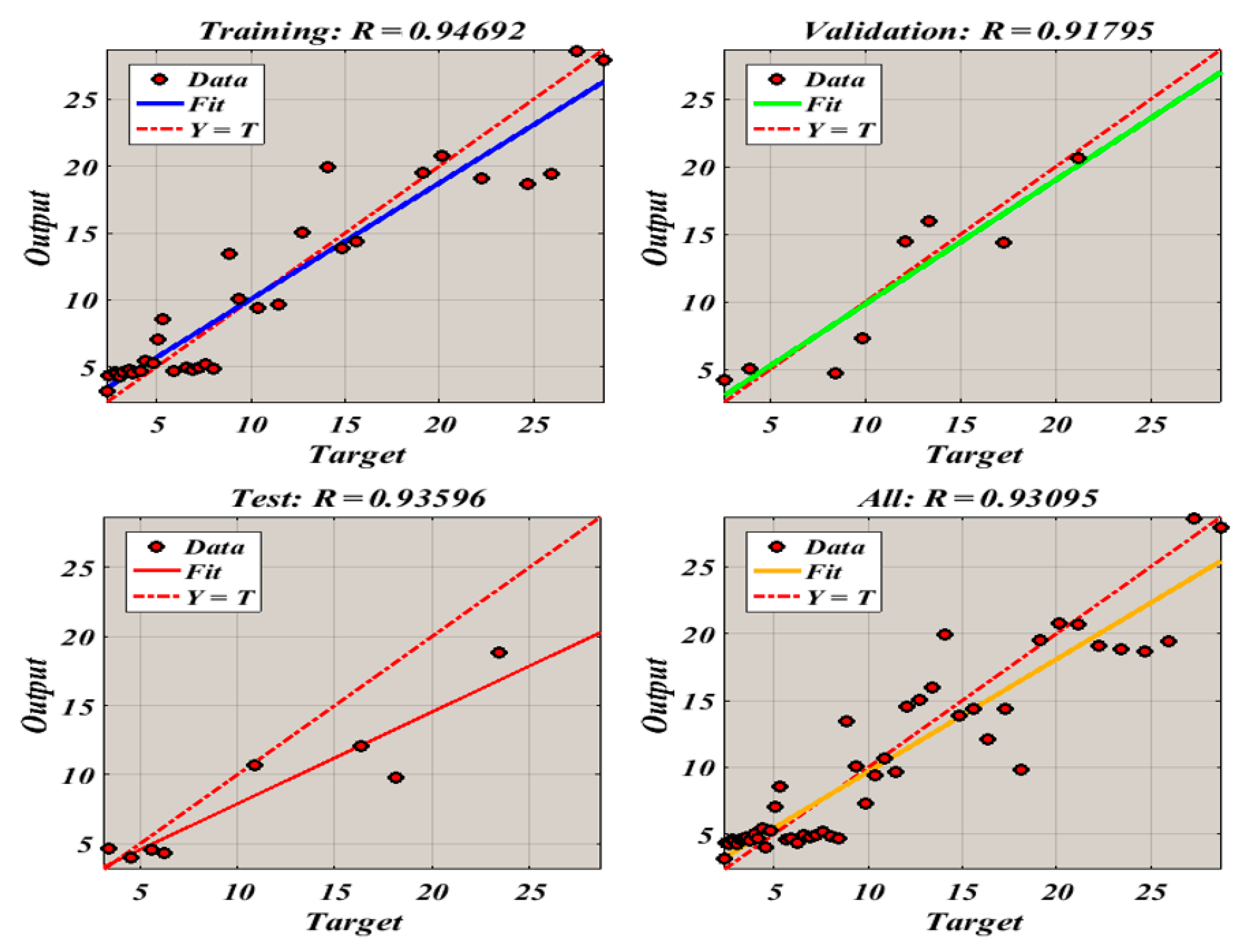
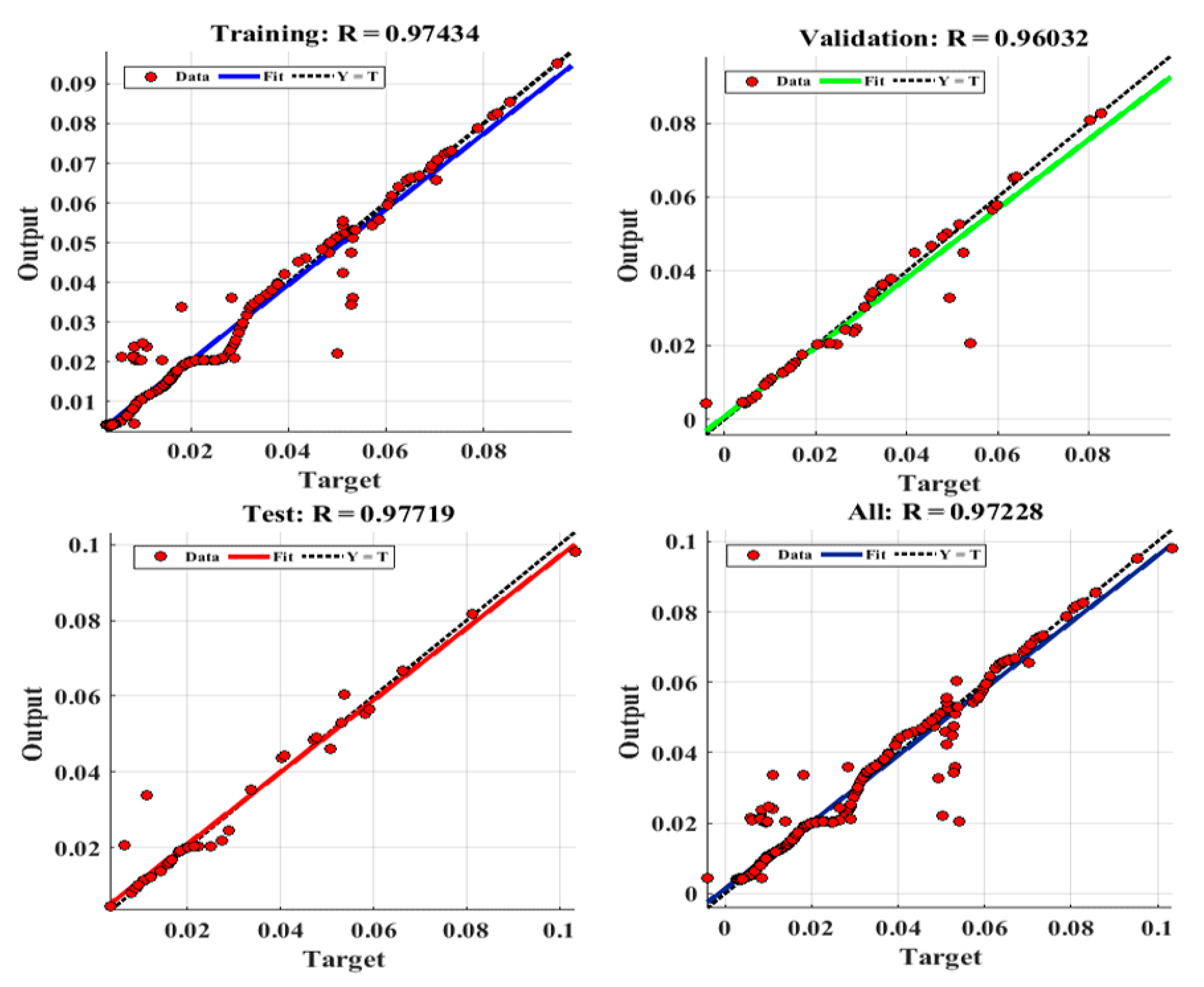
7.2. Artificial Neural Network
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Saha, B.; Goebel, K.; Poll, S.; Christophersen, J. Prognostics Methods for Battery Health Monitoring Using a Bayesian Framework. IEEE Trans. Instrum. Meas. 2009, 58, 291–296. [Google Scholar] [CrossRef]
- Misra, K.B. Maintenance Enginerring and Maintenability: An Introduction; Springer: London, UK, 2008. [Google Scholar]
- Tondon, N.; Choudhury, A. A review of vibration and acoustics measurement methods for the detection of defects in rolling element bearing. Tribol. Int. 1999, 32, 469–480. [Google Scholar] [CrossRef]
- Okoh, C.; Roy, R.; Mehnen, J.; Redding, L. Overview of Remaining Useful Life prediction techniques in Through-life Engineering Services. Procedia CIRP 2014, 16, 158–163. [Google Scholar] [CrossRef]
- Li, N.; Lei, Y.; LiN, J.; Ding, S.X. An Improved Exponential Model for Predicting Remaining Useful Life of Rolling Element Bearings. IEEE Trans. Ind. Electron. 2015, 62, 7762–7773. [Google Scholar] [CrossRef]
- Wu, J.; Wu, C.; Cao, S.; Or, S.W.; Deng, C.; Shao, X. Degradation Data-Driven Time-To-Failure Prognostics Approach for Rolling Element Bearings in Electrical Machines. IEEE Trans. Ind. Electron. 2018, 66, 529–539. [Google Scholar] [CrossRef]
- Sutrisno, E.; Oh, H.; Vasan, A.S.S.; Pecht, M. Estimation of remaining useful life of ball bearings using data driven methodologies. In Proceedings of the 2012 IEEE Conference on Prognostics and Health Management, Denver, CO, USA, 18–21 June 2012; Volume 2, pp. 1–7. [Google Scholar]
- Goebel, K.; Saha, B.; Saxena, A. A comparison of three data-driven techniques for prognostics. In Proceedings of the 62nd Society for Machinery Failure Prevention Technology, Virginia Beach, VA, USA, 6–8 June 2008; pp. 1–13. [Google Scholar]
- Loukopoulos, P.; Zolkiewski, G.; Bennett, I.; Sampatha, S.; Pilidis, P.; Li, X.; Mba, D. Abrupt fault remaining useful life estimation using measurements from a reciprocating compressor valve failure. Mech. Syst. Signal Process. 2019, 121, 359–372. [Google Scholar] [CrossRef]
- Kim, H.-E.; Andy, C.C.; Mathew, J.; Eric, Y.H.; Choi, B.-K. Machine Prognostics Based on Health State Estimation Using Svm. In Proceedings of the Third World Congress on Engineering Asset Management and Intelligent Maintenance Systems Conference, Beijing, China, 27–30 October 2008; pp. 834–845. [Google Scholar]
- Zhang, S.; Ganesan, R.; Xistris, G.D. Self-organising neural networks for automated machinery monitoring systems. Mech. Syst. Signal Process. 1996, 10, 517–532. [Google Scholar] [CrossRef]
- Mandal, D.; Pal, S.K.; Saha, P. Modeling of electrical discharge machining process using back propagation neural network and multi-objective optimization using non-dominating sorting genetic algorithm-II. J. Mater. Process. Technol. 2007, 186, 154–162. [Google Scholar] [CrossRef]
- Elasha, F.; Mba, D.; Togneri, M.; Master, I.; Teixeira, J.A. A hybrid prognostic methodology for tidal turbine gearboxes. Renew. Energy 2017, 114, 1051–1061. [Google Scholar] [CrossRef]
- Li, X.; Duan, F.; Loukopoulos, P.; Bennett, I.; Mba, D. Canonical variable analysis and long short-term memory for fault diagnosis and performance estimation of a centrifugal compressor. Control Eng. Pract. 2018, 72, 177–191. [Google Scholar] [CrossRef]
- Cheng, F.; Qu, L.; Qiao, W. Fault Prognosis and Remaining Useful Life Prediction of Wind Turbine Gearboxes Using Current Signal Analysis. IEEE Trans. Sustain. Energy 2018, 9, 157–167. [Google Scholar] [CrossRef]
- Elforjani, M.; Shanbr, S. Prognosis of Bearing Acoustic Emission Signals Using Supervised Machine Learning. IEEE Trans. Ind. Electron. 2017, 0046, 5864–5871. [Google Scholar] [CrossRef]
- Heng, R.B.W.; Nor, M.J.M. Statistical analysis of sound and vibration signals for monitoring rolling element bearing condition. Appl. Acoust. 2002, 53, 211–226. [Google Scholar] [CrossRef]
- Zhu, J.; Nostrand, T.; Spiegel, C.; Morton, B. Survey of Condition Indicators for Condition Monitoring Systems. In Proceedings of the Annual Conference of the Prognostics and Health Management Society, Fort Worth, TX, USA, 29 September–2 October 2014; Volume 5, pp. 1–13. [Google Scholar]
- Eftekharnejad, B.; Carrasco, M.R.; Charnley, B.; Mba, D. The application of spectral kurtosis on Acoustic Emission and vibrations from a defective bearing. Mech. Syst. Signal Process. 2011, 25, 266–284. [Google Scholar] [CrossRef]
- Wang, L.; Gao, R.X. Condition Monitoring and Control for Intelligent Manufacturing; Springer: London, UK, 2006. [Google Scholar]
- Bates, D.M.; Watts, D.G. Nonlinear Regression Analysis; Wiley: New York, NY, USA, 2007; 392p. [Google Scholar]
- Mahamad, A.K.; Saon, S.; Hiyama, T. Predicting remaining useful life of rotating machinery based artificial neural network. Comput. Math. Appl. 2010, 60, 1078–1087. [Google Scholar] [CrossRef]
- Levenberg, K.; Arsenal, F. A Method for the Solution of Certain Non-Linear Problems in Least Squares. Q. Appl. Math. 1943, 1, 536–538. [Google Scholar] [CrossRef]
- Bechhoefer, E.; van Hecke, B.; He, D. Processing for Improved Spectral Analysis. In Proceedings of the Annual Conference of Prognostics and Health Management Society, New Orleans, LU, USA, 14–17 October 2013; pp. 1–6. [Google Scholar]



| Machine State | Increasing Inner Race Bearing Fault |
|---|---|
| Power rating | 2 MW flux |
| Nominal speed | 1800 rpm |
| Measurement Channel | Sensor |
| Sample rate | 97,656 Hz |
| Record length | 6 s |
| Sensor type | Accelerometer |
| Parameter | Measurement |
|---|---|
| External Diameter (Pitch) | 84.14 mm |
| Internal Diameter (Bore) | 40.00 mm |
| Pitch Circle Diameter | 62.71 mm |
| Roller Diameter | 11.91 mm |
| Number of Rollers | 10 |
| Weight of the Specimen | 1.2 kg |
| Condition Indicators | Dataset 1 | Dataset 2 | ||||||
|---|---|---|---|---|---|---|---|---|
| Model Constants | RMSE | Adj. R2 | Model Constants | RMSE | Adj. R2 | |||
| a | b | a | b | |||||
| RMS | 2.235 | 0.0511 | 0.05248 | 0.957 | 0.003835 | 0.3797 | 0.000717 | 0.995 |
| KU | 3.439 | 0.1121 | 0.9469 | 0.975 | 7.87 | 0.2548 | 0.2494 | 0.990 |
| Condition Indicators | Dataset 1 | Dataset 2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model Constants | RMSE | Adj. R2 | Model Constants | RMSE | Adj. R2 | |||||
| a0 | a1 | a2 | a0 | a1 | a2 | |||||
| RMS | 2.19 | 0.117 | 0.0044 | 0.1644 | 0.5947 | 0.000552 | 0.001365 | 0.003602 | 0.0007735 | 0.853 |
| KU | 3.24 | 0.5718 | 0.3004 | 0.2172 | 0.881 | 0.244 | 1.971 | 7.786 | 0.3851 | 0.792 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Elasha, F.; Shanbr, S.; Mba, D. Remaining Useful Life Prediction of Rolling Element Bearings Using Supervised Machine Learning. Energies 2019, 12, 2705. https://doi.org/10.3390/en12142705
Li X, Elasha F, Shanbr S, Mba D. Remaining Useful Life Prediction of Rolling Element Bearings Using Supervised Machine Learning. Energies. 2019; 12(14):2705. https://doi.org/10.3390/en12142705
Chicago/Turabian StyleLi, Xiaochuan, Faris Elasha, Suliman Shanbr, and David Mba. 2019. "Remaining Useful Life Prediction of Rolling Element Bearings Using Supervised Machine Learning" Energies 12, no. 14: 2705. https://doi.org/10.3390/en12142705
APA StyleLi, X., Elasha, F., Shanbr, S., & Mba, D. (2019). Remaining Useful Life Prediction of Rolling Element Bearings Using Supervised Machine Learning. Energies, 12(14), 2705. https://doi.org/10.3390/en12142705






