Energy Saving Operation of Manufacturing System Based on Dynamic Adaptive Fuzzy Reasoning Petri Net
Abstract
1. Introduction
2. Related Works
3. Problem Statement and Fuzzy Operation Knowledge Representation
3.1. System Description and Assumptions
- Machine Mi, i = 1, 2, …, n, has a constant cycle time . The cycle time of machines can be the same or different, which means the system can be synchronous or asynchronous lines.
- Buffer Bi, i = 1, 2, …, n−1, has a finite buffer capacity Li. The buffer level of Bi at time t is represented as bi(t) at the beginning of each discrete time slot.
- The reliability models of machines are assumed to follow a known but not definitive probability distribution. The time dependent failure mode is used in this study.
- At the beginning of a discrete time slot, Mi is starved if it is powered on and its upstream buffer Bi-1 is empty. It is assumed that the first machine is never starved.
- At the beginning of a discrete time slot, Mi is blocked if it is powered on and its downstream buffer Bi is full. It is assumed that the last machine is never blocked.
- A power-on machine consumes materials, such as electricity, fuel, gas and compressed air. All consumed materials will be converted into energy.
- In this study, a machine has following states: Processing (PS), starvation (ST), blockage (BL), failure (FL), and sleep for energy saving (SL).
3.2. Knowledge Representation of Machine Energy Saving Operations
- bi(t) is the level of upstream buffer of Mi at time point t.
- bi+1(t) is the level of downstream buffer of Mi at time point t.
- UB and DB are the fuzzy sets of buffer levels which are described in 3 linguistic variables {Low, Medium, High} in this paper.
- si(t) is the decided machine state, i.e., SR = {Sleep, Running}, at time t.
- The parameter μx = {μs, μr} defined in the universe of discourse [0,1] is the certainty factor (CF) representing the strength of the certainty of WFPRs when si(t) is {sleep} and {running} respectively.
- wub,x and wdb,x are the set of weights, which are defined in the universe of discourse [0,1] and assigned to the first and second antecedent propositions in the rules. The weights show the relative importance of each antecedent proposition to the consequence proposition. The sum of the proposition weights equals to 1.
4. Dynamic Adaptive Fuzzy Reasoning Petri Net for Energy Efficient Operation
4.1. Formal Definition of Dynamic Adaptive Fuzzy Reasoning Petri Net
- is a finite set of propositions or called places, , including a set of starting places , a set of terminating places . Here, is the set of all input transitions of p, and is the set of all output transitions of p. Variable m is the number of propositions in the rules. In this paper, there are 8 places, i.e., m = 8. , which represent three linguistic levels of upstream buffers and three linguistic levels of downstream buffers. represents the two decision states {sleep, running} of a machine.
- is a finite set of transitions, representing a set of fuzzy inference rules. Variable is the number of rules. In this paper, there are 9 rules and Transitions correspond to rules shown in Table 1.
- , a finite set of propositions in the fuzzy knowledge base. . . For example, the proposition {UBL} describes the fuzzy level of upstream and the proposition {Sleep} is the decision result of the machine at the next decision cycle.
- , the input function, defining the directed arcs from starting places to transitions.
- , the output function, defining the directed arcs from transitions to terminating places.
- , an input function whose elements are the weights of input places, which indicates that how much an input place (or corresponding antecedent proposition) impacts on its transition. The sum of the antecedent proposition weights of a transition is equal to 1.
- , an output function whose elements are the certainty factors of the transitions/rules, indicating how much a transition/rule impacts on its output places, i.e., the decided machine state. is adjusted automatically based on the changing production conditions.
- , a correlation function, representing mapping from a set of places to a set of real values in [0,1]. is the fuzzy value of a starting place, indicating the truth degree of proposition
- , a correlation function, represents a bidirectional mapping between a set of places and a set of propositions. For example, {UBL}.
4.2. Knowledge Reasoning for Energy Saving State Decisions of A Machine
5. Numerical Experiments and Discussions
5.1. A Serial Automotive Powertrain Line
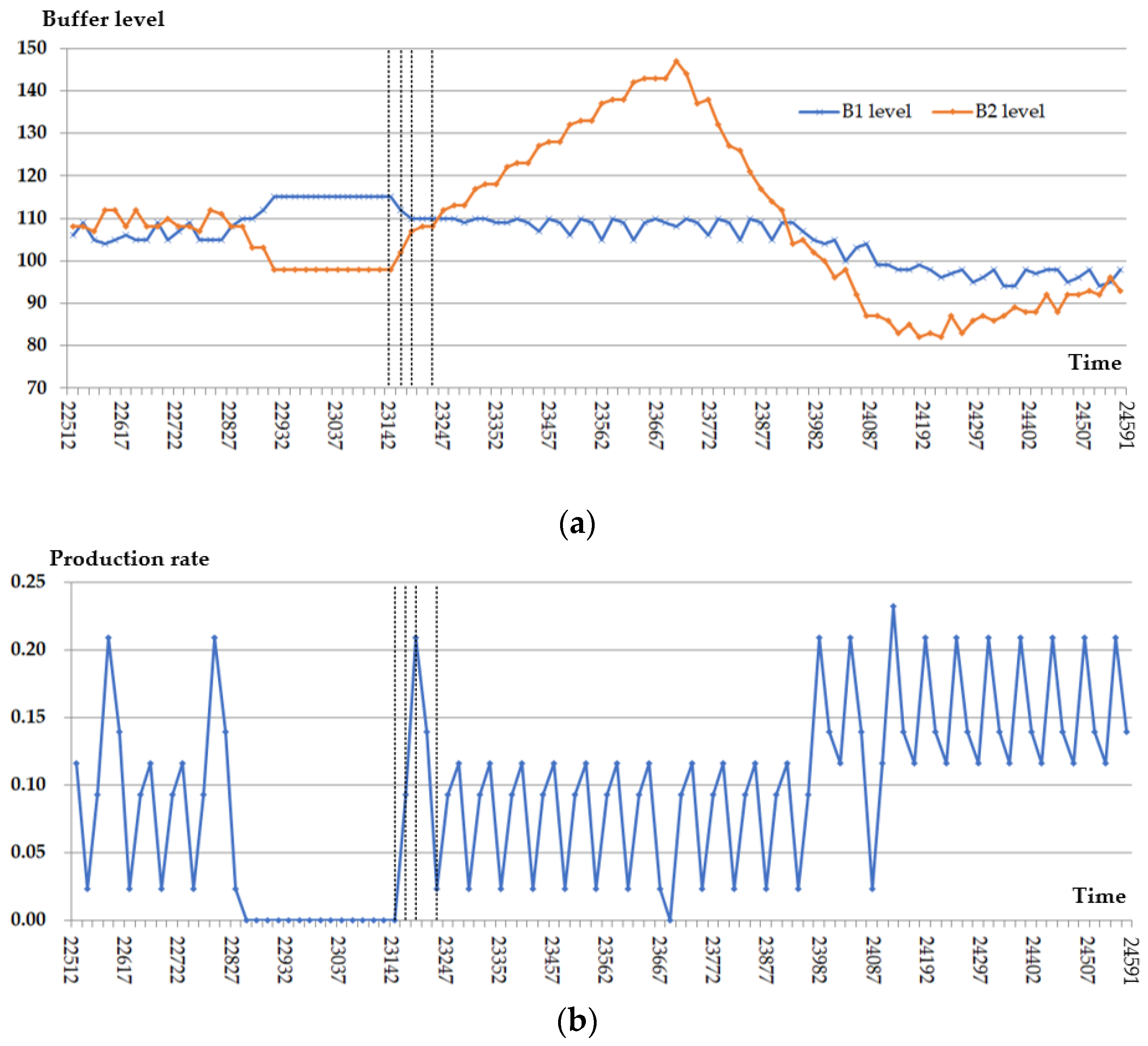
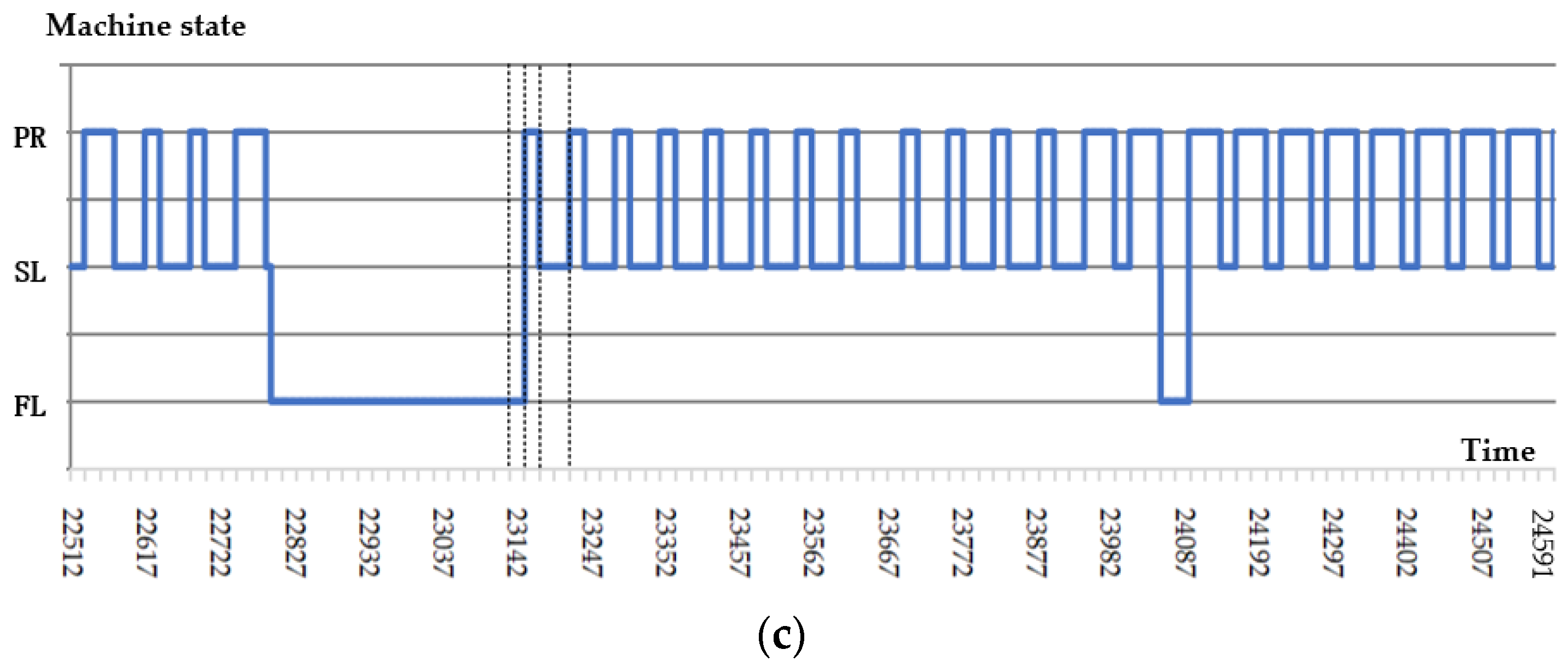
5.2. Discussions
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations and Nomenclature
| Abbreviations | Description |
| PNs | Petri nets |
| FRPNs | Fuzzy reasoning Petri nets |
| FPRs | Fuzzy production rules |
| WFPRs | Weighed fuzzy production rules |
| DAFRPN | Dynamic adaptive fuzzy reasoning Petri net |
| PS | Processing state |
| ST | Starvation state |
| BL | Blockage state |
| FL | Failure state |
| SL | Sleep state |
| CF | Certainty factor |
| UBL | The level of the upstream buffer is low |
| DBM | The level of the downstream buffer is medium |
| CI | Confidence interval |
| TPL | Throughput loss |
| ECR | Energy cost reduction |
| Starting places | |
| Terminating places | |
| Cycle time of Mi, | |
| Li | Buffer capacity of Bi |
| bi(t) | Buffer level of Bi at time t |
| Eps,i | Energy consumption of processing state |
| Eid,i | Energy consumption of idle state |
| Esl,i | Energy consumption of sleep state |
| Tps,i | Time length of processing state |
| Tid,i | Time length of idle state |
| Tsl,i | Time length of sleep state |
| Energy consumption of Mi in time (0,T] | |
| Energy consumption of the system during time (0,T] | |
| bi(t) | Level of the upstream buffer of Mi at time point t |
| bi+1(t) | Level of the downstream buffer of Mi at time point t |
| si(t) | Decided machine state |
| μs | Certainty factor of WFPR when si(t) is sleep |
| μr | Certainty factor of WFPR when si(t) is running |
| wub,x | Weight of the first antecedent proposition in the rule |
| wdb,x | Weight of the second antecedent proposition in the rule |
| ri(t) | Production rate of Mi within decision cycle |
| dc | Decision cycle |
| TPi(t) | Throughput of Mi at time point t |
References
- Park, C.W.; Kwon, K.S.; Kim, W.B.; Min, B.K.; Park, S.J.; Sung, I.H.; Seok, J. Energy consumption reduction technology in manufacturing–a selective review of policies, standards, and research. Int. J. Precis. Eng. Manuf. 2009, 10, 151–173. [Google Scholar] [CrossRef]
- Energy Information Administration. Available online: http://www.eia.gov/outlooks/aeo/pdf/0383(2015).pdf (accessed on 20 December 2016).
- Zhang, X.P.; Cheng, X.M. Energy consumption, carbon emissions, and economic growth in China. Ecol. Econ. 2009, 68, 2706–2712. [Google Scholar] [CrossRef]
- Thomas, Z.; Charlotte, M. Evaluating the management system approach for industrial energy efficiency improvements. Energies 2016, 9, 774. [Google Scholar]
- Lawrence, A.; Thollander, P.; Andrei, M.; Karlsson, M. Specific energy consumption/use (SEC) in energy management for improving energy efficiency in industry: Meaning, usage and differences. Energies 2019, 12, 247. [Google Scholar] [CrossRef]
- International Energy Agency. Available online: http://indiaenvironmentportal.org.in/files/Indicators_2008.pdf (accessed on 20 October 2008).
- Gutowski, T.G.; Allwood, J.M.; Herrmann, C.; Sahni, S. A global assessment of manufacturing: Economic development, energy use, carbon emissions, and the potential for energy efficiency and materials recycling. Annu. Rev. Environ. Resour. 2013, 38, 81–106. [Google Scholar] [CrossRef]
- Patrik, T.; Jenny, P. Industrial energy management decision making for improved energy efficiency—strategic system perspectives and situated action in combination. Energies 2015, 8, 5694–5703. [Google Scholar]
- Twomey, J.; Yildirim, M.; Whitman, B.L.; Liao, H.; Ahmad, J. Energy Profiles of Manufacturing Equipment for Reducing Energy Consumption in A Production Setting. Working Paper; Wichita State University: Wichita, KS, USA, 2008. [Google Scholar]
- Peng, C.; Peng, T.; Zhang, Y.; Tang, R.; Hu, L. Minimising non-processing energy consumption and tardiness fines in a mixed-flow shop. Energies 2018, 11, 3382. [Google Scholar] [CrossRef]
- Mouzon, G.; Yildirim, M.B.; Twomey, J. Operational methods for minimization of energy consumption of manufacturing equipment. Int. J. Prod. Res. 2007, 45, 4247–4271. [Google Scholar] [CrossRef]
- Prabhu, V.V.; Jeon, H.W.; Taisch, M. Modeling green factory physics-an analytical approach. In Proceedings of the 8th IEEE International Conference on Automation Science and Engineering, Seoul, Korea, 20–24 August 2012. [Google Scholar]
- Mashaei, M.; Lennartson, B. Energy reduction in a pallet-constrained flow shop through on–off control of idle machines. IEEE Trans. Autom. Sci. Eng. 2013, 10, 45–56. [Google Scholar] [CrossRef]
- Frigerio, N.; Matta, A. Energy-efficient control strategies for machine tools with stochastic arrivals. IEEE Trans. Autom. Sci. Eng. 2015, 12, 50–61. [Google Scholar] [CrossRef]
- Jia, Z.; Zhang, L.; Arinez, J.; Xiao, G. Performance analysis for serial production lines with Bernoulli machines and real-time WIP-based machine switch-on/off control. Int. J. Prod. Res. 2016, 54, 1–17. [Google Scholar] [CrossRef]
- Chang, Q.; Xiao, G.; Biller, S.; Li, L. Energy saving opportunity analysis of automotive serial production systems. IEEE Trans. Autom. Sci. Eng. 2013, 10, 334–342. [Google Scholar] [CrossRef]
- Sun, Z.; Li, L. Opportunity estimation for real time energy control of sustainable manufacturing systems. IEEE Trans. Autom. Sci. Eng. 2013, 10, 38–44. [Google Scholar] [CrossRef]
- Li, L.; Sun, Z. Dynamic energy control for energy efficiency improvement of sustainable manufacturing systems using Markov decision process. IEEE Trans. Syst. Man Cybern. Syst. 2013, 43, 1195–1205. [Google Scholar] [CrossRef]
- Li, Y.; Chang, Q.; Ni, J.; Brundage, M.P. Event-based supervisory control for energy efficient manufacturing systems. IEEE Trans. Autom. Sci. Eng. 2018, 15, 92–103. [Google Scholar] [CrossRef]
- Li, Y.; Wang, J.; Chang, Q. Event-based production control for energy efficiency improvement in sustainable multistage manufacturing systems. ASME J. Manuf. Sci. Eng. 2018, 141. [Google Scholar] [CrossRef]
- Zou, J.; Arinez, J.; Chang, Q.; Lei, Y. Opportunity window for energy saving and maintenance in stochastic production systems. Trans. ASME J. Manuf. Sci. Eng. 2016, 138, 121009. [Google Scholar] [CrossRef]
- Zou, J.; Chang, Q.; Arinez, J.; Xiao, G.X. Data-driven modeling and real-time distributed control for energy efficient manufacturing systems. Energy 2017, 127, 247–257. [Google Scholar] [CrossRef]
- Hibino, H.; Yanaga, K. Decision support for energy-saving idle production facility operations in a production line based on an M2M environment. Procedia CIRP 2017, 61, 399–403. [Google Scholar] [CrossRef]
- Azadegan, A.; Porobic, L.; Ghazinoory, S.; Samouei, P.; Kheirkhah, A.S. Fuzzy logic in manufacturing: A review of literature and a specialized application. Int. J. Prod. Econ. 2011, 132, 258–270. [Google Scholar] [CrossRef]
- Tsourveloudis, N.C.; Doitsidis, L.; Ioannidis, S. Work-in-process scheduling by evolutionary tuned fuzzy controllers. Int. J. Adv. Manuf. Technol. 2007, 34, 748–761. [Google Scholar] [CrossRef]
- Tamani, K.; Boukezzoula, R.; Habchi, G. Application of a continuous supervisory fuzzy control on a discrete scheduling of manufacturing systems. Eng. Appl. Artif. Intell. 2011, 24, 1162–1173. [Google Scholar] [CrossRef][Green Version]
- Precup, R.E.; Hellendoorn, H. A survey on industrial applications of fuzzy control. Comput. Ind. 2011, 62, 213–226. [Google Scholar] [CrossRef]
- Wang, J.; Fei, Z.; Chang, Q.; Li, S.; Fu, Y. Multi-state decision of unreliable machines for energy-efficient production considering work-in-process inventory. Int. J. Adv. Manuf. Technol. 2019, 102, 1009–1021. [Google Scholar] [CrossRef]
- Wang, J.; Fei, Z.; Chang, Q.; Fu, Y.; Li, S. Energy saving operation of multi-stage stochastic manufacturing systems based on fuzzy logic. Int. J. Simul. Model. 2019, 18, 138–149. [Google Scholar] [CrossRef]
- Liu, H.C.; You, J.X.; Li, Z.W.; Tian, G. Fuzzy petri nets for knowledge representation and reasoning: A literature review. Eng. Appl. Artif. Intell. 2017, 60, 45–56. [Google Scholar] [CrossRef]
- Xie, N.; Duan, M.; Chinnam, R.B.; Li, A.; Xue, W. An energy modeling and evaluation approach for machine tools using generalized stochastic petri nets. J. Clean. Prod. 2016, 113, 523–531. [Google Scholar] [CrossRef]
- Pang, C.K.; Le, C.V. Optimization of total energy consumption in flexible manufacturing systems using weighted p-timed petri nets and dynamic programming. IEEE Trans. Autom. Sci. Eng. 2014, 11, 1083–1096. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, X.; Yang, S. Energy modeling and simulation of flexible manufacturing system based on colored timed Petri net. J. Ind. Ecol. 2014, 18, 558–566. [Google Scholar] [CrossRef]
- Li, Y.; He, Y.; Wang, Y.; Wang, Y.; Yan, P.; Lin, S. A modeling method for hybrid energy behaviors in flexible machining systems. Energy 2015, 86, 164–174. [Google Scholar] [CrossRef]
- Fei, Z.; Li, S.; Chang, Q.; Wang, J.; Huang, Y. Fuzzy petri net based intelligent machine operation of energy efficient manufacturing system. In Proceedings of the 14th IEEE Conference on Automation Science and Engineering (CASE), Munich, Germany, 20–24 August 2018; pp. 1593–1598. [Google Scholar]
- Gao, M.; Zhou, M.C.; Huang, X.; Wu, Z. Fuzzy reasoning Petri nets. IEEE Trans. Syst. Man Cybern. A 2013, 33, 314–323. [Google Scholar]
- Yeung, D.S.; Tsang, E.C.C. Weighted fuzzy production rules. Fuzzy Sets Syst. 1997, 88, 299–313. [Google Scholar] [CrossRef]
- Liu, H.C.; Lin, Q.L.; Mao, L.X.; Zhang, Z.Y. Dynamic adaptive fuzzy petri nets for knowledge representation and reasoning. IEEE Trans. Syst. Man Cybern. S 2013, 43, 1399–1410. [Google Scholar] [CrossRef]
- Li, J.; Meerkov, S.M.; Zhang, L. Production systems engineering: Problems, solutions, and applications. Annu. Rev. Control. 2010, 34, 73–88. [Google Scholar] [CrossRef]



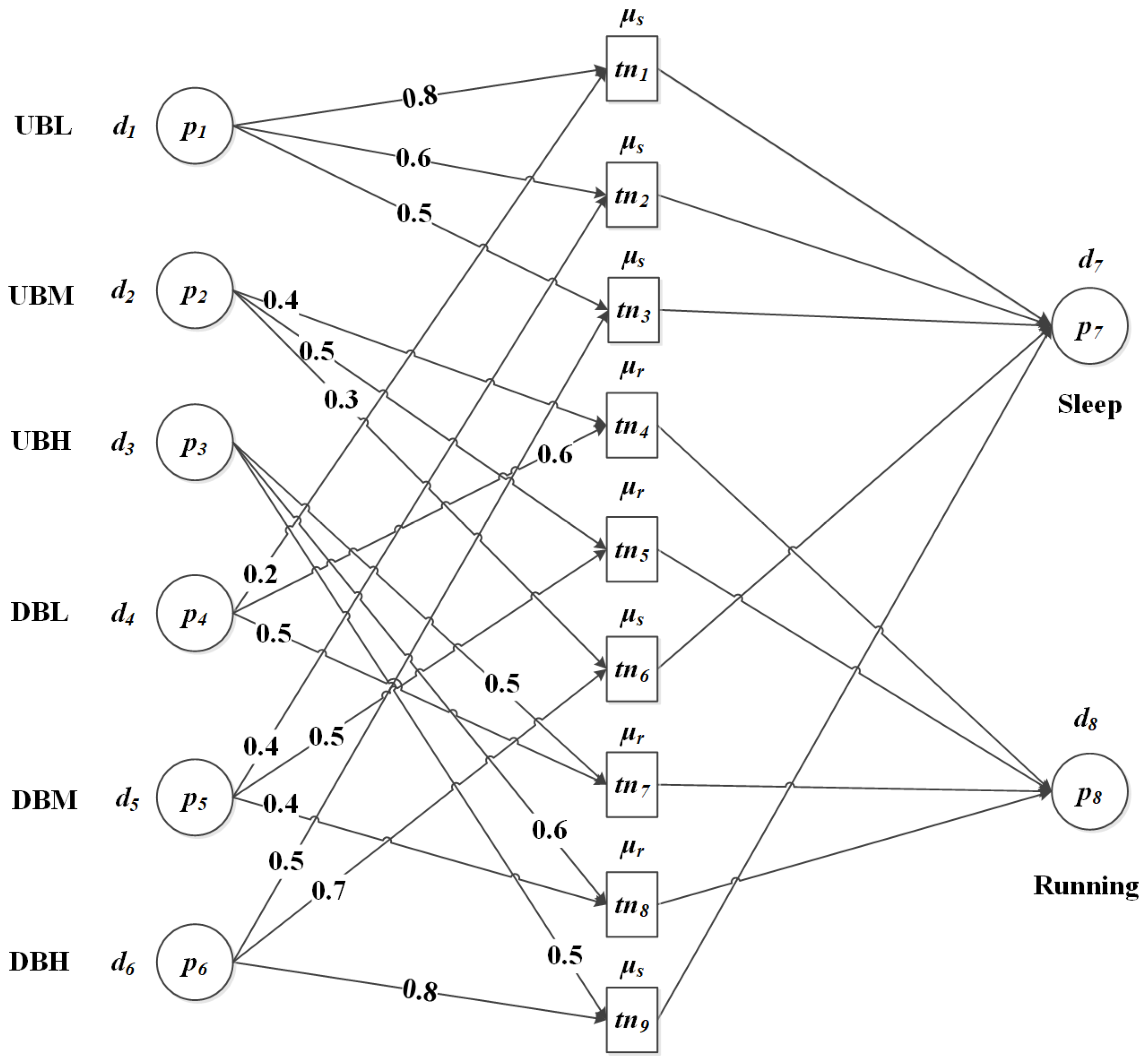
| No. | bi(t) | ub,x | bi+1(t) | db,x | si(t) | cfi(t) |
|---|---|---|---|---|---|---|
| 1 | Low | 0.8 | Low | 0.2 | Sleep | μs |
| 2 | Low | 0.6 | Medium | 0.4 | Sleep | μs |
| 3 | Low | 0.5 | High | 0.5 | Sleep | μs |
| 4 | Medium | 0.4 | Low | 0.6 | Running | μr |
| 5 | Medium | 0.5 | Medium | 0.5 | Running | μr |
| 6 | Medium | 0.3 | High | 0.7 | Sleep | μs |
| 7 | High | 0.5 | Low | 0.5 | Running | μr |
| 8 | High | 0.6 | Medium | 0.4 | Running | μr |
| 9 | High | 0.2 | High | 0.8 | Sleep | μs |
| No. | ri | μs | μr |
|---|---|---|---|
| 1 | Low | Small | Big |
| 2 | Medium | Middle | Middle |
| 3 | High | Big | Small |
| Machine | M1 | M2 | M3 | M4 | M5 | M6 |
|---|---|---|---|---|---|---|
| MTBF (min) | 5422 | 6301.2 | 11872.2 | 5440.2 | 6412.8 | 6250.8 |
| MTTR (min) | 130.8 | 208.2 | 409.8 | 279.6 | 205.2 | 250.8 |
| Cycle time (min) | 3.5 | 4.3 | 2.7 | 9.4 | 1.1 | 5.9 |
| Working energy (kWh) | 450 | 300 | 240 | 288 | 660 | 360 |
| Buffer | B1 | B2 | B3 | B4 | B5 |
|---|---|---|---|---|---|
| Capacity | 120 | 150 | 160 | 50 | 150 |
| Initial level | 70 | 30 | 50 | 40 | 50 |
| Scenario | Sleep Time(min) [95% CI] | Throughput [95% CI] | Total Energy Cost [95% CI] | Energy Cost Per Part ($) |
|---|---|---|---|---|
| S1 | - | 3168.45 [3149.72,3187.18] | 225727.80 [224839.67,226615.94] | 71.24 |
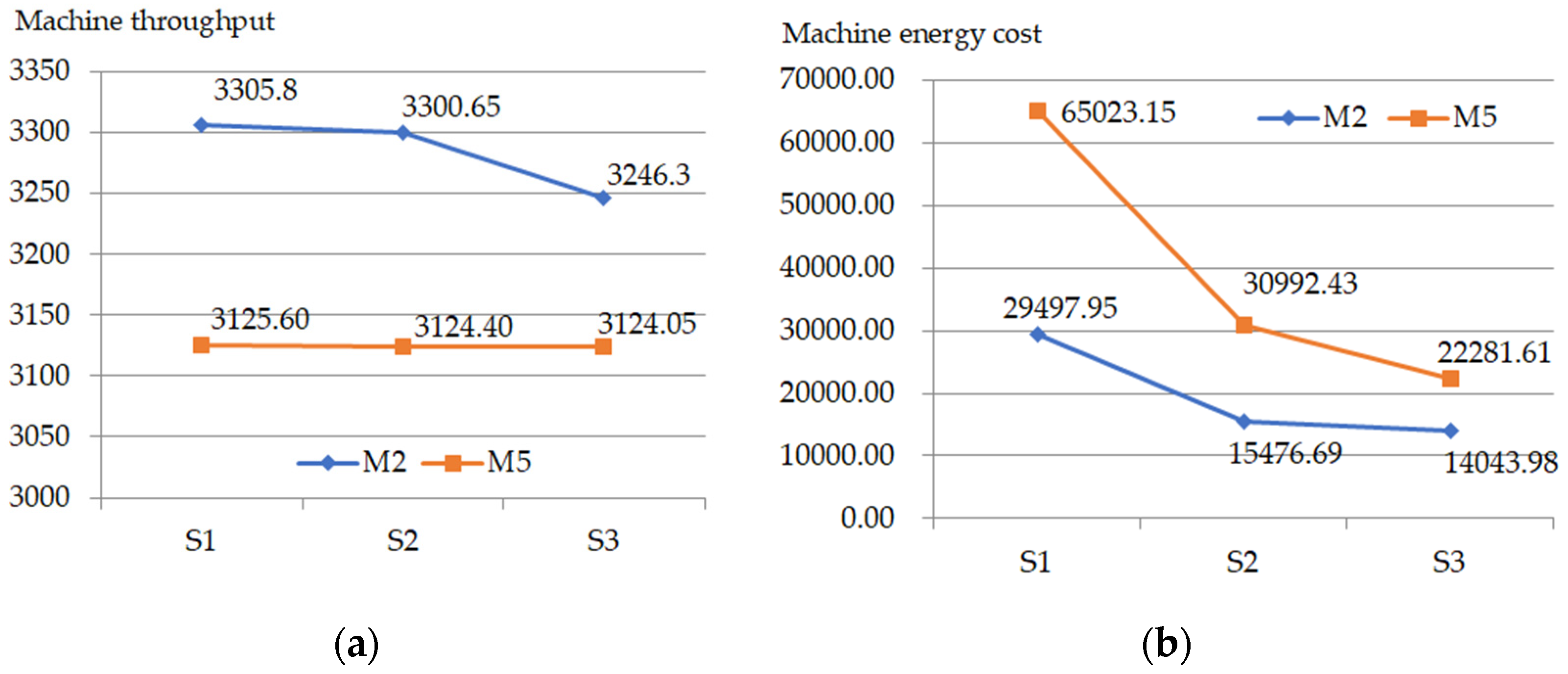
| S2 (M2) | 14021.62 [13877.85,14165.38] | 3168.45 [3149.72,3187.18] | 211707.56 [210800.94,212614.18] | 66.82 |
| S2 (M5) | 15468.38 [15346.97,15589.78] | 3167.05 [3148.41,3185.69] | 191700.72 [190945.86,192455.59] | 60.53 |
| S3 | 73722.71 [73323.99,74121.42] | 3166.55 [3147.81,3185.29] | 123747.56 [123055.63,124439.49] | 39.08 |
| Time Length | Scenario | M1 | M2 | M3 | M4 | M5 | M6 |
|---|---|---|---|---|---|---|---|
| PS | S1 S3 | 11744.60 11475.28 | 14214.94 13959.09 | 8615.97 8563.86 | 29008.40 29007.46 | 3438.16 3436.46 | 18693.86 18682.65 |
| BL | S1 S3 | 17894.49 0.00 | 15283.01 84.89 | 20841.81 373.36 | 6.26 7.20 | 0.00 0.00 | 0.00 0.00 |
| ST | S1 S3 | 0.00 0.00 | 0.00 0.00 | 156.00 0.00 | 0.00 0.00 | 26117.82 6691.55 | 10641.95 10655.03 |
| FL | S1 S3 | 600.91 600.15 | 742.05 742.21 | 626.21 626.35 | 1225.34 1225.34 | 684.02 684.10 | 904.19 902.33 |
| SL | S3 | 18164.58 | 15453.81 | 20676.43 | 0.00 | 19427.90 | 0.00 |
| TPL | % | 2.29% | 1.80% | 0.60% | 0.00% | 0.05% | 0.06% |
| ECR | % | 61.28% | 52.39% | 69.82% | 0.00% | 65.73% | 0.01% |
| Methods | [22] | M5 | M1, M2, M3, M5 | ||
|---|---|---|---|---|---|
| [29] | Our | [29] | Our | ||
| Throughput loss (%) | 2.70% | 0.69% | 0.04% | 0.23% | 0.06% |
| Energy cost reduction (%) | 27.00% | 25.48% | 15.07% | 51.76% | 45.18% |
| Energy cost reduction per part (%) | 24.98% | 24.95% | 15.03% | 51.66% | 45.14% |
| Increase of system profit (%) (300 $) | 5.15% | 7.07% | 4.64% | 15.90% | 13.99% |
| Increase of system profit (%) (600 $) | 0.68% | 2.67% | 1.98% | 6.74% | 6.02% |
| Decision Cycle (Times) | Sleep Time (min) [95% CI] | Throughput [95% CI] | Total Energy Cost [95% CI] | Energy Cost Per Part ($) |
|---|---|---|---|---|
| 2 | 78560.86 [78103.31,79018.40] | 3166.85 [3148.16,3185.54] | 113726.48 [113025.77,114427.20] | 35.91 |
| 5 | 73722.71 [73323.99,74121.42] | 3166.55 [3147.81,3185.29] | 123747.56 [123055.63,124439.49] | 39.08 |
| 10 | 66122.12 [65619.01,66625.22] | 3166.75 [3148.06,3185.44] | 136515.89 [135625.89,137405.89] | 43.11 |
| Input Weights Group 1 | Sleep Time (min) [95% CI] | Throughput [95% CI] | Total Energy Cost [95% CI] | Energy Cost Per Part ($) |
|---|---|---|---|---|
| G1 | 73722.71 [73323.99,74121.42] | 3166.55 [3147.381,3185.29] | 123747.56 [123055.63,124439.49] | 39.08 |
| G2 | 73667.62 [73266.93,74068.31] | 3166.55 [3147.81,3185.29] | 123793.75 [123097.26,124490.24] | 39.09 |
| G3 | 60671.83 [60280.04,61063.62] | 3167.35 [3148.63,3186.07] | 152435.80 [151310.40,153561.20] | 48.13 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Fei, Z.; Chang, Q.; Li, S. Energy Saving Operation of Manufacturing System Based on Dynamic Adaptive Fuzzy Reasoning Petri Net. Energies 2019, 12, 2216. https://doi.org/10.3390/en12112216
Wang J, Fei Z, Chang Q, Li S. Energy Saving Operation of Manufacturing System Based on Dynamic Adaptive Fuzzy Reasoning Petri Net. Energies. 2019; 12(11):2216. https://doi.org/10.3390/en12112216
Chicago/Turabian StyleWang, Junfeng, Zicheng Fei, Qing Chang, and Shiqi Li. 2019. "Energy Saving Operation of Manufacturing System Based on Dynamic Adaptive Fuzzy Reasoning Petri Net" Energies 12, no. 11: 2216. https://doi.org/10.3390/en12112216
APA StyleWang, J., Fei, Z., Chang, Q., & Li, S. (2019). Energy Saving Operation of Manufacturing System Based on Dynamic Adaptive Fuzzy Reasoning Petri Net. Energies, 12(11), 2216. https://doi.org/10.3390/en12112216






