1. Introduction
Integration of renewable energy resources into the power grid causes major deregulation in the electricity market. Keeping the generation cost down in the deregulated power system as well as providing a reliable load to customers necessitates the use of remote measurements and smart metering in the power system, which leads to smart grid development. A smart grid is able to establish a two-way communication by means of advanced sensors to improve the reliability and performance of a system. While these cyber resources enable market operators to enhance the performance of a system, they bring new challenges to the infrastructure. Cyber-physical systems (CPSs) render smart grids more vulnerable to cutting-edge undetectable cyber-physical attacks. Therefore, the impact assessment of cyber-attacks on smart grids is considered as one of the most serious issues in recent years [
1].
Several types of cyber-attacks have been investigated, which are divided into three different categories, namely, data availability, confidentiality, and integrity. Cyber-attacks on availability or named denial-of-service (DoS) attacks effort to delay, deny, or alter transferring information at different layers of a communication network. Attacks on confidentiality aim to obtain unauthorized information from networks in smart grids. Attacks on integrity intend to deliberately and illegally modify or disrupt data exchange in a smart grid. Such attacks attempt to stealthily manipulate data to corrupt critical information exchange in smart grids [
2]. Recently, the method of false data injection attack (FDIA) has been attracting the attention of researchers. The false data injection attack was designed to impact the state estimation [
3] and real-time electricity market [
4] by manipulating the data in the SCADA system. Another type of cyber-attack on a smart grid’s integrity, namely, alter-and-hide (AaH) is used to change the true values of digital variables such as substation switches and breakers. This kind of attack affects the topology processor and brings catastrophic consequences [
5]. However, owing to the basic difference in the modeling of the various cyber-attacks, and the vast literature on this type of attack, the FDIA is modeled and formulated in this study to be investigated.
FDIAs aim to modify data at the control center or measurement units to reach a predetermined end. FDIAs target analog measured data from the power system, i.e., the nodal voltage magnitudes and angles, nodal power injections, line power flows, and digital data such as the status of breakers and switches [
6]. Such data are essential to the power system operator (PSO) to perform state estimation (SE) in order to monitor and control the power grid operation. The result of SE is also exploited in the security constraint economic dispatch (SCED) to settle in the real-time power electricity market. Thus, the data integrity guarantees an accurate SE as well as effective monitoring and control of the power system operation.
The concept of FDIAs on SE in smart grids was first raised in [
7]. The authors in [
7] illustrated that by having adequate knowledge of the power system configuration, an adversary can launch FDIA without being detected. That investigation was an inspiration for other researchers to work on impacts of this type of attack on the power system and appropriate techniques to defend it. The authors in [
8] presented analytical approaches to analyze the influence of FDIAs on AC state estimation. The authors in [
9,
10,
11,
12,
13] discussed various methods of FDIA on SE in smart grids considering complete and incomplete knowledge about the topology of the considered power system.
As mentioned earlier, the estimated variables are utilized in SCED and real-time electricity market settlement. This issue can be considered as a motivation for the adversary to stealthily attack the SE by altering locational marginal price (LMP) values in the real-time electricity market. Wide areas of research have been carried out to investigate this matter. The economic consequences of FDIA on the real-time ex-ante market were discussed in [
6]. FDIA on analog and digital measurements were studied in [
14], and an optimized attack problem was presented. Given the Australian real-time electricity market mechanism, the authors in [
15] proposed a compact FDIA-based approach to cyber topology. The researchers in [
16,
17] provided a thorough review of FDIAs on power system state estimation and their influence on the electricity market up to the year 2017.
Several methods in the literature have been developed to mitigate and detect FDIAs on SE in smart grids [
18,
19,
20,
21,
22]. The authors in [
18] developed a heuristic algorithm to find an undetectable vector of FDIA and correspondingly, an infinite norm bad data detection (BDD) processor is defined to detect the attack vector efficiently. Liu et al. [
19] presented an approach utilizing the correlation and history of measurements as well as the sparse attribute of malicious attacks to detect FDIAs in smart grids. By applying the Kullback–Leibler distance (KLD) and assuming a probability distribution function for historical data, a statistical method for FDIA was introduced in [
20]. Another statistical outlier idea was proposed in [
21] to estimate the density ratio by using machine learning. By utilizing load forecasting, generation schedules and Phasor Measurement Units (PMUs), the author in [
22] proposed an online bad data detection algorithm.
Recently, machine learning techniques have been widely applied for bad data detection and identification in smart grids. The authors in [
23] proposed a hybrid machine learning method to detect stealthy attacks in smart grids. Data was labeled in the preprocessing stage by a supervised algorithm followed by training the labeled data with a support vector machine (SVM). Similarly, a deep-learning-based approach for detection of FDIA on smart meters’ data was investigated in [
24]. The model used a state vector estimator (SVE) and a deep-learning-based identification algorithm to prevent electricity theft. Multiple hidden layers were considered in this method to enhance the detection accuracy. A sparse principal component analysis and approximation approach were developed in [
25] to identify a stealthy FDIA on a smart grid. The accuracy of the method depended on the sparsity of data and it was less efficient for sparse vectors. Wang et al. [
26] investigated a data-centric paradigm to identify FDIAs in smart grids and the developed model employed a margin setting algorithm to categorize a huge amount of data. It was illustrated in [
26] that, by increasing the false data rate, the detection accuracy is decreased. In order to detect sparse cyber-attacks in smart grids, the authors in [
26,
27] developed a deep-learning-based interval state estimation algorithm. A multi-layer stacked autoencoder was used in that method, in which the last layer detected anomalies in electric load forecasting.
To the best knowledge of the authors, nonlinear autoregressive exogenous (NARX) (a special configuration of ANN) has not been utilized to detect stealthy optimized FDIA on contingency analysis. In spite of the distribution system, a transmission system is facilitated with adequate measurement devices; hence, analytical methods reveal accurate results of the state of the system. Still, measurements at the transmission level are exposed to FDIAs. There are BDD processors in the state estimator procedure even though, under specific conditions, FDIAs can pass through them. This paper aims to develop a novel BDD procedure based on a recurrent architecture of ANN, namely, nonlinear autoregressive exogenous (NARX) model, to identify FDIAs that could not be observed by conventional BDD processors.
The NARX neural network (NARXNN) is a robust engine for times series prediction by using historical data. Thus, it is practical to apply this learning engine to predict step-ahead values of the state by considering measurement values and historical data as input variables. However, owing to the nonlinear characterization of the forecast, the output would contain subtle errors in comparison to real values and SE results by analytical methods. Meanwhile, the results of analytical methods can be utilized without any restriction to validate and evaluate the estimated state.
This paper represents potential FDIAs that can be launched on smart grids without being detected by conventional BDDs. Moreover, by introducing NARXNN and its prominent features, which renders it an attractive predictor engine for estimation of the states, a novel FDIA detector is introduced and evaluated. The rest of this paper is organized as follows.
Section 2 briefly presents the main concept of state estimation in power systems as well as bad data identification tests.
Section 3 provides a review and formulation of undetectable FDIAs by conventional methods. A novel ANN-based bad data detection method is introduced and formulated in
Section 4. Finally, numerical analyses are provided in
Section 5, followed by conclusions in
Section 6.
3. Undetected False Data Injection Attack on State Estimation
In order to attack the state estimation, the adversary would inject an attack vector
to the measurement vector
. Thus, the residual vector would be altered as follows:
Correspondingly, the power flow vector is manipulated according to the following equation:
where
indicates the deviation of estimated state vector as a result of the attacked vector
. It is indicated in [
14] that the congested line has a direct impact on dual variables in the LMP equation. Consequently, each congested line set is associated with a unique LMP vector. Considering this theorem, most publications focused on FDIAs that target congested line sets without being detected by the conventional BDD. Similar to [
11,
14,
15,
16,
17], this paper assumes that FDIAs are launched without being detected by changing congested lines from their original situations. According to
norm-based residual test, in order to launch an unidentified attack, the following constraint should be satisfied:
In practice,
; therefore, provided that
, it can be guaranteed that the BDD process cannot detect the injected data. Equation (14) is extended by using the previous equations as follows:
where
is an arbitrary non-zero vector. It is shown in [
19] that, in cases
, a perfect and unidentifiable attack is launched to the state estimation. However, it is not feasible to assume that the system topology is completely known to an attacker. The attacker has to ensure
to launch an imperfect attack to avoid detection with high probability.
On the other hand, according to the LNR test, the following condition should be satisfied for each array of the residual vector to pass a BDD process:
hence
where
is the vector of absolute values of residual vector and
is the threshold vector. Equation (17), at the presence of an attack, is rewritten as follows:
therefore, in order to have a hidden attack, the attacker should consider the following constraint:
where
is the threshold vector for the residual vector to have an undetected attack.
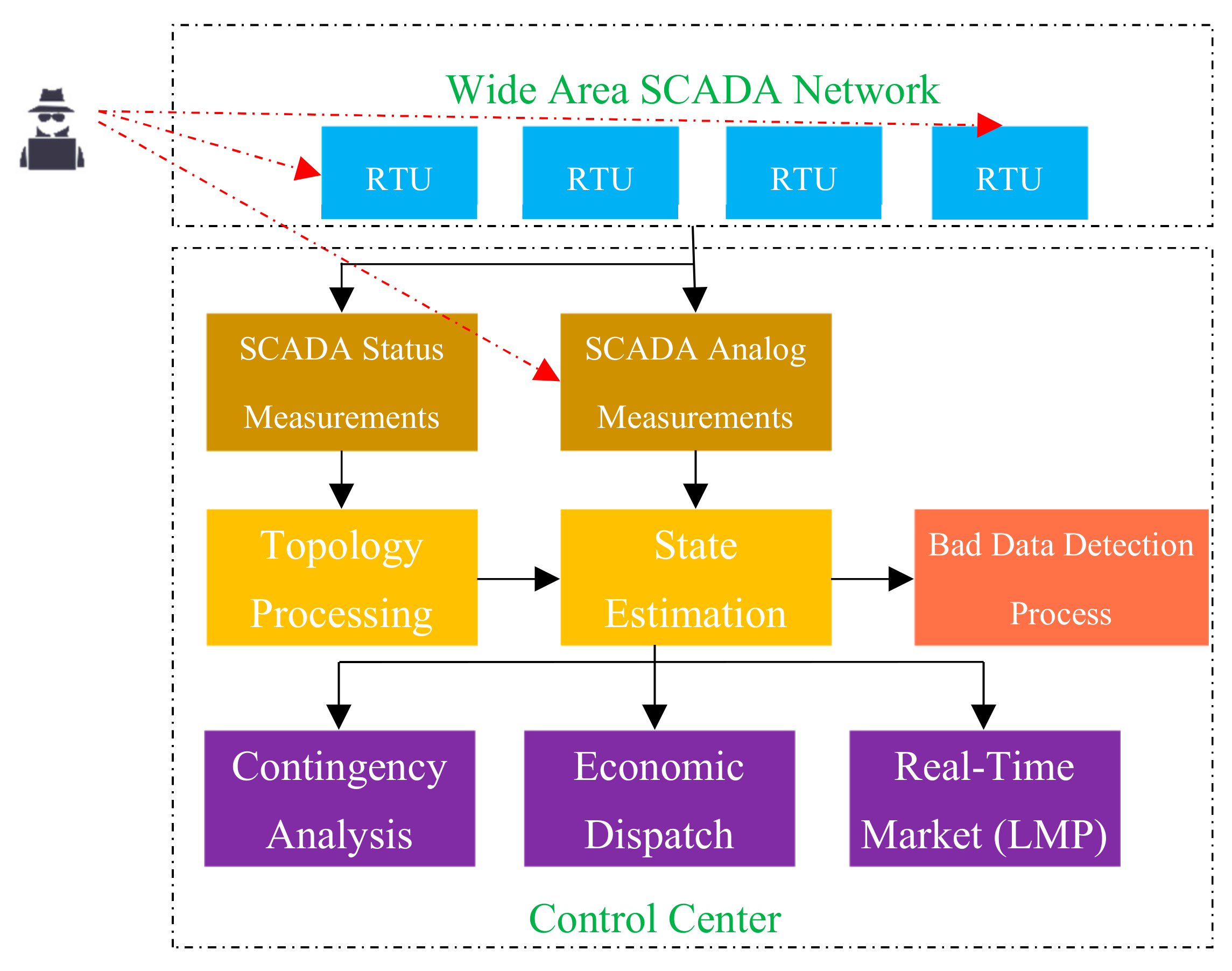
As shown in
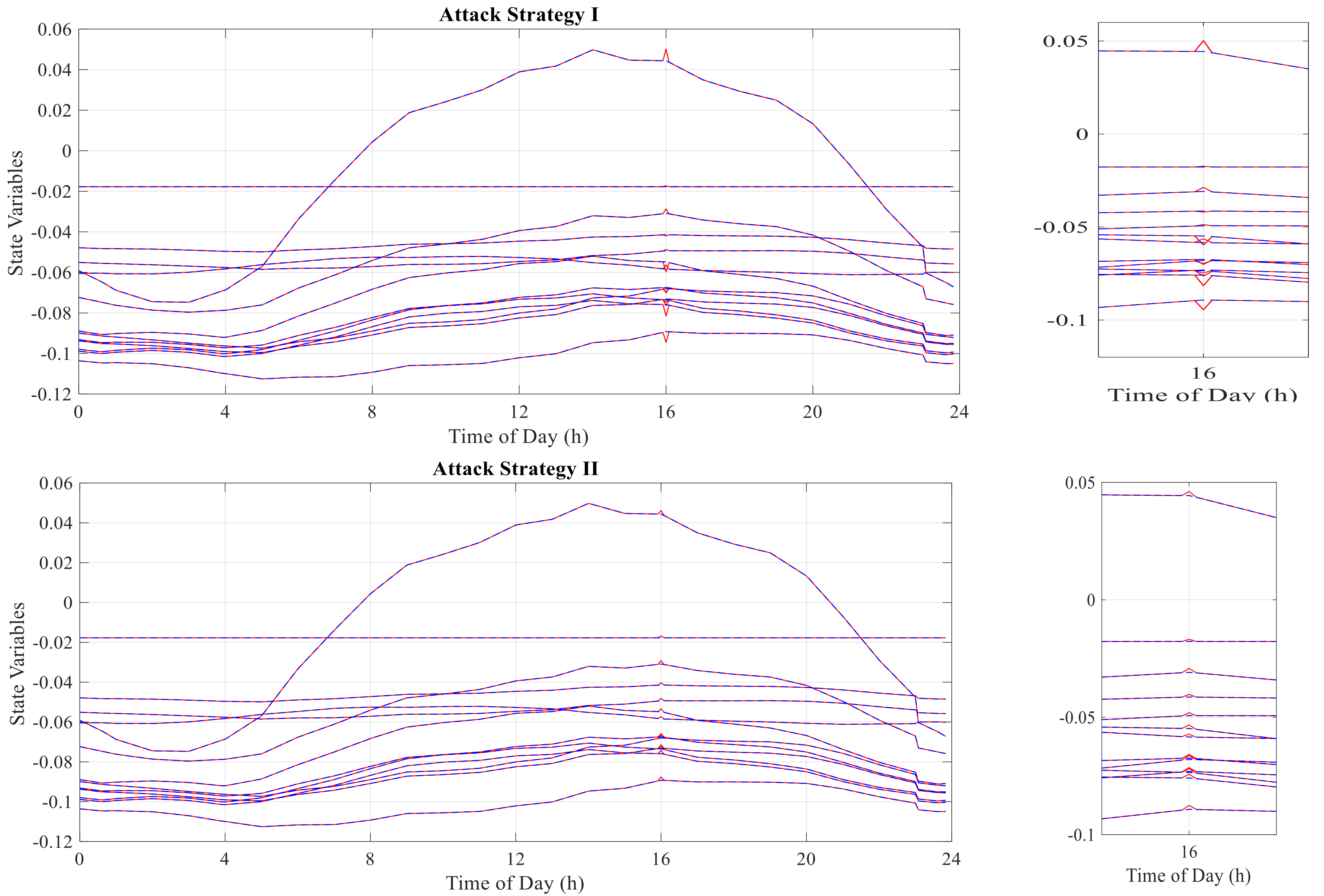
Figure 1, the attacker may either attack an individual measurement throughout the power system or gathered measurement vectors in the control center. Therefore, two different attack strategies can be considered. The attacker may try to attack the control center directly and alter the aggregated measurement vector in the first scenario. In this case, the number of available measurements that can be changed by the attacker is not restricted. However, in order to keep the attack unidentified, the size of the attack vector must be as small as possible. On the other hand, the attacker can launch an unidentified attack by changing the measurements values directly. In this case, limited measurements should be altered locally and simultaneously. Therefore, the lowest number of measurements that should be attacked to have an undetected and effective attack would be determined in this scenario. Both scenarios are introduced and explained in the following sections:
3.1. Attack Strategy I
In order to attack a SCADA system in a control center, before sending the gathered measurements to the state estimator, there is no limitation for the adversary to attack the number of measurements; whereas, limiting the
norm of the attack vector can effectively impact on finding a feasible attack vector. In this case, the optimization problem is as follows:
s.t.
where
is the sum of squared arrays of
,
is the transposed vector of
, and
is the identity symmetric matrix representing the quadratic function.
is
lth row of the admittance matrix,
is the uncertainty relaxation constant (because of the random distribution of measurements errors and the uncertainty of the real-time power generation and demand, in order to assure the effectiveness of the attack this parameter is needed to be adjusted),
is the
lth estimated power flow line in the original state,
is the attacker’s desired congested line, and
is the imperfect attack threshold. Equation (21) is the objective function of the optimization problem that the attacker uses to manipulate the gathered measurements in the SCADA system. Equations (22) and (23) lead the state estimation to a situation that the attacker can change the congestion pattern. Equations (24) and (25) restrict the residual vector for each measurement to have an unidentified attack vector in the
norm-based residual test and the LNR test, respectively. Equation (24) restricts and controls the sum of residual values for all measurements. Hence, the attacker cannot alter the value of measurements freely and there is a limitation in the aggregated value of the residual vector. Consequently, based on Equation (25) the attacker cannot alter the value of an individual measurement. In this case, there is an upper limit for each array in the attack vector. This constraint leads to change a large number of measurements to launch an undetectable attack. Finally, (26) guarantees that the uncertainty relaxation constant acquires a positive value.
3.2. Attack Strategy II
As illustrated in
Figure 1, the attacker may want to attack individual measurements before being gathered by the SCADA system. In this case, the minimum sparsity objective function is considered by the attacker as the following optimization problem:
s.t. Equations (22)–(26).
Where indicates the number of non-zero arrays or sparsity of . Equation (27) is the objective function of an optimization problem, by which the minimum number of manipulated measurements are found to achieve a successful attack. The constraints are the same as the constraints of the first attack strategy.
Finding the minimum sparsity of the attack vector is a nonlinear and nonconvex problem. Hence, in order to make the optimization problem solvable, the
norm optimization problem can be estimated with
norm or
norm problems [
27,
29]. Here, in order to have a convex problem with a positive infinite symmetric matrix, a weighted
norm optimization problem is substituted with the original problem. In addition, an iterative algorithm similar to the method in [
30] is utilized.
The equivalent
norm optimization problem is formulated as follows:
s.t. Equations (22)–(26).
Where is a weight matrix representing a quadratic function.
An iterative algorithm is performed to compute the optimum solution. The details are illustrated in Algorithm 1. The problem is solved several times to reach the stop criterion constraint.
| Algorithm 1. Iteratively reweighted norm minimum sparsity. |
| Input: congestion pattern, imperfect attack relaxation, residual vector relaxation constraints |
| Output: attack vector , |
| , initial weights |
| while stop criterion false do |
| , s.t. |
| where is a small positive value |
|
|
| end while |
4. Methodology
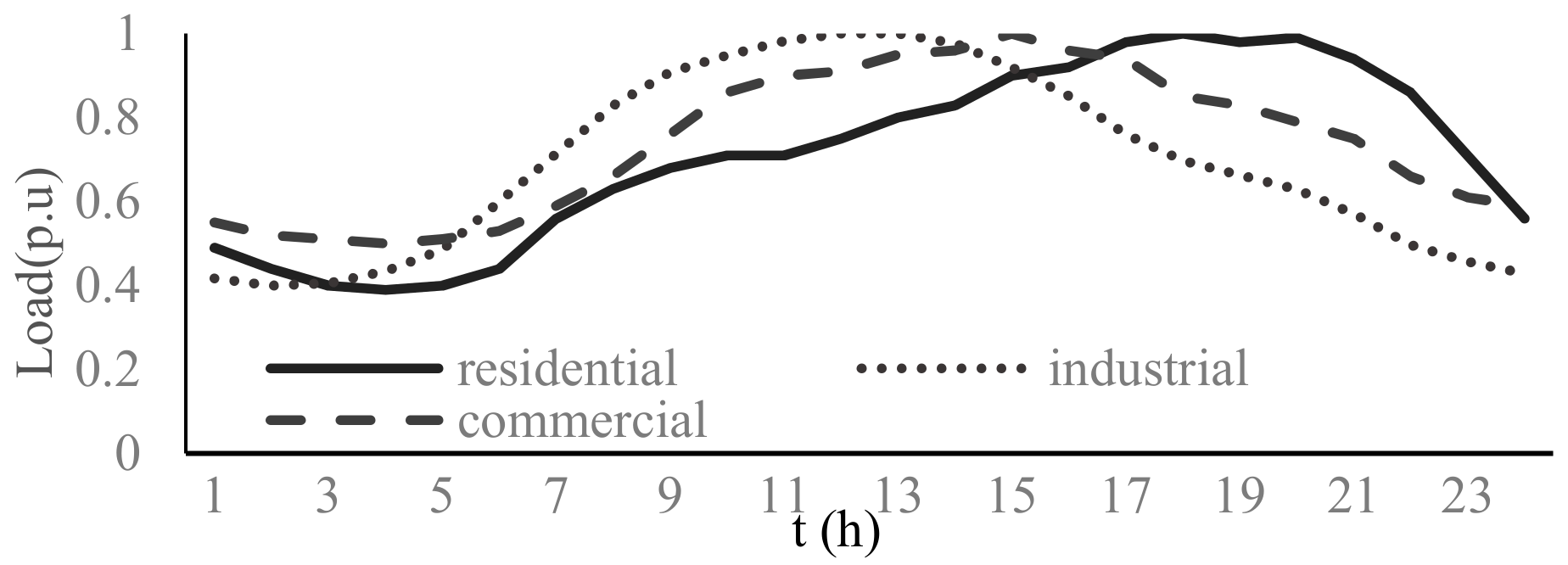
State variables of a power system have repetitive daily behavior in a midterm viewpoint. This periodic behavior is a remarkable indicator with valuable information in historical data. Moreover, an integrated structure of a power network creates identifiable dependencies between state variables and measurements across the grid.
NARX is an important class of discrete-time nonlinear system that employs historical values of output variable and exogenous input variables into the model. The equation for NARX is expressed as follows:
where
and
indicate input and output variables for nonlinear time series modeling, respectively;
and
represent the input and output delay, respectively; and
is a nonlinear function. The output variable is a function of the previous values of the output signal and past values of independent input variables. The function
can be approximated by a neural network.
ANN has been widely employed in electrical engineering for forecasting undetermined parameters. ANN is a robust engine for prediction, classification, clustering, pattern recognition, and process modeling. It provides nonlinear mapping solutions between input features and output, due to its learning, generalization, error tolerance, and parallel processing abilities. The advantage of not requiring a clear relationship between inputs and outputs renders a neural network an attractive choice for forecasting [
31].
A further developed neural network configuration is the recurrent neural network (RNN), namely, a supervised learning engine that contains feedback loops. The memorizing ability in RNN renders it interesting for time series prediction and modeling with historical data. The recurrent NARX neural network (RNARXNN) is a proper engine for chaotic nonlinear forecasting problems. RNARXNN uses feedback from the output layer, instead of hidden layers in the conventional RNN structure. This configuration improves the learning capability, convergence, and generalization performances of the learning engine [
32].
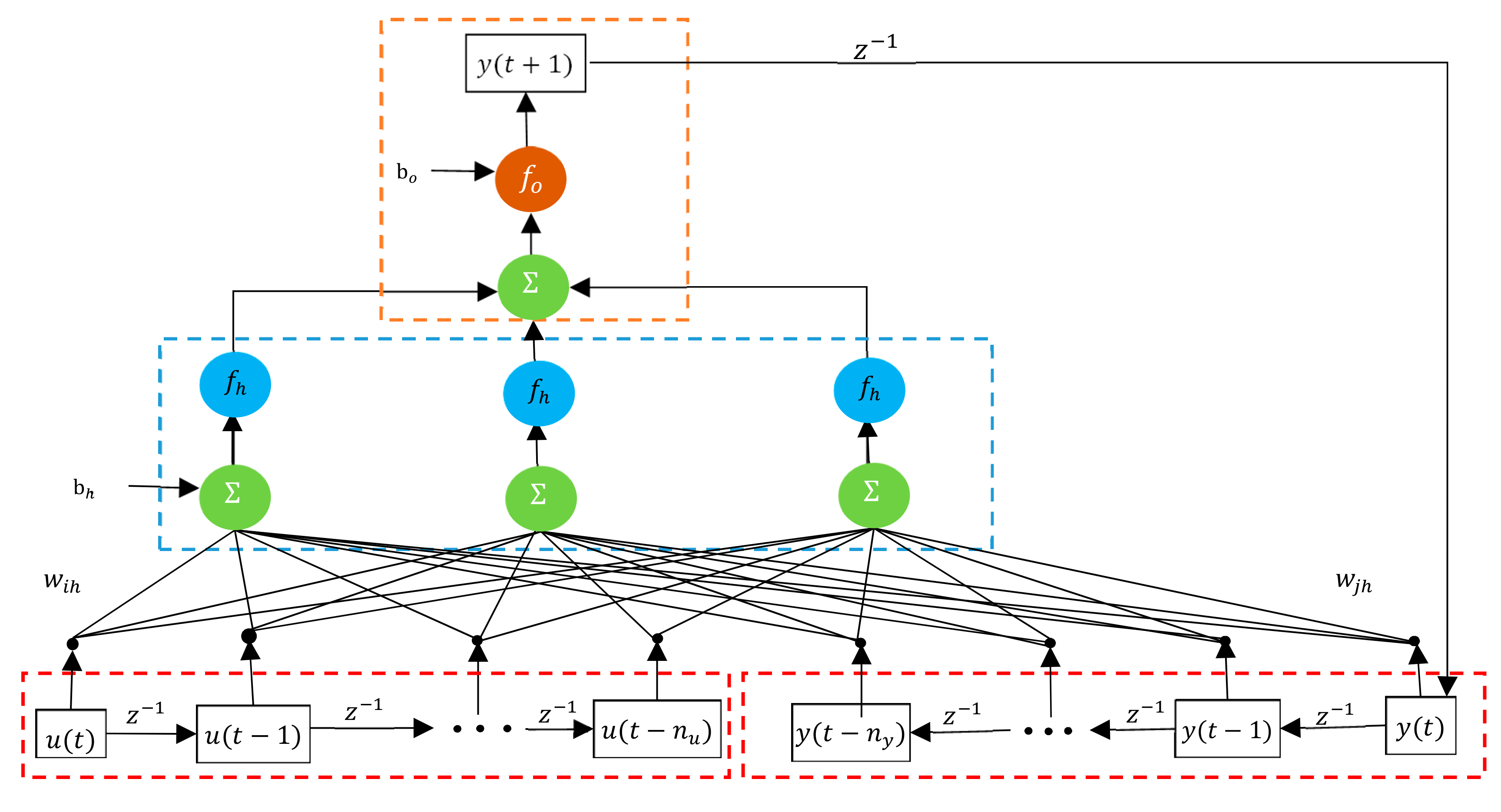
A schematic diagram of the RNARXNN model with one time-series is depicted in
Figure 2. The formulated RNARXNN is shown as follows.
where
,
and
are weights between independent input to the hidden layers, weights between input with past values of output to the hidden layer and weights between the hidden layer to the output layer, respectively.
and
are biases, and
and
are activation functions (linear) of the hidden layer and output layer, respectively.
A recent formulation is used to predict state variables of a power system. In this case, the input variable is the historical value of the measurement vector and the output is the state variables of the power system. Accordingly, in order to develop RNARXNN, Equation (30) is restated as follows:
where
indicates the measurement vector at the time interval
and
is the predicted state variable by using the RNARXNN method.
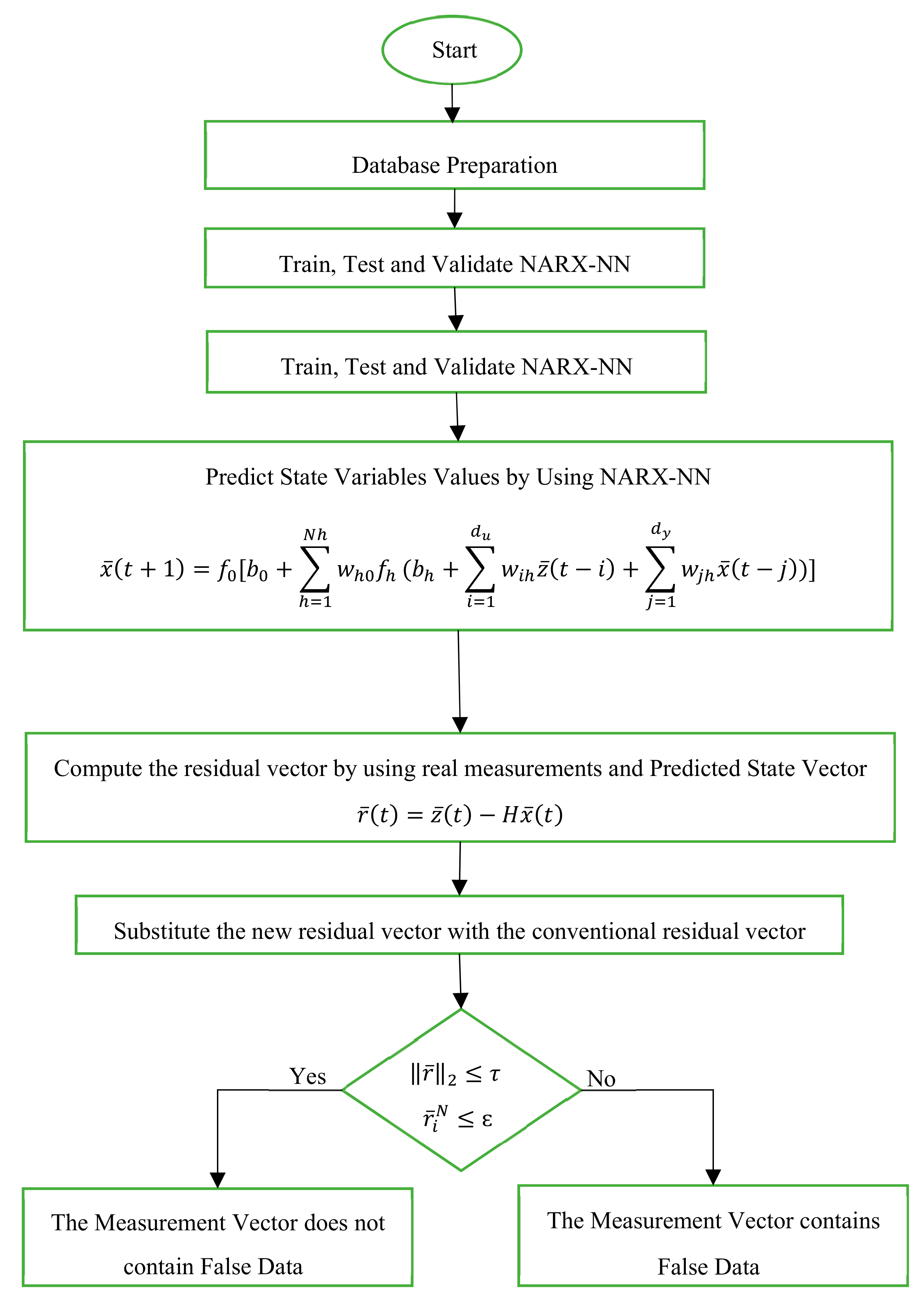
By applying this method, state variables of a power system can be forecast with previous measurement values as input vectors. The result of forecasting may contain uncertainty and approximation, which is not as accurate as analytical methods like WLS for the estimation of states. However, it can be exploited to evaluate the accuracy of measurements and detect false data.
Therefore, by using the forecasted states, the residual vector is computed as follows:
where
is the estimated residual vector by using the predicted state variables. Instead of the conventional computation method for the residual vector (Equation (6)), the RNARXNN-based residual vector is utilized to test the measurements. Hence, the
norm-based residual test equation will be updated as follows:
consequently, the LNR test is changed to the following:
Therefore, the FDIA will be identified using the updated value of the residual vector in the conventional tests; however, this type of attack could alter the power system characteristics without being detected by the conventional BDD procedure. The flowchart of the proposed method is illustrated in
Figure 3.
7. Conclusions
This paper proposes a NARX-based BDD processor to identify FDIAs on power system state estimation. The desired state variables are predicted by using a NARX network and are compared to computed state variables. Hence, by using the residual vector, potentially bad data are identified. The computed state variables passing the BDD processor can be applied as accurate results in power system operation and market clearance.
Two different FDIA strategies are considered to formulate and simulate a cyber-attack on power system state estimation. It is illustrated that this kind of attack can be launched on state estimation and can alter the line congestion pattern without being detected by conventional bad data detection processors. The results depict that only less than 10% of the formulated attacks are detected by conventional processors.
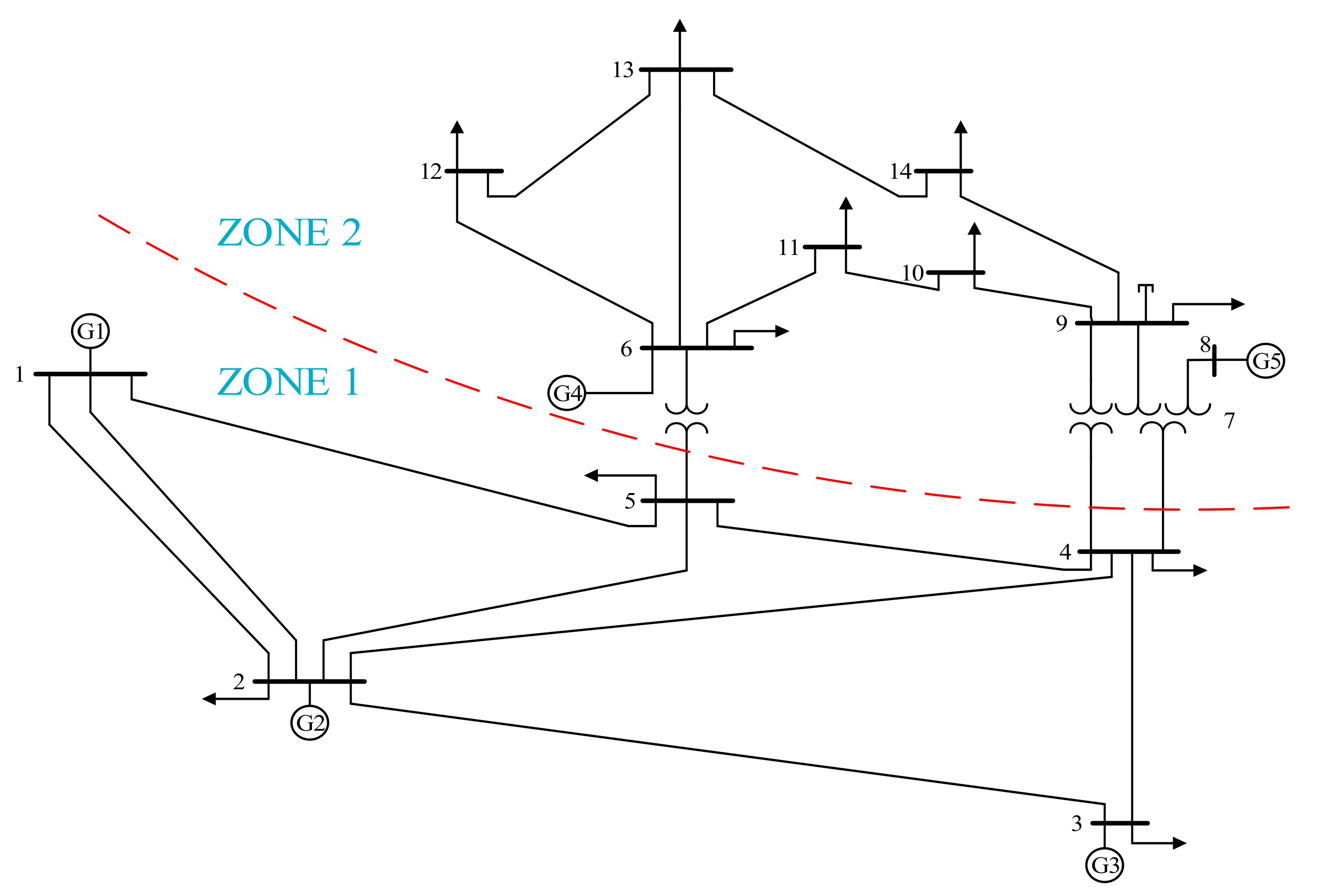
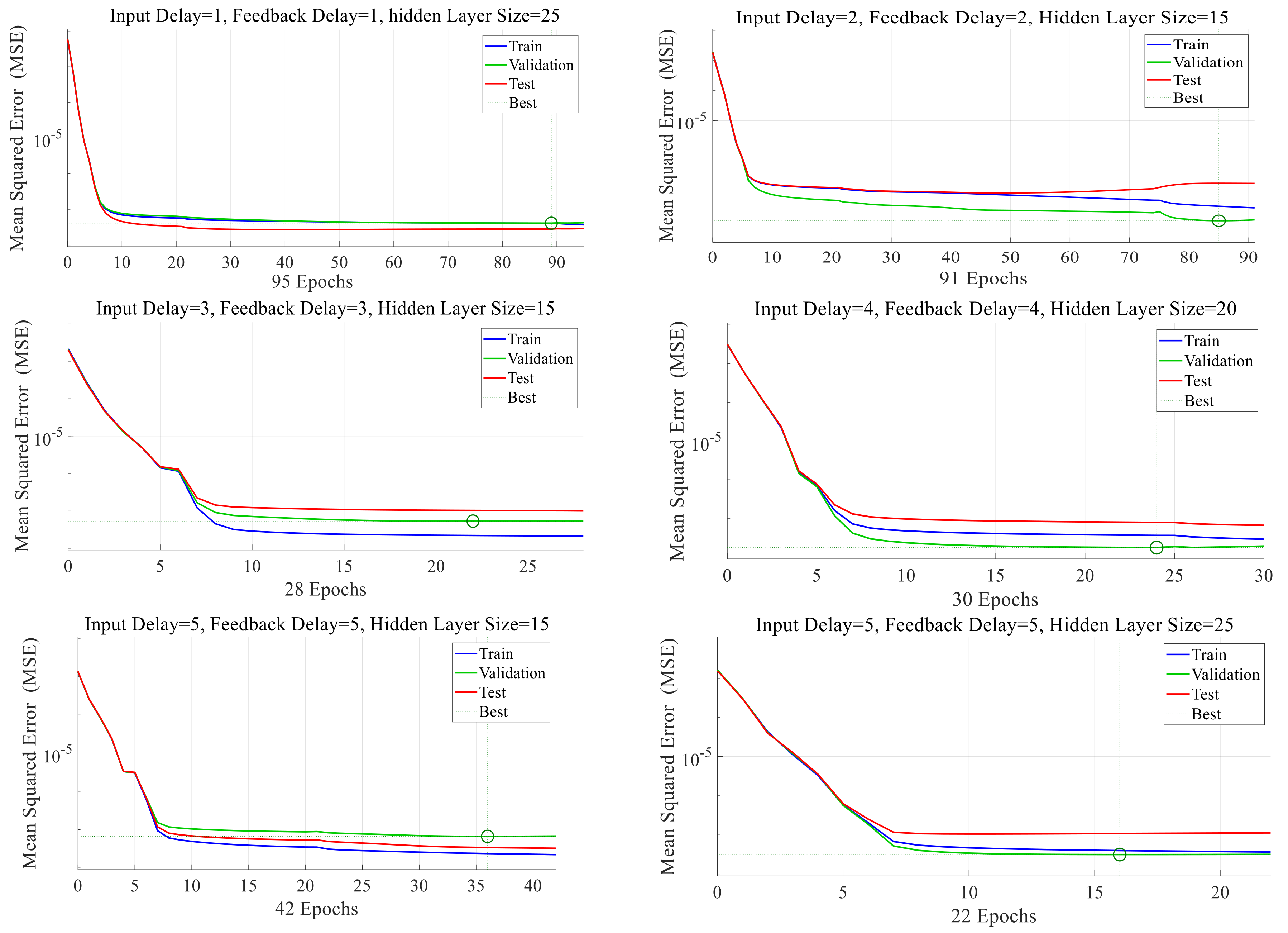
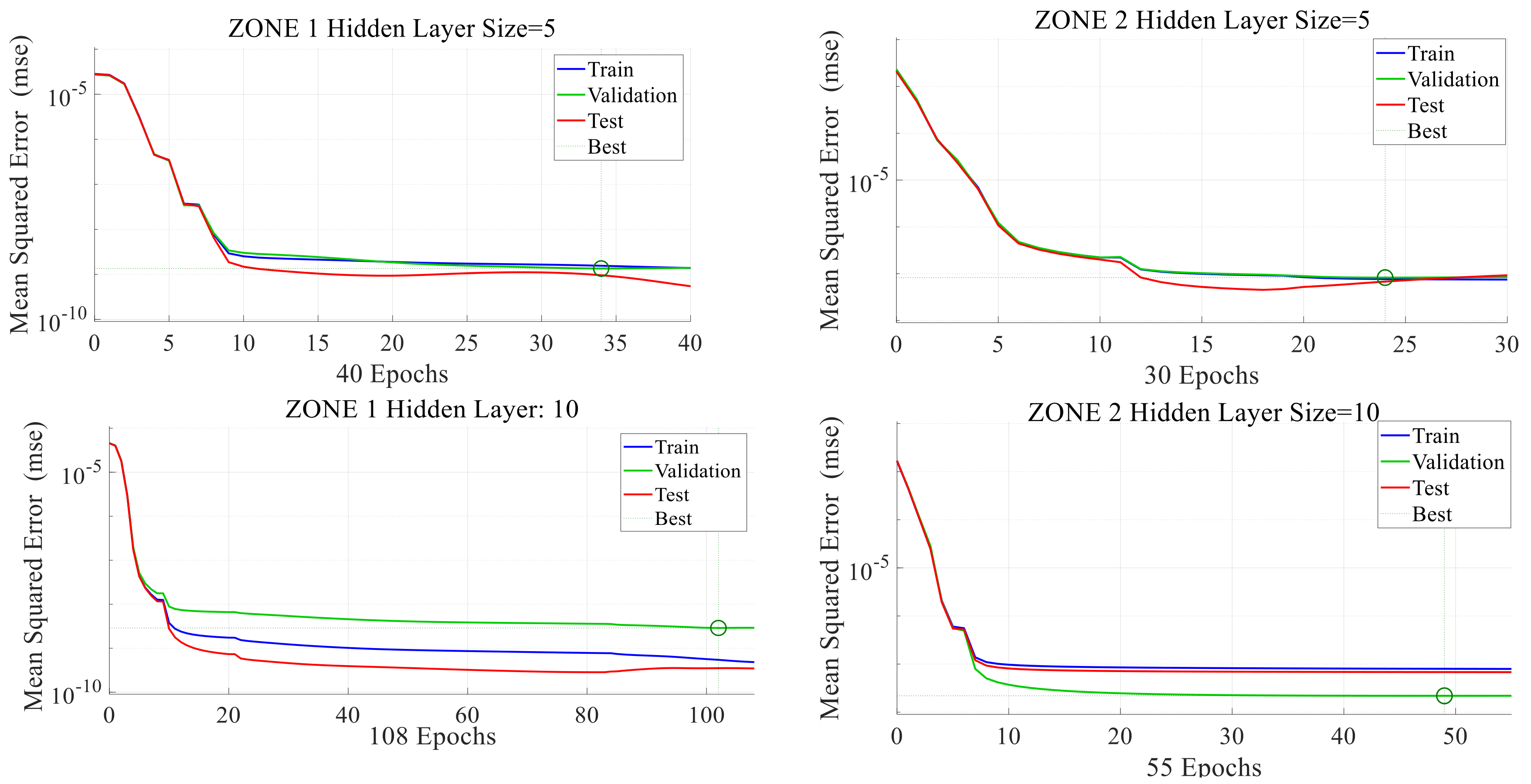
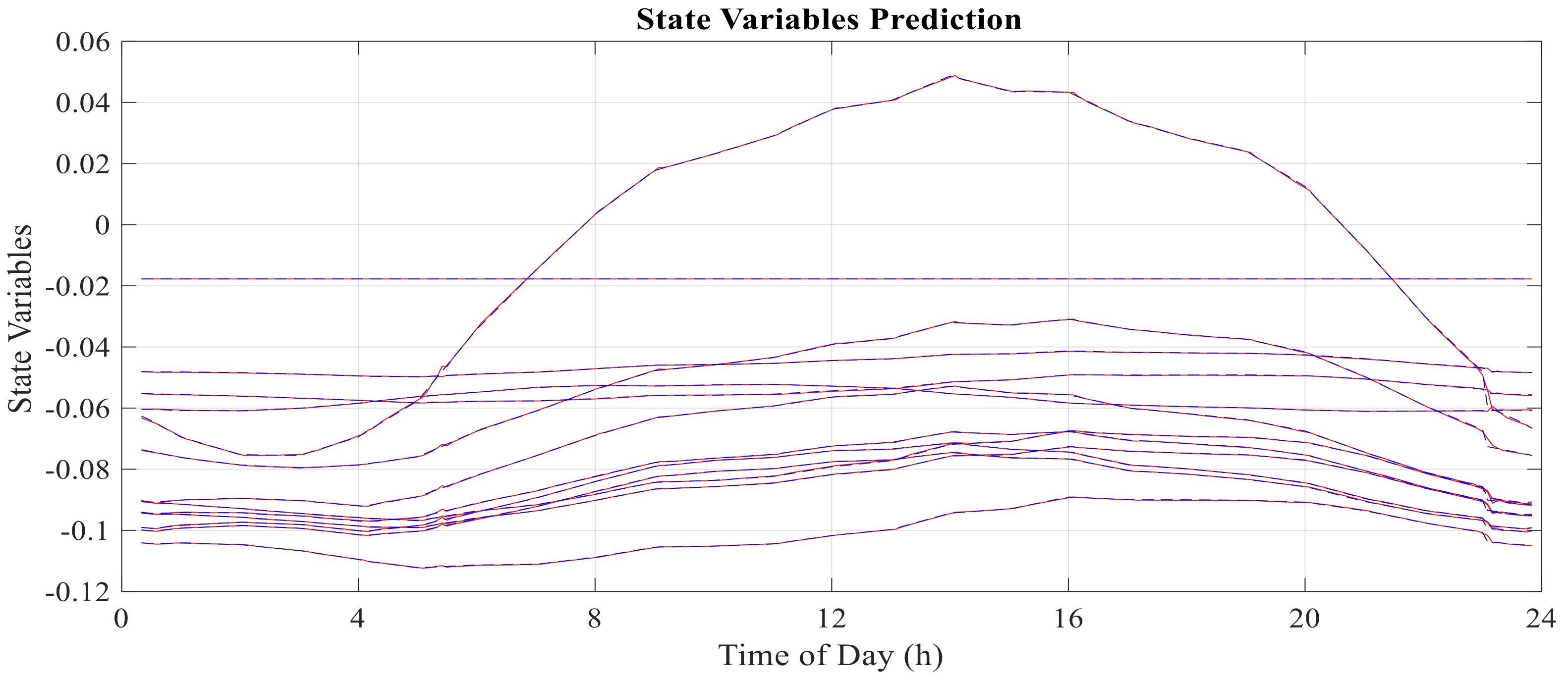
The proposed method is implemented in the IEEE 14-bus standard test system. After having prepared adequate historical data for power system measurements and state variables, an RNARXNN-based model is developed to train, test, and validate the data in order to identify FDIAs on state estimation. According to the results, owing to the correlation between input and feedback variables, the network is trained and tested with great performance and can predict the state variable vector appropriately. The results illustrate the high efficiency of the proposed method for bad data detection of FDIA on state estimation.
The proposed method can be implemented on large scale power systems by dividing the power system into several subsystems and training individual network for each subsystem. This method can decrease the training time duration by keeping the performance of the network as nearly accurate as the results of the primary system.
In future work, the presented method can be extended for AC state estimation by adding reactive power measurements and PMUs to the measurement vector and voltage magnitude to state variables.