Dynamic Modeling of Wind Turbines Based on Estimated Wind Speed under Turbulent Conditions
Abstract
1. Introduction
2. Mathematical Model of Wind Energy System
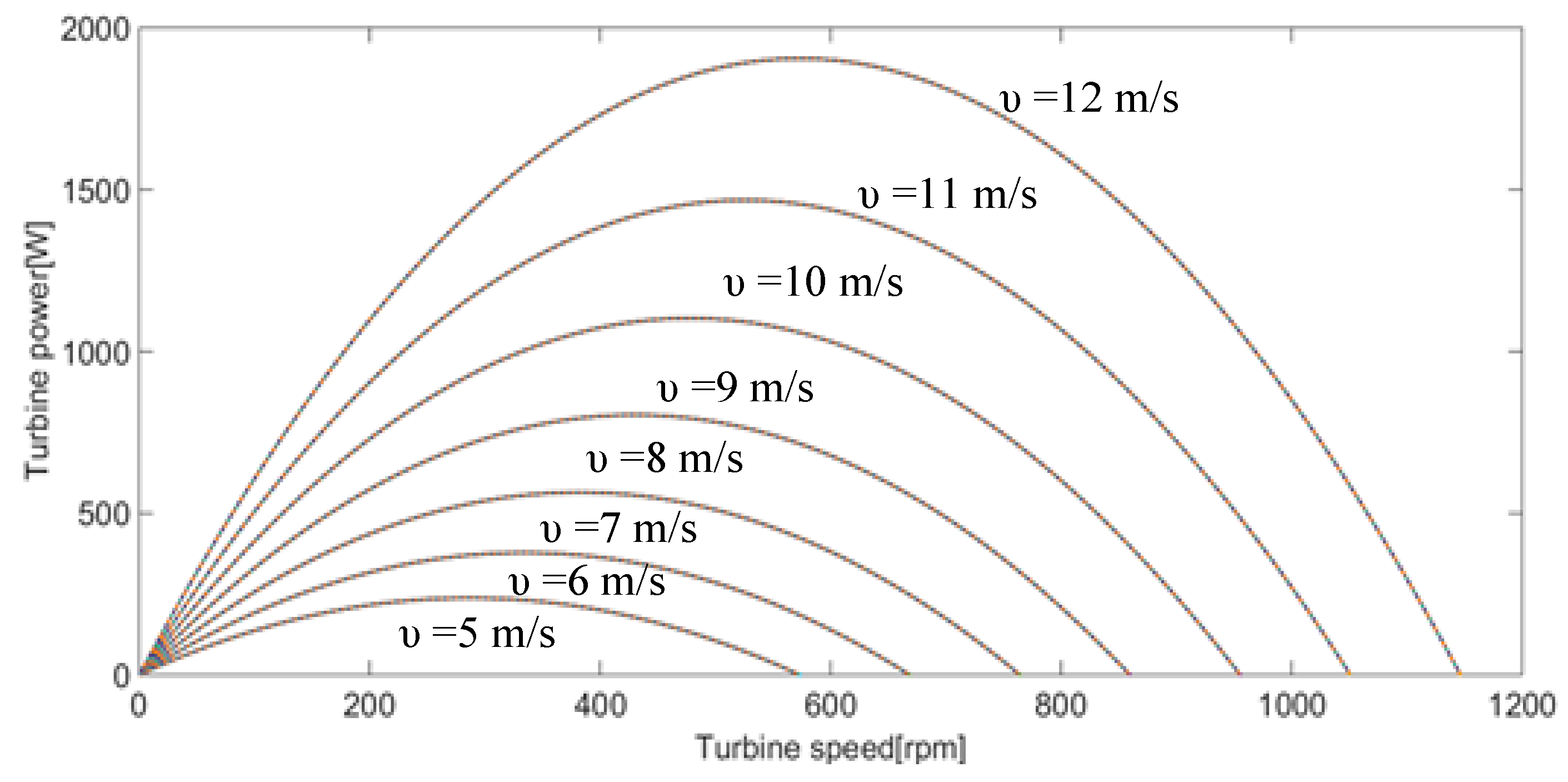
2.1. Wind Turbine Model
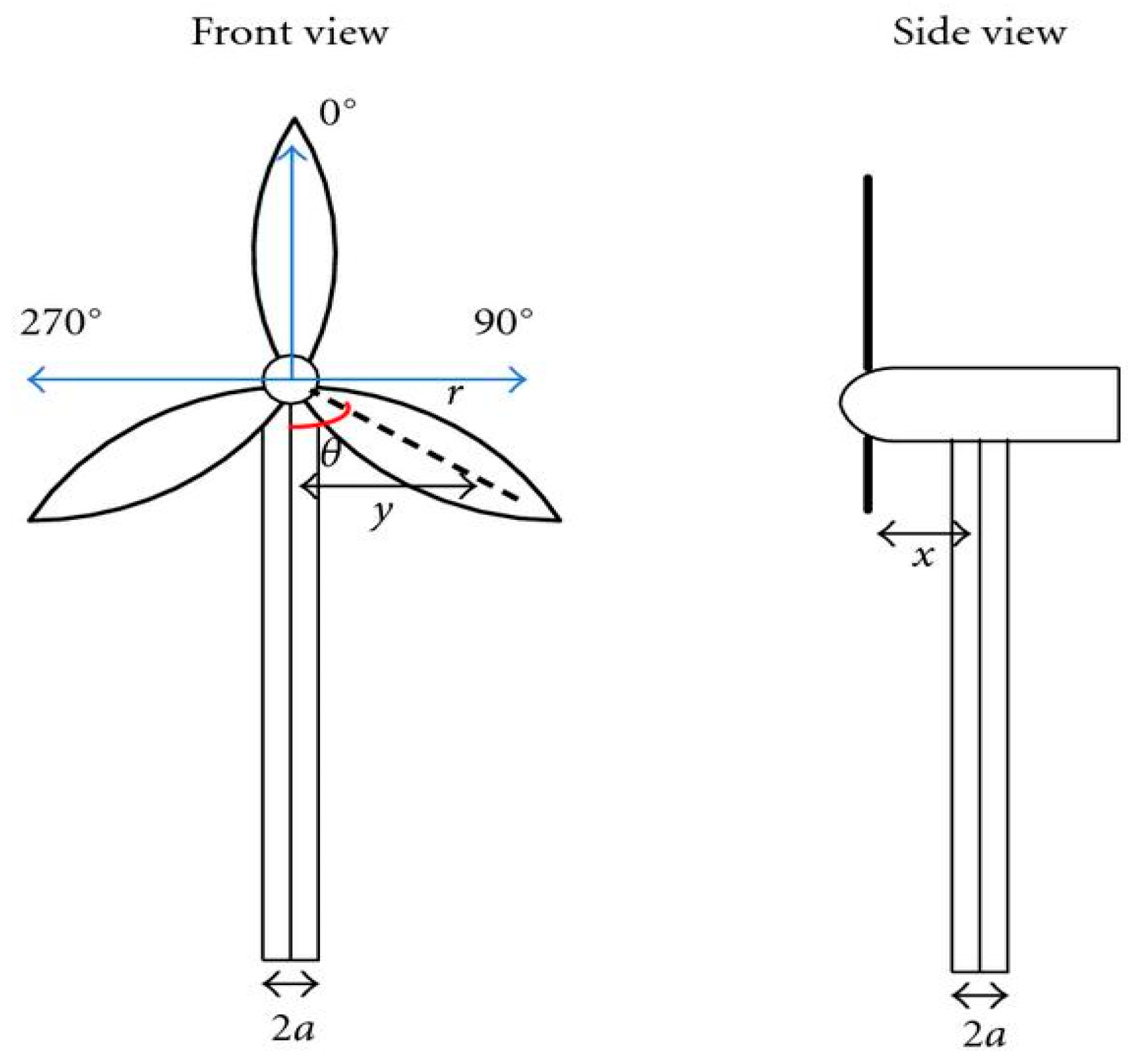
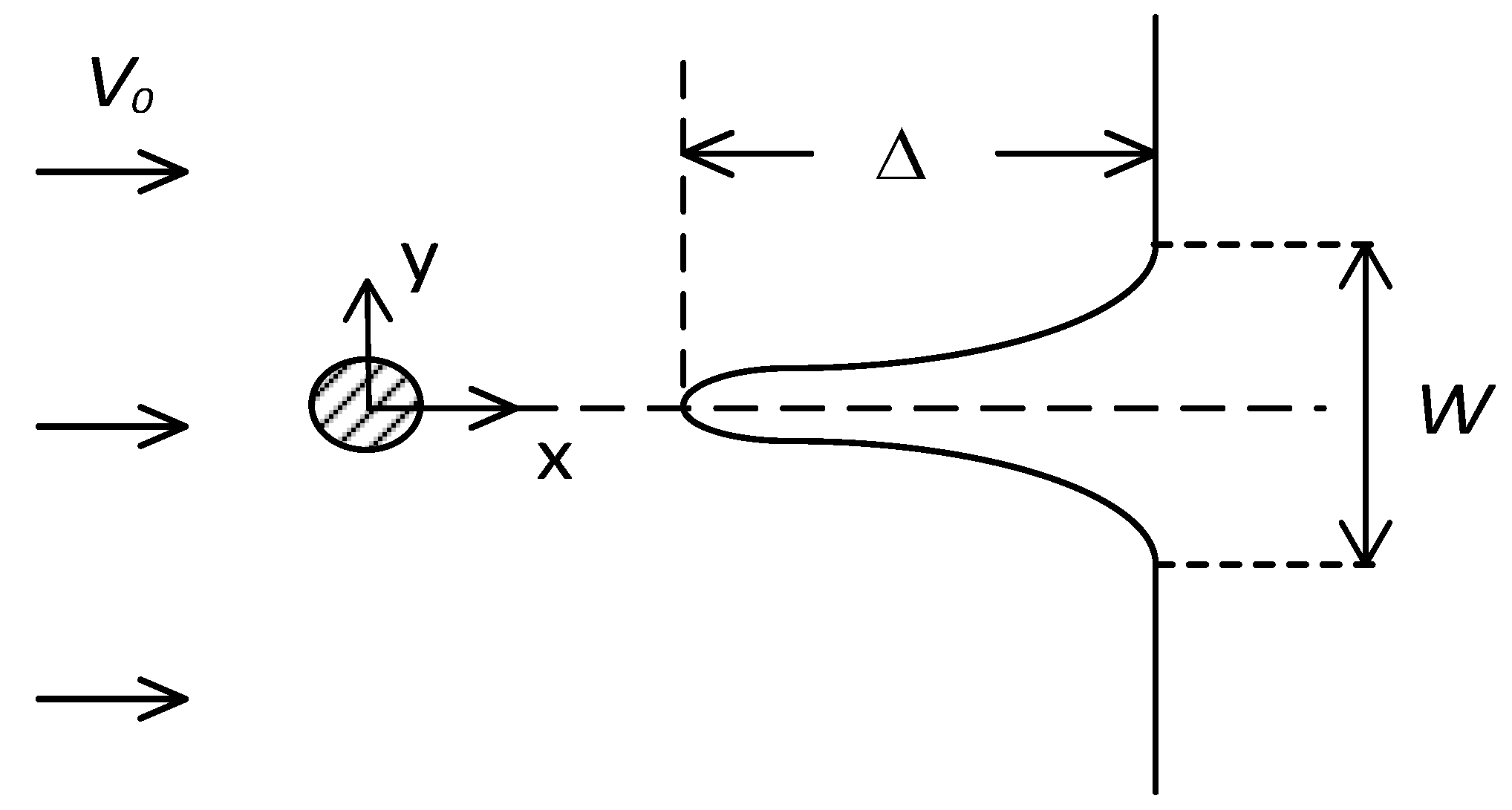
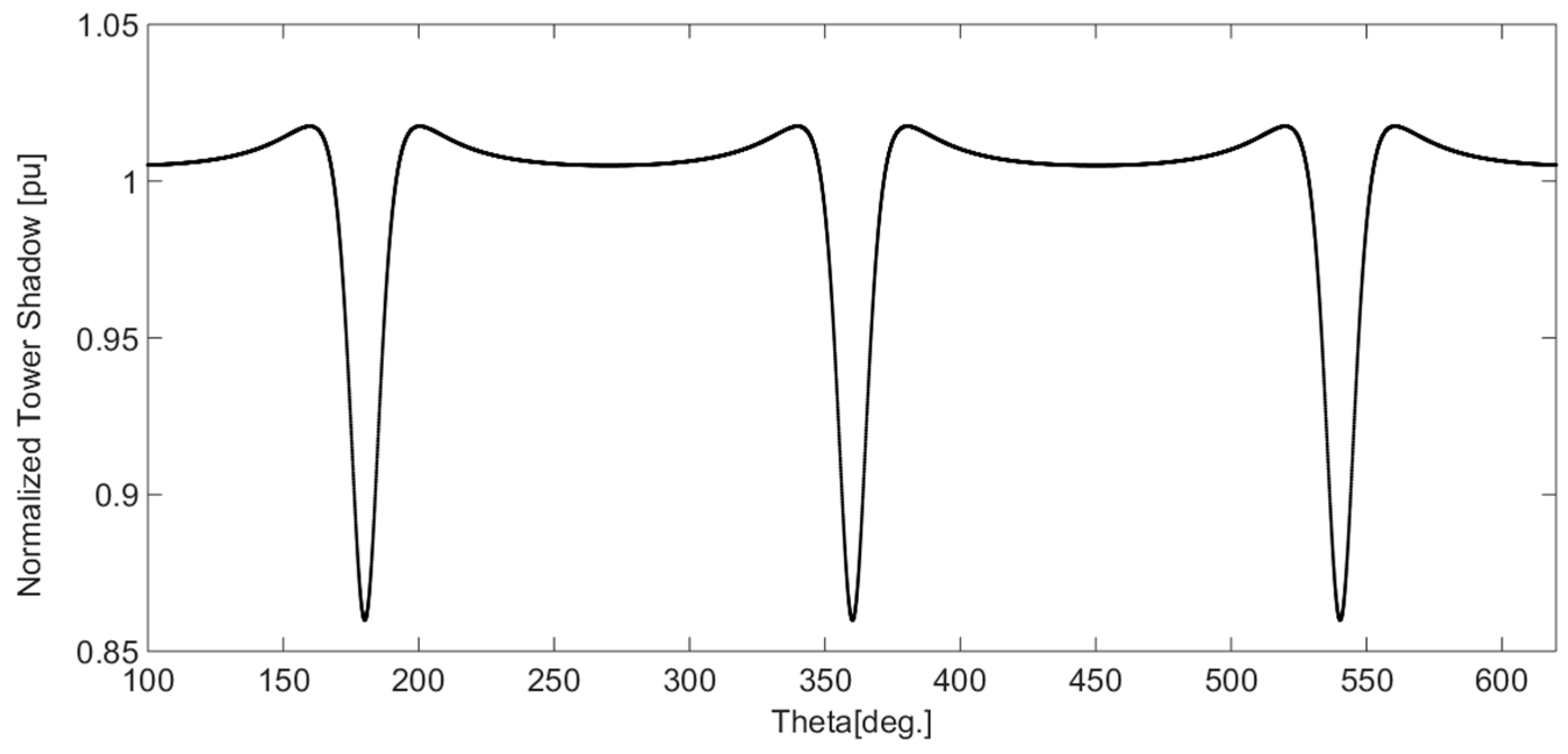
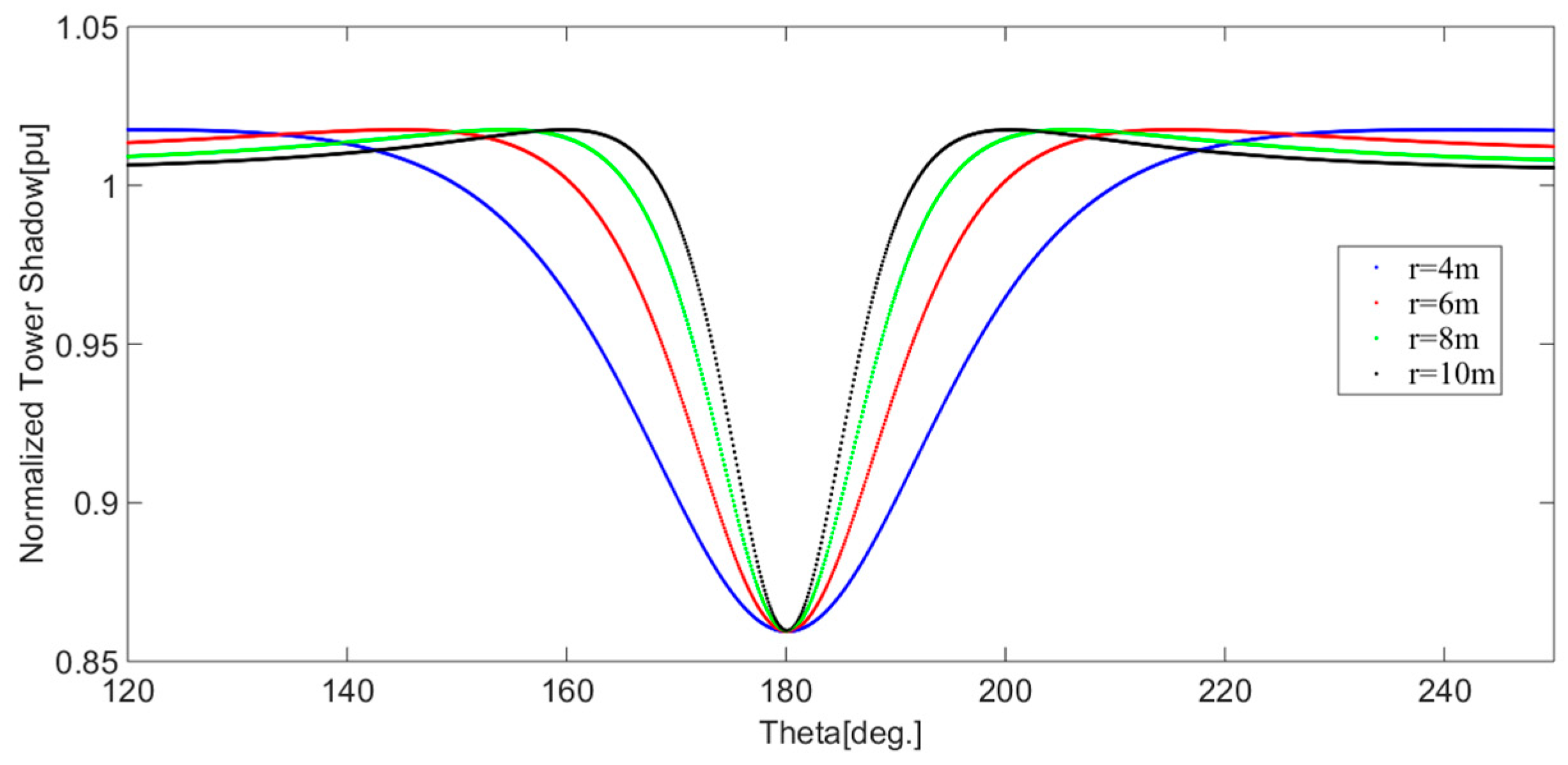
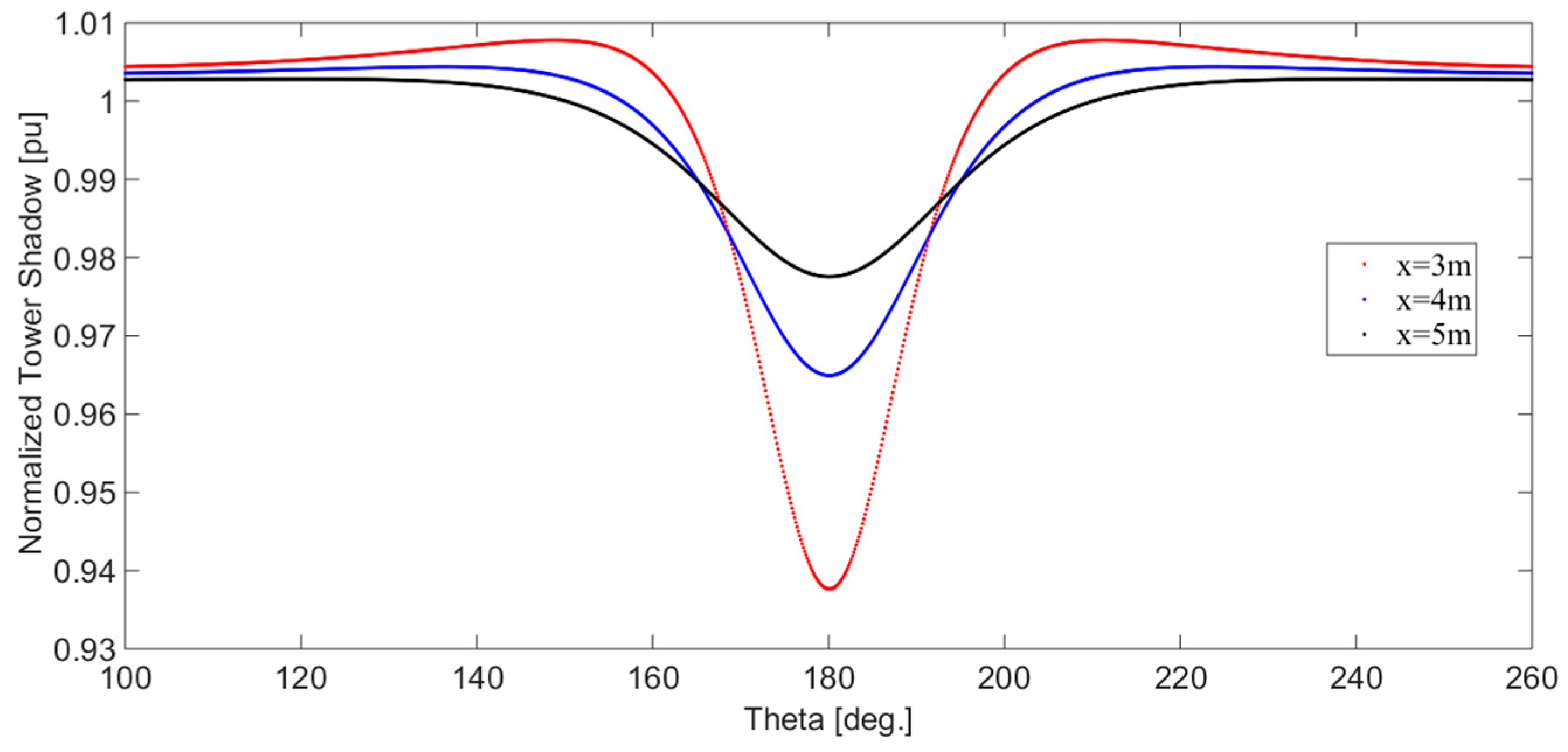
2.2. Wind Shear and Tower Shadow Model
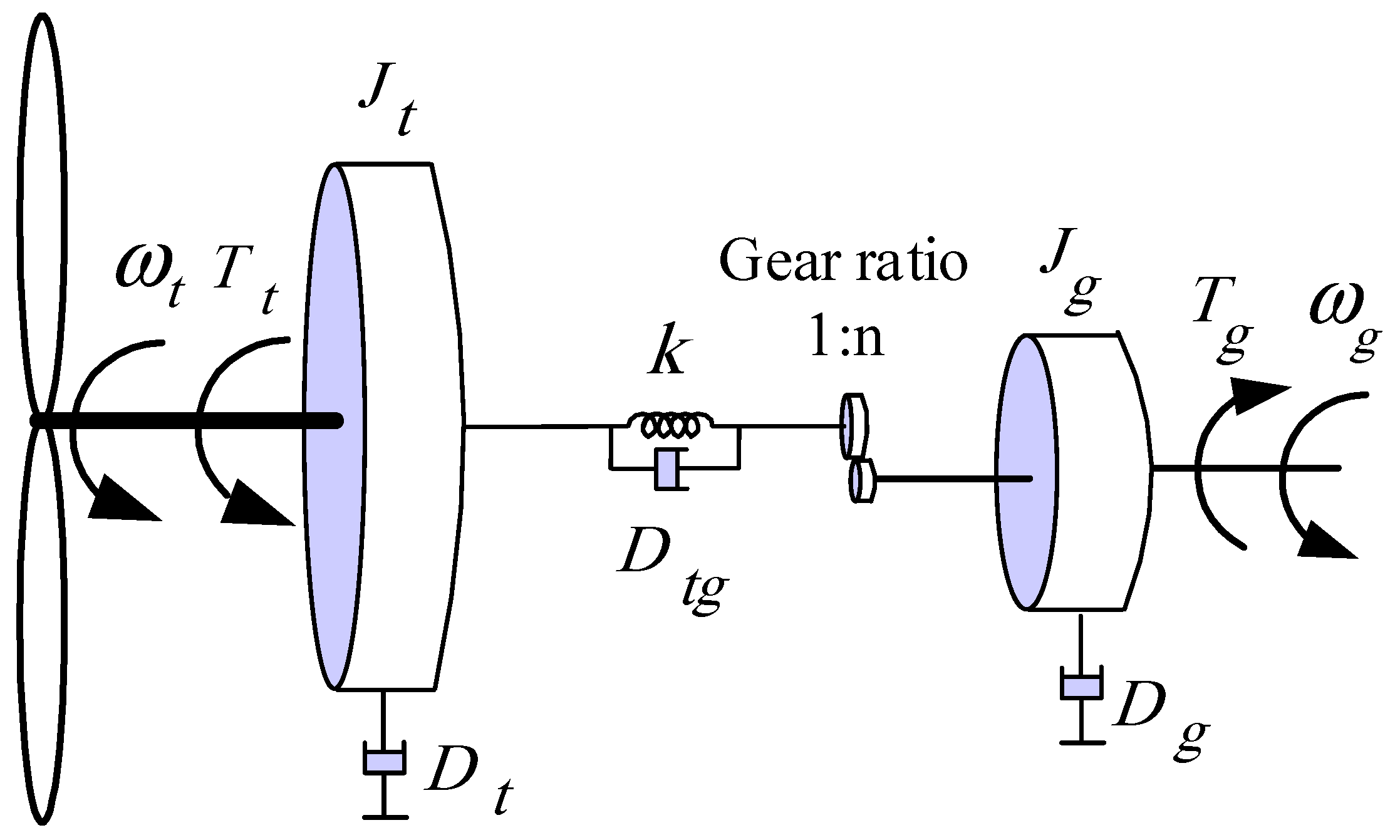
2.3. Dynamic of the Rotating Masses in the Wind Turbine
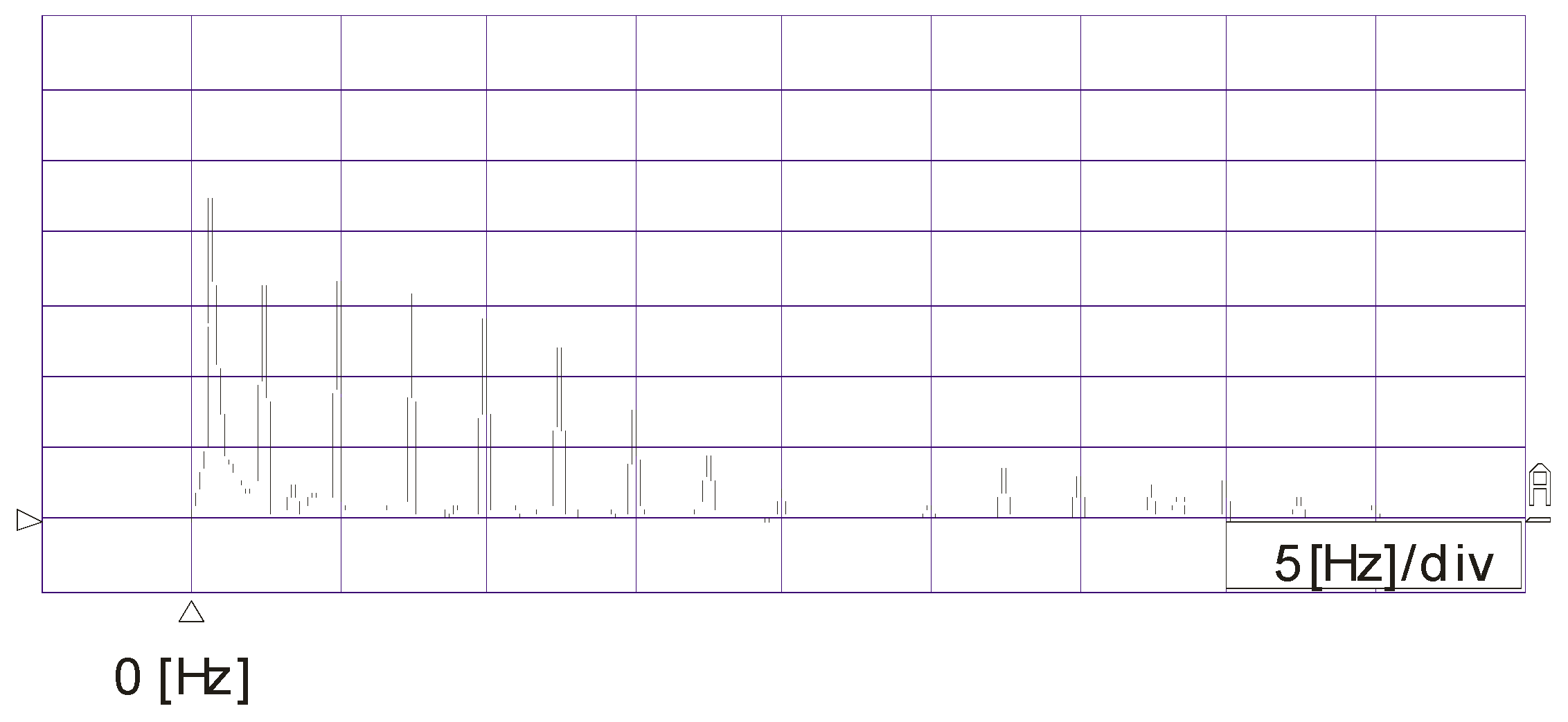
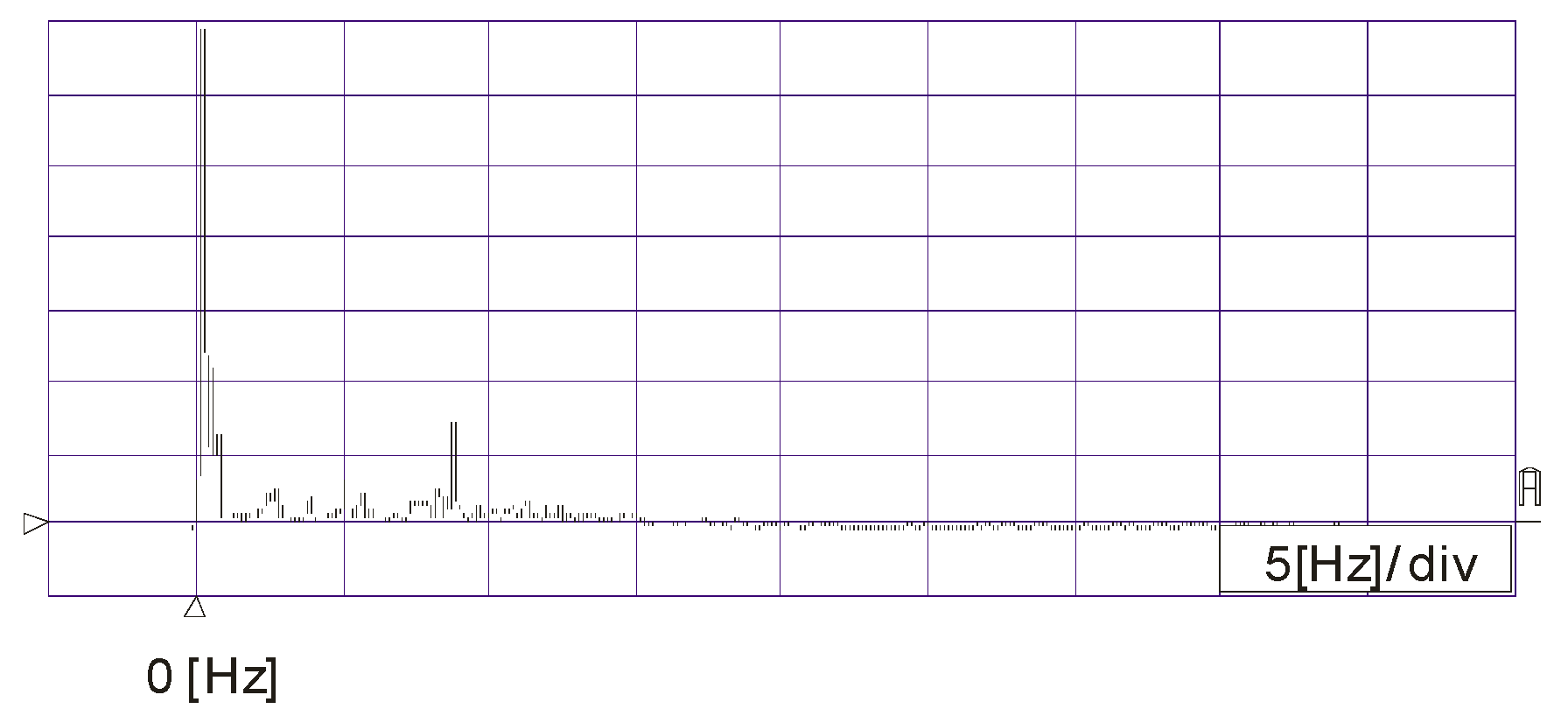
2.4. The Wind Speed Simulator
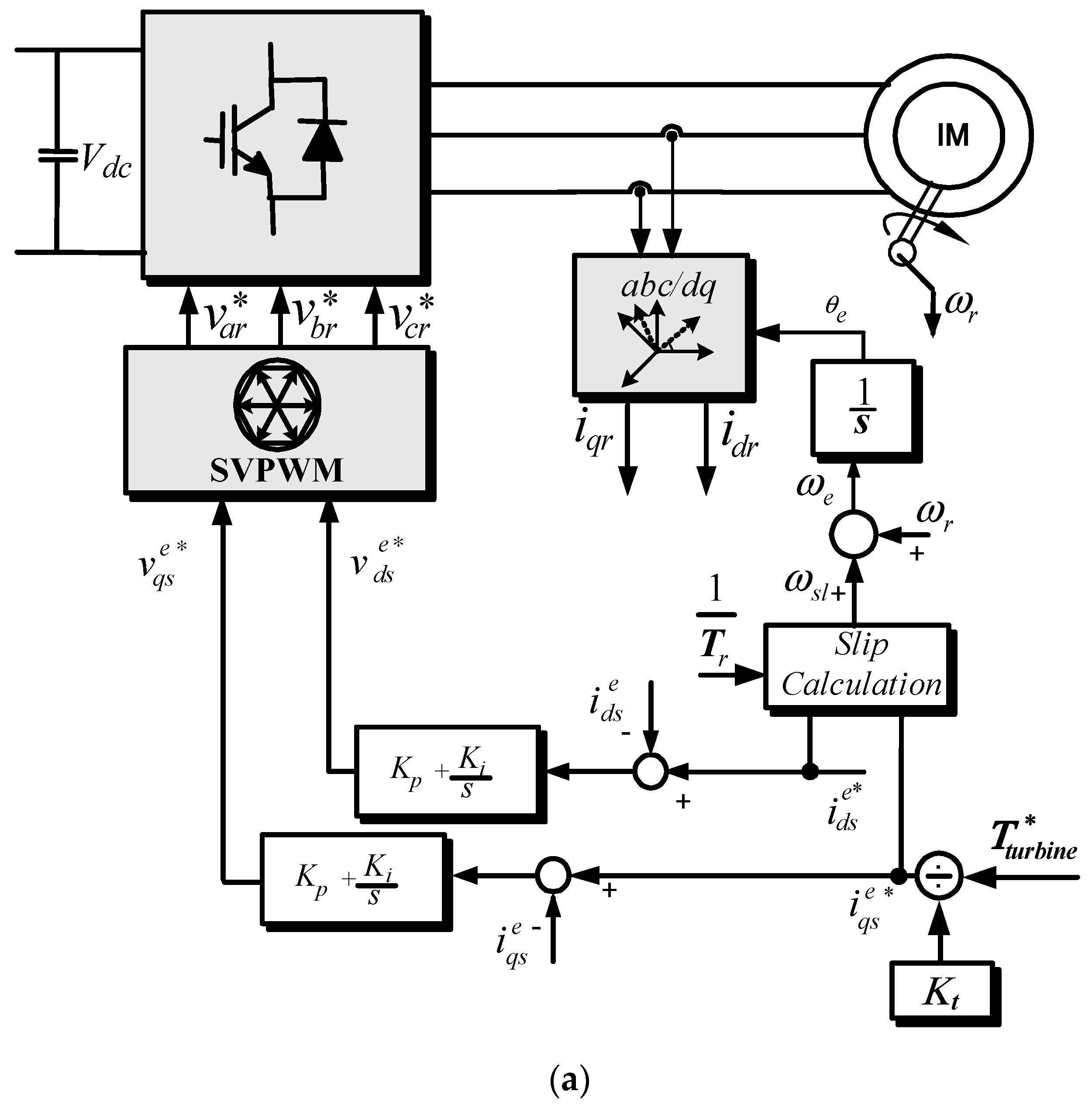
3. Induction Motor Control
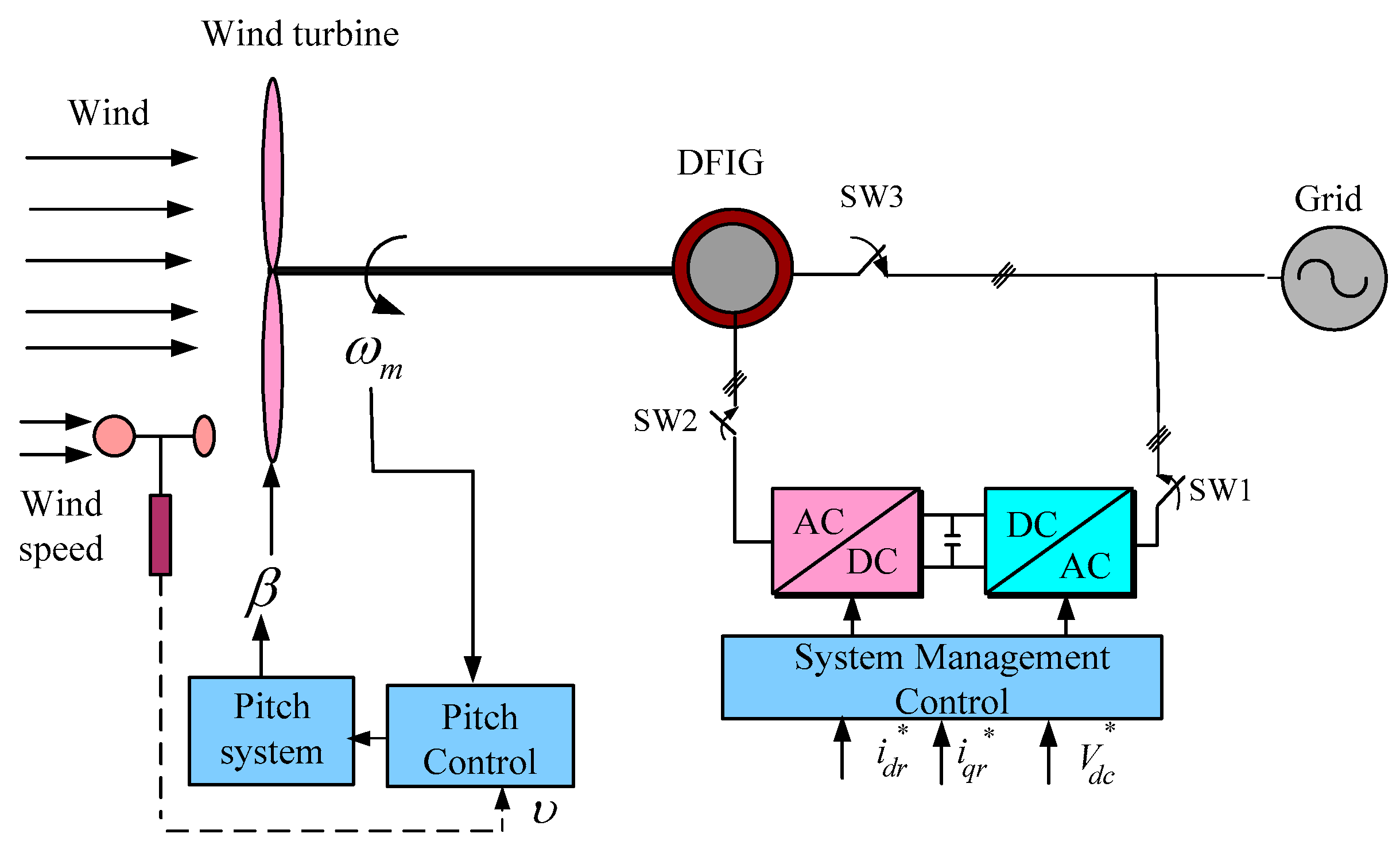
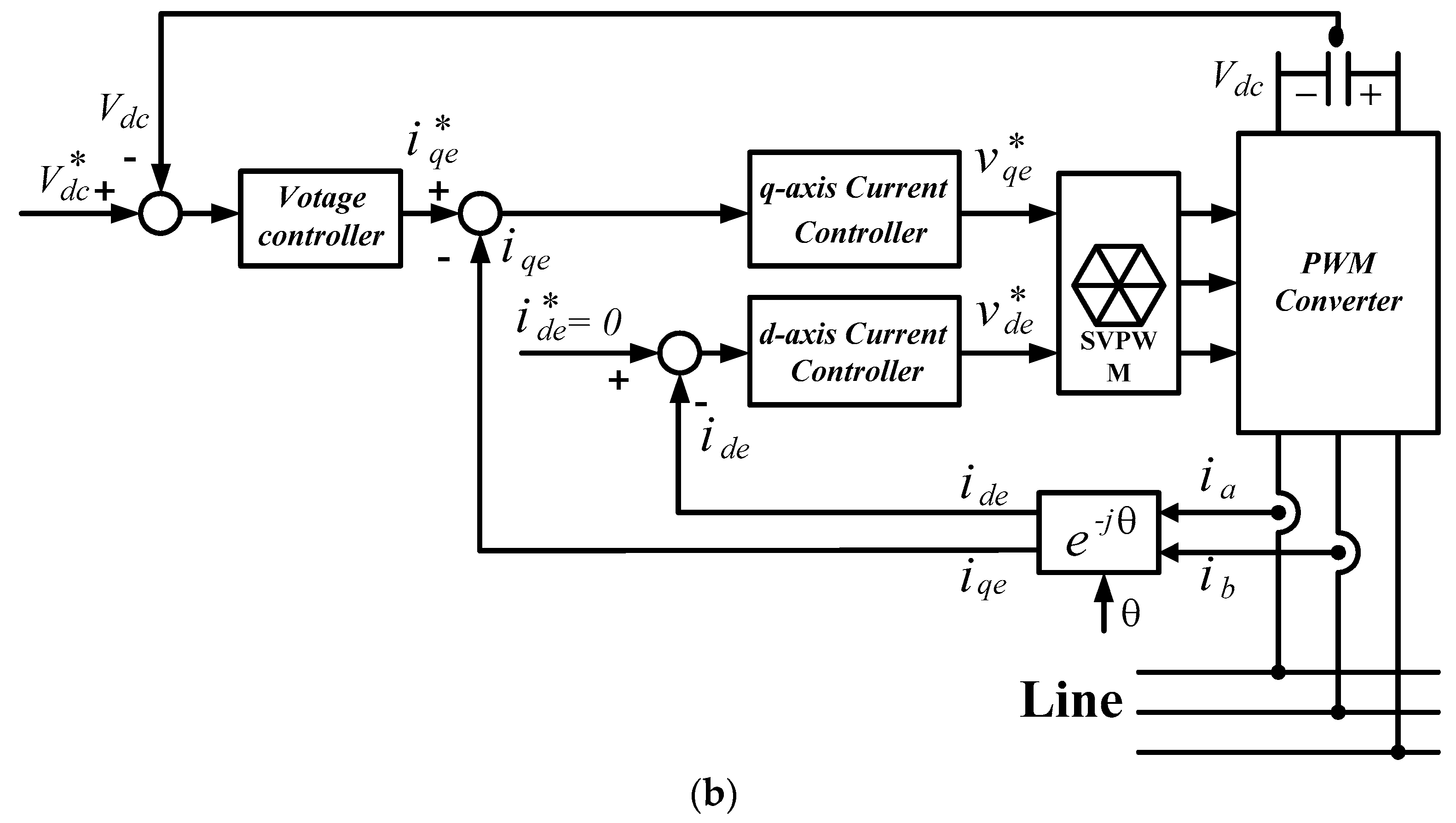
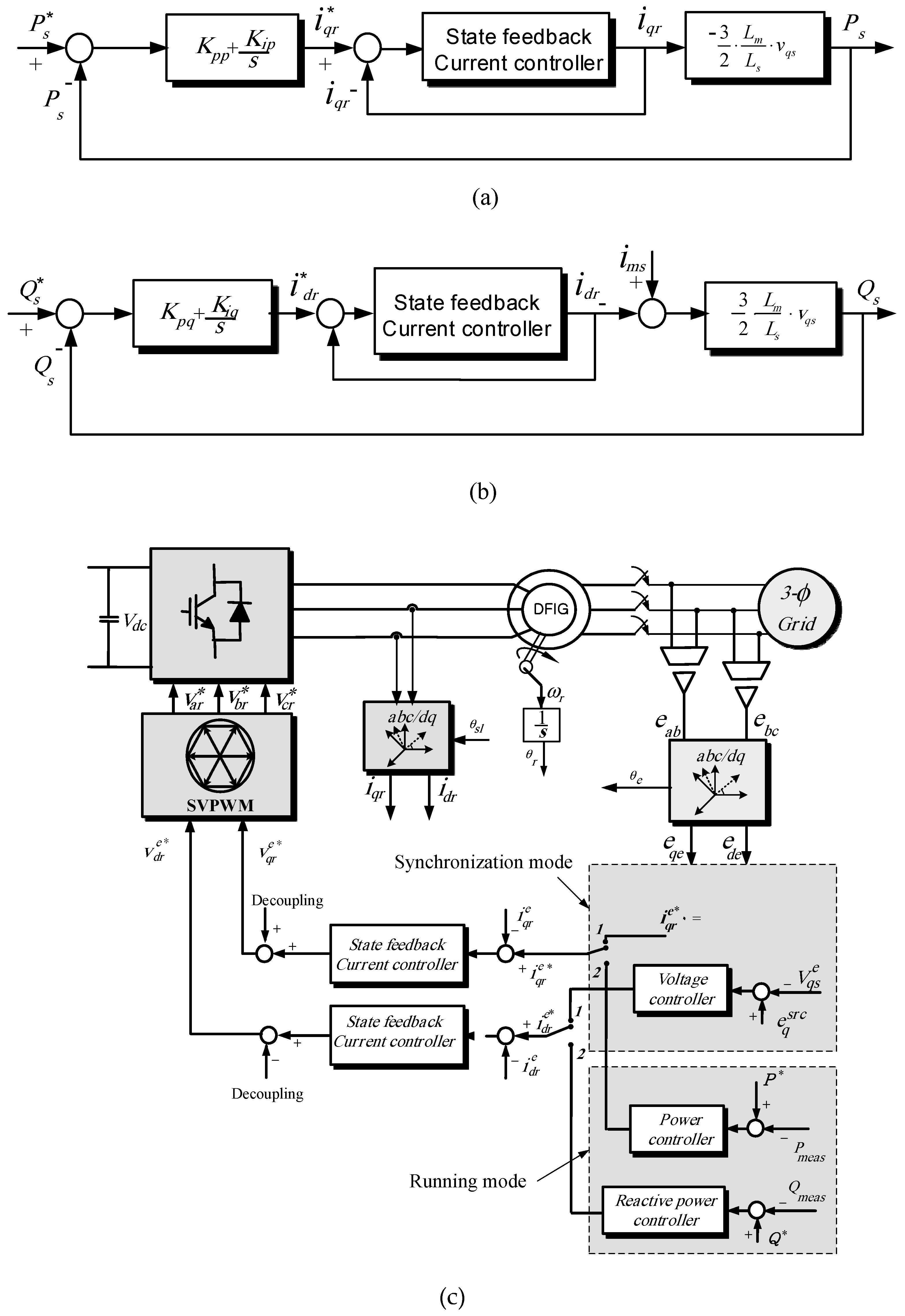
4. Control Scheme of DFIG
5. Wind Speed Estimation
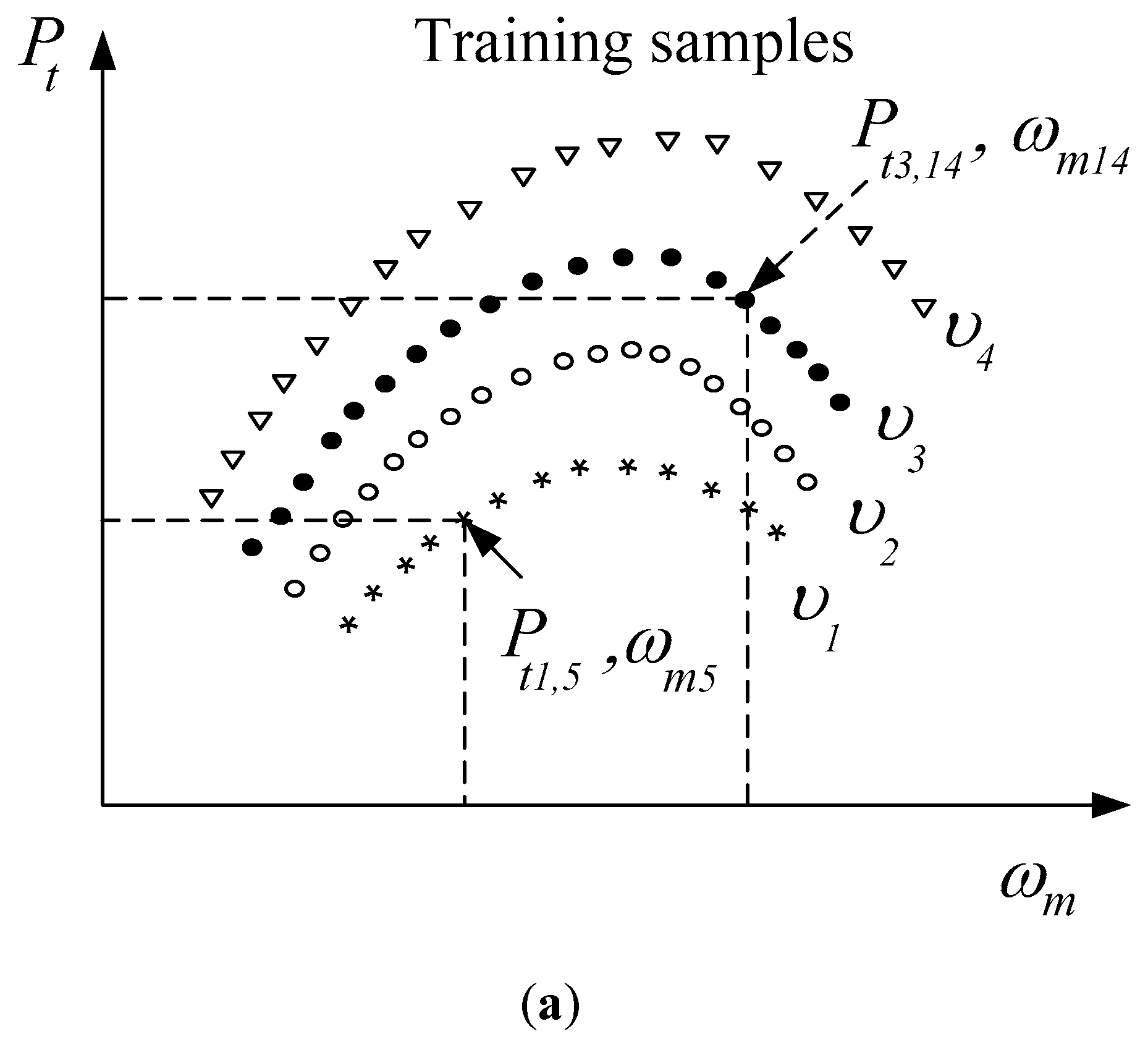
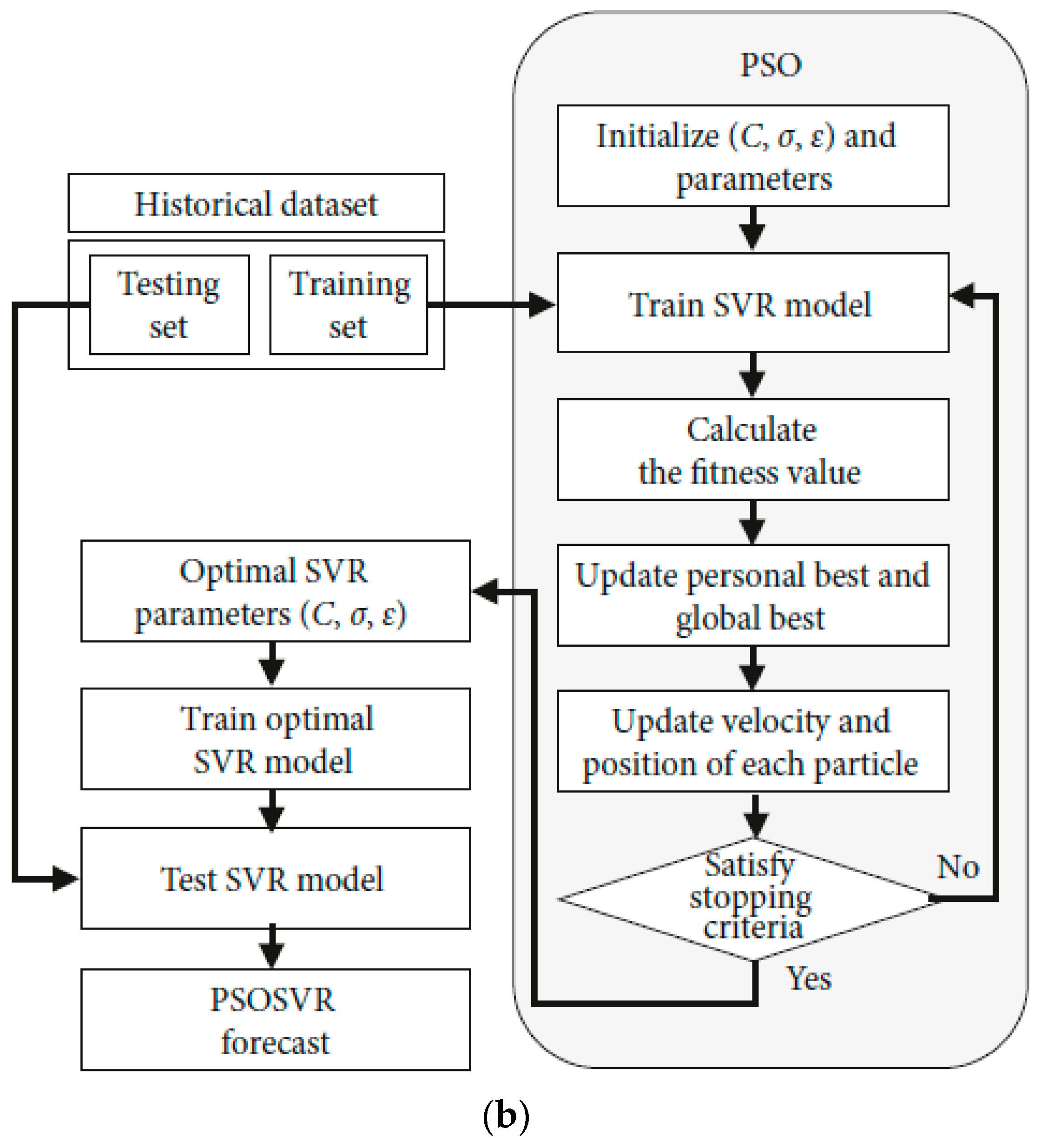
5.1. Support Vector Regression
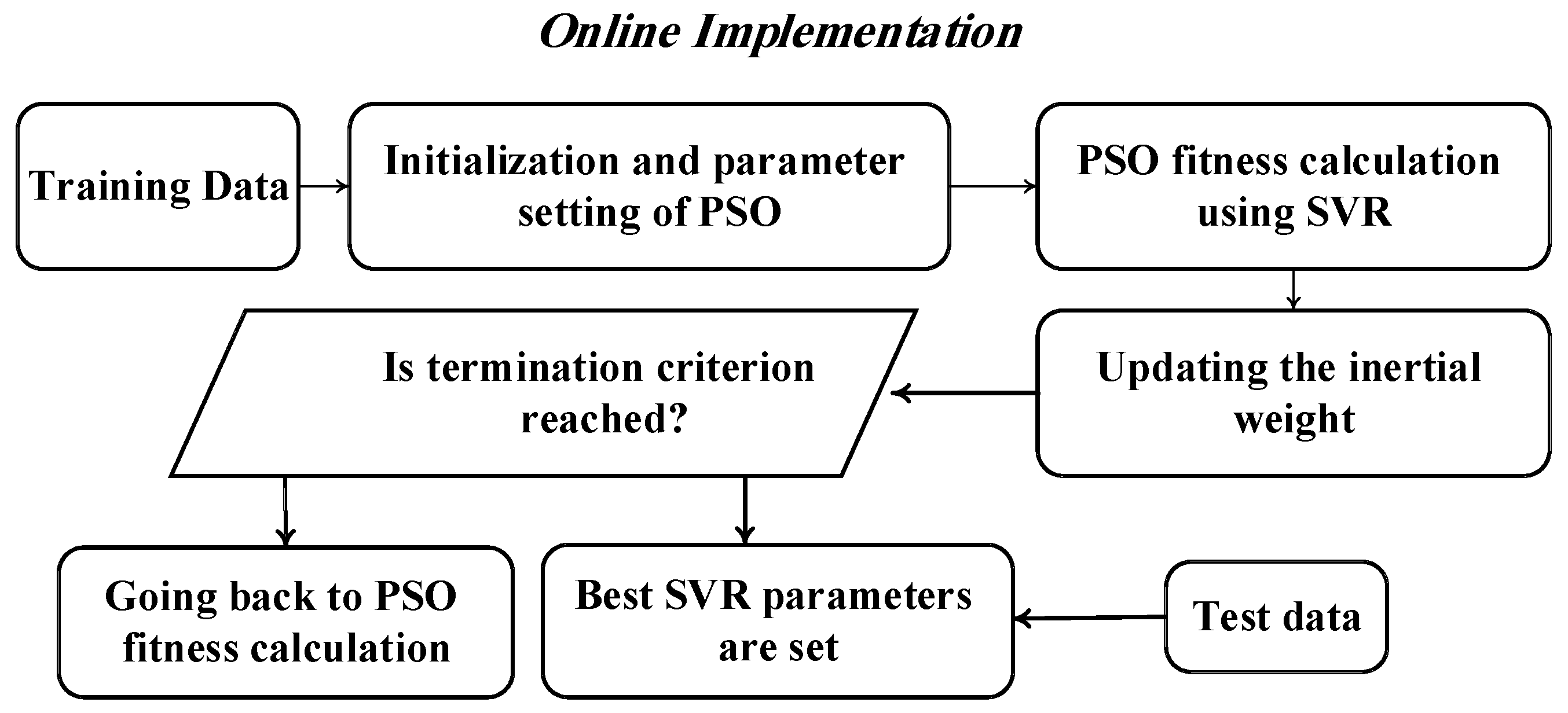
5.2. Particle Swarm Optimization
- Enter original data for estimation, known as the data preparation step;
- Initialize the particles with random velocities and positions, known as particles optimization;
- Perform an offline training process for SVR with training samples assessing each particle fitness value of the PSO for the SVR;
- Update each particle velocity and position until the termination condition is satisfied;
- Construct and retrain the SVR estimation model based on the optimal parameters.
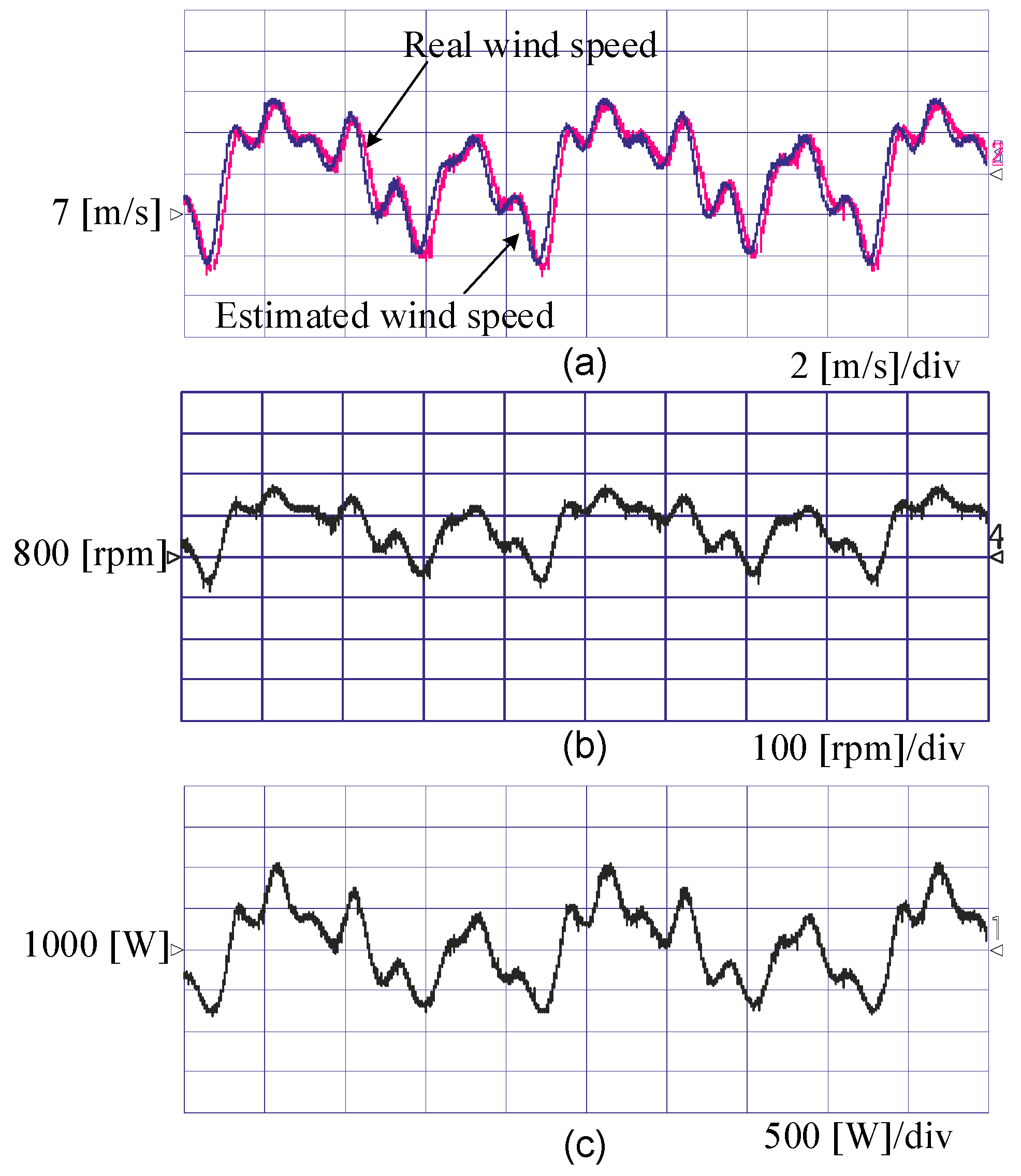
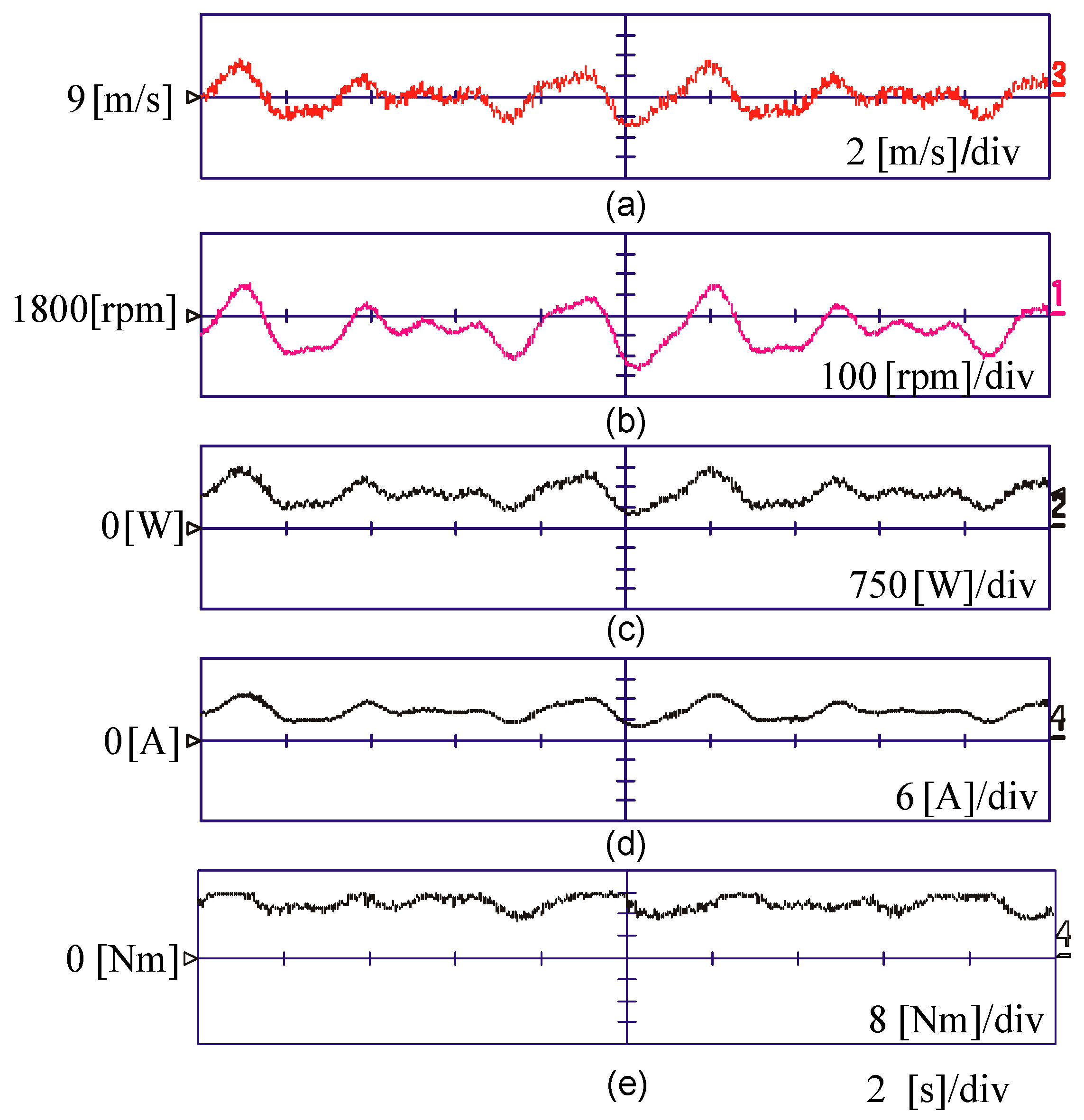
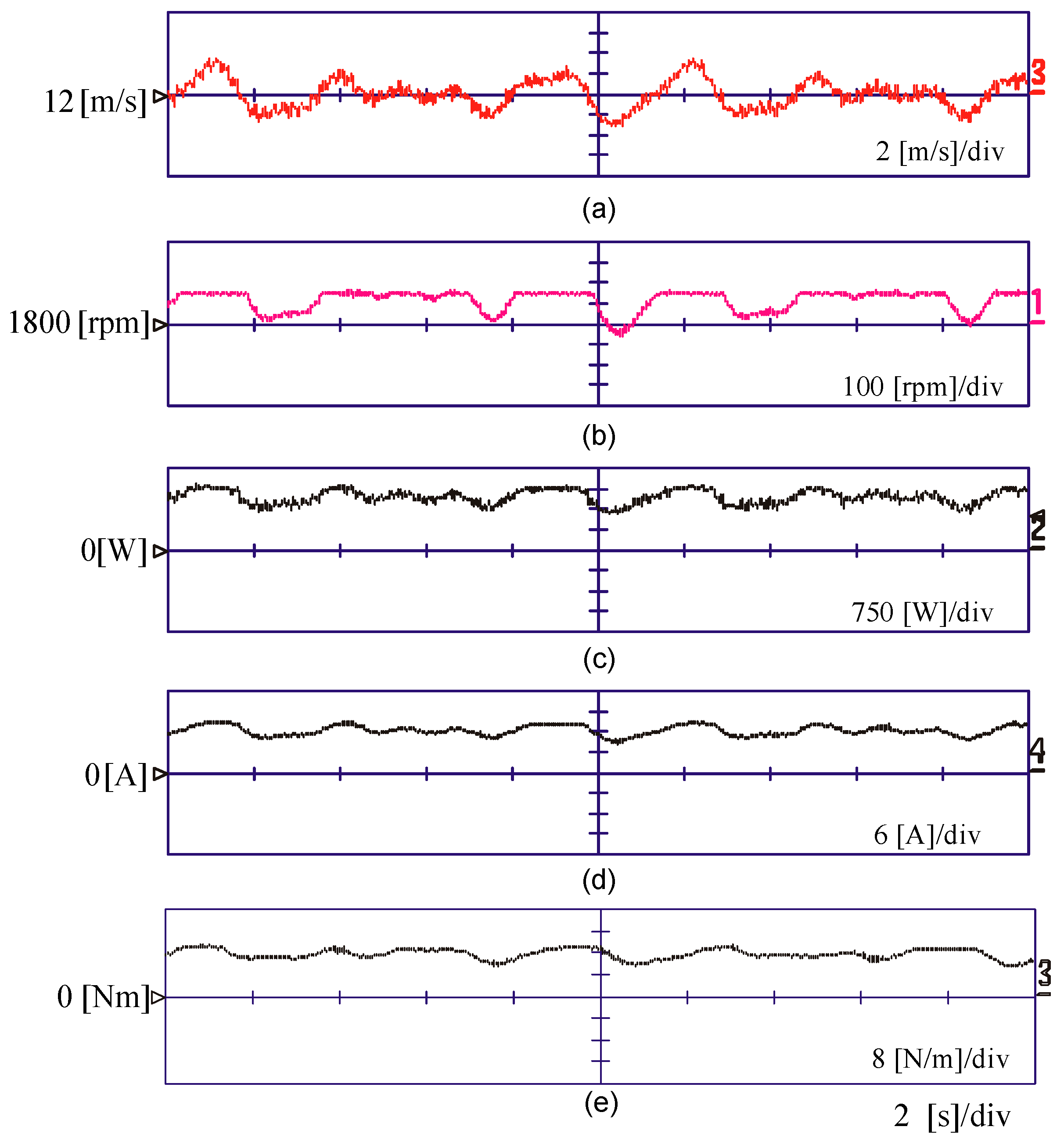
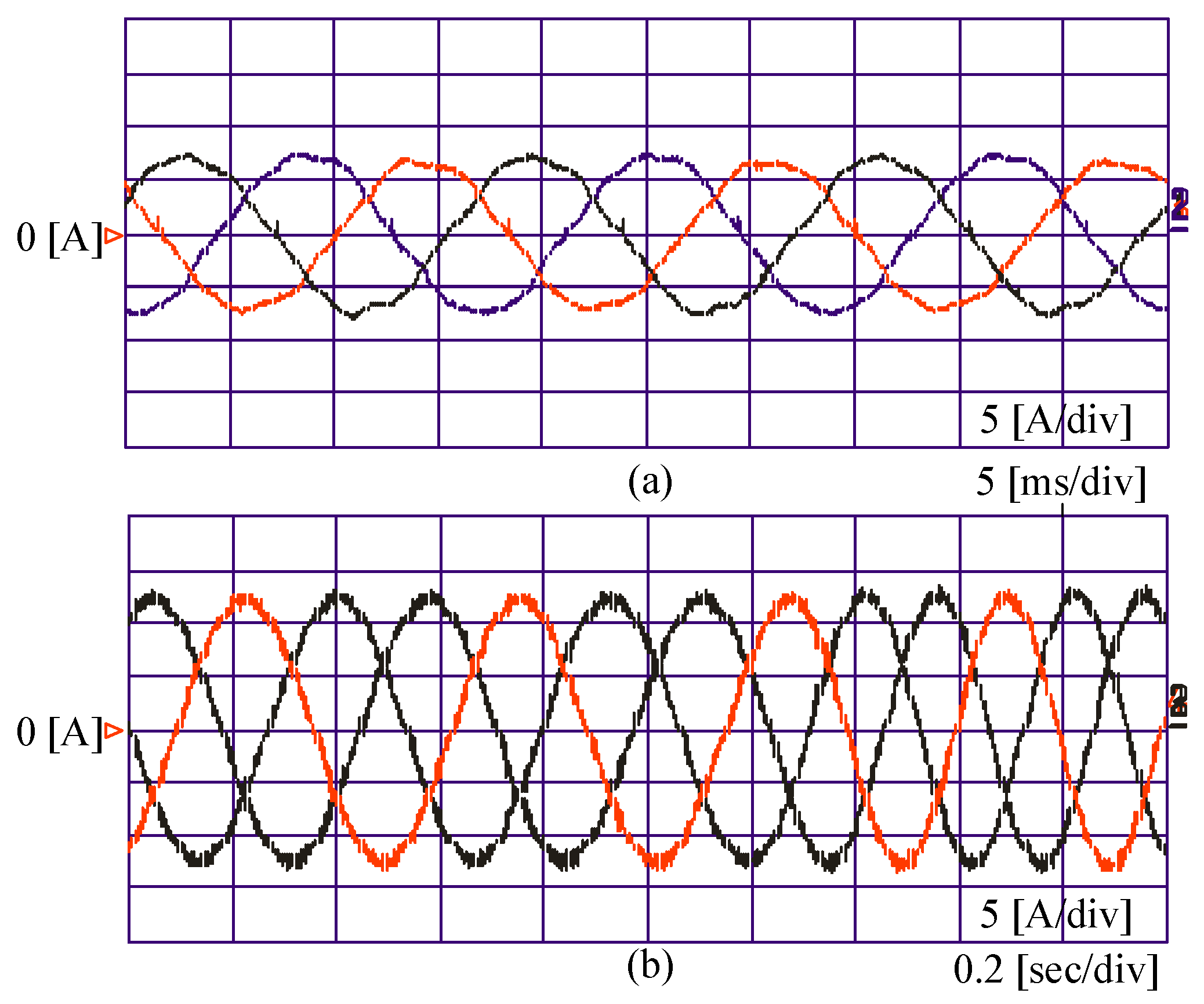
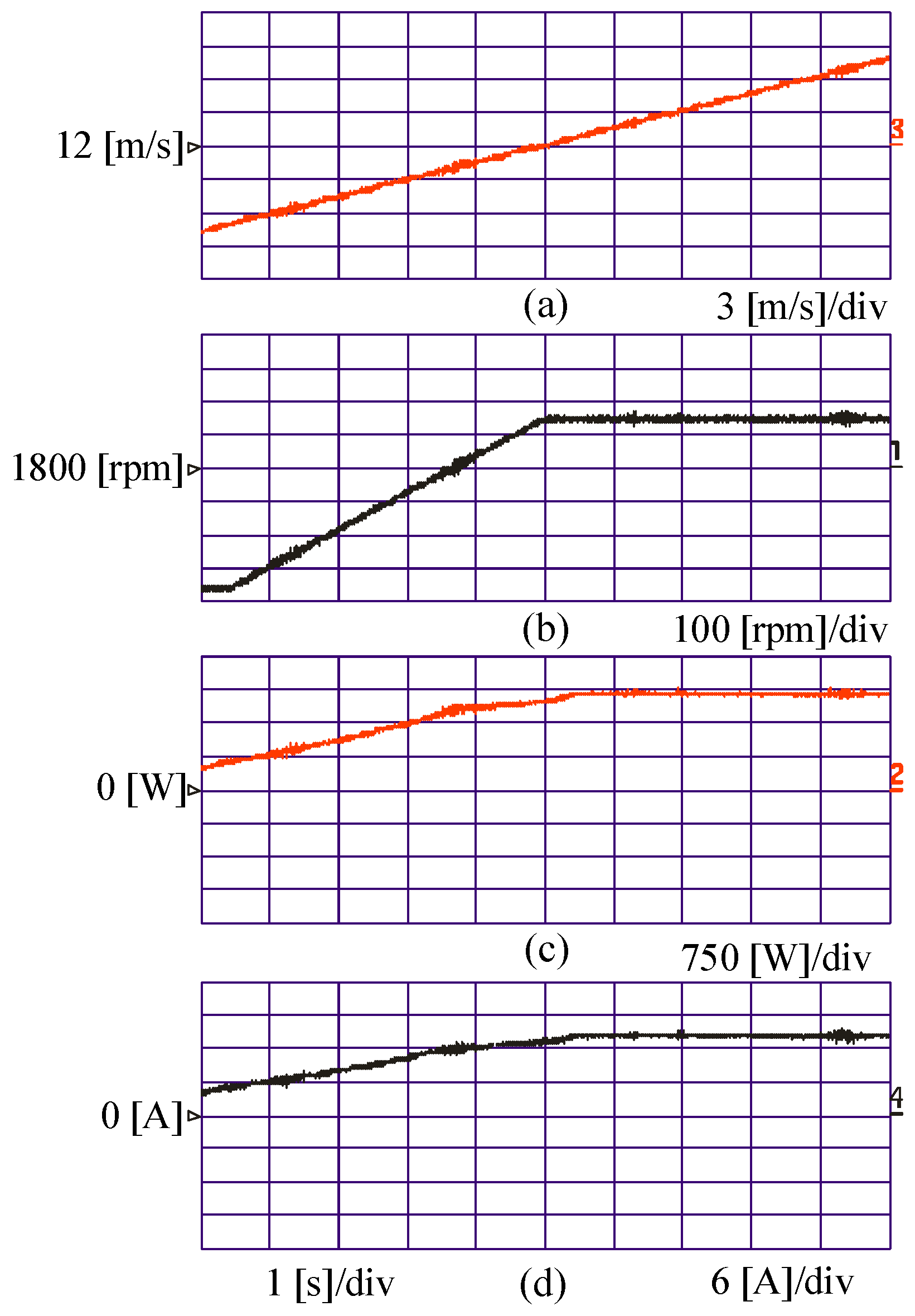
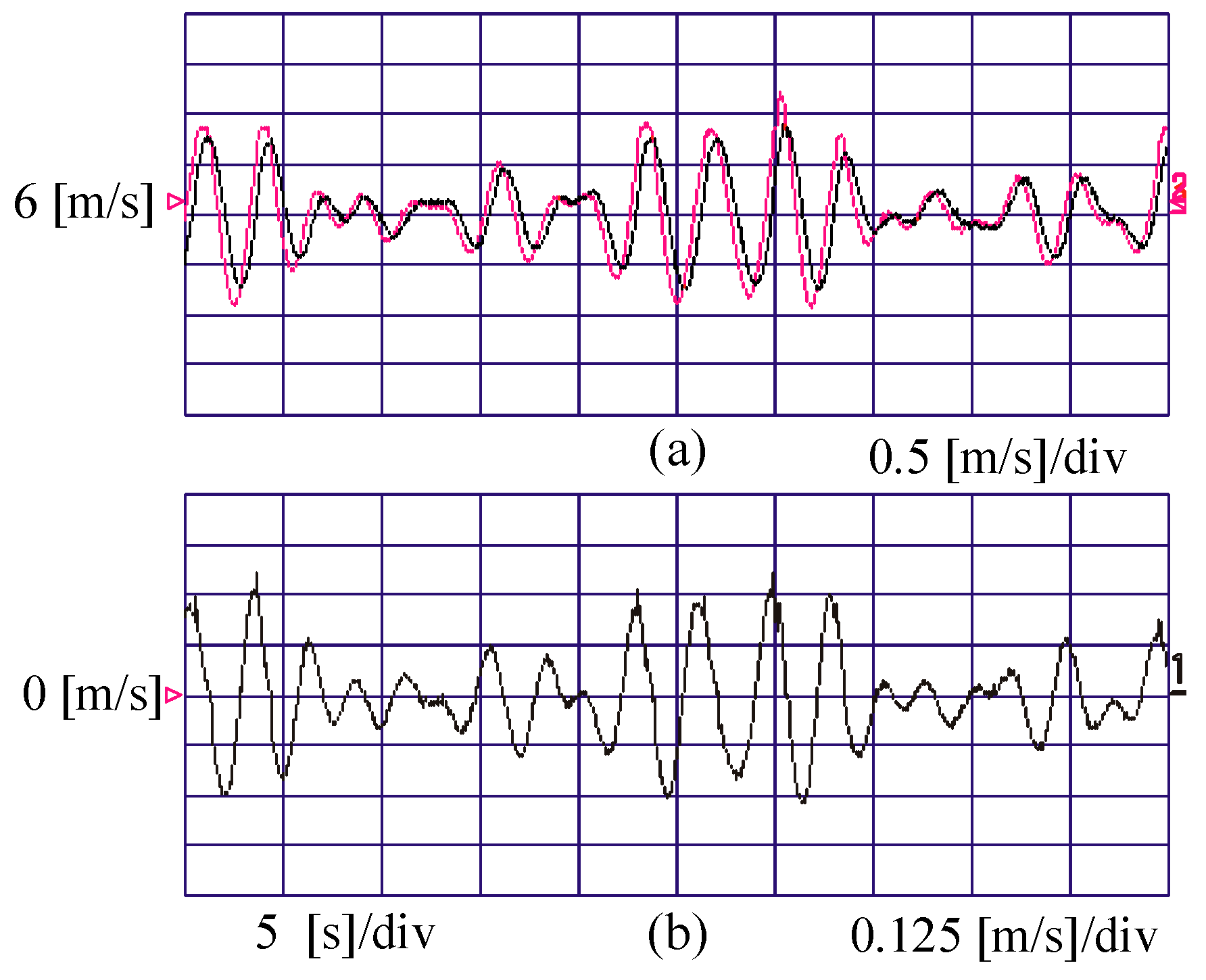
6. Experimental Results
- -
- Region AB, when the wind speed is less than the cut-in speed when the rotational speed is less than the minimum rotational speed for optimum operation.
- -
- Region BC, when the wind speed is higher than the cut-in speed and less than the rated value. The output power is given by .
- -
- Region CD, when the rotational speed approaches to its rated value.
- -
- Region DE, when the wind speed is beyond the limits and the generator output power is controlled to its rated value. The blade pitch controller is activated in this region.
7. Conclusions
- The turbine steady-state characteristics are modeled using the turbine torque equation, which is a function of the wind speed, tip-speed ratio, and blade pitch angle.
- A derivation for the wind shear and tower shadow torque components are obtained as a function of the turbine dimensions and the estimated effective wind speed.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Turbine power | |
| standard air specific density [kg/m3] | |
| power conversion coefficient | |
| pitch angle of turbine blades [degree] | |
| wind speed [m/s] | |
| tip-speed ratio (TSR) | |
| R | blade radius [m] |
| h | corresponding height of point under consideration |
| empirical parameter, which increases with the terrain roughness | |
| z | the elevation above ground |
| H | hub height |
| wind speed at hub height | |
| blade rotational angle | |
| radial distance from the rotor axis | |
| the wind shear disturbance | |
| a | the tower radius |
| x | the distance from the blade origin to the tower midline |
| y | the lateral distance of the blade from the tower midline |
| Vts | the tower shadow |
| Tt | turbine torque |
| Tts | disturbance in torque due to tower shadow |
| Tws | disturbance in torque due to wind shear |
| JT | moment of inertia of the wind turbine |
| JG | moment of inertia of the generator |
| k | stiffness of coupling shaft |
| D | coupling shaft damping |
| n | transmission ratio of the gearbox |
| Pg | the generator power |
| the turbine speed | |
| J | the system moment of inertia |
| instantaneous wind speed | |
| effective average value of wind speed | |
| N | harmonic samples order |
| harmonic frequency | |
| harmonic amplitude | |
| turbulence intensity | |
| Lu | turbulence length |
| , | the d-q voltages in the stator |
| , | the d-q currents in the stator |
| the frequency in the rotor | |
| , | the d-q flux linkages in the stator side |
| equivalent magnetizing inductance | |
| equivalent stator self-inductance | |
| equivalent rotor self-inductance | |
| equivalent d-q flux linkage in the stator | |
| equivalent rotor d -q flux linkage | |
| magnetizing d-axis currents in the stator and rotor | |
| the torque constant | |
| Ps, Qs | Stator active and reactive power |
| the d-q voltages in the rotor | |
| rotor equivalent resistance | |
| slip angular frequency | |
| the stator resistance | |
| the synchronous frame angle | |
| the SVR weight vector | |
| the bias | |
| the allowable error | |
| the penalty factor | |
| , | Lagrange multipliers. |
| and is the velocity weight at iteration . | |
| social learning factor | |
| , | cognition factor are random numbers in the range |
Appendix A
| Parameters | Value |
|---|---|
| Blade radius | 0.95 m |
| Max. power conv. coeff. | 0.45 |
| Optimal tip-speed ratio | 7 |
| Cut-in speed | 4 m/s |
| Rated wind speed | 13 m/s |
| Parameters | Value |
|---|---|
| Stator resistance | 0.93 Ω |
| Rotor resistance | 0.533 Ω |
| Iron loss resistance | 190 Ω |
| Stator leakage inductance | 0.003 H |
| Rotor leakage inductance | 0.003 H |
| Mutual inductance | 0.076 H |
References
- Gan, L.K.; Shek, J.K.H.; Mueller, M.A. Modeling and characterization of downwind tower shadow effects using a wind turbine emulator. IEEE Trans. Ind. Electron. 2017, 64, 7087–7097. [Google Scholar] [CrossRef]
- de Kooning, J.D.M.; Vandoorn, T.L.; van de Vyver, J.; Meersman, B.; Vandevelde, L. Shaft speed ripples in wind turbines caused by tower shadow and wind shear. IET Renew. Power Gener. 2014, 8, 195–202. [Google Scholar] [CrossRef]
- Weihao, H.; Chi, S.; Zhe, C. Impact of wind shear and tower shadow effects on power system with large-scale wind power penetration. In Proceedings of the IECON 2011 37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, Australia, 7–10 November 2011; pp. 878–883. [Google Scholar]
- Ahshan, R.; Iqbal, M.T.; Mann, G.K.I. Controller for a small induction generator-based wind turbine. Appl. Engery 2008, 85, 218–227. [Google Scholar] [CrossRef]
- Martinez, F.; Herrero, L.C.; Pablo, S.D. Open-loop wind turbine emulator. Renew. Energy 2014, 63, 212–221. [Google Scholar] [CrossRef]
- Kojabadi, H.M.; Chang, L.; Boutot, T. Development of a novel wind turbine simulator for wind energy conversion systems using an inverter-controlled induction motor. IEEE Trans. Energy Convers. 2004, 19, 547–552. [Google Scholar] [CrossRef]
- Mihet-Popa, L.; Blaabjerg, F.; Boldea, I. Wind turbine generator modeling and simulation where rotational speed is the controlled variable. IEEE Trans. Ind. Appl. 2004, 40, 3–10. [Google Scholar] [CrossRef]
- Monfared, M.; Kojabadi, H.M.; Rastegar, H. Static and dynamic wind turbine simulator using a converter controlled DC motor. Renew. Energy 2008, 33, 906–913. [Google Scholar] [CrossRef]
- Sajadi, A.; Rosłaniec, Ł.; Kłos, M. An emulator for fixed pitch wind turbine studies. Renew. Energy 2016, 87, 391–402. [Google Scholar] [CrossRef]
- Hughes, F.M.; Anaya-Lara, O.; Ramtharan, G. Influence of tower shadow and wind turbulence on the performance of power system stabilizers for DFIG-based wind farms. IEEE Trans. Energy Convers. 2008, 23, 519–528. [Google Scholar] [CrossRef]
- Wan, S.; Cheng, L.; Sheng, X. Effects of yaw error on wind turbine running characteristics based on the equivalent wind speed model. Energies 2015, 8, 6286–6301. [Google Scholar] [CrossRef]
- Tan, J.; Hu, W.; Wang, X. Effect of tower shadow and wind shear in a wind farm on AC tie-line power oscillations of interconnected power systems. Energies 2013, 6, 6352–6372. [Google Scholar] [CrossRef]
- Shamshirband, S.; Petkovic, D.; Anuar, N.B.; Kiah, M.L.M.; Akib, S.; Gani, A.; Cojbasic, Z.; Nikolic, V. Sensorless estimation of wind speed by adaptive neuro-fuzzy methodology. Int. J. Electr. Power Energy Syst. 2014, 62, 490–495. [Google Scholar] [CrossRef]
- Mohandes, M.; Rehman, S.; Rahman, S. Estimation of wind speed profile using adaptive neuro-fuzzy inference system (ANS). Appl. Energy 2011, 88, 4024–4032. [Google Scholar] [CrossRef]
- Li, H.; Shi, K.; McLaren, P. Neural-network-based sensorless maximum wind energy capture with compensated power coefficient. IEEE Trans. Ind. Appl. 2015, 41, 1548–1556. [Google Scholar] [CrossRef]
- Abo-Khalil, A.G.; Abo-Zied, H. Sensorless control for d-fig wind turbine based on support vector regression. In Proceedings of the IECON 2012 38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 3475–3480. [Google Scholar]
- Abo-Khalil, A.G.; Lee, D.C. MPPT control of wind generation systems based on estimated wind speed using SVR. IEEE Trans. Ind. Electron. 2008, 55, 1489–1490. [Google Scholar] [CrossRef]
- Abo-Khalil, A.G. Model-based optimal efficiency control of induction generators for wind power systems. In Proceedings of the 2011 IEEE International Conference on Industrial Technology (ICIT), Auburn, AL, USA, 14–16 March 2011; pp. 191–197. [Google Scholar]
- Abo-Khalil, A.G. Impacts of wind farms on power system stability. In Modeling and Control Aspects of Wind Power Systems; IntechOpen: London, UK, 2013; ISBN 980-953-307-562-9. [Google Scholar]
- Abo-Khalil, A.G. Synchronization of DFIG output voltage to utility grid in wind power system. Renew. Energy 2012, 44, 193–198. [Google Scholar] [CrossRef]
- Dolan, D.; Lehn, P. Simulation model of wind turbine 3p torque oscillations due to wind shear and tower shadow. IEEE Trans. Energy Convers. 2006, 21, 717–724. [Google Scholar] [CrossRef]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Tummala, A.; Velamati, R.K.; Sinha, D.K.; Indraja, V.; Krishna, V.H. A review on small scale wind turbines, Renew. Sustain. Energy Rev. 2016, 56, 1351–1371. [Google Scholar] [CrossRef]
- Lei, Y.; Mullane, A.; Lightbody, G.; Yacamini, R. Modeling of the wind turbine with a doubly fed induction generator for grid integration studies. IEEE Trans. Energy Convers. 2006, 21, 257–264. [Google Scholar] [CrossRef]
- Gregory, I.M.; Chowdhry, R.S.; McMinn, J.D.; Shaughnessy, J.D. Hypersonic Vehicle Model and Control Law Development Using H∞ and μ Synthesis; Langley Research Center: Hampton, VA, USA, 1994.
- Abo-Khalil, A.G.; Kim, H.G.; Lee, D.C.; Seok, J.K. Maximum output power control of wind generation system considering loss minimization of machines. In Proceedings of the 30th Annual Conference of IEEE Industrial Electronics Society, Busan, Korea, 2–6 November 2004; pp. 1676–1681. [Google Scholar]
- Abo-Khalil, A.G.; Lee, D.C. Grid connection of doubly-fed induction generators in wind Energy conversion system. In Proceedings of the 2006 CES/IEEE 5th International Power Electronics and Motion Control Conference, Shanghai, China, 14–16 August 2006; Volume 2, pp. 1–5. [Google Scholar]
- Park, H.G.; Abo-Khalil, A.G.; Lee, D.C.; Son, K.M. Torque ripple elimination for doubly fed induction motors under unbalanced source voltage. In Proceedings of the 2007 7th International Conference on Power Electronics and Drive Systems, Bangkok, Thailand, 27–30 November 2007; Volume 7, pp. 1301–1306. [Google Scholar]
- Abo-Khalil, A.G.; Park, H.G.; Lee, D.C. Loss minimization control for doubly fed induction generators in variable speed wind turbines. In Proceedings of the IECON 2007 33rd Annual Conference of the IEEE Industrial Electronics Society, Taipei, Taiwan, 5–8 November 2007; pp. 1109–1114. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Nuller, K.R.; Smola, A.J.; Ratsch, G.; Scholkopf, B.; Kohlmorgen, J.; Vapnik, V. Predicting time series with support vector machine. In International Conference on Artificial Neural Networks; Springer: Berlin/Heidelberg, Germany, 1997; pp. 999–1004. [Google Scholar]
- Senthil, M.A.; Rao, M.V.C.; Chandramohan, A. Competitive approaches to PSO algorithms via new-acceleration coefficient variant with mutation operators. In Proceedings of the Sixth International Conference on Computational Intelligence and Multimedia Applications (ICCIMA’05), Las Vegas, NV, USA, 16–18 August 2005. [Google Scholar]
- Vukosavic, S.N.; Levi, E. Robust DSP-based efficiency optimization of a variable speed induction motor drive. IEEE Trans. Ind. Electron. 2003, 50, 560–570. [Google Scholar] [CrossRef]
- Lin, S.W.; Ying, K.C.; Chen, S.C.; Lee, Z.J. Particle swarm optimization for parameter determination and feature selection of support vector machines. Expert Syst. Appl. 2008, 35, 1817–1824. [Google Scholar] [CrossRef]
- Cho, K.R.; Seok, J.K.; Lee, D.C. Mechanical parameter identification of servo systems using robust support vector regression. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No.04CH37551), Aachen, Germany, 20–25 June 2004; Volume 5, pp. 3425–3430. [Google Scholar]
- Liu, H.-H.; Chang, L.-C.; Li, C.-W.; Yang, C.-H. Particle swarm optimization-based support vector regression for tourist arrivals forecasting. Comput. Intell. Neurosci. 2018, 2018, 1–13. [Google Scholar] [CrossRef]
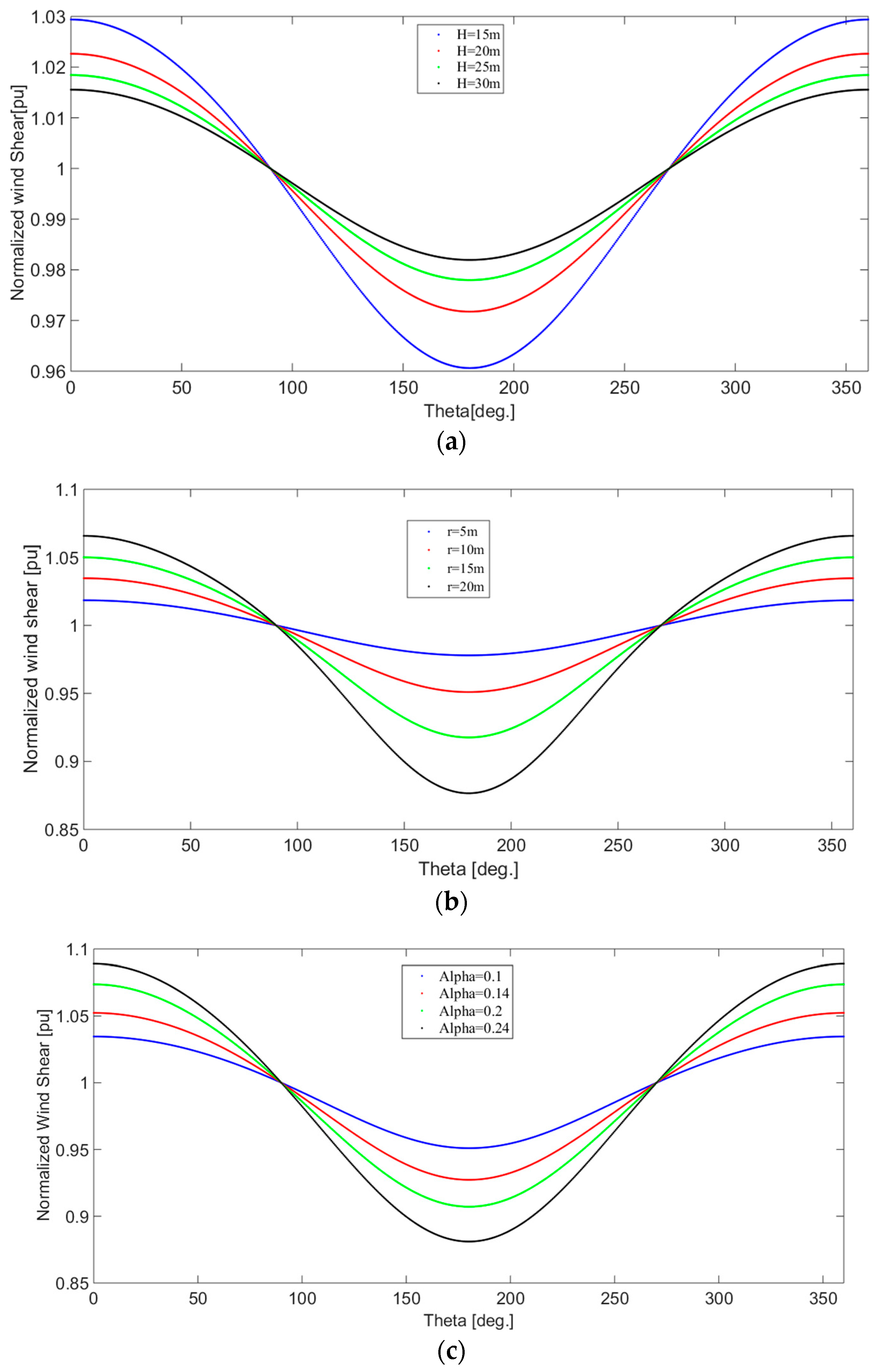



| Terrain | Empirical Wind Shear Exponent |
|---|---|
| Smooth, hard ground, lake, or ocean | 0.1 |
| Smooth, level, grass-covered | 0.14 |
| Tall row crops, low bushes with few trees | 0.2 |
| Many trees, occasional buildings | 0.24 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abo-Khalil, A.G.; Alyami, S.; Sayed, K.; Alhejji, A. Dynamic Modeling of Wind Turbines Based on Estimated Wind Speed under Turbulent Conditions. Energies 2019, 12, 1907. https://doi.org/10.3390/en12101907
Abo-Khalil AG, Alyami S, Sayed K, Alhejji A. Dynamic Modeling of Wind Turbines Based on Estimated Wind Speed under Turbulent Conditions. Energies. 2019; 12(10):1907. https://doi.org/10.3390/en12101907
Chicago/Turabian StyleAbo-Khalil, Ahmed G., Saeed Alyami, Khairy Sayed, and Ayman Alhejji. 2019. "Dynamic Modeling of Wind Turbines Based on Estimated Wind Speed under Turbulent Conditions" Energies 12, no. 10: 1907. https://doi.org/10.3390/en12101907
APA StyleAbo-Khalil, A. G., Alyami, S., Sayed, K., & Alhejji, A. (2019). Dynamic Modeling of Wind Turbines Based on Estimated Wind Speed under Turbulent Conditions. Energies, 12(10), 1907. https://doi.org/10.3390/en12101907





