Analytical and Numerical Investigation of Fe3O4–Water Nanofluid Flow over a Moveable Plane in a Parallel Stream with High Suction
Abstract
1. Introduction
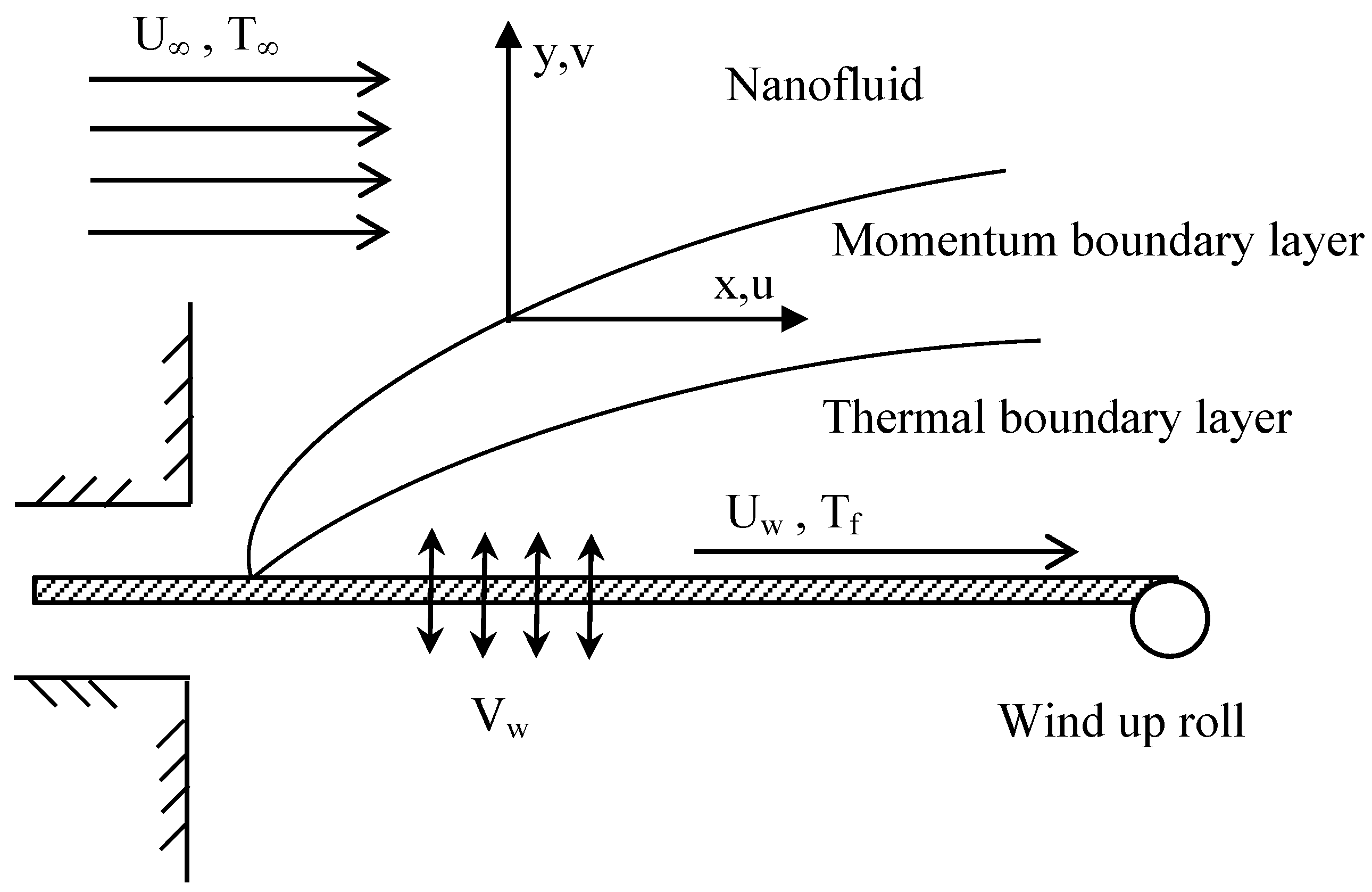
2. Modeling
3. Analytical Solutions via Singular Perturbation Technique
3.1. An Analytical Solution of Energy Equation
3.2. An Analytical Solution of the Blasuis Equation
4. Analytical Parametric Study
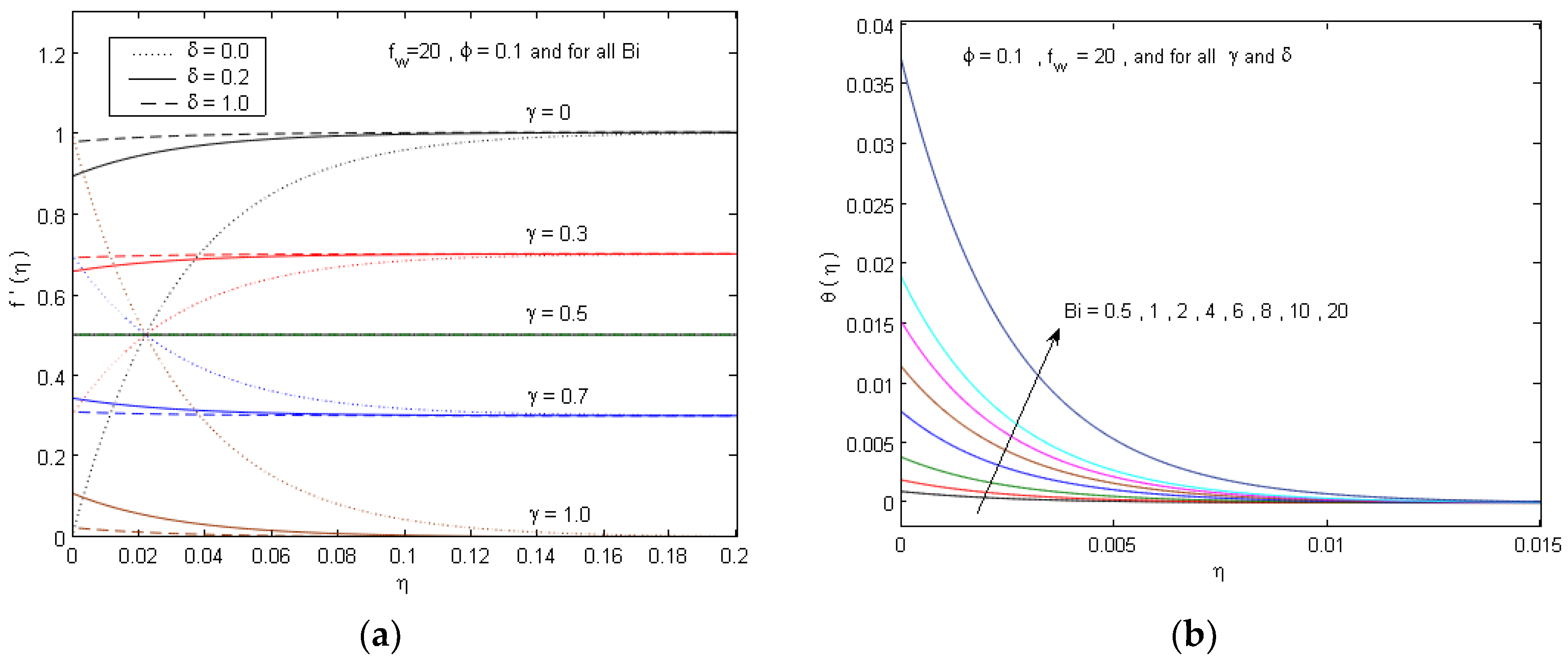
- Solutions in Equations (20) and (21) show that the temperatures profiles have exponential distributions.
- We notice that the solutions in Equations (20) and (21) do not contain the velocity ratio parameter or the slip factor , which indicates that, for high suction, the effect of these parameters on the temperature profiles and the local Nusselt number can be neglected compared to other existing parameters.
- Since we have , , and , , and the solution in Equation (21) results in a positive local Nusselt number.
- Additionally, since we have , , and , and . This means that, as the solid volume fraction increases the initial temperature of the wall layer, , decreases, while the thermal boundary layers thickness increases, which suggests that there are intersections points among curves and the temperature profiles decrease non-monotonically.
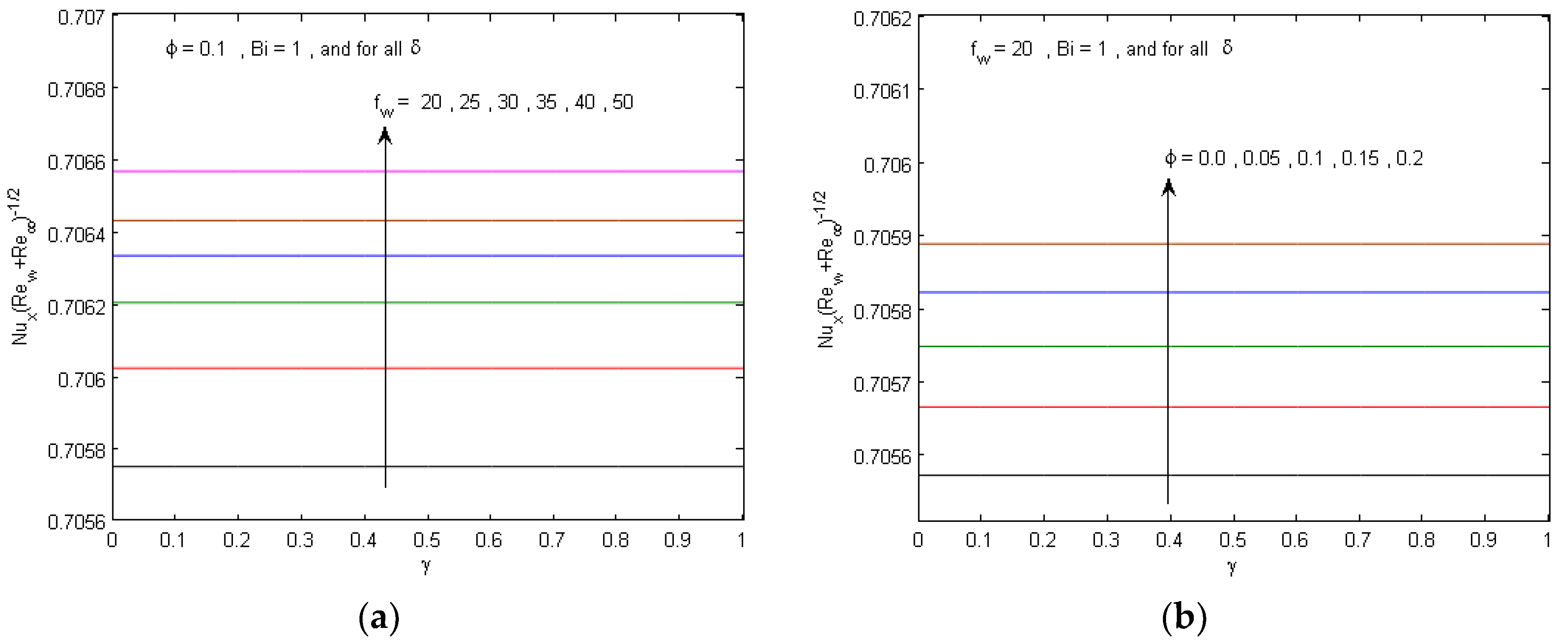
- Moreover, the solution in Equation (20) shows that, as the suction parameter increases or the Biot number decreases, the temperature profiles decrease monotonically.
- Additionally, the solution in (21) shows that as the suction parameter or the Biot number increases the wall temperature gradients (at ) and the local Nusselt number increase.
- The solution in Equation (20) shows that, as the suction parameter increases the wall temperature and the temperature profile decrease; therefore, the thermal boundary layers thickness decreases, while the Biot number has a neglected effect on the temperature layer’s thickness compared to other parameters.
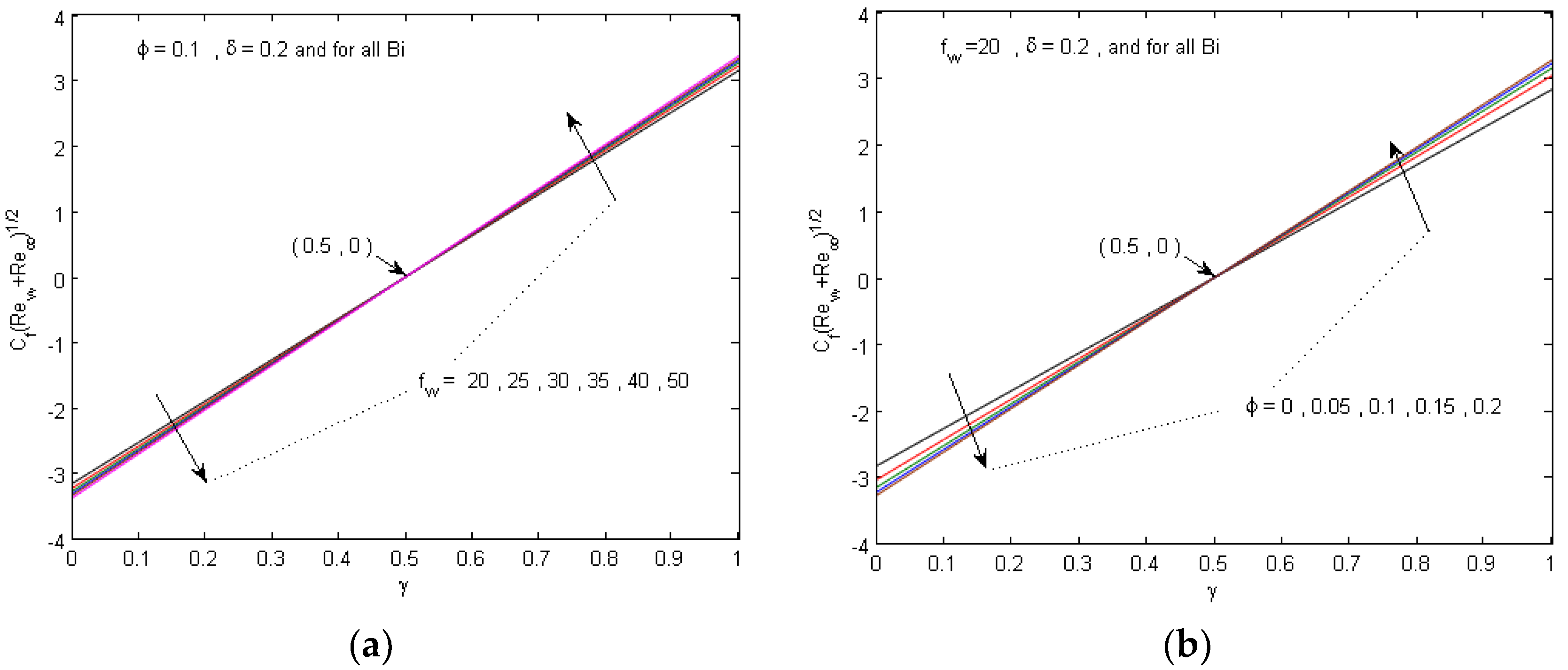
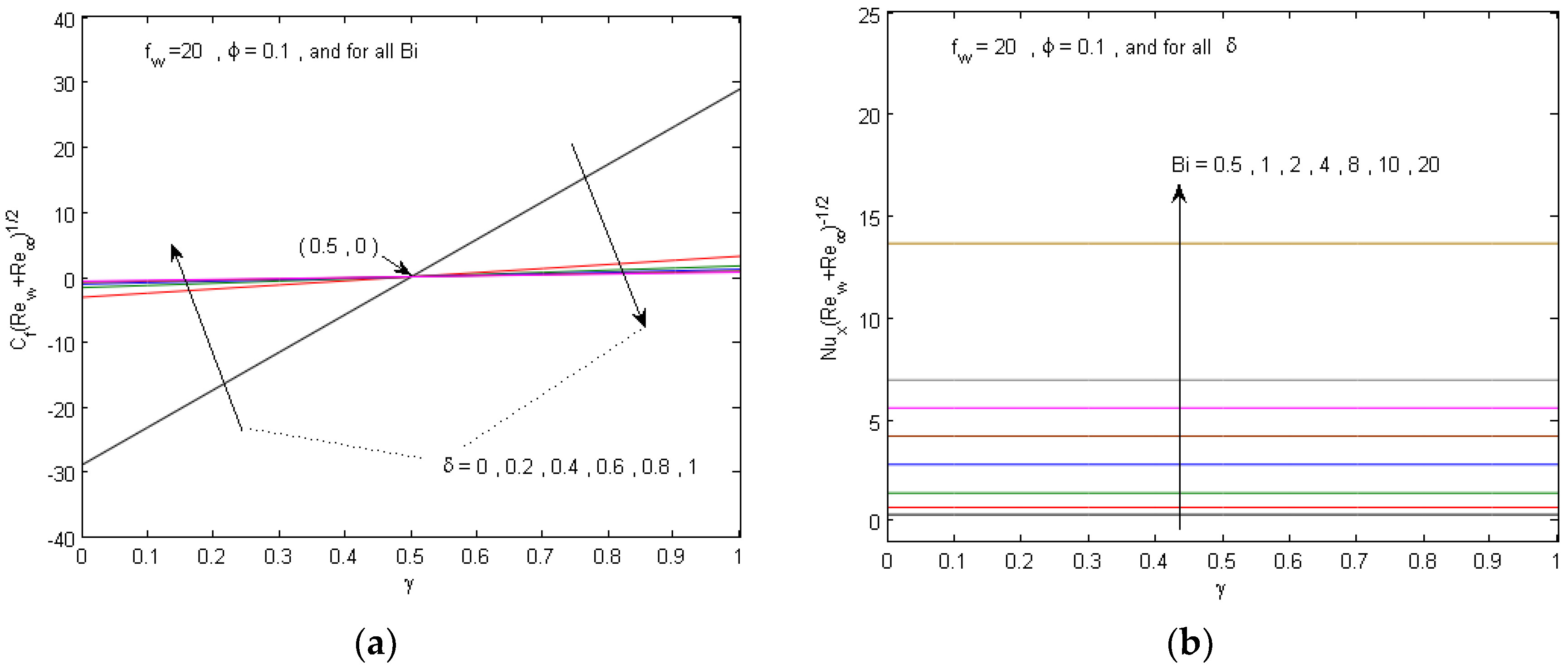
- The solutions in Equations (27)–(29) do not contain the Biot number , which indicates that it has no effect on the fluid velocity and the Local skin friction coefficient.
- Since we have and , , and the solution in Equation (29) always results in a negative local skin friction coefficient for and a positive one for .
- Since we have and and for (), as the solid volume fraction parameter increases, the velocity profiles decrease (increases).
- The value of at which can be determined from Equation (27) and is given bywhich shows that, at fixed values of and , we have one intersection point of the velocity curves regardless of the values of . This intersection point lies in the right (left) half plane for () which confirm that for high suction, , and positive slip factor , the intersection point lies in the left half plane.
- Moreover, based on Equations (27)–(29), for () and (), as the suction parameter or the slip parameter increases, the velocity profiles decrease (increases) monotonically.
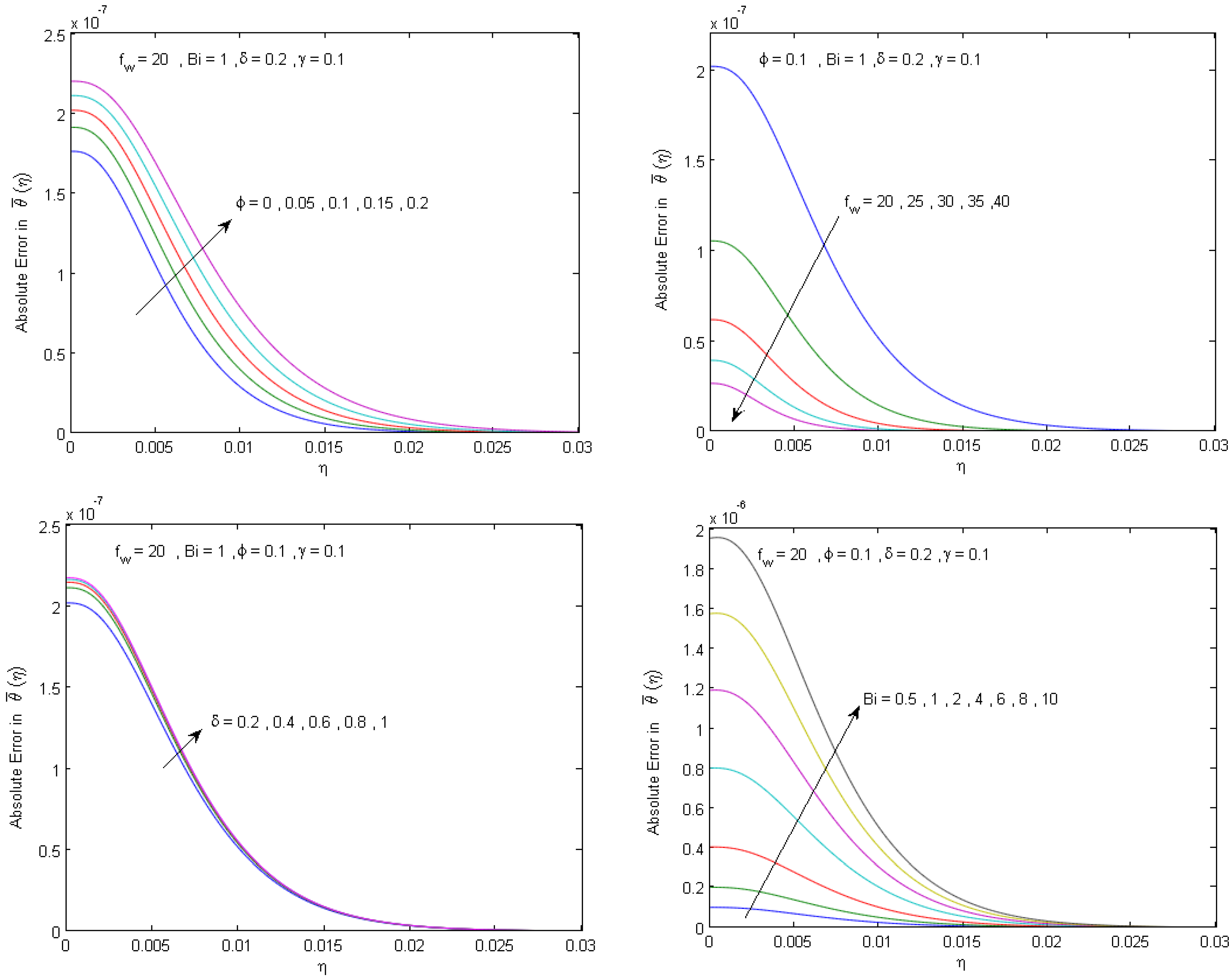
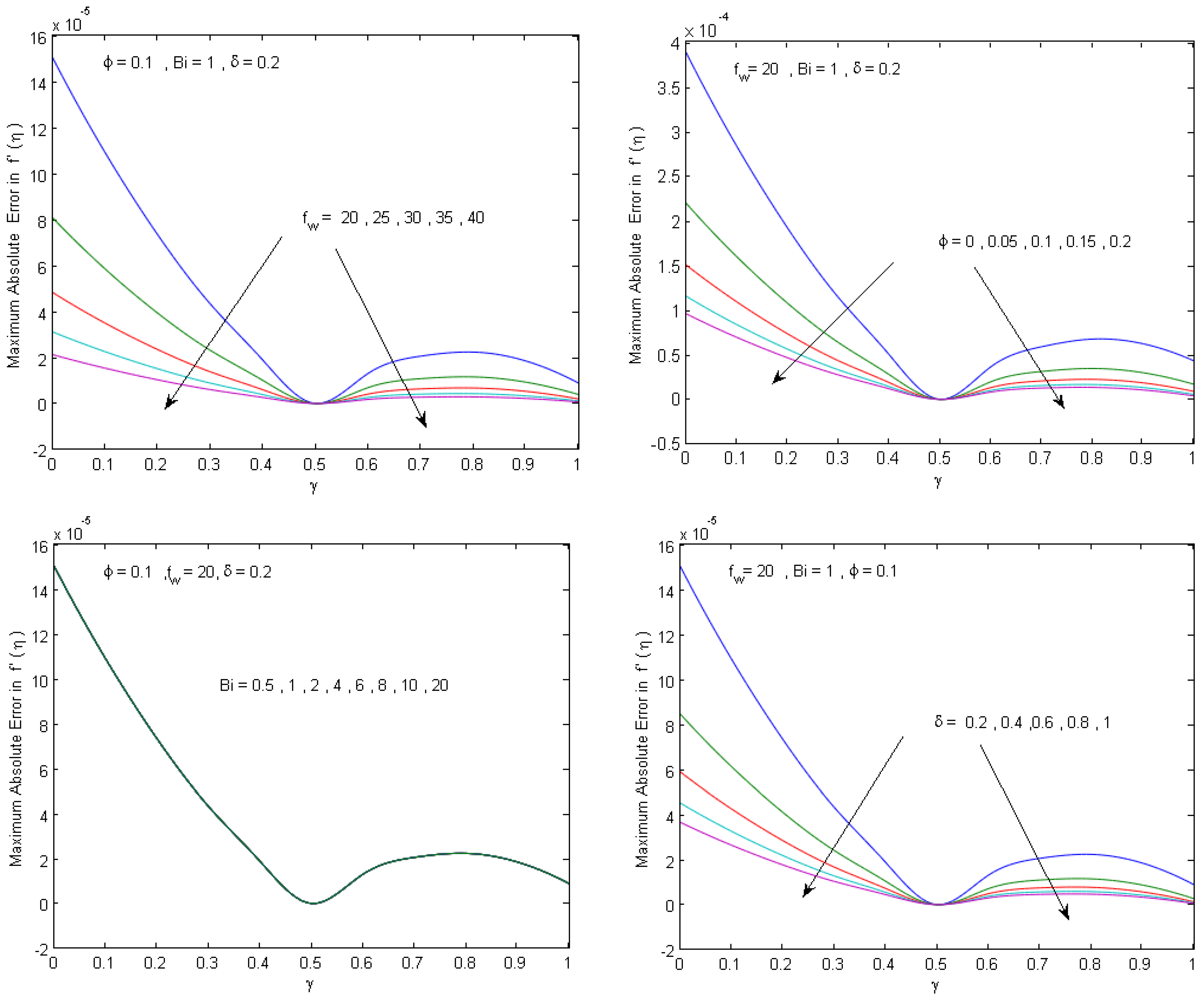
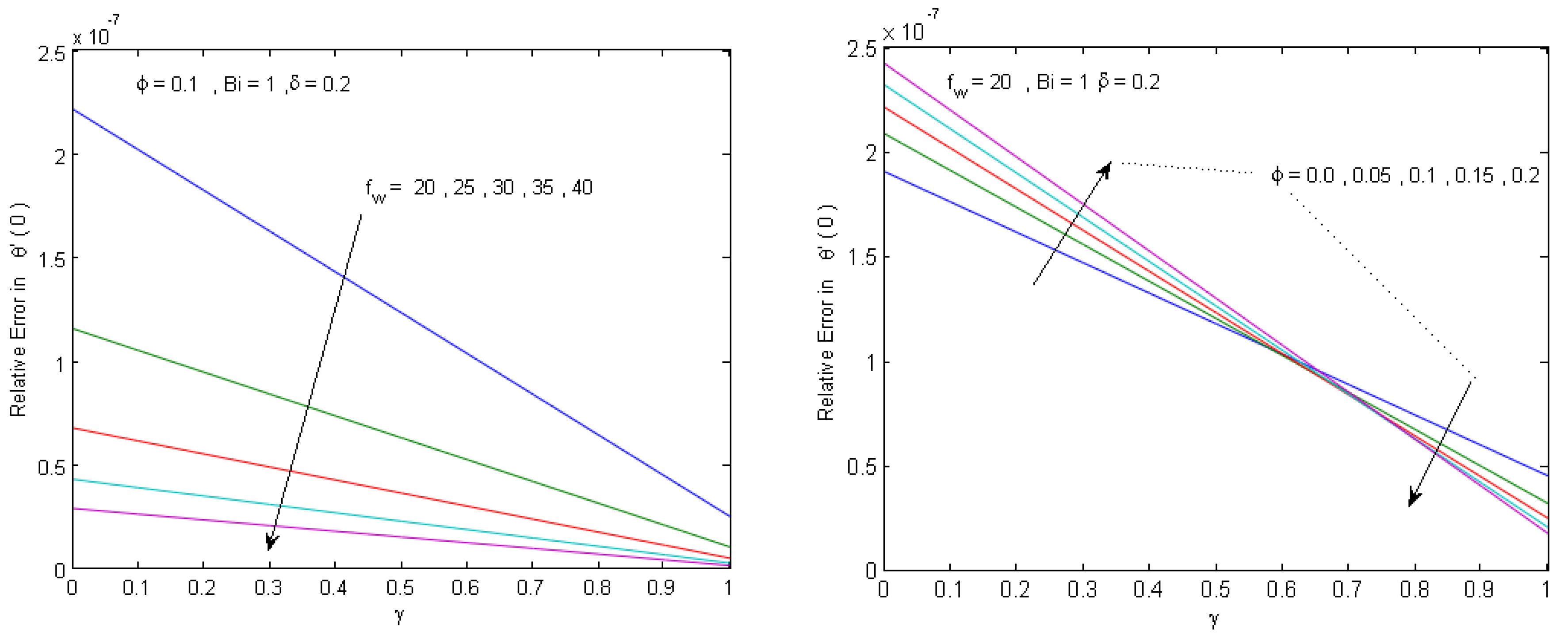
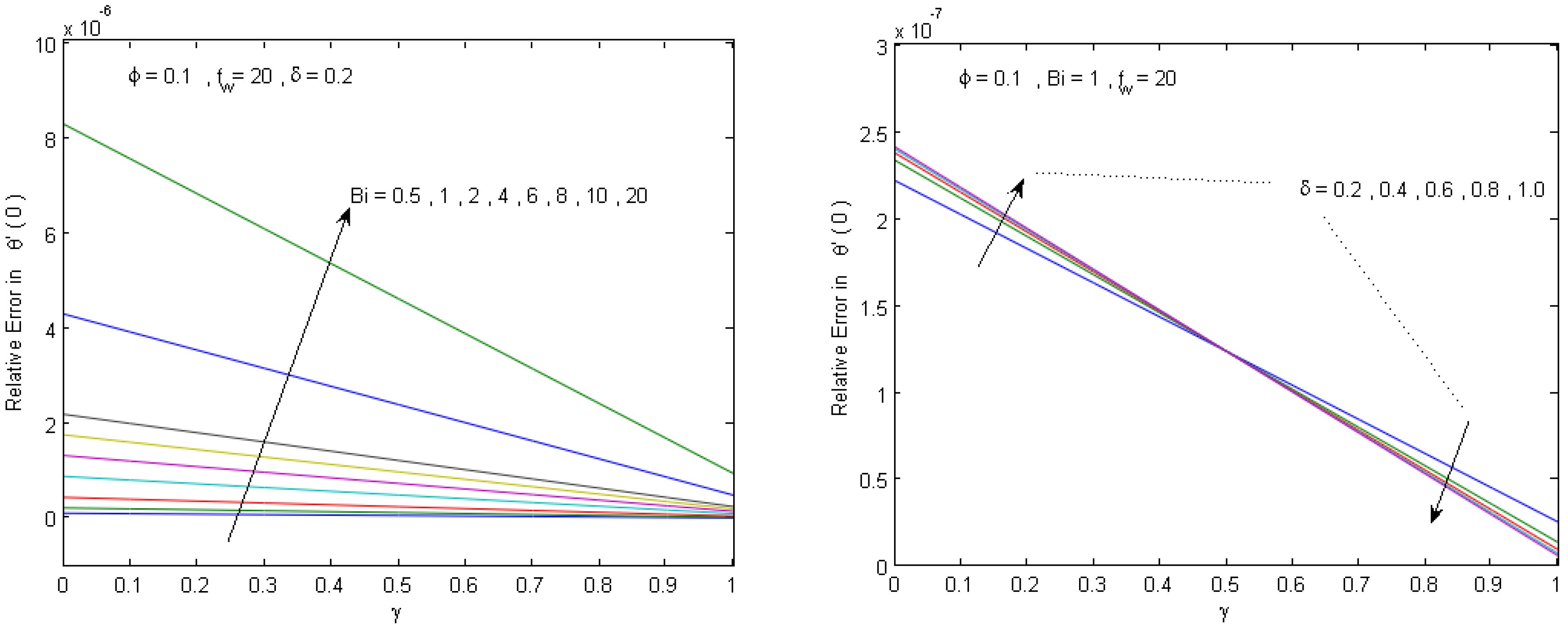
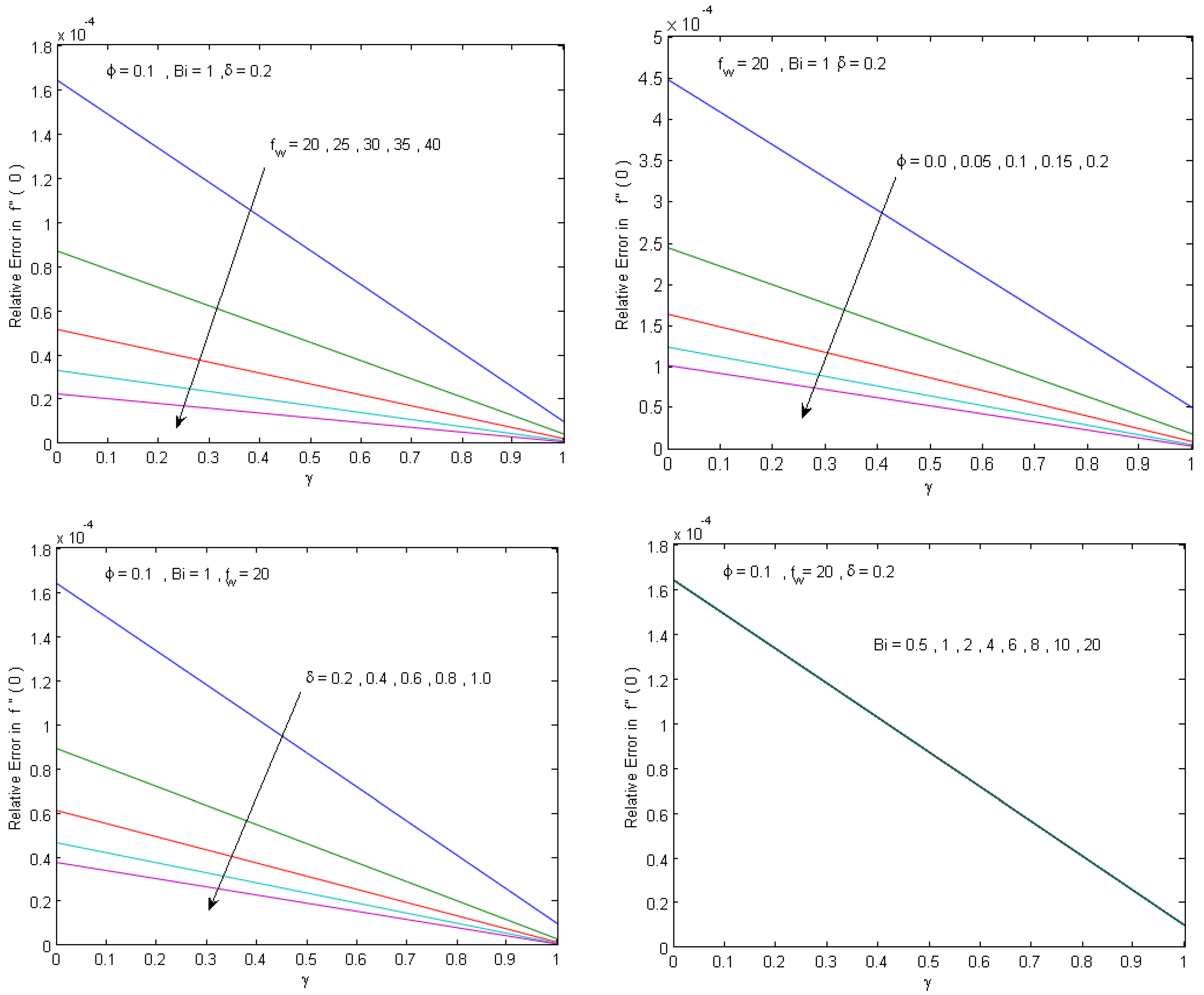
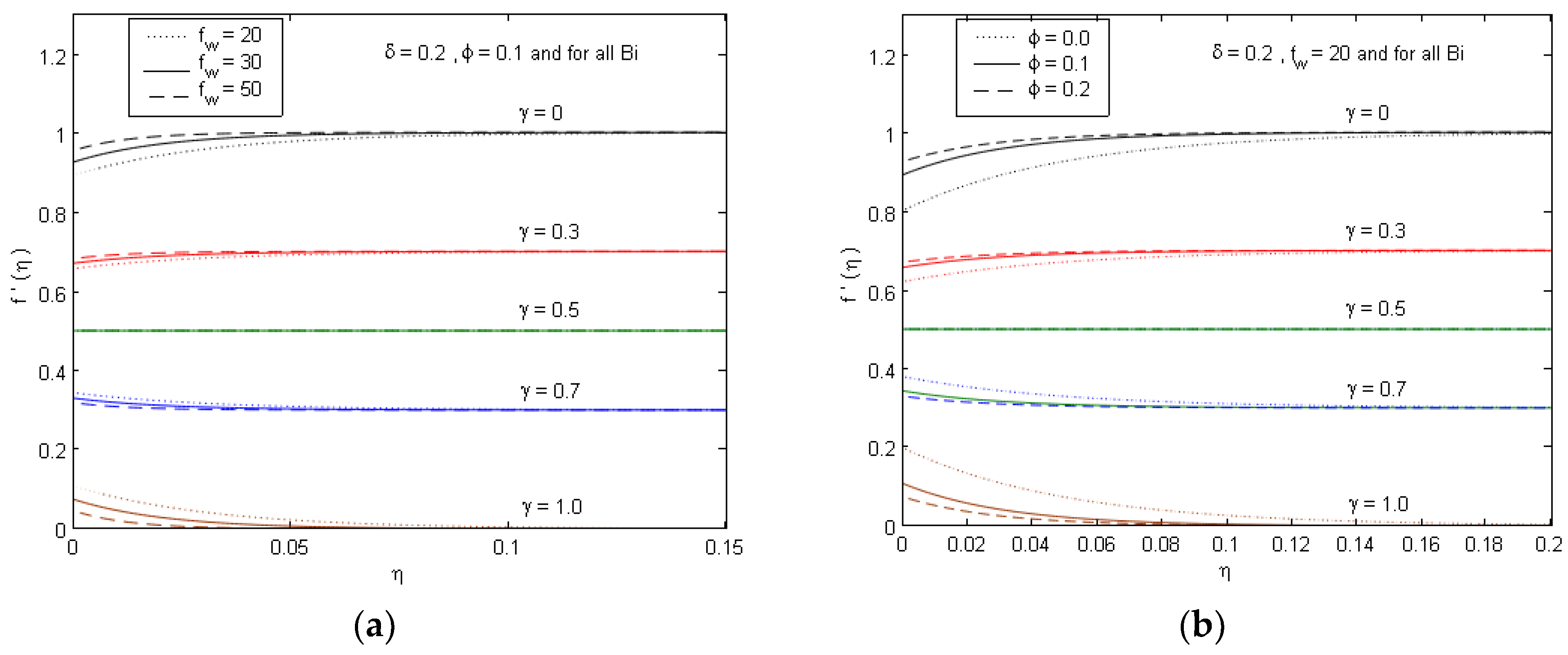
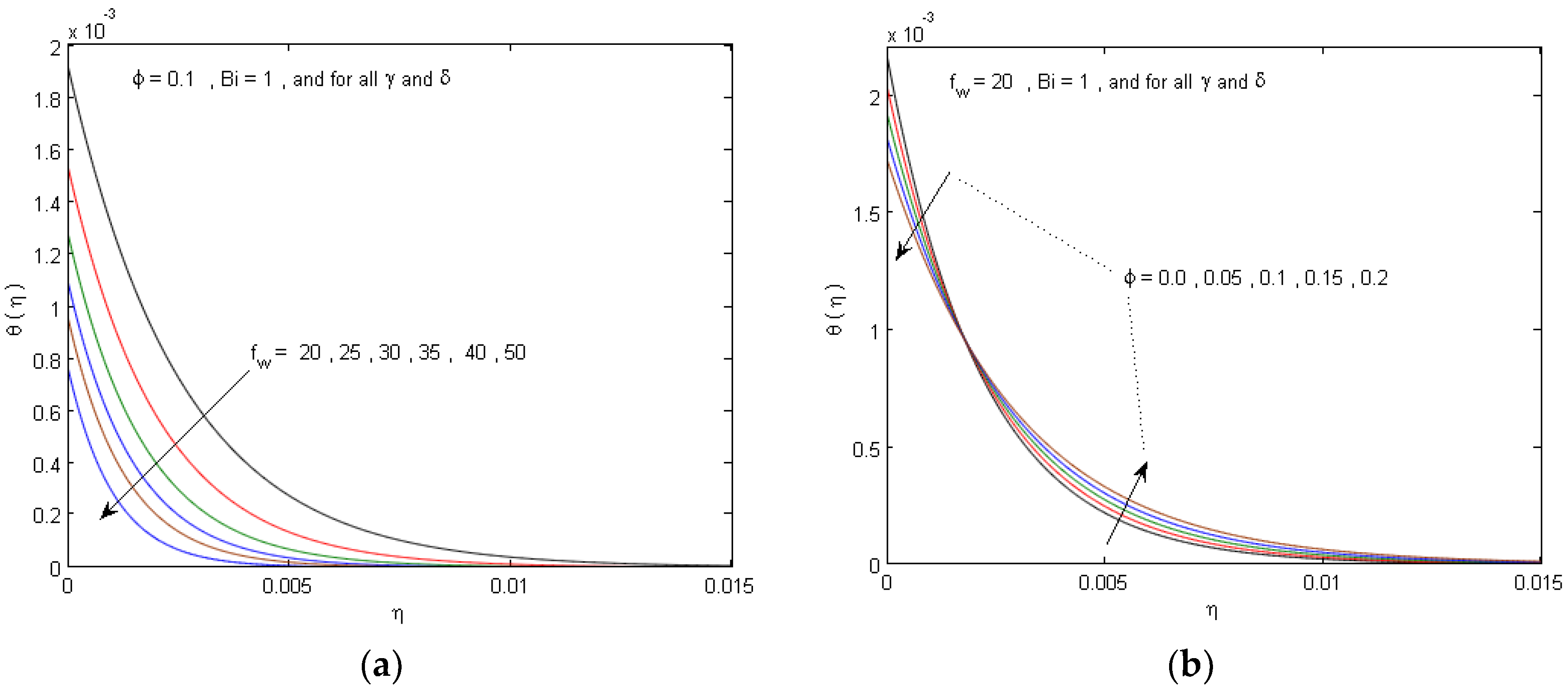
5. Numerical Results and Discussion
6. Conclusions
- The present singular perturbation technique results in a closed form asymptotic solution of the energy and Blasuis equations as a function of the physical parameters.
- The rapid calculation of the system solution (dynamic response) with acceptable accuracy demonstrates that the analytical solutions are effective for performing analytical parametric studies.
- An analytical parametric study is carried out to predict the impact of the system physical parameters on the temperature and velocity behaviors.
- The results of the numerical study confirms a high validation of the present analytical parametric study and their main results can be summarized as follows:
- Both the nanofluid velocity and temperature distributions are decelerated for growing the solid volume fraction and suction parameters.
- The raising in slip parameter causes an increment in the velocity profiles, and the raising in Biot number causes an increment in the temperature profiles.
- The local Nusselt number elevates along with boosting values of Biot number solid volume fraction and suction parameters.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Nomenclature | |
| Bi | Biot number |
| Cp | specific heat at constant pressure (J·kg−1·K−1) |
| Cf | local skin-friction coefficient |
| fw | suction parameter value |
| dimensionless velocity | |
| hf | convective heat transfer coefficient (W/m2 k) |
| k | thermal conductivity (m2 s−1) |
| N | velocity slip coefficient |
| Nux | local Nusselt number |
| Pr | Prandtl number, n/am |
| Rew, Re∞ | Reynolds numbers |
| T | temperature (K) |
| u, v | velocity components along and axes (m/s) |
| Uw, U∞ | the plate velocity and free stream velocity, respectively (m/s) |
| x | coordinate in flow direction (m) |
| y | coordinate perpendicular to flow direction (m) |
| Vw | uniform transpiration velocity (m/s) |
| Greek Symbols | |
| α | thermal diffusivity (m2 s−1) |
| β | coefficient of thermal expansion (1/K) |
| γ | velocity ratio parameter |
| η | similarity variable |
| θ | dimensionless temperature |
| solid volume fraction parameter | |
| ψ | non-dimensional stream function |
| δ | velocity slip parameter |
| μ | dynamic viscosity (m2 s−1) |
| ν | kinematic viscosity (m2 s−1) |
| ρCp | heat capacity (J·kg−3·K−1) |
| ρ | density (kg/ m3) |
| Subscripts | |
| f | fluid |
| nf | ferrofluid |
| s | nanoparticle |
| w | condition at the wall |
| ∞ | condition at infinity |
References
- He, J.H. Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Keimanesh, M. Using differential transform method and the Padé approximant for solving MHD flow in a laminar liquid film from a horizontal stretching surface. Math. Prob. Eng. 2010, 20, 14. [Google Scholar] [CrossRef]
- Shi, J.; Wang, L.; Wang, Y.; Zhang, J. Generalized energy flow analysis considering electricity gas and heat subsystems in local-area energy systems integration. Energies 2017, 10, 514. [Google Scholar] [CrossRef]
- Habib, H.M.; El-Zahar, E.R. Mathematical modeling of heat-transfer for a moving sheet in a moving fluid. J. Appl. Fluid Mech. 2013, 6, 369–373. [Google Scholar]
- El-Zahar, E.R.; Rashad, A.M.; Gelany, A.M. Studying high suction effect on boundary-layer flow of a nanofluid on permeable surface via singular perturbation technique. J. Comput. Theoret. Nanosci. 2015, 12, 4828–4836. [Google Scholar] [CrossRef]
- Sakiadis, B.C. Boundary layers on continuous solid surfaces. AIChE J. 1961, 7, 26–28, 221–225, 467–472. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plane. ZAMP 1970, 21, 645–647. [Google Scholar]
- Tsou, F.; Sparrow, E.; Goldstein, R. Flow and heat transfer in the boundary layer on a continuous moving surface. Int. J. Heat Mass Transf. 1967, 10, 219–235. [Google Scholar] [CrossRef]
- Magyari, E.; Keller, B. Heat and mass transfer in the boundary layers on an exponentially stretching continuous surface. J. Phys. D: Appl. Phys. 1999, 32, 577–585. [Google Scholar] [CrossRef]
- Magyari, E.; Keller, B. Exact solutions for self-similar boundary-layer flows induced by permeable stretching walls. Eur. J. Mech. B/Fluids. 2000, 19, 109–122. [Google Scholar] [CrossRef]
- El-Kabeir, S.M.M.; Rashad, A.M.; Gorla, R.S.R. Unsteady MHD combined convection over a moving vertical sheet in a fluid saturated porous medium with uniform surface heat flux. Math. Comput. Model. 2007, 46, 384–397. [Google Scholar] [CrossRef]
- Bataller, R.C. Radiation effects in the blasius flow. Appl. Math. Comput. 2008, 198, 333–338. [Google Scholar]
- Ishak, A. Radiation effects on the flow and heat transfer over a moving plate in a parallel stream. Chin. Phys. Lett. 2009, 26, 034701. [Google Scholar] [CrossRef]
- El-Kabeir, S.M.M.; El-Hakiem, M.A.; Rashad, A.M. Lie group analysis of unsteady MHD three dimensional by natural convection from an inclined stretching surface saturated porous medium. J. Comput. Appl. Math. 2008, 213, 582–603. [Google Scholar] [CrossRef]
- Rashad, A.M.; Bakier, A.Y.; Gorla, R.S.R. Viscous dissipation and ohmic heating effects on MHD mixed convection along a vertical moving surface embedded in a fluid saturated porous medium. J. Porous Med. 2010, 13, 159–170. [Google Scholar] [CrossRef]
- El-Kabeir, S.M.M.; Rashad, A.M.; Gorla, R.S.R. Heat transfer in a micropolar fluid flow past a permeable continuous moving surface. ZAMM 2011, 91, 1–11. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, San Francisco, CA, USA, 12–17 November 1995; Volume 231, pp. 99–103. [Google Scholar]
- Buongiorno, J. Convective transport in nanofluids. ASME J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Rashad, A.M.; Al-Meshaiei, E. Melting effect on unsteady hydromagnetic flow of a nanofluid past a stretching sheet. Int. J. Chem. React. Eng. 2011, 9, 1–23. [Google Scholar] [CrossRef]
- Rashad, A.M.; El-Hakiem, M.A.; Abdou, M.M.M. Natural convection boundary layer of a non-Newtonian fluid about a permeable vertical cone embedded in a porous medium saturated with a nanofluid. Comput. Math. Appl. 2011, 62, 3140–3151. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Rashad, A.M. Natural convection from a vertical permeable cone in nanofluid saturated porous media for uniform heat and nanoparticles volume fraction fluxes. Int. J. Numer. Method. Heat Fluid Flow. 2012, 22, 1073–1085. [Google Scholar] [CrossRef]
- Bég, O.A.; Ferdows, M. Explicit numerical simulation of magnetohydrodynamic nanofluid flow from an exponential stretching sheet in porous media. Appl. Nanosci. 2013, 1–15. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Rashad, A.M.; Aly, A.M. Transient natural convection flow of a nanofluid over a vertical cylinder. Meccanica 2013, 48, 71–81. [Google Scholar] [CrossRef]
- Noghrehabadi, A.; Behseresht, A.; Ghalambaz, M.; Behseresht, J. Natural convection flow of nano fluids over a vertical cone embedded in a non-Darcy porous medium. J. Thermophys. Heat Transf. 2013, 27, 334–341. [Google Scholar] [CrossRef]
- Behseresht, A.; Noghrehabadi, A.; Ghalambaz, M. Natural convection heat and mass transfer from a vertical cone in porous media filled with nano fluids using the practical ranges of nano fluids thermophysical properties. Chem. Eng. Res. Des. 2014, 92, 447–452. [Google Scholar] [CrossRef]
- Rashad, A.M.; Abbasbandy, S.; Chamkha, A.J. Non-Darcy natural convection from a vertical cylinder embedded in a thermally stratified and nanofluid-saturated porous media. ASME J. Heat Transf. 2014, 136, 002503. [Google Scholar] [CrossRef]
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticle. In Developments and Applications of Non-Newtonian Flows, Proceedings of the ASME FED International Mechanical Engineering Congress & Exposition, San Francisco, CA, USA, 12–17 November 1995; Siginer, D.A., Wang, H.P., Eds.; US Department of Energy, Basic Energy Sciences-Material Sciences: Washington, DC, USA, 1995; Volume 231, pp. 99–105. [Google Scholar]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Tran. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- El-Kabeir, S.M.M.; Chamkha, A.J.; Rashad, A.M. The effect of thermal radiation on non-Darcy free convection from a vertical cylinder embedded in a nanofluid porous media. J. Porous Med. 2014, 17, 269–278. [Google Scholar] [CrossRef]
- El-Kabeir, S.M.M.; Modather, M.; Rashad, A.M. Effect of thermal radiation on mixed convection flow of a nanofluid about a solid sphere in a saturated porous medium under convective boundary condition. J. Porous Med. 2015, 18, 569–584. [Google Scholar] [CrossRef]
- Rashad, A.M. Impact of thermal radiation on MHD slip flow of a ferrofluid over a nonisothermal wedge. J. Magn. Mater. 2017, 422, 25–31. [Google Scholar] [CrossRef]
- Rashad, A.M. Unsteady nanofluid flow over an inclined stretching surface with convective boundary condition and anisotropic slip impact. Int. J. Heat Technol. 2017, 35, 82–90. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Abbas, T.; Rashidi, M.M.; Ali, M.E.; Yang, Z. Entropy generation on MHD eyring—Powell nanofluid through a permeable stretching surface. Entropy 2016, 18, 224. [Google Scholar] [CrossRef]
- Garoosi, F.; Hoseininejad, F.; Rashidi, M.M. Numerical study of heat transfer performance of nanofluids in a heat exchanger. Appl. Therm. Eng. 2016, 105, 436–455. [Google Scholar] [CrossRef]
- Khalili, S.; Tamim, H.; Khalili, A.; Rashidi, M.M. Unsteady convective heat and mass transfer in pseudoplastic nanofluid over a stretching wall. Adv. Powder Technol. 2015, 26, 1319–1326. [Google Scholar] [CrossRef]
- Bashirnezhad, K.; Rashidi, M.M.; Yang, Z.; Bazri, S.; Yan, W.M. A comprehensive review of last experimental studies on thermal conductivity of nanofluids. J. Therm. Anal. Calorim. 2014, 9, 863–884. [Google Scholar] [CrossRef]
- Mohebbi, R.; Rashidi, M.M. Numerical simulation of natural convection heat transfer of a nanofluid in an L-shaped enclosure with a heating obstacle. J. Taiwan Instit. Chem. Eng. 2017, 72, 70–84. [Google Scholar] [CrossRef]
- Li, Y.; Yan, H.; Massoudi, M.; Wu, W.T. Effects of anisotropic thermal conductivity and Lorentz force on the flow and heat transfer of a ferro-nanofluid in a magnetic field. Energies 2017, 10, 1065. [Google Scholar] [CrossRef]
- Salleh, S.N.A.; Bachok, N.; Arifin, N.M.; Ali, F.M.; Pop, I. Magnetohydrodynamics flow past a moving vertical thin needle in a nanofluid with stability analysis. Energies 2018, 11, 3297. [Google Scholar] [CrossRef]
- O’Malley, R.E. Introduction to Singular Perturbations; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Bender, C.M.; Orszag, S.A. Advanced Mathematical Methods for Scientists and Engineers, International Series in Pure and Applied Mathematic; McGraw-Hill: New York, NY, USA, 1978. [Google Scholar]
- Doolan, E.P.; Miller, J.J.H.; Schilders, W.H.A. Uniform Numerical Methods for Problems with Initial and Boundary Layers; Boole Press: Dublin, Ireland, 1980. [Google Scholar]
- Kadalbajoo, M.K.; Patidar, K.C. A survey of numerical techniques for solving singularly perturbed ordinary differential equations. Appl. Math. Comput. 2002, 130, 457–510. [Google Scholar] [CrossRef]
- Kumar, M.; Singh, P.; Mishra, H.K. A recent survey on computational techniques for solving singularly perturbed boundary value problems. Int. J. Comput. Math. 2007, 84, 1–25. [Google Scholar] [CrossRef]
- Miller, J.J.; O’Riordan, E.; Shishkin, G.I. Fitted Numerical Methods for Singular Perturbation Problems: Error Estimates in the Maximum Norm for Linear Problems in One and Two Dimensions; World Scientific: Singapore, 2012. [Google Scholar]
- Verhulst, F. Methods and Applications of Singular Perturbations: Boundary Layers and Multiple Timescale Dynamics; Springer Science and Business Media: Berlin, Germany, 2006. [Google Scholar]
- Ross, H.G.; Stynes, M.; Tobiska, L. Robust Numerical Methods for Singularly Perturbed Differential Equations: Convection-Diffusion-Reaction and Flow Problems; Springer Science & Business Media: Berlin, Germany, 2008; Volume 24. [Google Scholar]
- Habib, H.M.; El-Zahar, E.R. Variable step size initial value algorithm for singular perturbation problems using locally exact integration. Appl. Math. Comput. 2008, 200, 330–340. [Google Scholar] [CrossRef]
- El-Zahar, E.R.; EL-Kabeir, S.M.M. A new method for solving singularly perturbed boundary value problems. Appl. Math. Inf. Sci. 2013, 7, 927–938. [Google Scholar] [CrossRef]
- Vulanovic, R. A uniform numerical method for quasilinear singular perturbation problems without turning points. Computing 1989, 41, 97–106. [Google Scholar] [CrossRef]
- Kierzenka, J.; Shampine, L.F. A BVP solver based on residual control and the MATLAB PSE. ACM Trans. Math. Softw. 2001, 27, 299–316. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chamkha, A.J.; Rashad, A.M.; EL-Zahar, E.R.; EL-Mky, H.A. Analytical and Numerical Investigation of Fe3O4–Water Nanofluid Flow over a Moveable Plane in a Parallel Stream with High Suction. Energies 2019, 12, 198. https://doi.org/10.3390/en12010198
Chamkha AJ, Rashad AM, EL-Zahar ER, EL-Mky HA. Analytical and Numerical Investigation of Fe3O4–Water Nanofluid Flow over a Moveable Plane in a Parallel Stream with High Suction. Energies. 2019; 12(1):198. https://doi.org/10.3390/en12010198
Chicago/Turabian StyleChamkha, A. J., A. M. Rashad, E. R. EL-Zahar, and Hamed A. EL-Mky. 2019. "Analytical and Numerical Investigation of Fe3O4–Water Nanofluid Flow over a Moveable Plane in a Parallel Stream with High Suction" Energies 12, no. 1: 198. https://doi.org/10.3390/en12010198
APA StyleChamkha, A. J., Rashad, A. M., EL-Zahar, E. R., & EL-Mky, H. A. (2019). Analytical and Numerical Investigation of Fe3O4–Water Nanofluid Flow over a Moveable Plane in a Parallel Stream with High Suction. Energies, 12(1), 198. https://doi.org/10.3390/en12010198






