1. Introduction
China is a major energy consumer. Since the first half of 2018, coal, natural gas, petrol, and electricity consumption has been on the rise, among which the highest increase was coal consumption with an increase of 3.1%, and we found thermal power was a major factor of the continued growth of coal consumption. According to “BP Statistical Review of World Energy” [
1], China’s renewable energy consumption accounts for 36% of global volume in 2017, among which natural gas consumption accounted for 32.6% of global natural gas consumption. This showed that China’s energy consumption has an important role in world energy consumption. At present, China’s energy consumption structure upgraded gained initial success, however there is still a distance from the long-term goal to build a low-carbon clean energy consumption structure. Therefore, based on a multitude of influencing factors of energy consumption, it is imperative to apply highly accurate predictive model to forecast energy consumption, and then study more economic information about China’s energy consumption. A high-precision energy consumption forecasting model can provide a quantitative basis for decision-making by relevant Chinese institutions, enabling China to better understand energy consumption trends and solve energy-related problems such as pollutant emissions and carbon emissions. In this article, a breakthrough is made in the machine intelligence algorithm. The PSO-LSSVM forecasting model optimized by the Tabu search algorithm is put forward, which avoids PSO-LSSVM falling into local optimum and speeds up the global search at the same time. Finally, the comparison of various forecasting models proves the fact that the accuracy and generalization ability of the TS-PSO-LSSVM forecasting model proposed in this article is higher than the others.
Energy consumption can be influenced by many factors directly or indirectly. Up to now, there are many factors affecting energy consumption have been studied [
2,
3,
4,
5,
6]. Energy consumption problem is a complex nonlinear problem. So far, scholars have proposed various forecasting models, including grey prediction theory [
7,
8,
9], multiple regression [
10,
11,
12], input-output method [
13,
14], and time-series forecasting models [
15,
16].
Hsu et al. [
7] applied artificial neural network and an improved gray model to predict electricity consumption of Taiwan, and the examples showed that the improved grey prediction model has higher prediction accuracy. Sehgal, V et al. [
10] proposed the wavelet-bootstrap-multiple linear regression (WBMLR) predictive model to forecast India Mahathir Power Load Nadi River Basin, and the examples showed that the model owns higher accuracy than the artificial neural networks (ANN), wide area network (WAN), machine learning in
R (MLR) model. Erdogdu E [
16] applied co-integration analysis and auto-regressive integrated moving average (ARIMA) model to predict power load of the Republic of Turkey, and proved the high power load forecasting officially.
Up to now, a multitude of scholars have proposed robustness problem of the principal component analysis (PCA) based on various ways and put forward their own optimized algorithm. Luong et al. [
17] considered a new method named online robust principal component analysis (RPCA) for time-varying decomposition problems and proposed a compressive online RPCA algorithm that can combine various information about decomposed vectors via an
n −
l1 minimization method. Chretien et al. [
18] proposed a robust principal component analysis (RPCA) method to build the Low Rank + Sparse models when the used data is corrupted by outliers and applied it to estimate the topology in power grid networks. Sadeghian et al. [
19] thought that traditional robust principal component analysis (RPCA) algorithms only focused on output outliers, however, both input and output data can make mistakes in developing soft sensors. They built a robust probabilistic predictive model to overcome this problem by appropriate formulation of noise distributions. Wu et al. [
20] proposed a multi-component groups sparse RPCA model to solve the problems under the condition of complex dynamic background and applied alternating direction method of multipliers algorithm to the proposed model. Experiments demonstrated that the proposed method has better performance than others.
Along with the wide application of intelligent algorithms, more and more scholars have proposed various intelligent algorithms in all areas. Least squares support vector machine (LSSVM) prediction algorithm is one of the most widely used and has high accuracy and applicability. Roushangar et al. [
21] built three types of models about flow characteristics, flow and bedform characteristics, and sediment characteristics based on the Least Squares Support Vector Machine optimized by Particle Swarm Optimization (PSO-LSSVM) and proved the forecasting model can predict the roughness coefficient precisely. Huan et al. [
22] proposed a forecasting model based on integrated empirical mode decomposition (EEMD) and Least Squares Support Vector Machine (LSSVM) and showed that EEMD-LSSVM model is a better predictor algorithm than wavelet denoising least squares support machine (WD-LSSVM) and traditional LSSVM. Xue [
23] optimized the LSSVM by improved particle swarm optimization algorithm (IMPSO-LSSVM) and proposed the combined concrete compressive strength prediction model. Then, he compared IMPSO-LSSVM, PSO-LSSVM, GA-LSSVM (the Least Squares Support Vector Machine optimized by genetic algorithm) and back-propagation neural network to prove the proposed model is an effective tool to forecast concrete compressive strength. Lu et al. [
24] presented a new forecasting model based on empirical mode decomposition integrated permutation entropy (EEMD-PE), LSSVM, and gravitational search algorithm (GSA) to overcome the nonlinear prediction of wind power and volatility difficulties and predicted ultra-short-term forecasting of wind power accurately. Zhao et al. [
25] used the salp swarm algorithm (SSA) on LSSVM to optimize two machine parameters in LSSVM algorithm, and showed that the forecasting model have higher accuracy than traditional LSSVM, PSO-LSSVM and BP neural network through integrated statistical indicators. Wen et al. [
26] proposed the GA-LSSVM prediction model to predict landslide displacement and showed that the model can predict high-precisive consistency between measured displacement and predicted displacement. Liu et al. [
27] proposed an improved gravitational search algorithm (AC-GSA) to improve the performance of GSA and optimize LSSVM parameters. They used a novel model to forecast heat rate of a 600 MW supercritical steam turbine unit. Results indicate that the AC-GSA–LSSVM model is a powerful technique to forecast load. Gorjaei et al. [
28] applied the LSSVM model to predict liquid flow rate for two-phase flow through wellhead chokes and used particle swarm optimization (PSO) to optimize two parameters of the LSSVM algorithm. The PSO-LSSVM model is excellently consistent with actual measured rates. Results indicated that the PSO-LSSVM model demonstrated better regression precision and generalization capability. Zhang [
29] proposed a hybrid model that combines fuzzy clustering (FC), LSSVM, and the wolf pack algorithm (WPA), and used two cases to train and test data. The results proved that the proposed model obtains higher prediction accuracy and stability.
In recent years, the Tabu search algorithm is widely used to shorten the computing time of the algorithm [
30,
31,
32,
33]
Peng et al. [
30] added a Tabu search procedure into the framework of path relinking to generate solutions to the job shop scheduling problem (JSP). The results showed that Tabu search/Path relinking (TS/PR) obtained better performance than the traditional state-of-the-art algorithms for JSP. Escobar et al. [
31] proposed a hybrid Granular Tabu Search algorithm to solve the Multi-Depot Vehicle Routing Problem (MDVRP). The results of cases showed that the proposed algorithm solved problems with short computing time and got best solutions. Li et al. [
32] applied a hybrid algorithm (HA) to the genetic algorithm (GA) and used Tabu search (TS) at the same time to solve the flexible job shop scheduling problem with the aim to minimize the make span and proved that the proposed method can provide the best solutions. Sicilia et al. [
33] presented a novel algorithm to solve the problem of the capillary distribution of goods in major urban areas. The proposed Tabu search algorithm can minimize the wide variety of constraints and complexities and reduced costs, which made problems quickly solved in time.
In order to accurately predict China’s energy consumption, this article proposes a native PSO-LSSVM model optimized by the Tabu search algorithm based on robust principal component analysis. The innovations of this article are as follows:
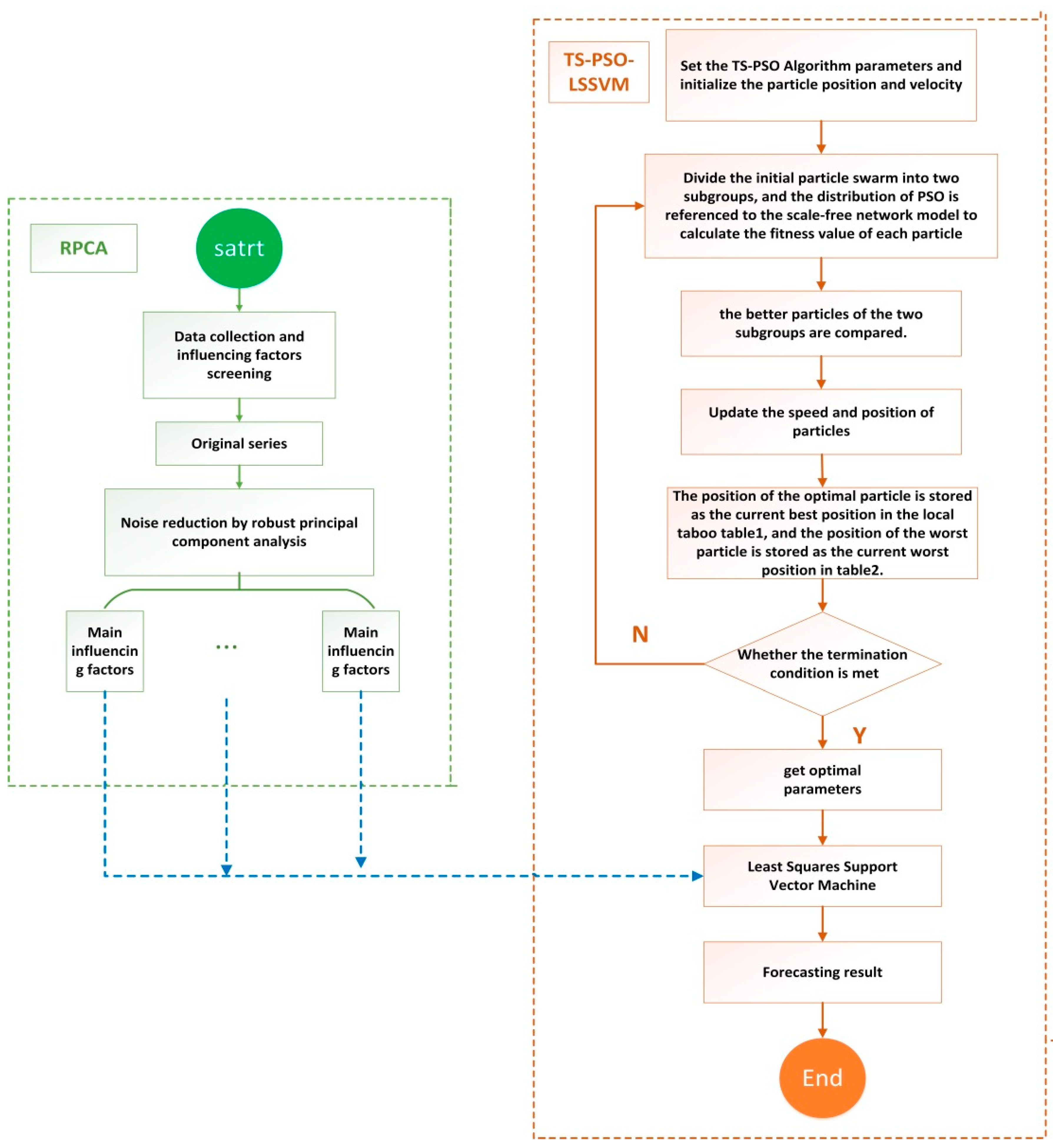
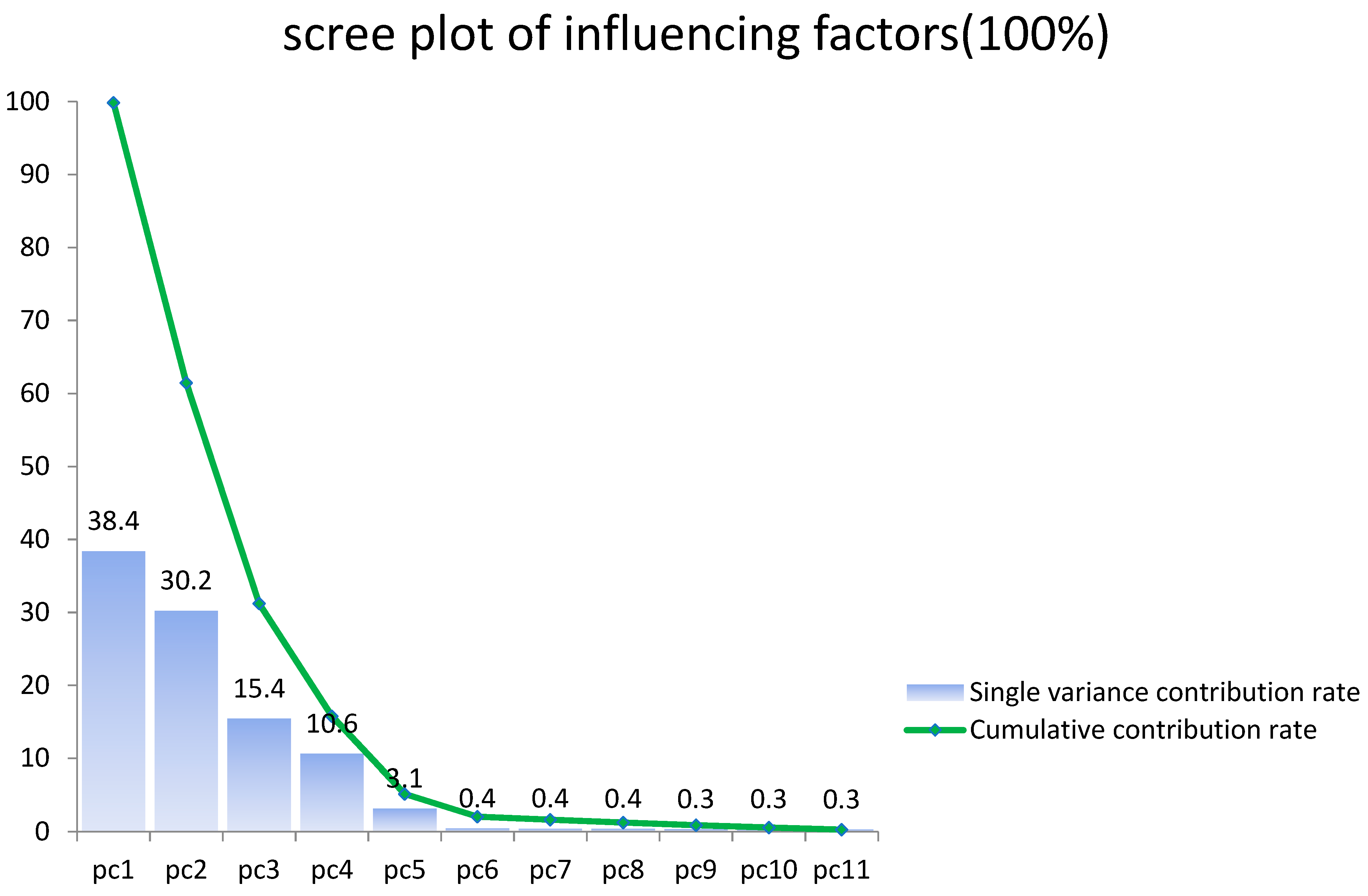
(1) Energy consumption is a macroeconomic issue and is affected by many influencing factors. In order to achieve accurate prediction of China’s energy consumption, based on a large amount of literature research, combined with China’s energy consumption characteristics, we selected GDP, population, industrial structure, energy consumption structure, energy intensity, total import and export, social fixed Asset investment, energy utilization rate, urbanization rate, household consumption level, and fixed investment in energy industry as the set of initial influencing factors. In this article, the main influencing factors are selected by robust optimized principal component analysis (RPCA) method. Based on the idea of signal reconstruction, the judgment basis of a “bad point” sample is given, which can reduce the difficulty of data collection. The first five influencing factors have the ability to represent the information of other influencing factors. By comparing the classification results, it is concluded that the RPCA algorithm is significantly better than the traditional PCA, and the classification effect is more accurate. The information of the original sample can be more comprehensively represented. This operation also greatly improves the accuracy of the forecasting mode.
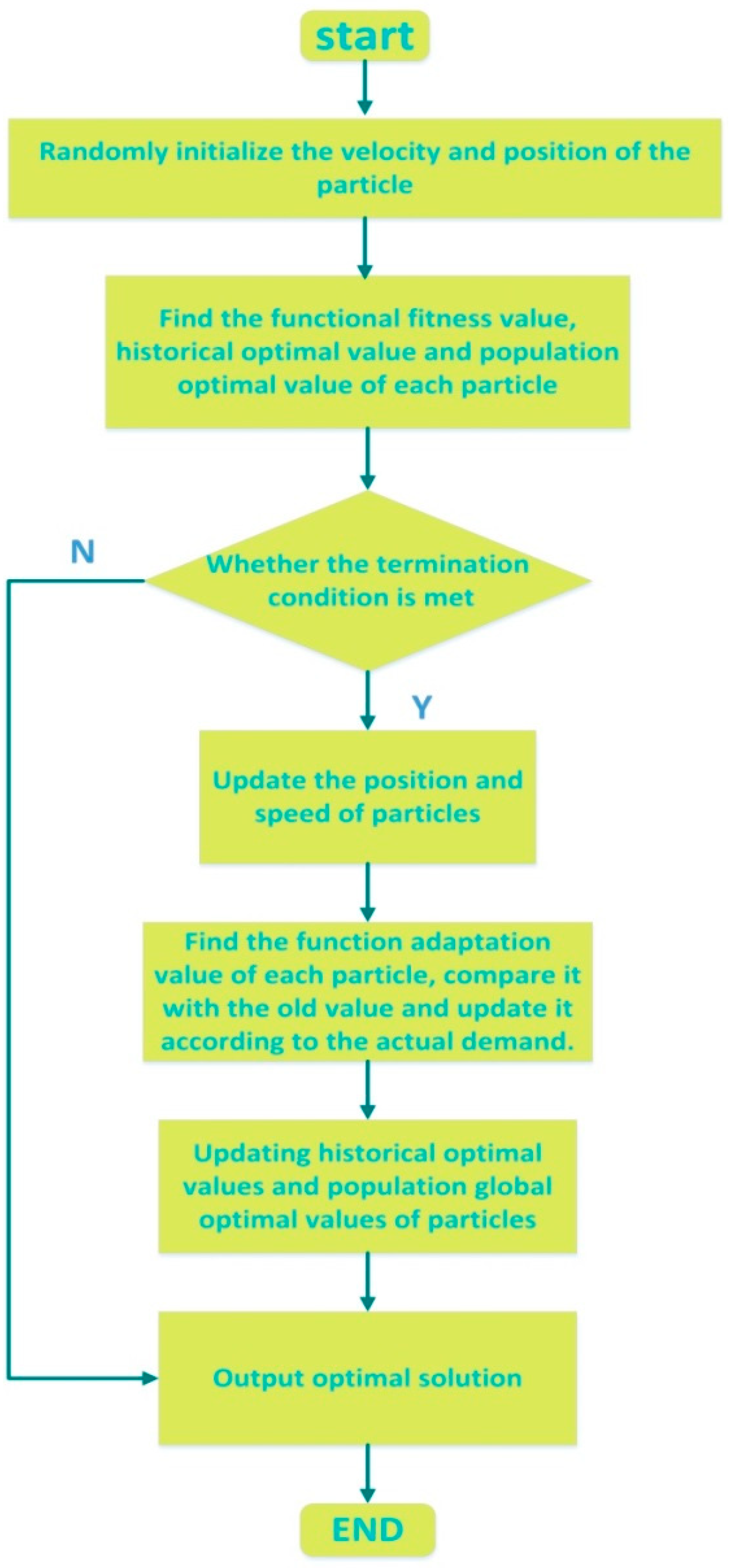
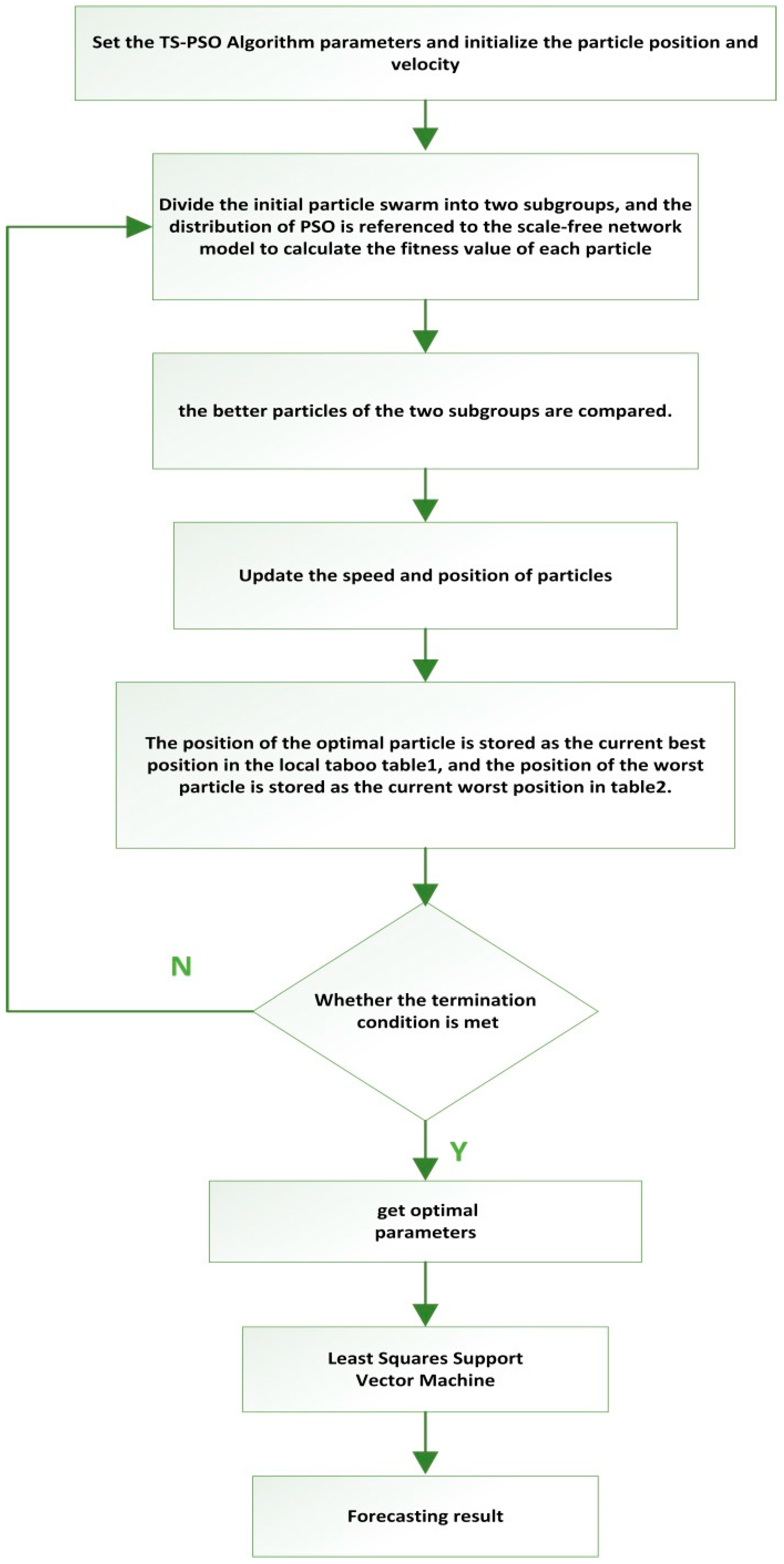
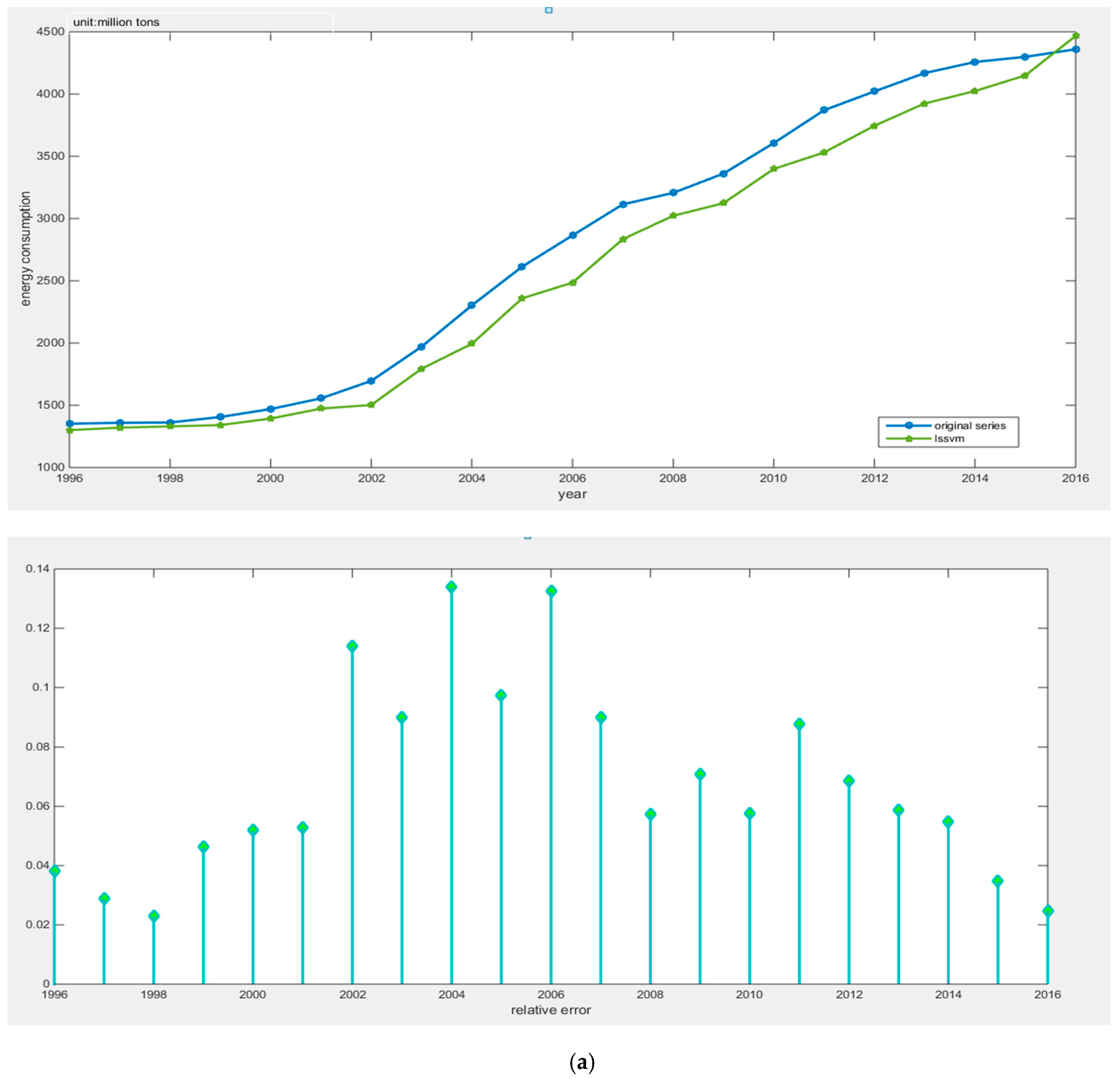
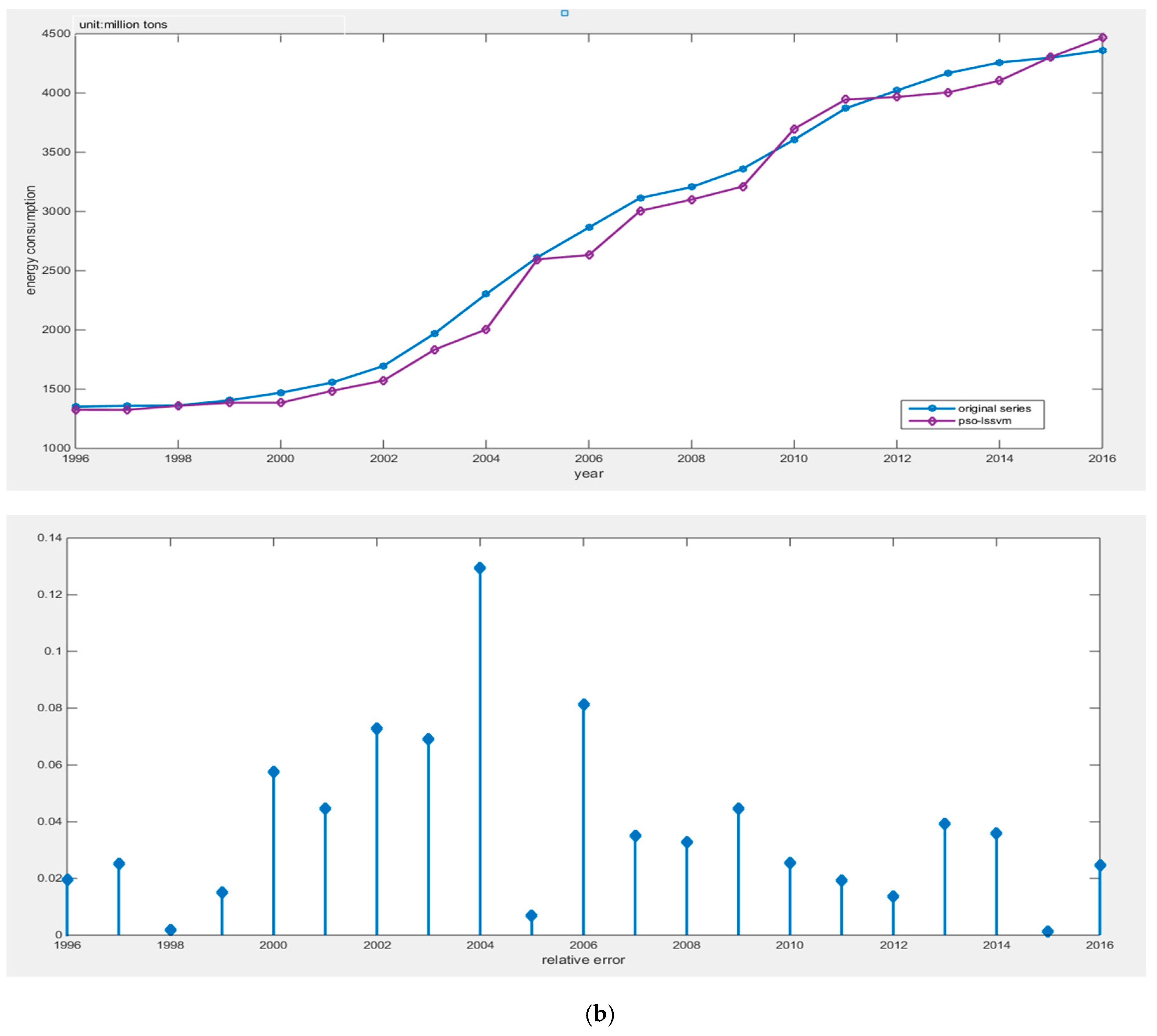
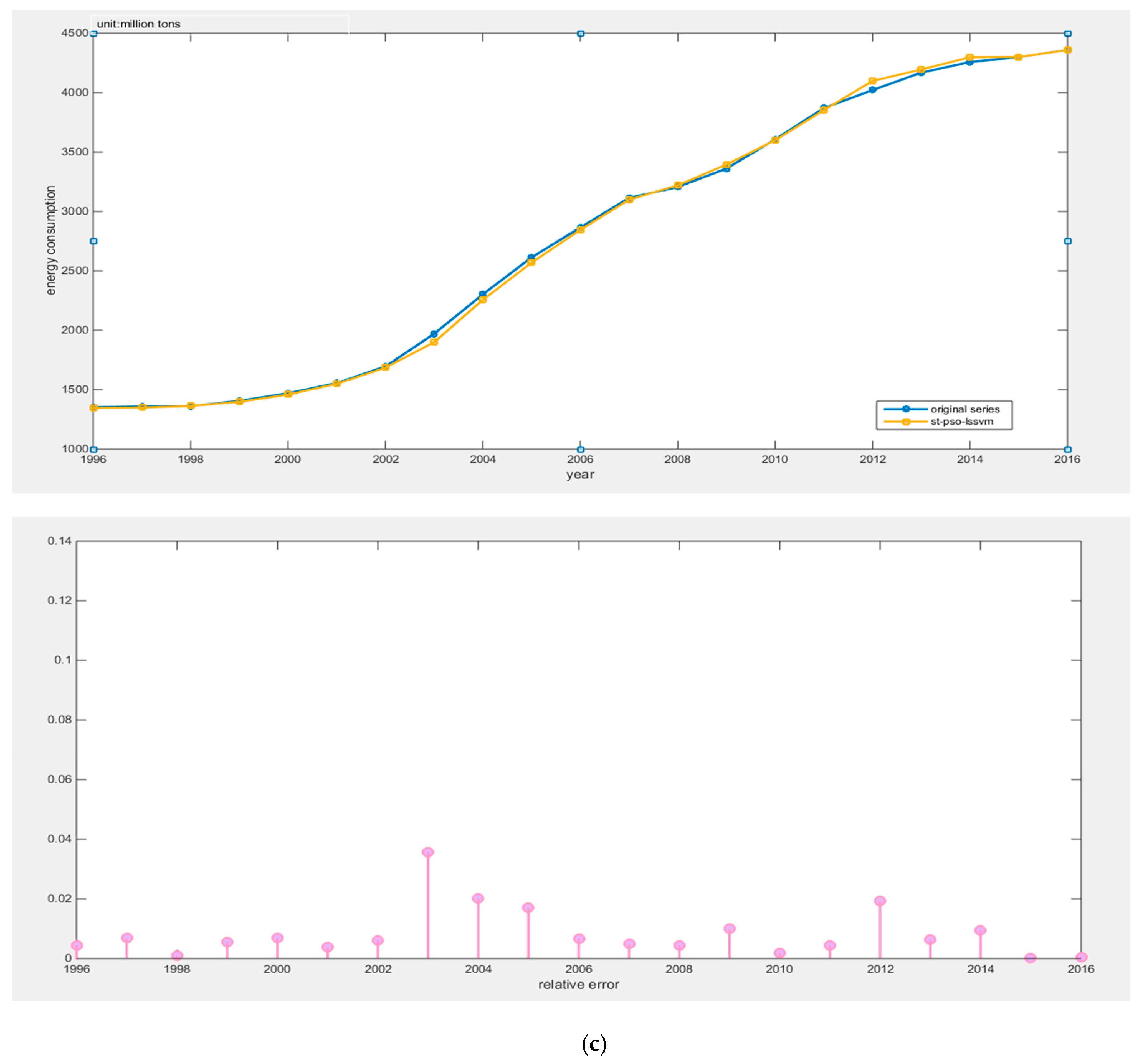
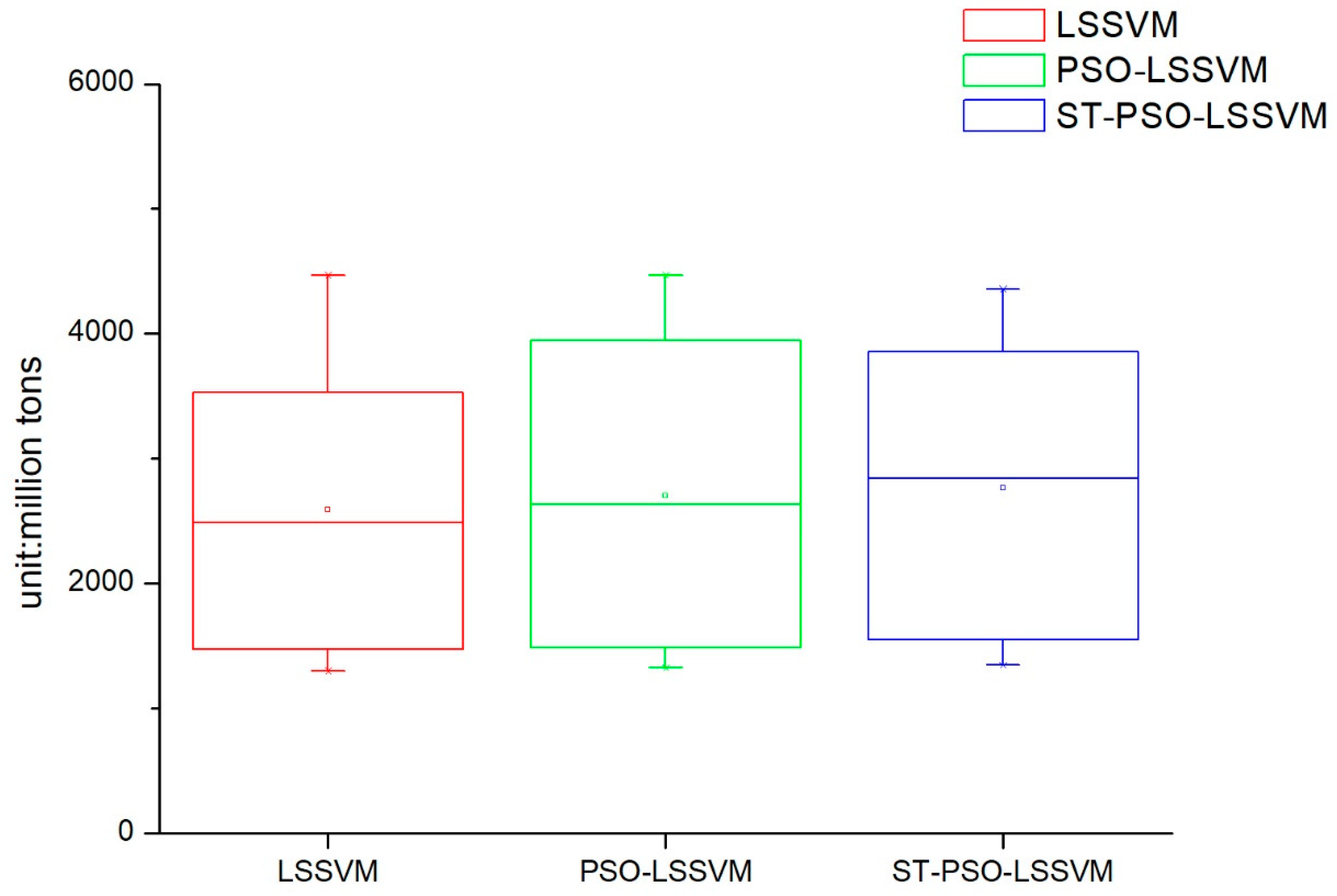
(2) This article innovatively applies the Tabu search algorithm to optimizing the PSO-LSSVM algorithm. The combined forecasting model greatly improves the search ability of parameters and reduces the search time, then, it can avoid local optimal results. The empirical analysis proves that the TS-PSO-LSSVM model has strong generalization ability and can reliably forecast China’s energy consumption, and its prediction accuracy is better than PSO-LSSVM and LSSVM.
(3) This article innovatively applies the machine learning algorithm into the hot spot of international research about forecasting China’s energy consumption. The traditional methods to forecast energy consumption mainly includes mathematical statistics methods, such as linear regression, time series analysis, gray prediction, etc. These methods all regard energy consumption as a linear problem, which is greatly limited by the choice of influencing factors, so it is difficult to be rational and scientific. However, the machine learning algorithm used in this article can consider more influencing factors, which can turn the energy consumption problem into a nonlinear problem with higher rationality and adaptability.
The main contents of the article are as follows: the second section describes the mathematical principle of robust principal component analysis and PSO-LSSVM optimized by the Tabu search algorithm; the third part proves that the proposed forecasting model has higher prediction accuracy, generalization ability, and higher training speed by compared results with traditional LSSVM and PSO-LSSVM models, and then we apply the model to forecast the energy consumption in China from 2017 to 2030; the fourth part makes forward-looking conclusions according to the results of the RPCA-TS-PSO-LSSVM forecasting model.
4. Conclusions
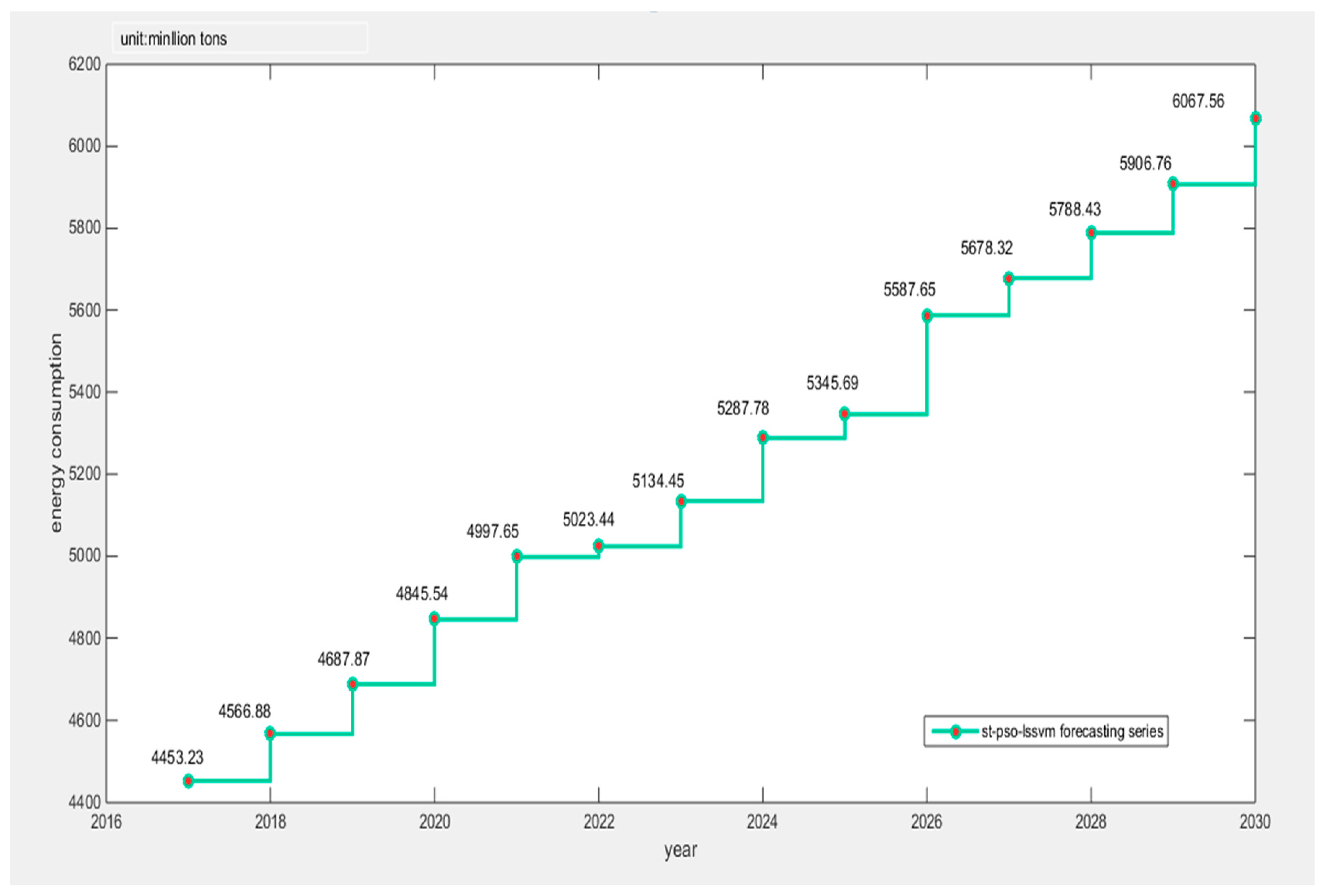
This article combined the Tabu search algorithm with the PSO-LSSVM algorithm to construct the TS-PSO-LSSVM forecasting model for prediction of China’s energy consumption. Because the study of energy consumption is a complex issue and energy consumption is influenced by a multitude of factors, we adopted RPCA to select the main factors of GDP, population, industrial structure and energy consumption structure, urbanization, energy intensity, total imports and exports, fixed asset investment, energy efficiency, energy industry fixed investment, household consumption, and level of noise reduction. The main influential factors can contain information about other factors, while reducing the complexity of the studied factors. Compared with the traditional PCA, RPCA was proved to be better for generalizing information. After selecting the five main influential factors, we used data from 1996 to 2010 as the training set for the TS-PSO-LSSVM, PSO-LSSVM, and LSSVM forecasting models, and data from 2011 to 2016 as the test set. Then, we compared the results from forecasting of the test set form the perspective of both accuracy and operation speed. Finally, we applied the RPCA-TS-PSO-LSSVM forecasting model to forecast the future energy consumption of China in 2017–2030. We found that China’s energy consumption will break through 5000 million tons in 2020, and energy consumption will increase year by year, eventually reaching 6000 million tons in 2030. Our final conclusions and policy recommendations are as follows:
(1) From 2018 to 2030, China’s energy consumption shows a gradual upward trend, but the growth rate is gradually tightening. From the perspective of technological progress, this forecast proves that China’s energy efficiency will increase year by year.
(2) China’s energy consumption economy will transfer into the stage of diminishing returns around 2026. At that time, excessive energy investment will not bring about sustained GDP growth. Therefore, China should give priority to improving energy efficiency in the future, and continue to develop renewable energy technologies. Meanwhile, China needs to look for better opportunities in the energy investment field and continue to reduce pollutants and carbon emissions.
(3) China should pay more attention to the development of energy consumption terminal power for energy conservation and emissions reduction of the international community. At the same time, in the field of energy investment, China must attach importance to the development of the Belt and Road and grasp the opportunities of international cooperation in energy-based society. According to the forecasting results, the energy strategy of the next ten years must be carefully planned.
The forecasting results and corresponding conclusions drawn in this article have laid a strong foundation for our future research, especially the research hotspots of China’s carbon emission related to energy consumption and China’s investment ability in Belt and Road countries.