Flow Separation Control in a Curved Diffuser with Rigid Traveling Wave Wall and Its Mechanism
Abstract
:1. Introduction
2. Numerical Simulation of Flow Control in a Curved Diffuser Using Traveling Wave Wall
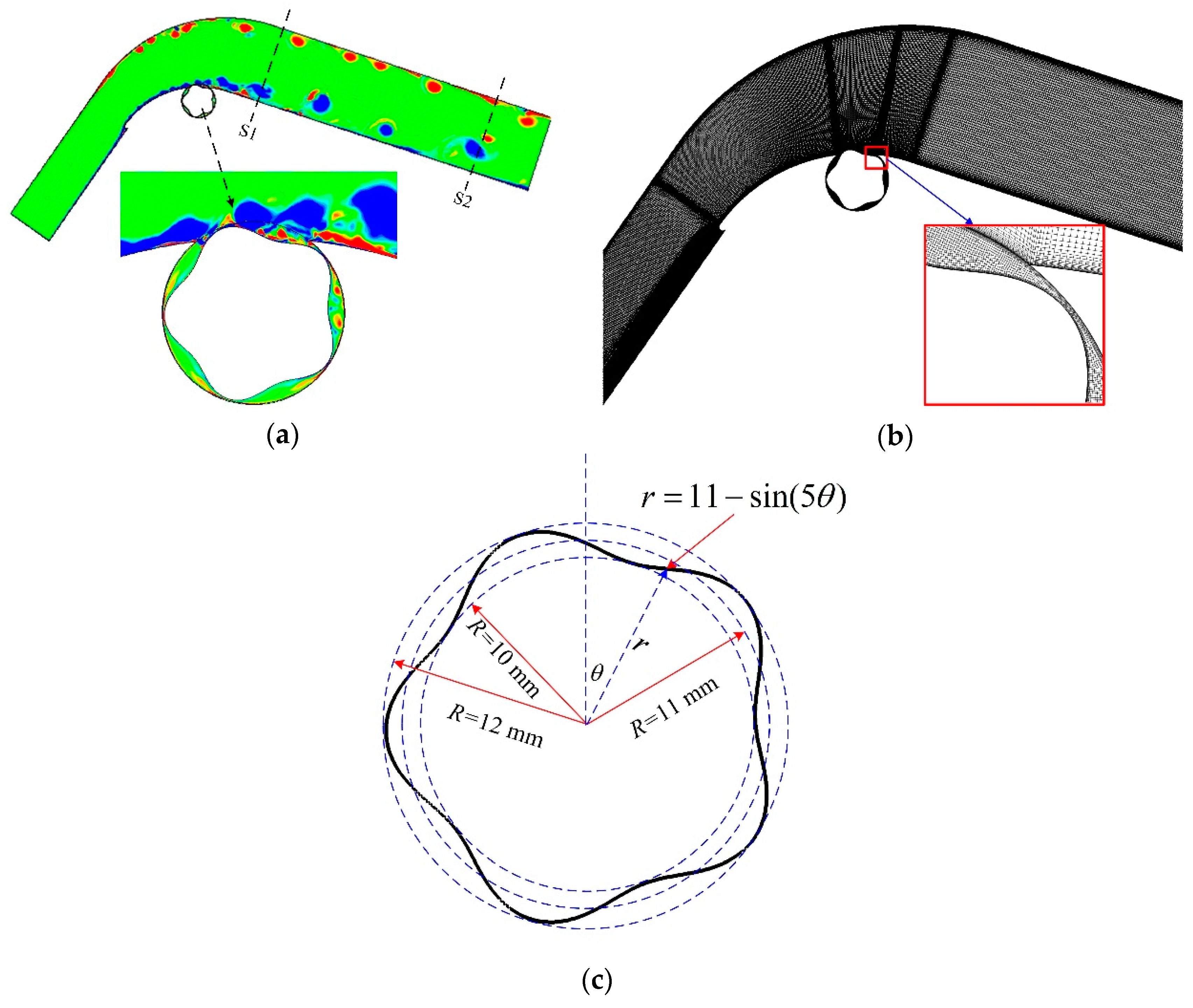
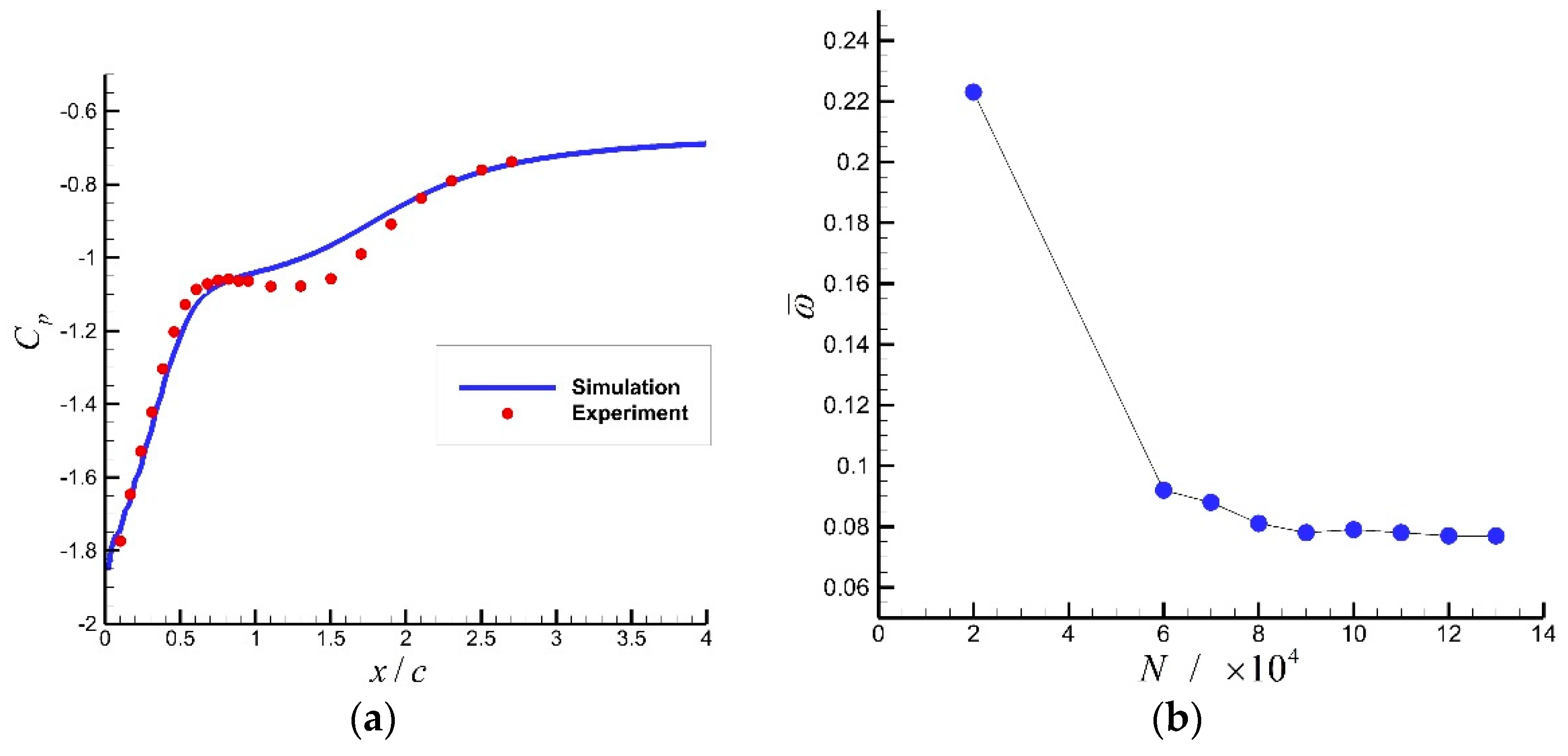
2.1. Diffuser and Its Numerical Method
2.2. Dimensionless Parameters and Evaluation Indexes of Control Effect
2.3. Results and Analysis of the Numerical Simulation
3. Nonlinear Simplified Model and Its Analysis
3.1. Duffing-Based Model for Traveling Wave Control
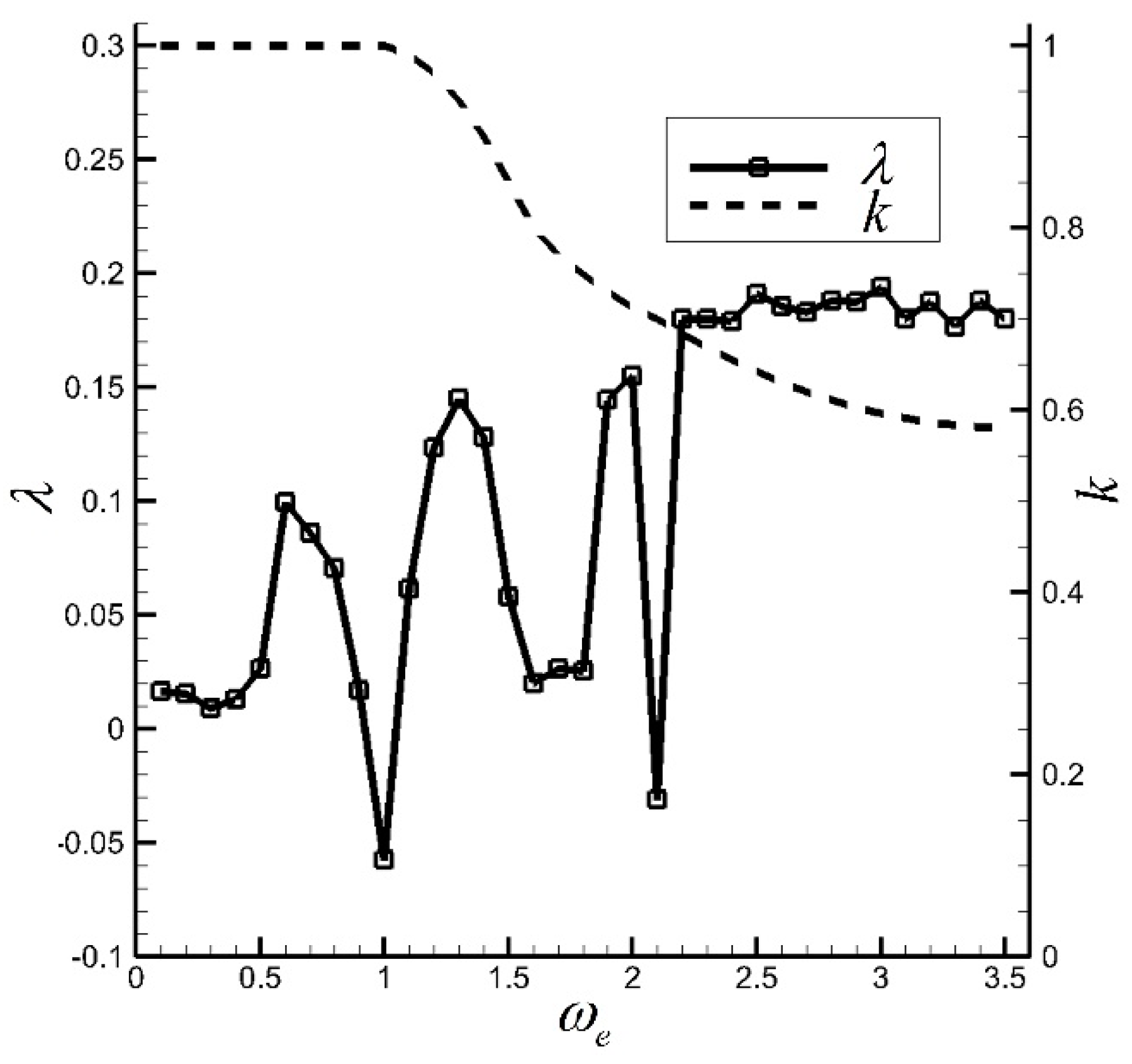
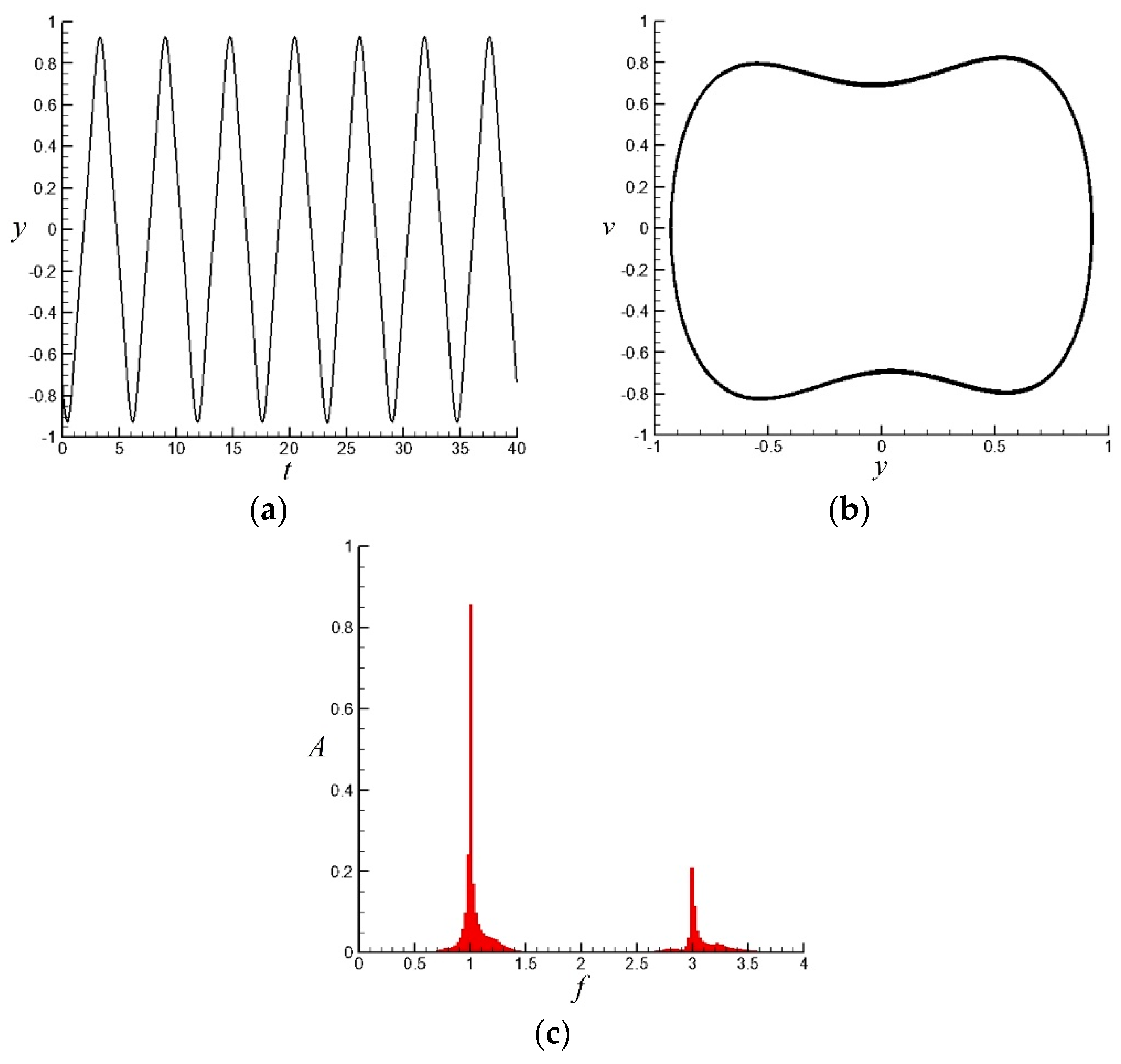
3.2. Characteristics of the Nonlinear Simplified Model without and with Traveling Wave Wall Control
4. Mechanism Analysis of Flow Control Using Traveling Wave Wall
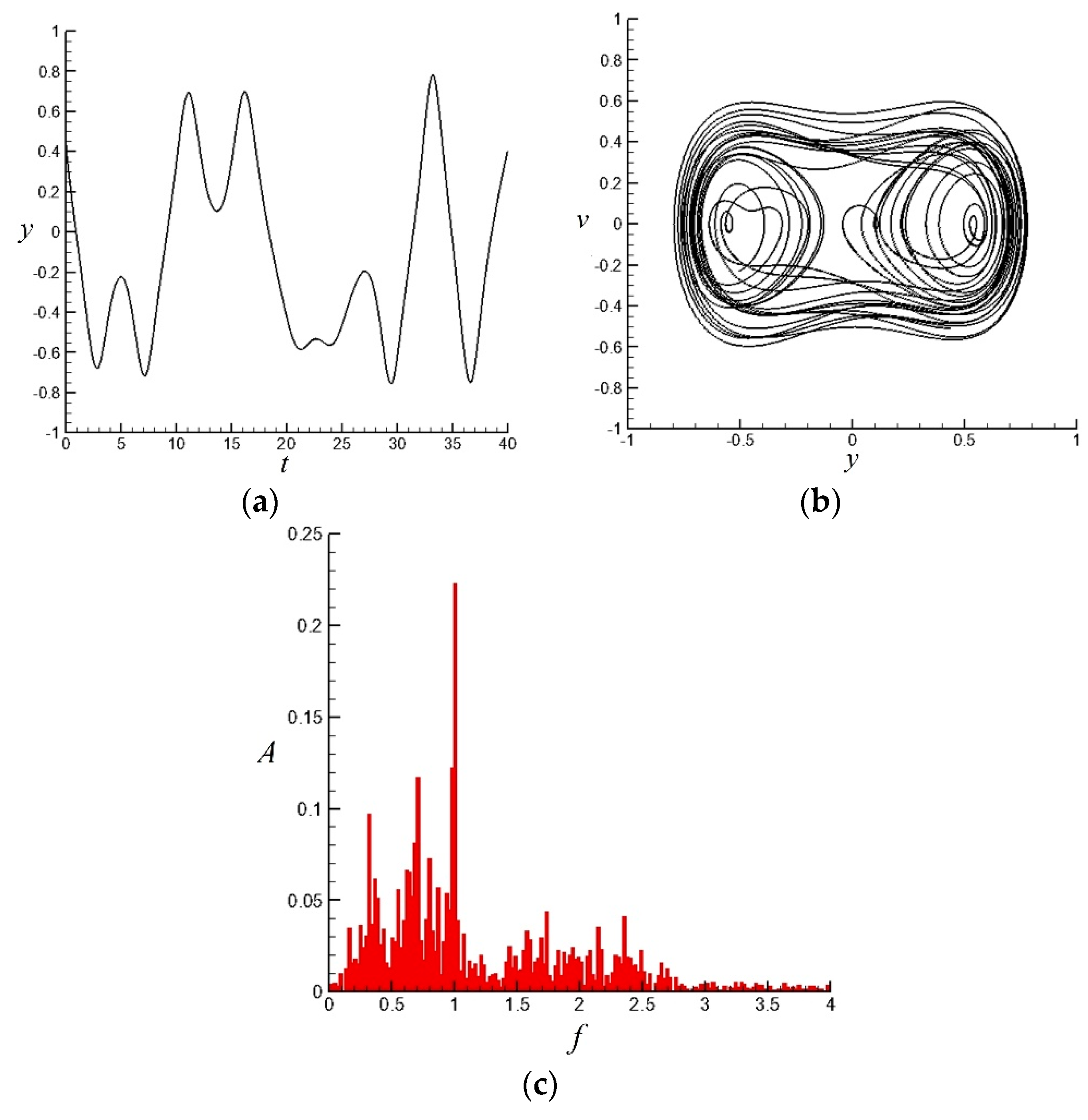
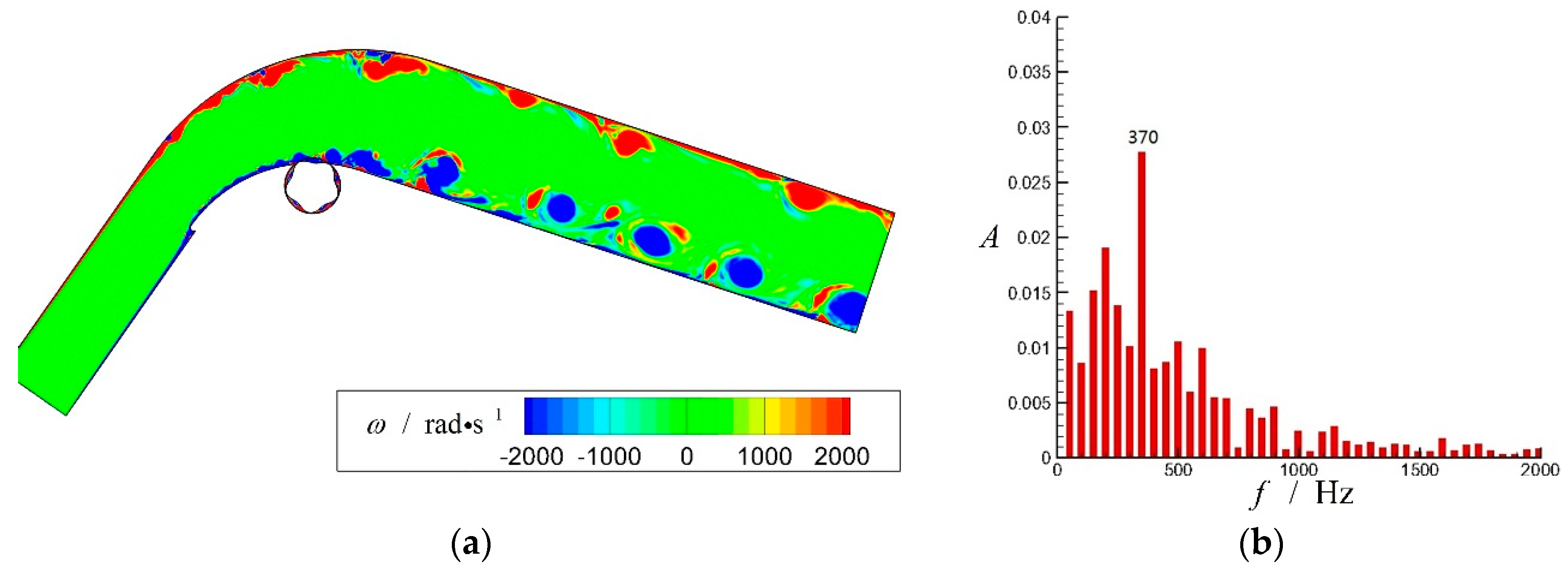
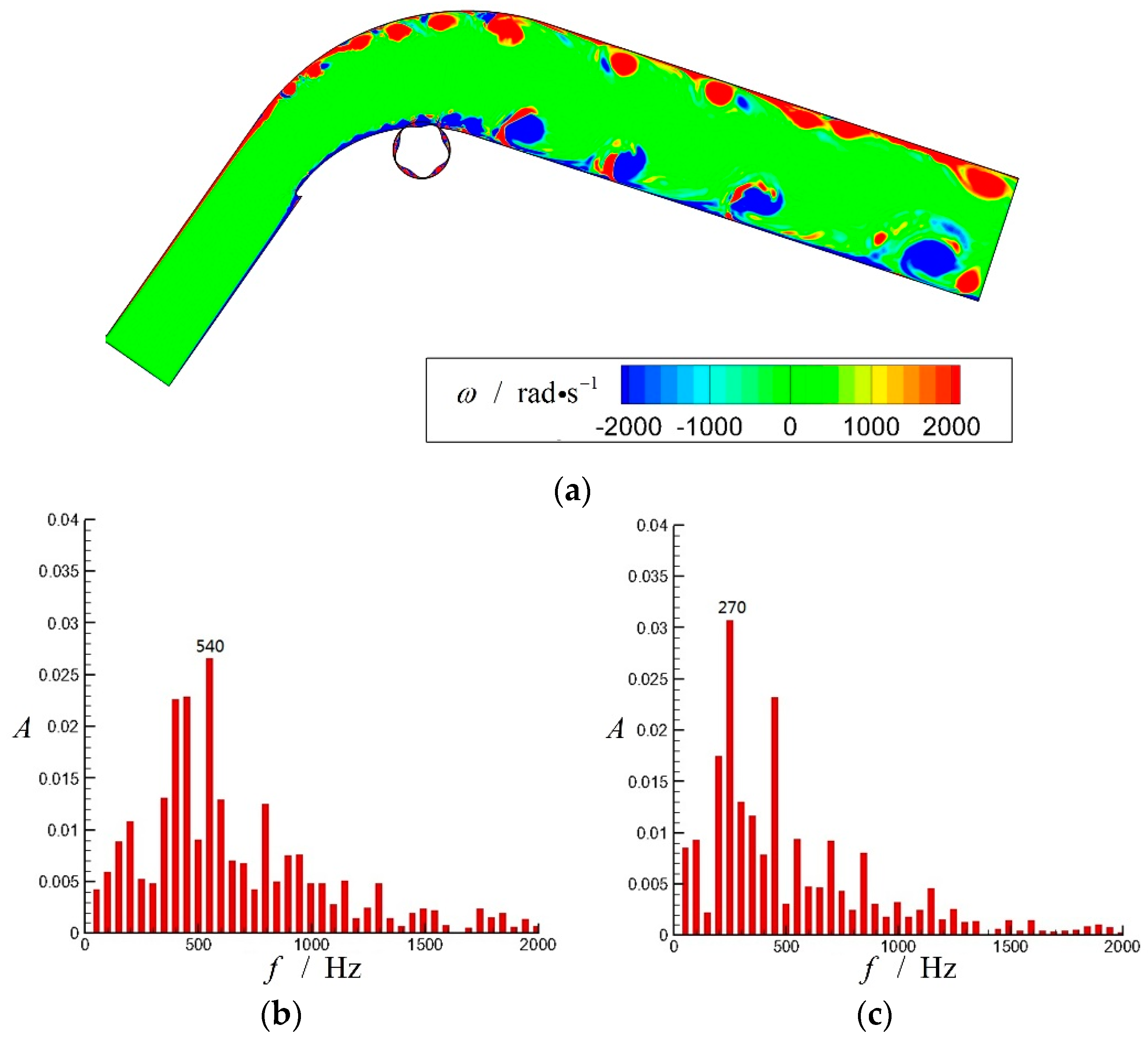
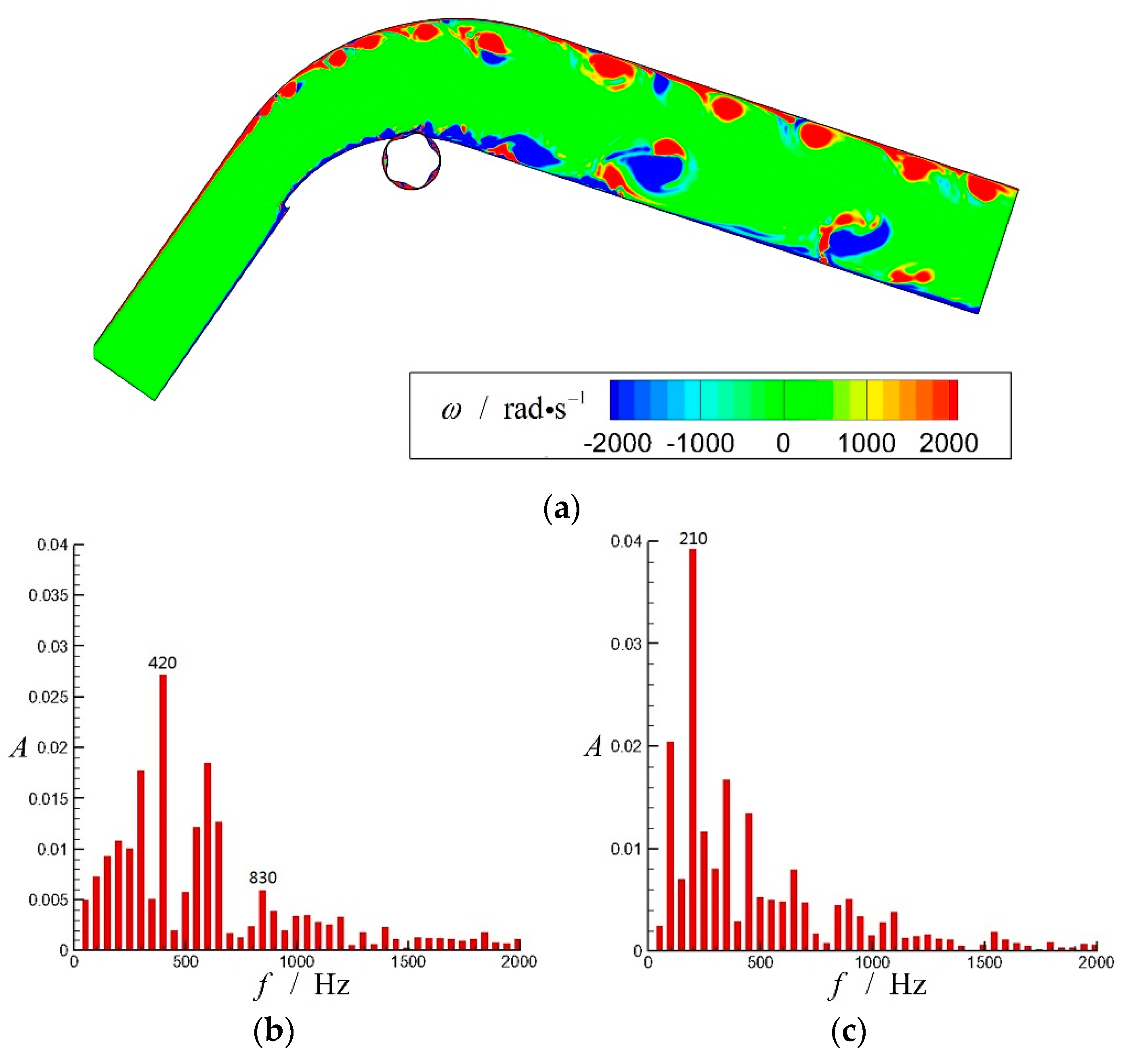
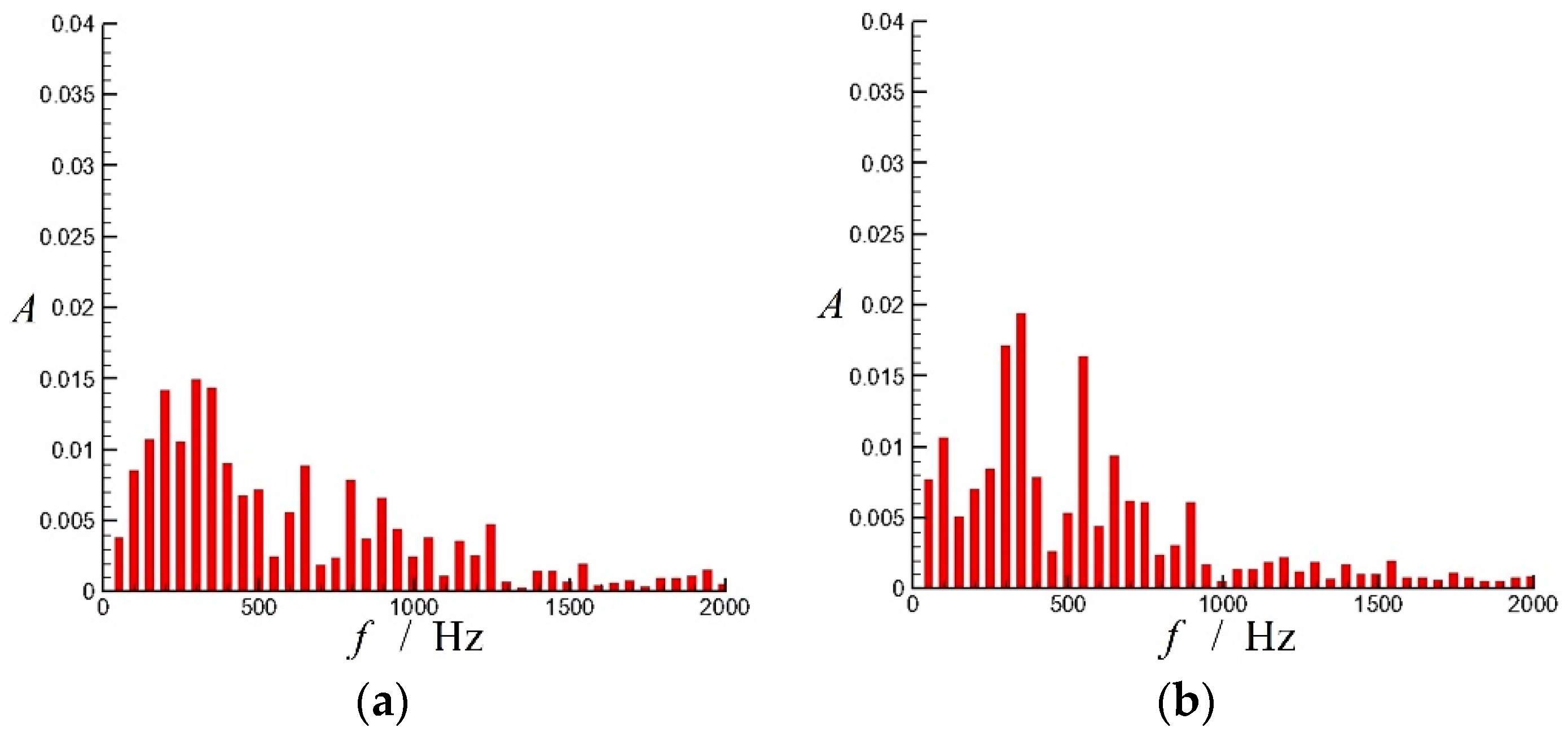
4.1. FFT Analysis of the Diffuser without Flow Control and with Typical Control of Traveling Wave Wall
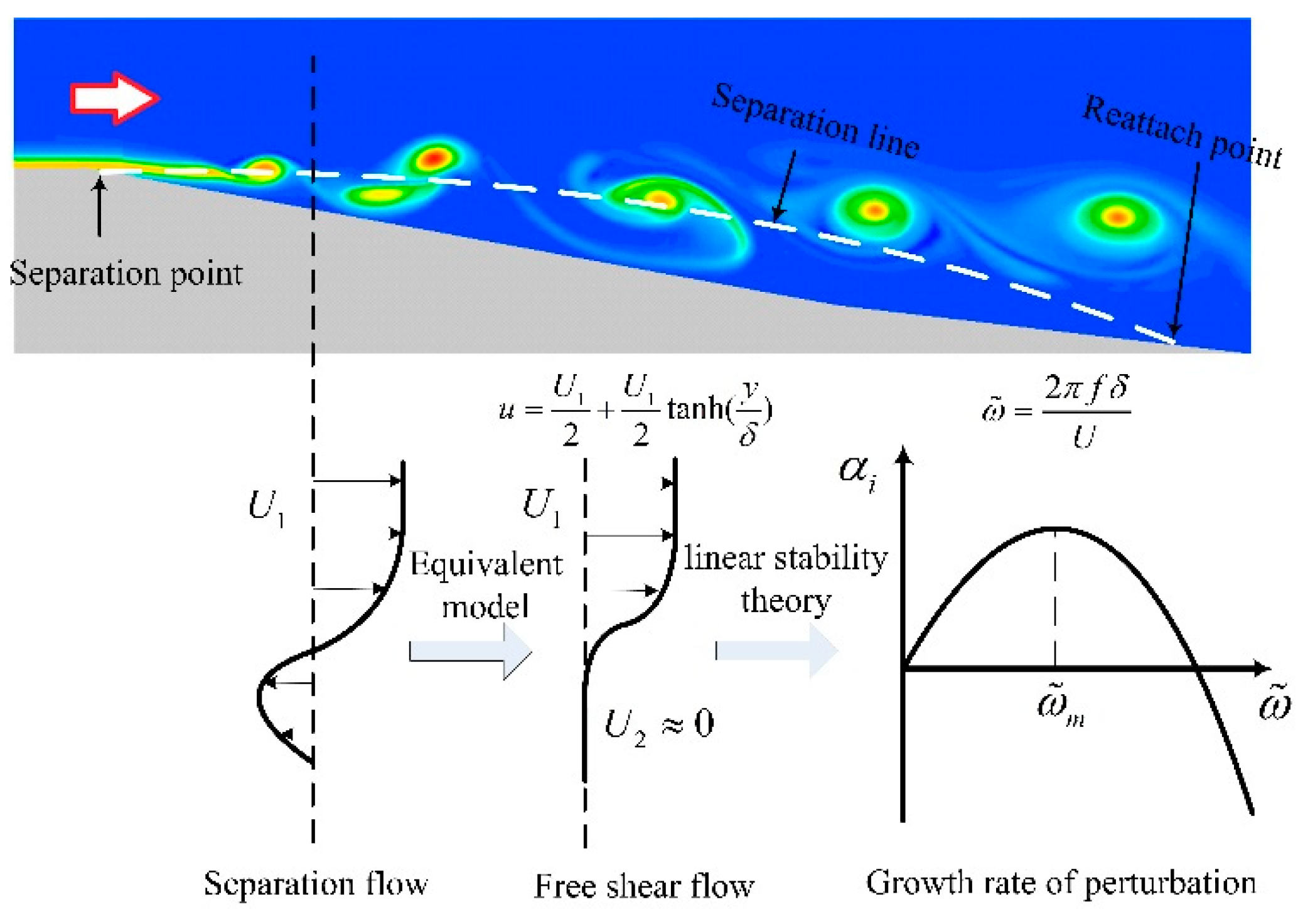
4.2. Free Shear Flow Stability Interpretation
4.3. Mechanism Analysis of Flow Control Using Traveling Wave Wall
5. Conclusions
- (1)
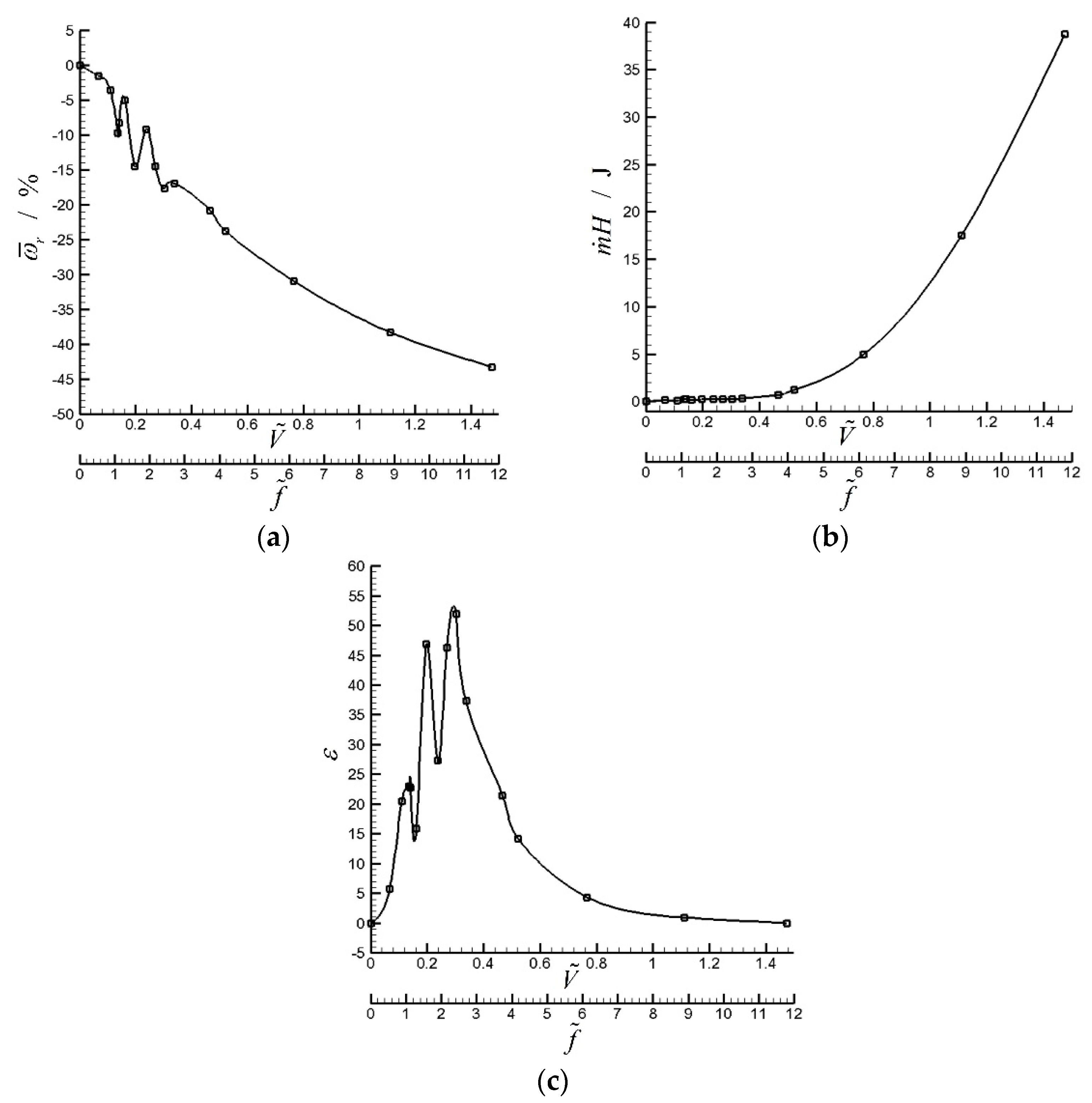
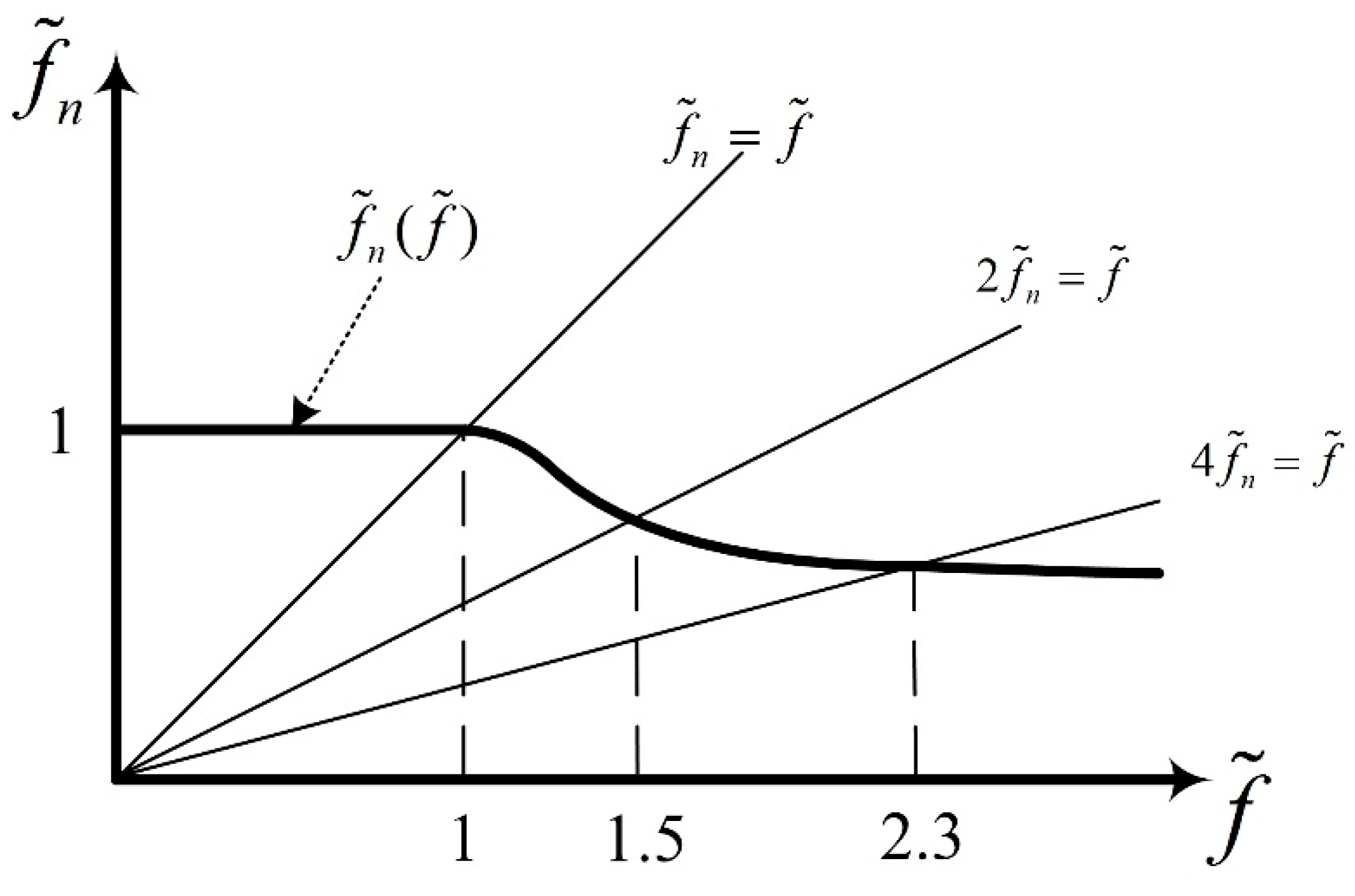
- Numerical simulation of a diffuser controlled by a rigid traveling wave wall is performed, and a parameter named energy efficiency is defined to evaluate the control effect. In this case, energy efficiency increases first and then decreases as the phase velocity or the reduced frequency of the traveling wave wall increases. However, three discrete reduced frequencies of 1, 1.5, and 2.3 have better control effect than the adjacent frequencies, and the corresponding relative total pressure loss coefficients are about –10%, –15%, and –18%, respectively. This property serves as a unique characteristic of traveling wave wall control. Also, the maximum energy efficiency is about 50, which means the traveling wave wall control is very economical. Both of the high effectiveness and economy indicate the engineering practicability of traveling wave wall controls.
- (2)
- Duffing-based nonlinear simplified model for traveling wave wall control is used. The interaction of the traveling wave wall to this dynamic system is modeled as a periodic external excitation and the change in natural frequency. External periodic excitation, which imitates the form of a K–H wave, is added into the model. Thus, the complete nondimensional form of the model can be stated as:
- (3)
- With a given k, which is a function of reduced frequency, the characteristic of the simplified model is obtained using MLE. MLE is considerably decreased when the reduced frequencies equal 1, 1.6, and 2.1. This case indicates high orderliness compared that of adjacent frequencies. This deduction is supported by the time–displacement and velocity–displacement phase diagrams and FFT analysis of displacement. Furthermore, the same phenomenon in the numerical simulation reflects that the nonlinear model can effectively explain the behavior of such chaotic flows.
- (4)
- FFT analysis of numerical simulation proves the red shift of natural frequency and merging of vortices, which are also theoretically explained by linear stability theory of free shear layers.
- (5)
- Using numerical simulation, a simplified nonlinear model, FFT analysis, and linear stability theory, three mechanisms are found responsible for the peculiar phenomena in traveling wave wall control: unitary orderliness of frequency, red shift of the natural frequency, and merging of vortices. Therefore, as phase velocity increases, natural frequency drops continuously. The merging of vortices results in that the reduced frequency is one, two, or four times the natural frequency. This condition will strengthen the dominant separation vortices and make the flow field orderly, thereby resulting in good control effect.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hertel, H. Structure Form Movement; Reinhold: New York, NY, USA, 1966. [Google Scholar]
- Choi, K.S. Emerging Techniques in Drag Reduction; John Wiley & Sons: London, UK, 1996. [Google Scholar]
- Wu, C.J.; Wang, L.; Wu, J.Z. Suppression of the Von Karman Vortex Street Behind a Circular Cylinder by a traveling Wave Generated by a Flexible Surface. J. Fluid Mech. 2007, 574, 365–391. [Google Scholar] [CrossRef]
- Wu, C.J.; Xie, Y.Q.; Wu, J.Z. “Fluid Roller Bearing” Effect and Flow Control. Acta Mech. Sin. 2003, 19, 476–484. [Google Scholar]
- Wu, J.M.; Wu, J.Z.; Wu, C.J.; Vakili, A.D. Preliminary Study of Nonlinear Flow over Traveling Wavy Wall. Int. Symp. Nonsteady Fluid Dyn. 1990, 92, 359–368. [Google Scholar]
- Wu, J.Z.; Wu, J.M. Vorticity Dynamics on Boundaries. Adv. Appl. Mech. 1996, 32, 119–275. [Google Scholar]
- Yang, Z.; Wu, J.Z. Drag Reduction by Axisymmetric Traveling Wavy Wall. J. Univ. Sci. Technol. China 2005, 35, 471–479. [Google Scholar]
- Wu, Q.Y. Study on Numerical Simulation of Active Control by Using Traveling Wave Wall of Flow Around a Circular Cylinder. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2013; pp. 37–38. (In Chinese). [Google Scholar]
- Chen, W.; Liu, Y.; Hu, H. Suppression of Vortex Shedding from a Circular Cylinder by using a Traveling Wave Wall. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014. AIAA 2014-0399. [Google Scholar]
- Zheng, X.Q.; Zhou, X.B.; Zhou, S. Investigation on a type of flow control to weaken unsteady separated flows by unsteady excitation in axial flow compressors. J. Turbomach. 2005, 127, 489–496. [Google Scholar] [CrossRef]
- Greenblatt, D.; Wygnanski, I.J. The Control of Flow Separation by Periodic Excitation. Prog. Aerosp. Sci. 2000, 36, 487–545. [Google Scholar] [CrossRef]
- Chatterjee, A. An introduction to the proper orthogonal decomposition. Curr. Sci. 2000, 78, 809–817. [Google Scholar]
- Lumley, J.L. The Structure of Inhomogeneous Turbulent Flows. In Atmospheric Turbulence and Radio Wave Propagation; Nauka: Moscow, Russian, 1967; pp. 166–178. [Google Scholar]
- Vinuesa, R. Synergetic Computational and Experimental Studies of Wall-Bounded Turbulent Flows and Their Two-Dimentionality; Illinois Institute of Technology: Chicago, IL, USA, 2013. [Google Scholar]
- Qi, L.; Zou, Z.; Wang, P.; Cao, T.; Liu, H. Control of secondary flow loss in turbine cascade by streamwise vortex. Comput. Fluids 2012, 54, 45–55. [Google Scholar] [CrossRef]
- Batcheler, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 1967. [Google Scholar]
- Kovacic, I.; Brennan, M.J. The Duffing Equation: Nonlinear Oscillators and Their Behavior; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Huang, G.; Lu, W.; Zhu, J.; Fu, X.; Wang, J. A nonlinear dynamic model for unsteady separated flow control and its mechanism analysis. J. Fluid Mech. 2017, 826, 942–974. [Google Scholar] [CrossRef]
- Zhuang, L.X.; Yi, X.Y.; Ma, H.Y. Fluid Mechanics, 2nd ed.; Press of University of Science and Technology of China: Hefei, China, 2012. [Google Scholar]
- Benettin, G.; Galgani, L.; Giorgilli, A.; Strelcyn, J.M. Lyapunov characteristic exponents for smooth dynamical systems; a method for computing all of them: Part I: Theory, Part II: Numerical applications. Meccanica 1980, 15, 9–20. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic non periodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Stuart, J.T. On finite amplitude oscillations in laminar mixing layers. J. Fluid Mech. 1967, 29, 417–440. [Google Scholar] [CrossRef]
- Drazinm, P.C. Hydrodynamic Stabilty, 2nd ed.; Cambridge Mathematical Library: Cambridge, UK, 2012. [Google Scholar]
- Oster, D.; Wygnanski, I. The forced mixing layer between parallel streams. J. Fluid Mech. 1982, 123, 91–130. [Google Scholar] [CrossRef]

| Part | Parameter | Value |
|---|---|---|
| Diffuser | Inlet Mach number | 0.1 |
| Inlet attack angle/degree | 9 | |
| Chord length of the blade/mm | 80 | |
| Inlet width/mm | 34.3 | |
| Outlet width/mm | 55 | |
| Traveling wave | Wavelength/mm | 13.8 |
| Wave amplitude/mm | 1 | |
| Rotation radius/mm | 11 | |
| Number of full waves | 5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, W.; Huang, G.; Wang, J.; Yang, Y. Flow Separation Control in a Curved Diffuser with Rigid Traveling Wave Wall and Its Mechanism. Energies 2019, 12, 192. https://doi.org/10.3390/en12010192
Lu W, Huang G, Wang J, Yang Y. Flow Separation Control in a Curved Diffuser with Rigid Traveling Wave Wall and Its Mechanism. Energies. 2019; 12(1):192. https://doi.org/10.3390/en12010192
Chicago/Turabian StyleLu, Weiyu, Guoping Huang, Jinchun Wang, and Yuxuan Yang. 2019. "Flow Separation Control in a Curved Diffuser with Rigid Traveling Wave Wall and Its Mechanism" Energies 12, no. 1: 192. https://doi.org/10.3390/en12010192
APA StyleLu, W., Huang, G., Wang, J., & Yang, Y. (2019). Flow Separation Control in a Curved Diffuser with Rigid Traveling Wave Wall and Its Mechanism. Energies, 12(1), 192. https://doi.org/10.3390/en12010192






