State of Charge Estimation for Lithium-Bismuth Liquid Metal Batteries
Abstract
:1. Introduction
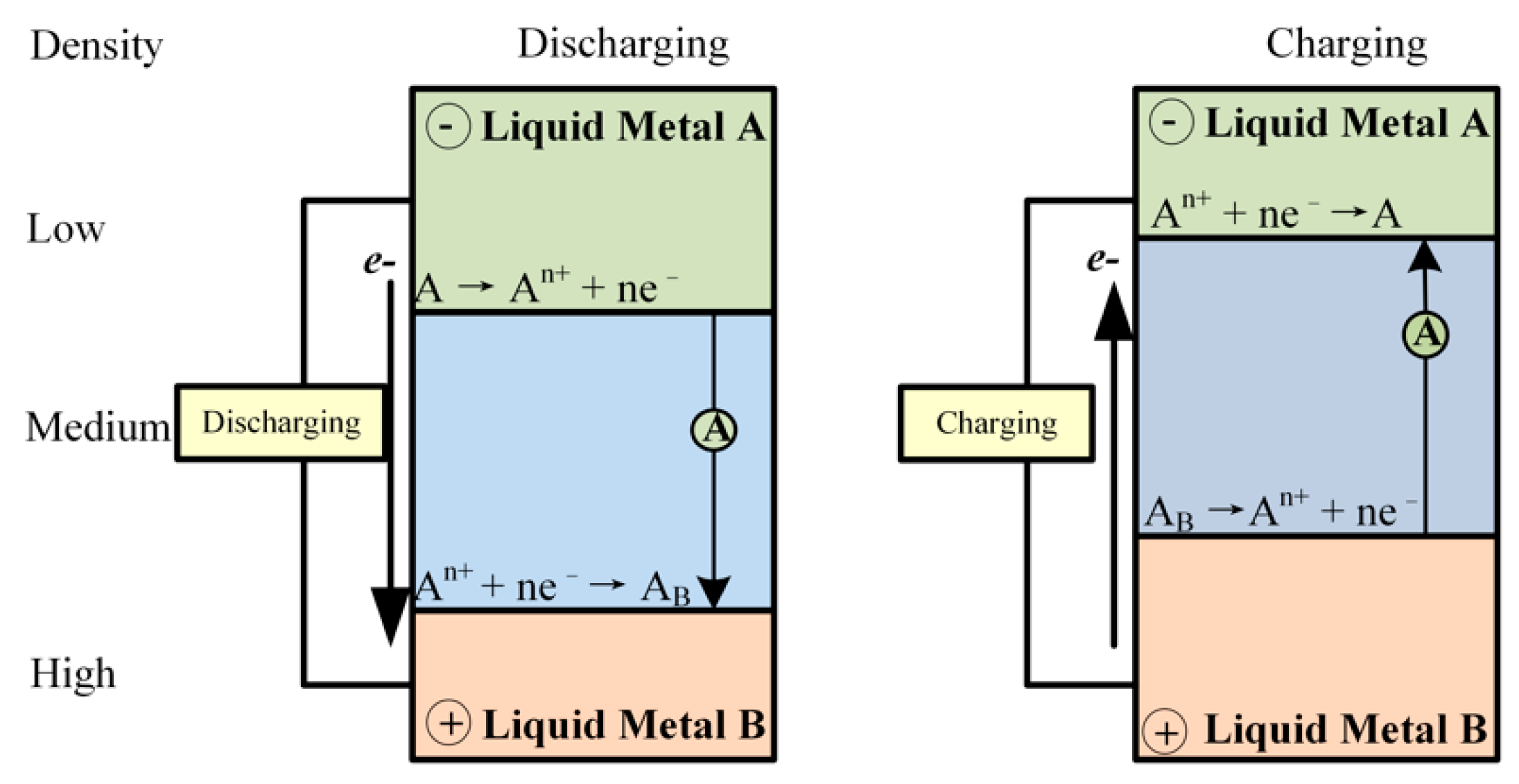
2. Lithium-Bismuth Liquid Metal Battery
3. Experimental Details and Equivalent Circuit Model
3.1. Experiment Details
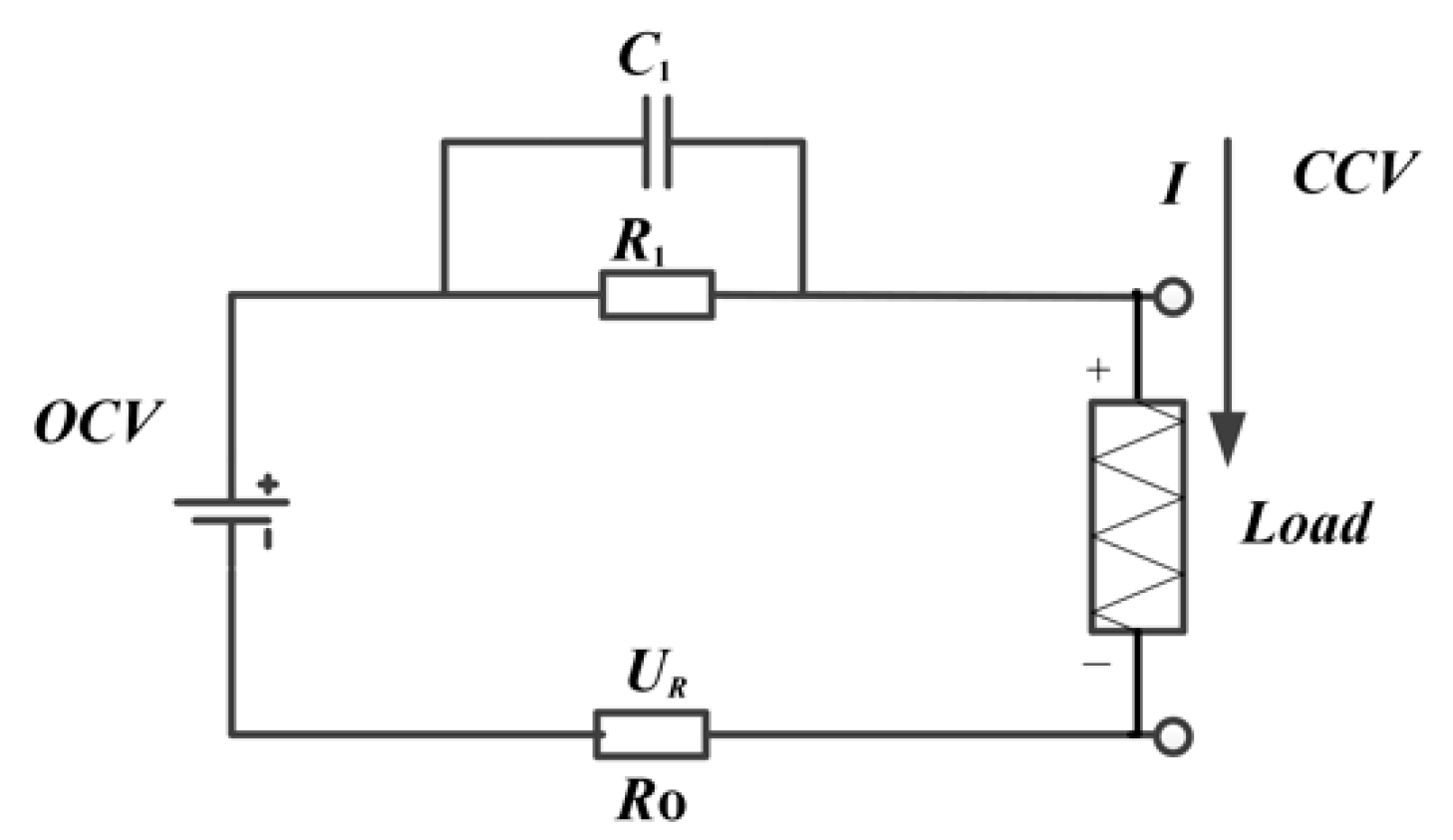
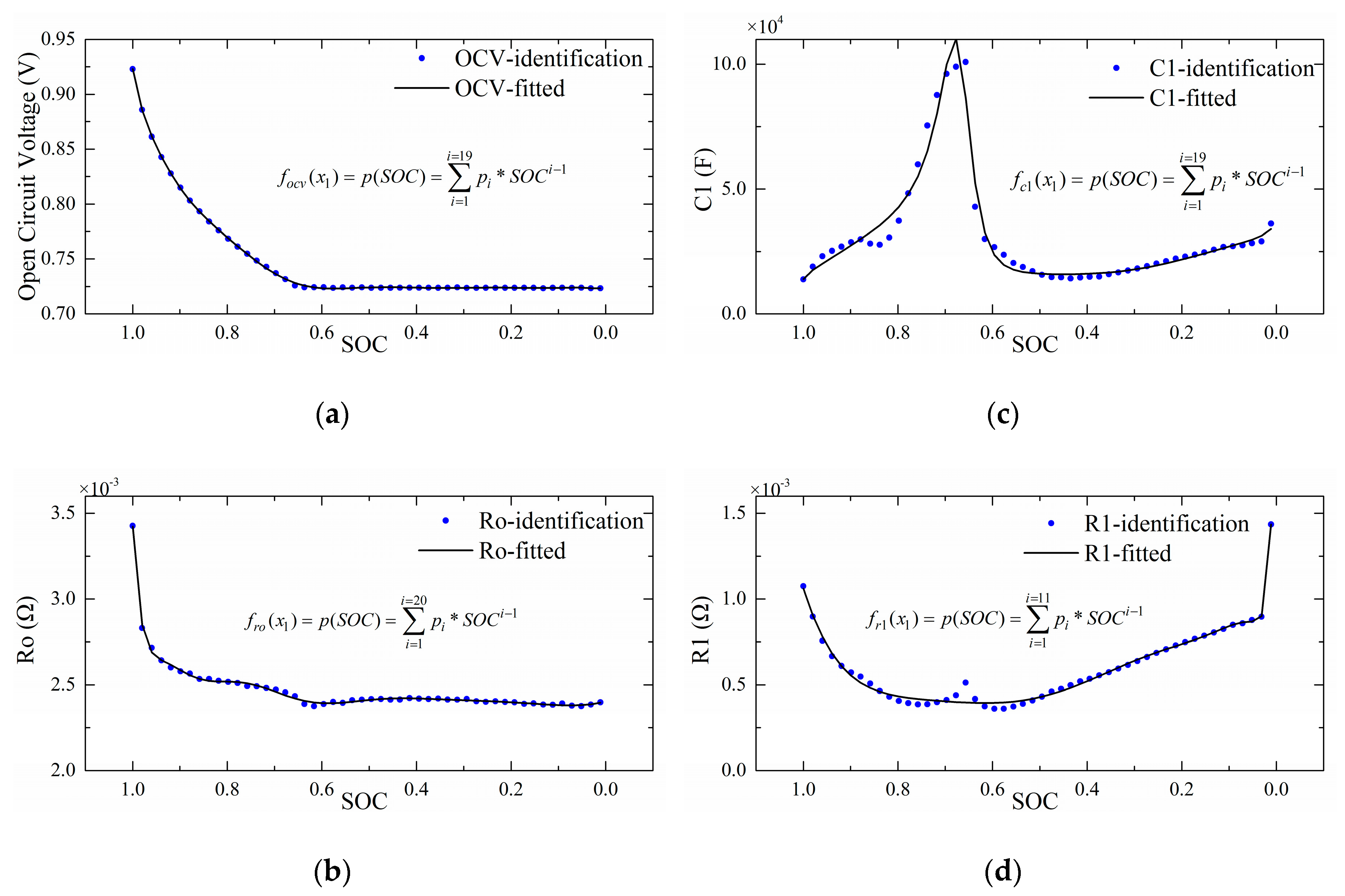
3.2. Equivalent Circuit Model and Parameter Identification
4. SoC Estimation Algorithms
4.1. Applicability of Traditional Techniques
4.1.1. Open Circuit Voltage Method
4.1.2. Ampere Hour Counting Method
4.1.3. Data-Driven Methodology
4.1.4. Model-Based Methods
4.2. Extended Kalman Filter
4.3. Unscented Kalman Filter
4.4. Particle Filter
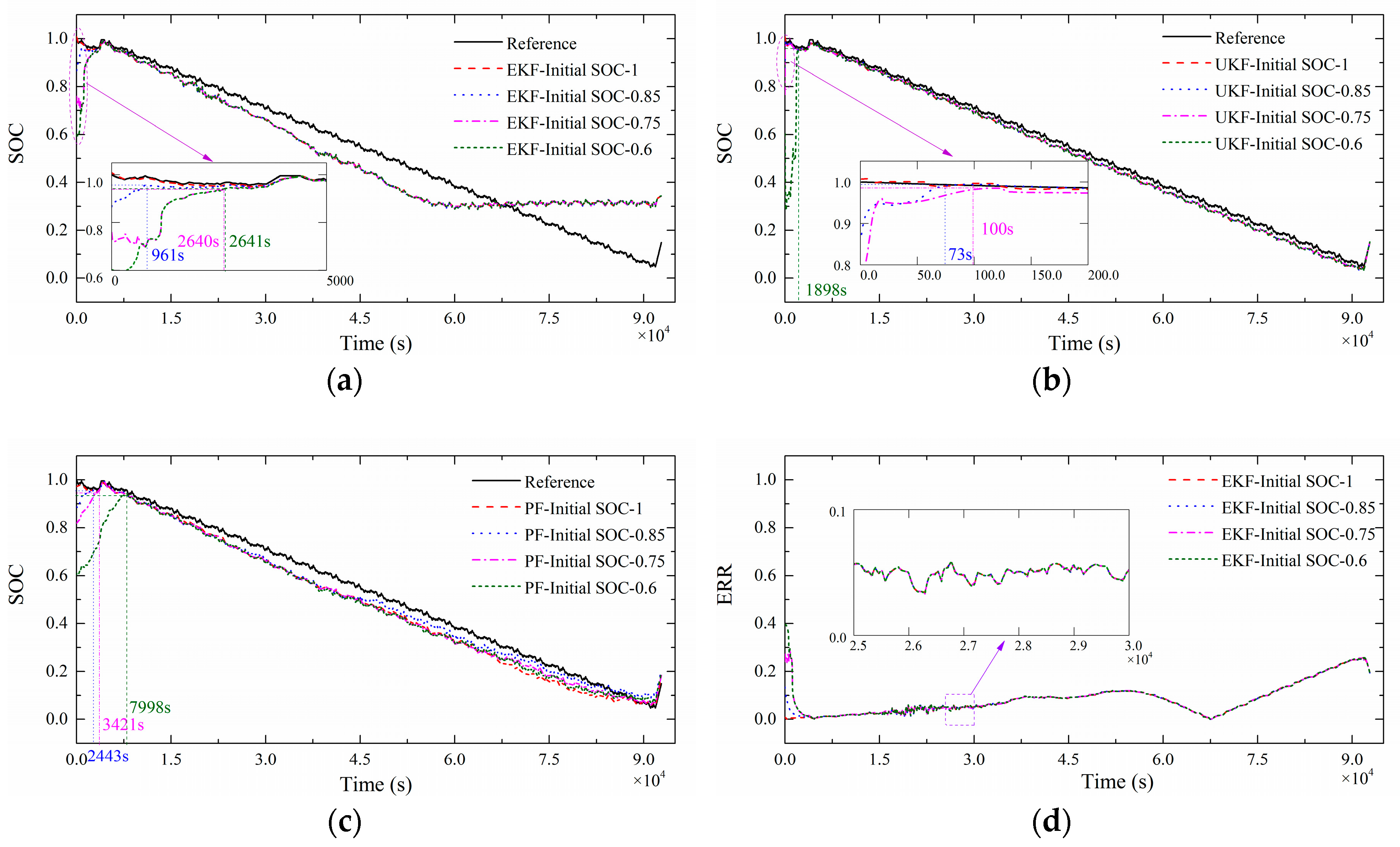
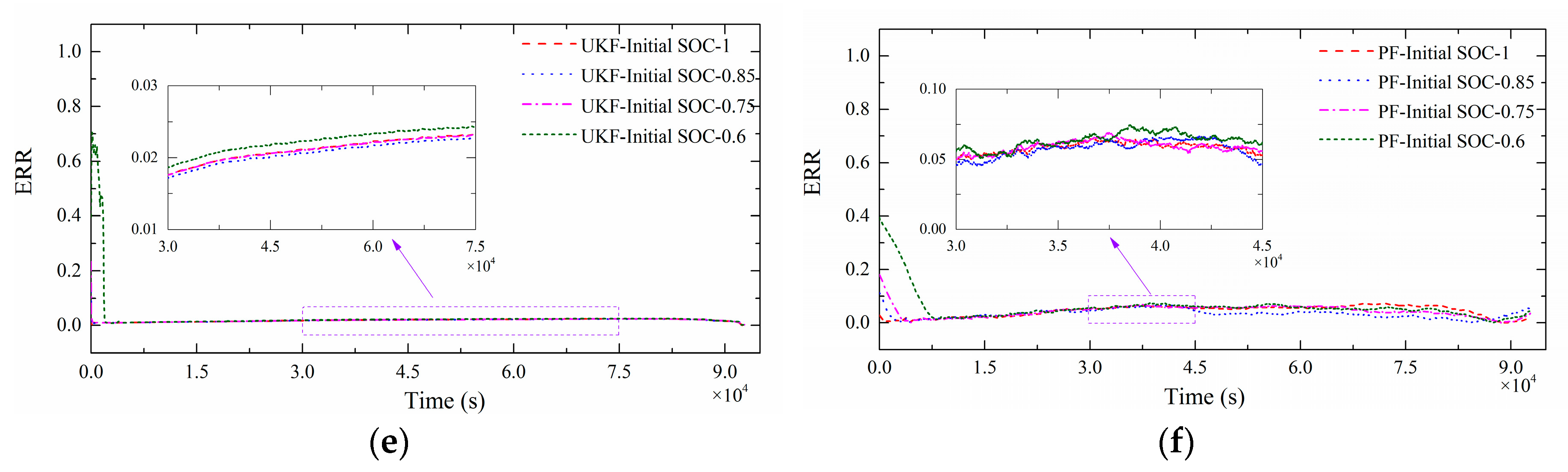
5. Results and Discussion
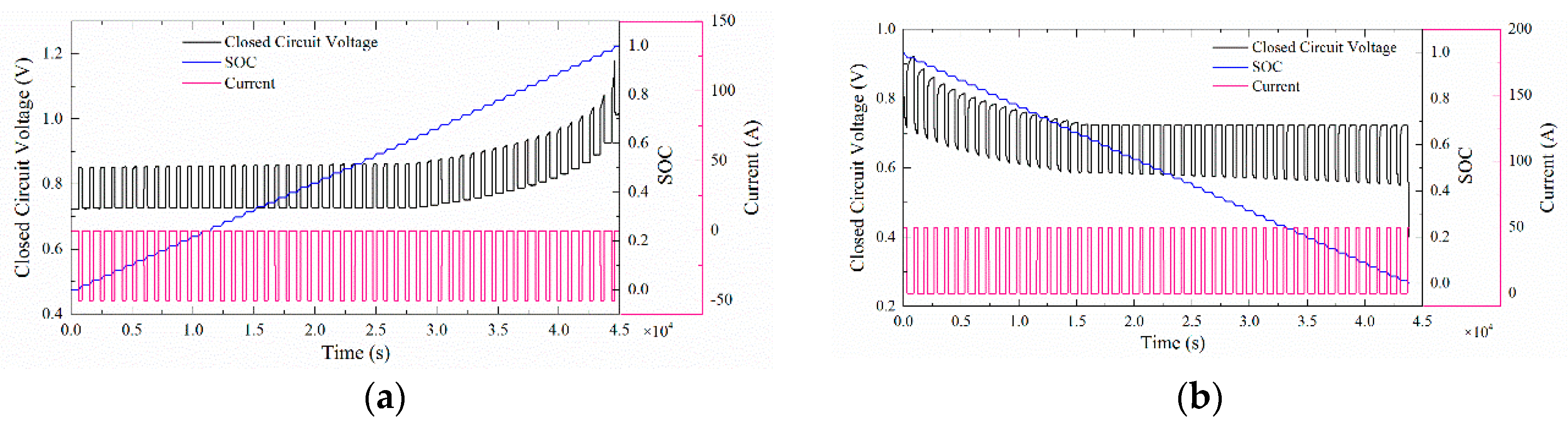
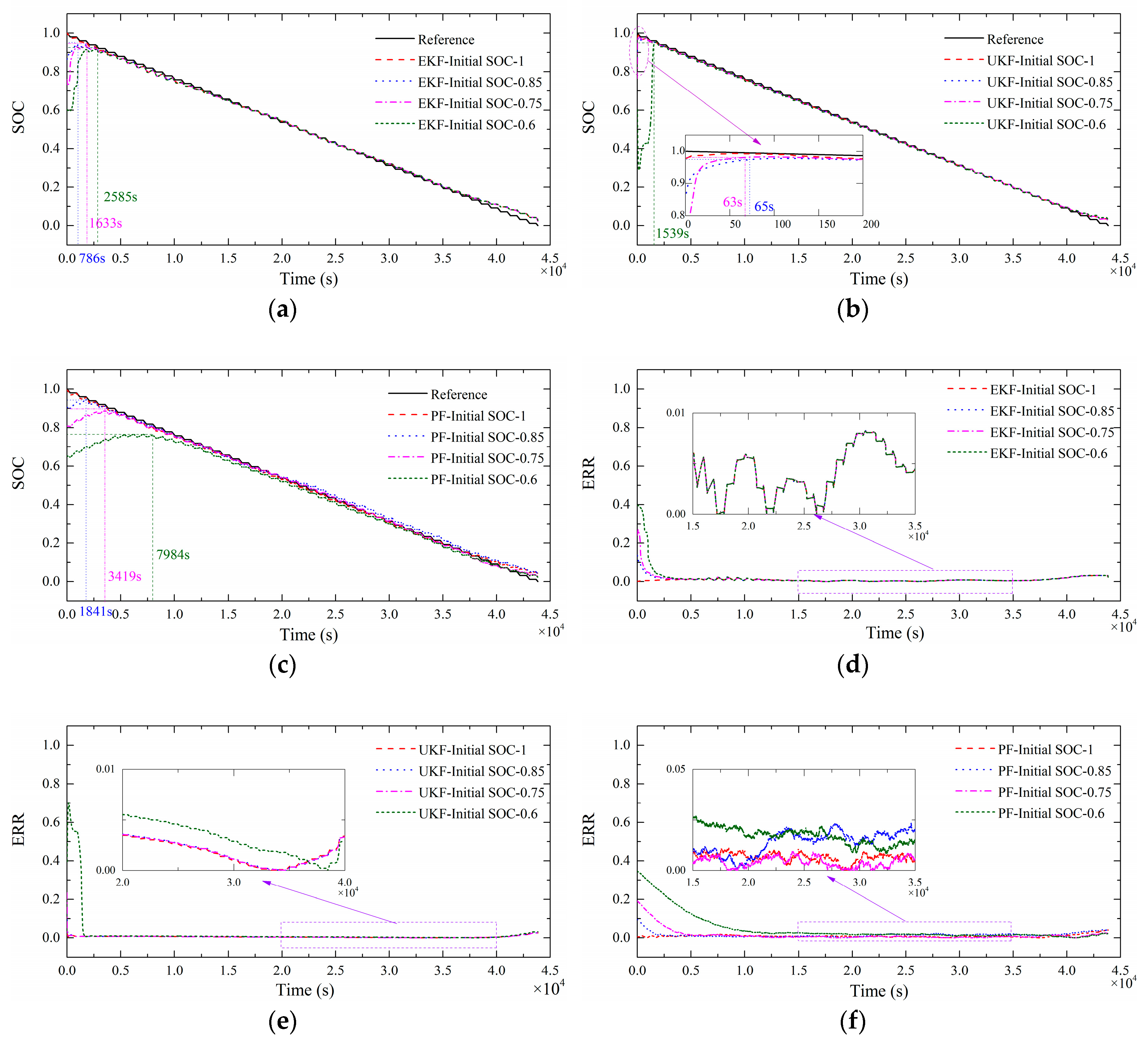
5.1. SoC Estimation Results in Pulse Discharge Mode
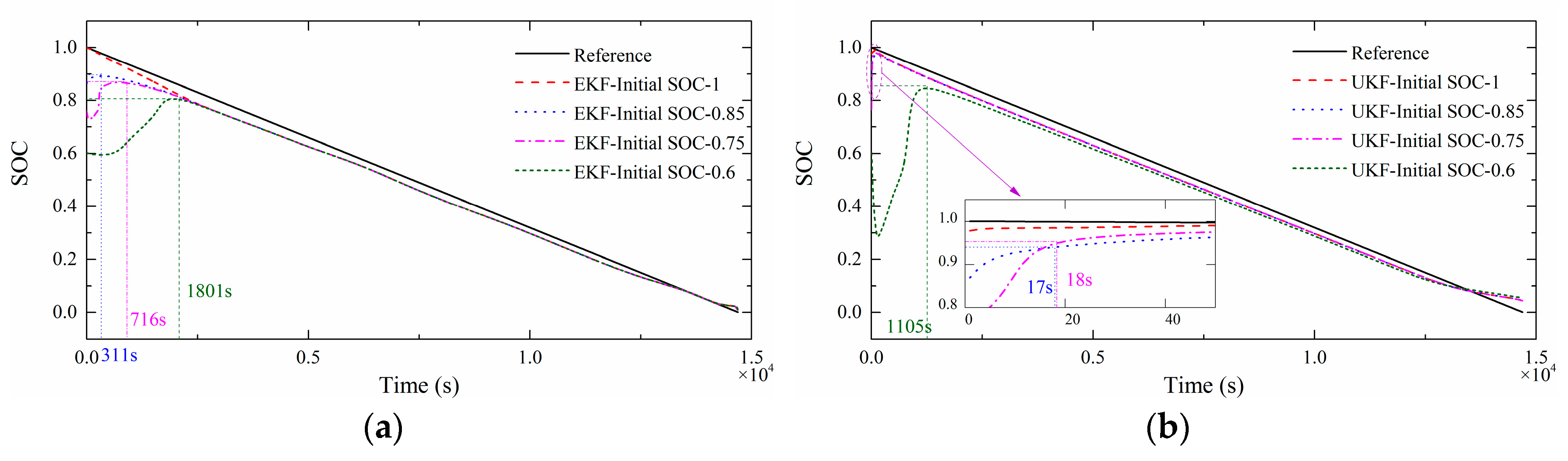
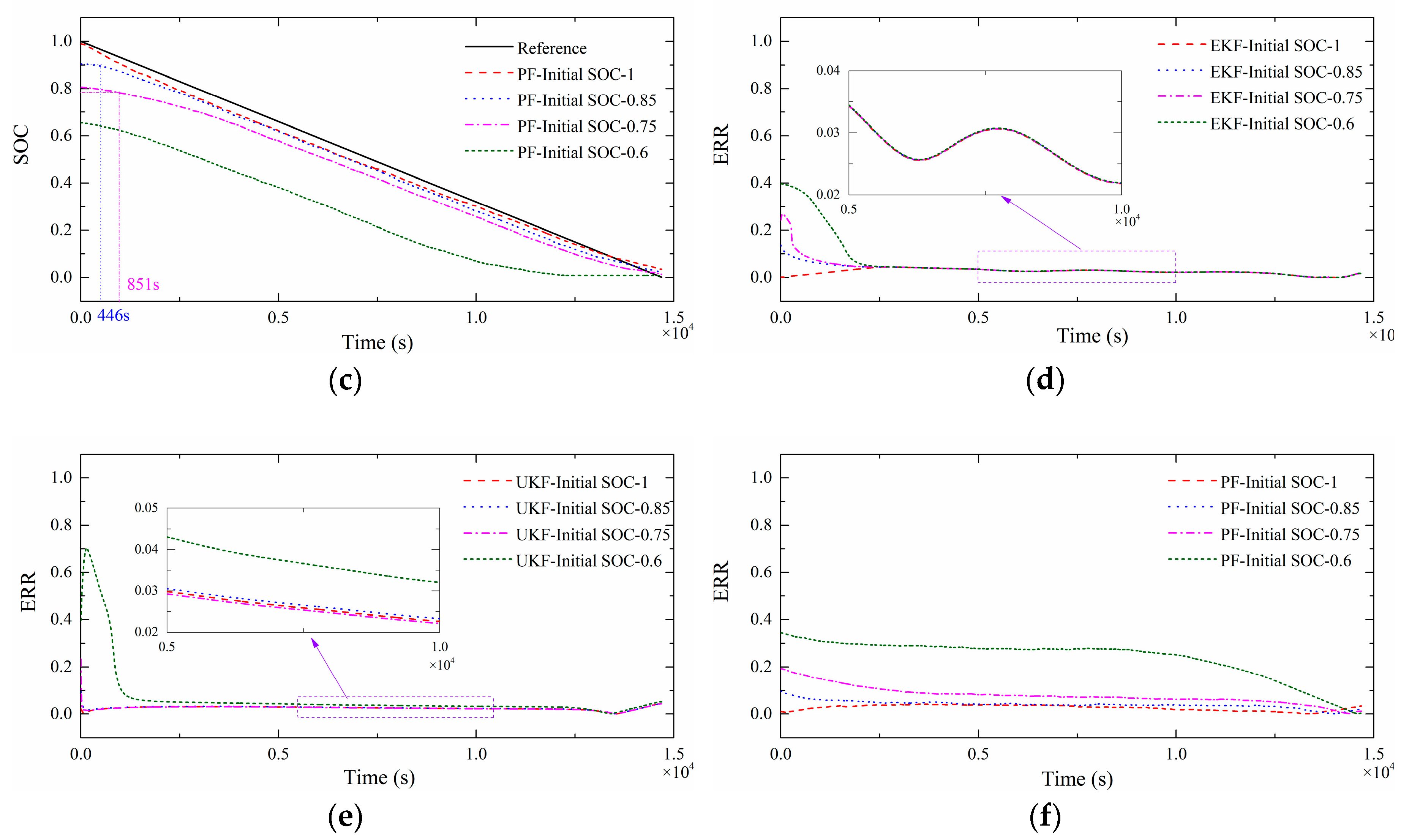
5.2. SoC Estimation Results in Current Discharge Mode
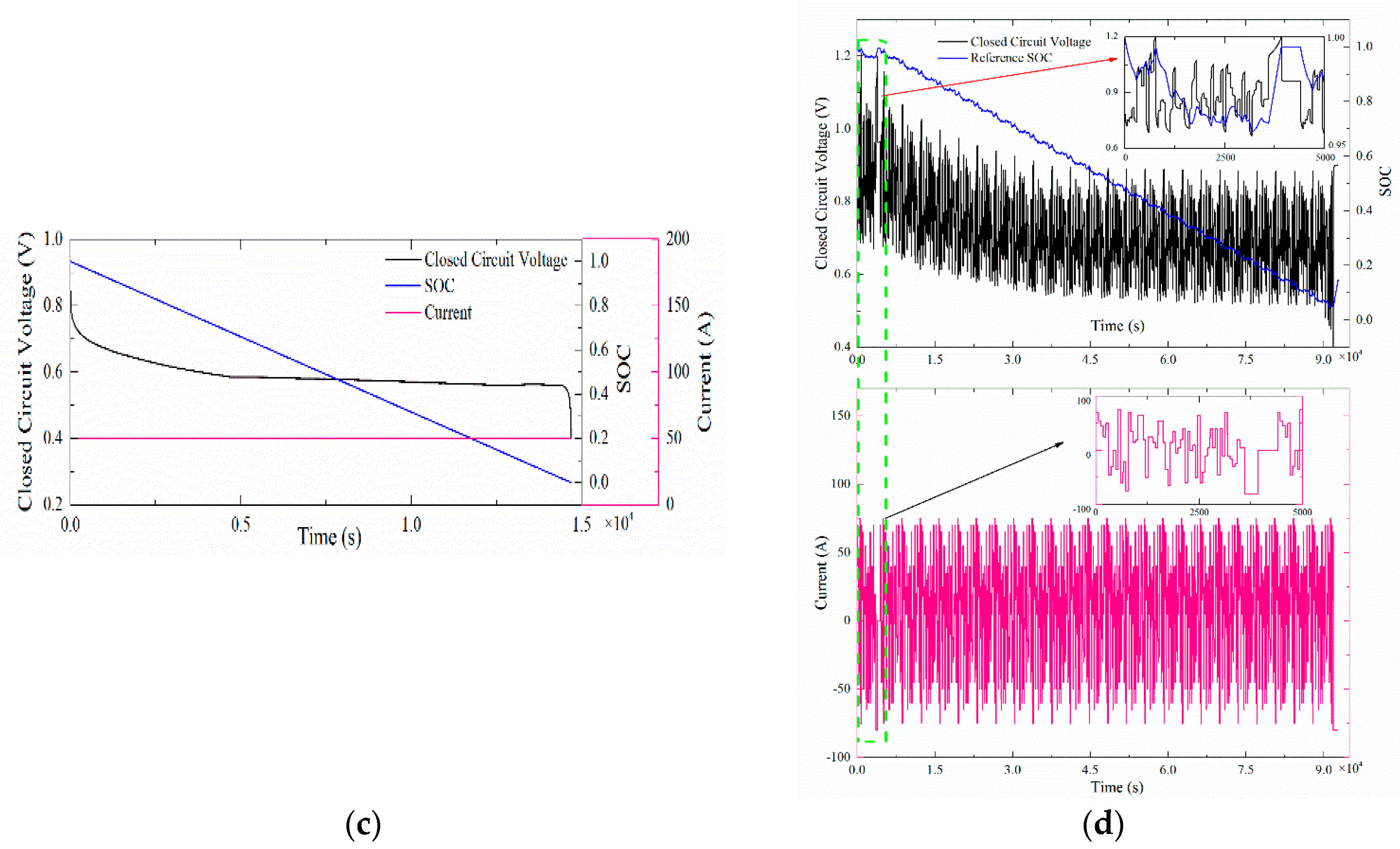
5.3. SoC Estimation Results in Hybrid Pulse Charge/Discharge
5.4. Further Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Soloveichik, G.L. Battery technologies for large-scale stationary energy storage. Annu. Rev. Chem. Biomol. Eng. 2011, 2, 503–527. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Jiang, K.; Chung, B.; Ouchi, T.; Burke, P.J.; Boysen, D.A.; Bradwell, D.J.; Kim, H.; Muecke, U.; Sadoway, D.R. Lithium-antimony-lead liquid metal battery for grid-level energy storage. Nature 2014, 514, 348–350. [Google Scholar] [CrossRef] [PubMed]
- Ashour, R.F.; Kelley, D.H.; Salas, A.; Starace, M.; Weber, N.; Weier, T. Competing forces in liquid metal electrodes and batteries. J. Power Sources 2018, 378, 301–310. [Google Scholar] [CrossRef] [Green Version]
- Bradwell, D.J.; Kim, H.; Sirk, A.H.; Sadoway, D.R. Magnesium-antimony liquid metal battery for stationary energy storage. J. Am. Chem. Soc. 2012, 134, 1895–1897. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Boysen, D.A.; Newhouse, J.M.; Spatocco, B.L.; Chung, B.; Burke, P.J.; Bradwell, D.J.; Jiang, K.; Tomaszowska, A.A.; Wang, K.; et al. Liquid metal batteries: Past, present, and future. Chem. Rev. 2013, 113, 2075–2099. [Google Scholar] [CrossRef] [PubMed]
- Newhouse, J.M. Modeling the Operating Voltage of Liquid Metal Battery Cells. Ph.D. Thesis, MIT, Cambridge, MA, USA, 2014. [Google Scholar]
- Ning, X.; Phadke, S.; Chung, B.; Yin, H.; Burke, P.; Sadoway, D.R. Self-healing Li–Bi liquid metal battery for grid-scale energy storage. J. Power Sources 2015, 275, 370–376. [Google Scholar] [CrossRef] [Green Version]
- Wei, Z.; Leng, F.; He, Z.; Zhang, W.; Li, K. Online state of charge and state of health estimation for a Lithium-Ion battery based on a data–model fusion method. Energies 2018, 11, 1810. [Google Scholar] [CrossRef]
- Liu, S.; Cui, N.; Zhang, C. An Adaptive Square Root Unscented Kalman Filter Approach for State of Charge Estimation of Lithium-Ion Batteries. Energies 2017, 10, 1345. [Google Scholar] [Green Version]
- Piller, S.; Perrin, M.; Jossen, A. Methods for state-of-charge determination and their applications. J. Power Sources 2001, 96, 113–120. [Google Scholar] [CrossRef]
- He, H.; Zhang, X.; Xiong, R.; Xu, Y.; Guo, H. Online model-based estimation of state-of-charge and open-circuit voltage of lithium-ion batteries in electric vehicles. Energy 2012, 39, 310–318. [Google Scholar] [CrossRef]
- Chiang, Y.H.; Sean, W.Y.; Ke, J.C. Online estimation of internal resistance and open-circuit voltage of lithium-ion batteries in electric vehicles. J. Power Sources 2011, 196, 3921–3932. [Google Scholar] [CrossRef]
- Lee, S.; Kim, J.; Lee, J.; Cho, B. State-of-charge and capacity estimation of lithium-ion battery using a new open-circuit voltage versus state-of-charge. J. Power Sources 2008, 185, 1367–1373. [Google Scholar] [CrossRef]
- Hu, X.S.; Sun, F.C.; Zou, Y.A. Estimation of state of charge of a lithium-ion battery pack for electric vehicles using an adaptive luenberger observer. Energies 2010, 3, 1586–1603. [Google Scholar] [CrossRef]
- Chin, C.; Gao, Z. State-of-charge estimation of battery pack under varying ambient temperature using an adaptive sequential extreme learning machine. Energies 2018, 11, 711. [Google Scholar] [CrossRef]
- Piao, C.H.; Fu, W.L.; Lei, G.H.; Cho, C.D. Online parameter estimation of the Ni-MH batteries based on statistical methods. Energies 2010, 3, 206–215. [Google Scholar] [CrossRef]
- Hansen, T.; Wang, C.J. Support vector based battery state of charge estimator. J. Power Sources 2005, 141, 351–358. [Google Scholar] [CrossRef]
- Anton, J.A.; Nieto, P.G.; Viejo, C.B.; Vilan, J.V. Support vector machines used to estimate the battery state of charge. IEEE Trans. Power Electron. 2013, 28, 5919–5926. [Google Scholar] [CrossRef]
- Hu, J.N.; Hu, J.J.; Lin, H.B.; Li, X.P.; Jiang, C.L.; Qiu, X.H.; Li, W.S. State-of-charge estimation for battery management system using optimized support vector machine for regression. J. Power Sources 2014, 269, 682–693. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Z.; Lü, Z.; Li, J.; Ji, B.; Wei, H.; Pan, H. A novel state-of-charge estimation method of lithium-ion batteries combining the Grey model and Genetic Algorithms. IEEE Trans. Power Electron. 2018, 33, 8797–8807. [Google Scholar] [CrossRef]
- Singh, P.; Vinjamuri, R.; Wang, X.; Reisner, D. Design and implementation of a fuzzy logic-based state-of-charge meter for Li-ion batteries used in portable defibrillators. J. Power Sources 2006, 162, 829–836. [Google Scholar] [CrossRef]
- Waag, W.; Fleischer, C.; Sauer, D.U. Critical review of the methods for monitoring of lithium-ion batteries in electric and hybrid vehicles. J. Power Sources 2014, 258, 321–339. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 1. Background. J. Power Sources 2004, 134, 252–261. [Google Scholar] [CrossRef]
- Lee, K.T.; Dai, M.J.; Chuang, C.C. Temperature-compensated model for lithium-ion polymer batteries with extended Kalman filter state-of-charge estimation for an implantable charger. IEEE Trans. Ind. Electron. 2018, 65, 589–596. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Zhang, X.; Sun, F.; Fan, J.X. State-of-charge estimation of the lithium-ion battery using an adaptive extended Kalman filter based on an improved Thevenin model. IEEE Trans. Veh. Technol. 2011, 60, 1461–1469. [Google Scholar]
- Yang, J.; Xia, B.; Shang, Y.; Huang, W.; Mi, C.C. Adaptive state-of-charge estimation based on a split battery model for electric vehicle applications. IEEE Trans. Veh. Technol. 2017, 66, 10889–10898. [Google Scholar] [CrossRef]
- Plett, G.L. Sigma-point Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 1: Introduction and state estimation. J. Power Sources 2006, 161, 1356–1368. [Google Scholar] [CrossRef]
- Liu, C.; Liu, W.; Wang, L.; Hu, G.; Ma, L.; Ren, B. A new method of modeling and state of charge estimation of the battery. J. Power Sources 2016, 320, 1–12. [Google Scholar] [CrossRef]
- Schwunk, S.; Armbruster, N.; Straub, S.; Kehl, J.; Vetter, M. Particle filter for state of charge and state of health estimation for lithium–iron phosphate batteries. J. Power Sources 2013, 239, 705–710. [Google Scholar] [CrossRef]
- Dong, G.; Chen, Z.; Wei, J.; Zhang, C.; Wang, P. An online model-based method for state of energy estimation of lithium-ion batteries using dual filters. J. Power Sources 2016, 301, 277–286. [Google Scholar] [CrossRef]
- Hua, Y.; Cordoba-Arenas, A.; Warner, N.; Rizzoni, G. A multi time-scale state-of charge and state-of-health estimation framework using nonlinear predictive filter for lithium-ion battery pack with passive balance control. J. Power Sources 2015, 280, 293–312. [Google Scholar] [CrossRef]
- Hu, C.; Youn, B.D.; Chung, J. A multiscale framework with extended Kalman filter for lithium-ion battery SOC and capacity estimation. Appl. Energy 2012, 92, 694–704. [Google Scholar] [CrossRef]
- Pan, H.; Lü, Z.; Lin, W.; Li, J.; Chen, L. State of charge estimation of lithium-ion batteries using a grey extended kalman filter and a novel open-circuit voltage model. Energy 2017, 138, 764–775. [Google Scholar] [CrossRef]
- Wei, J.; Dong, G.; Chen, Z. On-board adaptive model for state of charge estimation of lithium-ion batteries based on Kalman filter with proportional integral-based error adjustment. J. Power Sources 2017, 365, 308–319. [Google Scholar] [CrossRef]
- Lim, K.; Bastawrous, H.A.; Duong, V.H.; See, K.W.; Zhang, P.; Dou, S.X. Fading Kalman filter-based real-time state of charge estimation in LiFePO4 battery-powered electric vehicles. Appl. Energy 2016, 169, 40–48. [Google Scholar] [CrossRef]
- Liu, X.; Chen, Z.; Zhang, C.; Wu, J. A novel temperature-compensated model for power Li-ion batteries with dual-particle-filter state of charge estimation. Appl. Energy 2014, 123, 263–272. [Google Scholar] [CrossRef]
- Cai, M.; Chen, W.; Tan, X. Battery state-of-charge estimation based on a dual unscented Kalman filter and fractional variable-order model. Energies 2017, 10, 1577. [Google Scholar] [CrossRef]
- Xiong, R.; Sun, F.; Chen, Z.; He, H. A data-driven multi-scale extended Kalman filtering based parameter and state estimation approach of lithium-ion polymer battery in electric vehicles. Appl. Energy 2014, 113, 463–476. [Google Scholar]
- Tran, N.T.; Khan, A.B.; Choi, W. State of Charge and State of Health Estimation of AGM VRLA Batteries by Employing a Dual Extended Kalman Filter and an ARX Model for Online Parameter Estimation. Energies 2017, 10, 137. [Google Scholar] [CrossRef]
- Li, Y.; Chattopadhyay, P.; Xiong, S.; Ray, A.; Rahn, C.D. Dynamic data-driven and model-based recursive analysis for estimation of battery state-of-charge. Appl. Energy 2016, 184, 266–275. [Google Scholar] [CrossRef]
- Propp, K.; Auger, D.J.; Fotouhi, A.; Longo, S.; Knap, V. Kalman-variant estimators for state of charge in lithium-sulfur batteries. J. Power Sources 2017, 343, 254–267. [Google Scholar] [CrossRef] [Green Version]
- Fotouhi, A.; Auger, D.J.; Propp, K.; Longo, S. Lithium-sulfur battery state-of-charge observability analysis and estimation. IEEE Trans. Power Electron. 2018, 33, 5847–5859. [Google Scholar] [CrossRef]
- Pickard, W.F.; Shen, A.Q.; Hansing, N.J. Parking the power: Strategies and physical limitations for bulk energy storage in supply–demand matching on a grid whose input power is provided by intermittent sources. Renew. Sustain. Energy Rev. 2009, 13, 1934–1945. [Google Scholar] [CrossRef]
- Kroeze, R.C.; Krein, P.T. Electrical battery model for use in dynamic electric vehicle simulations. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 1336–1342. [Google Scholar]
- Gao, W.; Jiang, M.; Hou, Y. Research on PNGV model parameter identification of LiFePO4 Li-ion battery based on FMRLS. In Proceedings of the 2011 6th IEEE Conference on Industrial Electronics and Applications, Beijing, China, 21–23 June 2011; pp. 2294–2297. [Google Scholar]
- Yao, L.W.; Wirun, A.; Aziz, M.J.B.A.; Sutikno, T. Battery state-of-charge estimation with extended Kalman-filter using third-order Thevenin model. Telkomnika 2015, 13, 401–412. [Google Scholar] [CrossRef]
- Freedom CAR Program Electrochemical Energy Storage Team. Freedom CAR Battery Test Manual for Power Assist Hybrid Electric Vehicles; U.S. Department of Energy: Washington, DC, USA, 2003.
- Hoque, M.M.; Hannan, M.A.; Mohamed, A. Charging and discharging model of lithium-ion battery for charge equalization control using particle swarm optimization algorithm. J. Renew. Sustain. Energy 2016, 8, 7847–7858. [Google Scholar] [CrossRef]
- Rahman, M.A.; Anwar, S.; Izadian, A. Electrochemical model parameter identification of a lithium-ion battery using particle swarm optimization method. J. Power Sources 2016, 307, 86–97. [Google Scholar] [CrossRef]
- Guo, X.; Kang, L.; Yao, Y.; Huang, Z.; Li, W. Joint estimation of the electric vehicle power battery state of charge based on the least squares method and the Kalman filter algorithm. Energies 2016, 9, 100. [Google Scholar] [CrossRef]
- Zhan, R.; Wan, J. Neural network-aided adaptive unscented Kalman filter for nonlinear state estimation. IEEE Signal Process. Lett. 2006, 13, 445–448. [Google Scholar] [CrossRef]
- An, D.; Choi, J.H.; Kim, N.H. Prognostics 101: A tutorial for particle filter-based prognostics algorithm using Matlab. Reliab. Eng. Syst. Saf. 2013, 115, 161–169. [Google Scholar] [CrossRef]
- Li, T.; Bolic, M.; Djuric, P.M. Resampling Methods for Particle Filtering: Classification, implementation, and strategies. IEEE Signal Process. Mag. 2015, 32, 70–86. [Google Scholar] [CrossRef]
- Jouin, M.; Gouriveau, R.; Hissel, D.; Péra, M.C.; Zerhouni, N. Particle filter-based prognostics: Review, discussion and perspectives. Mech. Syst. Signal Process. 2016, 72–73, 2–31. [Google Scholar] [CrossRef]

| Nominal capacity | 200 Ah |
| Nominal voltage | 0.7 V |
| Cut-off voltage (charging, discharging) | 1.2 V, 0.4 V |
| Self-discharge current | 0.4 A |
| Rated working current | 50 A (0.25 C) |
| Operating temperature | 500 °C |
| Weight | 4.8 kg |
| Size (diameter, height) | 18 cm, 10 cm |
| Cost | 240 $ kWh−1 [7] |
| Non-linear state-space model and linearized model |
| Step 1: Initialization |
| For k = 1, 2, ..., n, loop from step 2 to step 10. Step 2: Update Jacobian matrices: Ak, Bk, |
| Step 3: Priori state update |
| Step 4: Priori error covariance update |
| Step 5: Update Jacobian matrices: Ck, Dk |
| Step 6: Kalman gain update |
| Step 7: Measurement update |
| Step 8: Posteriori state update |
| Step 9: Posteriori error covariance update |
| Non-linear state-space model |
| Step 1: Initialization , , |
| For k = 1, 2, ..., n, loop from step 2 to step 12. Step 2: Create sigma points |
| Step 3: Priori sigma points update |
| Step 4: Priori state update |
| Step 5: Priori error covariance update |
| Step 6: Measurement for sigma points update |
| Step 7: Measurement update |
| Step 8: Measurement covariance update |
| Step 9: State/measurement cross covariance update |
| Step 10: Kalman gain update |
| Step 11: Posteriori state update |
| Step 12: Posteriori error covariance update |
| Non-linear state-space model |
| Step 1: Initialization |
| For k = 1, 2, ..., n, loop from step 2 to step 6. Step 2: Prediction Prior probability distribution Corresponding observational values |
| Step 3: Update-importance sampling Likelihood distribution |
| Step 4: Weighting value normalization |
| Step 5: Resampling- Eliminate particles with low weights and duplicate particles with high weights |
| Step 6: State update |
| Algorithm | SoC0 | Overall RMSE | Convergence Time (s) | RMSE after Convergence |
|---|---|---|---|---|
| EKF | 1 | 0.0118 | 1 | 0.0118 |
| 0.85 | 0.0171 | 786 | 0.0130 | |
| 0.75 | 0.0263 | 1622 | 0.0124 | |
| 0.6 | 0.0533 | 2585 | 0.0121 | |
| UKF | 1 | 0.0063 | 1 | 0.0063 |
| 0.85 | 0.0067 | 63 | 0.0063 | |
| 0.75 | 0.0071 | 65 | 0.0063 | |
| 0.6 | 0.0988 | 1539 | 0.0080 | |
| PF | 1 | 0.0114 | 1 | 0.0114 |
| 0.85 | 0.0195 | 1841 | 0.0158 | |
| 0.75 | 0.0327 | 3419 | 0.0092 | |
| 0.6 | 0.0857 | 7984 | 0.0188 |
| Algorithm | SoC0 | Overall RMSE | Convergence Time (s) | RMSE after Convergence |
|---|---|---|---|---|
| EKF | 1 | 0.0271 | 1 | 0.0271 |
| 0.85 | 0.0367 | 311 | 0.0334 | |
| 0.75 | 0.0503 | 716 | 0.0310 | |
| 0.6 | 0.1071 | 1801 | 0.0279 | |
| UKF | 1 | 0.0255 | 1 | 0.0255 |
| 0.85 | 0.0264 | 17 | 0.0263 | |
| 0.75 | 0.0256 | 18 | 0.0250 | |
| 0.6 | 0.1377 | 1105 | 0.0376 | |
| PF | 1 | 0.0288 | 1 | 0.0288 |
| 0.85 | 0.0429 | 446 | 0.0403 | |
| 0.75 | 0.0871 | 851 | 0.0764 | |
| 0.6 | 0.2524 | - | - |
| Algorithm | SoC0 | Overall RMSE | Convergence Time (s) | RMSE after Convergence |
|---|---|---|---|---|
| EKF | 1 | 0.1021 | 1 | 0.1021 |
| 0.85 | 0.1024 | 961 | 0.1021 | |
| 0.75 | 0.1064 | 2640 | 0.1021 | |
| 0.6 | 0.1089 | 2641 | 0.1021 | |
| UKF | 1 | 0.0190 | 1 | 0.0190 |
| 0.85 | 0.0186 | 73 | 0.0186 | |
| 0.75 | 0.0191 | 100 | 0.0190 | |
| 0.6 | 0.0817 | 1898 | 0.0199 | |
| PF | 1 | 0.0486 | 1 | 0.0486 |
| 0.85 | 0.0373 | 2443 | 0.0361 | |
| 0.75 | 0.0486 | 3421 | 0.0447 | |
| 0.6 | 0.0818 | 7998 | 0.0475 |
| Algorithm | Scenario (a) | Scenario (b) | Scenario (c) |
|---|---|---|---|
| EKF | 11.908 (s) | 4.13 (s) | 25.863 (s) |
| UKF | 23.717 (s) | 8.291 (s) | 52.215 (s) |
| PF | 73.820 (s) | 24.810 (s) | 158.264 (s) |
| Test time | 12.179 (h) | 4.081 (h) | 25.778 (h) |
| Algorithm | SoC0 | Scenario (a) | Scenario (b) | Scenario (c) |
|---|---|---|---|---|
| PF (100) | 1 | 0.0296 | 0.0274 | 0.0412 |
| 0.85 | 0.0184 | 0.0323 | 0.0505 | |
| 0.75 | 0.0357 | 0.0563 | 0.0507 | |
| 0.6 | 0.0672 | 0.2051 | 0.0761 | |
| Time | 397.378 (s) | 132.327 (s) | 918.940 (s) | |
| PF (20) | 1 | 0.0114 | 0.0288 | 0.0486 |
| 0.85 | 0.0195 | 0.0429 | 0.0373 | |
| 0.75 | 0.0327 | 0.0871 | 0.0486 | |
| 0.6 | 0.0857 | 0.2524 | 0.0818 | |
| Time | 73.820 (s) | 24.810 (s) | 158.264 (s) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Song, Z.; Yang, K.; Yin, X.; Geng, Y.; Wang, J. State of Charge Estimation for Lithium-Bismuth Liquid Metal Batteries. Energies 2019, 12, 183. https://doi.org/10.3390/en12010183
Wang X, Song Z, Yang K, Yin X, Geng Y, Wang J. State of Charge Estimation for Lithium-Bismuth Liquid Metal Batteries. Energies. 2019; 12(1):183. https://doi.org/10.3390/en12010183
Chicago/Turabian StyleWang, Xian, Zhengxiang Song, Kun Yang, Xuyang Yin, Yingsan Geng, and Jianhua Wang. 2019. "State of Charge Estimation for Lithium-Bismuth Liquid Metal Batteries" Energies 12, no. 1: 183. https://doi.org/10.3390/en12010183
APA StyleWang, X., Song, Z., Yang, K., Yin, X., Geng, Y., & Wang, J. (2019). State of Charge Estimation for Lithium-Bismuth Liquid Metal Batteries. Energies, 12(1), 183. https://doi.org/10.3390/en12010183





