An Aero-acoustic Noise Distribution Prediction Methodology for Offshore Wind Farms
Abstract
1. Introduction
2. Materials and Methods
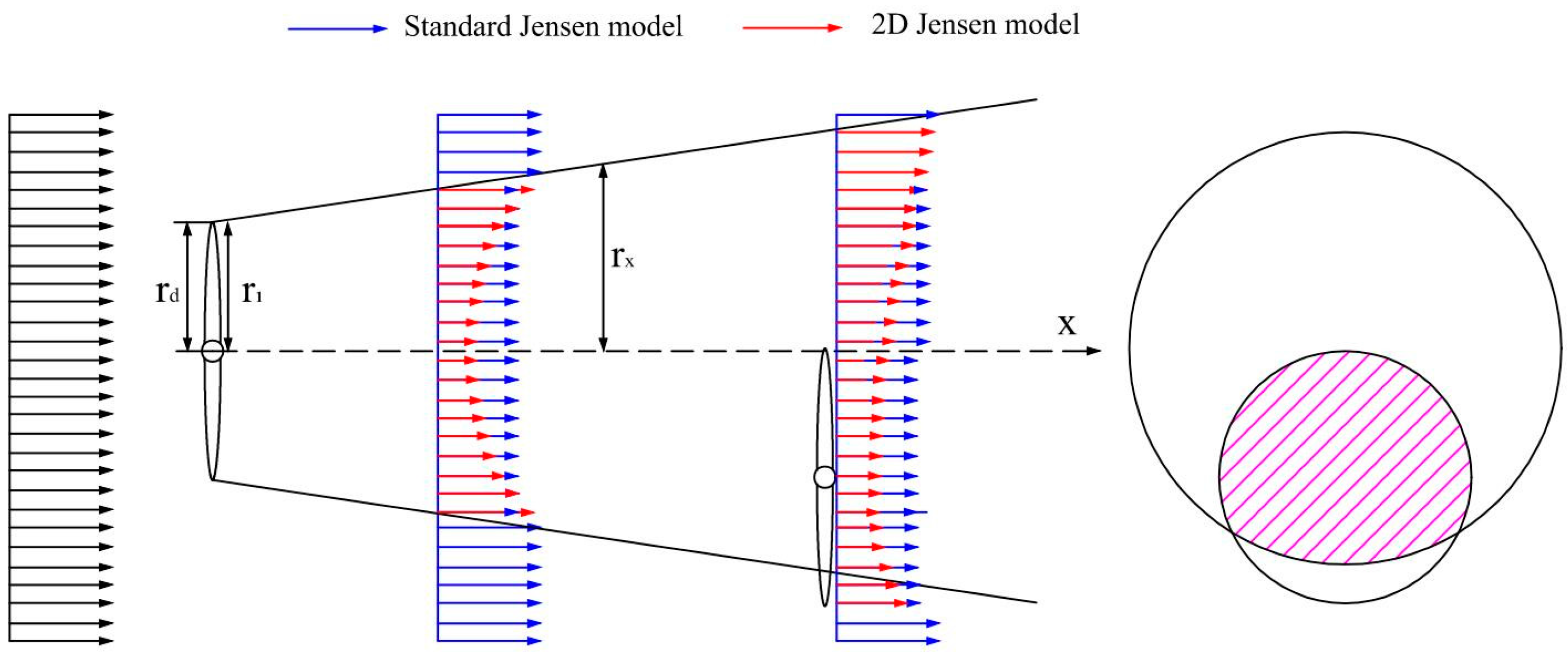
2.1. 2D-Wake Modeling
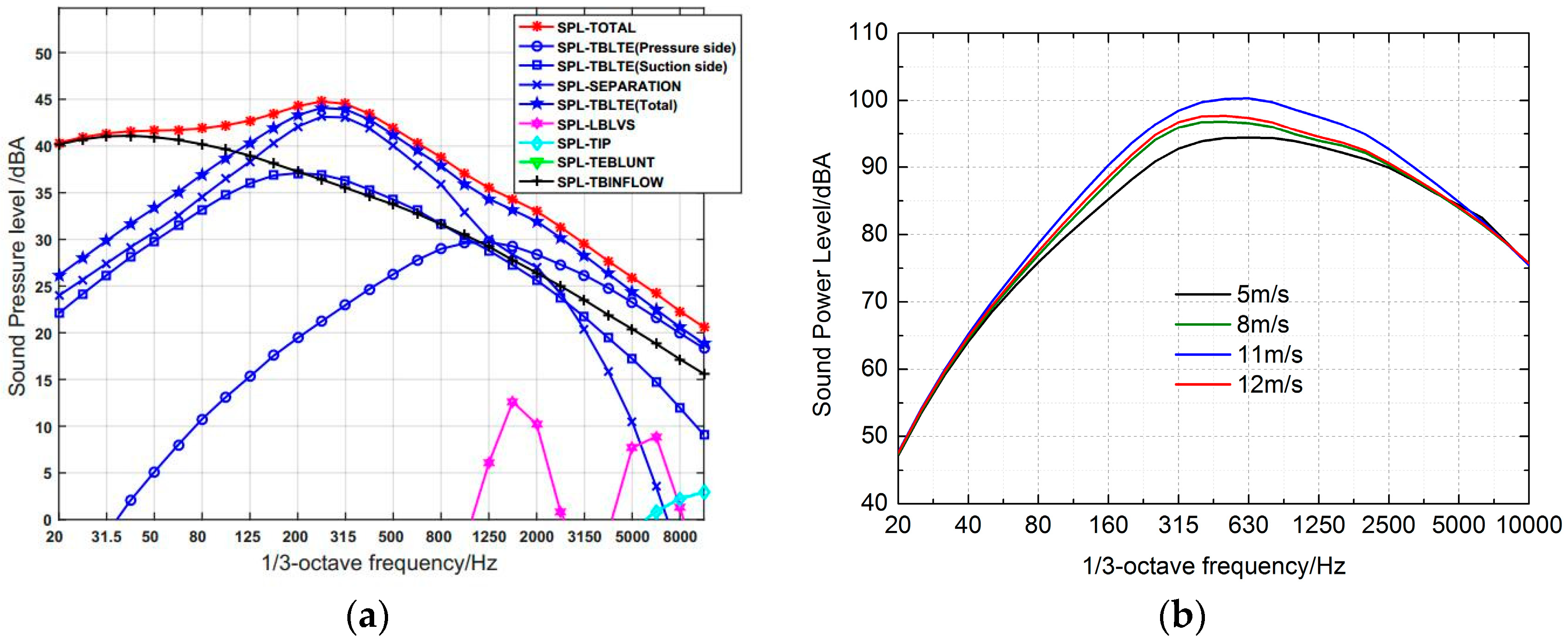
2.2. Wind Turbine Noise Source
- Turbulent Boundary Layer Trailing Edge (TBL-TE) noise, including pressure side and suction side
- Separation-Stall (SEP) noise
- Laminar Boundary Layer Vortex Shedding (LBL-VS) noise
- Tip Vortex Formation (TIP) noise
- Trailing Edge Bluntness Vortex Shedding (TEB-VS) noise
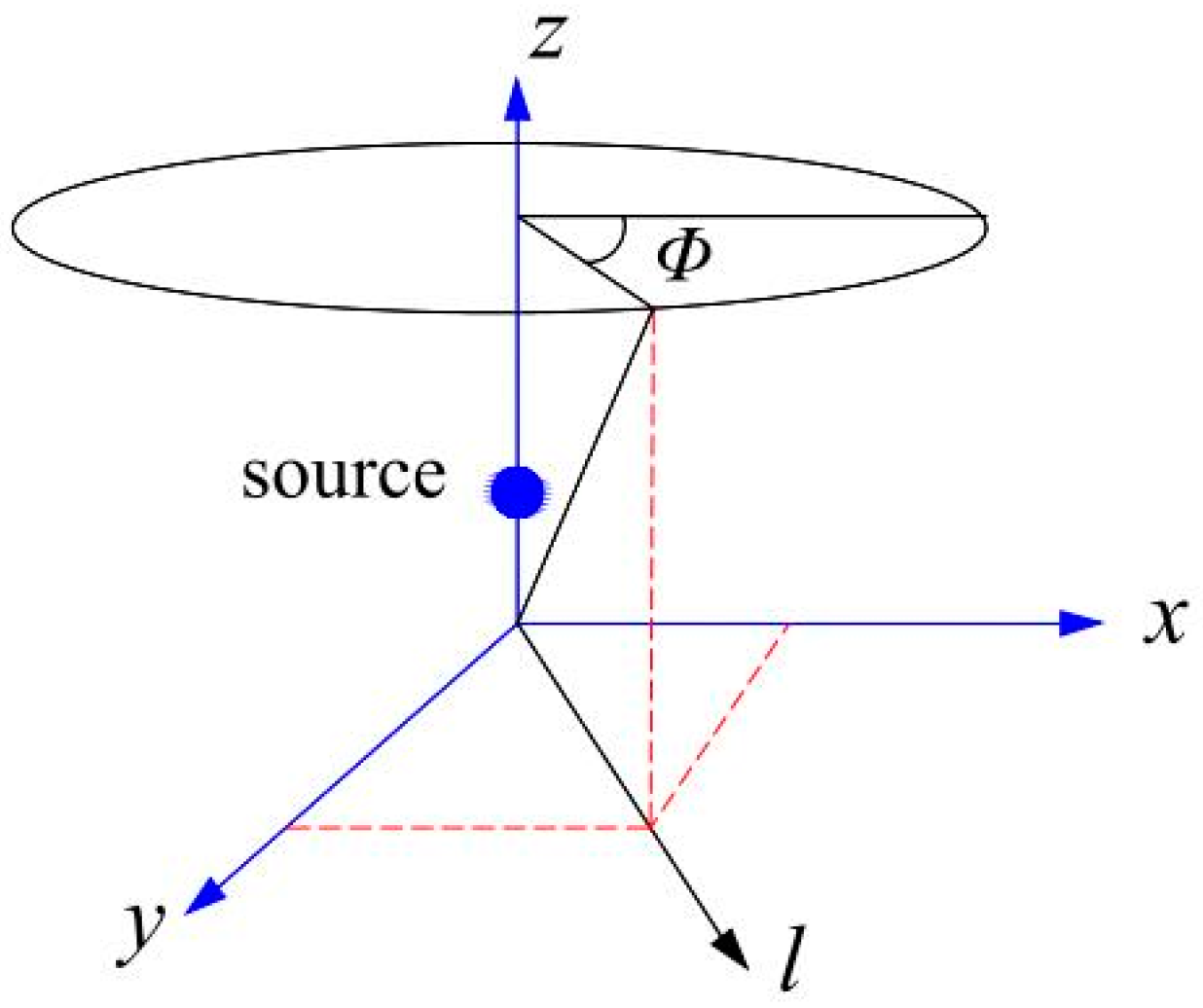
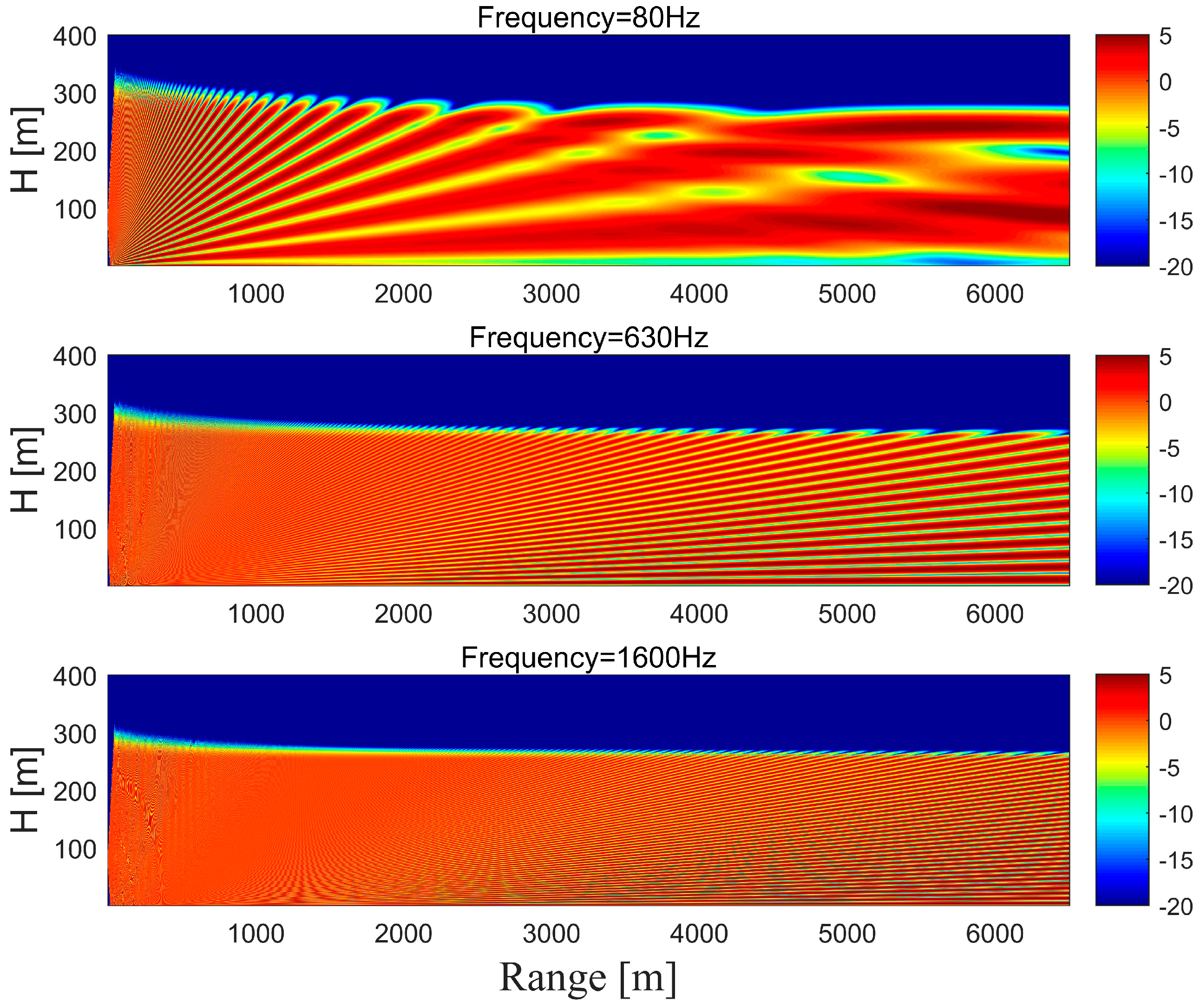
2.3. Wind Turbine Noise Propagation
3. Numerical Results
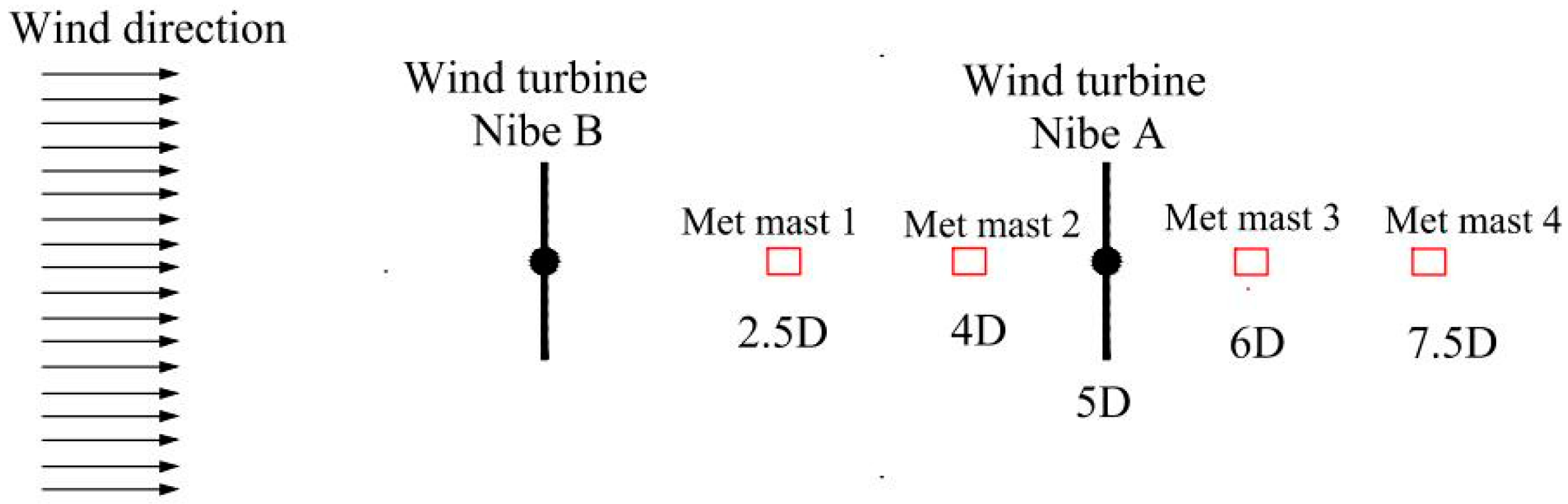
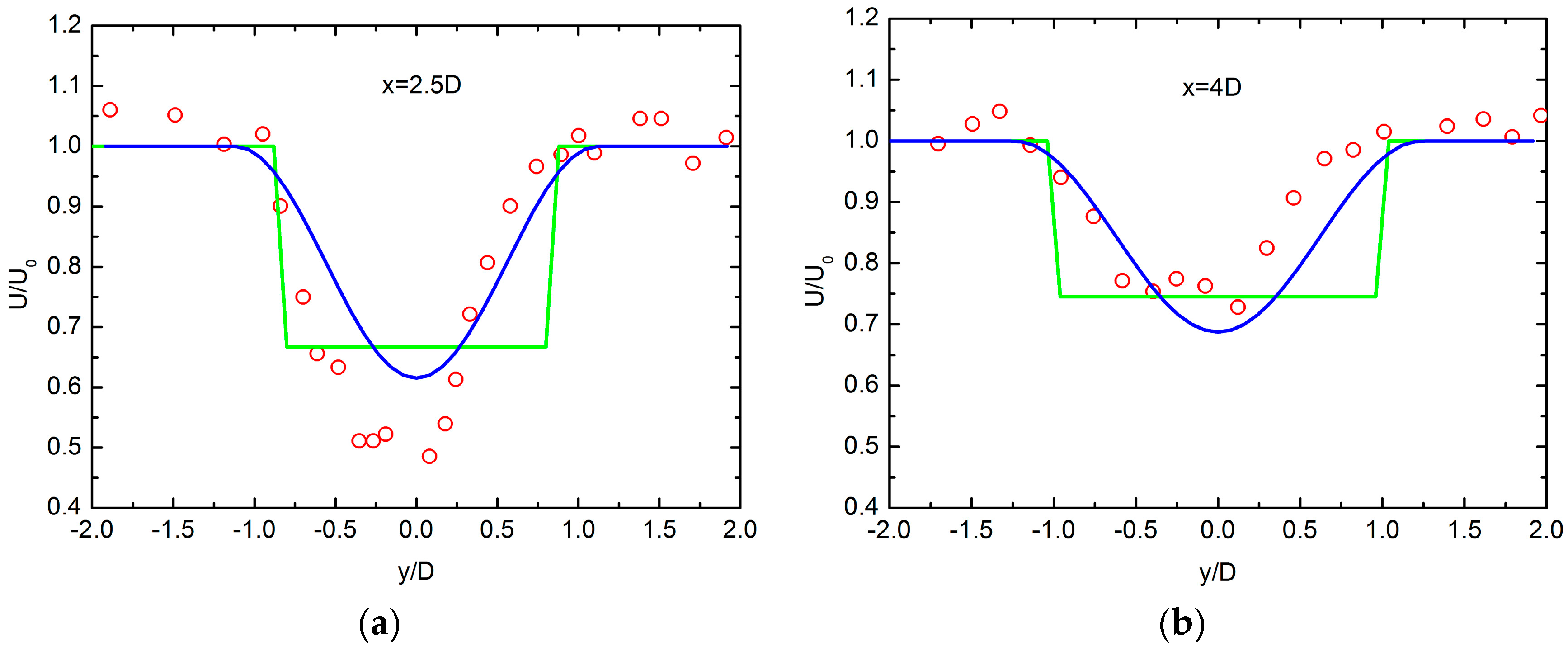
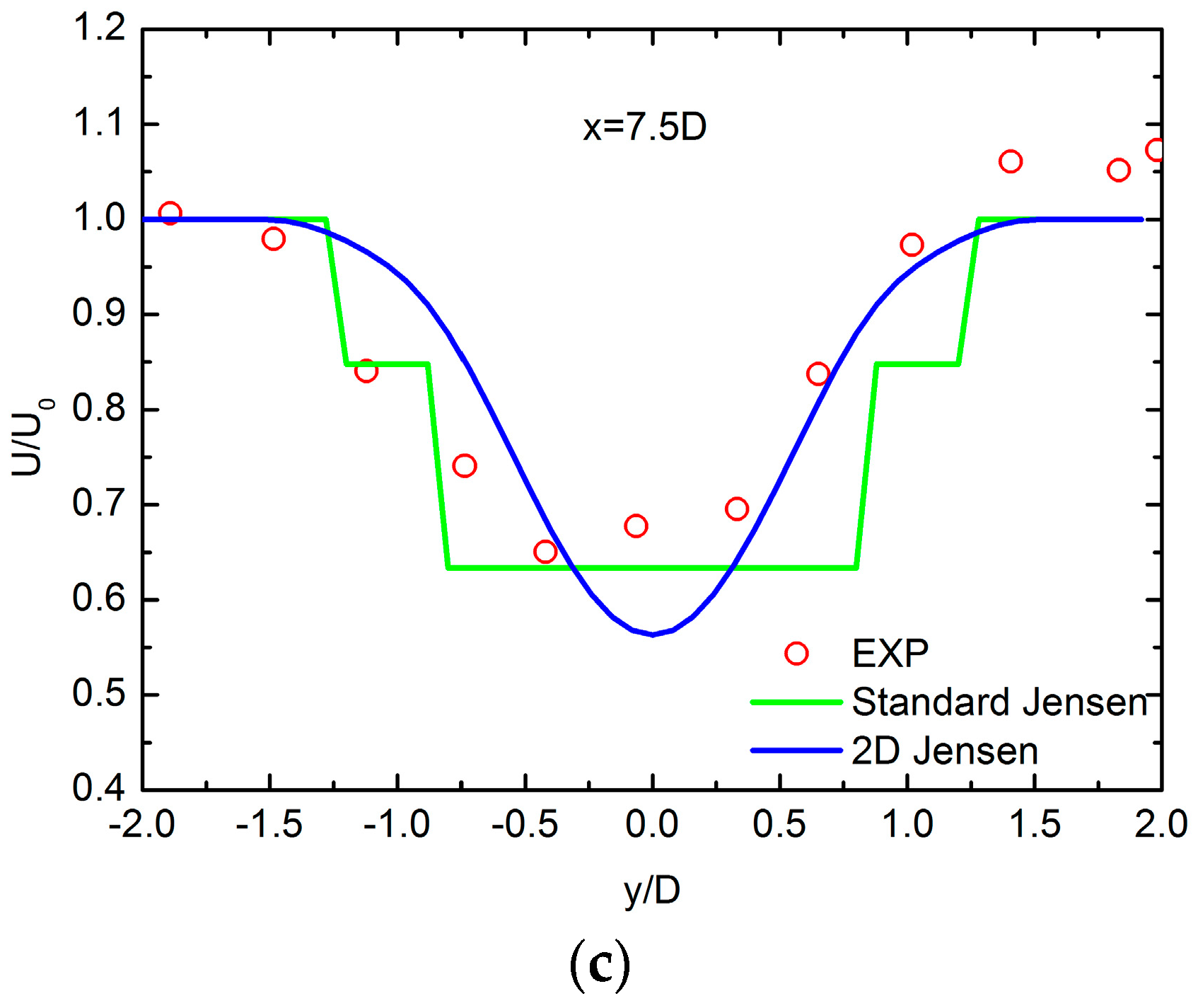
3.1. Wake Modeling Validations
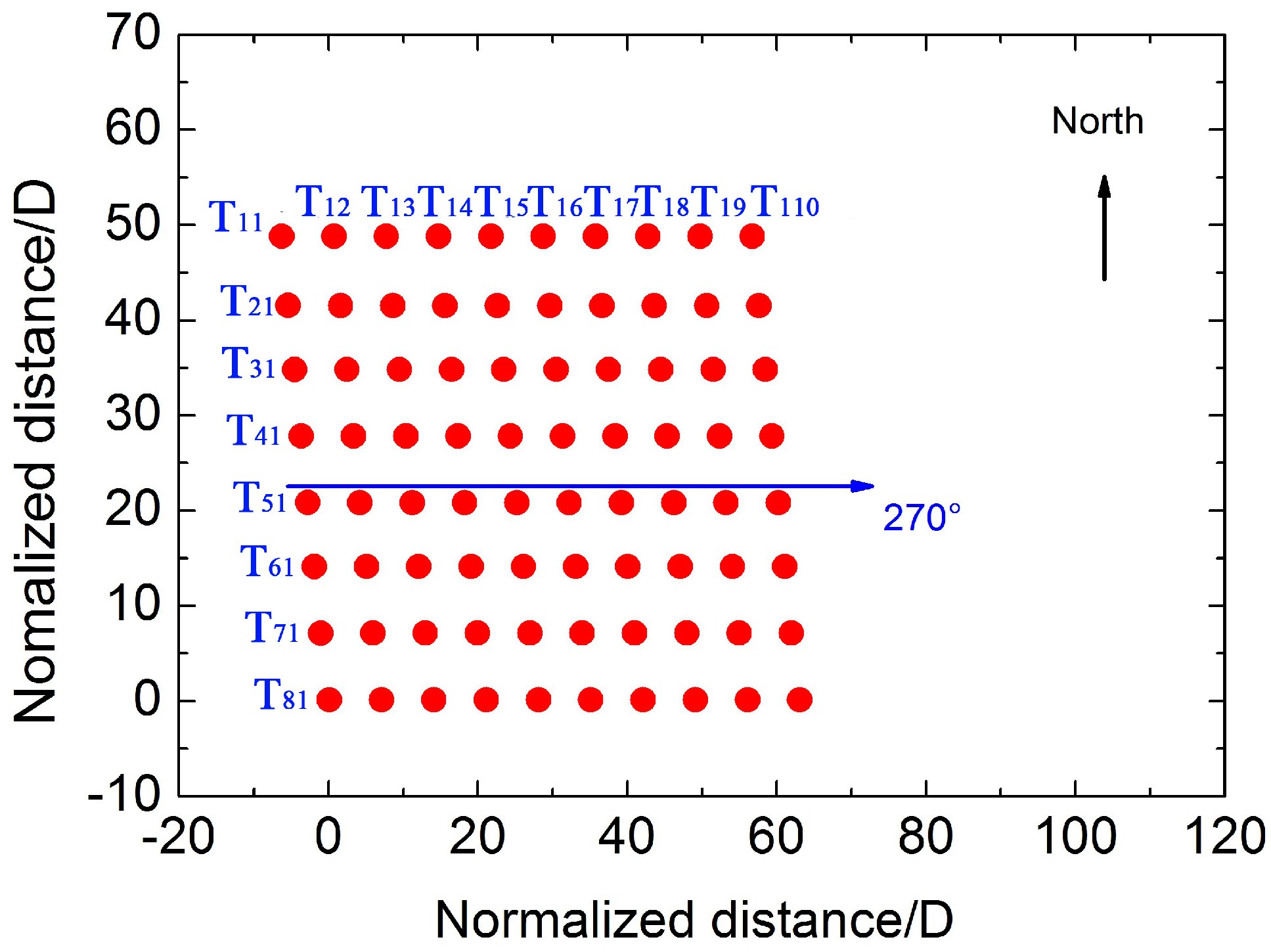
3.2. Horns Rev Wind Farm Case
3.2.1. Noise Propagation from a Single Wind Turbine
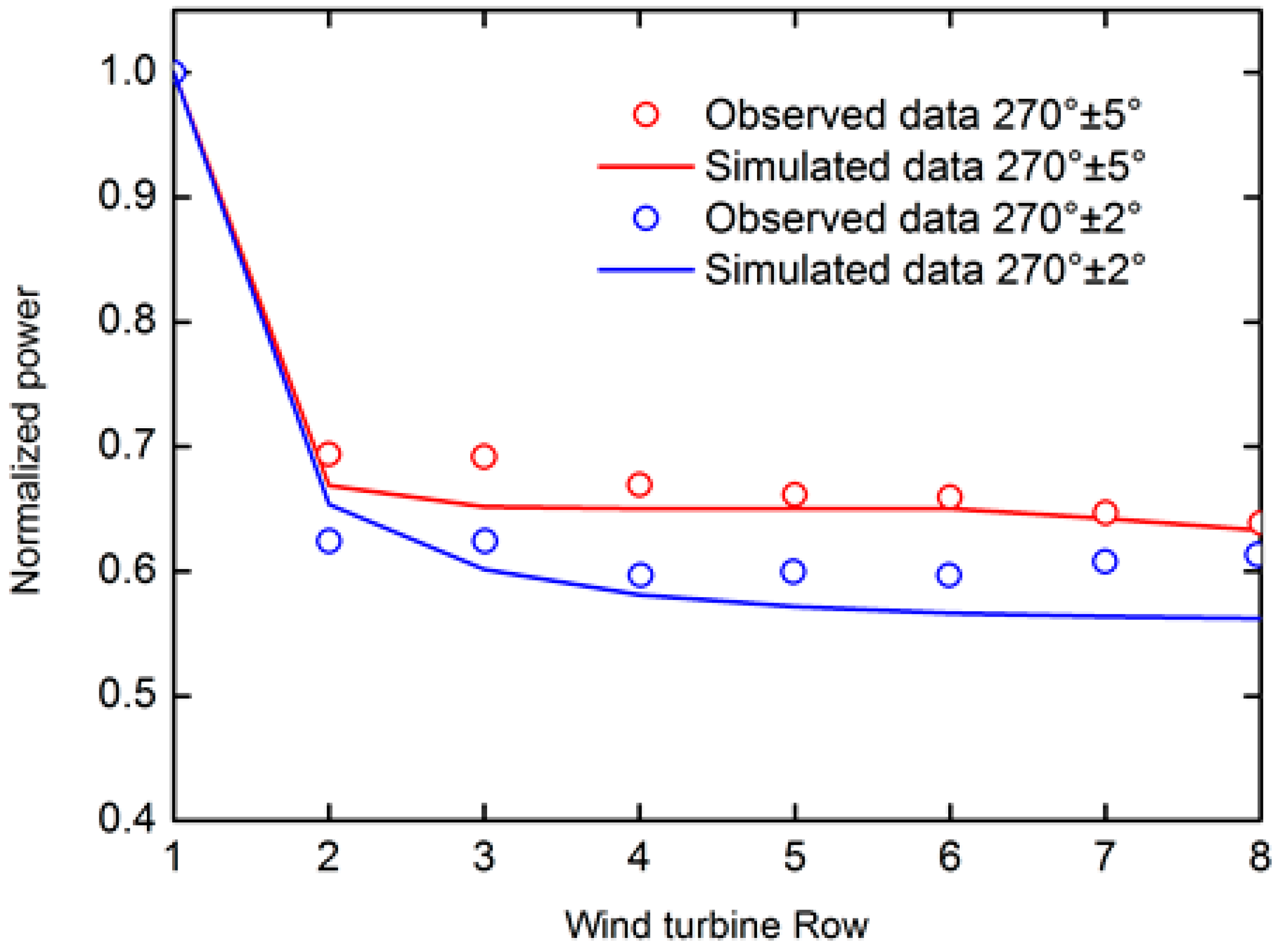
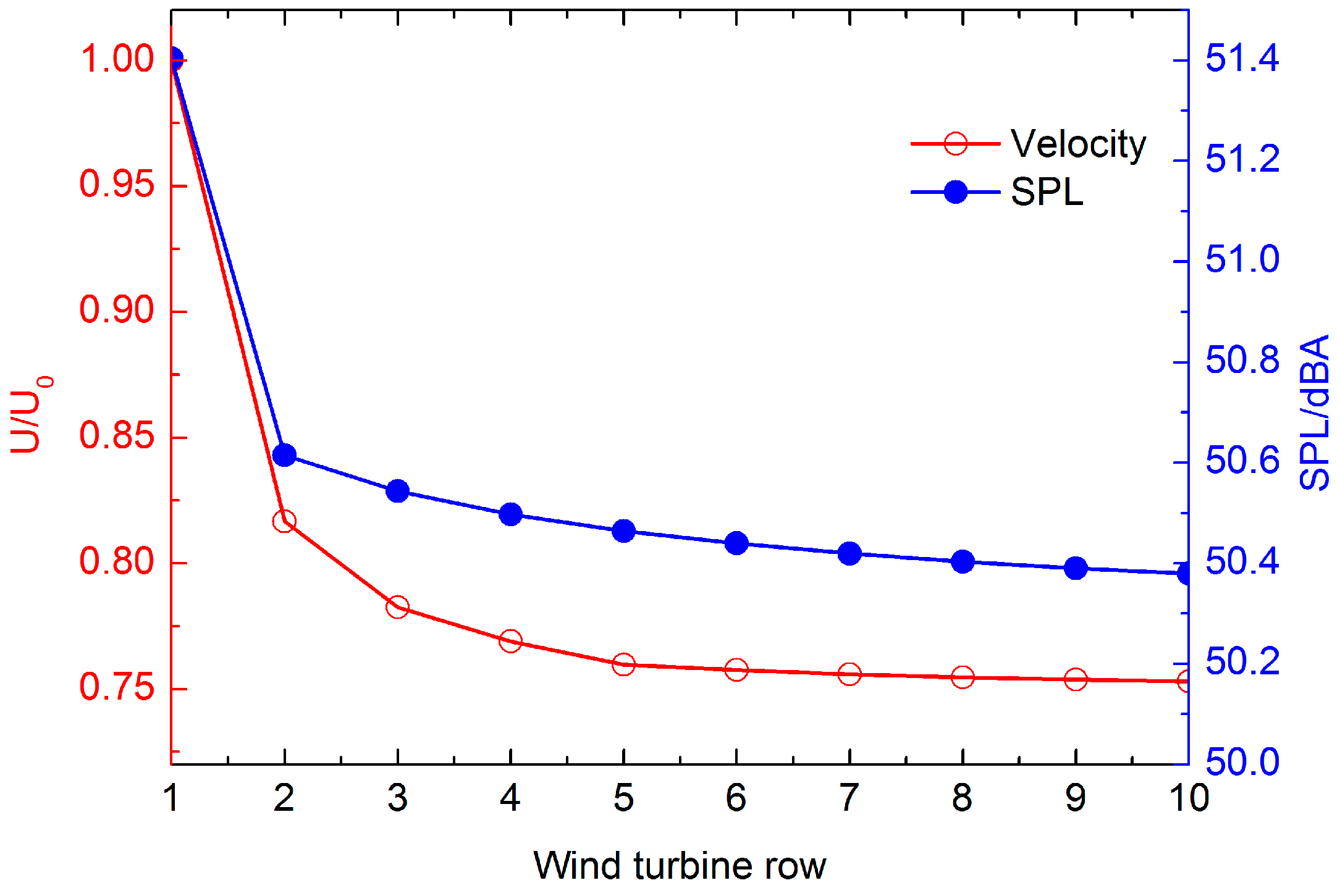
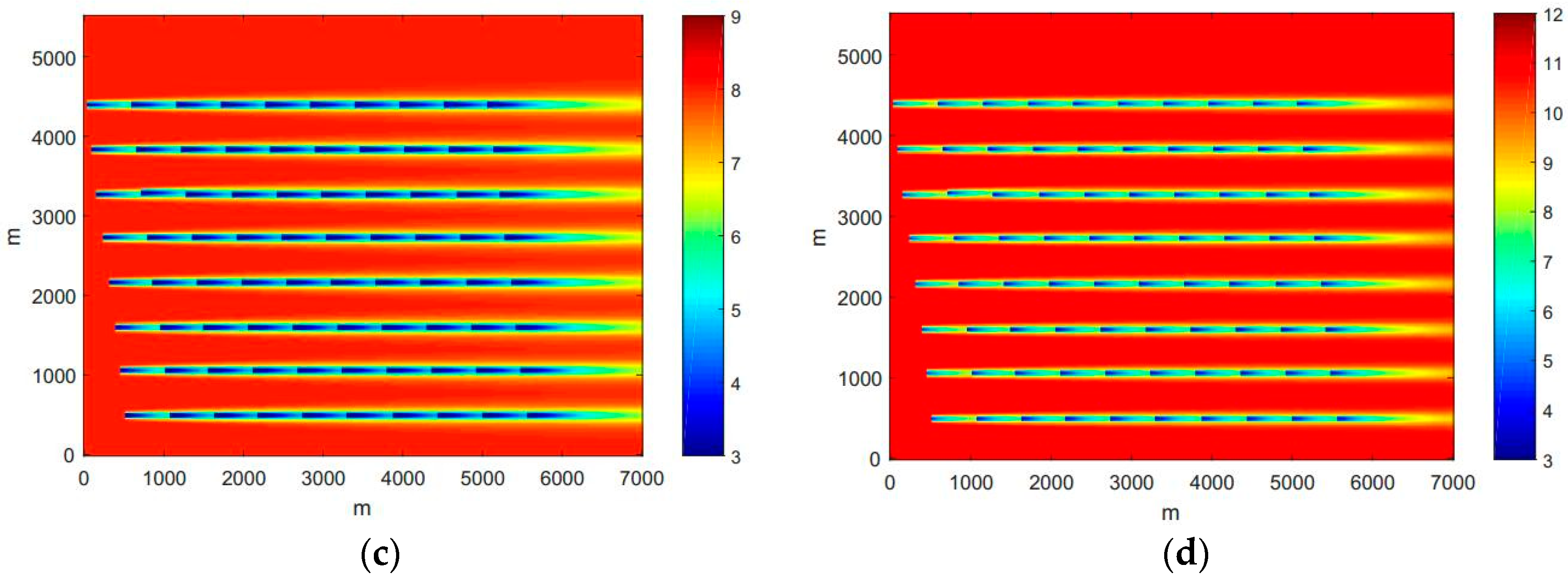
3.2.2. Multiple Wind Turbine Noise
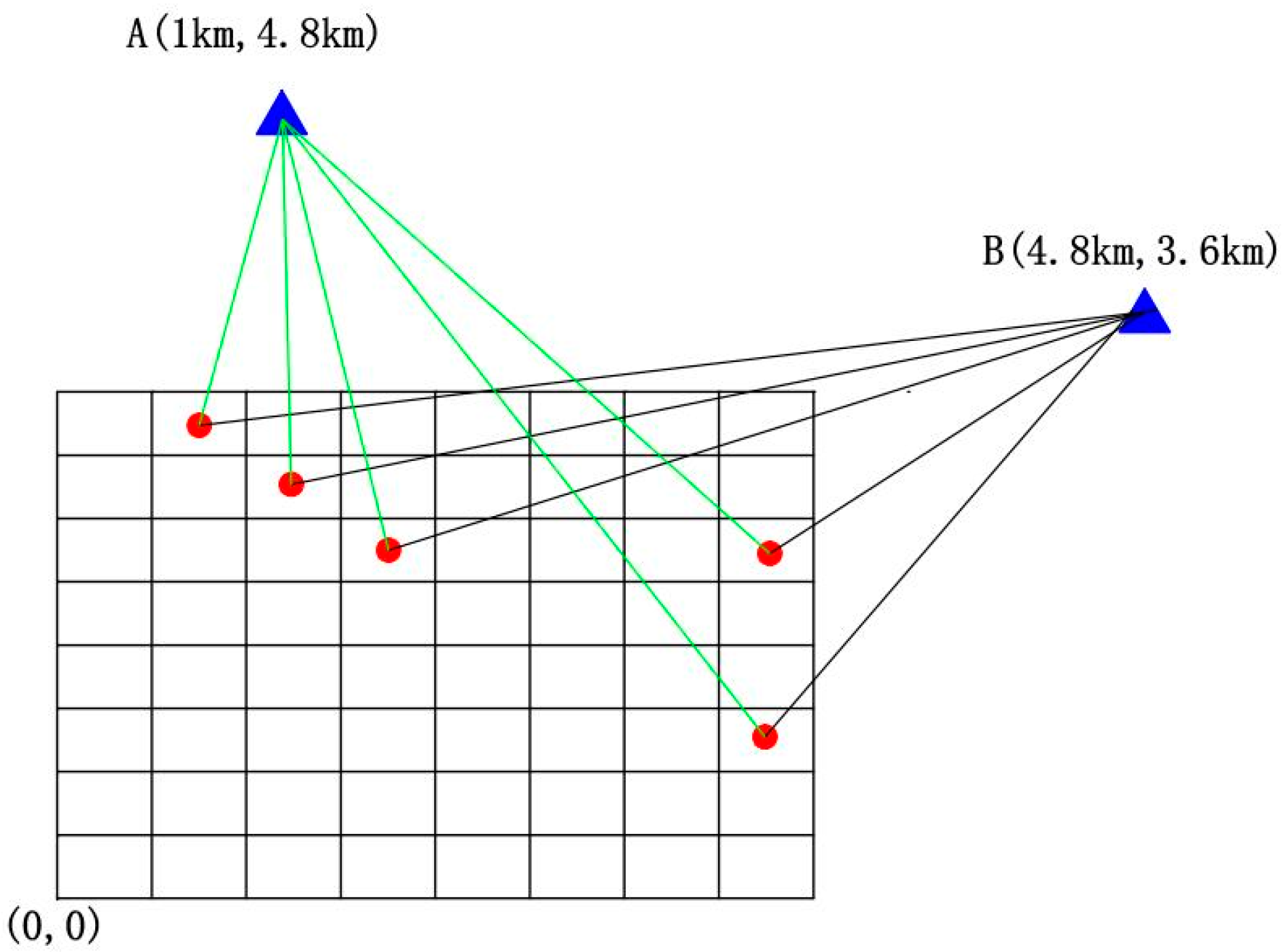
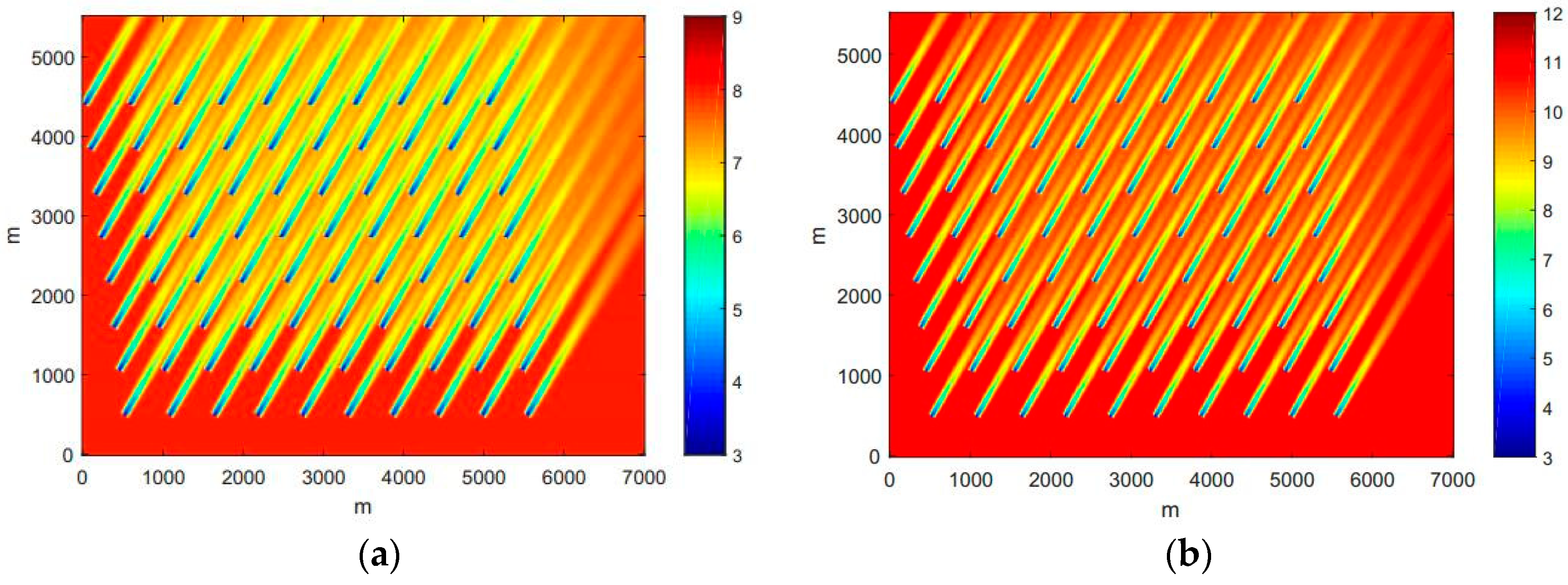
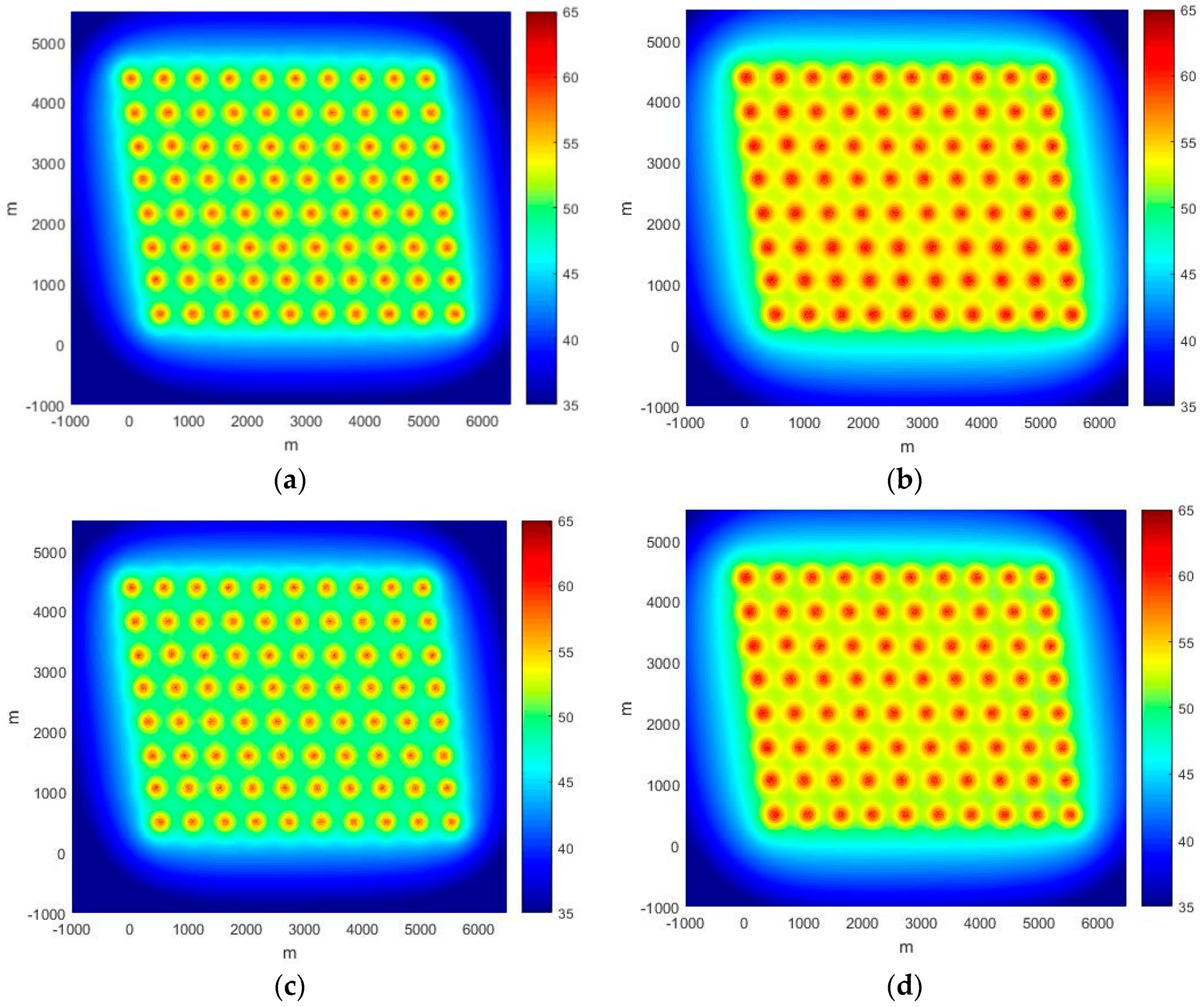
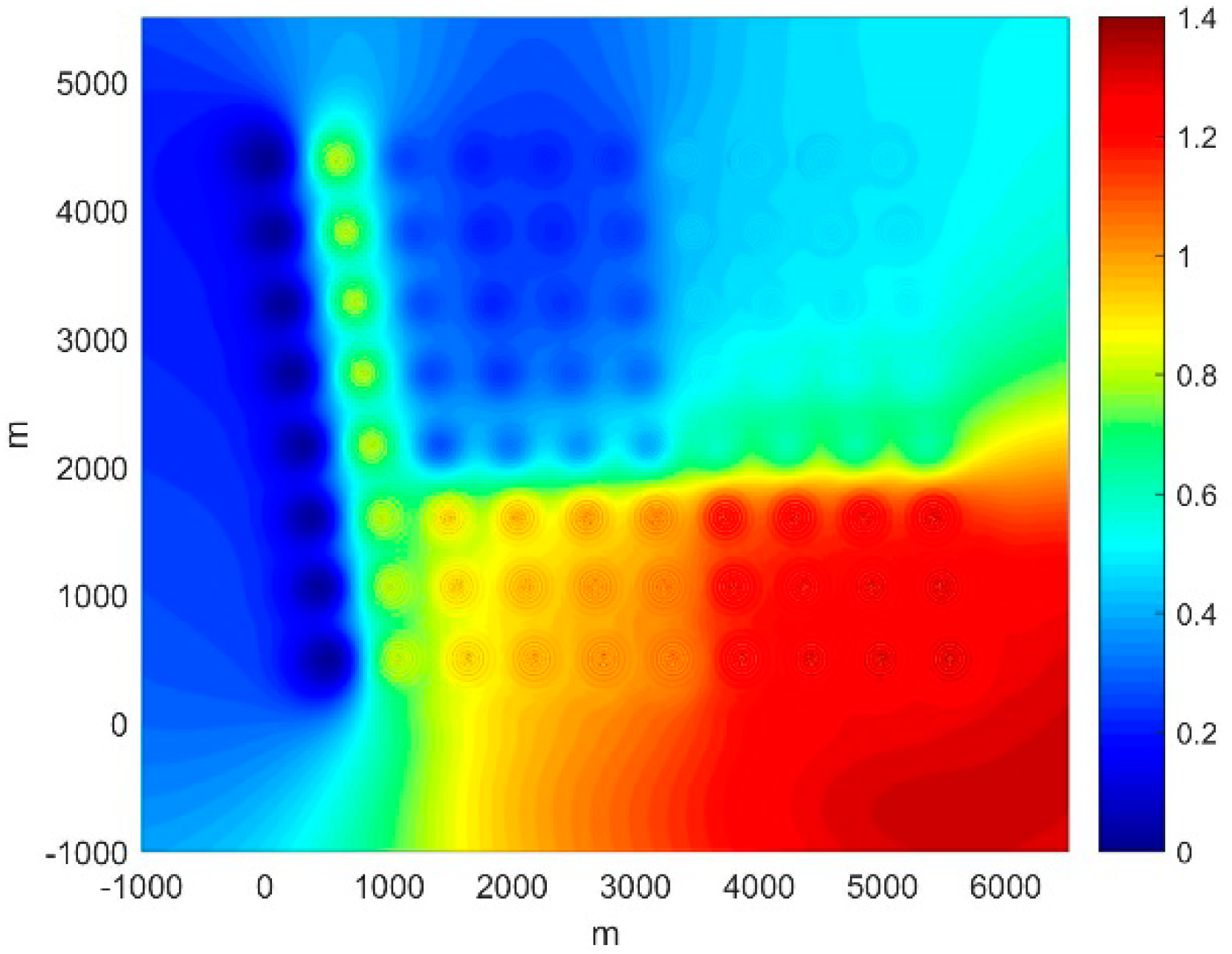
3.2.3. Offshore Wind Farm Noise
4. Discussions
5. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Andersson, M. Offshore Wind Farms Ecological Effects of Noise and Habitat Alteration on Fish; Stockholm University: Stockholm, Sweden, 2011. [Google Scholar]
- Gocmen, T.; Van der Laan, P.; Rethore, P.-E.; Diaz, A.P.; Larsen, G.C.; Ott, S. Wind turbine wake models developed at the technical university of Denmark: A review. Renew. Sustain. Energy Rev. 2016, 60, 752–769. [Google Scholar] [CrossRef]
- Mikkelsen, R. Actuator Disc Methods Applied to Wind Turbines; MEK-FM-PHD 2003-02; Technical University of Denmark: Lyngby, Denmark, 2003. [Google Scholar]
- Sørensen, J.N.; Shen, W.Z.; Munduate, X. Analysis of wake states by a full-field actuator disc model. Wind Energy 1998, 1, 73–88. [Google Scholar] [CrossRef]
- Wu, Y.-T.; Porté-Agel, F. Modeling turbine wakes and power losses within a wind farm using LES: An application to the Horns Rev offshore wind farm. Renew. Energy 2015, 75, 945–955. [Google Scholar] [CrossRef]
- Shen, W.Z.; Zhu, W.J.; Sørensen, J.N. Actuator line/Navier-Stokes computations for the MEXICO rotor: Comparison with detailed measurements. Wind Energy 2012, 15, 811–825. [Google Scholar] [CrossRef]
- Troldborg, N.; Larsen, G.C.; Madsen, H.A.; Hansen, K.S.; Sørensen, J.N.; Mikkelsen, R. Numerical simulations of wake interaction between two wind turbines at various inflow conditions. Wind Energy 2010, 14, 859–876. [Google Scholar] [CrossRef]
- Ciri, U.; Petrolo, G.; Salvetti, M.V.; Leonardi, S. Large-Eddy Simulations of Two in-line Turbines in a Wind Tunnel with Different Inflow Conditions. Energies 2017, 10, 821. [Google Scholar] [CrossRef]
- Frandsen, S. On the wind speed reduction in the center of large clusters of wind turbines. J. Wind Eng. Ind. Aerodyn. 1992, 39, 251–265. [Google Scholar] [CrossRef]
- Jensen, N.O. A Note on Wind Generator Interaction; Risø-M-2411 Risø National Laboratory Roskilde: Roskilde, Denmark, 1983; pp. 1–16. [Google Scholar]
- Larsen, G.C.; Madsen, H.A.; Thomsen, K.; Larsen, T.J. Wake meandering: A pragmatic approach. Wind Energy 2008, 11, 377–395. [Google Scholar] [CrossRef]
- Herbert-Acero, J.F.; Probst, O.; Rethore, P.E.; Larsen, G.C.; Castillo-Villar, K.K. A Review of Methodological Approaches for the Design and Optimization of Wind Farms. Energies 2014, 7, 6930–7016. [Google Scholar] [CrossRef]
- Tian, L.; Zhu, W.; Shen, W.; Zhao, N.; Shen, Z. Development and validation of a new two-dimensional wake model for wind turbine wakes. J. Wind Eng. Ind. Aerodyn. 2015, 137, 90–99. [Google Scholar] [CrossRef]
- Tian, L.; Zhu, W.; Shen, W.; Song, Y.; Zhao, N. Prediction of multi-wake problems using an improved Jensen wake model. Renew. Energy 2017, 102, 457–469. [Google Scholar] [CrossRef]
- Brooks, T.F.; Pope, D.S.; Marcolini, M.A. Airfoil Self-Noise and Prediction; National Aeronautics and Space Administration: Washington, DC, USA, 1989.
- Zhu, W.J.; Heilskov, N.; Shen, W.Z.; Sørensen, J.N. Modeling of Aerodynamically Generated Noise from Wind Turbines. J. Sol. Energy Eng. 2005, 127, 517–528. [Google Scholar] [CrossRef]
- Salomons, E.M. Computational Atmospheric Acoustics; Springer Sciences & Bussiness Media: Berlin, Germany, 2012. [Google Scholar]
- Lowson, M.V. Assessment and Prediction of Wind Turbine Noise; Flow Solutions Report 92/19, ETSU W/13/00284/REP; Energy Technology Support Unit: Harwell, UK, 1993; pp. 1–59.
- West, M.; Gilbert, K.; Sack, R.A. A tutorial on the parabolic equation (PE) model used for long range sound propagation in the atmosphere. Appl. Acoust. 1992, 37, 31–49. [Google Scholar] [CrossRef]
- Taylor, G.L. Wake Measurements on the Nibe Wind Turbines in Denmark; National Power-Technology and Environment Center: Leatherhead, UK, 1990. [Google Scholar]
- Heimann, D.; Englberger, A.; Schady, A. Sound propagation through the wake flow of a hilltop wind turbine—A numerical study. Wind Energy 2018, 21, 650–662. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, J.; Zhu, W.; Wu, X.; Wang, T.; Xu, H. An Aero-acoustic Noise Distribution Prediction Methodology for Offshore Wind Farms. Energies 2019, 12, 18. https://doi.org/10.3390/en12010018
Cao J, Zhu W, Wu X, Wang T, Xu H. An Aero-acoustic Noise Distribution Prediction Methodology for Offshore Wind Farms. Energies. 2019; 12(1):18. https://doi.org/10.3390/en12010018
Chicago/Turabian StyleCao, Jiufa, Weijun Zhu, Xinbo Wu, Tongguang Wang, and Haoran Xu. 2019. "An Aero-acoustic Noise Distribution Prediction Methodology for Offshore Wind Farms" Energies 12, no. 1: 18. https://doi.org/10.3390/en12010018
APA StyleCao, J., Zhu, W., Wu, X., Wang, T., & Xu, H. (2019). An Aero-acoustic Noise Distribution Prediction Methodology for Offshore Wind Farms. Energies, 12(1), 18. https://doi.org/10.3390/en12010018





