Adaptive Air-Fuel Ratio Regulation for Port-Injected Spark-Ignited Engines Based on a Generalized Predictive Control Method
Abstract
:1. Introduction
2. Modelling of Dynamic AFR of the SI Engine
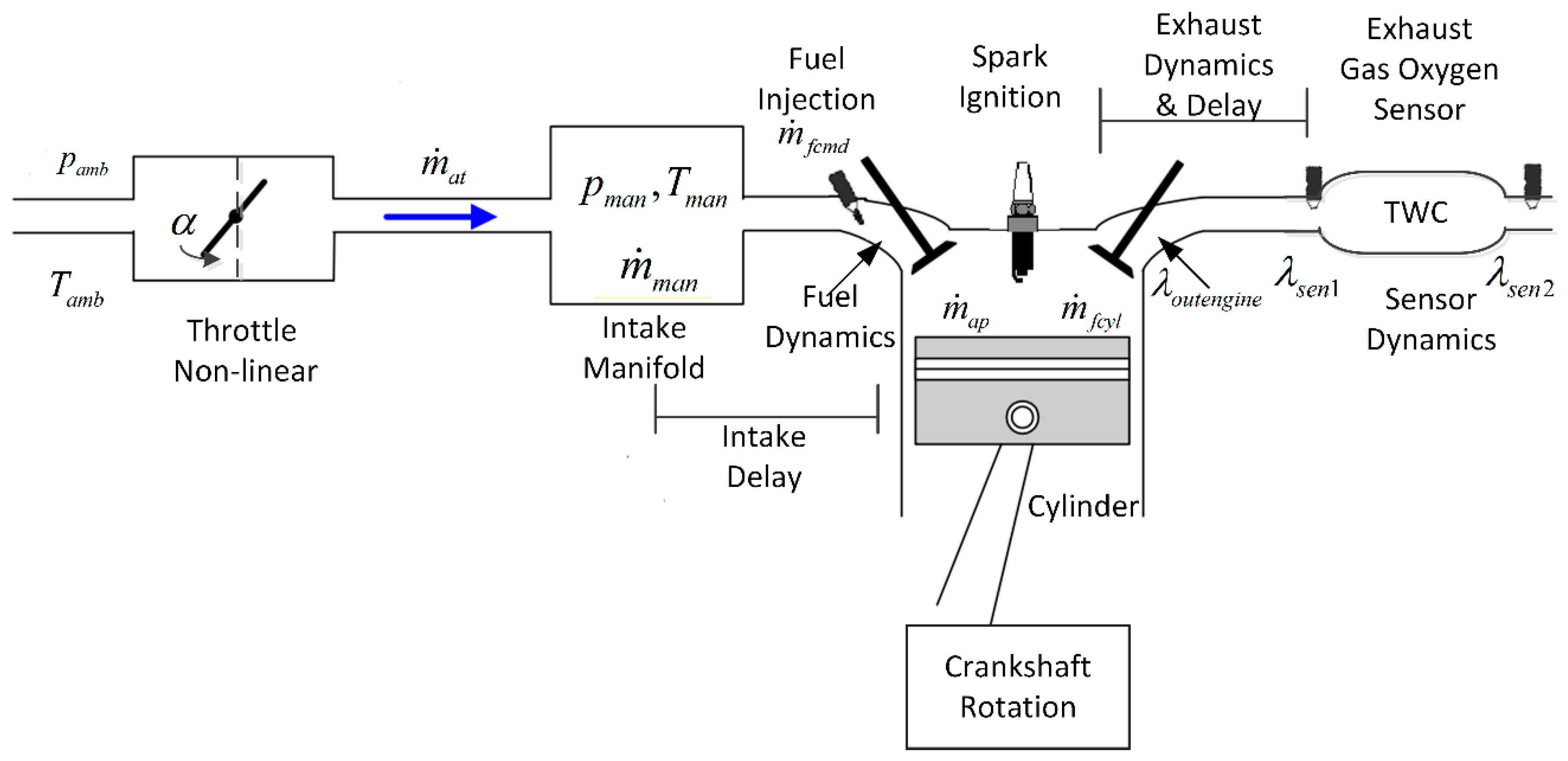
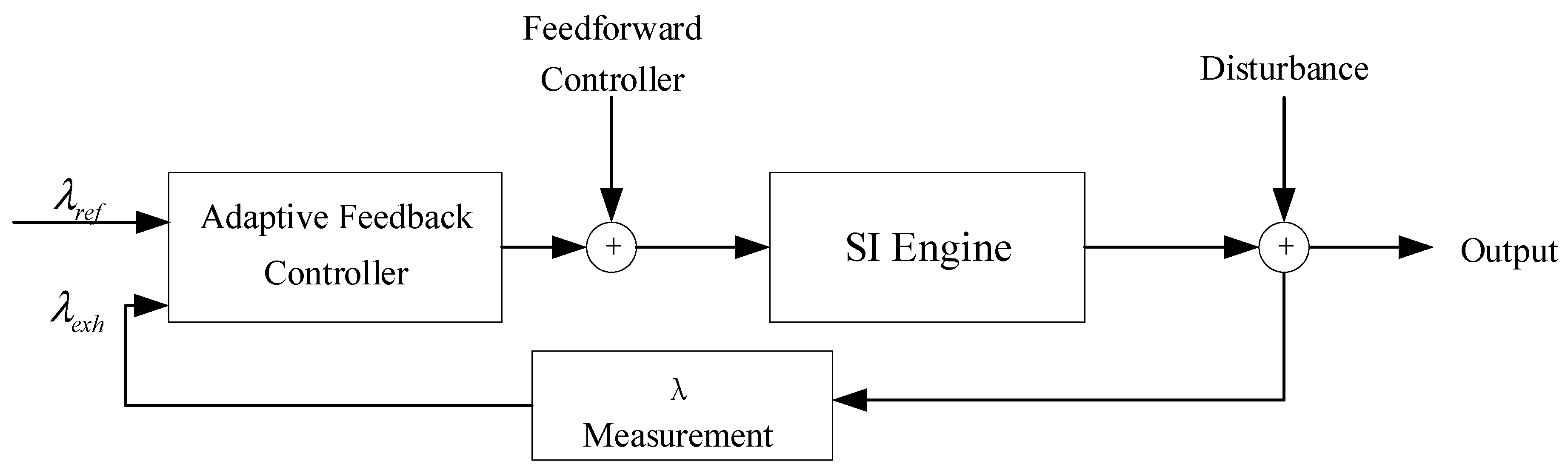
2.1. System Description
2.2. The Dynamic AFR in the SI Engine
2.2.1. The Air Path Dynamic Model
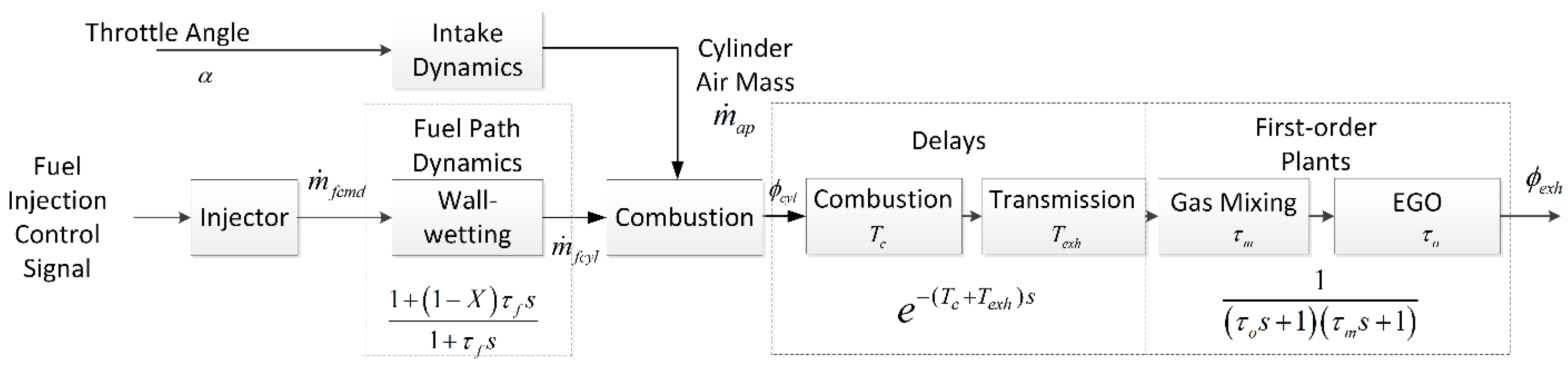
2.2.2. The Fuel Path Dynamic Model
2.2.3. The Crankshaft Dynamic
2.2.4. AFR Path Dynamic Model
3. Adaptive AFR Regulation Controller Design
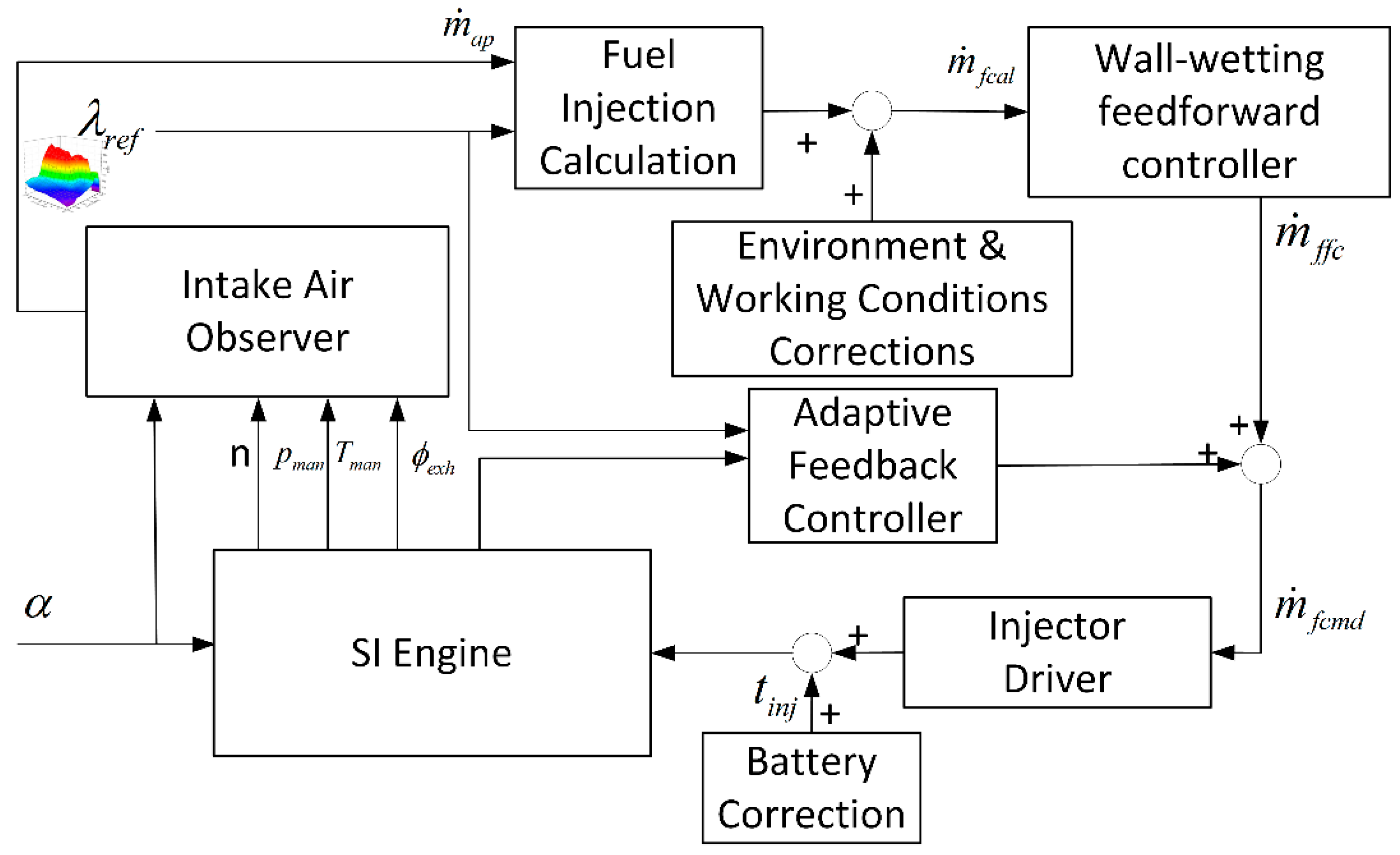
3.1. Problem Formulation of AFR Regulation
3.2. Observer-Based Intake Air Estimation
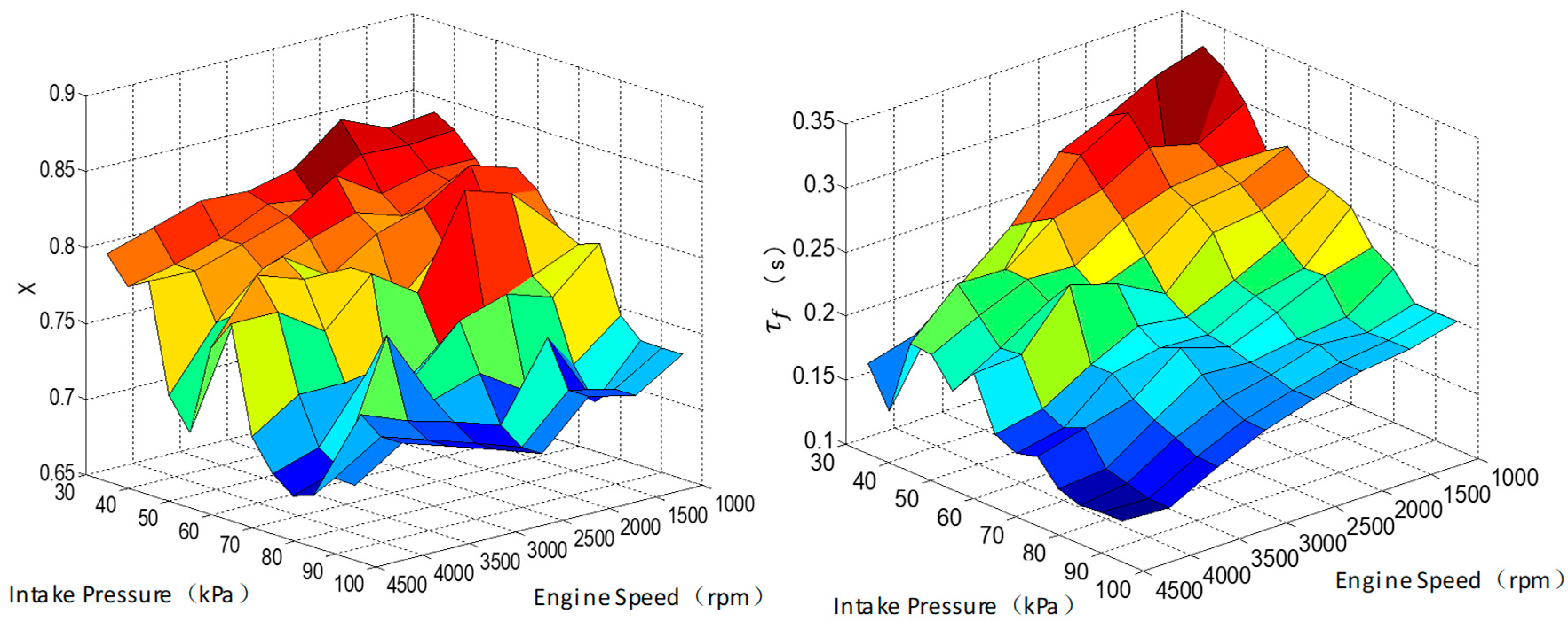
3.3. Wall-Wetting Feedforward Controller Design
3.4. Adaptive Feedback Controller Design
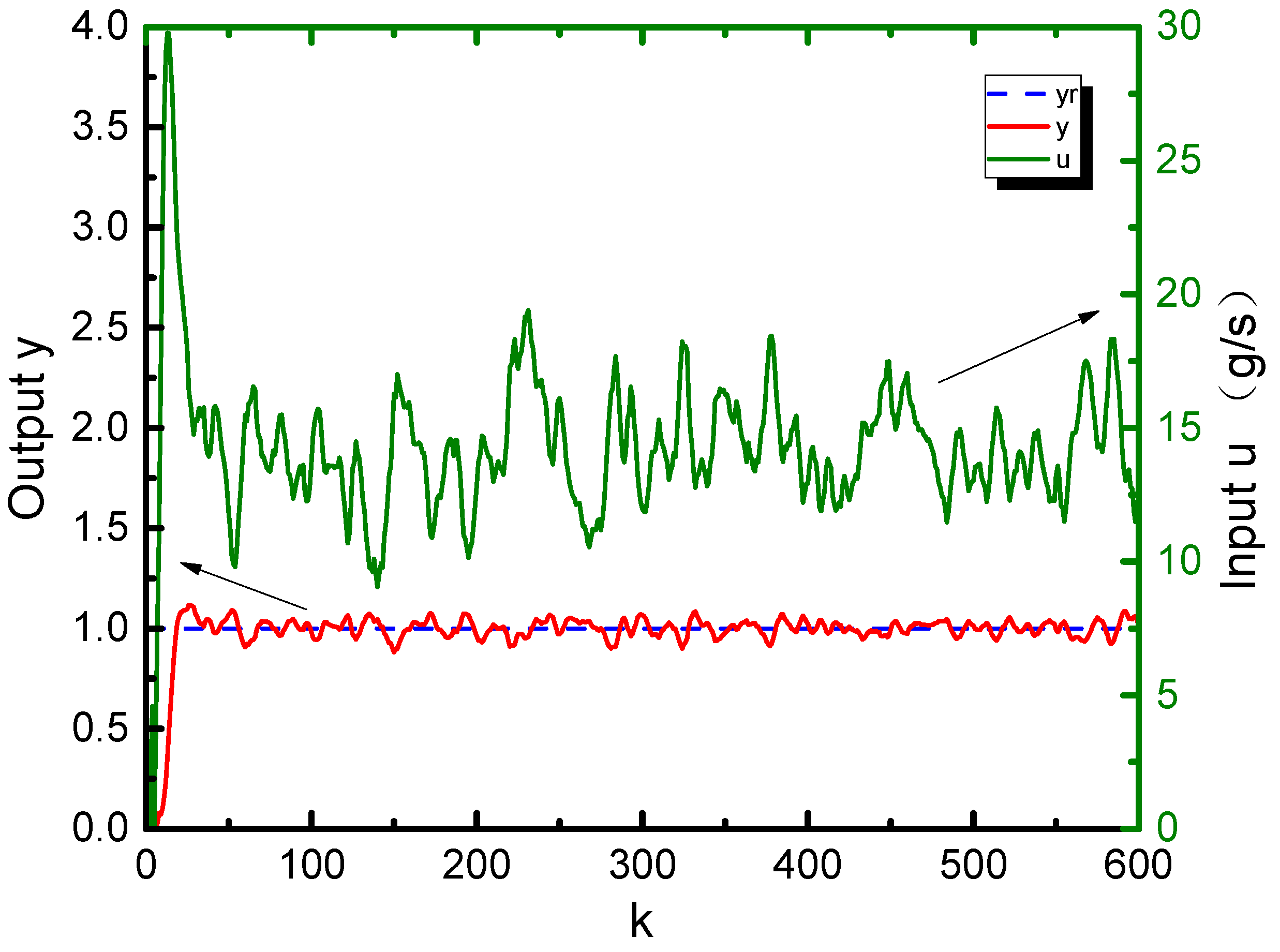
4. Simulation Validation
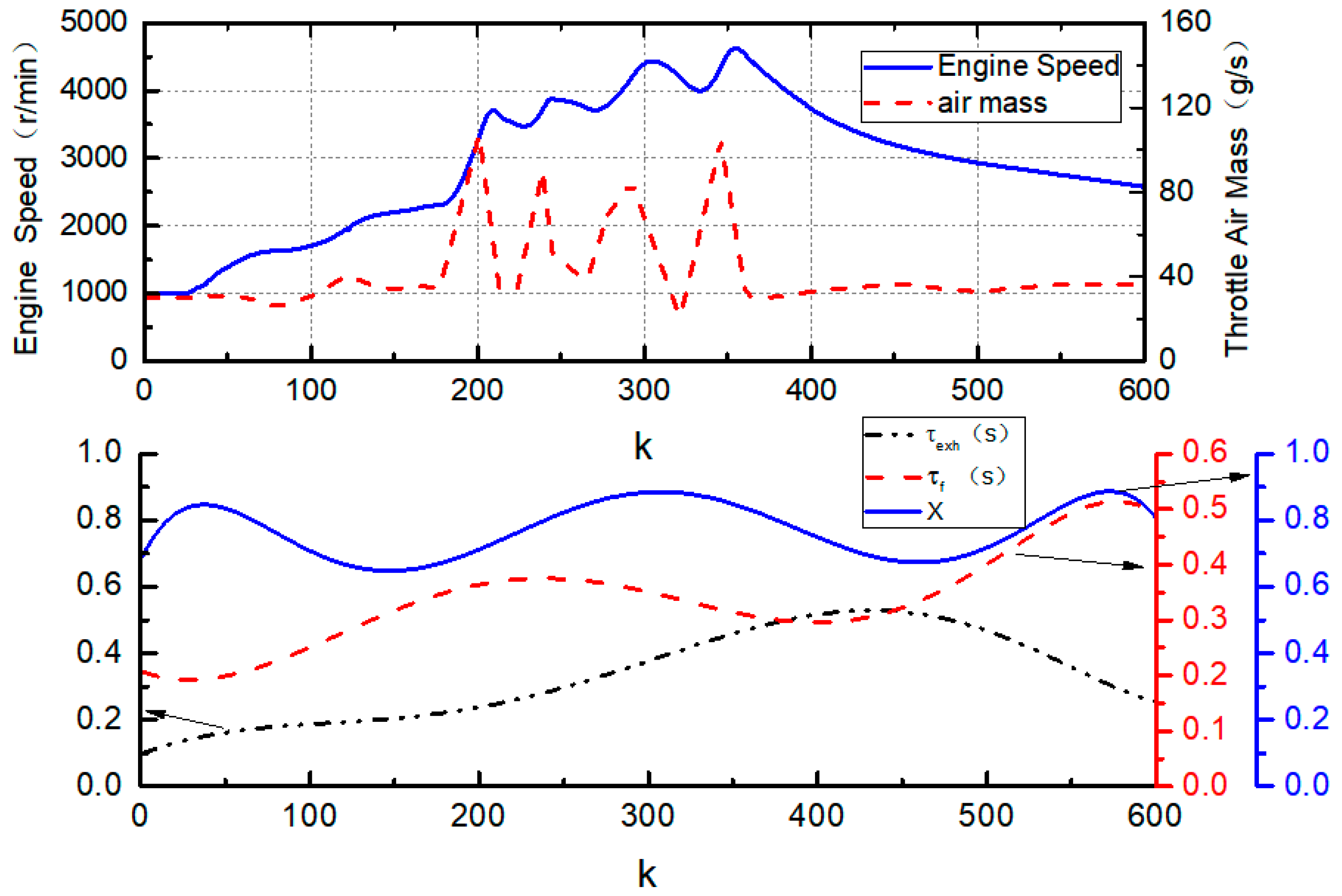
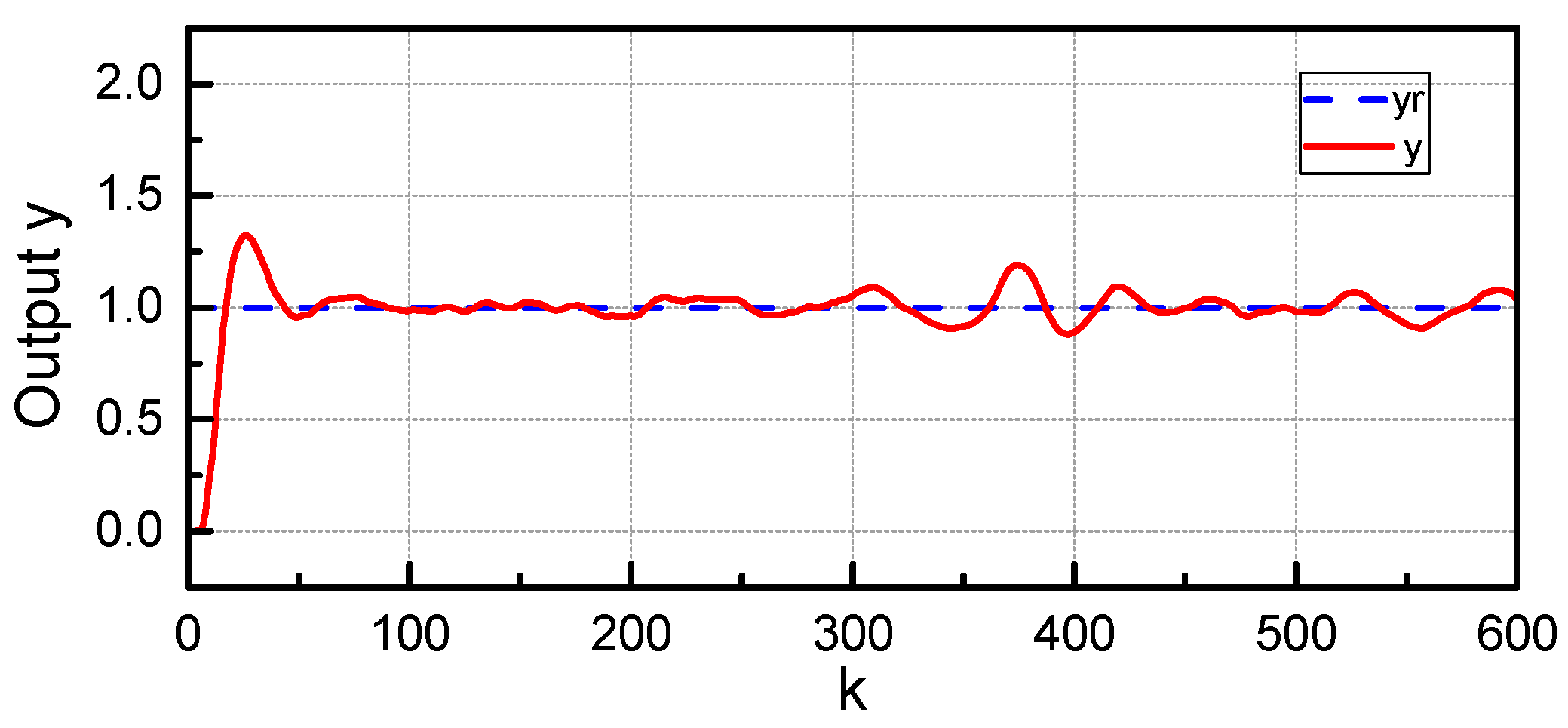
5. Experimental Implementation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Symbol: Description | Unit |
| : throttle position angle | ° |
| : constant fitting parameters | - |
| : stoichiometric air fuel ratio | - |
| : actual air fuel ratio | - |
| : volumetric efficiency | - |
| : fuel heating value | J/kg |
| : inertia of the engine and load | kg∙m2 |
| : air mass in the engine cylinder | kg/s |
| : air mass through the throttle plate | kg/s |
| : fitting constant | - |
| : injected fuel mass flow followed the control command | kg/s |
| : fuel mass flow entering the cylinder | kg/s |
| : fuel mass flow of the wall film evaporation | kg/s |
| : fuel mass flow of the directly evaporation | kg/s |
| : calculated fuel mass amount | kg/s |
| : fuel feedforward controller output | kg/s |
| , : the fraction and its estimation value of the fuel flow into film | - |
| , : the fuel film evaporation time constant and its estimation value | s |
| : time constant of the gas mixing | s |
| : time constant of the oxygen sensor | s |
| : AFR transmission delay | s |
| : time constant of the gas exhausting | s |
| : time of the injector opening | ms |
| : torque of indicated, friction and load | N∙m |
| : time delay of the combustion and gas exhausting | s |
| : sampling time | s |
| : temperature of the intake manifold and ambient | K |
| : engine speed | r/min |
| : intake air pressure | kPa |
| : ambient air pressure | kPa |
| : pressure constant parameter | kPa |
| : ratio of air pressure before and after the throttle | - |
| : indicated efficiency | - |
| : gas constant | J/(kg∙K) |
| : engine velocity | rad/s |
| : spark advance angle | ° |
| : volume of the intake manifold | L |
| : lambda, ratio of AFR and the stoichiometric ratio | - |
| : referenced lambda | - |
| : fuel/air equivalence ratio | - |
| , : fuel/air equivalence ratio in the cylinder and exhaust pipe | - |
| : the maximum costing horizon and control horizon of GPC | - |
| : control weighting in GPC | - |
| : delay step in GPC | - |
| , : the order of the CARIMA model | - |
References
- Jiao, X.; Zhang, J.; Shen, T.; Kako, J. Adaptive air-fuel ratio control scheme and its experimental validations for port-injected spark ignition engines. Int. J. Adapt. Control 2015, 29, 41–63. [Google Scholar] [CrossRef]
- Shen, T.; Zhang, J.; Jiao, X.; Kang, M.; Kako, J.; Ohata, A. Transient Control of Gasoline Engines; CRC Press: Boca Ratonn, FL, USA, 2015. [Google Scholar]
- Wong, K.I.; Wong, P.K. Adaptive air-fuel ratio control of dual-injection engines under biofuel blends using extreme learning machine. Energy Convers. Manag. 2018, 165, 66–75. [Google Scholar] [CrossRef]
- Carbot-Rojas, D.A.; Escobar-Jiménez, R.F.; Gómez-Aguilar, J.F.; Téllez-Anguiano, A.C. A survey on modeling, biofuels, control and supervision systems applied in internal combustion engines. Renew. Sustain. Energy Rev. 2017, 73, 1070–1085. [Google Scholar] [CrossRef]
- Powell, J.D.; Fekete, N.P.; Chen-Fang, C. Observer-based air fuel ratio control. Control Syst. IEEE 1998, 18, 72–83. [Google Scholar] [CrossRef]
- Jensen, P.B.; Olsen, M.B.; Poulsen, J.; Hendricks, E.; Fons, M.; Jepsen, C. A New Family of Nonlinear Observers for SI Engine Air/Fuel Ratio Control; SAE Technical Paper 9706155. 1997. Available online: https://www.sae.org/publications/technical-papers/content/970615/ (accessed on 4 January 2019).
- Bresch-Pietri, D.; Chauvin, J.; Petit, N. Adaptive backstepping controller for uncertain systems with unknown input time-delay. Application to SI engines. In Proceedings of the 49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 15–17 December 2010; pp. 3680–3687. [Google Scholar]
- White, A.; Guoming, Z.; Jongeun, C. Hardware-in-the-Loop Simulation of Robust Gain-Scheduling Control of Port-Fuel-Injection Processes. IEEE Trans. Control Syst. Technol. 2011, 19, 1433–1443. [Google Scholar] [CrossRef]
- Postma, M.; Nagamune, R. Air-Fuel Ratio Control of Spark Ignition Engines Using a Switching LPV Controller. IEEE Trans. Control Syst. Technol. 2012, 20, 1175–1187. [Google Scholar] [CrossRef]
- Pace, S.; Zhu, G.G. Sliding mode control of both air-to-fuel and fuel ratios for a dual-fuel internal combustion engine. J. Dyn. Syst. Measur. Control 2012, 134. [Google Scholar] [CrossRef]
- Wu, H.; Tafreshi, R. Fuzzy Sliding-mode Strategy for Air-fuel Ratio Control of Lean-burn Spark Ignition Engines. Asian J. Control 2018, 20, 149–158. [Google Scholar] [CrossRef]
- Kahveci, N.E.; Jankovic, M.J. Adaptive controller with delay compensation for Air-Fuel Ratio regulation in SI engines. In Proceedings of the American Control Conference (ACC), Baltimore, MD, USA, 30 June–2 July 2010; pp. 2236–2241. [Google Scholar]
- Kahveci, N.E.; Impram, S.T.; Genc, A.U. Adaptive Internal Model Control for Air-Fuel Ratio regulation. In Proceedings of the Intelligent Vehicles Symposium, Dearborn, MI, USA, 8–11 June 2014; pp. 1091–1096. [Google Scholar]
- Prucka, R.G.; Filipi, Z.S.; Hagena, J.R.; Assanis, D.N. Cycle-by-Cycle Air-to-Fuel Ratio Calculation During Transient Engine Operation Using Fast Response CO and CO2 Sensors. In Proceedings of the ASME 2012 Internal Combustion Engine Division Fall Technical Conference, Vancouver, BC, Canada, 23–26 September 2012; pp. 303–311. [Google Scholar]
- Hendricks, E. Engine Modelling for Control Applications: A Critical Survey. Meccanica 1997, 32, 387–396. [Google Scholar] [CrossRef]
- Guzzella, L.; Onder, C.H. Introduction to Modeling and Control of Internal Combustion Engine Systems; Springer: Berlin/Heidelberg, Germany, 2010; Volume 25, pp. 96–99. [Google Scholar]
- Hendricks, E.; Vesterholm, T. The Analysis of Mean Value SI Engine Models; SAE Technical Paper 920682. 1992. Available online: https://www.sae.org/publications/technical-papers/content/920682/ (accessed on 4 January 2019).
- Lei, M.; Zeng, C.; Hong, L.; Jie, L.; Wen, L.; Li, X. Research on Modeling and Simulation of SI Engine for AFR Control Application. Open Autom. Control Syst. J. 2014, 6, 803–812. [Google Scholar] [CrossRef]
- Hendricks, E.; Chevalier, A.; Jensen, M.; Sorenson, S.C.; Trumpy, D.; Asik, J. Modelling of the Intake Manifold Filling Dynamics; SAE Technical Paper 960037. 1996. Available online: https://www.sae.org/publications/technical-papers/content/960037/ (accessed on 4 January 2019).
- Hendricks, E.; Vesterholm, T.; Sorenson, S.C. Nonlinear, Closed Loop, SI Engine Control Observers; SAE Technical Paper 920237. 1992. Available online: https://www.sae.org/publications/technical-papers/content/920237/ (accessed on 4 January 2019).
- Kiencke, U.; Nielsen, L. Automotive Control Systems: For Engine, Driveline, and Vehicle; Springer: Berlin/Heidelberg, Germany, 2005; pp. 56–70. ISBN 978-3-540-26484-2. [Google Scholar]
- Clarke, D.W.; Mohtadi, C.; Tuffs, P.S. Generalized predictive control—Part I. The basic algorithm. Automatica 1987, 23, 137–148. [Google Scholar] [CrossRef]
- Wang, Z.; Zhu, Q.; Prucka, R. A Review of Spark-Ignition Engine Air Charge Estimation Methods; SAE Technical Paper 2016-01-0620. 2016. Available online: https://www.sae.org/publications/technical-papers/content/2016-01-0620/ (accessed on 4 January 2019).
- Hendricks, E.; Vesterholm, T.; Kaidantzis, P.; Rasmussen, P.; Jensen, M. Nonlinear Transient Fuel Film Compensation (NTFC); SAE Technical Paper 930767. 1993. Available online: https://www.sae.org/publications/technical-papers/content/930767/ (accessed on 4 January 2019).
- Vijayagopal, R.; Michaels, L.; Rousseau, A.P.; Halbach, S.; Shidore, N. Automated Model Based Design Process to Evaluate Advanced Component Technologies; SAE Technical Paper 2010-01-0936. 2010. Available online: https://www.sae.org/publications/technical-papers/content/2010-01-0936/ (accessed on 4 January 2019).

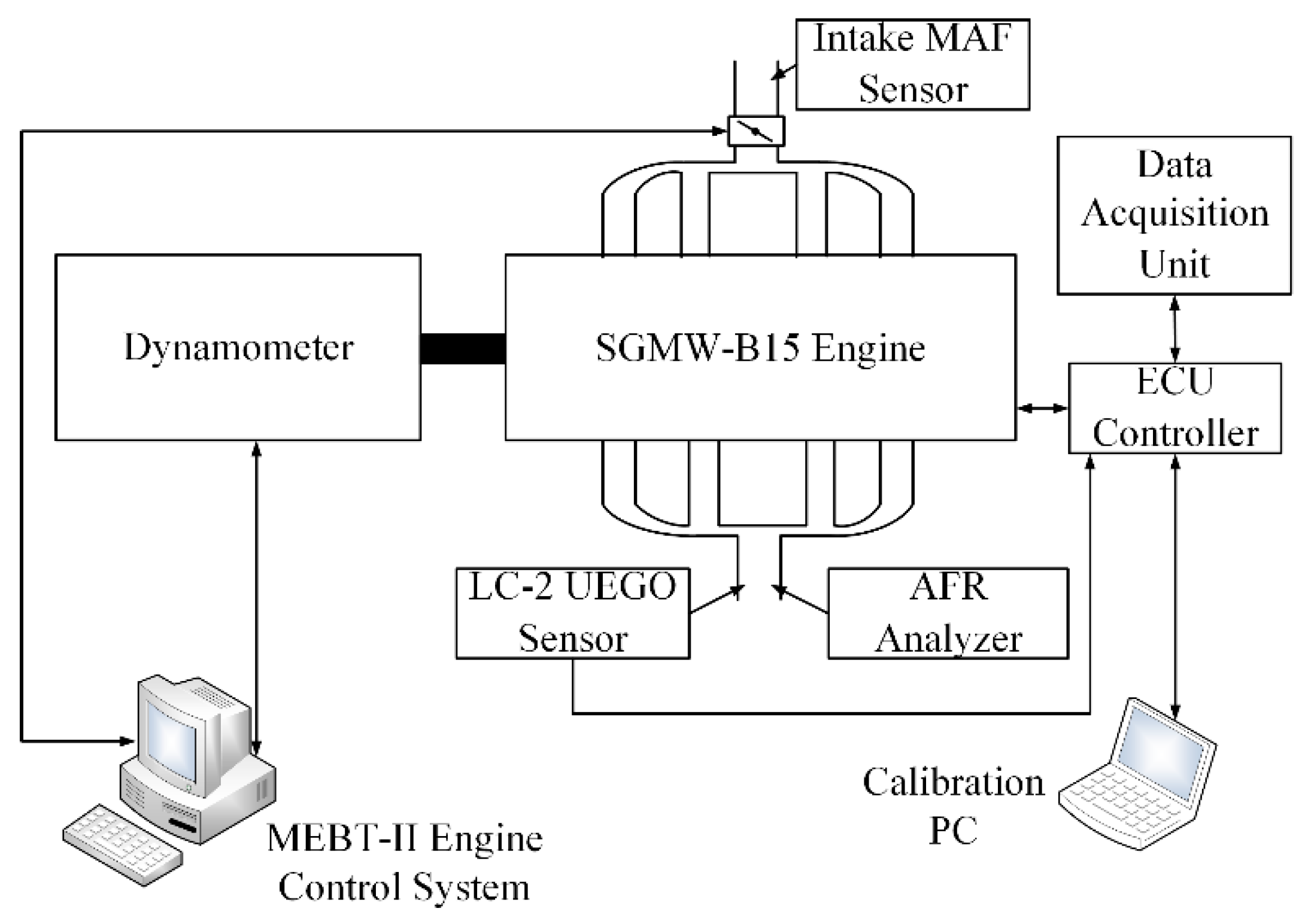
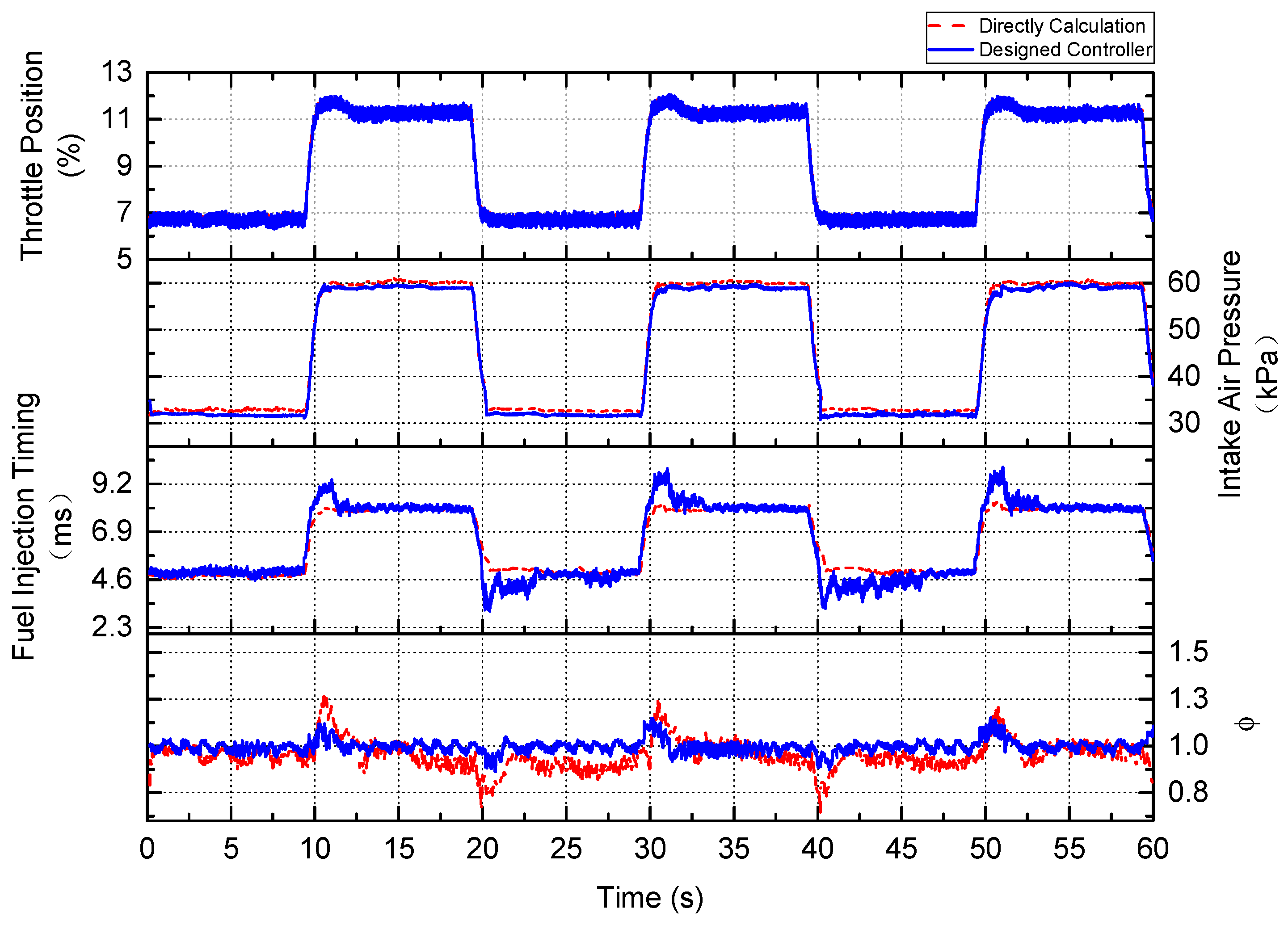
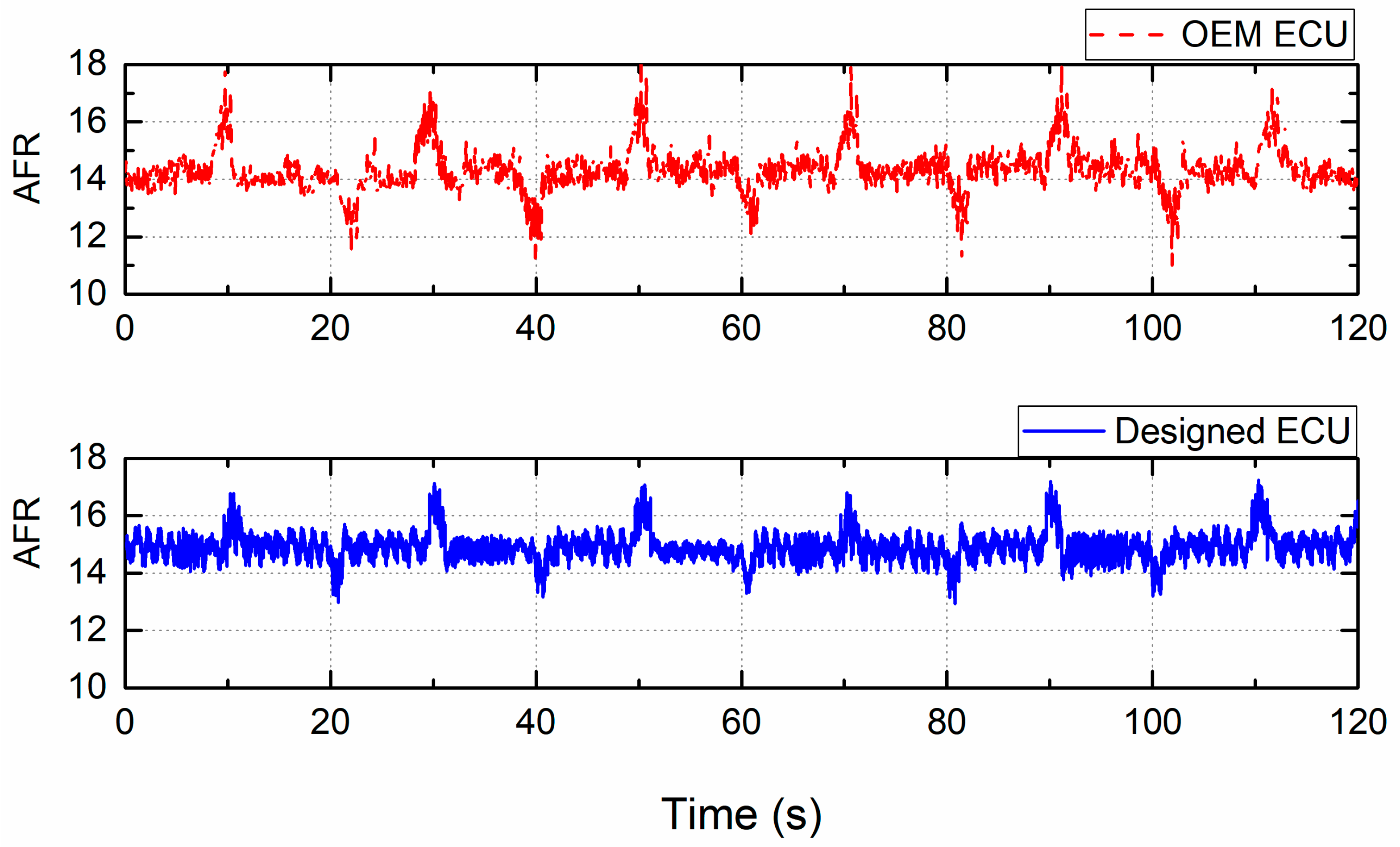
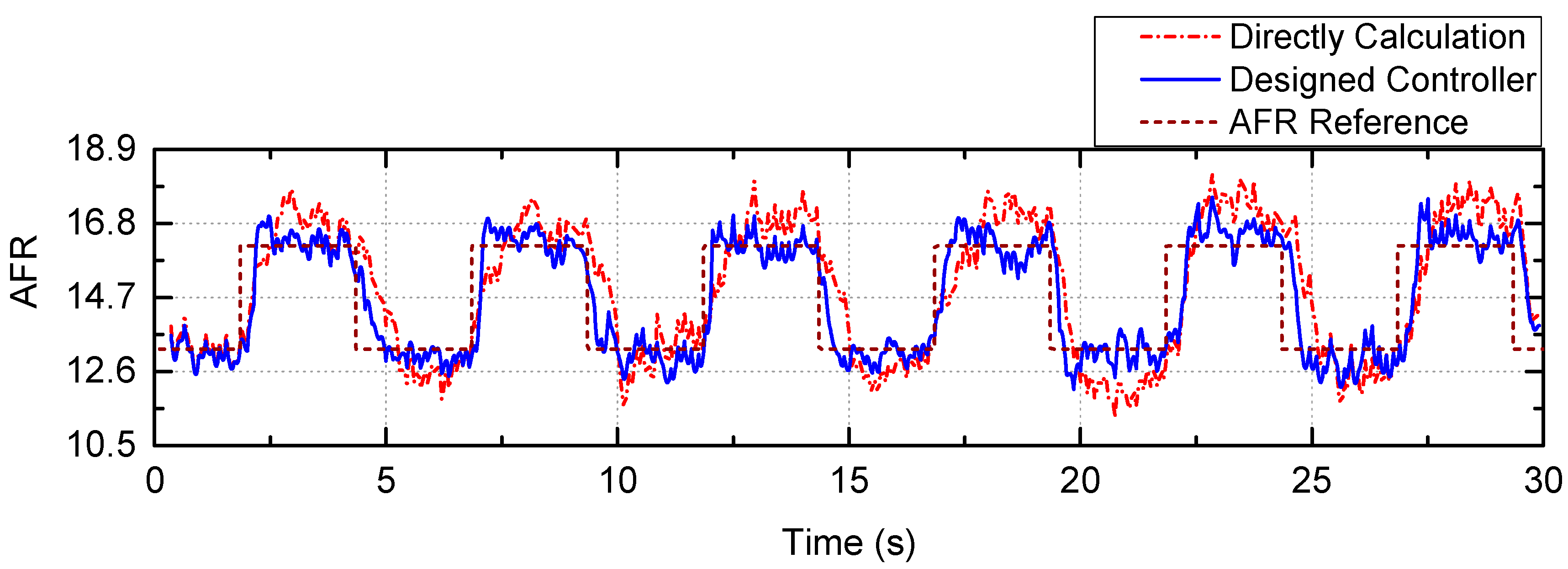
| Parameter Type | Value |
|---|---|
| Engine Type | SI,4 cylinders, In-line |
| Displacement (liters) | 1.485 L |
| Compression Ratio | 10.2:1 |
| Bore (mm) | 74.7 |
| Stroke (mm) | 84.7 |
| Maximum torque | 146 N∙m/3600–4000 rpm |
| Maximum power | 82 kW/5800 rpm |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, L.; Wang, X.; Zeng, C.; Luo, J. Adaptive Air-Fuel Ratio Regulation for Port-Injected Spark-Ignited Engines Based on a Generalized Predictive Control Method. Energies 2019, 12, 173. https://doi.org/10.3390/en12010173
Meng L, Wang X, Zeng C, Luo J. Adaptive Air-Fuel Ratio Regulation for Port-Injected Spark-Ignited Engines Based on a Generalized Predictive Control Method. Energies. 2019; 12(1):173. https://doi.org/10.3390/en12010173
Chicago/Turabian StyleMeng, Lei, Xiaofeng Wang, Chunnian Zeng, and Jie Luo. 2019. "Adaptive Air-Fuel Ratio Regulation for Port-Injected Spark-Ignited Engines Based on a Generalized Predictive Control Method" Energies 12, no. 1: 173. https://doi.org/10.3390/en12010173
APA StyleMeng, L., Wang, X., Zeng, C., & Luo, J. (2019). Adaptive Air-Fuel Ratio Regulation for Port-Injected Spark-Ignited Engines Based on a Generalized Predictive Control Method. Energies, 12(1), 173. https://doi.org/10.3390/en12010173




